EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 557 (September 2013) A&A, 557 (2013) A28 Full HTML
Free Access
Issue
A&A
Volume 557, September 2013
Article Number A28
Number of page(s) 5
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201321754
Published online 15 August 2013

© ESO, 2013

1. Introduction

Optical brightness measurements of the quasar OJ287 have shown cyclical behavior with two well-defined cycles: a 60-year cycle and a 12-year cycle (Valtonen et al. 2006). In 1995 a model was constructed that gave a good account of the 12-year cycle that occurs in two major bursts separated by one to two years (Lehto & Valtonen 1996; Sundelius et al. 1997). The model predicted the optical brightness level for every two-week interval from 1996 until 2030, and also explained the brightness of OJ287 at similar steps from 1900 up to 1996. Even though the number of historical data points has increased by an order of magnitude since 1995, the calculated two-week averages give a fair explanation of the past behavior (Hudec et al. 2013). As to the future predictions, the two-week points have been correct from 1996 to 2010 with surprisingly small errors. Other suggested models that produce a quasi-periodic 12-year cycle can be excluded at a 5 sigma significance level at present (Valtonen et al. 2011). In the future if OJ287 continues to produce the expected optical magnitudes at each two-week step, this confidence level will go up.

A new challenge has arisen with the discovery of the complex behavior of the resolved radio jet that makes it possible to identify the same 12-year cycle in the position angle of the radio jet in the sky in the cm wave radio maps (Tateyama & Kingham 2004). Moreover, the 12-year cycle is clearly modulated by a longer time scale variation (Valtonen & Wiik 2012) even though it is too soon to claim that the 60-year cycle has also been detected since the radio jet observations cover only about 30 years, in contrast to the 120-year optical light curve. A new twist in the story is the radio jet measurements at mm waves: they show variations of much larger amplitude (Agudo et al. 2012b; Tateyama 2013). The first radio maps at these frequencies go back less than twenty years, and thus it would not be useful to model these data alone. However, a combination of optical variability data together with the jet variations at these two frequency ranges provides enough challenging data to attempt a model.

Valtonen & Wiik (2012) looked at the variations of the rotation axis of the inner accretion disk in the well-defined binary model which gives a detailed account of the optical variations (Valtonen et al. 2008). They found that the disk shows a wobble in the 12-year time scale that could be associated with the jet variations at cm wavelengths. They also found that a small timing delay of about 16 years is necessary between the disk wobble and the jet changes to give the best account of the data. The model produces two cycles, a short one of about 11 years, and a long cycle of about 120 years. The latter is understood to result from the Kozai cycle in the inner accretion disk, inside the pericenter of the binary orbit (Innanen et al. 1997). Subsequently, Valtonen et al. (2012b) investigated the possibility of including the mm wave observations in the same model. They found that the jet cannot be straight and have the different orientation angles arise at the same time.

This leads us to a jet model which has been found useful in S5 0836+710 and in other jet sources (Perucho et al. 2012, 2013): a helical jet. This is a way, even if not a unique way, of producing different viewing angles at different distances from the origin of the jet. When we add to this the disk wobble that arises from the model based exclusively on optical data, we get a new attempt to model the complex situation in OJ287.

2. The inner disk

Our basic model is a binary black hole system where a small companion black hole periodically perturbs the disk of the much larger primary black hole (Valtonen et al. 2010). The parameters are very tightly constrained by the optical data which leaves practically no free parameters in the model. The only exception is the orbital inclination of the secondary orbit relative to the disk which was unknown until recently. Its determination requires the identification of one of the spectral lines of the secondary and the measurement of the relative radial velocity. From the recent detection of a spectral line of the secondary (T. Pursimo, priv. comm.) we determined the inclination to be close to 50 degrees. Previously the inclination of 90 degrees was used for simplicity; here we calculate both the 50 and 90 degree cases.

We placed a ring of particles around the primary, and starting from year 1856, followed the evolution of each disk particle. The calculations were carried out as in Valtonen & Wiik (2012): in the present simulation the number of disc particles is 1500. They were placed in circular orbits between 1.7 and 14 Schwarzschild radii of the primary. For every particle, and for every time step, we calculated the orbital elements of the orbits with respect to the primary. The elements were averaged per calendar year. As there are many integration steps per year, typically each annual mean is based on the average of 105 values. By varying the number of particles it was found that the mean values generated in this way are very robust. Figure 1 shows the time evolution of two of the elements, inclination i and ascending node Ω.

thumbnail Fig. 1

Variation of the inclination with respect to the initial value of 50 degrees (solid line) of the inner accretion disk, and the variation of the node with respect to initial value of zero (dashed line).

As in Valtonen et al. (2006), the variation of Ω is negligible in comparison with the variation of i. (Valtonen & Wiik 2012 had interchanged i and Ω by mistake; this, however, had no consequences in that paper apart from wrong labels. Correcting this error, the results agree with the present work.) The evolution of the element i may be well represented by a doubly periodic function (1)The amplitudes A1 and A2 depend on the initial inclination i0 as well as on the distance r of the ring from the primary black hole. The values of the coefficients are shown in Fig. 2.

thumbnail Fig. 2

Amplitudes A1 and A2 (in degrees) of the two periodic components of the inclination variation as a function of the distance from the center r in units of 10 Schwarzschild radii of the primary. The first number in the label gives the initial inclination in degrees, the second number the subscript of the amplitude coefficient.

We were particularly interested in the inner edge of the disk that presumably connects to the jet that is launched perpendicular to the disk. Therefore, we used the values of A1 and A2 which are appropriate for the inner disk, with r between 1.7 and 3.4 Schwarzschild radii. The smaller value corresponds to the last stable orbit in the accretion disk. We also considered the case of i0 = 50 degrees only, with A1 = 3.5. We notice from Fig. 2 that the amplitudes are somewhat greater for i0 = 90 degrees than for i0 = 50 degrees. The calculation below would lead to small changes in the jet parameters if we used i0 = 90 degrees instead of i0 = 50 degrees. The two periods P1 = 116.6 yr and P2 = 11.0 yr are insensitive to i0.

One of the differences between a gaseous disk and the simulated particle disk is the need to transport information between particles in order to mimic gas behavior. We do this by simply averaging the results over a period longer than one-year in order to allow time for dissipative processes. The one-year averaging was arbitrarily chosen. Considering that the period rotation of the innermost disk is about 0.5 yr, and that the viscous time scale of the inner disk is about an order of magnitude greater than this, the appropriate averaging time scale is in the range of 5 to 10 years (Krolik et al. 2005). We use ten-year averaging (as in Valtonen & Wiik 2012) that lowers the coefficient A2 from 2.24 to 0.75. The values for t1 = 1903.9 and t2 = 1893.5 are insensitive to the inclination i0 and to the averaging time scale, while the value of C = 3.13 is of no importance to what follows.

3. The helix model

We assume that a helical jet emanates from the center of the accretion disk, perpendicular to the disk. This assumption should be correct independent of the direction of the spin of the primary black hole (Palenzuela et al. 2010; McKinney et al. 2013). The jet flow is assumed to follow a helical path because of the helical Kelvin-Helmholtz instability (Hardee 2000, 2011; Mignone et al. 2010; Mizuno et al. 2012). The parameters of the helix, the half-opening angle of the helix cone θ, and the wavelength λ of the helix are determined by fitting to the observational data. Also the viewing angle φ of the jet at a given time and at a given distance from the origin is a free parameter; however, the evolution of the viewing angle follows from the wobble of the disk and contains only one free parameter, the time delay d between the changes in the disk and the corresponding changes at the emitting region (Valtonen et al. 2012b).

We will first consider the region of optical emission in the jet. After experimenting with different parameter values, we find that the overall brightness evolution is well modeled if θ = 4 degrees, and the minimum viewing angle of the cone axis is φmin = 1.8 degrees. As the first step to obtain these values, the best sinusoidal long-period fit to the optical magnitude data was determined. This fit is shown in Fig. 3. Then the angular parameters of the helical model were varied at intervals of 0.1 degrees, and for each model a light curve was produced, and for each theoretical light curve a similar sinusoidal fit was performed. The best match with the observations was obtained with the above mentioned values. Their uncertainty may be estimated as ±0.1 degrees.

thumbnail Fig. 3

Optical V-magnitude of OJ287 as a function of time. The line is a fit of the long-period component of the model. The model parameters are given in the figure.

The time delay d = 1.4 yr. It could also be 58.3 + 1.4 yr, i.e., with a shift of one half of the cycle period. However, the distance of the optically emitting region is more likely to be around 1.4 × Γ lyr than 60 × Γ lyr from the center (Agudo et al. 2012a; Kushwaha et al. 2013). Moreover, the rather abrupt jump of the optical polarization by ~90 degrees around 1995 occurs only in the model with the shorter time delay (Fig. 4). The theoretical values in Fig. 4 were calculated assuming that the electric vector of the radiating electrons is always perpendicular to the jet and the assumed prevailing parallel magnetic field. The jump in calculated values is noticeably larger than observed. However, as discussed in Valtonen & Wiik (2012), there is a possibility that the electric vector is not strictly perpendicular to the jet direction, but at a small angle to it. This is expected as the optical emission is likely to originate from a compression in the jet, which in turn strengthens the perpendicular component of the magnetic field, and causes the magnetic field direction to bend at the compression. In the case of OJ287, the magnetic field along the jet has been observed to vary all the way from parallel to perpendicular (Gabuzda & Gómez 2001). If we do assume an angle offset of about 15 degrees, the calculated values match the observations.

thumbnail Fig. 4

Evolution of optical polarization in OJ287. Data points are based on Valtonen & Wiik (2012), while the curve corresponds to a model where the electric vector of the radiating electrons lies perpendicular to the jet direction in the optical emission region.

In this model the magnetic field of the optical emission region lies more or less parallel to the jet, as was also concluded in a previous work (Valtonen & Wiik 2012). The required Lorentz Γ = 14 is in agreement with other determinations (Jorstad et al. 2005, Γ = 16.5 ± 4; Hovatta et al. 2009, Γ ~ 15.4; Savolainen et al. 2010, Γ ~ 9.3; and Agudo et al. 2012, Γ = 14 ± 5). The viewing angles reported from observations also fall within the range of the model (Jorstad et al. 2005, φ = 3.2 ± 0.9 degrees; Hovatta et al. 2009, φ ~ 3.3 degrees; Savolainen et al. 2010, φ ~ 1.9 degrees; and Agudo et al. 2012b, φ = 2 ± 1.3 degrees). The spectral index is − 0.8, which takes into consideration the internal extinction in the OJ287 host galaxy (Valtonen et al. 2012a).

Since the properties of the helix cone are now fully determined by the optical data, we may apply the model to radio data. Figure 5 plots the rotation of jet direction in the sky. The x-axis represents Ω while the y-axis represents i. The position angle of the jet is calculated as arctan(y/x). These position angles are plotted in Fig. 6 to show the fit to the mm wave data points (Agudo et al. 2012b).

thumbnail Fig. 5

Path of the jet in the sky plane. The different lines refer to slightly different time delays. The x-axis corresponds to Ω and the y-axis to i, both given in degrees. The center of the helix is at (1.8, 0), and there is a foreshortening factor of 3.5 which flattens the circular jet profile along the x-axis to an ellipse. The jet is taken to move to the positive x-direction. The cross marks the origin of the jet.

thumbnail Fig. 6

Position angle of the radio jet at mm waves, shown as points with error bars, compared with the model. The model parameters are given in the figure.

The time delay is 50 yr with respect to optical. It could also be 50 + 116.6 yr, but we choose the smallest possible value. For the cm wave data (Valtonen & Wiik 2012), the fit is shown in Fig. 7.

thumbnail Fig. 7

Comparison of the observed position angle of the cm wave radio jet, points with error bars, with the model at two different time delays (the two curves). The model parameters are described in the figure.

The two curves in the figure present a 3 yr difference in the timing. Since the resolution of the observations has improved during the 30 year period, it is expected that the early part and the latter part of the observations would fit a slightly different model. Overall, the time delay with respect to optical data is ~218 yr. This is a much greater value than was considered by Valtonen & Wiik (2012). The value could be even greater, 218 + 116.6 yr, but we choose again the smallest possible delay.

In Fig. 5, the jet direction is taken at the point in the helix which corresponds to x = 0.5. This scale is subsequently associated with the mm wave jet. It then leads to a definite physical scale (see the discussion below). In Fig. 5 we trace a point in the jet in the sky plane as a function of time. Ten different (closely spaced) values of time delay are used. No forward motion of this point is included, but if you imagine such a motion towards the right in the figure, then one may guess that the outward moving structure would look like multiple streams. In Fig. 8 the outward motion is included, and the positions projected in the sky are averaged in the form of a contour map of the density of points. This is also the observed pattern at high resolution (Tateyama 2013).

thumbnail Fig. 8

Jet moving on the sky plane in the x-direction in the model. Discrete points in the model jet spanning several helix wavelengths were calculated and projected to the sky plane. The sky plane was binned in 15 bins along the x and y-axis and smoothed by a factor of 3 using cubic splines. Density contours were then calculated with 10 levels of contours. The right-hand edge represents the cm wave scale while the left-hand edge represents the mm wave scale.

The only unsolved helix parameter remaining is the helix wavelength. The cm and mm emitting regions are 218 − 50 yr = 168 yr apart in the model, which is 168/116.6 ~ 1.4 cycles. We use this value later to find the wavelength, after the positions of the mm and cm regions are estimated in the following.

4. Jet properties

Using the typical viewing angle φ = 2 degrees, the deprojection factor is ~30. The projected linear scale of the jet in the sky is ~4.6 parsec per milliarcsec. The mm wave jet is observed with a resolution of ~0.2 milliarcsec, while the cm wave jet has a resolution of ~1 milliarcsec. Thus the apparent speed at which the changes at the foot of the jet proceed outwards is ~28 pc/50 yr ~ 1.7c. The value calculated for the cm wave jet, ~130 pc/218 yr ~ 2c, is similar. Thus the kink also moves relativistically.

We may estimate the kink speed as follows. The time it takes the VLBI knots to move through the mm wave jet is Δtknot ~ 1 yr. This may be compared with the kink travel time Δtkink ~ 50 yr for the same distance. These quantities are functions of the relative velocities βknot and βkink, respectively, and of the viewing angle φ. The two time intervals are related by 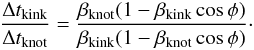(2)Putting φ = 2 degrees, βknot = 0.9974 (corresponding to Γ = 14), and 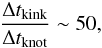(3)we get 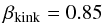(4)corresponding to Γ ~ 3.5. Thus the true time delay is ~175 yr between optical and mm waves. The corresponding true delay between mm and cm waves is ~630 yr. Since the two emitting regions are 1.4 cycles apart in the model, the true wavelength of the helical wave is about 70 pc. Considering the projection factors, this corresponds to about 0.5 milliarcsec separation in the sky. Sinusoidal features with this wavelength may be recognized in the maps of Tateyama (2013).

5. Discussion

Perucho et al. (2012) discuss fitting a helical jet model to S5 0836+710 which has wiggly jet. Even though the source of the wiggles is not known in their case, they discuss parameters that could lead to the observed pattern. These parameters are not very different from the parameters that we found for OJ287. The big advantage in the case of OJ287 is the well-specified origin of the jet wobble which is completely determined by the optical variability data. In this paper we use the optical data to determine the basic properties of the helical jet, its opening angle, and the direction at a given time so there is only the wavelength of the helix and the flow speed to be determined. These are found by fitting the model to the mm wave and the cm wave jet orientation data.

Note that in this model there are two flow speeds, the jet flow with Γ = 14, and a slower flow with Γ ~ 3.5 that carries the information about the jet wobble from the base of the jet outward. This requires a spine-sheath structure for the jet (Hardee 2007; Hardee et al. 2007), with the sheath bulk flow moving with Γ ~ 3.5. However, we cannot rule out the possibility that the information of the jet wobble is carried by an oscillating disturbance in the sheath, for example. In this case the wave motion may propagate with Γ ~ 3.5 with actual bulk flow of the sheath being much slower. This picture is qualitatively supported by considering 3D animations of the entire jet given by the model. These demonstrate the visibly oscillatory character of the resulting 3D jet. The fast jet is narrow; its value is not specified in the model, but observationally its half opening angle should be θfast = 0.8 ± 0.4 degrees (Jorstad et al. 2005). The slow jet is wide, with the half-opening angle of θslow = 4 degrees. These opening angles follow the mean relation between θ and Γ found by Pushkarev et al. (2009).

It is interesting that this simple model explains the apparently complex dual jet seen in observations by Tateyama (2013).

6. Summary

The complex behavior of the radio jet has been shown to result from a model with three main assumptions: first, OJ287 is a binary black hole system whose orbit is described by the celestial mechanical solution of parameters. This solution is complemented by the missing parameter, the inclination of the binary with respect to the disk of the primary, determined from recent spectroscopy. Second, the jet propagates along the rotation axis of the inner disk. And third, the jet has spine-sheath structure, and the spine follows a helical path.

The model allows us to determine the jet parameters. There is prior information on some, but not all of the parameters. Thus the model increases our knowledge of the jet in this case. The value for the spine Γ = 14 agrees with previous determinations, as does the typical sheath viewing angle of 2 degrees. The sheath opening angle of 4 degrees was not previously known, nor the Lorentz Γ = 3.5 for the sheath. The helical wavelength of ~70 pc is also determined for the first time, even though it could also be determined from the high resolution maps of Tateyama (2013). It is also interesting that the period of the helical motion

agrees in order of magnitude with the Kozai cycle of inner accretion disk. Moreover, the fact that the variation of optical polarization follows the model allows us to state definitely that the magnetic field is parallel to the jet in the optical emission region, a conclusion which was only tentative in earlier work (Valtonen & Wiik 2012).

Acknowledgments

P. Pihajoki is supported by the Magnus Ehrnrooth foundation. We thank the anonymous referee for helpful comments that improved the article.

References

  1. Agudo, I., Jorstad, S. G., Marscher, A. P., et al. 2012a, J. Phys. Conf. Ser., 355, 012032 [NASA ADS] [CrossRef] [Google Scholar]
  2. Agudo, I., Marscher, A. P., Jorstad, S. G., et al. 2012b, ApJ, 747, 63 [CrossRef] [Google Scholar]
  3. Gabuzda, D. C., & Gómez, J. L. 2001, MNRAS, 320, L49 [Google Scholar]
  4. Hardee, P. E. 2000, ApJ, 533, 176 [NASA ADS] [CrossRef] [Google Scholar]
  5. Hardee, P. E. 2007, ApJ, 664, 26 [NASA ADS] [CrossRef] [Google Scholar]
  6. Hardee, P. E. 2011, in IAU Symposium, eds. G. E. Romero, R. A. Sunyaev, & T. Belloni, IAU Symp., 275, 41 [Google Scholar]
  7. Hardee, P., Mizuno, Y., & Nishikawa, K.-I. 2007, Astrophys. Space. Sci., 311, 281 [Google Scholar]
  8. Hovatta, T., Valtaoja, E., Tornikoski, M., & Lähteenmäki, A. 2009, A&A, 494, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Hudec, R., Bašta, M., Pihajoki, P., & Valtonen, M. 2013, A&A, in press DOI: 10.1051/0004-6361/201219323 [Google Scholar]
  10. Innanen, K. A., Zheng, J. Q., Mikkola, S., & Valtonen, M. J. 1997, AJ, 113, 1915 [NASA ADS] [CrossRef] [Google Scholar]
  11. Jorstad, S. G., Marscher, A. P., Lister, M. L., et al. 2005, AJ, 130, 1418 [NASA ADS] [CrossRef] [Google Scholar]
  12. Krolik, J. H., Hawley, J. F., & Hirose, S. 2005, ApJ, 622, 1008 [NASA ADS] [CrossRef] [Google Scholar]
  13. Kushwaha, P., Sahayanathan, S., & Singh, K. P. 2013, MNRAS, 433, 2380 [NASA ADS] [CrossRef] [Google Scholar]
  14. Lehto, H. J., & Valtonen, M. J. 1996, ApJ, 460, 207 [NASA ADS] [CrossRef] [Google Scholar]
  15. McKinney, J. C., Tchekhovskoy, A., & Blandford, R. D. 2013, Science, 339, 49 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  16. Mignone, A., Rossi, P., Bodo, G., Ferrari, A., & Massaglia, S. 2010, MNRAS, 402, 7 [NASA ADS] [CrossRef] [Google Scholar]
  17. Mizuno, Y., Lyubarsky, Y., Nishikawa, K.-I., & Hardee, P. E. 2012, ApJ, 757, 16 [NASA ADS] [CrossRef] [Google Scholar]
  18. Palenzuela, C., Garrett, T., Lehner, L., & Liebling, S. L. 2010, Phys. Rev. D, 82, 044045 [NASA ADS] [CrossRef] [Google Scholar]
  19. Perucho, M., Kovalev, Y. Y., Lobanov, A. P., Hardee, P. E., & Agudo, I. 2012, ApJ, 749, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Perucho, M., Kovalev, Y. Y., Hardee, P. E., et al. 2013 [arXiv:1301.2049] [Google Scholar]
  21. Pushkarev, A. B., Kovalev, Y. Y., Lister, M. L., & Savolainen, T. 2009, A&A, 507, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Savolainen, T., Homan, D. C., Hovatta, T., et al. 2010, A&A, 512, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Sundelius, B., Wahde, M., Lehto, H. J., & Valtonen, M. J. 1997, ApJ, 484, 180 [NASA ADS] [CrossRef] [Google Scholar]
  24. Tateyama, C. E. 2013, ApJS, 205, 15 [NASA ADS] [CrossRef] [Google Scholar]
  25. Tateyama, C. E., & Kingham, K. A. 2004, ApJ, 608, 149 [NASA ADS] [CrossRef] [Google Scholar]
  26. Valtonen, M. J., & Wiik, K. 2012, MNRAS, 421, 1861 [NASA ADS] [CrossRef] [Google Scholar]
  27. Valtonen, M. J., Lehto, H. J., Sillanpää, A., et al. 2006, ApJ, 646, 36 [NASA ADS] [CrossRef] [Google Scholar]
  28. Valtonen, M. J., Lehto, H. J., Nilsson, K., et al. 2008, Nature, 452, 851 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  29. Valtonen, M. J., Mikkola, S., Merritt, D., et al. 2010, ApJ, 709, 725 [NASA ADS] [CrossRef] [Google Scholar]
  30. Valtonen, M. J., Lehto, H. J., Takalo, L. O., & Sillanpää, A. 2011, ApJ, 729, 33 [NASA ADS] [CrossRef] [Google Scholar]
  31. Valtonen, M. J., Ciprini, S., & Lehto, H. J. 2012a, MNRAS, 427, 77 [NASA ADS] [CrossRef] [Google Scholar]
  32. Valtonen, M. J., Gopakumar, A., Mikkola, S., Wiik, K., & Lehto, H. J. 2012b, in Proc. ICGC Intern. Conf., Goa [arXiv:1208.4524] [Google Scholar]

All Figures

thumbnail Fig. 1

Variation of the inclination with respect to the initial value of 50 degrees (solid line) of the inner accretion disk, and the variation of the node with respect to initial value of zero (dashed line).
In the text
thumbnail Fig. 2

Amplitudes A1 and A2 (in degrees) of the two periodic components of the inclination variation as a function of the distance from the center r in units of 10 Schwarzschild radii of the primary. The first number in the label gives the initial inclination in degrees, the second number the subscript of the amplitude coefficient.
In the text
thumbnail Fig. 3

Optical V-magnitude of OJ287 as a function of time. The line is a fit of the long-period component of the model. The model parameters are given in the figure.
In the text
thumbnail Fig. 4

Evolution of optical polarization in OJ287. Data points are based on Valtonen & Wiik (2012), while the curve corresponds to a model where the electric vector of the radiating electrons lies perpendicular to the jet direction in the optical emission region.
In the text
thumbnail Fig. 5

Path of the jet in the sky plane. The different lines refer to slightly different time delays. The x-axis corresponds to Ω and the y-axis to i, both given in degrees. The center of the helix is at (1.8, 0), and there is a foreshortening factor of 3.5 which flattens the circular jet profile along the x-axis to an ellipse. The jet is taken to move to the positive x-direction. The cross marks the origin of the jet.
In the text
thumbnail Fig. 6

Position angle of the radio jet at mm waves, shown as points with error bars, compared with the model. The model parameters are given in the figure.
In the text
thumbnail Fig. 7

Comparison of the observed position angle of the cm wave radio jet, points with error bars, with the model at two different time delays (the two curves). The model parameters are described in the figure.
In the text
thumbnail Fig. 8

Jet moving on the sky plane in the x-direction in the model. Discrete points in the model jet spanning several helix wavelengths were calculated and projected to the sky plane. The sky plane was binned in 15 bins along the x and y-axis and smoothed by a factor of 3 using cubic splines. Density contours were then calculated with 10 levels of contours. The right-hand edge represents the cm wave scale while the left-hand edge represents the mm wave scale.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.