EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 557 (September 2013) A&A, 557 (2013) A127 Full HTML
Free Access
Issue
A&A
Volume 557, September 2013
Article Number A127
Number of page(s) 6
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201321741
Published online 20 September 2013

© ESO, 2013

1. Introduction

PSR B1259-63 is a 47.7 ms radio pulsar in a 3.5 year orbit around a Be star (Johnston et al. 1992). The pulsar has a high spindown power Ė ≈ 8 × 1035 erg s-1. An outburst of very high energy gamma ray (VHE, >100 GeV), X-ray, and radio emission occurs at periastron passage (τ ≡ 0 d), when the pulsar wind interacts with the stellar wind and the equatorial disc surrounding the Be companion. A bow shock structure forms, whose appearance changes according to which component (stellar wind or Be disc) the pulsar wind interacts with. The e−e+ pairs present in the pulsar wind are isotropised and energised at the shock. The pairs radiate non-thermal emission as they flow away from the binary, producing a small-scale pulsar wind nebula (PWN).

High-energy gamma-ray emission (HE, >100 MeV) was detected for the first time during the last passage in 2010 (Tam et al. 2011; Abdo et al. 2011). A weak ≈5σ “brightening” of the emission was detected starting at least 20 days before periastron (τ − 30 d), ending a couple of weeks after (τ + 15 d). The system was not detected in HE gamma rays for the next two weeks, and its activity related to periastron passage was thought to be over when it surprisingly brightened in HE gamma rays at τ + 30 d. This “GeV flare” reached a luminosity close to the pulsar spindown power, lasting nearly 2 months up to τ + 80 d. The average spectrum was a power law of photon index Γ = 1.4 with an exponential cutoff at 0.3 GeV, hardening with decreasing flux. The GeV flare was not accompanied by concurrent changes in emission in radio, X-rays, or VHE gamma rays (Abdo et al. 2011; Abramowski et al. 2013), suggesting that the particles responsible for this GeV emission component have a narrow energy distribution, distinct from the power-law distributed pairs attributed to the shocked pulsar wind.

The origin of the flare remains puzzling: how is the spindown power so efficiently converted to gamma rays and why does this occur suddenly one month after periastron passage? The double-peaked shape of the radio and X-ray lightcurves has been associated with the pulsar “crossings” of the dense Be disc (Tavani & Arons 1997; Johnston et al. 1999; Chernyakova et al. 2006; Takata et al. 2012), which is thought to be inclined with respect to the orbital plane (Melatos et al. 1995). However, the GeV flare starts ≈10 days after the post-periastron radio/X-ray peak, well after the presumed disc crossing times. The pulsar is far from the densest regions, being 60 to 100 R⋆ away from the star during the GeV flare (Fig. 1). Indeed, the radio pulsations, eclipsed by the circumstellar material starting at τ − 16 d, turn back on two weeks prior to the GeV flare (Abdo et al. 2011). Hence, the mechanism for the GeV flare also appears distinct from that causing the radio/X-ray variability.

A high conversion efficiency to HE gamma-rays can be obtained if the pairs present in the pulsar wind (and its nebula) cool rapidly due to inverse Compton scattering. The companion star has a high luminosity so most models have considered the anisotropic upscattering of stellar photons (Kirk et al. 1999; Khangulyan et al. 2007; Takata & Taam 2009; Pétri & Dubus 2011). The lightcurve peaks slightly before periastron, when the orbital geometry allows close to head-on scattering. This lightcurve is compatible with the brightening but not with the GeV flare. Taking the contribution from the Be disc does not change this conclusion since disc photons come predominantly from the region closest to the star, leading to the same lightcurve (van Soelen & Meintjes 2011; van Soelen et al. 2012; Yamaguchi, pers. comm.). Khangulyan et al. (2012) proposed that the flare is related to the rapidly changing shape of the bow shock as the pulsar exits the Be disc. The unshocked pulsar wind becomes unconfined along the direction of weakest external pressure, giving the cold pairs present in the wind more space (and time) to cool. A high energy density of seed photons with a favourable scattering geometry is still required: Khangulyan et al. (2012) postulated that this would be provided by local heating of the Be disc due to the pulsar crossing.

A possible clue is that the orbital phase of the GeV flare brackets inferior conjunction of the pulsar (τ+60 d, Fig. 1). The observational evidence presented above suggests the pulsar is away from the Be disc material, so that its ram pressure balances the stellar wind ram pressure. In this case, the bow shock is oriented towards the observer at inferior conjunction (Tam et al. 2011). For parameters appropriate to PSR B1259-63, the wind momentum ratio η is 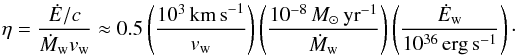(1)Semi-analytical approximations and numerical simulations show that the shock region asymptotes to a hollow cone far from the binary axis; its minimum (θin) and maximum (θout) opening angle depend only on η (Bogovalov et al. 2008; Lamberts et al. 2011, and references therein). For η ≈ 0.5, the shocked pulsar wind fills a cone from 50° to 65°, while the shocked stellar wind fills a cone from 65° to 110° (Bogovalov et al. 2008). With an orbital inclination i ≈ 30°, the line-of-sight goes through the whole length of the shocked pulsar wind cone at inferior conjunction (Fig. 2). Material in this cone has a speed c/3 immediately after the shock with the flow directed towards the observer, boosting the shocked pulsar wind emission due to relativistic effects (Dubus et al. 2010). Hence, Tam et al. (2011) and Kong et al. (2012) proposed that the GeV flare is due to Doppler-boosted synchrotron emission, providing an attractive explanation for its orbital phase. However, all co-located emission is impacted by Doppler boosting so the lack of simultaneous flaring at other frequencies (X-rays, VHE) is puzzling in this model. In addition, Khangulyan et al. (2012) commented that it would be a remarkable coincidence that the Doppler-boosted GeV luminosity happens to be nearly equal to the spindown luminosity.

Here, we investigate whether the GeV flare could have been due to inverse Compton scattering of photons from the shocked pulsar wind. The scattering geometry will be favourable if the emitting pairs are close to the pulsar and the seed photons originate from the “cometary tail” of shocked pulsar wind material. The seed photons will then be back-scattered to the observer at inferior conjunction, when the shock cone sweeps the line-of-sight, providing a geometric explanation for the orbital phase of the GeV flare. Indeed, radio VLBI maps taken in 2010–11 show large changes in the position angle of the resolved emission from the shocked flow between periastron passage and τ + 100 d (Moldón et al. 2012, and in prep.). A detailed model would require a simulation of the interaction region coupled with radiative codes. For this exploratory work we computed the expected lightcurve using a simplified toy model, sufficient to discuss its consequences on the properties of the pairs in the pulsar wind and to point out a possible test: the detection of an MeV flare prior to periastron passage.

thumbnail Fig. 1

Orbit of PSR B1259-63 close to periastron, projected assuming an inclination i = 30°. Be star is the red dot at center (to scale). Black dots mark the pulsar position in 10 day intervals. The times of the GeV “brightening” and “flare” are highlighted.

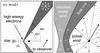thumbnail Fig. 2

Left: geometry of the toy model for inverse Compton scattering of X-ray emission from the cone of shocked pulsar wind (dark shaded region in both panels). Right: zoom on the region delimited by a dashed rectangle on the left, showing possible sources of high energy electrons. The direction to the observer is ≈60° during the GeV flare (full line arrow in both panels).

2. Model

2.1. Assumptions

We assume that the pulsar wind interacts only with the fast stellar wind at the time of the GeV flare (Sect. 1) and approximate the shock region as a hollow cone, characterised by two opening angles measured from the cone axis θin ≈ 50° and θout ≈ 65° (see left panel of Fig. 2). This hollow cone represents the shocked pulsar wind region and is the source of seed photons for inverse Compton scattering in our toy model. The particles in this cone are assumed to emit the seed photons isotropically (note, however, that the emission from the cone seen at a given location is not isotropic). The cone axis is oriented along the line-of-centres joining the Be star to the pulsar. The cone apex is located at the standoff distance between the two winds (≈0.6 × the orbital separation from the Be star for η = 0.5) although its precise location is not important here.

This geometry does not provide a precise description of the interaction region close to the pulsar, where the shock width is finite and the respective location of the high-energy pairs and seed photons is complex (see right panel of Fig. 2). The pairs responsible for the GeV emission could be localised in the pulsar wind, in the shocked pulsar wind, or in the shocked stellar wind. Here, we assume that the pairs are located at the apex of the cone, and come back to their origin later (Sect. 3.2). Localising the pairs at the apex is reasonable if the seed photons are emitted on a much larger scale.

The pairs at the cone apex see a constant intensity Iν of seed photons where the cone is filled in, and no intensity in the hollowed-out region or outside the cone. The radial distribution of emissivity in the cone is not needed to calculate the radiation energy density at the apex. As discussed in Sect. 1, the GeV spectrum suggests a narrow energy distribution for the pairs. We took mono-energetic electrons of Lorentz factor γ.

The inverse Compton emission from the pairs is expected to be dominated by the upscattering of soft X-rays from the shocked pulsar wind. The inverse Compton power depends on the energy density of the seed photons: it is maximum for interaction on X-ray photons since the observed spectral energy distribution breaks at a few keV (Uchiyama et al. 2009). The Lorentz factor of the pairs must be γ ≈ 500 to boost 1 keV photons to 300 MeV, where the spectrum cuts off. The inverse Compton interaction is at the limit between Thomson and Klein-Nishina regime, hence the cooling timescale is the smallest possible, maximizing the radiative efficiency. Other consequences of being close to the Klein-Nishina limit are that (1) seed photons with energies >1 keV contribute little to the inverse Compton emission; (2) emission ≥1 GeV may be absorbed due to pair production on the X-ray photons, depending on how the X-ray emission is distributed in the cone.

The soft X-ray emission is likely to arise in an extended region, larger than the zone where the pairs are located at the cone apex. Just like a PWN, the shocked pulsar wind is expected to radiate synchrotron emission from radio up to the radiative limit at ≈30 MeV (e.g. de Jager et al. 1996), with the higher energy photons emitted from the regions closest to the apex of the termination shock (e.g. Kennel & Coroniti 1984; Dubus 2006). Emission in X-rays involves particles that have significantly cooled and have been advected away from the shock apex. There is observational evidence that in LS 5039, where a comparable interaction is thought to occur, the X-rays are emitted far out of the system in an extended region (Bosch-Ramon et al. 2007; Szostek & Dubus 2011). The shocked stellar wind may also contribute thermal X-rays: we have neglected it since the observations show that the non-thermal component dominates.

2.2. Lightcurve

The spectrum from the mono-energetic electrons is highly peaked at 300 MeV so the HE lightcurve follows closely the bolometric lightcurve. With the assumption described above, the bolometric lightcurve is straightforward to compute in the Thomson regime by following Henri & Petrucci (1997). 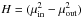We find that the total power radiated by an electron of Lorentz factor γ (velocity β = v/c) travelling at an angle μ = cosθ from the hollow cone axis is given by (2)where J = (μin − μout), /2, 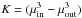/3, μin = cosθin, μout = cosθout, σT is the Thomson cross-section, ne is the number of electrons, and 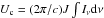is the radiation energy density of the hollow cone at its apex. Under the head-on approximation, appropriate for relativistic pairs, the bolometric lightcurve is set by the emission of the pairs travelling directly towards the observer. If the pair distribution is isotropic, the lightcurve is given by Eq. (2) with θ representing the angle between the line-of-sight and the cone axis. This angle, which varies from π/2 + i (superior conjunction) to π/2 − i (inferior conjunction) with i the system inclination, is calculated using the formulae in Dubus et al. (2010). For comparison, the total power radiated by scattering photons from the star, taken as a point source, is (3)where 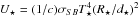with T⋆ the star temperature, R⋆ its radius, d⋆ its distance to the electron. This can be rederived from Eq. (2) in the limit μin = 1, μout = 1 − (R⋆/d⋆)2/2 ≈ 1, with μ →  − μ because the star is oriented directly opposite to the cone.

thumbnail Fig. 3

Top: lightcurve for inverse Compton scattering on photons from the star (dashed line) and from the hollow shock cone (solid line). Middle: X-ray (1–10 keV) lightcurve from Abdo et al. (2011). Bottom: the cone lightcurve is multiplied by the X-ray lightcurve and compared to the Fermi/LAT lightcurve. See text for details.

2.3. Results

The lightcurve obtained for scattering off photons from the hollow cone is shown in Fig. 3 (top panel), with θin ≈ 50°, θout ≈ 65°. The lightcurve for scattering off stellar photons is shown for comparison (dashed line). Both are normalised by the same factor 2neσTcγ2U with U constant and taken equal to U⋆ at periastron passage (at the pulsar location). The “cone” lightcurve peaks at inferior conjunction, as expected, but decays very slowly because the orientation of the cone changes slowly for the observer along this part of the orbit, by a few degrees. The observations show a much faster decline (data in the bottom panel of Fig. 3). Changing the opening angles of the cones has a mild influence on the normalisation or the fractional variability. However, the main characteristics (peak at τ + 60 d and slow decay) remain unchanged.

Other factors must come into play to obtain a better match with the GeV lightcurve. The interaction occurs far from the star, hence the stellar wind has already accelerated to its terminal velocity so η is unlikely to change with orbital phase (in as much as we ignore the effects of the Be disc, for the reasons given in Sect. 1). Alternatively, the orientation of the cone could deviate from being radially away from the star. The cone has a large opening angle so parts of it are affected by the Be disc (Takata et al. 2012). However, this effect is unlikely to persist beyond τ + 60 d and, hence, to significantly impact the lightcurve. Finally, the intrinsic emission from the cone could have a strong orbital dependence. The lightcurves shown in the top panel of Fig. 3 assume that Uc stays constant along the orbit. Actually, Uc is expected to vary with phase because the changing location and size of the shock region have an impact on the magnetisation at the shock, on the flow timescales, on radiative and adiabatic losses (Tavani et al. 1996; Kirk et al. 1999; Dubus 2006; Khangulyan et al. 2007; Uchiyama et al. 2009; Takata & Taam 2009). Modelling these effects is beyond the scope of this work. To highlight the possible impact on the lightcurve, we have assumed in the lower panel of Fig. 2 that Uc varies together with the observed X-ray lightcuve (taken from Abdo et al. 2011). The impact of the X-ray variations is evident: the geometrical dependence of the inverse Compton cross-section quenches the first X-ray peak and enhances the second X-ray peak in the upscattered lightcurve. Note that both GeV brightening and flare are explained by the same process in this model.

Although the agreement with the observations is improved, the model does not explain the delay between the (second) X-ray peak and the GeV flare. Here, more subtle effects could play a role such as a changing spectral shape for the seed photons, or taking into account a more complex geometry for the location of the high-energy pairs and the seed photons. Doppler boosting may also influence the lightcurve. The shocked pulsar wind accelerates to relativistic velocities away from the apex (Bogovalov et al. 2008) so radiation from particles embedded in the flow will be Doppler boosted in the direction of bulk motion. The effect will be to enhance the emission from the part of the cone moving directly towards the observer, which may slightly modify the lightcurve as our line-of-sight crosses the cone differently with orbital phase. An accurate calculation requires knowledge of the emission and velocity structure inside the cone. However, we note that if the pairs are located at the apex and the X-ray emission is in the wings, where the flow velocity is higher, the seed photon density seen by the pairs will be deboosted, making inverse Compton emission less efficient.

3. Discussion

3.1. Radiative efficiency

The peak gamma-ray luminosity is nearly equal to the pulsar spindown power. The radiative process responsible for the GeV flare must be able to cool the electrons efficiently, before they move away from the gamma-ray emission zone, setting a strict limit on the seed photon energy density (Khangulyan et al. 2012).

We start by considering particles in the unshocked pulsar wind. Cold particles in the pulsar wind rest frame naturally leads to emission in a narrow band. The pairs travel radially away from the pulsar with γ interpreted as the bulk Lorentz factor of the wind Γ. We see only emission from those pairs that travel directly towards us because of relativistic beaming. They radiate before reaching the termination shock, on a timescale τesc ~ d/v with d the orbital separation and v ≈ c the speed of the wind. Assuming that the pairs see an isotropic radiation field U, their inverse Compton cooling timescale is 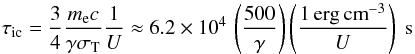(4)assuming the Thomson regime (the timescale using the exact cross-section will be longer by a factor ~a few at the transition to the Klein-Nishina regime). The lower limit on U is 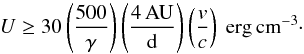(5)The pairs do not necessarily see an isotropic field. If they scatter stellar photons then the relevant energy loss rate is given by Eq. (3). Since θ = 60° at τ + 60 d, the timescale for anisotropic loss rate on stellar photons is ≈5 times longer than given by the isotropic case (Eq. (4)). Stellar photons clearly cannot cool pairs in the unshocked wind since the required field U is much higher than U⋆ ≈ 0.1  erg   cm-3 (at the pulsar position and τ + 60 d). However, if the pairs scatter radiation from the cone, the loss rate given by Eq. (2) is 1.4 times smaller than the isotropic case (Eq. (4)), so Uc ≥ 20    erg   cm-3 is a reasonable estimate. The isotropic estimate also holds for the case of particles in the shocked winds because their velocity is isotropized at the shock. Their escape timescale is still roughly estimated as τesc ~ d/v, with v the wind speed (Stevens et al. 1992).

The high radiation field density required by efficient cooling is difficult to reconcile with the observed luminosity. The X-ray luminosity is related to Uc in our geometry by 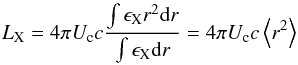(6)where ϵX is the X-ray emissivity of the cone, which we assume to depend only on the radius r from apex and to be isotropic. 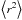is typically the inner radius of the X-ray emission zone 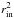when ϵX decreases more steeply than r-2. The characteristic size is 3   ×   1010  (γ/500)1/2(d/4   AU)1/2(c/v)1/2   cm since the observed X-ray flux translates to a luminosity LX ≈ 1034 erg s-1. The estimated size is very small compared to the natural scale d.

Khangulyan et al. (2012) face the same difficulty. They considered electrons in the unshocked pulsar wind scattering optical or IR photons, hence they have γ ≈ 104. The required density U ≥ 1  erg   cm-3 (Eq. (5)) is 10 times greater than the stellar radiation density at τ + 60 d. If this is Be disc material heated and disrupted by the pulsar passage, they find its luminosity should be as large as the stellar luminosity (Eq. (6) with r ≈ d). The limit is even greater if the seed photon field is seen behind the gamma-ray emitting electrons by the observer, leading to inefficient Compton scattering, so part of this material must be on our line-of-sight without preventing the detection of radio pulses.

3.2. Location of the high-energy particles

Efficient inverse Compton cooling requires a high radiation energy density U, posing a major caveat on such models – including the present one. We propose that this favours locating the gamma-ray emitting particles in the post-shock region, where higher U may be reached, rather than in the pulsar wind. The longer advection timescale means that the particles have more time to radiate, especially if they are mixed with the shocked stellar wind which has v/c ≈ 0.003. Particles at the apex, near the “stagnation point”, may take longer to escape than we assume. Our simplified geometry and other assumptions (scattering of X-rays, U independent of exact electron location, isotropic emissivity) also entail significant uncertainties. All of this alleviates the discrepancy in size, although it is unclear whether they can be fully reconciled. Numerical simulations including radiation are required to quantify this.

The GeV-emitting particles could be accelerated at the termination shock of the stellar wind as proposed by Bednarek (2011). However, this should produce a power-law distribution of particles instead of the narrow distribution of HE particles suggested by observations. Instead, we propose to associate the HE particles with the Maxwellian distribution at energy Γmec2 that models of magnetised pair outflows typically produce at the pulsar wind termination shock. In particular, Sironi & Spitkovsky (2011) found in their simulations that shock-driven reconnection of a striped pulsar wind produces thermal distributions at high latitudes, where there is a net magnetic field averaged over a stripe wavelength, and broad non-thermal distributions in the equatorial plane of the pulsar, where the net field averages to zero and particles undergo Fermi acceleration. These broad distributions are obtained for values of 4πκRLC/RTS ≳ 10, which is verified here since the termination shock RTS is at 104–105 times the light cylinder radius RLC. Hence, we speculate that the GeV emission and the X-ray/TeV emission arise from particles situated at different pulsar latitudes in the post-shock region. In any case, assuming as we did that the pairs upscatter X-ray photons from the shocked flow has for consequence a much lower bulk velocity Γ than usually invoked at the termination shock of pulsars like the Crab. There may not be enough room in PSR B1259-63 to accelerate the wind to higher Lorentz factors before it meets its fate at the termination shock.

3.3. An MeV flare

A consequence of the model that we propose is that the GeV flare should be preceded by a MeV flare. The high energy pairs responsible for the GeV flare have a Lorentz factor γ ≈ 500 (see Sect. 2.1). These pairs can also upscatter the ϵ⋆ ≈ 10 eV stellar photons, resulting in emission peaked at ≈2 MeV. The lightcurve of this component behaves like the dashed curve in Fig. 3 (top panel), peaking a few days before periastron. The luminosity depends on ne. The density of particles is 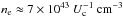to reproduce the peak GeV flare luminosity LGeV ≈ Ė. Assuming ne stays roughly at the same value during periastron passage, using Eq. (3) gives a peak MeV luminosity LMeV ≲ 4 × 1034  erg   s-1 for Uc ≥ 30  erg   cm-3. Since this is comparable to LX, a hard component may therefore emerge in hard X-rays beyond 100 keV in the days preceding periastron passage, something that can be tested in the future by the soft gamma-ray detector onboard ASTRO-H.

4. Conclusion

We have explored the possibility to generate a HE gamma-ray flare by inverse Compton scattering X-ray photons emitted by the shocked pulsar wind instead of optical photons from the star. The main advantage of this model is that the associated lightcurve naturally peaks after periastron passage, when the cone of shocked material passes through the line-of-sight, while scattering on stellar or Be disc photons produces a peak before periastron passage. The evolution of the intrinsic emission of the cone with orbital phase needs to be taken into account to reproduce the HE gamma-ray lightcurve, notably the fast decline after τ + 60 d. The high gamma-ray luminosity suggests a high radiative efficiency. As with all models invoking inverse Compton emission, we find that a significant drawback is the very high energy density of seed photons required to have a high radiative efficiency. We speculate that this may be easier to attain in the shock region. The same model could be at work in other gamma-ray binaries, notably LSI +61°303 where the GeV emission peaks after periastron passage (Hadasch et al. 2012).

Finally, we remark that all the proposed models for the GeV flare have tied it to the orbital motion of the pulsar. Hence, all predict a similar GeV flare should occur at the next periastron passage. Its absence, or the detection of a GeV flare at some other orbital phase, could indicate that it was a random occurrence. In this case, the GeV flare of PSR B1259-63 would be more akin to the GeV flares observed in the Crab pulsar wind nebula (Buehler et al. 2012), which have been interpreted as random reconnection events downstream the termination shock (Uzdensky et al. 2011; Cerutti et al. 2013). This is a tempting analogy, although we note that the duration and the radiative efficiency of the flare in PSR B1259-63 are quite different from the day- to week-long Crab flares, where at most 1% of the spin-down luminosity is radiated away. On the other hand, there is no obvious reason to expect strictly similar particle acceleration and emission from the AU-scale nebula in PSR B1259-63 and the 0.1 pc nebula in the Crab.

Acknowledgments

We thank Gilles Henri for pointing out that the scattered power (Eq. (2)) can be cast in analytical form. G.D. acknowledges support from the European Union via contract ERC-StG-200911 and from CNES.

References

  1. Abdo, A. A., Ackermann, M., Ajello, M., et al. (Fermi/LAT collaboration) 2011, ApJ, 736, L11 [NASA ADS] [CrossRef] [Google Scholar]
  2. Abramowski, A., Acero, F., Aharonian, F., et al. (H.E.S.S. collaboration), 2013, A&A, 551, A94 [Google Scholar]
  3. Bednarek, W. 2011, MNRAS, 418, L49 [NASA ADS] [Google Scholar]
  4. Bogovalov, S. V., Khangulyan, D., Koldoba, A. V., Ustyugova, G. V., & Aharonian, F. A. 2008, MNRAS, 387, 63 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bosch-Ramon, V., Motch, C., Ribó, M., et al. 2007, A&A, 473, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Buehler, R., Scargle, J. D., Blandford, R. D., et al. 2012, ApJ, 749, 26 [NASA ADS] [CrossRef] [Google Scholar]
  7. Cerutti, B., Werner, G. R., Uzdensky, D. A., & Begelman, M. C. 2013, ApJ, 770, 147 [NASA ADS] [CrossRef] [Google Scholar]
  8. Chernyakova, M., Neronov, A., Lutovinov, A., Rodriguez, J., & Johnston, S. 2006, MNRAS, 367, 1201 [NASA ADS] [CrossRef] [Google Scholar]
  9. de Jager, O. C., Harding, A. K., Michelson, P. F., et al. 1996, ApJ, 457, 253 [NASA ADS] [CrossRef] [Google Scholar]
  10. Dubus, G. 2006, A&A, 456, 801 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Dubus, G., Cerutti, B., & Henri, G. 2010, A&A, 516, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Hadasch, D., Torres, D. F., Tanaka, T., et al. 2012, ApJ, 749, 54 [NASA ADS] [CrossRef] [Google Scholar]
  13. Henri, G., & Petrucci, P. O. 1997, A&A, 326, 87 [NASA ADS] [Google Scholar]
  14. Johnston, S., Manchester, R. N., Lyne, A. G., et al. 1992, ApJ, 387, L37 [Google Scholar]
  15. Johnston, S., Manchester, R. N., McConnell, D., & Campbell-Wilson, D. 1999, MNRAS, 302, 277 [NASA ADS] [CrossRef] [Google Scholar]
  16. Kennel, C. F., & Coroniti, F. V. 1984, ApJ, 283, 710 [NASA ADS] [CrossRef] [Google Scholar]
  17. Khangulyan, D., Hnatic, S., Aharonian, F., & Bogovalov, S. 2007, MNRAS, 380, 320 [NASA ADS] [CrossRef] [Google Scholar]
  18. Khangulyan, D., Aharonian, F. A., Bogovalov, S. V., & Ribó, M. 2012, ApJ, 752, L17 [NASA ADS] [CrossRef] [Google Scholar]
  19. Kirk, J. G., Ball, L., & Skjaeraasen, O. 1999, Astropart. Phys., 10, 31 [NASA ADS] [CrossRef] [Google Scholar]
  20. Kong, S. W., Cheng, K. S., & Huang, Y. F. 2012, ApJ, 753, 127 [NASA ADS] [CrossRef] [Google Scholar]
  21. Lamberts, A., Fromang, S., & Dubus, G. 2011, MNRAS, 418, 2618 [NASA ADS] [CrossRef] [Google Scholar]
  22. Melatos, A., Johnston, S., & Melrose, D. B. 1995, MNRAS, 275, 381 [NASA ADS] [Google Scholar]
  23. Moldón, J., Ribó, M., & Paredes, J. M. 2012, in Proc. Gamma 2012, Heidelberg, July 2012, eds. F. A. Aharonian, W. Hofmann, & F. M. Rieger, AIP Conf. Proc., 1505, 386 [Google Scholar]
  24. Pétri, J., & Dubus, G. 2011, MNRAS, 417, 532 [NASA ADS] [CrossRef] [Google Scholar]
  25. Sironi, L., & Spitkovsky, A. 2011, ApJ, 741, 39 [NASA ADS] [CrossRef] [Google Scholar]
  26. Stevens, I. R., Blondin, J. M., & Pollock, A. M. T. 1992, ApJ, 386, 265 [NASA ADS] [CrossRef] [Google Scholar]
  27. Szostek, A., & Dubus, G. 2011, MNRAS, 411, 193 [NASA ADS] [CrossRef] [Google Scholar]
  28. Takata, J., & Taam, R. E. 2009, ApJ, 702, 100 [NASA ADS] [CrossRef] [Google Scholar]
  29. Takata, J., Okazaki, A. T., Nagataki, S., et al. 2012, ApJ, 750, 70 [NASA ADS] [CrossRef] [Google Scholar]
  30. Tam, P. H. T., Huang, R. H. H., Takata, J., et al. 2011, ApJ, 736, L10 [NASA ADS] [CrossRef] [Google Scholar]
  31. Tavani, M., & Arons, J. 1997, ApJ, 477, 439 [NASA ADS] [CrossRef] [Google Scholar]
  32. Tavani, M., Grove, J. E., Purcell, W., et al. 1996, A&AS, 120, C221 [NASA ADS] [Google Scholar]
  33. Uchiyama, Y., Tanaka, T., Takahashi, T., Mori, K., & Nakazawa, K. 2009, ApJ, 698, 911 [NASA ADS] [CrossRef] [Google Scholar]
  34. Uzdensky, D. A., Cerutti, B., & Begelman, M. C. 2011, ApJ, 737, L40 [NASA ADS] [CrossRef] [Google Scholar]
  35. van Soelen, B., & Meintjes, P. J. 2011, MNRAS, 412, 1721 [NASA ADS] [CrossRef] [Google Scholar]
  36. van Soelen, B., Meintjes, P. J., Odendaal, A., & Townsend, L. J. 2012, MNRAS, 426, 3135 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1

Orbit of PSR B1259-63 close to periastron, projected assuming an inclination i = 30°. Be star is the red dot at center (to scale). Black dots mark the pulsar position in 10 day intervals. The times of the GeV “brightening” and “flare” are highlighted.
In the text
thumbnail Fig. 2

Left: geometry of the toy model for inverse Compton scattering of X-ray emission from the cone of shocked pulsar wind (dark shaded region in both panels). Right: zoom on the region delimited by a dashed rectangle on the left, showing possible sources of high energy electrons. The direction to the observer is ≈60° during the GeV flare (full line arrow in both panels).
In the text
thumbnail Fig. 3

Top: lightcurve for inverse Compton scattering on photons from the star (dashed line) and from the hollow shock cone (solid line). Middle: X-ray (1–10 keV) lightcurve from Abdo et al. (2011). Bottom: the cone lightcurve is multiplied by the X-ray lightcurve and compared to the Fermi/LAT lightcurve. See text for details.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.