EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 557 (September 2013) A&A, 557 (2013) A2 Full HTML
Free Access
Issue
A&A
Volume 557, September 2013
Article Number A2
Number of page(s) 5
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/201220628
Published online 12 August 2013

© ESO, 2013

1. Introduction

The most common technique used to investigate plasmas properties is spectroscopical observations of photon emission that is a result of electron-ion collisions. Dielectronic recombination (DR) is one of the most important sources of emission lines from astrophysical and laboratory plasmas. When observing lines from such processes, it is possible to study the initial mass function of the earliest generation of stars and the chemical evolution of the universe (Savin 2000). Reliable DR rate coefficients are essential for determining the ionization balance and interpreting spectra from most types of astrophysical and laboratory plasmas (Zatsarinny et al. 2004; Ferland et al. 1998; Savin 2000). Fluorine is an astrophysically abundant element (La Cognata et al. 2011) and is currently believed to be present in different astrophysical objects, such as in Type II supernovae and Galactic asymptotic giant branch (AGB) stars (Lodders 2003; Abia et al. 2011; Zhang & Liu 2005). It is used to probe nucleosynthesis scenarios because its abundance is very sensitive to the physical conditions within the stars (Lucatello et al. 2011).

The importance of the DR mechanism was first recognized by Burgess (1964) for hot plasmas, where highly charged ions are present. DR is a two-step resonant recombination process of a continuum electron with a non-bare ion. In the first step, an incoming electron is captured to some bound state of the ion, with the simultaneous excitation of a core electron, forming a doubly excited state. In the second step, the produced doubly excited state decays through autoionization or by radiative decay. The radiative decay leads to the completion of DR, the system is stable against autoionization and the charge state of the ion decreases by one unit. In addition to radiative recombination (RR) and DR, a third resonant recombination channel, called trielectronic recombination (TR) is possible in Be-like ions. In this process, two electrons from the 2s state are excited to 2p state during the attachment of a free electron to a certain nl Rydberg state, forming a triply excited state (Schnell et al. 2003; Fogle et al. 2005). This occurs because of the strong mixing between the 2s2 and 2p2 configurations and the low excitation energy of the two 2s electrons (Schnell et al. 2003). Throughout this paper, we use the convention of identifying the charge state prior to recombination.

The calculations for DR rate coefficients are a challenging task since DR is a resonant process that involves doubly excited intermediate states, which can be highly correlated and thus makes the calculations extremely difficult (Lindroth & Schuch 2003). The available DR data used in plasma modelling codes are frequently obtained from calculations based on simplified models. These data are often not verified experimentally and contains uncertainties, especially at low energies below 3 eV. At these very low energies, the DR plasma rate coefficients are very sensitive to the energy position of the resonances. A few meV uncertainty in the position of DR resonances changes the low-temperature plasma DR rate coefficients by an order of magnitude (Schippers et al. 2004). A critical evaluation of the uncertainties in the existing calculated high-temperature DR rate coefficients has been performed by Savin & Laming (2002). They have found that for some ions the uncertainties in different calculations can be as large as a factor of 2−5. More recently, Bryans et al. (2006) used updates to archived DR and RR data to find differences in peak fractional abundances of up to 60% compared to the commonly used data. Because of these uncertainties in low-temperature plasma rates, the relative elemental abundance inferred from the solar and stellar upper atmosphere, needed for modelling the astrophysical plasmas is affected to a large extent (Chen 2002). Laboratory measurements are therefore essential for testing and improving the theoretical approaches to produce reliable recombination data for plasma modelling.

The most prominent and reliable experimental technique for deriving absolute recombination rate coefficients utilizes ion storage rings equipped with electron coolers (Schuch & Böhm 2007). These laboratory instruments provide an excellent and extraordinary environment for studying recombination processes with extreme precision to generate valuable atomic data. For example, in a recent experiment performed at TSR for lithium-like scandium (Sc+18), an uncertainty of less than 5 ppm has been reported for DR resonances having energies below 100 meV (Lestinsky et al. 2008).

In the past, most of the recombination measurements for fluorine have been performed for H- to Li-like and C-like ions (Andersen 1991; Andersen et al. 1992; Schmidt et al. 1992; Glans et al. 1999; Tokman et al. 2002). Only a few measurements for Be-like fluorine have been reported so far (Dittner et al. 1987; Badnell et al. 1991). The statistics and energy resolution in these measurements are poor, and the data are contaminated by unknown fractions of metastable ions. This does not allow one to derive reliable absolute recombination rate coefficients. In this publication, experimental results of absolute recombination rate coefficients for Be-like F VI recombining into B-like F V, measured at the CRYRING storage ring are presented.

2. Experiment and data analysis

The F5+ ions were produced in an electron cyclotron resonance ion source and injected into the CRYRING storage ring (Abrahamsson et al. 1993), located in the Manne Siegbahn Laboratory at Stockholm University, Sweden. Following injection, the ions were accelerated inside the ring up to an energy of 6.65 MeV/amu. In the electron cooler section of the storage ring, a low-temperature electron beam with a diameter of 4 cm and electron density of 3.92 × 106 cm-3 was merged with the circulating ion beam over an effective interaction length of 80 cm. The ions were electron cooled for 1.5 s. As a result of repeated Coulomb collisions between the constantly refreshed cold electrons and hot ions, the diameter of the ion beam was reduced to approximately 1 mm from its initial 2 cm diameter. After electron cooling, the electron energy was scanned in a zig-zag pattern to cover an energy range up to 25 eV. An ultra high vacuum of the order of 10-11 mbar was maintained in the entire ring during the experiments.

Apart from the ion beam cooling, the electron cooler also acted as an electron target for the stored ions. In the electron cooler, electron recombines with F5+ ions to produce F4+ ions. The recombined ions were separated from the parent ion beam as they pass through the first dipole bending magnet after the electron cooler. There, the charge-changed ions were detected with 100% efficiency by using a solid state surface barrier detector. For each recombination event detected by the detector, the program records the pulse height, electron acceleration potential, and time. After the electron energy scan, the acquisition window was closed and the ion beam dumped. The above sequence was repeated by starting a new cycle with the ion beam injection into the CRYRING.

For each data point, the space-charge-corrected electron energy, Ee, and the drag-force-corrected ion energy, Ei, were used to obtain the collision energy in the centre-of-mass frame ECM. A detailed procedure of data analysis is described in Madzunkov et al. (2001); DeWitt et al. (1996). The absolute recombination rate coefficient, α(E), as a function of ECM was obtained by normalizing the count rate, R(E), associated with each electron-ion collision energy value, to the number of ions, Ni, and electron density, ne. This is accomplished by using the following equation: 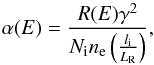(1)where γ is the Lorentz factor. The time spent by the ions during interactions with the electrons is given by the ratio of electron-ion interaction length, li, to the orbit length, LR, of the ions.

thumbnail Fig. 1

Recombination rate coefficients for Be-like F recombining into B-like F. The grey area represents the experimentally derived recombination rate coefficients. The red solid curve shows calculated ground-state recombination rate coefficients (DR +TR), and the blue solid curve (and corresponding white area) shows calculated TR rate coefficients, both scaled to 85%, as discussed in the text to account for the metastable fraction of the ion beam present in the experiment. The black dotted line is the calculated field-ionization-free rate coefficients, scaled to 85%. The RR contribution to the experimental spectrum is shown by the hatched area in the inset. The vertical bars show the approximate DR resonance positions calculated with Eq. (2). Vertical arrows show TR resonance positions and their configurations obtained from the AUTOSTRUCTURE calculations.

3. Results and discussion

3.1. Merged-beam recombination rate coefficients

The experimental merged beam recombination rate coefficients for F VI are shown in Fig. 1 for the electron-ion collision energy range of 0−25 eV. The non-resonant background, which increases with the decrease in electron-ion collision energy, is due to the RR contribution to the experimental spectrum. Quantum mechanically RR and DR are indistinguishable processes when occurring in the same final states, and can interfere with each other. However, Pindzola et al. (1992) have concluded that the interference between these two mechanisms is very small and can be safely neglected. The RR contribution in our experimental spectrum is shown in the inset of Fig. 1. This contribution was estimated by using Bethe & Salpeter (1957) formula, after correcting by the Gaunt factors (Lindroth & Schuch 2003) for recombination into low-n states.

In the investigated energy range △ n = 0, recombination resonance are observed due to the excitation of a 2s core electron to the 2s2p (3PJ) and 2s2p (1P1) states (1s2 core is omitted for simplicity). The approximate energy positions of different DR resonances corresponding to the above two series are marked in Fig. 1. These resonance positions were estimated by using the Rydberg formula 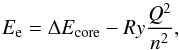(2)where Ee is the kinetic energy of the free electron, △ Ecore the excitation energy of the excited core (Ralchenko et al. 2012), Ry = 13.6 and q = 5 the Rydberg constant and charge number of the ion, respectively. In the investigated energy range the lowest possible values of the principal quantum number for which DR can take place in the 2s2p (3PJ) and 2s2p (1P1) series are four and six, respectively. Individual resonance can be seen clearly resolved up to n = 12 for 2s2p (3PJ) and n = 14 for 2s2p (1P1) series.

The recombined ions with Rydberg electrons in the principal quantum number n > ncutoff = 18 are field-ionized as they pass through the analysing dipole magnet behind the electron cooler section. These ions return to their parent charge states and are lost for detection. However, some of the ions recombined into states with n > 18 can radiatively decay into n < 18 during the flight time from the electron cooler to the dipole magnet. These ions survive the field-ionization region and are detected. This contribution extends the experimental rate coefficients over the field-ionization limit in the experimental spectrum as can be seen at the 2s2p (1P1) series limit.

In the merged beam experiments, the contamination of the stored ion beam with metastable ions is a concern when deriving the absolute recombination rate coefficients. Calculations are used to correct the experimental spectrum for metastable contributions. In the present experiment a small amount of metastable contributions is observed owing to the population of metastable ions associated with 2s2p (3P0) states in the primary ion beam. Cheng et al. (2008) calculated a radiative rate of 1.208 × 10-1 s-1 for the 3P0 level, and Andersen et al. (2009) calculated a rate of 1.182 × 10-1 s-1 giving radiative life time of 8.28 and 5.5 s, respectively. Life times for the other metastable states (3P01,2) are very short, and they decay to the ground state before the measurement cycle started. Thus a small contribution from metastable states is expected in the spectrum. With increasing kinetic energy, the free electron is attached predominantly into high nl states for the same excitation of the core electron. As a result the DR resonances pile up, which can be seen clearly in the 2s2p (1P1)nl series. It is also interesting to note that the strengths of DR peaks belonging to the 2s2p (3PJ)nl series decreases towards the series limit. The radiative decay of the 3PJ core is dipole forbidden, which implies that the radiative decay needed to complete DR is forced to take place through the decay of the Rydberg electrons. The probability that the Rydberg electrons to decay via radiative cascade decreases rapidly for high nl states. This in turn decreases sharply the DR strength along the 3PJ resonance series.

The calculated DR rate coefficients shown in Fig. 1, were obtained using the AUTOSTRUCTURE code (Badnell 1986). The calculations were performed with a similar approach to the one described by Fogle et al. (2005). The code calculates the energy levels, radiative and autoionization rates needed to calculate DR cross sections. Accounting for the stabilization of recombined electrons before field ionization, the calculations use a 50 ns mean time-of-flight between the interaction zone and the magnet (Schuch et al. 1999). To compare the theoretical results with the experimentally derived recombination rate coefficients, the calculated recombination cross sections, σ(E), were convoluted with the velocity distribution of the electrons from the experiment 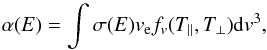(3)where fv(T∥, T⊥) is the Maxwellian velocity distribution, characterizing the electron beam in the interaction region of the electron cooler, with T∥ = 0.1 meV and T⊥ = 1.0 meV.

Excellent agreement can be observed at energies above 13 eV between the experimentally derived recombination rate coefficients and the calculated results if we apply a scaling factor of 0.85 to the calculated data for the n = 2−18 resonances. This suggests a 15% metastable fraction in the experimental spectra as discussed before. In the energy region between 4 eV to 13 eV, the calculated peak intensity of some of the DR peaks is slightly lower than the experimental results and few small peaks are not observed in the calculated data. At low energies below 4 eV, the agreement is less satisfactory between both the spectra in resonance positions and intensities. In the inset of Fig. 1 the low-energy part of the experimental spectrum is shown to represent the RR contributions to the experimental spectrum estimated using the same procedure as discussed by Fogle et al. (2003).

As discussed above, field-ionization of the recombined ions in the bending dipole magnet does not allow all the recombined ions to be detected . To account for the resonances not detected in the experiment, the results from the AUTOSTRUCTURE calculations, containing recombination into principal quantum number n up to 1000, are used as shown in Fig. 1. This approximation is considered to be reasonable, since the calculations are quite accurate for high n value and DR into states with n > 1000 are insignificant. In the rest of the paper the recombination data up to n = 1000 will be referred to as field-ionization-free rate coefficients.

A small background from electron capture in residual gas of around 0.1 × 10-10 cm3 s-1 as seen in Fig. 1 above the series limit was not subtracted from the data. Its contribution is in the size of the statistical error, which is in the channels with the lowest number of counts 10% in the region of the highest peaks around 5%. The total systematic error in the measured DR rate coefficients is found to be 15%. This includes 10% uncertainties in the beam current, 5% in the electron-ion interaction length, the uncertainty of 7% in the metastable fraction of the ion-beam, and a possible 5% contribution from residual gas capture (background).

3.2. Plasma rate coefficients

The temperature-dependent plasma rate coefficients, α(Te), were obtained by convoluting the merged beam recombination rate coefficients spectra with the Maxwell-Boltzmann energy distribution of the electrons in a plasma at temperature Te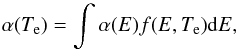(4)where α(E) is the merged-beam rate coefficients, and f(E,Te) is the Maxwell-Boltzmann distribution of the electron energies at electron temperature Te, which is given by 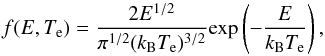(5)where kB is the Boltzmann constant. The convolution of the measured recombination rate coefficients was made over the temperature range of 103−106 K and the resulting temperature-dependent rate coefficients are shown in Fig. 2. The above approach of convolution is valid as long as the electron temperatures in the experiment is much lower than the temperature of the Maxwell-Boltzmann energy distribution in plasma (Schippers et al. 2001).

To derive field-ionization-free plasma rate coefficients, we used the same procedure as described in Schippers et al. (2001) and Fogle et al. (2005). The field-effected part of the experimental spectrum was estimated using the calculated results for Rydberg states with n up to 1000 as discussed in the previous section. The resulting recombination spectra were then convoluted using Eq. (4), to obtain the field-free plasma rate coefficients as shown in Fig. 2. Since 85% of the circulating ions are in their ground state, the final field-free plasma rate coefficients are obtained by dividing the above convoluted rate coefficients by 0.85. This gives our experimental rate for a pure ground state. At temperatures lower than 2 × 104 K, ncutoff and field-ionization-free plasma rate coefficients have the same values, and above this temperature high Rydberg states affected by field-ionization begin to contribute significantly, resulting in low ncutoff plasma rate coefficients compared to the field-free case.

thumbnail Fig. 2

Plasma recombination rate coefficients for Be-like F as a function of electron temperatures. The black solid line and grey shaded area represent the experimentally derived ncutoff and field-ionization-free total (DR+TR) recombination rate coefficients, respectively. The open circles show field-ionization-free DR+TR rate coefficients from AUTOSTRUCTURE calculations. The calculated results from the literature are shown by the following symbols: open stars – Dittner et al. (1987); filled stars – Colgan et al. (2003); filled squares – Mazzotta et al. (1998); and open triangles – Badnell et al. (1991)

To facilitate plasma modellers, use of our data, we have fitted our derived plasma rate coefficients results using the following expression 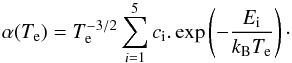(6)The resulting values of the fitting parameters ci and Ei are summarized in Table 1. The given fitting parameters are only valid for calculating plasma rate coefficients in the temperature range of 103−106 K. The fit deviates no more than 0.7% below 2.5 × 103 K and 0.4% above temperature of 2.5 × 103 K from our experimentally derived curve.

In Fig. 2 the experimentally derived field-ionization-free plasma rate coefficients are compared with the calculated results available in the literature. The existing calculated data in the literature show a wide spread at temperatures below 104 K and are significantly different from our experimentally derived rate coefficients. The reason for these discrepancies is the sensitivity of the rate coefficients at low-energy resonance positions and intensities. Most of the calculations neglect or underestimate the low-energy DR resonances resulting in a low value of rate coefficients by orders of magnitude. For example, the results of Dittner et al. (1987) contain DR resonances above 8 eV and only include states with n ≤ 64. Similarly, the calculations of Badnell et al. (1991) contain DR only in states with principal quantum number n up to 51. Their data show the same behaviour as observed in our rate coefficients but significantly lower than our rate coefficients. The calculated rate coefficients of Mazzotta et al. (1998) severely underestimate our recombination rate coefficients below 105 K.

The calculated results of Colgan et al. (2003) show a similar shape to our experimental rate coefficients and our AUTOSTRUCTURE results. In the temperatures range of 3 × 103−106 K, our AUTOSTRUCTURE calculations agree very well with the rate coefficients of Colgan et al. (2003). Below 3 × 103, the AUTOSTRUCTURE results show the opposite behaviour to Colgan et al. (2003) calculations. The rate coefficients from our AUTOSTRUCTURE calculations have lower values than our experimentally derived results within 25% in the temperature range of 8 × 104−106 K. The experimental rate is much higher than the calculated DR rate coefficients in the temperature range of 3 × 103 K to 8 × 104 K. This enhancement in the experimental plasma rate coefficients is due to high intensity of DR resonances in the energy range of 4 eV to 13 eV compared to the calculations. At 103 K the rate coefficients from AUTOSTRUCTURE calculations is 32% higher than our derived plasma rate coefficients due to the presence of a strong DR peak at ~0.07 eV, which is not observed in the experimental spectrum.

Table 1

Fit coefficients for the ncutoff and field-ionization-free plasma rate coefficients of F VI obtained by using Eq. (6).

4. Conclusions

We present high-resolution recombination rate coefficients of Be-like F ions from the measurements performed at a storage ring. Above 4 eV, an overall good agreement is observed between the experimentally derived rate coefficients and the results of our AUTOSTRUCTURE calculations. Below an energy of 4 eV, the agreement between the results is not satisfactory in both resonance energy positions and intensities. The temperature-dependent rate coefficients are presented and compared with the AUTOSTRUCTURE calculations and the calculated data available in literature. Above 8 × 104 K, good agreement is found between the experimentally derived plasma rate coefficients and the calculated results (within 25%). Below 104 K the data from literature and our AUTOSTRUCTURE results show a wide spread and deviate strongly from our experimental results. The temperature-dependent plasma rate coefficient from the AUTOSTRUCTURE calculation is 32% higher than the experimental result at 103 K.

Acknowledgments

We acknowledge the financial support from Swedish Research Council VR and thank the CRYRING staff members for assisting during the experiments.

References

  1. Abia, C., Cunha, K., Cristallo, S., et al. 2011, ApJ, 737, L8 [NASA ADS] [CrossRef] [Google Scholar]
  2. Abrahamsson, K., Andler, G., Bagge, L., et al. 1993, NIMPRB, 79, 269 [Google Scholar]
  3. Andersen, L. H. 1991, Supplement to Z. Phys. D-Atoms Molecules and Clusters, 21, S29 [Google Scholar]
  4. Andersen, L. H., Pan, G.-Y., Schmidt, H. T., Badnell, N. R., & Pindzola, M. S. 1992, Phys. Rev. A, 45, 7868 [NASA ADS] [CrossRef] [Google Scholar]
  5. Andersson, M., Zou, Y., Hutton, R., & Brage, T. 2009, Phys. Rev. A, 79, 032501 [NASA ADS] [CrossRef] [Google Scholar]
  6. Badnell, N. R. 1986, J. Phys. B: At. Mol. Phys., 19, 3827 [NASA ADS] [CrossRef] [Google Scholar]
  7. Badnell, N. R., Pindzola, M. S., Andersen, L. H., Bolko, J., & Schmidt, H. T. 1991, J. Phys. B: At. Mol. Phys., 24, 4441 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bethe, H., & Salpeter, E. 1957, The quantum mechanics of one and two electron systems, Handbuch der Physik (Berlin: Springer), 35 [Google Scholar]
  9. Bryans, P., Badnell, N. R., Gorczyca, T. W., et al. 2006, ApJS, 167, 334 [Google Scholar]
  10. Burgess, A. 1964, ApJ, 139, 776 [NASA ADS] [CrossRef] [Google Scholar]
  11. Chen, M. H. 2002, Phys. Rev. A, 66, 052715 [NASA ADS] [CrossRef] [Google Scholar]
  12. Cheng, K. T., Chen, M. H., & Johnson, W. R. 2008, Phys. Rev. A, 77, 052504 [NASA ADS] [CrossRef] [Google Scholar]
  13. Colgan, J., Pindzola, M. S., Whiteford, A. D., & Badnell, N. R. 2003, A&A, 412, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. DeWitt, D. R., Schuch, R., Gao, H., et al. 1996, Phys. Rev. A, 53, 2327 [NASA ADS] [CrossRef] [Google Scholar]
  15. Dittner, P. F., Datz, S., Krause, F., et al. 1987, Phys. Rev. A, 36, 33 [NASA ADS] [CrossRef] [Google Scholar]
  16. Ferland, G. J., Korista, K. T., Verner, D. A., et al. 1998, PASP, 110, 761 [Google Scholar]
  17. Fogle, M., Badnell, N. R., Eklöw, N., Mohamed, T., & Schuch, R. 2003, A&A, 409, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Fogle, M., Badnell, N. R., Glans, P., et al. 2005, A&A, 442, 757 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Glans, P., Lindroth, E., Eklöw, N., et al. 1999, NIMPRB, 154, 97 [NASA ADS] [Google Scholar]
  20. Cognata La, M., Mukhamedzhanov, A. M., & Spitaleri, C., et al. 2011, ApJ, 739, L54 [Google Scholar]
  21. Lestinsky, M., Lindroth, E., Orlov, D. A., et al. 2008, Phys. Rev. Lett., 100, 033001 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  22. Lindroth, E., & Schuch, R. 2003, The Physics of Multiply and Highly Charged Ions (Netherlands: Kluvert Academic Publishers), 1, 231 [CrossRef] [Google Scholar]
  23. Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
  24. Lucatello, S., Masseron, T., Johnson, J. A., Pignatari, M., & Herwig, F. 2011, ApJ, 729, 40 [NASA ADS] [CrossRef] [Google Scholar]
  25. Madzunkov, S., Eklöw, N., Lindroth, E., Tokman, M., & Schuch, R. 2001, Phys. Scr., T92, 357 [NASA ADS] [CrossRef] [Google Scholar]
  26. Mazzotta, P., Mazzitelli, G., Colafrancesco, S., & Vittorio, N. 1998, A&ASS, 133, 403 [Google Scholar]
  27. Pindzola, M. S., Badnell, N. R., & Griffin, D. C. 1992, Phys. Rev. A, 46, 5725 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  28. Ralchenko, Yu., Kramida, A. E., Reader, J., & NIST ASD Team 2012, NIST Atomic Spectra Database (ver. 4.1.0), National Institute of Standards and Technology, Gaithersburg, MD [Google Scholar]
  29. Savin. D. W. 2000, ApJ, 533, 106 [NASA ADS] [CrossRef] [Google Scholar]
  30. Savin, D. W., & Laming, J. M. 2002, ApJ, 566, 1166 [NASA ADS] [CrossRef] [Google Scholar]
  31. Schippers, S., Müller, A., Gwinner, R. G., et al. 2001, ApJ, 555, 1027 [NASA ADS] [CrossRef] [Google Scholar]
  32. Schippers, S., Schnell, M., Brandau, C., et al. 2004, A&A, 421, 1185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Schmidt, H. T., Pan, G. Y., & Andersen, L. H. 1992, J. Phys. B: At. Mol. Opt. Phys., 25, 3165 [NASA ADS] [CrossRef] [Google Scholar]
  34. Schnell, M., Gwinner, G., Badnell, N. R., et al. 2003, Phys. Rev. Lett., 91, 043001 [NASA ADS] [CrossRef] [Google Scholar]
  35. Schuch, R., & Böhm, S. 2007, J. Phys. Conf. Ser., 88, 012002 [NASA ADS] [CrossRef] [Google Scholar]
  36. Schuch, R., Zong, W., & Badnell, N. R., 1999, Int. J. Mass Spectrom., 192, 225 [NASA ADS] [CrossRef] [Google Scholar]
  37. Tokman, M., Eklöw, N., Glans, P., et al. 2002, Phys. Rev. A, 66, 012703 [NASA ADS] [CrossRef] [Google Scholar]
  38. Zatsarinny, O., Gorczyca, T. W., Korista, K. T., Badnell, N. R., & Savin, D. W. 2004, A&A, 417, 1173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Zhang, Y., & Liu, X. -W. 2005, ApJ, 631, L61 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Fit coefficients for the ncutoff and field-ionization-free plasma rate coefficients of F VI obtained by using Eq. (6).

In the text

All Figures

thumbnail Fig. 1

Recombination rate coefficients for Be-like F recombining into B-like F. The grey area represents the experimentally derived recombination rate coefficients. The red solid curve shows calculated ground-state recombination rate coefficients (DR +TR), and the blue solid curve (and corresponding white area) shows calculated TR rate coefficients, both scaled to 85%, as discussed in the text to account for the metastable fraction of the ion beam present in the experiment. The black dotted line is the calculated field-ionization-free rate coefficients, scaled to 85%. The RR contribution to the experimental spectrum is shown by the hatched area in the inset. The vertical bars show the approximate DR resonance positions calculated with Eq. (2). Vertical arrows show TR resonance positions and their configurations obtained from the AUTOSTRUCTURE calculations.
In the text
thumbnail Fig. 2

Plasma recombination rate coefficients for Be-like F as a function of electron temperatures. The black solid line and grey shaded area represent the experimentally derived ncutoff and field-ionization-free total (DR+TR) recombination rate coefficients, respectively. The open circles show field-ionization-free DR+TR rate coefficients from AUTOSTRUCTURE calculations. The calculated results from the literature are shown by the following symbols: open stars – Dittner et al. (1987); filled stars – Colgan et al. (2003); filled squares – Mazzotta et al. (1998); and open triangles – Badnell et al. (1991)
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.