| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201220025 | |
| Published online | 12 August 2013 | |
Clouds in the atmospheres of extrasolar planets
IV. On the scattering greenhouse effect of CO2 ice particles: Numerical radiative transfer studies
1 Zentrum für Astronomie und Astrophysik, Technische Universität Berlin, Hardenbergstr. 36, 10623 Berlin, Germany
e-mail: kitzmann@astro.physik.tu-berlin.de
2 Institut für Planetenforschung, Deutsches Zentrum für Luft- und Raumfahrt (DLR), Rutherfordstr. 2, 12489 Berlin, Germany
Received: 16 July 2012
Accepted: 17 June 2013
Context. Owing to their wavelength-dependent absorption and scattering properties, clouds have a strong impact on the climate of planetary atmospheres. The potential greenhouse effect of CO2 ice clouds in the atmospheres of terrestrial extrasolar planets is of particular interest because it might influence the position and thus the extension of the outer boundary of the classic habitable zone around main sequence stars. Such a greenhouse effect, however, is a complicated function of the CO2 ice particles’ optical properties.
Aims. We study the radiative effects of CO2 ice particles obtained by different numerical treatments to solve the radiative transfer equation. To determine the effectiveness of the scattering greenhouse effect caused by CO2 ice clouds, the radiative transfer calculations are performed over the relevant wide range of particle sizes and optical depths, employing different numerical methods.
Methods. We used Mie theory to calculate the optical properties of particle polydispersion. The radiative transfer calculations were done with a high-order discrete ordinate method (DISORT). Two-stream radiative transfer methods were used for comparison with previous studies.
Results. The comparison between the results of a high-order discrete ordinate method and simpler two-stream approaches reveals large deviations in terms of a potential scattering efficiency of the greenhouse effect. The two-stream methods overestimate the transmitted and reflected radiation, thereby yielding a higher scattering greenhouse effect. For the particular case of a cool M-type dwarf, the CO2 ice particles show no strong effective scattering greenhouse effect by using the high-order discrete ordinate method, whereas a positive net greenhouse effect was found for the two-stream radiative transfer schemes. As a result, previous studies of the effects of CO2 ice clouds using two-stream approximations overrated the atmospheric warming caused by the scattering greenhouse effect. Consequently, the scattering greenhouse effect of CO2 ice particles seems to be less effective than previously estimated. In general, higher order radiative transfer methods are needed to describe the effects of CO2 ice clouds accurately as indicated by our numerical radiative transfer studies.
Key words: planets and satellites: atmospheres / scattering / radiative transfer
© ESO, 2013
1. Introduction
Clouds can have a strong impact on the climate of terrestrial planetary atmospheres by either scattering the incident stellar radiation back to space (albedo effect) or by trapping the infrared radiation in the atmosphere (greenhouse effect). The extension of the habitable zone around different types of stars depends, therefore, on the presence of clouds (see e.g. Kasting et al. 1993; Selsis et al. 2007). The position of the inner boundary of the habitable zone is determined by the efficiency of the albedo effect by water droplet clouds (Kasting 1988). The outer boundary, on the other hand, might be influenced by the formation of CO2 ice clouds and their corresponding climatic impact (e.g. Kasting et al. 1993; Forget & Wordsworth 2010). Selsis et al. (2007) discuss the potential effects of CO2 clouds for the outer boundary of the habitable zone around the star Gliese 581. In particular the planet Gliese 581d has been studied with one and three-dimensional atmospheric models by Wordsworth et al. (2010b, 2011), which included a simplified model for describing CO2 clouds. Their results show that the CO2 clouds contribute to the greenhouse effect by increasing the surface temperature of Gliese 581d.
 |
Fig. 1 Real part (black line) and imaginary part (red line) of the refractive index of CO2 ice. The solid lines indicate the data published by Hansen (1997, 2005), the dashed lines mark the data compilation from Warren (1986). |
The effects of CO2 ice clouds, however, differ from those of water droplets or ice clouds due to the very different optical properties. Additionally, whether the greenhouse or albedo effect dominates for a given cloud of CO2 ice crystals depends on a variety of cloud properties. Apart from the wavelength-dependent optical depths, the crystal size is the most important quantity for determining the climatic effect of CO2 clouds (Pierrehumbert & Erlick 1998; Forget & Pierrehumbert 1997).
The only CO2 clouds observed so far in planetary atmospheres are found in the atmosphere of Mars. Most of the observed clouds near the Martian equator are composed of particles with rather small effective radii (aeff < 3 μm) and with optical depths below 0.5 in the visible wavelength region (Määttänen et al. 2010; Montmessin et al. 2007; Vincendon et al. 2011). Larger particles (aeff ~ 10 μm) are found at high latitudes during the polar night (Forget et al. 1995; Colaprete et al. 2003), for example.
Clouds composed of CO2 ice crystals are also thought to play a major role in the conditions of the early Martian atmosphere. For a dense early Mars atmosphere, Forget & Pierrehumbert (1997) have shown that CO2 ice clouds can exhibit a greenhouse effect by scattering of infrared radiation if the effective particle radii are larger than ~6 μm. Smaller particle radii yield a dominating albedo effect that leads to lower surface temperatures. A similar approach for early Mars, but including a more detailed radiative transfer treatment, was used by Mischna et al. (2000). Their results indicate that the altitude of CO2 clouds influence the efficiency of the greenhouse effect. The formation of CO2 clouds in the atmosphere of early Mars has been studied by Colaprete & Toon (2003) with a detailed microphysical model using laboratory data from Glandorf et al. (2002) for the description of the CO2 ice nucleation. The microphysical model was coupled with a time-dependent one-dimensional radiative-convective atmospheric model. According to their model calculations, the mean particle size in a dense CO2-dominated atmosphere of early Mars is of the order of 1000 μm. The results of Colaprete & Toon (2003) also indicate that the (scattering) greenhouse effect is limited overall by the evaporation of CO2 ice particles due to the large amount of latent heat released during their formation. The greenhouse effect of such CO2 clouds is thereby self-limited. Besides early Mars, CO2 clouds may have also contributed to the climate of the early Earth (see e.g. Caldeira & Kasting 1992).
In this paper we study the radiative effects of CO2 ice particles. Mie theory is used to calculate the optical properties for assumed gamma particle size distributions for a broad range of effective radii (Sect. 2). In Sect. 3 discrete ordinate radiative transfer schemes are applied to obtain the spectral reflectance and transmittance of given CO2 clouds for different optical depths. The net radiative effects of such CO2 ice clouds for the particular case of a cool M-type dwarf star are discussed in Sect. 4. To make a comparison with previous model studies on the climatic effects of CO2 ice clouds, we also apply two-stream radiative transfer methods. These additional calculations are compared with our findings obtained from a high-order discrete ordinate method.
2. Optical properties of CO2 ice particles
2.1. Refractive index of CO2 ice
Two different (main) compilations of the refractive index are available for CO2 ice covering the wavelength range from the far UV up to the microwave region and are shown in Fig. 1. The first set of this refractive index was published by Warren (1986). The imaginary part was compiled from various published measurements by different authors, connected by extrapolation and interpolation. Gaps in the data are present in the visible and far-infrared (FIR) wavelength range (see Fig. 1) where no published measurements were available at that time. Based on the compiled imaginary part, Warren (1986) calculated the corresponding real part by using the Kramers-Kronig relations (Kramers 1927; Kronig 1926).
The second compilation was published by Hansen (1997, 2005). For the imaginary part of the refractive index laboratory measurements by Hansen were used from 0.174 μm up to 333 μm. Below 0.174 μm and above 333 μm, the compilation was extended with data from Warren (1986). The corresponding real part of the refractive index was also obtained via the Kramers-Kronig relations.
The imaginary part of the refractive index is directly related to the absorption coefficient. For CO2 it shows considerable variations of about twelve orders of magnitudes throughout the whole wavelength range. Especially in the IR it exhibits a complicated oscillatory behaviour with several strong absorption bands. Besides these strong bands, the imaginary part suggests that the overall absorption of CO2 ice seems to be small in the IR in comparison to, say, water ice (see Warren & Brandt 2008, for details on the refractive index of H2O ice). Compared to the imaginary part, the real part does not show any such large variations. It, however, has two distinct large features in the IR near 4.3 μm and 15.2 μm.
Besides these two large data compilations, other measurements are also available for the astrophysically important strong absorption bands in the IR and FIR. The refractive index for these bands was published by Johnson & Atreya (1996), Hudgins et al. (1993), Ehrenfreund et al. (1996), or Baratta & Palumbo (1998), among others. The wavelengths positions of these absorption bands agree overall with those of the Hansen (1997, 2005) and Warren (1986) data compilations. However, the band widths and heights are strong functions of temperature and can, therefore, vary between the different measurements. For this study the refractive index from Hansen (1997, 2005) is used.
2.2. Mie theory calculations
To calculate the optical properties of CO2 ice particles Mie theory (Mie 1908) is used in this study by assuming a spherical particle shape. From observations in the Earth atmosphere, it is well known that water-ice crystals are rarely spherical but show a broad distribution of different particle shapes. In contrast to H2O, the unit cell of CO2 ice has a face-centred cubic structure. Therefore, as found in in-situ laboratory measurements by Behnken (1912), Wahl (1913), or Wergin et al. (1997), for instance, CO2 crystals can have cubic or octahedral shapes. Combinations of both (cuboctahedra) or more complicated shapes also occur, such as rhobic-dodecahedral crystals. In-situ measurements of the shapes of CO2-ice cloud particles in, for example, the Martian atmosphere are not yet available. Furthermore, the scattering properties of such non-spherical particles are extremely demanding to calculate so that we use the approximation of spherical particles in this study, which has also been done in all previous studies on the climatic impact of CO2 ice clouds.
Following the approach of Forget & Pierrehumbert (1997), we describe the size distribution of the cloud particles by a modified gamma distribution: 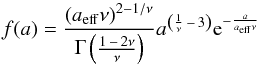 (1)where aeff is the effective radius, ν the effective variance, and Γ the gamma function. For the effective variance we adopt the value ν = 0.1 also used by Forget & Pierrehumbert (1997). The effective radii are varied between 0.1 μm and 200 μm in this study. Mie theory (Wiscombe 1980, 1979) is used to obtain the optical properties for a distinct single particle size. These optical properties are then averaged over the assumed size distribution functions. The optical properties from Mie scattering calculations are shown in Fig. 2 for four different exemplary effective particle radii and an optical depth1 of τ = 1.
(1)where aeff is the effective radius, ν the effective variance, and Γ the gamma function. For the effective variance we adopt the value ν = 0.1 also used by Forget & Pierrehumbert (1997). The effective radii are varied between 0.1 μm and 200 μm in this study. Mie theory (Wiscombe 1980, 1979) is used to obtain the optical properties for a distinct single particle size. These optical properties are then averaged over the assumed size distribution functions. The optical properties from Mie scattering calculations are shown in Fig. 2 for four different exemplary effective particle radii and an optical depth1 of τ = 1.
 |
Fig. 2 Calculated optical properties of CO2 for four different size distributions: aeff = 0.1 μm (black line), aeff = 1 μm (blue line), aeff = 20.0 μm (red line), aeff = 200 μm (green line). Upper diagram: optical depth, middle diagram: single scattering albedo ω, lower diagram: asymmetry parameter g. |
The optical depth of the larger particles is almost constant from the EUV up to the EHF wavelength region. This corresponds directly to the large-particle limit of Mie theory (Bohren & Huffman 1998), which predicts a constant value for the extinction efficiency independent of the refractive index and, therefore, from the considered material. For the largest particles (aeff = 200 μm), this limit is reached for almost the whole wavelength range up to the FIR (Fig. 2). For each size distribution the optical depths show a distinct maximum at different wavelengths. This maximum value is located near the wavelengths roughly corresponding to the particle size. For example, the particles with aeff = 20 μm (aeff = 1 μm) have their maximum optical depth in the IR at λ = 27 μm (λ = 1.2 μm). The positions of these maxima will largely determine the radiative effects of the CO2 ice particles.
The single scattering albedo is shown in the middle panel of Fig. 2. The resulting albedo values indicate that scattering dominates over a wide wavelength range for the large CO2-ice crystals. Independent of the particle size, the single scattering albedo is almost unity from the near UV up to the NIR. As a direct consequence the incident stellar radiation will mostly be scattered and not absorbed at this wavelength range.
The albedo of CO2 ice in the IR shows complicated behaviour as a function of the effective particle size. Within the strong absorption bands, the albedo can be as low as zero, indicating dominating absorption. However, outside of these bands the scattering albedo of the 200 μm and 20 μm particle size distributions are almost unity up to the EHF and FIR, respectively. The particles with aeff = 0.1 μm show much stronger variations in the single scattering albedo than the distributions with larger effective radii. In the IR, however, the single scattering albedo quickly approaches a value of almost zero for these small particles.
The single scattering albedo emphasises that the interaction of the radiation field with CO2-ice particles is quite different compared to, say, water-ice clouds. While water-ice clouds exhibit a greenhouse effect by absorption and re-emission of thermal radiation, CO2-ice particles will affect the thermal radiation mostly by scattering processes. To produce a corresponding (scattering) greenhouse effect (Forget & Pierrehumbert 1997) the thermal radiation must be scattered back to the planetary surface by the CO2-ice clouds. Thus, the efficiency of the greenhouse effect of CO2 ice also depends on the mean scattering angle and, therefore, on the value of the asymmetry parameter.
The asymmetry parameters averaged over the size distributions are shown in the lower panel of Fig. 2. The resulting asymmetry parameters are always larger than or equal to zero (Rayleigh scattering limit), which indicates dominating forward scattering. For the largest particles with aeff = 200 μm the asymmetry parameter has almost a constant value of about 0.9 from the UV up to the FIR except for strong variations in the absorption bands. With a value of about 0.8, the asymmetry for aeff = 20 μm is smaller in the wavelength regime from the UV up to the NIR. It then steadily increases up to 0.9 in the MIR before slowly declining for wavelength λ > 30 μm. Only for wavelengths larger than 300 μm the asymmetry parameter approaches the limit of Rayleigh scattering (g = 0) as expected. The smallest particles considered here (aeff = 0.1 μm) show a constant decline in g already at λ = 0.3 μm and approach the Rayleigh limit in the NIR.
3. Radiative transfer calculations
Radiative transfer calculations are performed for each particle size distribution to determine the radiative effects of the considered CO2-ice particles. In these calculations only one single cloud layer is studied, assuming plane-parallel geometry.
We consider the radiative transfer equation: 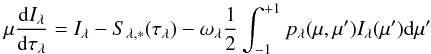 (2)with the scattering phase function pλ, the single scattering albedo ωλ, and the contribution due to an external illumination by a central star Sλ, ∗(τλ). The scattering phase function can be represented as an infinite series of Legendre polynomials (Chandrasekhar 1960)
(2)with the scattering phase function pλ, the single scattering albedo ωλ, and the contribution due to an external illumination by a central star Sλ, ∗(τλ). The scattering phase function can be represented as an infinite series of Legendre polynomials (Chandrasekhar 1960) 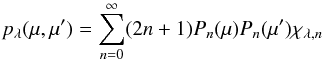 (3)with the Legendre polynomials Pn(μ) and the phase function moments χλ,n. In practice the series is truncated at a certain n = Nmax. For discrete ordinate methods the number of moments Nmax used to describe the phase function expansion series is a direct function of the number of ordinates (streams) considered (Chandrasekhar 1960).
(3)with the Legendre polynomials Pn(μ) and the phase function moments χλ,n. In practice the series is truncated at a certain n = Nmax. For discrete ordinate methods the number of moments Nmax used to describe the phase function expansion series is a direct function of the number of ordinates (streams) considered (Chandrasekhar 1960).
In this study the scattering phase function is approximated by the Henyey-Greenstein function (Henyey & Greenstein 1941). This phase function only depends on the asymmetry parameter g and is an approximation of the full Mie scattering phase function. Although lacking many detailed features and complicated structure of the Mie phase function, the Henyey-Greenstein function preserves its average quantities, most notably its asymmetry parameter. The Henyey-Greenstein phase function is usually a good replacement for the much more complicated Mie phase function in case of higher optical depths because the finer details of the Mie phase functions are effaced by the multiple scattering effects. Only the averaged quantities (such as the asymmetry parameter) then determine the overall properties of the radiation field, especially the angular integrated quantities of the intensity, such as the radiation flux. However, at very small optical depths, the results obtained by using the Henyey-Greenstein function may not be so accurate.
For the solution of the radiative transfer equation Eq. (2) we employ different discrete ordinate methods (Chandrasekhar 1960). In particular, we use the well established and very flexible atmospheric radiative transfer code DISORT (Stamnes et al. 1988). Following the previous studies of Mischna et al. (2000) or Colaprete & Toon (2003), we additionally also use two-stream methods for comparison, namely a δ-Eddington quadrature method for the incident stellar radiation and a hemispheric two-stream method in the IR (see Toon et al. 1989, for details on these methods).
The simple two-stream solution methods use only one stream for the upward and one for the downward direction. In this case only the first two moments of the phase function expansion would enter into the radiative transfer calculations. However, even the simplest phase functions, such as the Rayleigh scattering phase function, require the first three moments of the expansion for an accurate representation. Therefore, the two-stream methods, such as the δ-Eddington quadrature method or the hemispheric mean two-stream radiative transfer, cannot use the usual expansion series but must rely on different, simplified approximations of the phase function. For example, the hemispheric mean method uses a phase function of 1 + g in the forward and 1 − g in the backward direction (Toon et al. 1989).
For applying of the more general discrete ordinate solver DISORT, we use here 24 streams in all calculations, i.e. Nmax + 1 = 24. This allows for a much better description of the phase function than in the case of the two-stream methods. Such an approach usually should give more accurate results for systems dominated by angular dependent radiative transfer processes such as in particular anisotropic scattering.
To make an estimate, the scattering and absorption behaviour of atmospheric CO2 molecules and of the planetary surface has been approximately included in the radiative transfer calculations for the stellar radiation with a wavelength-dependent albedo ap,λ below the cloud layer. The albedo ap,λ roughly describes the impact of an Earth-like surface with a 2 bar CO2 atmosphere as an example. Therefore, we assume a constant (measured) Earth-like surface albedo of 0.13 (Kitzmann et al. 2010), lowered to 0.1 to account for the NIR absorption of CO2 molecules. In addition to this constant albedo describing the impact of the planetary surface, we added a Rayleigh-scattering-like albedo with the well-known λ-4 dependence to account for molecular Rayleigh scattering. The Rayleigh scattering contribution is important for central stars with higher effective temperatures, whereas the influence of the (reduced) surface albedo is important for cooler stars. Figure 4 shows the resulting (clear-sky) planetary albedo ap as a function of the effective temperatures of the central stars. We note that the surface albedo and the amount of gas that influences the Bond albedo due to Rayleigh scattering can have a strong impact on the net effect of a CO2 cloud. For example, low surface albedos (e.g. due to oceans) will yield a smaller net greenhouse effect, while a more reflective, Martian-like surface albedo can result in an increase in the scattering greenhouse effect. As mentioned by Forget & Pierrehumbert (1997), the thermal emission by the cloud itself would only make a minor contribution and is therefore neglected in our study.
 |
Fig. 3 Spectral transmittance (left column) and reflectance (right column) for two different optical depths: τ = 4 (upper panels) and τ = 10 (lower panels). Results are shown for four different size distributions: aeff = 0.1 μm (red line), aeff = 1 μm (blue line), aeff = 20.0 μm (black line), and aeff = 200 μm (green line). Calculations using DISORT (two-stream methods) are denoted by solid lines (dashed lines). |
A zenith angle for the incident stellar radiation of 60 degrees is used here, which corresponds to the mean zenith angle in a one-dimensional global average atmospheric model. As a result of our radiative transfer calculations we obtain the fraction of the incident stellar radiation in downward direction ϵs,λ at the cloud base for each wavelength λ by 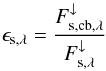 (4)where
(4)where 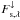 denotes the incident stellar radiation at the top of the atmosphere and
denotes the incident stellar radiation at the top of the atmosphere and 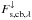 the downward shortwave radiation flux at the cloud base. The flux
the downward shortwave radiation flux at the cloud base. The flux 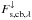 is composed of the incident stellar light that is transmitted and forward scattered through the cloud layer, as well as contributions from multiple scattering of that shortwave radiation between the cloud base and the lower atmosphere/planetary surface (approximated here by the wavelength-dependent albedo ap,λ). Additionally, we obtain the spectral transmittance of the cloud layer and the percentage of thermal IR radiation scattered back towards the surface (spectral reflectance ϵa,r,λ of the cloud) given by
is composed of the incident stellar light that is transmitted and forward scattered through the cloud layer, as well as contributions from multiple scattering of that shortwave radiation between the cloud base and the lower atmosphere/planetary surface (approximated here by the wavelength-dependent albedo ap,λ). Additionally, we obtain the spectral transmittance of the cloud layer and the percentage of thermal IR radiation scattered back towards the surface (spectral reflectance ϵa,r,λ of the cloud) given by 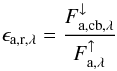 (5)where
(5)where 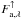 is the thermal radiation flux emitted from the atmosphere/surface and
is the thermal radiation flux emitted from the atmosphere/surface and 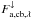 denotes the downward longwave flux at the cloud base. The incident fluxes for each wavelength are set to unity to simplify the numerical boundary conditions in the radiative transfer calculations. Obviously, this does not affect the computed values of the ratios ϵa,r,λ and ϵs,λ.
denotes the downward longwave flux at the cloud base. The incident fluxes for each wavelength are set to unity to simplify the numerical boundary conditions in the radiative transfer calculations. Obviously, this does not affect the computed values of the ratios ϵa,r,λ and ϵs,λ.
To illustrate the basic differences between the two-stream methods and DISORT, Fig. 3 summarises the resulting spectral transmittance and reflectance of the CO2 cloud for several different cloud properties. Additionally, the ratio ϵs,λ is depicted in Fig. 5.
 |
Fig. 4 Planetary albedo (clear-sky condition) as a function of the effective temperatures of the central stars. |
 |
Fig. 5 Calculated fraction of the incident stellar radiation in downward direction at the cloud base (ϵs,λ) for τ = 4. Results are shown for four different size distributions: aeff = 0.1 μm (red line), aeff = 1 μm (blue line), aeff = 20.0 μm (black line), and aeff = 200 μm (green line). Calculations using DISORT (two-stream methods) are denoted by solid lines (dashed lines). |
The smallest particles (aeff = 0.1 μm) yield an almost 100% transmittance for wavelengths larger than 1 μm even for a high optical depth of 10. This implies that their effect on the incident stellar radiation will be small if the maximum of the stellar radiation is located in this wavelength region. On the other hand, they also have a reflectance of almost zero, which means that these small particles will not yield a scattering greenhouse effect (see Fig. 3).
The transmittance of larger particles is always less than 100% and decreases at higher optical depth. The strongest negative impact on the transmittance is obtained for particles with aeff = 1 μm because these particles have their largest contribution to the opacity in this wavelength region (see Fig. 2). The transmittance is almost equal for the largest particles. This is the result of the large-particle limit discussed in Sect. 2.2 yielding the same optical properties (optical depth, asymmetry parameter, and single scattering albedo) for all big particles at short wavelengths.
The spectral reflectance for the aeff = 1 μm particles is very low (Fig. 3), especially in the wavelength region where most of the atmospheric thermal radiation is transported (λ > 8 μm). This and their strong negative impact on the transmittance suggests that these particles will more likely cool the lower atmosphere than cause a net scattering greenhouse effect.
However, larger particles can show high reflectance values in the IR wavelength range. The reflectance for aeff = 20 μm is overall almost 20% higher than for the largest particles with aeff = 200 μm. This is caused by the higher optical depth of the 20 μm particles in the thermal IR wavelength range (cf. Fig. 2) and, on the other hand, by the higher asymmetry parameter for aeff = 200 μm, which leads to a larger fraction of the thermal radiation being scattered in forward direction to space rather than backwards to the planetary surface. This indicates that the scattering greenhouse effect will be most efficient for particles with sizes comparable to the wavelength of the thermal radiation.
 |
Fig. 6 Ratios Fa,c/Fa,cs as a function of optical depth τ and the effective radius aeff of the gamma size distribution for an effective temperature of Teff = 3000 K and two values of the atmospheric temperatures Ta: 160 K (upper diagrams), 273 K (lower diagrams). Results are shown for calculations using DISORT (left column) and two-stream methods (right column). The same colour scaling is used for each diagram. (This figure is available in colour in the electronic form.) |
Figures 3 and 5 also show the results of the two-stream methods. The results indicate that the two-stream methods overestimate both
-
the transmission/scattering of stellar radiation, and
-
and the back-scattering of thermal radiation.
For the δ-Eddington two-stream method the differences are about 6% while the hemispheric mean two-stream yields deviations up to 20%. Thus, two-stream methods will in general overate the positive net scattering greenhouse effect of CO2 clouds by allowing more stellar radiation to be transmitted through the cloud layer and more thermal radiation back-scattered to the planetary surface. However, the exact climatic impact will depend on the spectral distributions of the radiation incident on the cloud. These effects are therefore discussed for different central stars and atmospheric temperatures in the following
4. Radiative impact of CO2 clouds
By using the results of the radiative transfer calculations with normalised boundary conditions presented in the previous section we now determine the net radiative effect of a given CO2 cloud for different incident stellar spectra and atmospheric temperatures.
We let 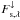 denote the downward flux from the central star incident at the top of the atmosphere which can be written as
denote the downward flux from the central star incident at the top of the atmosphere which can be written as 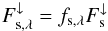 (6)where fs,λ is the normalised spectral distribution and
(6)where fs,λ is the normalised spectral distribution and 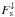 is the total (wavelength-integrated) flux. For simplicity we describe
is the total (wavelength-integrated) flux. For simplicity we describe 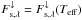 by black-body radiation with a given stellar effective temperature2Teff. Likewise, the upward thermal radiation incident at the cloud base is denoted by
by black-body radiation with a given stellar effective temperature2Teff. Likewise, the upward thermal radiation incident at the cloud base is denoted by 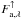 , which can also be factorised in analogy to Eq. (6):
, which can also be factorised in analogy to Eq. (6): 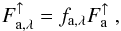 (7)where
(7)where 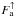 is the wavelength-integrated flux and fa,λ the corresponding normalised spectral distribution. The infrared radiation from the lower atmosphere Fa,λ is assumed to be black-body radiation of a given temperature Ta. This temperature Ta is not necessarily the surface temperature of the planet but could be any temperature below the cloud base where the atmosphere becomes transparent in the IR.
is the wavelength-integrated flux and fa,λ the corresponding normalised spectral distribution. The infrared radiation from the lower atmosphere Fa,λ is assumed to be black-body radiation of a given temperature Ta. This temperature Ta is not necessarily the surface temperature of the planet but could be any temperature below the cloud base where the atmosphere becomes transparent in the IR.
In the cloud-free case the total amount of incident shortwave radiation being absorbed by the planet is determined as usual by 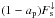 , where ap is the (cloud-free) planetary albedo (see Fig. 4) given by
, where ap is the (cloud-free) planetary albedo (see Fig. 4) given by 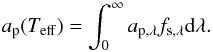 (8)Conservation of energy implies that this absorbed energy is balanced by the emitted (clear sky – cs) thermal flux
(8)Conservation of energy implies that this absorbed energy is balanced by the emitted (clear sky – cs) thermal flux 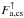 :
: 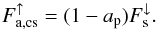 (9)In contrast to a clear sky, the amount of shortwave radiation absorbed by the planet in the cloudy case (c) is given by
(9)In contrast to a clear sky, the amount of shortwave radiation absorbed by the planet in the cloudy case (c) is given by 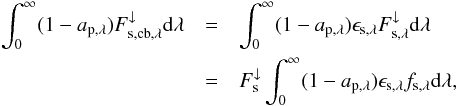 (10)using Eq. (4) for ϵs,λ and Eq. (6) for
(10)using Eq. (4) for ϵs,λ and Eq. (6) for 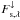 .
.
Thus, for each considered stellar effective temperature we calculate the total percentage ϵs of the incident shortwave radiation being absorbed by the planet according to 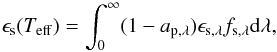 (11)using an adaptive Gauss-Kronrod quadrature method. On the other hand, the amount of thermal radiation scattered back towards the surface by the cloud is given by (see Eqs. (5) and (7))
(11)using an adaptive Gauss-Kronrod quadrature method. On the other hand, the amount of thermal radiation scattered back towards the surface by the cloud is given by (see Eqs. (5) and (7)) 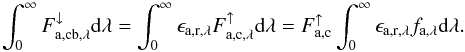 (12)Therefore, the total percentage ϵa,r of the upwelling thermal flux
(12)Therefore, the total percentage ϵa,r of the upwelling thermal flux 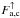 back-scattered by the cloud is obtained by
back-scattered by the cloud is obtained by 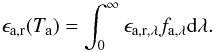 (13)The wavelength region (14 μm − 16 μm) around the 15 μm absorption band of CO2 is excluded in this integration. Both, the CO2 gas molecules and the CO2 cloud can strongly absorb and re-emit thermal radiation in that particular spectral region, which might result in a classical greenhouse effect. Because the cloud’s thermal emission, as well as the absorption and thermal emission by CO2 molecules, is not considered in our radiative transfer calculations (see previous section), this wavelength region is omitted from the analysis of the scattering greenhouse effect. Calculations by, say, Forget & Pierrehumbert (1997), which also included the CO2 gas, however, showed that the contribution of this spectral region to the greenhouse effect of the CO2 cloud seems to be small.
(13)The wavelength region (14 μm − 16 μm) around the 15 μm absorption band of CO2 is excluded in this integration. Both, the CO2 gas molecules and the CO2 cloud can strongly absorb and re-emit thermal radiation in that particular spectral region, which might result in a classical greenhouse effect. Because the cloud’s thermal emission, as well as the absorption and thermal emission by CO2 molecules, is not considered in our radiative transfer calculations (see previous section), this wavelength region is omitted from the analysis of the scattering greenhouse effect. Calculations by, say, Forget & Pierrehumbert (1997), which also included the CO2 gas, however, showed that the contribution of this spectral region to the greenhouse effect of the CO2 cloud seems to be small.
According to the conservation of energy, the upwelling thermal flux in the cloudy case 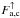 is balanced by the absorbed downward shortwave flux
is balanced by the absorbed downward shortwave flux 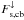 and back-scattered thermal flux
and back-scattered thermal flux 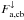 :
: 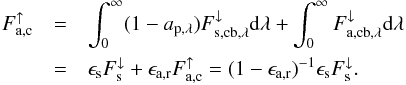 (14)We therefore define the ratio of the thermal radiation fluxes of the cloudy (Fa,c, Eq. (15)) and clear-sky case (Fa,cs, Eq. (9)):
(14)We therefore define the ratio of the thermal radiation fluxes of the cloudy (Fa,c, Eq. (15)) and clear-sky case (Fa,cs, Eq. (9)): 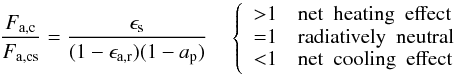 (15)which gives an indication of the net radiative effect of the cloud layer. For a ratio greater than one, the cloud has a net heating effect on the atmosphere below the cloud, while for values lower than one the lower atmosphere is cooled by the cloud layer. A ratio of exactly one represents radiatively neutral cloud particles.
(15)which gives an indication of the net radiative effect of the cloud layer. For a ratio greater than one, the cloud has a net heating effect on the atmosphere below the cloud, while for values lower than one the lower atmosphere is cooled by the cloud layer. A ratio of exactly one represents radiatively neutral cloud particles.
To study the effectiveness of the (net) scattering greenhouse effect, several calculations are performed for a broad range of stellar effective temperatures between 8000 K and 2000 K. Since cool M-type dwarf stars seem to be particularly important in view of the detectability of (potentially) habitable planets (Rauer et al. 2011), detailed results for a low effective stellar temperature of 3000 K are presented in the next section.
For the thermal radiation we assume two limiting cases: first we consider the atmosphere below the cloud to be optically thin, such that Ta would correspond to the surface temperature of a habitable planet at the outer boundary of the habitable zone (i.e. Ta = 273 K, freezing point of water). In the second case we consider the atmosphere below the cloud to be opaque such that only thermal radiation directly from below the cloud base reaches the cloud. In this case we adopt a temperature Ta = 160 K that roughly corresponds to the temperature where CO2 would condense (cf. model calculations of Mischna et al. 2000; or Colaprete & Toon 2003).
 |
Fig. 7 Ratios Fa,c/Fa,cs as a function of optical depth τ for an effective temperature of Teff = 3000 K and the two different atmospheric temperatures: Ta = 160 K (upper diagram) and Ta = 273 K (lower diagram). Results are shown for different size distributions in each diagram: aeff = 25 μm (black line, upper diagram), aeff = 17 μm (black line, lower diagram), aeff = 0.1 μm (red line), aeff = 1.0 μm (blue line), and aeff = 200 μm (green line). Calculations using DISORT (two-stream methods) are denoted by solid lines (dashed lines). |
 |
Fig. 8 Ratios Fa,c/Fa,cs as a function of effective particle radius aeff for an effective temperature of Teff = 3000 K and the two different atmospheric temperatures: Ta = 160 K (upper diagram) and Ta = 273 K (lower diagram). Results are shown for different values of the optical depth τ in each diagram: τ = 0.5 (black line), τ = 4 (red line), and τ = 10 (blue line). Calculations using DISORT (two-stream methods) are denoted by solid lines (dashed lines). |
4.1. Results for a cool M-dwarf star
In the following we discuss our results for a stellar effective temperature of 3000 K, roughly corresponding to a cool M5 dwarf star. The ratios Fa,c/Fa,cs are shown in Fig. 6 as a function of the optical depth τ and effective particle radius aeff for both considered atmospheric temperatures. The results of two-stream radiative transfer calculations are also shown for comparison. For a more detailed analysis, different slices through the two-dimensional parameter space are shown in Figs. 7 and 8 for several different particle sizes and optical depths.
The results depicted in Figs. 6–8 suggest that the CO2 particles have a negative or neutral impact over a wide range of the considered parameter space. Only particles with sizes comparable to the wavelength of the thermal radiation contribute to a net greenhouse effect if the optical depth is not too large. For higher optical depths, again a cooling effect is found. This kind of behaviour as a function of the optical depth is consistent with the results of Mischna et al. (2000) and Colaprete & Toon (2003).
Thus, CO2 ice clouds have a certain parameter range of particle radii and optical depths where the heating effect is most efficient. These particle radii are a function of temperature Ta and increase with decreasing temperature; i.e., the most efficient particle radius is about 25 μm (17 μm) for Ta = 160 K (Ta = 273 K). Apart from the shift in the particle size, the efficiency also increases with lower atmospheric temperature, which leads to a stronger scattering greenhouse effect if the cloud layer were, say, located at higher altitudes within the atmosphere (cf. Mischna et al. 2000). However, even the highest ratios are only slightly larger than 1; i.e., the resulting quantitative radiative forcing would be small.
For larger or smaller particle sizes a cooling effect is found that is very strong for particles with effective radii near 1 μm. This is caused by the large optical depth of these particles at short wavelengths where the maximum of the incident stellar radiation is located (see Sect. 3 and Fig. 3). These kinds of particles would lead to massive cooling if present in the atmosphere.
 |
Fig. 9 Ratios Fa,c/Fa,cs as a function of optical depth τ and the effective radius aeff of the gamma size distribution for three different effective temperatures of the central star: 7300 K (upper diagrams), 5800 K (middle diagrams), and 3000 K (lower diagrams). Results are shown for calculations using DISORT (left column) and two-stream methods (right column). The same colour scheme is used in each diagram. (This figure is available in colour in the electronic form.) |
Very small particles (0.1 μm) are almost radiatively neutral, independent of the considered optical depth. Even at τ = 20 they show only a weak cooling effect. The reason for this behaviour is that these particles make their main contribution to the optical depth at very short wavelengths (cf. Sect. 3). Since the maximum of the incident stellar radiation for the chosen low effective temperature is located near λ = 1 μm the impact of these small particles is very small. This effect is similar to the known low efficiency of Rayleigh scattering by the gas molecules for cool M-type stars.
According to the comparison of the different radiative transfer methods (Figs. 6–8) the efficiency of warming by CO2-ice clouds differs quite noticeably for different approximations in the numerical treatment that solves the radiative transfer equation. Consistent with previous reports of Forget & Pierrehumbert (1997) or Mischna et al. (2000), among others, the two-stream methods predict a strong scattering greenhouse effect at medium optical depths near τ = 4. In contrast to this, the application of DISORT, however, results in an almost radiatively neutral cloud. As already mentioned, only at small optical depths near 0.5 is a slight positive effect found that is much less than the two-stream results. Obviously the largest deviations occur for particle sizes that roughly correspond to the wavelength of the thermal radiation because this is the region where Mie scattering is important. The hemispheric mean two-stream method in particular seems to yield quite inaccurate results compared to a more elaborate discrete ordinate radiative transfer. The errors are also clearly a function of the optical depth. For lower optical depths the differences are small, whereas they are greatest in the region of the most efficient greenhouse effect. The deviations decrease again for more increasing optical depths.
4.2. Other main sequence stars
Figure 9 shows the ratio Fa,c/Fa,cs for three different stellar effective temperatures: 7300 K (comparable to an F2V star), 5800 K (G2V star), and 3000 K (M5V star). All figures use the same colour scheme to make them directly comparable. Results are only shown for Ta = 160 K. As noted in the previous section, the values of Fa,c/Fa,cs would be lower for higher atmospheric temperatures. Additionally, Fig. 10 shows the resulting ratios as a function of the effective temperature for several chosen values of the particles effective radii and optical depths.
The results in Fig. 9 indicate that the most efficient particle size for a net scattering greenhouse effect does not vary with the type of the central star. Rather, it is only a function of the lower atmospheric temperatures Ta. As discussed for Ta = 160 K, the corresponding effective particle size is about 25 μm. As shown in Fig. 10, this particle size yields a small net greenhouse effect for cool stars which increases towards higher effective temperatures. This increase is caused by the higher (clear-sky) planetary albedos due to the stronger Rayleigh scattering at shorter wavelengths.
Other particle sizes, however, exhibit larger variations as a function of the central star temperature. For example, lower ratios of Fa,c/Fa,cs are obtained for increasing stellar effective temperatures in case of the particles with aeff = 0.1 μm. For cooler stars they are almost radiatively neutral, whereas they show a strong cooling effect for higher stellar temperatures. This is directly related to the optical properties (see Fig. 2) and the resulting transmittance from the radiative transfer calculations. As depicted in Fig. 3 a clear decline at shorter wavelength (λ < 1 μm) is present in the spectral transmittance, which makes the albedo effect more efficient at higher effective temperatures of the central star. The greatest negative impact is still obtained for particle size distributions with effective radii close to 1 μm. This result is almost independent of the stellar effective temperatures.
As already discussed for the cool M-type star, the two-stream methods again strongly overestimate the positive effect of the CO2 cloud. The ratios Fa,c/Fa,cs obtained by DISORT are in every case less than those found by the two-stream methods. Especially at medium optical depths of τ = 4, large deviations from the more accurate radiative transfer calculations are found. Here, the two-stream methods yield a large scattering greenhouse effect, which also increases at higher stellar effective temperatures. For cooler stars, a less efficient greenhouse effect is obtained (see also Wordsworth et al. 2011). At smaller optical depths, the differences between the two different radiative transfer methods are again smaller. These results indicate that the scattering greenhouse effect was most likely overrated in all previous model studies of the climatic impact of CO2 clouds.
 |
Fig. 10 Ratios Fa,c/Fa,cs as a function of the stellar effective temperature. Results are shown for different values of the optical depth τ and effective radii of the gamma size distributions. Black line: aeff = 25 μm,τ = 4, blue line: aeff = 25 μm,τ = 0.5, red line: aeff = 0.1 μm,τ = 4, green line: aeff = 1 μm,τ = 4. Calculations using DISORT are denoted by solid lines, two-stream methods are marked by dashed lines. |
5. Summary
In this study we investigated the radiative effects of CO2 ice clouds. The particle size distribution were assumed to be gamma distributions with different effective radii. Mie theory was used to calculate the optical properties (optical depths, single scattering albedo, and asymmetry parameter) of CO2 ice particles with effective radii from 0.1 μm to 200 μm. Radiative transfer calculations using different discrete ordinate methods were performed to obtain the spectral reflectance and transmittance of a single layer of CO2 ice particles. In particular, a high-order discrete ordinate solver (DISORT) was employed. Additionally, we also applied simpler two-stream radiative transfer methods for comparison with previous studies. We then studied the net radiative effect of the CO2 ice cloud for different spectral distributions of the incident stellar and the atmospheric thermal radiation.
A net scattering greenhouse effect by CO2 clouds was only obtained for very specific cloud properties. Only particles with sizes comparable to the wavelength of the thermal radiation incident on the cloud base yielded a net greenhouse effect. For larger or smaller particles, a net cooling effect was found. In particular, particles with aeff ~ 1 μm lead to strong cooling. Very small particles (aeff = 0.1 μm) were found to be radiatively neutral for very cool stars even at high optical depths. In general, the net heating effect of the CO2 cloud increases with increasing stellar effective temperatures. For cooler stars, however, even the most efficient particle sizes yield only a radiatively neutral cloud.
As suggested by Eq. (15), the planetary surface albedo and the albedo due to molecular Rayleigh scattering can have a strong impact on the net climatic effect of a CO2 cloud. While planets with low surface albedos (e.g. ocean planets) would result in a weaker net heating effect, planets with, e.g., a Martian-like surface albedo can show an increased scattering greenhouse effect. Increasing the amount of CO2 gas, on the other hand, would yield a stronger Rayleigh scattering but also more NIR absorption of the stellar radiation. Thus, for central stars with higher effective temperatures one can expect an increased net heating effect by the cloud, while for cooler M-type stars, the CO2 cloud would remain more or less radiatively neutral.
We also compared these results with those of two-stream radiative transfer calculations. Here, a strong greenhouse effect was found at optical depth larger than one and smaller than ten for particle sizes comparable to the wavelength of the thermal radiation, which agrees with, e.g., Forget & Pierrehumbert (1997) or Mischna et al. (2000). Overall, the two-stream methods yielded large deviations from the calculations using a higher order discrete ordinate method in the important parameter range where a net greenhouse effect was obtained in previous model studies.
Therefore, all these previous studies of the effects of CO2 ice clouds on the outer boundary of the habitable zone that were restricted to two-stream approximations overestimated the positive scattering greenhouse effect. It is evident that more accurate radiative transfer methods are necessary to accurately describe the radiative effects of CO2 clouds. Our study suggests that the scattering greenhouse effect still occurs. However, it is much weaker than previously expected and only efficient for a narrow range of parameters (optical depths, particle sizes). Therefore, we suggest using higher order radiative transfer schemes in future atmospheric model calculations, which include CO2 ice clouds.
In combination with the reduced classical greenhouse effect by CO2 gas molecules due to a revised description of the collisional induced absorption reported by Wordsworth et al. (2010a), this indicates that the outer boundary of the habitable zone should be located closer to the central star than previously considered (e.g. Selsis et al. 2007). A quantitative analysis of the scattering greenhouse effect of CO2 clouds and their impact on the position of the outer boundary of the habitable zone would, however, require an atmospheric model for more detailed calculations.
We used a zenith angle of 60 degree in this study, which corresponds to the global average zenith angle for a one-dimensional model. By using smaller zenith angles (e.g. locally in a three-dimensional atmospheric model), one could still obtain higher ratios of Fa,c/Fa,cs, resulting in a greater scattering greenhouse effect.
Acknowledgments
The authors thank Gary Hansen for providing his refractive index of CO2 ice and Tom Rother, as well as Philip von Paris and Mareike Godolt, for the fruitful discussions. Additionally, we thank the referee Francois Forget for his suggestions for improving the manuscript. This work has been partly supported by the research alliance Planetary Evolution and Life of the Helmholtz Association (HGF).
References
- Baratta, G. A., & Palumbo, M. E. 1998, J. Opt. Soc. Am. A, 15, 3076 [Google Scholar]
- Behnken, H. E. 1912, Phys. Rev. (Series I), 35, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Bohren, C. F., & Huffman, D. R. 1998, Absorption and Scattering of Light by Small Particles (Weinheim: Wiley-VH) [Google Scholar]
- Caldeira, K., & Kasting, J. F. 1992, Nature, 359, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1960, Radiative transfer (Dover Publications Inc.) [Google Scholar]
- Colaprete, A., & Toon, O. B. 2003, J. Geophys. Res. Planets, 108, 5025 [NASA ADS] [CrossRef] [Google Scholar]
- Colaprete, A., Haberle, R. M., & Toon, O. B. 2003, J. Geophys. Res. Planets, 108, 5081 [Google Scholar]
- Ehrenfreund, P., Boogert, A. C. A., Gerakines, P. A., et al. 1996, A&A, 315, L341 [NASA ADS] [Google Scholar]
- Forget, F., & Pierrehumbert, R. T. 1997, Science, 278, 1273 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Forget, F., & Wordsworth, R. D. 2010, in Pathways Towards Habitable Planets, eds. V. Coudé Du Foresto, D. M. Gelino, & I. Ribas, ASP Conf. Ser., 430, 55 [Google Scholar]
- Forget, F., Hansen, G. B., & Pollack, J. B. 1995, J. Geophys. Res., 1002, 21219 [NASA ADS] [CrossRef] [Google Scholar]
- Glandorf, D. L., Colaprete, A., Tolbert, M. A., & Toon, O. B. 2002, Icarus, 160, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, G. B. 1997, J. Geophys. Res., 102, 21569 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, G. B. 2005, J. Geophys. Res. Planets, 110, 11003 [Google Scholar]
- Henyey, L. G., & Greenstein, J. L. 1941, ApJ, 93, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Hudgins, D. M., Sandford, S. A., Allamandola, L. J., & Tielens, A. G. G. M. 1993, ApJS, 86, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, B. R., & Atreya, S. K. 1996, Icarus, 119, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Kasting, J. F. 1988, Icarus, 74, 472 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kasting, J. F., Whitmire, D. P., & Reynolds, R. T. 1993, Icarus, 101, 108 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kitzmann, D., Patzer, A. B. C., von Paris, P., et al. 2010, A&A, 511, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kramers, H. A. 1927, Atti Cong. Intern. Fisica, 2, 545 [Google Scholar]
- Kronig, R. D. L. 1926, J. Opt. Soc. Am., 12, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Määttänen, A., Montmessin, F., Gondet, B., et al. 2010, Icarus, 209, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Mie, G. 1908, Annalen der Physik, 330, 377 [Google Scholar]
- Mischna, M. A., Kasting, J. F., Pavlov, A., & Freedman, R. 2000, Icarus, 145, 546 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Montmessin, F., Gondet, B., Bibring, J.-P., et al. 2007, J. Geophys. Res. Planets, 112, 11 [Google Scholar]
- Pierrehumbert, R. T., & Erlick, C. 1998, J. Atmos. Sci., 55, 1897 [NASA ADS] [CrossRef] [Google Scholar]
- Rauer, H., Gebauer, S., Paris, P. V., et al. 2011, A&A, 529, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Selsis, F., Kasting, J. F., Levrard, B., et al. 2007, A&A, 476, 1373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stamnes, K., Tsay, S.-C., Jayaweera, K., & Wiscombe, W. 1988, Appl. Opt., 27, 2502 [Google Scholar]
- Toon, O. B., McKay, C. P., Ackerman, T. P., & Santhanam, K. 1989, J. Geophys. Res., 94, 16287 [NASA ADS] [CrossRef] [Google Scholar]
- Vincendon, M., Pilorget, C., Gondet, B., Murchie, S., & Bibring, J.-P. 2011, J. Geophys. Res. Planets, 116, [CrossRef] [Google Scholar]
- Wahl, W. 1913, Roy. Soc. London Proc. Ser. A, 89, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, S. G. 1986, Appl. Opt., 25, 2650 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, S. G., & Brandt, R. E. 2008, J. Geophys. Res., 26, 14220 [Google Scholar]
- Wergin, W. P., Foster, J. L., Chang, A. T. C., et al. 1997, Microsc. Microanalysis, 3, 1235 [Google Scholar]
- Wiscombe, W. J. 1979, MIE scattering calculations, advances in technique and fast, vector-shaped computer codes, Tech. Rep. (Boulder: NCAR Library) [Google Scholar]
- Wiscombe, W. J. 1980, Appl. Opt., 19, 1505 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wordsworth, R., Forget, F., & Eymet, V. 2010a, Icarus, 210, 992 [NASA ADS] [CrossRef] [Google Scholar]
- Wordsworth, R. D., Forget, F., Selsis, F., et al. 2010b, A&A, 522, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wordsworth, R. D., Forget, F., Selsis, F., et al. 2011, ApJ, 733, L48 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Real part (black line) and imaginary part (red line) of the refractive index of CO2 ice. The solid lines indicate the data published by Hansen (1997, 2005), the dashed lines mark the data compilation from Warren (1986). |
| In the text | |
 |
Fig. 2 Calculated optical properties of CO2 for four different size distributions: aeff = 0.1 μm (black line), aeff = 1 μm (blue line), aeff = 20.0 μm (red line), aeff = 200 μm (green line). Upper diagram: optical depth, middle diagram: single scattering albedo ω, lower diagram: asymmetry parameter g. |
| In the text | |
 |
Fig. 3 Spectral transmittance (left column) and reflectance (right column) for two different optical depths: τ = 4 (upper panels) and τ = 10 (lower panels). Results are shown for four different size distributions: aeff = 0.1 μm (red line), aeff = 1 μm (blue line), aeff = 20.0 μm (black line), and aeff = 200 μm (green line). Calculations using DISORT (two-stream methods) are denoted by solid lines (dashed lines). |
| In the text | |
 |
Fig. 4 Planetary albedo (clear-sky condition) as a function of the effective temperatures of the central stars. |
| In the text | |
 |
Fig. 5 Calculated fraction of the incident stellar radiation in downward direction at the cloud base (ϵs,λ) for τ = 4. Results are shown for four different size distributions: aeff = 0.1 μm (red line), aeff = 1 μm (blue line), aeff = 20.0 μm (black line), and aeff = 200 μm (green line). Calculations using DISORT (two-stream methods) are denoted by solid lines (dashed lines). |
| In the text | |
 |
Fig. 6 Ratios Fa,c/Fa,cs as a function of optical depth τ and the effective radius aeff of the gamma size distribution for an effective temperature of Teff = 3000 K and two values of the atmospheric temperatures Ta: 160 K (upper diagrams), 273 K (lower diagrams). Results are shown for calculations using DISORT (left column) and two-stream methods (right column). The same colour scaling is used for each diagram. (This figure is available in colour in the electronic form.) |
| In the text | |
 |
Fig. 7 Ratios Fa,c/Fa,cs as a function of optical depth τ for an effective temperature of Teff = 3000 K and the two different atmospheric temperatures: Ta = 160 K (upper diagram) and Ta = 273 K (lower diagram). Results are shown for different size distributions in each diagram: aeff = 25 μm (black line, upper diagram), aeff = 17 μm (black line, lower diagram), aeff = 0.1 μm (red line), aeff = 1.0 μm (blue line), and aeff = 200 μm (green line). Calculations using DISORT (two-stream methods) are denoted by solid lines (dashed lines). |
| In the text | |
 |
Fig. 8 Ratios Fa,c/Fa,cs as a function of effective particle radius aeff for an effective temperature of Teff = 3000 K and the two different atmospheric temperatures: Ta = 160 K (upper diagram) and Ta = 273 K (lower diagram). Results are shown for different values of the optical depth τ in each diagram: τ = 0.5 (black line), τ = 4 (red line), and τ = 10 (blue line). Calculations using DISORT (two-stream methods) are denoted by solid lines (dashed lines). |
| In the text | |
 |
Fig. 9 Ratios Fa,c/Fa,cs as a function of optical depth τ and the effective radius aeff of the gamma size distribution for three different effective temperatures of the central star: 7300 K (upper diagrams), 5800 K (middle diagrams), and 3000 K (lower diagrams). Results are shown for calculations using DISORT (left column) and two-stream methods (right column). The same colour scheme is used in each diagram. (This figure is available in colour in the electronic form.) |
| In the text | |
 |
Fig. 10 Ratios Fa,c/Fa,cs as a function of the stellar effective temperature. Results are shown for different values of the optical depth τ and effective radii of the gamma size distributions. Black line: aeff = 25 μm,τ = 4, blue line: aeff = 25 μm,τ = 0.5, red line: aeff = 0.1 μm,τ = 4, green line: aeff = 1 μm,τ = 4. Calculations using DISORT are denoted by solid lines, two-stream methods are marked by dashed lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


