| Issue |
A&A
Volume 556, August 2013
|
|
|---|---|---|
| Article Number | A148 | |
| Number of page(s) | 15 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201321860 | |
| Published online | 09 August 2013 | |
Three-dimensional modeling of radiative disks in binaries
Department of Physics & AstronomyUniversity of
Padova,
via Marzolo 8,
35131
Padova,
Italy
e-mail:
picogna@pd.infn.it
Received:
8
May
2013
Accepted:
25
June
2013
Context. Circumstellar disks in binaries are perturbed by the companion gravity causing significant alterations of the disk morphology. Spiral waves due to the companion tidal force also develop in the vertical direction and affect the disk temperature profile. These effects may significantly influence the process of planet formation.
Aims. We perform 3D numerical simulations of disks in binaries with different initial dynamical configurations and physical parameters. Our goal is to investigate their evolution and their propensity to grow planets.
Methods. We use an improved version of the SPH code VINE modified to better account for momentum and energy conservation via variable smoothing and softening length. The energy equation includes a flux-limited radiative transfer algorithm. The disk cooling is obtained with the use of “boundary particles” populating the outer surfaces of the disk and radiating to infinity. We model a system made of star/disk + star/disk where the secondary star (and relative disk) is less massive than the primary.
Results. The numerical simulations performed for different values of binary separation and disk density show that trailing spiral shock waves develop when the stars approach their pericenter. Strong hydraulic jumps occur at the shock front, in particular for small separation binaries, creating breaking waves, and a consistent mass stream between the two disks. Both shock waves and mass transfer cause significant heating of the disk. At apocenter these perturbations are reduced and the disks are cooled down and less eccentric.
Conclusions. The disk morphology is substantially affected by the companion perturbations, in particular in the vertical direction. The hydraulic jumps may slow down or even halt the dust coagulation process. The disk is significantly heated up by spiral waves and mass transfer, and the high gas temperature may prevent the ice condensation by moving the “snow line” outward. The disordered motion triggered by the spiral waves may, on the other hand, favor direct formation of large planetesimals from pebbles. The strength of the hydraulic jumps, disk heating, and mass exchange depends on the binary separation, and for larger semi-major axes, the tidal spiral pattern is substantially reduced. The environment then appears less hostile to planet formation.
Key words: protoplanetary disks / binaries: close / planets and satellites: formation / hydrodynamics
© ESO, 2013
1. Introduction
According to Duquennoy & Mayor (1991), more than 50% of G type stars are in multiple systems. The multiplicity appears to depend on the stellar mass with a higher frequency for massive stars, roughly 70% (Mason et al. 1998), and a lower frequency of about 30% for less massive M stars (see Lada 2006 for a review of the data). It is also suspected that most stars could form in binary or higher multiplicity systems disintegrating at later times via dynamical interactions or decay (Reipurth 2000). As for single stars, binary stars in the early stages of their evolution are surrounded by protoplanetary disks. An example is the L1551 IRS 5 system, which contains two protostars, each surrounded by a circumstellar disk (Rodríguez et al. 1998; Osorio et al. 2003). Spatially resolved observations of disks in binaries in the Orion nebula cluster (Daemgen et al. 2012) suggest that the fraction of circumstellar disks around individual components of binary systems is about 40%, only slightly lower than that for single stars (roughly 50%). This is possibly due to the impact of the companion star on the disk evolution which causes disk truncation, eccentric shape, warping, and heating (Nelson 2000; Kley & Nelson 2008; Paardekooper et al. 2008; Marzari et al. 2009, 2012).
The physical properties of circumstellar disks are relevant for forming planetary systems. Perturbed disks, like those in close binaries, may affect planet accretion at different stages, producing a population of planets that differ from those around single stars. The process by which dust particles evolve into kilometer-sized planetesimals, which is still not fully understood for single stars (Weidenschilling 1977; Blum & Wurm 2008), may be altered in disks around binaries. Spiral waves excited by the companion perturbations may, via Epstein drag coupling, affect the relative velocity of the colliding particles, the drift rate towards the star and the vertical settling speed. All these parameters strongly influence the collisional sticking process and dust agglomeration into larger bodies, and the binary perturbations appear to act against a fast dust coagulation. On the other hand, the large scale motions in these disks, excited by the gravitational pull of the companion star, may locally favor concentration and subsequent accumulation of dust and pebbles directly into planetesimals (Johansen et al. 2007; Cuzzi et al. 2008). Even the planetesimal accretion phase appears more complex in close binary systems due to the increase in the mutual impact velocity between the planetesimals caused by the combined action of secular perturbations by the companion star and gas drag effects (Marzari & Scholl 2000; Thébault et al. 2004, 2006, 2008; Kley & Nelson 2008; Thébault et al. 2009; Marzari et al. 2009, 2012; Xie & Zhou 2009; Xie et al. 2010; Paardekooper et al. 2008).
In spite of all these additional complications, which seem to lower the efficiency of planet formation, about 50 planets are known to date in binary stars, among which are also the newly discovered planet in the α Centauri system (Dumusque et al. 2012). In addition, according to Bonavita & Desidera (2007) and Mugrauer & Neuhäuser (2009), the frequency of planets in binaries do not appear to differ much from that of planets orbiting single stars. However, it is reasonable to expect that the differences in the two initial steps of planet formation – dust coagulation and planetesimal accretion – would have a significant impact on the final physical properties and dynamical architecture of planetary systems around single and binary stars. For example, Zucker & Mazeh (2002); Eggenberger et al. (2004); Mugrauer et al. (2005); Desidera & Barbieri (2007) find some discrepancies in the mass-period and eccentricity-period diagrams of planets in binaries and single stars.
The dynamical structure of circumstellar disks in binaries is crucial not only to understand the processes of planet formation but also to predict the migration of planets. Their morphology, temperature, and density profiles are significantly affected by the excitation of eccentric modes (Paardekooper et al. 2008; Kley & Nelson 2008; Marzari et al. 2009), shock waves formation, and mass exchange (Nelson 2000). These differences, compared to disks around single stars, may influence the migration speed and direction. Population synthesis calculations, like those described in Mordasini et al. (2012), have shown that differences in migration may lead to distinct predictions concerning the final orbital and mass distributions of planets. To understand the architecture of planetary systems in binaries, in particular those with small separations, it is then important to know the morphology and physical state of circumstellar disks in the crucial phases of planet growth, i.e., during dust coagulation and planetesimal accumulation.
In this paper we model the 3D evolution of circumstellar disks in binaries using the SPH code VINE (Wetzstein et al. 2009; Nelson et al. 2009). The original code had been upgraded to improve both momentum and energy conservation. In addition, to better model optically thick disks in their initial stages of evolution, we have implemented a radiative energy equation. This is particularly recommended since the companion star induces strong spiral waves in the disks that may generate local strong shocks and compressional heating violating the local isothermal approximation. In addition, these shocks may also produce notable effects in the vertical direction, potentially affecting the dust coagulation process.
In Sect. 2 we focus on the upgrades to the SPH code VINE and on the implementation of the radiation hydrodynamics. In Sect. 3 we describe the initial conditions of the simulations concerning different density disks in close and wide binary configurations. In Sect. 4 we analyze the outcomes of the simulations and discuss some theoretical implications. Finally in Sect. 5 we summarize our results, discuss their relevance for planet formation, and comment on possible future improvements in the study of disks in binaries.
2. The model
To compute the evolution of the disks surrounding the stars in the binary system, we use the hydrodynamical code VINE (Wetzstein et al. 2009; Nelson et al. 2009). It is based on the smoothed particle hydrodynamics (SPH) algorithm that solves the equations of fluid dynamics by replacing the fluid with a set of particles (Gingold & Monaghan 1977).
We have updated the code with some important features that improve momentum and energy conservation during the simulations. In addition, we have implemented a fully radiative approach so that the viscous heating is diffused in the disk and emitted at the disk’s outer borders. The flux-limited approximation, as described in Levermore & Pomraning (1981), is used in the code. Here below we describe in detail the substantial modifications to the code.
2.1. Variable smoothing length
The basic idea of the variable smoothing length method (Price & Monaghan 2004; Springel
& Hernquist 2002) is that the smoothing length h is
related to the particle coordinates through a relation between h and the
particle density ρ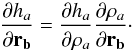 (1)The ansatz on the
dependence of h on ρ is of the form
(1)The ansatz on the
dependence of h on ρ is of the form 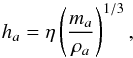 (2)where
η is a dimensionless parameter that specifies the size of the smoothing
length in terms of averaged particle spacing (setting η to 1.2 gives in
3D about 60 particles around any given one). The derivative of the above equation respect
to ρ gives
(2)where
η is a dimensionless parameter that specifies the size of the smoothing
length in terms of averaged particle spacing (setting η to 1.2 gives in
3D about 60 particles around any given one). The derivative of the above equation respect
to ρ gives 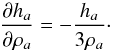 (3)The density definition in
VINE is given by
(3)The density definition in
VINE is given by 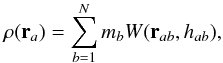 (4)where
rab = |ra − rb |
and
hab = (ha + hb)/2,
so we have a nonlinear equation to be solved for both h and
ρ.
(4)where
rab = |ra − rb |
and
hab = (ha + hb)/2,
so we have a nonlinear equation to be solved for both h and
ρ.
To find a self-consistent solution to Eqs. (2)–(4), we have to solve the
following equation 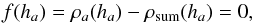 (5)with a Newton-Raphson
method until convergence is reached. The derivative of the function
f(ha) is
(5)with a Newton-Raphson
method until convergence is reached. The derivative of the function
f(ha) is
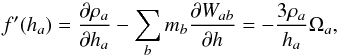 (6)where
(6)where
![\begin{equation} \Omega_a = \left [ 1 - \frac{\partial h_a } {\partial \rho_a} \sum_b m_b \frac {\partial W_{ab}}{\partial h} \right], \end{equation}](/articles/aa/full_html/2013/08/aa21860-13/aa21860-13-eq16.png) (7)accounts for the gradient
of the smoothing length. Convergence is assumed to occur when
| hnew − h|/h0 < ϵ = 10-3.
Due to the dependence of h on ρ, the equations of motion
are changed accordingly
(7)accounts for the gradient
of the smoothing length. Convergence is assumed to occur when
| hnew − h|/h0 < ϵ = 10-3.
Due to the dependence of h on ρ, the equations of motion
are changed accordingly 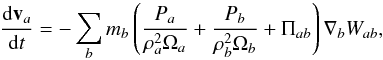 (8)where
Πab is the artificial viscous pressure term. The
continuity equation becomes
(8)where
Πab is the artificial viscous pressure term. The
continuity equation becomes 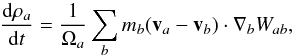 (9)and the energy
equation
(9)and the energy
equation 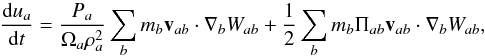 (10)where
vab = va − vb.
(10)where
vab = va − vb.
The artificial viscosity term is added a) to correctly model shock waves that inject
entropy into the flow over distances that are much shorter than a smoothing length and b)
to simulate the evolution of viscous disks. The Π term broadens the shock over a small
number of smoothing lengths and correctly resolves it ensuring at the same time that the
Rankine-Hugoniot equations are satisfied. In this way it prevents discontinuities in
entropy, pressure, density, and velocity fields. SPH simulations (Monaghan & Gingold 1983) include both a linear term (bulk
viscosity), which dissipates kinetic energy as particles approach each other to reduce
subsonic velocity oscillations following a shock, and a quadratic term (von
Neumann-Richtmyer viscosity), which convert kinetic energy to thermal energy preventing
particle interpenetration in shocks
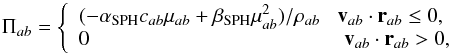 (11)where
all quantities are symmetrized. The term μab
plays the role of the velocity divergence,
(11)where
all quantities are symmetrized. The term μab
plays the role of the velocity divergence,
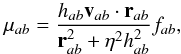 (12)with
η ≪ 1 to prevent singularities as particles approach, while
fab (Balsara
1995) is introduced to avoid large entropy generation in pure shear flows and is
defined as
(12)with
η ≪ 1 to prevent singularities as particles approach, while
fab (Balsara
1995) is introduced to avoid large entropy generation in pure shear flows and is
defined as 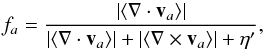 (13)where again
η′ ≪ 1 is a factor used to prevent singularities, and
αSPH and βSPH determine the
strength of the artificial viscosity. In general they are set initially to 0.1 and 0.2,
respectively, but they can vary during the simulation, keeping only their ratio fixed
(Morris & Monaghan 1997; Rosswog et al. 2000).
(13)where again
η′ ≪ 1 is a factor used to prevent singularities, and
αSPH and βSPH determine the
strength of the artificial viscosity. In general they are set initially to 0.1 and 0.2,
respectively, but they can vary during the simulation, keeping only their ratio fixed
(Morris & Monaghan 1997; Rosswog et al. 2000).
The shear viscosity contribution deriving from the linear and quadratic artificial
viscosity terms can be compared to the Shakura &
Sunyaev (1973) viscosity αSS as in Meru & Bate (2012): 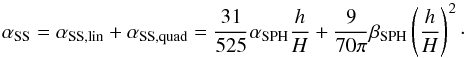 (14)It has been shown
(Monaghan 1985; Lodato & Price 2010; Meru & Bate
2012) that even in the continuum limit, the artificial viscosity terms
αSPH and βSPH mimic a
Navier-Stokes viscosity.
(14)It has been shown
(Monaghan 1985; Lodato & Price 2010; Meru & Bate
2012) that even in the continuum limit, the artificial viscosity terms
αSPH and βSPH mimic a
Navier-Stokes viscosity.
2.2. Variable softening length
The variable softening length method is needed when self-gravity is included in the model
(Price & Monaghan 2007). The modified
gravitational potential per unit mass may be written in the form
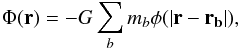 (15)where
φ is a softening kernel that is a function of the particle separation
and the softening length (h, which corresponds to the smoothing length as
in Price & Monaghan 2007). The form of
φ is given below. The gravitational force in r is computed
as
(15)where
φ is a softening kernel that is a function of the particle separation
and the softening length (h, which corresponds to the smoothing length as
in Price & Monaghan 2007). The form of
φ is given below. The gravitational force in r is computed
as 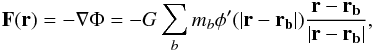 (16)where
φ′ = ∂φ/∂|r − rb |,
and we have neglected the spatial variation of h. To get an expression
for φ, the Poisson’s equation is used
(16)where
φ′ = ∂φ/∂|r − rb |,
and we have neglected the spatial variation of h. To get an expression
for φ, the Poisson’s equation is used
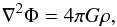 (17)and by using the
SPH definition for the density (Eq. (4)),
it is possible to derive a relation between the smoothing kernel W and
the softening kernel
φ
(17)and by using the
SPH definition for the density (Eq. (4)),
it is possible to derive a relation between the smoothing kernel W and
the softening kernel
φ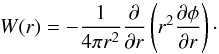 (18)The kernel softens the
gravity from neighbor particles while it is the usual
1/r potential for those far away. The additional
terms to the equation of motion due to the self-gravity are (Price & Monaghan 2007)
(18)The kernel softens the
gravity from neighbor particles while it is the usual
1/r potential for those far away. The additional
terms to the equation of motion due to the self-gravity are (Price & Monaghan 2007)
![\begin{eqnarray} \frac{{\rm d}\vec{v}_a}{{\rm d}t} = &&-G \sum_b m_b \phi'_{ab}(h_{ab}) \frac{\vec{r_a}-\vec{r_b}}{|\vec{r_a}-\vec{r_b}|} \nonumber \\ &&- \frac{G}{2} \sum_b m_b \left[\frac{\zeta_a}{\Omega_a}+ \frac{\zeta_b}{\Omega_b}\right] W'_{ab}(h_{ab}), \end{eqnarray}](/articles/aa/full_html/2013/08/aa21860-13/aa21860-13-eq46.png) (19)where
the first term represents the softened gravitational force, and the second one is used
when the adapting softening length is adopted and restore the energy conservation with
(19)where
the first term represents the softened gravitational force, and the second one is used
when the adapting softening length is adopted and restore the energy conservation with
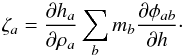 (20)
(20)
2.3. SPH implementation of radiation hydrodynamics in the flux-limited diffusion
The coupled energy equations describing the evolution of the specific gas internal energy
ug and of the total frequency-integrated radiation energy
ξ are the following (Mihalas &
Mihalas 1984; Whitehouse & Bate
2004): ![\begin{eqnarray} \frac {D \xi} {Dt} & =& - \frac {\grad \cdot \vec F} {\rho} - \frac { \grad \vec v : {\vec P}} {\rho} - a c \kappa \left[ \frac {\rho \xi} {a} - \left( \frac {u_{\rm g}} {c_v} \right )^4 \right], \label{radeneqn} \\ \frac {D u_{\rm g}} {Dt} & =& - \frac {P \grad \cdot \vec v} {\rho} + a c \kappa \left[ \frac{\rho \xi} {a} - \left( \frac {u_{\rm g}} {c_v} \right )^4 \right], \label{spceneqn} \end{eqnarray}](/articles/aa/full_html/2013/08/aa21860-13/aa21860-13-eq50.png) where
a = 4σB/c
and κ is the mean absorption opacity. The term
where
a = 4σB/c
and κ is the mean absorption opacity. The term
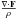 on the
right-hand side of Eq. (21) is the
radiation flux term. For an isotropic radiation field (Eddington approximation), the
radiative flux is given by
on the
right-hand side of Eq. (21) is the
radiation flux term. For an isotropic radiation field (Eddington approximation), the
radiative flux is given by 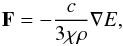 (23)where
χ is the total opacity, which is the sum of absorption and scattering
terms; E is the radiative energy density
E = ξ·ρ; and c is
the light speed. In optically thin regions where χ → 0 the Eddington
approximation fails (F → ∞), since photons travel freely and their free paths
may exceed characteristic lengths of the system, making the radiation field anisotropic.
In this case the flux-limited approximation is used (Levermore & Pomraning 1981) and the radiation flux can be written as a
Fick’s law of diffusion
(23)where
χ is the total opacity, which is the sum of absorption and scattering
terms; E is the radiative energy density
E = ξ·ρ; and c is
the light speed. In optically thin regions where χ → 0 the Eddington
approximation fails (F → ∞), since photons travel freely and their free paths
may exceed characteristic lengths of the system, making the radiation field anisotropic.
In this case the flux-limited approximation is used (Levermore & Pomraning 1981) and the radiation flux can be written as a
Fick’s law of diffusion 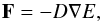 (24)where
D = cλ/(χρ) is a
diffusion coefficient, and the dimensionless function
λ = λ(E) is the flux-limiter defined
as (Levermore & Pomraning 1981; Whitehouse & Bate 2004)
(24)where
D = cλ/(χρ) is a
diffusion coefficient, and the dimensionless function
λ = λ(E) is the flux-limiter defined
as (Levermore & Pomraning 1981; Whitehouse & Bate 2004)
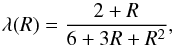 (25)where R
is the dimensionless quantity
R = |∇E|/(χρE).
In the optically thin limit (R → ∞) the flux limiter tends towards
(25)where R
is the dimensionless quantity
R = |∇E|/(χρE).
In the optically thin limit (R → ∞) the flux limiter tends towards
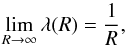 (26)so the magnitude of the
flux approaches
| F| = c|∇E|/(χρR) = cE.
In the optically thick (or diffusion) limit, R → 0 so the flux-limiter
(26)so the magnitude of the
flux approaches
| F| = c|∇E|/(χρR) = cE.
In the optically thick (or diffusion) limit, R → 0 so the flux-limiter
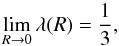 (27)and the flux takes the
value given by Eq. (23).
(27)and the flux takes the
value given by Eq. (23).
The second term on the rigth-hand side of Eq. (21) 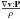 ,
describing the radiation pressure, contains the radiation pressure tensor P
that, in the flux-limited approximation, can be expressed in terms of the radiation energy
density
,
describing the radiation pressure, contains the radiation pressure tensor P
that, in the flux-limited approximation, can be expressed in terms of the radiation energy
density 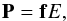 (28)where
f is the Eddington tensor, defined as
(28)where
f is the Eddington tensor, defined as 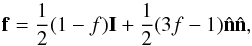 (29)where
(29)where
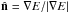 is the unit vector in the direction of the radiation energy density gradient and
f = f(E) is a scalar function called
the Eddington factor. The flux limiter and the Eddington factor are related through
is the unit vector in the direction of the radiation energy density gradient and
f = f(E) is a scalar function called
the Eddington factor. The flux limiter and the Eddington factor are related through
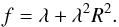 (30)The last term in
both Eqs. (21) and (22) controls the interaction between the
radiation and the gas. In fact we can rewrite the term inside the square bracket as
(30)The last term in
both Eqs. (21) and (22) controls the interaction between the
radiation and the gas. In fact we can rewrite the term inside the square bracket as
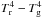 .
.
In non-irradiated protoplanetary disks, the temperatures are low enough that the energy
stored in radiation is negligible compared to the thermal energy of the gas
(ξ ≪ ug). Under this condition, the
so-called one-temperature approach (Kley et al.
2009), the two coupled equations, Eqs. (21) and (22), reduce to a single
equation for the gas internal energy ug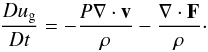 (31)The radiation flux
term can be rewritten using the flux-limiter λ as
(31)The radiation flux
term can be rewritten using the flux-limiter λ as ![\begin{eqnarray} \label{eneq} - \frac {\grad \cdot \vec F} {\rho} & = &\frac {1} {\rho} \grad \cdot \left( \frac{c \lambda}{\kappa_{\rm R} \rho} \grad E \right), \\ & = &\frac {1} {\rho} \grad \cdot \left[ \frac{c \lambda}{\kappa_{\rm R} \rho} \grad \left( \frac{4\sigma_{\rm B}}{c}T^4\right)\right], \nonumber \\ & =& \frac {1} {\rho} \grad \cdot \left[\frac{16 \sigma_{\rm B} \lambda} {\kappa_{\rm R} \rho} T^3 \grad T \right], \end{eqnarray}](/articles/aa/full_html/2013/08/aa21860-13/aa21860-13-eq84.png) where
κR, the Rosseland mean opacity, approximates
χ. To compute κR we use a power-law
dependence on temperature and density
κR = κ0ρaTb
as in Bell & Lin (1994) where the
coefficients κ0, a, and b
depend on the opacity regime. The previous equation has the same form of the heat
conduction equation
where
κR, the Rosseland mean opacity, approximates
χ. To compute κR we use a power-law
dependence on temperature and density
κR = κ0ρaTb
as in Bell & Lin (1994) where the
coefficients κ0, a, and b
depend on the opacity regime. The previous equation has the same form of the heat
conduction equation 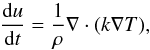 (34)where
k is the thermal conductivity. This similarity is useful when we try to
implement the energy equation (Eq. (32))
in the SPH formalism. Cleary & Monaghan
(1999) give in fact the following SPH expression for the heat transport equation
(34)where
k is the thermal conductivity. This similarity is useful when we try to
implement the energy equation (Eq. (32))
in the SPH formalism. Cleary & Monaghan
(1999) give in fact the following SPH expression for the heat transport equation
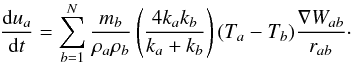 (35)In the case of
radiative diffusion, the coefficients ka and
kb have to be substituted by (Whitehouse & Bate 2004)
(35)In the case of
radiative diffusion, the coefficients ka and
kb have to be substituted by (Whitehouse & Bate 2004)
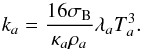 (36)
(36)
2.3.1. Cooling via boundary particles
While the disk is heated by the viscous dissipation (we neglect star irradiation effects), it is at the same time cooled by the thermal emission into the vacuum at the upper and lower surfaces. To model the radiation escape, we introduce “boundary” particles into the algorithm. These particles populate the regions where the optical depth of the disk τ is equal to 1 (Ayliffe & Bate 2009; Meru 2010). To identify the boundary particles among all the particles representing the disk we proceed as follows:
-
1.
The disk is divided in sectors(r + Δr, θ + Δθ);
-
2.
In each sector, SPH particles are sorted along both r and z;
-
3.
The parameter zb is defined as the height at which the optical depth τ is ≈1 so that
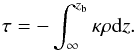 (37)Under the
assumption of low temperature and density in the outer layers of the disk, the
vertical isothermal approximation can be locally used (thin disk condition) so
that the opacity κ is approximately constant and can be taken out
of the integral leading to the following expression
(37)Under the
assumption of low temperature and density in the outer layers of the disk, the
vertical isothermal approximation can be locally used (thin disk condition) so
that the opacity κ is approximately constant and can be taken out
of the integral leading to the following expression
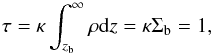 (38)where
Σb is the surface mass density of the boundary particles;
(38)where
Σb is the surface mass density of the boundary particles; -
4.
In the SPH formalism, the superficial density can be computed as
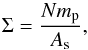 (39)where
mp is the SPH particle mass, N the
total number of particles present in the sector (independently of the
z coordinate), and As the sector
area;
(39)where
mp is the SPH particle mass, N the
total number of particles present in the sector (independently of the
z coordinate), and As the sector
area; -
5.
Knowing Σb we can compute Nb, the number of particles populating the layer with τ = 1. This number is given by
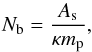 (40)this is done in
both the positive and negative vertical directions.
(40)this is done in
both the positive and negative vertical directions.
The boundary particles evolve normally, but they interact radiatively with the “normal” SPH particles in the bulk of the disk absorbing radiation without releasing it. The amount of heat they are supposed to radiatively transfer to their neighbors, which is computed from the energy equation, is lost to infinity. In this way they act as cooling particles radiating away energy. It is noteworthy that the temperature of the boundary particles is not set to a low value but is in equilibrium with the local temperature profile of the disk. This prevents them from rapidly migrating towards the median plane of the disk due to their low pressure value. However, they absorb the energy of the other particles and act as energy sinks. In Fig. 1 we show two representative vertical temperature profiles obtained from our simulations of disks in binaries. They are computed in a quiet ring far from the center of both the primary and secondary disks to avoid the heating due to strong spiral waves, which also act when the binary is at the apocenter. The cooling due to boundary particles is effective and leads to a decrease in the temperature towards the surfaces of the disk.
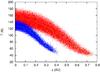 |
Fig. 1 Temperature profiles as a function of the height over the median plane of the disk (z component) for the primary disk at r ~ 6 AU and for the secondary disk at r ~ 3 AU. These locations are far from the center of the disk where the heating due to the spiral waves, even at apocenter, is the strongest. The dots are the individual temperatures of the SPH particles encompassed between 6 and 6.3 AU for the primary disk and 3 and 3.3 AU for the secondary disk. The continuous lines are the average temperature values. The SPH particles of the primary disk are represented by red dots, while blue dots are relative to the secondary disk. |
3. Initial setup of the disks in the binary system
The parameter space of a binary system with a circumstellar disk surrounding each stellar component is very wide so we focus in this paper on a configuration that is supposed to be the more plausible one according to observations. A mass ratio of μ = Ms/Mp = 0.4 and an eccentricity of e = 0.4 are adopted in the definition of our standard case since these values are statistically the most frequent among the binary systems observed so far (Duquennoy & Mayor 1991). Two different values of the binary semi-major axis are adopted in our models: a = 30 and a = 50 AU. Coplanarity is assumed between the disks and the binary orbit, even if in the future we plan to relax this constraint. We consider a high-density disk with a midplane density ρ0(r = 1,z = 0) = 1 × 10-9 g /cm3, which is a value close to that prescribed by the minimum mass solar nebula model. A second less massive case, with ρ0(r = 1,z = 0) = 5 × 10-10 g /cm3, is also modeled to test the influence of the initial density profile on the morphology and physical properties of the disks. Hereinafter, the four different runs are named in the following way: the high-density case with binary semi-major axis aB = 30 AU is called HIDECL, while the low density case with the same value of aB is named LODECL. The two runs with aB = 50 AU are called HIDEFA and LODEFA, respectively.
Parameters of the simulations.
The density midplane radial profile is computed as
ρ0(r) ∝ r-1.5.
The initial vertical density stratification of the disks is computed as in Bitsch & Kley (2010) using a Gaussian-like
dependence of the density on z. This is a good approximation for a
stationary disk where the pressure balances the z-component of the central
star gravity ![\begin{equation} \rho(r,z)=\rho_0(r,z) \exp\left[-\frac{z^2}{2H^2}\right], \end{equation}](/articles/aa/full_html/2013/08/aa21860-13/aa21860-13-eq132.png) (41)with the scale height
h = H/r initially
set to a constant value of 0.04. The circumprimary disk extends from 0.5 AU to 8 AU and the
circumsecondary to 5.5 AU, both within the tidal truncation limits computed by Artymowicz & Lubow (1994) in the case where the
binary semi-major axis is set to 30 AU. For the second case where
aB = 50 AU our configuration with relatively small disks is
similar to that observed for the system L1551 IRS 5 (Rodríguez et al. 1998) where the circumstellar disks of the binary system are well
separated and smaller than the tidal truncation radius. We did not increase the size of the
disks up to the tidal truncation radius since we wanted to explore whether a less perturbed
configuration with the stars moving farther away affects the same disks of the simulations
with aB = 30 AU. At the outer border, the disk density is
smoothly truncated with ρ(r,z) exponentially decreasing.
The mass of the primary disk in the HIDECL and HIDEFA models is
0.015 M⊙, while that of the secondary is
0.003 M⊙. The secondary disk is less massive since we scale
its initial density with the stellar mass and its initial radius is also smaller. In the
LODECL and LODEFA models the masses of the disks are 0.0075 M⊙
and 0.0015 M⊙, respectively since the density is reduced by a
factor 2.
(41)with the scale height
h = H/r initially
set to a constant value of 0.04. The circumprimary disk extends from 0.5 AU to 8 AU and the
circumsecondary to 5.5 AU, both within the tidal truncation limits computed by Artymowicz & Lubow (1994) in the case where the
binary semi-major axis is set to 30 AU. For the second case where
aB = 50 AU our configuration with relatively small disks is
similar to that observed for the system L1551 IRS 5 (Rodríguez et al. 1998) where the circumstellar disks of the binary system are well
separated and smaller than the tidal truncation radius. We did not increase the size of the
disks up to the tidal truncation radius since we wanted to explore whether a less perturbed
configuration with the stars moving farther away affects the same disks of the simulations
with aB = 30 AU. At the outer border, the disk density is
smoothly truncated with ρ(r,z) exponentially decreasing.
The mass of the primary disk in the HIDECL and HIDEFA models is
0.015 M⊙, while that of the secondary is
0.003 M⊙. The secondary disk is less massive since we scale
its initial density with the stellar mass and its initial radius is also smaller. In the
LODECL and LODEFA models the masses of the disks are 0.0075 M⊙
and 0.0015 M⊙, respectively since the density is reduced by a
factor 2.
Each disk is initially evolved as a single disk around its star until it reaches a steady state both in density and temperature. Once this state is reached, the stars and their disks are combined into a binary system with the desired orbital parameters. Each SPH simulation uses about 1 × 106 particles distributed in both disks according to their size and density. The distinctive parameters of the four different models are summarized in Table 1. Those SPH particles traveling within 0.5 AU are accreted by the star. Their number is limited in time, and for this reason, we do not correct for their effects on the pressure and viscous forces on particles moving inside the border as in Bate et al. (1995).
The initial values of αSPH and βSPH adopted in the simulations are 0.1 and 0.2, respectively. The αSS viscosity, estimated from Eq. (14), is about (2−4) × 10-3 for the primary disk and (1−2) × 10-3 for the disk around the secondary star. The αSS of the primary disk is very close to that of Nelson (2000).
4. Results
In the forthcoming sections, we describe the evolution of the disks in the four different models. We focus on the disk morphology, the occurrence of shock waves, and the mass exchange between the two disks (in particular for the cases with aB = 30 AU). Shock waves cause the onset of hydraulic jumps along the vertical axis, which might significantly affect the dust accumulation towards the median plane of the disk and possibly inhibit the planetesimal formation via pairwise accumulation. In addition, in the models with small aB, the high temperature induced by the pericenter passages, and not fully dissipated at the apocenter, may further inhibit planet formation, as already guessed by Nelson (2000). The asymmetry in the disk shape will also be explored as a potential prediction for observers.
 |
Fig. 2 Top plot: logarithm of the superficial density (column integrated) of the circumstellar disks for HIDECL (high density, small binary semi-major axis) shown during the pericenter passage of the secondary star. Bottom panels: density (non-integrated) drawn along the x − z and y − z sections of the primary disk (2nd and 3rd panels) and secondary disk (4th and 5th panels). |
4.1. High-density disks
In the top panel of Fig. 2 we illustrate the integrated density of the circumstellar disks in the HIDECL model. The secondary star is close to the pericenter of its orbit around the primary, the most perturbing configuration for the two disks. This is the third pericenter passage of our simulation, which took about three months of CPU time on a dedicated 32-processor machine (VINE is parallelized with OPENMP). This long integration time is due to the radiative transfer, which requires a very short time step, in particular close to the pericenter when strong spiral waves are excited in both disks, and mass is transferred from one disk to the other.
The primary disk displays two prominent, tidally generated trailing spiral arms that tightly wind towards the center of the disk. The appearance of this pattern, initially at the outer edges of the disk, begins when the companion star approaches the primary star, and they reach their maximum intensity shortly after the pericenter passage. They are transient features, and they are gradually damped when the stars evolve towards the apocenter. The gas density is significantly higher at the location of the spirals as is the temperature (see Fig. 5). The arms cover a substantial portion of the disk affecting its overall evolution even by locally changing the shear viscosity and heating rate. In Fig. 2 the secondary disk seems to have a more complex spiral pattern with three arms, but an additional arm, as we see later on, is simply excited by the impact of stream material coming from the primary disk. A significant mass transfer occurs during the pericenter passage mostly from the primary star to the secondary. This phenomenon might in the long term lead to a redistribution of mass between the two disks with the initially smaller one becoming slowly more massive and gradually loosing memory of its initial density profile. The spiral waves are also visible in the x − z and y − z sections of the disks as regions of higher density and inflated in the vertical direction.
4.2. Spiral shock waves, hydraulic jumps and dust settling
Three-dimensional waves in accretion disks act like fundamental modes that correspond to large surface distortions in the disk (Lubow & Ogilvie 1998). Boley et al. (2005) have shown that shock waves in 3D disks cause abrupt increases in the disk scale height. These jumps convert part of the flow’s initial kinetic energy into potential energy, while some is irreversibly lost into heat. Breaking waves, generated at the jump, crash onto the pre-shock flow creating additional disordered motion and possibly affecting the chondrule formation and dust settling processes. This shock-related splashing, observed in the bottom plots of Fig. 2, is evidently highly nonlinear and has the characteristics of hydraulic jumps that behave, in part, like gravity modes (Martos & Cox 1998).
To verify that the waves excited during the pericenter passage are indeed shock waves, we
performed two tests. First we estimated a 2D vortensity by computing the ratio between a
column integrated vorticity ω derived for each SPH particle as
ω = ẑ·(∇ × v) and the superficial density Σ
as the average of the 3D density ρ over concentric rings 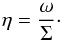 (42)This quantity is
used locally as an indicator of shocks since vortensity is generated when the material
passes through a shock. In Fig. 3 the spiral waves
are clearly outlined, and the vortensity perturbations are superimposed on the density
waves observed in the superficial density plots.
(42)This quantity is
used locally as an indicator of shocks since vortensity is generated when the material
passes through a shock. In Fig. 3 the spiral waves
are clearly outlined, and the vortensity perturbations are superimposed on the density
waves observed in the superficial density plots.
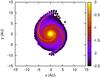 |
Fig. 3 Vertically integrated vortensity in the primary disk during the pericenter passage in the HIDECL model. |
The second test relies entirely on the fact that spiral shocks also lead to hydraulic jumps (Durisen 2011). In general, a hydraulic jump occurs when the flow reaches a region where there is an abrupt decrease in its speed. Conservation of mass, momentum, and energy requires that the bulk kinetic energy of the prejump flow be converted across the jump into gravitational potential energy and disordered motion. There is an increase in the flow vertical height at the shock wave passage, according to the Rankine-Hugoniot equations, and the consequent fallback of gas onto the disk causes additional disordered motion and the developing of vortices. Even though the gas in the protoplanetary disk is compressible, the formation of a shock wave, in our scenario forced by the gravitational perturbations of the companion star, produces a similar phenomenon. We can estimate quantitatively how much the scale height of the disk is affected by the shock wave using a simplified model developed by Boley et al. (2005), which assumes that the shock is planar, is vertically stratified in the direction perpendicular to the wave propagation, and has the pre-shock region in vertical hydrostatic equilibrium.
Defining the jump factor Jf as the ratio between the pressure
body forces and self-gravitating potentials in the pre-shock and post-shock regions Boley et al. (2005) find that for strong shock waves
(M ≫ 1) and when the background potential dominates the gas potential
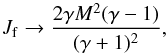 (43)where M
is the Mach number and γ is the adiabatic index. The two limiting cases
are
(43)where M
is the Mach number and γ is the adiabatic index. The two limiting cases
are
-
Jf > 1, the gas is overpressured, and it will expand vertically;
-
Jf < 1, self-gravity cause the gas to compress.
A strong adiabatic shock (M → ∞) disrupts vertical hydrostatic
equilibrium, because Jf > 1 and the
material expands upward at the sound speed on a timescale of approximately
H/cs ≈ Ω-1 = trot/2π.
As shown in the bottom panels of Fig. 2, at the
spiral waves the density distribution along the z-axis is puffed up, and
this confirms that in our models we are in the
J > 1 case where the gas expands vertically. To
predict the height of the shock bore, Boley et al.
(2005) adopt a classical hydraulic jump model, where
gz = cost. The jump of
the fluid behind the shock is determined by the Froude number 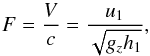 (44)which is defined as the
ratio of a characteristic velocity (V) to a gravitational wave velocity
(c) or as the ratio of a body’s inertia to gravitational forces, and it
is an analogous to the Mach number. In a non-dissipative jump,
(44)which is defined as the
ratio of a characteristic velocity (V) to a gravitational wave velocity
(c) or as the ratio of a body’s inertia to gravitational forces, and it
is an analogous to the Mach number. In a non-dissipative jump, 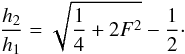 (45)In the limit of a
strong jump (F ≫ 1) we would have
h2/h1 ~ F.
Using this classical result as a model for understanding the maximum height, a shock bore
reaches during the post-shock vertical expansion, Boley et
al. (2005) derive, for a non self-gravitating disk,
(45)In the limit of a
strong jump (F ≫ 1) we would have
h2/h1 ~ F.
Using this classical result as a model for understanding the maximum height, a shock bore
reaches during the post-shock vertical expansion, Boley et
al. (2005) derive, for a non self-gravitating disk, 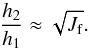 (46)This ratio has a behavior
similar to that of the Froude number described in Eq. (45). When M = 1,
h2/h1 ~ 1,
and
h2/h1 ~ M
when M ≫ 1. This does not mean that any fluid element close to the shock
wave shows a jump in the vertical direction, but it does imply that the disk scale height
will change. As an example, material near the midplane
(dΦ/dz → 0, Jf → 0) will
not be affected by a single shock wave passage, while higher altitude gas will have the
strongest response.
(46)This ratio has a behavior
similar to that of the Froude number described in Eq. (45). When M = 1,
h2/h1 ~ 1,
and
h2/h1 ~ M
when M ≫ 1. This does not mean that any fluid element close to the shock
wave shows a jump in the vertical direction, but it does imply that the disk scale height
will change. As an example, material near the midplane
(dΦ/dz → 0, Jf → 0) will
not be affected by a single shock wave passage, while higher altitude gas will have the
strongest response.
 |
Fig. 4 Velocity field and density of a slice in the (x,z) plane in the region of hydraulic jumps for the primary (top panel) and secondary (bottom panel) in the HIDECL model. Both disks are centered on their parent stars to properly compute the gas velocity field. The scales in x and z are different in the two plots and, in addition, the star is on the right in the top plot (circumprimary disk), while it is on the left in the bottom one (circumsecondary disk). |
In our HIDECL case, we can apply this model to the spiral waves observed in Fig. 2 and estimate the jump factor Jf and the corresponding Froude number. In Fig. 4 we show a detail of both disks in the (x − z) plane around the shock wave. In Fig. 4a (upper plot), we show a slice of the circumprimary disk where the star is on the right. In Fig. 4b (lower plot) we instead show a detail of the circumsecondary disk where the star is on the left. Different scales are used in the plots to magnify the density variations. The formation of hydraulic jumps at the spiral waves is clearly visible with a significant increase of the gas vertical height and the formation of breaking waves on top of the jumps. The motion of the gas is evidenced by velocity vectors which are superimposed to the 2D density plot. There is a significant decrease in the velocity magnitude across the wave and an abrupt change in the gas density. A rough estimate of the jump-factor Jf from Fig. 4a by using Eq. (46) gives a value of Jf ≈ 3.2 and a Froude number (from Eq. (45)) F ≈ 1.6.
Similar values are also found in the secondary disk. The velocity field evidences the formation of breaking fronts at the top of the hydraulic jump and the splashing of material from the top of the jump. Shock bores not only generate the vertical displacement of fluid elements illustrated in Fig. 4a,b, but they also drive gas to large radial excursions from their circular orbits, causing large amounts of wave energy to be transformed into kinetic energy stirring and mixing the disk. This is also at the origin of the disk heating. When the gas crosses the shock front, the shock normal component of the fluid element velocity diminishes, according to the Rankine-Hugoniot equations, while the tangential component is preserved and the flow become supersonic after the shock. This leads to streaming along the spiral arms (Roberts et al. 1979). Moreover, when the gas expands upwards, the pressure confinement normal to the shock loosens and the fluid expands radially, causing some gas to flow back over the top of the shock. The resulting morphology is a spiral pattern moving through the disk in the (x − y), as illustrated in Fig. 2, while the pattern appears as a breaking wave in the vertical direction.
In the inner part of the disk we do not observe breaking waves, but this is due to the fast crossing of winding spiral arms. The orbital period of a fluid element is much shorter than the pattern period of a spiral wave. Shortly after the first shock, the gas therefore encounters another arm before it can settle back onto the disk, ending up elevated between shock passages. However, in the outer part of the disk the periods become comparable and the shock bores have the time to develop into breaking waves.
 |
Fig. 5 Temperature distribution in the two disks computed at their median plane when the stars are close to the pericenter (upper panel) and apocenter (lower panel) in the HIDECL model. |
The evolution of the gas disk into hydraulic jumps may have critical consequences for the dust settling towards the disk midplane. When the gas is pumped up at the shock waves, via aerodynamic effects, it can drag the smaller components of the dust inverting their settling motion. As a consequence, at each pericenter passage, the disk will develop strong spiral waves able to stir up the dust significantly slowing the sedimentation process down, if not suppressing it. In addition, it would also increase the relative velocity between dust particles halting the coagulation process at small dust sizes and possibly preventing the formation of planetesimals through the conventional scenario of dust coagulation. On the other hand, turbulent motion that may develop in the proximity of spiral waves, may favor the fast accretion of pebbles into large planetesimals, as suggested by Johansen et al. (2007) and Cuzzi et al. (2008).
4.3. Temperature profile: Chondrule formation at shocks?
In Fig. 5 we show the midplane temperature distribution of the two disks during the pericenter passage. At the shocks generated by the spiral structures, the temperature is raised to high values that might cause vaporization of some grains, as suggested by Nelson (2000), and chondrule formation (Boley et al. 2005). The secondary disk is cooler than the primary and this is due to its lower density. It appears also overheated at the outer edge, more than the circumprimary, since mass coming from the more massive circumprimary disk strikes its outer borders thereby increasing its temperature.
During the pericenter approach, there is a considerable transient internal thermal energy generation in the disks by means of shock waves and mass transfer. Once the stars depart from each other traveling towards the apocenter, the disks cool down due to radiative cooling possibly reaching an equilibrium state. This effect is shown in Fig. 6 where we compare the azimuthally and vertically averaged temperature profiles for both disks when the stars are at pericenter and apocenter, respectively. The difference is more marked in the outer parts of the disks, and it can be as large as 200 K. This phenomenon was also observed by Nelson (2000) in his simulations of an equal mass binary system with aB = 50 AU and eb = 0.3. He performed 2D SPH numerical simulations of such a binary star/disk + star/disk system finding a relatively mild difference in temperature between pericenter and apocenter. Our larger difference may be attributed to the different dynamical configuration. In effect, our HIDECL model system is more compact (smaller semimajor axis), and it also has higher eccentricity. This dynamical configuration leads to a stronger heating at shock waves and a larger mass exchange that causes a consistent local temperature increase where the transferred flow impacts the disk. Both these effects can explain the larger difference in the temperature profiles between pericenter and apocenter we find in our model. On the other hand, we have lower temperatures in the disks on average compared to the ones obtained in Nelson (2000) but this may be related to the different initial density adopted in his simulations, the different orbital architecture and the different cooling algorithm. The Nelson (2000) case compares better with our models where the stars have a larger separation (aB = 50 AU), which is discussed later on. Our temperature profiles appear to be comparable or slightly higher than those in Müller & Kley (2012), even if a different initial density profile is adopted (Σ ∝ r-1 while ours declines as Σ ∝ r− 1/2). In addition, Müller & Kley (2012) consider a single disk around the primary, and as a consequence, the mass exchange between the two disks, with its consequent heating, is not included in their model. Also, since our simulations are performed in 3D, the amount of heating due to gas compression at the shock waves where hydraulic jumps occur is higher.
 |
Fig. 6 Azimuthally and vertically averaged temperature profiles of both disks in the HIDECL model when the stars are at pericenter and apocenter, respectively. The secondary disk is less dense than around the primary, so its temperature is on average lower. |
While high temperatures appear to prevent the condensation of icy dust particles and then the growth of giant planet cores, they may favor the formation of chondrules. They form as melt droplets that were heated to high temperatures, while they were independent, free-floating objects in the protoplanetary nebula. After they were heated, cooled, and crystallized, chondrules were incorporated into the parent bodies in which chondrites originate. There are constraints on chondrule formation like a peak temperature of about 1300 K followed by a fast cooling (100–1000 K per hour) as suggested in Armitage (2010). In our simulations we find that the temperature along the shock waves is higher than 1000 K, and it drops quickly after the wave passage. This may favor chondrules formation in such disks, in particular in more compact and eccentric binary configurations where stronger and possibly hotter spiral waves develop. This mechanism is not local since the shock waves induced by the companion star covers the whole disk, since the spiral wave extends from inside to the outer borders. As a consequence, it would not be necessary to invoke additional heating mechanisms or local shock fronts of different origins (Urey & Craig 1953; Urey 1967; Sanders & Taylor 2005; Asphaug et al. 2011; Levy & Araki 1989; Joung et al. 2004; Morfill et al. 1993; Pilipp et al. 1998; Desch & Cuzzi 2000; Nakamoto et al. 2005; Boss & Graham 1993; Ruzmaikina & Ip 1994; Hood et al. 2009; Hood 1998; Weidenschilling et al. 1998; Ciesla et al. 2004; Morris et al. 2012; Wood 1996; Desch & Connolly 2002; Boss & Durisen 2005; Boley & Durisen 2008). In this picture, the strong shock waves generated by binary interaction during pericenter passages might be an additional and very efficient mechanism for chondrule formation over the whole disk.
4.4. Mass exchange between the disks
When the two stars are at the pericenter, the gravitational interaction of the companion on each disk is the strongest. Spiral shock waves tidally induced by the gravitational perturbations of the stars propagate within each disk causing a significant mass transfer between the two disks in addition to disk heating. The mass exchange is bidirectional, but in absolute value, the primary disk donates more mass to the secondary, possibly because of its higher mass and its stronger shock waves that extend farther out from the disk center.
Where the mass stream coming from one disk hits the other and is accreted, heat is generated. This effect can been seen in the temperature distribution illustrated in Fig. 5a. At the edge of both disks, where the exchanged mass is accreted, the temperature is locally higher. This heating is subsequently spread around within the disk, contributing to the overall disk temperature profile. For this reason, in modeling disks in close binaries, it is important to include the secondary disk since the final temperature profile will depend on the amount of mass exchanged between the disks.
The mass accreted by the secondary disk generates an additional spiral arm in the disk as illustrated in Fig. 7. There are three spiral arms in the disk, two generated by the primary star tidal field and an additional one produced by the the impact of a stream from the primary.
The morphology of the mass flux moving from the primary to the secondary reflects the shape of the shock wave. It appears as a concave structure continuing in the shock wave direction and propagating towards the secondary disk. In Fig. 8 we show a 3D plot of the material transferred from the primary disk to the secondary and its temperature. The concave structure (like a water wave) is visible, and the gas impacting the secondary disk is heated up by the compressional motion.
 |
Fig. 7 Density distribution of the secondary disk when the stars are at the pericenter in the HIDECL model. A new spiral arm is created by the material transferred from the primary disk and impacting the outer edge of the secondary. |
 |
Fig. 8 Temperature distribution of the material flowing from the circumprimary disk to the circumsecondary in the HIDECL model. The impact on the secondary of the flow from the primary is marked by a raise in the temperature. |
The mass flow from the primary to the secondary disk induced by the formation of spiral waves during the pericenter passage can have significant effects in the long term. It can reduce the viscous mass loss of the secondary disk and change the initial post-formation mass ratio of the two disks. If this ratio was similar to the stellar mass ratio during the protostar contraction, later on this ratio could be different. The lifetime of the secondary disk may be longer, thereby increasing the probability of finding a planet around a less massive companion star, as suggested by the discovery of the planet around α Centauri B (Dumusque et al. 2012). However, a longer integration timespan is required to confirm this trend.
4.5. Disk eccentricity
The disk eccentricity is an important parameter for the evolution of a putative planetesimal population born in the disk. As shown in Paardekooper et al. (2008), Marzari et al. (2012), and Kley & Nelson (2008), an eccentric shape for the disk may perturb the evolution of the planetesimal eccentricity and orbital alignment, which may lead to destructive collisions rather than growth. The azimuthally averaged eccentricity profile of both disks (primary and secondary) at apocenter, where the spiral waves are dissipated, is shown in Fig. 9 for the HIDECL model. The disk eccentricity is low in the inner parts of both disks and it increases in the outer more perturbed regions. The eccentricity values agree with those derived in both Müller & Kley (2012) and Marzari et al. (2012) for radiative disks on a longer timescale. In our model the secondary disk is significantly more eccentric compared to the primary and this might be due to the stronger perturbations of the primary star, which is more massive, and to a reduced self-gravity related damping effect Marzari et al. (2012). It is noteworthy that the eccentricity profile we obtain after three pericenter passages is similar to that of Müller & Kley (2012) and Marzari et al. (2012), derived after more binary periods, making us confident that our results also hold in the long term. In particular, Fig. 3 of Müller & Kley (2012) shows that, for radiative disks, the eccentricity profile does not vary significantly with time. This behavior is different from isothermal disks where the disk eccentricity requires more time to reach a quasi-stationary (and more eccentric) state (Müller & Kley 2012; Marzari et al. 2012, 2009; Kley & Nelson 2008). As suggested in Marzari et al. (2012) and Cassen & Woolum (1996), the energy loss by radiation may be at the origin of this different evolution, leading to a faster damping of density waves in radiative disks.
 |
Fig. 9 Disk eccentricity profiles, averaged on azimuth and vertical direction, of the primary and secondary disks in the HIDECL and LODECL models. The eccentricity is computed at the apocenter when the strong spiral arms have almost completely dissipated. |
4.6. Low-density disks
The morphology of the disks in the LODECL model does not differ significantly from that of the HIDECL and strong trailing spiral patterns form in the both disks close to pericenter dissipating by the time the stars move to the apocenter. The main difference between the LODECL and HIDECL scenarios concern the temperature distribution and the vertical height of the hydraulic jump at the shock waves. In Fig. 10 we compare the temperature profiles of the two cases with aB = 30 AU. As expected, the lower density case has an overall lower temperature, and it is similarly heated up at the pericenter when shock waves develop and mass transfer occurs. Concerning the hydraulic jump at the shock waves, values as high as 2.2 for the h2/h1 ratio are found in the shock waves giving Jf ~ 4.8 and F ~ 1.9. These values are slightly higher compared to the HIDECL case and might be related to the lower sound speed in the LODECL disk, leading to larger Mach numbers. Figure 11 is a 3D picture of the two lower density disks showing the large vertical jumps at the shock waves.
 |
Fig. 10 Azimuthally and vertically averaged temperature profiles of the low-density disk (LODECL model) around the primary star compared to the high-density case (HIDECL) with the binary at pericenter and apocenter. The lower density disk is cooler in both cases. |
 |
Fig. 11 3D picture of the density distribution of the disks in the LODECL model close to the binary pericenter. Large vertical jumps can be observed at the shock waves. The surfaces are drawn at τ ~ 2. |
The eccentricity of both disks is compared in Fig. 9 to that of the HIDECL case and they show a similar behavior. As a consequence, the reduction of a factor two in density is not enough to significantly affect the shape of the disks. Even if the self-gravity damping effect is less strong Marzari et al. (2009), the lower temperature profile of the LODECL case might somehow help in keeping the overall disk eccentricity (Marzari et al. 2012) within 0.1 for both disks.
4.7. Binary systems with larger separation
In the models HIDEFA and LODEFA the semimajor axis of the binary system is increased to 50 AU, a configuration similar to the one explored by Nelson (2000). The orbital elements of the binary are the same, but Nelson (2000) considers two equal mass solar type stars and equal mass disks, while we model a system where the secondary star is less massive (0.4 M⊙), and the disk is scaled in density of the same ratio and is less radially extended. Differences are then expected in terms of physical properties of the disks in the simulations. We did not match the configuration of Nelson (2000) since we wanted to test the dependence of the disk evolution on the binary semimajor axis so we kept the same architecture of the previous models but we increase the binary semimajor axis.
Figure 12 illustrates the integrated density distribution of the two disks in the proximity of the binary pericenter in the HIDEFA model. Two-armed spiral shock waves are still present in the secondary disk, while they are reduced to density waves in the primary. These waves are weaker than those observed in the model disks of Nelson (2000), owing to the lower mass of the companion star in our simulations and to the different disk densities and sizes. The disk around the secondary shows shock bores as in the cases with aB = 30 AU (HIDECL and LODECL). This is illustrated in the lower panel of Fig. 12 from which a value of the jump factor Jf ~ 2 is estimated. This value is significantly lower than that computed for the HIDECL and LODECL cases as a consequence of the less perturbative configuration in the HIDEFA model. An almost negligible mass transfer between the two disks occurs in this configuration, due to the lack of strong shock waves on the primary disk.
In Fig. 13 the averaged temperature profiles are compared in the close and distant cases with the stars at pericenter and apocenter. At pericenter the close case (aB = 30 AU) is hotter compared to the distant (aB = 50 AU) case. This is an expected outcome since both disks in the HIDECL case are significantly more perturbed by shock waves, and a remarkable mass transfer occurs. At apocenter, the primary disks have approximately the same temperature profiles since the shock waves have dissipated, and the viscous heating and cooling are almost in equilibrium. The secondary disk is instead still very hot in the HIDECL case, possibly because its dissipation timescale is longer than the binary orbital period, and its excitation at pericenter was much stronger than in the HIDEFA case, as also shown by the lower value of Jf. Compared to the temperature profiles given in Nelson (2000), our values are lower, and this may be ascribed to the differences in the architecture of the system, in the cooling algorithm and in the fact that our models are 3D.
In Fig. 14 we compare the temperatures in the LODEFA and HIDEFA cases at pericenter and, as expected, the low-density disks are cooler. In this less perturbed case, the difference in temperature between the LODEFA and HIDEFA models must be mostly ascribed to a different balance between viscous heating and radiative cooling. In both cases the temperature rise at pericenter is negligible when compared to the close cases (aB = 30 AU). This can be inferred by comparing the upper panel of Fig. 13, where the stars are at pericenter, with the bottom panel where the stars are at apocenter. While there is a significant difference between the temperature profiles of the close case (HIDECL) in the two dynamical configurations, for the HIDEFA case the increase in temperature at pericenter is significantly less marked for both disks.
 |
Fig. 12 Integrated density profile of the disks in the HIDEFA model shortly after the pericenter (upper panel). The non-integrated density of the disk around the secondary star is shown in the x − z plane. Shock bores are visible even if less marked than in the HIDECL case. The hydraulic jumps in the primary are of negligible height. |
 |
Fig. 13 Comparison of the azimuthally and vertically averaged temperature profiles in the HIDEFA and HIDECL cases at pericenter (upper panel) and apocenter (lower panel) for both disks. At apocenter the temperature of the primary disk in the HIDEFA and HIDECL cases is very similar. |
In the distant configurations, the disk eccentricity is small independently of the initial gas density, as shown in Fig. 15. We expect that in this more quiet configuration, planetesimal accumulation can proceed less perturbed by the disk gravity.
5. Summary and discussion
We have performed 3D simulations of circumstellar disks in binary systems using VINE, an SPH algorithm that has been modified to model a fully radiative disk. The cooling has been simulated by including boundary particles that populate the outer surfaces of the disks (defined by τ ≥ 1) and effectively radiate away the heat transported from the inner regions via radiative transfer. Four different binary and disk configurations are modeled to explore the influence of the companion star perturbations on the disk morphology, temperature, and eccentricity. Two close configurations (aB = 30 AU) with different initial gas densities scaled by a factor 2 and two distant configurations (aB = 50 AU) with the same scale factor in density.
In the close configurations the spiral shock waves excited during the pericenter approach of the two stars generate hydraulic jumps whose height can be calculated from the simulations leading to an estimate of the Froude number. A significant mass transfer occurs between the disks at the binary pericenter when tidal trailing spiral waves are excited. This is an additional source of heat for both disks, and it can also increase the mass and lifetime of the smaller secondary disk enhancing the possibility of planet formation in it. It is also noteworthy that the mass ratio between the two disks at later stages of evolution may not reflect the primordial value due to the flux of mass from the primary to the secondary.
In the secondary disks, the impact of material coming from the primary disks excites the formation of an additional shock wave. The temperature profiles show a large difference between pericenter and apocenter related to the heating generated by shock waves and mass transfer at pericenter. The disk eccentricity is relatively low for the primary disks with values compatible with previous 2D studies. The secondary disk is more eccentric compared to the primary in particular in the outer regions where the eccentricity can be as high as 0.1. There is no notable difference in the disk morphology and disk eccentricity when we model less massive disks. On the other hand, the temperature profiles, due to the dependence of the viscous heating on the density, are instead significantly different.
 |
Fig. 14 Temperature profiles at the binary pericenter in the LODEFA and HIDEFA cases for both the primary and secondary disks. |
 |
Fig. 15 Eccentricity profiles for both disks in the two distant (aB = 50 AU) HIDEFA and LODEFA cases. The same scale of Fig. 9 is adopted for comparison. |
In the models with a higher value of the binary separation (aB = 50 AU), hydraulic jumps appear only in the secondary disks, while in the primaries the spiral waves, even at the pericenter, do not cause a significant change in the disk morphology. This implies that there is a limiting binary separation beyond which the strength of the tidal spiral patterns on the primary disk is not enough to excite the motion of the gas in the vertical direction and lead to mass transfer. In these less perturbed configurations, the disk eccentricity is lower even for the secondary disks with an upper limit of ≈0.03 over the full radial extent of the disks. Owing to the reduced strength of the spiral waves and negligible mass exchange, the distant configurations have lower temperature profiles with the stars at pericenter compared to the close configurations. At apocenter the primary disks in the distant and close configurations have the same temperature while the secondary disk is hotter possibly because it did not dissipate all the heat accumulated during the pericenter passage. As for the close configurations, the temperature profiles of the less dense disks is lower than in higher density cases.
5.1. Implications for planet formation
As already pointed out by Nelson (2000), the high temperature of the disks and the consequent shifting outside of the “snow line” may inhibit the condensation of ices reducing the amount of available mass for accreting the core of giant planets. Although in our models the temperature profiles are lower than those found by Nelson (2000), even if with a different system architecture, the temperature is still too high in the close configurations. In the dense close configuration (HIDECL) at pericenter, the “snow line” is at about 8 AU for the primary and 6 AU for the secondary disk. In both cases, the “snow line” location almost coincides with the outer borders of the disks. At apocenter, the two values shrink to 6 AU and 4 AU, respectively. In the more distant configurations, the “snow line” is at 6 AU for the primary with negligible differences between pericenter and apocenter, while it shifts from 2 to 3 AU for the secondary disk. Even locally, at the shock waves, the temperatures are high enough to prevent icy dust condensation, but on the other hand, they might favor the formation of chondrules.
In addition to the high temperature of the disk, our simulations show that the spiral waves generate hydraulic jumps that would invert the dust settling to the disk midplane induced by the aerodynamic drag. This would significantly affect the settling velocity and timescale and, as a consequence, the coagulation process into larger particles. The relationship between the size and vertical height would be destroyed and a substantial remixing of the dust would occur at the shock bores. An additional nasty effect for particle growth would be the increase in the mutual relative velocities at the shock, in particular where breaking waves crash back onto the disk.
The two effects described above seem to work against the coagulation of dust into large planetesimals, thereby preventing the formation of planets in binaries. Even the subsequent planetesimal accretion process appears critical in binary systems as already pointed out by Marzari & Scholl (2000); Thébault et al. (2004, 2006, 2008, 2009); Kley & Nelson (2008); Marzari et al. (2009); Xie & Zhou (2009); Xie et al. (2010); Paardekooper et al. (2008), and Marzari et al. (2012). However, close binary systems hosting giant planets have been detected, such as γ Cephei (Campbell et al. 1988), Gliese 86 (Queloz et al. 2000), HD 41004 (Zucker et al. 2004), HD 196885 (Correia et al. 2008), and the small terrestrial planet in α Centauri (Dumusque et al. 2012). There are two possible scenarios for the formation of the present dynamical architectures of these systems. The first is that the binary system hosting the planet had a larger separation in the past compatible with the growth of planets according to the standard core-accretion model. The subsequent dynamical evolution of the stellar system – either because it is part of an unstable triple stellar system or because it suffered a close encounter with a third (background) star (Marzari & Barbieri 2007b,a; Martí & Beaugé 2012) – led to a shrinking of the binary orbit without ejecting the planet(s) from the system. A second possibility is related to the new model for planetesimal formation based on the direct formation of large planetesimals from the accumulation of small solid particles in turbulent structures of the gaseous disk (Johansen et al. 2007; Cuzzi et al. 2008). The onset of disordered motions is strongly favored in circumstellar disks in binaries due to the formation of strong spiral waves that not only affect the radial evolution of the disk but also influence the vertical structure of the disk, as shown in our models. The quick formation of large planetesimals may bypass the crucial stage of dust coagulation and subsequent planetesimal accumulation, even if it would not solve the problem of the high temperature able to prevent the condensation of icy dust grains.
5.2. Speculations on the long-term evolution
One limitation of our approach is related to the heavy computational load needed to complete a simulation. Even the 2D simulations performed by Nelson (2000) are limited to a few binary revolutions. The main cause of this is related to the energy equation solution that requires a very short time step owing to the large and short-term variations in internal energy of the gas at the shock waves and at the location where material from one disk impacts the other. In effect, our models and those presented in Nelson (2000) are the only ones where each star of the binary system has its own disk. Simulations of radiative disks with grid codes model only the disk around the primary star, and they do not have to deal with the mass exchange between the two disks. In SPH simulations it would in theory be possible to speed up the computations by implicitly solving the energy equation. However, this approach fails to properly follow the behavior of the gas internal energy in the highly perturbed environment of disks in binaries, as discussed in more detail in the next section. Concerning the long-term evolution of the system we have studied, it is encouraging that 2D simulations of radiative and self-gravitating disks in binaries (Müller & Kley 2012; Marzari et al. 2012) show stable behavior, that does not evolve significantly even at later stages. This is possibly related to the fast radiative damping of density waves as suggested in Marzari et al. (2012). The disk eccentricity and temperature profiles we obtain in 3D are similar to those observed for disks around the primary star in the previously mentioned papers, and they are self-similar after many binary revolutions. As a consequence, we may infer that the features we find in our simulations, such as the hydraulic jumps, are preserved during the subsequent evolution of the disks. As an additional test, we performed an isothermal simulation of the HIDECL model assuming a temperature profile similar to that of our radiative model at apocenter. After 20 binary revolutions, the main features due to the binary perturbations (spiral waves and vertical excursions) are still present and have the same morphology at any pericenter passage during the full length of the simulation. However, we have to point out that there are significant differences between the radiative and isothermal runs. As already pointed out by 2D simulations, spiral waves are damped more quickly in the radiative model as illustrated in the bottom plots of Fig. 16. The integrated density distribution of the primary disks in the radiative (left) and isothermal (right) models are compared in the same orbital configuration after the pericenter passage. The density waves are significantly less marked in the radiative case, suggesting that they are more effectively damped than in the isothermal one. The scale height of the disk is higher in the radiative case, and the hydraulic jumps have a significantly larger jump factor Jf (see Fig. 2) compared to the isothermal case illustrated in Fig. 16 top plot.
 |
Fig. 16 Upper plot: vertical slice of an isothermal disk with the HIDECL parameters shown after 20 binary revolutions near the pericenter passage. Lower plots: primary disks shortly after the binary pericenter. They show how density waves dissipate more quickly in the radiative disk (left plot) than in the isothermal disk (right plot). |
From Fig. 16 (top plot) it also appears that the
density beyond the shock wave is higher in the isothermal model. This may be analytically
justified when taking into account that in a radiative disk the ratio between the pre- and
post-shock densities can be estimated, according to Durisen (2011), as 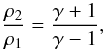 (47)for
M ≫ 1. In an isothermal disk, on the other hand, the ratio can be
approximated by
(47)for
M ≫ 1. In an isothermal disk, on the other hand, the ratio can be
approximated by 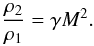 (48)In this last case,
the post-shock density is expected to be higher than in the radiative case.
(48)In this last case,
the post-shock density is expected to be higher than in the radiative case.
5.3. Future improvements
Alternative cooling algorithms can be explored to test their influence on the physical behavior of the disks. We tested the cooling algorithm proposed in Stamatellos et al. (2007) to solve the energy equation with an implicit time step with two different approaches: using the polytropic cooling term or with the hybrid approach proposed by Forgan et al. (2009) where the cooling is coupled to the flux-limited radiation diffusion already implemented in our algorithm. In both cases we observed the formation of unphysical mass condensations in the midplane of the disk after the passage of shock waves and significant spikes in the gas temperatures all over the disk. This is not due to the cooling and radiative transfer algorithms but to the application of the implicit time step. Using the same algorithms but with an explicit time step for the VINE leapfrog scheme, both problems disappeared, suggesting that they were related to the too long time step assumed in the implicit method not able to correctly follow the fast evolution of the internal energy in our type of system. We propagated our standard model HIDECL for a perihelion passage with the hybrid method proposed by Forgan et al. (2009) without the implicit time step, and the outcome is very similar to what is obtained with the boundary particle algorithm. The only noticeable difference is a slightly lower temperature of the gas where material from one disk impacts the other one. In Fig. 17 we show a vertical slice of the disk to be compared with that in Fig. 2 of the standard model HIDECL with boundary particles. Marked hydraulic jumps are visible in both figures, and only minor differences appear in the vertical density distribution.
 |
Fig. 17 Non-integrated disk density of the primary disk of the HIDECL model on the x − z plane. The hybrid method proposed by Forgan et al. (2009) for radiative cooling is used with an explicit time step. |
In our model we neglect stellar irradiation, which might be important at least in the outer parts of the disk where the viscous heating is less intense. However, it appears a complex problem to include the stellar flux since the hydraulic jumps in the vertical direction can shield the outer parts of the disk from stellar irradiation. Disk self-shadowing due to spiral waves may strongly reduce the amount of stellar irradiation on the disk surfaces. It would be necessary to adopt a ray-tracing approach for each particle. This appears feasible but might further increase the CPU load. In addition, the outer parts of the disks in our “close” models are strongly perturbed by tidal waves and mass exchange whose effects on the temperature may overcome those due to stellar irradiation.
It would also be interesting to explore the evolution of non coplanar disks to test the formation of spiral waves, warping, disk precession, and relaxation in this configuration. Previous SPH models (Larwood et al. 1996) were based on the polytropic approximation, while Fragner & Nelson (2010) used the isothermal approximation. Even in this case, the radiative part of the code might be critical in terms of CPU time possibly reducing the model timespan.
Acknowledgments
We thank an anonymous referee for useful comments and suggestions. Many of our plots were made with the SPLASH software package (Price 2007). We also thank D. Stamatellos for giving us his tabulated pseudo-mean opacities and internal energies.
References
- Armitage, P. J. 2010, Astrophysics of Planet Formation (Cambridge: Cambridge University Press) [Google Scholar]
- Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Asphaug, E., Jutzi, M., & Movshovitz, N. 2011, Earth Planet. Sci. Lett., 308, 369 [Google Scholar]
- Ayliffe, B. A., & Bate, M. R. 2009, MNRAS, 393, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Balsara, D. S. 1995, J. Comput. Phys., 121, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Bate, M. R., Bonnell, I. A., & Price, N. M. 1995, MNRAS, 277, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, K. R., & Lin, D. N. C. 1994, ApJ, 427, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Bitsch, B., & Kley, W. 2010, A&A, 523, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blum, J., & Wurm, G. 2008, ARA&A, 46, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boley, A. C., & Durisen, R. H. 2008, ApJ, 685, 1193 [NASA ADS] [CrossRef] [Google Scholar]
- Boley, A. C., Durisen, R. H., & Pickett, M. K. 2005, in Chondrites and the Protoplanetary Disk, eds. A. N. Krot, E. R. D. Scott, & B. Reipurth, ASP Conf. Ser., 341, 839 [Google Scholar]
- Bonavita, M., & Desidera, S. 2007, A&A, 468, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boss, A. P., & Durisen, R. H. 2005, ApJ, 621, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Boss, A. P., & Graham, J. A. 1993, Icarus, 106, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, B., Walker, G. A. H., & Yang, S. 1988, ApJ, 331, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Cassen, P., & Woolum, D. S. 1996, ApJ, 472, 789 [NASA ADS] [CrossRef] [Google Scholar]
- Ciesla, F. J., Hood, L. L., & Weidenschilling, S. J. 2004, Meteorit. Planet. Sci., 39, 1809 [NASA ADS] [CrossRef] [Google Scholar]
- Cleary, P. W., & Monaghan, J. J. 1999, J. Comput. Phys., 148, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Correia, A. C. M., Udry, S., Mayor, M., et al. 2008, A&A, 479, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuzzi, J. N., Hogan, R. C., & Shariff, K. 2008, ApJ, 687, 1432 [NASA ADS] [CrossRef] [Google Scholar]
- Daemgen, S., Correia, S., & Petr-Gotzens, M. G. 2012, A&A, 540, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desch, S. J., & Connolly, Jr., H. C. 2002, Meteor. Planet. Sci., 37, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Desch, S. J., & Cuzzi, J. N. 2000, Icarus, 143, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Desidera, S., & Barbieri, M. 2007, A&A, 462, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumusque, X., Pepe, F., Lovis, C., et al. 2012, Nature, 491, 207 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
- Durisen, R. H. 2011, Disk Hydrodynamics, ed. P. J. V. Garcia (Chicago: University of Chicago Press), 149 [Google Scholar]
- Eggenberger, A., Udry, S., & Mayor, M. 2004, A&A, 417, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Forgan, D., Rice, K., Stamatellos, D., & Whitworth, A. 2009, MNRAS, 394, 882 [NASA ADS] [CrossRef] [Google Scholar]
- Fragner, M. M., & Nelson, R. P. 2010, A&A, 511, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gingold, R. A., & Monaghan, J. J. 1977, MNRAS, 181, 375 [Google Scholar]
- Hood, L. L. 1998, Meteor. Planet. Sci., 33, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Hood, L. L., Ciesla, F. J., Artemieva, N. A., Marzari, F., & Weidenschilling, S. J. 2009, Meteorit. Planet. Sci., 44, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., Oishi, J. S., Mac Low, M.-M., et al. 2007, Nature, 448, 1022 [Google Scholar]
- Joung, M. K. R., Mac Low, M.-M., & Ebel, D. S. 2004, ApJ, 606, 532 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., & Nelson, R. P. 2008, A&A, 486, 617 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W., Bitsch, B., & Klahr, H. 2009, A&A, 506, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lada, C. J. 2006, ApJ, 640, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Larwood, J. D., Nelson, R. P., Papaloizou, J. C. B., & Terquem, C. 1996, MNRAS, 282, 597 [NASA ADS] [Google Scholar]
- Levermore, C. D., & Pomraning, G. C. 1981, ApJ, 248, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Levy, E. H., & Araki, S. 1989, Icarus, 81, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Lodato, G., & Price, D. J. 2010, MNRAS, 405, 1212 [NASA ADS] [Google Scholar]
- Lubow, S. H., & Ogilvie, G. I. 1998, ApJ, 504, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Martí, J. G., & Beaugé, C. 2012, A&A, 544, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martos, M. A., & Cox, D. P. 1998, ApJ, 509, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Marzari, F., & Barbieri, M. 2007a, A&A, 472, 643 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marzari, F., & Barbieri, M. 2007b, A&A, 467, 347 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marzari, F., & Scholl, H. 2000, ApJ, 543, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Marzari, F., Scholl, H., Thébault, P., & Baruteau, C. 2009, A&A, 508, 1493 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marzari, F., Baruteau, C., Scholl, H., & Thebault, P. 2012, A&A, 539, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, B. D., Gies, D. R., Hartkopf, W. I., et al. 1998, AJ, 115, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Meru, F. 2010, Ph.D. Thesis [Google Scholar]
- Meru, F., & Bate, M. R. 2012, MNRAS, 427, 2022 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, D., & Mihalas, B. W. 1984, Foundations of radiation hydrodynamics (New York: Oxford University Press), 731 [Google Scholar]
- Monaghan, J. J. 1985, Comp. Phys. Rep., 3, 71 [Google Scholar]
- Monaghan, J. J., & Gingold, R. A. 1983, J. Comput. Phys., 52, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Mordasini, C., Alibert, Y., Klahr, H., & Henning, T. 2012, A&A, 547, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morfill, G., Spruit, H., & Levy, E. H. 1993, in Protostars and Planets III, eds. E. H. Levy, & J. I. Lunine, 939 [Google Scholar]
- Morris, J. P., & Monaghan, J. J. 1997, J. Comput. Phys., 136, 41 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Morris, M. A., Boley, A. C., Desch, S. J., & Athanassiadou, T. 2012, ApJ, 752, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Mugrauer, M., & Neuhäuser, R. 2009, A&A, 494, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mugrauer, M., Neuhäuser, R., Seifahrt, A., Mazeh, T., & Guenther, E. 2005, A&A, 440, 1051 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, T. W. A., & Kley, W. 2012, A&A, 539, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakamoto, T., Hayashi, M. R., Kita, N. T., & Tachibana, S. 2005, in Chondrites and the Protoplanetary Disk, eds. A. N. Krot, E. R. D. Scott, & B. Reipurth, ASP Conf. Ser., 341, 883 [Google Scholar]
- Nelson, A. F. 2000, ApJ, 537, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, A. F., Wetzstein, M., & Naab, T. 2009, ApJS, 184, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Osorio, M., D’Alessio, P., Muzerolle, J., Calvet, N., & Hartmann, L. 2003, ApJ, 586, 1148 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J., Thébault, P., & Mellema, G. 2008, MNRAS, 386, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Pilipp, W., Hartquist, T. W., Morfill, G. E., & Levy, E. H. 1998, A&A, 331, 121 [NASA ADS] [Google Scholar]
- Price, D. J. 2007, PASA, 24, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D. J., & Monaghan, J. J. 2004, MNRAS, 348, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D. J., & Monaghan, J. J. 2007, MNRAS, 374, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Queloz, D., Mayor, M., Weber, L., et al. 2000, A&A, 354, 99 [NASA ADS] [Google Scholar]
- Reipurth, B. 2000, AJ, 120, 3177 [CrossRef] [Google Scholar]
- Roberts, Jr., W. W., Huntley, J. M., & van Albada, G. D. 1979, ApJ, 233, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez, L. F., D’Alessio, P., Wilner, D. J., et al. 1998, Nature, 395, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Rosswog, S., Davies, M. B., Thielemann, F.-K., & Piran, T. 2000, A&A, 360, 171 [NASA ADS] [Google Scholar]
- Ruzmaikina, T. V., & Ip, W. H. 1994, Icarus, 112, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, I. S., & Taylor, G. J. 2005, in Chondrites and the Protoplanetary Disk, eds. A. N. Krot, E. R. D. Scott, & B. Reipurth, ASP Conf. Ser., 341, 915 [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Springel, V., & Hernquist, L. 2002, MNRAS, 333, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Stamatellos, D., Whitworth, A. P., Bisbas, T., & Goodwin, S. 2007, A&A, 475, 37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thébault, P., Marzari, F., Scholl, H., Turrini, D., & Barbieri, M. 2004, A&A, 427, 1097 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thébault, P., Marzari, F., & Scholl, H. 2006, Icarus, 183, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Thébault, P., Marzari, F., & Scholl, H. 2008, MNRAS, 388, 1528 [NASA ADS] [CrossRef] [Google Scholar]
- Thébault, P., Marzari, F., & Scholl, H. 2009, MNRAS, 393, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Urey, H. C. 1967, Icarus, 7, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Urey, H. C., & Craig, H. 1953, Geochim. Cosmochim. Acta, 4, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J., Marzari, F., & Hood, L. L. 1998, Science, 279, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Wetzstein, M., Nelson, A. F., Naab, T., & Burkert, A. 2009, ApJS, 184, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Whitehouse, S. C., & Bate, M. R. 2004, MNRAS, 353, 1078 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, J. A. 1996, Meteorit. Planet. Sci., 31, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Xie, J.-W., & Zhou, J.-L. 2009, ApJ, 698, 2066 [NASA ADS] [CrossRef] [Google Scholar]
- Xie, J.-W., Zhou, J.-L., & Ge, J. 2010, ApJ, 708, 1566 [NASA ADS] [CrossRef] [Google Scholar]
- Zucker, S., & Mazeh, T. 2002, ApJ, 568, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Zucker, S., Mazeh, T., Santos, N. C., Udry, S., & Mayor, M. 2004, A&A, 426, 695 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Temperature profiles as a function of the height over the median plane of the disk (z component) for the primary disk at r ~ 6 AU and for the secondary disk at r ~ 3 AU. These locations are far from the center of the disk where the heating due to the spiral waves, even at apocenter, is the strongest. The dots are the individual temperatures of the SPH particles encompassed between 6 and 6.3 AU for the primary disk and 3 and 3.3 AU for the secondary disk. The continuous lines are the average temperature values. The SPH particles of the primary disk are represented by red dots, while blue dots are relative to the secondary disk. |
| In the text | |
 |
Fig. 2 Top plot: logarithm of the superficial density (column integrated) of the circumstellar disks for HIDECL (high density, small binary semi-major axis) shown during the pericenter passage of the secondary star. Bottom panels: density (non-integrated) drawn along the x − z and y − z sections of the primary disk (2nd and 3rd panels) and secondary disk (4th and 5th panels). |
| In the text | |
 |
Fig. 3 Vertically integrated vortensity in the primary disk during the pericenter passage in the HIDECL model. |
| In the text | |
 |
Fig. 4 Velocity field and density of a slice in the (x,z) plane in the region of hydraulic jumps for the primary (top panel) and secondary (bottom panel) in the HIDECL model. Both disks are centered on their parent stars to properly compute the gas velocity field. The scales in x and z are different in the two plots and, in addition, the star is on the right in the top plot (circumprimary disk), while it is on the left in the bottom one (circumsecondary disk). |
| In the text | |
 |
Fig. 5 Temperature distribution in the two disks computed at their median plane when the stars are close to the pericenter (upper panel) and apocenter (lower panel) in the HIDECL model. |
| In the text | |
 |
Fig. 6 Azimuthally and vertically averaged temperature profiles of both disks in the HIDECL model when the stars are at pericenter and apocenter, respectively. The secondary disk is less dense than around the primary, so its temperature is on average lower. |
| In the text | |
 |
Fig. 7 Density distribution of the secondary disk when the stars are at the pericenter in the HIDECL model. A new spiral arm is created by the material transferred from the primary disk and impacting the outer edge of the secondary. |
| In the text | |
 |
Fig. 8 Temperature distribution of the material flowing from the circumprimary disk to the circumsecondary in the HIDECL model. The impact on the secondary of the flow from the primary is marked by a raise in the temperature. |
| In the text | |
 |
Fig. 9 Disk eccentricity profiles, averaged on azimuth and vertical direction, of the primary and secondary disks in the HIDECL and LODECL models. The eccentricity is computed at the apocenter when the strong spiral arms have almost completely dissipated. |
| In the text | |
 |
Fig. 10 Azimuthally and vertically averaged temperature profiles of the low-density disk (LODECL model) around the primary star compared to the high-density case (HIDECL) with the binary at pericenter and apocenter. The lower density disk is cooler in both cases. |
| In the text | |
 |
Fig. 11 3D picture of the density distribution of the disks in the LODECL model close to the binary pericenter. Large vertical jumps can be observed at the shock waves. The surfaces are drawn at τ ~ 2. |
| In the text | |
 |
Fig. 12 Integrated density profile of the disks in the HIDEFA model shortly after the pericenter (upper panel). The non-integrated density of the disk around the secondary star is shown in the x − z plane. Shock bores are visible even if less marked than in the HIDECL case. The hydraulic jumps in the primary are of negligible height. |
| In the text | |
 |
Fig. 13 Comparison of the azimuthally and vertically averaged temperature profiles in the HIDEFA and HIDECL cases at pericenter (upper panel) and apocenter (lower panel) for both disks. At apocenter the temperature of the primary disk in the HIDEFA and HIDECL cases is very similar. |
| In the text | |
 |
Fig. 14 Temperature profiles at the binary pericenter in the LODEFA and HIDEFA cases for both the primary and secondary disks. |
| In the text | |
 |
Fig. 15 Eccentricity profiles for both disks in the two distant (aB = 50 AU) HIDEFA and LODEFA cases. The same scale of Fig. 9 is adopted for comparison. |
| In the text | |
 |
Fig. 16 Upper plot: vertical slice of an isothermal disk with the HIDECL parameters shown after 20 binary revolutions near the pericenter passage. Lower plots: primary disks shortly after the binary pericenter. They show how density waves dissipate more quickly in the radiative disk (left plot) than in the isothermal disk (right plot). |
| In the text | |
 |
Fig. 17 Non-integrated disk density of the primary disk of the HIDECL model on the x − z plane. The hybrid method proposed by Forgan et al. (2009) for radiative cooling is used with an explicit time step. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


