| Issue |
A&A
Volume 556, August 2013
|
|
|---|---|---|
| Article Number | A118 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201321811 | |
| Published online | 06 August 2013 | |
The occultation of HIP 107302 by Jupiter⋆
1
Armagh Observatory,
College Hill,
Armagh,
BT61 9DG
UK
e-mail:
aac@arm.ac.uk
2 International Occultation Timing Association – European
Section
3 Institut de Ciències de l’ Espai (IEEC – CSIC), Spain
4
Agrupació Astronòmica de Sabadell, 08200
Barcelona,
Spain
5 Instituto de Astrofísica de Canarias, 38205 La Laguna
( Tenerife), Spain
6
Universidade Federal do Rio de Janeiro, Observatorio do
Valongo, Ladeira Pedro Antonio
43, 20080-090
Rio de Janeiro,
Brazil
7
IMCCE/Observatorie de Paris, 77 Avenue Denfert Rochereau, 75014
Paris,
France
8
Observatorio Nacional/MCT, R. General Jose Cristino 77, 20921-400
Rio de Janeiro,
Brazil
9
Observatoire de Paris/LESIA, bâtiment 10, 92195
Meudon Cedex,
France
10
IAS Observatory, 9000
Hakos,
Namibia
11
Astronomical Union of Sparta, 23100
Sparta,
Greece
12
Ellinogermaniki Agogi Observatory, Dimitrios Panegeas Str., 153 51
Pallini,
Greece
13
Department of Astrophysics, Astronomy and Mechanics, University of
Athens, Panepistimiopolis, 157 84
Zografos, Athens,
Greece
Received: 1 May 2013
Accepted: 21 June 2013
Aims. Occultations of bright stars by planets provide information on the state of their atmospheres. An occultation of the bright star 45 Capricornii (HIP 107302) by Jupiter occurred on the night of 3/4 August 2009.
Methods. The event was observed at multiple sites in Europe, Africa and South America and with instruments ranging in aperture from 0.4 m to 2.2 m. All observations, except one, were carried out in methane absorption bands centred at 0.89 μm and 2.2 μm to minimise the planetary contribution to the measured stellar flux. Following the application of special post-processing techniques, differential photometry was performed. Nearby bright satellites were used as reference sources.
Results. Fifteen lightcurves were obtained. The photometric time series for fourteen of these were fitted to a model atmosphere of constant scale height (H). Estimates of H for most lightcurves lie within the range 20−30 km with an inverse-variance weighted mean of 23.6 ± 0.4 km, in good agreement with previous works. A comparison between half-light times at ingress and at egress implies an astrometric offset of 10−15 mas in Jupiter’s position relative to the star. Five lightcurves – two for ingress and three for egress – were numerically inverted into profiles of pressure versus temperature. Isothermal, mutually consistent behaviour is observed within the pressure range 3−10 μbar. The inferred temperature of 165 ± 5 K is consistent with, but slightly higher than, that measured by the Galileo Probe at 5° S latitude in 1995 at the same pressure level. Subtraction of isothermal models for nine cases show the presence of at least one, and possibly two, non-isothermal layers a few tens of km below the half-light datum. Their altitudes are similar to those of features previously reported during the occultation of HIP 9369 in 1999. Our temperature estimates are consistent with the expected small magnitude of the perturbation of the atmosphere following the impact event on Jupiter in July 2009.
Key words: planets and satellites: atmospheres / planets and satellites: individual: Jupiter / occultations / methods: observational / methods: data analysis
Data for the lightcurves are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/556/A118
© ESO, 2013
1. Introduction
Photometric monitoring of stellar occultations is an established method of determining the structure and variability of planetary and satellite atmospheres (Elliot & Olkin 1996). In the case of ground-based optical observations, the objective is to measure starlight attenuated by the intervening atmosphere due to differential refraction. This is complementary to monitoring a spacecraft’s radio signal as the latter disappears and reappears behind the planetary body (e.g. Lindal et al. 1981; Lindal 1992) or by direct observation of a stellar source in the UV where attenuation of the stellar flux is due to absorption (e.g. Festou et al. 1981; Greathouse et al. 2010). In particular, the optical method generally samples a different atmospheric pressure regime than the other methods and does not require a spaceborne platform. On the other hand, the ground-based method requires a sufficiently bright star to act as source and such opportunities are relatively rare. In addition, the organising of an observing campaign appropriately resourced to ensure a successful outcome is not a trivial undertaking. For the case of Jupiter, scientifically useful ground-based results have been obtained from campaigns involving the stars σ Arietis (V = 5.5; Baum & Code 1953), β Scorpii A & C (V = 2.63/4.92; Hubbard et al. 1972; Vapillon et al. 1973; Veverka et al. 1974), SAO 78505 (V = 8.7; Hubbard et al. 1995) and HIP 9369 (V = 7.6; Raynaud et al. 2003). The β Scorpii campaign, in particular, highlighted the numerous difficulties involved in the process of “inverting” the observed lightcurves into atmospheric temperature/pressure/density profiles.
 |
Fig. 1 Left: co-added images obtained during the ingress in the K-band with the Carlos Sánchez Telescope (Observatorio del Teide, Tenerife, Canary Islands; SCHMAS). North is towards the lower left and East towards the lower right. The bright feature near the south pole transiting the central meridian is the spot left by the impact of an asteroid or comet on July 19th. Right: co-added images for Egress. Note that the impact spot has rotated towards the western limb of the planet. |
Summary of observations.
A new campaign was organised in 2009 to observe the occultation of the bright star HIP 107302 (45 Capricornii, V = 5.5; hereafter referred to as “45 Cap”) by Jupiter during the night of 3rd to 4th August 2009. Its occurrence during the summer encouraged the participation of a large number of both amateur and professional observers as a “stress test” for an amateur-professional collaboration. Moreover, the latitude of the star’s ingress and egress locations in Jupiter’s atmosphere (46−59° S; planetographic latitudes are used throughout this paper unless otherwise stated) was similar to that of β Scorpii A during its 1971 occultation by the planet (47−60° S). Therefore, a direct comparison between the two sets of results could be made. Finally, the fortuitous detection of an impact-generated dark spot on Jupiter’s atmosphere on 2009 July 19th, two weeks prior to the occultation (CBET 1882) and at a similar latitude (57° S), raised the question of whether changes in Jupiter’s atmosphere could be detected on this occasion, as a result.
This paper presents and discusses the results of this campaign. The following Section reports on the observations and data reduction. Section 3 reports on the results and their analysis. Section 4 discusses the 2009 impact while Sect. 5 presents our conclusions and future plans.
2. Observations and data reduction
The occultation was recorded by both fixed and mobile observing stations in Europe, Africa and South America wherever Jupiter was sufficiently high in the sky at ingress, egress or both (Table 1). In all cases but one, the observations were made in those regions of Jupiter’s spectrum where deep absorption bands due to methane are present (Karkoschka 1994) in order to minimise the contribution of the atmosphere to the observed flux. As an example, we present in Fig. 1 the full image sequence obtained at SCHMAS during stellar ingress and egress. The cadence used by the different observers was in the range 0.4−10 s. The egress lightcurve of BATH (Hakos, Namibia) was cut short due to technical problems. Egress was missed at RCASAS (Sabadell, Spain) due to clouds while Jupiter was too low in the sky from ASRIB (Pico dos Dias, Brazil) during ingress. Seven ingress profiles were acquired at the planetographic coordinates 105° W (System III), 46−56° S on the IAU_JUPITER reference ellipsoid (Seidelmann et al. 2007) and eight egress profiles at 300° W, 47−59° S.
Even with the reduced contribution of Jupiter’s scattered light, measuring the flux from the star is not straightforward. After bias, dark and flat field correction and treatment of bad pixels, either one of the following two methods were used to reduce the data:
-
1.
The images were aligned using Jupiter as a reference. Using those images obtained while the star was occulted by Jupiter, a template for the planet was created. Following removal of satellites and replacement with a synthetic background, the template was subtracted from each image in the corresponding series. An example of an image after template subtraction may be seen in Fig. 2. Photometry was then carried out by using static apertures of different sizes and a satellite as reference. In the case of stellar reappearance at SCHMAS no reference was used because no satellites were present in the images (right panel of Fig. 1).
-
2.
Firstly, the photocentre of the star relative to a nearby moon – JII (Europa) for Ingress and JI (Io) for Egress – was determined. Then the intensity of 45 Cap, the Jovian limb, the sky background and the Jovian background with apertures with radii from 2 to 7 pixels with an increment of 1 pixel were determined. Subtracting the intensities of the background from the aperture intensities of 45 Cap yielded the final intensity. The procedure was tested by checking the uniformness of the Jovian background several tens of minutes after the star was occulted. The fractional variation of Jupiter’s background flux was found to be 0.5% of the flux from the star.
 |
Fig. 2 Single frame from the sequence obtained at RCASAS and at 22:55:01 UT, mask subtracted and showing the star (close to the planetary limb) and two satellites (Europa and Ganymede). The bright feature indicated by the arrow is the Great Red Spot. Image orientation is the same as in Fig. 1. |
 |
Fig. 3 Lightcurves of the occultation’s ingress (left column) and egress (right column) phases obtained in this work. |
3. Data analysis
3.1. Reproducing the event geometry
To convert the reduced data into information on Jupiter’s atmosphere requires that the relative geometry between the star, Jupiter and the observer was reproduced to the degree allowed by the respective ephemeris uncertainties. This was done using subroutines and ephemeris kernels available within the SPICE package (Acton 1999) and implemented within a wrapper programme written in C by one of us (AAC). The observed lightcurves were referred to altitudes above the IAU_JUPITER reference ellipsoid – an oblate spheroid of revolution with major and minor axes of 71 492 and 66 854 km respectively (Seidelmann et al. 2007) – corresponding to the 1-bar pressure level. The stellar coordinates at the epoch of observation were computed from the first edition of the Hipparcos catalogue (Perryman 1997) and shown in Table 2. The stated positional uncertainties have been propagated to the observation epoch based on the proper motion uncertainties and those of the star’s position at the catalogue epoch. These are principally due to the propagation of the proper motion uncertainties to the epoch of observation. We have compared the obtained position with that propagated from the new edition of the Hipparcos catalogue and found a difference of ~2 milliarcsec (mas), well within the stated uncertainties. We could find no evidence for variability or duplicity in the literature. As a further attempt to quantify the uncertainty in the star’s position, we have compared its Hipparcos position with that given in the Tycho-2 catalogue (Hog et al. 2000). A difference of 12 mas, principally in the direction of right ascension, was found. This corresponds to a height increment of 30 km in Jupiter’s atmosphere or 3 s in time.
Astrometric and spectroscopic data on 45 Capricornii.
3.2. Baum-Code fits
Assuming an isothermal atmosphere at the altitudes sampled by the data, a fit of the altitude and observed stellar flux pairs 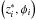 yields estimates of the scale height H and ephemeris altitude at half-light
yields estimates of the scale height H and ephemeris altitude at half-light 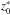 (or, equivalently, the time of half-light t0 if the observation times ti are used as the independent parameter). We note here that this altitude corresponds to the closest approach of the observer-star line-of-sight to the Jovian reference ellipsoid, as provided by the ephemeris, and is approximately proportional to time. To distinguish it from the altitude z of the refracted light ray calculated from inverting the lightcurves (Sect. 3.4), we shall refer to the former as the “ephemeris altitude” and denote it by z∗. The model fitted to the observations is that of Baum & Code (1953):
(or, equivalently, the time of half-light t0 if the observation times ti are used as the independent parameter). We note here that this altitude corresponds to the closest approach of the observer-star line-of-sight to the Jovian reference ellipsoid, as provided by the ephemeris, and is approximately proportional to time. To distinguish it from the altitude z of the refracted light ray calculated from inverting the lightcurves (Sect. 3.4), we shall refer to the former as the “ephemeris altitude” and denote it by z∗. The model fitted to the observations is that of Baum & Code (1953): 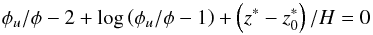 (1)where φu is the flux of the unocculted star and log denotes the natural (base e) logarithm.
(1)where φu is the flux of the unocculted star and log denotes the natural (base e) logarithm.
A nonlinear fit to Eq. (1) was carried out using the Levenberg-Marquardt method as implemented in the Mathematica v8 package (Wolfram 1991). The results are shown in Table 3, where the stated uncertainties correspond to the 95% confidence level (1.96σ). As a check of the procedure, a linear regression fit, where the first two terms in Eq. (1) were treated as the ordinate, was carried out on the SCHMAS (ingress + egress) lightcurves independently by one of us. The resulting estimates of t0 and H were found to be within 1.5 s and 2 km respectively of the corresponding values in Table 3. Following Raynaud et al. (2004), we also investigated the effect of adding a pedestal to the model in order to account for imperfections in the subtraction of the background flux. An additive constant k was fitted to the normalised stellar flux simultaneously with the other two parameters. We find that in all cases | k| < 0.03 with a median of 0.01. We have decided to adopt the three-parameter fit for all lightcurves.
Results of Baum-Code fits.
Inspection of the parameter estimates from the Baum-Code model fit indicates that the ephemeris altitudes of half-light at ingress are systematically higher than those at egress. A Student t-test carried out on the differences (ingress – egress) rejects the hypothesis that these were drawn from a zero mean distribution at a >99% level. The least square estimate of the offsets is 127.9 ± 16.3 (93.3 ± 2.3) km, where the brackets indicate that the measurements were weighted with the inverses of the 1σ variances from Table 3.
Assuming a typical Jovian latitude for both ingress and egress of 55° S, the corresponding ephemeris shift required to eliminate this asymmetry in the ingress (egress) altitudes at half-light is 111.5 ± 3.6 (81.3 ± 1.3) km or 30 (22) mas in right ascension. This is somewhat higher than the correction due to relativistic effects (~50 km; cf. Eq. (3) of Cooray et al. 1998). Applying the shift, the respective means for ingress and egress become 505 and 471 km.
A short discussion of the uncertainties is appropriate here. These are probably underestimated due to systematics in some of the lightcurves. For example, timing errors at each observing site would introduce an error of 10 km for every second of clock offset. However, we deem it unlikely that such systematics, originating from many independent observations, would coherently combine in such a way as to produce an offset of this magnitude. In conclusion, we attribute the inferred ephemeris offset, minus the relativistic correction, of ~50 km or 10−15 mas in the ephemeris of Jupiter relative to the star to a combination of the uncertainty in the star’s (see Sect. 3.1) as well as Jupiter’s position with respect to the Earth (Folkner et al. 2009).
 |
Fig. 4 Scale heights from fitting the Baum-Code law to our lightcurves, compared to the estimates from previous works. |
3.3. Isothermal scale heights and temperatures
Our estimates of the scale height H are compared with those obtained by other authors in Fig. 4 as a function of planetographic latitude. This is essentially an update of Fig. 4 from Hubbard et al. (1995). We considered only those past estimates (filled red circles) that were accompanied by uncertainty information. These cluster in three groups. Group I contains 20 data points, at high southern latitudes, including our data as well as data corresponding to the 1971 β Scorpii A occultation from Hubbard et al. (1972) and Raynaud et al. (2004). The latter authors recalculated previous estimates from Vapillon et al. (1973), correcting for the contribution of the background flux to the lightcurves. Group II has 5 data points, at near equatorial latitudes, containing the SAO 78505 data from Hubbard et al. (1995) as well as β Scorpii B data from Hubbard et al. (1972). Finally, Group III has 8 data points, at high northern latitude, the estimates by Raynaud et al. (2003) corresponding to the occultation of HIP 9369. To facilitate the comparison, our estimates are shown as open diamonds if the 2σ formal uncertainty is 5 km or less and open circles otherwise.
To compare these three groups, we calculated the respective means, where the individual estimates of H are weighted with their inverse variances. The uncertainties in Table 3, as well as those in Raynaud et al. (2003, 2004), were divided by 1.96 to convert them to Gaussian 1σ variates. Estimates from the MCDIAZ observations were assigned zero weight since the cadence was insufficient to resolve an H ~ 25 km atmosphere. While carrying out the fit, it was recognised that the very small uncertainty for one of two estimates from Raynaud et al. (0.2 km; 2004) was driving the final result for Group I. For that reason, and because this value is an order of magnitude smaller than the smallest formal uncertainties in the remainder of the sample, we relaxed the uncertainty for this estimate to 1.7 km. The weighted means for Groups I, II and III respectively are then 23.8 ± 0.3, 28.8 ± 1.4 and 24.5 ± 0.5 km. Considering the subset of Group I containing the results for 45 Cap alone yields an estimate of 23.6 ± 0.4 km while considering all the data together yields 24.2 ± 0.3 km. In an isothermal atmosphere, the temperature T is related to the scale height H through the relationship T = Hμg/R where μ is the mean molecular weight, g the gravitational acceleration and R the universal gas constant. Adopting μ = 2.29 g from Raynaud et al. (2003) and g = 25 m s-2, the corresponding temperatures for the different groups are 164 ± 2 K, 198 ± 10 K, 168 ± 4 K respectively. The estimate that results from considering all the data together is 166 ± 2 K.
 |
Fig. 5 Sensitivity of the numerical inversion of a model lightcurve to Gaussian random noise (left) and the pedestal value (right). See text for details. |
 |
Fig. 6 Atmospheric profiles derived in this work compared with in situ data from the Galileo Probe ASI investigation. Left: ingress profiles from data acquired at Teide (SCHMAS), Calar Alto (EBACAS) and Hakos (BATH). Right: egress profiles from data acquired at Pico dos Dias (ASRIB) and Teide (SCHMAS). |
Taken at face value, these results indicate that a different scale height, and a different effective temperature by implication, applies to high and low latitudes. However, it is pertinent to state the following caveats: (i) the three groups are represented by different sample sizes, (ii) as we have just indicated, the weighted least squares procedure is driven by the highest quality (i.e. smaller σ) subset of the sample where systematic errors such as timing offsets or imperfect background estimation and subtraction during data reduction (Hubbard et al. 1972; Raynaud et al. 2004) could creep in, and (iii) as pointed out by Wasserman & Veverka (1973), the isothermal (i.e. constant scale height) assumption is not a necessary condition for a good Baum-Code fit to the lightcurves; this model produces an “effective” scale height.
An alternative method of comparing the three groups is by considering that, under certain assumptions, the sample median is a maximum likelihood estimator (MLE; see Appendix). This alleviates the above caveats to a degree, since it is independent of the uncertainties related to the individual estimates of H. The MLEs for the three Groups are then 23.8 (164), 30.0 (207) and 26.6 (183) km (K) while the MLE for the entire sample is 25.0 km (172 K).
From these results, the strongest statement we feel justified in making is that the typical “effective” scale height corresponding to the half-light altitude appears to be smaller (implying colder temperatures) at high latitudes than at the equator. The issue of temperature determination is revisited in the following two Sections.
3.4. Lightcurve inversion
Occultation lightcurves of sufficient quality (i.e. of low enough systematic and random error) can be inverted to provide information on atmospheric temperature and density as a function of height or an equivalent parameter (e.g. pressure). For this reason, a programme was written in C based on the algorithm for the numerical inversion of the Abelian integral described by Wasserman & Veverka (1973). Assuming that refracted light rays from the star do not cross and for an assumed atmospheric composition, one obtains the atmospheric refractivity as a function of altitude followed by the density, temperature and pressure. The performance of the method is dependent on the starting conditions at the top of the atmosphere and can typically be relied upon to converge below the half-light level. To choose suitable starting conditions, we have adopted Wasserman & Veverka’s “Method A”, whereby the algorithm is iterated with a quasi-scale height
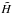 computed by a linear regression fit at the previous iteration and used to estimate a new boundary condition at the top of the atmosphere for the next iteration. In our case, the temperature and pressure are set to zero for the first iteration while the refractivity is given a value of 10-15. In those authors’ notation, the pressure P1 at the top of the atmosphere for the next iteration is back-extrapolated from a level N by
computed by a linear regression fit at the previous iteration and used to estimate a new boundary condition at the top of the atmosphere for the next iteration. In our case, the temperature and pressure are set to zero for the first iteration while the refractivity is given a value of 10-15. In those authors’ notation, the pressure P1 at the top of the atmosphere for the next iteration is back-extrapolated from a level N by
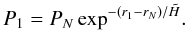 Usually, the pressure boundary converges to some non-zero value after 2−3 iterations.
Usually, the pressure boundary converges to some non-zero value after 2−3 iterations.
Inversion algorithms of this type have been shown to be sensitive to the correct separation of the stellar flux from the background (Veverka et al. 1974; Raynaud et al. 2004). A variational study is usually done to establish the sensitivity of the result to the various parameters (e.g. Raynaud et al. 2003). Here, we restrict ourselves to: (a) the effects of random photometric noise; and (b) systematics in estimating the stellar flux. We have generated a synthetic lightcurve that obeys the Baum-Code law (Eq. (1)) evaluated at the same times as the SCHMAS ingress lightcurve and with the same scale height (H ≃ 21 km). This synthetic lightcurve is then populated with different amounts of Gaussian random noise in the first instance and, in the second, a small “pedestal” value is added to the model flux. The result of processing these lightcurves with our programme is shown in Fig. 5. In the ideal case, the algorithm recovers the temperature corresponding to the chosen value of the scale height. The addition of moderate amounts of noise (2−3%) delays convergence to the correct temperature to higher pressures but a precision of ±10 K is achieved at and below the ~5 μbar level. Increasing the noise level to 5% renders the issue of determining convergence itself problematic; nevertheless, an estimate not too different (by 15 K) from the actual value is obtained at the 10 μbar level. On the other hand, the presence of even a small (0.35%) systematic under- or over-estimate in the flux has more severe consequences. There, the computed profiles exhibit a slope at higher pressure levels so that the computed temperatures are within 10 K of the model value below 5 and above 100 μbar.
 |
Fig. 7 Profile of stellar flux with model lightcurve subtracted against altitude relative to the instant of half-light in every case. The arrows indicate the position of prominent features (“spikes”) observed in the ingress profiles (left) and their expected locations in the egress ones (right). Profiles at ingress (egress) are horizontally separated by 0.5 (0.4) units for clarity. |
3.5. Pressure vs. temperature profiles
Based on these tests, we have chosen to apply the algorithm to the 9 highest quality lightcurves: SCHMAS, ASRIB, EBACAS, EPPICH and BATH. The convergence to a profile is reached when (a) a segment of the derived profile is isothermal; (b) the constant scale height that corresponds to this segment is within a few km (typical rms in Table 3) of the ones obtained in the isothermal fits. During this procedure, the algorithm failed to converge for 4 of the profiles. The remaining 5 are shown in Fig. 6 for ingress (left panel) and egress (right panel). The profile obtained by the Atmospheric Structure Investigation (ASI) experiment onboard the Galileo Probe (Seiff et al. 1996) is also plotted for comparison. In the interval 3−10 μbar, our data show an isothermal profile with a temperature in the range 160−170 K for both ingress and egress, consistent with a temperature of 164 ± 2 K calculated from the isothermal fits in Sect. 4.1. It is also in agreement with the two profiles analysed by Raynaud et al. (2003) at the same planetographic latitude as our observations, albeit in the northern hemisphere of the planet. In addition, it compares favourably with temperatures of 155−165 K found by ASI over the same range of pressures. Raynaud et al. (2004) re-analysed occultation photometry of β Scorpii A obtained in 1971 at latitudes of 56−59°. They found significantly different temperatures between ingress and egress, 190 K and 150 K respectively. Those data were, however, obtained at planetographic (System III) longitudes 320 W and 200 W respectively, significantly different than ours and those of Raynaud et al. (2003). Our data highlight the uniqueness of the 1971 profiles and suggests either temporal or longitudinal variability in Jupiter’s atmosphere at the altitudes probed by ground-based stellar occultation techniques.
Finally we discuss the Calar Alto profile in the left panel of Fig. 6. It approaches isothermal behaviour at significantly lower altitudes (>20 μbar) and shows significantly higher temperatures, 200−220 K. Such high temperatures have been reported previously and attributed to auroral heating (Raynaud et al. 2003) at latitudes ~70°S. However, the Calar Alto observations sampled lower latitudes (55−60 S) for which Raynaud et al. found temperatures of 160−170 K, similar to our results for our other profiles, which sampled the same latitude range as Calar Alto. An inspection of the original frames showed the pixel signal within the available reference satellite sources to be close to the saturation level of the detector. This may be responsible for the significant amount of noise (1σ of 10%) in the photometry of the star before immersion and following emersion (Fig. 3). The Baum-Code fit procedure is likely minimally affected – the procedure effectively “averages through” the noise – but the impact on the lightcurve inversion procedure may have been sufficient to produce an anomalous profile due to the top-down nature of the algorithm. For these reasons, we believe that the Calar Alto result should be treated with caution.
3.6. Non-isothermal layers
Our best quality, highest time resolution lightcurves (Fig. 3) show fluctuations of the stellar brightness (“spikes”) that rise significantly above the ambient noise level. As pointed out by Raynaud et al. (2003), these are due to non-isothermal features i.e. where significant temperature fluctuations take place at specific altitudes in the Jovian atmosphere. In an attempt to correlate spikes between different lightcurves and thus identify such features in our data, we have subtracted a Baum-Code model lightcurve from each profile using its estimated scale height from Table 3 and referred the result to the altitude of half-light. We remind the reader that the process of retrieving the altitudes z as a function of time is a byproduct of the retrieval of the refractivity. The results have been plotted in Fig 7 for ingress (left panel) and egress (right panel) respectively. As the BATH an EPPICH observations took place within a few hundreds of m of each other and have similar time resolutions we expect that real atmospheric structure will result in mutually correlated features in those photometric profiles. In the ingress case, one prominent feature (hereafter referred to as “top”; top arrow) is identified at approximately 10−20 km below the half light level in the BATH and EPPICH data. It also appears in the EBACAS lightcurve and is probably present in the coarser time resolution SCHMAS data as well. A second feature (“bottom”; bottom arrow) of lesser amplitude in the interval 25−40 km appears in the BATH and EPPICH profiles with evidence for it in the other two profiles as well. We regard the top feature to be real and the bottom one probably so. The egress profiles, on the other hand, are generally devoid of structure with no clear evidence of the features identified in the ingress data or strong correlations of features seen between different lightcurves. A different distribution of features at ingress and egress was also observed in the temperature gradient profiles by Raynaud et al. where photometric spikes take the form of local minima (their Fig. 10). Our top feature occurs at the same altitude as their feature “B” and a similar, albeit weaker, statement can be made for our bottom feature and their feature “C”. Since the top feature was detected at both Namibia and Calar Alto, its spatial extent in Jupiter’s atmosphere corresponds to ~9° of latitude or ~2000 km.
4. The 2009 July 19th impact on Jupiter
Two weeks previous to these observations, the sudden appearance of a dark feature on Jupiter’s southern hemisphere (57°S) was reported by A. Wellesley (CBET 1882). Subsequent follow-up (IAUC 9060) established it as being most likely due to an impact by a comet or asteroid on the planet, similar to the D/1993 F2 (Shoemaker-Levy) impact in 1994. For the latter event, elevated atmospheric temperatures – by several tens of deg K – were observed near several of the impact sites and at pressure levels of 3 μbar which persisted for several days. These perturbations attenuated over time, but remained detectable up to 8−10 days post-impact. Temperatures 10 K colder than pre-impact conditions were reported by Moreno et al. (2001) at the 10 μbar pressure level 2−3 weeks after the impacts.
At the time of our observations, the impact feature spanned ~30° in longitude and ~7° in latitude, from 60° S to 53° S (Sánchez-Lavega et al. 2011). Although the impact debris resided deeper into the atmosphere (most likely below the 1 mbar pressure level) than the region probed by our observations (de Pater et al. 2010), this fortuitous coincidence allowed us to test for observable effects and, at the same time, use the intensive monitoring of Jupiter during this time to further validate our results. Based on the observations, no residual temperature perturbation above the 1mbar pressure regime in Jupiter’s atmosphere was detectable five days after the impact (Fletcher et al. 2011). Fletcher et al. (2010) estimated a temperature of 170−180 K in the 3−10 μbar level from observations taken on July, 26th (i.e. immediately following the impact) and on August, 13th with a maximum temperature difference between the two epochs of 2 ± 2 K (1σ) occurring at the few-mbar pressure level. Our temperature estimate of 165 ± 5 K applicable to the lower pressure region is consistent with theirs and bolsters our confidence that our estimated uncertainties are sound. Furthermore, it is consistent with the expected temperature perturbation being at least several times smaller than our formal noise level.
5. Conclusions and future prospects
This work has utilised observational data collected worldwide of an occultation of a bright star by Jupiter in order to constrain the state of its atmosphere at a particular location, time and altitude interval. Our results are, where comparable, entirely consistent with those from past work and add to a growing set of ground-based occultation measurements. In addition, they highlight: (a) the potential for instruments as small as 0.5 m in aperture (i.e. BATH) to produce lightcurves of a quality sufficient for numerical inversion into profiles of temperature vs. pressure; (b) the value of having many independent observations of the same event in hand as a means to cross-check the obtained atmospheric parameter estimates (e.g. layers) and the uncertainties intrinsic to them; and (c) the potential for high-quality ground-based occultation measurements, in the long intervals between in situ investigations (i.e. by the Pioneer, Voyager, Galileo, Juno and JUICE missions), towards characterising atmospheric state and variability.
Future opportunities for observing additional occultations of bright stars by Jupiter’s atmosphere in the next 10 yr1 include those at 12th April 2016 and at 2nd April 2021. These involve the stars HIP 54057 (K0, V = 7.2) and HIP 107232 (44 Capricornii; F0, V = 5.9) respectively. The former is observable from E Europe, E Africa, the Middle East and large parts of Asia and Australia, while the latter is visible from the Americas. The 2016 event samples similar planetographic latitudes as the 45 Cap occultation and may take on added significance in view of the expected arrival of the Juno mission to the Jovian system that year (Bolton & the Juno Science Team 2010). The same star will be occulted by Jupiter’s largest satellite Ganymede, some 18h after its egress from behind the planet. The 2021 event occurs near Jupiter’s equator. Egress is followed 20 min later by an occultation of the star by the satellite Io. Only one ground-based observation of an occultation of a star by Io has been reported in the literature, that of β Sco C in 1971 (Bartholdi & Owen 1972), where an upper limit of 7 × 10-9(T/μ)3/2 bar was placed on any atmosphere. For an SO2-dominated atmosphere (μ = 64.066 g) and temperatures of 150 K and 500 K (McGrath et al. 2006), this upper limit translates to 0.025 and 0.15 μbar respectively. More recently, localised pressure highs of 0.1 μbar have been reported for Io’s tenuous atmosphere (McGrath et al. 2006). It can be argued that modern CCD detectors, in combination with larger aperture instruments (a photomultiplier tube and a 0.4 m instrument was used for the 1971 observations) will be sufficiently sensitive to yield significant new information on the Ionian atmosphere.
Predictions generated by D. Mink; http://tdc-www.harvard.edu/occultations/jupiter/jupiter.ppm2000.html
Acknowledgments
We wish to thank the referee, W. B. Hubbard, for his comments which improved the manuscript. Astronomical research at the Armagh Observatory is funded by the Northern Ireland Department of Culture, Arts and Leisure (DCAL). M.A. acknowledges CNPq/Brazil grants 482080/2009-4 and 308721/2011-0. F.B.R. thanks the financial support by the CAPES/Brazil. R.C. was supported by Spanish Science Ministry Grant AYA2009-13936, Consolider-Ingenio CSD2007-00060 and project 2009SGR1398 from Generalitat de Catalunya. This article is based on observations made with the TCS operated on the island of Tenerife by the Instituto de Astrofsica de Canarias in the Spanish Observatorio del Teide; observations collected at the Centro Astronómico Hispano Alemán (CAHA) at Calar Alto, operated jointly by the Max-Planck Institut für Astronomie and the Instituto de Astrofísica de Andalucía (CSIC); and observations made at the Laboratório Nacional de Astrofisica (LNA), Itajubá-MG, Brazil.
Appendix:
A maximum likelihood estimate for H
Assuming that: (a) the sample is drawn from the same error function; (b) this function is symmetric about some constant value (a function parameter), then for any value H0 of the distribution of the estimates for H and for every estimate Hk we can define the Bernoulli random variable: 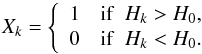 (2)with P(Xk = 1) = P(Xk = 0) = 1/2.
(2)with P(Xk = 1) = P(Xk = 0) = 1/2.
The number of estimates larger than H0 in the sample is given by Sn = X1 + ··· + Xn where n is the sample size. Sn follows the binomial distribution: 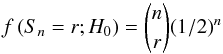 (3)which depends on the parameter H0 implicitly through the definition of X. This is maximised for r = [n/2] − 1 (r odd) and r = n/2 or r = n/2 + 1 for r even. In other words, the likelihood of the sample is maximised if H0 is the sample median.
(3)which depends on the parameter H0 implicitly through the definition of X. This is maximised for r = [n/2] − 1 (r odd) and r = n/2 or r = n/2 + 1 for r even. In other words, the likelihood of the sample is maximised if H0 is the sample median.
References
- Acton, C. H. 1999, in 3th LPSC, Houston, TX, Abs. 1323 [Google Scholar]
- Bartholdi, P., & Owen, F. 1972, AJ, 77, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Baum, W. A., & Code, A. D. 1953, AJ, 58, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Bolton, S. J., & the Juno Science Team. 2010, in Galileo’s Medicean Moons: their impact on 400 years of discovery, eds. C. Barbieri, S. Chakrabarti, M. Coradini, & M. Lazzarin (Cambridge: Cambridge University Press), Proc. IAU Symp., 269, 92 [Google Scholar]
- Cooray, A. R., Elliot, J. L., Bosh, A. S., Young, L. A., & Shure, M. A. 1998, Icarus, 132, 298 [NASA ADS] [CrossRef] [Google Scholar]
- de Pater, I., Fletcher, L. N., Pérez-Hoyos, S., et al. 2010, Icarus, 210, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Elliot, J. L., & Olkin, C. B. 1996, Annu. Rev. Earth Planet. Sci., 24, 89 [Google Scholar]
- Festou, M. C., Atreya, S. K., Donahue, T. M., et al. 1981, J. Geophys. Res., 86, 5717 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, L. N., Orton, G. S., de Pater, I., & Mousis, O. 2010, A&A, 524, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fletcher, L. N., Orton, G. S., de Pater, I., et al. 2011, Icarus, 211, 568 [NASA ADS] [CrossRef] [Google Scholar]
- Folkner, et al. 2009, JPL Interplanetary Network Progress Report, 24, http://ipnpr.jpl.nasa.gov/progress_report/42-178/178C.pdf [Google Scholar]
- Greathouse, T. K., Gladstone, G. R., Moses, J. I., et al. 2010, Icarus, 208, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Hog, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS] [Google Scholar]
- Hubbard, W. B., Nather, R. E., Evans, D. S., et al. 1972, AJ, 77, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Hubbard, W. B., Hammerle, V., Porco, C. C., & Rieke, G. H. 1995, Icarus, 113, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Karkoschka, E. 1994, Icarus, 111, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Lindal, G. F. 1992, AJ, 103, 967 [NASA ADS] [CrossRef] [Google Scholar]
- Lindal, G. F., Wood, G. E., Levy, G. S., et al. 1981, J. Geophys. Res., 86, 8721 [NASA ADS] [CrossRef] [Google Scholar]
- McGrath, M. A., Lellouch, E., Strobel, D. F., Feldman, P. D., & Johnson, R. E. 2006, in Jupiter: the planet, satellites and magnetosphere, eds. F. Bagenal, T. Dowling, & W. McKinnon (Cambridge: Cambridge University Press), 457 [Google Scholar]
- Moreno, R., Marten, A., Biraud, Y., et al. 2001, Planet. Space Sci., 49, 473 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C. 1997, ESA SP, Noordwijk, The Netherlands, 1200 [Google Scholar]
- Raynaud, E., Drossart, P., Matcheva, K., et al. 2003, Icarus, 162, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Raynaud, E., Drossart, P., Matcheva, K., et al. 2004, Icarus, 168, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Lavega, W. B., et al. 2011, Icarus, 211, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Seidelmann, P. K., Archinal, B. A., et al. 2007, Cel. Mech. Dyn. Astron., 98, 155 [Google Scholar]
- Seiff, A. K., Donn, B., Knight, T. C. D., et al. 1996, Science, 5263, 844 [NASA ADS] [CrossRef] [Google Scholar]
- Vapillon, L., Combes, M., & Lecacheux, J. 1973, A&A, 29, 135 [NASA ADS] [Google Scholar]
- Veverka, J., Wasserman, L. H., Elliot, J., Sagan, C., & Liller, W. 1974, AJ, 79, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Wasserman, L., & Veverka, J. 1973, Icarus, 20, 322 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Left: co-added images obtained during the ingress in the K-band with the Carlos Sánchez Telescope (Observatorio del Teide, Tenerife, Canary Islands; SCHMAS). North is towards the lower left and East towards the lower right. The bright feature near the south pole transiting the central meridian is the spot left by the impact of an asteroid or comet on July 19th. Right: co-added images for Egress. Note that the impact spot has rotated towards the western limb of the planet. |
| In the text | |
 |
Fig. 2 Single frame from the sequence obtained at RCASAS and at 22:55:01 UT, mask subtracted and showing the star (close to the planetary limb) and two satellites (Europa and Ganymede). The bright feature indicated by the arrow is the Great Red Spot. Image orientation is the same as in Fig. 1. |
| In the text | |
 |
Fig. 3 Lightcurves of the occultation’s ingress (left column) and egress (right column) phases obtained in this work. |
| In the text | |
 |
Fig. 4 Scale heights from fitting the Baum-Code law to our lightcurves, compared to the estimates from previous works. |
| In the text | |
 |
Fig. 5 Sensitivity of the numerical inversion of a model lightcurve to Gaussian random noise (left) and the pedestal value (right). See text for details. |
| In the text | |
 |
Fig. 6 Atmospheric profiles derived in this work compared with in situ data from the Galileo Probe ASI investigation. Left: ingress profiles from data acquired at Teide (SCHMAS), Calar Alto (EBACAS) and Hakos (BATH). Right: egress profiles from data acquired at Pico dos Dias (ASRIB) and Teide (SCHMAS). |
| In the text | |
 |
Fig. 7 Profile of stellar flux with model lightcurve subtracted against altitude relative to the instant of half-light in every case. The arrows indicate the position of prominent features (“spikes”) observed in the ingress profiles (left) and their expected locations in the egress ones (right). Profiles at ingress (egress) are horizontally separated by 0.5 (0.4) units for clarity. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


