| Issue |
A&A
Volume 556, August 2013
|
|
|---|---|---|
| Article Number | A31 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201321409 | |
| Published online | 22 July 2013 | |
The quenching of star formation in accretion-driven clumpy turbulent tori of active galactic nuclei
1
CDS, Observatoire astronomique de Strasbourg, UMR 7550,
11 rue de l’université,
67000
Strasbourg,
France
e-mail: Bernd.Vollmer@astro.unistra.fr
2
Max-Planck Insitut für extraterrestrische Physik, Postfach 1312,
85741
Garching,
Germany
Received:
5
March
2013
Accepted:
28
May
2013
Galactic gas-gas collisions involving a turbulent multiphase interstellar medium (ISM) share common ISM properties: dense extraplanar gas visible in CO, large linewidths (≳50 km s-1), strong mid-infrared H2 line emission, low star formation activity, and strong radio continuum emission. Gas-gas collisions can occur in the form of ram pressure stripping caused by the rapid motion of a spiral galaxy within the intracluster medium, galaxy head-on collisions, compression of the intragroup gas and/or galaxy ISM by an intruder galaxy which flies through the galaxy group at a high velocity, or external gas accretion on an existing gas torus in a galactic center. We suggest that the common theme of all these gas-gas interactions is adiabatic compression of the ISM leading to an increase of the turbulent velocity dispersion of the gas. The turbulent gas clouds are then overpressured and star formation is quenched. Within this scenario we developed a model for turbulent clumpy gas disks where the energy to drive turbulence is supplied by external infall or the gain of potential energy by radial gas accretion within the disk. The cloud size is determined by the size of a continuous (C-type) shock propagating in dense molecular clouds with a low ionization fraction at a given velocity dispersion. We give expressions for the expected volume and area filling factors, mass, density, column density, and velocity dispersion of the clouds. The latter is based on scaling relations of intermittent turbulence whose open parameters are estimated for the circumnuclear disk in the Galactic center. The properties of the model gas clouds (~0.1 pc, ~100 M⊙, Δv ≳ 6 km s-1) and the external mass accretion rate necessary for the quenching of the star formation rate due to adiabatic compression (Ṁ ~ 1−10 M⊙ yr-1) are consistent with those derived from high-resolution H2 2.12 μm line observations. Based on these findings, a scenario for the evolution of gas tori in galactic centers is proposed and the implications for star formation in the Galactic center are discussed.
Key words: galaxies: active / galaxies: nuclei / ISM: clouds / ISM: structure / ISM: kinematics and dynamics
© ESO, 2013
1. Introduction
What do the circumnuclear disk (CND) in the Galactic center, a thick obscuring active galactic nucleus (AGN) torus, the ram-pressure stripped and tidally distorted Virgo spiral galaxy NGC 4438, the colliding Taffy galaxies, and Stephan’s Quintet, all have in common? At first glance all systems are very different. First of all, the spatial scales and timescales differ enormously. The CND and AGN tori have spatial extents of about 10 pc and rotation timescales of 104 yr, whereas the relevant scales and timescales in NGC 4438, the Taffy galaxies, and Stephan’s Quintet are on the order of tens of kpc and 100 Myr. The common property of all systems is that they are undergoing gas-gas collisions with high energy injection rates. In these collisions, one gaseous body is the turbulent clumpy multiphase interstellar medium (ISM), while the other can be of different mean density and temperature (e.g. ISM, intragroup or intracluster gas): NGC 4438 is affected by ongoing ram pressure caused by its rapid motion through the Virgo intracluster medium (Vollmer et al. 2005, 2009), the Taffy galaxies recently experienced a head-on ISM-ISM collision (Condon et al. 1993; Vollmer et al. 2012), and the intragroup gas of the Stephan’s Quintet is compressed by a high-velocity intruder galaxy.
NGC 4438 had a tidal interaction ~100 Myr ago (Combes et al. 1988) probably associated with an ISM-ISM collision (Kenney et al. 1995). In addition, the galaxy undergoes strong on-going ram pressure stripping leading to extraplanar CO emission and a characteristic double-line profile in the extraplanar region (Vollmer et al. 2005). Strong radio continuum emission is associated with the extraplanar gas (Vollmer et al. 2009). The Taffy system attracted attention through its strong radio synchrotron bridge, a very unusual feature. The bridge is Hi-rich (Condon et al. 1993) and was subsequently found to be rich in molecular gas as well through CO observations (Gao et al. 2003; Braine et al. 2003). The CO lines have particularly large linewidths. Strong H2 emission is associated with the bridge gas (Peterson et al. 2012). Whereas the ISM-ISM collision of the Taffy galaxies occurred ~20 Myr ago, the gas-gas collision in Stephan’s Quintet is on-going and involves an intruder galaxy hitting the intra-group medium of this compact group with a velocity of ~1000 km s-1. The resulting large-scale shock (~40 kpc) emits in X-ray (Trinchieri et al. 2003) and radio continuum emission (van der Hulst 1981). Powerful high-velocity dispersion molecular hydrogen is associated with the intergalactic shock wave (Appleton et al. 2006; Guillard et al. 2009). About 5 × 108 M⊙ of warm H2 spread over ~480 kpc2 were found in the main shock region (Cluver et al. 2010). In addition, CO(1–0), (2–1) and (3–2) line emission have been detected in this region with complex profiles, spanning a velocity range ~1000 km s-1 (Guillard et al. 2012). The intra-group material involved has most probably been tidally stripped by a past galaxy–galaxy interaction (Renaud et al. 2010; Hwang et al. 2012).
All these regions outside the galactic disks formed by galactic gas-gas collisions involving high energy injection rates, have high gas densities (CO emission), involve huge molecular gas masses, show large linewidths, and have strong associated H2 and radio continuum emission. In addition, star formation is significantly reduced in all these regions (NGC 4438: Vollmer et al. 2009; Taffy galaxies: Vollmer et al. 2012; Stephan’s Quintet: Guillard et al. 2012). Gas tori in active galactic centers have many of these properties in common with these regions: they involve huge gas masses (Hicks et al. 2009), display high gas densities and large linewidths (Davies et al. 2007; Sani et al. 2012), and have a significantly reduced star formation rate, i.e. they are classified as post-starburst regions (Davies et al. 2007). Based on these similarities, we suggest that the thick, obscuring AGN gas tori undergo a violent ISM-ISM collision caused by infalling material which hits the torus. The mechanical energy input drives the gas turbulence and quenches star formation as in galaxy-scale ISM-ISM collisions.
The ISM in galaxies and galactic center gas tori is clumpy. Thermal instabilities triggered by small-scale gas compression lead to the condensation of dense cold clouds (Parravano 1987). If the turbulent crossing time is smaller than the free-fall time, the clouds become selfgravitating and might collapse. The CND in the Galactic center is made of gas clouds with masses of a few 10 M⊙, an area filling factor of ΦA ~ 0.1 and a volume filling factor of ΦV ~ 0.01 (Jackson et al. 1993; however, Requena-Torres et al. 2012 suggest a much higher volume filling factor of ΦV ~ 0.2). Since the densities derived from the HCN lines (Jackson et al. 1993) are close to those of selfgravitating clouds with a thermal sound speed of ~1 km s-1, Vollmer & Duschl (2001a) and Vollmer et al. (2004) proposed a model of a collisional disk made of stable gas clouds. This model was extended to AGN gas tori in Vollmer et al. (2008). These authors suggested the following scenario for the evolution of an AGN gas torus: during a rapid massive infall1, gas accumulates at a distance of ~10 pc around the central black hole (Davies et al. 2007; Lira et al. 2013). At this stage the torus forms stars giving rise to a nuclear starburst. After ~10 Myr the SN explosions remove the torus intercloud gas leaving a torus made of dense clumps. Due to a high mass accretion rate, the torus has a high velocity dispersion, i.e. it is thick. Its radial mass accretion is high enough to power the central AGN. This collisional torus has a rather low star formation rate. Once the external mass accretion rate decreases the collisional torus eventually becomes thin.
In the present article, we modify this scenario by replacing the collisional torus (Sect. 2) by a turbulent clumpy torus (Sect. 4). We show that both types of models lead to gas clouds of comparable masses and sizes (Sect. 6). However, the turbulent torus clouds have a much higher velocity dispersion (≥ 6 km s-1) than the collisional CND clouds (≥ 1 km s-1). Since the collisional clouds are by definition selfgravitating, the torus clouds are overpressured with respect to their turbulent pressure. This prevents gravitational collapse and quenches star formation (Sect. 7). The model cloud properties are compared to those derived from subarcsecond molecular gas emission line observations of two Seyfert galaxies in Sect. 8. The implications for the recent star formation history in the Galactic center are discussed in Sect. 9 and we give our conclusions in Sect. 10.
2. The theory of clumpy gas disks
Galactic accretion disks generally are clumpy: gas disks of spiral galaxies contain gas
clumps of cold neutral hydrogen (e.g., Strasser et al. 2007) with embedded giant molecular clouds (e.g., Solomon et al. 1987); gas tori around central galactic black holes also
contain clumps of high volume densities (e.g., Krolik & Begelman 1988; Güsten et al. 1987). The formation of regions of overdense gas is caused by thermal
instabilities and selfgravity. In turbulent galactic disks, gas clumps are of transient
nature with lifetimes of about a crossing time (e.g., Dobbs & Pringle 2013). The governing gas physics of such disks are highly
time-dependent and intrinsically stochastic. Over a long-enough timescale, turbulent motion
of clumps is expected to redistribute angular momentum in the gas disk like an effective
viscosity would do. This allows accretion of gas toward the center and makes it possible to
treat the disk as an accretion disk (e.g., Pringle 1981). This gaseous turbulent accretion disk rotates in a given gravitational
potential Φ with an angular velocity 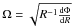 ,
where R is the disk radius. The disk has an effective turbulent viscosity
that is responsible for mass accretion and outward angular momentum transport. The turbulent
velocity can be driven by SN explosions or external gas infall, which stir the disk and lead
to viscous transport of angular momentum. In addition, star formation might remove gas from
the viscous evolution. Following Lin & Pringle (1987), the evolution of the gas surface density is given by
,
where R is the disk radius. The disk has an effective turbulent viscosity
that is responsible for mass accretion and outward angular momentum transport. The turbulent
velocity can be driven by SN explosions or external gas infall, which stir the disk and lead
to viscous transport of angular momentum. In addition, star formation might remove gas from
the viscous evolution. Following Lin & Pringle (1987), the evolution of the gas surface density is given by ![\begin{equation} \frac{\partial \Sigma}{\partial t}=-\frac{1}{R}\frac{\partial}{\partial R}\left( \frac{(\partial/\partial R)[\nu \Sigma R^3 ({\rm d}\Omega/{\rm d}R)]}{({\rm d}/{\rm d}R)(R^2 \Omega)}\right) -\dot{\Sigma}_{*}+\dot{\Sigma}_{\rm sph} , \label{eq:linpringle} \end{equation}](/articles/aa/full_html/2013/08/aa21409-13/aa21409-13-eq21.png) (1)where ν is
the gas disk viscosity, Ω the angular velocity. Gas which does not accrete within the disk
plane gives rise to the spherical mass accretion rate
(1)where ν is
the gas disk viscosity, Ω the angular velocity. Gas which does not accrete within the disk
plane gives rise to the spherical mass accretion rate
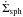 .
In contrast to Lin & Pringle (1987) we assume
a continuous and non-zero spherical gas mass accretion rate. By approximating
∂/∂R ~ 1/R,
the global viscous evolution becomes
.
In contrast to Lin & Pringle (1987) we assume
a continuous and non-zero spherical gas mass accretion rate. By approximating
∂/∂R ~ 1/R,
the global viscous evolution becomes 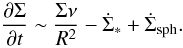 (2)Radial integration of
Eq. (2) then gives
(2)Radial integration of
Eq. (2) then gives
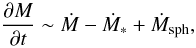 (3)where
M is the disk gas mass and Ṁ the radial disk accretion
rate. The external mass accretion rate is thus
Ṁext = Ṁ + Ṁsph.
We note that in thick gas disks or tori, the disk occupies a significant solid angle and
Ṁsph decreases in favor of Ṁ.
(3)where
M is the disk gas mass and Ṁ the radial disk accretion
rate. The external mass accretion rate is thus
Ṁext = Ṁ + Ṁsph.
We note that in thick gas disks or tori, the disk occupies a significant solid angle and
Ṁsph decreases in favor of Ṁ.
If, in thin starforming galactic disks, the external mass accretion rate keeps the combined Toomre parameter of the gas and stars smoothed over a few rotation periods constant, the gas surface density will only vary slowly with changes in the dark halo mass distribution (via Ω) and the stellar disk structure, the gas loss due to star formation is balanced by spherical accretion as suggested by Fraternali et al. (2008) and Marinacci et al. (2010), and the gas disk can be regarded as being stationary2 (∂M/∂t = 0).
In the absence of star formation in thick gas tori around central galactic black holes (see Sect. 7), the disk can be regarded as stationary if (i) the external infall mainly occurs within the disk plane, i.e. Ṁsph ≪ Ṁ or Ṁext ~ Ṁ; and (ii) over a sufficiently large timescale, the time-averaged external mass infall is constant. Condition (i) is quite naturally fulfilled for a thick gas disk/torus which is mainly fed at the outer edge. The relevant timescale for disk evolution is then the viscous timescale. Condition (ii) is a quite strong assumption which might not be fulfilled in all cases. In a recent numerical work, Gaspari et al. (2013) studied the behavior of cold accretion down to the central part of an elliptical galaxy. They showed that in a cooling, heated and turbulent atmosphere of elliptical galaxies, thermal instabilities become quickly nonlinear, leading to the condensation of dense cold clouds in a turbulent medium, up to several kpc from the center. The clouds then fall toward the very inner region and strongly collide within 10–100 pc. The inelastic collisions promote angular momentum cancellation, strongly boosting black hole accretion. Thus, the collision of gas clumps can dominate the distribution of angular momentum and thus gas accretion. Within this scenario, the external mass accretion rate is highly time-dependent and intrinsically stochastic (Figs. 3 and 5 of Gaspari et al. 2013). For our purpose, one has to time-average the external mass accretion rate on scales of Δt ~ 5 Myr, the typical timescale of the fluctuations of the mass accretion rate. This timescale is comparable to the viscous timescale of a thick torus (tvisc = R2/ν; see Eq. (43)).
For a stationary gas disk which fulfills conditions (i) and (ii) the local mass and
momentum conservations yield: 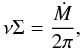 (4)where Ṁ is
the radial mass accretion rate within the disk plane.
(4)where Ṁ is
the radial mass accretion rate within the disk plane.
In this work we are not interested in the detailed radial distributions of the disk
properties, but look at the integrated values. To measure the gas content of the gas disk,
we use the Toomre parameter Q of the gas
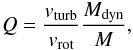 (5)where
vturb and vrot are the turbulent
and rotation velocities, and Mdyn is the total enclosed mass.
Hicks et al. (2009) and Sani et al. (2012) found
Q > 1 in AGN gas tori where star formation is
quenched.
(5)where
vturb and vrot are the turbulent
and rotation velocities, and Mdyn is the total enclosed mass.
Hicks et al. (2009) and Sani et al. (2012) found
Q > 1 in AGN gas tori where star formation is
quenched.
The present rather simple analytical model of steady clumpy accretion disks aims at capturing the basic gas physics of (i) turbulent and (ii) collisional disks within the framework set by Vollmer & Beckert (2002, 2003) and Vollmer et al. (2004). In case (i) the ISM is regarded as a single entity which changes phase (molecular, atomic, ionized) according to internal (gas density, pressure, magnetic field) and external (gravitation, radiation field, winds) conditions. Energy is injected into a turbulent cascade at the driving lengthscale (large scale) and dissipated at the dissipation lengthscale (small scale). In Vollmer & Beckert (2002, 2003) we identified the dissipation lengthscale with the characteristic size of selfgravitating clouds in starforming disks. These clouds decouple from the turbulent cascade and constitute the first energy sink. The source of energy which is injected at the driving scale to maintain turbulence can be either (i) mass accretion in the gravitational potential of the galactic center (fully gravitational FG model) or (ii) supernova explosions (SN model). AGN feedback, which represents an additional energy source for turbulence is not included in the model. In the collisional case energy is also supplied in the process of mass accretion in the gravitational potential of the galactic center and dissipated via partially inelastic cloud-cloud collisions. The actual dissipation rate in individual collisions is largely unknown. The disk evolution is mainly driven by the external mass accretion rate. Since these models are equilibrium models, we assume that the mass accretion rate is constant throughout the region of interest when averaged for a sufficiently long time (~Ω-1; here Ω is the angular velocity of circular orbits in the gravitational potential of the galactic nucleus) and maintained for at least the turnover timescale R/vturb of gas in the disk, where R is the distance from the center of the galaxy and vturb the characteristic speed of turbulent eddies. All models provide the global parameters of the disk and the local parameters of the most massive clouds (see Table 1). The free parameters of the models are the Toomre parameter Q, the mass accretion rate Ṁ, the disk transparency ϑ (Eq. (7)) for the collisional model, and the scaling parameter between the driving lengthscale and the cloud size in the turbulent model. Other parameters are fixed using the Galactic values (Vollmer & Beckert 2002, 2003). Each model has an associated star formation rate. In the following we describe these models in more detail.
Model parameters and their meaning.
In the present article we extend this theory to non-starforming clumpy accretion disks where the source of energy to maintain turbulence is external gas infall (mechanical energy) and subsequent mass accretion in the gravitational potential of the galactic center. We assume that the external mass infall occurs mainly within the disk plane. The disk mass accretion rate is thus equivalent to the external mass accretion rate. The turbulent energy is mainly dissipated by molecular line radiation (CO, H2, H2O; see, e.g., Neufeld & Kaufman 1993) from the dense clouds. In contrast to the previous work, dense clouds do not need to be selfgravitating.
3. Collisional disks
The disk clouds are supposed to be stable (via selfgravitation and magnetic fields) and
long-lived (several rotation periods). In this case their collisions will give rise to
angular momentum redistribution which can be described by an effective viscosity. An
equilibrium disk can be formed if there are fragmenting collisions or partially inelastic
collisions (the clouds are supposed to be magnetized). It follows that the collisional
energy dissipation rate can be written as 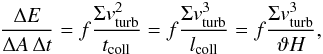 (6)where
Σ = 2ρH is the mean gas surface density, ρ the mean gas
density, H the disk height, vturb the turbulent
velocity, tcoll the collision timescale,
lcoll the collision lengthscale, and ϑ the
disk transparency. The disk mean density is linked to the cloud density via the volume
filling factor ρ = ρclΦV.
(6)where
Σ = 2ρH is the mean gas surface density, ρ the mean gas
density, H the disk height, vturb the turbulent
velocity, tcoll the collision timescale,
lcoll the collision lengthscale, and ϑ the
disk transparency. The disk mean density is linked to the cloud density via the volume
filling factor ρ = ρclΦV.
The factor f accounts for the mean fraction of cloud mass participating in
the highly supersonic cloud collisions. For constant density clouds Krolik &
Begelman (1988) argue that f = 0.2.
For more centrally condensed, self-gravitating clouds we will use a factor
f = 0.1 as in Vollmer et al. (2008). If the collisional timescale tcoll is longer or
equal to the dynamical timescale, the resulting viscosity can be written as 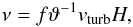 (7)where the disk
transparency
ϑ = tcollΩ > 1 and
H is the disk height.
(7)where the disk
transparency
ϑ = tcollΩ > 1 and
H is the disk height.
The cloud size rcl and the volume filling factor ΦV
of clouds can be derived using their mean free path (see Vollmer et al. 2004)
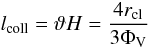 (8)and
the fact that the clouds are selfgravitating
(8)and
the fact that the clouds are selfgravitating 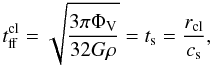 (9)where
(9)where
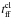 is the free fall
timescale within clouds,
ρ = Ω2/π/G/Q
the disk overall gas density, ts the sound crossing timescale,
cs the sound speed, and G the gravitation
constant. The area filling factor of the clouds is then
is the free fall
timescale within clouds,
ρ = Ω2/π/G/Q
the disk overall gas density, ts the sound crossing timescale,
cs the sound speed, and G the gravitation
constant. The area filling factor of the clouds is then 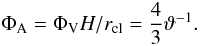 (10)Eqs. (9), (10), and
H = vturb/Ω lead to
(10)Eqs. (9), (10), and
H = vturb/Ω lead to
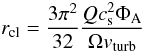 (11)and
(11)and
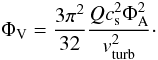 (12)The cloud mass is then
(12)The cloud mass is then
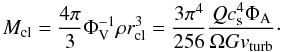 (13)Based on the results of
Vollmer et al. (2004), Vollmer et al. (2008) assumed that the cloud mass of all disks is close
to that of the CND (Jackson et al. 1993),
Mcl = 10 M⊙. This is
equivalent to a common size, density, and column density of all clouds
(13)Based on the results of
Vollmer et al. (2004), Vollmer et al. (2008) assumed that the cloud mass of all disks is close
to that of the CND (Jackson et al. 1993),
Mcl = 10 M⊙. This is
equivalent to a common size, density, and column density of all clouds  \arraycolsep1.75ptAssuming
a sound speed of cs = 1.5 km s-1 leads to
rcl = 0.02 pc,
ρcl = 107 cm-3, and
Ncl = 5 × 1023 cm-2. The value for the
sound speed corresponds to a cloud temperature of ~500 K (Krips et al. 2011 found T ≥ 200 K for NGC 1068,
Hailey-Dunsheath et al. 2012, derived
T ~ 600 K for NGC 1068, Davies et al. 2012, favor T ~ 300 K for NGC 3227) when only thermal gas
pressure is considered. The sound speed is a measure of the pressure support against
self-gravity and additional contributions to the pressure gradient inside clouds like
magnetic fields may contribute. With Q = 5 (Vollmer et al. 2008; Hicks et al. 2009) and Ω = 100 km s-1/10 pc, we obtain for the volume filling factor
\arraycolsep1.75ptAssuming
a sound speed of cs = 1.5 km s-1 leads to
rcl = 0.02 pc,
ρcl = 107 cm-3, and
Ncl = 5 × 1023 cm-2. The value for the
sound speed corresponds to a cloud temperature of ~500 K (Krips et al. 2011 found T ≥ 200 K for NGC 1068,
Hailey-Dunsheath et al. 2012, derived
T ~ 600 K for NGC 1068, Davies et al. 2012, favor T ~ 300 K for NGC 3227) when only thermal gas
pressure is considered. The sound speed is a measure of the pressure support against
self-gravity and additional contributions to the pressure gradient inside clouds like
magnetic fields may contribute. With Q = 5 (Vollmer et al. 2008; Hicks et al. 2009) and Ω = 100 km s-1/10 pc, we obtain for the volume filling factor
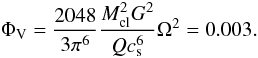 (17)The area filling
factor is then
(17)The area filling
factor is then 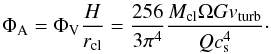 (18)Assuming a thick disk with
a height of H = 5 pc
(vturb = HΩ = 50 km s-1) yields an
area filling factor of ΦA = 0.8, i.e. the disk obscures the central engine.
(18)Assuming a thick disk with
a height of H = 5 pc
(vturb = HΩ = 50 km s-1) yields an
area filling factor of ΦA = 0.8, i.e. the disk obscures the central engine.
Since the clouds are assumed to be stable and long-lived, they have to resist tidal shear
ρcl ≥ Ω2/π/G.
This translates into a minimum sound speed at the inner edge of the torus where tidal shear
is maximum of 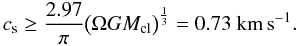 (19)
(19)
4. Turbulent disks
In contrast to the previous models of turbulent clumpy accretion disks (Vollmer & Beckert 2002, 2003; Vollmer et al. 2004, 2008), we do not assume that the clouds are selfgravitating. We thus have to estimate the cloud size in a different way. As in the previous models, the disk evolution is mainly driven by the external mass accretion rate. Since these models are equilibrium models, we assume that the mass accretion rate is constant throughout the region of interest when averaged and maintained for a sufficiently long time (tvisc = R2/ν ~ 5 Myr). External accretion onto an existing gas disk leads to shocks in the dense magnetized molecular gas. In such a dense gas (n ≳ 104 cm-3) with low ionization fraction (xi ≲ 10-6) the ionic Alfvén speed is higher than the shock speed so that ions and magnetic fields smoothly transit between upstream and downstream conditions without discontinuities. As a result of the ion-neutral drag forces, the transition in the neutrals is also modified and, in the presence of significant cooling, all physical quantities vary smoothly in the shock region, forming a continuous (C-type) shock (Draine 1980). The combination of low ionization fraction, strong cooling, and significant (but not high) magnetic fields thus results in a shock in which ion-neutral drag provides the viscosity, cooling keeps the gas supersonic and the field via the ions provides an extended cushioning layer which inhibits molecular dissociation (Draine & McKee 1993). For high shock velocities (>50 km s-1 at n = 105 cm-3) molecular hydrogen is dissociated in the shock layer due to the high temperature and the shock becomes J-type (Le Bourlot et al. 2002). Strong multifluid (neutral and ionized medium, magnetic field) J-type shocks behave like classical single fluid shocks. These shocks have magnetic/ionic precursors in which ion-neutral drift preheats the incoming gas before the shock itself. For the considered gas densities n ≤ 105 and shock velocities ≲60 km s-1, the shocks are mainly C-type. Extreme shock velocities might lead to J-type shocks with magnetic precursors. The compression ratio and thickness of these shocks are assumed to be close to those of C-type shocks.
Within the strong shock approximation the gas compression rate in the shock is given by
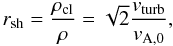 (20)where the
vA,0 = B/
(20)where the
vA,0 = B/ is the neutral Alfvén speed in the diffuse medium with magnetic field B
(see, e.g. Chen & Ostriker 2012). The neutral
Alfvén speed of the ISM clouds of different densities is almost constant
vA,0 ~ 1 km s-1 (Crutcher
1999). Assuming recombination-ionization
equilibrium, the shock thickness is given by Eq. (43) of Chen & Ostriker (2012):
is the neutral Alfvén speed in the diffuse medium with magnetic field B
(see, e.g. Chen & Ostriker 2012). The neutral
Alfvén speed of the ISM clouds of different densities is almost constant
vA,0 ~ 1 km s-1 (Crutcher
1999). Assuming recombination-ionization
equilibrium, the shock thickness is given by Eq. (43) of Chen & Ostriker (2012): 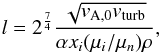 (21)where
α = 3.7 × 1013 cm3 s-1g-1
(Draine et al. 1983) is the collision coefficient,
xi the ionization fraction, and
(μi/μn) = (30/2.3) = 13
the fraction between the mean ion and neutral molecular weights. If the so-called frozen-in
condition
(nivi = const.,
where ni and
vi are the ionized gas density and
velocity; e.g. Wardle 1990) is used instead of
recombination-ionization equilibrium, Eq. (21) and the following equations change. This case is developed in Appendix A.
(21)where
α = 3.7 × 1013 cm3 s-1g-1
(Draine et al. 1983) is the collision coefficient,
xi the ionization fraction, and
(μi/μn) = (30/2.3) = 13
the fraction between the mean ion and neutral molecular weights. If the so-called frozen-in
condition
(nivi = const.,
where ni and
vi are the ionized gas density and
velocity; e.g. Wardle 1990) is used instead of
recombination-ionization equilibrium, Eq. (21) and the following equations change. This case is developed in Appendix A.
The ionization fraction is given by
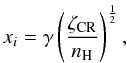 (22)where
γ = 600−2000 cm−3/2 s1/2
(Williams et al. 1998; McKee et al. 2010) and
nH = ρ/(2.3 × mp).
For the cosmic ray ionization rate we take the value for the Galactic center region of
ζCR = 2 × 10-15 s-1 (Yusef-Zadeh et al.
2013). With
γ = 600 cm−3/2 s1/2
the size of the C-shock is
(22)where
γ = 600−2000 cm−3/2 s1/2
(Williams et al. 1998; McKee et al. 2010) and
nH = ρ/(2.3 × mp).
For the cosmic ray ionization rate we take the value for the Galactic center region of
ζCR = 2 × 10-15 s-1 (Yusef-Zadeh et al.
2013). With
γ = 600 cm−3/2 s1/2
the size of the C-shock is 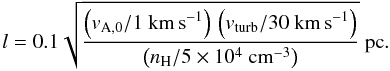 (23)The
ionization-recombination approximation is justified, because the ionization and
recombination timescales
(ti ~ xi/ζCR
and
trec ~ γ2ni)
are very short (years) compared to shock crossing timescale
(tcross = lcl/vturb).
(23)The
ionization-recombination approximation is justified, because the ionization and
recombination timescales
(ti ~ xi/ζCR
and
trec ~ γ2ni)
are very short (years) compared to shock crossing timescale
(tcross = lcl/vturb).
Within the shock the magnetic field is compressed in the direction of shock propagation.
The shock might become unstable and converging gas flows will form within the shock plane.
In this way gas clouds are created which do not need to become selfgravitating. Within a
simplified picture a converging flow bounded by C-shocks has a breadth at least twice the
shock size (Chen & Ostriker 2012) which we
identify with the cloud size: lcl = 2 × l. An
approximation for the volume filling factor is 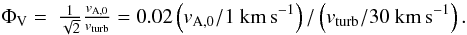 (24)With
the mean density of
ρ = Ω2/(πGQ) the cloud
size becomes
(24)With
the mean density of
ρ = Ω2/(πGQ) the cloud
size becomes ![\begin{equation} \begin{array}{ll} l= & 0.1 \left(\Omega/1 \times 10^{-5}~{\rm yr}^{-1}\right)^{-1} \\[4mm] &\times~ \sqrt{(Q/5)\,\left(v_{\rm A,0}/1~{\rm km\,s}^{-1}\right)\,\left(v_{\rm turb}/30~{\rm km\,s}^{-1}\right)}~{\rm pc} \end{array} \label{eq:lturb} \end{equation}](/articles/aa/full_html/2013/08/aa21409-13/aa21409-13-eq150.png) (25)and
the area filling factor is
(25)and
the area filling factor is 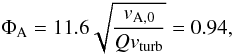 (26)the mass of the clouds
(26)the mass of the clouds
![\begin{equation} \begin{array}{ll} M_{\rm cl}=&\displaystyle \frac{4}{3}\pi \Phi_{\rm V}^{-1} \rho \left(\frac{l}{2}\right)^{3}=23\,\left(\Omega/1.5 \times 10^{-5}~{\rm yr}^{-1}\right)^{-1} \\[4mm] &\displaystyle \times~\left(\left(Q/5)(v_{\rm A,0}/1~{\rm km\,s}^{-1}\right)\right)^{\frac{1}{2}} \left(v_{\rm turb}/30~{\rm km\,s}^{-1}\right)^{\frac{5}{2}}~{M}_{\odot} , \end{array} \label{eq:mcl} \end{equation}](/articles/aa/full_html/2013/08/aa21409-13/aa21409-13-eq152.png) (27)and
the cloud surface density
(27)and
the cloud surface density ![\begin{equation} \begin{array}{ll} N_{\rm cl}=&\displaystyle 7 \times 10^{23}\,\left(\Omega/1.5 \times 10^{-5}~{\rm yr}^{-1}\right) \\[4mm] &\displaystyle\!\! \!\!\!\!\times~\left(\left(Q/5)(v_{\rm A,0}/1~{\rm km\,s}^{-1}\right)\right)^{-\frac{1}{2}} \left(v_{\rm turb}/30~{\rm km\,s}^{-1}\right)^{\frac{3}{2}}~{\rm cm}^{-2} . \end{array} \label{eq:Nturb} \end{equation}](/articles/aa/full_html/2013/08/aa21409-13/aa21409-13-eq153.png) (28)The
gas within the clouds is heated via dissipation and the heating is
(28)The
gas within the clouds is heated via dissipation and the heating is
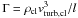 with
l = 2rcl. The gas is cooled via molecular
line radiation and the cooling is
Λ = ℒncln(M), where
n(M) is the particle density of the coolant (CO,
H2, or H2O) and the cooling rate coefficient ℒ has the units of
erg cm3 s-1. The equilibrium between heating and cooling sets the
gas temperature in the cloud.
with
l = 2rcl. The gas is cooled via molecular
line radiation and the cooling is
Λ = ℒncln(M), where
n(M) is the particle density of the coolant (CO,
H2, or H2O) and the cooling rate coefficient ℒ has the units of
erg cm3 s-1. The equilibrium between heating and cooling sets the
gas temperature in the cloud.
One of the most striking (and least understood) features of turbulence is its intermittent
spatial and temporal behavior (Balkovsky & Falkovich 1998). The structures that arise in a turbulent flow manifest themselves as high
peaks at random places and at random times. This is reflected in the probability
distribution functions of dynamical variables or passively advected scalars. They are
sensitive measures of deviations from Gaussian statistics. Rare strong fluctuations are
responsible for extended tails, whereas the much larger regions of low intensity contribute
to the peak of the PDF near zero (Balkovsky & Falkovich 1998). In the case of incompressible turbulence the rate of transfer of
energy per unit mass in turbulent eddies of size l is
constant 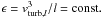 (Kolmogorov 1941).
Within the framework of the β-model for intermittent turbulence, where the
turbulent eddies become less and less space filling, the conserved quantity is
(Kolmogorov 1941).
Within the framework of the β-model for intermittent turbulence, where the
turbulent eddies become less and less space filling, the conserved quantity is
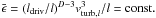 (Frisch et al. 1978), where D is the fractal dimension.
For D = 3 the Kolmogorov turbulence is recovered.
(Frisch et al. 1978), where D is the fractal dimension.
For D = 3 the Kolmogorov turbulence is recovered.
In the case of compressible turbulence the mean volume rate of energy transfer becomes
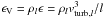 (e.g.,
Fleck 1996). If the density scales with
ρl ∝ l−3α,
the turbulent velocity dispersion obeys the relation
vl ∝ l1/3 + α
(Fleck 1996; Kritsuk et al. 2007). Extending the β-model to compressible turbulence
leads to
(e.g.,
Fleck 1996). If the density scales with
ρl ∝ l−3α,
the turbulent velocity dispersion obeys the relation
vl ∝ l1/3 + α
(Fleck 1996; Kritsuk et al. 2007). Extending the β-model to compressible turbulence
leads to 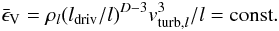 (29)With
ρl ∝ l−3α,
the turbulent velocity dispersion obeys the relation
(29)With
ρl ∝ l−3α,
the turbulent velocity dispersion obeys the relation 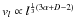 . For
D = 2 (see Sect. 6.1) one obtains
vl ∝ lα
and the energy flux
. For
D = 2 (see Sect. 6.1) one obtains
vl ∝ lα
and the energy flux 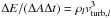 is conserved.
In this case the scaling relation (Eq. (29))
becomes
is conserved.
In this case the scaling relation (Eq. (29))
becomes 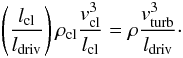 (30)With
ΦA = ΦVH/rcl = ρ/ρclH/rcl
one obtains
(30)With
ΦA = ΦVH/rcl = ρ/ρclH/rcl
one obtains 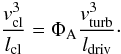 (31)If the energy
dissipation rate at large-scales is dominated by the energy dissipation rate in the dense
clouds,
(31)If the energy
dissipation rate at large-scales is dominated by the energy dissipation rate in the dense
clouds, 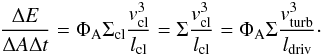 (32)Since the viscous
energy dissipation rate of the disk is given by
(32)Since the viscous
energy dissipation rate of the disk is given by 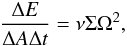 (33)the effective
turbulent viscosity is
(33)the effective
turbulent viscosity is 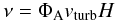 (34)for
D = 2. If D = 3, it becomes
ν = ΦVvturbH. The
disk mass accretion rate Ṁ can be estimated using mass conservation (see,
e.g., Pringle 1981)
(34)for
D = 2. If D = 3, it becomes
ν = ΦVvturbH. The
disk mass accretion rate Ṁ can be estimated using mass conservation (see,
e.g., Pringle 1981)
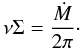 (35)In general, the viscosity
is expected to be of the form
(35)In general, the viscosity
is expected to be of the form 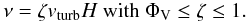 (36)We will estimate
ζ in Sect. 6.1. Figure 1 visualizes the differences between the collisional and
turbulent clumpy disk models.
(36)We will estimate
ζ in Sect. 6.1. Figure 1 visualizes the differences between the collisional and
turbulent clumpy disk models.
 |
Fig. 1 Schematic of the collisional and turbulent disk/torus models. |
5. Turbulent versus collisional disks
Within the collisional model the assumption of a constant cloud mass and sound speed leads
to a constant density, size, and surface density of the clouds independent of the distance
to the galactic center (Fig. 1):
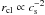 (Eq. (14)),
(Eq. (14)),
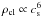 (Eq. (15)),
(Eq. (15)), 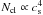 (Eq. (16)). On the other hand, the area and volume
filling factors depend on the sound speed and the angular velocity:
(Eq. (16)). On the other hand, the area and volume
filling factors depend on the sound speed and the angular velocity:
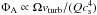 (Eq. (18)),
(Eq. (18)), 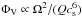 (Eq. (17)). In the case of a constant sound speed the
obscuration of the nucleus is mainly due to a higher area filling factor of clouds of same
mass, density, and size at the inner edge of the torus where the area filling factor
ΦA is maximum. Thus clouds at the inner edge obscure the nucleus with the
highest probability.
(Eq. (17)). In the case of a constant sound speed the
obscuration of the nucleus is mainly due to a higher area filling factor of clouds of same
mass, density, and size at the inner edge of the torus where the area filling factor
ΦA is maximum. Thus clouds at the inner edge obscure the nucleus with the
highest probability.
The situation is different in the turbulent model, where the volume and area filling
factors are constant (Eqs. (24), (26), and (A.3)). Thus, clouds located at all distance to the galactic center
obscure the nucleus with the same probability at optical wavelengths. On the other hand, the
cloud size and mass vary with the inverse of the angular velocity:
lcl ∝ Ω-1 (Eqs. (25) and (A.2)),
Mcl ∝ Ω-1 (Eqs. (27) and (A.4)). For the
cloud density and surface density we found 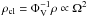 and
Ncl ∝ Ω (Eqs. (28) and (A.5)). For a constant
rotation velocity Ω ∝ R-1. Thus, clouds at the inner edge of the
torus have the highest surface densities. If an AGN torus is Compton thick in X-ray
emission, the optical thickness is most probably provided by a cloud located close to the
central engine.
and
Ncl ∝ Ω (Eqs. (28) and (A.5)). For a constant
rotation velocity Ω ∝ R-1. Thus, clouds at the inner edge of the
torus have the highest surface densities. If an AGN torus is Compton thick in X-ray
emission, the optical thickness is most probably provided by a cloud located close to the
central engine.
Another difference between the turbulent and collisional models lies in the turbulent viscosity and thus the derived disk mass accretion rate. The effective viscosity of the collisional disk is νcoll ~ 3/4 fΦAvturbH (Eq. (7)), that of the turbulent disk is νturb = ζvturbH with ΦV ≤ ζ ≤ 1 (Eq. (36)). For D = 2, the turbulent viscosity and the associated mass accretion rate is a factor of ~1/f ~ 10 higher than the effective viscosity of a collisional disk.
Are the collisional and turbulent disk models exclusive? It is remarkable that the CND clouds have densities close to stability limit against tidal shear and can be modeled by Bonner-Ebert spheres with sound or Alfvénic speeds of ~1 km s-1 (Vollmer et al. 2001a,b). We can only speculate that intermittent turbulence knows about stability, in the sense that if the kinetic energy of a turbulent clump with a velocity dispersion of 6–7 km s-1 is rapidly dissipated, the resulting cloud with an Alfvénic speed of ~1 km s-1 will be marginally stable.
6. Application of the models
The collisional model (Sect. 3) was successfully applied to the CND (Vollmer et al. 2004) and thick obscuring tori in nearby AGNs (Vollmer et al. 2008). We thus concentrate on the turbulent model (Sect. 4) and its relation to the collisional model.
6.1. The circumnuclear disk in the Galactic center
The central black hole of the Galaxy is surrounded by a clumpy structure of gas and dust forming a disk or a ring (CND, see e.g. Güsten et al. 1987) up to a radius of ~5 pc3. The CND has a total gas mass of a few times 104 M⊙ (Etxaluze et al. 2011; Requena-Torres et al. 2012) which is distributed in clouds with an estimated area filling factor of φA ~ 0.1 and a volume filling factor of φV ~ 0.01. The clouds have densities of ~105−6 cm-3, sizes of ~0.1 pc and gas temperatures ≳200 K. A typical dusty cloud has a visual extinction AV > 30m and Mcl ~ 30 M⊙. Further properties of the clouds in the central 2 pc are listed in Jackson et al. (1993). The vertical thickness (2 H) of the CND increases from ~0.5 pc at a radius of 2 pc to about 2 pc at the outer radius of 7 pc. The disk rotates with a velocity of ~110 km s-1 which corresponds to a dynamical mass of ~5 × 106 M⊙ at the inner edge. The velocity dispersion (0.4 times the linewidth) of the clumpy gas disk is ~20 km s-1 (Güsten et al. 1987), that of the clouds is ~7–15 km s-1 (Montero-Castaño et al. 2009). The observed properties of the CND and its gas clouds are summarized in Table 2.
Observed/assumed CND and derived cloud properties within the turbulent clumpy disk model.
For the moment, the CND represents the only gas torus for which we can estimate the
turbulent viscosity via its luminosity-to-mass ratio. The model luminosity-to-mass ratio
due to turbulent viscous energy dissipation is (Eq. (33) and (36)):
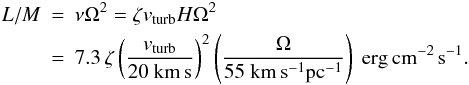 (37)Since
the temperature of the molecular gas is high (≳200 K), the luminosity due to turbulent
viscous energy dissipation is dominated by Oi, H2, H2O, and
high-level CO emission. Submillimeter continuum emission can be used to determine the
total gas mass of the CND. Bradford et al. (2005)
observed the CND up to a radius of ~2 pc in the CO(7–6) rotational transition. The
combination with lower CO rotational transitions yielded temperatures
of T ~ 200−300 K and a total mass of warm gas of at
least 2000 M⊙. The derived luminosity-to-mass ratio
is
(37)Since
the temperature of the molecular gas is high (≳200 K), the luminosity due to turbulent
viscous energy dissipation is dominated by Oi, H2, H2O, and
high-level CO emission. Submillimeter continuum emission can be used to determine the
total gas mass of the CND. Bradford et al. (2005)
observed the CND up to a radius of ~2 pc in the CO(7–6) rotational transition. The
combination with lower CO rotational transitions yielded temperatures
of T ~ 200−300 K and a total mass of warm gas of at
least 2000 M⊙. The derived luminosity-to-mass ratio
is 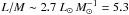 erg s-1 g-1
taking CO, H2, H2O, and Oi emission of the warm gas into
account. Given that the total gas mass of the CND is about a factor of 5–10 higher than
the estimated mass of warm gas (Etxaluze et al. 2011; Requena-Torres et al. 2012), the
total luminosity-to-mass ratio of the CND is
L/M ~ 0.5−1 erg s-1 g-1.
By inserting this value into Eq. (37), we
derive ζ ~ 0.1. This is consistent with D = 2, for
which ζ = ΦA ~ 0.1 (Eq. (34)). We thus suggest that intermittency leads to a fractal dimension
of D = 2 and lowers the turbulent viscosity of accretion-driven clumpy
gas tori by one tenth or the area filling factor.
erg s-1 g-1
taking CO, H2, H2O, and Oi emission of the warm gas into
account. Given that the total gas mass of the CND is about a factor of 5–10 higher than
the estimated mass of warm gas (Etxaluze et al. 2011; Requena-Torres et al. 2012), the
total luminosity-to-mass ratio of the CND is
L/M ~ 0.5−1 erg s-1 g-1.
By inserting this value into Eq. (37), we
derive ζ ~ 0.1. This is consistent with D = 2, for
which ζ = ΦA ~ 0.1 (Eq. (34)). We thus suggest that intermittency leads to a fractal dimension
of D = 2 and lowers the turbulent viscosity of accretion-driven clumpy
gas tori by one tenth or the area filling factor.
In the following, we derive the scaling of the density and turbulent velocity dispersion
with cloud size. We have seen in Sect. 4 that for
D = 2 the scaling is
vl ∝ lα
if
ρl ∝ l−3α.
The exponent α can thus be determined with the ratios
ρ/ρcl = ΦV
and 2H/lcl. We set the
disk thickness to be
2H = 2vturbΩ-1 = 0.7 pc, the
total gas mass of the CND within a radius of 2 pc to
be MCND = 104 M⊙,
and thus
Q ~ (vturb/vrot)(Mdyn/MCND) = 100.
With ρ = Ω2/(πGQ), the
cloud size is lcl = 0.1 pc (Eq. (23)). With a density ratio between the two scales
lcl and 2H
of 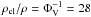 , we
derive α = 0.56. This exponent is very close to that found for galactic
molecular clouds (α = 0.5; Larson 1981; Solomon et al. 1987; however, Heyer
et al. 2009 found a
, we
derive α = 0.56. This exponent is very close to that found for galactic
molecular clouds (α = 0.5; Larson 1981; Solomon et al. 1987; however, Heyer
et al. 2009 found a
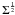 dependence of
dependence of 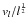 ).
The turbulent velocity thus scales with
vl ∝ l0.5 and
the turbulent velocity of the clouds is
).
The turbulent velocity thus scales with
vl ∝ l0.5 and
the turbulent velocity of the clouds is 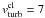 km s-1. This is
compatible with, but at the lower end of the observed velocity dispersion (Montero-Castaño
et al. 2009).
km s-1. This is
compatible with, but at the lower end of the observed velocity dispersion (Montero-Castaño
et al. 2009).
According to Eqs. (24), (27), and (28), the mass of a model gas cloud is Mcl ~ 30 M⊙, the column density is Ncl ~ 3 × 1023 cm-2, and the density is ncl ~ 106 cm-3. This density is consistent with the estimates based on HCN lines (Jackson et al. 1993), but at odds with cloud densities derived from multi-transition CO observations (Requena-Torres et al. 2012). The area filling factor of the clouds is ΦA = 0.26 (Eq. (26)). Since these clouds are not selfgravitating, the Virial theorem cannot be applied to derive their masses. With the Virial cloud masses of Christopher et al. (2005) the CND would have a gas mass and a mass accretion rate of an AGN torus. The mass accretion rate of the CND (Eq. (36) with ζ = ΦA) is Ṁ = 10-2 M⊙ yr-1. The assumed disk parameters and calculated cloud parameters for the turbulent disk model are summarized in Table 2. In comparison to this, we now turn to the collisional disk model.
In this framework of a collisional disk, the CND has an area filling factor of ΦA = 4/3ϑ-1 ≃ 0.1 (ϑ = 15; Vollmer et al. 2004) within a radius of 7 pc. According to Eq. (13), the area filling factor at a radius of R = 2 pc has to increase to ΦA = 0.35 to obtain a cloud mass of Mcl = 10 M⊙. The cloud radius, density, and column density are then rcl = 0.03 pc, ρcl = 1.3 × 106 cm-3, and Ncl = 1.3 × 1023 cm-2. The volume filling factor at this radius is ΦV = 0.03.
The turbulent and collisional models thus give similar cloud properties, except for the cloud velocity dispersion, which is 1 km s-1 in the collisional model and 7 km s-1 in the turbulent model. Since in the collisional model the clouds are marginally selfgravitating by definition, the clouds of the turbulent model are highly overpressured with respect to the turbulent pressure at a given mass. A further difference between the turbulent and collisional disks is the mass accretion rate. The collisional model yields a ~10 times smaller mass accretion rate (Vollmer et al. 2004) than the turbulent model.
6.2. Clumpy gas tori in active galactic nuclei
Obscuring gas tori in local AGNs have a high velocity dispersion (vturb ~ 40−80 km s-1) and are therefore thick (Davies et al. 2007). For a representative AGN torus, we chose vturb = 50 km s-1. This corresponds to the maximum shock velocity which allows C-type shocks at a mean density of n = 105 cm-3 (Le Bourlot et al. 2002). The typical total gas mass is a few 106 M⊙ within a radius of ~10 pc (Hicks et al. 2009) and the Toomre parameter is Q ~ 5 (Vollmer et al. 2008). The torus height at a radius of 5 pc is H = vturbΩ-1 = 2.3 pc. The area filling factor of these clouds (Eq. (26)) is ΦA = 0.7, i.e. the torus is obscuring, as it is expected. The volume filling factor of the clouds (Eq. (24)) is ΦV = 0.01, comparable to that of the CND.
The assumed torus parameters and calculated cloud parameters are summarized in Table 3. The mass accretion rate of the torus (Eq. (36) with ζ = ΦA) is Ṁ = 4.8 M⊙ yr-1. Thus, the mass accretion rate of a turbulent, thick, obscuring gas tori is a factor of ~500 higher than that of a turbulent CND.
The cloud mass and size at a radius of 5 pc are Mcl ~ 100 M⊙ and lcl = 0.08 pc. The cloud density and column density are ncl = 9 × 106 cm-3 and Ncl = 2 × 1024 cm-2. These clouds are thus Compton-thick. The velocity dispersion of the clouds is vcl ~ vturb (lcl/(2H))0.5 ~ 6 km s-1. The torus clouds are more massive, smaller, have an about ten times higher density and surface density, but, most importantly, have a comparable velocity dispersion compared to the CND clouds.
Observed/assumed torus and derived cloud properties within the turbulent clumpy disk model.
Since typical radial extents of obscuring tori in nearby AGNs are about 10 pc (Davies et al. 2007; Lira et al. 2013; Müller-Sanchez et al. 2013), the typical cloud sizes and masses have to be multiplied by a factor 2 (both quantities depend on Ω-1): Mcl ~ 230 M⊙, lcl ~ 0.16 pc. The cloud density has to be divided by a factor 4 and the column density by a factor 2: ρcl = 2 × 106 cm-3 and Ncl = 1024 cm-2.
As for the CND (Sect. 6.1), the cloud properties of the turbulent model are very similar to those of the collisional model, except for the cloud velocity dispersion, which is ~ 5 times higher in the turbulent model compared to the collisional model. The derived mass accretion rate of the turbulent torus is about a factor of 10 higher than the mass accretion rate for collisional tori (Vollmer et al. 2008). This is mainly due to the mean fraction of cloud mass participating in the highly supersonic cloud collisions f = 0.1 (Eq. (6)), which enters the viscosity prescription in the collisional model.
7. The quenching of star formation in accretion-driven turbulent gas disks
As shown in Sect. 6, the main difference between the
gas cloud in the collisional and turbulent clumpy disk models lies in the velocity
dispersion of the clouds. Whereas it is ~1–1.5 km s-1 in the collisional model,
it is 6–7 km s-1 in the turbulent model. By definition, the clouds in the
collisional model are marginally selfgravitating, i.e. their free fall time equals the
turbulent crossing time: tff = tturb
(Eq. (9)). To assess the role of
selfgravitation of the clouds, we calculate the fraction 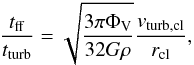 (38)where
vturb,cl is the turbulent velocity dispersion
of the cloud. A cloud is selfgravitating if
tff/tturb < 1.
(38)where
vturb,cl is the turbulent velocity dispersion
of the cloud. A cloud is selfgravitating if
tff/tturb < 1.
Inserting Eqs. (24), (25),
rcl = l/2, and
ρ = Ω2/(πGQ) into
Eq. (38) yields 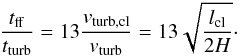 (39)We recall that the disk
height is H = vturb/Ω. The
cloud properties of Tables 2 and 3 lead to
tff/tturb ~ 5
for the CND
and tff/tturb ~ 2
for a thick, obscuring torus. Since our value of the velocity dispersion of CND gas clouds
is at the lower limit of the observed velocity dispersion (Montero-Castaño et al. 2009), the values of
tff/tturb can
also be seen as lower limits.
(39)We recall that the disk
height is H = vturb/Ω. The
cloud properties of Tables 2 and 3 lead to
tff/tturb ~ 5
for the CND
and tff/tturb ~ 2
for a thick, obscuring torus. Since our value of the velocity dispersion of CND gas clouds
is at the lower limit of the observed velocity dispersion (Montero-Castaño et al. 2009), the values of
tff/tturb can
also be seen as lower limits.
Thus, for both types of clouds selfgravitation does not play a role, i.e. these clouds are overpressured with respect to the turbulent pressure and do not collapse to form stars. The high turbulent energy input caused by external mass accretion thus leads to overpressured gas clouds with high velocity dispersions which cannot form stars. The accretion-driven turbulence thus suppresses or quenches star formation in the clumpy disk. We suggest that the increase of the turbulent velocity in the torus gas is due to adiabatic compression of the torus gas by material that falls onto the torus from outside.
We suggest two ways to estimate the necessary external mass accretion rate onto the torus, which leads to an enhanced gas velocity dispersion and thus an enhanced Toomre Q parameter of the large-scale, smeared-out gas disk (with a mean density and a mean velocity dispersion4):
-
1.
Following Robertson & Goldreich (2012; Eq. (6)) the necessary condition for adiabatic compression of the torus gas is that the compression timescale has to be smaller than the turbulent timescale times the efficiency of the energy cascade η:
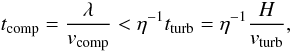 (40)where
λ is the characteristic compression lengthscale. Assuming
λ = H for convenience and taking intermittency
(η = ζ) into account, this condition translates
into
vcomp > ζvturb
with ΦV ≤ ζ ≤ 1 (see Eq. (36)). The compression velocity can be calculated from the
conservation of the rate of momentum transfer:
(40)where
λ is the characteristic compression lengthscale. Assuming
λ = H for convenience and taking intermittency
(η = ζ) into account, this condition translates
into
vcomp > ζvturb
with ΦV ≤ ζ ≤ 1 (see Eq. (36)). The compression velocity can be calculated from the
conservation of the rate of momentum transfer: 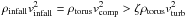 . It is assumed
that the gas radially hits the outer border of the torus which has an area of
2πRH. The external mass accretion rate is
. It is assumed
that the gas radially hits the outer border of the torus which has an area of
2πRH. The external mass accretion rate is
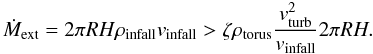 (41)With
vturb/vrot = H/R,
Σtorus = ρtorusH, and
vinfall = vrot one obtains
(41)With
vturb/vrot = H/R,
Σtorus = ρtorusH, and
vinfall = vrot one obtains
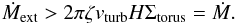 (42)The external mass
accretion rate has thus to be higher than the disk/torus mass accretion rate. This is
expected, because the torus is fed by the external mass infall. Based on the results
of Sect. 6.2 the external mass accretion rate is
expected to be on the order of a few solar masses per year.
(42)The external mass
accretion rate has thus to be higher than the disk/torus mass accretion rate. This is
expected, because the torus is fed by the external mass infall. Based on the results
of Sect. 6.2 the external mass accretion rate is
expected to be on the order of a few solar masses per year. -
2.
the energy supply due to accretion ΔE/(ΔAΔt) ~ ṀΩ2, where Ṁ is the disk/torus mass accretion rate, has to be larger than the energy supply from supernovae (Vollmer & Beckert 2003)
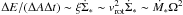 .
The star formation rate can be estimated
via Ṁ∗ ~ 0.02MgasΩ (Genzel
et al. 2010; Daddi et al. 2010). We thus
find Ṁ > 0.02MgasΩ.
For vrot = 100 km s-1,
R = 10 pc, and
Mgas = 5 × 106 M⊙,
the lower limit for the mass accretion rate is
Ṁ = 1 M⊙ yr-1.
.
The star formation rate can be estimated
via Ṁ∗ ~ 0.02MgasΩ (Genzel
et al. 2010; Daddi et al. 2010). We thus
find Ṁ > 0.02MgasΩ.
For vrot = 100 km s-1,
R = 10 pc, and
Mgas = 5 × 106 M⊙,
the lower limit for the mass accretion rate is
Ṁ = 1 M⊙ yr-1.
The impact of AGN feedback on gas expulsion and driving of turbulence is not considered,
because it is beyond the scope of this work. We conclude that continuous external mass
accretion rate of a few solar masses per year leads to large-scale adiabatic compression of
the torus gas which increases the mean velocity dispersion and quenches star formation. At
small-scales, it is likely that adiabatic compression due to infall will be followed by
adiabatic expansion, especially in turbulent flows. Here we only consider the overall
behavior of the whole gas disk in the presence of continuous external mass accretion. If the
external mass accretion is time-dependent and stochastic (e.g., Gaspari et al. 2013), the initial massive gas infall makes the
disk/torus thick. In the presence of a sufficient external mass accretion rate at the outer
edge averaged over a viscous timescale, the torus can sustain its thickness during a viscous
timescale  (43)For the model to be
valid, the variation timescale of the external mass accretion rate thus should not exceed
the viscous timescale of the disk/torus.
(43)For the model to be
valid, the variation timescale of the external mass accretion rate thus should not exceed
the viscous timescale of the disk/torus.
Once the external mass accretion has significantly decreased, the turbulent energy is dissipated in a crossing time H/vturb = Ω-1, the disk becomes thinner and begins to form stars. In the case of a massive AGN torus, the subsequent star formation will most likely be qualified as a nuclear starburst.
Vollmer et al. (2008) proposed an evolutionary model which is divided into three phases: Phase I – initial massive infall and formation of a turbulent, massive gas disk: an initial infall of a large amount of gas, Mgas ~ 106 M⊙ leads to the formation of a massive (Q ~ 1), moderately thin (vturb/vrot < 5) gas disk in which star formation proceeds. Phase II – torus evolution at constant turbulent velocity: during the first phase of its evolution the massive collisional torus stays thick. This implies that the mass accretion rate within the torus, and thus also the external mass accretion rate Ṁ, do not decrease significantly during this phase. Phase III – torus evolution at constant gas mass: once the external mass accretion rate has significantly decreased, the torus evolves at constant gas mass.
The evolution of a thick, obscuring torus is proposed to proceed in the following way: due to an initial, massive infall a massive (Q ~ 1) turbulent star-forming disk is formed (Phase I). The turbulence in this disk is maintained through the energy supply by feedback from rapid star formation. The subsequent SN explosions destroy the disk structure after 10 Myr, i.e. the intercloud medium is removed leaving only the densest, most massive clouds which remain Jeans-stable. The disk becomes collisional and stays geometrically thick (Phase II). After ~100 Myr the mass accretion rate decreases and the disk becomes thin (Phase III) and ultimately transparent.
Based on the present work, we suggest an alternative evolution scenario including the three phases of Vollmer et al. (2008) which depends on the external gas infall timescale tinfall = Mgas/Ṁ. For tinfall ≲ 100 Ω-1 the torus becomes thick and star formation is quenched.
-
Phase I a torus with a small amount of gas (~104 M⊙) becomes thick for Ṁ ≳ 10-3 M⊙ yr-1. In this phase gas is added to the torus without a significant gas consumption by star formation.
-
Phase II once the torus has acquired a gas mass exceeding Mgas ≳ Mdyn(10 km s-1/vrot) ~ 106 M⊙ and tinfall ≳ 100 Ω-1, star formation sets in with Ṁ∗ ~ 0.02MgasΩ. Since the infall is slow, the star formation rate exceeds the mass accretion rate (Ṁ∗ > Ṁ), and turbulence is maintained through the energy supply by feedback from rapid star formation. The subsequent SN explosions might destroy the disk structure after 10 Myr, removing the intercloud medium. Otherwise, star formation consumes the gas within a timescale of t∗ = Mgas/Ṁ∗.
-
Phase III - if the mass accretion rate increases, exceeding the expected star formation rate according to Ṁ∗ ~ 0.02 × MgasΩ (implying tinfall ≲ 100Ω-1), the torus gas is adiabatically compressed. This leads to an increase of the velocity dispersion and the Toomre Q parameter. The turbulent energy supply of the torus gas becomes dominated by the gain of potential energy via gas accretion. The turbulent torus clouds become overpressured with respect to the turbulent pressure and cannot collapse anymore. Therefore, star formation is quenched in the turbulent, thick, obscuring torus. The subsequent high mass accretion rate powers the central AGN.
If the external mass accretion rate decreases significantly, star formation sets in again, producing a nuclear starburst (Phase II). The torus looses gas via star formation, SN gas expulsion, and radial gas accretion within the torus. The necessary mass accretion rate to form a thick torus thus varies significantly with time depending on the torus gas mass (Ṁ ≳ 3 × 10-3MgasΩ). The thickness and star formation rate of the torus entirely depend on the external mass accretion rate.
8. Comparison with NGC 3227 and NGC 1068
The dense molecular gas in AGNs generally has temperatures in excess of 100 K. Krips et al. (2011) analyzed various lower CO, HCN and HCO+ transitions observed at <2′′ ~ 140 pc resolution in NGC 1068. They concluded that the gas is at temperatures >200 K. Hailey-Dunsheath et al. (2012) detected far-IR CO rotational emission from the central 10′′ ~ 700 pc of NGC 1068. The detected transitions were modeled as arising from two different components at 170 and 570 K with densities exceeding 4 × 105 cm-3.
Davies et al. (2012) presented an LVG analysis of subarcsecond-resolution observations of CO(2–1) and HCN(1–0) line emissions in the central region of the Seyfert galaxy NGC 3227. Based on the high HCN(1–0)/CO(2–1) ratio in the central 80 pc of NGC 3227 and the central regions of NGC 6951 and NGC 1068, Davies et al. (2012) suggested that the dense gas in all three galaxies is warm (T ~ 300 K), dense (ncl ~ 105.5 cm-3, and have large velocity gradients (dV/dr ~ 100 km s-1 pc-1)5. Assuming a cloud size of 0.1 pc, the clouds have a turbulent velocity dispersion of 10 km s-1.
Within our turbulent torus model (Sect. 6.2), the
derived cloud density
(ρcl = Ω2/(πGQ))
corresponds to an outer torus radius of R ~ 30 pc. The clumps at this
radius have sizes between 0.3 and 0.5 pc and masses between 180 and
720 M⊙. Since the cloud size
lcl and the torus height H are both
proportional to the angular velocity Ω, the turbulent velocity of the clouds is the same for
all radii R: vcl = 5−7 km s-1.
These cloud properties are consistent with those derived by Davies et al. (2012). All tori clouds are overpressured with respect to
the turbulent pressure expected for selfgravitating clouds (Eq. (39)). To estimate the temperature of gas in the
model clouds, we follow Bradford et al. (2005) and
require equilibrium between turbulent dissipation and (H2, H2O,
CO)-line cooling within the turbulent clouds:
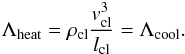 (44)For the cooling we
use the model of Neufeld & Kaufman (1993)
with CO and H2O abundances of 10-4 and 10-6, respectively.
With a cloud density of
ncl = 3 × 105 cm-3, a cloud size
of 0.3 pc, and a turbulent velocity dispersion of
vcl = 7 km s-1, we obtain a gas temperature
of T = 170 K. Half of the cooling is provided by H2
line-emission, 40% by CO line-emission, and the rest by H2O line-emission. To
reach a gas temperature of 300 K a velocity dispersion of
vcl = 14 km s-1 is required. As already suggested
in Sect. 6.1 for the CND, our model cloud velocity
dispersion might be seen as a lower limit.
(44)For the cooling we
use the model of Neufeld & Kaufman (1993)
with CO and H2O abundances of 10-4 and 10-6, respectively.
With a cloud density of
ncl = 3 × 105 cm-3, a cloud size
of 0.3 pc, and a turbulent velocity dispersion of
vcl = 7 km s-1, we obtain a gas temperature
of T = 170 K. Half of the cooling is provided by H2
line-emission, 40% by CO line-emission, and the rest by H2O line-emission. To
reach a gas temperature of 300 K a velocity dispersion of
vcl = 14 km s-1 is required. As already suggested
in Sect. 6.1 for the CND, our model cloud velocity
dispersion might be seen as a lower limit.
Müller-Sanchez et al. (2009) presented subarcsecond-resolution H2 2.12 μm line observations of the inner 300 pc of the Seyfert galaxy NGC 1068. They found two prominent linear structures leading to the AGN from the north and south. The kinematics of the gas in these features are dominated by noncircular motions and indicate that material streams toward the nucleus on highly elliptical or parabolic trajectories. These gas streamers provide the central 10 pc with fresh gas, corresponding to the external mass accretion rate discussed in Sect. 7. From their data, Müller-Sanchez et al. (2009) derive an upper limit for this external mass accretion rate of Ṁext ~ 15 M⊙ yr-1. This limit is entirely consistent with the theoretical limit for external mass accretion rate of a few solar masses per year which leads to adiabatic compression and subsequent quenching of the star formation rate (Sect. 7). The absence of rotation in the H2 velocity field of the inner 20 pc implies that the torus is probably hidden by the southern gas streamer (Müller-Sanchez et al. 2009). This leads to a torus size of ~7 pc, comparable to that of the CND. We thus suggest that the nucleus is in a Phase III, where the torus is still formed through massive external accretion.
9. Implications for star formation in the Galactic center
The quenched star formation in gas with a high turbulent velocity (Q > 1) might also help to elucidate the paradox of youth in the Galactic center (Ghez et al. 2003; Genzel et al. 2010). The central parsec of the Galaxy contains ~200 young, massive stars, and is one of the richest and massive star formation regions in the entire Galaxy. This is highly surprizing. The presence of so many young stars in the immediate vicinity of the central massive black hole is unexpected (Allen & Sanders 1986; Morris 1993; Ghez et al. 2003; Alexander 2005). For gravitational collapse to occur in the presence of the tidal shear from the central mass, gas clouds have to be denser than the critical Roche density, which is higher than 1010 cm-3 at a distance of 0.1 pc from the black hole. A population of 100 young, massive stars is arranged mainly in two coherent disk structures (Bartko et al. 2009). Since the transport of massive stars from more benign sites of formation is not favored by current observations, in situ star formation is the most probable explanation for the paradox of youth. Recent simulations suggest that rapid dissipation and cooling in a molecular cloud plunging into the vicinity of a massive black hole or in two clouds colliding near near a massive black hole can plausibly overcome the critical Roche density at ~0.1 to 1 pc (Bonnell & Rice 2008; Hobbs & Nayakshin 2009). The resulting clumpy, filamentary disk fragments and may form stars efficiently.
Quenched star formation due to strong shocks at high velocities in colliding gas filaments can help to bring a fairly large amount of gas (≥ 104 M⊙) near the central black hole without star formation occuring on its way to the center. This gas can then settle at a distance of 0.1 pc from the black hole without a previous considerable gas consumption by star formation. This might help to explain the lack of young massive stars at galactic radii >0.5 pc and the relatively low eccentricities of these stars within the central parsec of the Galaxy (Bartko et al. 2009).
10. Conclusions
Galactic gas-gas collisions involving a turbulent multiphase ISM share common properties: dense extraplanar gas visible in CO, large linewidths (≳50 km s-1), strong mid-infared H2 line emission, low star formation activity, and strong radio continuum emission in the absence of a high star formation rate. Gas-gas collisions can occur in the form of ram pressure stripping caused by the rapid motion of a spiral galaxy within the intracluster medium (NGC 4438; Vollmer et al. 2005, 2009), a galaxy head-on collision (NGC 4438; Taffy galaxies, Condon et al. 1993; Gao et al. 2003; Braine et al. 2003; Vollmer et al. 2012), or a compression of the intragroup gas and/or galaxy ISM by an intruder galaxy which flies through the galaxy group at a high velocity (Stephan’s Quintet; Appleton et al. 2006; Guillard et al. 2009; Cluver et al. 2010; Guillard et al. 2012).
Gas tori in AGNs share many properties with these systems. The gas which falls from larger galactic radii onto an existing gas torus hits the torus gas at high relative velocities. Shocks form which give rise to gas turbulence within the torus. Davies et al. (2007) showed that the gas tori of nearby AGNs have high velocity dispersions, i.e. they are thick, and that there have been recent, but no longer active, starbursts in the last 10–300 Myr, i.e. the star formation has recently decreased despite the large torus gas masses (~106 M⊙).
Inspired by these similarities, we developed an analytical model for turbulent clumpy gas disks where the energy to drive turbulence is supplied by external infall or the gain of potential energy by radial gas accretion within the disk (Sect. 2). The gas disk is assumed to be stationary (∂Σ/∂t = 0) and the external mass accretion rate to be close to the mass accretion rate within the disk (the external mass accretion rate feeds the disk at its outer edge). The external and disk mass accretion rates averaged over the viscous timescale are assumed to be constant. In reality, the external mass accretion rate is certainly time-dependent and stochastic (see, e.g. Gaspari et al. 2013). Therefore, nonsteady hydrodynamics should prevail in real gas tori. Our model might be applied when all time-dependent quantities are averaged over a sufficiently long timescale, i.e. the viscous timescale of the disk or several Myr. Within the model, the disk is characterized by the disk mass accretion rate Ṁ and the Toomre Q parameter which is used as a measure of the gas content of the disk. We suggest that the velocity dispersion of the torus gas is increased through adiabatic compression by the infalling gas.
In contrast to our previous collisional and turbulent models, the gas clouds are not assumed to be selfgravitating. The disk velocity dispersion is fixed by the mass accretion rate and the gas surface density (Eq. (36)) (via Q). Turbulence is assumed to be supersonic, creating shocks in the weakly ionized dense molecular gas. For not too high shock velocities (<50 km s-1) these shocks will be continuous (C-type). The cloud size is determined by the size of a C-shock at a given velocity dispersion (Eq. (23)). If the turbulent velocity dispersion is much higher, strong dissociative J-type shocks will develop and our determination of the cloud size can no longer be applied. We give expressions for the expected volume and area filling factors, mass, density, column density, and velocity dispersion of the clouds. The latter is based on scaling relations of intermittent turbulence (Eq. (29)) whose open parameters are estimated for the CND in the Galactic center.
The results for the turbulent disk model were compared to those of the collisional model
developed in Vollmer et al. (2004, 2008). In the collisional model with constant cloud mass,
the cloud size, density, and column density only depend on the gas temperature, whereas the
cloud area and volume filling factors depend on Ω and Ω2, respectively. In the
case of a constant sound speed the obscuration of the nucleus is mainly due to a higher area
filling factor of clouds of same mass, density, and size at the inner edge of the torus
where the area filling factor ΦA is maximum. Within the turbulent model, we found
lcl ∝ Ω-1,
Mcl ∝ Ω-1, 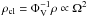 , and
Ncl ∝ Ω. Thus, clouds at the inner edge of the torus have the
highest surface densities. If an AGN torus is Compton thick in X-ray emission, the optical
thickness is most probably provided by a cloud located close to the central engine. The mass
accretion rates of the turbulent torus is expected to be a factor of ~10 higher than those
of the collisional model.
, and
Ncl ∝ Ω. Thus, clouds at the inner edge of the torus have the
highest surface densities. If an AGN torus is Compton thick in X-ray emission, the optical
thickness is most probably provided by a cloud located close to the central engine. The mass
accretion rates of the turbulent torus is expected to be a factor of ~10 higher than those
of the collisional model.
The turbulent and collisional model were applied to the CND and thick obscuring tori in AGNs. Despite the different gas masses (CND: 104 M⊙; AGN torus: 106 M⊙) and velocity dispersions (CND: 20 km s-1; AGN torus: 50 km s1), both models share gas clouds of similar masses and sizes. However, whereas the expected FWHM linewidths are ~2.5 km s-1 in the collisional model, they are ~17 km s-1 in the turbulent model. Whereas the clouds are by definition selfgravitating in the collisional model, they are overpressured with respect to the turbulent pressure in the turbulent model. This prevents gravitational collapse and star formation is significantly reduced in the torus. This is consistent with the findings of Davies et al. (2007) in nearby AGNs and the large observed linewidths of CND clouds (Montero-Castaño et al. 2009). In particular, the model gas cloud properties and the external mass accretion rate necessary for the quenching of the star formation rate due to adiabatic compression are consistent with those derived from observations (Müller-Sanchez et al. 2009; Davies et al. 2012).
With these ideas in mind, we propose the following scenario for the evolution of a galactic center gas torus: a torus with a small amount of gas (~104 M⊙) becomes thick for Ṁ ≳ 10-3 M⊙ yr-1. In this phase gas is added to the torus without a significant gas consumption by star formation. Once the torus has acquired a gas mass exceeding Mgas ≳ Mdyn(10 km s-1/vrot) ~ 106 M⊙ and tinfall ≳ 100 Ω-1, star formation sets in with Ṁ∗ ~ 0.02 MgasΩ. Since the infall is slow, the star formation rate exceeds the mass accretion rate (Ṁ∗ > Ṁ), and turbulence is maintained through the energy supply by feedback from rapid star formation. The subsequent SN explosions might destroy the disk structure after 10 Myr, removing the intercloud medium. Otherwise, star formation consumes the gas within a timescale of t∗ = Mgas/Ṁ∗. If the mass accretion rate increases above the expected star formation rate Ṁ∗ ~ 0.02 × MgasΩ within a timescale smaller than the star formation timescale (tinfall ≲ 100 Ω-1), the torus gas is adiabatically compressed. This leads to an increase of the velocity dispersion and the Toomre Q parameter. The turbulent energy supply of the torus gas becomes dominated by the gain of potential energy via gas accretion. The turbulent torus clouds become overpressured with respect to the turbulent pressure and cannot collapse anymore. Therefore, star formation is quenched in the turbulent, thick, obscuring torus. The subsequent high mass accretion rate powers the central AGN. If the external mass accretion rate decreases significantly, star formation sets in again, producing a nuclear starburst. The necessary mass accretion rate to form a thick torus thus varies significantly with time depending on the torus gas mass. The thickness and star formation rate of the torus entirely depend on the external mass accretion rate.
We suggest that quenched star formation due to strong shocks at high velocities in colliding gas streams (a gas cloud falling onto a pre-existing torus) and subsequent adiabatic compression can help to bring a fairly large amount of gas (≥ 104 M⊙) from a torus near the central black hole without star formation occuring on its way to the center. This gas can then settle around at a distance of 0.1 pc from the black hole without a previous considerable gas consumption by star formation. This might help to explain the paradox of youth (Ghez et al. 2003), i.e. the lack of young massive stars at galactic radii >0.5 pc and the relatively low eccentricities of these stars within the central parsec of the Galaxy (Bartko et al. 2009).
Indeed, local spiral galaxies show a Qtot not too far away from unity (1.3–2.5; Leroy et al. 2008).
For Q > 1 the Toomre parameter corresponds to a measure of the gas content with Q = 1 for the maximum gas content (see Sect. 2).
References
- Alexander, T. 2005, Phys. Rep., 419, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, D. A., & Sanders, R. H. 1986, Nature, 319, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Appleton, P. N., Xu, K. C., Reach, W., et al. 2006, ApJ, 639, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Balkovsky, E., & Falkovich, G. G. 1998, Phys. Rev. E, 57, 1231 [NASA ADS] [CrossRef] [Google Scholar]
- Bartko, H., Martins, F., Fritz, T. K., et al. 2009, ApJ, 697, 1741 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A., & Rice, W. K. M. 2008, Science, 321, 1060 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bradford, C. M., Stacey, G. J., Nikola, T., et al. 2005, ApJ, 623, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Braine, J., Davoust, E., Zhu, M., et al. 2003, A&A, 408, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, C.-Y., & Ostriker, E. C. 2012, ApJ, 744, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Christopher, M. H., Scoville, N. Z., Stolovy, S. R., & Yun, M. S. 2005, ApJ, 622, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Cluver, M. E., Appleton, P. N., Boulanger, F., et al. 2010, ApJ, 710, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Combes, F., Dupraz, C., Casoli, F., & Pagani, L. 1988, A&A, 203, L9 [NASA ADS] [Google Scholar]
- Condon, J. J., Helou, G., Sanders, D. B., & Soifer, B. T. 1993, AJ, 105, 1730 [Google Scholar]
- Crutcher, R. M. 1999, ApJ, 520, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. I., Müller Sánchez, F., Genzel, R., et al. 2007, ApJ, 671, 1388 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R., Mark, D., & Sternberg, A. 2012, A&A, 537, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dobbs, C. L., & Pringle, J. E. 2013, MNRAS, 1187 [Google Scholar]
- Draine, B. T. 1980, ApJ, 241, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & McKee, C. F. 1993, ARA&A, 31, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., Roberge, W. G., & Dalgarno, A. 1983, ApJ, 264, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Etxaluze, M., Smith, H. A., Tolls, V., Stark, A. A., & González-Alfonso, E. 2011, AJ, 142, 134 [Google Scholar]
- Fleck, R. C., Jr. 1996, ApJ, 458, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Fraternali, F., & Binney, J. J. 2008, MNRAS, 386, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, U., Sulem, P.-L., & Nelkin, M. 1978, J. Fluid Mech., 87, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, Y., Zhu, M., & Seaquist, E. R. 2003, AJ, 126, 2171 [NASA ADS] [CrossRef] [Google Scholar]
- Gaspari, M., Ruszkowski, M., & Oh, S. P. 2013, MNRAS, 432, 3401 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Eisenhauer, F., & Gillessen, S. 2010, RvMP, 82, 3121 [NASA ADS] [Google Scholar]
- Ghez, A. M., Duchêne, G., Matthews, K., et al. 2003, ApJ, 586, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Guillard, P., Boulanger, F., Pineau Des Forêts, G., & Appleton, P. N. 2009, A&A, 502, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillard, P., Boulanger, F., Pineau des Forłts, G., et al. 2012, ApJ, 749, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Güsten, R., Genzel, R., Wright, M. C. H., et al. 1987, ApJ, 318, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Hailey-Dunsheath, S., Sturm, E., Fischer, J., et al. 2012, ApJ, 755, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Heyer, M., Krawczyk, C., Duval, J., & Jackson, J. M. 2009, ApJ, 699, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Hicks, E. K. S., Davies, R. I., Malkan, M. A., et al. 2009, ApJ, 696, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, A., & Nayakshin, S. 2009, MNRAS, 394, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Hwang, J.-S., Struck, C., Renaud, F., & Appleton, P. N. 2012, MNRAS, 419, 1780 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, J. M., Geis, N., Genzel, R., et al. 1993, ApJ, 402, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Kenney, J. D. P., Rubin, V. C., Planesas, P., & Young, J. S. 1995, ApJ, 438, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Krips, M., Martin, S., Eckart, A., et al. 2011, ApJ, 736, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Kritsuk, A. G., Norman, M. L., Padoan, P., & Wagner, R. 2007, ApJ, 665, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Krolik, J. H., & Begelman, M. C. 1988, ApJ, 329, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1981, MNRAS, 194, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bourlot, J., Pineau des Forêts, G., Flower, D. R., & Cabrit, S. 2002, MNRAS, 332, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A.K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D. N. C., & Pringle, J. E. 1987, ApJ, 320, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Lira, P., Videla, L., Wu, Y., et al. 2013, ApJ, 764, 159 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., Li, P. S., & Klein, R. I. 2010, ApJ, 720, 1612 [NASA ADS] [CrossRef] [Google Scholar]
- Marinacci, F., Binney, J., Fraternali, F., et al. 2010, MNRAS, 404, 1464 [NASA ADS] [Google Scholar]
- Montero-Castaño, M., Herrnstein, R. M., & Ho, P. T. P. 2009, ApJ, 695, 1477 [Google Scholar]
- Morris, M. 1993, ApJ, 408, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Müller Sánchez, F., Davies, R. I., Genzel, R., et al. 2009, ApJ, 691, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Müller-Sánchez, F., Prieto, M. A., Mezcua, M., et al. 2013, ApJ, 763, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., & Kaufman, M. J. 1993, ApJ, 418, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Parravano, A. 1987, A&A, 172, 280 [NASA ADS] [Google Scholar]
- Peterson, B. W., Appleton, P. N., Helou, G., et al. 2012, ApJ, 751, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Pringle, J. E. 1981, ARA&A, 19, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Renaud, F., Appleton, P. N., & Xu, C. K. 2010, ApJ, 724, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Requena-Torres, M. A., Güsten, R., Weiß, A., et al. 2012, A&A, 542, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robertson, B., & Goldreich, P. 2012, ApJ, 750, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Sani, E., Davies, R. I., Sternberg, A., et al. 2012, MNRAS, 424, 1963 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., Rivolo, A. R., Barrett, J., & Yahil, A. 1987, ApJ, 319, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Strasser, S. T., Dickey, J. M., Taylor, A. R., et al. 2007, AJ, 134, 2252 [NASA ADS] [CrossRef] [Google Scholar]
- Trinchieri, G., Sulentic, J., Breitschwerdt, D., & Pietsch, W., 2003, A&A, 401, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Hulst, J. M., & Rots, A. H. 1981, AJ, 86, 1775 [NASA ADS] [CrossRef] [Google Scholar]
- Vollmer, B., & Beckert, T. 2002, A&A, 382, 872 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., & Beckert, T. 2003, A&A, 404, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., & Duschl, W. J. 2001, A&A, 377, 1016 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Beckert, T., & Duschl, W. J. 2004, A&A, 413, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Braine, J., Combes, F., & Sofue, Y. 2005, A&A, 441, 473 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Beckert, T., & Davies, R. I. 2008, A&A, 491, 441 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Soida, M., Chung, A., et al. 2009, A&A, 496, 669 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Braine, J., & Soida, M. 2012, A&A, 547, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wardle, M. 1990, MNRAS, 246, 98 [NASA ADS] [Google Scholar]
- Williams, J. P., Bergin, E. A., Caselli, P., Myers, P. C., & Plume, R. 1998, ApJ, 503, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Yusef-Zadeh, F., Hewitt, J. W., Wardle, M., et al. 2013, ApJ, 762, 33 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Frozen-in magnetic field
If the so-called frozen-in condition
(nivi = const.,
where ni and
vi are the ionized gas density and
velocity; e.g. Wardle 1990) is used instead of
recombination-ionization equilibrium Eq. (21) becomes 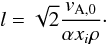 (A.1)With
γ = 600 cm−3/2 s1/2
and ζCR = 10-15 s-1 the size of the
C-shock is
(A.1)With
γ = 600 cm−3/2 s1/2
and ζCR = 10-15 s-1 the size of the
C-shock is 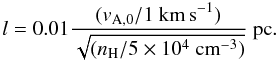 (A.2)The area filling
factor and cloud mass then become
(A.2)The area filling
factor and cloud mass then become 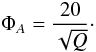 (A.3)For the cloud mass and
surface density we find
(A.3)For the cloud mass and
surface density we find ![\appendix \setcounter{section}{1} \begin{eqnarray} M_{\rm cl}&=&0.03\,\left(\Omega/1.5 \times 10^{-5}~{\rm yr}^{-1}\right)^{-1} \nonumber \\[2mm] &&\times~(Q/5)^{\frac{1}{2}}\left(v_{\rm A,0}/1~{\rm km\,s}^{-1}\right)^{2}\left(v_{\rm turb}/30~{\rm km\,s}^{-1}\right)~{M}_{\odot} , \label{eq:Amcl} \end{eqnarray}](/articles/aa/full_html/2013/08/aa21409-13/aa21409-13-eq373.png) (A.4)
(A.4)![\appendix \setcounter{section}{1} \begin{eqnarray} N_{\rm cl}&= & 8 \times 10^{22}\,\left(\Omega/1.5 \times 10^{-5}~{\rm yr}^{-1}\right)\nonumber \\[2mm] & & \times~ (Q/5)^{-\frac{1}{2}}\left(v_{\rm turb}/30~{\rm km\,s}^{-1}\right)~{\rm cm}^{-2}\ . \label{eq:ANcl} \end{eqnarray}](/articles/aa/full_html/2013/08/aa21409-13/aa21409-13-eq374.png) (A.5)The
cloud mass and surface density thus increase linearly with the turbulent velocity of the
disk, whereas in the recombination-ionization equilibrium model
(A.5)The
cloud mass and surface density thus increase linearly with the turbulent velocity of the
disk, whereas in the recombination-ionization equilibrium model
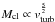 and
and 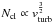 .
The frozen-in magnetic field approximation yields much too small cloud sizes and masses in
the CND for the high cosmic ray ionization rate measured by Yusef-Zadeh et al. (2013) in the inner 100 pc of the Galaxy.
.
The frozen-in magnetic field approximation yields much too small cloud sizes and masses in
the CND for the high cosmic ray ionization rate measured by Yusef-Zadeh et al. (2013) in the inner 100 pc of the Galaxy.
All Tables
Observed/assumed CND and derived cloud properties within the turbulent clumpy disk model.
Observed/assumed torus and derived cloud properties within the turbulent clumpy disk model.
All Figures
 |
Fig. 1 Schematic of the collisional and turbulent disk/torus models. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


