| Issue |
A&A
Volume 556, August 2013
|
|
|---|---|---|
| Article Number | A147 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201321296 | |
| Published online | 09 August 2013 | |
The relation between magnetic and material arms in models for spiral galaxies
1
School of Mathematics, University of Manchester,
Manchester
M13 9PL,
UK
e-mail:
moss@ma.man.ac.uk
2
MPI für Radioastronomie, Auf dem Hügel 69,
53121
Bonn,
Germany
3
Department of Physics, Moscow State University,
129337
Moscow,
Russia
4
Institute of Continuous Media Mechanics,
Korolyov str. 1,
614061
Perm,
Russia
5
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Str. 77,
50937
Köln,
Germany
6
Byurakan Astrophysical Observatory, Armenia and Isaac Newton
Institute of Chile, 378433
Byurakan, Armenian Branch
7 State National Research Polytechnical, University of Perm,
Russia
Received:
14
February
2013
Accepted:
24
June
2013
Context. Observations of polarized radio emission show that large-scale (regular) magnetic fields in spiral galaxies are not fully axisymmetric, but generally stronger in interarm regions. In some nearby galaxies such as NGC 6946 they are organized in narrow magnetic arms situated between the material spiral arms.
Aims. The phenomenon of magnetic arms and their relation to the optical spiral arms (the material arms) calls for an explanation in the framework of galactic dynamo theory. Several possibilities have been suggested but are not completely satisfactory; here we attempt a consistent investigation.
Methods. We use a 2D mean-field dynamo model in the no-z approximation and add injections of small-scale magnetic field, taken to result from supernova explosions, to represent the effects of dynamo action on smaller scales. This injection of small scale field is situated along the spiral arms, where star-formation mostly occurs.
Results. A straightforward explanation of magnetic arms as a result of modulation of the dynamo mechanism by material arms struggles to produce pronounced magnetic arms, at least with realistic parameters, without introducing new effects such as a time lag between Coriolis force and α-effect. In contrast, by taking into account explicitly the small-scale magnetic field that is injected into the arms by the action of the star forming regions that are concentrated there, we can obtain dynamo models with magnetic structures of various forms that can be compared with magnetic arms. These are rather variable entities and their shape changes significantly on timescales of a few 100 Myr. Properties of magnetic arms can be controlled by changing the model parameters. In particular, a lower injection rate of small-scale field makes the magnetic configuration smoother and eliminates distinct magnetic arms.
Conclusions. We conclude that magnetic arms can be considered as coherent magnetic structures generated by large-scale dynamo action, and associated with spatially modulated small-scale magnetic fluctuations, caused by enhanced star formation rates within the material arms.
Key words: galaxies: spiral / galaxies: magnetic fields / galaxies: evolution / galaxies: individual: NGC 6946 / dynamo
© ESO, 2013
1. Introduction
Large-scale regular) magnetic fields in the discs of spiral galaxies are thought to be maintained by dynamo action, the joint action of differential rotation and mirror asymmetric interstellar turbulence associated with the entire galactic disc. According to mean-field dynamo theory (e.g. Ruzmaikin et al. 1988; Beck et al. 1996), the dynamo organizes the field lines of the large-scale magnetic field into spiral form. The tangent of the pitch angle of the field is given by the ratio of the radial and azimuthal magnetic field components, and can also be expressed as a function of the dynamo governing parameters. The observed pitch angles of the large-scale magnetic field are in the range between approximately 10° and 40° (e.g. Fletcher 2010). Comparing these pitch angles with the pitch angles of the material (optical) spiral arms of such galaxies shows that they are similar at least across significant parts of the galactic discs; this cannot be understood in the framework of the basic conventional form of the mean-field dynamo alone.
The field structure most readily generated by the mean-field dynamo is axisymmetric (ASS, the m = 0 mode). Radio observations of nearby galaxies show, however, that while the total magnetic field is stronger in the spiral arms, the ordered magnetic field (traced by polarized emission)1 is generally stronger in the interarm regions (i.e. between the spiral arms). This was first detected in the grand-design galaxy M 81 (Krause et al. 1989b) and has been confirmed in most nearby galaxies observed so far at centimetre wavelengths (Beck 2005; Beck & Wielebinski 2013). A few galaxies with strong large-scale gas compression such as the density-wave galaxy M 51 (Fletcher et al. 2011) and the barred galaxy NGC 1097 (Beck et al. 2005) show additional polarized emission in the compression regions.
This result cannot be simply explained by stronger turbulence or enhanced Faraday depolarization within the spiral arms but seems to indicate an interaction between processes in the material spiral arms and the dynamo action that generates large-scale field.
In particular, the magnetic configurations in some nearby spiral galaxies are clearly organized into narrow “magnetic arms”, e.g. in IC 342 and NGC 6946. Shifts between the magnetic and material arms are observed in IC 342 (Krause 1993). There is a prominent spiral arm in the south which splits into two branches. The most spectacular example is provided by NGC 6946, a galaxy with massive spiral arms, but without density-wave shock fronts. The magnetic arms are clearly situated between material arms (Beck & Hoernes 1996; Beck 2007). The magnetic arms in NGC 6946 are most prominent in polarized emission. Strong Faraday rotation in the magnetic arms shows that the field is large-scale (regular). On the other hand, the random magnetic field (traced by the unpolarized emission) is strongest in the material arms.
There have been several attempts to introduce the interaction between spiral arms and magnetic arms. A direct effect of a density wave is a modulation of the axisymmetric velocity distribution of the gas in a galactic disk. The effect of this modulation on the galactic dynamo was examined by Chiba & Tosa (1990; see also Moss 1998) who found conditions for parametric resonance to occur, the so-called swing excitation of galactic magnetic fields. However, the rather special conditions that have to be satisfied for such resonances to occur suggest that they are unlikely to be of major physical importance.
Shukurov (1998) suggested that – as a result of the gas density contrast – random gas velocities in the material arms are larger than those in the interarm space, and that they destroy large-scale magnetic fields within the arms. Magnetic fields may survive in the interarm space, in the form of magnetic arms situated between the material arms, provided that dynamo action is not too strong.
The main problem here is that our knowledge concerning the arm/interarm contrast in dynamo governing parameters is very limited (Shukurov & Sokoloff 1998; Moss 1998; Rohde et al. 1999; Chamandy et al. 2013a). As we only have snapshots of the structure of few nearby galaxies it is not clear how general the example of NGC 6946 is. It might also be connected with the material arms rotating with an angular velocity that is different from that of the gas in the disc, so that sometimes both types of arms coincide and sometimes they are displaced.
It looks a priori plausible that by modifying the non-axisymmetric distribution of the dynamo-governing parameters, a magnetic arm configuration of the desired type might be obtained. In fact, Moss (1998) and Elstner et al. (2000) considered the enhancement of the turbulent diffusivity and the α-effect in the spiral arms due to density waves, and effects on the evolution of magnetic arms. In addition, Kulpa-Dybel et al. (2011) claim that some interlacing of magnetic and material arms can occur from the difference in angular velocity between the arm pattern and the gas.
However, the available observational information and theoretical ideas presented up to now are insufficient to isolate a completely plausible explanation for the phenomenon of magnetic arms. For example, while the parametric resonance mechanism can produce something like magnetic arms, rather special combinations of galactic parameters are necessary to produce significant effects. (We note that the problems associated with material arms themselves are not yet completely clear.) Chamandy et al. (2013a) do produce magnetic arms by a combination of a spatial modulation of the alpha effect and temporal nonlocality – see also Chamandy et al. (2013b).
In order to limit the variety of the models, we consider a dynamo model based on a particular parametrization of the arm-interarm contrast in the dynamo-governing parameters, suggested by Shukurov & Sokoloff (1998). (We acknowledge that any such estimates are subject to substantial uncertainty.) Then we focus our attention on a further idea that mean-field dynamos and large-scale magnetic fields exist in the presence of small-scale magnetic fields and various local distortions of a smooth dynamo action. We demonstrate that such small-scale mechanisms, when modulated by a spiral structure, are able to produce magnetic arms. The model used here is a modification of that of Moss et al. (2012).
Before moving to specific modelling we briefly present here the leading idea of this paper. We first confirm that it is possible to obtain magnetic arms situated between the material arms, just by spatial variation of the dynamo governing parameters (Sect. 3). This mechanism is in some ways not completely satisfactory, and we deduce that it is desirable to find another mechanism leading to magnetic arm formation. We suggest such a mechanism, based on the idea that the spatial scale of magnetic fluctuations associated with mean-field galactic dynamo is in fact not very much smaller than the spatial scale of the large-scale magnetic field, and that the contribution of the fluctuations to the evolution of the mean-field should be taken into account. The importance of fluctuations for the evolution of the mean-field field was stressed in general form by Hoyng (1988), and we apply the general idea in the specific framework of galactic dynamos. Following this approach we include these fluctuations in the conventional mean-field equations. We appreciate that such extension of the mean-field equations deserves further verification at a fundamental level; however we do not consider this as a goal of the current paper.
We exploit a plausible assumption that small-scale magnetic field injection is enhanced in the material arms, because of the higher star formation rate and increased occurrence of star forming regions there. In order to illuminate the effect suggested we deliberately assume that all other dynamo governing parameters are independent of azimuth. Of course, we appreciate that in practice variations in the injection rate will very likely be associated with some variations of the other dynamo governing parameters, and do not argue against the idea that such mechanisms can also contribute to the formation of magnetic structures. We emphasize that our aim in this paper is not to produce a comprehensive modelling of magnetic fields in spiral galaxies, including all possible relevant effects. Rather we attempt to isolate the effects of a novel mechanism, which we believe can contribute to the formation of regular interarm fields in some instances.
2. The dynamo model
We use here a plausible simplification of the 2D mean-field galactic dynamo in the form of the “no-z” model (e.g. Subramanian & Mestel 1993; Moss 1995), which restricts modelling to quantities which are accessible observationally and make the numerical implementation easily affordable. For the sake of clarity we briefly reproduce the relevant equations from Moss et al. (2012).
The code solves in the αω approximation explicitly for the field
components parallel to the disc plane, while the component perpendicular to this plane (i.e.
in the z-direction) is given by the solenoidality condition. The even
(quadrupole-like) magnetic field parity with respect to the disc plane is assumed. The field
components parallel to the plane are considered as mid-plane values, or as a form of
vertical average through the disc. The key parameters are the aspect ratio
λ = h0/R,
where h0 corresponds to the semi-thickness of the warm gas disc
and R is its radius, and the dynamo numbers
Rα = α0h0/η,
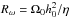 . We allow the disc semi-thickness
h = h(r) to vary with radius (see
below), and h0 = h(0) is our reference value.
λ must be a small parameter. η is the turbulent
diffusivity, assumed uniform, and
α0,Ω0 are typical values of the
α-coefficient and angular velocity respectively. Thus the dynamo
equations become in cylindrical polar coordinates (r,φ,z)
. We allow the disc semi-thickness
h = h(r) to vary with radius (see
below), and h0 = h(0) is our reference value.
λ must be a small parameter. η is the turbulent
diffusivity, assumed uniform, and
α0,Ω0 are typical values of the
α-coefficient and angular velocity respectively. Thus the dynamo
equations become in cylindrical polar coordinates (r,φ,z) ![\begin{eqnarray} % \frac{\partial B_r}{\partial t} &=& -R_\alpha\frac{h(r)}{h_0} B_\phi-\frac{\pi^2}{4}\left(\frac{h(r)}{h_0}\right)^2 B_r \nonumber\\ && +\, \lambda^2\left(\frac{\partial}{\partial r}\left[\frac{1}{r}\frac{\partial}{\partial r}(rB_r)\right]+ \frac{1}{r^2}\frac{\partial^2B_r}{\partial\phi^2}-\frac{2}{r^2}\frac{\partial B_\phi}{\partial\phi}\right), \label{evolBr} \end{eqnarray}](/articles/aa/full_html/2013/08/aa21296-13/aa21296-13-eq19.png) (1)
(1)![\begin{eqnarray} % \frac{\partial B_\phi}{\partial t} &=& R_\omega r B_r\frac{{\rm d}\Omega}{{\rm d}r}-R_\omega\Omega\frac{\partial B_\phi}{\partial \phi}-\frac{\pi^2}{4} B_\phi\left(\frac{h(r)}{h_0}\right)^2 \nonumber\\ && +\, \lambda^2\left(\frac{\partial}{\partial r}\left[\frac{1}{r}\frac{\partial}{\partial r}(rB_\phi)\right] +\frac{1}{r^2}\frac{B_\phi^2}{\partial \phi^2}-\frac{2}{r^2}\frac{\partial B_r}{\partial \phi}\right), \label{evolBphi} \end{eqnarray}](/articles/aa/full_html/2013/08/aa21296-13/aa21296-13-eq20.png) (2)where
z does not appear explicitly. Here a flared disc with semi-thickness
(2)where
z does not appear explicitly. Here a flared disc with semi-thickness
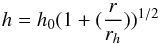 (3)is
assumed, with
h0,rh
being constants. The factors
h(r)/h0
are introduced in Eqs. (1), (2) to allow for the variation in disc height with
radius, following Ruzmaikin et al. (1988). (We note
that Lazio & Cordes 1998, argue that the
Milky Way disc is flat; there is no reliable evidence concerning disc flaring in external
galaxies. Limited experimentation suggests that our results do not depend significantly on
this assumption, within the uncertainty in the dynamo parameters.) This equation has been
calibrated by introduction of the factors
π2/4 in the vertical diffusion terms. In
principle, in the αω approximation the parameters
Rα,Rω
can be combined into a single dynamo number
D = RαRω,
but we choose to keep them separate. Length, time and magnetic field are non-dimensionalized
in units of R,
(3)is
assumed, with
h0,rh
being constants. The factors
h(r)/h0
are introduced in Eqs. (1), (2) to allow for the variation in disc height with
radius, following Ruzmaikin et al. (1988). (We note
that Lazio & Cordes 1998, argue that the
Milky Way disc is flat; there is no reliable evidence concerning disc flaring in external
galaxies. Limited experimentation suggests that our results do not depend significantly on
this assumption, within the uncertainty in the dynamo parameters.) This equation has been
calibrated by introduction of the factors
π2/4 in the vertical diffusion terms. In
principle, in the αω approximation the parameters
Rα,Rω
can be combined into a single dynamo number
D = RαRω,
but we choose to keep them separate. Length, time and magnetic field are non-dimensionalized
in units of R, 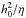 and the
equipartition field strength Beq, respectively.
α0 = α0(r) is
taken proportional to h(r)Ω(r), and is
unaffected by the arms. This, together with the presence of uniform turbulent diffusivity,
implies the presence of a background level of turbulence throughout the disc. A naive
algebraic α-quenching nonlinearity is assumed,
and the
equipartition field strength Beq, respectively.
α0 = α0(r) is
taken proportional to h(r)Ω(r), and is
unaffected by the arms. This, together with the presence of uniform turbulent diffusivity,
implies the presence of a background level of turbulence throughout the disc. A naive
algebraic α-quenching nonlinearity is assumed,
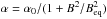 , where
Beq is the strength of the equipartition field in the general
disc environment.
, where
Beq is the strength of the equipartition field in the general
disc environment.
We take the same rotation law as used in Moss et al. (2012), namely 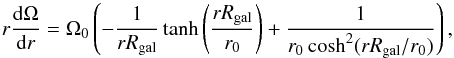 where
r0 corresponds to the turnover radius for the rotational
velocity: we take r0 = 0.2.
where
r0 corresponds to the turnover radius for the rotational
velocity: we take r0 = 0.2.
 |
Fig. 1 Evolution of magnetic field configurations. Left-hand column is model 75, middle column model 76, right-hand column model 77. Models (a), (b), (c) (first row) at approximate time 11.7 Gyr; models (d), (e), (f) (second row) at time 12.5 Gyr; models (g), (h), (i) (third row) at 12.9 Gyr; models (j), (k), (l) (bottom row) at approximately 13.2 Gyr (i.e. “now”). For model 76 the rotation parameter Rω has been increased from that of model 75, and in model 77 the magnitude of the injected field, Binj0, has been decreased from that used in model 75. The continuous contours delineate the regions (“arms”) where field is injected; these rotate rigidly, with pattern speed such that the corotation radius is at fractional radius r ≈ 0.7. |
The alpha effect is assumed to depend on angular velocity and disc thickness, α ∝ Ωh-1, whereas Beq is assumed to be uniform because our restricted knowledge of physical conditions gives no secure basis for more realistic assumptions. We continue our simulations to a time corresponding to the present day where knowledge of particular galaxies is rather better, and we emphasize that we are studying generic properties of thin disc dynamos.
Taking typical galactic values, we can estimate Rα = O(1), Rω = O(10) (i.e. D = O(10)). We adopt values R = 10 kpc, rh = 1,h0 = 350 pc. This gives h ≈ 500 pc at r = R = 10 kpc. This gives a time unit of 0.78 Gyr. We use a fixed integration timestep of approximately 0.04 Myr.
We superimpose on this rather standard dynamo model the injection of random magnetic fields of rms strength Binj0 with energy density comparable to that of the turbulent motions, at discrete time intervals and at a number of randomly determined discrete locations. We take the interval between injections to be about 107 yr – see Moss et al. (2012) for details. (In the context of our models this time can be interpreted as a convenient interval at which to maintain/renew the injection of small-scale field. This interval is close to the turnover time of vortices in the interstellar turbulence, which in turn determines the time scale of small-scale magnetic field evolution.) The new feature of this paper is that injection only occurs within a spiral pattern representing the material spiral arms. This pattern is assumed to rotate rigidly with the pattern speed ωP. We choose ωP such that the corotation radius rcorr = 0.7 R in each case. For simplicity, the injection rate falls discontinuously to zero at the boundaries of the arms. The shape of the arms, and of the centrally enhanced central injection region, can be seen in, e.g., Fig. 1. This is combined with an enhancement of the injection field strength near the galactic centre (an increase by a factor 2 at the centre, decreasing to unity at r = 0.1 or 1 kpc in dimensional units). This is a token recognition of the increased star formation expected to occur in the central part. We stress that Binj0 should be considered only as a proxy for the typical field strength generated by the small-scale dynamo action associated with star-forming regions. Thus we allow it to take a range of values, to compensate for inherent deficiencies in the model.
Our expectation is that as the material arms sweep through the ambient gas (or v.v. depending on the position relative to the corotation radius), outside of the regions where field is injected the differential rotation will be able to organise the small-scale field into large-scale. Inside the arms, both small- and large-scale field will be present. Effectively, the ISM will be “reseeded” by the ongoing injections.
The dynamo equations are integrated on a 537 × 537 Cartesian grid which is just large enough to provide a “dead zone” around the dynamo active region – see e.g. Fig. 1. To enable reproducibility and for ease of inter-comparison, the same sequence of pseudo-random numbers was used in each simulation.
3. Arm-interarm contrast of dynamo governing parameters
In this section we use the parametrization of the arm-interarm contrast for the dynamo governing parameters introduced by Shukurov & Sokoloff (1998). As the α-coefficient is larger in the interarm regions, whereas the kinetic energy density of turbulence is larger in the arms, the turbulent magnetic diffusivity can only be weakly affected by the spiral pattern. In turn, these parameters are reduced via more or less conventional scaling to the turbulent rms velocity v, the basic scale of galactic turbulence l, the scale height of the ionized gaseous galactic disc h, the galactic angular velocity Ω and the gas density ρ. The arm-interarm contrast is estimated as va/vi ≈ 2 for v, and ρa/ρi ≈ 3 for the gas density (indexes a and i stands for arm and interarm region, respectively), based on available observational data for the Milky Way (Rohlfs & Kreitschman 1987) and M 51 (Garcia-Burillo et al. 1993; see also Fletcher et al. 2011). The contrast in turbulent energies is estimated as Ea/Ei ≈ 10. The scale heights ha and hi were taken to be equal, because the sound crossing and passage times for the spiral density wave were estimated to be almost the same, and so the density wave affects the mean hydrostatic equilibrium only. The estimate of the turbulent diffusivity contrast is based on the assumption that the correlation time scales as the inverse supernova rate, which gives ηa/ηi ≈ 1. The correlation length l is identified with the radius of supernova remnants (SNR). Shukurov & Sokoloff (1998) take a conventional estimate la/li ≈ 0.5. Assuming that Ω is the same in arms and in the interarm regions, they obtain the estimate αa/αi ≈ 0.25. We accept these estimates as representing the current state of knowledge.
 |
Fig. 2 Early evolution of the magnetic field in model 75. Models (a), (b), (c) (first row) at approximate time 0.078,0.78,2.34 Gyr respectively; models (d), (e) (second row) at times 3.9,7.8 Gyr. The continuous contours delineate the regions (“arms”) where field is injected; these rotate rigidly, with pattern speed such that the corotation radius is at fractional radius r ≈ 0.7. As time proceeds, the large-scale organization of the field increases – see also the first column of Fig. 1. |
 |
Fig. 3 Colour coded images of our model galaxies: from top to the bottom models 75, 76 and 77, from left to right: azimuthal component of magnetic field, azimuthal component of large-scale magnetic field and azimuthal component of small-scale magnetic field at approximate times 13.2 Gyr. The large-scale field is averaged over 1 kpc. The continuous contours delineate the regions (“arms”) where field is injected; these rotate rigidly, with pattern speed such that the corotation radius is at fractional radius r ≈ 0.7. |
As context for our main calculations, we performed dynamo simulations with α increased by a maximum factor of about 3.3 between the arms with a smooth quasi-parabolic profile of α. With Rα = 1, Rω = 4.5, the dynamo is only slightly supercritical. Here we were guided by the experience of Shukurov (1998) that weak dynamo action is more favourable for the production of interarm fields by this mechanism. For a weak initial field it is possible to see a slight enhancement of the (regular) field within the interam region (we do not display this result in detail here). This run started with a random field with rms strength 10-6 (but no further field injections). The resulting magnetic configuration becomes more complicated for a more substantial initial field (with a strength of order of equipartition), but again there are no very pronounced features localized in the interarm regions. Apart from these small azimuthal variations, there is also a radial field reversal, but nothing like the magnetic arms of NGC 6946. Note that for a weak initial field the time to saturation is about 17 Gyr (see also the discussion in Moss & Sokoloff 2012a). This time becomes much shorter and realistic with a strong initial field (cf. Arshakian et al. 2009). This mechanism, taken alone, does not seem particularly promising. We note that a more elaborate model of this general type by Chamandy et al. (2013a) produces potentially more interesting results.
We conclude that special variations of dynamo governing parameters, e.g. as considered by Moss (1996), can in principle give magnetic arms, but requires some fine tuning of parameters (see also Rohde et al. 1999). We deduce that variations which correspond to the naive estimates of Shukurov & Sokoloff (1998) fail to produce pronounced magnetic arms. It follows that to explain the magnetic arms in the framework of the model under consideration, we need something more than just modulations of α by spiral arms, such as continuous small-scale field injections, modulated by spiral structure. We emphasize that azimuthal variations of dynamo quantities (here α) are considered only in this section, for illustrative purposes.
 |
Fig. 4 Colour coded figures for the azimuthal component of the mean magnetic field at time evolution from left to right: 11.7, 12.5 and 12.9 Gyr. Fields are averaged over lengths 1 kpc. The top row shows model 75, the lower model 76. The continuous contours delineate the regions (“arms”) where field is injected; these rotate rigidly, with pattern speed such that the corotation radius is at fractional radius r ≈ 0.7. |
4. Magnetic configurations with field injections modulated by spiral arms
Moss et al. (2012) included the injection of small-scale magnetic fields as a proxy for the effects of the dynamical star-formation process in their model for the evolution of magnetic fields in disc galaxies. They assumed that the star-formation rate governs the rate of supernova explosions, which in turn drive the turbulence of the gas in these galaxies and are the main source of small-scale magnetic fields via small-scale dynamo action. In this paper, we simulate the evolution of the large-scale magnetic field, by assuming the injection rate of small-scale field, of strength of order the equipartition strength, to be high only in the material spiral arms – since more gas resides in the arm regions (and hence the star-formation rate is higher there) compared to the interarm regions. In the following discussions, we do not allow any arm/interarm variation of the unquenched alpha-coefficient, in order to isolate clearly the effects of field injection in the arms.
 |
Fig. 5 Colour coded images showing the ratio of mean (large-scale) to rms for the galaxies: from left to right models 75, 76 and 77 at approximate times 13.2 Gyr. The fields are averaged over 1 kpc. The continuous contours delineate the regions (“arms”) where field is injected; these rotate rigidly, with pattern speed such that the corotation radius is at fractional radius r ≈ 0.7. |
 |
Fig. 6 Magnetic arms in a 4-armed galaxy (model 402) at approximate times 11.7, 12.5, 12.9 and 13.2 Gyr. The dynamo parameters are the same as for model 75. The contours delineate the material arms. |
We discuss some representative models; the adopted values of Rω give a rotational velocity of around 200 km s-1, comparable to that in the Milky Way. In the first column of Fig. 1 we show our reference model (model 75) for which Rα = 3, Rω = 12, h0 = 350 pc (so h ~ 500 pc at radius 10 kpc) and Binj0 = 10, from time 11.7 Gyr to 13.2 Gyr, corresponding to the present day. (In this, and other models discussed, the corotation radius is about 7 kpc, i.e. r = 0.7.) It is clearly visible that the magnetic field is more regular between the spiral arms than in them. We also show in Fig. 2 snapshots of the earlier evolution of model 75. These two figures demonstrate a gradual development of large-scale magnetic field in the interarm regions. Indeed, we can see in these two figures the progression in model 75 from a largely disorganized field (localized in the arms), to a fully developed global field with large-scale structure. By playing with the dynamo governing parameters we can modify the result. A reasonable increase of differential rotation (to Rω = 20) adds a global magnetic reversal in the central part of the galaxy (model 76, Fig. 1, second column) while a lower injection rate gives some regular field in the material arms (model 77, Fig. 1, third column).
Decomposition of magnetic field into large-scale and small-scale components can be performed in various ways and it is far from clear in advance which particular way is more physically meaningful (cf. Gent et al. 2013). As an example, we present in Fig. 3 the total, large-scale and small-scale azimuthal magnetic field obtained by applying a Gaussian filter with width σ = 500 pc to the computed magnetic field. We can compare panels of the second column of Fig. 3, showing the large-scale field, with the panels of the third column which show the small-scale field which in our model coincides with the position of the material arms. In addition Fig. 4 shows also some earlier stages of the evolution of the azimuthal component of the mean field in models 75 and 76. Models 75 and 76 exhibit dynamical evolution of magnetic arms which can either be located between the material arms or cross them, whereas it can be seen clearly that model 77 has an almost completely axisymmetric large-scale magnetic field. There is no fixed certain correlation between the large-scale structure of the magnetic fields and the material arms. The arm/interarm contrast is clearly shown by the ratio of large-scale field to the root-mean-square of the fluctuations (see Fig. 5).
Note that the reference model 75 shows many local reversals, which can be compared with local reversals detected in the Milky Way (Van Eck et al. 2011). In contrast, model 76 shows a global reversal. A plausible argument for larger differential rotation (Rω) favouring reversals can be made as follows. To get reversals we need relatively strong magnetic fields to be present at the early stages of galactic evolution. This is (as we have seen) more likely for stronger initial fields with “enough” lumpiness. With too much lumpiness, the initial conditions are near-uniform, which may, for suitable choices, give no reversals. Larger Rω means that the initial inhomogeneities grow faster, without diffusing radially – they get stretched into rings. There is more chance of the subsequent radial merger of these rings giving extended radial regions with opposing Bφ – i.e. reversals. Further discussion is given in Moss & Sokoloff (2012b).
We see a marginal effect (visible clearly only away from corotation, in certain models), that the magnetic field upstream of the arms (rcorr = 0.7 R) is slightly more disordered than that downstream. Note that the downstream side of the arm changes between the regions inside and outside of corotation.
We also investigated a similar model with 4-armed spiral structure, and show, in Fig. 6, snapshots of the magnetic field at later times for a model with the same dynamo parameters as model 75. The magnetic arms situated between the material arms now look much less pronounced than in the corresponding 2-armed model (model 75), plausibly because there is now not enough time for an ordered field to arise in the interarm regions, before the next arm comes along and disturbs it. Again, when we vary the intensity of the field injections, we find that the magnetic arms are smoothed out if less small-scale field is injected.
The evolution of magnetic patterns in model 75 is presented in Fig. 1. We see that details of the magnetic pattern shape are variable on timescales comparable with the galactic rotation period. A magnetic arm (quite smooth in Fig. 1a) is much sharper in Fig. 1b. The main point is that the random injection of the small-scale magnetic field, which mimics the role of supernovae in star-forming regions in generating small-scale field, is important and determines the instantaneous shape of the magnetic configuration. This is an intrinsic property of our dynamo model. A further, more artificial, effect is that our injections of field occur simultaneously at discrete intervals in time. The anomalously large isolated B-vectors visible in Figs. 1d, e probably arise from such an immediately previous injection, coupled with the intrinsically random distribution of the injection sites, strengths and the choice of the locations at which vectors are plotted. The contemporary state of observational studies of galactic magnetism does not support or reject this conclusion, because we have snapshots of magnetic patterns in a very few galaxies only. However we stress that this conclusion could be supported by observations of a representative sample of spiral galaxies. The prediction is that we would expect to see a rich variety of magnetic patterns in such a sample. Fine tuning of parameters of a particular dynamo model to mimic, say, the magnetic patterns in NGC 6946 is less useful in the framework of our dynamo model, because snapshots of magnetic configurations over relatively short time intervals (on galactic time scales, of course) can differ quite significantly.
Some dynamical simulations (e.g. Wada et al. 2011) of the evolution of spiral galaxies show that material arms dissolve and reform on relatively short timescales, typically several rotation periods. In contrast, in the models discussed above, the arms are permanent features. To assess the importance of this simplification, we ran a model with the parameters of model 75, in which the position of the arms changed discontinuously and at random at intervals of about 5 × 108 yr. In this case, at least, the field at large times was not generically different to that shown in Fig. 1. Of course, immediately after such a jump there will be some differences, such as temporary non-coincidence of disordered field and material arms, but this is short-lived. If the jump is by an angle near 0° or 180°, there is little gross effect, even immediately.
Additionally, we ran simulations with parameters as model 75 with the equipartition field strength in the material arms increased by ca. 25% and ca. 70%. This (maybe unsurprisingly) resulted in a modest increase in magnetic energy, but caused very little difference to the overall field morphology. In particular, the marked contrast between arm and interarm regions remained.
5. Discussion and conclusions
We have presented a galactic dynamo model that attempts to explain the phenomenon that the degree of uniformity of the magnetic field is higher in the interarm regions. This work is largely motivated by observations such as those of IC 342 (Krause 1993) and the prototypical case of NGC 6946 (Beck 2007) that magnetic arms can be situated between material arms. M 51 is one of the rare cases where magnetic and material spiral arms almost coincide because of compression (Fletcher et al. 2011). Density-wave shock fronts cause velocity perturbations which are not included in our model. The key feature of our model is that it includes small-scale magnetic field injections from small-scale dynamo action, associated with strong turbulence in star-forming regions that are predominantly found in spiral arms and near the galactic centre. When the gas in which this small-scale field is embedded leaves the material arms, conventional large-scale dynamo action can use it as an ongoing “seed” to produce ordered (regular) field between the material arms. We have demonstrated that modulation of the small-scale magnetic field injection rate allows a mimicking of the phenomenology of ordered interarm fields. We obtain snapshots of magnetic fields that look broadly similar to the observational plots of the polarized intensity of many galaxies including NGC 6946 (Beck 2007) – contemporary ordered fields in model 75 are situated between the material arms. But we note that in model 77 the ordered field almost fills the whole interarm and arm space, and does not form distinct magnetic arms.
A more realistic approach might, e.g., have the field injection decrease more slowly and smoothly away from the arms. This could be expected to result in narrower regions of regular field (“magnetic arms”).
Our results are generally consistent with a process in which disordered field injected within the material arms continually finds itself in the interarm regions, as the material arms move relative to the gas in the disc. Once outside of an arm, large-scale order is imposed by the action of the global dynamo (which is now unperturbed by field injections) together with the stretching associated with the differential rotation. Of course, the large-scale dynamo action occurs within the material arms also, but there its effects are obscured by the injected random field. We believe that this is the key mechanism of our model.
We note that the magnetic structures are more tightly wound than the material arms, and thus intersect them. We did not see a strong influence of the corotation radius in our models, except perhaps that the magnetic arms may cross the material arms near or just inside the corotation radius. This is visible in models 75 and 76, but not in model 77 (Fig. 1), where discrete magnetic structures do not occur. As the magnetic structures are quite broad in our models, it is difficult to be more precise. This also means that the large-scale field seems to be more widely distributed in radius than in the models of Chamandy et al. (2013a,b).
A quantification of the phenomenon in terms of the concepts of mean-field theory is faced with the problem of how to distinguish mean and large-scale features. We have made a preliminary attempt to contrast mean field and fluctuations in Fig. 5. The breadth of the material arms is quite small in comparison with the length of the ring centred at the galactic centre at a typical radius; the global perturbation to the basic axisymmetric structure is small. A consequence is that the magnetic arms give only a weak m = 2 (or m = 1) mode with amplitude changing relatively quickly with time, when decomposed into azimuthal modes (see Fig. 7). It seems more satisfactory to say that the magnetic arms should be considered as mesoscale phenomenon of the magnetic field configuration. In any case, the magnetic arm phenomenon cannot be considered as an excitation of one of just one or two of the lower non-axisymmetric modes of the mean field. Rather it is a coherent structure which can be represented by many coherent Fourier modes.
In the context of the arm-interarm contrast, Fig. 8 shows that the magnitude of the large-scale field in the arms is not very different to that in the interarm regions in all the models, in contradiction to observations – our models predict a significant large-scale field in the arms, almost as strong as in the interarm regions. There are several mechanisms that can reduce the expected polarized emission in the arms: tangling by SNR shocks and shear motions, Faraday depolarization and averaging effects due to the limited beam size. Another possible resolution of this point is that we were unable to include consistently an enhancement of turbulent diffusivity in the arms, as we were unable to represent gradients satisfactorily in the code. However, experiments with enhanced diffusivity, without inclusion of gradient terms, suggest that this mechanism is capable of alleviating the problem by reducing the large-scale field in the arms.
 |
Fig. 7 Amplitudes of azimuthal modes of large-scale of Bφ vs. radius: m = 0 – left hand column; m = 1 – middle column; m = 2 – right hand column. The first row is at approximate time 12.5 Gyr and the second row at 12.9 Gyr. |
Note that our models neglect Faraday depolarization effects and hence should be compared only to radio polarization maps at high frequencies where Faraday depolarization is small, typically at wavelengths of ≲6 cm where most polarization observations were performed (as for NGC 6946, see Beck 2007). At longer wavelengths, polarized radio emission traces not only large-scale magnetic fields, but also the amount of Faraday depolarization.
We have emphasized models with relatively well-developed magnetic arms – our main purpose in this paper is to demonstrate “proof of concept”, rather than to present an exhaustive survey of parameter space. However we note that both a weaker strength of injected field, and stronger differential rotation (Rω) make magnetic arms less pronounced in the sense that magnetic field in the arms becomes less disordered, and the large-scale field becomes more homogeneous globally – see Fig. 1.
We calculated the averaged amplitude of the large-scale magnetic field and rms of the small-scales over arm and interarm regions separately. The panels of Fig. 8 should be compared with Fig. 1, where the arm-interarm contrast looks pronounced for the models 75 and 76, but very much weaker for model 77. We see clearly from Fig. 8 that the small-scale field in the arms is noticeably larger than the large-scale field in the models 75 and 76, and is substantially weaker in the later stage of the evolution of model 77. As a result, the magnetic field in the arm region looks disordered for models 75 and 76, and quite ordered for model 77. We verified that this quantification remains stable for filter widths up to σ = 1 kpc, while larger filter widths become more comparable with the arm width and the contrast is smoothed out.
From the above analysis our result looks quite straightforward: the magnetic field becomes less ordered in the regions where the field injections are stronger. The outcome is nevertheless nontrivial, because we have seen that enhanced dynamo action alone does not lead to a similar contrast.
We stress however that the analysis used to generate Fig. 8 does not reproduce the visual impression of Fig. 1 in that the large-scale field in the arms is not significantly weaker than in the interarm regions. The reason for this behaviour seems to be that the large-scale dynamo operates throughout the disc, and produces a global scale field. In the arms, small-scale field is added, which is converted to large-scale field in the interarm region before entering the next arm. It is not clear in advance how this is related to the processing of the observational data. In other words, interpretation of the results depends on the algorithmic distinction between the concepts of large-scale, mean, regular, ordered and other characteristics of the visual impression of the magnetic field, which are applied in interpretation of observational data. Progress in this direction is obviously strongly required, but it is however obviously far beyond the scope of this paper.
 |
Fig. 8 Quantification of arm/interarm contrast for large-scale (thick lines) and small-scale (thin lines) fields for material arms (red dashed lines) and interarm regions (blue solid lines), for models 75, 76, 77 (from top to bottom). The peak in small-scale field at approximate time 12 Gyr as well as other details of small-scale magnetic field distribution are probably caused by the chance coincidence of an injection event with the analysed snapshot of the field. |
Studies in the far-UV, optical and Hα integrated light in regions of recent star formation of NGC 5236 (M 83) (Lundgren et al. 2008; Silva-Villa & Larsen 2012) allow estimates of the star formation rate to be made. It was found that the surface star formation rate densities are higher in arms than that in the interarm regions by approximately 0.6 dex, and that the star formation rate changes along the spiral arm, being higher in the leading part than in the trailing part of the arm (Martínez-García et al. 2009; Silva-Villa & Larsen 2012). As was shown in our simulations (models 75, 76 in Figs. 1j,k), the higher injection rate of turbulent magnetic field suggested to be associated with a higher star formation rate in the arm compared to the rate in the interarm regions, leads to a less ordered field in the arms and large-scale regular fields in the interarm regions. The offset of the star-formation rate in the arm and interarm regions is thus able to explain the contrast of the regular magnetic field in those regions. The variation of the star-formation rate along the spiral arm may have a specific imprint on the ordering of the magnetic field along the arm. High resolution and high sensitivity observations of a dozen or so nearby galaxies with the SKA are needed to address this issue. We intend to study the effect of the variation of the star formation rate on regularity of the field along a spiral arm in subsequent papers. We note that some of our models possess large-scale field reversals of the type believed to be present in the Milky Way (e.g. van Eck et al. 2011; Farrar & Jansson 2012), while they seem to be rare or absent in external galaxies. Polarisation observations with forthcoming radio telescopes like the Square Kilometre Array (SKA) and its precursors can help elucidate this issue (Beck 2011).
Following the temporal evolution of the magnetic arms, we find that they are quite variable entities and that their shape can change significantly from one snapshot to the other. An arm which looks quite diffuse in one snapshot may become concentrated in another, and the relative position of magnetic and material arms can vary in time – see e.g. Fig. 4. In this sense magnetic arms are – similarly to material spiral arms – much less stable than large-scale magnetic reversals, which are sometimes present, e.g. in model 76.
Our models have the potential to describe a wide range of types of galactic magnetic field structures. We can note that situations such as shown in model 77 seem to be rarely observed. The only possible candidate is M 31 where the large-scale field seems to fill both arm and interarm regions (Berkhuijsen et al. 2003), but the high inclination of M 31 does not allow a definite statement.
An increase in the number of material arms tends to produce less axisymmetric global magnetic structure (Fig. 6) and, as expected, decreasing the injection rate also makes magnetic arm structure weaker. We note that some studies suggest that the Milky Way has a thicker disc than adopted in our models (Schnitzeler 2012), and that the disc may not be flared (Lazio & Cordes 1998). We stress that we are not trying specifically to model the Milky Way. However we can note that a thicker disc would mean the dynamo was more efficient, and so similar results to ours could be obtained for smaller values of the dynamo numbers – while staying within the intrinsic uncertainties in our knowledge of these quantities. This would not affect significantly the operation of our proposed mechanism for magnetic arms. (Of course, in a model that includes an explicit z-dependence, rather than our two dimensional, vertically averaged, approximation, the thickness of the disc is a significant input quantity.) In general, we believe our results will be quite robust with respect to plausible changes in galactic parameters, such as disc thickness and flaring, within the uncertainty of the basic dynamo parameters.
In conclusion, we have demonstrated that the process studied, namely the contrast in star formation rate between arm and interarm regions, can make a major contribution to the large-scale ordering of field in the arm/interarm regions, including the phenomenon of magnetic arm generation and the presence of magnetic arms situated between material arms, for suitable choices of parameters. We have examined in isolation the simplest modelling of field injection, but a more realistic modelling would certainly include other mechanisms, with corresponding modulation of our preliminary results.
Linearly polarized emission traces “ordered” magnetic fields, which can be either “regular” (or large scale) magnetic fields (preserving their direction over large scales) or “anisotropic turbulent” fields (with multiple field reversals within the telescope beam). To distinguish between these two components observationally, additional Faraday rotation data is needed.
Acknowledgments
The authors thank the referee, Anvar Shukurov, for making a number of comments that led to substantial improvements to the paper. D.M., D.S. and R.S. are grateful to MPIfR for hospitality. The paper was partially supported by RFBR under grant 12-02-00170. R.B. acknowledges support by DFG grant FOR1254. The work was also partially supported by DFG project number Os 177/2-1. R.S. acknowledges grant YD-520.20132 from the Council of the President of the Russian Federation and RFBR grant 11-01-96031-ural.
References
- Arshakian, T. G., Beck, R., Krause, M., & Sokoloff, D. 2009, A&A, 494, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, R. 2005, in Cosmic Magnetic Fields, eds. R. Wielebinski, & R. Beck (Berlin: Springer), 41 [Google Scholar]
- Beck, R. 2007, A&A, 470, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, R. 2011, in Magnetic Fields in the Universe: From Laboratory and Stars to Primordial Structures, eds. M. Soida, K. Otmianowska-Mazur, E. M. de Gouveia Dal Pina, & A. Lazarian [arXiv:1111.5802] [Google Scholar]
- Beck, R., & Hoernes, P. 1996, Nature, 379, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., & Wielebinski, R. 2013, in Planets, Stars and Stellar Systems Vol. 5, eds. D. T. Oswalt, & G. Gilmore (Dordrecht: Springer), 641 [arXiv:1302.5663B] [Google Scholar]
- Beck, R., Brandenburg, A., Moss, D., Shukurov, A., & Sokoloff, D. 1996, ARA&A, 34, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., Fletcher, A., Shukurov, A., et al. 2005, A&A, 444, 739 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berkhuijsen, E. M., Beck, R., & Hoernes, P. 2003, A&A, 398, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chamandy, L., Subramanian, K., & Shukurov, A. 2013a, MNRAS, 428, 356 [Google Scholar]
- Chamandy, L., Subramanian, K., & Shukurov, A. 2013b, MNRAS, submitted [arXiv:1301.4761] [Google Scholar]
- Chiba, M., & Tosa, M. 1990, MNRAS, 244, 714 [NASA ADS] [Google Scholar]
- Fan, Z., & Lou, Y.-Q. 1996, Nature, 383, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, A. 2010, in The Dynamic Interstellar Medium, eds. R. Kothes, T. L. Landecker, & A. G. Williset, ASP Conf. Ser., 438, 197 [Google Scholar]
- Fletcher, A., Beck, R., Shukurov, A., Berkhuijsen, E. M., & Horellou, C. 2011, MNRAS, 412, 2396 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Garcia-Burillo, S., Combes, F., & Cerin, M. 1993, A&A, 274, 148 [NASA ADS] [Google Scholar]
- Gent, F. A., Shukurov, A., Sarson, G. R., Fletcher, A., & Mantere, M. J. 2013, MNRAS, 430, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyng, P. 1988, ApJ, 332, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Jansson, R., & Farrar, G. R. 2011, ApJ, 757, 14 [Google Scholar]
- Krause, M. 1993, The cosmic dynamo, eds. F. Krause, K. H. Rädler, & G. Rüdiger, IAUS, 157, 305 [Google Scholar]
- Krause, M., Hummel, E., & Beck, R. 1989a, A&A, 217, 4 [NASA ADS] [Google Scholar]
- Krause, M., Beck, R., & Hummel, E. 1989b, A&A, 217, 17 [NASA ADS] [Google Scholar]
- Kulpa-Dybel, K., Otmianowska-Mazur, K., Kulesza-Zydzik, B., et al. 2011, ApJ, 733, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Lazio, T. J. W., & Cordes, J. M. 1998, ApJ, 497, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Lundgren, A. A., Olofsson, H., Wiklind, T., & Beck, R. 2008, in Pathways Through an Eclectic Universe, eds. J. H. Knapen, T. J. Mahoney, & A. Vazdekis, ASP Conf. Ser., 390, 144 [Google Scholar]
- Martínez-García, E. E., González-Lópezlira, R. A., & Bruzual-A, G. 2009, ApJ, 694, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Moss, D. 1995, MNRAS, 275, 191 [NASA ADS] [Google Scholar]
- Moss, D. 1996, A&A, 308, 381 [NASA ADS] [Google Scholar]
- Moss, D. 1998, MNRAS, 297, 860 [NASA ADS] [CrossRef] [Google Scholar]
- Moss, D., & Sokoloff, D. 2012a, Geophys. Astrophys. Fluid Dyn., 107, 3 [Google Scholar]
- Moss, D., & Sokoloff, D. 2012b, Geophys. Astrophys. Fluid Dyn., DOI: 10.1080/03091928.2012.732575 [Google Scholar]
- Moss, D., Stepanov, R., Arshakian, T. G., et al. 2012, A&A, 350, 423 [Google Scholar]
- Rohde, R., Beck, R., & Elstner, D. 1999, A&A, 350, 423 [NASA ADS] [Google Scholar]
- Rohlfs, W. W., & Kreitschmann, J. 1987, A&A, 178, 95 [NASA ADS] [Google Scholar]
- Ruzmaikin, A. A., Shukurov, A. M., & Sokoloff, D. D. 1988, Magnetic Fields of Galaxies (Dordrecht: Kluwer), Asrophys. Space Sci. Lib., 133 [Google Scholar]
- Schnitzeler, D. H. F. M. 2012, MNRAS, 427, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Shukurov, A. 1998, MNRAS, 299, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Shukurov, A., & Sokoloff, D. 1998, Studia Geoph. Geod., 42, 391, www.mas.ncl.ac.uk/~nas13/AS/1998_StGG_arms.pdf [CrossRef] [Google Scholar]
- Silva-Villa, E., & Larsen, S. S. 2012, A&A, 537, 145 [Google Scholar]
- Sokoloff, D., & Nesme-Ribes, E. 1994, A&A, 288, 293 [NASA ADS] [Google Scholar]
- Subramanian, K., & Mestel, L. 1993, MNRAS, 265, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Van Eck, C. L., Brown, J. C., Stil, J. M., et al. 2011, ApJ, 728, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., Baba, J., & Saitoh, T. R. 2011, ApJ, 735, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Zweibel, E. G. 1996, Nature, 383, 758 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Evolution of magnetic field configurations. Left-hand column is model 75, middle column model 76, right-hand column model 77. Models (a), (b), (c) (first row) at approximate time 11.7 Gyr; models (d), (e), (f) (second row) at time 12.5 Gyr; models (g), (h), (i) (third row) at 12.9 Gyr; models (j), (k), (l) (bottom row) at approximately 13.2 Gyr (i.e. “now”). For model 76 the rotation parameter Rω has been increased from that of model 75, and in model 77 the magnitude of the injected field, Binj0, has been decreased from that used in model 75. The continuous contours delineate the regions (“arms”) where field is injected; these rotate rigidly, with pattern speed such that the corotation radius is at fractional radius r ≈ 0.7. |
| In the text | |
 |
Fig. 2 Early evolution of the magnetic field in model 75. Models (a), (b), (c) (first row) at approximate time 0.078,0.78,2.34 Gyr respectively; models (d), (e) (second row) at times 3.9,7.8 Gyr. The continuous contours delineate the regions (“arms”) where field is injected; these rotate rigidly, with pattern speed such that the corotation radius is at fractional radius r ≈ 0.7. As time proceeds, the large-scale organization of the field increases – see also the first column of Fig. 1. |
| In the text | |
 |
Fig. 3 Colour coded images of our model galaxies: from top to the bottom models 75, 76 and 77, from left to right: azimuthal component of magnetic field, azimuthal component of large-scale magnetic field and azimuthal component of small-scale magnetic field at approximate times 13.2 Gyr. The large-scale field is averaged over 1 kpc. The continuous contours delineate the regions (“arms”) where field is injected; these rotate rigidly, with pattern speed such that the corotation radius is at fractional radius r ≈ 0.7. |
| In the text | |
 |
Fig. 4 Colour coded figures for the azimuthal component of the mean magnetic field at time evolution from left to right: 11.7, 12.5 and 12.9 Gyr. Fields are averaged over lengths 1 kpc. The top row shows model 75, the lower model 76. The continuous contours delineate the regions (“arms”) where field is injected; these rotate rigidly, with pattern speed such that the corotation radius is at fractional radius r ≈ 0.7. |
| In the text | |
 |
Fig. 5 Colour coded images showing the ratio of mean (large-scale) to rms for the galaxies: from left to right models 75, 76 and 77 at approximate times 13.2 Gyr. The fields are averaged over 1 kpc. The continuous contours delineate the regions (“arms”) where field is injected; these rotate rigidly, with pattern speed such that the corotation radius is at fractional radius r ≈ 0.7. |
| In the text | |
 |
Fig. 6 Magnetic arms in a 4-armed galaxy (model 402) at approximate times 11.7, 12.5, 12.9 and 13.2 Gyr. The dynamo parameters are the same as for model 75. The contours delineate the material arms. |
| In the text | |
 |
Fig. 7 Amplitudes of azimuthal modes of large-scale of Bφ vs. radius: m = 0 – left hand column; m = 1 – middle column; m = 2 – right hand column. The first row is at approximate time 12.5 Gyr and the second row at 12.9 Gyr. |
| In the text | |
 |
Fig. 8 Quantification of arm/interarm contrast for large-scale (thick lines) and small-scale (thin lines) fields for material arms (red dashed lines) and interarm regions (blue solid lines), for models 75, 76, 77 (from top to bottom). The peak in small-scale field at approximate time 12 Gyr as well as other details of small-scale magnetic field distribution are probably caused by the chance coincidence of an injection event with the analysed snapshot of the field. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


