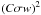| Issue |
A&A
Volume 556, August 2013
|
|
|---|---|---|
| Article Number | A132 | |
| Number of page(s) | 14 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201220752 | |
| Published online | 08 August 2013 | |
Astronomical image denoising using dictionary learning⋆
1 Laboratoire AIM, UMR CEA-CNRS-Paris 7, Irfu, SAp/SEDI, Service d’Astrophysique, CEA Saclay, 91191 Gif-sur-yvette Cedex, France
e-mail: simon@beckouche.fr
2 GREYC CNRS-ENSICAEN-Université de Caen, 6 Bd du Maréchal Juin, 14050 Caen Cedex, France
Received: 16 November 2012
Accepted: 27 January 2013
Astronomical images suffer a constant presence of multiple defects that are consequences of the atmospheric conditions and of the intrinsic properties of the acquisition equipment. One of the most frequent defects in astronomical imaging is the presence of additive noise which makes a denoising step mandatory before processing data. During the last decade, a particular modeling scheme, based on sparse representations, has drawn the attention of an ever growing community of researchers. Sparse representations offer a promising framework to many image and signal processing tasks, especially denoising and restoration applications. At first, the harmonics, wavelets and similar bases, and overcomplete representations have been considered as candidate domains to seek the sparsest representation. A new generation of algorithms, based on data-driven dictionaries, evolved rapidly and compete now with the off-the-shelf fixed dictionaries. Although designing a dictionary relies on guessing the representative elementary forms and functions, the framework of dictionary learning offers the possibility of constructing the dictionary using the data themselves, which provides us with a more flexible setup to sparse modeling and allows us to build more sophisticated dictionaries. In this paper, we introduce the centered dictionary learning (CDL) method and we study its performance for astronomical image denoising. We show how CDL outperforms wavelet or classic dictionary learning denoising techniques on astronomical images, and we give a comparison of the effects of these different algorithms on the photometry of the denoised images.
Key words: methods: data analysis / methods: statistical
The current version of the code is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/556/A132
© ESO, 2013
1. Introduction
1.1. Overview of sparsity in astronomy
The wavelet transform (WT) has been extensively used in astronomical data analysis during the last ten years, and this holds for all astrophysical domains, from the study of the sun through cosmic microwave background (CMB) analysis (Starck & Murtagh 2006). X-ray and Gamma-ray source catalogs are generally based on wavelets (Pacaud et al. 2006; Nolan et al. 2012). Using multiscale approaches such as the wavelet transform, an image can be decomposed into components at different scales, and the wavelet transform is therefore well-adapted to the study of astronomical data (Starck & Murtagh 2006). Furthermore, since noise in physical sciences is not always Gaussian, modeling in wavelet space of many kinds of noise such as Poisson noise has been a key motivation for the use of wavelets in astrophysics (Schmitt et al. 2010). If wavelets represent well isotropic features, they are far from optimal for analyzing anisotropic objects such as filaments, jets, etc. This has motivated the construction of a collection of basis functions possibly generating overcomplete dictionaries, e.g., cosine, wavelets, curvelets (Starck et al. 2003). More generally, we assume that the data X is a superposition of atoms from a dictionary D such that X = Dα, where α are the synthesis coefficients of X from D. The best data decomposition is the one which leads to the sparsest representation, i.e., few coefficients have a large magnitude, while most of them are close to zero (Starck et al. 2010b). Hence, for some astronomical data sets containing edges (planetary images, cosmic strings, etc.), curvelets should be preferred to wavelets. But for a signal composed of a sine, the Fourier dictionary is optimal from a sparsity standpoint since all information is contained in a single coefficient. Hence, the representation space that we use in our analysis can be seen as a prior we have on our observations. The larger the dictionary is, the better the data analysis will be, but also the larger the computation time to derive the coefficients α in the dictionary will be. For some specific dictionaries limited to a given set of functions (Fourier, wavelet, etc.) we have very fast implicit operators allowing us to compute the coefficients with a complexity of 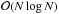 , which makes these dictionaries very attractive. But what can we do if our data are not well represented by these fixed existing dictionaries? Or if we do not know the morphology of features contained in our data? Is there a way to optimize our data analysis by constructing a dedicated dictionary? To answer these questions, a new field has recently emerged, called dictionary learning (DL). Dictionary learning techniques offer the possibility of learning an adaptive dictionary D directly from the data (or from a set of exemplars that we believe to represent the data well). Dictionary Learning is at the interface of machine learning, optimization, and harmonic analysis.
, which makes these dictionaries very attractive. But what can we do if our data are not well represented by these fixed existing dictionaries? Or if we do not know the morphology of features contained in our data? Is there a way to optimize our data analysis by constructing a dedicated dictionary? To answer these questions, a new field has recently emerged, called dictionary learning (DL). Dictionary learning techniques offer the possibility of learning an adaptive dictionary D directly from the data (or from a set of exemplars that we believe to represent the data well). Dictionary Learning is at the interface of machine learning, optimization, and harmonic analysis.
1.2. Contributions
In this paper, we show how classic dictionary learning for denoising behaves with astronomical images. We introduce a new variant, the centered dictionary learning (CDL), developed to process more efficiently point-like features that are extremely common in astronomical images. Finally, we perform a study comparing how wavelet and dictionary learning denoising methods behave regarding the photometry of sources, showing that dictionary learning is better at preserving the source flux.
1.3. Paper organization
This paper is organized as follows. Section 2 presents the sparsity regularization problem where we introduce notations and the paradigm of the dictionary for sparse coding. We introduce in Sect. 3 the methods for denoising by dictionary learning and we introduce the CDL technique. We give in Sect. 4 our results on astronomical images and we conclude with some perspectives in Sect. 5.
2. Sparsity regularization
2.1. Notations
We use the following notations. Uppercase letters are used for matrices notation and lowercase for vectors. Matrices are written column-wise D = [d1,...,dm] ∈ Rn × m. If D is a dictionary matrix, the columns di ∈ Rn represent the atoms of the dictionary. We define the ℓp pseudo-norm (p > 0) of a vector x ∈ Rn as 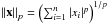 . As an extension, the ℓ∞ norm is defined as ∥x∥∞ = max1 ≤ i ≤ n{xi}, and the pseudo-norm ℓ0 stands for the number of non-zero entries of a vector: ∥x∥0 = #{i,xi ≠ 0}. Given an image Y of Q × Q pixels, a patch size n = τ × τ, and an overlapping factor Δ ∈ [1,...,n], we denote by R(i1,i2)(Y) the patch extracted from Y at the central position i = (i1,i2) ∈ [0,...,Q/Δ] 2 and converted it into a vector of Rn, such that ∀j1,j2 ∈ [ − τ/2,...,τ/2],
. As an extension, the ℓ∞ norm is defined as ∥x∥∞ = max1 ≤ i ≤ n{xi}, and the pseudo-norm ℓ0 stands for the number of non-zero entries of a vector: ∥x∥0 = #{i,xi ≠ 0}. Given an image Y of Q × Q pixels, a patch size n = τ × τ, and an overlapping factor Δ ∈ [1,...,n], we denote by R(i1,i2)(Y) the patch extracted from Y at the central position i = (i1,i2) ∈ [0,...,Q/Δ] 2 and converted it into a vector of Rn, such that ∀j1,j2 ∈ [ − τ/2,...,τ/2], ![\begin{eqnarray} {\vec Y} (i_1\Delta+j_1,i_2\Delta+j_2). = R_i({\vec Y})[\tau j_1+j2], \end{eqnarray}](/articles/aa/full_html/2013/08/aa20752-12/aa20752-12-eq25.png) (1)which corresponds to stacking the extracted square patch into a column vector. Given a patch Ri,j(Y) ∈ Rn, we define the centering operator Ci,j as the translation operator
(1)which corresponds to stacking the extracted square patch into a column vector. Given a patch Ri,j(Y) ∈ Rn, we define the centering operator Ci,j as the translation operator ![\begin{eqnarray} C_{i,j}R_{i,j}[l] = \left\{ \begin{array}{l l} R_{i,j}[l\!+\!\delta_{i,j}] & \text{ if } 1\!\leq\! l \leq n-\delta_{i,j}\\[2.5mm] R_{i,j}[l\!+\!\delta_{i,j}-n] & \text{ if } n-\delta_{i,j}< l \leq n \end{array} \right. \label{centering_operator} \end{eqnarray}](/articles/aa/full_html/2013/08/aa20752-12/aa20752-12-eq28.png) (2)and δi,j is the smallest index verifying
(2)and δi,j is the smallest index verifying ![\begin{eqnarray} \left\{ \begin{array}{l l} C_{i,j}R_{i,j}[n/2] = \underset{l}{\max}\{R_{i,j}[l]\}\quad \text{if }n\text{ is even}\\[2.5mm] C_{i,j}R_{i,j}[(n-1)/2] = \underset{l}{\max}\{R_{i,j}[l]\}\quad \text{if }n\text{ is odd.} \end{array} \right. \end{eqnarray}](/articles/aa/full_html/2013/08/aa20752-12/aa20752-12-eq30.png) (3)The centering operator translates the original vector values to place the maximum values in the central index position. When the original vector has more than one entry that reaches its maximum value, the smallest index with this value is placed at the center in the translated vector. Finally, to compare two images M1 and M2, we use the peak signal-to-noise ratio
(3)The centering operator translates the original vector values to place the maximum values in the central index position. When the original vector has more than one entry that reaches its maximum value, the smallest index with this value is placed at the center in the translated vector. Finally, to compare two images M1 and M2, we use the peak signal-to-noise ratio 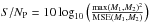 , where MSE(M1,M2) is the mean square error of the two images and max(M1,M2) is the highest value contained in M1 and M2.
, where MSE(M1,M2) is the mean square error of the two images and max(M1,M2) is the highest value contained in M1 and M2.
2.2. Sparse recovery
A signal α = [α1,...,αn], is said to be sparse when most of its entries αi are equal to zero. When the observations do not satisfy the sparsity prior in the direct domain, computing their representation coefficients in a given dictionary might yield a sparser representation of the data. Overcomplete dictionaries, which contain more atoms than their dimension and so are redundant, when coupled with sparse coding framework have shown in the last decade to lead to more significant and expressive representations which help to better interpret and understand the observations (Starck & Fadili 2009; Starck et al. 2010a). Sparse coding concentrates around two main axes: finding the appropriate dictionary, and computing the encodings given this dictionary.
Sparse decomposition requires the summation of the relevant atoms with their appropriate weights. However, unlike a transform coder that comes with an inverse transform, finding such sparse codes within overcomplete dictionaries is non-trivial, in particular because the decomposition of a signal on an overcomplete dictionary is not unique. The combination of a dictionary representation with sparse modeling was first introduced in the pioneering work of Mallat & Zhang (1993), where the traditional wavelet transforms were replaced by the more generic concept of a dictionary for the first time.
We use in this paper a sparse synthesis prior. Given an observation x ∈ Rn, and a sparsifying dictionary D ∈ Rn × k, sparse decomposition refers to finding an encoding vector α ∈ Rk that represents a given signal x in the domain spanned by the dictionary D, while minimizing the number of elementary atoms involved in synthesizing it: 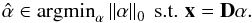 (4)When the original signal is to be reconstructed only approximately, the equality constrain is replaced by an ℓ2 norm inequality constrain
(4)When the original signal is to be reconstructed only approximately, the equality constrain is replaced by an ℓ2 norm inequality constrain 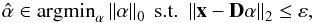 (5)where ε is a threshold controlling the misfitting between the observation x and the recovered signal
(5)where ε is a threshold controlling the misfitting between the observation x and the recovered signal 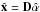 .
.
The sparse prior can also be used from an analysis point of view (Elad et al. 2007). In this case, the computation of the signal coefficient is simply obtained by the sparsifying dictionary and the problem becomes 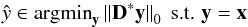 (6)or
(6)or 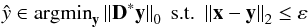 (7)whether the signal x is contaminated by noise or not. This approach has been explored more recently than the synthesis model and has thus far yielded promising results (Rubinstein et al. 2012). We chose to use the synthesis model for our work because it offers more guarantees as it has been proved to be an efficient model in many different contexts.
(7)whether the signal x is contaminated by noise or not. This approach has been explored more recently than the synthesis model and has thus far yielded promising results (Rubinstein et al. 2012). We chose to use the synthesis model for our work because it offers more guarantees as it has been proved to be an efficient model in many different contexts.
Solving Eq. (5) proves to be conceptually Np-hard and numerically intractable. Nonetheless, heuristic methods called greedy algorithms were developed to approximate the sparse solution of the ℓ0 problem, while considerably reducing the resources requirements. The process of seeking a solution can be divided into two effective parts: finding the support of the solution and estimating the values of the entries over the selected support (Mallat & Zhang 1993). Once the support of the solution is found, estimating the signal coefficients becomes a straightforward problem since a simple least-squares application can often provide the optimal solution regarding the selected support. This class of algorithms includes matching pursuit (MP), orthogonal matching pursuit (OMP), gradient pursuit (GP), and their variants.
A popular alternative to the problem Eq. (5) is to use the ℓ1-norm instead of the ℓ0 to promote a sparse solution. Using the ℓ1 norm as a sparsity prior results in a convex optimization problem (Basis Pursuit Denoising or Lasso) that is computationally tractable, finding 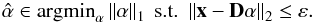 (8)The optimization problem Eq. (8) can also be written in its unconstrained penalized form
(8)The optimization problem Eq. (8) can also be written in its unconstrained penalized form 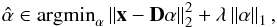 (9)where λ is a Lagrange multiplier, controlling the sparsity of the solution (Chen et al. 1998). The larger λ is, the sparser the solution becomes. Many frameworks have been proposed in this perspective, leading to multiple basis pursuit schemes. Readers interested in an in-depth study of sparse decomposition algorithms can be referred to Starck et al. (2010a), Elad (2010).
(9)where λ is a Lagrange multiplier, controlling the sparsity of the solution (Chen et al. 1998). The larger λ is, the sparser the solution becomes. Many frameworks have been proposed in this perspective, leading to multiple basis pursuit schemes. Readers interested in an in-depth study of sparse decomposition algorithms can be referred to Starck et al. (2010a), Elad (2010).
2.3. Fixed dictionaries
A data set can be decomposed in many dictionaries, but the best dictionary for solving Eq. (5) is the one with the sparsest (most economical) representation of the signal. In practice, it is convenient to use dictionaries with a fast implicit transform (such as Fourier transform, wavelet transform, etc.) which allows us to directly obtain the coefficients and reconstruct the signal from these coefficients using fast algorithms running in linear or almost linear time (unlike matrix-vector multiplications). The Fourier, wavelet and discrete cosine transforms certainly provide the most well-known dictionaries.
Most of these dictionaries are designed to handle specific contents, and are restricted to signals and images that are of a certain type. For instance, Fourier represents stationary and periodic signals well, wavelets are good for analyzing isotropic objects of different scales, curvelets are designed for elongated features, etc. They cannot guarantee sparse representations of new classes of signals of interest, that present more complex patterns and features. Thus, finding new approaches to design these sparsifying dictionaries becomes of the utmost importance. Recent works have shown that designing adaptive dictionaries and learning them upon the data themselves, instead of using predesigned selections of analytically-driven atoms, leads to state-of-the-art performance in various tasks such as image denoising (Elad & Aharon 2006), inpainting (Mairal et al. 2010), source separation (Bobin et al. 2008, 2013), and so forth.
2.4. Learned dictionaries
The question of dictionary learning in its non-overcomplete form (that is, when the number of atoms in the dictionary is smaller than or equal to the dimension of the signal to decompose) has been studied in depth and can be approached using many viable techniques, such as principal component analysis (PCA) and its variants, which are based on algorithms minimizing the reconstruction errors upon a training set of samples while representing them as a linear combination of the dictionary elements (Bishop 2007). Inspired by an analogy to the learning mechanism in the simple cells in the visual cortex, Olshausen & Field (1996) proposed a minimization process based on a cost function that balances a misfitting term and a sparsity inducing term. The optimization process is performed by alternating the optimization with respect to the sparse encodings, and to the dictionary functions. Most of the overcomplete dictionary learning methods are based on a similar alternating optimization scheme, while using specific techniques to induce the sparsity prior and update the dictionary elements. This problem shares many similarities with the blind sources separation (BSS) problem (Zibulevsky & Pearlmutter 1999), although in BSS the sources are assumed to be sparse in a fixed dictionary and the learning is performed on the mixing matrix.
A popular approach is to learn patch-sized atoms instead of a dictionary of image-sized atoms. This allows faster processing and makes the learning possible even with a single image to train on as many patch exemplars can be extracted from a single training image. Section 3 gives more details about the variational problem of patch learning and denoising. This patch-based approach leads to different learning algorithms such as method of optimal direction (MOD) (Engan et al. 1999), pojected gradient descent methods (Lin 2007), or K-SVD (Aharon et al. 2006) that have proven efficient for image processing (Elad & Aharon 2006; Mairal et al. 2010; Peyré et al. 2010).
3. Denoising by centered dictionary learning
3.1. General variational problem
The goal of denoising with dictionary learning is to build a suitable n × k dictionary D, a collection of atoms [di] i = 1,...,P ∈ RN × P, that offers a sparse representation of the estimated denoised image. As is it not numerically tractable to process the whole image as a large vector, Elad & Aharon (2006), Mairal et al. (2010), and Peyré et al. (2010) propose breaking down the image into smaller patches and learning a dictionary of patch-sized atoms. When simultaneously learning a dictionary and denoising an image Y, the problem amounts to solving 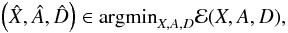 (10)where
(10)where ![\begin{eqnarray} \mathcal{E} (X,A,D) &=& \frac{\lambda}{2}\left\|Y-X\right\|_2^2 \nonumber\\[1.5mm] && +\sum_{i,j}\left ( \frac{\mu_{i,j}}{2}\left\|C_{i,j}R_{i,j}(X)-D\alpha_{i,j}\right\|_2^2 + \left\|\alpha_{i,j}\right\|_1\right) \label{denoising_energy} \end{eqnarray}](/articles/aa/full_html/2013/08/aa20752-12/aa20752-12-eq60.png) (11)such that the learned dictionary D is in
(11)such that the learned dictionary D is in 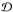 , the set of dictionaries whose atoms are scaled to the unit ℓ2-ball
, the set of dictionaries whose atoms are scaled to the unit ℓ2-ball ![\begin{eqnarray} \forall j\in[1,\dots,k], \quad \left\|d_j\right\|^2 = \sum_{i=1}^N \left|d_j[i]\right|^2\leq1. \label{bounded_atoms} \end{eqnarray}](/articles/aa/full_html/2013/08/aa20752-12/aa20752-12-eq62.png) (12)Here, Y is the noisy image, X the estimated denoised image, A = (αi,j)i,j is the sparse encoding matrix such that αi,j is a sparse encoding of Ri,j(X) in D, and Ci,j is a centering operator defined by Eq. (2). The parameters λ and (μi,j)i,j balance the energy between sparsity prior, data fidelity, and denoising. The dictionary is constrained to obey Eq. (12) to avoid classical scale indeterminacy in the bilinear model (the so-called equivalence class corresponds to scaling, change of sign, and permutation). Indeed, if (A,D) is a pair of sparsifying dictionary and coefficients, then the pair
(12)Here, Y is the noisy image, X the estimated denoised image, A = (αi,j)i,j is the sparse encoding matrix such that αi,j is a sparse encoding of Ri,j(X) in D, and Ci,j is a centering operator defined by Eq. (2). The parameters λ and (μi,j)i,j balance the energy between sparsity prior, data fidelity, and denoising. The dictionary is constrained to obey Eq. (12) to avoid classical scale indeterminacy in the bilinear model (the so-called equivalence class corresponds to scaling, change of sign, and permutation). Indeed, if (A,D) is a pair of sparsifying dictionary and coefficients, then the pair 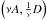 , for any non-zero real ν, leads to the same data fidelity. Thus, discarding the normalization constraint in the minimization problem Eq. (11) would favor arbitrary small coefficients and arbitrary large dictionaries. It is also worth mentioning that the energy Eq. (11) is not minimized with respect to the translation operators (Ci,j)i,j. Rather, we chose to use fixed translation operators that translate the patch such that the pixel of its maximum value is at its center. The rationale behind this is to increase the sensitivity of the algorithm to isotropic structures such as stars, which are ubiquitous in astronomical imaging. This will be clearly shown in the numerical results described in Sect. 4.
, for any non-zero real ν, leads to the same data fidelity. Thus, discarding the normalization constraint in the minimization problem Eq. (11) would favor arbitrary small coefficients and arbitrary large dictionaries. It is also worth mentioning that the energy Eq. (11) is not minimized with respect to the translation operators (Ci,j)i,j. Rather, we chose to use fixed translation operators that translate the patch such that the pixel of its maximum value is at its center. The rationale behind this is to increase the sensitivity of the algorithm to isotropic structures such as stars, which are ubiquitous in astronomical imaging. This will be clearly shown in the numerical results described in Sect. 4.
It is possible to learn a dictionary without denoising the image simultaneously, thus minimizing 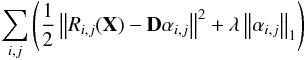 (13)with respect to D and A. This allows a dictionary to be learned from a noiseless training set, or from a small noisy training set extracted from a large noisy image when it is numerically not tractable to process the whole image directly. Once the dictionary is learned, an image can be denoised solving Eq. (5) as we show in Sect. 4. The classical scheme of dictionary learning for denoising dos not include the centering operators and has proven to be an efficient approach (Elad & Aharon 2006; Peyré et al. 2010).
(13)with respect to D and A. This allows a dictionary to be learned from a noiseless training set, or from a small noisy training set extracted from a large noisy image when it is numerically not tractable to process the whole image directly. Once the dictionary is learned, an image can be denoised solving Eq. (5) as we show in Sect. 4. The classical scheme of dictionary learning for denoising dos not include the centering operators and has proven to be an efficient approach (Elad & Aharon 2006; Peyré et al. 2010).
An efficient way to find a minimizer of Eq. (11) is to use an alternating minimization scheme. The dictionary D, the sparse coding coefficient matrix A, and the denoised image X are updated one at a time, the other being fixed. We give more details about each step and how we tuned the parameters below.
3.2. Alternating minimization
3.2.1. Sparse coding
We consider here that the estimated image X and the dictionary D are determined to minimize ℰ with respect to A. Estimating the sparse encoding matrix, A comes down to solve Eq. (9) using iterative soft thresholding (Daubechies et al. 2004) or interior point solver (Chen et al. 1998). We chose to use the Orthogonal Matching Pursuit (OMP) algorithm (Pati et al. 1993), a greedy algorithm that finds an approximate solution of Eq. (5). OMP yields satisfying results while being very fast and its parameters are simple to tune. When learning on a noisy image, we let OMP find the sparsest representation of a vector up to an error threshold that has been set depending on the noise level. In the case of learning an image on a noiseless image, we reconstruct an arbitrary number of component of OMP.
3.2.2. Dictionary update
We consider that the encoding matrix A and the training image Y are fixed here, and we explain how the dictionary D can be updated. The dictionary update consists in finding 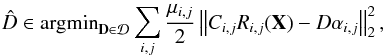 (14)which can be rewritten in a matrix form as
(14)which can be rewritten in a matrix form as 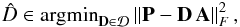 (15)where each column of P contains a patch Ci,jRi,j(X). We chose to use the MOD algorithm that minimizes the mean square error of the residuals, introduced in Engan et al. (1999). The MOD algorithm uses a single conjugate gradient step and gives the following dictionary update
(15)where each column of P contains a patch Ci,jRi,j(X). We chose to use the MOD algorithm that minimizes the mean square error of the residuals, introduced in Engan et al. (1999). The MOD algorithm uses a single conjugate gradient step and gives the following dictionary update 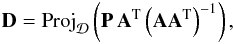 (16)where
(16)where 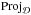 is the projection on
is the projection on 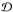 such that for
such that for 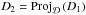 , d2i = d1i/∥d1i∥2 for each atom d2j of D2. The MOD algorithm is fast and easy to implement. An exact minimization is possible with an iterative projected gradient descend (Peyré et al. 2010) but the process is slower and require precise parameter tuning. Another successful approach, the K-SVD algorithm, updates the atoms of the dictionary one by one, using for the update of a given atom only the patches that significantly use this atom in their sparse decomposition (Aharon et al. 2006).
, d2i = d1i/∥d1i∥2 for each atom d2j of D2. The MOD algorithm is fast and easy to implement. An exact minimization is possible with an iterative projected gradient descend (Peyré et al. 2010) but the process is slower and require precise parameter tuning. Another successful approach, the K-SVD algorithm, updates the atoms of the dictionary one by one, using for the update of a given atom only the patches that significantly use this atom in their sparse decomposition (Aharon et al. 2006).
 |
Fig. 1 Hubble images used for numerical experiments: a) Pandora’s galaxy cluster Abell 2744; b) an ACS image of 47 Tucanae; c) an image of WFC3 UVIS full field; and d) a cosmic strings simulation. |
3.2.3. Image update
When D and A are fixed, the energy from Eq. (11) is a quadratic function of X minimized by the closed -form solution ![\begin{eqnarray} \widehat{X} &= & \left(\sum_{i,j} \mu_{i,j}R^*_{i,j}R_{i,j}+\lambda \mathrm{Id}\right)^{-1} \nonumber\\[3mm] &&\times \left(\sum_{i,j} \mu_{i,j}R^*_{i,j}C^*_{i,j}{\bf D}\alpha_{i,j} + \lambda {\vec Y}\right). \label{image_update} \end{eqnarray}](/articles/aa/full_html/2013/08/aa20752-12/aa20752-12-eq84.png) (17)Updating X with Eq. (17) simply consists in applying on each patch the “de-centering” operator
(17)Updating X with Eq. (17) simply consists in applying on each patch the “de-centering” operator 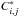 and reconstructing the image by averaging overlapping patches.
and reconstructing the image by averaging overlapping patches.
3.2.4. Algorithm summary
The centered dictionary learning for denoising algorithm is summarized in Algorithm 1. It takes as input a noisy image to denoise and an initial dictionary, and iterates the three steps previously described to yield a noiseless image, a dictionary, and an encoding matrix.

3.3. Parameters
 |
Fig. 2 Results of denoising with galaxy cluster image: a) noisy image, with a S/NP of 26.52 dB; b) the learned dictionary; c) the result of the wavelet shrinkage algorithm that reaches a S/NP of 38.92 dB; and d) the result of denoising using the dictionary learned on the noisy image, with a S/NP of 39.35 dB. |
 |
Fig. 3 Results of denoising with star cluster image: a) the image noisy image, with a S/NP of 27.42 dB; b) the learned dictionary; c) the result of the wavelet shrinkage algorithm that reaches a S/NP of 37.28 dB; d) the result of denoising using the dictionary learned on the noisy image, with a S/NP of 37.87 dB. |
 |
Fig. 4 Results of denoising with nebula image: a) the image used both for learning a noisy dictionary and denoising, with a S/NP of 26.67 dB; b) the learn dictionary; c) the result of the wavelet shrinkage algorithm that reaches a S/NP of 33.61 dB; d) the result of denoising using the dictionary learned on the noisy image, with a S/NP of 35.24 dB. |
Algorithm 1 requires several parameters. All images are 512 × 512 in our experiments.
Patch size and overlap:
we use n = 9 × 9 patches for our experiments and take an overlap of 8 pixels between two consecutive patches. An odd number of pixels is more convenient for patch centering, and this patch size has proven to be a good trade off between speed and robustness. A high overlap parameter allows us to reduce block artifacts.
Dictionary size:
we learn a dictionary of p = 2n = 162 atoms, which gives a ratio of 2 between the size of the dictionary and the dimension of its atoms. It makes the dictionary redundant and allows to capture different morphologies, without inducing an unreasonable computing complexity.
Training set size:
we extract 80n training patches when learning patches of n pixels. Extracting more training samples allows us tor capture the image morphology with more precision, and while it leads to very similar dictionaries, it allows a slightly sparser representation and a slightly better denoising. Reducing the size of the training set might lead us to miss some features from the image used to learn from, depending on the diversity of the morphology it contains.
 |
Fig. 5 a) shows a simulated cosmic string map (1′′ × 1′′); and b) shows the learned dictionary. |
 |
Fig. 6 Example of cosmic string simulation denoising with a high noise level, using the learned dictionary from Fig. 5 and the wavelet algorithm. a) is the source image; b) shows the noisy image with a S/NP of 17.34 dB; c) shows the wavelet denoised version with a S/NP of 30.19 dB; and d) shows the learned dictionary denoised version with a S/NP of 31.04 dB. |
Sparse coding stop criterion:
we stop OMP when the sparse coding xs of a vector x verifies 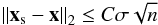 (18)and we use C = 1.15 as gain parameter, as do Elad & Aharon (2006). When learning on noiseless images, we stop OMP computation when it finds the three first components of xs.
(18)and we use C = 1.15 as gain parameter, as do Elad & Aharon (2006). When learning on noiseless images, we stop OMP computation when it finds the three first components of xs.
Training set:
we do not use every patch available in Y as it would be too computationally costly, so we select a random subset of patch positions that we extract from Y. We extract 80n training patches and after learning, we perform a single sparse coding step with the learned dictionary on every noisy patch from Y that are then averaged using Eq. (17). Extracting more training sample does not have a significant effect on the learned dictionary in our examples.
4. Application to astronomical imaging
In this section, we report the main results of the experiments we conducted to study the performance of the presented strategy of centering dictionary learning and image denoising in the case of astronomical observations. We performed our tests on several Hubble images and cosmic string simulations (see Fig. 1). Cosmic string maps are not standard astronomical images, but are interesting because they have a complex texture and are extremely difficult to detect. Wavelet filtering has been proposed for their detection (Hammond et al. 2009) and it is interesting to investigate if DL could eventually be an alternative to wavelets for this purpose. It should, however, be clear that the level of noise that we are using here is not realistic, and this experiment has to be seen as a toy-model example rather than a cosmic string scientific study which would require us to consider as well CMB as well as more realistic cosmic string simulations. The three Hubble images are Pandora’s Galaxy Cluster Abell 2744, an ACS image of the 47 Tucanae star field, and a WFC3 UVIS Full Field Nebula image. These images contain a mixture of isotropic and linear features, which make them difficult to process with the classical wavelet or curvelet-based algorithms.
We study two different cases where we perform dictionary learning and image denoising at the same time, and where the dictionary is learned on a noiseless image and used afterward to denoise a noisy image. We show for these two cases how DL is able to capture the natural features contained in the image, even in the presence of noise, and how it outperforms wavelet-based denoising techniques.
4.1. Joint learning and denoising
We give several examples of astronomical images denoised with the method presented above. For all experiments we show the noisy image, the learned dictionary, and the denoised images, processed respectively with the wavelet shrinkage and the dictionary learning algorithms. We add white Gaussian noise to a noiseless image. We then denoise them using Algorithm 1 and a wavelet shrinkage algorithm, and compare their performance in term of peak S/N. Figure 2 shows the processing of a Hubble image of the Pandora’s Galaxy Cluster, Fig. 3 shows our results on a star cluster image, and Fig. 4 shows our results on a nebula image. The CDL proves to be superior to the wavelet-based denoising algorithm for each example. The dictionary learning method is able to capture the morphology of each kind of image and manages to give a good representation of point-like features.
 |
Fig. 7 Benchmark comparing the wavelet shrinkage algorithm to the dictionary learning denoising algorithm when dealing with various noise levels, using the dictionary from Fig. 5. Each experiment is repeated 100 times and the results are averaged. We use the maximum value for the patch-overlaping parameter. The sparse coding uses OMP and is set to reach an error margin |
 |
Fig. 8 Images used in CDL benchmark: a) a panoramic view of a turbulent star-making region; b) an ACS/WFC image of Abell 1689. |
4.2. Separate learning and denoising
We now apply the presented method to cosmic string simulations. We use a second image similar to the cosmic string simulation from Fig. 1 to learn a noiseless dictionary shown in Fig. 5. We add a high-level white Gaussian noise on the cosmic string simulation from Fig. 1 and we compare how classic DL and wavelet shrinkage denoising perform in Fig. 6. We chose not to use CDL because the cosmic string images do not contain stars but more textured features. In Fig. 7 we give a benchmark of the same process repeated for different noise levels. The peak S/N between the denoised and source image is displayed as a function of the peak S/N between the noisy and the original source image. The reconstruction score is higher for the dictionary learning denoising algorithm than for the wavelet shrinkage algorithm for any noise level. This shows that the atoms computed during the learning are more sensitive to the features contained in the noisy image, compared to wavelets. The learned dictionary was able to capture the morphology of the training image, which is similar to the morphology of the image to denoise. Hence, the coefficients of the noisy image’s decomposition in the learned dictionary are more significant that its coefficient in the wavelet space, which leads to a better denoising.
We show now how DL behaves when learning on real astronomical noiseless images, that is images that present an extremely low level of noise or that have been denoised and thus are considered noiseless. We give several benchmarks to show how the centered dictionary learning is able to outperform the classic approach. We denoise two previously presented images, and two additional images shown in Fig. 8. We perform the learning step on similar noiseless images, see Fig. 9. The benchmark results are presented in Figs. 10–13. Figure 13 illustrates a particular case where the classical dictionary learning becomes less efficient than the wavelet-based denoising algorithm, while using the centered learning and denoising yields better results at any noise level. For each benchmark, we added a white Gaussian noise with a varying standard deviation to one image and learn a centered dictionary and a non-centered dictionary on a second similar noiseless image. We use the same set of parameters for both learning. The CDL method performs better than the classic DL method and wavelet-based denoising. A consequence of the better sparsifying capability of the centered dictionary is a faster computation during the sparse coding step. The noiseless dictionaries prove to be efficient for any level of noise.
 |
Fig. 9 Hubble images used for noiseless dictionary learning: a) Pandora’s Cluster Abell; b) a galaxy cluster; c) a region in the Large Magellanic Cloud; and d) is an additional image of Pandora’s Cluster Abell. |
 |
Fig. 10 Benchmark for nebula image from Fig. 1 comparing CDL to DL and wavelet denoising methods: a) centered learned dictionary that was learned on a second, noiseless image and used for denoising; and b) the peak S/N curve for the three methods. The centered dictionary learning method is represented by the green curve, the classic dictionary learning in blue, and the wavelet-based method in red. The horizontal axis represents the peak S/N (dB) between the image before and after adding noise. For denoising, we use OMP with a stopping criterion fixed depending on the level of noise that was added. 100 experiments were repeated for each value of noise. |
4.3. Photometry and source detection
Although the final photometry is generally done on the raw data (Pacaud et al. 2006; Nolan et al. 2012), it is important that the denoising does not introduce a strong bias on the flux of the different sources because it would dump their amplitude and reduce the number of detected sources.
 |
Fig. 11 Benchmark for galaxy cluster image from Fig. 1 comparing CDL to DL and wavelet denoising methods: a) a centered learned dictionary that was learned on a second, noiseless image and used for denoising; b) the peak S/N curve for the three methods. Centered dictionary learning method is represented by the green curve, the classic dictionary learning in blue and the wavelet-based method in red. The horizontal axis represents the peak S/N (dB) between the image before and after adding noise. For denoising, we use OMP with a stopping criterion fixed depending on the level of noise that was added. 100 experiments were repeated for each value of noise. |
 |
Fig. 12 Benchmark for star-making region image from Fig. 8 comparing CDL to DL and wavelet denoising methods: a) a centered learned dictionary that was learned on a second, noiseless image and used for denoising; b) the peak S/N curve for the three methods. Centered dictionary learning method is represented by the green curve, the classic dictionary learning in blue and the wavelet-based method in red. The horizontal axis represents the peak S/N (dB) between the image before and after adding noise. For denoising, we use OMP with a stopping criterion fixed depending on the level of noise that was added. 100 experiments were repeated for each value of noise. |
 |
Fig. 13 Benchmark for Abell 1689 image from Fig. 8 comparing CDL to DL and wavelet denoising methods: a) a centered learned dictionary that was learned on a second, noiseless image and used for denoising; b) the peak S/N curve for the three methods. Centered dictionary learning method is represented by the green curve, the classic dictionary learning in blue and the wavelet-based method in red. The horizontal axis represents the peak S/N (dB) between the image before and after adding noise. For denoising, we use OMP with a stopping criterion fixed depending on the level of noise that was added. 100 experiments were repeated for each value of noise. |
 |
Fig. 14 Source photometry comparison between CDL and wavelet denoising: a) number of sources with a flux above a varying threshold after denoising; and b) how the flux is dampened by denoising, representing the source flux after denoising as a function of the source flux before denoising. |
 |
Fig. 15 Zoomed features extracted from a galaxy cluster image: a) the full source image before adding noise; b) the noiseless source; c) the noisy version, and d); e); and f) the denoised feature, using wavelets, classic dictionary learning and centered dictionary learning, respectively. |
We provide in this section a photometric comparison of the wavelet and dictionary learning denoising algorithms. We use the top-left quarter of the nebula image from Eq. (4). We run Sextractor (Bertin & Arnouts 1996) using a 3σ detection threshold on the noiseless image, and we store the detected sources with their respective flux. We then add white Gaussian noise with a standard deviation of 0.07 to the image which has a standard deviation of 0.0853 (S/NP = 10.43 dB), and use the different algorithms to denoise it. We then use Sextractor, using the source location stored from the clean image analysis and processing the denoised images. We show two curves in Fig. 14. The first is the number of sources in the image with a flux above a varying threshold for the original, wavelet denoised, and CDL denoised images. The second curve shows how the flux is dampened by the different denoising methods. We also show in Figs. 15–17 several features after denoising the galaxy cluster images using the different methods. It appears that denoising using centered dictionary learning restores objects with better contrast, less blur, and is more sensitive to small sources. Finally, we give several benchmarks to show how the centered dictionary learning is able to overcome the classic approach.
The learned-dictionary-based techniques show much better behavior in term of flux comparison. This is consistent with the aspect of the features shown in Figs. 15–17. The CDL method induces less blurring of the sources and is more sensitive to point-like features.
 |
Fig. 16 Zoomed features extracted from the previously shown nebular image: a) the full source image before adding noise; b) the noiseless source; c) the noisy version; and d); e); and f) show the denoised feature using wavelets, classic dictionary learning and centered dictionary learning, respectively. |
 |
Fig. 17 Zoomed features extracted from the previously shown nebular image: a) the full source image before adding noise; b) the noiseless source; c) the noisy version; and d); e); and f) show the denoised feature using wavelets, classic dictionary learning and centered dictionary learning, respectively. |
5. Software
We provide the matlab functions and script related to our numerical experiment at the URL http://www.cosmostat.org/software.html.
6. Conclusion
We introduce a new variant of dictionary learning, the centered dictionary learning method, for denoising astronomical observations. Centering the training patches yields an approximate translation invariance inside the patches and leads to significant improvements in terms of global quality as well as photometry or feature restoration. We conducted a comparative study of different dictionary learning and denoising schemes, and compared the performance of the adaptive setting to the state-of-the-art in this matter. The dictionary learning appears as a promising paradigm that can be exploited for many tasks. We showed its efficiency in astronomical image denoising and how it overcomes the performances of state-of-the-art denoising algorithms that use non-adaptive dictionaries. The use of dictionary learning requires us to chose several parameters like the patch size, the number of atoms in the dictionary or the sparsity imposed during the learning process. Those parameters can have a significant impact on the quality of the denoising, or the computational cost of the processing. The patch-based framework also brings additional difficulties as one has to adapt it to the problem being dealt with. Some tasks require a more global processing of the image and might require a more subtle use of the patches than the sliding window used for denoising.
Acknowledgments
The authors thank Gabriel Peyre for useful discussions. This work was supported by the French National Agency for Research (ANR -08-EMER-009-01) and the European Research Council grant SparseAstro (ERC-228261).
References
- Aharon, M., Elad, M., & Bruckstein, A. 2006, Signal Processing, IEEE Trans., 54, 4311 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bishop, C. M. 2007, Pattern Recognition and Machine Learning Information Science and Statistics (Springer) [Google Scholar]
- Bobin, J., Moudden, Y., Starck, J. L., Fadili, M., & Aghanim, N. 2008, Statistical Methodology, 5, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Bobin, J., Starck, J.-L., Sureau, F., & Basak, S. 2013, A&A, 550, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, S. S., Donoho, D. L., Michael, & Saunders, A. 1998, SIAM J. Scientific Computing, 20, 33 [Google Scholar]
- Daubechies, I., Defrise, M., & De Mol, C. 2004, Comm. Pure Appl. Math., 57, 1413 [Google Scholar]
- Elad, M. 2010, Sparse and Redundant Representations: From theory to applications in signal and image processing (Springer) [Google Scholar]
- Elad, M., & Aharon, M. 2006, Image Processing, IEEE Trans., 15, 3736 [Google Scholar]
- Elad, M., Milanfar, P., & Rubinstein, R. 2007, Inverse Problems, 23, 947 [NASA ADS] [CrossRef] [Google Scholar]
- Engan, K., Aase, S. O., & Hakon Husoy, J. 1999, IEEE International Conf. on Acoustics, Speech, and Signal Processing, 5, 2443 [Google Scholar]
- Hammond, D. K., Wiaux, Y., & Vandergheynst, P. 2009, MNRAS, 398, 1317 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, C. 2007, Neural Computation, 19, 2756 [CrossRef] [Google Scholar]
- Mairal, J., Bach, F., Ponce, J., & Sapiro, G. 2010, The Journal of Machine Learning Research, 11, 19 [Google Scholar]
- Mallat, S., & Zhang, Z. 1993, IEEE Transactions on Signal Processing, 41, 3397 [NASA ADS] [CrossRef] [Google Scholar]
- Nolan, P. L., Abdo, A. A., Ackermann, M., et al. 2012, ApJS, 199, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Olshausen, B., & Field, D. 1996, Nature, 381, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Pacaud, F., Pierre, M., Refregier, A., et al. 2006, MNRAS, 372, 578 [NASA ADS] [CrossRef] [Google Scholar]
- Pati, Y. C., Rezaiifar, R., Rezaiifar, Y. C. P. R., & Krishnaprasad, P. S. 1993, in Proc. 27th Annual Asilomar Conference on Signals, Systems, and Computers, 40 [Google Scholar]
- Peyré, G., Fadili, J., & Starck, J. L. 2010, SIAM J. Imaging Sciences, 3, 646 [Google Scholar]
- Rubinstein, R., Peleg, T., & Elad, M. 2012, in ICASSP 2012, Kyoto, Japon [Google Scholar]
- Schmitt, J., Starck, J. L., Casandjian, J. M., Fadili, J., & Grenier, I. 2010, A&A, 517, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Starck, J.-L., & Fadili, M. J. 2009, An overview of inverse problem regularization using sparsity [Google Scholar]
- Starck, J.-L., & Murtagh, F. 2006, Astronomical Image and Data Analysis (Springer), 2nd edn. [Google Scholar]
- Starck, J.-L., Candes, E., & Donoho, D. 2003, A&A, 398, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Starck, J., Murtagh, F., & Fadili, J. 2010a, Sparse Image & Signal Processing Wavelets, Curvelets, Morphological Diversity (Cambridge University Press) [Google Scholar]
- Starck, J.-L., Murtagh, F., & Fadili, M. 2010b, Sparse Image and Signal Processing (Cambridge University Press) [Google Scholar]
- Zibulevsky, M., & Pearlmutter, B. A. 1999, Neural Computation, 165 [Google Scholar]
All Figures
 |
Fig. 1 Hubble images used for numerical experiments: a) Pandora’s galaxy cluster Abell 2744; b) an ACS image of 47 Tucanae; c) an image of WFC3 UVIS full field; and d) a cosmic strings simulation. |
| In the text | |
 |
Fig. 2 Results of denoising with galaxy cluster image: a) noisy image, with a S/NP of 26.52 dB; b) the learned dictionary; c) the result of the wavelet shrinkage algorithm that reaches a S/NP of 38.92 dB; and d) the result of denoising using the dictionary learned on the noisy image, with a S/NP of 39.35 dB. |
| In the text | |
 |
Fig. 3 Results of denoising with star cluster image: a) the image noisy image, with a S/NP of 27.42 dB; b) the learned dictionary; c) the result of the wavelet shrinkage algorithm that reaches a S/NP of 37.28 dB; d) the result of denoising using the dictionary learned on the noisy image, with a S/NP of 37.87 dB. |
| In the text | |
 |
Fig. 4 Results of denoising with nebula image: a) the image used both for learning a noisy dictionary and denoising, with a S/NP of 26.67 dB; b) the learn dictionary; c) the result of the wavelet shrinkage algorithm that reaches a S/NP of 33.61 dB; d) the result of denoising using the dictionary learned on the noisy image, with a S/NP of 35.24 dB. |
| In the text | |
 |
Fig. 5 a) shows a simulated cosmic string map (1′′ × 1′′); and b) shows the learned dictionary. |
| In the text | |
 |
Fig. 6 Example of cosmic string simulation denoising with a high noise level, using the learned dictionary from Fig. 5 and the wavelet algorithm. a) is the source image; b) shows the noisy image with a S/NP of 17.34 dB; c) shows the wavelet denoised version with a S/NP of 30.19 dB; and d) shows the learned dictionary denoised version with a S/NP of 31.04 dB. |
| In the text | |
 |
Fig. 7 Benchmark comparing the wavelet shrinkage algorithm to the dictionary learning denoising algorithm when dealing with various noise levels, using the dictionary from Fig. 5. Each experiment is repeated 100 times and the results are averaged. We use the maximum value for the patch-overlaping parameter. The sparse coding uses OMP and is set to reach an error margin |
| In the text | |
 |
Fig. 8 Images used in CDL benchmark: a) a panoramic view of a turbulent star-making region; b) an ACS/WFC image of Abell 1689. |
| In the text | |
 |
Fig. 9 Hubble images used for noiseless dictionary learning: a) Pandora’s Cluster Abell; b) a galaxy cluster; c) a region in the Large Magellanic Cloud; and d) is an additional image of Pandora’s Cluster Abell. |
| In the text | |
 |
Fig. 10 Benchmark for nebula image from Fig. 1 comparing CDL to DL and wavelet denoising methods: a) centered learned dictionary that was learned on a second, noiseless image and used for denoising; and b) the peak S/N curve for the three methods. The centered dictionary learning method is represented by the green curve, the classic dictionary learning in blue, and the wavelet-based method in red. The horizontal axis represents the peak S/N (dB) between the image before and after adding noise. For denoising, we use OMP with a stopping criterion fixed depending on the level of noise that was added. 100 experiments were repeated for each value of noise. |
| In the text | |
 |
Fig. 11 Benchmark for galaxy cluster image from Fig. 1 comparing CDL to DL and wavelet denoising methods: a) a centered learned dictionary that was learned on a second, noiseless image and used for denoising; b) the peak S/N curve for the three methods. Centered dictionary learning method is represented by the green curve, the classic dictionary learning in blue and the wavelet-based method in red. The horizontal axis represents the peak S/N (dB) between the image before and after adding noise. For denoising, we use OMP with a stopping criterion fixed depending on the level of noise that was added. 100 experiments were repeated for each value of noise. |
| In the text | |
 |
Fig. 12 Benchmark for star-making region image from Fig. 8 comparing CDL to DL and wavelet denoising methods: a) a centered learned dictionary that was learned on a second, noiseless image and used for denoising; b) the peak S/N curve for the three methods. Centered dictionary learning method is represented by the green curve, the classic dictionary learning in blue and the wavelet-based method in red. The horizontal axis represents the peak S/N (dB) between the image before and after adding noise. For denoising, we use OMP with a stopping criterion fixed depending on the level of noise that was added. 100 experiments were repeated for each value of noise. |
| In the text | |
 |
Fig. 13 Benchmark for Abell 1689 image from Fig. 8 comparing CDL to DL and wavelet denoising methods: a) a centered learned dictionary that was learned on a second, noiseless image and used for denoising; b) the peak S/N curve for the three methods. Centered dictionary learning method is represented by the green curve, the classic dictionary learning in blue and the wavelet-based method in red. The horizontal axis represents the peak S/N (dB) between the image before and after adding noise. For denoising, we use OMP with a stopping criterion fixed depending on the level of noise that was added. 100 experiments were repeated for each value of noise. |
| In the text | |
 |
Fig. 14 Source photometry comparison between CDL and wavelet denoising: a) number of sources with a flux above a varying threshold after denoising; and b) how the flux is dampened by denoising, representing the source flux after denoising as a function of the source flux before denoising. |
| In the text | |
 |
Fig. 15 Zoomed features extracted from a galaxy cluster image: a) the full source image before adding noise; b) the noiseless source; c) the noisy version, and d); e); and f) the denoised feature, using wavelets, classic dictionary learning and centered dictionary learning, respectively. |
| In the text | |
 |
Fig. 16 Zoomed features extracted from the previously shown nebular image: a) the full source image before adding noise; b) the noiseless source; c) the noisy version; and d); e); and f) show the denoised feature using wavelets, classic dictionary learning and centered dictionary learning, respectively. |
| In the text | |
 |
Fig. 17 Zoomed features extracted from the previously shown nebular image: a) the full source image before adding noise; b) the noiseless source; c) the noisy version; and d); e); and f) show the denoised feature using wavelets, classic dictionary learning and centered dictionary learning, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.