EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 555 (July 2013) A&A, 555 (2013) A50 Full HTML
Free Access
Issue
A&A
Volume 555, July 2013
Article Number A50
Number of page(s) 9
Section Galactic structure, stellar clusters and populations
DOI https://doi.org/10.1051/0004-6361/201321421
Published online 27 June 2013

© ESO, 2013

1. Introduction

Westerlund 2 is a compact young open cluster embedded in the H ii region RCW 49. The cluster lies in the direction of the Carina spiral arm (l, b = 284°̣4, -0°̣34), and descriptions of prior studies of the object and region are provided in Ascenso et al. (2007) and Vargas Álvarez et al. (2013). Most noteworthy is that the distance to Westerlund 2 has been the subject of lively debate (e.g., Rauw et al. 2007; Ascenso et al. 2007), with estimates ranging from 2 kpc to more than 8 kpc from the Sun. That range propagates into uncertainties in the size, mass, and luminosity determinations for the cluster. Consequently, establishing a reliable cluster distance is vital and directly depends on how interstellar extinction is treated because of the high reddening for Westerlund 2 members. Such an analysis is particularly important given the cluster’s location in the vicinity of the Great Carina Nebula and complex (e.g., Carraro et al. 2004), where anomalous dust extinction (RV = AV/EB − V ≃ 4) appears to be widespread (Turner 2012, see also Baume et al. 2009).

Westerlund 2 is also located in the direction of one of the Galaxy’s strongest sources of γ-rays (Aharonian et al. 2007; Abramowski et al. 2011), and is also coincident with a strong source of X-rays (Tsujimoto et al. 2007), which suggests that the physical conditions necessary for producing these radiation sources must be present in the cluster (see Bednarek 2007) if a physical association with Westerlund 2 is confirmed. Several Wolf-Rayet stars in the cluster and surroundings (Moffat et al. 1991; Roman-Lopes et al. 2011) are potential sources of high-energy radiation, as is the case, for example, for the northern hemisphere cluster Berkeley 87 (Manchanda et al. 1996; Tluczykont 2001; Abdo et al. 2009). Berkeley 87 is spatially coincident with the strongest northern hemisphere source of γ-rays and contains the WO2 Wolf-Rayet star WR 142 as well as several unusual high-mass objects (Turner & Forbes 1982). Strong mass loss has been demonstrated to be a feature of luminous members of Berkeley 87 (Turner et al. 2010), which may also be the case for luminous members of Westerlund 2. Such characteristics are important considerations for identifying potential sources of high-energy radiation from the clusters (Bednarek 2007), in addition to the observed frequency dependence of radiation from them.

An important consideration in all such studies is to establish the correct distance to Westerlund 2. The present analysis employs new UBVRIc photometry (see also Carraro et al. 2012) to tackle the cluster distance through zero-age main-sequence (ZAMS) fitting, including a new analysis of the reddening law in the region. The revised results have ramifications for the determination of the cluster mass and the reputed membership of the Wolf-Rayet stars WR20aa and WR20c (Roman-Lopes et al. 2011).

thumbnail Fig. 1

40 s exposure in the R band showing a portion of the field studied here. To highlight the cluster core, the original image was cropped to a 9′ × 9′ field. Two important WR stars discussed here are highlighted in the figure.

2. Observations and data reduction

Westerlund 2 was originally observed at the Cerro Tololo Inter-American Observatory on the nights of March 10 and 13, 2010, using the 1-m ex-YALO telescope, operated by the SMARTS consortium1. The camera is equipped with an STA 4064 × 4064 CCD2 with 15-μm pixels, yielding a scale of 0.289″/pixel and a field-of-view (FOV) of 20′ × 20′ at the Cassegrain focus of the CTIO 1-m telescope. The CCD was operated without binning at a nominal gain of 1.44 e−/ADU, implying a readout noise of 7 e− per quadrant (the detector is read by means of four different amplifiers).

All observations were carried out in good seeing conditions (always less than 1.3″), but not photometric conditions. Our UBV instrumental photometric system was defined by the use of a standard broad-band Kitt Peak UBV set of filters3. The set of images obtained is listed in Table 1.

Table 1

UBVIc photometric observations of Westerlund 2 obtained at the CTIO in March 2010.

To secure photometric calibration and add R-band and deep Ic-band images, the field under analysis was observed at Las Campanas Observatory (LCO) on the night of May 17, 2010, as summarized in Table 2, which lists useful details of the observations, such as filter coverage, air mass range, and exposure times and sequences. The observations made use of the SITe#3 CCD detector on the Swope 1.0m telescope4. With its pixel scale of 0.435″/pixel, the CCD gives a coverage of 14.8′ × 22.8′ on the sky. The night of observation was photometric with seeing ranging from 0.9 to 1.4″ . The field observed is shown in Fig. 1, where a bias- and flat-field-corrected image in the R band (40 s) is shown.

The transformation from the instrumental system to the standard Johnson-Kron-Cousins system, as well as corrections for atmospheric extinction, were determined through multiple observations of stars in Landolt areas PG 1047, PG 1323, and MarkA (Landolt 1992). Broad ranges in air mass (~1.06 to ~1.91) and color (− 0.5 ≤ (B − V) ≤ 1.5) were covered.

Table 2

UBVRIc photometric observations of Westerlund 2 and standard-star fields at LCO in May 2010.

2.1. Photometric reductions

Basic calibration of the CCD frames was performed with the IRAF5 package CCDRED. Zero exposure frames and twilight sky flats were taken every night for standardization purposes. All frames were pre-reduced applying trimming, bias, and flat-field correction. Prior to flat-fielding, all LCO frames were corrected for linearity, following the recipe discussed in Hamuy et al. (2006).

Photometry was then performed using the IRAF DAOPHOT/ALLSTAR and PHOTCAL packages. Instrumental magnitudes were extracted following the point-spread function (PSF) method (Stetson 1987). A quadratic, spatially variable, master PSF (PENNY function) was adopted because of the large FOV of the detector. Aperture corrections were then determined using aperture photometry of a suitable number (typically 15 to 20) of bright, isolated, stars across the field. The corrections were found to be stable across the field, and vary from 0.130 to 0.270 mag, depending upon the filter. Lastly, the PSF photometry was aperture corrected, filter by filter.

2.2. Photometric calibration

After removing problematic stars and stars with only a few observations in Landolt’s catalog (Landolt 1992), a photometric solution for the run was extracted from a total of 43 measurements per filter. The resulting calibration relations are (see also Fig. 2):

U = u + (4.902 ± 0.010) + (0.41 ± 0.01) × X + (0.129 ± 0.020) × (U − B) B = b + (3.186 ± 0.012) + (0.31 ± 0.01) × X + (0.057 ± 0.008) × (B − V) V = v + (3.115 ± 0.007) + (0.17 ± 0.01) × X − (0.057 ± 0.011) × (B − V) R = r + (2.986 ± 0.008) + (0.11 ± 0.01) × X − (0.039 ± 0.011) × (V − R) I = i + (3.426 ± 0.011) + (0.07 ± 0.01) × X + (0.091 ± 0.012) × (V − I) .

The final rms residuals of the fitting in the present case are ± 0.025, ± 0.020, ± 0.013, ± 0.018, and ± 0.013 in U, B, V, R, and Ic, respectively.

Global photometric uncertainties were estimated using the scheme developed by Patat & Carraro (2001, Appendix A.1), which takes into account the uncertainties resulting from the PSF fitting procedure (i.e., from ALLSTAR), and the calibration uncertainties corresponding to the zero point, color terms, and extinction corrections. The final catalog contains 3481 UBVRIc and 12 879 VIc entries.

2.3. Completeness and astrometry

Completeness corrections were determined by running artificial star experiments on the data. Basically, several simulated images were created by adding artificial stars to the original frames. The artificial stars were added at random positions and had the same color and luminosity distribution as the sample of true stars. To avoid potential overcrowding, up to 20% of the original number of stars were added in each simulation. Depending on the frame, between 1000 and 5000 stars were added in this way. The results are summarized in Table 3.

Table 3

Completeness study as a function of the filter.

The optical catalog was then cross-correlated with 2MASS, which resulted in a final catalog that included UBVRIc and JHKs photometry. As a by-product, pixel (i.e., detector) coordinates were converted to RA and Dec for equinox J2000.0, thus providing 2MASS-based astrometry useful for spectroscopic follow- e.g.

2.4. Comparison with previous photometry

Optical data for Westerlund 2 are scarse. Moffat & Vogt (1975) obtained photoelectric photometry for nine stars in the cluster, we caution that the region is complicated and most stars could be binaries. Photoelectric fixed-aperture photometry in crowded fields also carries the classical difficulties of handling blends of stars (Patat & Carraro 2001). The CCD photometry by Moffat et al. (1991) extends the observed sample of cluster stars to V ≃ 19, with the photometry being calibrated using the Moffat & Vogt (1975) observations. Carraro & Munari (2004) remarked that their U-band photometry was offset by upward of 0.2 mag relative to the Moffat et al. (1991) data. Moffat noted in a private communication that the offset could be related to unaccounted-for color terms in the Moffat et al. (1991) dataset. Another source for the discrepancy may be related to aperture corrections when PSF photometry is used for cluster stars and fixed aperture photometry is used for standard stars. No details about that procedure are reported in Moffat et al. (1991).

An independent set of optical data has recently been published by Rauw et al. (2007). These authors found that the Carraro & Munari (2004) photometry is brighter in V by ~0.2 mag than their own photometry. No mention is made by Rauw et al. (2007) concerning the size of the aperture correction. To our knowledge, no other photometric studies have been conducted on the cluster to date.

thumbnail Fig. 2

Photometric solution in UBVRI for standard stars (see Table 2 for details). σ, on the right-hand side, indicates the rms of the fit.

thumbnail Fig. 3

Comparisons of the photometry presented in this paper with that of Moffat et al. (1991).

thumbnail Fig. 4

Comparisons of the photometry presented in this paper with that of Rauw et al. (2007).

thumbnail Fig. 5

Observed colors for stars in Westerlund 2, with data for the Wolf-Rayet stars WR 20a and WR 20b plotted as circled yellow points. The intrinsic relation for dwarfs is plotted as a solid black curve, with the same relation reddened by EB − V = 1.65 as a gray curve. Reddening lines of slope EU − B/EB − V = 0.64 are plotted relative to the hottest O stars and A3 dwarfs (red lines), and B5 dwarfs (blue line). A similar reddening line of slope EU − B/EB − V = 0.75 is shown for the hottest O stars (green line).

Since the panchromatic response of current CCD detectors is not well suited to the replication of the Johnson UBV system, particularly for the U-band, it is important to establish the general accuracy of the present observations prior to an analysis of Westerlund 2. To begin, a comparison of the new photometry presented here was made with the data of Moffat et al. (1991). A cross-correlation of the two catalogs revealed 61 stars in common with UBV photometry. A comparison is illustrated in Fig. 3, where the differences in V, B − V, and U − B are plotted in the sense Moffat et al. (M91) minus the present photometry (C13). The comparison yields offsets of 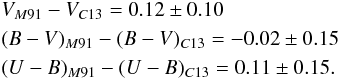The strong deviation at faint V magnitudes is the result of poor detector sensitivity, which is common when comparing photometry from modern detectors to older data sets (Carraro et al. 2011).

The study by Rauw et al. (2007) is tied to BV observations. A cross-correlation with their photometry yields 226 stars in common, with the comparisons shown in Fig. 3. The offsets are 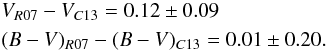The same V offset exists as in the comparison with the Moffat et al. (1991) data, yet the B − V colors agree.

3. Photometric analysis

The accuracy of the CCD photometry presented here was tested using the observations themselves, particularly in light of the offsets from previously published photometry described in Sect. 2.4. The UBV data appear to be closely matching the Johnson system, as shown in Fig. 5, which is a color–color diagram for observed stars in the field of Westerlund 2. The observations are plotted relative to the intrinsic UBV relation for dwarf stars, the same relation reddened by EB − V = 1.65, and reddening lines of slope EU − B/EB − V = 0.64 and 0.75 for the hottest O-type stars, with the former also plotted relative to the intrinsic colors for B5 and A3 dwarfs. There are a number of highly deviant points in Fig. 5, a situation typical of stars in crowded fields or stars near the limits of reliable photometry with the detector. Yet it is noteworthy that there are also many stars that closely match the intrinsic relation for unreddened dwarfs, which is often a good test of how closely the observations match the Johnson UBV system (see Turner et al. 2012b).

3.1. Reddening law

The clump of stars near (B − V, U − B) = (1.65, 0.00) represents the reddened colors of massive O-type members of Westerlund 2. The two plotted reddening lines from the earliest main-sequence spectral types are consistent with the run of observed colors for the stars only for a reddening slope near EU − B/EB − V = 0.64. A steeper reddening relation such as that plotted for EU − B/EB − V = 0.75 does not match the observations for the O-stars; the run of colors for the stars is noticeably different and would imply sizable ultraviolet excesses for most of them, a highly improbable situation. Reddening lines of slope 0.64 are also a close match to the colors of stars reddened from the A3 “kink” in the intrinsic relation for dwarfs at B − V = 0.08, as well as from the intrinsic colors for B5 dwarfs, the latter appearing to form a consistent blue limit for the colors of less-reddened foreground stars in the Westerlund 2 field. If there were a color-dependent error in the U − B colors from the CCD photometry, such consistent trends would not be evident in the data.

Another test was made by examining the color excesses for spectroscopically observed members of Westerlund 2, including stars classified spectroscopically by Vargas Álvarez et al. (2013). The intrinsic colors of O-type dwarfs and giants vary little with spectral type, but for consistency we rederived spectral types for those stars in the compilation of spectra plotted by Rauw et al. (2007), without reference to earlier classifications, although the results are generally similar. The temperature and luminosity subtypes were tied closely to the Walborn system (Walborn 1971a,b, 1972; Walborn & Fitzpatrick 1990), particularly in luminosity, with reference to published spectral line criteria. Color excesses, EB − V and EU − B, were derived for the stars using an unpublished set of intrinsic colors for early-type stars established by DGT (see Turner et al. 2012a) through a combination of published tables by Johnson (1966) and FitzGerald (1970), in conjunction with observational studies of young clusters. The Vargas Álvarez et al. (2013) classifications were adopted as published. The results are summarized in Table 4, where the star numbering is taken from Moffat et al. (1991).

Table 4

Spectroscopic data for brighter Westerlund 2 members.

Color excesses were also calculated for less-reddened stars lying within 1° of Westerlund 2 using UBV photometry and spectral types from the literature compiled in Simbad, with the results depicted in Fig. 6. The data for faint members of Westerlund 2 (mainly from Vargas Álvarez et al. 2013) and stars lying near the cluster core exhibit noticeable scatter, most likely because of the effects of crowding by nearby stars on the photometry, and for stars in the surrounding field partly because of variations in the extinction properties of dust affecting individual stars (see Turner 2012). Overall, there is good agreement with a reddening relation described by EU − B/EB − V = 0.63 + 0.02EB − V, where the reddening slope matches that found by Turner (2012) for dust affecting the heavily reddened group of stars associated with WR38, which also belongs to the Great Carina Nebula complex, and the curvature term is adopted from Turner (1989). Only 5 of the spectroscopically observed stars deviate significantly from the adopted relation; that appears to be a consequence of crowding from the close companions for many of the stars.

thumbnail Fig. 6

UBV color excesses for spectroscopically observed stars in Westerlund 2 (filled circles) and within 1° of it (open circles). Circled yellow points represent spectra for Westerlund 2 stars from Vargas Álvarez et al. (2013). The plotted reddening relation is described by EU − B/EB − V = 0.63 + 0.02EB − V.

3.2. Extinction law RV

UBV membership assignment in clusters is routinely based on reddening. The UBV data for Westerlund 2 stars in Table 4, and stars without spectroscopic observations identified from dereddening as probable zero-age main-sequence (ZAMS) objects, were used for a variable-extinction study (see Johnson 1968) of Westerlund 2. For the former the absolute visual magnitudes are linked closely to the calibration of Walborn (1971b), while for the latter they were inferred by means of ZAMS fitting techniques (see Turner 1976a,b), where the ZAMS for O-type stars is that of Turner (1976a) updated to include the hottest O-type stars with intrinsic colors of (B–V)0 = −0.33.

Spectroscopically observed stars in Table 4 anchored the analysis through their apparent distance moduli, although adjustments were necessary for some stars within their assigned luminosity classifications (see notes to Table 4). Differences of up to or more exist between the luminosities of dwarfs (class V) and ZAMS stars on one hand, and dwarfs (class V) and subgiants (class IV) on the other, and since it is impossible to distinguish these differences in luminosity class spectroscopically from the available spectra, one must be careful to avoid assigning individual stars erroneous absolute magnitudes that make their parameters appear inconsistent with cluster membership (i.e., reddening, apparent distance modulus). Luminosity adjustments were therefore applied to the few stars indicated above to make them consistent with the general trend of apparent distance modulus versus color excess observed for the large majority of other Westerlund 2 stars. The luminosity calibration used for the spectroscopic absolute magnitudes is tied to the same ZAMS relation (Turner 1980).

The resulting analysis for Table 4 stars in conjunction with ZAMS-fitted stars produced the results depicted in Fig. 7. Best-fitting relations obtained from least-squares and non-parametric techniques restricted to Westerlund 2 stars yielded 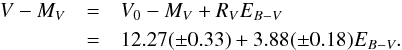I.e., RV = AV/EB − V = 3.88 ± 0.18 for the ratio of total-to-selective extinction and V0 − MV = 12.27 ± 0.33 for the intrinsic distance modulus, the latter corresponding to a distance of 2.85 ± 0.43 kpc, closely coincident with the value of 2.8 kpc adopted by Ascenso et al. (2007) in their independent near-infrared study of Westerlund 2. The large uncertainty in the present distance estimate is the result of the high reddening of cluster stars in conjunction with the extrapolation to EB − V = 0.00 of the best-fitting relation from a reddening of EB − V ≃ 1.75.

Such a high value of RV is consistent with the shallow slope of the reddening line, as also inferred for adjacent regions of Carina (Turner et al. 2005, 2009; Turner 2012), and also matches the value of RV = 3.77 ± 0.09 obtained by Vargas Álvarez et al. (2013) from spectral energy distribution fitting of Hubble Space Telescope (HST) spectra for cluster stars (see Table 5).

thumbnail Fig. 7

Variable-extinction diagram for members of Westerlund 2 from ZAMS fitting (filled circles) and spectroscopic distance moduli (circled yellow points), and for members of IC 2581 (open circles). The gray line represents the best-fitting parameters (see text).

Table 5

Recent RV estimates for the region hosting Westerlund 2.

A similar variable-extinction analysis restricted to stars in Fig. 7 associated with IC 2581 (Turner 1978) yielded values of RV = 3.77 ± 0.19 and V0 − MV = 12.01 ± 0.09, the latter corresponding to a distance of 2.52 ± 0.11 kpc. Many young aggregates in the region of the Great Carina Nebula cluster toward distances of ~2.1 kpc (Turner 2012). Westerlund 2 and IC 2581 appear to lie on the far side of the group.

3.3. Color-difference results

The high value of RV obtained from the variable-extinction analysis is confirmed by color-difference data for Table 4 stars, and is consistent with other recent studies for the extinction properties of the dust in the region surrounding Westerlund 2, as summarized in Table 5. The present use of the color-difference method (see Johnson 1968) used UBVRIc data from this study in combination with JHKs data from 2MASS (Cutri et al. 2003) and intrinsic JHKs colors for hot O-stars from Turner (2011). The results depicted in Fig. 8 yield an average value of RV = 3.85 ± 0.07 for 19 spectroscopically-observed stars using the relationship of Fitzpatrick & Massa (2007) to extrapolate to λ-1 = 0 from the infrared region. The curve fitting the data in Fig. 3 is adapted from Zagury & Turner (2012) for that value of RV.

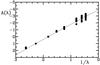thumbnail Fig. 8

Color-difference method applied to the UBVRIcJHKs magnitudes for Westerlund 2 stars. The fitted relation has RV = AV/EB − V = 3.85 ± 0.07.

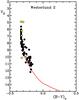thumbnail Fig. 9

Unreddened color–magnitude diagram for Westerlund 2 for the parameters cited in the text, with the Wolf-Rayet stars plotted as circled yellow points, from top to bottom: WR20a, WR20b, WR20c, WR20aa, and WR21a. The red line represents the ZAMS for V0 − MV = 12.27 ± 0.33, and an arrow depicts the main-sequence gap discussed in the text.

4. Westerlund 2

The unreddened color–magnitude diagram for Westerlund 2 members with good quality UBV photometry (Fig. 9) dereddened individually to the intrinsic color–color relation (see Turner 1996; Turner et al. 2012b) is that of an extremely young cluster. Very few hot O-type members are evolved by more than 1m from the ZAMS, except for the two Wolf-Rayet stars WR 20a and WR 20b, which are akin to O-type supergiants, WR 20a having a suspected O-supergiant companion (Roman-Lopes et al. 2011). The two Wolf-Rayet stars have luminosities of MV = −7.37 and − 7.33, typical of binary late-WN stars (e.g., Morris et al. 1993). According to standard stellar evolutionary models (e.g., Meynet et al. 1993), this implies an age of no more than τ ~ 2 × 106 yr for cluster stars.

Apparent in the cluster color–magnitude diagram (Fig. 9) is a gap in the main sequence at V0 ≃ 10. The gap also appears in Fig. 5 as a dearth of reddened cluster members with intrinsic colors of (B − V)0 ≃ −0.28, corresponding to B0.5 V stars. The existence of gaps in the distribution of B-type stars lying on the main sequences in color–magnitude diagrams for young open clusters has been recognized for years (see Mermilliod 1982). Turner (1996) noted from simulations that gap characteristics are generally consistent with expectations for mergers of close binaries, namely an increased luminosity by ~ to 3m of the former “main-sequence” stars from their original position on the cluster main sequence, and a redward spread in color arising from rapid rotation of the newly-merged systems. That may also be true for Westerlund 2. Such a feature would explain the curious red-ward spread of the cluster main sequence both above and below the gap in Fig. 9. Presumably the color spread below the B0.5 V gap arises from an additional gap farther down the main-sequence in the undersampled region of the cluster color–magnitude diagram.

4.1. Wolf-Rayet members

The parameters of the Wolf-Rayet stars near Westerlund 2 are summarized in Table 6, where the broad-band magnitudes and colors are from the present study, Roman-Lopes et al. (2011), and Simbad, and the spectral types are from Roman-Lopes et al. (2011). The inferred broad-band luminosities are based upon the assumption of membership in Westerlund 2. The close similarity in broad band magnitudes and colors for WR20a and WR20b from this study (Table 6) differs markedly from the sizably different narrow-band magnitudes and colors for the same stars (Shara et al. 1991), and deserves a more detailed investigation.

WR20a and WR20b are indicated to be members of Westerlund 2 on the basis of their reddening and location in the core region of the cluster. The assumption of membership in Westerlund 2 also works well for WR20aa and WR20c, despite their location in more distant portions of the cluster corona. Their inferred luminosities are consistent with results for other late-type WN stars in open clusters. Roman-Lopes et al. (2011) suggest that they are runaway stars from the cluster. The case for WR21a is much more interesting. Its inferred luminosity as a member of Westerlund 2 is much too low, which suggested that it must lie beyond the cluster. And yet it is also bright with a much lower reddening than members of Westerlund 2, which would normally imply foreground status to the cluster. The anomaly for this star defies a simple explanation. Roman-Lopes et al. (2011) summarized the case for this star as uncertain.

The dominance of Westerlund 2 members in the X-ray cleaned color–magnitude data of Fig. 10 also suggests that the source of high-energy radiation originating from this direction (Sect. 1) must be associated with the cluster stars themselves. Presumably, strong stellar winds from the hot stars are responsible for much of the γ-ray and X-ray flux from this region of Carina.

Table 6

Wolf-Rayet stars near Westerlund 2.

thumbnail Fig. 10

Left panel, VIc data for stars within 1.2′ of the cluster center. Right panel, X-ray (Chandra) cleaned data for that same area reveals the cluster’s main-sequence and pre-main-sequence populations. A Siess et al. (2000)τ = 1.5 × 106 yr isochrone was applied using the parameters established in Sect. 3.

5. X-ray-cleaned VIc CMD

The cluster age determined from the UBV analysis is corroborated by applying a Siess et al. (2000) isochrone to the VIc photometry (Fig. 10). The latter data are deeper and sample the cluster’s pre-main-sequence stars. The VIc photometry was subsequently matched with Chandra X-ray observations (Tsujimoto et al. 2007). The correlation was performed using the cross-match service provided by CDS, Strasbourg. Tsujimoto et al. (2007) noted that the X-ray observations were obtained in August 2003 via the Advanced CCD Imaging Spectrometer (ACIS). ACIS features a 17′ × 17′ FOV, and the cluster was imaged for 40 ks. The size of the ACIS field is smaller than the optical field (Sect. 2), but the cluster core is sampled. Chandra’s arc-second resolution is particularly pertinent here given that Westerlund 2 is a compact (crowded) cluster, thus ensuring that sources are reliably matched between the X-ray/optical data.

The benefits of employing X-ray observations for studying stellar clusters are numerous (Evans 2011; Majaess et al. 2012). In this instance the X-ray observations are used to segregate field stars from bona fide cluster members, thereby fostering a reliable application of the isochrone. Field stars are typically old slow rotators that have become comparatively X-ray-quiet. The X-ray observations highlight the members of Westerlund 2 that feature a late-type companion (chromospherically active), and earlier-type members that exhibit prominent stellar winds. The brightest X-ray sources may be linked to colliding mass-loss from the binary WR stars (Table 6, see also Tsujimoto et al. 2007).

The left panel in Fig. 10 displays the color–magnitude diagram for all VIc sources within of the cluster center, whereas the right panel contains only X-ray sources occupying that area. Field star contamination is apparent in the former panel, while the cluster’s prominence is revealed in the latter. The main-sequence and pre-main-sequence stars are clearly discernible in the X-ray-cleaned sample of Fig. 10, in addition to the gap described in Sect. 4. The VIc X-ray data are well represented by a τ = 1.5 × 106 yr isochrone (Siess et al. 2000), which was applied using parameters established in Sect. 3. The results confirm the approximate age estimated for Westerlund 2 in Sect. 4 from the main-sequence turnoff.

6. Discussion and conclusions

Westerlund 2 is found to be 2.85 ± 0.43 kpc distant, in close agreement with the distance to the cluster derived from near-infrared photometry by Ascenso et al. (2007). Differences with respect to other estimates can be explained by the anomalous extinction law that applies in the cluster field. For 1 kpc discrepancy relative to the Vargas Álvarez et al. (2013) study using HST spectra and a similar value of RV, the difference probably originates in the manner of ZAMS fitting, which for Vargas Álvarez et al. (2013) was closer to main-sequence fitting. As noted in Sect. 3.2, main-sequence absolute magnitudes are ~ more luminous than ZAMS values for O-type stars of identical intrinsic color.

Variable-extinction analyses of members of Westerlund 2 and IC 2581 yield values of RV = 3.88 ± 0.18 and 3.77 ± 0.19, respectively, while the color-difference method applied to 19 Westerlund 2 members observed spectroscopically yields a best estimate of RV = 3.85 ± 0.07. The agreement of all three estimates is consistent with previous arguments for the existence of anomalous extinction throughout much of the Carina region (Turner 2012, and Table 5).

The Wolf-Rayet stars WR20a and WR20b are almost certainly members of Westerlund 2 according to their derived parameters and location in the cluster core. WR20aa and WR20c appear to be members of Westerlund 2 as well, although whether they are runaway cluster members (Roman-Lopes et al. 2011) or simply members of the cluster corona is left for future study. The cluster color–magnitude diagram (Fig. 9) displays characteristics that have been noted previously to be consistent with close binary mergers and rapid rotation (Turner 1996), which, in conjunction with the strong flux of γ-rays and X-rays (Fig. 10) from the cluster, reveals Westerlund 2 as an extremely active site for dynamical interactions and mass loss for cluster stars.

The distance established for Westerlund 2 (~3 kpc) implies that the cluster lies within the Carina spiral arm.

5

IRAF is distributed by the National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy, Inc., under cooperative agreement with the National Science Foundation.

Acknowledgments

This study is based on data acquired at Las Campanas Observatory. G.C. is grateful for the technical support and pleasant environment provided at the observatory. We made use of B. Skiff’s Catalogue of Stellar Spectral Classifications, and the WEBDA database maintained in Vienna by E. Paunzen and J.-C. Mermilliod, and the SIMBAD database. G.C. expresses his gratitude to Edgardo Costa for securing part of the observations discussed in this paper, and Rodolfo Barba for useful comments on spectral classification. This study was initiated during a visit by G.C. to Saint Mary’s University in July 2012. ESO funding via the DGDF program for the visit is deeply acknowledged. The scientific results reported here are based in part on observations made by the Chandra X-ray Observatory and published previously by M. Tsujimoto.

References

  1. Abdo, A. A., Allen, B. T., Aune, T., et al. 2009, ApJ, 700, L127 [Google Scholar]
  2. Abramowski, A., Acero, F., Aharonian, F., et al. 2011, A&A, 525, A46 [Google Scholar]
  3. Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2007, A&A, 472, 489 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Ascenso, J., Alves, J., Beletsky, Y., & Lago, M. T. V. T. 2007, A&A, 466, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Baume, G., Carraro, G., & Momany, Y. 2009, MNRAS, 398, 221 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bednarek, W. 2007, MNRAS, 382, 367 [NASA ADS] [CrossRef] [Google Scholar]
  7. Carraro, G., & Munari, U. 2004, MNRAS, 347, 625 [NASA ADS] [CrossRef] [Google Scholar]
  8. Carraro, G., Romaniello, M., Ventura, P., & Patat, F. 2004, A&A, 418, 525 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Carraro, G., Anthony-Twarog, B. J., Costa, E., Jones, B. J., & Twarog, B. A. 2011, AJ, 142, 127 [NASA ADS] [CrossRef] [Google Scholar]
  10. Carraro, G., Turner, D., Majaess, D., & Baume, G. 2012, Proc. IAU Symp. 292, in press [arXiv:1209.2080] [Google Scholar]
  11. Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, The IRSA 2MASS All-Sky Point Source Catalog of Point Sources, NASA/IPAC Infrared Science Archive [Google Scholar]
  12. Dean, J. F., Warren, P. R., & Cousins, A. W. J. 1978, MNRAS, 183, 569 [NASA ADS] [CrossRef] [Google Scholar]
  13. Evans, N. R. 2011 [arXiv:1112.1046] [Google Scholar]
  14. FitzGerald, M. P. 1970, A&A, 4, 234 [NASA ADS] [Google Scholar]
  15. Fitzpatrick, E. L., & Massa, D. 2007, ApJ, 603, 320 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Hamuy, M., Folatelli, G., Morrell, N. I., et al. 2006, PASP, 118, 2 [NASA ADS] [CrossRef] [Google Scholar]
  17. Johnson, H. L. 1965, ApJ, 141, 923 [NASA ADS] [CrossRef] [Google Scholar]
  18. Johnson, H. L. 1966, ARA&A, 4, 193 [NASA ADS] [CrossRef] [Google Scholar]
  19. Johnson, H. L. 1968, in Nebulae and Interstellar Matter, eds. B. M. Middlehurst, & L. H. Aller (Chicago: Univ. Chicago Press), 167 [Google Scholar]
  20. Landolt, A. U. 1992, AJ, 104, 340 [NASA ADS] [CrossRef] [Google Scholar]
  21. Majaess, D., Turner, D. G., Gallo, L., et al. 2012, ApJ, 753, 144 [NASA ADS] [CrossRef] [Google Scholar]
  22. Manchanda, R. K., Polcaro, V. F., Norci, L., et al. 1996, A&A, 305, 457 [NASA ADS] [Google Scholar]
  23. Massey, P. 2002, ApJS, 141, 81 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  24. Mermilliod, J.-C. 1982, A&A, 109, 37 [NASA ADS] [Google Scholar]
  25. Meynet, G., Mermilliod, J.-C., & Maeder, A. 1993, A&AS, 98, 477 [NASA ADS] [Google Scholar]
  26. Moffat, A. F. J., & Vogt, N. 1975, A&AS, 20, 125 [NASA ADS] [Google Scholar]
  27. Moffat, A. F. J., Shara, M. M., & Potter, M. 1991, AJ, 102, 642 [NASA ADS] [CrossRef] [Google Scholar]
  28. Morris, P. W., Brownsberger, K. R., Conti, P. S., Massey, P., & Vacca, W. D. 1993, ApJ, 412, 324 [NASA ADS] [CrossRef] [Google Scholar]
  29. Patat, F., & Carraro, G. 2001, MNRAS, 325, 1591 [NASA ADS] [CrossRef] [Google Scholar]
  30. Rauw, G., Manfroid, J., Gosset, E., et al. 1977, A&A, 463, 981 [Google Scholar]
  31. Roman-Lopes, A., Barba, R. H., & Morrell, N. I. 2011, MNRAS, 416, 501 [NASA ADS] [Google Scholar]
  32. Shara, M. M., Moffat, A. F. J., Smith, L. F., & Potter, M. 1991, AJ, 102, 716 [NASA ADS] [CrossRef] [Google Scholar]
  33. Shorlin, S. L., Turner, D. G., & Pedreros, M. H. 2004, PASP, 116, 170 [NASA ADS] [CrossRef] [Google Scholar]
  34. Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [NASA ADS] [Google Scholar]
  35. Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
  36. Tluczykont, M. 2001, Proc. ICRC 2001, 2558 [Google Scholar]
  37. Tsujimoto, M., Feigelson, E. D., Townsley, L. K., et al. 2007, ApJ, 665, 719 [NASA ADS] [CrossRef] [Google Scholar]
  38. Turner, D. G. 1976a, AJ, 81, 97 [NASA ADS] [CrossRef] [Google Scholar]
  39. Turner, D. G. 1976b, AJ, 81, 1125 [NASA ADS] [CrossRef] [Google Scholar]
  40. Turner, D. G., 1978, AJ, 83, 1081 [NASA ADS] [CrossRef] [Google Scholar]
  41. Turner, D. G. 1980, ApJ, 240, 137 [NASA ADS] [CrossRef] [Google Scholar]
  42. Turner, D. G. 1989, AJ, 98, 2300 [NASA ADS] [CrossRef] [Google Scholar]
  43. Turner, D. G. 1996, in ASP Conf. Ser. 90, The Origins, Evolution, and Destinies of Binary Stars in Clusters, eds. E. F. Milone, & J.-C. Mermilliod, 443 [Google Scholar]
  44. Turner, D. G. 2011, Rev. Mex. Astron. Astrofis., 47, 127 [NASA ADS] [Google Scholar]
  45. Turner, D. G. 2012, Ap&SS, 338, 303 [NASA ADS] [CrossRef] [Google Scholar]
  46. Turner, D. G., & Forbes, D. 1982, PASP, 94, 655 [NASA ADS] [CrossRef] [Google Scholar]
  47. Turner, D. G., Forbes, D., van den Bergh, S., Younger, P. F., & Berdnikov, L. N. 2005, AJ, 130, 1194 [NASA ADS] [CrossRef] [Google Scholar]
  48. Turner, D. G., Forbes, D., Leonard, P. J. T., et al. 2009, MNRAS, 397, 1046 [NASA ADS] [CrossRef] [Google Scholar]
  49. Turner, D. G., Majaess, D. J., Lane, D. J., & Balam, D. D. 2010, BAAS, 42, 566 [NASA ADS] [Google Scholar]
  50. Turner, D. G., Majaess, D. J., Lane, D. J., et al. 2012a, MNRAS, 422, 2501 [NASA ADS] [CrossRef] [Google Scholar]
  51. Turner, D. G., van den Bergh, S., Younger, P. F., et al. 2012b, AJ, 144, 187 [NASA ADS] [CrossRef] [Google Scholar]
  52. Vargas Álvarez, C. A., Kobulnicky, H. A., Bradley, D. R., et al. 2013, AJ, in press [Google Scholar]
  53. Walborn, N. R. 1971a, ApJ, 167, L31 [NASA ADS] [CrossRef] [Google Scholar]
  54. Walborn, N. R. 1971b, ApJS, 23, 257 [NASA ADS] [CrossRef] [Google Scholar]
  55. Walborn, N. R. 1972, AJ, 77, 312 [NASA ADS] [CrossRef] [Google Scholar]
  56. Walborn, N. R., & Fitzpatrick, E. L. 1990, PASP, 102, 379 [NASA ADS] [CrossRef] [Google Scholar]
  57. Zagury, F., & Turner, D. G. 2012, AN, 333, 640 [Google Scholar]

All Tables

Table 1

UBVIc photometric observations of Westerlund 2 obtained at the CTIO in March 2010.

In the text
Table 2

UBVRIc photometric observations of Westerlund 2 and standard-star fields at LCO in May 2010.

In the text
Table 3

Completeness study as a function of the filter.

In the text
Table 4

Spectroscopic data for brighter Westerlund 2 members.

In the text
Table 5

Recent RV estimates for the region hosting Westerlund 2.

In the text
Table 6

Wolf-Rayet stars near Westerlund 2.

In the text

All Figures

thumbnail Fig. 1

40 s exposure in the R band showing a portion of the field studied here. To highlight the cluster core, the original image was cropped to a 9′ × 9′ field. Two important WR stars discussed here are highlighted in the figure.
In the text
thumbnail Fig. 2

Photometric solution in UBVRI for standard stars (see Table 2 for details). σ, on the right-hand side, indicates the rms of the fit.
In the text
thumbnail Fig. 3

Comparisons of the photometry presented in this paper with that of Moffat et al. (1991).

In the text
thumbnail Fig. 4

Comparisons of the photometry presented in this paper with that of Rauw et al. (2007).
In the text
thumbnail Fig. 5

Observed colors for stars in Westerlund 2, with data for the Wolf-Rayet stars WR 20a and WR 20b plotted as circled yellow points. The intrinsic relation for dwarfs is plotted as a solid black curve, with the same relation reddened by EB − V = 1.65 as a gray curve. Reddening lines of slope EU − B/EB − V = 0.64 are plotted relative to the hottest O stars and A3 dwarfs (red lines), and B5 dwarfs (blue line). A similar reddening line of slope EU − B/EB − V = 0.75 is shown for the hottest O stars (green line).
In the text
thumbnail Fig. 6

UBV color excesses for spectroscopically observed stars in Westerlund 2 (filled circles) and within 1° of it (open circles). Circled yellow points represent spectra for Westerlund 2 stars from Vargas Álvarez et al. (2013). The plotted reddening relation is described by EU − B/EB − V = 0.63 + 0.02EB − V.
In the text
thumbnail Fig. 7

Variable-extinction diagram for members of Westerlund 2 from ZAMS fitting (filled circles) and spectroscopic distance moduli (circled yellow points), and for members of IC 2581 (open circles). The gray line represents the best-fitting parameters (see text).
In the text
thumbnail Fig. 8

Color-difference method applied to the UBVRIcJHKs magnitudes for Westerlund 2 stars. The fitted relation has RV = AV/EB − V = 3.85 ± 0.07.
In the text
thumbnail Fig. 9

Unreddened color–magnitude diagram for Westerlund 2 for the parameters cited in the text, with the Wolf-Rayet stars plotted as circled yellow points, from top to bottom: WR20a, WR20b, WR20c, WR20aa, and WR21a. The red line represents the ZAMS for V0 − MV = 12.27 ± 0.33, and an arrow depicts the main-sequence gap discussed in the text.
In the text
thumbnail Fig. 10

Left panel, VIc data for stars within 1.2′ of the cluster center. Right panel, X-ray (Chandra) cleaned data for that same area reveals the cluster’s main-sequence and pre-main-sequence populations. A Siess et al. (2000)τ = 1.5 × 106 yr isochrone was applied using the parameters established in Sect. 3.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.