| Issue |
A&A
Volume 555, July 2013
|
|
|---|---|---|
| Article Number | A130 | |
| Number of page(s) | 11 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201321212 | |
| Published online | 12 July 2013 | |
Transfer of polarized line radiation in 2D cylindrical geometry
1
UMR 7293 J.L. Lagrange Laboratory, Université de Nice Sophia Antipolis,
CNRS, Observatoire de la Côte d’Azur,
Campus Valrose,
06108
Nice,
France
2
Astronomical observatory Belgrade, Volgina 7,
11060
Belgrade,
Serbia
e-mail: milic@aob.rs
Received:
31
January
2013
Accepted:
12
April
2013
Aims. This paper deals with multidimensional NLTE polarized radiative transfer in the case of two level atom in the absence of lower level polarization. We aim to develop an efficient and robust method for 2D cylindrical geometry and to apply it to various axi-symmetrical astrophysical objects such as rings, disks, rotating stars, and solar prominences.
Methods. We review the methods of short characteristics and Jacobi iteration applied to axisymmetric geometry. Then we demonstrate how to use a reduced basis for polarized intensity and polarized source function to self-consistently solve the coupled equations of radiative transfer and statistical equilibrium for linearly polarized radiation. We discuss some peculiarities that do not appear in Cartesian geometry, such as angular interpolation in performing the formal solution. We also show how to account for two different types of illuminating radiation.
Results. The proposed method is tested on homogeneous, self-emitting cylinders to compare the results with those in 1D geometries. We demonstrate a possible astrophysical application on a very simple model of circumstellar ring illuminated by a host star where we show that such a disk can introduce a significant amount of scattering polarization in the system.
Conclusions. This method is found to converge properly and, apparently, to allow for substantial time saving compared to 3D Cartesian geometry. We also discuss the advantages and disadvantages of this approach in multidimensional radiative transfer modeling.
Key words: methods: numerical / line: formation / radiative transfer / polarization
© ESO, 2013
1. Introduction
The importance of the multidimensional approach to radiative transfer is now a well-established and important topic. Many astrophysical objects do not possess symmetries and homogeneities that would allow us to use the assumption of one-dimensionality, where physical parameters and radiation field would only depend on one spatial coordinate. Here are some examples: inhomogeneous stellar atmospheres, circumstellar disks, extrasolar planet atmospheres, and solar prominences... To properly model emergent radiation from this kind of objects, it is required to account for the dependence of physical parameters and the radiation field on multiple spatial coordinates. In that case, the radiation field also becomes dependent on both angles that determine the direction of propagation. (Recall that in a 1D approach one usually deals only with the polar angle, θ.) It is evident that this greatly increases the problem’s complexity. It has been more than 40 years now, however, since the first scalar (i.e. modeling only the intensity component of the Stokes vector) radiative transfer calculations accounting for the multidimensionality of the medium have been carried out by Monte Carlo methods (Avery et al. 1969). In their seminal paper, Mihalas et al. (1978) performed detailed radiative transfer computations in 2D Cartesian coordinates in the presence of inhomogeneities and velocity fields, using a second-order differential form of radiative transfer equation. An important breakthrough in the field has been achieved by introducing the so called “short characteristics” approach to a formal solution of the radiative transfer equation, combined with the approximate lambda operator (ALO) technique, by Olson & Kunasz (1987), Kunasz & Auer (1988), and Kunasz & Olson (1988). Most of the work has so far dealt with Cartesian coordinates. However, other coordinate systems have been considered as well. Stenholm (1977) described radiative transfer in 2D cylindrical coordinates, using the core saturation method. In a more recent paper, van Noort et al. (2002, from now on, VHL02) explicitly described 2D radiative transfer in Cartesian, cylindrical, and spherical coordinate systems using the ALO method. In the series of papers by Gouttebroze (2005, the first paper on 2D geometry), another variant of 2D cylinders has been considered, where inhomogeneity in r and ϕ coordinates has been assumed, instead of r and z.
We aim to generalize the previous research by modeling not only the intensity but also scattering polarization (Q and U components of the Stokes vector). Scattering polarization in spectral lines is a linear polarization, which is the result of selective absorption and/or emission of photons via electrons that belong to different Zeeman sub-states. It is also known as a quantum counterpart of Rayleigh’s scattering. Scattering polarization is greatly influenced by the anisotropy of the radiation field, which is, in turn, influenced by the object geometry and by the inhomogeneities in the medium. It is of great importance and diagnostic value to evaluate the effects of multidimensionality on scattering polarization in various astrophysical objects. Solar prominences, accretion disks, and exoplanet atmospheres are the objects that scatter light and are also illuminated by anisotropic radiation.
A very detailed framework for dealing with scattering polarization in multidimensional geometries, which also accounts for effects of partial frequency redistribution (PRD) and magnetic fields (also known as Hanle effect), has been recently given by Anusha & Nagendra (2011a), Anusha et al. (2011), and Anusha & Nagendra (2011b). We follow that approach here but adopt an approximation of complete frequency redistribution (CRD), which makes the problem simpler and less memory-consuming. For spectral lines where PRD is assumed to be important, our method can easily be modified to allow for this effect. The same holds for the macroscopic Hanle effect (i.e. Hanle effect created by a large-scale, oriented, magnetic field), but it should be stressed that this field would have to be axially symmetric, which reduces the range of objects one can model with this geometry. In this paper, the effects of the magnetic fields are not considered. This approach is, in a way, similar to the method of Busche & Hillier (2000) in that both papers are dealing with the short characteristics method in axi-symmetric medium and in inclusion of polarization. Their method is, however, more suitable for spherical objects.
We consider a 2D cylindrical coordinate system, where physical quantities depend on r and z coordinates only. The radiation field has an additional dependence on direction of propagation, which is described by the angles θ and ϕ (as customary, θ is the polar angle, while ϕ is the azimuthal angle, which is measured in the counterclockwise direction from the x axis), and since we are dealing with line transfer, it also depends on the frequency of radiation. This results in the specific intensity being 5-dimensional, which is a significant increase in complexity compared to the 1D case, where the radiation field depends on three quantities only. For the moment, we consider a 2-level atom model. In a polarized case, the reduced intensity basis framework is used. In this formalism, intensity and source function are written as six-component vectors, which are known as the reduced intensity and the reduced source function. The reduced intensity vector is angle and frequency dependent, while the reduced source function is both angle and frenquency independent, as in the unpolarized case. This transformation is of great importance in practical applications as it significantly reduces both memory requirements and computing time.
The issue that needs to be addressed at the beginning is why choose 2D cylindrical coordinates over 2D or 3D Cartesian coordinates? Compared to the 2D Cartesian approach, cylindrical coordinates account for a much greater degree of realism, since they allow modeling of the objects that are still finite in all three dimensions (e.g., disks, rings, and cylindrical threads), while keeping similar numerical effort. The assumption of invariance on rotation of the object along the azimuth is often encountered in modeling of astrophysical objects. Now, 3D Cartesian coordinates would allow us to relax that assumption, but it should be noted that the 3D approach also increases numerical effort and memory requirements by a factor of N (where N is the “typical” size of spatial grid). In cases of interest, N is usually of order of 100, which is a major increase, and often calls for parallelization of the code and significant computing time. It is our opinion that modeling via 2D cylindrical geometry is an optimal choice for certain objects. As it will be explained in the paper, this approach however introduces greater inaccuracy and more complicated formulation of some quantities that are relatively straightforward in Cartesian geometry.
The paper is structured as follows. In Sect. 2 we will briefly recap the approach by VHL02 which is adopted in this work. We will also further comment on some possibly problematic aspects, such as boundary conditions, angular interpolation, and choice of angular quadrature. We also explain there how to deal with scattering polarization (to model also Q and U components of the intensity vector). Section 3 compares our computations with some well-known 1D cases. Section 4 shows a simple astrophysical example where this approach can be used. In Sect. 5, we further discuss on advantages and drawbacks of the method and comment on possible improvements and the future work.
2. Method
2.1. Scalar radiative transfer in cylindrical geometry
Since the inclusion of scattering polarization in radiative transfer calculations is a
relatively straightforward generalization of an unpolarized problem (in the case where
lower level of the line has no atomic polarization), we first describe solution in the
case where only the I component of the intensity vector is considered. To
compute the emerging intensity from an object, the equation of radiative transfer needs to
be solved at each point in the grid, in each direction of propagation, and on each
frequency. It is convenient to cast the radiative transfer equation (RTE) in the so-called
along-the-ray form: 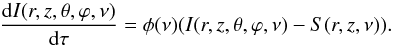 (1)Here,
ν is the frequency of radiation, and
φ(ν) is the line absorption profile.
τ is the line-integrated optical depth along the ray:
(1)Here,
ν is the frequency of radiation, and
φ(ν) is the line absorption profile.
τ is the line-integrated optical depth along the ray:
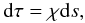 (2)where χ
is the line-integrated absorption coefficient and ds is an elementary
path along the ray. We assume CRD, which makes the source function independent of
frequency. In general, the source function has contributions from local thermal emission
of the medium and also from the scattered (i.e., absorbed and then re-emitted) radiation.
In the case of a two level atom model, the source function is given by
(2)where χ
is the line-integrated absorption coefficient and ds is an elementary
path along the ray. We assume CRD, which makes the source function independent of
frequency. In general, the source function has contributions from local thermal emission
of the medium and also from the scattered (i.e., absorbed and then re-emitted) radiation.
In the case of a two level atom model, the source function is given by 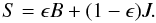 (3)For brevity, we
omitted dependence on spatial coordinates. B is the Planck function, and
J is the line profile-integrated mean intensity. ϵ is
defined as a photon destruction probability, which depends on the inverse radiative and
collisional lifetimes of the upper level of the line. That is
(3)For brevity, we
omitted dependence on spatial coordinates. B is the Planck function, and
J is the line profile-integrated mean intensity. ϵ is
defined as a photon destruction probability, which depends on the inverse radiative and
collisional lifetimes of the upper level of the line. That is
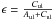 ,
where Aul is the inverse radiative lifetime (also known as
Einstein coefficient of spontaneous emission), and Cul is
inverse collisional lifetime. Smaller ϵ, greater the departures of the
radiation field from the Planck function and the source function is more dominated by the
mean intensity:
,
where Aul is the inverse radiative lifetime (also known as
Einstein coefficient of spontaneous emission), and Cul is
inverse collisional lifetime. Smaller ϵ, greater the departures of the
radiation field from the Planck function and the source function is more dominated by the
mean intensity: 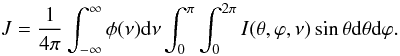 (4)Equations (1) and (3) form an integro-differential equation which can be directly solved only in
some restricted cases. A direct solution in the multidimensional case also showed to be
far from optimal in terms of computing time. Various iterative methods that exist are far
superior in the solution of the problem posed here. The simplest way is to solve in turn
the two equations until convergence. That method is known as “Λ iteration”. It is named
after Schwartzshild’s notation, where mean intensity is formally given by
(4)Equations (1) and (3) form an integro-differential equation which can be directly solved only in
some restricted cases. A direct solution in the multidimensional case also showed to be
far from optimal in terms of computing time. Various iterative methods that exist are far
superior in the solution of the problem posed here. The simplest way is to solve in turn
the two equations until convergence. That method is known as “Λ iteration”. It is named
after Schwartzshild’s notation, where mean intensity is formally given by
![\begin{equation} J=\Lambda[S]. \end{equation}](/articles/aa/full_html/2013/07/aa21212-13/aa21212-13-eq26.png) (5)Equation (5) is now
known as a process of formal solution, where the Λ operator is a way of obtaining the
specific intensity, and subsequently, the mean intensity from a given source function on a
spatial grid.
(5)Equation (5) is now
known as a process of formal solution, where the Λ operator is a way of obtaining the
specific intensity, and subsequently, the mean intensity from a given source function on a
spatial grid.
The most widely used way to improve the convergence rate is the local ALO method, also known as Jacobi iteration (for a seminal paper on the method, see Olson et al. 1986). Faster iterative processes are needed because Λ iteration not only converges extremely slowly, but also relative difference between consecutive iterations changes very slowly. It is therefore hard to establish convergence criteria. For more in-depth discussion, see Mihalas (1978).
An accurate and fast formal solution should be used in the iterative method to efficiently solve the coupled equation of radiative transfer and the equation of statistical equilibrium. For the best compromise of accuracy and speed, the method of choice for performing a formal solution today is the short characteristics method (Olson & Kunasz 1987).
2.1.1. Short characteristics on a cylindrical grid
The short characteristics method is based on the integral form of RTE:
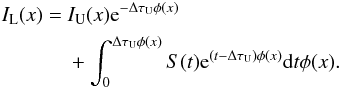 (6)As
it is customary, we use x as the frequency displacement from the line
center, expressed in the units of the line Doppler width. In the equation above, the
line absorption profile φ(x) is shown as independent
of the spatial coordinates for notational simplicity. The subscript L stands for the
grid point under the consideration (local point), while the subscript U stands for the
upwind point, which is the specifically chosen point lying in the upwind direction on
the line of the propagation of the radiation (so-called “ray”). In numerical
computations of this kind, one chooses a finite number of rays to describe the angular
variation of the specific intensity. The upwind point is at the location where the
upwind portion of the ray intersects the boundary of the grid cell.
ΔτU is the line-integrated optical path between the upwind
and the local point. We assume a quadratic dependence upon the source function on
optical depth and, in that case the integral equation above can be analytically solved
to obtain
(6)As
it is customary, we use x as the frequency displacement from the line
center, expressed in the units of the line Doppler width. In the equation above, the
line absorption profile φ(x) is shown as independent
of the spatial coordinates for notational simplicity. The subscript L stands for the
grid point under the consideration (local point), while the subscript U stands for the
upwind point, which is the specifically chosen point lying in the upwind direction on
the line of the propagation of the radiation (so-called “ray”). In numerical
computations of this kind, one chooses a finite number of rays to describe the angular
variation of the specific intensity. The upwind point is at the location where the
upwind portion of the ray intersects the boundary of the grid cell.
ΔτU is the line-integrated optical path between the upwind
and the local point. We assume a quadratic dependence upon the source function on
optical depth and, in that case the integral equation above can be analytically solved
to obtain 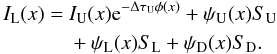 (7)Here,
subscript D stands for the downwind point, which is the point of intersection of the
downwind portion of the ray with the neighbor cell boundary. Coefficients
ψ depend on the optical path differences between the upwind and the
local point and the local and the downwind point, thus depending implicitly on the
angles that determine the orientation of the ray. To obtain values of the source
function, opacity and the specific intensity in U and D points, since they are not, in
general, located on given spatial grid, one needs to perform spatial interpolation.
Here, we use the method suggested by Auer &
Paletou (1994). It is a simple quadratic interpolation where an additional
check is performed to test whether an interpolated value induces new maximum or minimum
on the interval. If that is the case, the extremum is artificially suppressed. More
accurate interpolating strategies, both for interpolation of needed quantities at upwind
and downwind points and for the behavior of the source function on the interval in
question has been recently explained in detail by Ibgui
et al. (2013) and by de la Cruz Rodríguez
& Piskunov (2013). These approaches are based on Hermite and Bezier
interpolations which allow for third-order accuracy and guarantee either smoothness
(Hermite) or monotonicity (Bezier). We plan to implement one of these kinds of spatial
interpolation in future versions of our code.
(7)Here,
subscript D stands for the downwind point, which is the point of intersection of the
downwind portion of the ray with the neighbor cell boundary. Coefficients
ψ depend on the optical path differences between the upwind and the
local point and the local and the downwind point, thus depending implicitly on the
angles that determine the orientation of the ray. To obtain values of the source
function, opacity and the specific intensity in U and D points, since they are not, in
general, located on given spatial grid, one needs to perform spatial interpolation.
Here, we use the method suggested by Auer &
Paletou (1994). It is a simple quadratic interpolation where an additional
check is performed to test whether an interpolated value induces new maximum or minimum
on the interval. If that is the case, the extremum is artificially suppressed. More
accurate interpolating strategies, both for interpolation of needed quantities at upwind
and downwind points and for the behavior of the source function on the interval in
question has been recently explained in detail by Ibgui
et al. (2013) and by de la Cruz Rodríguez
& Piskunov (2013). These approaches are based on Hermite and Bezier
interpolations which allow for third-order accuracy and guarantee either smoothness
(Hermite) or monotonicity (Bezier). We plan to implement one of these kinds of spatial
interpolation in future versions of our code.
With the above strategy, the process of a formal solution proceeds as follows:
-
1.
Given a direction of the ray, one starts from an appropriateboundary of the grid, where the incident radiation is given.
-
2.
Sweeping the grid in the given direction, one first finds upwind and downwind points and interpolates to obtain needed physical quantities in these points.
-
3.
Equation (7) can then be solved for all the frequencies. The specific intensity is easily computed from the interpolated values at the upwind point and used for computation of the upwind intensity in subsequent points.
-
4.
Steps 1−3 are repeated for each given direction, starting from the appropriate boundary.
Applying the short characteristics method to the formal solution on a cylindrical grid is slightly different than in the Cartesian case. It is explained in detail in VHL02, and here, we will try to sum up some main ideas.
First, we recall that in Cartesian geometry (see, e.g. Auer & Paletou 1994), a characteristic can intersect a neighbor cell either along horizontal or vertical border. This leads to two different types of characteristics, requiring interpolation either along the vertical or horizontal coordinate. The upwind point also always “precedes” the local point, if we observe along the direction of propagation of the ray, while the downwind point always “follows” the local point. It is natural and intuitive, because we are projecting three-dimensional space on 2D plane.
In cylindrical coordinates, the characteristics are, strictly speaking, curved (see VHL02 for a nice illustration and in-depth discussion). Of course, it is always possible to treat them as straight lines, by simply integrating along the line connecting upwind and local point. This introduces some inaccuracies, which depend on the resolution of the spatial grid. A third kind of characteristic also appears. We give an illustration of possible types of characteristics one encounters (Fig. 1). In this case types 1 and 2 are “ingoing” rays, where the radial coordinate of the upwind point is greater than that of the local point. They are similar to those found in Cartesian case. A ray can intersect the cell at a boundary with either r = const. or with z = const. Depending on the outcome, spatial interpolation is performed along either the r or the z coordinate. The same two types are encountered in the case of “outgoing” rays, however, type 3 can also appear, because of the curvature of the grid. In this case, the upwind point lies on the same r circle as the local point. Spatial interpolation is done along z, while angular interpolation in intensity is not needed (see below for the details on angular interpolation). It is very important to notice that the azimuth of the upwind intensity lies in a different quadrant than the azimuth of the local intensity for a type 3 ray. Type 3 appears only in the outgoing intensity. It is easily seen that ϕU = π − ϕ for this type of characteristic. Since the whole grid is swept quadrant-at the time, this introduces an awkward problem in dynamic intensity deallocation. This kind of memory manipulation is very important and straightforward on Cartesian grids since the intensity can be deallocated as soon as it is not needed for interpolation. This way, much larger grids can be handled than if one keeps values of the intensity in memory.
2.1.2. Angular interpolation and angular quadrature
As explained in detail in VHL02 and given in Fig. 2, the angle, which describes the azimuth of the very same ray, is different in the local and the upwind point. We denote the azimuth of the ray in the upwind point with ϕU. In general, that value is not in the prescribed angular grid, and the value of I(θ,ϕU) has to be found by interpolation in azimuth. A straightforward way of performing this interpolation is to simply interpolate linearly between two closest points. However, higher order accuracy is recommended − for example, second order interpolation with suppression of maxima and minima as in Auer & Paletou (1994). In our experience, the choice can significantly alter the final solution of the problem (i.e., the converged values of the source function on a grid). For relatively simple problems, such as the homogeneous cylinders that are described in Sect. 3, differences are smaller than 1% and considered acceptable. In situations where the radiation field is highly anisotropic and inhomogeneous, differences can be much larger. We note and consider this as a very serious drawback of this approach to multidimensional radiative transfer in an axially symmetric media.
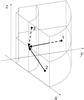 |
Fig. 1 Different types of rays in the cylindrical geometry. Types 1 and 2 are similar to Cartesian geometry and they intersect either a horizontal or vertical cell border. Type 3 is unique to the cylindrical geometry, as the upwind point has the same r coordinate as the local point. |
There exists more sophisticated interpolation strategies, such as the one suggested by Gouttebroze (2005) in which the interpolation is done by a Fourier expansion of the radiation field in azimuth. This allows us to consider explicitly the periodic nature of I(ϕ). Note that it has been used to perform spatial interpolation in azimuth in the original paper. We have implemented this method in our code but this time for angular interpolation of the upwind intensity. For simple test problems (as those given in Sect. 3) we find good agreement with the method of Auer & Paletou (1994), but we have found that Fourier interpolation is more time consuming than other schemes.
Finally, we have adopted the Bezier interpolation technique, which was originally introduced in the astrophysical context by Auer (2003) and used recently for purposes of spatial interpolation in radiative transfer computations (for example, de la Cruz Rodríguez & Piskunov 2013). This kind of interpolation guarantees second or third order accuracy where possible, while automatically preserving monotonicity of the function. This thus avoids creation of artificial maxima and minima. To perform interpolation which is used to find f(x), one needs the values of the function in four points, so that x1 < x2 < x3 < x4 and x2 < x < x3. Thanks to the symmetry properties of the radiation field one can always “shift” appropriate x values for 2π, regardless of the location of x in the angular grid, so that the above conditions are satisfied and the interpolation is possible. Since angular interpolation of the specific intensity on cylindrical grids is inevitable, the Bezier interpolation scheme seems to introduce as little numerical artifacts as possible. We note that we are using it only for angular interpolation at the moment.
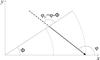 |
Fig. 2 Difference between the azimuthal angles of the ray in the local and in the upwind point. This difference makes angular interpolation necessary. |
The choice of the angular quadrature is another important point of the multidimensional numerical radiative transfer. As described above, the equation of radiative transfer is solved for a prescribed number of rays with given values of θ and ϕ, and obtained intensity is then numerically integrated over angles and frequencies to obtain the required moments of the radiation field (e.g. mean intensity, J). While integration over frequencies in the case of CRD, for which frequencies close to the line center are considered, is straightforward and the trapezoid quadrature is sufficient, the choice of angular quadrature can significantly affect accuracy and convergence properties of the code.
The most straightforward choice is to use an equidistant grid in both angles and a trapezoid quadrature to compute integration weights. However, a relatively large number of angles is needed to obtain sufficient accuracy. As both computation time and memory requirements scale linearly with the number of angles, it is desired to choose a different quadrature which preserves the accuracy while reducing the number of angles. One way to do it is to keep an equidistant grid in ϕ and adopt a Gaussian grid in cosθ (i.e., μ from plane-parallel, 1D geometry). However, this only slightly reduces the number of angles needed in θ mesh, so a better strategy is needed. The most used quadrature at the moment is probably the so-called Carlson’s set B (Carlson 1963).
This quadrature set mimics a Gaussian quadrature (which is very favorable in 1D geometry) in both angles while also being invariant to a 90° rotation along axis. This set is used in several recent works (e.g. Anusha & Nagendra 2011a; Ibgui et al. 2013). In this work, Carlson’s sets with n = 8 and n = 10 were tested. In simple test cases no significant differences in accuracy were noticed. Results given below are computed with the set with n = 10. In general, it would be of great benefit to be able to compute Carlson’s set B for an arbitrary number of angles because it significantly increases accuracy. However, the systems of equations for computation of the values of angles and weights become indeterminate for n > 10, and it is not possible to use the strategy described in the original paper to find them.
Testing these various quadratures, differences on the order of 0.5% have been found in the simple cases. In more realistic problems, differences are expected to be much larger. Obviously, both the interpolation strategy and angular quadrature are crucial for the accuracy of the method and the choice should be carefully made to find the most appropriate ones. It is also advantageous to use different quadratures for different problems and to increase the mesh resolution in the cases where radiation field is significantly anisotropic.
2.1.3. Boundary conditions
Most works on cylindrical geometry dealt with either non-illuminated finite objects (Stenholm 1977, VHL02) or some sort of simple illumination from below and/or from the sides. Since the principal goal of this paper is to show methods that deal with scattering polarization, which is sensitive to the anisotropy of the radiation field, it is of great importance to account for illumination of the object by external sources in a proper way. Take, for example, the modeling of solar prominences: not only the mean intensity of the illuminating radiation is needed, but also its angular dependence because of limb darkening needs to be properly treated. In such case, there is also an abrupt discontinuity in the function Iinc(θ), where Iinc is the specific intensity of the incident radiation. A similar situation appears if we consider the example of a circumstellar disk illuminated by the host star.
For such cases, an accurate strategy was given by Gouttebroze (2005). If the anisotropy of the illuminating radiation is known in great detail (e.g., from limb darkening tables), we create a very fine angular grid (100 times more dense than the angular grid used for the rest of computations), spanning in the angular region of the ray in question for each of the incoming rays. We can then average the incoming radiation over the given range. In principle, this can create errors in the emergent intensity but not in the source function, as the source function depends only on the moments of the radiation field, which are more accurately computed by this approach. After the converged solution has been found, one additional formal solution without the averaging incident radiation needs to be performed to find correct emergent intensity.
Another important aspect is the “inner” boundary condition at
r = rmin. If
rmin = 0, one needs to first integrate in the ingoing
direction and then use the symmetry properties of the cylinder to find the inner
boundary conditions. It turns out that:
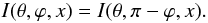 (8)We note here, in
advance, that this type of boundary condition is also valid for the reduced intensity
components used in computing the polarized radiation field, because they do not
(contrary to some of the Stokes components) change sign with rotation. We also noticed
that it is of great importance to compute the lambda operator (i.e., ψ
coefficients) with second order short characteristics in this case, even though it is
customary to use first order short characteristics on the grid boundaries. Contrary to
the “outer” boundaries, setting up a second order characteristic is possible here,
because of the same symmetry properties used above (i.e., even though the local point is
on the edge of the grid the “downwind” point still does exist).
(8)We note here, in
advance, that this type of boundary condition is also valid for the reduced intensity
components used in computing the polarized radiation field, because they do not
(contrary to some of the Stokes components) change sign with rotation. We also noticed
that it is of great importance to compute the lambda operator (i.e., ψ
coefficients) with second order short characteristics in this case, even though it is
customary to use first order short characteristics on the grid boundaries. Contrary to
the “outer” boundaries, setting up a second order characteristic is possible here,
because of the same symmetry properties used above (i.e., even though the local point is
on the edge of the grid the “downwind” point still does exist).
On the other hand, inner boundary conditions need to be specified if rmin ≠ 0. An example of this case is the modeling of a disk or ring, which illuminated by the host star. In such case, “ingoing” rays, emerging from the inner boundary, are treated as being absorbed by the illuminating object. The incident radiation on the inner boundary can be computed in a similar way as explained above for the other boundaries.
An additional complication arises when the object is illuminated by radiation from the
point source. For example, this situation would arise if a laboratory gas is illuminated
by a radiation coming from a laser or if an exoplanet is illuminated by a distant star.
It is very impractical and cumbersome to pick the appropriate angular quadrature to deal
with such cases with the approach described above. A much more convenient method is
proposed by Chandrasekhar (1950). It is necessary
to split the radiation field in two components: i) the incident radiation, which
penetrates into the object and is responsible for one part of the mean intensity, and
therefore, source function; and ii) the diffuse radiation, which originates in the
scattering processes (or thermal emission of the gas). The radiation field is as
follows: 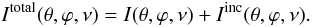 (9)Here I
is the diffuse part of the intensity. Since the incident intensity comes from one
direction, we treat the incident radiation as a delta function in θ and
ϕ. Now, the RTE can be split in two equations, where one is for each
part of the total intensity. The diffuse radiation obeys a RTE with no incident
radiation (Eq. (1)) and source function
has the form given by Eq. (3). The RTE
for the incident part is much simpler, because there is no source function for the
incident radiation, which only gets attenuated because of the absorption in the medium.
We also split the mean intensity at each point into a diffuse and an incident part. The
incident part is:
(9)Here I
is the diffuse part of the intensity. Since the incident intensity comes from one
direction, we treat the incident radiation as a delta function in θ and
ϕ. Now, the RTE can be split in two equations, where one is for each
part of the total intensity. The diffuse radiation obeys a RTE with no incident
radiation (Eq. (1)) and source function
has the form given by Eq. (3). The RTE
for the incident part is much simpler, because there is no source function for the
incident radiation, which only gets attenuated because of the absorption in the medium.
We also split the mean intensity at each point into a diffuse and an incident part. The
incident part is: 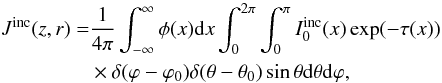 (10)where
θ0 and ϕ0 determine the
direction of the incident radiation. Taking advantage of the properties of the delta
function,
(10)where
θ0 and ϕ0 determine the
direction of the incident radiation. Taking advantage of the properties of the delta
function, 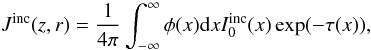 (11)where
τ(x) is the monochromatic optical path that the
incident radiation traveled through the object. This mean intensity is added to the mean
intensity of the diffuse radiation field to properly compute the source function for the
diffuse part of the radiation field. Since the incident radiation has the form of a
delta function, it contributes directly to emerging radiation in some cases only. If we
are, for example, interested in the contribution of the scattering processes to the
transmission spectrum, diffuse intensity is to be added to the properly attenuated
incident intensity. This situation would arise if one wants to accurately compute the
transmission spectrum of an exoplanet with a scattering-dominated atmosphere.
(11)where
τ(x) is the monochromatic optical path that the
incident radiation traveled through the object. This mean intensity is added to the mean
intensity of the diffuse radiation field to properly compute the source function for the
diffuse part of the radiation field. Since the incident radiation has the form of a
delta function, it contributes directly to emerging radiation in some cases only. If we
are, for example, interested in the contribution of the scattering processes to the
transmission spectrum, diffuse intensity is to be added to the properly attenuated
incident intensity. This situation would arise if one wants to accurately compute the
transmission spectrum of an exoplanet with a scattering-dominated atmosphere.
2.1.4. Acceleration of convergence
A simple Λ iteration method is too slow and unreliable to self-consistently solve the coupled equations of radiative transfer and statistical equilibrium. There are numerous ways to improve the rate of convergence. Apart from methods that use physical considerations to achieve that goal, such as ALO (Olson et al. 1986), Gauss-Seidel (Trujillo Bueno & Fabiani Bendicho 1995), or FBILI (Atanackovic-Vukmanovic et al. 1997), there are also numerical accelerating techniques that improve the rate of convergence, such as Ng acceleration (Ng 1974) or CG-BiSTAB (for an astrophysical application, see Anusha et al. 2011). For computations given here, we use the standard ALO technique (also known as Jacobi iteration). Here, we briefly recap the method.
Both RTE and SE equations for a two-level atom written together in operator form are
given by ![\begin{equation} S = \epsilon B + (1-\epsilon) \Lambda[S]. \label{Lambda} \end{equation}](/articles/aa/full_html/2013/07/aa21212-13/aa21212-13-eq62.png) (12)Here, Λ is to be
understood as a process of computing the mean intensity from some assumed value of the
source function. An ordinary Λ iteration solves the above equation over and over again.
In principle, Eq. (12) could be solved
directly if one can compute the Λ operator explicitly (note that this is never done in
practice, as formal solution proceeds as given in previous sections). This is not
practical for two reasons: i) the computation of the full Λ operator is cumbersome and
time consuming; and ii) the inversion of the full Λ matrix leads to the inversion of
huge matrices. An optimal “middle ground” between the Λ iteration and direct solution is
to use some sort of approximate operator that is easy to invert and to iteratively
correct the solution:
(12)Here, Λ is to be
understood as a process of computing the mean intensity from some assumed value of the
source function. An ordinary Λ iteration solves the above equation over and over again.
In principle, Eq. (12) could be solved
directly if one can compute the Λ operator explicitly (note that this is never done in
practice, as formal solution proceeds as given in previous sections). This is not
practical for two reasons: i) the computation of the full Λ operator is cumbersome and
time consuming; and ii) the inversion of the full Λ matrix leads to the inversion of
huge matrices. An optimal “middle ground” between the Λ iteration and direct solution is
to use some sort of approximate operator that is easy to invert and to iteratively
correct the solution: ![\begin{equation} S = \epsilon B + (1-\epsilon) \Lambda^{*}[S] + (\Lambda-\Lambda^{*})[S]. \end{equation}](/articles/aa/full_html/2013/07/aa21212-13/aa21212-13-eq63.png) (13)If one uses a local
operator as suggested by Olson et al. (1986),
Λ∗ reduces to a simple multiplication and its inversion to a division, so
the correction to the old value of the source function becomes
(13)If one uses a local
operator as suggested by Olson et al. (1986),
Λ∗ reduces to a simple multiplication and its inversion to a division, so
the correction to the old value of the source function becomes
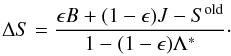 (14)This equation is solved
iteratively until ΔS/S is smaller
than some predefined value δ. Here, we use the value of
δ = 10-5. A detailed review of ALO (also known as ALI)
technique is given in Hubeny (2003). This method
increases the rate of convergence as compared to the Λ iteration by several orders of
magnitude which is absolutely necessary in practical computations. Λ∗ is
equal to the frequency and the angle-integrated ψL
coefficient, which is properly modified for a negative contribution of the downwind
point, as described in detail by Asensio Ramos &
Trujillo Bueno (2006). We note that (even though VHL02 claim that modification
is not needed) we found it absolutely necessary for high-density angular grids. In these
cases upwind and downwind optical path lengths can differ from each other significantly.
The use of strictly monotonous interpolation techniques (e.g. Bezier interpolation)
would eliminate the need for such modification of the local operator. Note that there
are also non-local multidimensional approximate operators, such as the one proposed by
Hauschildt & Baron (2006).
(14)This equation is solved
iteratively until ΔS/S is smaller
than some predefined value δ. Here, we use the value of
δ = 10-5. A detailed review of ALO (also known as ALI)
technique is given in Hubeny (2003). This method
increases the rate of convergence as compared to the Λ iteration by several orders of
magnitude which is absolutely necessary in practical computations. Λ∗ is
equal to the frequency and the angle-integrated ψL
coefficient, which is properly modified for a negative contribution of the downwind
point, as described in detail by Asensio Ramos &
Trujillo Bueno (2006). We note that (even though VHL02 claim that modification
is not needed) we found it absolutely necessary for high-density angular grids. In these
cases upwind and downwind optical path lengths can differ from each other significantly.
The use of strictly monotonous interpolation techniques (e.g. Bezier interpolation)
would eliminate the need for such modification of the local operator. Note that there
are also non-local multidimensional approximate operators, such as the one proposed by
Hauschildt & Baron (2006).
A greater increase in the convergence rate can be achieved by some of the numerical techniques mentioned above. Here, we apply Ng acceleration, which uses several (typically 3−5) previous values of the source function to compute the new value of the source function via residual minimization. A very clear and straightforward way of implementing Ng acceleration is given by Olson et al. (1986). For problems given in Sect. 3, we usually achieve a faster convergence of 2.5−3 times with Ng acceleration.
2.2. Inclusion of scattering polarization
2.2.1. Polarized radiative transfer formalism
If we consider only scattering polarization in the situation where the radiation field
is not axially symmetric, the intensity becomes a three-component vector:
Î = (I,Q,U) where
(I,Q,U) are Stokes components defined by Chandrasekhar (1950) (also see the monograph by Landi Degl’Innocenti & Landolfi 2004). In the case where
polarization of the lower level of the transition is negligible, all the components
share the same optical depth scale and the source function is also three-component
vector that is now also angle dependent. The equation of radiative transfer becomes
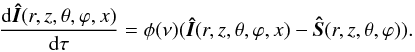 (15)The statistical
equilibrium equation has the following form (omitting dependence on coordinates):
(15)The statistical
equilibrium equation has the following form (omitting dependence on coordinates):
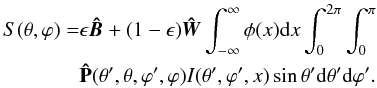 (16)Here
(16)Here
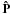 is the angular redistribution matrix, describing anisotropic scattering. Primed
quantities refer to incident radiation, while unprimed quantities refer to scattered
radiation.
is the angular redistribution matrix, describing anisotropic scattering. Primed
quantities refer to incident radiation, while unprimed quantities refer to scattered
radiation. 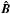 is
again the Planck function equal to (B,0,0). The vector
Ŵ describes the intrinsic line polarizability and
depends on J quantum numbers of upper and lower level of the
transition. For computations here, we have used Ŵ = 1.
This formalism, known as a scattering matrix formalism, keeps the same form of the
problem as in the unpolarized case. An alternative to this is a density matrix formalism
used by Landi Degl’Innocenti & Landolfi
(2004). The scattering matrix formalism enables one to account for PRD effects
but restricts its applicability to two level atoms. There is no satisfactory framework
to account for PRD effects on scattering polarization in multilevel atoms at the moment.
For the two level atom problem with CRD, both approaches are equivalent.
is
again the Planck function equal to (B,0,0). The vector
Ŵ describes the intrinsic line polarizability and
depends on J quantum numbers of upper and lower level of the
transition. For computations here, we have used Ŵ = 1.
This formalism, known as a scattering matrix formalism, keeps the same form of the
problem as in the unpolarized case. An alternative to this is a density matrix formalism
used by Landi Degl’Innocenti & Landolfi
(2004). The scattering matrix formalism enables one to account for PRD effects
but restricts its applicability to two level atoms. There is no satisfactory framework
to account for PRD effects on scattering polarization in multilevel atoms at the moment.
For the two level atom problem with CRD, both approaches are equivalent.
One can easily see that the angular dependence of the source function greatly increases the memory requirements in practical computations, because one always needs to keep values of the source function in the memory, which is contrary to the values of the intensity that can be dynamically deallocated. This problem would render models with large grids and/or dense angular meshes hard to handle. However, it has been known that the polarized source function can be decomposed in scalar (i.e., angle-independent) quantities (e.g., Rees 1978). This technique is also applicable in multidimensional radiative transfer, as given in detail by Anusha & Nagendra (2011a). Here, we summarize their main results to show the application in our computations.
2.2.2. Polarized RTE in reduced basis
It has been shown that both polarized intensity and a polarized source function can be
decomposed via irreducible spherical tensors, which change the basis of the problem to a
six-component angle and a frequency-dependent intensity,
Îr = (Ii);
where i = 0...5 and an angle and a frequency (in case of CRD) −
independent source function,
Ŝr = (Si);
where i = 0..5. The reduced intensity vector still satisfies a RTE with
the same opacity scale: 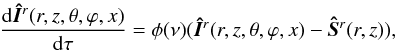 (17)and the reduced
source function vector is given by
(17)and the reduced
source function vector is given by
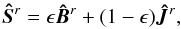 (18)where the reduced mean
intensity vector Ĵr is
(18)where the reduced mean
intensity vector Ĵr is
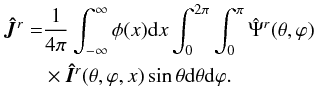 (19)Here,
(19)Here,
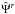 is a 6 × 6 angle-dependent matrix that describes coupling between different components
of the reduced intensity vector and reduced source function vector. Its form is given in
the Appendix D of Anusha & Nagendra
(2011b).
is a 6 × 6 angle-dependent matrix that describes coupling between different components
of the reduced intensity vector and reduced source function vector. Its form is given in
the Appendix D of Anusha & Nagendra
(2011b). 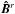 is the Planck function in the reduced basis:
is the Planck function in the reduced basis: 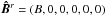 .
To compute the emergent radiation from an object, it is now necessary to
self-consistently solve the coupled Eqs. (17) to (19). We use the
following strategy: with the first guess for the values of the reduced intensity vector
and reduced source function taken from the solution of the non-polarized case, we solve
Eqs. (17)−(19) in turn, until convergence. This is a Λ
iteration for the polarized radiation. Since the polarization of the light should not
change values of the Stokes I significantly, corrections are relatively
small, and the method converges quickly. The whole procedure of obtaining a
self-consistent solution for the Stokes vector proceeds as follows:
.
To compute the emergent radiation from an object, it is now necessary to
self-consistently solve the coupled Eqs. (17) to (19). We use the
following strategy: with the first guess for the values of the reduced intensity vector
and reduced source function taken from the solution of the non-polarized case, we solve
Eqs. (17)−(19) in turn, until convergence. This is a Λ
iteration for the polarized radiation. Since the polarization of the light should not
change values of the Stokes I significantly, corrections are relatively
small, and the method converges quickly. The whole procedure of obtaining a
self-consistent solution for the Stokes vector proceeds as follows:
-
1.
A self-consistent solution of the unpolarized problem isobtained via Jacobi iteration with Ng acceleration.
-
2.
Initial values of the reduced intensity vector are set to (I0,I1,I2,I3,I4,I5) = (Iscalar,0,0,0,0,0).
-
3.
SE and RTE equations are then solved, in turn, until the convergence criterion is achieved. We use δ = |ΔS0/S0| < 10-5.
-
4.
The Stokes components are then computed from the reduced intensity vector via Eqs. (36)−(38) in Anusha & Nagendra (2011a).
2.2.3. Boundary conditions
As we are also interested in dealing with externally illuminated objects, it is
necessary to set-up proper boundary conditions for the polarized part of the
computation. In principle, one can describe incident polarized radiation with
appropriate values of Stokes parameters. However, there is no unique transformation from
the Stokes basis to the reduced intensity basis, so one would, in principle, have to
describe the incident radiation in reduced intensity basis. However, reduced intensity
components are not measurable quantities, except for the
component I0, which can be considered equal to Stokes
I. At the moment, we are only able to deal with the illumination by
an unpolarized radiation. For the examples given here, it is a good approximation for
two reasons: i) the illuminating radiation is indeed unpolarized or very weakly
polarized, and the polarization in the object arises because of the scattering of the
anisotropic incident radiation; or: ii) the optical thickness of the object is large
enough that initial polarization of the illuminating light is destroyed in multiple
scatterings and the resulting polarization is “re-created”. In the case where the object
is illuminated by a single “ray” of radiation, a similar equation to Eq. 11 can be written for the components of the
source function in the reduced basis:
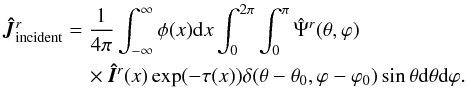 (20)Here
the angular dependence of incident radiation also has the form of a delta function. The
parameter
Îr(x) = (I(x),0,0,0,0,0),
where I(x) is the first component of incident Stokes
vector, while the other two components are assumed to be zero.
(20)Here
the angular dependence of incident radiation also has the form of a delta function. The
parameter
Îr(x) = (I(x),0,0,0,0,0),
where I(x) is the first component of incident Stokes
vector, while the other two components are assumed to be zero.
 can then be analytically found and computed at each point of the grid, as in the
unpolarized case. We now test the method on several well-known problems.
can then be analytically found and computed at each point of the grid, as in the
unpolarized case. We now test the method on several well-known problems.
3. Comparison with one-dimensional solutions
The method described above has been implemented in a C++ code. Grid points are considered as objects, which makes operations, such as calculating the formal solution and interpolation more intuitive and modular. All computations given in this section are performed with Carlson’s set B using n = 10 for angular quadrature and using 17 equidistant points for frequency integration, which spans from zero to four Doppler widths. For these computations, we have used a logarithmic spatial grid with 10 points per decade with finer spacing toward the edges of the object. Opacity is set to unity, so the geometrical grid is identical to optical depth grid. Cylinders are self-emitting with no illuminating source from the inside. For the scalar (unpolarized) case and for grid made of 132 × 263 points, one iteration (with computation of a lambda operator), compiled on a free g++ compiler, takes about 25 s on the Intel i7-2600 3.4 GHz CPU. For the polarized case, an iteration takes approximately six times longer.
To test the radiative transfer code, we first attempt to reproduce the known results in 1D
plane-parallel geometry. In the case where the total optical thickness of the cylinder along
both the z and r are much larger than the thermalization
length (1/ϵ), the source function saturates to the value
of the Planck function, and in regions far from the lateral boundaries, it should behave as
in simpler case of a 1D geometry. Here, we consider homogeneous cylinders with a total
optical thickness along both z and r equal
to 1011. The Planck function is set to unity, and the scalar radiative transfer
problem is solved for ϵ = 10-4, 10-6, and
10-8. In all of these cases, the cylinder is significantly larger than the
thermalization length. The behavior of the source function along z for
r = Rmin is the same as in a semi-infinite
atmosphere. That is, it saturates at approximately the same optical depth as the
thermalization length and reaches the value of 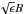 at the
surface. Since radial optical thickness is also very large, we do not see effects of
curvature of the cylinder, since the region where the source function is non-thermalized is
much smaller than the region where S = B. Thus, the
behavior of the source function along r for z equal to
zmax/2 should also mimic a 1D case.
Figure 3 shows that this is true for all used values
of ϵ. In the three cases, convergence was achieved after 82, 121, and 224
iterations, respectively, using Ng acceleration. Now, we turn to the computations for the
polarized case.
at the
surface. Since radial optical thickness is also very large, we do not see effects of
curvature of the cylinder, since the region where the source function is non-thermalized is
much smaller than the region where S = B. Thus, the
behavior of the source function along r for z equal to
zmax/2 should also mimic a 1D case.
Figure 3 shows that this is true for all used values
of ϵ. In the three cases, convergence was achieved after 82, 121, and 224
iterations, respectively, using Ng acceleration. Now, we turn to the computations for the
polarized case.
 |
Fig. 3 Behavior of scalar source function with optical depth, mimicking 1D plane-parallel atmosphere. Upper panel: S(z) for r = 0. Lower panel: S(r) for z = zmax/2. |
Results of academic problems for polarized radiative transfer are not so well-known, and moreover, there are no analytical solutions to compare with numerical computations. Scattering polarization in semi-infinite atmospheres has been extensively studied by Faurobert (1988). She considered polarized line transfer in scattering-dominated atmospheres for various frequency redistributions. Here, we compare our results with hers. If one considers point with coordinates (zmax,0), one would expect emergent scattering polarization to behave as in an 1D atmosphere again. Stokes components are defined as in Chandrasekhar (1950), where intensity is decomposed in components Ir and Il. The component Ir corresponds to the component of the electric field that oscillates parallel to the plane θ = π/2, and Il is perpendicular to it.
Outgoing Q/I profiles should have the same behavior as in Faurobert (1988), while U/I profiles should be zero, since the point is far from lateral boundaries and no azimuthal asymmetry is expected. We show in Fig. 4 that this is, indeed, the case. Q/I shows the same qualitative properties as given in Faurobert’s paper (differences are because of the different angular quadrature), while U/I is negligibly small compared to the Q/I and can really be considered zero. Of course, different behavior close to the boundaries is to be expected, because azimuthal anisotropy in radiation field will appear. To our knowledge, there are no suitable test cases or comparisons for polarized line transfer in cylindrical objects. In Fig. 5 we show the variation of Q/I and U/I profiles with the azimuth for θ = 84° on the edge point of the cylinder, (zmax,rmax) for the case ϵ = 10-4, to illustrate the effects of the anisotropy. We note that the polarization magnitudes, both in Q/I and U/I are significantly higher than in the 1D case. The explanation for this is that both horizontal and vertical inhomogeneities in the source function are high near the edges of the object because of the radiative losses through multiple boundaries. Obviously, axial symmetry is broken near the edge of the cylinder, hence, we also see high values of the Stokes parameter U. It can also be noticed that values of Q/I are not strictly monotonic with respect to azimuth. We cannot relate the interpretation to the 1D case, because in this case, object is three-dimensional. It is, however, important to understand that different azimuths probe vertical inhomogeneities in different ways, which result in different Q/I profiles for different azimuths. Note that Q/I is negative, which corresponds to an absorption line formed in the semi-infinite atmosphere.
These results can be used as benchmark to some degree. It would be valuable to compare them with different approaches, such as those computed with 3D Cartesian geometry, since the method described here aims to provide a simpler substitute for 3D Cartesian models in the cases where axial symmetry is assumed.
 |
Fig. 4 Q/I and U/I profiles emerging from the point with coordinates (zmax,0) for θ = 84°. Since this point is far from lateral boundaries, scattering polarization profiles correspond to those formed in the 1D atmosphere. We note that U/I is on the order of 10-8%, which is negligible compared to Q/I, as expected. |
 |
Fig. 5 Q/I and U/I profiles emerging from the edge of the cylinder, or from the point with coordinates (zmax,rmax), for θ ≈ 84° and various azimuths. |
4. Astrophysical example: line scattering on a circumstellar disk
An obvious example of a disk-like structure is an accretion or circumstellar disk illuminated by a host star. The disk scatters the incident radiation and/or emits by itself. It is of great interest and diagnostic value to properly account for radiative transfer effects in these structures (for example, see Papkalla 1995; Elitzur et al. 2012). A recent study on continuum polarization originating from circumstellar disks has been performed by Halonen et al. (2013). Circumstellar disks are gaseous disks, which are situated, for example, around Be stars. Spherical stars do not emit detectable scattering polarization as the polarization cancels on the opposite limbs. However, some polarization signature can be expected if there is a disk to break the spherical symmetry of the system.
Here, we consider a simple case to illustrate application of our cylindrical code. The disk
is situated in the equatorial plane of the star with
Rmax = 10R∗ and
Rmin = R∗. Following the density
distribution from Halonen et al. (2013), it is
assumed to have the following opacity distribution:
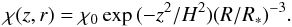 (21)The constants
χ0 and H are chosen so that the radial
line-integrated optical thickness of the disk is 100 and the disk is confined to equatorial
plane. That is, regions far from the plane z = 0 are essentially
transparent. It is assumed that the disk only scatters radiation (ϵ = 0).
The disk is illuminated from the inside, by the limb-darkened radiation of the host star.
The boundary conditions are
(21)The constants
χ0 and H are chosen so that the radial
line-integrated optical thickness of the disk is 100 and the disk is confined to equatorial
plane. That is, regions far from the plane z = 0 are essentially
transparent. It is assumed that the disk only scatters radiation (ϵ = 0).
The disk is illuminated from the inside, by the limb-darkened radiation of the host star.
The boundary conditions are 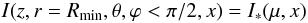 (22)and
(22)and
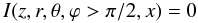 (23)elsewhere. Here
I∗ denotes the illuminating stellar radiation. Note that
μ stands for the cosine of the polar angle of the stellar radiation in
the coordinate system placed on the stellar surface in this case, while θ
and ϕ are angles in the disk coordinate system. Generally
μ = μ(θ,ϕ). The illuminating radiation
has following angular dependence:
(23)elsewhere. Here
I∗ denotes the illuminating stellar radiation. Note that
μ stands for the cosine of the polar angle of the stellar radiation in
the coordinate system placed on the stellar surface in this case, while θ
and ϕ are angles in the disk coordinate system. Generally
μ = μ(θ,ϕ). The illuminating radiation
has following angular dependence: 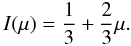 (24)This is a very simple model
of linear limb darkening, where we introduce stellar continuum radiation as an illuminating
source. The boundary conditions are found by the averaging process introduced by Gouttebroze (2005) and briefly recapped in Sect. 2.1.3.
We again use 17 frequency points and Carlsons’s set B with n = 10. We are
interested in Q/I and
U/I line profiles as measurable
quantities, where Q and U are assumed to be emerging from
a disk only, while I is the combination of directly received and scattered
stellar radiation. One has to integrate over the visible surface of the disk to find total
Q and U emitted from the disk. If the x
axis is pointing toward the observer, the expressions for the total Stokes vector emitted by
the disk are
(24)This is a very simple model
of linear limb darkening, where we introduce stellar continuum radiation as an illuminating
source. The boundary conditions are found by the averaging process introduced by Gouttebroze (2005) and briefly recapped in Sect. 2.1.3.
We again use 17 frequency points and Carlsons’s set B with n = 10. We are
interested in Q/I and
U/I line profiles as measurable
quantities, where Q and U are assumed to be emerging from
a disk only, while I is the combination of directly received and scattered
stellar radiation. One has to integrate over the visible surface of the disk to find total
Q and U emitted from the disk. If the x
axis is pointing toward the observer, the expressions for the total Stokes vector emitted by
the disk are 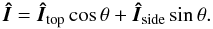 (25)We note that angle
θ has the same meaning as the inclination angle used in the binary stars
community (e.g., for an observer in the plane of the disk,
θ = i = π/2). Here,
“top” and “side” subscripts stand for the contribution of the “top” of the disk (plane with
z = zmax) and the “side of the cylinder”
(surface with r = rmax). The corresponding
equations are:
(25)We note that angle
θ has the same meaning as the inclination angle used in the binary stars
community (e.g., for an observer in the plane of the disk,
θ = i = π/2). Here,
“top” and “side” subscripts stand for the contribution of the “top” of the disk (plane with
z = zmax) and the “side of the cylinder”
(surface with r = rmax). The corresponding
equations are: 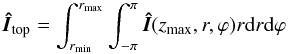 (26)and
(26)and
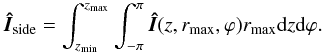 (27)Here, we have
omitted the dependence on θ and x for brevity. Care should
also be taken here to see which components of the reduced intensity cancel in the above
angular integration over ϕ. Emerging scattering polarization profiles for
various values of the inclination angle of the disk are given in Fig. 6. Note that the disk introduces significant amount of polarization in the
system. Levels of line-center polarization are expected to be different in reality (most
likely, smaller), because of the intrinsic line polarizability and the pure absorption in
the disk. We see a similar dependence of total polarization (defined as
(27)Here, we have
omitted the dependence on θ and x for brevity. Care should
also be taken here to see which components of the reduced intensity cancel in the above
angular integration over ϕ. Emerging scattering polarization profiles for
various values of the inclination angle of the disk are given in Fig. 6. Note that the disk introduces significant amount of polarization in the
system. Levels of line-center polarization are expected to be different in reality (most
likely, smaller), because of the intrinsic line polarizability and the pure absorption in
the disk. We see a similar dependence of total polarization (defined as
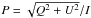 ) on the inclination angle as
found in Halonen et al. (2013), where total linear
polarization reaches the maximum around 75°.
) on the inclination angle as
found in Halonen et al. (2013), where total linear
polarization reaches the maximum around 75°.
A completely clear interpretation of these results is not possible, since this computation is model-dependent. We would like to draw attention to a very deep and thorough analysis done by Poeckert & Marlborough (1978) of the star γ Cas. Perhaps the most interesting and useful result is the dependence of total polarization on inclination (panel 4 of Fig. 6), since it might be difficult to obtain precise, high-resolution polarization spectra of these stars. If a disk was illuminated by a point-like source, total polarization would behave as P ∝ sin2i/(2 + sin2i) which is the monotonically increasing function in interval (0,π). We see, however, that polarization starts decreasing after i ≈ 75°. The reason for this is that the disk is geometrically thin and confined to equatorial plane of the star in this model. For high inclinations, we see the disk more and more “edge-on”, thus seeing less of the polarized disk radiation and more of unpolarized star radiation.
The intensity profiles are almost completely in emission, thus resulting in a positive Q/I. For the large inclination, we can see self-absorption in the line, because this radiation crosses the largest portion of the disk and passes largest optical path. Please note that each profile in panel 3 of Fig. 6 is normalized with respect to itself thus resulting in apparently different continuum levels.
The shape of Q/I profiles, which are dominant in the total polarization are typical CRD profiles created by scattering of incident radiation on a relatively thin object. We note that Poeckert & Marlborough (1978) also consider Hα polarization profiles, but in much more detail than here. They include multilevel computations and velocity fields. However, their results show that polarization is also dominated by Stokes Q and that the profiles are relatively simple, although double peaked because of the effects of velocity fields. The reason why Stokes Q dominates scattering polarization is that we perform integration over azimuth. Thus, a large part of reduced intensity components that influence Stokes U cancels out.
 |
Fig. 6 Emergent Q/I (first panel) and U/I (second panel) profiles from a system disk and a star, where polarization is assumed to be only induced by a line scattering in the disk. Instead of a polar angle θ here, we use inclination i, so that the inclination is zero if the observer is in the plane of the disk. Intensity profiles (third panel) combine disk line scattering and star continuum radiation (note that legend is the same as in the top two panels). In the fourth panel, we show the variation of line-center scattering polarization with the inclination. |
We would like to stress that the brief discussion given here is just a simple example of the 2D cylindrical polarized radiative transfer code that was presented in the paper. We note that a major departure from the reality here is the absence of velocity fields. More detailed work on more realistic disk models, with velocity fields is planned for the near future.
5. Conclusions
This paper describes a method of solving NLTE polarized radiative transfer in a 2D cylindrical geometry, where cylinders are assumed to be homogeneous in azimuth and physical quantities depend only on z and r coordinates. A formal solution is performed via the method of short characteristics of the second order and to consistently solve the equations of radiative transfer and statistical equilibrium, the Jacobi method with Ng acceleration is applied. The expansion of the method to handle scattering polarization is also presented. At the moment, CRD is assumed, but the method can handle PRD with slight adjustments. Two ways, depending on illuminating objects, of dealing with external illumination are shown.
The code has been tested by comparing the results to the well-known 1D solutions where it accurately reproduces the behavior of the source function in the scalar case and emerging scattering polarization profiles. Its applicability is illustrated on a very simple example of line scattering in a circumstellar disk. In the concluding discussion, we would like to weigh the pros and cons of this approach once again and in more detail.
Pros:
-
The method allows one to model axially symmetric objectswithout the need of using 3D Cartesian grids, thus saving a lot ofcomputing time and memory requirements. A 2D cylindricalgeometry is much more realistic than 2D Cartesian geometry, as itallows modeling of the objects that are finite in all dimensions. Italso allows simple modeling of thin rings or disks, which wouldotherwise require 3D geometry with numerous grid points. Inthese cases, axial symmetry is also automatically satisfied.
-
It can be used without parallelization while still having moderate execution time which allows one to experiment with various parameters, or, if needed, to even create large grids of models.
-
In certain cases, inversion techniques from observed data would be possible where the model can be described with several parameters only.
Cons:
-
Angular interpolation in the process of a formal solution is needed, which renders the code slower and reduces its accuracy. This is especially important for polarized RT computations, because the polarization is sensitive to the anisotropies of the radiation field, which can be polluted via computational artifacts in extreme cases.
-
Ray characteristics are more complicated than in Cartesian geometry. Specifically, the process of intensity interpolation sometimes requires the values of the intensity in other grid points in directions that belong to a different angular octant. This makes dynamic deallocation of the intensity problematic, because some intensities must be kept in memory all the time, which increases the memory requirements.
-
The possibility of implementing magnetic fields is greatly limited as they are required to be axisymmetric.
Keeping in mind all of the above, we can conclude that this approach can be useful in various applications, especially if observations cannot be done with sufficient precision. It would be of great benefit to compare these computations with computations done with a 3D Cartesian solver and to carefully evaluate not only accuracy but also memory requirements and speed of the code. It is our main long-term goal. The next extension of the method will be inclusion of arbitrary velocity fields in the observer’s frame and then in a co-moving frame. It would allow modeling of objects, such as accretion disks, which are known to be dynamic and whose velocity fields introduce important radiative transfer effects.
Acknowledgments
I am indebted to my doctoral advisors, Professor Marianne Faurobert of University of Nice Sophia-Antipolis and Professor Olga Atanacković of University of Belgrade, who not only greatly improved this manuscript but also carefully and pedagogically guided my work on this subject and on my whole thesis. I thank Nikola Vitas for useful discussions and for providing me with code to compute arbitrary Carlson’s B sets and Milica Vučetić for careful reading of the manuscript and useful comments. The manuscript has been greatly improved by the referee’s remarks. This work has been partially funded by the Serbian Ministry of Science and Education through the project 176004,
“Stellar Physics”, and my stay in Nice has been supported by the Eiffel scholarship from the French Government. I want to dedicate this paper to the memory of my father, Zoran A. Milić, who passed away in the summer of 2012 and who was always a person I admired.
References
- Anusha, L. S., & Nagendra, K. N. 2011a, ApJ, 726, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Anusha, L. S., & Nagendra, K. N. 2011b, ApJ, 738, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Anusha, L. S., Nagendra, K. N., & Paletou, F. 2011, ApJ, 726, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Asensio Ramos, A., & Trujillo Bueno, J. 2006, in EAS Pub. Ser. 18, ed. P. Stee, 25 [Google Scholar]
- Atanackovic-Vukmanovic, O., Crivellari, L., & Simonneau, E. 1997, ApJ, 487, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Auer, L. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 3 [Google Scholar]
- Auer, L. H., & Paletou, F. 1994, A&A, 285, 675 [NASA ADS] [Google Scholar]
- Avery, L. W.,House, L. L., &Skumanich, A. 1969, J. Quant. Spectr. Rad. Transf. 9, 519 [Google Scholar]
- Busche, J. R., & Hillier, D. J. 2000, ApJ, 531, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Carlson, B. G. 1963, in Statistical Physics, eds. B. Adler, S. Fernbach, & M. Rotenberg (New York: Academic Press), Meth. Comput. Phys., 1, 1 [Google Scholar]
- Chandrasekhar, S. 1950, Radiative Transfer (London: Oxford University Press) [Google Scholar]
- de la Cruz Rodríguez, J., & Piskunov, N. 2013, ApJ, 764, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Elitzur, M., Asensio Ramos, A., & Ceccarelli, C. 2012, MNRAS, 422, 1394 [NASA ADS] [CrossRef] [Google Scholar]
- Faurobert, M. 1988, A&A, 194, 268 [NASA ADS] [Google Scholar]
- Gouttebroze, P. 2005, A&A, 434, 1165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Halonen, R. J., Mackay, F. E., & Jones, C. E. 2013, ApJS, 204, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Hauschildt, P. H., & Baron, E. 2006, A&A, 451, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubeny, I. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 17 [Google Scholar]
- Ibgui, L., Hubeny, I., Lanz, T., & Stehlé, C. 2013, A&A, 549, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kunasz, P., & Auer, L. H. 1988, J. Quant. Spectr. Rad. Transf., 39, 67 [Google Scholar]
- Kunasz, P. B., & Olson, G. L. 1988, J. Quant. Spectr. Rad. Transf., 39, 1 [Google Scholar]
- Landi Degl’Innocenti, E., & Landolfi, M. 2004, Polarization in Spectral Lines, Astrophys. Space Sci. Lib., 307 [Google Scholar]
- Mihalas, D. 1978, Stellar atmospheres 2nd edn. (San Francisco: W. H. Freeman & Company) [Google Scholar]
- Mihalas, D., Auer, L. H., & Mihalas, B. R. 1978, ApJ, 220, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Ng, K.-C. 1974, J. Chem. Phys., 61, 2680 [NASA ADS] [CrossRef] [Google Scholar]
- Olson, G. L., Auer, L. H., & Buchler, J. R. 1986, J. Quant. Spectr. Rad. Transf., 35, 431 [Google Scholar]
- Olson, G. L., & Kunasz, P. B. 1987, J. Quant. Spectr. Rad. Transf., 38, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Papkalla, R. 1995, A&A, 295, 551 [NASA ADS] [Google Scholar]
- Poeckert, R., & Marlborough, J. M. 1978, ApJ, 220, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, D. E. 1978, PASJ, 30, 455 [Google Scholar]
- Stenholm, L. G. 1977, A&A, 54, 577 [NASA ADS] [Google Scholar]
- Trujillo Bueno, J., & Fabiani Bendicho, P. 1995, ApJ, 455, 646 [NASA ADS] [CrossRef] [Google Scholar]
- van Noort, M., Hubeny, I., & Lanz, T. 2002, ApJ, 568, 1066 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Different types of rays in the cylindrical geometry. Types 1 and 2 are similar to Cartesian geometry and they intersect either a horizontal or vertical cell border. Type 3 is unique to the cylindrical geometry, as the upwind point has the same r coordinate as the local point. |
| In the text | |
 |
Fig. 2 Difference between the azimuthal angles of the ray in the local and in the upwind point. This difference makes angular interpolation necessary. |
| In the text | |
 |
Fig. 3 Behavior of scalar source function with optical depth, mimicking 1D plane-parallel atmosphere. Upper panel: S(z) for r = 0. Lower panel: S(r) for z = zmax/2. |
| In the text | |
 |
Fig. 4 Q/I and U/I profiles emerging from the point with coordinates (zmax,0) for θ = 84°. Since this point is far from lateral boundaries, scattering polarization profiles correspond to those formed in the 1D atmosphere. We note that U/I is on the order of 10-8%, which is negligible compared to Q/I, as expected. |
| In the text | |
 |
Fig. 5 Q/I and U/I profiles emerging from the edge of the cylinder, or from the point with coordinates (zmax,rmax), for θ ≈ 84° and various azimuths. |
| In the text | |
 |
Fig. 6 Emergent Q/I (first panel) and U/I (second panel) profiles from a system disk and a star, where polarization is assumed to be only induced by a line scattering in the disk. Instead of a polar angle θ here, we use inclination i, so that the inclination is zero if the observer is in the plane of the disk. Intensity profiles (third panel) combine disk line scattering and star continuum radiation (note that legend is the same as in the top two panels). In the fourth panel, we show the variation of line-center scattering polarization with the inclination. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


