| Issue |
A&A
Volume 555, July 2013
|
|
|---|---|---|
| Article Number | A28 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220698 | |
| Published online | 24 June 2013 | |
Pulse-to-pulse flux density modulation from pulsars at 8.35 GHz
1
Kepler Institute of Astronomy, University of Zielona Góra,
ul. Lubuska 2,
65-265
Zielona Góra,
Poland
e-mail:
olaf@astro.ia.uz.zgora.pl
2
Station de Radioastronomie de Nançay, Observatoire de Paris,
CNRS/INSU, 18330
Nançay,
France
3
Laboratoire de Physique et Chimie de l’Environnement et de
l’Espace, LPC2E UMR 7328 CNRS, 45071
Orléans Cedex 2,
France
4
National Centre for Radio Astrophysics, PO Bag 3, Pune University
Campus, 411 007,
Pune,
India
5
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69, 53121
Bonn,
Germany
Received: 6 November 2012
Accepted: 29 April 2013
Aims. We aim to investigate the flux density modulation from pulsars and the specific behaviour of the modulation index versus frequency.
Methods. Several pulsars were observed with the Effelsberg radio telescope at 8.35 GHz. Their flux density time series were corrected for interstellar scintillation effects.
Results. We present measurements of modulation indices for eight pulsars. We confirm the presence of a critical frequency at ~1 GHz for these pulsars (including three new ones from this study). We derived intrinsic modulation indices for the resulting flux density time series. Our data analysis revealed strong single pulses detected from five pulsars.
Key words: pulsars: general / pulsars: individual: B1133+16
© ESO, 2013
1. Introduction
A typical pulsar spectrum is steep compared to spectra of other non-thermal radio sources and can be described by a power law (S ∝ να) in the radio frequency range. The average spectral index of pulsars is −1.8 (Maron et al. 2000), which indicates that pulsars are weak radio sources when observed at high frequencies. According to radius-to-frequency mapping (Cordes 1978; Kijak & Gil 2003), high-frequency radiation originates close to the pulsar surface. Therefore, single-pulse observations of pulsars at short wavelengths can provide valuable information for studies of pulsar radio emission close to the neutron star surface.
Pulsar radiation undergoes various propagation effects as it passes through the interstellar medium. Depending on the strength of the turbulence and on the homogeneity of the scattering material, these effects cause a phase modulation of the propagating pulsar signal. This modulation manifests itself by variations in signal intensity over a wide range of observation time scales and bandwidths. These modulations are correlated over a characteristic scintillation bandwidth that is exponentially proportional to the observing frequency (Δf ∝ f4) as presented by Scheuer (1968). Scintillation effects are generally more pronounced at frequencies below 1 GHz. However, observing pulsars at high frequencies can also serve as a probe of properties of the interstellar medium, as shown by Bhat et al. (2000) and Lewandowski et al. (2011). These authors used high-frequency observations of pulsars to study the structure and dynamics of the local interstellar medium and to directly determine the interstellar electron density spectrum.
The pulse-energy distribution can be used to investigate different possible models of pulsar emission physics. In a series of papers, Cairns and collaborators (Cairns et al. 2001, 2003a,b, 2004) investigated different possible models of the emission physics using observations of three pulsars. They have shown that the pulse-energy distributions appear to be log-normal and are representative of the normal pulsar radio emission, can be fitted with a single-emission model or with a convolution of Gaussian-log-normal or double log-normal models. The approximately power-law distributions was ascribed to the emission of “giant pulses”, i.e. pulses whose integrated flux density is greater than ten times the integrated flux density of the average profile. These pulses are believed to be associated with the high-energy emission in the outer magnetosphere (Johnston & Romani 2002; Cairns 2004).
Moreover, measuring the modulation index can be used to study the physical processes that create pulsar radio emission. Jenet & Gil (2003) used the pulse-to-pulse modulation index to test different radio emission models. They used four “complexity parameters” that represented a sparking-gap model (Gil & Sendyk 2000), a continuous-current outflow instabilities model (Arons & Scharlemann 1979; Hibschman & Arons 2001), a surface magneto-hydrodynamic wave instabilities model (Lou 2001), and an outer magnetospheric instabilities model (Jenet & Gil 2003). The anti-correlation of these parameters with measured pulse-to-pulse modulation indices of a sample of 12 pulsars led them to dismiss the surface magneto-hydrodynamic wave instabilities model. The results from a survey of pulsars at 21 and 92 cm made by Weltevrede et al. (2006, 2007) have shown that the modulation index increases at lower frequencies, but despite large samples of pulsars, none of the models could be favoured over the others so far.
The analysis of the pulse-to-pulse modulation index shows that the degree of modulation depends on the observing frequency, with an apparent minimum around 1 GHz for the majority of analysed pulsars (Bartel et al. 1980). In this paper we argue that this phenomenon is not intrinsic to pulsar emission mechanism, but depends on the sensitivity of the observations and the presence of so-called pseudo-nulls. The outline of this paper is as follows: we summarise our observations and data reduction for a set of 12 pulsars, followed by our flux density measurements and corrections for the effect of interstellar scintillation. Then, we derive intrinsic modulation indices. Next, we compare the pulse-energy distributions from our observations with those made at other frequencies. We also report the detection of numerous strong single pulses from PSR B1133+16 and from four other sources, albeit less abundant. Finally, we discuss our results in the last section.
2. Observations and data reduction
We carried out our observations with the 100-m radio telescope of the Max-Planck-Institut für Radioastronomie at Effelsberg in 2002 (March and December) and 2004 (April and June). The observations were made with the cooled secondary focus receiver with HEMT amplifiers at the observing frequency of 8350 MHz and bandwidth of 1100 MHz. The receiver provided LHC and RHC signals that were digitised and independently sampled into 1024 pulse phase bins synchronously folded with the topocentric pulse period P, using the Effelsberg Pulsar Observation System (EPOS, Jessner 1996), which recorded the calibrated data in single-pulse mode and stored for future off-line analysis. The aim of our observations was to detect single pulses from pulsars at this frequency.
To calibrate the received pulsar signal at the Effelsberg radio telescope, a noise diode is installed in every receiver. This diode is switched on synchronously with every pulse period. The signal output of the noise diode is then compared with the energy received from the pulsar. The energy from the noise diode is calibrated by comparing its output with the flux density of a known continuum source. This pointing procedure was performed on well-known flux calibrators during our observations. For the 2002 observations we used the following flux calibrators: 3C 295, 3C 147, and 3C 279; for the 2004 observations we used 3C 273, 3C 196, NGC 7027 and 3C 286. In order to estimate the mean flux density Smean (which represents the total on-pulse energy E averaged over an entire pulse period P, i.e. Smean = E/P), we used the calibration procedure described in detail in Kramer (1995). The pulsar signal was sampled by dividing the pulsar period into 1024 bins of the entire pulse window. For the observations of PSR B1133+16 made in April and June 2004 the resolution was increased to 60 μs by using the part of the pulsar period enclosing the pulse profile and dividing it into 1024 bins. Finally, the flux-calibrated time series were produced for the subsequent analysis. Table 1 summarises the parameters of the observed pulsars.
List of observed pulsars, their observing parameters, and the values derived from the observations.
3. Data analysis and results
 |
Fig. 1 Calibrated time series from PSR B0329+54. The decrease of the signal strength due to the weak interstellar scintillation is clearly visible. |
 |
Fig. 2 Calibrated time series from PSR B0355+54 showing signal variation due to the strong interstellar scintillation that causes the signal to have significant variation over a very short time scale. |
3.1. Scintillation and modulation effects
To analyse the data and produce the flux-calibrated time series, we must first investigate the influence of effects that can alter the intrinsic pulsar flux. As a first effect we considered interstellar scattering. Since, as mentioned above, the pulsar scatter broadening time is strongly dependent on frequency (τs ∝ f-4, Lorimer & Kramer 2005), we expect the effects of scattering to have little influence on our observations. The empirical relationship between τs and the dispersion measure, presented in Bhat et al. (2004), allowed us to estimate τs, and confirm that this effect is negligible at high observing frequency of 8.35 GHz for the pulsars used in our study.
We now move to the second effect, interstellar scintillation. It is well known that the scintillation strength changes according to observational parameters such as frequency and the bandwidth at which the pulsar is observed, or according to its dispersion measure. Lorimer & Kramer (2005) estimated the transition frequency from the strong to the weak scintillation regime as a function of pulsar’s dispersion measures. They showed that pulsars with a dispersion measure lower than 40 cm-3pc observed at 8.35 GHz will be in the weak scintillation regime. This is evident in Fig. 1, where a decrease of signal strength is seen through the observation. All pulsars presented in Table 1, except for two sources, have met this criterion. The first pulsar, B2154+40, does not show these variations in its time series despite its high dispersion measure, 70 857 cm-3pc, probably because of fortuitous scintillation conditions during the observations. The second source, B0355+54, shows significant variations in flux density over a short time scale, which can be seen in Fig. 2. This behaviour is clearly due to the strong interstellar scintillation and makes flux measurements of this source uncertain. According to the work of Lewandowski et al. (2011), the pulsar B0329+54 has a transition frequency between 8 and 10 GHz, which suggests that it may have undergone occasional changes between the weak and strong scintillation regime during our observations.
To derive the intrinsic modulation indices (mint) we used the method described in Kramer et al. (2003). They used 200-s running median to correct the pulsar signal for the effects of interstellar scintillation. The time scale of 200 seconds is longer than a typical pulsar intrinsic pulse-to-pulse modulation (Weltevrede et al. 2006, 2007) and shorter than the expected scintillation times. By dividing the calibrated flux of each pulse by the running median corresponding to its location, we corrected our observations for the effects of interstellar observations. To obtain the corrected flux density time series for interstellar scintillation effects, the flux density of each pulse was divided by the running median corresponding to its location. Then the each of the data sets was rescaled to be consistent with the initial average flux density. For every observation we integrated individual pulses to obtain the average pulse profile and calculated its flux density (see Table 1). For existing multiple observations of the pulsars B0329+54, B0823+26, and B1133+16 we also present calculated average values and their uncertainties. Our flux density measurements are consistent with values available in the literature (e.g. Maron et al. 2000). After correcting the data sets for the effects of interstellar scintillation, we calculated the intrinsic modulation indices mint. We used the following equation: 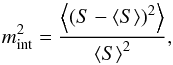 (1)
(1)
where S is the flux measurement from an individual pulse, while ⟨S⟩ is the average flux from an entire observation. The last column in Table 1 holds the calculated values of mint. When a pulsar was observed multiple times, we present the average mint with its uncertainty. For pulsars B0355+54, B0450+55, B2154+40, and B2310+42 the observation times were too short to provide reliable estimates of mint. In Fig. 4 we collate our modulation index values as a function of frequency with the results presented in Bartel et al. (1980) and Kramer et al. (2003). It is clearly seen that mint first decreases with frequency, and after it reaches the so-called critical frequency 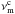 (with a value of ~1 GHz), it rises again.
(with a value of ~1 GHz), it rises again.
3.2. Null and on states
In Fig. 5 we present pulse energy distributions for PSR B1133+16 spanning a frequency range from 325 MHz to 8.35 GHz. The panels for distributions obtained from observations at lower frequencies were prepared using data from Bhat et al. (2007). The panel showing the distribution of pulse energies at 8.35 GHz was chosen from a number of similar distributions produced from our data sample. In Fig. 5 one can see that the distribution at lower frequencies is bimodal with a classical separation into two components. At higher frequencies the distributions merge with each other into positively skewed distribution (Bhat et al. 2007). The distribution around zero at lower frequencies (e.g. 325 MHz) most probably represents so-called pseudo-nulls (Herfindal & Rankin 2007), while the right-hand side of the histogram is nothing else but a Gaussian energy distribution of pulses around the pulsar energy mean value. The change of the distribution with increasing frequency is mainly caused by the decrease of average pulsar energy with the value of spectral index of −1.9 for this pulsar (Maron et al. 2000). The change of distribution character from bimodal to skewed normal is caused by the increasing number of genuine nulls as a result of spectral dependency of the observed energy (decreasing with frequency) and low sensitivity of the receiver. However, the careful analysis of our data sets performed by Honnappa et al. (2012) confirmed the pseudo-nulls – they wrote “we found a clear evidence for periodic pseudonulls in the form of apparent “null zones” in the folded modulation pattern”.
In Fig. 6 we present a similar analysis of pulse-energy distributions for two peripheral observing frequencies, i.e. 327 MHz and 8.35 GHz. The panel with the low-frequency distribution was prepared using data reported in Herfindal & Rankin (2007), while the distribution at 8.35 GHz was produced from our data. The above-mentioned effect is not as pronounced as for PSR B1133+16, which is consistent with the modulation index distribution independent of frequency. In Figs. 5 and 6 the raw un-normailzed data were used.
Inspecting Fig. 5 (histograms of single-pulse energy distributions) and comparing it with Fig. 4, which shows the dependency of the modulation index as a function of frequency, we conclude that these results are related and one dependency follows the other. Namely, when we observe a “saddle” (bimodal) distribution (see histograms at 325 MHz), the modulation index for this case has a higher value than that for 1.4 GHz, where the “saddle” disappears and the distribution becomes almost symmetrical with a wide plateau around its mean value. This behaviour reflects a low value of modulation index. When the histogram represents a skewed distribution (8.35 GHz), the modulation index increases. Figure 4 suggests that the pseudo-nulls may be present for more pulsars than these previously mentioned (e.g. PSR B0809+74), whereas PSR B0823+26 shows the flat modulation index spectrum that may be caused by the absence of the pseudo-nulls. The pulsar B0823+26 is well known for its mode changing, which is a variation between active (radio-on, hereafter) and quiescent (radio-off or null, hereafter) emission modes. For observations at frequencies higher than 1 GHz, which we propose in this paper as a critical frequency, it is possible that the changes of emission modes may show the flat distribution of modulation indices as a function of the observing frequency. This is also seen in the shape of the energy distribution of single pulses, which may be described by a normal distribution, while the measurements at lower frequencies (i.e. 327 MHz for PSR B0823+26) show the bimodal distribution. We emphasize the importance of simultaneous observations at low and high frequencies to identify this behaviour. Several anomalously high points in Fig. 4 may be due to nulling and mode-changing phenomena, as suggested by Bartel et al. (1980).
3.3. Strong single pulses in PSR B1133+16
In his review, Cairns (2004) defined so-called “giant pulses” as single pulses whose mean flux density exceeds the average flux density by 10 × ⟨ S ⟩. They also have tendency to be narrower than the pulsar’s average pulse, with time scales down to nano-seconds (e.g. Hankins et al. 2003), and occur at specific range of pulse phases, mostly at the trailing edge of average pulse profile. Giant pulses are also known to show a steep power-law in their energy distributions, as shown in Knight et al. (2006) and Knight (2007).
Pulsar B1133+16 is well known for emitting strong single pulses visible at a wide range of frequencies (e.g. Karuppusamy et al. 2011; Kramer et al. 2003). During our analysis we also detected strong single pulses originating from PSR B1133+16. The strongest detected pulse was about 48 × ⟨S⟩. Figure 3 presents the calibrated time series of B1133+16 with clearly visible frequently occurring strong pulses. In all observational sessions we detected 156 pulses originating from this pulsar, whose mean flux density exceeds 10 × ⟨S⟩. During the longest observations of PSR B1133+16 in April 2004, a total of 54 strong single pulses were detected. Figure 7 shows the integrated pulse profile (dotted line) magnified by a factor of 35 and the pulse profile resulting from averaging only the strong single pulses observed in April 2004. One can easily see that the peak of this profile is located at the trailing edge of the first component of the average profile. Figure 8 shows the three strongest observed single pulses from our longest observation. It is easily seen that they present a very complicated structure with multiple narrow components. Although these pulses meet the “working definition” of giant pulses, we cannot acknowledge them as “classical” giant pulses produced in the outer gap region. In Fig. 9 we show the computed cumulative probability distribution of single-pulse flux densities for the longest observation of PSR B1133+16 in April 2004. In this plot we indicate the mean flux density ⟨S⟩ by a dashed line and a dotted-dashed line marks the value of 10 × ⟨S⟩. There is no noticeable evidence for any change in the slope of the cumulative probability function and hence, power-law in their energy distribution. The lack of the typical steep power law in the distribution prevents us from classifying them as “classical” giant pulses.
We also report the detection of strong single pulses (S > 10 × ⟨S⟩) from four other pulsars during our observations: two pulses for PSR B0329+54, five pulses for PSR B0355+54, two pulses for PSR B0823+26, and three pulses for PSR B0950+08.
 |
Fig. 3 Longest calibrated time series (6061 pulses) from PSR B1133+16. Frequent strong single pulses can be seen. A technical break in the observations resulted in a 1-min gap in the time series, visible around the 60-min mark. |
 |
Fig. 4 Modulation indices m versus frequency for the observed pulsars. It is clearly seen that mint first decreases with frequency, and after it reaches so-called critical frequency |
 |
Fig. 5 Pulse-energy distributions for the pulsar B1133+16. Panels presenting distribution for frequencies from 325 MHz to 4800 MHz are produced using data from Bhat et al. (2007). The panel for 8.35 GHz presents the pulse-energy distribution prepared from our data. The vertical dotted line represents an integrated-intensity threshold of 0.10 ⟨ S ⟩ to distinguish the nulls. Filled grey regions show the on-pulse energy, while the black contour denotes the off-pulse energy. The offpulse noise is included for every pulse, but due to the large number of offpulse values near zero, their distributions were scaled according to the highest onpulse bin. 139 pulses with S langleS ⟩ above 6 were removed from the 8.35 GHz panel to retain the same scale of the plots. |
 |
Fig. 6 Pulse-energy distributions for the pulsar B0823+26. The vertical dotted line represents an integrated-intensity threshold of 0.10 ⟨ S ⟩ to distinguish the nulls. The upper panel presents the distribution prepared using data from Herfindal & Rankin (2009) and shows the observations at 327 MHz. The lower panel shows our observations at 8.35 GHz. Filled grey regions show the on-pulse energy, while the black contour plots the off-pulse energy. The offpulse noise is included for every pulse, but due to the large number of offpulse values near zero, their distributions were scaled according to the highest onpulse bin. |
 |
Fig. 7 Average profile (solid line) made by folding strong pulses from observations of PSR B1133+16 in April 2004 relative to the integrated profile (dotted line), multiplied by a factor of 35. The tendency of the strong single pulses to occurr at the trailing edge of the first component can be seen. |
 |
Fig. 8 Three strongest pulses (solid, dashed and dot-dashed lines) from observations of PSR B1133+16 in April 2004 relative to the first component of the integrated profile (dotted line), multiplied by a factor of 150. The complex pulse structure and tendency to occurr at the trailing edge of the first component is shown. |
 |
Fig. 9 Cumulative probability function of single-pulse flux density of PSR B1133+16 for data presented in Fig. 3. The dashed line denotes the mean value of the flux density, ⟨S⟩, while the dot-dashed line indicates 10 × ⟨S⟩. |
4. Discussion and conclusions
The research presented in this paper concerned pulse-to-pulse flux density modulation of pulsars at high frequency. We measured flux densities of integrated pulse profiles for 12 pulsars, which agreed with the known literature values (Maron et al. 2000). For multiple observational sessions available for three pulsars, we calculated average values of flux densities and their uncertainties. For two pulsars we encountered long-term variations of their flux density time series. PSR B0355+54 showed very strong variations over very short time scales (i.e. 9 min). This resulted in large uncertainty in flux density (see Table 1). The origin of the variations can be assigned to the strong interstellar scintillations.
The analysis of the behaviour of the modulation indices as a function of frequency showed that its value in most cases is lowest around 1 GHz. The distribution changes from bimodal to normal symmetrical with its maximum around zero. The changes of pulse-energy distributions of the observed pulses result in changes of modulation indices depending on frequency. The bimodal distribution at lower frequencies occurs because the maximum around zero represents so-called pseudo-nulls (no detection due to properties of the radiation beam structure) and the right side of the histogram is nothing else but a Gaussian pulse-energy distribution around the average value. The change of this bimodal distribution into the normal one with a maximum around zero with increasing observing frequency is mainly caused by decreasing average pulsar energy with the approximate value of spectral index of −2.0. Therefore the number of so-called genuine nulls (no detection due to inadequate receiver sensitivity) increases.
We reported the detection of strong single pulses from PSR B1133+16. Although they meet the “working definition” of giant pulses, (i.e. 10 × ⟨S⟩ and constrains on appearance at the trailing edge of first component), the complexity of the structure in single pulses and no visible power-law behaviour in their distribution energy suggest that other phenomena are responsible for this behaviour. It is possible that those “giant pulses” come from the polar cap, as suggested by Gil & Melikidze (2005). Therefore longer observation with a higher resolution are required to obtain a better signal-to-noise ratio and a more detailed structure of single pulses for this pulsar. This will show if there is a power-law in the energy distribution and will provide a clue for existence of giant-pulse phenomenon in this source.
Acknowledgments
This paper is based on observations with the 100-m telescope of the MPIfR (Max-Planck-Institut für Radioastronomie) at Effelsberg. The authors would like to thank Michael Kramer for valuable suggestions during the data analysis and W. Lewandowski for fruitful discussions. M.S. would like to thank Joanna Rankin, Jeffrey Herfindal and Ramesh Bhat for providing the data used to calculate the pulse-energy distributions. This paper was supported by the grant DEC-2012/05/B/ST9/03924 of the Polish National Science Centre. This work made use of the NASA ADS astronomical data system.
References
- Arons, J., & Scharlemann, E. T. 1979, ApJ, 231, 854 [NASA ADS] [CrossRef] [Google Scholar]
- Bartel, N., Sieber, W., & Wolszczan, A. 1980, A&A, 90, 58 [NASA ADS] [Google Scholar]
- Bhat, N. D. R., Kramer, M., Gupta, Y., & Lambert, H. C. 2000, in BAAS, Amer. Astron. Soc. Meet. Abstracts, 32, 1502 [NASA ADS] [Google Scholar]
- Bhat, N. D. R., Cordes, J. M., Camilo, F., Nice, D. J., & Lorimer, D. R. 2004, ApJ, 605, 759 [CrossRef] [Google Scholar]
- Bhat, N. D. R., Gupta, Y., Kramer, M., et al. 2007, A&A, 462, 257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cairns, I. H. 2004, ApJ, 610, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Cairns, I. H., Johnston, S., & Das, P. 2001, ApJ, 563, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Cairns, I. H., Das, P., Robinson, P. A., & Johnston, S. 2003a, MNRAS, 343, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Cairns, I. H., Johnston, S., & Das, P. 2003b, MNRAS, 343, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Cairns, I. H., Johnston, S., & Das, P. 2004, MNRAS, 353, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M. 1978, ApJ, 222, 1006 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gil, J., & Melikidze, G. I. 2005, A&A, 432, L61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gil, J. A., & Sendyk, M. 2000, ApJ, 541, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Hankins, T. H., Kern, J. S., Weatherall, J. C., & Eilek, J. A. 2003, Nature, 422, 141 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Herfindal, J. L., & Rankin, J. M. 2007, MNRAS, 380, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Herfindal, J. L., & Rankin, J. M. 2009, MNRAS, 393, 1391 [NASA ADS] [CrossRef] [Google Scholar]
- Hibschman, J. A., & Arons, J. 2001, ApJ, 560, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Honnappa, S., Lewandowski, W., Kijak, J., et al. 2012, MNRAS, 421, 1996 [NASA ADS] [CrossRef] [Google Scholar]
- Jenet, F. A., & Gil, J. 2003, ApJ, 596, L215 [NASA ADS] [CrossRef] [Google Scholar]
- Jessner, A. 1996, in Large Antennas in Radio Astronomy, eds. C. G. M. van’t Klooster & A. van Ardenne, 185 [Google Scholar]
- Johnston, S., & Romani, R. W. 2002, MNRAS, 332, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Karuppusamy, R., Stappers, B. W., & Serylak, M. 2011, A&A, 525, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kijak, J., & Gil, J. 2003, A&A, 397, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knight, H. S. 2007, MNRAS, 378, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Knight, H. S., Bailes, M., Manchester, R. N., & Ord, S. M. 2006, ApJ, 653, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Kramer, M. 1995, Ph.D. Thesis, University of Bonn [Google Scholar]
- Kramer, M., Karastergiou, A., Gupta, Y., et al. 2003, A&A, 407, 655 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lewandowski, W., Kijak, J., Gupta, Y., & Krzeszowski, K. 2011, A&A, 534, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lorimer, D. R., & Kramer, M. 2005, Handbook of Pulsar Astronomy (Cambridge University Press) [Google Scholar]
- Lou, Y.-Q. 2001, ApJ, 563, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Maron, O., Kijak, J., Kramer, M., & Wielebinski, R. 2000, A&AS, 147, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scheuer, P. A. G. 1968, Nature, 218, 920 [NASA ADS] [CrossRef] [Google Scholar]
- Weltevrede, P., Edwards, R. T., & Stappers, B. W. 2006, A&A, 445, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weltevrede, P., Stappers, B. W., & Edwards, R. T. 2007, A&A, 469, 607 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
List of observed pulsars, their observing parameters, and the values derived from the observations.
All Figures
 |
Fig. 1 Calibrated time series from PSR B0329+54. The decrease of the signal strength due to the weak interstellar scintillation is clearly visible. |
| In the text | |
 |
Fig. 2 Calibrated time series from PSR B0355+54 showing signal variation due to the strong interstellar scintillation that causes the signal to have significant variation over a very short time scale. |
| In the text | |
 |
Fig. 3 Longest calibrated time series (6061 pulses) from PSR B1133+16. Frequent strong single pulses can be seen. A technical break in the observations resulted in a 1-min gap in the time series, visible around the 60-min mark. |
| In the text | |
 |
Fig. 4 Modulation indices m versus frequency for the observed pulsars. It is clearly seen that mint first decreases with frequency, and after it reaches so-called critical frequency |
| In the text | |
 |
Fig. 5 Pulse-energy distributions for the pulsar B1133+16. Panels presenting distribution for frequencies from 325 MHz to 4800 MHz are produced using data from Bhat et al. (2007). The panel for 8.35 GHz presents the pulse-energy distribution prepared from our data. The vertical dotted line represents an integrated-intensity threshold of 0.10 ⟨ S ⟩ to distinguish the nulls. Filled grey regions show the on-pulse energy, while the black contour denotes the off-pulse energy. The offpulse noise is included for every pulse, but due to the large number of offpulse values near zero, their distributions were scaled according to the highest onpulse bin. 139 pulses with S langleS ⟩ above 6 were removed from the 8.35 GHz panel to retain the same scale of the plots. |
| In the text | |
 |
Fig. 6 Pulse-energy distributions for the pulsar B0823+26. The vertical dotted line represents an integrated-intensity threshold of 0.10 ⟨ S ⟩ to distinguish the nulls. The upper panel presents the distribution prepared using data from Herfindal & Rankin (2009) and shows the observations at 327 MHz. The lower panel shows our observations at 8.35 GHz. Filled grey regions show the on-pulse energy, while the black contour plots the off-pulse energy. The offpulse noise is included for every pulse, but due to the large number of offpulse values near zero, their distributions were scaled according to the highest onpulse bin. |
| In the text | |
 |
Fig. 7 Average profile (solid line) made by folding strong pulses from observations of PSR B1133+16 in April 2004 relative to the integrated profile (dotted line), multiplied by a factor of 35. The tendency of the strong single pulses to occurr at the trailing edge of the first component can be seen. |
| In the text | |
 |
Fig. 8 Three strongest pulses (solid, dashed and dot-dashed lines) from observations of PSR B1133+16 in April 2004 relative to the first component of the integrated profile (dotted line), multiplied by a factor of 150. The complex pulse structure and tendency to occurr at the trailing edge of the first component is shown. |
| In the text | |
 |
Fig. 9 Cumulative probability function of single-pulse flux density of PSR B1133+16 for data presented in Fig. 3. The dashed line denotes the mean value of the flux density, ⟨S⟩, while the dot-dashed line indicates 10 × ⟨S⟩. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


