EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 554 (June 2013) A&A, 554 (2013) A64 Full HTML
Free Access
Issue
A&A
Volume 554, June 2013
Article Number A64
Number of page(s) 6
Section The Sun
DOI https://doi.org/10.1051/0004-6361/201220550
Published online 05 June 2013

© ESO, 2013

1. Introduction

The electron and proton distribution functions detected in the solar wind and the magnetosphere of the Earth display a bidirectional temperature anisotropy A ≡ T⊥/T∥ ≠ 1, where the parallel and perpendicular subscripts indicate directions with respect to the uniform magnetic field (Pilipp et al. 1990; Salem et al. 2003; Hellinger et al. 2006; Stverak et al. 2008; Bale et al. 2009). However, these deviations from isotropy are not large as predicted by the low-collisional exospheric models, implying the existence of some constraints, e.g., instabilities or collisions, that should limit the growth of the anisotropy and explain the observations. Collisions are less effective at time and space scales in the solar wind plasma, but the limits observed for the temperature anisotropy seem to be well explained by the resulting wave fluctuations and their effects on plasma particles. Thus, for electrons, linear dispersion theory predicts that any excess of temperature in the direction parallel to the magnetic field (T∥ > T⊥) is constrained by the firehose instability (Paesold & Benz 1999; Gary & Nishimura 2003; Stverak et al. 2008), while perpendicular temperature (T⊥ > T∥) is limited by the whistler instability (Gary & Wang 1996; Stverak et al. 2008; Schlickeiser et al. 2011).

The electron whistler-cyclotron signals with frequencies between the electron and ion gyro-frequencies, | Ωe |  < ω < Ωi, and a prevailing right-handed (RH) circular polarization have first been observed in atmospherics (Helliwell et al. 1956). These electromagnetic modes are triggered by the kinetic anisotropies and suprathermal populations of electrons (Mace 1998; Lazar et al. 2008a), expecting to play a major role at dissipative scales in the solar wind and planetary magnetospheres (Pilipp et al. 1990; Salem et al. 2003; Stverak et al. 2008). Because plasma is diluted and poor-collisional in these environments, only the wave-particle interactions can explain the deviations from Maxwellian equilibrium, which are permanently confirmed by the observations. Suprathermal populations are present at all altitudes in the solar wind (Feldman et al. 1975; Pilipp et al. 1987; Fisk & Gloeckler 2006) and corona (Pierrard et al. 1999; Scudder 1992), being associated with the high energy tails of the measured distributions, which are overall best modeled by the family of Kappa functions (Vasyliunas 1968; Scudder 1992; Maksimovic et al. 1997; Pierrard et al. 2001).

Distribution functions of Kappa-type are power-laws, with the power-index κ determining the slope of the high-energy tails in the velocity spectrum of plasma particles. For high values of κ → ∞, the Kappa function degenerates into a Maxwellian (Summers & Thorne 1991). An anisotropic distribution (T⊥ ≠ T∥) can be modeled using a bi-Kappa function introduced here in Eq. (1). This distribution has widely been exploited to describe kinetic instabilities of a drifting or a non-drifting plasma, e.g., the ion acoustic instability (Summers & Thorne 1992), the electromagnetic ion-cyclotron and the firehose instabilities (Summers & Thorne 1992; Xue et al. 1996a,b; Lazar & Poedts 2009; Lazar 2012), the mirror unstable mode (Leubner & Schupfer 2000, 2001; Pokhotelov et al. 2002), the electron whistler and cyclotron instabilities (Mace 1998; Xiao et al. 1998; Tripathi & Singhal 2008; Lazar et al. 2008a), and the weakly propagating instabilities in low magnetized plasmas (Lazar et al. 2008b; 2009; 2010).

Suprathermal populations can significantly alter both the dispersion and stability properties. Thus, a bi-Kappa model predicts that the instability of the whistler-cyclotron modes is, in general, inhibited (Lazar et al. 2008a; 2011a), but for low anisotropies, A < 2, the effect is opposite, the growth rate decreasing with the increase of κ-index (Mace 1998; Tripathi & Singhal 2008; Mace & Sydora 2010). The same effect must therefore govern the lowest threshold conditions close to the marginal stability, but this seems to contradict recent claims that the instability thresholds do not depend on the power index κ, and the maximum growth rate depends strongly on it.

To clarify these contradictory issues, in the present paper we present a new rigorous investigation of the threshold conditions for the whistler-cyclotron instability, driven by the temperature anisotropy of a bi-Kappa distributed plasma. The electrons are assumed to be anisotropic, with an excess of perpendicular temperature (T⊥ > T∥). In these conditions linear theory predicts destabilization of the whistler-cyclotron branch (Kennel & Petschek 1966). Moreover, if the initial distribution function decreases monotonically with increasing energy, the parallel-propagating modes are the most unstable1. Numerical simulations confirm the excitation of transverse field fluctuations in the frequency range Ωp < ωr <  | Ωe | for both the idealized bi-Maxwellian (Gary & Wang 1996, and references therein) and the generalized bi-Kappa model (Lu et al. 2010). These waves have subluminal phase velocities (ω/k < c, where c is the speed of light in vacuum) and right-handed (RH) polarization, and their frequency is sufficiently high to neglect the ion dynamics.

2. Dispersion and stability theory

To characterize the anisotropic distributions with high-energy tails we use a bi-Kappa distribution function F(v∥,v⊥)=1π3/2θ⊥2θ∥ Γ[κ+1]κ3/2Γ[κ−1/2](1+v∥2κθ∥2+v⊥2κθ⊥2)−κ−1,\begin{eqnarray} F (v_{\parallel}, v_{\perp}) = {1 \over \pi^{3/2} \theta_{\perp}^2 \theta_{\parallel}} \, {\Gamma[\kappa +1] \over \kappa^{3/2} \Gamma[\kappa -1/2]} \left(1 + {v_{\parallel}^2\over \kappa \theta_{\parallel}^2 } + {v_{\perp}^2\over \kappa \theta_{\perp}^2 }\right)^{-\kappa-1}, \label{e1} \end{eqnarray}(1)which is normalized to unity, ∫d3v   F = 1, and is defined using the equivalent thermal velocities θ∥ , ⊥ given by 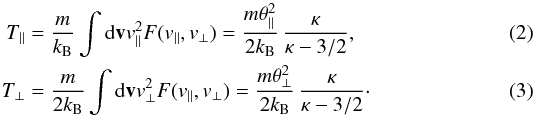T∥=T⊥=\begin{eqnarray} T_{\parallel} &= & {m \over k_{\rm B}} \int {\rm d}{\bf v} v_{\parallel}^2 F (v_{\parallel}, v_{\perp}) = {m \theta_{\parallel}^2 \over 2 k_{\rm B}} \, {\kappa \over \kappa -3/2}, \label{e2} \\ T_{\perp} &=& {m \over 2 k_{\rm B}} \int {\rm d}{\bf v} v_{\perp}^2 F (v_{\parallel}, v_{\perp}) = {m \theta_{\perp}^2 \over 2 k_{\rm B}} \, {\kappa \over \kappa -3/2} \cdot\label{e3} \end{eqnarray}In the limit of a very large power index κ → ∞, 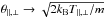θ∥,⊥→2kBT∥,⊥/m\hbox{$\theta_{\parallel, \perp} \to \sqrt{2k_{\rm B} T_{\parallel, \perp}/m}$}, and the bi-Kappa distribution function approaches the standard bi-Maxwellian.

Assuming an excess of perpendicular temperature (T⊥ > T∥), the electromagnetic whistler-cyclotron mode is enhanced, leading to a wave instability of finite frequency Re(ω) ≡ ωr ≠ 0, and growth rate Im(ω) ≡ ωi > 0. We restrict the analysis to propagation parallel to the uniform magnetic field (k = k∥), because, in this case, the instability decouples from the electrostatic modes, and exhibits maximum growth rates. The RH-modes are described by the general dispersion relation (Gary 1993) 0=1−k2c2ω2+πω2∑aωp,a2∫−∞∞ dv∥ω−kv∥+Ωa∫0∞ dv⊥\begin{eqnarray} 0 &= & 1 -{k^2c^2 \over \omega^2} + {\pi \over \omega^2} \sum_a \omm_{{\rm p},a}^2 \int_{-\infty}^{\infty} \, {{\rm d}v_{\parallel} \over \omm - k v_{\parallel} + \Omega_a} \int_0^{\infty} \, {\rm d}v_{\perp} \notag \\ && \times v_{\perp}^2 \left[(\omm - k v_{\parallel}) {\partial F_{a,\kappa} \over \partial v_{\perp}} + k v_{\perp} {\partial F_{a,\kappa} \over \partial v_{\parallel}} \right], \label{e4} \end{eqnarray}(4)where Ωa = qaB0/(mac) is the (non-relativistic) gyrofrequency, and ωp,a = (4πnae2/ma)1/2 is the plasma frequency for the particles of sort a. For the bi-Kappa distribution (1), partial derivatives in Eq. (4) are calculated in Appendix A, yielding the dispersion relation k2c2= ω2+∑aωpa2{(Ta⊥Ta∥−1)\begin{eqnarray} k^2c^2 &= & \, \omega^2 + \sum_a \omega_{{\rm p}a}^2 \Biggl\{ \left({T_{a\perp}\over T_{a\parallel}} -1 \right) \notag \\ && + \left[{T_{a\perp}\over T_{a\parallel}} \, {\omega \pm \Omega_a \over k \theta_{a\parallel}} \mp {\Omega_a \over k\theta_{a\parallel}} \right] Z^0_{\kappa} (f_1) \Biggr\}. \label{e5} \end{eqnarray}(5)Here we use the modified (Kappa) plasma dispersion function (Lazar et al. 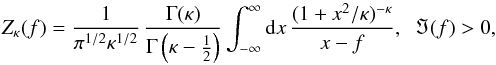2008b) Zκ(f)=1π1/2κ1/2 Γ(κ)Γ(κ−12)∫−∞∞dx (1+x2/κ)−κx−f,ℑ(f)>0,\begin{eqnarray} Z_{\kappa}(f) = {1 \over \pi^{1/2} \kappa^{1/2}} \, {\Gamma (\kappa) \over \Gamma \left( \kappa -{1 \over 2}\right)} \int_{-\infty}^{\infty} {\rm d}x \, {(1+x^2/\kappa)^{-\kappa } \over x - f}, \;\; \Im(f)>0, \label{e6} \end{eqnarray}(6)of argument 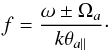f=ω±Ωakθa∥·\begin{equation} f = {\omega \pm \Omega_a \over k \theta_{a\parallel}}\cdot \label{e7} \end{equation}(7)The dispersion relation in Eq. (5) enables one to consider an arbitrary number of plasma species, and for high values of the power index κ → ∞, it reduces exactly to the standard form of a bi-Maxwellian model (Gary 1993). At high frequencies of the whistler-cyclotron modes, ions do not react, and the dispersion relation simplifies to 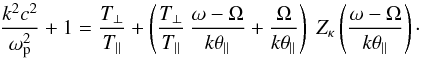k2c2ωp2+1=T⊥T∥+(T⊥T∥ ω−Ωkθ∥+Ωkθ∥)Zκ(ω−Ωkθ∥)·\begin{eqnarray} {k^2c^2 \over \omega_{\rm p}^2} + 1 = {T_{\perp}\over T_{\parallel}} + \left({T_{\perp}\over T_{\parallel}} \, {\omega - \Omega \over k \theta_{\parallel}} + {\Omega \over k\theta_{\parallel}} \right) \; Z_{\kappa} \left({\omega - \Omega \over k \theta_{\parallel}}\right)\cdot \label{e8} \end{eqnarray}(8)We neglect ω2 ≪ k2c2 (subluminal modes), and, for simplicity, we note Ω =  | Ωe | and omit the subscript “e” for all other symbols.

Table 1

Electron temperature anisotropy fitting parameters from Eq. (9).

2.1. Instability thresholds

The unstable wave-numbers are usually limited between a maximum cutoff (kM), which increases with the temperature anisotropy T⊥/T∥, and a minimum cutoff wave number (km), which increases with the magnetic field (compare, for instance the three panels in Fig. 2, or in Fig. 3). Increasing the magnetic field strength will also reduce the (maximum) growth rate, and can even suppress the instability if the anisotropy is not large enough. At the limit of marginal stability, the maximum growth rate γm → 0, and the two cutoffs approach each other km = kM. Theoretically, this is the condition of marginal stability, but an exact analytical form conditioning plasma parameters is not easily provided because km can be expressed analytically only for a large | f |  > 1, while kM for a small | f |  < 1. These cutoffs can, however, be derived exactly numerically, but, again, to correlate plasma parameters for the limit condition km = kM at marginal stability (γm = 0) is not straightforward. At very low values of γ → 0 (or, equivalently, close to kmin = kmax) plasma parameters do not change very much and differences are difficult to distinguish. Moreover, a numerical computation of the marginal threshold γm = 0 also restricts one to the precision limit, setting to zero any values of the growth rate that are lower than this limit. Instead, we adopted a procedure that is very well established (see papers published in the past two decades by Gary and his group), and adequate for our purposes, as it is sufficient to identify the lowest thresholds governed by the same effects of the suprathermal populations and relevant for the marginal stability. Thus, we derive the instability thresholds corresponding to (finite) low levels of the maximum growth rate. These must be chosen low enough that the effects of the suprathermals may be representative for all the other lower thresholds, down to the marginal limit of stability (γm → 0).

thumbnail Fig. 1

Effect of power-index κ = 2, 6, ∞ (Maxwellian) on the thresholds of the electron whistler-cyclotron instability for four levels of the maximum growth rates γm/Ω = 10-1, 10-2, 10-3, and 10-4.

Using the dispersion relation (8), the electron whistler-cyclotron instability thresholds are derived exactly numerically for four different levels of the maximum growth rates γm/Ω = 10-4, 10-3, 10-2, and 10-1. The anisotropy thresholds are calculated for an extended range of the plasma beta parameter 0.01 ≤ β∥ ≤ 10, including conditions in the solar wind and magnetospheric plasma. The inverse correlation law between temperature anisotropy, A = T⊥/T∥, and plasma beta, β∥, is obtained by fitting thresholds with (Gary & Wang 1996) 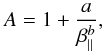A=1+aβ∥b,\begin{eqnarray} A = 1 + {a \over \beta_{\parallel}^b}, \label{e9} \end{eqnarray}(9)where the fitting parameters a and b are shown in Table 1. Contours of the maximum growth rates (in units of Ω) are displayed in Fig. 1, with solid lines for the bi-Maxwellian, and dashed lines for the bi-Kappa model (κ = 2,6). As expected, the anisotropy thresholds decrease with plasma beta because we need lower anisotropies to ignite the instability for a hotter plasma.

For high levels of the maximum growth rates, e.g., 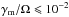\hbox{$\gamma_{\rm m}/\Omega \leqslant 10^{-2}$}, the anisotropy threshold increases in the presence of suprathermal populations, making this instability less effective in a bi-Kappa distributed plasma. This could explain the stable plasma configurations in the fast solar wind, which are restrained to narrow limits of small β∥ ≲ 1 (Stverak et al. 2008). However, for the lowest levels of the maximum growth rates, e.g., γm/Ω < 10-2, which are more relevant for the marginal stability (γ → 0), the anisotropy threshold is markedly lowered in the presence of suprathermal electrons for the full range of plasma beta \hbox{$10^{-2} \leqslant \beta_{\parallel} \leqslant 10$}. In this case, only two instability thresholds are displayed in Fig. 1 (the last two panels) corresponding to γm/Ω = 10-3 and 10-4, because suprathermal effects have been found to be similar for all other lower thresholds down to 10-6 (see Table 1).

Thus, the effect of suprathermal populations is found to be non-uniform, and the switch between these two opposite behaviors is localized close to the level γm/Ω = 10-2, where the anisotropy threshold does not change much with values of the power-index κ.

thumbnail Fig. 2

Effect of power-index κ = 2, 4, 6, 8, ∞ (Maxwellian) on the growth rates of the electron whistler-cyclotron instability for β∥ = 0.01, and three values of the temperature anisotropies A = T⊥/T∥ = 4.5 (top), 2.2 (middle), 1.5 (bottom).

thumbnail Fig. 3

Effect of power-index κ = 2, 4, 6, 8, ∞ (Maxwellian) on the growth rates of the electron whistler-cyclotron instability for β∥ = 1.0, and three values of the temperature anisotropies A = T⊥/T∥ = 2.0 (top), 1.3 (middle), 1.2 (bottom).

thumbnail Fig. 4

Effect of power-index κ = 2, 4, 6, 8, ∞ (Maxwellian) on the frequencies of the electron whistler-cyclotron instability for β∥ = 1, and two values of the temperature anisotropies A = T⊥/T∥ = 2.0 (top), 1.3 (bottom).

2.2. Correlating thresholds and growth rates

Growth rates of the electron whistler-cyclotron instability are derived exactly numerically and are displayed in Figs. 2 and 3 for two relevant values of the plasma beta parameter, βp, ∥ = 0.01 and βp, ∥ = 1, respectively. Again, two opposite effects of suprathermal populations can easily be recognized when we compare the top and bottom panels. These effects depend on the temperature anisotropy and the plasma parameter. Thus, while the higher growth rates are suppressed (top panels), the lower growth rates are enhanced (bottom panels) by a decreasing κ → 2. To correlate with the instability threshold conditions, temperature anisotropies were chosen to be in the same range as the threshold values, see Fig. 1. The effect of suprathermal electrons on the growth rates is now consistent with that found above for the thresholds. At lower thresholds (γm/Ωp < 10-2), close to marginal stability, growth rates increase with enhancing suprathermal populations (low values of κ-index). The influence of power index κ is lowest only close to the switch level (γm/Ωp = 10-2). As mentioned above, this critical switching level of the threshold is not always the same, but it depends on plasma beta: for βp, ∥ = 0.01 it is found to be close to Ap = 2.2, while for βp, ∥ = 1 it approaches Ap = 1.3. Above this critical level, growth rates are inhibited by the suprathermal populations, and the anisotropy thresholds (γm/Ωp = 10-1) increase.

The influence of suprathermals on the oscillatory frequency of this instability is shown in Fig. 4, with the remark that the effect can be significant (lowering the wave frequency) only for a sufficiently high anisotropy, far from thresholds. Otherwise, for low anisotropies, changes of the wave frequency are minimal.

Concluding, the present results provide an explicit and coherent characterization of the electron whistler-cyclotron instability in bi-Kappa distributed plasmas. We have found that the instability thresholds can be very sensitive to the value of the κ-index. The lowest (including marginal) thresholds (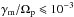\hbox{$\gamma_{\rm m} / \Omega_{\rm p} \leqslant 10^{-3}$}) decrease in the presence of suprathermal electrons, in perfect agreement with an enhancing of the growth rates. The effect is opposite at higher anisotropies, raising questions about the physics that underly this dual behavior, and the switching critical anisotropy. The answer resides in the number of resonant electrons that transfer energy to the instability. At large anisotropies, the transverse profile of the distribution function is wide enough so that an increase of power-index κ → ∞ is equivalent with an increase of this number of resonant electrons. For low anisotropies, the resonant wave-phase speed increases due to a significant Doppler shift introduced by the parallel thermal velocity, so that the number of resonant electrons (in the tail) decreases with increasing power-index κ → ∞.

3. Conclusions

Distributions of electrons measured in the solar wind and magnetosphere exhibit a constant and finite thermal spread and are overall better described by the Kappa distribution functions, which incorporate both the cooler core, and the suprathermal and highly anisotropic halo populations. We have investigated the electron whistler-cyclotron instability driven by a temperature anisotropy (T⊥ > T∥) of a bi-Kappa distributed plasma for conditions typically encountered in magnetosphere and different altitudes in the solar wind. This instability stimulates the electron cyclotron emissions that are widely invoked in astrophysics and fusion plasma experiments.

Although many studies have extensively described the effects of suprathermal electrons (parameterized by the power index κ) on the growth rates of the whistler instability, details have not been given to the instability threshold condition, but only some contradictory statements. Thus, the large temperature anisotropies invoked by some previous investigations cannot be relevant for the instability threshold. Moreover, the conclusion that thresholds are not affected by the presence of suprathermals is not consistent with the enhancing effect of the growth rates at low anisotropies. Here, instead, we provided a unitary characterization of this instability, showing rigorously that, depending on their levels, the instability thresholds (including the marginal stability) can be very sensitive to the value of κ-index.

The instability thresholds have been determined exactly numerically and in close correlations with the growth rates, which exhibit a nonuniform dependence of the power-index κ and implicitly of the density of suprathermal populations. Consequently, the effect of suprathermal electrons is found to be markedly dependent on the temperature anisotropy and the plasma beta. Thus, the lowest thresholds, 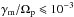\hbox{$\gamma_{\rm m} / \Omega_{\rm p} \leqslant 10^{-3}$}, close to the marginal stability conditions, decrease with the increase of suprathermal populations. This result is fully predicted by the enhanced fluctuations of this instability for sufficiently low anisotropies. For higher anisotropies, far from threshold conditions, the presence of suprathermal electrons has an opposite effect, suppressing the growth rates and increasing the thresholds. This evolution does not apply to the marginal conditions of instability, but could be relevant in the context of an interplay with the mirror instability, driven principally by protons (with T⊥ > T∥), and for which the (linear) dispersion theory predicts lower growth rates. For a large βp, ∥ > 1, the increase of parallel temperature is constrained by the firehose instability (Lazar & Poedts 2009; Lazar et al. 2011b). The new marginal thresholds calculated with a bi-Kappa model are expected to provide better predictions for the limits of the temperature anisotropy in the solar wind.

1

Growth rates diminish with increasing angle to the magnetic field, and vanish at some critical angle. Harder distributions with high-energy tails, like the Kappa power-law, will produce a larger cone of instability, but the maximum remains at parallel propagation (Kennel & Petschek 1966).

Acknowledgments

We are grateful to the anonymous referee for valuable criticism and suggestions that helped us to improve the paper. M.L. acknowledges financial support from the EU Commission and Research Foundation Flanders (FWO) as FWO Pegasus Marie Curie Fellow (grant 1.2.070.13). The authors acknowledge support from the Ruhr-Universität Bochum, the Deutsche Forschungsgemeinschaft (DFG), grant Schl 201/21-1, and by the Katholieke Universiteit Leuven. These results were obtained in the framework of the projects GOA/2009-009 (KU Leuven), G.0729.11 (FWO-Vlaanderen), and C 90347 (ESA Prodex 9). The research leading to these results has also received funding from the European Commission’s Seventh Framework Programme (FP7/2007-2013) under the grant agreements SOLSPANET (project No. 269299, http://www.solspanet.eu), SPACECAST (project No. 262468, fp7-spacecast.eu), eHeroes (project No. 284461, http://www.eheroes.eu) and SWIFF (project No. 263340, http://www.swiff.eu).

References

  1. Bale, S. D., Kasper, J. C., Howes, G. G., et al. 2009, Phys. Rev. Lett., 103, 211101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  2. Feldman, W. C., Asbridge, J. R., Bame, S. J., Montgomery, M. D., & Gary, S. P. 1975, JGR, 80, 4181 [Google Scholar]
  3. Fisk, L. A., & Gloeckler, G. 2006, ApJ, 640, L79 [NASA ADS] [CrossRef] [Google Scholar]
  4. Gary, S. P. 1993, Theory of Space Plasma Microinstabilities (Cambridge: University Press) [Google Scholar]
  5. Gary, S. P., & Karimabadi, H. 2006, JGR, 111, A11224 [Google Scholar]
  6. Gary, S. P., & Nishimura, K. 2003, Phys. Plasmas, 10, 3571 [NASA ADS] [CrossRef] [Google Scholar]
  7. Gary, S. P., & Wang, J. 1996, JGR, 101, 10,749 [Google Scholar]
  8. Gary, S. P., Lavraud, B., Thomsen, M. F., Lefebvre, B., & Schwartz, S. 2005, GRL, 32, L13109 [NASA ADS] [CrossRef] [Google Scholar]
  9. Hellinger, P., Travnicek, P., Kasper, J. C., & Lazarus, J. J. 2006, Geophys. Res. Lett., 33, L09101 [NASA ADS] [CrossRef] [Google Scholar]
  10. Helliwell, R., Crary, J., Pope, J., & Smith, R. 1956, JGR, 61, 139 [Google Scholar]
  11. Kennel, C. F., & Petschek, H. E. 1966, JGR, 71, 1 [NASA ADS] [CrossRef] [Google Scholar]
  12. Lazar, M. 2012, A&A, 547, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Lazar, M., & Poedts, S. 2009, A&A, 494, 311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Lazar, M., Schlickeiser, R., Poedts, S., & Tautz, R. C. 2008a, MNRAS, 390, 168 [NASA ADS] [CrossRef] [Google Scholar]
  15. Lazar, M., Schlickeiser, R., & Shukla, P. K. 2008b, Phys. Plasmas, 15, 042103 [NASA ADS] [CrossRef] [Google Scholar]
  16. Lazar, M., Schlickeiser, R., & Poedts, S. 2009, Phys. Plasmas, 16, 012106 [NASA ADS] [CrossRef] [Google Scholar]
  17. Lazar, M., Schlickeiser, R., & Poedts, S. 2010, Phys. Plasmas, 17, 062112 [NASA ADS] [CrossRef] [Google Scholar]
  18. Lazar, M., Poedts, S., & Schlickeiser, R. 2011a, MNRAS, 410, 663 [NASA ADS] [CrossRef] [Google Scholar]
  19. Lazar, M., Poedts, S., & Schlickeiser, R. 2011b, A&A, 534, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Leubner, M. P., & Schupfer, N. 2000, JGR, 105, 27387 [NASA ADS] [CrossRef] [Google Scholar]
  21. Leubner, M. P., & Schupfer, N. 2001, JGR, 106, 12993 [NASA ADS] [CrossRef] [Google Scholar]
  22. Lu, Q., Zhou, L., & Wang, S. 2010, JGR, 115, A02213 [NASA ADS] [CrossRef] [Google Scholar]
  23. Mace, R. L. 1998, JGR, 103, 14643 [Google Scholar]
  24. Mace, R. L., & Sydora, R. D. 2010, JGR, 115, A07206 [Google Scholar]
  25. Maksimovic, M., Pierrard, V., & Lemaire, J. F. 1997, A&A, 324, 725 [NASA ADS] [Google Scholar]
  26. Maruca, B. A., Kasper, J. C., & Bale, S. D. 2011, Phys. Rev. Lett., 107, 201101 [NASA ADS] [CrossRef] [Google Scholar]
  27. Paesold, G., & Benz, A. O. 1999, A&A, 351, 741 [NASA ADS] [Google Scholar]
  28. Pierrard, V., Maksimovic, M., & Lemaire, J. F. 1999, JGR, 104, 17021 [Google Scholar]
  29. Pierrard, V., Maksimovic, M., & Lemaire, J. F. 2001, JGR, 106, 29305 [Google Scholar]
  30. Pilipp, W. G., Miggenrieder, H., Montgomery, M. D., et al. 1987, JGR, 92, 1075 [NASA ADS] [CrossRef] [Google Scholar]
  31. Pilipp, W. G., Miggenrieder, H., Montgomery, M. D., et al. 1990, JGR, 95, 6305 [NASA ADS] [CrossRef] [Google Scholar]
  32. Pokhotelov, O. A., Treumann, R. A., Sagdeev, R. Z., et al. 2002, JGR, 107, 1312 [CrossRef] [Google Scholar]
  33. Salem, C., Hubert, D., Lacombe, C., et al. 2003, ApJ, 585, 1147 [NASA ADS] [CrossRef] [Google Scholar]
  34. Schlickeiser, R., Lazar, M., & Skoda, T. 2011, Phys. Plasmas, 18, 012103 [NASA ADS] [CrossRef] [Google Scholar]
  35. Scudder, J. D. 1992, ApJ, 398, 299 [NASA ADS] [CrossRef] [Google Scholar]
  36. Stverak, S., Travnicek, P., Maksimovic, M., et al. 2008, JGR, 113, A03103 [Google Scholar]
  37. Summers, D., & Thorne, R. M. 1991, Phys. Fluids B, 3, 1835 [NASA ADS] [CrossRef] [Google Scholar]
  38. Summers, D., & Thorne, R. M. 1992, JGR, 97, 16827 [Google Scholar]
  39. Xue, S., Thorne, R. M., & Summers, D. 1996a, JGR, 101, 15457 [NASA ADS] [CrossRef] [Google Scholar]
  40. Xue, S., Thorne, R. M., & Summers, D. 1996b, JGR, 101, 15467 [Google Scholar]
  41. Xiao, F., Thorne, R. M., & Summers, D. 1998, Phys. Plasmas, 5, 2489 [NASA ADS] [CrossRef] [Google Scholar]
  42. Tripathi, A. K., & Singhal, R. P. 2008, Planet. Space Sci., 56, 310 [NASA ADS] [CrossRef] [Google Scholar]
  43. Vasyliunas, V. M. 1968, JGR, 73, 2839 [Google Scholar]

Appendix A: Derivatives of the distribution function

The partial derivatives in the dispersion relation (4) are provided here for the bi-Kappa function (1) ∂F∂v∥=−2π3/2θ⊥2θ∥ Γ(κ+2)κ5/2Γ(κ−1/2)×{ϵ1 v∥−v1θ12 [1+(v∥−v1)2κθ12+v⊥2κθ⊥2]−κ−2+ϵ2 v∥+v2θ22 [1+(v∥+v2)2κθ22+v⊥2κθ⊥2]−κ−2},∂F∂v⊥=−2v⊥π3/2θ⊥4θ∥ Γ(κ+2)κ5/2Γ(κ−1/2)×{ϵ1 [1+(v∥−v1)2κθ12+v⊥2κθ⊥2]−κ−2+ϵ2 [1+(v∥+v2)2κθ22+v⊥2κθ⊥2]−κ−2}.\appendix \setcounter{section}{1} \begin{eqnarray} {\partial F \over \partial v_{\parallel}} &= &- {2 \over \pi^{3/2} \theta_{\perp}^2 \theta_{\parallel}} \, {\Gamma (\kappa +2) \over \kappa^{5/2} \Gamma(\kappa -1/2)} \notag \\ && \times \Biggl\{\epsilon_1 \, {v_{\parallel}-v_1 \over \theta_1^2} \, \left[1 + {(v_{\parallel}-v_1)^2 \over \kappa \theta_1^2} +{v_{\perp}^2 \over \kappa \theta_{\perp}^2}\right]^{-\kappa -2} \notag \\ & & +\epsilon_2 \, {v_{\parallel}+ v_2 \over \theta_2^2}\, \left[1+{(v_{\parallel}+v_2)^2 \over \kappa \theta_2^2} +{v_{\perp}^2 \over \kappa \theta_{\perp}^2} \right]^{-\kappa -2} \Biggr\}, \\ {\partial F \over \partial v_{\perp}}& = &- {2 v_{\perp} \over \pi^{3/2} \theta_{\perp}^4 \theta_{\parallel}} \, {\Gamma (\kappa +2) \over \kappa^{5/2} \Gamma(\kappa -1/2)} \notag \\ && \times \Biggl\{\epsilon_1 \, \left[1 + {(v_{\parallel}-v_1)^2 \over \kappa \theta_1^2} +{v_{\perp}^2 \over \kappa \theta_{\perp}^2}\right]^{-\kappa -2} \notag \\ & & +\epsilon_2 \, \left[1+{(v_{\parallel}+v_2)^2 \over \kappa \theta_2^2} +{v_{\perp}^2 \over \kappa \theta_{\perp}^2} \right]^{-\kappa -2} \Biggr\}. \end{eqnarray}

All Tables

Table 1

Electron temperature anisotropy fitting parameters from Eq. (9).

In the text

All Figures

thumbnail Fig. 1

Effect of power-index κ = 2, 6, ∞ (Maxwellian) on the thresholds of the electron whistler-cyclotron instability for four levels of the maximum growth rates γm/Ω = 10-1, 10-2, 10-3, and 10-4.
In the text
thumbnail Fig. 2

Effect of power-index κ = 2, 4, 6, 8, ∞ (Maxwellian) on the growth rates of the electron whistler-cyclotron instability for β∥ = 0.01, and three values of the temperature anisotropies A = T⊥/T∥ = 4.5 (top), 2.2 (middle), 1.5 (bottom).
In the text
thumbnail Fig. 3

Effect of power-index κ = 2, 4, 6, 8, ∞ (Maxwellian) on the growth rates of the electron whistler-cyclotron instability for β∥ = 1.0, and three values of the temperature anisotropies A = T⊥/T∥ = 2.0 (top), 1.3 (middle), 1.2 (bottom).
In the text
thumbnail Fig. 4

Effect of power-index κ = 2, 4, 6, 8, ∞ (Maxwellian) on the frequencies of the electron whistler-cyclotron instability for β∥ = 1, and two values of the temperature anisotropies A = T⊥/T∥ = 2.0 (top), 1.3 (bottom).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.