| Issue |
A&A
Volume 554, June 2013
|
|
|---|---|---|
| Article Number | A111 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201220171 | |
| Published online | 13 June 2013 | |
Modeling the processing of interstellar ices by energetic particles
Engineering Research Institute “Ventspils International Radio Astronomy Center” of Ventspils University College (VIRAC), Latvia
e-mail: kalvans@lu.lv
Received: 6 August 2012
Accepted: 30 April 2013
Context. Interstellar ice is the main form of metal species in dark molecular clouds. Experiments and observations have shown that the ice is significantly processed after the freeze-out of molecules onto grains. The processing is caused by cosmic-ray particles and cosmic-ray-induced UV photons. These transformations are included in current astrochemical models only to a very limited degree.
Aims. We aim to establish a model of the “cold” chemistry in interstellar ices and to evaluate its general impact on the composition of interstellar ices.
Methods. The ice was treated as consisting of two layers – the surface and the mantle (or subsurface) layer. Subsurface chemical processes are described with photodissociation of ice species and binary reactions on the surfaces of cavities inside the mantle. Hydrogen atoms and molecules can diffuse between the layers. We also included deuterium chemistry.
Results. The modeling results show that the content of chemically bound H is reduced in subsurface molecules by about 30% on average. This promotes the formation of more hydrogen-poor species in the ice. The enrichment of ice molecules with deuterium is significantly reduced by the subsurface processes. On average, it follows the gas-phase atomic D/H abundance ratio, with a delay. The delay produced by the model is on the order of several Myr.
Conclusions. The processing of ice may place new constraints on the production of deuterated species on grains. In a mantle with a two-layer structure the upper layer (CO) should be processed substantially more intensively than the lower layer (H2O). Chemical explosions in interstellar ice might not be an important process. They destroy the structure of the mantle, which forms over long timescales. Besides, ices may lack the high radical content needed for the explosions.
Key words: astrochemistry / molecular processes / ISM: molecules / ISM: clouds
© ESO, 2013
1. Introduction
One of the important periods in the transformation process of gas into stars is the pre-stellar core (PSC) phase. This period lasts not much longer than one Myr (Lee & Myers 1999; Enoch et al. 2008; Schnee et al. 2012). Most elements heavier than He (referred to throughout as metals) are either locked in the interstellar dust-grains, or freeze onto the grains as icy mixtures.
The ice is formed by the accretion of atoms and the subsequent formation of molecules on the surface, such as H2O and most other species, or by the direct accretion of molecules, such as CO (Öberg et al. 2011a). The formation occurs first in steps that affect the chemical composition and physical structure of the ice. In the dark PSCs it is processed mainly by cosmic rays (CR) and cosmic-ray-induced photons as well as interstellar ultraviolet (UV) and X-ray photons, radioactive decay events, and heating by exothermic reactions. Particularly important are heavy cosmic rays, mostly Fe nuclei (Fe-CR) (Leger et al. 1985).
Astrochemical models usually include gas and grain surface as the chemically active phases (e.g. Hasegawa & Herbst 1993b; Roberts et al. 2007; Albertsson et al. 2011). However, both observations of interstellar matter and astrochemistry laboratory simulations have shown that the processing of ice is not limited to the outer surface.
First, the interstellar ice seems to be compact instead of porous. The porous structure is expected to form from molecules accreting on the surface at 10 K. The timescale for mantle compaction calculated from experiments with UV photons, exothermic reactions, and energetic ions is from a few up to 50 Myr (Raut et al. 2008; Palumbo et al. 2010; Accolla et al. 2011). The icy mantles tend to be mixtures. Their compaction is slower than that of pure substances and it could never be completed during the cloud lifetime (Palumbo 2006). Observations of pure ices and mixtures consisting of two species indicate that the mantle is segregated in chemically different layers (Pontoppidan et al. 2003; Öberg et al. 2011a; Linnartz et al. 2011). The segregation can be attributed to the heating for ices already in the protostellar phase (Öberg et al. 2009b). Temporal heating events by UV photons and cosmic rays may induce ice segregation in prestellar phases. Among other things, the observation of differentiated layers indicates the ability of molecules to move along the thickness of the ice over timescales relevant to PSCs.
Second, the ice mantle on the grains is subjected to chemical processing by UV photons and cosmic rays. Multiple experiments (e.g. Gerakines et al. 1996, 2004; Andersson & van Dishoeck 2008; Öberg et al. 2009b,a, 2011b, among recent papers) show that the composition of ice irradiated by ionizing photons can be quite different from the initial one, regardless of whether it was pure substance or a mixture. Similarly, suprathermal reactions and the appearance of new species are induced by ice irradiation by fast ions (e.g. Millar & Williams 1993, Chap. 14). Mechanisms for these processes include the generation of radicals, migration, and reactions of species in elevated temperature.
A solution was proposed to quantitatively describe the “cold” processing of the mantle by Kalvāns & Shmeld (2010, Paper I). The model described there includes a few key concepts:
-
The molecules frozen onto the grains are assumed to be dividedinto two layers – the surface and the mantle. The mantle alsoincludes molecules on the surfaces of closed cavities inside theice. Thus, there is a total of three phases – the outer surface, themantle volume, and the cavities.
-
Molecules in these phases are subjected to photodissociation by UV photons. In the dark conditions of PSCs, only CR-induced photons have a sufficiently high flux to be important.
-
Reactions occur on the outer surface and the surface of the cavities. The inclusion of the chemically active cavity phase makes the system different from the three-phase model of Hasegawa & Herbst (1993b). The reactions in the cavities consume the radicals generated in mantle by photodissociation.
-
The cavities themselves are processed (resurfaced, destroyed, generated again) by cosmic-ray hits. Most of the molecules and radicals in the mantle are cycled through the cavity phase and thus the reactions on the inner surfaces are able to affect the whole mantle.
-
The diffusion of hydrogen occurs through the mantle. This process is described as a transition from one ice phase to another. Only surfaces are considered as the stable residence sites for H and H2, following Strauss et al. (1994). In Paper I only the outer and cavity surfaces were considered for the diffusion of H. In this work (Sect. 4.2) the mantle volume phase is included, too. It is represented by micropores that can host one or several H atoms, but are too small for reactions involving metal atoms to occur.
Notably, the model does not include chemical transformations induced directly by cosmic-ray hits. The astrochemical database used (udfa06) does not contain dissociation reactions for metal molecules hit by cosmic-ray protons.
In this paper we aim to study the effects of subsurface mantle chemistry in more detail. The approach outlined in Paper I is kept with some improvements. The time-dependence for the evolution of the composition of the mantle and deuterium chemistry are investigated. Molecules with a high enrichment of deuterium are characteristic for PSCs (see, e.g. Caselli 2011). There are indications that the solid species of the icy grain-mantles are highly deuterated, too, and evaporate to the gas-phase (e.g. Mangum et al. 1991). The deuteration is usually attributed to gas phase chemistry with the isotopologs of 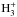 (Millar et al. 1989; Roberts & Millar 2000; Roberts et al. 2004) that act as important intermediate reactants. They produce an overabundance of atomic D, which then accretes onto dust-grains and reacts with other surface molecules, producing highly deuterated species. When the accretion continues, surface is covered and surface molecules are incorporated into the mantle. In our model they are still subjected to the dissociation by CR-induced UV photons and chemical reactions on cavity surfaces.
(Millar et al. 1989; Roberts & Millar 2000; Roberts et al. 2004) that act as important intermediate reactants. They produce an overabundance of atomic D, which then accretes onto dust-grains and reacts with other surface molecules, producing highly deuterated species. When the accretion continues, surface is covered and surface molecules are incorporated into the mantle. In our model they are still subjected to the dissociation by CR-induced UV photons and chemical reactions on cavity surfaces.
The paper is organized as follows. General chemical input data, information on the gas-phase chemistry, and specific information about photoreactions are given in Sect. 2. All processes that are directly related to surfaces are described in Sect. 3. The most important novelty introduced in the model is the concept of cavities within the ice mantle. The processes related specifically to the cavities are described in Sect. 4. At the end of the description of the calculation methodology the summary rate equations are given in Sect. 5. The outcome of the simulation is described in detail in Sect. 6. Finally, the conclusions form the results are briefly discussed in Sect. 7.
2. Chemical data
A cloud with constant density of hydrogen atoms nH = 105 cm-3, gas temperature Tg = 15 K, and dust temperature Td = 10 K was modeled for the integration times up to t = 9.5 × 1013 s, which equals approximately 3 Myr. The integration times used are beginning from 1.4 × 1012 s, multiplied by a factor of 1.42 and rounded to two significant numbers until a total of 13 steps was reached. Initially, all elements were assumed to be in atomic form. Calculations with shorter integration times were considered to be scientifically irrelevant.
2.1. Species and reactions
The UMIST udfa06 dipole astrochemistry database (Woodall et al. 2007) was used to provide the gas-phase chemical reaction set (Sect. 2.3). The permitted elements were H, D, He, C, N, O, Na, Mg, S, and Fe, and their relative abundance and depletion are specified in Table 1.
In total, the model includes 450 chemical species with more than 10 000 reactions. No species with more than four heavy atoms and four hydrogen atoms are included, with the sole exception of CH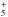 and its hydrogen isotopologs. Of these species, 186 neutral species are refractory, accreting and participating in the chemistry on the grains. We reduced the number of chemical species to facilitate the calculations. The aim of this paper is to investigate the general effects of the subsurface processes, not to model the whole chemistry of an interstellar cloud core.
and its hydrogen isotopologs. Of these species, 186 neutral species are refractory, accreting and participating in the chemistry on the grains. We reduced the number of chemical species to facilitate the calculations. The aim of this paper is to investigate the general effects of the subsurface processes, not to model the whole chemistry of an interstellar cloud core.
Outer and cavity surface reactions are described with the approach described by Hasegawa et al. (1992) (Sect. 3.3). The dissociation by CR-induced photons for all ice species is included, with the rates provided in the gas-phase udfa06 database and modified by the respective dissociation yield for each ice phase (Sect. 2.4).
Adopted abundances and depletion of elements in the model.
All processes in the model are described in terms of rate equations. This applies to first and second order chemical reactions and phase transitions (Sects. 2.3, 2.4, 3.1, 3.2, 4). The general rate equation for a first-order process is 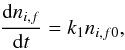 (1)where dni,f is the abundance change (cm-3 s-1) of species i in phase f, k1 is the rate coefficient (s-1), and ni,f0 is the abundance of i in the initial phase (cm-3). The phases f and f0 are either gas g, outer-surface S, cavity-surface C, or mantle M. For chemical reactions (usually) f = f0.
(1)where dni,f is the abundance change (cm-3 s-1) of species i in phase f, k1 is the rate coefficient (s-1), and ni,f0 is the abundance of i in the initial phase (cm-3). The phases f and f0 are either gas g, outer-surface S, cavity-surface C, or mantle M. For chemical reactions (usually) f = f0.
The rate (cm-3 s-1) of second-order reactions of type l + j → i is calculated by the equation 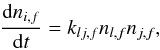 (2)where klj,f (cm3 s-1) is the second-order rate coefficient.
(2)where klj,f (cm3 s-1) is the second-order rate coefficient.
2.2. Including H isotopolog reactions
Deuterium is involved in the reaction network following the approach by Rodgers & Millar (1996). That is, the rate of a gas-phase reaction is equal for deuterated and non-deuterated species and statistical branching ratios for reaction outcomes are assumed. For surface reactions, the reaction rate of deuterium species is modified to take into account their different molar mass according to Hasegawa et al. (1992). An approximation is made that in a molecule there is no distinction between H or D atoms attached to different heavy atoms. For example, methanol is treated as CH4O, not CH3OH. This approximation facilitates calculations at the cost of only little loss of information because the actual fate of different hydrogen atoms in a reaction is usually unknown anyway. The gas-phase deuterium exchange reactions given by Roberts & Millar (2000) and Roberts et al. (2004) are added to the reaction list.
2.3. Gas-phase reactions
The rate of first-order reactions in gas phase (f = f0 = g) is calculated according to Eq. (1) with the rate coefficient kudfa1 (s-1) from the udfa06 database. It is obtained as explicitly given in Woodall et al. (2007), Eqs. (2)–(4). The first-order reactions are direct cosmic-ray ionization, cosmic-ray-induced photoreactions, and interstellar photoreactions. For the latter the extinction of the interstellar UV radiation field AV = 20 mag, which makes these photoreactions rather unimportant.
The rate of second-order gas-phase reactions is calculated in accordance with Eq. (2) (f = g). The respective rate constant kudfa2 is obtained by the reaction coefficients given in udfa06, as in Woodall et al. (2007), Eq. (1).
2.4. Solid-phase cosmic-ray-induced photodissociation
The dissociation by cosmic-ray-induced UV photons for gas, surface, mantle, and cavity phase molecules is based on data from the udfa06 database. The photodissociation rate for a solid-phase molecule (f = f0 = S,C or M) i is a first-order process, calculated according to Eq. (1) with a rate coefficient 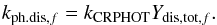 (3)kCRPHOT is the respective rate coefficient from the udfa06 database (s-1) and Ydis,tot,f is the quantum yield for dissociation in the solid phases. We assumed that the dissociation properties for molecules in ice remain the same as in the gas-phase. Ionization is not taken into account for solid-phase species. Ydis,tot,f is different for each of the three ice phases and is calculated by
(3)kCRPHOT is the respective rate coefficient from the udfa06 database (s-1) and Ydis,tot,f is the quantum yield for dissociation in the solid phases. We assumed that the dissociation properties for molecules in ice remain the same as in the gas-phase. Ionization is not taken into account for solid-phase species. Ydis,tot,f is different for each of the three ice phases and is calculated by 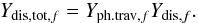 (4)Yph.trav,f is the probability for a photon to reach a monolayer of certain (average) depth in the mantle, characteristic for the phase f. Ydis,f is the probability that the dissociation products survive in the phase f and do not recombine in situ. For mantle- and cavity-phase molecules Yph.trav,f corresponds to the middle of a 100-monolayer thick mantle. The absorption in UV for each monolayer is 0.02 (Hartquist & Williams 1990).
(4)Yph.trav,f is the probability for a photon to reach a monolayer of certain (average) depth in the mantle, characteristic for the phase f. Ydis,f is the probability that the dissociation products survive in the phase f and do not recombine in situ. For mantle- and cavity-phase molecules Yph.trav,f corresponds to the middle of a 100-monolayer thick mantle. The absorption in UV for each monolayer is 0.02 (Hartquist & Williams 1990).
Ydis,f is largely unknown, especially for astronomically relevant timescales, although many photolysis experiments have been conducted (see Sect. 1). We used values that produce feasible results and seem physically adequate. Higher photodissociation yields need a higher proportion of ice species in the chemically active cavity phase Xcav, so that the radicals can be consumed and turned into molecules. Ydis,f is adjusted for Xcav ≈ 1% with a radical content of a few per cent at most. On the outer surface, dissociation products H and H2 and their deuterium analogs escape into the gas phase as described in Hartquist & Williams (1990) (see also Paper I).
In addition to the three solid phases, photodissociation is separately considered for mantle-phase molecules that happen to reside directly next to a cavity. The proportion in ice of these species is assumed to be equal to Xcav, i.e., 1%. In the model their dissociation products enter the cavity and thus change their phase (f = C and f0 = M). The dissociation yield for these molecules is the same as for other mantle-phase species, and the rate coefficient (s-1) is 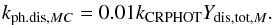 (5)
(5)
3. Surface-related processes
3.1. Accretion
The outer surface is defined as the porous layer of molecules on top of the denser mantle. Surface-phase species are exposed to surface reactions and desorption processes. The rates of neutral molecule and atom accretion onto grains are calculated according to the first-order rate Eq. (1) with f = S and f0 = g. The relevant rate coefficient (s-1) is calculated according to Willacy & Williams (1993): 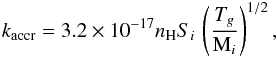 (6)where Si is the assumed sticking coefficient, Mi is the molecular mass of species i in atomic mass units, and nH is the total hydrogen nucleon density. Following Brown & Charnley (1990), Smetal = 1.0. For the light species H, D, H2, HD, and D2 a lower value is used, SH = 1/3Smetal, as in Paper I, i.e. SH = 0.33.
(6)where Si is the assumed sticking coefficient, Mi is the molecular mass of species i in atomic mass units, and nH is the total hydrogen nucleon density. Following Brown & Charnley (1990), Smetal = 1.0. For the light species H, D, H2, HD, and D2 a lower value is used, SH = 1/3Smetal, as in Paper I, i.e. SH = 0.33.
3.2. Desorption
The desorption rate of species from the surface into the gas-phase (f = g,f0 = S) is a first-order process, Eq. (1). kdes, s-1, is the rate coefficient. There are five desorption mechanisms included in the model. For thermal evaporation the rate coefficient is the inverse evaporation time tevap from Hasegawa et al. (1992), Table 1. The desorption via grain heating by cosmic rays is treated as in Hasegawa & Herbst (1993a): 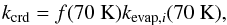 (7)where f(70 K) is the fraction of the time spent by grains in the vicinity of 70 K and kevap,i (70 K) is the evaporation rate coefficient for species i at 70 K, (Hasegawa & Herbst 1993a, Eq. (14)). f(70 K) is calculated as
(7)where f(70 K) is the fraction of the time spent by grains in the vicinity of 70 K and kevap,i (70 K) is the evaporation rate coefficient for species i at 70 K, (Hasegawa & Herbst 1993a, Eq. (14)). f(70 K) is calculated as 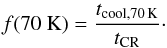 (8)tcool, s, is the time-scale for grain cooling via desorption of volatiles (10-5 s) and tCR is the average time between two successive Fe-CR hits on the grain. tCR = 10-12 s from Bringa & Johnson (2004) results in a rate coefficient higher than that in Hasegawa & Herbst (1993a).
(8)tcool, s, is the time-scale for grain cooling via desorption of volatiles (10-5 s) and tCR is the average time between two successive Fe-CR hits on the grain. tCR = 10-12 s from Bringa & Johnson (2004) results in a rate coefficient higher than that in Hasegawa & Herbst (1993a).
The rate coefficient for desorption by CR-induced photons (Prasad & Tarafdar 1983; Willacy & Williams 1993) is calculated by 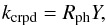 (9)where the photon hit rate Rph (s-1) for a single grain is
(9)where the photon hit rate Rph (s-1) for a single grain is 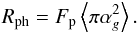 (10)The desorption yield Y is taken as 0.1, Fp is photon flux, 4875 cm-2 s-1, both from Roberts et al. (2007).
(10)The desorption yield Y is taken as 0.1, Fp is photon flux, 4875 cm-2 s-1, both from Roberts et al. (2007). 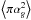 is the average cross section of a grain (1.0 × 10-10 cm2).
is the average cross section of a grain (1.0 × 10-10 cm2).
The rate of desorption of surface molecules by energy released by H2 molecule formation on grains is calculated according to the rate coefficient (Roberts et al. 2007): 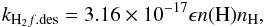 (11)where ϵ = 0.01 is number of molecules desorbed per act of H2 molecule formation, n(H) is the number density of atomic hydrogen in gas-phase (Roberts et al. 2007). The species desorbed are those with binding energies Eb ≤ 1210 K, with binding energies from Aikawa et al. (1997).
(11)where ϵ = 0.01 is number of molecules desorbed per act of H2 molecule formation, n(H) is the number density of atomic hydrogen in gas-phase (Roberts et al. 2007). The species desorbed are those with binding energies Eb ≤ 1210 K, with binding energies from Aikawa et al. (1997).
Summarizing the desorption rate coefficients: 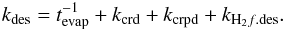 (12)In addition to desorption from the surface, we included a process of direct impulsive ejection of mantle species into the gas (Johnson et al. 1991) (f = g,f0 = M). The rate coefficient (s-1) is calculated as in Paper I:
(12)In addition to desorption from the surface, we included a process of direct impulsive ejection of mantle species into the gas (Johnson et al. 1991) (f = g,f0 = M). The rate coefficient (s-1) is calculated as in Paper I: 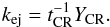 (13)YCR is the number of mantle molecules ejected by this process in each hit, assumed to be 1000 here, close to the upper limit from Johnson et al. (1991). It is the only direct mechanism for molecules to escape the subsurface layers of the frozen ice on grains. Impulsive ejection for surface species is insignificant compared to the desorption rates for other mechanisms and is not included in the model.
(13)YCR is the number of mantle molecules ejected by this process in each hit, assumed to be 1000 here, close to the upper limit from Johnson et al. (1991). It is the only direct mechanism for molecules to escape the subsurface layers of the frozen ice on grains. Impulsive ejection for surface species is insignificant compared to the desorption rates for other mechanisms and is not included in the model.
3.3. Binary reactions on surfaces
The rate of binary reactions (second-order process, cm-3 s-1) on the outer surface (f = S) and the cavity surface (f = C) is calculated according to Eq. (2). The respective rate coefficient is calculated as in Hasegawa et al. (1992): 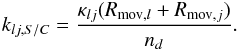 (14)Rmov is the movement (diffusion on surface) rate for each respective reactant, κlj is the probability for molecules to overcome the activation energy barrier upon encounter for the reaction to take place (Eq. (6) in Hasegawa et al. 1992), and nd = 1.33 × 10-12nH cm-3 is the abundance of dust-grains. Rmov is given by
(14)Rmov is the movement (diffusion on surface) rate for each respective reactant, κlj is the probability for molecules to overcome the activation energy barrier upon encounter for the reaction to take place (Eq. (6) in Hasegawa et al. 1992), and nd = 1.33 × 10-12nH cm-3 is the abundance of dust-grains. Rmov is given by 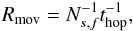 (15)where Ns,f is the number of adsorption sites on one of the two chemically active surface types (phases), thop is the hopping time from one adsorption site to the next for a particular molecule, calculated as given by Hasegawa et al. (1992), Eqs. (2), (3) and (10). For deuterium-containing species the movement rates are recalculated taking into account their increased molecular mass.
(15)where Ns,f is the number of adsorption sites on one of the two chemically active surface types (phases), thop is the hopping time from one adsorption site to the next for a particular molecule, calculated as given by Hasegawa et al. (1992), Eqs. (2), (3) and (10). For deuterium-containing species the movement rates are recalculated taking into account their increased molecular mass.
Hasegawa et al. (1992) used a value Ns,S = 106 for their surface reaction rate calculations. An increased value of Ns,S = 2 × 106 fits this simulation better, because surface roughness is an important feature of the model. The abundance of metal atoms in outer-surface and cavity phases is similar in the final integration time steps (Sect. 6.2), so Ns,C can be taken to be similar to Ns,S × Ns,C = 106, because the abundance of cavity species is significantly below the abundance of surface species and molecules will have fewer options for adsorption in the cramped cavities. For a simple representation one can imagine a mantle consisting of 100 monolayers that includes 1000 cavities that have 1000 adsorption sites each. It is important to note that Ns,C and Ns,S are assumed to be constant in the model, although the relative abundance of metals in surface- and mantle phases changes with time (Sects. 3.4 and 6.2).
3.4. Formation of the mantle
The mantle is formed by the transfer of molecules from the surface- to the mantle-phase. It is described as a reversible first-order phase transition, Eq. (1) with f = M and f0 = S for the forward and f = S and f0 = M for the reverse process. The gradual compaction of the ice layer is described by this approach in the model (see below).
Currently the structure of the ice phase on grains is usually described by two different methods in astrochemical modeling. Both are capable of yielding feasible results. Subsurface chemistry is not taken into account by any means in either of the calculation methods.
One method is to describe the ice mantle as a rigid structure, as e.g. in Hasegawa & Herbst (1993b) or Cuppen et al. (2009). The surface species are mobile, reactive, and subjected to desorption. Molecules in the layers below are frozen in place, forming a densely packed permanent structure divided into monolayers.
However, repeated experiments have shown that ices formed at cryogenic temperatures are porous (Accolla et al. 2011; Palumbo et al. 2010; Raut et al. 2007b, 2008). Molecules of considerable size (CO, CH4) are able to diffuse through an accumulate in these interstellar ice analogs (Palumbo 2006; Raut et al. 2007a). These molecules are initially deposited on the surface. Their diffusion into the depth of the ice layer means that the molecules in the porous ice are available for surface reactions. Moreover, the compaction of ice (see below) indicates that the molecules are able to move within the mantle in conditions and timescales relevant to dark clouds. One can conclude that a rigid mantle is a rough approximation of the astrophysical reality.
A simpler way is to treat the ice as a single phase, consisting of reactive (surface) species (e.g. Roberts et al. 2007; Semenov et al. 2010; van Weeren et al. 2009). In terms of this model it can be described as a porous layer, fully exposed to surface reactions. The experiments mentioned above have also shown that the porous ice becomes compact when subjected to energetic processes (ion and UV-photon irradiation, exothermic reactions). Observations of interstellar ices indicate that they are dense and segregated in chemically different layers (e.g. Jenniskens et al. 1995; Öberg et al. 2009a). The time of compaction is estimated to be from a few to 50 Myr, depending on the process considered. Icy mixtures, characteristic of interstellar ices, may be never completely compacted (Palumbo 2006).
When depleted metal abundances are used, one can assume that the single-ice-phase model includes the very upper layer of the ice mantle only. The surface phase is intimately connected to the gas phase. The model contains no direct information about the composition of the bulk of the ice.
We propose a simple way to include the behavior of interstellar ices in the model, taking into account the experimental findings. It is reasonable to assume that the time of ice compaction (Sect. 1) is longer than the time of accretion of molecules onto grains in dense cores (105 years, Schutte & Greenberg 1991). As a basic assumption, the accretion and ice compaction does not occur simultaneously. More than 90% of the metal atoms are already present in the ice phases in the first integration time-step of the simulation.
The calculation of the transition rate of species into the mantle phase is related to the rate of heavy cosmic-ray hits on the grain. In our view light CRs, UV, and X-ray photons, exothermic reactions, and other events all contribute to the compaction of ice. The rate of this first-order process is calculated according to Eq. (1), with f = M and f0 = S. The rate coefficient (s-1) is 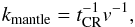 (16)where v is the number of Fe-CR strikes, during which all surface species are converted into mantle species.
(16)where v is the number of Fe-CR strikes, during which all surface species are converted into mantle species.
The percentage of outer-surface species in completely compacted ice with a thickness of 100 monolayers can never be lower than 1%. A reverse process – the transition of ice species from the dense mantle-phase to the porous and exposed surface-phase (f = S,f0 = M) helps to describe the formation and compaction of the ice. The respective rate coefficient is kdig − up. To have approximately 1% of ice-forming species in the outer-surface phase, kmantle is assumed 100kdig − up.
v = 50 and kdig − up:kmantle = 1:100 results in a slowly growing mantle-to-surface metal atom abundance ratio up to approximately 100:1. After 5 × 1013 s it remains roughly constant (Sect. 6.2). This simulates the gradual compaction of the ice.
The assumption of molecule transition from the mantle- to the surface phase is explained as follows. Cosmic-ray hits and other energetic events induce molecule movement within the ice that leads to compaction and segregation (Öberg et al. 2009b). As a side effect, some mixing occurs, and some molecules in the denser mantle become exposed to the outer surface or surface of open pores. However, the full mixing of the mantle is unlikely, and we regard the transition of mantle molecules to the surface as an approximation, only. Because the timescales of mantle circulation are much longer than those for other processes, this approximation can be considered tolerable for the purposes of the model. If the ice is initially porous in interstellar conditions, this model might be conceptually closer to the physical reality than most other current models. A low-level porosity of the mantle in the model is always maintained via the concept of the cavity phase (next section).
The generalized approach to modeling the mantle porosity and cavities is a tool for simulating the ice chemistry. The structure of the mantle is described essentially with a set of input parameters. This is different the work by Cuppen & Herbst (2007) and Cuppen et al. (2009), where detailed simulation of the formation and structure of the ice layer has been performed using the continuous-time random-walk Monte Carlo simulation technique.
4. System of cavity-related transformations
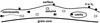 |
Fig. 1 Schematic drawing of the mantle, as reflected in the model. The ice phases – surface, cavities, and mantle volume, which includes micropores, are shown. Not to scale. |
In Sect. 1 (this paper) and in Paper I, we have described the model that reflects the processing of the mantle. Figure 1 shows a sketch of the present mantle model. There are improvements over Paper I, because hydrogen diffusion to micropores (see Sect. 4.2 below) and CR-induced photoreactions of mantle-phase species (Sect. 2.4) are included in this model. For short, the mantle always has some degree of porosity and its molecules are subjected to photodissociation, which produces chemically active radicals. The lighter radicals can move across the surfaces of pores and react when an appropriate reactant is found. In this way, they are converted into stable molecules again. Meanwhile, hydrogen diffuses between the mantle and the outer surface. That means, H and H2 released by dissociation may escape the mantle. They may also diffuse into the mantle from the surface, which is exposed to the gas phase. The calculations show that these two effects do not exactly balance out.
4.1. Formation of the cavities
We assumed that molecules are periodically cycled through the chemically active cavity phase by movement induced by heating from Fe-CR hits and other energetic events. The rate of molecule transition between the cavity phase and the mantle phase is described as a first-order phase transition, Eq. (1). The respective rate coefficients are kact for f = C,f0 = M and kinact for f = M,f0 = C: 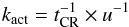 (17)and
(17)and 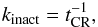 (18)where u is the number of Fe-CR strikes during which the grain mantle is fully reorganized. That means, the amount of molecules exposed to a cavity surface is equivalent to the total number of molecules per mantle. u is assumed 100 (see below) and all existing cavity surfaces are lost (resurfaced) upon the next Fe-CR hit (Eq. (18)). The activation of intact molecules by cosmic-ray hits and dissociation by CR-induced UV radiation of molecules nearby to the cavities (Eq. (5)) are the two processes in the model that change the molecules exposed in the cavities in the mantle.
(18)where u is the number of Fe-CR strikes during which the grain mantle is fully reorganized. That means, the amount of molecules exposed to a cavity surface is equivalent to the total number of molecules per mantle. u is assumed 100 (see below) and all existing cavity surfaces are lost (resurfaced) upon the next Fe-CR hit (Eq. (18)). The activation of intact molecules by cosmic-ray hits and dissociation by CR-induced UV radiation of molecules nearby to the cavities (Eq. (5)) are the two processes in the model that change the molecules exposed in the cavities in the mantle.
The rate coefficients of mantle-cavity phase transitions are attached to the rate of Fe-CR hits in a way similar to the case of mantle formation. The ratio kact/kinact = 0.01 determines the proportion of mantle species in the cavity phase (Xcav). It is assumed that the continuous bombardment by high-energy particles always keep 1% of subsurface mantle species on the surfaces of large, closed pores, channels, or cracks. They are considered chemically active. In our opinion it is close to the maximum percentage that is still consistent with the view that interstellar ices are amorphous and dense (Raut et al. 2008; Accolla et al. 2011; Palumbo 2006). It ensures sufficiently rapid consumption of radicals in the mantle, although their content is still considerable at 1%.
4.2. Hydrogen diffusion through the mantle
For hydrogen diffusion each of the three solid phases plays an important role. According to the conclusions by Strauss et al. (1994), hydrogen almost always resides on a surface, and H and H2 residing in the lattice is only a rare intermediate state. The model assumptions are as follows. First, hydrogen atoms and molecules accrete onto the grain (mantle) outer surface. They also reside on inner surfaces in the cavity phase and in the more densely packed amorphous volume phase – in microcavities. A microcavity is too small to provide enough surface and reactants for chemical reactions, but it is large enough to provide a stable surface for one or a few hydrogen atoms/molecules to reside on. Thus the two mantle phases also represent two kinds of cavities, when regarding the diffusion of hydrogen in the model. This two-level division of pores in interstellar ices is consistent with the experimental findings by Raut et al. (2007a). The rate of transition for H and H2 from solid-phase f0 to solid-phase f is calculated as a first-order process by Eq. (1). The respective rate coefficient is 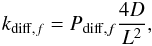 (19)where D is the diffusion coefficient (cm2 s-1), Pdiff is the probability for diffusing species to find an appropriate surface of the phase f, hereafter referred to as P for short. L is the length of the diffusion path, 4 × 10-6 cm, approximately half the thickness of the mantle. DH = 2.5 × 10-21 cm2 s-1 from Awad et al. (2005) and DH2 = 5.9 × 10-8 cm2 s-1, as estimated from the data by Strauss et al. (1994) in Paper I.
(19)where D is the diffusion coefficient (cm2 s-1), Pdiff is the probability for diffusing species to find an appropriate surface of the phase f, hereafter referred to as P for short. L is the length of the diffusion path, 4 × 10-6 cm, approximately half the thickness of the mantle. DH = 2.5 × 10-21 cm2 s-1 from Awad et al. (2005) and DH2 = 5.9 × 10-8 cm2 s-1, as estimated from the data by Strauss et al. (1994) in Paper I.
The diffusion coefficient of deuterium species through the icy mantle is very poorly known. In fact, no usable calculation or measurement data could be found on D for D, HD, and D2 at cryogenic temperatures in an environment similar to interstellar ices. We estimated the coefficients from the available literature on the diffusion of deuterium species in cryogenic temperatures (Guil et al. 1973; Kappesser & Wipf 1996; Martin et al. 1996; Forsythe & Makri 1998; Kua et al. 2001; Coulomb et al. 2003). For the sake of convenience D for D and HD, D2 is expressed as DH or DH2, respectively, modified by a multiplier. The multipliers for D, HD and D2 are 10-7, 10-6 and 10-8, respectively. In our opinion these values could be at the lower-end of plausible values for D, i.e., meaning rather slow diffusion.
The hydrogen diffusion probabilities to the outer surface PS, to cavities PC, and to the volume of the mantle (microcavities) PM are dependent on their relative surface area and the number of available adsorption sites. They are summarized in Table 2. Figure 2 shows the respective probabilities for diffusion to each of the ice phases.
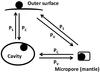 |
Fig. 2 Diffusion scheme of H, H2 and their isotopologs. PS: the probability for diffusion to the outer-surface phase, i.e., f = S, PC: f = C, PM: f = M. |
5. Rate equations
The actual rate of abundance change is calculated by summing the rate of the first-order phase transitions i(f0) → i(f), first-order reactions j → i, second-order reactions l + j → i, and i + j. The total rate of change for the abundance of gas-phase species i can be expressed as 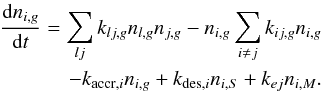 (20)For the outer-surface phase species total rate of abundance change is
(20)For the outer-surface phase species total rate of abundance change is 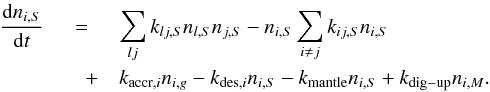 (21)For the cavity-surface phase species:
(21)For the cavity-surface phase species: 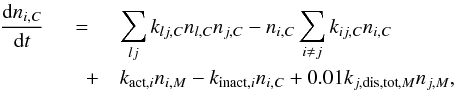 (22)and for the mantle-phase species:
(22)and for the mantle-phase species: 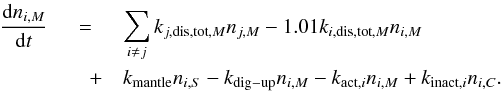 (23)For the light hydrogen species H, H2, D, HD, and D2 the ice diffusion terms (Sect. 4.2) have to be added for rate calculation in S,C, and M phases.
(23)For the light hydrogen species H, H2, D, HD, and D2 the ice diffusion terms (Sect. 4.2) have to be added for rate calculation in S,C, and M phases.
6. Calculation results
6.1. Method for comparing of abundances in the ice phases
We here and in Paper I investigate for the first time the chemical transformation of subsurface ice in the mantles of interstellar dust grains. The most important task is to study the changes in molecular abundances introduced by the subsurface chemistry relative to outer-surface abundances. To compare this, the ratio between the mantle- and surface phase relative abundances for species can be used (mantle-to-surface ratio, M/S), 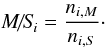 (24)However, as described in Paper I, the best tool for demonstrating the relative changes in mantle and surface abundances is the normalized mantle-to-surface ratio, nM/S. It allows one to avoid the effects caused by different proportion of various elements in the ice phases and different distribution of the total number of metal atoms among the mantle and surface phases, both of which can vary over the integration period. The full calculation formula for nM/S is
(24)However, as described in Paper I, the best tool for demonstrating the relative changes in mantle and surface abundances is the normalized mantle-to-surface ratio, nM/S. It allows one to avoid the effects caused by different proportion of various elements in the ice phases and different distribution of the total number of metal atoms among the mantle and surface phases, both of which can vary over the integration period. The full calculation formula for nM/S is 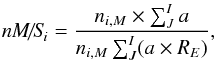 (25)where a (the index in a molecular formula) is the number of atoms of elements i to J in the molecule i. RE is the total M/S ratio for each element that is in the molecule i (C, N, O, S from i through J). Na, Mg, and Fe do not form molecules in the model. Because hydrogen wanders rather freely between the surface and the mantle, it is not counted here. RE for an element is calculated by
(25)where a (the index in a molecular formula) is the number of atoms of elements i to J in the molecule i. RE is the total M/S ratio for each element that is in the molecule i (C, N, O, S from i through J). Na, Mg, and Fe do not form molecules in the model. Because hydrogen wanders rather freely between the surface and the mantle, it is not counted here. RE for an element is calculated by 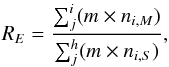 (26)i.e., RE is the total relative abundance of the element E over all species i through j in the mantle-phase divided by the total relative abundance of this element in the surface-phase.
(26)i.e., RE is the total relative abundance of the element E over all species i through j in the mantle-phase divided by the total relative abundance of this element in the surface-phase.
 |
Fig. 3 Top: evolution of the total relative abundance for the mantle-forming metal elements C, N, O, S, and for hydrogen, chemically bound in metal molecules. Bottom: evolution of the M/S ratio for metals and chemically bound H. |
6.2. Structure of the mantle
The structure of the mantle (surface roughness, porosity, except for closed cavities) is characterized by the M/S ratio for the total abundance of metal atoms in the mantle and surface phases. Figure 3 shows the abundance and M/SE for chemically active ice metal elements and chemically bound H in ice. The enhancement of the cumulative M/SCNOS reflects the compaction of the mantle over time, i.e., the reduction of the abundance of molecules in the outer surface phase.
One can conclude from the data of Fig. 3 that an approximate state of equilibrium in the mantle-forming process is reached in the last two time-steps only, when the differences between M/SCNOS,t have become smaller than 1%. At t = 6.7 × 1013 s M/SCNOS = 99.9, at t = 9.5 × 1013 s M/SCNOS = 100.5, and at t = 1015 s, which is another 6–7 time steps forward, M/SCNOS = 101.0. The corresponding metal total relative abundances nM,CNOS and nS,CNOS change only slightly, below 1% if t ≥ 6.7 × 1013 s.
6.3. General results
 |
Fig. 4 Evolution of the solid-phase relative abundance (surface + mantle) for selected species. Note the scale of each graph. |
 |
Fig. 5 Evolution of the normalized mantle-to-surface nM/S ratio for selected species. Note the scale of each graph. |
This section includes the analysis of the calculated abundances for surface and mantle phase species. Figures 4 and 5 show the relative abundance of species in ice phases and the nM/S ratio, respectively. These are the main results of the calculations.
The most important species in ice phase are small molecules H2O, CO2, and H2CO, and also NH3, H2S, CO, and N2. The total proportion of single atoms and other radicals (O, C, S, OH, NH2, NH, etc.) is lower than 1%, and they contain an even lower proportion of metal atoms. A growing abundance curve and high nM/S is characteristic of radicals such as free atoms, OH, SO, CN, CH2, C2H, etc.
 |
Fig. 6 Examples of calculation results on the abundance of deuterated species. The evolution of the solid-phase (surface + mantle) relative abundance of selected hydrogen-isotopologs is shown. Note the scale of each graph. |
 |
Fig. 7 Examples of calculation results on the nM/S ratio for deuterated species. The evolution of the nM/S for all D isotopologs of selected species is shown. Note the scale of each graph. |
The mantle has a lower hydrogen content, which indicates that the outward hydrogen diffusion plays a more important role than inward diffusion. When the integration time becomes longer than approximately 1013 s, M/SH ≈ 0,7M/SCNOS (compare Fig. 3). This means that the hydrogen content bound in metal molecules in the mantle is only around 70% of that in surface molecules. This is mostly because nM/S < 1 for the important H2O, H2CO, NH3, and H2S molecules. The oxygen disposed by the reduction of H2O abundance ends up as part of CO2. This is a significant result since it testifies to the capability of the novelties in the model to address an important astrochemical problem – the route of synthesis of CO2 in interstellar ice. It is produced in subsurface processes, where CO is oxidized by the products of H2O photodissociation, mainly O (see also Ioppolo et al. 2009, 2011; Oba et al. 2010a,b; Roser et al. 2001). The CO conversion in H2O matrix may address the difficulty in observing features related to CO:H2O mixture in interstellar ices (Pontoppidan et al. 2003).
Carbon monoxide is the main gas-phase molecule and is the main form of C and O accreting onto grain surface at conditions given (Kalvāns & Shmeld 2012). On the surface it can attach itself to either H or O and transform into H2CO or CO2. Formaldehyde is the most abundant form of hydrogenated CO. The relative abundance of methanol, which is an abundant hydrogenation product of CO in interstellar ice (Öberg et al. 2011a; Peng et al. 2012), is negligible. This is because the data from Hasegawa et al. lack the hydrogenation reactions of formaldehyde.
OCS is the only ice-phase, sulfur-bearing molecule that has been observed in space (Gibb et al. 2004; Aikawa et al. 2012). It is among the molecules with highest nM/S. Other molecules whose abundance in the mantle is much higher than the abundance in the surface (nM/S > 100) are CN, HCS, carbon chains, and smaller radical-type compounds (mobile species). These species have been directly or indirectly created by the dissociation by CR-photons of stable molecules. CO has the highest nM/S of the stable major molecules, because it is also the dissociation product of H2CO and CO2. The production of carbon-chain compounds in ice complies with the observations of protostars (Bottinelli et al. 2004; Kuan et al. 2004).
The general results of this model (less H and H2O, CO2 as the dominating species in the ice) agree with the results in Paper I. They also approximately agree with observations (e.g. Öberg et al. 2011a). The previously calculated distribution of sulfur compounds in the ice (with a similar abundance for H2S, SO2, SO, H2CS, and CS) better agrees with observations (Hatchell et al. 1998; van der Tak et al. 2003; Wakelam et al. 2004; Herpin et al. 2009; Ren et al. 2011) than the current results with H2S as the single most important sulfur molecule. This and the calculation results at t = 1015 s (Sect. 6.5) may indicate that the ice is more intensively processed before the protostar evaporates the mantle. The cause can be the chemical changes induced by cosmic rays, and the heating of ice in young stellar objects (YSO).
The main difference between the composition of the surface and the mantle is the amount of CO hydrogenation products. The relative abundance of H2CO on the surface surpasses even that of H2O, while in the mantle it is significantly lower and complies better with reality. This can be an evidence for the usefulness of subsurface processes in explaining the composition of interstellar ices. The total calculated abundance of hydrogenated CO still significantly exceeds the observed H2O:CH3OH 100:4 ratio. This is probably due to the limited reaction set and the absence of any measure to take into account the discrete nature of the reactions on grains (modified rate-equation or Monte-Carlo approach, e.g. Charnley 2001; Stantcheva et al. 2001; Stantcheva & Herbst 2004). In real ices some of these molecules are turned into complex organic molecules (Öberg et al. 2011c).
6.4. Results and discussion on deuterium species
The calculation results regarding the molecule enrichment in deuterium are shown in four figures. Figure 6 shows the total abundance in ice (mantle + surface phases) for selected species. The nM/S ratio is shown in Fig. 7 and the deuteration ratio in Fig. 8. The deuteration ratio or RD is the abundance ratio XD: XH, where X is the remainder of a molecule with H or D atom. Figure 9 shows the total abundance ratio for chemically bound H and D in surface- and mantle phases.
 |
Fig. 8 Calculated deuteration level for selected species. The evolution of the abundance ratio (RD) for singly deuterated to non-deuterated molecules in the solid phase (mantle + surface) is shown. |
The hydrogen-containing heavy molecules can be divided into three broad classes. First, there are those that are intensively produced in the mantle. These include HCN, C3H, C4H, H2S2, HCOOH, and others. At the first stage they are produced with some level of deuteration on the surface, then they are buried and become part of the mantle. There they are produced additionally, with a deuteration characteristic of the mantle and their level of deuteration may even not grow with time, unlike all other species.
The second group of molecules (e.g. HNO, C2H4, CH4, H2CO, NH3) are mostly destroyed, not produced in the mantle, so they keep the comparatively high level of deuteration achieved by their synthesis in the gas phase and on the outer surface, and with time it only becomes higher.
Between these two groups are species with nM/S values around unity, most notably H2O as the most abundant hydrogenated heavy molecule. The abundance, nM/S, and deuteration level for examples of all three groups are shown in Figs. 6–8.
Figure 9 shows that the D enrichment in surface molecules is much higher than in the mantle. For both surface and mantle, RD is higher than the cosmic D/H ratio of 2 × 10-5. Generally, modeling results indicate that the mantle molecules lose a significant proportion of D when they are included in the mantle. RD grows with time in the solid phases. For most cases, the relative abundance of D-containing molecules correlates with their protium analogs.
Free hydrogen atoms have RD > 200 at t ≈ 3 Myr, it is the highest of all species in the mantle. Metal molecules with highest RD are organic species with a rather high hydrogen content (CH4, C2H4, CH2NH, CH3CN, CH3OH, H2CO, etc.) and H2S, NH3. Species with lowest RD are radicals, HCN, H2S2, and organic species with low hydrogen content (HC3N, C4H, C3H, C2H, and HCOOH, see Fig. 8).
The RD for gas-phase species is similar to the surface molecules, it is 1–3 times higher than the RD for solid phase (total) species. The observed pattern of D enrichment can be explained assuming that the maximum RD is reached in reactions in the gas-phase. The molecules on the surface are in direct contact with molecules accreting from the gas and are cycled through gas- and surface phases by desorption and accretion processes. They mostly keep their high RD. When they are incorporated into the mantle, they lose connection to the efficient gas-phase deuterium enrichment “factory”. Their RD is determined by the proportion of H and D that is incorporated into ice, with atomic hydrogen as the most important form. D/H in the gas-phase (also shown in Fig. 9) is typically lower than RD for heavy molecules, so ice molecules lose their high deuteration ratios inherited from gas-phase chemistry. This mechanism can also serve as a partial explanation of selective D enrichment in ice compounds, because molecules hydrogenated in different phases have different RD.
 |
Fig. 9 Evolution of the chemically bound deuterium to chemically bound hydrogen total abundance ratio in the solid phases and the gas-phase atomic D-to-H abundance ratio. |
The most important hydrogen-containing molecule is water. Its calculated final abundance in ice is similar to the observed one, with the HDO content a few times 10-4 (Peng et al. 2012) and [D2O]/[HDO] 10-3 (Butner et al. 2007). The RD for formaldehyde are higher than those of H2O (as expected) but lower than the values from observations (see e.g. Cazaux et al. 2011, Table 1 and references therein). Formaldehyde is overproduced in the model. The average RD is approximately consistent with D enrichment in starless prestellar core, which is the main subject of this paper. For most other molecules the maximum calculated RD is 0.5% or less. RD is far from the observed maximum enrichment of several per cent (Cazaux et al. 2011; Coutens et al. 2012). Observed values exceed 10%, especially for molecules with several hydrogen atoms (up to 30% CH2DOH for methanol, Parise et al. (2002)). The highest RD is observed in protostars.
The calculated RD and the dynamics of enrichment growing over time generally agree with observations of molecular gas and YSOs. However, the modeling results are different from the existing view that interstellar ice molecules are always highly enriched in D. Such a product can be an artifact due to the approximations used in the model. For example, the cause may be the difference in the photodissociation rate and reaction branching ratios between H and D species.
If the effect is real, it may place some constraints on the interpretation of PSC, YSO and protoplanetary disk observations. This product is different from our previously published results (Kalvāns & Shmeld 2011) because of a different and more cautious approach to the description of the diffusion of H and D. The overall modeling results, including those at t = 1015 s, point to a possible measurable delay in the D-enrichment process of ice molecules. The delay might be shorter than that obtained from model results (at least several Myr), because high RD can be reached more rapidly due to the chemical changes induced directly by cosmic rays.
6.5. Calculation results and discussion for a model at t = 1015 s
Parameters for the content of chemically bound H and D in the mantle and surface phases for integration times 9.5 × 1013s and 1015 s.
There are indications from the modeling results that the interstellar ice has been more intensively processed than assumed in the model. Because of this, and also to bridge the integration time gap between this work and Paper I, calculations with a prolonged integration time of 1015 s were performed. They are also relevant to long-lived ices in non-starforming cores. The results obtained are different from results with shorter t and interesting enough to be briefly analyzed. To facilitate the interpretation, these results are compared with results with t = 9.5 × 1013 ≈ 1014 s in Table 3.
The total M/S ratio for both simulations is similar (Sect. 6.2), but the content of H and D in mantle molecules differs (Table 3). At t = 1015 s the content of chemically bound H in subsurface molecules has increased by 8%, and by 4% for surface species. This is reflected in the abundance of major species, because the most abundant molecule is now H2O, not CO2. The HCN:HNC ratio is still higher, the abundance of N2 has increased, and H2CO, CH3OH have diminished. These changes affect important molecules and are more consistent with observations. The abundance has grown considerably (more than five times) for several species with different nM/S. This suggests that the enhanced production is phase-independent and is a result of the reaction net, where the molecule is involved. The abundance of atoms and other free radicals has remained approximately the same.
The next important result for the t = 1015 s model is the increase of the proportion of chemically bound D. The total RD for mantle species is now 2/3 of the surface RD. The gas-phase atomic D/H ratio, which determines RD for subsurface ice species, is growing over time. The average RD for mantle molecules is growing with a delay, because of the inefficient processing of the mantle.
At 1015 s, RD has increased for virtually all molecules, except H2. For important species, such as H2O, H2CO, and NH3, this increase is four times. Like the changes in species abundance, the enhancement of RD is independent from the nM/S ratio. Moreover, changes in D enrichment are practically independent of the abundance changes in results at t = 1014 and 1015 s.
Generally, the results with t = 1015s make the impression that the ice on grains is perhaps subjected to a more prolonged or more intense chemical and physical processing than permitted by the model, because they are more consistent with observations.
7. Discussion
The model used for calculations includes a full system that is able to at least partially describe subsurface processes in the mantle. It is rather general and superficial in terms of the reactant and reaction databases. It seldom reproduces abundances of specific molecules that are consistent with observations. The approach used was to analyze the differences produced by subsurface chemistry relative to the “conventional” chemistry on the outer surface. In addition to the results described in Sect. 6, it allowed us to draw some more general conclusions regarding the chemistry of interstellar ice.
The developed model allows proposing an interpretation of the processes that occur in ice with two chemically different layers (Schutte & Greenberg 1991). The inner layer (closer to the grain nucleus) consists of H2O, CO2, NH3, and other molecules, mostly characterized by the ability to form hydrogen bonds. Volatile species, such as CO, CH4, and N2 form the outer layer. This is more exposed to radiation and absorbs a larger dose of UV photons that tear down its molecules. However, thanks to the weaker binding between molecules, the radicals are more mobile and able to recombine effectively (i.e., in terms of our model, its cavities would resurface more frequently). The layer underneath is more shielded and fewer radicals are produced there, while its sturdier, hydrogen-bound structure is less affected by Fe-CR hits and other energetic events. This picture improves the current view on the processes in ice layers (see, e.g. Linnartz et al. 2011).
Our work allows us to suggest that desorption by chemical explosions (Greenberg & Yencha 1973; D’Hendecourt et al. 1982; Schutte & Greenberg 1991) is perhaps insignificant in interstellar clouds. In an explosion the grain loses whole segments of ice, which leads to the destruction of the dense, layered mantle structure. At 10 K or at an even lower temperature the ice formed by accretion can be expected to be porous. Ice segregation and compaction is a long-term process and no ice layers of different chemical composition will be able to form if repeated explosions occur. Instead, the individual reactions in ice slowly decrease the excess abundance of radicals, and are an important feature in explaining the observed ice composition. Additionally, according to our model, a long lifetime of ice is required to explain the high observed D enrichment in molecules.
Atomic hydrogen may provide an important contribution to the reactions producing an ice explosion (Rawlings et al. 2013). However, according to our calculation results, during astronomical timescales H will diffuse from the mantle to the surface before evaporating to the gas phase, i.e., it does not accumulate in the ice mantle and cannot take part in explosive processes. DH is the most trustworthy of all diffusion coefficients for light hydrogen species used in this paper. It was obtained by Awad et al. (2005) from the experiments by Watanabe et al. (2003) with interstellar ice analogs, H2O:CO mixture. Yet no significant accumulation of H in the mantle was observed in the calculation results (Table 2). This further decreases the likelihood for chemical explosions to play a significant role in processes regarding interstellar ices.
Calculation results regarding the deuterium enrichment in molecules (Sect. 6.4) predict that there might be a prolonged period in the evolution of starless and star-forming cores, when the enrichment in ice molecules is low. It is possible that this period is shorter than the results indicate (around 10 Myr) because of the additional processing by cosmic rays. The conclusion that in quiescent cloud cores RD for molecules in the ice mantles is lower than in matter affected by the formation of a protostar agrees with observations, but there are other possible explanations, too (Parise et al. 2005; Bergman et al. 2011).
Acknowledgments
The publication of this article is financed by ERDF project SATTEH, No. 2010/0189/2DP/2.1.1.2.0/10/APIA/VIAA/019, being implemented in Engineering Research Institute “Ventspils International Radio Astronomy Center” of Ventspils University College (ERI VIRAC). The authors are thankful to Institute of Astronomy, University of Latvia, for providing technical support for the calculations performed for the article. We thank the anonymous referee for many valuable comments and suggestions. This research has made use of NASA’s Astrophysics Data System.
References
- Accolla, M., Congiu, E., Dulieu, F., et al. 2011, Phys. Chem. Chem. Phys. (Incorporating Faraday Transactions), 13, 8037 [NASA ADS] [CrossRef] [Google Scholar]
- Aikawa, Y., Umebayashi, T., Nakano, T., & Miyama, S. M. 1997, ApJ, 486, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Aikawa, Y., Kamuro, D., Sakon, I., et al. 2012, A&A, 538, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Albertsson, T., Semenov, D. A., & Henning, T. 2011 [arXiv:1110.2644] [Google Scholar]
- Andersson, S., & van Dishoeck, E. F. 2008, A&A, 491, 907 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Awad, Z., Chigai, T., Kimura, Y., Shalabiea, O. M., & Yamamoto, T. 2005, ApJ, 626, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Bergman, P., Parise, B., Liseau, R., & Larsson, B. 2011, A&A, 527, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bottinelli, S., Ceccarelli, C., Neri, R., et al. 2004, ApJ, 617, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Bringa, E. M., & Johnson, R. E. 2004, ApJ, 603, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, P. D., & Charnley, S. B. 1990, MNRAS, 244, 432 [NASA ADS] [Google Scholar]
- Butner, H. M., Charnley, S. B., Ceccarelli, C., et al. 2007, ApJ, 659, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P. 2011, in IAU Symp. 280, eds. J. Cernicharo, & R. Bachiller, 19 [Google Scholar]
- Cazaux, S., Caselli, P., & Spaans, M. 2011, ApJ, 741, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Charnley, S. B. 2001, ApJ, 562, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Coulomb, J. P., Floquet, N., Martin, C., & Kahn, R. 2003, EPJE, 12, 25 [CrossRef] [EDP Sciences] [Google Scholar]
- Coutens, A., Vastel, C., Caux, E., et al. 2012, A&A, 539, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cuppen, H. M., & Herbst, E. 2007, ApJ, 668, 294 [Google Scholar]
- Cuppen, H. M., van Dishoeck, E. F., Herbst, E., & Tielens, A. G. G. M. 2009, A&A, 508, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Hendecourt, L. B., Allamandola, L. J., Baas, F., & Greenberg, J. M. 1982, A&A, 109, L12 [NASA ADS] [Google Scholar]
- Enoch, M. L., Evans II, N. J., Sargent, A. I., et al. 2008, ApJ, 684, 1240 [NASA ADS] [CrossRef] [Google Scholar]
- Forsythe, K. M., & Makri, N. 1998, J. Chem. Phys., 108, 6819 [NASA ADS] [CrossRef] [Google Scholar]
- Gerakines, P. A., Schutte, W. A., & Ehrenfreund, P. 1996, A&A, 312, 289 [NASA ADS] [Google Scholar]
- Gerakines, P. A., Moore, M. H., & Hudson, R. L. 2004, Icarus, 170, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Gibb, E. L., Whittet, D. C. B., Boogert, A. C. A., & Tielens, A. G. G. M. 2004, ApJS, 151, 35 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Greenberg, J. M., & Yencha, A. J. 1973, in Interstellar Dust and Related Topics, eds. J. M. Greenberg, & H. C. van de Hulst, IAU Symp., 52, 369 [Google Scholar]
- Guil, J. M., Hayward, D. O., & Taylor, N. 1973, Proc. Roy. Soc. London A, 335, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Hartquist, T. W., & Williams, D. A. 1990, MNRAS, 247, 343 [NASA ADS] [Google Scholar]
- Hasegawa, T. I., & Herbst, E. 1993a, MNRAS, 261, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, T. I., & Herbst, E. 1993b, MNRAS, 263, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, T. I., Herbst, E., & Leung, C. M. 1992, ApJS, 82, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Hatchell, J., Thompson, M. A., Millar, T. J., & MacDonald, G. H. 1998, A&A, 338, 713 [NASA ADS] [Google Scholar]
- Herpin, F., Marseille, M., Wakelam, V., Bontemps, S., & Lis, D. C. 2009, A&A, 504, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ioppolo, S., Palumbo, M. E., Baratta, G. A., & Mennella, V. 2009, A&A, 493, 1017 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ioppolo, S., van Boheemen, Y., Cuppen, H. M., van Dishoeck, E. F., & Linnartz, H. 2011, MNRAS, 413, 2281 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, E. B. 2009, ApJ, 700, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P., Blake, D. F., Wilson, M. A., & Pohorille, A. 1995, ApJ, 455, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, R. E., Donn, B., Pirronello, V., & Sundqvist, B. 1991, ApJ, 379, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Kalvāns, J., & Shmeld, I. 2010, A&A, 521, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalvāns, J., & Shmeld, I. 2011, in IAU Symp. 280, eds. J. Cernicharo, & R. Bachiller, 212 [Google Scholar]
- Kalvāns, J., & Shmeld, I. 2012, Baltic Astron., 21, 447 [NASA ADS] [Google Scholar]
- Kappesser, B., & Wipf, H. 1996, J. Phys. IV France, 06, C8 [Google Scholar]
- Kua, J., Lauhon, L. J., Ho, W., & Goddard, W. A. 2001, J. Chem. Phys., 115, 5620 [NASA ADS] [CrossRef] [Google Scholar]
- Kuan, Y.-J., Huang, H.-C., Charnley, S. B., et al. 2004, ApJ, 616, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C. W., & Myers, P. C. 1999, ApJS, 123, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Leger, A., Jura, M., & Omont, A. 1985, A&A, 144, 147 [NASA ADS] [Google Scholar]
- Linnartz, H., Bossa, J.-B., Bouwman, J., et al. 2011, in IAU Symp. 280, eds. J. Cernicharo, & R. Bachiller, 390 [Google Scholar]
- Mangum, J. G., Plambeck, R. L., & Wootten, A. 1991, ApJ, 369, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, C., Coulomb, J. P., & Ferrand, M. 1996, Europhys. Lett., 36, 503 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Millar, T. J., & Williams, D. A. 1993, Dust and chemistry in astronomy (Bristol and Philadelphia: Institute of Physics Publishing) [Google Scholar]
- Millar, T. J., Bennett, A., & Herbst, E. 1989, ApJ, 340, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Oba, Y., Watanabe, N., Kouchi, A., Hama, T., & Pirronello, V. 2010a, ApJ, 712, L174 [NASA ADS] [CrossRef] [Google Scholar]
- Oba, Y., Watanabe, N., Kouchi, A., Hama, T., & Pirronello, V. 2010b, ApJ, 722, 1598 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Fayolle, E. C., Cuppen, H. M., van Dishoeck, E. F., & Linnartz, H. 2009a, A&A, 505, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Öberg, K. I., Garrod, R. T., van Dishoeck, E. F., & Linnartz, H. 2009b, A&A, 504, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Öberg, K. I., Boogert, A. C. A., Pontoppidan, K. M., et al. 2011a, ApJ, 740, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Garrod, R. T., van Dishoeck, E. F., & Linnartz, H. 2011b, in 2010 NASA Laboratory Astrophysics Workshop, C44 [Google Scholar]
- Öberg, K. I., van der Marel, N., Kristensen, L. E., & van Dishoeck, E. F. 2011c, ApJ, 740, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Pagel, B. E. J. 1997, Nucleosynthesis and Chemical Evolution of Galaxies (Cambridge University Press) [Google Scholar]
- Palumbo, M. E. 2006, A&A, 453, 903 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Palumbo, M. E., Baratta, G. A., Leto, G., & Strazzulla, G. 2010, J. Mol. Struct., 972, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Parise, B., Ceccarelli, C., Tielens, A. G. G. M., et al. 2002, A&A, 393, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parise, B., Caux, E., Castets, A., et al. 2005, A&A, 431, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peng, T.-C., Despois, D., Brouillet, N., Parise, B., & Baudry, A. 2012, A&A, 543, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Phillips, A. P., Pettini, M., & Gondhalekar, P. M. 1984, MNRAS, 206, 337 [NASA ADS] [Google Scholar]
- Pontoppidan, K. M., Fraser, H. J., Dartois, E., et al. 2003, A&A, 408, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prasad, S. S., & Tarafdar, S. P. 1983, ApJ, 267, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Prodanović, T., Steigman, G., & Fields, B. D. 2010, MNRAS, 406, 1108 [NASA ADS] [Google Scholar]
- Raut, U., Famá, M., Teolis, B. D., & Baragiola, R. A. 2007a, J. Chem. Phys., 127, 713 [Google Scholar]
- Raut, U., Teolis, B. D., Loeffler, M. J., et al. 2007b, J. Chem. Phys., 126, 511 [Google Scholar]
- Raut, U., Famá, M., Loeffler, M. J., & Baragiola, R. A. 2008, ApJ, 687, 1070 [NASA ADS] [CrossRef] [Google Scholar]
- Rawlings, J. M. C., Williams, D. A., Viti, S., Cecchi-Pestellini, C., & Duley, W. W. 2013, MNRAS, 430, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Ren, J. Z., Liu, T., Wu, Y., & Li, L. 2011, MNRAS, 415, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, H., & Millar, T. J. 2000, A&A, 361, 388 [NASA ADS] [Google Scholar]
- Roberts, H., Herbst, E., & Millar, T. J. 2004, A&A, 424, 905 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roberts, J. F., Rawlings, J. M. C., Viti, S., & Williams, D. A. 2007, MNRAS, 382, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Rodgers, S. D., & Millar, T. J. 1996, MNRAS, 280, 1046 [NASA ADS] [CrossRef] [Google Scholar]
- Roser, J. E., Vidali, G., Manicò, G., & Pirronello, V. 2001, ApJ, 555, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Schnee, S., Di Francesco, J., Enoch, M., et al. 2012, ApJ, 745, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Schutte, W. A., & Greenberg, J. M. 1991, A&A, 244, 190 [NASA ADS] [Google Scholar]
- Semenov, D., Hersant, F., Wakelam, V., et al. 2010, A&A, 522, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stantcheva, T., & Herbst, E. 2004, A&A, 423, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stantcheva, T., Caselli, P., & Herbst, E. 2001, A&A, 375, 673 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strauss, H. L., Chen, Z., & Loong, C.-K. 1994, J. Chem. Phys., 101, 7177 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tak, F. F. S., Boonman, A. M. S., Braakman, R., & van Dishoeck, E. F. 2003, A&A, 412, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Weeren, R. J., Brinch, C., & Hogerheijde, M. R. 2009, A&A, 497, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., Castets, A., Ceccarelli, C., et al. 2004, A&A, 413, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watanabe, N., Shiraki, T., & Kouchi, A. 2003, ApJ, 588, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Willacy, K., & Williams, D. A. 1993, MNRAS, 260, 635 [NASA ADS] [Google Scholar]
- Woodall, J., Agúndez, M., Markwick-Kemper, A. J., & Millar, T. J. 2007, A&A, 466, 1197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Parameters for the content of chemically bound H and D in the mantle and surface phases for integration times 9.5 × 1013s and 1015 s.
All Figures
 |
Fig. 1 Schematic drawing of the mantle, as reflected in the model. The ice phases – surface, cavities, and mantle volume, which includes micropores, are shown. Not to scale. |
| In the text | |
 |
Fig. 2 Diffusion scheme of H, H2 and their isotopologs. PS: the probability for diffusion to the outer-surface phase, i.e., f = S, PC: f = C, PM: f = M. |
| In the text | |
 |
Fig. 3 Top: evolution of the total relative abundance for the mantle-forming metal elements C, N, O, S, and for hydrogen, chemically bound in metal molecules. Bottom: evolution of the M/S ratio for metals and chemically bound H. |
| In the text | |
 |
Fig. 4 Evolution of the solid-phase relative abundance (surface + mantle) for selected species. Note the scale of each graph. |
| In the text | |
 |
Fig. 5 Evolution of the normalized mantle-to-surface nM/S ratio for selected species. Note the scale of each graph. |
| In the text | |
 |
Fig. 6 Examples of calculation results on the abundance of deuterated species. The evolution of the solid-phase (surface + mantle) relative abundance of selected hydrogen-isotopologs is shown. Note the scale of each graph. |
| In the text | |
 |
Fig. 7 Examples of calculation results on the nM/S ratio for deuterated species. The evolution of the nM/S for all D isotopologs of selected species is shown. Note the scale of each graph. |
| In the text | |
 |
Fig. 8 Calculated deuteration level for selected species. The evolution of the abundance ratio (RD) for singly deuterated to non-deuterated molecules in the solid phase (mantle + surface) is shown. |
| In the text | |
 |
Fig. 9 Evolution of the chemically bound deuterium to chemically bound hydrogen total abundance ratio in the solid phases and the gas-phase atomic D-to-H abundance ratio. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


