| Issue |
A&A
Volume 554, June 2013
|
|
|---|---|---|
| Article Number | A42 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201219971 | |
| Published online | 03 June 2013 | |
The Herschel view of the massive star-forming region NGC 6334⋆,⋆⋆
1 Aix Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de Marseille), UMR 7326, 13388 Marseille, France
e-mail: delphine.russeil@oamp.fr
2 Laboratoire AIM Paris-Saclay, CEA/DSM – INSU/CNRS – Université Paris Diderot, IRFU/SAp, CEA-Saclay, Orme des Merisiers, 91191 Gif-sur-Yvette, France
3 Department of Physics, West Virginia University, Morgantown, WV 26506, USA
4 INAF – Istituto Astrofisica e Planetologia Spaziale, via Fosso del Cavaliere 100, 00133 Roma, Italy
5 Laboratoire d’Astrophysique de Bordeaux, OASU – UMR 5804, CNRS – Université de Bordeaux 1, 2 rue de l’Observatoire, BP 89, 33270 Floirac, France
6 I. Physik. Insitut, Zülpicher Str. 77, University of Cologne, Germany
7 Université de Toulouse, UPS, CESR, 9 av. du colonel Roche, 31028 Toulouse, France
8 National Research Council of Canada, 5071 West Saanich Road, Victoria, BC V9E 2E7, Canada
9 National Astronomical Observatories of the Chinese Academy of Sciences, 100012 Beijing, PR China
10 The Canadian Institute for Theoretical Astrophysics (CITA), University of Toronto, 60 St. George Street, Toronto, Ontario, M5S 3H8, Canada
11 Department of Astrophysics, Faculty of Physics, University of Athens, Panepistimiopolis, 15784 Zografos, Athens, Greece
12 Institut d’Astrophysique de Paris, UMR 7095 CNRS, Université Pierre & Marie Curie, 98 bis Boulevard Arago, 75014 Paris, France
13 ESO, Karl Schwarzschild str. 2, 85748 Garching, Germany
14 Herschel Science Centre, ESA-ESAC, PO Box 78, 28691 Villanueva de la Caada, Madrid, Spain
15 Jeremiah Horrocks Institute, University of Central Lancashire, PR1 2HE, UK
16 Department of Physics and Astronomy, The Open University, Walton Hall, Milton Keynes, MK7 6AA, UK
17 RAL Space, STFC Rutherford Appleton Laboratory, Chilton, Didcot, Oxfordshire, OX11 0QX, UK
Received: 9 July 2012
Accepted: 28 March 2013
Aims. Fundamental to any theory of high-mass star formation are gravity and turbulence. Their relative importance, which probably changes during cloud evolution, is not known. By investigating the spatial and density structure of the high-mass star-forming complex NGC 6334 we aim to disentangle the contributions of turbulence and gravity.
Methods. We used Herschel PACS and SPIRE imaging observations from the HOBYS key programme at wavelengths of 160, 250, 350, and 500 μm to construct dust temperature and column density maps. Using probability distribution functions (PDFs) of the column density determined for the whole complex and for four distinct sub-regions (distinguished on the basis of differences in the column density, temperature, and radiation field), we characterize the density structure of the complex. We investigate the spatial structure using the Δ-variance, which probes the relative amount of structure on different size scales and traces possible energy injection mechanisms into the molecular cloud.
Results. The Δ-variance analysis suggests that the significant scales of a few parsec that were found are caused by energy injection due to expanding H ii regions, which are numerous, and by the lengths of filaments seen everywhere in the complex. The column density PDFs have a lognormal shape at low densities and a clearly defined power law at high densities for all sub-regions whose slope is linked to the exponent α of an equivalent spherical density distribution. In particular with α = 2.37, the central sub-region is largly dominated by gravity, caused by individual collapsing dense cores and global collapse of a larger region. The collapse is faster than free-fall (which would lead only to α = 2) and thus requires a more dynamic scenario (external compression, flows). The column density PDFs suggest that the different sub-regions are at different evolutionary stages, especially the central sub-region, which seems to be in a more evolved stage.
Key words: stars: formation / ISM: clouds / ISM: individual objects: NGC 6334
Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with important participation from NASA.
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
The transformation of a molecular cloud several tens of parsec in size into OB-stars is not understood well. Self-gravitating, hydrodynamic simulations of molecular cloud formation and evolution point towards a scenario in which the cloud’s filamentary structure is determined by large-scale driven turbulence (e.g., Heitsch et al. 2001; MacLow et al. 2004; Ballesteros-Paredes & MacLow 2002; Federrath et al. 2010). It is known that shock compression and high accretion rates lead to the creation of clumps and cores of high densities and mass that then fragment and collapse to form stars (e.g., Klessen et al. 2000; Klessen & Hennebelle 2010). Only recently, however, has the importance of filaments been recognized (e.g., Vazquez-Semadeni et al. 2007; Toala et al. 2012). Filaments may provide a mass flow onto massive structures that become gravitationally unstable and fragment into cores and finally stars. This scenario is suggested by observations of both low-mass (e.g., André et al. 2010; Arzoumanian et al. 2011) and high-mass star-forming regions (e.g., Schneider et al. 2010a; Hennemann et al. 2012). The high accretion rates provided by merging filaments (Schneider et al. 2012) may be particularly important for the formation of massive clusters.
In the scenario described above, one would expect that sub-regions within one molecular cloud complex may be in different states with regard to turbulence and gravity, i.e., star-forming versus non-star-forming sub-regions. This implies that different sub-regions have different density structures. We may trace these differences using probability distribution functions (PDFs) from sensitive, high angular resolution column density maps obtained with the Herschel satellite. These PDFs (e.g., Federrath et al. 2008) are useful tools for investigating the column density structure of atomic/molecular gas in observations and simulations. PDFs characterize the probability that a volume of gas has a quantity, e.g., density (n) in the range [n, n+Δn]. PDFs determined from column density maps of molecular clouds are typically lognormal over a wide range of densities, but deviations from the lognormal shape have been found in both the low- and high-density range. Generally, the width of the lognormal portion of the PDF measures the turbulent velocity field and the tail of the PDF gives an indication of the progress of gravitational collapse. In particular, strongly self-gravitating systems produce a deviation (e.g. Klessen 2000; Kainulainen et al. 2009) from the turbulence-dominated lognormal PDF, traced as a power-law tail at high densities.
 |
Fig. 1 Three-colour Herschel image of NGC 6334 with 500 μm data in red, 160 μm data in green, and 70 μm data in blue. The size of the image is 2 |
One way to quantify the relative contribution of turbulence in a cloud is to determine the power-spectrum or the Δ-variance (Ossenkopf et al. 2008a,b) of a cloud. The Δ-variance characterizes size scales that are present in the cloud, caused by energy injection on different scales. This includes scales on which the entire molecular cloud and individual filaments were formed, where star formation has generally propagated or feedback has shaped the cloud, and where turbulence produces smaller sub-structures.
For this study, we use observational data of NGC 6334 from the Herschel imaging survey of OB young stellar objects (HOBYS), which is the first systematic survey of a complete sample of nearby (within 3 kpc high-mass star-forming regions, Motte et al. 2010). The HOBYS programme targets ten molecular complexes forming OB-type stars at five wavelengths from 70 μm to 500 μm. The advantage of Herschel is that high- and low-mass star formation sites at all evolutionary stages are probed: from filaments, prestellar cores, and protostars to more evolved objects like H ii regions (e.g., Motte et al. 2010; André et al. 2010; Molinari et al. 2010; Anderson et al. 2012).
2. The NGC 6334 star-formation complex
NGC 6334 is a very active star forming region (see review by Persi & Tapia 2008). At sub-millimetre wavelengths, the central part of NGC 6334 consists of a 10-pc long filament that is also associated with strong extinction (Russeil et al. 2010). Several sites of high-mass star formation have been identified (e.g., Loughran et al. 1986), by the presence of water masers, UC H ii regions (e.g., Rodriguez et al. 1982; Carral et al. 2002), molecular outflows, and H ii regions (GUM 61, 62, 63, and 64 (Gum 1955), and GM1-24, indicated in Fig. 1). The large number of H ii regions spread across the complex is remarkable. For example, NGC 6334 has 7 compact and optical H ii regions per square degree while its neighboring star-forming complex, NGC 6357, has ~ 4 per square degree. Many of these H ii regions have a “bubble” morphology at Herschel wavelengths but also at IR- or radio wavelengths1. The typical size scales of the H ii bubbles visible in Fig. 1 is one to a few parsec.
The Hα emission of NGC 6334 (Fig. A.1) extends to the north-west up to ~ 0.5 from the main dust filament. The optical H ii regions are excited by a few stars (Neckel 1978). However, Tapia et al. (1996) estimated that the ionization of the radio H ii regions, NGC 6334I and NGC 6334E, is due to a rich embedded young cluster and a cluster of B-stars, respectively. Bica et al. (2003) listed seven embedded clusters/groups associated with radio sources, and from dozens of likely OB stars, both in clusters and dispersed throughout the region, Feigelson et al. (2009) suggested that star formation in the complex has taken place over millions of years. On the north-west border of NGC 6334 there is a 12 Myr old (Kharchenko et al. 2009) cluster Bochum 13 (l = 351.201°, b = + 1.36°) containing five O-B3 stars (McSwain & Gies 2005), giving rise to diffuse and extended Hα emission. The south-west part of NGC 6334 is dominated by the optical H ii region GM 1-24 excited by a cluster of about ten young massive stars (Tapia et al. 1991).
The distance of NGC 6334, 1.74 kpc, has previously been derived by Persi & Tapia (2008) and confirmed by Russeil et al. (2012) who found a distance of 1.75 kpc for the exciting stars of NGC 6334. We adopt 1.75 kpc throughout this paper. There is no sign of a recent (younger than ~10 000 yr) supernova remnant (SNR) in NGC 6334. There is one well-known SNR in the field, G351.7+0.8 (Green 2009), located at a distance of ~13 kpc (Tian et al. 2007), and thus not associated with NGC 6334.
3. Observations
NGC 6334 was observed with the ESA Herschel Space Observatory (Pilbratt et al. 2010) with the PACS (Poglitsch et al. 2010) and SPIRE (Griffin et al. 2010) instruments2 as part of the HOBYS (Motte et al. 2010) key programme (OBSIDs: 1342204421 and 1342204422). Data were taken in five wavelength bands: 70 μm and 160 μm for PACS at FWHM resolutions of 5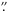 6 and 11
6 and 11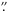 4, respectively, and 250 μm, 350 μm, and 500 μm for SPIRE at FWHM resolutions of 18
4, respectively, and 250 μm, 350 μm, and 500 μm for SPIRE at FWHM resolutions of 18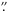 1, 25
1, 25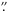 2, and 36
2, and 36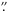 6, respectively. The observations were performed in parallel scan map mode, observing with both instruments simultaneously, with a scan speed of 20s. Two perpendicular scans were taken. The photometric calibration is good to within 10% for all bands of SPIRE while they are 5% and 10% for the 70 μm and 160 μm PACS bands respectively (see the respective observers’ manuals)
6, respectively. The observations were performed in parallel scan map mode, observing with both instruments simultaneously, with a scan speed of 20s. Two perpendicular scans were taken. The photometric calibration is good to within 10% for all bands of SPIRE while they are 5% and 10% for the 70 μm and 160 μm PACS bands respectively (see the respective observers’ manuals)
We reduced the Herschel data using the Herschel interactive processing environment (HIPE) software, version 4.0. More recent versions of HIPE (Version 7.0 onwards) contain a destriper module that significantly removes striping effects compared to the maps produced in previous HIPE versions. We found, however, that the Scanamorphos software (Roussel et al. 2012), version 4.0, applied to the level 1 data produces better quality maps for both, PACS and SPIRE, and we used the Scanamorphos output for the current work. Scanamorphos estimates the value at each sky position by exploiting the redundancy in the data.
In addition, the astrometry of the PACS and SPIRE Herschel data produced by HIPE-4.0 have offsets relative to each other, and also relative offsets to higher resolution Spitzer maps. Using bright point sources across the field, we first aligned the 70 μm PACS data to the 24 μm Spitzer MIPSGAL data (Carey et al. 2009). We then aligned the PACS 160 μm data to the PACS 70 μm data, and so on for all the Herschel PACS and SPIRE bands. The resulting relative offsets are smaller than 10.
 |
Fig. 2 Three-colour image of the central part of NGC 6334 with the same colour mapping as in Fig. 1. The image is 33 |
We show a global view of NGC 6334 as seen by Herschel in Fig. 1 and a zoom-in of the central part in Fig. 2. In Fig. 1, we label H ii regions in the field from Anderson et al. (2011), Caswell & Haynes (1987), and Gum (1955). These images illustrate the complexity of NGC 6334, in particular the relative distribution of the warm and cold dust. In the central region, warm dust traced by the 70 μm emission dominates but is spatially bounded by cold dust traced by the longer wavelengths. The warm dust spatially coincident with the ionized gas of the optical H ii regions (Figs. A.1 and A.2).
Several young active star-forming regions (labelled I to V) are located in the main filament (Fig. 2). With the exception of NGC 6334I(N), which exhibits only weak centimetre-wave emission, all these active regions are associated with compact or ultra-compact H ii regions that are traced here by their 70 μm emission. That NGC 6334I is an UC H ii region (Beuther et al. 2005) while NGC 6334I(N) is an IR-quiet protostellar object (Russeil et al. 2010) suggests that NGC 6334I(N) is younger than NGC 6334I. We note that the well-studied I(N) and I are saturated in SPIRE bands. This has no impact on the Δ-variance (the pixel size is too small) or PDFs (these pixels are ignored). NGC 6334I(N) is known to be a very active massive star formation site.
 |
Fig. 3 H2 column density (left) and temperature (right) maps of NGC 6334, determined using the 160 μm, 250 μm, 350 μm, and 500 μm Herschel wavebands. The different sub-regions discussed in the text are indicated with white dashed-line polygons. The H ii regions GUM61 to 64a,b,c are indicated with triangles. |
4. Dust temperature and column density maps
4.1. The maps
We simultaneously created dust temperature and column density (NH2) maps following Anderson et al. (2012). We rebinned all images to the pixel size and grid spacing of the 500 μm data (36) and applied the intensity offsets to recover the absolute intensity level following Bernard et al. (2010). No background substraction has been performed. At each grid location, we created a spectral energy distribution from the Herschel data and fit a grey-body Planck function by adopting β = 2 and a dust opacity per unit mass (dust + gas, assuming a gas-to-dust ratio of 100) κν = 0.1 (ν/1000 GHz)β cm g (Beckwith et al. 1990; Hildebrand 1983). This assumes that the emission is optically thin. This assumption is valid everywhere, with the exception of a few pixels along the central ridge, and even then it only fails for the 160 μm data. The resulting maps are shown in Fig. 3. The column density map exhibits a range of column densities of 1.7 × 1021 to 3 × 1023 cm and an average column density of 0.76 × 1022 cm. This corresponds to a total mass of 3.8 × 105 M⊙ using a mean molecular weight of μ = 2.36 and integrating over the whole map.
The column density map may be affected by foreground and background contributions along the line-of-sight. NGC 6334 is located ~0.8 deg above the Galactic plane (i.e. 25 pc above the plane at a distance of 1.7 kpc), while at the distance of the two next arms (~3 and 4 kpc away) the line-of-sight passes at ~50 pc above the plane. Since the distribution of the cold dust emission appears to be confined to the plane with a mean scale height of 46 pc (Beuther et al. 2012), we thus expect a very low level of extinction from the background. Molecular line data help us to roughly estimate the foreground and background contributions. The foreground column density level was estimated by Emprechtinger et al. (2012) to be ~1.8 × 1021 cm from Herschel absorption measurements of the HF radical. They calculated the H-column density of four different foreground clouds at −3, 0, +6.5, and +8 km s (the bulk emission of the NGC 6334 cloud is between − 6 to − 8 km s). This value converts to AV ~ 1.9 mag and is compatible with the foreground extinction found by Neckel (1978). A lower limit for the background component can be estimated from the blue-shifted velocity components seen in CO 2 → 1 data (Kraemer & Jackson 1999) at −40 km s and −100 km s. However, their CO intensity is on average a factor 30 less than the one from the NGC 6334 bulk cloud so we do not expect an increase in column density more than ~2−3 mag in AV. Our Herschel column density map at the edges of the map only has a value of AV ~ 2 mag, which we consider as the typical background level3.
We created two sets of temperature and column density maps, one set including and one set excluding the lowest-resolution 500 μm data. For the Δ-variance analysis, we wanted the highest possible angular resolution, so we used the column density map made without the 500 μm data. This map is very similar to the one shown in Fig. 3. It differs less than 10% from column density map produced including the 500 μm data, (after re-gridding both maps to the same resolution), but has a resolution of 25.
Since we are mostly interested in the distribution of the cold gas, for all temperature and column density maps we excluded the 70 μm data (this is also done in other HOBYS papers, e.g. Hill et al. 2011; Nguyen-Luong et al. 2011; Schneider et al. 2012; Hennemann et al. 2012). At 70 μm, there are two effects that may limit the reliability of temperature and column density maps. First, 70 μm emission may be optically thick for cold high column density gas, and thus the derived temperature may be too low for dense structures. In a study of bright H ii regions (including their associated condensations and photodissociation regions), however, Anderson et al. (2012) find that including the 70 μm data only affects the derived temperatures by ~5% on average. The 70 μm band also traces contributions from a warmer dust component, which may result in overestimating dust temperatures. Compiègne et al. (2010) estimate that in diffuse regions the contribution from warm dust to the 70 μm flux ranges between 12% to 35%. They find that this contribution increases when the very small grain abundance increases relative to the big grain abundance and/or if the radiation field decreases. Owing to the important variation in the radiation field through NGC 6334, we may thus expect a large variation in the contribution of the warm dust component to the 70 μm flux.
We also investigated in detail the temperature and column density uncertainties that reflect the combined effects of noise in the data, uncertainties in the absolute calibration, and the contribution from multiple emitting components along the line of sight. Since the fit errors arise in part from the calibration uncertainties, which are correlated across the map, the relative error in column density between regions in the map is not necessarily represented well by the values in the error map. The mean error in temperature for these maps is 8% (11% when excluding the 500 μm data) with a standard deviation of 1% (2%). The mean error in column density is 22% (29%) with a standard deviation of 2% (2%). For the temperature maps, there is a strong positive relationship between the uncertainty and the temperature value itself, beginning at ~25 K. Below ~25 K there is essentially no relationship. This illustrates that at higher temperatures where the dust emits stronger at 70 μm, the exclusion of the 70 μm data leads to greater uncertainties in high temperature values. There is no such relationship for the column density maps.
The assumed form of the opacity law also adds uncertainty to the derived column density values, and this source of uncertainty is not accounted for in our error maps. Taking the Ossenkopf et al. (1994) and Ormel et al. (2011) opacity values in addition to the parameterization of Beckwith et al. (1990) that we use here, we evaluate the uncertainty associated with the assumed opacity law. For Ossenkopf et al. (1994) we tabulate opacity values for thick and thin ice mantles and densities of zero (effectively, assuming no coagulation), 106 cm-3, and 107 cm-3. For Ormel et al. (2011), we tabulate opacity values for silicates and graphite, with or without ice-coatings, and coagulation timescales of 105 to 106.5 years. The standard deviation of the opacity values of Beckwith et al. (1990), Ossenkopf et al. (1994), and Ormel et al. (2011), evaluated at 350 μm, is 2.0 cm g. The average value is 8.4 cm g, while the value we are using is 7.3 cm g. There is therefore approximately 25 − 30% uncertainty in the opacity value. Finally, we are using a single opacity for the entire field of NGC 6334, which has both low and high density areas. The true opacity uncertainty may even be larger than our above estimate of 27% if all of the opacities considered are not appropriate for some areas of the field (i.e., the lower column density regions). Arzoumanian et al. (2011) find that the 7.3 cm g value we are using is appropriate for intermediate density gas, as shown by the agreement with extinction maps (see their appendix). For low-density regions, the Planck collaboration (Abergel et al. 2011) found an opacity value of 4.2 cm g.
4.2. Definition of sub-regions
Comparing the temperature map, the column density map, and the Hα image it is obvious that there are different physical environments with different spatial and density structures, UV illuminations, temperatures, and star-formation activities. We thus define several sub-regions that clearly differ in one or more parameters. This selection is subjective; it does not use a single criterion such as a multi-resolution analysis of the column density (e.g. Hill et al. 2011), but is appropriate for our needs because it takes several properties of the cloud into account. Our aim is to analyse these sub-regions with structure and density analysis tools (Sect. 5) to understand the physical processes that lead to their contrasting properties4. As suggested by their different characteristics, we name the sub-regions “Centre”, “Cold”, “Filaments”, and “Quiet” (see Fig. 3 and below).
In addition, we perform basic measurements of the width and length of the filaments from the column density map (see Arzoumanian et al. 2011 or Hennemann et al. 2012 for more sophisticated methods). At several positions along the filamentary structures, we extract perpendicular column density profiles and establish the central width (above the background) of each profile (deconvolved full width at half maximum, FWHM) using a Gaussian fitting. For each sub-region we give the average FWHM. We estimate the length of the filaments by measuring their width on the column density map above a threshold of 4 × 10 cm, 9 × 10 cm and 2.5 × 10 cm for the “Cold”, “Centre” and “Filaments” sub-regions, respectively. The chosen threshold defines the first isocontour delimitating the filaments. In the “Quiet” sub-region no clear filament can be extracted. To help us distinguish the sub-regions, we also evaluate the filament mass per unit length (Mline), which allows us to characterize their thermal stability (e.g. Ostriker 1964 for isothermal, non-magnetized filaments without turbulent support, Inutsuka & Miyama 1992) because only above the critical value5, Mcrit, is the filament able to collapse. As a possible evolutionary scheme, it is expected that starless clouds have Mline that increase with time during the collapse and star-formation process (Beuther et al. 2011).
An inspection of the temperature map shows a clear temperature contrast between the north-eastern and the central parts of the map. Indeed, the northern part of NGC 6334, i.e. the “Cold” sub-region, clearly stands out as the coldest part of the complex with Tdust = 15−17 K and H column densities of up to ~7 × 1022 cm. The boundary of this sub-region encompasses the coldest gas in the temperature map (Fig. 3). The spatial structures are dominated by a rather thick ( ⟨ FWHM ⟩ = 0.5 ± 0.21 pc) patched distribution of gas following a global filamentary pattern. Four filament-like structures with lengths between 3 and 9 pc can be measured with Mline between 72 and 204 M⊙ pc. With Mcrit = 24 M⊙ pc the filaments are just barely supercritical. This sub-region corresponds to the “inter-filament region” in Russeil et al. (2010) connecting NGC 6334 to NGC 6357. No optical H ii region has been observed in this area.
The “Centre” sub-region is dominated by the optical H ii regions and thus by a strong radiation field. It exhibits very high column densities, more than 2 × 10 cm, and also has the highest temperatures (up to 37 K). Star formation is actively taking place along one main filament, as shown by the optical H ii regions and the young active star-forming regions NGC 6334I(N) and NGC 6334I (see Sects. 2 and 3). The filament’s length is 9 pc with an average FWHM of 0.24 ± 0.14 pc. It is largely supercritical since Mline = 1033 M⊙ pc, while Mcrit = 35 M⊙ pc. This sub-region encompasses all the ionized gas.
The “Centre” sub-region contrasts to the “Filaments” sub-region, which has well-defined and numerous thinner filaments ( ⟨ FWHM ⟩ = 0.16 ± 0.04 pc), including one warm filament with active star-formation traced by the GM1-24 Hα region (see Fig. 7 nicely outlining the filamentary structure). Up to eight filaments can be measured above the chosen threshold with length between 1.5 and 6 pc. In this sub-region the temperature is between 17 K and 22 K and the column densities reach ~ 10 cm. The filaments exhibit a mean Mline = 75 M⊙ pc (between 22 and 109 M⊙ pc) suggesting that most are just barely supercritical (Mcrit = 28 M⊙ pc). In Hα (see Fig. A.1) this sub-region shows strong extinction, suggesting it is located at the front of the complex and no such behaviour is observed for the “Cold” sub-region. The boundary of this sub-region encompasses all the optical extinction associated with GM1-24.
Finally, we identify a fourth sub-region called “Quiet” at the north-west of the field. This sub-region is characterized by a more uniform column density distribution (no clear filaments can be measured) with an intermediate temperature (~19 K), low mean column density density (up to ~ 1.5 × 10 cm), and intense, but diffuse Hα emission (Fig. A.1).
5. Data analysis and results
5.1. Column density and temperature probability distribution functions
We determine the PDFs (e.g., Federrath et al. 2008) of the column density maps to investigate the (column) density structure of the cloud6. Deviations in the PDF from the lognormal shape have been found in both the low- and high-density ranges. The excess at high densities, as seen for example in extinction maps (Kainulainen et al. 2009) and Herschel column density maps (Hill et al. 2011; Schneider et al. 2012, 2013), is ascribed to star formation activity. From a theoretical point of view, a purely lognormal distribution is expected if the cloud structure is due to supersonic turbulence. Deviations from lognormal are predicted for self-gravitating clouds (Klessen et al. 2000; Ballesteros-Paredes et al. 2011). Observational studies of low- to intermediate-mass star-forming regions (Kainulainen et al. 2009) have confirmed theoretical predictions (Klessen 2000; Vázquez-Semadeni et al. 2008; Federrath et al. 2008) that strongly-self-gravitating systems produce a deviation from the turbulence-dominated lognormal column density PDF at high densities and that the column-density PDF develops a power-law tail.
Figures 4 and 5 show the column-density (expressed in visual extinction using the conversion formula given in Sect. 4.1) PDFs of the total NGC 6334 region and the sub-regions, created using the lower resolution column density map that includes the SPIRE 500 μm emission (resolution 36). Common to all PDFs is a lognormal distribution for low densities and a power-law tail for higher column densities. The low-density range is affected by noise, low sampling, and possible line-of-sight confusion. The PDF of the total NGC 6334 region shows a perturbed PDF at low column densities with deviations from the lognormal at AV ~ 2 and ~ 4. These components may indeed result from fore- and background emission (see Sect. 4.1) but can also be due to compression from the expanding H ii region as seen in the Rosette cloud (Schneider et al. 2012).
Another caveat can be that the assumption of isothermal gas is no longer fulfiled. In view of Fig. 6, showing the temperature PDFs, this is the case for all except the “Quiet” region. However, the deviation from the ideal isothermal case is not large (not several orders of magnitude) so though it is not possible to determine how a more complex temperature distribution (like the bimodal one for the “Filament” region) imprints on the density PDF, we do not expect a strong influence. Assuming that the high-density tail is only due to the effect of gravity, Federrath et al. (2011) show that the exponent α of the spherical density distribution ρ(r) = ρ0 (r/r0) − α is linked to the slope of the power-law tail of the high-density end of the column density PDF. Thus, α may be used to characterize the star formation processes at work and the relative contribution of turbulence and gravitation in a cloud.
 |
Fig. 4 Column density PDF of NGC 6334 produced without the 70 μm band. The x-axis labelling is in column density at the bottom x-axis and in ln(N/ ⟨ N ⟩ ) at the top x-axis. The labelling of the y-axis is a probability on the left and number of pixels per log bin on the right. The green curve indicates the best lognormal fit PDF, and the red line is the best-fit power-law fit to the high-density tail. In the panel the deviation point of the PDF from lognormal (AV), the width σ, the slope s, and the exponent α are given. |
 |
Fig. 5 Column density PDFs of the 4 sub-regions in NGC 6334 produced without the 70 μm band. The x-axis labelling is in visual extinction at the bottom x-axis and in ln (N/ ⟨ N ⟩ ) at the top x-axis. The labelling of the y-axis is a probability. The green curves indicate the best lognormal fit PDF (Eq. (1)), and the red line is a fit to the high-density part of the PDF that follows a power law. The width of the PDF, σ, and the exponent of the spherical density profile, α, are given in each panel. |
 |
Fig. 6 Same as Fig. 5 for temperature. The x-axis labelling for the temperature PDF is in Kelvin at the bottom x-axis and in ln (T/ ⟨ T ⟩ ) at the top x-axis. The width, σ, and the peak temperature, in Kelvin, of the PDF are given in each panel. |
 |
Fig. 7 Individual column-density maps of the sub-regions expressed in visual extinction AV (in the range of AV-values for the PDF) with the contour level of the lower limit used for fitting the slope in the high-density tail of the PDF (Fig. 5). The corresponding values are given in each panel. |
We applied this technique to the column density PDFs obtained for the different sub-regions of NGC 6334. For the “Centre” region, there is excess in the PDF for AV > 100 so we did not include the single power law in the fit. However, we emphasize that the pixel statistic for this column density range is still high enough to consider that the distribution is significant. The characteristic properties of the PDF (width, peak), were fitted with the lognormal function ![\begin{equation} p_\eta\,{\rm d}\eta=\frac{1}{\sqrt{2\pi\sigma^2}}{\rm exp}\left[ -\frac{(\eta-\mu)^2}{2\sigma^2} \right]{\rm d}\eta \end{equation}](/articles/aa/full_html/2013/06/aa19971-12/aa19971-12-eq77.png) (1)where σ is the dispersion, η = ln(N/ ⟨ N ⟩ ), and μ is the mean of the lognormal function. We do this systematically by performing several fits on a grid of parameters for η and μ and then calculate the positive and negative residuals. We select fits with the least negative residuals and determine the range of lognormality, when the difference between the model and pη is less than three times the statistical noise in pη. To determine the slope, we numerically determined the AV value where the fitted lognormal part of the PDF intersects the observed curve.
(1)where σ is the dispersion, η = ln(N/ ⟨ N ⟩ ), and μ is the mean of the lognormal function. We do this systematically by performing several fits on a grid of parameters for η and μ and then calculate the positive and negative residuals. We select fits with the least negative residuals and determine the range of lognormality, when the difference between the model and pη is less than three times the statistical noise in pη. To determine the slope, we numerically determined the AV value where the fitted lognormal part of the PDF intersects the observed curve.
Figure 7 shows the column density maps of each sub-region with a different AV-contour (in red) overlaid on it. These contours indicate where the deviation of the PDF from the lognormal form starts (AV = 8 , 22 mag, 12 mag, 26 mag for “Quiet”, “Cold”, “Filaments”, and “Centre” sub-regions, respectively.) The resulting fit of the power-law tail in the high-density range is indicated as a red line in Fig. 5, and the exponent α and the AV value of the break point in the PDF are listed in Table 1.
In summary, all column-density PDFs except that of the “Quiet” sub-region peak around AV of 7–9, deviate from the lognormal shape at AV ~ 12–26 and have a dispersion (“width”) σ of 0.30 − 0.35. The “Quiet” sub-region, however, has a narrower column-density PDF (σ = 0.2) and a rather steep higher density tail. The peak of this PDF lies at AV = 5, i.e., significantly lower than for all other sub-regions and is thus more comparable to the study of Kainulainen et al. (2009) in which molecular clouds with a lower average column density were studied. The results of NGC 6334 are in the same line like the ones obtained for Vela (Hill et al. 2011) also showing that for high-mass star-forming regions, the lognormal part of the PDF and its peak is shifted towards higher AV values (peak > 7).
We emphasize that the main results are unaffected by the possible diffuse component along the line of sight, unless such component is clearly more substantial than what we estimated in Sect. 4.1, and it varies spatially along the cloud. The variation in AV for the deviation of the PDF from lognormal would still be present and would not have a universal value, and the slope would not be affected at all. The only value that can be affected is the mass calculation. We are, however, more interested in the relative fraction of mass contained in the high-density regime indicated by the power-law tail. As seen in Table 1, for the “Centre” subregion the gravitationally collapsing gas makes up 62% of the total mass. These values gradually decrease to 21% and 27% for the “Cold” and “Filaments” sub-regions to the lowest value of 14% for the “Quiet” subregion. The other parameters of the column-density PDF fits are summarized in Table 1.
The temperature PDFs of the sub-regions (Fig. 6) show that the “Quiet” and “Cold” sub-regions each have a very narrow, nearly lognormal temperature distributions peaking around 20 K. In contrast, the “Filaments” sub-region has a bimodal distribution with the majority of dust at a temperature of ~21 K and – with a lower pixel statistics – an additional dust component at ~30 K. This bimodality is most likely due to the single H ii region GM1-24 observed in the temperature map (Fig. 3) at 17h16m30s, –3620. A bimodal distribution was also observed in Vela-C (Hill et al. 2011). Finally, the temperature PDF of the “Centre” sub-region shows that it is clearly the warmest part of NGC 6334, with a peak at 23 K and a wide range of temperatures covering 20 K to 40 K. There is, however, no clear separation into two different temperature regimes (as seen for the “Filaments” sub-region).
Results for probability distribution functions.
5.2. The spatial structure of NGC 6334
5.2.1. The Δ-variance method
We performed a Δ-variance analysis7, on the column density maps. This method can characterize spatial structure in a 2D map (denoted s). The Δ-variance, 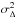 , is defined as
, is defined as 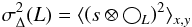 where ◯ L is a wavelet filtre function (a smooth or a step-shaped function, e.g., “Mexican hat” or “French hat”) convolved with the map to determine the power contained in all spatial (length) scales L (called lag) and derive possible characteristic size scales. For the present work, we use the “Mexican-hat” filtre because it is more robust compared to the “French-hat” filtre, which can produce ripples at large lags (Ossenkopf et al. 2008a).
where ◯ L is a wavelet filtre function (a smooth or a step-shaped function, e.g., “Mexican hat” or “French hat”) convolved with the map to determine the power contained in all spatial (length) scales L (called lag) and derive possible characteristic size scales. For the present work, we use the “Mexican-hat” filtre because it is more robust compared to the “French-hat” filtre, which can produce ripples at large lags (Ossenkopf et al. 2008a).
The Δ-variance is directly linked to the power spectrum of an image because for any 2D image with a power spectrum P(k) ∝ | k | − α, in which k is the spatial frequency, the 2D Δ-variance varies as 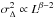 . Fitting the slope β thus provides a measure for the amount of structure on various scales in a given image. See Ossenkopf et al. (2008a,b) for a description of the method and, e.g., Sun et al. (2006) and Schneider et al. (2011) for its observational application.
. Fitting the slope β thus provides a measure for the amount of structure on various scales in a given image. See Ossenkopf et al. (2008a,b) for a description of the method and, e.g., Sun et al. (2006) and Schneider et al. (2011) for its observational application.
We perform the Δ-variance analysis here on the higher angular resolution column density map (25 resolution), derived by excluding the SPIRE 500 μm data. We used the column-density error map to determine the reliability of the Δ-variance spectrum because noise contributions in the map can be separated from the intrinsic structure of the cloud complex. Weighting the image with the signal-to-noise map (the column density map divided by the error map) enables us to distinguish the variable noise from real small-scale structure (see Ossenkopf et al. 2008b for details). The error bars shown in Figs. 8 and 9 are determined from Poisson statistics. As discussed in detail in Appendix D in Schneider et al. (2011), the error bars give absolute errors of the individual points in the spectrum that are not independent, but follow a mutual slope that is somewhere between the slope seen at the two ends of the error bars. Therefore, we have a very robust determination of the relative scaling behaviour between different lags, which is much more accurate than the size of the error bars.
Results for Δ-variance.
5.2.2. The Δ-variance applied to NGC 6334
To gain insight into different spatial structures in the sub-regions, we applied the Δ-variance to the sub-regions used in the PDF analysis. Figure 8 shows the respective curves, Δ-variance (in logarithmic display in order to determine the slope β and in linear scaling to emphasize the differences in the curves) against the length scale (lag) in arcseconds (lower axis) and parsecs (upper axis) and reveals interesting details, which are not visible in the curve for the whole complex (Fig. 9) that will be discussed afterwards. Table 2 summarizes the values of β of the Δ-variance.
 |
Fig. 8 Left: Δ-variance results including errorbars for the four sub-regions in NGC 6334 in logarithmic scaling. The lower x-axis gives the length scale in arcseconds, while the upper x-axis gives it in parsec. The grey dashed line indicates the angular resolution limit of 25. β was fitted starting from the resolution limit of 0.2 pc (25) until the first significant structure relevant for all regions (2 pc). This range is indicated as a line at the bottom of the figure. However, this fit is not always a perfect power law. Right: the same Δ-variance for the sub-regions shown in linear scaling in order to emphasize the differences in the curves. The curves are normalized to the value of the Δ-variance for 30. |
The Δ-variances for all sub-regions shows a steady increase in structure with increasing length scales starting at the resolution limit of 25 (0.2 pc at a distance of 1.75 kpc) to ~2 pc. The flatter increase with a plateau around 1 pc is found for the “Filaments” subregion. Though the curves show only subtle differences in their shape, these are significant, as becomes obvious in the linear display.
The curves gradually decrease after 2 pc, except for the “Cold” sub-region that shows a second peak around 8 pc. The “Filaments” sub-region has a plateau between ~0.5 pc and 2 pc; for higher lags, the Δ-variance drops faster than for the other sub-regions. Though it is tempting to interprete the lower value of 0.5 pc as being due to the filament width8, it is likely that the finite telescope beam (25) is still noticeable (Bensch et al. 2001). However, this value is also the typical filament width we determined from our preliminary method, and it corresponds to the width of the filaments measured for other high-mass star-forming regions, the DR21 filament in Cygnus X (Hennemann et al. 2012) and Vela-C (Hill et al. 2011). In contrast, for low-mass star-forming regions, Schneider et al. (2011) found characteristic scales between 0.2 pc and 1 pc interpreted as due to the filament width. From recent Herschel observations, Arzoumanian et al. (2011) measured a typical filament FWHM width of 0.1 pc (i.e. ~0.2 pc in our definition of filament width) for IC 5146 and other Herschel regions.
The dominating scales are between 1 and a few pc (up to 8 pc for the “Cold” sub-region). These scales should already be seen in the maps because the Δ-variance identifies scales in a systematic way. Accordingly, the three-colour map (Fig. 1) helps detect the “bubbles” of H ii regions (blue circular features) and the network of colder filaments (red).
To compare all regions, we fit the Δ-variance up to a common scale of 2 pc. All sub-regions except “Filaments” have a value of β around 2. This implies first that these regions are not fundamentally different in their spatial structure and second that small-scale structure dominates because the β-values are low. Interestingly, the “Filaments” sub-region has the lowest value, 1.7, which is indeed characteristic for filamentary structures (see Sun et al. 2006, who compared Δ-variance results from molecular line maps with different tracers and AV-maps).
Figure 9 shows the Δ-variance determined for the whole complex. The curve increases sharply until a peak at 2 pc and then falls off. However, this decrease does not follow the σ2 ∝ Lβ − 2 law; i.e., it is not determined by noise for high lags, but still contains significant structure. We overplotted the Δ-variance curve for the “Centre” sub-region on the curve and it becomes obvious that the global spatial structure of the complex is dominated by the peak around 2 pc, which is the prominent star-forming ridge apparent in the “Centre” sub-region.
A fit of the β exponent of the Δ-variance on smaller scales ( < 2 pc) gives a value of 2.53, which is typical of molecular clouds in general (Schneider et al. 2011). This higher value reflects that many structures are mixed and thus “smoothed” in the total Δ-variance curve.
 |
Fig. 9 Δ-variance results including errorbars for the whole NGC 6334 complex shown in black. Overplotted in red is the Δ-variance for the “Centre” region (scaled to fit the σ2 scale of the total region). The lower x-axis gives the length scale in arcseconds while the upper x-axis gives it in parsec. The grey dotted line indicates the angular resolution limit of 25. The fit range for the exponent β is indicated. |
6. Discussion
6.1. Impact of the H ii regions on the structure of the filaments
The characteristic size scales revealed by the Δ-variance analysis are created in general by the observed geometry, which is in turn linked to the injection scales of energy. In Schneider et al. (2011), and references therein, the interpretation is that the largest scales (tens of parsecs) correspond to expanding supernovae (SN) shells, while expanding H ii regions work on scales of a few parsecs and outflows on still smaller scales. The size scales of 1–7 pc may therefore be caused by the large number of optical H ii regions observed in NGC 6334, mainly in the “Centre” and “Filaments” sub-regions. The four main optical H ii regions, GUM64b, GUM63, GUM61, and G351.2+0.5, in the “Centre” sub-region have sizes of 5.6 pc, 15 pc, 4.2 pc, and 5.7 pc respectively, while the more compact radio sources have sizes between 0.2 pc and 1.4 pc. The optical extent of GM1-24 is ~ 5.6 pc × 2.1 pc. However, no distinct optical H ii region is present in the “Quiet” and “Cold” sub-regions. In the “Cold” sub-region there is indeed no scale limit (structures extend up to 8 pc), although it is less clear what causes the peak at ~2 pc for the “Quiet” sub-region. In this case, we may be observing the primordial structure of the cloud (note that the bubbles created by the H ii regions are still embedded in a network of filaments, see Fig. 1), or the formation of filaments due to expanding H ii regions that could well be the source of compressive energy, shaping the filaments. For example, Peretto et al. (2012) propose such a mechanism to explain the filamentary structure of the Pipe nebula.
It is the first time that these size scales are detected in a high-mass star-forming cloud where many density and spatial structures are present. In the study of Schneider et al. (2011) using extinction maps, none of the high-mass star-forming regions (e.g., Cygnus X, Vela, W3) indicated a characteristic size scale. This was mainly attributed to a confusion problem and the limitation imposed by the lower angular resolution, and not interpreted as a signature of self-similar turbulence. In studies of whole clouds (in particular along the Galactic plane), many scales are detected along the line-of-sight and no characteristic scale appears. With the Herschel column density maps, these problems can be resolved partly, although some regions are still too confused. The interest of using the Δ-variance for structure identification is that a direct link to the turbulent state of the cloud can be established. All structures already visible in the map, i.e., filaments and bubbles, are identified in the Δ-variance spectrum. It is not clear, however, whether the lower value of β = 1.7 for the “Filaments” region is a systematic difference, in contrast to the other sub-regions (β = 2). Applying the Δ-variance on a larger sample of clouds may give a more complete view of the significance of this finding.
6.2. The evolutionary state of NGC 6334
The column density PDFs deviate from the lognormal shape at AV ~ 12–26. In other Herschel studies (Vela C, Hill et al. 2011; Rosette et al. 2012) and in studies using extinction maps (Kainulainen et al. 2009; Froebrich & Rowles 2010; Schneider et al. 2011), including quiet, low-mass, and high-mass star-forming, this deviation point also shows a very large variation, i.e. from a few magnitudes up to very high values of up to 30 mag. This range is wide and implies that the deviation of the PDF from the lognormal should not be interpreted as a “threshold” of star formation as was proposed by Froebrich & Rowles (2010).
We observe a clear increase in α from the “Quiet” sub-region (α = 1.35) through the “Cold” and “Filaments” sub-regions (α = 1.61 and 1.66, respectively) to the “Centre” sub-region (α = 2.37). The most straightforward explanation is that self-gravity becomes gradually more important in the different sub-regions. The “Quiet” sub-region is thus turbulence-dominated, and indeed, it does not show active star-formation. Its column density PDF is lognormal over a large range of densities, with a narrow dispersion (σ = 0.2 in contrast to σ = 0.3–0.35 for the other sub-regions). The slope of the higher density range is steep, leading to a low value of α. Our analysis suggests that the “Cold” and “Filaments” sub-regions are in an intermediate evolutionary state, showing signposts of star formation (massive dense cores and protostellar objects are detected, Tigé et al., in prep.). The most active “Centre” sub-region, where the highest density and temperature values are found and where most of protostellar dense cores are located (Tigé et al., in prep.), has the shallowest high-density power-law tail and thus the highest value of α. Here, we are likely observing the density distribution of individual collapsing cores and/or the global collapse of the whole region. Previous studies (e.g., Schneider et al. 2010b; Csengeri et al. 2011; Peretto et al. 2006) have observationally confirmed the global collapse of high-mass star-forming regions. It is difficult, however, to distinguish the relative contributions of individual core collapse and a global collapse from an analysis of the column density PDF shape and the high-density slope. We plot in Fig. 7 the AV-contour where the PDF starts to develop a high-density power-law tail; i.e., from this column density value upwards, gravity should dominate. From that, we can speculate that the “Centre” sub-region is the best candidate for a global collapse; only the central, dominating ridge is included in the contour. For the “Filaments” sub-region, the AV = 12 mag contour nicely outlines the filamentary structures, which are all supercritical and thus gravitationally collapsing. In contrast, the AV -contours of the “Quiet” and “Cold” sub-regions outline less filamentary structures but rather clumpy regions and individual cores. These regions therefore probably show individual clump/core collapse.
Our results agree with the predictions from numerical simulations (Ballesteros-Paredes et al. 2011; Cho & Kim 2011; Kritsuk et al. 2011; Schneider et al., in prep.; Girichidis et al. 2012) where the column density PDF shape varies with time. All models (purely hydro-dynamic but with different forces on large or small scales and driven or decaying turbulence) have a perfect lognormal shape for a purely turbulent molecular cloud as a common starting situation. They develop steep power-law tails for initial time steps and shallow slopes for later stages. Though Ballesteros-Paredes (2011) correctly points out that the slope of the power-law tail varies with projection and thus changes from cloud to cloud, we are confident in our comparison because we have investigated sub-regions within a single cloud complex. To first order, we assume that there is no preferred direction in NGC 6334 and the absolute values of the slope indeed reflect an evolutionary sequence. The high value of α = 2.37 for the “Centre” region points toward a more dynamic and rapid scenario of star formation. Girichidis et al. (2012) shows that values of α > 2.1 are due to accelerated collapse and not only to free-fall gravitational collapse. Only dynamic processes that change the velocity field (e.g., converging flows, external compression via expansion of H ii -regions) can account for such an acceleration. As proposed by Girichidis et al. (2012), this leads to a “burst-like” mode of star formation that would be supported by our observations of the NGC 6334 “Centre” ridge with its high number of already formed H ii -regions and the protostellar sources.
7. Summary and conclusions
Using Herschel data we analysed the spatial and density structure in the star-forming region NGC 6334 with Δ-variance and PDFs for the column density. We applied both tools to four different sub-regions in NGC 6334 distinguished on the basis of differences in the column density, temperature, and radiation field. The investigations made through such tools can be used for “automatized” searches over large amounts of data to search for particular structures and/or to classify the ISM morphology in different regions. However, one needs to evaluate the performance of these methods in different situations. NGC 6334 represents a good case in the sense that it has zones with different evolutionary states, as well as numerous H ii regions. Our results represent observational constraints to the existing models of turbulence and cloud structure in general.
The Δ-variance analysis suggests that H ii regions are the most important agents for shaping the structure in the NGC 6334 complex. Most of the scales can be caused by the injection of energy due to expanding H ii regions. These may cause an acceleration of star formation that is seen in the slope of the column density PDF that is flatter than expected for a pure free-fall collapse of cores or filaments. The length of filaments is probably another characteristic scale, covering the same range of ~1 to ~8 pc. The width of filaments varies between 0.16 and 0.5 pc and is not clearly traced by the Δ-variance, probably also to the limited angular resolution. The column density PDFs suggest that the different sub-regions are at different evolutionary stages. As pointed out above, the “Centre” sub-region seems to be in a more evolved stage than the “Cold” and “Filaments” sub-regions.
Online material
Appendix A: Interplay between the ionized gas (Hα) and the dust
In this section, we show images combining Herschel and Hα images. The Hα image is from the UKST Hα survey (Parker et al. 2005).
 |
Fig. A.1 Hα image of NGC 6334 (2 |
 |
Fig. A.2 Three-colour image (1 |
See, e.g., http://www.eso.org/public/images/eso1017a/
The instrument parameters and calibration for PACS and SPIRE are given in the PACS Observers Manual and the SPIRE Observers Manual (see http://herschel.esac.esa.int/Documentation.shtml).
There remains a discrepancy with extinction maps obtained using near-IR data. The one published in Froebrich & Rowles (2010) shows a higher degree of extinction for the diffuse medium (7 mag < AV < 14 mag) along the NGC 6334 line of sight than we estimate. A possible contamination of the stellar background by giant stars throughout the whole galaxy and, especially, from the bulge may account for that, but in general, this discrepancy is not well understood.
We excluded in the sub-region definition (and analysis) the emission located on the map border around 172321.2, − 355410.4 because it belongs to a region located at larger distance (the radio source G351.61+00.17 with a velocity of − 43 km s-1; Caswell & Haynes 1987), hence not physically associated with NGC 6334.
After Brunt et al. (2010), the PDF of the log (normalized 2D column density) is only a compressed and shifted version of the PDF generated from the log (normalized 3D density). In the following, we rely on this approximation and use the general term “density”, although we use the column density. So far, PDFs determined from molecular cloud column density maps using extinction maps (Kainulainen et al. 2009) have suffered from a cut-off around AV ~ 25 and thus appeared to be lognormal over a wide range of low column densities without including the very high density. It is now possible to include the high densities using Herschel data.
All Δ-variance calculations have been done with the IDL-based routine deltavarwidget provided by V. Ossenkopf, available at http//:www.astro.uni-koeln.de/~ossk/ftpspace/deltavar
The Δ-variance traces the outer boundaries of structures while the measured filament width in Arzoumanian et al. (2011) or Hennemann et al. (2012), and our method corresponds to an FWHM that is a factor of ≈ 2 lower.
Acknowledgments
SPIRE has been developed by a consortium of institutes led by Cardiff Univ. (UK) and including Univ. Lethbridge (Canada); NAOC (China); CEA, LAM (France); IFSI, Univ. Padua (Italy); IAC (Spain); Stockholm Observatory (Sweden); Imperial College London, RAL, UCL-MSSL, UKATC, Univ. Sussex (UK); and Caltech, JPL, NHSC, Univ. Colorado (USA). This development has been supported by national funding agencies: CSA (Canada); NAOC (China); CEA, CNES, CNRS (France); ASI (Italy); MCINN (Spain); SNSB (Sweden); STFC, UKSA (UK); and NASA (USA). PACS has been developed by a consortium of institutes led by MPE (Germany) and including UVIE (Austria); KU Leuven, CSL, IMEC (Belgium); CEA, LAM (France); MPIA (Germany); INAF-IFSI/OAA/OAP/OAT, LENS, SISSA (Italy); IAC (Spain). This development has been supported by the funding agencies BMVIT (Austria), ESA-PRODEX (Belgium), CEA/CNES (France), DLR (Germany), ASI/INAF (Italy), and CICYT/MCYT (Spain). Part of this work was supported by the ANR (Agence Nationale pour la Recherche) projects “PROBeS” (ANR-08-BLAN-0241), and “STARFICH” (ANR-11-BS56-010). We thank C. Federrath, R. Klessen, and P. Girichidis for extensive discussions. This work was partially supported by the Deutsche Forschungsgemeinschaft, DFG, project number 0s 177/2-1. N. Schneider acknowledges funding by the DFG-priority programme 1573 (ISM-SPP). We thank the French Space Agency (CNES) for financial support.
References
- Abergel, A., Ade, P. A. R., Aghanim, N., et al. 2011, A&A, 536, A24 [Google Scholar]
- Anderson, L. D., Bania, T. M., Balser, D. S., et al. 2011, ApJS, 194, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, L. D., Zavagno, A., Deharveng, L., et al. 2012, A&A, 542, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, Ph., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arzoumanian, D., André, Ph., Didelon, P., et al. 2011, A&A, 529, L6 [Google Scholar]
- Ballesteros-Paredes, J., & Mac Low, M.-M. 2002, ApJ, 570, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Ballesteros-Paredes, J., Vázquez-Semadeni, E., Gazol, A., et al. 2011, MNRAS, 416, 1436 [NASA ADS] [CrossRef] [Google Scholar]
- Beckwith, S., Sargent, A., Chini, R., et al. 1990, AJ, 99, 924 [NASA ADS] [CrossRef] [Google Scholar]
- Bensch, F., Stutzki, J., & Ossenkopf, V. 2001, A&A, 266, 636 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., Thorwirth, S., Zhang, Q., et al. 2005, ApJ, 627, 834 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Kainulainen, J., Henning, T., et al. 2011, A&A, 533, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., Tackenberg, J., Linz, H., et al. 2012, ApJ, 747, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Bernard, J.-P., Paradis, D., Marshall, D., et al. 2010, A&A, 518, L88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bica, E., Dutra, C., & Barbuy, B. 2003, A&A, 397, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Brunt, C. M., Federrath, C., & Price, D. J. 2010, MNRAS, 403, 1507 [NASA ADS] [CrossRef] [Google Scholar]
- Carey, S. J., Noriega-Crespo, A., Mizuno, D. R., et al. 2009, PASP, 121, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Carral, P., Kurtz, S., & Rodriguez, L. 2002, AJ, 123, 2574 [NASA ADS] [CrossRef] [Google Scholar]
- Caswell, J. L., & Haynes, R. F. 1987, A&A, 171, 261 [NASA ADS] [Google Scholar]
- Cho, W., & Kim, J. 2011, MNRAS, 410, L8 [NASA ADS] [Google Scholar]
- Compiègne, M., Flagey, N., Noriega-Crespo, A., et al. 2010, ApJ, 724, 44 [Google Scholar]
- Csengeri, T., Bontemps, S., Schneider, N., et al. 2011, ApJ, 740, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Emprechtinger, M., Monje, R. R., van der Tak, F., et al. 2012, ApJ, 756, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Klessen, R. S., & Schmidt, W. 2008, ApJ, 688, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Duval, J., Klessen, R. S., et al. 2010, A&A, 512, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Federrath, C., Sur, S., Schleicher, D. R. G., et al. 2011, ApJ, 731, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Feigelson, E., Martin, A., McNeill, C., et al. 2009, AJ, 138, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Froebrich, D., & Rowles, J. 2010, MNRAS, 406, 1350 [NASA ADS] [Google Scholar]
- Gezari, D. 1982, ApJ, 259, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Girichidis, P., Konstandin, L., Whitworth, A., et al. 2012, ApJ, submitted [Google Scholar]
- Green, D. A. 2009, BASI, 37, 45 [NASA ADS] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Gum, C. S. 1955, MmRAS, 67, 155 [NASA ADS] [Google Scholar]
- Heitsch, F., Mac Low, M.-M., & Klessen, R. S. 2001, ApJ, 547, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Hennemann, M., Motte, F., Schneider, N., et al. 2012, A&A, 543, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
- Hill, T., Motte, F., Didelon, P., et al. 2011, A&A, 533, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inutsuka, S., & Miyama, S. 1992, ApJ, 388, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Kainulainen, J., Beuther, H., Henning, T., et al. 2009, A&A, 508, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kharchenko, N. V., Berczik, P., Petrov, M. I., et al. 2009, A&A, 495, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klessen, R. S. 2000, ApJ, 535, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S., & Hennebelle, P. 2010, A&A, 520, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klessen, R. S., Heitsch, F., & Mac Low, M.-M. 2000, ApJ, 535, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Kraemer, K. E., & Jackson, J. M. 1999, ApJS, 124, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Kritsuk, A. G., Norman, M. L., & Wagner, R. 2011, ApJ, 727, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Li, H., Griffin, G. S., Krejny, M., et al. 2006, ApJ, 648, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Loughran, L., McBreen, B., Fazio, G., et al. 1986, ApJ, 303, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Mc Breen, B., Fazio, G. G., Stier, M., et al. 1979, ApJ, 232, L183 [NASA ADS] [CrossRef] [Google Scholar]
- Mac Low, M.-M., & Klessen, R. S. 2004, RvMP, 76, 125 [Google Scholar]
- McSwain, M. V., & Gies, D. R. 2005, ApJS, 161, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Men’shchikov, A., André, Ph., Didelon, P., et al. 2012, A&A, 542, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, A&A, 518, L100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motte, F., Zavagno, A., Bontemps, S., et al. 2010, A&A, 518, L77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neckel, T. 1978, A&A, 69, 51 [NASA ADS] [Google Scholar]
- Nguyen Luong, Q., Motte, F., Hennemann, M., et al. 2011, A&A, 535, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ormel, C. W., Min, M., Tielens, A. G. G. M., et al. 2011, A&A, 532, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ossenkopf, V., & Henning, Th. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Ossenkopf, V., Krips, M., & Stutzki, J. 2008a, A&A, 485, 719 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ossenkopf, V., Krips, M., & Stutzki, J. 2008b, A&A, 485, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ostriker, J. 1964, ApJ, 140, 1056 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Parker, Q., Phillips, S., Pierce, M., et al. 2005, MNRAS, 362, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Persi, P., & Tapia, M. 2008, Handbook of Star Forming Regions, Volume II: The Southern Sky, ed. B. Reipurth (ASP Monograph Publications), 5, 456 [Google Scholar]
- Peretto, N., André, Ph., & Belloche, A. 2006, A&A, 445, 979 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peretto, N., André, Ph., Könyves, V., et al. 2012, A&A, 541, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roussel, H., et al. 2012, PASP, submitted [arXiv:1205.2576] [Google Scholar]
- Russeil, D., Zavagno, A., Motte, F., et al. 2010, A&A, 515, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Russeil, D., Zavagno, A., Adami, C., et al. 2012, A&A, 538, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodriguez, L. F., Canto’, J., & Moran, J. M. 1982, ApJ, 255, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., Csengeri, T., Bontemps, S., et al. 2010a, A&A, 520, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Motte, F., Bontemps, S., et al. 2010b, A&A, 518, L83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Bontemps, S., Simon, R., et al. 2011, A&A, 529, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Csengeri, T., Hennemann, M., et al. 2012, A&A, 540, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., André, Ph., Könyves, V., et al. 2013, ApJ, 766, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, K., Kramer, C., Ossenkopf, V., et al. 2006, A&A, 451, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tapia, M., Persi, P., & Roth, M. 1996, A&A, 316, 102 [NASA ADS] [Google Scholar]
- Tapia, M., Roth, M., Lopez, J., et al. 1991, A&A, 242, 388 [NASA ADS] [Google Scholar]
- Tian, W. W., Haverkorn, M., & Zhang, H. Y. 2007, MNRAS, 378, 1283 [NASA ADS] [CrossRef] [Google Scholar]
- Toala, J. A., Vázquez-Semadeni, E., & Gomez, G. C. 2012, ApJ, 744, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Vázquez-Semadeni, E., Gómez, G. C., Jappsen, A. K., et al. 2007, ApJ, 657, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Vázquez-Semadeni, E., Gonzales, R. F., Ballesteros-Paredes, J., et al. 2008, MNRAS, 390, 769 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Three-colour Herschel image of NGC 6334 with 500 μm data in red, 160 μm data in green, and 70 μm data in blue. The size of the image is 2 |
| In the text | |
 |
Fig. 2 Three-colour image of the central part of NGC 6334 with the same colour mapping as in Fig. 1. The image is 33 |
| In the text | |
 |
Fig. 3 H2 column density (left) and temperature (right) maps of NGC 6334, determined using the 160 μm, 250 μm, 350 μm, and 500 μm Herschel wavebands. The different sub-regions discussed in the text are indicated with white dashed-line polygons. The H ii regions GUM61 to 64a,b,c are indicated with triangles. |
| In the text | |
 |
Fig. 4 Column density PDF of NGC 6334 produced without the 70 μm band. The x-axis labelling is in column density at the bottom x-axis and in ln(N/ ⟨ N ⟩ ) at the top x-axis. The labelling of the y-axis is a probability on the left and number of pixels per log bin on the right. The green curve indicates the best lognormal fit PDF, and the red line is the best-fit power-law fit to the high-density tail. In the panel the deviation point of the PDF from lognormal (AV), the width σ, the slope s, and the exponent α are given. |
| In the text | |
 |
Fig. 5 Column density PDFs of the 4 sub-regions in NGC 6334 produced without the 70 μm band. The x-axis labelling is in visual extinction at the bottom x-axis and in ln (N/ ⟨ N ⟩ ) at the top x-axis. The labelling of the y-axis is a probability. The green curves indicate the best lognormal fit PDF (Eq. (1)), and the red line is a fit to the high-density part of the PDF that follows a power law. The width of the PDF, σ, and the exponent of the spherical density profile, α, are given in each panel. |
| In the text | |
 |
Fig. 6 Same as Fig. 5 for temperature. The x-axis labelling for the temperature PDF is in Kelvin at the bottom x-axis and in ln (T/ ⟨ T ⟩ ) at the top x-axis. The width, σ, and the peak temperature, in Kelvin, of the PDF are given in each panel. |
| In the text | |
 |
Fig. 7 Individual column-density maps of the sub-regions expressed in visual extinction AV (in the range of AV-values for the PDF) with the contour level of the lower limit used for fitting the slope in the high-density tail of the PDF (Fig. 5). The corresponding values are given in each panel. |
| In the text | |
 |
Fig. 8 Left: Δ-variance results including errorbars for the four sub-regions in NGC 6334 in logarithmic scaling. The lower x-axis gives the length scale in arcseconds, while the upper x-axis gives it in parsec. The grey dashed line indicates the angular resolution limit of 25. β was fitted starting from the resolution limit of 0.2 pc (25) until the first significant structure relevant for all regions (2 pc). This range is indicated as a line at the bottom of the figure. However, this fit is not always a perfect power law. Right: the same Δ-variance for the sub-regions shown in linear scaling in order to emphasize the differences in the curves. The curves are normalized to the value of the Δ-variance for 30. |
| In the text | |
 |
Fig. 9 Δ-variance results including errorbars for the whole NGC 6334 complex shown in black. Overplotted in red is the Δ-variance for the “Centre” region (scaled to fit the σ2 scale of the total region). The lower x-axis gives the length scale in arcseconds while the upper x-axis gives it in parsec. The grey dotted line indicates the angular resolution limit of 25. The fit range for the exponent β is indicated. |
| In the text | |
 |
Fig. A.1 Hα image of NGC 6334 (2 |
| In the text | |
 |
Fig. A.2 Three-colour image (1 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.