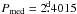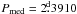| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A40 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220690 | |
| Published online | 29 April 2013 | |
Flip-flops of FK Comae Berenices⋆,⋆⋆
1 Department of Physics, PO Box 64, 00014 University of
Helsinki, Finland
e-mail: thomas.hackman@helsinki.fi
2
Finnish Centre for Astronomy with ESO (FINCA), University of
Turku, Väisäläntie
20, 21500
Piikkiö,
Finland
3 Tartu Observatory, Tõravere, 61602, Estonia
4
Aalto University, Department of Information and Computer
Science, PO Box
15400, 00076
Aalto,
Finland
5
Niels Bohr Institute, University of Copenhagen,
Juliane Maries Vej
30, 2100
København Ø,
Denmark
6
Centre for Star and Planet Formation, Natural History Museum of
Denmark, University of Copenhagen, Øster Voldgade 5 − 7, 1350
København Ø,
Denmark
7
Leibniz-Institut für Astrophysik Potsdam,
An der Sternwarte
16, 14882
Potsdam,
Germany
8
Nordic Optical Telescope, 38700
Santa Cruz de la Palma,
Spain
Received: 3 November 2012
Accepted: 5 March 2013
Context.FK Comae Berenices is a rapidly rotating magnetically active star, the light curve of which is modulated by cool spots on its surface. It was the first star where the “flip-flop” phenomenon was discovered. Since then, flip-flops in the spot activity have been reported in many other stars. Follow-up studies with increasing length have shown, however, that the phenomenon is more complex than was thought right after its discovery.
Aims. Therefore, it is of interest to perform a more thorough study of the evolution of the spot activity in FK Com. In this study, we analyse 15 years of photometric observations with two different time series analysis methods, with a special emphasis on detecting flip-flop type events from the data.
Methods. We apply the continuous period search and carrier fit methods on long-term standard Johnson-Cousins V-observations from the years 1995−2010. The observations were carried out with two automated photometric telescopes, Phoenix-10 and Amadeus T7 located in Arizona.
Results. We identify complex phase behaviour in 6 of the 15 analysed data segments. We identify five flip-flop events and two cases of phase jumps, where the phase shift is Δφ < 0.4. In addition we see two mergers of spot regions and two cases where the apparent phase shifts are caused by spot regions drifting with respect to each other. Furthermore we detect variations in the rotation period corresponding to a differential rotation coefficient of |k| > 0.031.
Conclusions. The flip-flop cannot be interpreted as a single phenomenon, where the main activity jumps from one active longitude to another. In some of our cases the phase shifts can be explained by differential rotation: two spot regions move with different angular velocity and even pass each other. Comparison between the methods show that the carrier fit utility is better in retrieving slow evolution especially from a low amplitude light curve, while the continuous period search is more sensitive in case of rapid changes.
Key words: stars: late-type / stars: activity / starspots / dynamo / stars: individual: FK Comae Berenices
Based on data obtained with the Amadeus T7 Automatic Photoelectric Telescope (APT) at Fairborn Observatory, jointly operated by the University of Vienna and AIP, the Phoenix-10 APT at Mt. Hopkins, Arizona, and the Nordic Optical Telescope, Observatorio Roque de los Muchachos, La Palma, Canary Islands.
The photometric observations are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/553/A40
© ESO, 2013
1. Introduction
FK Comae Berenices (HD 117555; hereafter FK Com) is the prototype of a class of single chromospherically active rapidly rotating G-K giants. Only a few stars fulfil the definition of the FK Com class (Bopp & Rucinski 1981). These stars may represent an intermediate state of coalesced W UMa binaries (e.g. Bopp & Stencel 1981) in the process of magnetic braking, which would explain why they are so rare.
FK Com itself is an extremely active late-type star and has been extensively studied with ground-based optical photometry and spectroscopy, radio observations, as well as satellite-based UV- and X-ray observations (e.g. Jetsu et al. 1994a; Oláh et al. 2006; Panov & Dimitrov 2007; Korhonen et al. 2009a; Hughes & McLean 1987; Bopp & Stencel 1981; Ayres et al. 2006; Drake et al. 2008).
The photometric rotation period of FK Com is 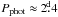 (Chugainov 1966; Jetsu et al. 1993). It has been proposed that its spectral class is between G5 iii (Korhonen et al. 1999, 2007) and G4 iii (Strassmeier 2009). Korhonen et al. (2000) concluded that vsini = 159 km s-1 gave the best fit for the spectral data.
(Chugainov 1966; Jetsu et al. 1993). It has been proposed that its spectral class is between G5 iii (Korhonen et al. 1999, 2007) and G4 iii (Strassmeier 2009). Korhonen et al. (2000) concluded that vsini = 159 km s-1 gave the best fit for the spectral data.
Analysing photometry spanning roughly over 25 years (1966−1990), Jetsu et al. (1993) reported a switch of activity between two longitudes separated by approximately 180°, and labelled this effect the “flip-flop”. The activity was observed to jump from one active longitude to the other three times during the period of analysis. Furthermore, the active longitude system was reported to be rotating with the photometric rotation period of 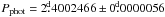 throughout the whole span of the data.
throughout the whole span of the data.
The flip-flop phenomenon has since then been suggested to occur in a number of stars (e.g. Jetsu 1996; Berdyugina & Tuominen 1998; Lehtinen et al. 2011). While further results of the stable active longitude system producing flip-flops on FK Com were published by Jetsu et al. (1994b), evidence for the phenomenon being more complex started building up, e.g. by the analysis of photometry by Strassmeier et al. (1997a). In this study, a gradual drift of the spots from one active longitude to the other was detected during 1993−1995, in contrast to the abrupt changes reported earlier, where spot migration over phase was not related to the phenomenon. With improved photometric data with denser timing piling up, the picture of a steady active longitude system rotating with one single period was abandoned. For instance in the study of Korhonen et al. (2002), where one-dimensional photometric inversions of FK Com were presented, the active longitude system exhibited three different periods: in the beginning of the observations, the system was rotating with the photometric rotation period of the star, slowed down during 1994−1997, and sped up to super-rotation for 1998−2004 (Korhonen et al. 2004). The first apparent semi-regularity of the flip-flops also became under doubt; the time between the flip-flops could range from a year to several years. Cycles of 5.2 and 5.8 years in the migration of the two active longitudes were reported by Oláh et al. (2006). Similarly, Panov & Dimitrov (2007) reported oscillatory spot migration with a cycle length of 5.8 ± 0.1 years. Furthermore Oláh et al. (2006) made a distinction between phase jumps and flip-flops. In the case of phase jumps, a new active region appears on the same hemisphere of the star as the old active region, resulting in a phase shift of less than 0.5. During a flip-flop the active longitude changes ~180°.
The behaviour of the active longitude system and the related flip-flops were spectroscopically confirmed by analysing the uniquely long series of Doppler images from the years 1993−2008 by Korhonen and collaborators (Korhonen et al. 2000, 2007; Ayres et al. 2006; Korhonen et al. 2009a,b). This work was based mainly on the observations with the SOFIN high-resolution spectrograph at the Nordic Optical Telescope (La Palma, Spain).
Jetsu et al. (1994b) detected variations in the photometric period, which could be a signature of differential rotation in FK Com. Korhonen et al. (2007) estimated the differential rotation by combining Doppler images and period analysis of photometry. They reported a rotation law of 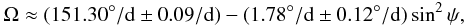 (1)where ψ is the stellar latitude. The estimated relative differential rotation coefficient was thus k ≈ 0.012. It should, however, be emphasised that estimating differential rotation using Doppler imaging is challenging, especially because of artifacts and errors in the spot latitudes.
(1)where ψ is the stellar latitude. The estimated relative differential rotation coefficient was thus k ≈ 0.012. It should, however, be emphasised that estimating differential rotation using Doppler imaging is challenging, especially because of artifacts and errors in the spot latitudes.
Observations of FK Com obtained with the Far Ultraviolet Spectroscopic Explorer (FUSE) revealed complex profiles suggesting that the transition region and the corona are highly structured, dominated by dynamic processes, and could be very extended (Ayres et al. 2006). The X-ray observations obtained with XMM-Newton imply that the corona of FK Com is dominated by large magnetic structures similar to the interconnecting loops in solar active regions, but significantly hotter (Gondoin et al. 2002). Similarly, using data from the Chandra X-ray Observatory, Drake et al. (2008) found indications of magnetic loops in the corona of FK Com. Their observations suggested that the observed X-ray emission originates from plasma residing predominantly in extended structures centred at a phase halfway between two spot regions, and that the coronal structures revealed by the Chandra observations correspond to magnetic loops joining these two spot regions. This would support a model where the two regions have opposite magnetic polarities.
We want to investigate the spot activity in more detail and combining different methods. Our main aim is to identify and study the flip-flops of FK Com. We apply two novel time series analysis methods on long-term photometric observations; the continuous period search method (hereafter CPS, Lehtinen et al. 2011) and the carrier fit utility (hereafter CF, Pelt et al. 2011). In particular, we are interested in the nature of the flip-flops. We want to isolate different types of proposed effects: i) abrupt jumps from one hemisphere to another representing the flip-flop phenomenon; ii) events better described as phase jumps (with a phase separation significantly less than 180°); and iii) gradual phase drifts of the active longitudes. We also aim at establishing whether, when properly classified and separated, there are any regularities related to the phenomena.
Our secondary aim is to compare the results from our two analysis methods. We anticipate that there is a great advantage of combining the two time series analysis methods because of their different solutions for modelling the data. It is also important to make a comparative study with real data.
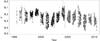 |
Fig. 1 All photometric V-data for FK Com. The Phoenix-10 data is marked with black dots and the Amadeus data is marked with grey pluses. |
 |
Fig. 2 The differential magnitudes of the comparison star HD 117567 for the Amadeus data: ΔV = VHD 117876 − VHD 117567. |
2. Observations
The photometric standard Johnson-Cousins V observations were collected with the 0.75 m Vienna University/AIP APT “Amadeus” (Strassmeier et al. 1997b, T7 in Table 1), located at Fairborn Observatory and the Phoenix-10 APT at Mt. Hopkins, Arizona (Ph10). Data points with errors greater than 0.02 were rejected and the differential magnitudes were transferred into apparent magnitudes using the comparison star HD 117567 just as in Jetsu et al. (1994a). A change corresponding to ΔV ~ 0.06 can be seen in the difference between the magnitudes of the check star HD 117876 and comparison star HD 117567 during 2006 (Fig. 2). The spectral type of the comparison star is F8, while the check star is classified as G8 ii-iii. Since no corresponding dip can be seen in the observations of FK Com, we concluded that it is the check star which has changed. For a more detailed description of the observations of FK Comae, we refer to the paper by Korhonen et al. (2001).
Most of the data has been included in earlier papers (Korhonen et al. 2002; Oláh et al. 2006, 2009; Korhonen et al. 2009a, and references therein). The data is summarised in Table 1 and published electronically at the CDS. Note that each observing season forms a segment. The new data consists of segments SEG14−SEG16.
Summary of the observations and labelling of each segment in the text.
3. Analysis methods
Both the CPS and CF analysis methods are based on an approach of continuous curve fitting. A main difference is that the CPS method allows the period to vary, while the CF uses a constant carrier period. Both approaches can be argued for. On one hand e.g. differential rotation will cause the photometric period to depend on the spot latitude or the anchoring depth of the spot structure. On the other hand, noise in the data and insufficient phase coverage will contribute to spurious period variations in the CPS method (Lehtinen et al. 2011). The CF method is more stable against such errors.
The main advantage of the CF- and CPS-methods is their flexible approach. The most common time series analysis methods used in astronomy are based on power spectrum analysis, e.g. the ones presented by Deeming (1975), Scargle (1982) and Horne & Baliunas (1986). These are limited in that there will be problems in dealing with higher harmonics and changes in the mean magnitude, light curve amplitude and minimum phase. This also means that the advantages of the CF- and CPS-methods become important when analysing long series of observations with a dense time coverage of a star with changing spot activity. The demand of dense timing of the observations is the reason why we omitted some part of the observations listed in Sect. 2 and some previously published observations of FK Com, e.g. the observations presented by Panov & Dimitrov (2007).
An alternative to time series analysis methods is offered by light curve modelling. With the availability of satellite observations, significant advances have been made in this area (see e.g. Croll et al. 2006). However, light curve modelling involves assumptions about considerable stability of the spots, which is clearly not the case for FK Com (see e.g. Fig. 4).
3.1. CF method
The CF method is based on the simple idea of decomposing the observed stellar light curves into two components: 1) a rapidly changing carrier modulation tracing the regular part of the signal, for instance rotation of a spotted star; and 2) a slowly changing modulation, such as evolution of the cool spots on the stellar surface. Such a situation can be described with the following model 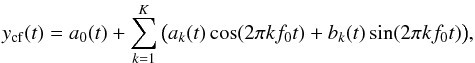 (2)
(2)
where a0(t) is the time-dependent mean level of the signal, K is the total number of harmonics included in the model, describing the overtones of the basic carrier frequency, while ak(t) and bk(t) are the low-frequency signal components. The carrier frequency f0 can be either known a priori, or determined using the CF utility, as the first step of the analysis. In this paper, we take the previous determinations of the photometric rotation period as the first guess of the carrier period 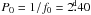 . The next step in the analysis is to formulate a suitable model for the modulating curves. In Pelt et al. (2011) we introduced two classes of models based on either trigonometric or spline approximation. In this paper, models based on the trigonometric approximation are used.
. The next step in the analysis is to formulate a suitable model for the modulating curves. In Pelt et al. (2011) we introduced two classes of models based on either trigonometric or spline approximation. In this paper, models based on the trigonometric approximation are used.
The trigonometric approximation model for the modulating signals is built in the following way. Let the time interval [tmin,tmax] be the full span of our input data. Then we can introduce a certain period D = C × (tmax − tmin) for which the coverage factor C is larger than unity (typically C = 1.1−1.5). Using the corresponding frequency, fD = 1/D, we can now build a trigonometric (truncated) series of the type: 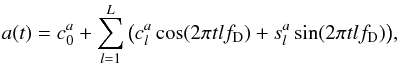 (3)and
(3)and 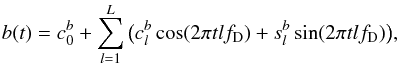 (4)where L is the total number of harmonics used in the modulator model. According to our definition of a slow process, the period D must be significantly longer than the carrier period P0. With the data segment lengths in the regime of 100−200 days, this condition is well satisfied with the chosen coverage factor. Next, proper expansion coefficient estimates are computed for every term in the series for the fixed carrier frequency f0 and the “data frequency” fD; this is a standard linear estimation procedure and can be implemented using standard mathematical (statistical) packages, as described in detail by Pelt et al. (2011). If the coefficients (ak,bk) consist of the same number of harmonics L and we approximate separate cycles by a K-harmonic model, then the overall count of linear parameters to be fitted is N = (2 × L + 1) ∗ (2 × K + 1). The actual choice of the representative parameters K and L depends on the particular object we are working with. The number of tones, K, depends on the complexity of the phase curves. The choice of L is constrained by the longest gaps in the time series. In this study, we adopt K = 2 and L = 3, resulting in the total number of free parameters to be fitted N = 35.
(4)where L is the total number of harmonics used in the modulator model. According to our definition of a slow process, the period D must be significantly longer than the carrier period P0. With the data segment lengths in the regime of 100−200 days, this condition is well satisfied with the chosen coverage factor. Next, proper expansion coefficient estimates are computed for every term in the series for the fixed carrier frequency f0 and the “data frequency” fD; this is a standard linear estimation procedure and can be implemented using standard mathematical (statistical) packages, as described in detail by Pelt et al. (2011). If the coefficients (ak,bk) consist of the same number of harmonics L and we approximate separate cycles by a K-harmonic model, then the overall count of linear parameters to be fitted is N = (2 × L + 1) ∗ (2 × K + 1). The actual choice of the representative parameters K and L depends on the particular object we are working with. The number of tones, K, depends on the complexity of the phase curves. The choice of L is constrained by the longest gaps in the time series. In this study, we adopt K = 2 and L = 3, resulting in the total number of free parameters to be fitted N = 35.
We visualise our results in the following way. First we calculate a continuous curve least-squares estimate ŷcf(t), from the randomly spaced and gapped data set. This approximation is continuous and does not contain gaps, and therefore allows us to get a smooth picture of the long-term behaviour. Next we divide this continuous curve into strips with a length of the carrier period 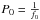 . We then normalise each strip so that the approximating values span the standard range of [−1,1] . After normalisation, we stack the strips along the time axis. To enhance the obtained plot, we extend every strip somewhat along phases, so that the actual display is wider (along phases) than a single period. The normalisation is a relevant part of our procedure because it helps to grasp the phase information we are interested in (trends, drifts, flip-flops etc.). This method of visualisation allows to verify that the model fits into the data and not into the gaps. If the number of nodes or harmonics L for the modulation model curves is chosen properly, then the phase plots do not reveal any underlying timing structure.
. We then normalise each strip so that the approximating values span the standard range of [−1,1] . After normalisation, we stack the strips along the time axis. To enhance the obtained plot, we extend every strip somewhat along phases, so that the actual display is wider (along phases) than a single period. The normalisation is a relevant part of our procedure because it helps to grasp the phase information we are interested in (trends, drifts, flip-flops etc.). This method of visualisation allows to verify that the model fits into the data and not into the gaps. If the number of nodes or harmonics L for the modulation model curves is chosen properly, then the phase plots do not reveal any underlying timing structure.
The data from both telescopes were merged for the CF-analysis. In principle merging V-magnitudes from two different sources may pose problems, even though the reduction is carefully done. In this case however, we concluded that the data was uniform enough for the CF-analysis. The CF analysis was applied on segments SEG2−16; in SEG1 there were not enough points to carry out the analysis.
The goodness of the fit was estimated with the coefficient of determination 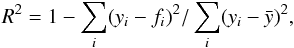 (5)
(5)
where 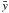 is the mean of the data. Our goal was to have R2 > 0.9. In five out of all the fifteen segments R2 was too small. Therefore, for SEG4, SEG5, SEG9, SEG10 and SEG15, we refined our analysis by excluding the 3σ outliers after an initial CF fit, and making a new fit. It is probably no coincidence, that four of these segments consisted of data from the two different telescopes. However, tests showed that excluding the outliers had no other significant influence on the result than that of improved goodness.
is the mean of the data. Our goal was to have R2 > 0.9. In five out of all the fifteen segments R2 was too small. Therefore, for SEG4, SEG5, SEG9, SEG10 and SEG15, we refined our analysis by excluding the 3σ outliers after an initial CF fit, and making a new fit. It is probably no coincidence, that four of these segments consisted of data from the two different telescopes. However, tests showed that excluding the outliers had no other significant influence on the result than that of improved goodness.
 |
Fig. 3 CF analysis results for each segment with the carrier period |
3.2. CPS method
The CPS method was originally developed for the analysis of photometric observations of late-type stars. In order to understand the spot activity of these stars, one has to take into account both short time scale (days) and long-term (years) changes (Lehtinen et al. 2011). The method is based on the Three Stage Period Analysis (TSPA, Jetsu & Pelt 1999). The model ![\begin{equation} y_\mathrm{cps}(t_i,\bar{\beta}) = a_0 + \sum_{k=1}^K{\left[a_k\cos{(2\pi k ft_i)} + b_k\sin{(2\pi k ft_i)}\right]}, \label{cpsmodel} \end{equation}](/articles/aa/full_html/2013/05/aa20690-12/aa20690-12-eq55.png) (6)is used to fit each set of the data. Here
(6)is used to fit each set of the data. Here 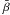 consists of the parameters (ai,bi,f), which are determined through a non-linear least squares optimisation. The three major improvements compared with the TSPA are:
consists of the parameters (ai,bi,f), which are determined through a non-linear least squares optimisation. The three major improvements compared with the TSPA are:
-
1.
We analyse the data with a sliding window of length ΔTmax in order to increase the time resolution.
-
2.
We test models of different orders and choose the final order K using a Bayesian information criterion .
-
3.
We derive the time scale TC of significant changes in the light curve.
With the CPS-analysis one can thus derive a continuous series of estimates for the mean magnitude (M), total light curve amplitude (A), photometric period (P) and epochs of the light curve minima (tmin). The temporal changes of the mean and amplitude are useful for studying variations in the level of spot activity, since the mean magnitude will be sensitive to the spot coverage and the amplitude is a measure of the non-axisymmetry of the spot configuration. Variations in the photometric period can be caused by differential rotation, or alternatively dynamo waves (Krause & Rädler 1980; Tuominen et al. 2002). The time scale of significant change TC can be used to estimate the stability of the light curve. It may also be related to the convective turnover time τc (Lehtinen et al. 2011, 2012).
The CPS-analysis was applied to the Phoenix 10 and Amadeus data separately. This method uses less data points in each fit than the CF-method, which makes it more vulnerable to errors in the data. Furthermore, with K = 2 the number of free parameters is six, i.e. much less than in the CF-method. Thus, the need to maximise the number of data points is less important than the homogeneity of the data for the CPS analysis. The maximum length of the moving window was ΔTmax = 24d. This length was chosen because the rotation period being ~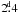 , it will give an optimal phase coverage in the case of evenly spaced observations. Normally ΔTmax would also define the division of the data into segments, as described in Lehtinen et al. (2011). However, for consistency reasons in this paper the segments are identical to the observing seasons. The maximum order of the fit, i.e. the largest tested K-value for the model (Eq. (6)), was Klim = 2.
, it will give an optimal phase coverage in the case of evenly spaced observations. Normally ΔTmax would also define the division of the data into segments, as described in Lehtinen et al. (2011). However, for consistency reasons in this paper the segments are identical to the observing seasons. The maximum order of the fit, i.e. the largest tested K-value for the model (Eq. (6)), was Klim = 2.
3.3. Kuiper test
Non-parametrical time-series analysis methods, such as the Kuiper test for phase distributions (Kuiper 1960), can be utilised to identify active longitudes from the epochs of light curve minima. We used the unweighted Kuiper-test as formulated by Jetsu & Pelt (1996). The Kuiper periodogram is calculated for a set of epochs of photometric minima tmin. The most significant periods are tested against the null hypothesis of a random phase distribution. Examples of application of this method can be found in Jetsu (1996), Lehtinen et al. (2011) and Lehtinen et al. (2012).
 |
Fig. 4 The CF fits for segments SEG4 and SEG5 using the carrier period |
 |
Fig. 5 The CPS analysis of segment SEG4 of the Amadeus photometry of FK Com. The phases in panel g) were calculated using the period |
We computed the Kuiper statistic periodogram for periodicities of 2.2−2.6 days using the epochs of photometric minima tmin derived both with the CF and CPS methods. A total of 1637 primary and secondary minima where retrieved from the CF-analysis. From the CPS-analysis we used separately the 136 independent minima and all 1837 minima. In addition to the minima, we also tested 1640 maxima from the CF-analysis.
 |
Fig. 6 The CPS analysis of segment SEG5 of the Amadeus photometry of FK Com. The phases in panel g) were calculated using the period |
4. Results
The results from the CF analysis are shown in the fifteen panels of Fig. 3, wrapped with the carrier period 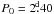 and assigning the phase φ = 0 to the first time point of each segment. The phase information of the segments is therefore not comparable. The dark-bright pattern is replicated as the phase-axis is extended around [0,1] to help the visualisation. The dark colours represent higher magnitude, i.e. lower temperatures. The results of the fitting procedures are summarised in Table 2, where
and assigning the phase φ = 0 to the first time point of each segment. The phase information of the segments is therefore not comparable. The dark-bright pattern is replicated as the phase-axis is extended around [0,1] to help the visualisation. The dark colours represent higher magnitude, i.e. lower temperatures. The results of the fitting procedures are summarised in Table 2, where 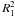 and
and 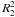 are the coefficients of determination (Eq. (5)) before and after the removal of the 3σ outliers, respectively. ΔN is the number of removed data points. As an example, the fits for two segments are shown in Fig. 4.
are the coefficients of determination (Eq. (5)) before and after the removal of the 3σ outliers, respectively. ΔN is the number of removed data points. As an example, the fits for two segments are shown in Fig. 4.
Summary of CF fit results for each segment.
The full CPS results of segments SEG4 and SEG5 are shown in Figs. 5 and 6. The values of the a priori period estimate P0, the median of all reliable periods Pmed, the limiting modelling order Klim and the maximum length of the dataset ΔTmax are given at the top of the plots. The panels show:
-
(a)
standard deviation of residualsσϵ(τ), τ being the mean epoch of each data set;
-
(b)
modelling order K(τ) (squares, units on the left y-axis); and number of observations per dataset n (crosses, units on the right y-axis);
-
(c)
mean V-magnitude M(τ);
-
(d)
time scale of change TC(τ);
-
(e)
amplitude A(τ);
-
(f)
period P(τ);
-
(g)
primary (squares) and secondary (triangles) minimum phases φmin,1(τ) and φmin,2(τ). These phases are calculated using the median period Pmed of the segment;
-
(h)
M(τ) versus P(τ);
-
(i)
A(τ) versus P(τ);
-
(j)
M(τ) versus A(τ).
In the subplots (a), (c) and (e)−(g), the reliable parameter estimates are indicated by filled symbols and unreliable ones by open symbols. The reliability is tested as described by Lehtinen et al. (2011). In subplot (d), the upward pointing arrows signify that the data fit the model, within the statistical limits explained by Lehtinen et al. (2011), from this point on throughout the segment.
In the correlation plots (h)−(j), the error bars have been drawn only for the independent parameter estimates. The linear Pearson correlation coefficients r0 for the independent datasets, as well as an estimate of the probabilities P(| r| > r0), are given.
 |
Fig. 7 Independent period, mean magnitude and amplitude estimates from the CPS analysis (squares with error bars). The mean magnitude and amplitude are plotted with the results from the CF analyses (dotted line). |
 |
Fig. 8 The phase distribution of the photometric minima folded with the period Pal = 2.4012. The epoch of the first minimum tmin1 = 2 4449 877.321 (HJD) corresponds to phase φ = 0.5. |
All independent CPS period estimates are shown in Fig. 7. The mean period and its standard deviation were 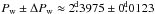 . There is no doubt, that the photometric period is varying. The probable reason is differential rotation. The variable period poses problems on what to use as a standard period for plots. We use the “old” ephemeris
. There is no doubt, that the photometric period is varying. The probable reason is differential rotation. The variable period poses problems on what to use as a standard period for plots. We use the “old” ephemeris 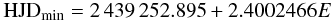 (7)derived by Jetsu et al. (1993) whenever we are combining results from the CF, CPS or Doppler imaging analysis. In the rest of the plots, we use either the carrier period (Fig. 3), the CPS median period for each segments (Figs. 5 and 6) or the best active longitude period (Fig. 8).
(7)derived by Jetsu et al. (1993) whenever we are combining results from the CF, CPS or Doppler imaging analysis. In the rest of the plots, we use either the carrier period (Fig. 3), the CPS median period for each segments (Figs. 5 and 6) or the best active longitude period (Fig. 8).
The independent CPS estimates of the mean magnitudes and light curve amplitudes are plotted together with the corresponding results from the CF analysis in Fig 7. In Fig. 9 we show the CF and CPS photometric minima for some interesting segments, together with results from Doppler imaging when available. In the latter cases we plot latitudinally averaged slices of Doppler images calculated by H. Korhonen (Ayres et al. 2006; Korhonen et al. 2007, 2009a,b). These slices were calculated from the original rectangular DI maps by weighting each surface element with its size. For segment SEG5 we also plot all reliable CPS light-curves in Fig. 10.
We can see that there is no discrepancy between the CF and CPS methods, since all differences can be explained by the different approaches. The results from the CF method look like a smooth fit to the more noisy CPS results.
The mean of TC(τ) is 32 d and the minimum 7 d. This is both surprising and worrying. In previous analysis of main sequence stars TC has been of the same order as the convective turnover time τc (Lehtinen et al. 2011, 2012). It is hard to determine τc for FK Com since it is an exceptional giant star with uncertain parameters. However, with an estimated radius of R ~ 10 R⊙, one would expect τc to be different than for main sequence stars. Thus one would expect also TC(τ) to differ. The worrying part is that about 30% of the TC(τ) are smaller than the ΔTmax = 24 d used as the time window for the CPS-analysis. Tests with reducing ΔTmax showed, however, that there was no significant change in the result, except that the reduced number of points in each CPS-set increased the errors. A low TC(τ) indicates that rapid changes occur in the spot configuration. It should be emphasised that TC(τ) of course depends on K: the higher the order of the model, the more sensitive it is to changes. Furthermore, the analysis is based on statistics, which explains why some low amplitude models may succeed in fulfilling the whole data, while subsequent models may be quickly rejected (see e.g. the three “arrows” in the upper left corner of panel (d) in Fig. 6). Details on the estimation of TC(τ) are found in Lehtinen et al. (2011).
 |
Fig. 9 The photometric minima from the CF and CPS analysis of segments from left to right SEG4, SEG5, SEG8, SEG11, SEG12 and SEG15 plotted with longitudinal average slices of simultaneous Doppler images, when available. The dotted lines represent the primary and secondary minima from the CF analysis. The squares (primary) and triangles (secondary) show the CPS minima. The phases were calculated using the ephemeris HJDmin = 2 439 252.895 + 2.4002466E. |
 |
Fig. 10 All reliable light curve fits for SEG5. The phases were calculated with the period derived for each set. |
4.1. Active longitudes
The overall result is that in about half of the segments only one active longitude can be detected. Two active longitudes usually seem to be present before and after longitudinal shifts in the activity, but there are also cases, e.g. SEG16, of two simultaneous active longitudes without indications of shifts. In some panels of Fig. 3 the pattern runs slanted upwards, in a couple it remains nearly horizontal, in a few panels it is slanted downwards, or in some segments disrupted in some way or another. The rising (e.g. segments SEG2 and SEG3) or falling (e.g. SEG6, SEG9 and SEG13) trends are indications of the carrier period not being optimal for the segment, i.e. rising trends could be corrected with increasing the carrier period somewhat, and correspondingly falling trends by decreasing it. As both types of trends are present in the segments, however, a global CF analysis of all the segments together would, in any case, give a carrier period very close to the one already adopted. The trends are relatively short-lived, as they are visible only in two, maximally three consecutive segments, i.e. last roughly one year.
A drift longer by an order of magnitude has been reported in the RS CVn binary II Peg (Lindborg et al. 2011; Hackman et al. 2011) during the years 1994−2001. It was interpreted as a possible azimuthal dynamo wave arising from the properties of the non-axisymmetric dynamo solution. During these years, the spot-generating structure was observed to rotate with a shorter, but constant period, i.e. forming a more or less rigidly rotating entity.
The short-lived trends are likely to be related to rotational non-uniformities either on the surface or at larger depth that the spots may be anchored to. This can also be seen in the varying photometric period retrieved with the CPS method (Fig. 7). With the seasonal gaps in the data, these trends make it hard to visually follow any long-lived active longitudes in FK Com (see e.g. Fig. 11).
However, the Kuiper periodogram analysis of the independent photometric minima from the CPS-analysis gave the best period 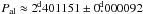 with a significance level of Q ≈ 5.3 × 10-11. The phases of the CPS minima, folded with this period, are displayed in Fig. 8. We also applied the Kuiper test on all photometric minima retrieved by the CPS method, as well as all minima and maxima from the CF-analysis. For these tests extremely low Q-values were derived, but since the measurements cannot be seen as independent, this has no statistical relevance. All the CPS-minima yielded the period
with a significance level of Q ≈ 5.3 × 10-11. The phases of the CPS minima, folded with this period, are displayed in Fig. 8. We also applied the Kuiper test on all photometric minima retrieved by the CPS method, as well as all minima and maxima from the CF-analysis. For these tests extremely low Q-values were derived, but since the measurements cannot be seen as independent, this has no statistical relevance. All the CPS-minima yielded the period 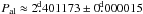 and the CF-minima gave the result
and the CF-minima gave the result 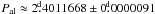 . However, the most significant period for the CF-maxima was
. However, the most significant period for the CF-maxima was 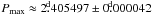 .
.
Thus, the analysis of the CF-minima gave practically the same Pal as for the CPS-minima. We note that Pal is slightly longer than the mean photometric period Pw. The value of Pal should describe the possible period of a magnetic structure within the star, while Pw may reflect the rotation at the surface. This would imply, that there is a magnetic structure rotating slightly slower than the surface of the star. The best period for the CF-maxima Pmax was again slightly longer than Pal. Thus, this periodicity may describe something else than the mere absence of spots, i.e. possibly bright surface features.
 |
Fig. 11 Longitudinal slices of Doppler images and photometric minima from the CF analysis. The phases were calculated using the same ephemeris as in Fig. 9. |
4.2. Flip-flop like events
Switching active longitudes were detected in six of the 15 analysed segments, namely SEG4, SEG5, SEG8, SEG11, SEG12 and SEG15. These events are summarised in Table 3 and plotted in Fig. 9 together with longitudinal slices of Doppler images. In many cases these events were not “proper” flip-flops. Either the phase jump was considerably less than 0.5, or the event involved more spot evolution, than just a shift from one active longitude to another one. In order to make a distinction between these events we use the definitions for a flip-flop suggested by Kajatkari et al. (2013):
-
the region of main activity shifts about 180 degrees from the oldactive longitude and then stays on the new active longitude. or
-
the primary and secondary minima are first separated by about 180 degrees, after which the secondary minimum evolves into a long-lived primary minimum, and vice versa.
In SEG4 (HJD0 = 2 450 778.043), two phase changes can be detected from the CF analysis (upper left panel of Fig. 9). During the first phase disruption, the primary minimum segregates into a secondary minimum roughly at HJD ≈ 2 450 870. The two minima have a phase separation of Δφ ≈ 0.4, which is close enough to 0.5 to call the event a flip-flop. At around HJD ≈ 2 450 880, the secondary minimum has become the main minimum. The CPS analysis shows, that the two parallel minima persist for approximately 35 days. In this respect, the phase change is, of course, very rapid, as it occurs during roughly a month. Towards the end of this segment, another phase jump is observed. The phase change is only Δφ ≈ 0.2 and based on the CPS analysis, it occurs gradually during ~20 days.
In the beginning of SEG5 (HJD0 = 2 451 144.0394) two active longitudes reside at opposite sides of the star. Both the CF- and CPS-method results show that the regions are not completely stable, but move in phase (upper right panel of Fig. 9). This is also evident from the evolution of the light curve during this segment (Fig. 10). At HJD ≈ 2 451 170 there is a flip-flop switch between the spot regions and the former secondary minimum becomes the new primary minimum. The CPS-analysis also reveals that at HJD ≈ 2 451 280 one of the spot regions starts drifting towards the other one and seems to pass it around HJD ≈ 2 451 300 (panel (g) in Fig. 6). The drift continues until HJD ≈ 2 451 330. This could be explained by the fact that differential rotation will make surface features at different latitudes or with different anchor depths move with different angular velocity. This drift is not apparent in the CF-analysis, as expected, because this method is not supposed to register such fast changes. Instead we see a phase jump of Δφ ≈ 0.3 occurring after HJD ≈ 24 515 300. From the plots of the individual light curves of the CPS-analysis we clearly see that the changes are actually gradual, and not just an effect of “interpolation” over an abrupt change (Fig. 10). Panels (h)−(j) of Fig. 6 show that there are clear connections between the light curve mean, amplitude and period. Especially interesting is the initial correlation between A and M, which is evolved to a loop in the (A,M) diagram. Correlations between neighbouring points in this kind of diagram are expected, since these are not independent measurements (see Lehtinen et al. 2011). But the loop indicates that there really is a more complex connection between A and M. However, no such connections can be seen in segment SEG4 (Fig. 5).
The next detectable phase shift occurs in SEG8 (middle left panel of Fig. 9), during which the primary minimum suddenly drops in strength, while a secondary minimum roughly Δφ ≈ 0.5 apart gains in magnitude, and during a few tens of days, the activity becomes concentrated to the location of the former secondary minimum. Although this event fulfils the criterion for a flip-flop, the new primary active longitude does not appear to become completely stable. Another minimum emerges at HJD ≈ 2 452 380 nearby it, gains in magnitude, and finally the two minima seem to merge.
In the beginning of SEG11 (middle right panel of Fig. 9), quite an abrupt phase shift, of nearly Δφ = 0.5, can be seen. This event, however, is very close to the beginning of the data set and it is not detectable from the CPS analysis, probably due to the low light curve amplitude.
In the beginning of SEG12 (lower left panel of Fig. 9), the primary minimum is located at φ = 0.6 roughly for the first 60 days of observations. At HJD ≈ 2 453 770 a secondary minimum emerges at φ = 0.9, and an exchange of activity levels occurs between the active longitudes. At the same time, the former primary minimum slowly drifts to φ = 0.2. This event takes over 100 days
In the beginning of segment SEG15 (lower right panel of Fig. 9), both the CF and CPS-analysis reveal two active regions separated by ~0.5 in phase. Shifts in the strengths of these seem to occur at HJD ≈ 2 454 830 and HJD ≈ 2 454 870. The two active longitudes seem to merge and form a common minimum at HJD ≈ 2 454 940.
In conclusion, the CF and CPS analysis disclose complex phase behaviour in six of the analysed segments, namely SEG4, SEG5, SEG8, SEG11, SEG12, and SEG15. The shifts in the primary minima in these segments can be explained by:
-
Flip-flops as defined earlier in this section (SEG4, SEG5, SEG8,SEG11, SEG15; denoted “ff” in Table 3)
-
Phase jumps of Δφ < 0.4 (SEG4, SEG12; denoted “phj”)
-
Two drifting active regions (SEG5, SEG12; denoted “dr”)
-
Merging of two active regions (SEG8, SEG15; denoted “mr”).
The main reason for differing between phase jumps and flip-flops is that this has consequences for the dynamo mode dominating the spot activity during a specific period. The merging of the active regions do not necessarily mean a physical merger, but rather that the two regions form a common minimum. As showed by Lehtinen et al. (2011), there is a minimum phase difference for spot regions under which these cannot be observed to cause separate minima.
The five flip-flops occur at times (in years) t ≈ 1998.2, 1999.0, 2002.0, 2005.0 and 2009.1. Thus, the interval between these events is 0.8−4.1 years and no clear periodicity can be seen. Furthermore, the division between flip-flops and phase jumps is not completely clear, since there is a “grey zone” of Δφ ≈ 0.4 phase shifts. We cannot rule out that the flip-flops and phase jumps play a role in the possible activity cycle, but the present data is not sufficient for any definite conclusions.
4.3. Differential rotation
In all segments we see drifts of the active regions. These indicate that the spots are not rotating with constant angular velocity. From the independent CPS period estimates we got the weighted mean period 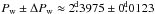 . If the variations in the photometric period were caused by differential rotation, we could estimate the differential rotation coefficient with the parameter
. If the variations in the photometric period were caused by differential rotation, we could estimate the differential rotation coefficient with the parameter 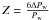 (Jetsu 1993). For FK Com, we got the value Z ≈ 0.0308, which would correspond to a differential rotation of ΔΩ > 4.6°/d.
(Jetsu 1993). For FK Com, we got the value Z ≈ 0.0308, which would correspond to a differential rotation of ΔΩ > 4.6°/d.
An alternative way to estimate the differential rotation is to study the drifts of active regions. During segment SEG5 the separation of the two active regions changed from −0.5 to 0.2 in 60 days. This would correspond to a differential rotation of ΔΩ ≈ 4.2°/d between the two spot structures. This is, as it should be, less than the value derived from the variations in the rotation period, but still more than twice the value derived by Korhonen et al. (2007) assuming a solar differential rotation law (Eq. (1)).
4.4. Comparison with previous results
Our analysis is partly based on the same data as used by Oláh et al. (2006) and covers in part the same time period as the photometric analysis of Panov & Dimitrov (2007) and the Doppler images by Korhonen and collaborators (Korhonen et al. 2007, 2009a,b). In Fig. 9 we already compared our results with simultaneous Doppler imaging maps. In Fig. 11 we compare the primary minima from the CF analysis with Doppler images from the years 1993−2008. This figure illustrates the rapid changes in the spot activity of FK Com. In general the consistency between the CF analysis and Doppler images is satisfactory. However, one must take into account that the photometric minimum is a result of the integrated effect of several spot regions, including the visibility effect. In calculating the longitudinal Doppler imaging stripes, visibility and limb darkening was not taken into account.
Flip-flops and phase jumps during the time period covered by the current analysis have been reported in several papers (Korhonen et al. 2002; Oláh et al. 2006; Panov & Dimitrov 2007; Korhonen et al. 2009a). Interestingly Oláh et al. (2006) also recognised the complex phase behaviour in SEG5. They conclude that a flip-flop occurred during this segment, similarly to Panov & Dimitrov (2007) and Korhonen et al. (2009a), while we detect both a flip-flop and drifting spot regions. Panov & Dimitrov (2007) reported a flip-flop occurring during the early 1998, which is also seen in the current analysis. Furthermore, Oláh et al. (2006) detected a phase jump in SEG3, and Korhonen et al. (2000) and Panov & Dimitrov (2007) reported a flip-flop in this segment. In our analysis this would be the “bump” visible in Fig. 3. Similar small bumps can be seen in several of the segments, which is why we did not focus on this case.
Our analysis includes observations of ~15 years, which is less than 3 × the cycles of 5.2 and 5.8 years reported by Oláh et al. (2006) and Panov & Dimitrov (2007). The long term changes of the mean magnitude in our analysis (middle panel in Fig. 7) shows signs of possibly cyclic variations on a time scale of 6 years, but no clear conclusions can be drawn from our analysis because of the limited time span.
Rotation periods used in the CF- and CPS-analysis and their mathematical or physical interpretation.
5. Discussion
Our analysis clearly shows, that the behaviour of FK Comae cannot be explained by a single rotation period. Instead, we find multiple periodicities, the explanation of the periods being listed in Table 4 in an attempt to remove any confusion about them. These periods are probably related to differential rotation as well as the interplay between rotation and varying surface spots.
Our close study of six flip-flop like events clearly shows that we are not dealing with a singular phenomenon. The shifts of the active longitudes can be a result of both abrupt and gradual changes. In one case the apparent flip-flop can be explained by two spot regions moving with different angular velocity and even passing each other. Since FK Comae is a late-type star with a convection zone, some amount of differential rotation, changing both as a function of depth and latitude, can be expected to be generated. The apparent flip-flop can thus be a consequence of differential rotation in two alternative ways:
-
The spot latitudes change and the spot or spot groups drift withrespect to each other because of surface differential rotation.
-
The anchor depth of the spot or spot groups change and the differences in the angular velocity is caused by the depth dependent differential rotation.
Furthermore, the situation will be complicated by rapid spot evolution. At times there are significant changes in the light curves within ~10 days. This time would probably be much shorter with light curves with denser spacing and higher accuracy, e.g. satellite observations. The changes in the light curves of FK Com cannot be explained just by differential rotation of a steady spot model (see e.g. Fig. 4). In reality we may thus be witnessing a combination of several effects: Rapid spot evolution combined with differential rotation in both depth and latitude, spiced with a possible dynamo wave.
We find that the differential rotation in FK Com is at least about ΔΩ ≈ 4.6°/d, which would correspond to a differential rotation coefficient of k ≈ 0.03. This is roughly three times larger than the value suggested by Korhonen et al. (2007) and about one sixth of the solar value. Our new value is in fair agreement with the observational and theoretical consensus (see e.g. Kitchatinov & Rüdiger 1999) of differential rotation diminishing proportional to 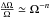 , where n ≈ 0.8−0.9. The rotation period of the Sun being roughly an order of magnitude slower than that of FK Com, indicates roughly 7 times weaker differential rotation for FK Com. However, we cannot conclude that this is a measure of the surface differential rotation, as it could also reflect geometric properties of the large-scale dynamo field, as described by Korhonen & Elstner (2011), and include a signal from a possible azimuthal dynamo wave (e.g. Krause & Rädler 1980; Lindborg et al. 2011).
, where n ≈ 0.8−0.9. The rotation period of the Sun being roughly an order of magnitude slower than that of FK Com, indicates roughly 7 times weaker differential rotation for FK Com. However, we cannot conclude that this is a measure of the surface differential rotation, as it could also reflect geometric properties of the large-scale dynamo field, as described by Korhonen & Elstner (2011), and include a signal from a possible azimuthal dynamo wave (e.g. Krause & Rädler 1980; Lindborg et al. 2011).
The finding of an active longitude period, which is slightly longer than the mean rotation period indicates the presence of an azimuthal dynamo wave. In the case of FK Com this would rotate slower than the star itself, as opposed to the RS CVn star II Peg (Lindborg et al. 2011; Hackman et al. 2011, 2012). Even though a clear long-term active longitude period can be detected, the short term spot evolution seems fast and random. Thus, it is not as easy to follow active longitudes over gaps in the data as in the case of e.g. II Peg. In this sense FK Com resembles some other single stars, e.g. HD 116956 (Lehtinen et al. 2011) and LQ Hya (Lehtinen et al. 2012). In general, the active longitudes of close binary stars may be more regular due to the tidal effects.
We also note that there is a clear tendency of having two active structures with a phase difference of considerably less than 0.5. This tendency can also be seen in the distribution of the minimum phases folded by Pal: The maximum in Fig. 8 is divided into two peaks with a separation of roughly 0.2. The same was already noted in earlier studies. E.g. Korhonen et al. (2009b) reported a pair of spots in 2008 with a phase difference of 0.25. This could resemble the pattern of leading and trailing spot pairs seen in much smaller scale on the Sun.
Concerning the possible existence of an activity cycle our study does not bring much conclusive evidence. The mean magnitude shows variability which is compatible with the cycle of 4.5−6.1 years found by Oláh et al. (2009). Naturally, when two active longitudes coexist, the amplitude tends to be lower. However, we do not see any other connection between the switches in the active longitudes and the long-term photometric
variability. Neither can we detect any regularity in the flip-flop like events of FK Com.
Acknowledgments
The work of T.H. was financed by the research programme “Active Suns” at the University of Helsinki. H.K. acknowledges the support from the European Commission under the Marie Curie Intra-European Fellowship. Financial support from the Academy of Finland grants No. 218159 (M.J.M.) and 141017 (J.P.) are gratefully acknowledged. The work of P.K. was supported by the Vilho, Yrjö and Kalle Väisälä Foundation.
References
- Ayres, T. R., Harper, G. M., Brown, A., et al. 2006, ApJ, 644, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugina, S. V., & Tuominen, I. 1998, A&A, 336, L25 [NASA ADS] [Google Scholar]
- Bopp, B. W., & Rucinski, S. M. 1981, in Fundamental Problems in the Theory of Stellar Evolution, eds. D. Sugimoto, D. Q. Lamb, & D. N. Schramm, IAU Symp., 93, 177 [Google Scholar]
- Bopp, B. W., & Stencel, R. E. 1981, ApJ, 247, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Chugainov, P. F. 1966, Inf. Bull. Var. Stars, 172, 1 [Google Scholar]
- Croll, B., Walker, G. A. H., Kuschnig, R., et al. 2006, ApJ, 648, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Deeming, T. J. 1975, Ap&SS, 36, 137 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Drake, J. J., Chung, S. M., Kashyap, V., et al. 2008, ApJ, 679, 1522 [NASA ADS] [CrossRef] [Google Scholar]
- Gondoin, P., Erd, C., & Lumb, D. 2002, A&A, 383, 919 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hackman, T., Mantere, M. J., Jetsu, L., et al. 2011, Astron. Nachr., 332, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Hackman, T., Mantere, M. J., Lindborg, M., et al. 2012, A&A, 538, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Horne, J. H., & Baliunas, S. L. 1986, ApJ, 302, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, V. A., & McLean, B. J. 1987, ApJ, 313, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Jetsu, L. 1993, A&A, 276, 345 [NASA ADS] [Google Scholar]
- Jetsu, L. 1996, A&A, 314, 153 [NASA ADS] [Google Scholar]
- Jetsu, L., & Pelt, J. 1996, A&AS, 118, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jetsu, L., & Pelt, J. 1999, A&AS, 139, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jetsu, L., Pelt, J., & Tuominen, I. 1993, A&A, 278, 449 [NASA ADS] [Google Scholar]
- Jetsu, L., Tuominen, I., Antov, A., et al. 1994a, A&AS, 103, 183 [NASA ADS] [Google Scholar]
- Jetsu, L., Tuominen, I., Grankin, K. N., Melnikov, S. Y., & Schevchenko, V. S. 1994b, A&A, 282, L9 [NASA ADS] [Google Scholar]
- Kajatkari, P., Hackman, T., Jetsu, L., Lehtinen, J., & Henry, G. W. 2013, A&A, submitted [Google Scholar]
- Kitchatinov, L. L., & Rüdiger, G. 1999, A&A, 344, 911 [NASA ADS] [Google Scholar]
- Korhonen, H., & Elstner, D. 2005, A&A, 440, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korhonen, H., & Elstner, D. 2011, A&A, 532, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korhonen, H., Berdyugina, S. V., Hackman, T., et al. 1999, A&A, 346, 101 [NASA ADS] [Google Scholar]
- Korhonen, H., Berdyugina, S. V., Hackman, T., Strassmeier, K. G., & Tuominen, I. 2000, A&A, 360, 1067 [NASA ADS] [Google Scholar]
- Korhonen, H., Berdyugina, S. V., Tuominen, I., et al. 2001, A&A, 374, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korhonen, H., Berdyugina, S. V., & Tuominen, I. 2002, A&A, 390, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korhonen, H., Berdyugina, S. V., & Tuominen, I. 2004, Astron. Nachr., 325, 402 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Korhonen, H., Berdyugina, S. V., Hackman, T., et al. 2007, A&A, 476, 881 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korhonen, H., Berdyugina, S. V., Ilyin, I. V., Strassmeier, K. G., & Hackman, T. 2009a, in Rev. Mex. Astron. Astrofis. Conf. Ser., 36, 323 [Google Scholar]
- Korhonen, H., Hubrig, S., Berdyugina, S. V., et al. 2009b, MNRAS, 395, 282 [NASA ADS] [CrossRef] [Google Scholar]
- Krause, F., & Rädler, K.-H. 1980, Mean-field magnetohydrodynamics and dynamo theory (Oxford: Pergamon Press) [Google Scholar]
- Kuiper, N. 1960, Proc. Koningkl. Nederl. Akad. van Wettenschappen, Ser. A, 63, 38 [Google Scholar]
- Lehtinen, J., Jetsu, L., Hackman, T., Kajatkari, P., & Henry, G. W. 2011, A&A, 527, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lehtinen, J., Jetsu, L., Hackman, T., Kajatkari, P., & Henry, G. W. 2012, A&A, 542, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindborg, M., Korpi, M. J., Hackman, T., et al. 2011, A&A, 526, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oláh, K., Korhonen, H., Kővári, Z., Forgács-Dajka, E., & Strassmeier, K. G. 2006, A&A, 452, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oláh, K., Kolláth, Z., Granzer, T., et al. 2009, A&A, 501, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Panov, K., & Dimitrov, D. 2007, A&A, 467, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pelt, J., Olspert, N., Mantere, M. J., & Tuominen, I. 2011, A&A, 535, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G. 2009, A&ARv, 17, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G., Bartus, J., Cutispoto, G., & Rodono, M. 1997a, A&AS, 125, 11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strassmeier, K. G., Boyd, L. J., Epand, D. H., & Granzer, T. 1997b, PASP, 109, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Tuominen, I., Berdyugina, S., & Korpi, M. 2002, Astron. Nachr., 323, 367 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Rotation periods used in the CF- and CPS-analysis and their mathematical or physical interpretation.
All Figures
 |
Fig. 1 All photometric V-data for FK Com. The Phoenix-10 data is marked with black dots and the Amadeus data is marked with grey pluses. |
| In the text | |
 |
Fig. 2 The differential magnitudes of the comparison star HD 117567 for the Amadeus data: ΔV = VHD 117876 − VHD 117567. |
| In the text | |
 |
Fig. 3 CF analysis results for each segment with the carrier period |
| In the text | |
 |
Fig. 4 The CF fits for segments SEG4 and SEG5 using the carrier period |
| In the text | |
 |
Fig. 5 The CPS analysis of segment SEG4 of the Amadeus photometry of FK Com. The phases in panel g) were calculated using the period |
| In the text | |
 |
Fig. 6 The CPS analysis of segment SEG5 of the Amadeus photometry of FK Com. The phases in panel g) were calculated using the period |
| In the text | |
 |
Fig. 7 Independent period, mean magnitude and amplitude estimates from the CPS analysis (squares with error bars). The mean magnitude and amplitude are plotted with the results from the CF analyses (dotted line). |
| In the text | |
 |
Fig. 8 The phase distribution of the photometric minima folded with the period Pal = 2.4012. The epoch of the first minimum tmin1 = 2 4449 877.321 (HJD) corresponds to phase φ = 0.5. |
| In the text | |
 |
Fig. 9 The photometric minima from the CF and CPS analysis of segments from left to right SEG4, SEG5, SEG8, SEG11, SEG12 and SEG15 plotted with longitudinal average slices of simultaneous Doppler images, when available. The dotted lines represent the primary and secondary minima from the CF analysis. The squares (primary) and triangles (secondary) show the CPS minima. The phases were calculated using the ephemeris HJDmin = 2 439 252.895 + 2.4002466E. |
| In the text | |
 |
Fig. 10 All reliable light curve fits for SEG5. The phases were calculated with the period derived for each set. |
| In the text | |
 |
Fig. 11 Longitudinal slices of Doppler images and photometric minima from the CF analysis. The phases were calculated using the same ephemeris as in Fig. 9. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.