| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 6 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201220447 | |
| Published online | 07 May 2013 | |
The Rh = ct universe without inflation
Department of Physics, The Applied Math Program, and Department of
AstronomyThe University of Arizona,
Tucson,
AZ
85721,
USA
e-mail:
fmelia@email.arizona.edu
Received:
26
September
2012
Accepted:
3
April
2013
Context. The horizon problem in the standard model of cosmology (ΛDCM) arises from the observed uniformity of the cosmic microwave background radiation, which has the same temperature everywhere (except for tiny, stochastic fluctuations), even in regions on opposite sides of the sky, which appear to lie outside of each other’s causal horizon. Since no physical process propagating at or below lightspeed could have brought them into thermal equilibrium, it appears that the universe in its infancy required highly improbable initial conditions.
Aims. In this paper, we demonstrate that the horizon problem only emerges for a subset of Friedmann-Robertson-Walker (FRW) cosmologies, such as ΛCDM, that include an early phase of rapid deceleration.
Methods. The origin of the problem is examined by considering photon propagation through a FRW spacetime at a more fundamental level than has been attempted before.
Results. We show that the horizon problem is nonexistent for the recently introduced Rh = ct universe, obviating the principal motivation for the inclusion of inflation. We demonstrate through direct calculation that, in this cosmology, even opposite sides of the cosmos have remained causally connected to us – and to each other – from the very first moments in the universe’s expansion. Therefore, within the context of the Rh = ct universe, the hypothesized inflationary epoch from t = 10-35 s to 10-32 s was not needed to fix this particular “problem”, though it may still provide benefits to cosmology for other reasons.
Key words: gravitation / cosmic background radiation / cosmological parameters / cosmology: theory / inflation / early Universe
© ESO, 2013
1. Introduction
The horizon problem arises out of the standard model of cosmology1, which posits that the universe began with a hot big bang, followed by an expansion calculable from the solution to two rather simple differential equations. In this picture, the cosmos we see today began its existence as a hot, dense plasma of thermalized matter and radiation, subjugated dynamically by its own self-gravity and the possible effects of an unspecified dark energy, whose principal role is to bring about the apparent acceleration we see today (Riess 1998; Perlmutter 1999). The initial hot state was followed by a gradual cooling and a drop in density and energy.
The observational evidence for a “beginning” appears to be overwhelming. Distant galaxies are receding from us at a speed proportional to their distance. A pervasive, relic microwave background radiation has been discovered with a Planck spectrum corresponding to a (highly diminished) temperature of 2.7 K. And the measured cosmic abundances are in agreement with the ratios predicted by big-bang nucleosynthesis, which produced elements with a composition of roughly 75% hydrogen by mass, and about 25% helium.
Couched in the language of general relativity, these observations confirm certain assumed symmetries implied by the Cosmological Principle, which holds that the universe is homogeneous and isotropic on large scales, certainly larger than 100 Mpc. The differential equations describing the universal expansion emerge directly from Einstein’s theory when these symmetries are adopted. They allow several different kinds of behavior as the constituents vary, and account very well for the global characteristics seen from the moment of the big bang all the way to the present time t0, some 13.7 billion years later.
The horizon problem is viewed as a major shortcoming of the standard model – not as a result of an observational or internal inconsistency but, rather, from the fact that the universe seems to have required special initial conditions that are highly improbable according to our current understanding of physics. In its most direct manifestation, the horizon problem arises from the observed uniformity of the microwave background radiation, which has the same temperature everywhere, save for fluctuations at the level of one part in 100 000 seen in WMAP’s measured relic signal (Spergel 2003). Regions on opposite sides of the sky, the argument goes, lie beyond each other’s horizon (loosely defined as the distance light could have traveled during a time t0), yet their present temperature is identical, even though they could not possibly have ever been in thermal equilibrium, since no physical process propagating at or below the speed of light could have causally connected them. The horizon problem therefore emerges as the inability of the standard model to account for this homogeneity on scales greater than the distance light could have traveled since the big bang, requiring some highly tuned spatial distribution of temperature that has no evident natural cause.
So serious has this shortcoming become that the inflationary model of cosmology (Guth 1981; 1982) was invented in part to resolve this possible discrepancy. In this picture, an inflationary spurt occurred from approximately 10-35 s to 10-32 s following the big bang, forcing the universe to expand much more rapidly than would otherwise have been feasible solely under the influence of matter, radiation, and dark energy, carrying causally connected regions beyond the horizon each would have had in the absence of this temporary acceleration.
In this paper, we will analyze the horizon problem more carefully than has been attempted before, demonstrating that the conflict between the observed properties of the cosmic microwave background (CMB) and ΛCDM is not generic to all FRW cosmologies. In particular, we will show that in the Rh = ct universe, even opposite sides of the cosmos have remained causally connected to us – and to each other – from the very first moments of the expansion. In this cosmology, therefore, the inflationary model may be attractive for other reasons, but there is actually no real horizon problem for it to resolve. We will argue that the inconsistency between the observed properties of the CMB and ΛCDM could be an indication that the standard model requires a new ingredient – inflation – to fix it, but could also just be evidence in support of the Rh = ct universe.
2. The Rh = ct universe
It will be helpful in what follows for us to briefly review what we know about the Rh = ct universe up to this point. From a theoretical standpoint, the Rh = ct condition is required when one adopts both the Cosmological principle and Weyl’s postulate together (Melia & Shevchuk 2012). If it turns out that the universe is indeed not correctly described by the Rh = ct cosmology, then either the Cosmological principle or (more likely) Weyl’s postulate would be called into question. That too would be quite interesting and profoundly important, but beyond the scope of our present discussion. (A more pedagogical description of the Rh = ct universe is given in Melia 2012.)
Over the past several decades, ΛCDM has developed into a comprehensive description of nature, in which a set of primary constituents (radiation, matter, and an unspecified dark energy) are assumed with a partitioning determined from fits to the available data. ΛCDM must therefore deal with the challenges of accounting for varied observations covering disparate properties of the universe, some early in its history (as seen in the relic CMB) and others more recently (such as the formation of large-scale structure).
It is therefore desirable to keep testing the basic premises of the theory, particularly those that have the most profound consequence, such as the possible role that inflation may have played in the early universe. In recent papers, we have demonstrated that the Rh = ct universe may be able to provide a physical basis for at least some of the features now emerging from the observations. For example, whereas one must infer empirically the overall equation-of-state of the constituents in ΛCDM, the total pressure p in Rh = ct must be given by the simple expression p = −ρ/3, in terms of the total energy density ρ. This leads to a great simplification of the observable quantities, such as the luminosity distance and the redshift-dependent Hubble constant, both of which appear to be consistent with the data (see, e.g., Melia & Maier 2013; Wei et al. 2013). A more comprehensive description of the Rh = ct universe, and tests of its predictions against the observations, may be found elsewhere (see, e.g., Melia 2012, 2013; Melia & Maier 2013; Wei et al. 2013). In the context of this paper, the Rh = ct cosmology provides a good counterpoint to ΛCDM because, unlike the latter, the former does not require a period of inflation.
3. A simple analogy in flat spacetime
Let us now begin our discussion of the horizon problem by considering a much simpler analogy in flat spacetime, in which two frames of reference, A and C, coincident with ours (frame B) at time t = 0 (with t measured in our frame), are receding from us at speed v (see Fig. 1). If v is close to c, inevitably we reach the point where 2vt > ct, and we would naively conclude that A and C are beyond each other’s “horizon”, here defined simply as ct. But there are actually several reasons why this statement is incorrect.
First, we cannot use the coordinates in our frame B to determine who is causally connected to A or C by simply adding velocities. To be specific, let’s assume that v = 0.9c. Then, A’s speed relative to C is not 2v = 1.8c but, by the relativistic addition of velocities, A is moving at speed 0.994475c relative to C, and is therefore a distance 0.994475ct′ (<ct′) away from C as measured after a time t′ in C’s frame. In other words, there is no violation of causality when A’s distance is measured by the observer in C using his coordinates, rather than those of another observer (in this case, ours) in frame B.
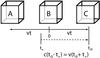 |
Fig. 1 Simple analogy in flat spacetime, in which 2 frames of reference (A and C) are moving away from us (situated in frame B), each at speed v, though in opposite directions. If v is close to c, after a time t in our frame, A and C are apparently beyond each other’s horizon (here defined as ct), but A and C could still have communicated after t = 0 (and before t0) if light were emitted by A at time t∗, such that c(t0 − t∗) = v(t0 + t∗). |
The second reason is that even though eventually
2vt > ct, we would still
conclude that A and C had communicated with each other after t = 0, as long
as they initiated the process very soon after separation had begun. Suppose we see A sending
a light signal to C at time t∗. We would conclude that the light
signal had reached C by the time t0, if
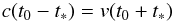 (1)or,
in other words, we would see that A and C had communicated with each other if their signals
had been sent prior to the time
(1)or,
in other words, we would see that A and C had communicated with each other if their signals
had been sent prior to the time 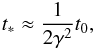 (2)where
γ ≡ (1− [v/c] )− 1/2
is the Lorentz factor. The emission time t∗ is small, but not
zero. So regardless of whether we argue from our perspective in B, or from that of the two
other frames, all observers would agree that A and C had been in causal contact after
t = t′ = 0, as long as all three frames were
coincident at the beginning. This is true in spite of the fact that
2vt0 > ct0
in our frame. As we shall see shortly, this example is quite instructive because an effect
similar to this emerges when we talk about proper distances between us and the various
patches of the CMB on opposite sides of the sky (see Fig. 2 below).
(2)where
γ ≡ (1− [v/c] )− 1/2
is the Lorentz factor. The emission time t∗ is small, but not
zero. So regardless of whether we argue from our perspective in B, or from that of the two
other frames, all observers would agree that A and C had been in causal contact after
t = t′ = 0, as long as all three frames were
coincident at the beginning. This is true in spite of the fact that
2vt0 > ct0
in our frame. As we shall see shortly, this example is quite instructive because an effect
similar to this emerges when we talk about proper distances between us and the various
patches of the CMB on opposite sides of the sky (see Fig. 2 below).
4. Null geodesics in the FRW spacetime
The Friedmann-Robertson-Walker (FRW) metric for a spatially homogeneous and isotropic
three-dimensional space may be written in terms of the cosmic (or proper) time
t measured by a co-moving observer, and the corresponding radial
(r) and angular (θ and φ) coordinates
in the co-moving frame, for which the interval ds is
![\begin{eqnarray} {\rm d}s^2 = c^2 {\rm d}t^2 - a^2(t)\left[{{\rm d}r^2\over (1 - kr^2)} + r^2\left({\rm d}\theta^2 + \sin^2\theta {\rm d}\phi^2\right)\right]. \end{eqnarray}](/articles/aa/full_html/2013/05/aa20447-12/aa20447-12-eq36.png) (3)The
constant k is + 1 for a closed universe, 0 for a flat, open universe, or
− 1 for an open universe. The spatial coordinates in this frame remain “fixed” for all
particles in the cosmos, while their physical separation varies by the scale factor
a(t). And to provide a framework for the analysis that
follows, let us point out that, for radial motion,
a(t)dr/(1 − kr2)
is the proper incremental distance realized when dt = 0,
but only for each specific observer at his/her location. Nowadays, it is common for people
to refer to the global quantity
(3)The
constant k is + 1 for a closed universe, 0 for a flat, open universe, or
− 1 for an open universe. The spatial coordinates in this frame remain “fixed” for all
particles in the cosmos, while their physical separation varies by the scale factor
a(t). And to provide a framework for the analysis that
follows, let us point out that, for radial motion,
a(t)dr/(1 − kr2)
is the proper incremental distance realized when dt = 0,
but only for each specific observer at his/her location. Nowadays, it is common for people
to refer to the global quantity 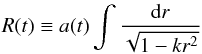 (4)as
the proper distance, but one must remember that R(t) is
calculated assuming the same common time t everywhere, which is not
the physical time for that observer at locations other than at
r = 0 (more on this below). Understanding this distinction will be critical
for a full appreciation of why these co-moving coordinates often lead to confusion regarding
what is – and what is not – causally connected.
(4)as
the proper distance, but one must remember that R(t) is
calculated assuming the same common time t everywhere, which is not
the physical time for that observer at locations other than at
r = 0 (more on this below). Understanding this distinction will be critical
for a full appreciation of why these co-moving coordinates often lead to confusion regarding
what is – and what is not – causally connected.
Utilizing the FRW metric in Einstein’s field equations of general relativity, one obtains
the corresponding FRW differential equations of motion alluded to in the introduction. These
are the Friedmann equation, 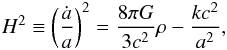 (5)and
the “acceleration” equation,
(5)and
the “acceleration” equation, 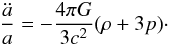 (6)An
overdot denotes a derivative with respect to cosmic time t, and
ρ and p represent the total energy density and total
pressure, respectively. A further application of the FRW metric to the energy conservation
equation in general relativity yields the final equation,
(6)An
overdot denotes a derivative with respect to cosmic time t, and
ρ and p represent the total energy density and total
pressure, respectively. A further application of the FRW metric to the energy conservation
equation in general relativity yields the final equation,
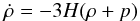 (7)which,
however, is not independent of Eqs. (5) and (6).
(7)which,
however, is not independent of Eqs. (5) and (6).
Using the definition of proper radius, we can now derive the differential equation for
photon trajectories in a cosmology consistent with the FRW metric (Eq. (3)). We have
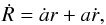 (8)and
the null condition applied to Eq. (3) yields
(8)and
the null condition applied to Eq. (3) yields
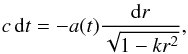 (9)where
we have assumed propagation of the photon along a radius toward the origin. The best
indications we have today are that the universe is flat so, for simplicity, we will assume
k = 0 in all the calculations described below. Therefore,
ṙ = −c/a for a
photon approaching the origin, and Eq. (8) becomes
(9)where
we have assumed propagation of the photon along a radius toward the origin. The best
indications we have today are that the universe is flat so, for simplicity, we will assume
k = 0 in all the calculations described below. Therefore,
ṙ = −c/a for a
photon approaching the origin, and Eq. (8) becomes
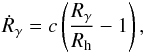 (10)where
we have added a subscript γ to emphasize the fact that this represents the
proper radius of a photon propagating toward the observer. This expression makes use of the
gravitational (or Hubble) radius (Melia 2007; Melia
& Shevchuk 2012)
(10)where
we have added a subscript γ to emphasize the fact that this represents the
proper radius of a photon propagating toward the observer. This expression makes use of the
gravitational (or Hubble) radius (Melia 2007; Melia
& Shevchuk 2012)
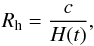 (11)and
we note that both Rγ and
Rh are functions of cosmic time t. When the
equation of state is written in the form p = wρ (for the
total pressure p in terms of the total energy density ρ),
it is not difficult to show from the Friedmann (5) and acceleration (6) equations that the
gravitational radius satisfies the dynamical equation (Melia & Abdelqader 2009)
(11)and
we note that both Rγ and
Rh are functions of cosmic time t. When the
equation of state is written in the form p = wρ (for the
total pressure p in terms of the total energy density ρ),
it is not difficult to show from the Friedmann (5) and acceleration (6) equations that the
gravitational radius satisfies the dynamical equation (Melia & Abdelqader 2009)
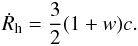 (12)Solving
Eqs. (10) and (12) simultaneously yields the null geodesic
Rγ(t) linking a source of
photons at proper distance
Rsrc(te) = Rγ(te)
and cosmic time te, with the observer who receives them at time
t0, when
Rγ(t0) = 0.
(12)Solving
Eqs. (10) and (12) simultaneously yields the null geodesic
Rγ(t) linking a source of
photons at proper distance
Rsrc(te) = Rγ(te)
and cosmic time te, with the observer who receives them at time
t0, when
Rγ(t0) = 0.
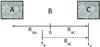 |
Fig. 2 An observer B is receiving light signals from two patches (A and C) of the CMB. We assume that the light was emitted by these sources at cosmic time te, when their proper distances from the observer were RBA(te) and RBC(te), respectively. In addition, we assume that A emitted an earlier light signal at time t∗ that reached C, a proper distance RAC(te) away, at time te. |
The geodesic Eq. (10) can sometimes be solved analytically, for example, in ΛCDM early in the universe’s history when radiation dominated ρ and p (for which w = + 1/3). To see how this works in practice, let us consider a specific scenario (not unlike the simple thought experiment of Sect. 2), in which observer B is exchanging signals with patches A and C in the CMB, as shown in Fig. 2. The photons emitted by A and C at time te reach the observer B at a later time t0 (and by symmetry, photons emitted by B at te also reach A and C at t0). Earlier, A emitted a signal at time t∗ (<te) in order to communicate with C at or before te. Thus, A and C will have been causally connected by the time their light was emitted at te toward B.
Now, by definition, the proper distance between A and C at time
t∗ is 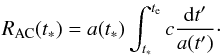 (13)We’ll
think of te as the time of recombination, when matter and
radiation separated. Therefore the universe was radiation dominated up to
te, and
(13)We’ll
think of te as the time of recombination, when matter and
radiation separated. Therefore the universe was radiation dominated up to
te, and
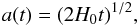 (14)where
H0 is the current value of the Hubble constant (Melia
& Abdelqader 2009). With this expansion
factor, Eq. (13) is easy to evaluate, yielding the result
(14)where
H0 is the current value of the Hubble constant (Melia
& Abdelqader 2009). With this expansion
factor, Eq. (13) is easy to evaluate, yielding the result
![\begin{eqnarray} R_{\rm AC}(t_*)=2ct_*\left[\left({t_{\rm e}\over t_*}\right)^{1/2}-1\right]. \end{eqnarray}](/articles/aa/full_html/2013/05/aa20447-12/aa20447-12-eq72.png) (15)But
in order for the signal emitted by A at t∗ to reach C at
te, we must also have
Rγe(t∗) = RAC(t∗),
and so for any arbitrary time t
(<te),
(15)But
in order for the signal emitted by A at t∗ to reach C at
te, we must also have
Rγe(t∗) = RAC(t∗),
and so for any arbitrary time t
(<te),
![\begin{eqnarray} R_{\gamma {\rm e}}(t)=2ct\left[\left({t_{\rm e}\over t}\right)^{1/2}-1\right]. \end{eqnarray}](/articles/aa/full_html/2013/05/aa20447-12/aa20447-12-eq75.png) (16)We
have added an “e” to the subscript to emphasize that this is the particular geodesic
reaching the observer (in this instance C) at time te. It is
straightforward to show that Eq. (16) is the solution to Eq. (10), since in this case
Rh(t) = 2ct. The properties
of this geodesic trajectory are representative of all such null paths in FRW spacetime
(Bikwa et al. 2012). Specifically,
Rγe(t) → 0 as
t → 0,
Rγe(t) → 0 as (in this
particular case) t → te, and
Rγe(t) has a maximum at
t = te/4, where
Rγe(te/4) = cte/2.
All of these features are evident in the photon geodesics shown schematically in Figs. 3–5.
(16)We
have added an “e” to the subscript to emphasize that this is the particular geodesic
reaching the observer (in this instance C) at time te. It is
straightforward to show that Eq. (16) is the solution to Eq. (10), since in this case
Rh(t) = 2ct. The properties
of this geodesic trajectory are representative of all such null paths in FRW spacetime
(Bikwa et al. 2012). Specifically,
Rγe(t) → 0 as
t → 0,
Rγe(t) → 0 as (in this
particular case) t → te, and
Rγe(t) has a maximum at
t = te/4, where
Rγe(te/4) = cte/2.
All of these features are evident in the photon geodesics shown schematically in Figs. 3–5.
5. The horizon problem in ΛCDM
Figure 3 explains why the observed properties of the CMB are in conflict with ΛCDM – a situation known as the “horizon problem” in cosmology. In the following discussion, we will find it easier to consider geodesics drawn from the perspective of someone in patch C. This should not matter as far as calculated proper distances are concerned, because the cosmic time t is the same everywhere and if we determine that C has received a light signal from B during a certain time interval, then it stands to reason that B will likewise have received a signal from C during that time.
 |
Fig. 3 Photon trajectories (solid curves) drawn from the perspective of an observer in patch C (see Fig. 2). The curve Rγe(t) is the null geodesic for light signals arriving at C at time te from any source at proper distance Rsrc(t) = Rγe(t) (for t < te), whereas Rγ0(t) is the corresponding null geodesic for photons arriving at C at time t0 (>te), though from sources at Rsrc(t) = Rγ0(t) (at any t < t0). The other curves and symbols are defined in the text. |
Drawn from the perspective of patch C, Fig. 3 shows the photon geodesics (solid curves) reaching the observer at two specific times. The first of these is the present (t0 in his frame), and some of the light propagating along this path was emitted by B at time te, a proper distance RBC(te) = Rγ0(te) away. The emission point is labeled δ in the figure. At time t0, C is also receiving light from patch A, radiated at time th (<te), from a proper distance RAC(th) = Rγ0(th) away, at the point labeled β. We’re calling this time th because no light emitted by A at t > th could have reached C by t0. In other words, patch A lies beyond C’s current photon horizon for t > th. (However, light emitted by A after th will become visible to C after t0, and similarly for light emitted by B after te).
For a given cosmology (in this case ΛCDM), the photon geodesic labeled Rγ0(t) is unique, and if we know the time te at which the light was emitted (say, because we know the redshift at which the CMB was produced), there is only one point δ that satisfies the necessary conditions for C to receive the signal at t0. Our observations of the CMB allow us to see light emitted by patches A and C at te ~ 380 000 years, apparently from equal proper distances on opposite sides of the sky, so that RAC(te) = 2RBC(te) in this diagram. Is it possible within the purview of ΛCDM for us to find a time t∗ to satisfy this proper-distance requirement, while A and C were still causally connected at time te?
The answer is yes, but not for a te as early as 380 000 years
after the big bang. Writing 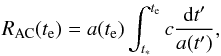 (17)we
can trivially show for a radiation-dominated universe prior to
te that
(17)we
can trivially show for a radiation-dominated universe prior to
te that
![\begin{eqnarray} R_{\rm AC}(t_{\rm e})=2ct_{\rm e}\left(1-\left[{t_*\over t_{\rm e}}\right]^{1/2}\right)\cdot \end{eqnarray}](/articles/aa/full_html/2013/05/aa20447-12/aa20447-12-eq99.png) (18)For
simplicity, and because the results don’t depend on the details of the calculation, we will
next calculate RBC(te) under the
assumption that the universe was matter-dominated between te and
t0. (The addition of dark energy would change the proper
distance by percentage points, but far from what is needed to change the answer.) So we will
put
(18)For
simplicity, and because the results don’t depend on the details of the calculation, we will
next calculate RBC(te) under the
assumption that the universe was matter-dominated between te and
t0. (The addition of dark energy would change the proper
distance by percentage points, but far from what is needed to change the answer.) So we will
put 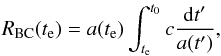 (19)where
a(t) = (3H0t/2)2/3
in Einstein-de-Sitter space. Thus
(19)where
a(t) = (3H0t/2)2/3
in Einstein-de-Sitter space. Thus ![\begin{eqnarray} R_{\rm BC}(t_{\rm e})=3ct_{\rm e}\left(\left[{t_0\over t_{\rm e}}\right]^{1/3}-1\right)\;. \end{eqnarray}](/articles/aa/full_html/2013/05/aa20447-12/aa20447-12-eq102.png) (20)Putting
RAC(te) = 2RBC(te)
therefore gives
(20)Putting
RAC(te) = 2RBC(te)
therefore gives 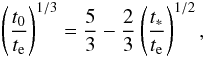 (21)which
shows that te is minimized when
t∗ → 0 and has the value
te ≈ 27t0/125,
or roughly 1/5 of t0. Thus, the early deceleration of the
universe following the big bang would not permit patches A and C to recede from each other
quickly enough for us to now see the light they emitted from opposite sides of the sky as
early as te = 380 000 years. We could, however, see their
light if it were emitted within the past 10 billion years or so, even though they
are on opposite sides of the sky.
(21)which
shows that te is minimized when
t∗ → 0 and has the value
te ≈ 27t0/125,
or roughly 1/5 of t0. Thus, the early deceleration of the
universe following the big bang would not permit patches A and C to recede from each other
quickly enough for us to now see the light they emitted from opposite sides of the sky as
early as te = 380 000 years. We could, however, see their
light if it were emitted within the past 10 billion years or so, even though they
are on opposite sides of the sky.
This point needs to be emphasized because the situation is similar to that of our thought experiment in Sect. 2. Just because two patches are moving in opposite directions from us is not a sufficient reason for them to be out of causal contact. Nonetheless, the fact that we see the CMB so early in the universe’s history means that either (1) there was some additional acceleration – possibly inflation – that increased RAC(te) to twice RBC(te) by te; or (2) the early deceleration was not as strong as that in ΛCDM, or was even completely absent. As we shall see in the next section, there is no such horizon problem in the Rh = ct universe.
 |
Fig. 4 Photon trajectories (solid curves) drawn from the perspective of an observer in patch B (see Fig. 2). By symmetry, the curve Rγe(t) is the null geodesic for light signals arriving at A or C at time te from B emitting from a proper distance RAB(t) = Rγe(t) (for t < te), whereas Rγ0(t) is the corresponding null geodesic for photons arriving at B at time t0 (>te). The other curves and symbols have the same meanings as in Fig. 3. |
Before jumping to that case, however, let us consider one more variation on the scenario we
have just explored, one in which the physical conditions in A and C are equilibrated by
virtue of a “beacon” sending out signals from B that reach these patches before they emit at
te. This situation is depicted in Fig. 4. Here, we need ![\begin{eqnarray} R_{\rm AB}(t_*)=R_{\rm BC}(t_*)=2ct_*\left(\left[{t_{\rm e}\over t_*}\right]^{1/2}-1\right), \end{eqnarray}](/articles/aa/full_html/2013/05/aa20447-12/aa20447-12-eq109.png) (22)but
also
(22)but
also ![\begin{eqnarray} R_{\rm AB}(t_{\rm e})=R_{\rm BC}(t_{\rm e})=3ct_{\rm e}\left(\left[{t_0\over t_{\rm e}}\right]^{1/3}-1\right) \end{eqnarray}](/articles/aa/full_html/2013/05/aa20447-12/aa20447-12-eq110.png) (23)(under
the same conditions as before). With
(23)(under
the same conditions as before). With
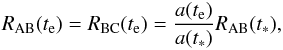 (24)it
is straightforward to see that the result for te is the same as
in Fig. 3, i.e., the earliest
te that would have allowed A and C to be causally connected –
and yet appear on opposite sides of the sky – is roughly 1/5 of
t0 within the context of ΛCDM. This is hardly surprizing, of
course, given the high degree of symmetry implicit in the FRW metric.
(24)it
is straightforward to see that the result for te is the same as
in Fig. 3, i.e., the earliest
te that would have allowed A and C to be causally connected –
and yet appear on opposite sides of the sky – is roughly 1/5 of
t0 within the context of ΛCDM. This is hardly surprizing, of
course, given the high degree of symmetry implicit in the FRW metric.
 |
Fig. 5 Photon trajectories (solid curves) drawn from the perspective of an observer in patch C (see Fig. 2) for a universe in which Rh = ct. All the symbols have the same meanings as those of Fig. 3. |
6. No horizon problem in the Rh = ct universe
The null geodesics and proper distances for the
Rh = ct universe are shown in Fig. 5, again from the perspective of an observer in patch C
(see Fig. 2). The principal difference between this
cosmology and ΛCDM is that here a(t) ∝ t
for all cosmic time t. Therefore, without necessarily having to go through
the same detailed derivations as before, we can immediately write down
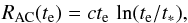 (25)and
(25)and
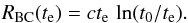 (26)The
question now is “under what conditions could A and C have been causally connected at
te, yet with
RAC(te) = 2RBC(te)
(which means that here on Earth we would be seeing light emitted by A and C at time
te from opposite sides of the sky)? Clearly, this condition is
met when
(26)The
question now is “under what conditions could A and C have been causally connected at
te, yet with
RAC(te) = 2RBC(te)
(which means that here on Earth we would be seeing light emitted by A and C at time
te from opposite sides of the sky)? Clearly, this condition is
met when  (27)and
just as was true for the thought experiment in Sect. 2, this time
t∗ may be small – but it is not zero.
(27)and
just as was true for the thought experiment in Sect. 2, this time
t∗ may be small – but it is not zero.
7. Conclusions
By carefully tracing null geodesics through the FRW spacetime, we have affirmed the well-known “horizon” problem in ΛCDM, highlighting its inability to account for the observed properties of the CMB without some additional early acceleration that would have permitted light emitted at te ~ 380 000 years after the big bang to now reach us from opposite sides of the sky. The inflationary model was invented largely to offset this flaw in the basic theory.
However, we have also demonstrated that the “horizon” problem is not generic to all FRW cosmologies. In particular, we have demonstrated that the recently introduced Rh = ct universe can easily accommodate a situation in which patches of the CMB, seemingly well beyond each other’s photon horizon on opposite sides of the sky, were nonetheless in causal contact with each other after the big bang and emitted the radiation we see today under identical physical conditions. To be clear, these patches were not really beyond each other’s photon horizon, though this mistaken inference is often made because of the confusion over the meaning of proper distance R = a(t)r. The reason is that R(t) does not represent the distance ct light has traveled during a time t. One can easily convince themselves of this by a quick inspection of Eq. (10). Therefore a simple comparison of the proper distance between two patches of CMB on opposite sides of the sky with the distance ct0 light could have traveled since the big bang is not sufficient to demonstrate whether or not these patches are causally connected.
For various reasons, some of which have been discussed elsewhere (Melia 2007, 2013; Melia & Shevchuk 2012; Melia & Maier 2013; Wei et al. 2013), we believe that the Rh = ct universe may provide a theoretical context for understanding at least some of the features that have emerged via fits to the data using the standard model. In this paper, we have extended the argument in favor of the Rh = ct universe by demonstrating that it can also explain how apparently disconnected regions of the CMB on opposite sides of the sky were nonetheless in physical equilibrium when they produced the microwave radiation we see today.
Therefore, inflation was not needed to fix a “horizon” problem that does not exist in this cosmology. In the end, this may
turn out to be the most important feature of the Rh = ct universe because the inflationary scenario is still not completely understood, and may not be able to overcome all of its inherent problems (e.g., the so-called monopole problem; Guth & Tye 1980; Einhorn 1980).
Today, the standard model of cosmology (ΛCDM) is taken to be a particular solution to Einstein’s equations of general relativity, in which the overall energy density is comprised of three principal components: (luminous and dark) matter, radiation, and an as yet unidentified dark energy, which is usually assumed to be a cosmological constant Λ.
Acknowledgments
This research was partially supported by ONR grant N00014-09-C-0032 at the University of Arizona, and by a Miegunyah Fellowship at the University of Melbourne. I am particularly grateful to Amherst College for its support through a John Woodruff Simpson Lectureship.
References
- Bikwa, O., Melia, F., & Shevchuk, A. 2012, MNRAS, 421, 3356 [NASA ADS] [CrossRef] [Google Scholar]
- Einhorn, M. B. 1980, Phys. Rev. D, 21, 3295 [NASA ADS] [CrossRef] [Google Scholar]
- Guth, A. H. 1981, Phys. Rev. D, 23, 347 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Guth, A. H., & Tye, S. 1980, Phys. Rev. Lett., 44, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Linde, A. 1982, Phys. Lett. B, 108, 389 [Google Scholar]
- Melia, F. 2007, MNRAS, 382, 1917 [NASA ADS] [CrossRef] [Google Scholar]
- Melia, F. 2012a, Austral. Phys., 49, 83 [Google Scholar]
- Melia, F. 2012b, AJ, 144, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Melia, F. 2013, ApJ, 764, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Melia, F., & Abdelqader, M. 2009, IJMP-D, 18, 1889 [NASA ADS] [CrossRef] [Google Scholar]
- Melia, F., & Maier, R. S. 2013, MNRAS, in press [arXiv:1304.1802] [Google Scholar]
- Melia, F., & Shevchuk, A. 2012, MNRAS, 419, 2579 [NASA ADS] [CrossRef] [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Wei, Jun-Jie, Wu, X., & Melia, F. 2013, ApJ, submitted [arXiv:1301.0894] [Google Scholar]
All Figures
 |
Fig. 1 Simple analogy in flat spacetime, in which 2 frames of reference (A and C) are moving away from us (situated in frame B), each at speed v, though in opposite directions. If v is close to c, after a time t in our frame, A and C are apparently beyond each other’s horizon (here defined as ct), but A and C could still have communicated after t = 0 (and before t0) if light were emitted by A at time t∗, such that c(t0 − t∗) = v(t0 + t∗). |
| In the text | |
 |
Fig. 2 An observer B is receiving light signals from two patches (A and C) of the CMB. We assume that the light was emitted by these sources at cosmic time te, when their proper distances from the observer were RBA(te) and RBC(te), respectively. In addition, we assume that A emitted an earlier light signal at time t∗ that reached C, a proper distance RAC(te) away, at time te. |
| In the text | |
 |
Fig. 3 Photon trajectories (solid curves) drawn from the perspective of an observer in patch C (see Fig. 2). The curve Rγe(t) is the null geodesic for light signals arriving at C at time te from any source at proper distance Rsrc(t) = Rγe(t) (for t < te), whereas Rγ0(t) is the corresponding null geodesic for photons arriving at C at time t0 (>te), though from sources at Rsrc(t) = Rγ0(t) (at any t < t0). The other curves and symbols are defined in the text. |
| In the text | |
 |
Fig. 4 Photon trajectories (solid curves) drawn from the perspective of an observer in patch B (see Fig. 2). By symmetry, the curve Rγe(t) is the null geodesic for light signals arriving at A or C at time te from B emitting from a proper distance RAB(t) = Rγe(t) (for t < te), whereas Rγ0(t) is the corresponding null geodesic for photons arriving at B at time t0 (>te). The other curves and symbols have the same meanings as in Fig. 3. |
| In the text | |
 |
Fig. 5 Photon trajectories (solid curves) drawn from the perspective of an observer in patch C (see Fig. 2) for a universe in which Rh = ct. All the symbols have the same meanings as those of Fig. 3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


