| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 9 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201219058 | |
| Published online | 18 April 2013 | |
A new extensive library of PHOENIX stellar atmospheres and synthetic spectra
1
Institut für Astrophysik, Georg-August-Universität Göttingen,
Friedrich-Hund-Platz 1,
37077
Göttingen, Germany
e-mail:
husser@astro.physik.uni-goettingen.de
2
CRAL, UMR 5574, CNRS, Université de Lyon, École Normale Supérieure de Lyon,
46 allée
d’Italie, 69364
Lyon Cedex 07,
France
3
Lowell Observatory, 1400 West Mars Hill Road, Flagstaff, AZ
86001,
USA
4
Hamburger Sternwarte, Gojenbergsweg 112,
21029
Hamburg,
Germany
Received:
16
February
2012
Accepted:
14
March
2013
Aims. We present a new library of high-resolution synthetic spectra based on the stellar atmosphere code PHOENIX that can be used for a wide range of applications of spectral analysis and stellar parameter synthesis.
Methods. The spherical mode of PHOENIX was used to create model atmospheres and to derive detailed synthetic stellar spectra from them. We present a new self-consistent way of describing micro-turbulence for our model atmospheres.
Results. The synthetic spectra cover the wavelength range from 500 Å to 5.5 μm with resolutions of R = 500 000 in the optical and near IR, R = 100 000 in the IR and Δλ = 0.1 Å in the UV. The parameter space covers 2300 K ≤ Teff ≤ 12 000 K, 0.0 ≤ log g ≤ +6.0, − 4.0 ≤ [Fe/H] ≤ +1.0, and − 0.2 ≤ [α/Fe] ≤ +1.2. The library is a work in progress and we expect to extend it up to Teff = 25 000 K.
Key words: stars: atmospheres / convection / stars: late-type
© ESO, 2013
1. Introduction
Stellar spectral libraries are an important tool for analysing observed spectra and can be used for a wide range of applications. The use of empirical libraries guarantees real physical spectra, which will match other observations well, e.g. absorption lines created by atomic and molecular transitions appear at the exact position with the correct shapes and strengths. However, these spectra are limited both in spectral resolution and wavelength coverage – and extensions of the library require some significant effort and observing time, if possible at all (e.g. changes in instrumentation). Furthermore, the chemical composition of the observed stars is not known exactly, resulting in possible systematic errors for abundance determinations, and the spectra cover only a limited parameter space, usually restricted to the effective temperature, the surface gravity, and the metallicity. Examples for empirical libraries covering the optical wavelength range are the Indo-US Library of Coudé Feed Stellar Spectra (Valdes et al. 2004), MILES (Sánchez-Blázquez et al. 2006), STELIB (Sánchez-Blázquez et al. 2006), and ELODIE (Prugniel & Soubiran 2004). Note that all these libraries contain only low to medium resolution spectra.
Synthetic spectra on the other hand are limited by the completeness of the spectral line lists and by the knowledge of line broadening parameters and numerical assumptions – e.g. plane-parallel versus spherical geometry and local thermodynamic equilibrium (LTE) versus statistical equilibrium (NLTE). Nevertheless, synthetic libraries have many advantages: the range of stellar parameters, elemental abundances, and both the wavelength range and the spectral resolution can be adjusted as needed. The best known set of model atmospheres currently available was created by Kurucz (1979), from which many spectral libraries have been derived (e.g. Rodríguez-Merino et al. (2005) in the UV, and Murphy & Meiksin (2004) and Munari et al. (2005) in the full optical domain). The NLTE stellar atmosphere code TLUSTY (Hubeny 1988) made possible a grid of NLTE atmospheres for O stars (Lanz & Hubeny 2003). Gustafsson et al. (2008) published a grid of spectra based on MARCS which, like our new grid, uses spherical-symmetry for its models.
Because we need a stellar spectral library for the analysis of spectra observed with MUSE (Bacon et al. 2010), X-shooter (Vernet et al. 2011), and CRIRES (Kaeufl et al. 2004) for example, a decision was made in favour of the flexibility of a synthetic library that can be extended on the fly – even in parameters that are not changed in the published grid. For example, varying the abundances of single elements enables us to determine the areas of the spectra that are mainly affected by those elements. In comparison with empirical spectra, this shows a major advantage of having a stellar atmosphere code available together with thousands of synthetic atmospheres that can be used as starting points for extensions. Instead of extending an existing synthetic library, we opted for creating a new one using the latest state-of-the-art version of the stellar atmosphere code PHOENIX (Hauschildt & Baron 1999).
The first published PHOENIX library consisted of 700 model atmospheres for M (sub)dwarf stars (Allard & Hauschildt 1995), all calculated under the assumption of LTE. This has also been the case for the NextGen library (Hauschildt et al. 1999a) with its temperatures ranging from 3000 K to 10 000 K, which has been used as the starting point for a grid of NLTE model atmospheres of dwarfs and giants. Furthermore, an upgrade to spherically symmetric models for giant stars with effective temperatures between 3000 K and 6800 K has been done by Hauschildt et al. (1999b). Further calculations of NLTE models have been conducted by Barman et al. (2000). The effects of dust settling in cool stars like brown dwarfs have been investigated by Allard et al. (2001) and extended to extra-solar planets by Witte et al. (2009, 2011). The latest comprehensive grid of spectra (Brott & Hauschildt 2005) was created for use with the GAIA mission (Lindegren et al. 2008). In the following we will refer to spectra created with that version of PHOENIX as AMES-cond-v2.6.
Our new spectral library is the first one using the current version 16 of PHOENIX, which has a new equation of state as well as an up-to-date atomic and molecular line list. This allowed us to produce spectra that match observations especially of cool stars significantly better than other synthetic libraries. A full discussion of this aspect will appear in a subsequent publication (Wende-von Berg & Reiners 2013). The use of spherical geometry guarantees a consistent model grid from the main sequence up to giants. We have adjusted the wavelength range and resolution to meet the requirements for science cases using existing and upcoming instruments.
In this paper we will first describe the basic parameters of the grid, namely its dimensions and the resolution of the spectra. Then we will discuss in detail some of the input parameters such as the used element abundances, the stellar mass, and the micro-turbulence for which we will also provide comparisons with observed data. We will characterise the equation of state used for calculating the models and show the improvements that we achieved compared to older PHOENIX models, other spectral libraries, and observations. Finally, we will explain how to download the FITS files containing the spectra and describe their content.
2. The library
2.1. Dimensions and resolution
Since the library is still a work in progress, we only present its current state which, however, already covers the parameter space of most stellar populations that are not part of starburst regions. Table 1 shows the current parameter space of the grid, a future extension will probably be towards higher effective temperatures, most probably up to 25 000 K. The grid is complete in its first three dimensions Teff, log g [cgs] and [Fe/H]. So far, a variation of the alpha element abundance ([α/Fe] ≠ 0) has only been calculated for effective temperatures 3500 K ≤ Teff ≤ 8000 K and metallicities − 3 ≤ [Fe/H] ≤ 0.
The standard spectroscopic abundance notation is used in this article which defines the
ratio of two elements A and B in a star relative to
their ratio in the Sun as ![\begin{equation} [A/B] \equiv \log\, [n(A)/n(B)] - \log\, [n(A)/n(B)]_\odot, \end{equation}](/articles/aa/full_html/2013/05/aa19058-12/aa19058-12-eq20.png) (1)with the number density
n. We assume that [X/H] = [Fe/H] for most elements and so,
[Fe/H] denotes the overall metallicity. The abundances of the α
elements (O, Ne, Mg, Si, S, Ar, Ca, and Ti) are defined as
(1)with the number density
n. We assume that [X/H] = [Fe/H] for most elements and so,
[Fe/H] denotes the overall metallicity. The abundances of the α
elements (O, Ne, Mg, Si, S, Ar, Ca, and Ti) are defined as
![\begin{equation} \rm [\alpha/H] = \feh + \afe. \end{equation}](/articles/aa/full_html/2013/05/aa19058-12/aa19058-12-eq24.png) (2)This implies that
the value of [Fe/H] is conserved in alpha-enhanced or depleted models, but the overall
metallicity Z changes.
(2)This implies that
the value of [Fe/H] is conserved in alpha-enhanced or depleted models, but the overall
metallicity Z changes.
Parameter space of the grid.
Sampling of the spectra in the grid.
The spectra cover the whole wavelength range from 500 Å up to 5.5 μm; the sampling is given in Table 2. Please note that these sampling rates are the direct output of PHOENIX, i.e. the spectra have never been resampled or convolved with any kernel.
The wavelength grid is identical for all models in the grid, which was made possible by a new option in PHOENIX v16, which has been introduced in this new version and allows us to disable the creation of new wavelength points to better account for opacity. We activated this option, since the sampling rate is high enough already. Furthermore, it allows us to store the wavelength grid only once for all spectra in the library and therefore save storage space.
2.2. Calculation of model atmospheres and synthetic spectra
Synthesising a spectrum with PHOENIX is a three-step process. First, a model atmosphere was calculated using a set of 766 atmospheres from a previously unpublished PHOENIX grid as start values. From those, the grid was extended step by step, always using an existing neighbouring model as the starting point. The PHOENIX code iterates a model atmosphere, until its criteria for convergence are reached. In order to limit the run time, we stopped after every 80 iterations and restarted PHOENIX if necessary. Parameter adjustments for many of the models had to be done individually in order to obtain fully converged model atmospheres.
The next step was to activate a mode in PHOENIX that triggers the use of special line profiles, which we used for the Ca lines, for example. In this mode no convergence is checked, so we carried out five more iterations by default in order to stratify the atmosphere again properly. Finally, the high resolution spectrum was synthesised from this intermediate model.
Having access to the model atmospheres as well as the spectra allows us to quickly expand the grid in any given direction. Furthermore, we can use the existing model atmospheres for other investigations – e.g. we activated the output of the full radiative field, which can be used for calculating limb darkening coefficients in PHOENIX for some models. The results will be discussed in a subsequent publication.
Even in its current state (end of 2012) with ~50 000 model atmospheres and corresponding synthetic spectra (of which ~30 000 will be published), it took about ~135 CPU years for the new PHOENIX library to be calculated on the Nehalem Cluster of the GWDG1 in about one year, parallelised on 20−50 nodes with 8 CPUs each.
2.3. PHOENIX settings
While most other synthetic libraries set many parameters to fixed values, we tried to use parametrisations, for the mass and the mixing length parameter α, for example, that better match observations. Below we introduce a new unique method for the micro-turbulence, which we calculate from convection velocities obtained from the atmospheric model. Furthermore our new stellar library is the first one to use the new equation of state introduced with the new version of PHOENIX and we use the most recent values for the solar element abundances.
All model atmospheres have been calculated in a spherical mode with 64 layers. The reference wavelength defining the mean optical depth grid, which should be set to a wavelength with sufficient flux, is fixed to λτ = 12 000 Å for Teff < 5000 K and λτ = 5000 Å for hotter stars.
Local thermodynamic equilibrium has been assumed for all the models in the library, which is sufficient for the temperature range that we have investigated so far – the extension to effective temperatures Teff ≥ 12 000 K will take into account NLTE effects. Nevertheless, even for the existing models with Teff ≥ 4000 K, we used the NLTE mode of PHOENIX to use special line profiles for some species (Li I, Na I, K I, Ca I, Ca II). The full sample of molecules is only used for models with Teff ≤ 8000 K, while it is stripped to a few important ones for hotter stars.
Condensation is included in the equation of state but ignored in the opacity (Cond setup, see Allard et al. 2001) and we do not handle dust settling at all in our model atmospheres, since all our models have effective temperatures Teff ≥ 2300 K.
2.3.1. Mass
While plane-parallel geometry is a valid assumption for main sequence star model atmospheres, this is no longer true for giants. For those, PHOENIX offers a mode for spherical symmetry, which we used for all models to guarantee a homogeneous grid. A model atmosphere with spherical geometry is then described by its effective temperature Teff, surface gravity log g, and mass M⋆, from which all the other physical parameters can be derived, i.e. adjusting the mass changes both the radius and the luminosity. In order to get numerically stable and realistic atmospheres, we used a varying mass throughout the grid and did not fix it to specific values (as Hauschildt et al. 1999b; and Gustafsson et al. 2008 do, for example).
For main sequence stars we use the mass-luminosity relation, which can be approximated
for solar type stars (Voigt 1991) as
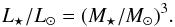 (3)Furthermore we can
calculate the luminosity from the effective temperature and radius. For the Sun the
radius can be substituted by the surface gravity and mass, which yields:
(3)Furthermore we can
calculate the luminosity from the effective temperature and radius. For the Sun the
radius can be substituted by the surface gravity and mass, which yields:
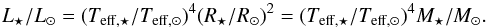 (4)By combining these two
equations we get:
(4)By combining these two
equations we get: 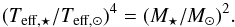 (5)For evolved stars,
we can naturally not prescribe a unique mass-radius relation, and it becomes more
challenging to define mass as a function of Teff and
log g, so we modify the main sequence relation with a variable
factor c for lower surface gravities to match observed values of giants
and super giants. Masses, especially of red giants and asymptotic giant branch stars,
show considerable spread even for identical atmospheric parameters, but we chose
adjustment factors such as matching the very-well-constrained values of Arcturus (Ramírez & Allende Prieto 2011) and the sample
of M giants studied by Dumm & Schild
(1998), roughly covering
3000 K ≤ Teff ≤ 4000 K,
− 0.5 ≤ log g ≤ 1.5 with masses between 0.8 and 4
M⊙. Therefore in the grid the mass is given by
(5)For evolved stars,
we can naturally not prescribe a unique mass-radius relation, and it becomes more
challenging to define mass as a function of Teff and
log g, so we modify the main sequence relation with a variable
factor c for lower surface gravities to match observed values of giants
and super giants. Masses, especially of red giants and asymptotic giant branch stars,
show considerable spread even for identical atmospheric parameters, but we chose
adjustment factors such as matching the very-well-constrained values of Arcturus (Ramírez & Allende Prieto 2011) and the sample
of M giants studied by Dumm & Schild
(1998), roughly covering
3000 K ≤ Teff ≤ 4000 K,
− 0.5 ≤ log g ≤ 1.5 with masses between 0.8 and 4
M⊙. Therefore in the grid the mass is given by
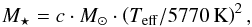 (6)with values for the
coefficient given in Table 3. Figure 1 shows the distribution of masses over the grid. For
solar-like stars, we obtain
M⋆ = 1 M⊙
and the masses increase for hotter and larger stars as expected.
(6)with values for the
coefficient given in Table 3. Figure 1 shows the distribution of masses over the grid. For
solar-like stars, we obtain
M⋆ = 1 M⊙
and the masses increase for hotter and larger stars as expected.
 |
Fig. 1 Distribution of stellar masses for different effective temperatures Teff and surface gravities log g, colour-coded in units of solar mass from 0 M⊙ (black) to 25 M⊙ (white). |
2.3.2. Convection
In PHOENIX, convection in the stellar atmosphere is described by the mixing length theory of turbulent transport, which goes back to Prandtl (1925) and, in the stellar context, to Vitense (1953) and Böhm-Vitense (1958). It is characterised by the mixing length parameter α, which describes the ratio between the characteristic length that a volume of gas can rise in a stellar atmosphere before mixing with its surrounding and the pressure scale height (α = l/Hp), i.e. it is a value for the efficiency of the convective energy transport – a large α indicates an efficient energy transport, while it is inefficient for a small α in which case the gas volume is allowed to rise to greater heights under the buoyant force, thus reaching higher velocities and carrying more heat before it is assumed to be dissipated.
For our spectra we describe the mixing length parameter α as discussed in Ludwig et al. (1999) where it has been calibrated using 3D radiative hydrodynamic models. Since the authors emphasise that it might be incorrect to extrapolate the mixing length outside the ranges given in the paper (4300 K ≤ Teff ≤ 7100 K and 2.54 ≤ log g ≤ 4.74), we restrict the result to an interval α ∈ [1,3.5].
 |
Fig. 2 Distribution of the mixing length parameter α in the grid. |
The distribution of mixing lengths in the grid is shown in Fig. 2. The majority of the models have an α roughly
between 1.5 and 2.5, while we had to cut off at α = 3.5 for models with
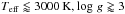 and at α = 1 for those with
and at α = 1 for those with 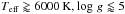 .
For almost all models with
.
For almost all models with 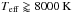 the mixing length is α = 1.
the mixing length is α = 1.
Because all the other changes introduced with the new PHOENIX library, we unfortunately are unable to comment on the impact of our choice of this varying alpha parameter on the final spectra.
2.3.3. Micro-turbulence
Micro-turbulence is an ad-hoc parameter that is used to match synthetic spectra with
observations. We use it in the sense that the large-scale (macro-) turbulent motion
triggers small-scale (micro-) turbulent motion below the length scale of the mean free
path of the photons. Unlike macro-turbulent motion, this motion affects the strength of
a spectral line (Gray 2005), since it directly
influences the line opacities, so it has to be included in the line forming process and
cannot be applied afterwards. Following this scheme, micro-turbulence is strongly
related to the macro-turbulent motion and we therefore use the relation
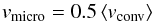 (7)to
determine its amount. This empirical approximation follows from 3D radiative
hydrodynamic investigations of cool M stars (Wende
et al. 2009), but also gives reasonable values for hotter stars (see Fig. 3). The mean value of the macro-turbulence
⟨vconv⟩ is taken from the PHOENIX atmospheres prior to
spectral synthesis. The convective velocities from all layers are averaged in a way that
only layers with non-zero values are included and then divided by a factor of two, i.e.
micro-turbulence is assumed to be half of the mean convective velocity in the
photosphere.
(7)to
determine its amount. This empirical approximation follows from 3D radiative
hydrodynamic investigations of cool M stars (Wende
et al. 2009), but also gives reasonable values for hotter stars (see Fig. 3). The mean value of the macro-turbulence
⟨vconv⟩ is taken from the PHOENIX atmospheres prior to
spectral synthesis. The convective velocities from all layers are averaged in a way that
only layers with non-zero values are included and then divided by a factor of two, i.e.
micro-turbulence is assumed to be half of the mean convective velocity in the
photosphere.
Since micro-turbulence mainly affects the strength and shape of the lines and not the structure of the atmosphere, it is only included in the computation of the high resolution synthetic spectra and not in the underlying model atmospheres. We did not attempt to further converge the atmospheres with the micro-turbulences derived from the previous iterations, which would have cost additional computational resources without noticeably changing the structure. Despite the lack of a self-consistent description derived from first principles, this empirical description removes micro-turbulence as a free parameter.
 |
Fig. 3 Distribution of micro-turbulence for models with solar abundances for different effective temperatures Teff and surface gravities log g (colour-coded). We had to disable the convection for the giants with Teff ≳ 5500 K and therefore no micro-turbulence was applied to these spectra. In and around this area we observe numerical instabilities causing single models to show differing results. Over-plotted are observational data points taken from Landstreet et al. (2009) (+) and Takeda et al. (2008) (×). |
Figure 3 shows the distribution of micro-turbulences for models with solar abundances. As one can see, for cool stars our micro-turbulences are a lot smaller that the 2 km s-1 frequently assumed in model atmospheres. Over-plotted are observational data points taken from Landstreet et al. (2009) and Takeda et al. (2008). The agreement with our values for stars on the upper main-sequence and the red giant branch is gratifying. For effective temperatures above 6500 K, however, convective turbulence predicted by our models decreases steadily and cannot reproduce the significant broadening velocities observed by Landstreet et al. (2009) in F and A stars.
We note however that the Landstreet et al. (2009) study does not display a unique relation of photospheric line broadening and atmospheric parameters, and includes a number of peculiar stars – e.g. all main sequence stars with vmicro ≥ 3 km s-1 in their sample are Am stars. They also conclude that the line shapes of these stars cannot be understood in a simple micro-turbulence concept. These findings are essentially confirmed by RHD simulations (Freytag et al. 2012, and references therein), but these still sample the hottest stars with convectively unstable atmospheres only very sparsely.
For giant stars with Teff ≈ 6500 K we encountered strong numerical instabilities in the PHOENIX convection module as a consequence of to the diminishing extension of the convectively unstable layer and had to disable it completely. For consistency with the rest of our grid, we have chosen to publish these spectra with zero vmicro; the users are advised that they cannot replace more detailed modelling using the micro-turbulence as a free parameter for those stars.
Other unexpected results appear in the region below 3000 K, where we see another peak
in the micro-turbulence. Those models develop a second convective zone at the outer edge
of the atmosphere, where the convection velocity increases towards lower optical depths,
which causes our method to produce values for the micro-turbulence that are higher than
expected. A similar behaviour has been observed in 3D radiative hydrodynamic simulations
by Wende et al. (2009). Although the effect of
this second convective zone on the spectrum is small, it does introduce changes as a
result of our new self-contained method for calculating the micro-turbulence. Thus, we
will provide an update for the spectral library for stars with
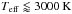 within a couple of months, in which we will limit the range of optical depths used for
calculating the micro-turbulence.
within a couple of months, in which we will limit the range of optical depths used for
calculating the micro-turbulence.
2.3.4. Equation of state
The Astrophysical Chemical Equilibrium Solver (ACES, Barman 2012) equation of state (EOS) that is used starting with PHOENIX version 16 is a state-of-the-art treatment of the chemical equilibrium in a stellar atmosphere. It uses the method of Smith & Missen (1982) with new experimental and theoretical thermodynamical data (Barman 2012) for 839 species (84 elements, 289 ions, 249 molecules, 217 condensates).
In each layer, the chemical equilibrium for all used atomic and molecular species is computed in dependence on the pressure, temperature, and density. After computing the atmospheric structure with the equations of radiation and hydrodynamics, a new chemical equilibrium is calculated in a second step. This iterative process continues until convergence. We did not not investigate which changes in the spectra were introduced specifically by using the new ACES equation of state.
2.3.5. Element abundances
The element abundances are scaled solar abundances taken from Asplund et al. (2009), where the abundances in both the photosphere and in meteorites are given. With the exception of Li, which is destroyed in the solar interior, and volatile elements that are depleted in meteorites, both sets of abundances agree within the errors; apart from the cases mentioned above, we have therefore chosen the measurements with respective smaller uncertainties (see Table 4) to best reproduce the proto-solar elemental composition (Lodders 2003).
2.4. Vacuum wavelengths
All our spectra are provided at vacuum wavelengths λvac. If
air wavelengths λair are required, one can use the following
equation taken from Ciddor (1996), where it is
applied for λ > 2000 Å only
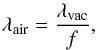 (8)with
(8)with
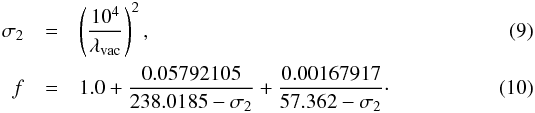
2.5. Interpolation
A few spectra are missing in the grid where PHOENIX was unable to compute the structure of the atmosphere for various reasons. Where possible, we provide interpolated spectra.
The interpolation is done point-wise, i.e. every wavelength point is interpolated independently using a cubic spline created from neighbouring spectra. The interpolation is done along the Teff axis only.
The difference in flux between an interpolated spectrum and one calculated with PHOENIX is usually less than 1%, but increases for lower temperatures and can reach up to 10% for the coolest stars in the grid.
3. Quality of the spectra
Many changes have been implemented with respect to previous PHOENIX models. For example, the more detailed treatment of the chemical equilibrium in the new EOS strongly affects the stellar structure and results in different line and molecular band strengths, which can introduce significant differences in comparison to older PHOENIX model spectra, especially for M stars as discussed below. But major changes can also be expected from the new list of element abundances and the new parametrisations for the mixing length and the micro-turbulence. Consequentially we observed some significant differences between spectra from previous PHOENIX grids and from this one.
We compared some temperature profiles with those of the original models that have been used
as a starting point for the new library. For 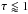 they match very well and we only see differences for τ ≫ 1, which are
irrelevant for the morphology of the final spectrum.
they match very well and we only see differences for τ ≫ 1, which are
irrelevant for the morphology of the final spectrum.
 |
Fig. 4 New PHOENIX ACES model spectra (full line) compared to PHOENIX AMES v2.6 spectra (dotted line); both models are calculated for a typical M 6 main sequence star (Teff = 2900 K, log g = 5.0) and smoothed to an effective resolution of R = 10 000. The ACES model spectra produce significantly deeper TiO bands than earlier PHOENIX models. |
3.1. M stars
In Fig. 4 we show a comparison between model spectra from our new PHOENIX grid and from a previous one using the old EOS AMES version 2.6 at the region around the TiO ϵ-band. In both cases, the Cond models are used. We show spectra at effective temperatures of Teff = 2900 K and log g = 5.0, typical values for an M6 main sequence star. The TiO bands are known as robust temperature indicators, because they only weakly depend on gravity but are very sensitive to temperature (Mohanty et al. 2004; Reiners 2005). In the new grid we now see TiO ϵ-bands that are significantly deeper than those in older PHOENIX versions for identical atmospheric parameters. In this example, the difference in temperature derived from the two models would be about 200 K.
 |
Fig. 5 Comparison between PHOENIX (full line) and ATLAS9 (dotted line) model spectra for Teff = 4000 K, log g = 4.0 and solar abundances. The PHOENIX spectrum has been convolved with a Gaussian kernel with a FWHM of 20 Å for wavelengths smaller than 1 μm and with a Gaussian with a FWHM of 50 Å for wavelengths larger than 1 μm. |
Element abundances used in grid, taken from Asplund et al. (2009).
3.2. Comparison with Kurucz models
In Figs. 5 and 6 the PHOENIX synthetic spectra are compared to corresponding ATLAS9 spectra (Castelli & Kurucz 2003) for two different effective temperatures. Note that they used the Grevesse & Sauval (1998) solar abundances, while we used the more recent abundances by Asplund et al. (2009). This will introduce systematic differences between the spectra. The PHOENIX spectra have been convolved with a Gaussian kernel with a FWHM of 20 Å for wavelengths smaller than 1 μm and with a Gaussian with a FWHM of 50 Å for wavelengths larger than 1 μm in order to match the spectral resolution of the ATLAS9 spectra better. In general the compared models agree well. For the 8000 K spectra we observe a ~3% lower flux at every single wavelength point in the PHOENIX spectrum than in the ATLAS9 spectrum, which is therefore just a difference in total luminosity that can easily be explained by the varying mass in our new library.
 |
Fig. 6 Comparison between PHOENIX (full line) and ATLAS9 (dotted line) model spectra for Teff = 8000 K, log g = 4.0 and solar abundances. The PHOENIX spectrum has been convolved with a Gaussian kernel with a FWHM of 20 Å. |
 |
Fig. 7 Comparison between PHOENIX (full line) and ATLAS9 (dotted line) model spectra for the Sun in full resolution (R = 500 000) in the upper plot. Below the PHOENIX spectrum (full line) is compared to a solar spectrum observed by Wallace et al. (2011). |
 |
Fig. 8 Comparison between PHOENIX (full line) and ATLAS9 (dotted line) model spectra for Vega, both convolved to 20 Å FWHM. |
Input parameters for PHOENIX and ATLAS9 models for Sun and Vega.
3.3. Sun
In the upper plot of Fig. 7a comparison between a PHOENIX and an ATLAS92 solar spectrum in full resolution is shown for the region around Hα. Table 5 lists the input parameters for both. The overall agreement is good, but the line profile is slightly different: in the PHOENIX spectrum the line is not as deep as in the ATLAS9 spectrum, which is compensated by broader wings. The lower plot of Fig. 7 compares the PHOENIX spectrum to a solar spectrum observed by Wallace et al. (2011). Obviously the real line is even broader and thus the PHOENIX spectrum is a better match than the ATLAS9 one.
Unfortunately, these comparisons also show one of the major drawbacks of synthetic spectra, i.e. they are missing some of the absorption lines present in the observed spectrum, e.g. the line at 6571 Å, which is present in the ATLAS9 spectrum but not in the PHOENIX spectrum.
Comparison of colour indices for different solar spectra.
Some colour indices calculated from the ATLAS9 and the PHOENIX spectrum are listed in Table 6. In addition, the colours for the solar spectrum from CALSPEC, which is a set of composite stellar spectra used for HST calibrations (see e.g. Turnshek et al. 1990; Colina & Bohlin 1997) are given. The transmission curves for the used filters have been adapted from Johnson (1965)3.
Altogether our solar spectrum seems to be quite accurate, which is gratifying for an all-purpose spectral library without special optimisations to match the solar spectrum well.
3.4. Vega
In Fig. 8 we show a comparison between spectra for Vega, calculated both with PHOENIX and ATLAS94 and the input parameters given in Table 5. The PHOENIX model has been interpolated from the existing grid instead of calculating a new one. Since the mass of that model differs from the real Vega because of our parametrisation of the stellar mass, the flux was scaled to match that of the ATLAS9 model. Further discrepancies are introduced by the differences in helium abundance, micro-turbulence, etc. Nevertheless, the overall shapes of the spectra match well.
Comparison of colour indices for different spectra of Vega.
Table 7 lists some colour indices. Since the magnitudes have been calculated in the VEGAmag system with the ATLAS9 model as reference, all colours are zero for these magnitudes. The results from our interpolated PHOENIX spectrum are in good agreement.
4. FITS files
4.1. Download
All the spectra presented in this paper are available for download from our homepage5. Single high-resolution spectra can be downloaded using a web form by specifying temperature, surface gravity, metallicity and alpha element abundance. In order to keep the amount of storage space to a minimum, these files contain only the flux; the wavelength grid must be obtained separately once for all spectra.
Furthermore we provide archives with full sub-grids of the library convolved to more convenient resolutions:
-
1.
Δλ = 1 Å in the optical wavelength range from λ = 3000 Å to 10 000 Å.
-
2.
R = 10 000, i.e. the resolution of the X-Shooter Spectral Library XSL (Chen et al. 2011), with the full wavelength range of X-Shooter, namely λ = 3000 Å to 24 800 Å.
These spectra are over-sampled by a factor of ten, so the 1 Å grid has a sampling rate of 0.1 Å, for example.
4.2. Naming scheme
The spectra are provided in a FITS file with the following naming scheme:
<grid>/<subgrid>/
(n)lte<Teff><log(g)><subgrid>.<grid>-HiRes.fits
where <grid> is the name of the grid. As for the spectra described in this paper, this will always be PHOENIX-ACES-AGSS-COND-2011.
The <subgrid> describes all the parameters in addition to Teff and log g and is empty when there are none. An example would be .Alpha=+0.30 for an alpha element enhancement of +0.3 dex. Abundances equal to those of the Sun are never included, i.e. there is no .Alpha=+0.00. Be aware that [Fe/H] is given as first parameter in the name of the sub-grid, not Z.
The filename itself always starts with either lte or nlte, describing whether the atmosphere has been calculated in LTE or NLTE.
The effective temperature <Teff> is always given by five digits with leading zeros, if necessary. The surface gravity <log(g)> is denoted by its negative with two digits after the decimal point. In the filename itself the Z describing the metallicity is dropped, since the metallicity is explicitly given for all files.
Two examples for the naming scheme would be
* PHOENIX-ACES-AGSS-COND-2011/Z-1.0.Alpha=+0.30/
lte08000-2.00-1.0.Alpha=+0.30.
PHOENIX-ACES-AGSS-COND-2011-HiRes.fits
* PHOENIX-ACES-AGSS-COND-2011/Z-0.0/
lte06800-4.50-0.0.
PHOENIX-ACES-AGSS-COND-2011-HiRes.fits
4.3. File content
The files always contain one single primary extension, which holds the flux of the spectrum in units of [erg/s/cm2/cm] on the stellar surface. The files for the high-resolution spectra contain a FITS keyword WAVE, which holds a reference to the file that stores the wavelength grid and is saved in the same format as the spectra, but with wavelength points instead of a flux array.
For the medium-resolution spectra, the wavelength grid is provided by a set of four FITS keywords. CRVAL1 defines the wavelength at pixel CRPIX1, which is always 1 for our spectra. The step size is given by CDELT1 and the number of points by NAXIS1. The type of the wavelength grid is defined by the CTYPE1 keyword – for this grid it will always be one of the two possible values for vacuum wavelengths, i.e. WAVE or WAVE-LOG, where the latter denotes a logarithmic scale. With this information the whole wavelength grid can be calculated easily.
4.4. Additional FITS keywords
In addition to the default FITS keywords, we added some more for documenting the atmospheric parameters for the spectrum.
The basic parameters are given as
-
PHXTEFF: [K] effective temperature;
-
PHXLOGG: [cm/s2] log (surface gravity);
-
PHXM_H: [M/H] metallicity (rel. sol. – Asplund et al. 2009);
-
PHXALPHA: [a/M] alpha element enhancement.
Additional parameters for the atmosphere are
-
PHXDUST: [T/F] Dust in atmosphere, always F for this grid;
-
PHXXI_L: [km s-1] micro-turbulent velocity for LTE lines;
-
PHXXI_M: [km s-1] micro-turbulent velocity for molec lines;
-
PHXXI_N: [km s-1] micro-turbulent velocity for NLTE lines;
-
PHXMASS: [kg] Stellar mass;
-
PHXREFF: [cm] Effective stellar radius;
-
PHXLUM: [W] Stellar luminosity;
-
PHXMXLEN: Mixing length.
Furthermore, we included some information about the PHOENIX run:
-
PHXBUILD: Build date of Phoenix;
-
PHXVER: Phoenix version;
-
DATE: [local] finishing date of model calculation;
-
PHXEOS: Equation of state.
As mentioned before, there are models within the grid for which we manually disabled the convection. For those we added another keyword PHXCONV with the value F. For the high-resolution spectra there is also a second FITS extension in the file containing a binary table listing all the element abundances that have been used in the model.
The files containing interpolated spectra only include the date of their creation and those FITS keywords from the lists above that specify the basic stellar parameters (Teff, log g, [Fe/H], and [α/Fe]). Furthermore, for these spectra we added the keyword INTERPOL with the value T.
5. Summary
The presented PHOENIX grid contains a comprehensive set of synthetic spectra that allows a detailed analysis of observed spectra for a wide range of applications. An extension taking into account NLTE treatment of important elements up to 25 000 K is a work in progress. Both resolution and wavelength range match existing and upcoming state-of-the-art instruments.
Gesellschaft für wissenschaftliche Datenverarbeitung mbH Göttingen, http://www.gwdg.de/index.php?id=2156
Acknowledgments
We warmly thank the anonymous referee for his/her comments that helped to improve this publication significantly. Derek Homeier has been funded under the Labex Lio programme of the Université Claude Bernard Lyon 1, the Agence Nationale de la Recherche (ANR), and the Programme National de Physique Stellaire (PNPS) of CNRS (INSU). Numerical calculations were performed at the Gesellschaft für Wissenschaftliche Datenverarbeitung Göttingen.
References
- Allard, F., & Hauschildt, P. H. 1995, ApJ, 445, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Allard, F., Hauschildt, P. H., Alexander, D. R., Tamanai, A., & Schweitzer, A. 2001, ApJ, 556, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bacon, R., Accardo, M., Adjali, L., et al. 2010, in SPIE Conf. Ser., 7735, 7 [Google Scholar]
- Barman, T. S., Hauschildt, P. H., Short, C. I., & Baron, E. 2000, ApJ, 537, 946 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm-Vitense, E. 1958, ZAp, 46, 108 [NASA ADS] [Google Scholar]
- Brott, I., & Hauschildt, P. H. 2005, in The Three-Dimensional Universe with Gaia, eds. C. Turon, K. S. O’Flaherty, & M. A. C. Perryman, ESA SP, 576, 565 [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2003, in Modelling of Stellar Atmospheres, eds. N. Piskunov, W. W. Weiss, & D. F. Gray, IAU Symp., 210, 20 [Google Scholar]
- Chen, Y., Trager, S., Peletier, R., & Lançon, A. 2011, J. Phys. Conf. Ser., 328, 012023 [NASA ADS] [CrossRef] [Google Scholar]
- Ciddor, P. E. 1996, Appl. Opt., 35, 1566 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Colina, L., & Bohlin, R. 1997, AJ, 113, 1138 [NASA ADS] [CrossRef] [Google Scholar]
- Dumm, T., & Schild, H. 1998, New A, 3, 137 [Google Scholar]
- Freytag, B., Steffen, M., Ludwig, H.-G., et al. 2012, J. Computat. Phys., 231, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. 2005, The observation and analysis of stellar photospheres (Cambridge University Press) [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hauschildt, P. H., & Baron, E. 1999, J. Computat. Appl. Math., 109, 41 [Google Scholar]
- Hauschildt, P. H., Allard, F., & Baron, E. 1999a, ApJ, 512, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Hauschildt, P. H., Allard, F., Ferguson, J., Baron, E., & Alexander, D. R. 1999b, ApJ, 525, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I. 1988, Comp. Phys. Comm., 52, 103 [Google Scholar]
- Johnson, H. L. 1965, ApJ, 141, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Kaeufl, H.-U., Ballester, P., Biereichel, P., et al. 2004, in SPIE Conf. Ser. 5492, eds. A. F. M. Moorwood, & M. Iye, 1218 [Google Scholar]
- Kurucz, R. L. 1979, ApJS, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Landstreet, J. D., Kupka, F., Ford, H. A., et al. 2009, A&A, 503, 973 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanz, T., & Hubeny, I. 2003, ApJS, 146, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Babusiaux, C., Bailer-Jones, C., et al. 2008, in IAU Symp. 248, eds. W. J. Jin, I. Platais, & M. A. C. Perryman, 217 [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Ludwig, H.-G., Freytag, B., & Steffen, M. 1999, A&A, 346, 111 [NASA ADS] [Google Scholar]
- Mohanty, S., Basri, G., Jayawardhana, R., et al. 2004, ApJ, 609, 854 [NASA ADS] [CrossRef] [Google Scholar]
- Munari, U., Sordo, R., Castelli, F., & Zwitter, T. 2005, A&A, 442, 1127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, T., & Meiksin, A. 2004, MNRAS, 351, 1430 [NASA ADS] [CrossRef] [Google Scholar]
- Prandtl, L. 1925, Zeitschr. Angewandt. Math. Mech., 5, 136 [Google Scholar]
- Prugniel, P., & Soubiran, C. 2004 [arXiv:astro-ph/0409214] [Google Scholar]
- Ramírez, I., & Allen de Prieto, C. 2011, ApJ, 743, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A. 2005, Astron. Nachr., 326, 930 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-Merino, L. H., Chavez, M., Bertone, E., & Buzzoni, A. 2005, ApJ, 626, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Blázquez, P., Peletier, R. F., Jiménez-Vicente, J., et al. 2006, MNRAS, 371, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, W., & Missen, R. 1982, in Chemical reaction equilibrium analysis: theory and algorithms, Wiley series in chemical engineering (Wiley) [Google Scholar]
- Takeda, Y., Sato, B., & Murata, D. 2008, PASJ, 60, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Turnshek, D. A., Bohlin, R. C., Williamson, II, R. L., et al. 1990, AJ, 99, 1243 [NASA ADS] [CrossRef] [Google Scholar]
- Valdes, F., Gupta, R., Rose, J. A., Singh, H. P., & Bell, D. J. 2004, ApJS, 152, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Vernet, J., Dekker, H., D’Odorico, S., et al. 2011, A&A, 536, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vitense, E. 1953, ZAp, 32, 135 [Google Scholar]
- Voigt, H.-H. 1991, Abriss der Astronomie (Spektrum Akademischer Verlag) [Google Scholar]
- Wallace, L., Hinkle, K. H., Livingston, W. C., & Davis, S. P. 2011, ApJS, 195, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Wende, S., Reiners, A., & Ludwig, H.-G. 2009, A&A, 508, 1429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Witte, S., Helling, C., & Hauschildt, P. H. 2009, A&A, 506, 1367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Witte, S., Helling, C., Barman, T., Heidrich, N., & Hauschildt, P. H. 2011, A&A, 529, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Distribution of stellar masses for different effective temperatures Teff and surface gravities log g, colour-coded in units of solar mass from 0 M⊙ (black) to 25 M⊙ (white). |
| In the text | |
 |
Fig. 2 Distribution of the mixing length parameter α in the grid. |
| In the text | |
 |
Fig. 3 Distribution of micro-turbulence for models with solar abundances for different effective temperatures Teff and surface gravities log g (colour-coded). We had to disable the convection for the giants with Teff ≳ 5500 K and therefore no micro-turbulence was applied to these spectra. In and around this area we observe numerical instabilities causing single models to show differing results. Over-plotted are observational data points taken from Landstreet et al. (2009) (+) and Takeda et al. (2008) (×). |
| In the text | |
 |
Fig. 4 New PHOENIX ACES model spectra (full line) compared to PHOENIX AMES v2.6 spectra (dotted line); both models are calculated for a typical M 6 main sequence star (Teff = 2900 K, log g = 5.0) and smoothed to an effective resolution of R = 10 000. The ACES model spectra produce significantly deeper TiO bands than earlier PHOENIX models. |
| In the text | |
 |
Fig. 5 Comparison between PHOENIX (full line) and ATLAS9 (dotted line) model spectra for Teff = 4000 K, log g = 4.0 and solar abundances. The PHOENIX spectrum has been convolved with a Gaussian kernel with a FWHM of 20 Å for wavelengths smaller than 1 μm and with a Gaussian with a FWHM of 50 Å for wavelengths larger than 1 μm. |
| In the text | |
 |
Fig. 6 Comparison between PHOENIX (full line) and ATLAS9 (dotted line) model spectra for Teff = 8000 K, log g = 4.0 and solar abundances. The PHOENIX spectrum has been convolved with a Gaussian kernel with a FWHM of 20 Å. |
| In the text | |
 |
Fig. 7 Comparison between PHOENIX (full line) and ATLAS9 (dotted line) model spectra for the Sun in full resolution (R = 500 000) in the upper plot. Below the PHOENIX spectrum (full line) is compared to a solar spectrum observed by Wallace et al. (2011). |
| In the text | |
 |
Fig. 8 Comparison between PHOENIX (full line) and ATLAS9 (dotted line) model spectra for Vega, both convolved to 20 Å FWHM. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


