| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201117723 | |
| Published online | 18 April 2013 | |
Spectral features of Earth-like planets and their detectability at different orbital distances around F, G, and K-type stars
1 Institut für Methodik der Fernerkundung, Deutsches Zentrum für Luft- und Raumfahrt, Oberpfaffenhofen, 82234 Weßling, Germany
e-mail: pascal.hedelt@dlr.de
2 Univ. Bordeaux, LAB, UMR 5804, 33270 Floirac, France
3 CNRS, LAB, UMR 5804, 33270 Floirac, France
4 Institut für Planetenforschung, Deutsches Zentrum für Luft- und Raumfahrt, Rutherfordstr. 2, 12489 Berlin, Germany
5 Zentrum für Astronomie und Astrophysik, Technische Universität Berlin, Hardenbergstr. 36, 10623 Berlin, Germany
Received: 18 July 2011
Accepted: 22 February 2013
Context. In recent years, more and more transiting terrestrial extrasolar planets have been found. Spectroscopy already yielded the detection of molecular absorption bands in the atmospheres of Jupiter and Neptune-sized exoplanets. Detecting spectral features in the atmosphere of terrestrial planets is the next great challenge for exoplanet characterization.
Aims. We investigate the spectral appearance of Earth-like exoplanets in the habitable zone (HZ) of different main sequence (F, G, and K-type) stars at different orbital distances. We furthermore discuss for which of these scenarios biomarker absorption bands and related compounds may be detected during primary or secondary transit with near-future telescopes and instruments.
Methods. Atmospheric profiles from a 1D cloud-free atmospheric climate-photochemistry model were used to compute primary and secondary eclipse infrared spectra. The spectra were analyzed taking into account different filter bandpasses of two photometric instruments planned to be mounted to the James Webb Space Telescope (JWST). We analyzed in which filters and for which scenarios molecular absorption bands are detectable when using the space-borne JWST or the ground-based European Extremely Large Telescope (E-ELT).
Results. Absorption bands of carbon dioxide (CO2), water (H2O), methane (CH4) and ozone (O3) are clearly visible in both high-resolution spectra as well as in the filters of photometric instruments. However, only during primary eclipse absorption bands of CO2, H2O and O3 are detectable for all scenarios when using photometric instruments and an E-ELT-like telescope setup. CH4 is only detectable at the outer HZ of the K-type star since here the atmospheric modeling results in very high abundances. Since the detectable CO2 and H2O absorption bands overlap, separate bands need to be observed to prove their existence in the planetary atmosphere. In order to detect H2O in a separate band, a ratio S/N > 7 needs to be achieved for E-ELT observations, e.g. by co-adding at least 10 transit observations. Using a space-borne telescope like the JWST enables the detection of CO2 at 4.3 μm, which is not possible for ground-based observations due to the Earth’s atmospheric absorption. Hence combining observations of space-borne and ground-based telescopes might allow to detect the presence of the biomarker molecule O3 and the related compounds H2O and CO2 in a planetary atmosphere. Other absorption bands using the JWST can only be detected for much higher S/Ns, which is not achievable by just co-adding transit observations since this would be far beyond the planned mission time of JWST.
Key words: planets and satellites: atmospheres / planets and satellites: composition / planets and satellites: detection / radiative transfer / techniques: imaging spectroscopy
© ESO, 2013
1. Introduction
Spectroscopic or photometric techniques enable the detection and even the investigation of the atmosphere of a transiting extrasolar planet (exoplanet). Increasing instrumental sensitivities allow for the detection of low-mass planets. Furthermore, long-term planet search programs are able to detect planets that are farther away from their host stars. Potentially rocky planets with masses lower than Neptune, which orbit within the habitable zone (HZ) of their central stars, are of main interest. Several potentially terrestrial planets orbiting in or close to the HZ are already known (Kepler-22 b: Borucki et al. 2012; HD 85512 b: Pepe et al. 2011; Gliese 581 c and d: Udry et al. 2007; Mayor et al. 2009; Gliese667C c: Bonfils et al. 2012; Anglada-Escudé et al. 2012; HD 40307 g: Tuomi et al. 2013). The search for more of these terrestrial planets and their characterization will eventually address the question, whether life on Earth is unique.
Analyzing the wavelength-dependent extinction of the stellar light passing through the planetary atmosphere during the primary transit allows for the chemical characterization of the planetary atmosphere. For hot-Jupiter planets, the detection of infrared molecular absorption bands of water (H2O) and methane (CH4), as well as of atomic lines in the visible using this technique have already been announced (see e.g. Charbonneau et al. 2002; Vidal-Madjar et al. 2003, 2004; Knutson 2007; Tinetti et al. 2007; Swain et al. 2008; Snellen et al. 2010a).
Up to now only two super-Earth planets (i.e. planets having masses below 10 MEarth) have been investigated in transmission (GJ 1214 b, Charbonneau et al. 2009 and CoRoT-7 b, Léger et al. 2009). Bean et al. (2010) obtained transmission spectra of GJ 1214 b (6.55 MEarth), which were lacking any spectral features. The nature of its atmosphere is currently under discussion (see e.g. Miller-Ricci Kempton et al. 2012; Bean et al. 2011; Croll et al. 2011; Désert et al. 2011; Crossfield et al. 2011; de Mooij et al. 2012; Berta et al. 2012). For CoRoT-7 b (6.9 MEarth, Hatzes et al. 2010), Guenther et al. (2011) were able to determine upper limits of the extension of its exosphere by observing the strength of different emission lines using high-resolution transmission spectroscopy.
From secondary eclipse observations, i.e. when the planet passes behind its star, both emission and reflection spectra can be obtained. Characteristics of the thermal emission of the planet can be investigated in the infrared, since here the planet-star flux ratio is orders of magnitudes higher than at optical wavelengths. The emergent spectrum holds information about the temperature structure of the atmosphere as well as the atmospheric components. The thermal emission of several hot Jupiter and Neptune-sized exoplanets has already been observed (see e.g. Snellen et al. 2010b; Richardson et al. 2007; Grillmair et al. 2007; Deming et al. 2006; Alonso et al. 2009b,a; Sing & López-Morales 2009; Demory et al. 2012).
In the optical regime, the stellar light that is reflected from the planet before it moves behind its host star may be observed and thus the planetary albedo could be determined (see e.g. Seager 2008). With reflection spectra the existence of clouds can be inferred and constraints on the energy budget can be made (see e.g. Rowe et al. 2008; Cowan & Agol 2011).
To determine whether a terrestrial planet is habitable or even inhabited, the detection of biomarker molecules plays a key role. These molecules are closely connected to or required for the existence of life as we know it. Biomarker molecules include nitrous oxide (N2O) and ozone (O3). N2O on Earth has an almost exclusively biogenic origin from nitrifying and denitrifying bacteria (Oonk & Kroeze 1998). O3 indicates the presence of oxygen in the atmosphere, which on Earth is almost exclusively produced by photosynthesis of plants and cyanobacteria. Selsis et al. (2002) and Segura et al. (2007) have discussed a possible abiotic formation of O3 in CO2 dominated atmospheres, whereas Domagal-Goldman & Meadows (2010) discussed a possible abiotic O3 buildup for Earth-like planets orbiting M-dwarfs.
Other related compounds connected to habitability and life are H2O, CH4 and carbon dioxide (CO2). Liquid H2O is necessary for life as we know it on Earth. It provides the majority of the greenhouse effect on modern Earth, warming the surface above the freezing point of water. CH4 has both biotic and abiotic sources and is also a strong greenhouse gas. CO2 is important for habitability mostly because of its greenhouse effect (especially toward the outer HZ) and the carbonate-silicate cycle (e.g. Walker et al. 1981).
Earth is so far the only known example of a habitable and inhabited planet, that can be used to investigate the parameter space of habitable conditions. It is straightforward (at least conceptually) to build a spectrum from a given arbitrary atmospheric composition. The inverse problem, however, i.e. to infer the characteristics of a planet from a spectrum, is much more difficult due to its ill-posed nature. It is nevertheless of paramount importance to understand what type of planet lies behind a given observed spectrum.
A huge number of parameters affect the atmospheric and spectral appearance of a given Earth-like planet. In this paper we investigate the influence of the central star type and the orbital distance to the central star within the HZ. We consider only small variations away from Earth, where our model assumptions (Earth development, Earth biomass, etc.) are more likely to be valid. We furthermore discuss for which conditions (in terms of orbital distance in the HZ and central star) molecular absorption bands can be detected with near-future telescope facilities.
Previous major modeling efforts which calculated synthetic spectra of hypothetical terrestrial extrasolar planets were performed, e.g. by Des Marais et al. (2002), Segura et al. (2003), Segura et al. (2005), Tinetti (2006), Ehrenreich et al. (2006), Kaltenegger et al. (2007), Kaltenegger & Traub (2009), and Rauer et al. (2011) to examine the influence of, e.g. different host stars, atmospheric abundances, and atmospheric evolution on the spectral appearance. Arnold et al. (2002), Arnold (2008), Ehrenreich et al. (2012), Pallé et al. (2009), Vidal-Madjar et al. (2010), Pallé et al. (2011), and Hedelt et al. (2011) analyzed observations of the terrestrial planets of the Solar System (i.e. Venus, Mars, and Earth) as proxies for exoplanets.
Segura et al. (2003) presented emission spectra for an Earth-like planet around F, G and K-type stars and discussed the spectral response due to varying O2 concentration. In this work, we vary the orbital distance to study the impact on emission and transmission spectra. In addition to calculating the spectral response, we furthermore discuss the detectability of the spectral features. For this purpose, we assume two telescope configurations and different instrument specifications. Improving upon the approach of Kaltenegger & Traub (2009) and Rauer et al. (2011), we present background-limited signal-to-noise ratios (S/Ns) instead of photon-limited S/Ns for a ground-based and a space-borne telescope setup.
Grenfell et al. (2007b, hereafter G07) investigated the effect on the atmospheric chemistry for slightly different scenarios than the ones considered in this work. We use an updated version of their atmospheric model and a slightly different position for the center HZ runs. In this paper we investigate if the chemical responses found lead to detectable spectral signatures.
Section 2 summarizes the atmospheric model, the radiative transfer model as well as the S/N model. Furthermore in this section the telescope and instrument parameters are shown as well as the considered model scenarios. The atmospheric and spectral response are discussed in Sect. 3, followed by a discussion about the detectability of molecular absorption lines. Section 4 discusses the results, before Sect. 5 presents our conclusions.
2. Methods and scenarios
2.1. Models
2.1.1. Atmospheric model
For this paper, we use the one-dimensional, cloud-free coupled climate and photochemical model of Rauer et al. (2011), which calculates global, diurnally-averaged atmospheric temperature, pressure and concentration profiles. It is based on the model used by G07, including improvements in the coupling of climate and photochemical modules as well as code optimization. A detailed model description can be found in Rauer et al. (2011), as well as in Segura et al. (2003), and Grenfell et al. (2007a). The code optimization includes an improved calculation of the climate module grid and a different convergence criterion (see Rauer et al. 2011, for details).
Since the model does not incorporate clouds, the model surface albedo (i.e. the reflectivity of the surface) is adjusted until the temperature profile of modern Earth is reproduced when simulating modern-day Earth conditions. In G07, a surface albedo of 0.218 was assumed, whereas for the profiles used in this paper the required value is 0.207 due to code optimization. Although the temperature profile is successfully reproduced, radiative fluxes (e.g. spectral albedos) calculated in the model do not reproduce modern Earth values since clouds are neglected, as stated above. We note that the influence of clouds on spectral albedos has been investigated by e.g. Robinson et al. (2011), and Kitzmann et al. (2011).
2.1.2. Radiative transfer model
The spherical line-by-line radiative transfer model MIRART-SQuIRRL (Schreier & Schimpf 2001; Schreier & Böttger 2003) has been used to calculate high-resolution synthetic emission and transmission spectra. It was designed for the analysis of terrestrial atmospheric measurements and has been verified by intercomparisons with other radiative transfer codes (see e.g. von Clarmann et al. 2003; and Melsheimer et al. 2005). MIRART-SQuIRRL uses HITRAN2008 (Rothman et al. 2009) for the calculation of absorption cross-sections and the temperature, pressure, water vapor and concentration profiles of 15 species from the atmospheric model, including H2O, CO2, CH4, O3, CO, and N2O. Furthermore continuum absorption corrections for H2O and CO2 are performed.
Emission spectra are calculated from the planetary surface up to the top of the atmosphere (located at 6.6 × 10-5 bar). To obtain a disk-integrated emission spectrum of the planet, we integrate a set of pencil beams with zenith angles from 0° (zenith) to 90° (horizon) in steps of 1°. Note that this approach is different to previous studies by, e.g. Rauer et al. (2011) or Segura et al. (2003), where only one single spectrum has been calculated at a viewing zenith angle of 38° and then multiplied by π in order to obtain a disk-integrated spectrum. Fully disk-integrated spectra take the atmospheric limb darkening into account. The difference between both approaches is mostly smaller than 10%, hence does not greatly influence the discussion presented hereafter. We furthermore take reflected stellar light that would be measured during secondary eclipse observations into account. The reflected component is in our scenarios important up to 4 μm. We added the contribution of reflected stellar light to the secondary eclipse spectrum by multiplying the stellar spectra with the spectral albedo of the atmosphere, which is calculated by the climate part of our atmospheric model. From these spectra brightness temperature spectra are calculated by identifying spectral fluxes with a blackbody temperature, assuming that the distance and radius of the planets are precisely known. This temperature is related to the physical temperatures of the contributing radiating atmospheric levels. We note that brightness temperature spectra calculated from secondary eclipse spectra yield temperatures which are in the near-infrared much warmer than the planetary temperatures since the spectra additionally include the reflected stellar component. We furthermore note that it might be possible to disentangle the planetary emission spectrum from the reflected component if the stellar spectrum is known. However, this will be challenging due to stellar variability and the low S/Ns found in the near-IR (see Sect. 3.4).
Transmission spectra (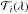 ) for 62 adjacent tangential beams through the atmosphere are calculated. The tangential heights hi correspond to the layer altitudes of the model atmosphere. The diameter of each beam is given by Δhi = hmax/nlayers, with hmax the altitude of the model lid (dependent on the scenario considered) and nlayers = 64, the number of layers in the photochemical model. The overall transmission
) for 62 adjacent tangential beams through the atmosphere are calculated. The tangential heights hi correspond to the layer altitudes of the model atmosphere. The diameter of each beam is given by Δhi = hmax/nlayers, with hmax the altitude of the model lid (dependent on the scenario considered) and nlayers = 64, the number of layers in the photochemical model. The overall transmission 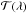 is simply the arithmetic mean of all
is simply the arithmetic mean of all 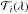 , since beams cross the atmosphere in equidistant grid points. The transit depth dTransit(λ) for all scenarios considered is calculated by:
, since beams cross the atmosphere in equidistant grid points. The transit depth dTransit(λ) for all scenarios considered is calculated by: 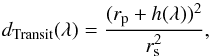 (1)with rp the planetary radius and rs the stellar radius. h(λ) is the effective height of the atmosphere at a given wavelength λ:
(1)with rp the planetary radius and rs the stellar radius. h(λ) is the effective height of the atmosphere at a given wavelength λ: 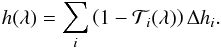 (2)The effective height of the atmosphere is the additional obscuring radius provided by the atmosphere that effectively increases the observed size of the planet during the primary transit.
(2)The effective height of the atmosphere is the additional obscuring radius provided by the atmosphere that effectively increases the observed size of the planet during the primary transit.
We note that a possible night-side pollution of a transit depth measurement, that was found by Kipping & Tinetti (2010) to be significant for hot-Jupiter planets, can be neglected in our scenarios. The contrast of the planetary to the stellar emission is ~10-5, whereas for hot-Jupiters it is ~10-3 (Kipping & Tinetti 2010). The night-side pollution is an effect arising from the normalization of the transit depth (measured from the different fluxes before and during the transit) to the out-of-transit flux.
2.1.3. S/N model
We will discuss the detectability of spectral features in Sect. 3.4 assuming the planets are observed by a ground-based or a space-borne telescope. For this we calculate background-limited S/Ns using the code of von Paris et al. (2011), which is based on the code of Rauer et al. (2011). Note that this reproduces the values found by Kaltenegger & Traub (2009), when using similar assumptions regarding spectral resolution and atmospheric profiles. We improved the code of von Paris et al. (2011) to calculate background-limited S/Ns for ground-based measurements by taking the thermal background as well as the transmission of Earth’s atmosphere into account.
To take the Earth’s atmospheric emission and transmission for ground-based measurements into account, we use spectra1 provided by ESO (Liske 2010) for the European Extremely Large Telescope (E-ELT) exposure time calculator (Liske 2008). The spectra are provided for different telescope sites and have been calculated using a tropical atmospheric profile and the HITRAN2004 database (Rothman et al. 2005). The water vapor profile has been adjusted to fit the mean precipitable water column value of the telescope site. For the ground-based telescope configuration we use the files for the “Paranal site” with an airmass of 1.0 (zenith viewing), a site altitude of 2600 m (743 mbar), an ambient temperature of 285 K, and a precipitable water column value of 2.3 mm. The E-ELT will be located at Cerro Armazones at an altitude of 3064 km. However, Earth atmospheric spectra and site parameters are not yet available. Calculated S/Ns are thus likely to be underestimated when using the Paranal site parameters.
For the calculation of S/Ns for ground-based observations, the simulated planetary spectrum is then multiplied with the Earth’s transmission spectrum. The atmospheric noise σA from the thermal emission of the Earth’s atmosphere is treated in the same way as the zodiacal noise (cf. Eq. (A.7) in von Paris et al. 2011) using the Earth’s emission spectrum as input. The telescope emission is modeled as a grey body (i.e. a black body multiplied by a constant emissivity).
We furthermore updated the code of von Paris et al. (2011) in order to calculate S/Ns for photometric instruments, which provide a different detector response. Instead of a refractive element for spectrometric instruments, photometric instruments are using transmissive windows to filter the incoming radiation in certain wavelength bandpasses. Hence the pixel area occupied on the detector is different than that for a dispersed spectrum. The number of pixels occupied on the detector npx(λ) is calculated from the angular diameter of the Airy disk θ and the pixel scale ps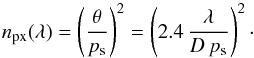 (3)
(3)
2.2. Telescope and instrument configurations
In this paper we investigate the spectral response of several absorption bands measured by high-resolution spectroscopic instruments, as well as by photometric instruments. Photometric instruments provide the ability to obtain high S/Ns by integrating the light over a fixed spectral bandpass. We are using the filter bandpasses of the Mid-InfraRed Instrument (MIRI, Wright et al. 2004) and the Near-InfraRed Camera (NIRCam), that are instruments planned for the space-borne James Webb Space Telescope (JWST). MIRI provides 9 filters in the range from 5 to 27.5 μm, whereas NIRCam provides filters in the range from 0.6 to 5.0 μm. Table 1 shows the wavelength bandpasses of all filters and their respective names that are used within this work. Note that we are not using all available filters, but only a selection of filters that are covering strong absorption bands (indicated in the table) or atmospheric windows (indicated as (R) in the table).
Operating wavelengths of photometric instrument filters used in this work.
We will furthermore discuss the detectability of molecular absorption bands, when using the JWST as an example of a space-borne telescope and the E-ELT of a ground-based telescope. JWST is scheduled for launch in 2018 and will provide a telescope aperture of 6.5 m diameter. The E-ELT will be located in the Atacama desert in Chile, on Mountain Cerro Armazones (3064 m altitude) and is planned to be operational by 2020. The E-ELT will have a primary mirror of 39.3 m diameter and a central obstruction of 11.76 m diameter. Ground-based telescopes observing in the infrared are restricted to certain atmospheric windows, where the Earth’s atmosphere has a high transmissivity.
The E-ELT will be equipped with the Exo-Planet Imaging Camera and Spectrograph (EPICS) which will be designed for the near-IR (0.6–1.65 μm) and with the Mid-infrared E-ELT Imager and Spectrograph (METIS) which will perform spectro-photometry in the wavelength range from 3 to 14 μm. Since the instrumentation is still in the planning phase and the filters are not yet defined, we use the wavelength bandpasses of the NIRCam filters for EPICS and that of MIRI for METIS, in order to allow for a comparison of JWST and E-ELT capabilities. The pixel scale ps and dark current dc for both instruments that are needed for the calculation of background-limited S/Ns are however already selected and will be used in our calculations. Table 2 lists the telescope and instrumental parameters that are used for the S/N calculations.
Telescope and instrument parameters used for S/N calculations.
2.3. Model scenarios
We model the atmosphere of an Earth-sized planet with a planetary radius of rp = 1 R⊕ and a mass of m = 1 M⊕. We employed for each stellar type the same initial Earth-like composition as G07 (1 bar surface pressure and, e.g. 21% O2, 355 ppm CO2, 1% Ar and N2 as filling gas) as well as Earth’s biomass surface emissions (prescribed as in Rauer et al. 2011). The sample stars used for the calculation of atmospheric profiles are the Sun as a well-known G2V star, σ Bootis as a representative of an F2V star and ϵ Eridani for the K2V star. Note that throughout the paper the different central star types used are referred to as G-type star, F-type star and K-type star, respectively.
The solar spectrum is constructed from high-resolution observations (Gueymard 2004) and the σ Bootis spectrum is taken from Segura et al. (2003). Compared to G07 and Segura et al. (2003), we use a different stellar spectrum for ϵ Eridani (see Kitzmann et al. 2010). We furthermore use a different stellar distance for the F-type reference star σ Bootis. Using the Hipparcos parallax of 64.66 mas for σ Bootis, we obtain a distance of 15.5 pc, which is confirmed by Habing et al. (2001). This is substantially larger than the 12 pc used by G07 and Segura et al. (2003).
The planets are positioned at orbital distances to their central star, such that for the “inner runs” (the model runs with the planetary orbital distance closest to their star) the model surface temperature reaches ~303 K (30 °C). The outer edge was defined with a surface temperature of ~273 K (0 °C). These limits corresponds to a definition of the HZ given by Dole (1964) for complex life. Note that modern day HZ definitions allow a much wider range, but it is challenging for this model setup to calculate the full range, since the photochemistry and climate calculations can only be carried out within a narrow temperature range. Classical studies of the runaway greenhouse effect at the inner edge of the HZ (e.g. Kasting 1988; Kasting et al. 1993), calculate a troposphere which is fully saturated with water vapor. These hot and humid conditions are difficult to study with our coupled climate and chemistry model. For the more-limited range of temperatures that we consider, we assume an Earth-like relative humidity profile from Manabe & Wetherald (1967) (see also G07). For the outer HZ the formation of clouds and their climatic impact as well as the carbonate-silicate cycle would become very important. This cycle controls the CO2 content of the atmosphere on the Earth such that it increases with decreasing surface temperature, thus stabilizing the climate and extending the outer HZ. This means that our outer runs are unlikely to represent fully self-consistent scenarios, since we keep the CO2 concentration constant over the entire range of orbital distances considered. However, such consistent coupling between atmospheric and geochemical processes is difficult and beyond the scope of this paper.
Scenarios considered in this paper.
For the central runs the modeled planets are positioned at an orbital distance from their central star where the stellar energy input equals that of the present-day mean total solar irradiance (FToA = 1366 W m-2), as in Kitzmann et al. (2010), and Rauer et al. (2011). This approach was chosen so that habitable surface temperatures were not enforced and which allowed the temperature to adjust in a consistent way to the different spectral energy distributions provided by the central stars. In this way the effects arising from the different spectral energy distributions are separated from variations of the total incoming flux. Note that in previous studies (e.g. Segura et al. 2003, 2005, and G07), the center of the HZ was defined such that the calculated surface temperature reached 288 K. However, the qualitative chemical responses on varying the orbital distance in this work are mostly similar to G07, although the absolute values change.
Table 3 lists all scenarios considered with estimated transit times ttransit and the top-of-atmosphere (ToA) wavelength-integrated fluxes FToA. Stellar radii needed for the calculation of transit depths are also given. The transit times are given for one single transit either during primary or secondary eclipse. Compared to G07, we need to apply different orbital positions for the planets orbiting F and K-type stars. For the F-type star this is related to the change in the normalization of the observed stellar spectrum, whereas for the K-type star the stellar input spectrum was differently constructed than that in G07 (see Kitzmann et al. 2011).
3. Results
In this section we will first shortly present the atmospheric response on varying the orbital distance. We will show the spectral response in high-resolution spectra before discussing what can be measured by the different filters provided by the instruments discussed in this paper, and if this would be detectable.
 |
Fig. 1 Pressure–temperature profiles of the Earth-like planets around different central stars (K-type star: dashed, G-type star: solid, F-type star: dotted) at different orbital distances (inner run: red, center run: black, outer run: blue). |
3.1. Atmospheric response
On increasing the orbital distance, the variation of the temperature profile is much smaller than for changing the central star type (see Fig. 1). Note that we find surface temperatures of about 300 K at an orbital distance of 0.94 AU for a planet orbiting a Sun-like star, whereas other authors find temperatures above ~350 K (see e.g. Kasting et al. 1993; Selsis et al. 2007). Our atmospheric model uses a fixed relative humidity profile of Manabe & Wetherald (1967) (see G07). Earlier calculations regarding the inner boundary of the HZ (Kasting 1988; Kasting et al. 1993) assumed instead a saturated troposphere, i.e. a relative humidity of unity. Using an isoprofile would result in higher temperatures by about 30 K, even for present solar insolation. We neglect the feedback between surface temperature and relative humidity, hence we are likely underestimating surface temperatures and water abundances for the inner runs.
 |
Fig. 2 Pressure–concentration profiles of five prominent spectral species of the Earth-like planets around different central stars (upper row: F-type star, center row: G-type star, lower row: K-type star). Columns from left to right show profiles of O3, CH4, N2O, H2O and HNO3. The orbital distance is indicated by colors as in Fig. 1. Note that CO2 is set to an isoprofile of 355 ppm and hence not shown. |
The orbital distance variation has the strongest effect on H2O and CH4. Figures 2 and 3 show the corresponding profiles of five prominent spectral species, whereas Table 4 shows the change in the total column amounts when increasing the orbital distance from the inner to the outer boundary. In comparison to G07 we find a somewhat stronger increase for O3 and CH4 and a smaller increase for N2O. H2O is controlled by the tropospheric water content, which is identical by construction. Nevertheless, the conclusions presented in G07 do not change when using the updated model.
3.2. Spectral response
Transmission spectroscopy during primary eclipse probes the molecular composition of the atmosphere. Furthermore, the height of the atmosphere which is related to the pressure and atmospheric structure can be determined, since the atmosphere becomes optically thick at different altitudes for different wavelengths.
Observation of the secondary eclipse provides contrast spectra of the planetary and stellar emission. In the near infrared up to 4 μm the reflection of the stellar spectrum dominates the secondary eclipse spectrum, whereas at higher wavelengths the planetary emission dominates. A brightness temperature spectrum computed from secondary eclipse radiance spectra shows the range of temperatures that can be found in a given atmosphere. We however note that to obtain a brightness temperature spectrum from a measured radiance spectrum, the planetary radius and the distance of the planet to the observer need to be well-known, which we assume to be the case here. The brightness temperature spectrum yields temperatures high above the planetary temperatures in the near-infrared due to the reflected stellar light (see Fig. 4, right). Thus the stellar and planetary fractions may be separated. We note that the spectral albedo is dominated by absorption rather than scattering, since Rayleigh scattering is negligible in the wavelength range from 2 to 4 μm and the main species responsible for Rayleigh scattering (N2, O2, CO2) are constant for all scenarios considered. With increasing orbital distance, the spectral albedo increases due to less H2O absorption (except for the outer K star run, where the CH4 absorption increases strongly). This increase in spectral albedo for the F and G star runs is approximately of the same amount as the stellar irradiation decreases (see Table 3). Thus the reflected component changes only slightly with increasing orbital distance. Note that Fig. 4 shows the brightness temperature difference to the model surface temperature. Since the surface temperature decreases by 30 K (by construction) and the reflected component changes only slightly, the reflected component seems to increase with increasing orbital distance.
 |
Fig. 3 Same as Fig. 2, but only the profiles of the planets at the center of the HZ are shown to visualize the dependency on central star type. The central star type used is color-coded (red: F-type star, black: G-type star and blue: K-type star). |
Relative change of total column amount when increasing the orbital distances from the inner to the outer boundary for different molecules and central star types.
 |
Fig. 4 Transit depth during primary eclipse (left) and brightness temperature difference with respect to the calculated surface temperature spectrum during secondary eclipse (right) for the scenarios considered. The spectral resolution is R = 100. Each center run with R = 3000 is shown in grey. The geometric transit depth (see Sect. 3.3) is indicated by a horizontal line for transmission spectra. The brightness temperature spectra include the reflected stellar component in the near-IR. Furthermore the bandpass of the filters considered in this work are shown. |
Figure 4 shows for two different spectral resolutions the transit depth for primary eclipse transmission spectra and the brightness temperature difference to the model surface temperature for the secondary eclipse. Both transit depth and brightness temperature spectra clearly show strong absorption bands of several molecules, as indicated in the figure. Note however that two bands, namely O3 (at 4.8 μm) and HNO3 (at 11.3 μm) are only evident in transmission spectra due to the longer path through the atmosphere for this transit geometry.
We note that in emission spectra CO2 features emission peaks at 4.3 and 15 μm for the G and F-star cases (Fig. 4, right) due to the atmospheric temperature inversion. For a spectral resolution of R = 3000 the brightness temperatures even exceed the model surface temperatures for the planets orbiting the F-type star due to the hot stratosphere (see Fig. 1). The spectral response seen for CO2 bands is exclusively related to the temperature response since the atmospheric CO2 content remains constant by construction.
The strongest spectral response on increasing the orbital distance is visible for H2O, since it not only features strong absorption bands at 2.7, 6.3 and above 17 μm, but also a strong continuum absorption over the entire wavelength range considered. On increasing the orbital distance the H2O absorption clearly decreases, which is visible in both emission and transmission spectra.
The CH4 bands at 3.3 and 7.7 μm show a negligible spectral response on increasing the orbital distance (i.e. the transit depth and brightness temperature in the band remain constant), although the spectrum in the vicinity of the bands changes drastically due to the H2O response. This is because the CH4 absorption increases with increasing orbital distance, whereas the H2O absorption decreases. For the planet around the K-type star the increase in CH4 absorption even overcomes the decrease in H2O absorption and both bands absorb slightly stronger for the outer runs than for the inner runs.
The response of O3 (at 4.8 and 9.6 μm) and HNO3 (at 11.3 μm) is not visible due to the strong H2O response. However, a strong response was not expected from the chemical analysis. N2O only features thin absorption bands at 4.5 and 7.8 μm, which are mainly masked by other absorption bands. An absorption band of N2O is visible in the vicinity of the 4.3 μm CO2 band in emission spectra, e.g. for the planets around the G and F-type star, but only in the case of a strong atmospheric temperature inversion, when the 4.3 μm CO2 band is seen in emission.
Atmospheric windows which provide a high atmospheric transmissivity provide in principle information on surface conditions. For Earth-like planets the atmosphere is transparent down to the surface at around 2.2, 3.7 and 11 μm for high zenith angles, i.e. only for secondary eclipse observations. However, the two near-IR windows cannot be used due to the reflected stellar light (see above). The brightness temperature in the 11 μm window is equal to the surface temperature for all outer runs, whereas for the inner runs, the brightness temperature found is about 9 K lower than the model surface temperature. This is due to the increase in optical thickness by higher water vapor concentrations. In primary eclipse, the atmosphere becomes opaque above about 20 km at these wavelengths.
3.3. Filter response
Photometric instruments provide high S/Ns, but at the cost of spectral information. To detect an absorption band, measurements in the filter of interest should be compared to measurements in so-called reference filters located in spectral regions where the atmosphere is assumed to be almost transparent. The measurable quantity is then the difference in the transit depth that is measured in both filters for primary eclipse transmission observations or the difference in the measured brightness temperature for secondary eclipse observations. Table 1 summarizes the filters used within this work. The position of the filters considered in this paper are shown in Fig. 4.
As reference filters we will use the NIRCam F356W (3.56 μm) and MIRI IM04 (11.3 μm) filters. The F356W filter covers the atmospheric window around 3.7 μm, but also the 3.3 μm CH4 absorption band. The IM04 filter covers the 11 μm atmospheric window, but also the H2O continuum absorption and in the case of transmission spectra an HNO3 absorption band at 11.3 μm.
We note that using a modified reference filter (e.g. a smaller F356W filter avoiding the CH4 absorption) is beyond the scope of this paper, since we only concentrate on the filters planned for JWST.
Geometric transit depth dGeo = (rP/rS)2 for planets orbiting different central stars.
3.3.1. Primary eclipse
First, we compare the transit depth d in the reference filters dFilter with the geometric transit depth dGeo given in Table 5, in order to estimate the systematic error due to absorption bands covered by the reference filters. The geometric transit depth is the squared ratio of the planetary to the stellar radius. For the planetary radius rP we use the Earth’s radius and the stellar radii rS from Table 3. The upper left plot in Fig. 5 shows the difference of transit depth measured in the reference filters to the geometric transit depth.
 |
Fig. 5 Transit depth differences for different filter combinations for primary eclipse transmission spectra. dFilter and dReference are the transit depths measured by the photometric filter and the reference filter, respectively, whereas dgeo is the geometric transit depth (i.e. the ratio of planetary and stellar radius squared). |
For the planets around the F and G-type star, the transit depth difference dF356W − dgeo (triangles) remains about the same over the entire HZ, since the increase in the CH4 abundance compensates for the decreasing scale height when increasing the orbital distance. Note that since the filter does not correctly track the decreasing atmospheric scale height with increasing orbital distance, this will lead to systematic errors when estimating the abundance of any atmospheric constituents when using this reference filter.
The CH4 absorption which is covered by the filter is strongest only for the outer run of the planet around the K-type star, and thus the F356W (3.56 μm) filter has to be used with caution as a reference and is hence not appropriate, especially when aiming at the detection of CH4. A reference filter spanning from 3.5 to about 4 μm would no longer cover the CH4 absorption band and would thus serve as a better reference filter in the near-IR.
The transit depth difference dIM04 − dGeo (diamonds) decreases with increasing orbital distance due to both the decreasing atmospheric scale height and the decrease of the H2O continuum absorption covered by the filter. The abundance of HNO3 did not change greatly over the HZ and has thus no influence on the IM04 (11.3 μm) filter.
H2O absorption bands are covered by the F277W (2.77 μm), IM01 (5.6 μm), IM02 (7.7 μm) and IM07 (18.0 μm) filters (see Table 1). We only use the F356W (3.56 μm) filter as a reference since the IM04 (11.3 μm) reference filter covers the H2O continuum absorption. The spectral response would thus not be visible. The strongest difference can be obtained from the F277W – F356W and IM01 – F356W filter combinations (diamonds and triangles in Fig. 5, upper right plot). This is related to the decrease in H2O absorption in the F277W and IM01 filter while the CH4 absorption increases in the F356W reference filter, when increasing the orbital distance.
Note that the transit depth difference in the F277W – F356W and IM01 – F356W filters becomes negative for the outer runs of the planets around the K-type star. In this case the CH4 absorption in the F356W filter is even stronger than the H2O/CO2 absorption in the F277W filter and the H2O absorption in the IM01 filter.
Note furthermore that the F277W (2.77 μm) filter covers both a CO2 and the H2O absorption band. To determine whether both molecules or only one them is present in the atmosphere, H2O and CO2 need to be detected independently in separate absorption bands, like e.g. in IM01 (at 5.6 μm) for H2O and F430M or IM06 (at 4.3 and 15 μm, respectively) for CO2 see below.
The signal difference from the IM02 – F356W filter combination (boxes) is slightly lower than for the afore-mentioned F277W – F356W and IM01 – F356W combinations since the IM02 (7.7 μm) filter also covers an CH4 absorption band at 7.7 μm, which is increasing with increasing orbital distance. However, this filter combination would help in order to minimize the effect of the CH4 absorption covered by the reference filter. The IM07 – F356W filter combination (at 18.0 and 3.56 μm, respectively) features the lowest signal and is thus not shown here.
O3 absorption bands are covered by the F480M (4.8 μm) and IM03 (10.0 μm) filters. The strongest signal can be inferred from the IM03 – IM04 filter combination, showing a slightly increasing O3 absorption with increasing orbital distance (see Fig. 5, lower right plot). This is almost exclusively an effect of the decreasing H2O continuum absorption covered by the IM04 (11.3 μm) reference filter when increasing the orbital distance, since the atmospheric O3 content remains nearly constant (see Table 4). When using the F356W (3.56 μm) filter as a reference also the influence of the CH4 absorption in this reference filter is clearly visible. Due the strong CH4 absorption in the F356W filter, the transit differences F480M – F356W and IM03 – F356W become negative for the outer runs of the K-type star.
CH4 absorption bands are covered by the F356W filter (which is also a reference filter) or by the IM02 (7.7 μm) filter, which also covers part of the strong H2O absorption band at 6.3 μm. Thus in principle only the IM04 reference filter can be used. Both filter combinations (F356W – IM04 and IM02-IM04) clearly increase with increasing orbital distance (see Fig. 5, lower left plot) due to the increasing CH4 absorption in IM02. However, as stated above also the F277W – F356W and IM01 – F356W filter combinations (which were used for the detection of H2O) and the F480M – F356W and IM03 – F356W filter combinations (for the detection of O3) can be used for the detection of CH4 for certain scenarios. For the outer runs of the planets orbiting a K-type star the absorption of CH4 in the F356W filter exceeds the absorption of H2O/CO2 in the F277W (2.7 μm) filter, the absorption of O3 in the F480M (4.8 μm) and IM03 (10.0 μm) filters and the absorption of H2O in the IM01 (5.6 μm) filter. The differences become negative (see diamonds and triangles in Fig. 5, upper right plot and lower right plot).
CO2 absorption bands are covered by the F277W (2.77 μm), F430M (4.3 μm) and IM06 (15.0 μm) filters. Since the CO2 content in our model atmospheres remains constant, each filter combination would only show the response of the reference filter, which are also covering CH4 and H2O absorption bands. Nevertheless the transit depth differences would be the strongest compared to all other filter combinations, reaching a transit depth difference of up to (dF430M − dIM04)/dgeo = 0.013 (not shown).
3.3.2. Secondary eclipse
From secondary eclipse observations, the brightness temperature measured in atmospheric windows provides estimates of the temperature in the lower troposphere and potentially the surface, where the emission originates for Earth-like atmospheres. The atmospheric water vapor content controls how deep the troposphere can be probed in the atmospheric window. For example for the inner runs the broadband water continuum absorption only allows the probing of the lower troposphere and not the surface. Reflected stellar light is dominant up to 4 μm and thus influences measurements in the near-IR filters F277W and F356W (at 2.77 and 3.56 μm, respectively). The near-IR reference filter F356W is furthermore influenced by atmospheric CH4 absorption at 3.3 μm. This is clearly visible in Fig. 6 (upper left plot), which shows the brightness temperature difference TSurf − TF356W, with Tsurf being the model surface temperature and TF356W the brightness temperature measured in the F356W filter. Note that the brightness temperature difference TSurf − TF356W (triangles) increases with orbital distance since the reflected stellar light changes only slightly, whereas the surface temperature decreases by 30 K (by construction, see Table 3).
 |
Fig. 6 Brightness temperature difference for different filter combinations for secondary eclipse emission spectra. The upper left panel shows the difference of the brightness temperature measured in the F356 and IM04 filter with respect to the model surface temperature, whereas the other panels show the difference of selected filters with respect to the reference filter IM04. Note the different vertical scales in the plots. |
If it would be possible to measure only the planetary emission, a temperature difference of about 7 K to the model surface temperature would be found. Since also the reflected stellar light needs to be taken into account, which increases the measured signal in the near-IR, the measured temperature difference is only about 1 K for the inner runs. For the outer runs the CH4 absorption is strongest, especially for the planets around the K-type star, thus dropping the brightness temperature difference slightly. Thus, the F356W filter can not be used, neither as a reference filter nor as a filter in order to estimate surface temperatures during secondary eclipse. Therefore, we will only use the IM04 (11.3 μm) filter as a reference filter in the following analysis.
The IM04 (11.3 μm) reference filter is not influenced by the reflected stellar signal. It can be clearly seen that the difference TSurf − TIM04 decreases with increasing orbital distance (diamonds). For all inner runs, H2O provides a strong continuum absorption over the entire IM04 filter, which influences the surface temperature determination. Inferred temperatures are thus lower than the model surface temperature by up to 9 K. For the outer runs, which are less influenced by H2O, the IM04 filter provides a surface temperature difference of below 2 K.
The strongest signal for the detection of H2O absorption bands can be found when comparing the IM01 (5.6 μm) filter with the IM04 (11.3 μm) reference filter (not shown). A brightness temperature difference of up to 40 K for all inner runs can be found. This difference decreases with increasing orbital distance. This is because the surface temperature (visible in the reference filter) decreases stronger than the temperature in the atmospheric layers contributing to the signal measured in the measurement filter IM01, when increasing the orbital distance.
CH4 features absorption bands at 3.3 and 7.7 μm. Due to the reflected stellar light, we omit the 3.3 μm band here. The 7.7 μm band (covered by the IM02 filter) is in most cases dominated by the band wings of the broad 6.3 μm H2O band, which is clearly visible in the brightness temperature difference TIM04 − TIM02 (see Fig. 6, upper right plot). The temperature difference remains nearly constant for the planets around G and F-type stars, since the increase in CH4 absorption compensates for the decreasing H2O continuum absorption in both filters. For the planets around the K-type star however, the temperature difference is increasing due to the strong increase in CH4 absorption, when increasing the orbital distance.
In the brightness temperature spectra shown in Fig. 4, CO2 features strong absorption bands at 2.7 μm, at 4.3 μm and 15 μm. We note that the 2.7 μm band overlaps with an absorption band of H2O and is furthermore influenced by the reflected stellar light. We thus do not take the F277W filter into account. The CO2 bands probe the lower to upper stratosphere, hence are extremely sensitive to stratospheric temperatures, which differ greatly between the different central star types (see e.g. Vasquez et al. 2013). This is related to the lower production of O3 in the atmosphere of the planet orbiting the K-type star and a weaker stellar radiation in the stellar UV bands in which O3 absorbs, which both result in a colder stratosphere (see e.g. G07 and Segura et al. 2003). Since surface temperatures are approximately equal for all scenarios (by construction), temperature differences between the brightness temperature and the surface temperature are consequently much larger for the planets around the K-type star (cf. Fig. 1).
 |
Fig. 7 Background limited S/Ns for secondary (right column) and primary transit observations (left column). The S/Ns for the central run of a planet orbiting a G-type star for two different telescope configurations are shown. The upper row shows S/Ns for one single transit observation, the lower row when co-adding five observations. The solid bars represent the filter bandpasses of NIRCam from 2 to 5 μm and of MIRI from 5 to 20 μm. Note that the F430M filter in transmission spectra is not visible due to a low S/N below 0.001. |
The strongest signal of up to about 70 K can be found for the planets around the K-type stars when comparing the brightness temperatures in the IM06 (15.0 μm) filter with the IM04 (11.3 μm) reference filter (diamonds in Fig. 6, lower left plot). Comparing the F430M (4.3 μm) filter with the IM04 reference filter yields only modest temperature differences below 10 K (triangles). The planets around the G and F-type stars furthermore feature lower brightness temperature differences, since the absorption in the CO2 band centers originate in the stratosphere at higher atmospheric temperatures due to the atmospheric temperature inversion (see Fig. 4). Thus the brightness temperature in the filter covering these bands are higher, hence the difference to the reference filter IM04 is much lower. A low brightness temperature difference would thus indicate a low-CO2 atmosphere or an atmosphere with a temperature inversion. The slight decrease in brightness temperature difference with increasing orbital distance for all scenarios considered is related to the decreasing H2O continuum absorption.
In secondary eclipse spectra O3 features only an absorption band at 9.6 μm in which the brightness temperature difference between the IM03 (10.0 μm) filter and the IM04 (11.3 μm) reference filter is rather low (see Fig. 6, lower right plot). Since the atmospheric response on increasing the orbital distance is weak (see Table 4) the filter response seen is only a result of the molecular absorption bands covered by the reference channels.
3.4. Detectability
The detectability of molecular absorption bands is investigated by calculating background-limited S/Ns for two different telescope configurations, namely JWST and E-ELT.
 |
Fig. 8 Transit depth differences for selected filter combinations (indicated by symbols) that provide S/Ns above unity, when co-adding five transits. Differences are shown for an E-ELT (left) and a JWST configuration (right) for the Earth-like planets around different types of central stars (F-star: red, G-star: black, K-star: blue) at different orbital distances (increasing from left to right, indicated by the increase in surface temperature). Error bars are only shown for filter combinations with differences larger than zero within their 1σ uncertainty. For clarity reasons the different filter combinations are shifted by 0.5 K. |
3.4.1. Calculated S/Ns
We calculate S/Ns for a hypothetical planet at a distance of 10 pc for one single transit observation (either primary or secondary transit with transit times shown in Table 3). In general the background-limited S/Ns are higher for primary eclipse transmission spectra than for secondary transit emission spectra, since the absorption of the stellar light is measured instead of the much fainter emission of the planet itself. Figure 7 shows the S/Ns for the central run of the G-type star in the bandpass of the photometric instruments. Since the Earth’s atmosphere is opaque at wavelengths where CO2 absorbs, the S/Ns for ground-based telescopes are low in the band centers of the 2.7, 4.3 and 15 μm CO2 bands. Since the filters F277W and IM06 at 2.7 and 15 μm, respectively, are broader than the absorption band, the S/Ns in these filters are dominated by the band wings.
In secondary eclipse emission spectra the highest S/Ns are obtained in the mid-IR above 10 μm (see Fig. 7, left panel) with values up to S/N = 0.3 during a single transit observation. Note that ground-based telescopes are limited by the thermal emission of the telescope and Earth’s atmosphere. By contrast, primary eclipse transmission observations provide the highest S/Ns in the near-IR (see Fig. 7, right panel), with S/Ns of up to 9 during a single transit observation for the near-IR filters for ground-based observations with the E-ELT. At wavelengths longer than 6 μm the thermal emission of the E-ELT dominates the overall noise.
We note that higher S/Ns may be conceivable when observing bigger planets (for secondary transit emission spectroscopy) around stars that are closer to the observer (the S/N increases quadratically with the planetary radius and decreases linearly with the distance, see e.g. Rauer et al. 2011). The distance to the planet is especially important for wavelengths where the noise is photon-dominated (i.e. in the near-IR). The zodiacal noise source decreases for targets at higher ecliptic latitudes. Currently we use measurements in the ecliptic plane for our zodiacal noise (Kelsall et al. 1998), which is a pessimistic assumption. This will be particularly important for measurements in the thermal-IR (i.e. in the MIRI IM06 filter). In addition, co-adding of transits could lead to increased S/Ns if systematic effects can be controlled. For example five transits can in principle be observed for a planet around a G-type star within the projected five-year mission time of JWST (i.e. the S/Ns increase by a factor of about two, see bottom row of Fig. 7). Finally the telescope and instrument designs can be improved to obtain higher S/Ns. The S/N increases linearly with the telescope’s aperture and with the square-root of the quantum efficiency (see, e.g. Rauer et al. 2011). Also the thermal emission of a space-borne telescope might be lowered. In total, a factor 10 higher S/Ns are conceivable.
3.4.2. Detectability of molecular absorption bands using filters
From the calculations shown above it is clear that the S/Ns are too low for a single transit observation in order to detect any absorption band in secondary eclipse spectra. For primary eclipse observations in the near infrared three filters provide S/Ns of larger than unity, when using an E-ELT-like telescope configuration (namely F277W at 2.7 μm, F356W at 3.56 μm, and F480M at 4.8 μm). These filters are covering the H2O/CO2 band at 2.7 μm (F277W), an atmospheric window at 3.7 μm which can be used as a reference (F356W) and an O3 band at 4.8 μm (F480M). When using a JWST-like telescope configuration, only the F277W and F430M (4.3 μm) filter provide S/Ns above unity during a single transit observation. The latter covers a CO2 absorption band at 4.3 μm.
During a single primary transit observation with the ELT (not shown), an absorption band in the F277W and F480M filter can be detected only for the planets around the F-type star. For planets orbiting a G-type star only an absorption band in the F277W filter can be detected, whereas no absorption bands are detectable for planets around K-type stars. Using the JWST, the CO2 absorption band at 4.3 μm can be detected in the F430M filter, but only for the planets around the F-type star. This is due to the strong transit depth difference of up to 0.013 between the F430M and the F356W reference filter. The S/N for the other stellar types are too low for a single transit observation.
Since both CO2 and H2O feature an absorption band at 2.7 μm, combining observations of JWST and E-ELT it is thus possible to determine the presence of H2O in the atmosphere of the planet around an F-type star: If the presence of a CO2 absorption at 4.3 μm can be ruled out using JWST measurements and an absorption band can be detected at 2.7 μm using E-ELT, than this might be attributed to the presence of H2O in the atmosphere. However, in order to detect H2O in a separate band (e.g. at 6.3 μm), a S/N > 7 needs to be achieved, hence about 10 transits need to be co-added for an E-ELT-telescope setup.
We assume here that during the five-year mission time of JWST about five transits of an Earth-like planet orbiting a main-sequence star in the HZ can be observed, assuming that instrumental effects can be neglected. This would increase the S/N by a factor of about two. Figure 8 shows the transit depth differences in the above-mentioned filters with 1σ error bars for five transit observations. The E-ELT configuration (left plot) would now allow the detection of both the 2.7 μm CO2/H2O band and the 4.8 μm O3 band in the F277W (2.77 μm) and F480M (4.8 μm) filters, respectively, for planets around G and F-type stars. For planets orbiting K-type stars only the 2.7 μm band can be detected. Most interestingly, a negative transit depth difference between the F277W and F356W filter in the outer run of the K-type planets can be detected. This is due to the strong 3.3 μm CH4 absorption covered by the F356W filter. Hence it would be possible to prove the existence of CH4 in the planetary atmosphere. Using the JWST (right plot) now also allows the detection of the 4.3 μm CO2 band for planets around G-type stars. Furthermore, the 2.7 μm CO2/H2O band can be detected for planets around F-type stars.
4. Discussion
We note that clouds can have a significant impact on the spectral appearance of a planet, as has been investigated by Robinson et al. (2011) and Kitzmann et al. (2011). With increasing cloud cover of either low or high-level clouds, Kitzmann et al. (2011) found that the overall IR emission of an Earth-like planet decreases and the absorption bands of O3, CO2 and H2O are weakened. Hence our S/Ns for emission spectra are already likely to be upper limits. For this work this means that the brightness temperature difference between the filter covering the 9.6 μm O3 band and the reference filter centered at 11.3 μm will decrease, when taking clouds into account. Furthermore, the uncertainty in the surface temperature determination will increase.
For primary eclipse transmission spectra, low level clouds have only a negligible effect, since the cloud layers are present below the tangential height, where the atmosphere is already optically thick. However, in order to study the effect of mid- or high-level clouds, 3-dimensional atmospheric and radiative transfer models need to be applied in order to account correctly for the absorption and scattering by the cloud layers.
The main challenge for ground-based observations of an Earth-like planet is to remove the contamination due to Earth’s atmospheric absorption. High-resolution observations may take advantage of the Doppler shift of single lines due to the proper motions of the star, the exoplanet, the Sun, and the Earth (see e.g. Vidal-Madjar et al. 2010), to distinguish between telluric absorption lines and lines forming in the atmosphere of the exoplanet. However, this is not applicable to absorption bands for low-resolution spectroscopy or photometry. These observations, however, may use multiobject spectroscopy or photometry in order to observe nearby reference stars, as in Bean et al. (2010).
We were able to show that the 4.8 μm absorption band of the biomarker molecule O3 and the absorption band at 6.3 μm of the related compound H2O are both detectable during primary eclipse, when co-adding several transit observations. The former molecule is on Earth directly related to the presence of plants and cyanobacteria that produce O2 from photosynthesis, whereas the latter is needed in its liquid phase on the surface for life as we know it.
Note that the detection of the presence of O3 in an exoplanetary atmosphere does not necessarily indicate the presence of a biosphere. It is currently discussed, if O3 can be formed in an abiotic way by the photodissociation of CO2 in e.g. a CO2 dominated atmosphere (Selsis et al. 2002) or in an atmosphere which is subject to strong UV irradiation (e.g. around active M-dwarfs). A combination of strong UV-C and weak UV-B irradiation is required for the latter process (see Domagal-Goldman & Meadows 2010). Segura et al. (2007) however showed that it is not possible to create O3 from the photolysis of CO2 in an Earth-like planet with an active hydrological cycle orbiting a Sun-like star.
Another way of forming substantial amounts of abiotic O3 is possible in an atmosphere that is subject to strong atmospheric escape, where atmospheric H2O is photolyzed, and H is efficiently removed. The atmosphere then becomes enriched in atomic oxygen, which can form O2 and O3 (Schindler & Kasting 2000). Such possible scenarios should be carefully evaluated before claiming the detection of life.
5. Summary and conclusions
In this paper we have studied the spectral appearance of cloud-free Earth-like atmospheres at different orbital distances within the HZ of three different main-sequence central stars. We have investigated under which conditions molecular absorption bands are detectable with near-future instruments and telescopes, either from ground or from space, and if surface temperatures can be inferred. For this we have calculated background-limited S/Ns for an E-ELT-type ground-based telescope and a JWST-like space-borne telescope, assuming that our target planets are located at a distance of 10 pc. For the instruments considered in this work, we used the specifications and bandpasses of two photometric instruments that are planned for the JWST. Of special interests are atmospheric species which are related to habitability (CO2, H2O) or could even be linked to biological activity (O3, CH4). Also the knowledge of surface temperature is central to the habitability problem.
In general, for an habitable Earth-sized planet, the contrast between the stellar emission and the planetary emission is too low as to provide a sufficient S/N in order to detect any absorption bands during secondary eclipse. However, during primary eclipse transmission spectroscopy much higher S/Ns (especially in the near-IR) can be obtained since the absorption of the stellar light in the planetary atmosphere is measured. Furthermore the geometry of the primary transit allows for weak absorption bands to produce significant features due to the longer lightpath in the atmosphere, which is e.g. the case for O3 at 4.8 μm and HNO3 at 11.3 μm, which are not visible in secondary eclipse emission spectra. This enhanced path length allows the detection of key compounds in an exoplanet atmosphere that are also present in the Earth’s atmosphere, as long as these compounds are observed from the ground in their optically thin bands. During a lunar eclipse e.g. Pallé et al. (2011) was able to detect from ground-based measurements a number of biomarker molecules as well as the dimers O2-O2 and O2-N2 in the transmission spectrum of our Earth’s atmosphere.
We found that ground-based observations using the E-ELT enables the detection of near-IR absorption bands of both CO2 and H2O at 2.7 and O3 at 4.8 μm for some cases, even for a single transit observation. In order to discriminate whether both CO2 and H2O or only one of them is present, separate bands need to be observed. This is e.g. possible using a space-borne telescope like the JWST, which allows the detection of the CO2 absorption band at 4.3 μm, which is not detectable for ground-based telescopes due to absorption in the Earth atmosphere. However, in order to detect H2O in a separate band at least a S/N > 7 need to be achieved for E-ELT observations, hence about 10 transits need to be co-added.
To increase the S/N, the observation of planets in the HZ around M-type stars would be a solution due to a much shorter period of about 32 days for planets in the HZ. Although the integration time during the transit is much shorter (3 h compared to 13 h) and the stellar luminosity is much lower for M-dwarfs than for e.g. G-type stars, a factor of about 11 more transits can be observed within one year, which would translate into a factor of about three times higher S/Ns during a one year mission time. The shorter integration time and lower stellar luminosity results in a factor of about two lower S/Ns for an M-dwarf planet than that for a planet orbiting a G-type star (see e.g. Rauer et al. 2011, for photon-limited S/Ns).
This paper shows for the first time, that photometric filters planned for the JWST or the E-ELT can also be used for the characterization of Earth-like exoplanet atmospheres, although the filter bandpasses have been defined for different scientific purposes. They can be used to characterize a given planetary atmosphere even if they provide only a very low spectral resolution. However, several filters need to be positioned over a broad wavelength range in order to obtain information about different biomarker molecules and surface conditions. To obtain information about the surface conditions and to perform a comparative filter analysis as performed in this paper, reference filters need to be chosen carefully in order not to be contaminated by spectral absorption bands. For primary eclipse transmission observations, two near-IR atmospheric windows from 2.1 to 2.4 μm and from 3.5 to 4.0 μm as well as in the mid-IR at around 11 μm could be used for reference filters when aiming at Earth-like atmospheres. The NIRCam F356W filter that has been used in this paper (which is planned for the JWST), is too broad (3.1−4.0 μm) and thus cover an CH4 absorption band at 3.3 μm. The near-IR windows provide much higher S/Ns than the mid-IR window. For secondary eclipse observations only the 11 μm atmospheric window can be used as a reference filter, since both near-IR windows feature very low S/Ns and are furthermore influenced by reflected stellar light.
Available online via http://www.eso.org/sci/facilities/eelt/science/drm/tech_data/data
Acknowledgments
We thank the referee V. Meadows for a thorough reading of and detailed comments on the manuscript. This research has been partly supported by the Helmholtz Gemeinschaft (HGF) through the HGF research alliance “Planetary Evolution and Life”. Pascal Hedelt, Philip von Paris and Franck Selsis acknowledge support from the European Research Council (Starting Grant 209622: E3ARTHs). Discussions with B. Stracke and A. Belu are gratefully acknowledged.
References
- Alonso, R., Alapini, A., Aigrain, S., et al. 2009a, A&A, 506, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso, R., Guillot, T., Mazeh, T., et al. 2009b, A&A, 501, L23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anglada-Escudé, G., Arriagada, P., Vogt, S. S., et al. 2012, ApJ, 751, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Arnold, L. 2008, Space Sci. Rev., 135, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Arnold, L., Gillet, S., Lardière, O., Riaud, P., & Schneider, J. 2002, A&A, 392, 231 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Bean, J. L., Kempton, E., & Homeier, D. 2010, Nature, 468, 669 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bean, J. L., Désert, J.-M., Kabath, P., et al. 2011, ApJ, 743, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Belu, A. R., Selsis, F., Morales, J., et al. 2011, A&A, 525, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berta, Z. K., Charbonneau, D., Désert, J.-M., et al. 2012, ApJ, 747, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Bonfils, X., Gillon, M., Udry, S., et al. 2012, A&A, 546, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D. G., Batalha, N., et al. 2012, ApJ, 745, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, D., Brown, T. M., Noyes, R. W., & Gilliland, R. L. 2002, ApJ, 568, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, D., Berta, Z. K., Irwin, J., et al. 2009, Nature, 462, 891 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cowan, N. B., & Agol, E. 2011, ApJ, 729, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Croll, B., Albert, L., Jayawardhana, R., et al. 2011, ApJ, 736, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Crossfield, I. J. M., Barman, T., & Hansen, B. M. S. 2011, ApJ, 736, 132 [NASA ADS] [CrossRef] [Google Scholar]
- de Mooij, E. J. W., Brogi, M., de Kok, R. J., et al. 2012, A&A, 538, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deming, D., Harrington, J., Seager, S., & Richardson, L. J. 2006, ApJ, 644, 560 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Deming, D., Seager, S., Winn, J., et al. 2009, PASP, 121, 952 [NASA ADS] [CrossRef] [Google Scholar]
- Demory, B.-O., Gillon, M., Seager, S., et al. 2012, ApJ, 751, L28 [Google Scholar]
- DesMarais, D. J., Harwit, M. O., Jucks, K. W., et al. 2002, Astrobiology, 2, 153 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Désert, J., Bean, J., Miller-Ricci Kempton, E., et al. 2011, ApJ, 731, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Dole, S. H. 1964, Habitable planets for man, 1st edn. (New York: Blaisdell Pub. Co.) [Google Scholar]
- Domagal-Goldman, S. D., & Meadows, V. S. 2010, in Pathways Towards Habitable Planets, eds. V. Coudé Du Foresto, D. M. Gelino, & I. Ribas, ASP Conf. Ser., 430, 152 [Google Scholar]
- Ehrenreich, D., Tinetti, G., Lecavelier Des Etangs, A., Vidal-Madjar, A., & Selsis, F. 2006, A&A, 448, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ehrenreich, D., Vidal-Madjar, A., Widemann, T., et al. 2012, A&A, 537, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grenfell, J. L., Grießmeier, J.-M., Patzer, B., et al. 2007a, Astrobiology, 7, 208 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Grenfell, J. L., Stracke, B., von Paris, P., et al. 2007b, Planetary and Space Science, 55, 661 [Google Scholar]
- Grillmair, C. J., Charbonneau, D., Burrows, A., et al. 2007, ApJ, 658, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Guenther, E. W., Cabrera, J., Erikson, A., et al. 2011, A&A, 525, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gueymard, C. 2004, Sol. Energy, 76, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Habing, H. J., Dominik, C., Jourdain de Muizon, M., et al. 2001, A&A, 365, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hatzes, A. P., Dvorak, R., Wuchterl, G., et al. 2010, A&A, 520, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hedelt, P., Alonso, R., Brown, T., et al. 2011, A&A, 533, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaltenegger, L., & Traub, W. A. 2009, ApJ, 698, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Kaltenegger, L., Traub, W. A., & Jucks, K. W. 2007, ApJ, 658, 598 [NASA ADS] [CrossRef] [Google Scholar]
- Kasper, M., Beuzit, J.-L., Verinaud, C., et al. 2010, in SPIE Conf. Ser., 7735 [Google Scholar]
- Kasting, J. F. 1988, Icarus, 74, 472 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kasting, J. F., Whitmire, D. P., & Reynolds, R. T. 1993, Icarus, 101, 108 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kelsall, T., Weiland, J. L., Franz, B. A., et al. 1998, ApJ, 508, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Kendrew, S., Jolissaint, L., Brandl, B., et al. 2010, in SPIE Conf. Ser., 7735, 179 [Google Scholar]
- Kipping, D. M., & Tinetti, G. 2010, MNRAS, 407, 2589 [NASA ADS] [CrossRef] [Google Scholar]
- Kitzmann, D., Patzer, A. B. C., von Paris, P., et al. 2010, A&A, 511, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kitzmann, D., Patzer, A. B. C., von Paris, P., Godolt, M., & Rauer, H. 2011, A&A, 534, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knutson, H. A. 2007, Nature, 448, 143 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Léger, A., Rouan, D., Schneider, J., et al. 2009, A&A, 506, 287 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Liske, J. 2008, E-ELT Spectroscopic ETC: Detailed Description, Technical Report [Google Scholar]
- Liske, J. 2010, E-ELT Programme. The E-ELT Design Reference mission: Technical Data used for Simulations., Tech. Rep. E-TRE-ESO-080-0718 Issue 1, ESO [Google Scholar]
- Manabe, S., & Wetherald, R. T. 1967, J. Atmos. Sci., 24, 241 [Google Scholar]
- Mayor, M., Bonfils, X., Forveille, T., et al. 2009, A&A, 507, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Melsheimer, C., Verdes, C., Buehler, S. A., et al. 2005, Radio Science, 40, 1007 [Google Scholar]
- Miller-Ricci Kempton, E., Zahnle, K., & Fortney, J. J. 2012, ApJ, 745, 3 [Google Scholar]
- Oonk, H., & Kroeze, C. 1998, Encyclopedia of Environmental Analysis and Remedation, ed. R. A. Meyers (London, UK: Wiley), 3035 [Google Scholar]
- Pallé, E., Zapatero Osorio, M. R., Barrena, R., Montañés-Rodríguez, P., & Martín, E. L. 2009, Nature, 459, 814 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pallé, E., García Muñoz, A., Zapatero Osorio, M. R., et al. 2011, in IAU Symp. 276, eds. A. Sozzetti, M. G. Lattanzi, & A. P. Boss, 385 [Google Scholar]
- Pepe, F., Lovis, C., Ségransan, D., et al. 2011, A&A, 534, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauer, H., Gebauer, S., von Paris, P., et al. 2011, A&A, 529, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richardson, L. J., Deming, D., Horning, K., Seager, S., & Harrington, J. 2007, Nature, 445, 892 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Robinson, T. D., Meadows, V. S., Crisp, D., et al. 2011, Astrobiology, 11, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Rothman, L. S., Jacquemart, D., Barbe, A., et al. 2005, J. Quant. Spectr. Radiat. Transf., 96, 139 [Google Scholar]
- Rothman, L. S., Gordon, I. E., Barbe, A., et al. 2009, J. Quant. Spectr. Radiat. Transf., 110, 533 [Google Scholar]
- Rowe, J. F., Matthews, J. M., Seager, S., et al. 2008, ApJ, 689, 1345 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2004, A&A, 415, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schindler, T. L., & Kasting, J. F. 2000, Icarus, 145, 262 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Schreier, F., & Böttger, U. 2003, Atmos. Ocean. Opt., 16, 262 [Google Scholar]
- Schreier, F., & Schimpf, B. 2001, in Int. Radiation Symp. IRS2000: Current Problems in Atmospheric Radiation, eds. W. Smith, & Y. Timofeyev (A. Deepak Publishing), 381 [Google Scholar]
- Seager, S. 2008, Space Sci. Rev., 135, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Segura, A., Krelove, K., Kasting, J. F., et al. 2003, Astrobiology, 3, 689 [Google Scholar]
- Segura, A., Kasting, J. F., Meadows, V., et al. 2005, Astrobiology, 5, 706 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Segura, A., Meadows, V. S., Kasting, J. F., Crisp, D., & Cohen, M. 2007, A&A, 472, 665 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Selsis, F., Despois, D., & Parisot, J.-P. 2002, A&A, 388, 985 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Selsis, F., Kasting, J. F., Levrard, B., et al. 2007, A&A, 476, 1373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sing, D. K., & López-Morales, M. 2009, A&A, 493, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Snellen, I. A. G., de Kok, R. J., de Mooij, E. J. W., & Albrecht, S. 2010a, Nature, 465, 1049 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Snellen, I. A. G., de Mooij, E. J. W., & Burrows, A. 2010b, A&A, 513, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Swain, M. R., Vasisht, G., & Tinetti, G. 2008, Nature, 452, 329 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tinetti, G. 2006, Origins of Life and Evolution of the Biosphere, 36, 541 [NASA ADS] [Google Scholar]
- Tinetti, G., Vidal-Madjar, A., Liang, M., et al. 2007, Nature, 448, 169 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tuomi, M., Anglada-Escudé, G., Gerlach, E., et al. 2013, A&A, 549, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Udry, S., Bonfils, X., Delfosse, X., et al. 2007, A&A, 469, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasquez, M., Schreier, F., Gimeno García, S., et al. 2013, A&A, 549, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vidal-Madjar, A., Lecavelier des Etangs, A., Désert, J., et al. 2003, Nature, 422, 143 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Vidal-Madjar, A., Désert, J., Lecavelier des Etangs, A., et al. 2004, ApJ, 604, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Vidal-Madjar, A., Arnold, L., Ehrenreich, D., et al. 2010, A&A, 523, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Clarmann, T., Höpfner, M., Funke, B., et al. 2003, J. Quant. Spectr. Radiat. Transf., 78, 381 [NASA ADS] [CrossRef] [Google Scholar]
- von Paris, P., Cabrera, J., Godolt, M., et al. 2011, A&A, 534, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walker, J. C. G., Hays, P. B., & Kasting, J. F. 1981, J. Geophys. Res., 86, 9776 [Google Scholar]
- Wright, G. S., Rieke, G. H., Colina, L., et al. 2004, in SPIE Conf. Ser. 5487, ed. J. C. Mather, 653 [Google Scholar]
All Tables
Relative change of total column amount when increasing the orbital distances from the inner to the outer boundary for different molecules and central star types.
Geometric transit depth dGeo = (rP/rS)2 for planets orbiting different central stars.
All Figures
 |
Fig. 1 Pressure–temperature profiles of the Earth-like planets around different central stars (K-type star: dashed, G-type star: solid, F-type star: dotted) at different orbital distances (inner run: red, center run: black, outer run: blue). |
| In the text | |
 |
Fig. 2 Pressure–concentration profiles of five prominent spectral species of the Earth-like planets around different central stars (upper row: F-type star, center row: G-type star, lower row: K-type star). Columns from left to right show profiles of O3, CH4, N2O, H2O and HNO3. The orbital distance is indicated by colors as in Fig. 1. Note that CO2 is set to an isoprofile of 355 ppm and hence not shown. |
| In the text | |
 |
Fig. 3 Same as Fig. 2, but only the profiles of the planets at the center of the HZ are shown to visualize the dependency on central star type. The central star type used is color-coded (red: F-type star, black: G-type star and blue: K-type star). |
| In the text | |
 |
Fig. 4 Transit depth during primary eclipse (left) and brightness temperature difference with respect to the calculated surface temperature spectrum during secondary eclipse (right) for the scenarios considered. The spectral resolution is R = 100. Each center run with R = 3000 is shown in grey. The geometric transit depth (see Sect. 3.3) is indicated by a horizontal line for transmission spectra. The brightness temperature spectra include the reflected stellar component in the near-IR. Furthermore the bandpass of the filters considered in this work are shown. |
| In the text | |
 |
Fig. 5 Transit depth differences for different filter combinations for primary eclipse transmission spectra. dFilter and dReference are the transit depths measured by the photometric filter and the reference filter, respectively, whereas dgeo is the geometric transit depth (i.e. the ratio of planetary and stellar radius squared). |
| In the text | |
 |
Fig. 6 Brightness temperature difference for different filter combinations for secondary eclipse emission spectra. The upper left panel shows the difference of the brightness temperature measured in the F356 and IM04 filter with respect to the model surface temperature, whereas the other panels show the difference of selected filters with respect to the reference filter IM04. Note the different vertical scales in the plots. |
| In the text | |
 |
Fig. 7 Background limited S/Ns for secondary (right column) and primary transit observations (left column). The S/Ns for the central run of a planet orbiting a G-type star for two different telescope configurations are shown. The upper row shows S/Ns for one single transit observation, the lower row when co-adding five observations. The solid bars represent the filter bandpasses of NIRCam from 2 to 5 μm and of MIRI from 5 to 20 μm. Note that the F430M filter in transmission spectra is not visible due to a low S/N below 0.001. |
| In the text | |
 |
Fig. 8 Transit depth differences for selected filter combinations (indicated by symbols) that provide S/Ns above unity, when co-adding five transits. Differences are shown for an E-ELT (left) and a JWST configuration (right) for the Earth-like planets around different types of central stars (F-star: red, G-star: black, K-star: blue) at different orbital distances (increasing from left to right, indicated by the increase in surface temperature). Error bars are only shown for filter combinations with differences larger than zero within their 1σ uncertainty. For clarity reasons the different filter combinations are shifted by 0.5 K. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


