| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A73 | |
| Number of page(s) | 10 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201321234 | |
| Published online | 28 March 2013 | |
The carbon-to-oxygen ratio in stars with planets⋆,⋆⋆
Stellar Astrophysics Centre, Department of Physics and AstronomyAarhus
University, Ny Munkegade
120, 8000
Aarhus C, Denmark
e-mail: pen@phys.au.dk
Received:
5
February
2013
Accepted:
2
March
2013
Context. In some recent works, the C/O abundance ratio in high-metallicity stars with planets is found to vary by more than a factor of two, i.e. from ~0.4 to C/O ≳ 1. This has led to discussions about the existence of terrestrial planets with a carbon-dominated composition that is very different from the composition of the Earth.
Aims. The mentioned C/O values were obtained by determining carbon abundances from high-excitation C i lines and oxygen abundances from the forbidden [O i] line at 6300 Å. This weak line is, however, strongly affected by a nickel blend at high metallicities. Aiming for more precise C/O ratios, oxygen abundances in this paper are derived from the high-excitation O i triplet at 7774 Å.
Methods. The C i lines at 5052 and 5380 Å in HARPS spectra were applied to determine carbon abundances of 33 solar-type stars for which FEROS spectra are available for determining oxygen abundances from the O iλ7774 triplet. Differential abundances with respect to the Sun were derived from equivalent widths using MARCS model atmospheres. Non-LTE corrections were included, and the analysis was carried out with both spectroscopic and photometric estimates of stellar effective temperatures and surface gravities.
Results. The results do not confirm the high C/O ratios previously found. C/O shows a tight, slightly increasing dependence on metallicity, i.e. from C/O ≃ 0.58 at [Fe/H] = 0.0 to C/O ≃ 0.70 at [Fe/H] = 0.4 with an rms scatter of only 0.06.
Conclusions. Recent findings of C/O ratios higher than 0.8 in high-metallicity stars seem to be spurious due to statistical errors in estimating the strength of the weak [O i] line in the Ni i blended λ6300 feature. Assuming that the composition of a proto-planetary disk is the same as that of the host star, the C/O values found in this paper lend no support to the existence of carbon-rich planets. The small scatter of C/O among thin-disk stars suggests that the nucleosynthesis products of Type II supernovae and low- to intermediate-mass stars are well mixed in the interstellar medium.
Key words: stars: abundances / stars: atmospheres / planetary systems
Based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory under programmes given in Table 1.
Tables 1 and 4 are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Recent high-resolution spectroscopic surveys suggest that the carbon-to-oxygen abundance ratio, C/O1, in the atmospheres of metal-rich F and G dwarf stars varies by more than a factor of two. Delgado Mena et al. (2010) find a range in C/O from ~0.4 to ≳1 for 370 stars observed with HARPS or CORALIE, including about 100 stars with detected planets. A similar range in C/O has been found by Petigura & Marcy (2011) for about 700 stars observed with HIRES of which 80 have detected planets. Even if one corrects the distribution of C/O for the quoted observational errors, there seems to be a small fraction (1–5%) of the stars having C/O ≳ 1, and a significant fraction (10–15%) having C/O > 0.8 (Fortney 2012) in contrast to the solar ratio of C/O ≃ 0.55.
Assuming that the composition of a proto-planetary disk is the same as that of the host star, variations in the C/O abundance ratio among solar-type stars may have interesting effects on the composition and structure of planets. Thus, Kuchner & Seager (2005) discuss the possible existence of extrasolar “carbon planets” consisting of carbides and graphite instead of “Earth-like” silicates. When modelling terrestrial planet formation, Bond et al. (2010) find that C/O > 0.8 leads to the formation of such carbon planets. A particularly interesting case is super-earth 55 Cancri e. Studies of its transit across the host star (Winn et al. 2011; Demory et al. 2011) lead to a radius R ≃ 2.0 R⊕ and a mass M ≃ 8.4 M⊕. Adopting an oxygen-rich composition, a massive water envelope over an Earth-like interior is required to explain the observed radius. Madhusudhan et al. (2012) have, however, shown that the mass and radius can also be explained by a carbon-rich interior without a volatile envelope. Interestingly, the star hosting this planet, i.e. 55 Cancri alias HD 75732, has C/O = 1.12 according to Delgado Mena et al. (2010).
The existence of dwarf stars with C/O > 1 has been questioned by Fortney (2012). Among cool K and M dwarfs, C/O > 1 leads to strong C2 and CN bands that are easy to detect. From various large spectroscopic surveys, including the SDSS, Fortney notes that the relative frequency of such “carbon” stars is less than ~10-3, and discusses various reasons that the C/O ratio may have been overestimated in solar-type stars.
In the works of Delgado Mena et al. (2010) and Petigura & Marcy (2011), carbon abundances were determined from high-excitation C i lines and oxygen abundances from the zero-excitation, forbidden [O i] line at 6300 Å. The large difference in excitation potential makes the derived C/O sensitive to errors in stellar effective temperature and to the temperature structure of the model atmospheres. Although the analysis in the two works was made differentially to the Sun, the use of homogeneous 1D model atmospheres might have introduced systematic errors of C/O as a function of metallicity. Furthermore, the [O i] line is overlapped by a Ni i line, which is calculated to have a strength of about 55% of the [O i] line in the solar flux spectrum (Caffau et al. 2008), if one adopts the gf-value determined by Johansson et al. (2003). Given that [O/Fe] decreases and [Ni/Fe] increases with increasing [Fe/H] (e.g. Bensby et al. 2005), the Ni i blend becomes more important at the high metallicities for which most of the high C/O values have been found. This makes it difficult to determine precise oxygen abundances from the [O i] line at high metallicities, and systematic errors in [O/H] are introduced if the Ni i blend is not correctly calibrated for the solar spectrum. Finally, the measured equivalent width of the weak [O i] line depends critically on the continuum setting, and sometimes it is difficult to correct for overlapping telluric O2 lines.
Instead of the [O i] line, the O i triplet at 7774 Å may be used to determine oxygen abundances. These three lines have a high excitation potential like the C i lines, which makes the derived C/O ratio insensitive to errors in effective temperature and the temperature structure of the model atmospheres. Furthermore, the lines are practically unblended. A drawback is that the triplet is affected by deviations from local thermodynamic equilibrium (non-LTE; Kiselman 2001), which is not the case for the forbidden [O i] line.
The ESO 3.6 m HARPS spectra (Mayor et al. 2003) used by Delgado Mena et al. (2010) have a maximum wavelength of 6900 Å, but for a good fraction of their stars, ESO 2.2 m FEROS spectra (Kaufer et al. 1999) covering the O i triplet are available. In this paper, these FEROS spectra have been used to derive oxygen abundances from the triplet together with carbon abundances from the C i lines in the HARPS spectra. Section 2 contains a description of the stellar spectra and the measurement of equivalent widths. The model-atmosphere analysis, including non-LTE corrections, is dealt with in Sect. 3, and the abundances obtained when adopting spectroscopic and photometric estimates of Teff and log g, respectively, are presented in Sects. 4 and 5. Finally, Sect. 6 provides a comparison with other works and a discussion of the Galactic dispersion and evolution of C/O.
2. Stellar spectra and equivalent widths
Tables 1 and 2 in Delgado Mena et al. (2010) contain a list of 100 dwarf stars with detected planets for which they have determined C and O abundances based on spectra from the HARPS GTO survey. Out of this sample, 38 stars have FEROS spectra available in the ESO Science Archive. Of these, five stars have Teff around 5100 K. The remaining 33 stars (listed in Table 1) have 5400 < Teff < 6400 K, which is a suitable range for a differential abundance analysis with respect to the Sun.
Pipeline extracted and wavelength calibrated spectra observed under the programmes listed in Table 1 were acquired from the ESO Science Archive. The HARPS spectra cover a wavelength range from 3800 to 6900 Å and have a resolution of R ≃ 115 000. After combination of many individual spectra, the signal-to-noise ratio (S/N) ranges from 250 to more than 1000. The FEROS spectra range from 3500 to 9200 Å with a resolution of R ≃ 48 000. Most of these spectra have S/N from 200 to 300 (in the region of the O i triplet), except for HD 216770 that has S/N = 120.
The spectra were normalized with the IRAF continuum task using a cubic spline fitting function of relatively low order, i.e. a wavelength scale >20 Å. The measurement of an equivalent width (EW) was carried out with reference to local continuum regions selected to be free of lines in the solar spectrum and situated within 4 Å from the line. Care was taken to use the same continuum windows in all stars.
The measurement of the equivalent widths of the O i triplet lines causes particular problems. These lines are somewhat strong and have very broad wings. If measured by fitting a Voigt profile, the equivalent width becomes very sensitive to the setting of the continuum. This is even a problem in solar spectra having extremely high resolution and S/N. Thus, the EWs of the O i triplet lines measured by Asplund et al. (2004) and Caffau et al. (2008) differ by 5 to 10 mÅ, which is a major reason for the difference in the solar oxygen abundance derived in these two 3D studies. In the present work, equivalent widths are, instead, measured by Gaussian fitting using the IRAF splot task, which for the resolution of FEROS turns out to provide nearly the same EW as obtained by direct integration over a range of ± 0.4 Å centred on the line. The method neglects the contribution from the broad wings, but this was compensated for by also calculating the EW in the model-atmosphere analysis over a window of ± 0.4 Å. The same procedure was followed for the two C i lines, although they are sufficiently weak to ensure that Gaussian fitting provides a good estimate of the total EW of the line.
The measured equivalent widths are given in Table 1. It is noted that weak CN and C2 lines are present in the region of the O i triplet, but fitting with a Gaussian profile minimizes the influence of such blends. In general, the equivalent widths of the O i lines have a precision of 2–3 mÅ and those of the C i lines a precision of about 1 mÅ.
To make a reliable differential analysis with respect to the Sun, it is important to apply a solar flux spectrum observed in the same way as the stellar spectra. Fortunately, this is possible; spectra of reflected sunlight from Ceres and Ganymede have been obtained with both HARPS and FEROS, and with S/Ns similar to those of the programme stars. As seen from Table 1, the equivalent widths measured for the two minor planets agree very well. Therefore, the average values have been applied in the model-atmosphere analysis.
Line data and derived solar abundances.
 |
Fig. 1 Carbon abundances of Delgado Mena et al. (2010) in comparison with carbon abundances derived in this paper. |
 |
Fig. 2 Oxygen abundances of Delgado Mena et al. (2010) in comparison with non-LTE oxygen abundances derived in this paper. |
3. Analysis
3.1. Model atmospheres and line broadening
For each star, a plane parallel (1D) model atmosphere was obtained from the standard MARCS grid (Gustafsson et al. 2008) by interpolating to the Teff, log g, and [Fe/H] values of the star, and the Uppsala program EQWIDTH was used to calculate equivalent widths of the C i and O i lines as a function of C or O abundance assuming LTE. Interpolation to the observed equivalent widths then yields the LTE abundances.
Line data used in the analysis are given in Table 2. The gf values of the C i lines are based on quantum mechanical calculations by Hibbert et al. (1993) and those of oxygen are taken from Hibbert et al. (1991). Doppler broadening by non-thermal, small-scale motions in the atmosphere is described by one parameter, ξturb, in the usual way. For the O i lines, collisional broadening caused by neutral hydrogen and helium atoms is based on the quantum mechanical calculations of Barklem et al. (2000). Their work does not include the two C i lines, for which the Unsöld (1955) approximation with an enhancement factor of two was adopted as in Asplund et al. (2005). The C i lines are sufficiently weak to be insensitive to the assumed enhancement factor; if it is changed from two to one, the derived [C/H] values change by less than 0.01 dex.
3.2. Non-LTE corrections
It is well know that the strength of the O i triplet is subject to large non-LTE effects (e.g. Kiselman 2001). The most advanced study is due to Fabbian et al. (2009), who calculated non-LTE corrections for a grid of MARCS models ranging from 4500 to 6500 K in Teff, from 2.0 to 5.0 in log g, and from − 3.0 to 0.0 in [Fe/H]. Their model atom contains 54 energy levels and includes electron collision cross sections based on quantum mechanical calculations by Barklem (2007). An IDL program, made available, allows interpolation of the non-LTE correction to the stellar values of Teff, log g, and [Fe/H] for a given LTE oxygen abundance. For stars with [Fe/H] > 0.0, one needs to make an extrapolation in [Fe/H], but because the correction changes only a little from [Fe/H] = −0.5 to 0.0 (see Fig. 7 in Fabbian et al.), this is not expected to introduce any significant errors.
The “dark horse” in the non-LTE calculations is the handling of inelastic collisions with hydrogen atoms, because no experimental or quantum mechanical estimates of cross sections are available. Therefore, Fabbian et al. adopted the classical Drawin formula (Drawin 1968) scaled by an empirical factor SH. According to the 3D, non-LTE study of the solar centre-to-limb variation of the O i triplet lines by Pereira et al. (2009), who applied the same atomic model as Fabbian et al., SH = 0.85 leads to the best agreement with the observations. Because Fabbian et al. (2009) provide non-LTE corrections for both SH = 0 (H collisions are neglected) and SH = 1 (Drawin’s formula), it is possible to interpolate their corrections to SH = 0.85, which is the value applied in the present paper.
According to Table 2, the solar non-LTE corrections range from − 0.22 to − 0.17 for the three O i lines, i.e. close to − 0.20 dex on average. As seen from Figs. 7 and 8 in Fabbian et al. (2009), the corrections become increasingly more negative for higher Teff and lower log g, whereas stars with lower Teff than the Sun have less negative non-LTE corrections. Altogether, this leads to significant differential non-LTE corrections of [O/H] ranging from about − 0.2 dex at Teff ≃ 6400 K to +0.1 dex at Teff ≃ 5400 K.
The non-LTE corrections for the C iλ5052 and λ5380 lines are much smaller than those for the O i triplet. According to the detailed calculations of Takeda & Honda (2005) adopted in this paper, the corrections are − 0.01 dex for the Sun and changes only slightly as a function of Teff and log g. Their calculations were made on the assumption that SH = 1. Assuming instead SH = 0, Asplund et al. (2005) find a solar non-LTE correction of − 0.03 dex. In this case the corrections of [C/H] would be somewhat higher, but still close to be negligible compared to other error sources.
3.3. Random and systematical errors
Random errors arise from the uncertainties of the measured equivalent widths and from the uncertainty of the adopted stellar atmospheric parameters. The first source is best estimated by comparing abundances obtained from different spectral lines of the same element. The [C/H] abundances derived from the two C i lines agree very well; the average standard deviation of the mean is σ[C/H] = 0.009 dex. From the three O i lines one gets σ[O/H](non-LTE) = 0.017 dex2. Adding these errors in quadrature, the one-sigma error of [C/O] due to EW uncertainties becomes ≃0.02 dex.
Based on the rms deviations between spectroscopic and photometric parameters discussed in Sect. 5, the one-sigma errors for each set of parameters are estimated to be σ(Teff) = 45 K, σ(log g) = 0.08, σ [Fe/H] = 0.04, and σ(ξturb) = 0.07 km s-1. The effects on the derived [C/H], [O/H], and [C/O] values of the corresponding changes in stellar parameters are shown in Table 3. As seen, the largest contribution to the abundance errors arises from the error in Teff with [O/H] being more affected than [C/H]. This is due to a higher excitation potential of the O i lines (9.15 eV) than in the case of the C i lines (7.69 eV), and to the high Teff-sensitivity of the O i non-LTE corrections. Still, there is some canceling effect of the Teff dependence for the C i and the O i lines; the error in [C/O] is only half the error in [O/H]. Furthermore, the derived [C/H] and [O/H] values have nearly the same gravity dependence, so that the log g-induced error on [C/O] becomes relatively small. Finally, it is noted that errors induced by the uncertainties in [Fe/H] and ξturb are negligible.
When adding all errors in quadrature, the total errors become σ [C/H] = 0.04, σ [O/H] = 0.07, and σ [C/O] = 0.04. These are the random one-sigma errors, but systematical errors may also be present. As discussed in Sect. 5, there may be a systematic error of Teff as a function of [Fe/H] ranging from +60 K at [Fe/H] = −0.5 to − 60 K at [Fe/H] = +0.3. The corresponding change in [C/O] ranges from +0.04 at [Fe/H] = −0.5 to − 0.04 at [Fe/H] = +0.3. There may also be an effect of applying 1D model atmospheres instead of more realistic 3D models. According to Asplund et al. (2004), the difference of the oxygen abundance derived from the O i triplet using a 3D and a MARCS model for the solar atmosphere is − 0.06 dex, whereas the corresponding difference for the solar carbon abundance determined from the C i lines is − 0.01 dex (Asplund et al. 2005). It remains to be seen if these 3D – MARCS differences change with Teff or [Fe/H], but because the range of parameters for the present sample of stars is less than ± 600 K in Teff and ± 0.5 dex in [Fe/H], I do not expect any major 3D effects on the derived [C/O] values. It is also noted that the uncertainty of the SH parameter for hydrogen collisions, say a change from the adopted value SH = 0.85 to an extreme of SH = 0, has only a small effect on [C/O]; the changes are within ± 0.02 dex.
4. Results based on spectroscopic stellar parameters
Carbon and oxygen abundances are first derived with MARCS model atmospheres having the same parameters as applied by Delgado Mena et al. (2010). The original source of these parameters is Sousa et al. (2008), who in a differential, LTE analysis with respect to the Sun determined Teff, log g, [Fe/H], and ξturb by requesting that iron abundances derived from Fe i and Fe ii lines have no systematic dependence on excitation potential, ionization stage, or equivalent width. The parameters are listed in Table 4 together with the LTE and non-LTE values of [C/H] and [O/H] derived in this paper.
As seen from Fig. 1, there is an excellent agreement between the carbon abundances derived by Delgado Mena et al. (2010) and the values derived in this paper. The rms deviation in [C/H] is only 0.025 dex. This is not surprising, because in both studies C abundances are derived from equivalent widths of the λλ5052,5380 C i lines in high S/N HARPS spectra using the same set of stellar parameters.
 |
Fig. 5 λ6300.3 [O i]+Ni i blend in HARPS spectra of HD 196050 (full drawn line) and HD 216435 (red dots). |
The situation is, however, very different when one compares the oxygen abundances derived by Delgado Mena et al. (2010) from the λ6300 [O i] line with O abundances derived in this paper from FEROS spectra of the λ7774 O i triplet (see Fig. 2). In this case, the rms deviation is as large as 0.12 dex. The problem can be illustrated by comparing the spectra of two stars with similar atmospheric parameters Teff, log g, and [Fe/H], i.e. HD 196050 (5917 K, 4.32, 0.23) and HD 216435 (6008 K, 4.20, 0.24). As seen from Figs. 3 and 4, the C i and O i lines have about the same strengths in the two stars. Actually, the lines of HD 216435 are a bit wider and have slightly larger EWs than those of HD 196050, but due to the small differences in Teff and log g between the two stars, this is to be expected for fixed values of [C/H] and [O/H]. As seen from Table 4, the model-atmosphere analysis provide very similar O abundances, i.e. [O/H] = 0.12 for HD 196050 and [O/H] = 0.09 in the case of HD 216435. This is in stark contrast to the results of Delgado Mena et al. (2010), who obtain [O/H] = 0.36 for HD 196050 and [O/H] = −0.02 for HD 216435.
Figure 5 shows a comparison of HARPS spectra of HD 196050 and HD 216435 in the 6300 Å region. The [O i]+Ni i blend is affected by a telluric O2 line in many of the available HARPS spectra of HD 196050, so the spectrum shown in Fig. 5 is an average of a subset of spectra from July 2004, when the topocentric radial velocity of HD 196050 shifts the telluric line away from the [O i] line. As seen from the figure the equivalent width of the [O i]+Ni i blend is nearly the same in the spectra of HD 196050 and HD 216435, i.e. EW = 8.0 and 7.5 mÅ, respectively. Adopting [Ni/H] = 0.28 and 0.29 for the two stars (as used by Delgado Mena et al.) and solar flux data EW[O i] = 3.5 mÅ and EW(Ni i) = 2.0 mÅ (Caffau et al. 2008), a differential analysis with respect to the Sun leads to [O/H] = 0.17 ± 0.10 for HD 196050 and [O/H] = 0.11 ± 0.10 for HD 216435, where the main contribution to the error arises from the uncertainty of setting the continuum level. These [O/H] values agree well with the non-LTE values derived from the O i triplet, but lend no support to the large difference in [O/H] found by Delgado Mena et al. (2010). Perhaps, they applied a different set of HARPS spectra for HD 196050; in any case, the analysis shows that oxygen abundances derived from the [O i]+Ni i blend in spectra of metal-rich stars are uncertain due to difficulties in setting the continuum level and correcting for the large contribution of the Ni i line.
 |
Fig. 6 Differences between photometric gravities determined via Hipparcos parallaxes and spectroscopic gravities used by Delgado Mena et al. (2010). |
5. Results based on photometric stellar parameters
In order to test the reliability of the derived C/O ratios, photometric atmospheric parameters of the stars have been determined as an alternative to the spectroscopic parameters adopted by Delgado Mena et al. (2010). Teff was taken as the mean value derived from the ( and ( colour indices using the IRFM calibrations of Casagrande et al. (2010) with V magnitudes and ( from Olsen (1983) and K magnitudes from the 2MASS catalogue (Skrutskie et al. 2006). All stars are closer than 60 pc according to their Hipparcos parallaxes, so reddening corrections can be neglected.
The surface gravities of the stars were determined from the fundamental relation 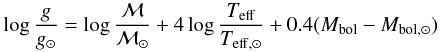 (1)where ℳ is the mass of the star and Mbol the absolute bolometric magnitude. Hipparcos parallaxes (van Leeuwen 2007) were used to derive MV and the bolometric correction adopted from Casagrande et al. (2010). The stellar mass was obtained by interpolating in the luminosity – log Teff diagram between the Yonsei -Yale evolutionary tracks by Yi et al. (2003) as described in detail by Nissen & Schuster (2012). Due to the small error of the Hipparcos parallaxes, the estimated error of log g is only 0.04 dex.
(1)where ℳ is the mass of the star and Mbol the absolute bolometric magnitude. Hipparcos parallaxes (van Leeuwen 2007) were used to derive MV and the bolometric correction adopted from Casagrande et al. (2010). The stellar mass was obtained by interpolating in the luminosity – log Teff diagram between the Yonsei -Yale evolutionary tracks by Yi et al. (2003) as described in detail by Nissen & Schuster (2012). Due to the small error of the Hipparcos parallaxes, the estimated error of log g is only 0.04 dex.
The metallicity was determined from 12 Fe ii lines with equivalent widths being measured from the HARPS spectra. By using Fe ii lines only, the derived [Fe/H] value is unlikely to be affected by departures from LTE (Mashonkina et al. 2011; Lind et al. 2012). The Fe ii lines have equivalent widths in the range 10 ≲EW ≲90 mÅ, which allows a determination of ξturb from the requirement that the derived [Fe/H] should not depend on EW.
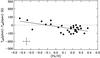 |
Fig. 7 Differences between photometric values of Teff determined from colour indices and spectroscopic values used by Delgado Mena et al. (2010). |
 |
Fig. 8 Difference between [C/O] values derived in this paper, when using photometric and spectroscopic stellar parameters, respectively. |
It is noted that this procedure for the determination of stellar parameters has to be iterated, because the Teff calibrations, bolometric corrections and mass determinations depend on [Fe/H].
When comparing the photometric and spectroscopic parameters, the following rms deviations are obtained: rms(ΔTeff) = 62 K, rms(Δlog g) = 0.12, rms(Δ [Fe/H] ) = 0.05, and rms(Δξturb) = 0.10 km s-1. The scatter for [Fe/H] and ξturb is as small as one would expect, if the one-sigma errors of each of the two studies are σ [Fe/H] ≃ 0.03 and σ(ξturb) = 0.07 km s-1. In the case of log g, the scatter is larger than expected from the estimated errors, i.e. σ(log g) = 0.06 for the spectroscopic gravities (Sousa et al. 2008) and σ(log g) = 0.04 for the photometric values obtained via the Hipparcos parallaxes. As shown in Fig. 6, this is mainly due to a significant dependence of Δlog g on Teff; the rms scatter around the fitted line is only 0.07 dex. This trend is not easy to explain; according to Lind et al. (2012, Fig. 4) non-LTE effects on the ionization balance of Fe (used to determine the spectroscopic gravities) are almost negligible for the effective temperatures, gravities and metallicities of the present sample of stars.
A similar problem is present, when one compares photometric and spectroscopic temperatures. In this case, the difference depends on [Fe/H] as shown in Fig. 7. Here, the rms deviation around the fit is 40 K. Again it is unclear, what is causing this trend with [Fe/H].
Despite of these systematic differences between the photometric and spectroscopic stellar parameters, the C/O ratios derived in this paper are not much affected as seen from Fig. 8. [C/O] is immune to changes in log g, whereas the trend of ΔTeff with [Fe/H] shown in Fig. 7 introduces a small dependence of Δ [C/O] on [Fe/H].
6. Discussion
Figure 9 shows the C/O ratios derived in this paper compared to the ratios derived by Delgado Mena et al. (2010) with the same set of spectroscopic stellar parameters applied in the two studies. Evidently, the C/O ratios of Delgado Mena et al. have a much larger scatter than the ratios obtained in this paper. Furthermore, the Delgado Mena et al. C/O ratios tend to be higher than the values in the present study, which is mainly due to the fact that they adopt a solar ratio (C/O)⊙ = 0.66 instead of the value (C/O)⊙ = 0.58 corresponding to the solar abundances derived in this paper (see Table 4). Recent 3D studies lead to nearly the same C/O ratio in the Sun, i.e. (C/O)⊙ = 0.55 ± 0.10 (Asplund et al. 2009; Caffau et al. 2008, 2010). The solar C/O ratio adopted by Delgado Mena et al. is on the high side of the quoted error range for these 3D studies.
 |
Fig. 9 Carbon-to-oxygen ratios derived in this paper (filled, black circles) in comparison with the C/O ratios determined by Delgado Mena et al. (2010) (open, red circles). The error bars shown refer to data from this paper. In the case of HD 196050 and HD 216435, the filled and open circles are connected by a straight line. |
Excluding two stars with [Fe/H] < −0.3 having thick-disk kinematics, one obtains a linear fit, C/O = 0.58 + 0.48 [Fe/H], to the data of this paper. If the two thick-disk are included the relation becomes C/O = 0.56 + 0.54 [Fe/H]. In both cases, the rms dispersion around the fit is σ (C/O) = 0.06. In comparison, the Delgado Mena et al. (2010) data have a scatter of σ = 0.14 relative to a linear fit with three stars having C/O ≃ 1 and 10 stars having C/O > 0.8. As discussed in Sect. 4, this difference in the C/O distribution is mainly due to the large differences in the oxygen abundances derived from the λ6300 [O i] line by Delgado Mena et al. and the O abundances derived in this paper from the O i triplet as exemplified by the comparison of HD 196050 and HD 215435. The small dispersion of C/O derived in this paper suggests that the high C/O values (>0.8) found by Delgado Mena et al. (2010) and by Petigura & Marcy (2011) are spurious due to difficulties in determining oxygen abundances from the λ6300 [O i]+Ni i blend especially at high metallicities. In the solar spectrum, the EWs of the Ni i and [O i] lines are 2.0 and 3.5 mÅ, respectively, (Caffau et al. 2008) i.e. a ratio of R ≃ 0.55, but in a solar-type star with [Fe/H] = +0.3, [O/Fe] = −0.15, and [Ni/Fe] = +0.1 (Bensby et al. 2005), the ratio is increased to R ≃ 1.
In view of the possible systematic errors in the 3D, non-LTE corrections for the C and O abundances derived from high-excitation C i and O i lines, it is important to check the trend and scatter of C/O obtained in this paper by independent determinations of C/O. Such a study has been carried out by Bensby et al. (2004) and Bensby & Feltzing (2006), who determined O and C abundances from weak forbidden lines, i.e. [O i] at 6300 Å and [C i] at 8727 Å. The non-LTE corrections for these lines are vanishing and 3D corrections are small in the solar case (Asplund et al. 2004, 2005; Caffau et al. 2008, 2010), but the lines are weak and affected by blends; in addition to the Ni i blend of the λ6300 [O i] line, a weak Fe i line is overlapping the λ8727 [C i] line. Hence, very high resolution and high S/N spectra are needed like those obtained with the Coudé Echelle Spectrograph at the ESO 3.6 m telescope by Bensby et al.
Figure 10 shows [C/O] versus [Fe/H] for a sample of 42 dwarf stars with 5000 < Teff < 6500 K from Table 1 in Bensby & Feltzing (2006), divided into thin- and thick-disk stars according to their kinematics. In addition, the figure shows data from the present study based on model atmospheres with photometric parameters. For this sample, three stars with a total space velocity relative to the Local Standard of Rest VLSR > 80 km s-1 (Holmberg et al. 2009) have been classified as belonging to the thick disk. Four stars are in common between the two samples; they show good agreement in [C/O], i.e. a mean and rms deviation (Bensby − this paper) Δ [C/O] = 0.02 ± 0.05.
As seen from Fig. 10, there is an excellent agreement between [C/O] data from Bensby & Feltzing (2006) and from this paper, including a systematic difference in [C/O] between thin- and thick-disk stars at low metallicity. A linear fit to the thin-disk data yields a trend 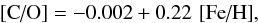 (2)with a standard deviation of ± 0.048 dex for 30 stars from this work and ± 0.068 dex for 27 stars from Bensby & Feltzing. This equation corresponds to [C/O] = 0.086 at [Fe/H] = +0.4 or C/O = 0.71, when adopting a solar ratio (C/O)⊙ = 0.58. If the solar ratio is (C/O)⊙ = 0.65, Eq. (2) corresponds to C/O = 0.79 at [Fe/H] = +0.4.
(2)with a standard deviation of ± 0.048 dex for 30 stars from this work and ± 0.068 dex for 27 stars from Bensby & Feltzing. This equation corresponds to [C/O] = 0.086 at [Fe/H] = +0.4 or C/O = 0.71, when adopting a solar ratio (C/O)⊙ = 0.58. If the solar ratio is (C/O)⊙ = 0.65, Eq. (2) corresponds to C/O = 0.79 at [Fe/H] = +0.4.
Another two high-precision studies of carbon and oxygen abundances in solar-type stars (Takeda & Honda 2005; Ramírez et al. 2009) also show good agreement with the [C/O]–[Fe/H] trend found in this paper as seen from Fig. 11. In both works, the adopted abundances are obtained from high-excitation C i and O i lines with non-LTE corrections based on their own calculations. The [C/O] values from Takeda & Honda, which include 27 planet-harbouring stars, distribute around the line given in Eq. (2) with an rms deviation of ± 0.070 dex, and the data from Ramírez et al. for solar twins and analogs have an rms deviation of 0.058 dex. In both cases, the scatter can be explained by the errors of the abundance determination, and although a few stars from Takeda & Honda fall above [C/O] = 0.14, which corresponds to C/O = 0.8, this may be accidental.
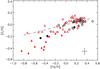 |
Fig. 10 [C/O] versus [Fe/H]. Data from this paper are plotted with circles and data from Bensby & Feltzing (2006) are shown with (red) triangles. Open symbols refer to stars with thin-disk kinematics and filled symbols to thick-disk stars. A linear fit to the thin-disk stars, given in Eq. (2), is shown by a dashed line. |
While oxygen is probably formed on a relatively short time-scale in massive stars exploding as Type II SNe, the origin of carbon is more uncertain with many possible sources including Type II supernovae, novae, winds from massive stars, and low- to intermediate-mass stars (Gustafsson et al. 1999). As shown by Akerman et al. (2004), [C/O] raises from a level of − 0.5 dex in halo stars with [O/H] < −1 to [C/O] ≃ 0 in disk stars with solar metallicity. A similar trend is found from H ii regions in spiral and irregular galaxies (Garnett et al. 2004). From this apparent universal metallicity dependence, Akerman et al. argue that the carbon enrichment in the Galactic disk is mainly due to metal-dependent winds from massive stars. In order to explain the difference in [C/O] between thin- and thick-disk stars shown in Fig. 10, it is, however, necessary to invoke a significant carbon contribution from low- and intermediate-mass stars ocurring on a relatively long time-scale in the Galactic thin disk (Chiappini et al. 2003; Carigi et al. 2005; Cescutti et al. 2009), whereas data for [C/O] in stars belonging to the thick disk and the Galactic bulge may be explained by metallicity-dependent C and O yields for massive stars alone (Cescutti et al. 2009). The situation is, however, complicated and the [C/O] data at high metallicity are not well explained, so more precise observations of C/O, more reliable yields, and realistic Galactic models are needed to advance the field.
7. Conclusions
The results in this paper and those of Bensby & Feltzing (2006), Takeda & Honda (2005), and Ramírez et al. (2009) show a tight [C/O]–[Fe/H] correlation for thin-disk stars. Furthermore, [C/O] is not reaching higher than [C/O] ≃ 0.1 dex (corresponding to C/O ≃ 0.7 for a solar ratio of (C/O)⊙ = 0.55) even at the highest metallicities. This suggests that the recent findings by Delgado Mena et al. (2010) and Petigura & Marcy (2011) of C/O > 0.8 in a significant fraction (10–15%) of solar-type stars are spurious due to difficulties in measuring the strength of the weak λ6300 [O i] + Ni i blend with sufficient precision and to correct for the Ni i contribution when deriving oxygen abundances.
 |
Fig. 11 [C/O] versus [Fe/H] with data from Takeda & Honda (2005) (circles) and Ramírez et al. (2009) (red triangles). Equation (2) is shown as a dashed line. |
As mentioned in the introduction, modelling of planet formation (Bond et al. 2010) indicates that C/O > 0.8 in proto-planetary disks with uniform composition lead to the formation of terrestrial “carbon planets” consisting of carbides and graphite instead of “Earth-like” silicates. Assuming that the composition of a proto-planetary disk is the same as that of the host star, the results in this paper (C/O < 0.8) lend no support to the existence of such carbon planets.
The separation of [C/O] between thin- and thick-disk stars suggests that carbon in the thin disk are mainly formed in low- and intermediate-mass stars. Assuming that oxygen comes from massive stars exploding as Type II SNe, the small dispersion of [C/O] indicates that the nucleosynthesis products of these objects are well mixed in the interstellar medium before new stars are formed. A detailed understanding of the formation of the two elements requires, however, further observational and theoretical studies.
Online material
ESO observing programme numbers, S/Ns, and equivalent widths measured by Gaussian fitting to line profiles.
Adopted atmospheric parameters and derived carbon and oxygen abundances.
Acknowledgments
The referee, Elisabetta Caffau, is thanked for comments that helped to improve the manuscript significantly. Funding for the Stellar Astrophysics Centre is provided by the Danish National Research Foundation (Grant agreement no.: DNRF106). The research is supported by the ASTERISK project (ASTERoseismic Investigations with SONG and Kepler) funded by the European Research Council (Grant agreement No. 267864). This publication made use of the SIMBAD database operated at CDS, Strasbourg, France, and of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by NASA and the National Science Foundation.
References
- Akerman, C. J., Carigi, L., Nissen, P. E., Pettini, M., & Asplund, M. 2004, A&A, 414, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., Allen de Prieto, C., & Kiselman, D. 2004, A&A, 417, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., Allen de Prieto, C., & Blomme, R. 2005, A&A, 431, 693 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Barklem, P. S. 2007, A&A, 462, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barklem, P. S., Piskunov, N., & O’Mara, B. J. 2000, A&AS, 142, 467 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Bensby, T., & Feltzing, S. 2006, MNRAS, 367, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Feltzing, S., & Lundström, I. 2004, A&A, 415, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., Lundström, I., & Ilyin, I. 2005, A&A, 433, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bond, J. C., O’Brien, D. P., & Lauretta, D. S. 2010, ApJ, 715, 1050 [NASA ADS] [CrossRef] [Google Scholar]
- Caffau, E., Ludwig, H.-G., Steffen, M., et al. 2008, A&A, 488, 1031 [CrossRef] [EDP Sciences] [Google Scholar]
- Caffau, E., Ludwig, H.-G., Bonifacio, P., et al. 2010, A&A, 514, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carigi, L., Peimbert, M., Esteban, C., & García-Rojas, J. 2005, ApJ, 623, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cescutti, G., Matteucci, F., McWilliam, A., & Chiappini, C. 2009, A&A, 505, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiappini, C., Matteucci, F., & Meynet, G. 2003, A&A, 410, 257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delgado Mena, E., Israelian, G., González Hernández, J. I., et al. 2010, ApJ, 725, 2349 [NASA ADS] [CrossRef] [Google Scholar]
- Demory, B.-O., Gillon, M., Deming, D., et al. 2011, A&A, 533, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drawin, H.-W. 1968, Z. Phys., 211, 404 [Google Scholar]
- ESA 1997, The Hipparcos and Tycho Catalogues, ESA SP-1200 [Google Scholar]
- Fabbian, D., Asplund, M., Barklem, P. S., Carlsson, M., & Kiselman, D. 2009, A&A, 500, 1221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fortney, J. J. 2012, ApJ, 747, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Garnett, D. R., Edmunds, M. G., Henry, R. B. C., Pagel, B. E. J., & Skillman, E. D. 2004, AJ, 128, 2772 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Karlsson, T., Olsson, E., Edvardsson, B., & Ryde, N. 1999, A&A, 342, 426 [NASA ADS] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hibbert, A., Biémont, E., Godefroid, M., & Vaeck, N. 1991, J. Phys. B, 24, 3943 [CrossRef] [Google Scholar]
- Hibbert, A., Biémont, E., Godefroid, M., & Vaeck, N. 1993, A&AS, 99, 179 [NASA ADS] [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2009, A&A, 501, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johansson, S., Litzén, U., Lundberg, H., & Zhang, Z. 2003, ApJ, 584, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Kaufer, A., Stahl, O., Tubbesing, K., et al. 1999, The Messenger, 95, 8 [Google Scholar]
- Kiselman, D. 2001, New Astron. Rev., 45, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Kuchner, M. J., & Seager, S. 2005, ApJ, submitted [arXiv:astro-ph/0504214] [Google Scholar]
- Lind, K., Bergemann, M., & Asplund, M. 2012, MNRAS, 427, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Madhusudhan, N., Lee, K. K. M., & Mousis, O. 2012, ApJ, 759, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Mashonkina, L., Gehren, T., Shi, J.-R., Korn, A. J., & Grupp, F. 2011, A&A, 528, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger , 114, 20 [NASA ADS] [Google Scholar]
- Nissen, P. E., & Schuster, W. J. 2012, A&A, 543, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olsen, E. H. 1983, A&AS, 54, 55 [NASA ADS] [Google Scholar]
- Pereira, T. M. D., Asplund, M., & Kiselman, D. 2009, A&A, 508, 1403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petigura, E. A., & Marcy, G. W. 2011, ApJ, 735, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., Meléndez, J., & Asplund, M. 2009, A&A, 508, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Takeda, Y., & Honda, S. 2005, PASJ, 57, 65 [NASA ADS] [Google Scholar]
- Unsöld, A. 1955, Physik der Sternatmosphären, 2nd edn. (Berlin: Springer Verlag) [Google Scholar]
- van Leeuwen, F. 2007, Hipparcos, the New Reduction of the Raw Data, (Dordrecht: Springer) Astrophys. Space Sci. Library, 350 [Google Scholar]
- Winn, J. N., Matthews, J. M., Dawson, R. I., et al. 2011, ApJ, 737, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Yi, S. K., Kim, Y. -C., & Demarque, P. 2003, ApJS, 144, 259 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
ESO observing programme numbers, S/Ns, and equivalent widths measured by Gaussian fitting to line profiles.
All Figures
 |
Fig. 1 Carbon abundances of Delgado Mena et al. (2010) in comparison with carbon abundances derived in this paper. |
| In the text | |
 |
Fig. 2 Oxygen abundances of Delgado Mena et al. (2010) in comparison with non-LTE oxygen abundances derived in this paper. |
| In the text | |
 |
Fig. 3 λ5380 C i line in HARPS spectra of HD 196050 (full drawn line) and HD 216435 (red dots). |
| In the text | |
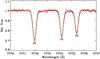 |
Fig. 4 O i triplet in FEROS spectra of HD 196050 (full drawn line) and HD 216435 (red dots). |
| In the text | |
 |
Fig. 5 λ6300.3 [O i]+Ni i blend in HARPS spectra of HD 196050 (full drawn line) and HD 216435 (red dots). |
| In the text | |
 |
Fig. 6 Differences between photometric gravities determined via Hipparcos parallaxes and spectroscopic gravities used by Delgado Mena et al. (2010). |
| In the text | |
 |
Fig. 7 Differences between photometric values of Teff determined from colour indices and spectroscopic values used by Delgado Mena et al. (2010). |
| In the text | |
 |
Fig. 8 Difference between [C/O] values derived in this paper, when using photometric and spectroscopic stellar parameters, respectively. |
| In the text | |
 |
Fig. 9 Carbon-to-oxygen ratios derived in this paper (filled, black circles) in comparison with the C/O ratios determined by Delgado Mena et al. (2010) (open, red circles). The error bars shown refer to data from this paper. In the case of HD 196050 and HD 216435, the filled and open circles are connected by a straight line. |
| In the text | |
 |
Fig. 10 [C/O] versus [Fe/H]. Data from this paper are plotted with circles and data from Bensby & Feltzing (2006) are shown with (red) triangles. Open symbols refer to stars with thin-disk kinematics and filled symbols to thick-disk stars. A linear fit to the thin-disk stars, given in Eq. (2), is shown by a dashed line. |
| In the text | |
 |
Fig. 11 [C/O] versus [Fe/H] with data from Takeda & Honda (2005) (circles) and Ramírez et al. (2009) (red triangles). Equation (2) is shown as a dashed line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


