| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A104 | |
| Number of page(s) | 11 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201220987 | |
| Published online | 09 April 2013 | |
Phase correction for ALMA with 183 GHz water vapour radiometers
1
Astrophysics Group, Cavendish Laboratory, University of
Cambridge,
JJ Thomson Avenue,
Cambridge
CB3 0HE,
UK
e-mail:
bnikolic@nrao.edu
2
Kavli Institute for Cosmology Cambridge,
Madingley Road
Cambridge, CB3
0HA, UK
3
Joint ALMA Observatory, Alonso de Cordova 3107, Vitacura, Santiago, Chile
Received:
21
December
2012
Accepted:
25
February
2013
Fluctuating properties of the atmosphere, and in particular its water vapour content, give rise to phase fluctuations of astronomical signals which, if uncorrected, lead to rapid deterioration of performance of (sub)-mm interferometers on long baselines. The Atacama Large Millimetre/submillimeter Array (ALMA) uses a 183 GHz water vapour radiometer (WVR) system to help correct these fluctuations and provide much improved performance on long baselines and at high frequencies. Here we describe the design of the overall ALMA WVR system, the choice of design parameters and the data processing strategy. We also present results of initial tests that demonstrate both the large improvement in phase stability that can be achieved and the very low contribution to phase noise from the WVRs. Finally, we describe briefly the main limiting factors to the accuracy of phase correction seen in these initial tests; namely, the degrading influence of cloud and the residual phase fluctuations that are most likely to be due to variations in the density of the dry component of the air.
Key words: atmospheric effects / instrumentation: high angular resolution / techniques: interferometric
© ESO, 2013
1. Introduction
The Atacama Large (sub-)Millimetre Array (ALMA) is an aperture-synthesis telescope that will consist of 66 antennas observing at millimetre and sub-millimetre wavelengths on baselines ranging in length from 9 m to 16 km. The Earth’s troposphere has a large degrading effect on astronomical observations at these wavelengths, and to minimise these effects ALMA is located at a very dry site in northern Chile with an altitude of 5000 m.
Even at this site, the troposphere will have a significant effect on most ALMA observations, consisting of two related phenomena (see, for example, Wilson et al. 2009):
-
1.
Absorption of incoming astronomical radiation (andcorresponding emission of incoherent thermal radiation).
-
2.
Delay to the incoming astronomical radiation (i.e., non-unit refractive index) that is variable in time and in position.
The two phenomena are physically related by the requirement of causality (see, e.g., Toll 1956) as mathematically described by the Kramers-Krönig relation. They are primarily caused by the molecules of oxygen, nitrogen and water in the troposphere. The degradation of the astronomical signals caused by the absorption is of course irreversible, but this is not the case for the delay. If (as is the case for ALMA) the individual elements of the interferometer are smaller than the characteristic length-scale over which delay varies, and the received signal is sampled faster than the characteristic time-scale over which the delay changes, then the effects of variable delay can in principle be corrected in the data processing step (Hinder & Ryle 1971). For this to be possible, it is however necessary to be able to estimate the delay variation due to the atmosphere. In the case of ALMA a system of water vapour radiometers (WVR) operating at 183 GHz is used for this purpose.
1.1. Structure of the atmosphere
Nitrogen, oxygen and other “dry” components of the troposphere are well-mixed with each other and are in near pressure equilibrium. As a result, the pressure and total column density of the troposphere generally vary only slowly with time and position. In contrast, the temperature of the dry air does vary rapidly in time and position. This is due to a combination of hydrostatic temperature variation, localised heating and cooling at the Earth’s surface and the effect of wind-induced turbulence. These temperature fluctuations have only a minor effect on the absorption by dry air but a significant effect on the refractive index, leading to fluctuations in apparent delay of astronomical signals. These delay fluctuations are, in turn, the dominant cause of seeing that impacts astronomical observations at optical and infrared wavelengths from the Earth’s surface. These “dry” delay fluctuations due to temperature differences of air also have a measurable effect at millimetre and sub-millimetre wavelengths, but are generally much smaller than the effects of water vapour.
Due to its large dipole moment, water vapour is a strong absorber at millimetre and sub-millimetre wavelengths. It also significantly increases the refractive index of air and therefore delays the radiation, with one millimetre of precipitable water vapour corresponding to an equivalent of approximately 6 millimetres of extra “electrical path”. Unlike the “dry” air components, water vapour is generally very poorly mixed with the other components of air, which means that its concentration (or partial pressure) varies rapidly in time and position. This in turn means that the integrated water vapour along the line of sight of each element of an interferometer, and consequently the apparent delay to each element, are fluctuating in time in a way that is different for each element.
If we assume that the differences in concentration of water vapour are driven by fully developed turbulence, then the likely difference in concentration of water vapour between two points in the atmosphere is an increasing function of the distance between these points up to some “outer length scale”. Carilli & Holdaway (1999) show evidence that, at the VLA site in New Mexico, USA, this outer length-scale at which the differences between two points no longer increase is at least as large as the maximum baseline length of ALMA. This increase in the differences in water vapour concentration with baseline length translates into an increase in the magnitude of path fluctuations on longer baselines, making measurements of astronomical signals less efficient and less accurate.
1.2. Impact of phase errors on science data
An aperture synthesis telescope is only sensitive to changes in the difference of delays between pairs of elements. A fluctuating difference in the delays leads to a fluctuation in the phase of the correlated signal (the “visibility”) recorded for that pair.
Such phase fluctuations have a number of effects on the images of the sky reconstructed
from the visibilities (see for example Nikolic et al.
2008; Lay 1997) two of which are most
important. Firstly, they cause decorrelation, i.e., a reduction of the apparent amplitude
of visibility recorded, because the signal is not fully coherent for the duration of
observation. The decorrelation causes a loss of amplitude by a factor
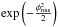 where φrms is the root-mean-square (rms) fluctuation of phase.
The magnitude of the noise in the measurements is unaffected by these phase fluctuations
and therefore the decorrelation leads to a reduction in the sensitivity of the telescope.
where φrms is the root-mean-square (rms) fluctuation of phase.
The magnitude of the noise in the measurements is unaffected by these phase fluctuations
and therefore the decorrelation leads to a reduction in the sensitivity of the telescope.
Secondly, the errors in the measured visibilities produce spurious features on the maps that are produced. These spurious features lead to a further reduction in the dynamic range of the maps. (The term “dynamic range” is the ratio of the highest peak on the map to the average noise in the parts of the map where there are no real astronomical sources.) Note that in addition to the errors in the phases caused directly by the atmospheric fluctuations, errors are also introduced into the measured amplitudes because the amount of decorrelation of each sample varies due to the random nature of the fluctuations. Both sorts of error contribute to the spurious features in the map.
The magnitude of the atmospheric fluctuations increases on longer baselines and, at millimetre and particularly sub-millimetre wavelengths, a baseline length is reached where the path variations are a large fraction of a wavelength and no useful astronomical signal can be reconstructed. This means that, without correction of the phase fluctuations, the angular resolution of the telescope will be limited by the effects of the atmosphere. The resolution achievable without correction is extremely variable, but a typical value is, coincidentally, similar to the optical seeing at good sites, i.e., around 0.5 arcsec (see for example the analysis of ALMA site-testing data by Evans et al. 2003).
1.3. Strategies for dealing with atmospheric phase fluctuations
If no phase correction method is available, the only option is to limit the observing to short baselines and/or to times when the atmosphere is sufficiently stable. This is effective because on short enough baselines, the elements of an interferometer look along similar lines of sight through the atmosphere and therefore suffer from almost the same total path fluctuations; this means that the differential path fluctuation, which is what determines phase fluctuation of the visibility, is small. This strategy however directly limits the maximum resolution attainable with the interferometer and reduces the amount of observing time available.
Alternatively, if the surface brightness of the objects being observed is sufficiently high, it may be possible to use the technique of self-calibration (e.g., by Pearson & Readhead 1984; Cornwell & Fomalont 1999). With this technique, the observed interferometric visibilities are used to solve simultaneously for the path errors to the antennas and for the reconstructed image of the sky. For this technique to be effective the signal-to-noise ratio in the time interval being solved for needs to be high enough to give phase errors smaller than those caused by the atmosphere. This technique works well at centimetre wavelengths, especially for compact non-thermal sources, but at millimetre and sub-mm wavelengths many objects will not have sufficiently high brightness temperatures to satisfy the signal-to-noise requirement, especially on the longer baselines. Several factors contribute to this increasing difficulty as one moves to shorter wavelengths. These include the nature of the emission, which is generally thermal, the higher system noise temperatures and the fact that the timescales of the atmospheric fluctuations that cause significant decorrelation are shorter. The large instantaneous bandwidth available provides some mitigation when the source has continuum emission, but that does not apply for objects where the emission is limited to a few spectral lines.
To alleviate the problems of low signal-to-noise ratio on the science target, phase referencing (also known as fast-switching) can be implemented. In this scheme a phase calibrator, nearby in the sky to the science target, is observed frequently and the phase measurements obtained for each antenna (from self-calibration) are used to generate an interpolated phase correction table for the source. This method is presented in Carilli & Holdaway (1999) and is in routine use at the (J)VLA at 22 GHz and higher frequencies. For centimetre wavelengths, calibration on timescales of order one minute is effective, but at millimetre and especially sub-mm wavelengths much shorter calibration times are needed to prevent significant decorrelation. Finding suitable phase calibrators that are sufficiently close to the target also becomes increasingly difficult at higher frequencies.
Another option is the paired-antennas method (see Asaki et al. 1996) where sub-arraying (i.e., independent interferometric arrays operating side-by-side) is used so that both the target source and a calibrator source are observed simultaneously. Provided that the science target and calibrator are close enough on the sky, phase measurements of the calibrator can be used to determine the phase correction required above each of the calibrator-array antennas and these can be transferred, directly or with interpolation, to nearby antennas in the science-subarray. This technique has been used successfully at mm wavelengths at the CARMA telescope (Pérez et al. 2010).
Although they are effective at improving phase noise from the atmosphere, both fast-switching and the paired-antennas methods come at a cost in terms of sensitivity, in the former case because time on source is reduced and in the latter because only a fraction of the array is available for science observing. In addition there are, in both cases, limitations on the accuracy that can be achieved. In fast-switching, the non-continuous measurement of the calibrator phase means that we are forced to interpolate in time to estimate the phase corrections to apply to the observations of the science source, and the lines of sight through the atmosphere necessarily differ because the source and calibrator are not co-located on the sky. In the paired antenna scheme, whilst there is continuous measurement of calibrator phase, the path through the atmosphere is different for the science and calibrator sources, both because of the different sky positions and because of the different positions of the antennas on the ground.
1.4. Radiometric phase correction
It was realised early on in the development of interferometric telescopes operating at cm-wavelengths that water vapour fluctuations are an important limitation on achievable resolution (Baars 1967; Hinder & Ryle 1971). By this time the basic technique of using passive radiometers to do remote-sensing of the water vapour content of the atmosphere was already developed (Barrett & Chung 1962) and it was therefore soon proposed that radiometers could be used to correct for the path delay due to water vapour and therefore phase errors in an interferometer (e.g., Schaper et al. 1970).
The principle of radiometric phase correction is to make measurements of the sky brightness as a function of time along the line of sight of the antennas and use these to infer the delays to the astronomical signal received at each antenna. Since water vapour is the largest contributor to the time-variable delays, radiometer systems have most often been designed to observe at frequencies around strong water-vapour transitions.
Most of the larger mm and sub-mm wave interferometric telescopes have either implemented or experimented with radiometric phase correction techniques in order to improve the coherence of the astronomical signal on longer baselines. Systems based on the 22 GHz water vapour line have been installed or experimented with at the IRAM Plateau de Bure Interferometer (PdBI) in the French Alps (Bremer 2002), at the NRAO Very Large Array in New Mexico and at the Owens Valley Radio Observatory in California (Woody et al. 2000). Only the system at PdBI is in routine operation. 22 GHz radiometers are also used on some VLBI telescopes, for example at Effelsberg (Roy et al. 2007).
A broadband continuum radiometric phase correction technique where the atmospheric emission away from specific transitions, but which is still mostly due to water vapour, has been tried at Berkley-Illinois-Maryland Array (Zivanovic et al. 1995), IRAM PdBI (Bremer et al. 1995) and at the Sub-Millimeter Array (Battat et al. 2004).
Finally, phase correction using the 183 GHz water vapour line has been demonstrated at the James Clerk Maxwell Telescope – Caltech Submillimeter Observatory interferometer (Wiedner et al. 2001). The ALMA radiometer system is to a large extent based on that concept.
2. System overview
The ALMA specification, at system level, for correction of phase fluctuations due to water
vapour is given by: 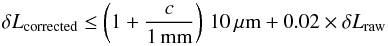 (1)where the
symbols have following meanings:
(1)where the
symbols have following meanings:
-
δ
L
raw
is the uncorrected path fluctuations on a baseline
-
c
is the Precipitable Water Vapour (PWV) column along the line of sight of an antenna
-
δ
L
corrected
is the specification for the per-antenna path fluctuations after the correction.
The quantity normally measured is the phase fluctuation on a baseline, which is allowed to
be up to 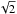 larger than the per-antenna specification. The specification in Eq. (1) applies on timescales shorter than 180 s; the
specification assumes that any residual errors on timescales longer than 180 s will be
adequately corrected by observations of point source phase calibrators near to the science
target.
larger than the per-antenna specification. The specification in Eq. (1) applies on timescales shorter than 180 s; the
specification assumes that any residual errors on timescales longer than 180 s will be
adequately corrected by observations of point source phase calibrators near to the science
target.
If these specifications are just met, they imply a 7% amplitude loss due to decorrelation (see discussion in Sect. 1.2) from residual phase errors if observing at λ = 350 μm in 0.5 mm PWV; 2.5% loss if observing at λ = 850 μm at 1.1 mm PWV; and less than 1% loss when observing at λ = 3 mm when the line of sight PWV is 3 mm. By comparison, the loss due to atmospheric absorption when observing at λ = 350 μm through 0.5 mm PWV is about 50%, i.e., much larger than the loss due to decorrelation. The losses due to decorrelation are however highly variable and hard to estimate. As a result they affect both the image quality and the flux calibration accuracy. By contrast, the losses due to absorption need not have a significant effect on imaging or accuracy, apart from the inevitable loss of sensitivity, so long as appropriate calibration techniques are applied.
The ALMA phase correction system consists of 183 GHz WVRs installed on all of the 12 m diameter antennas. The WVRs measure the observed sky signal, integrate the signal for an operator-selected time interval and apply an internal calibration, so that the output values are in units of antenna temperature. The integration times used are typically around one second, as this corresponds to characteristic minimum timescale (~D/u where D = 12 m is the antenna diameter and u ~ 10 m s-1 is the wind speed) over which the observed signal varies. The WVR measurements are collected by the ALMA correlator subsystem, recorded to the permanent data store and optionally used for on-line phase-correction.
3. WVR instrument design
A block diagram of the conceptual design of the radiometers deployed by ALMA is shown in Fig. 1. This is an evolution of the design originally described by Wiedner et al. (2001) which was used as a starting point for two ALMA prototype WVRs designed and built by a collaboration between the University of Cambridge and Onsala Space Observatory. These prototypes were in turn used as input for the detailed design and production of the final production WVRs by Omnisys Instruments AB, Sweden. The detailed design of production units is described by Emrich et al. (2009). In this section we describe the design parameters of the WVRs and their justification.
 |
Fig. 1 Conceptual design of the water vapour radiometers. |
3.1. Frequency response
The objectives of the frequency response and filter design of the WVRs were:
-
Maximum sensitivity to water vapour fluctuations over a range oftotal water vapour column conditions.
-
Sufficient frequency resolution to avoid using the saturated part of the line when conditions are wet and to avoid the wings when conditions are dry.
-
Measurement of both the inner part of the water vapour line and the wings to allow inference of atmospheric properties such as total water vapour column and also constraints on its vertical distribution.
-
Keep the design as simple as possible and limit the costs.
To maximise the sensitivity, the entire region of the spectrum around the 183 GHz water vapour line is sampled simultaneously using a double-sideband (DSB) mixing system with four fixed Intermediate Frequency (IF) filters. The alternative arrangement of using a single filter, sideband separation and tunable local oscillators (LOs) to scan a single detection band across the line is used in some commercial atmospheric sounders but would lead to extra complexity and lower sensitivity (as only a part of the spectrum is sampled at any one time) while the additional frequency resolution is not thought to be an advantage in our application.
During the design and prototyping stages the effects of clouds were recognised as potential sources of errors in the WVR phase correction technique. In order to try to reduce this problem, a sideband-separation design leading to a dual-single-sideband (2SB) system was considered and implemented in one of the prototypes. Such a 2SB system can distinguish a sloping continuum spectrum from one which is symmetric around the LO frequency and can therefore be used to separate the contribution to the sky brightness from water vapour and from cloud droplets (which has opacity that approximately varies as ν2). The extra complexity and cost of sideband separation was however judged to outweigh the benefits and this option was therefore descoped for the ALMA production radiometers.
Selection and optimisation of the filters frequencies and bandwidths is discussed in detail by Hills (2007). The main conclusions of this optimisation study are that:
-
For optimum sensitivity it is best to divide the entire available IF bandwidth between the filters.
-
Estimates of the continuum (which is dominated by clouds when they are present) are most constrained by the outermost channel and therefore this channel should be kept relatively narrow so that is contains only a small contribution from the wing of the line.
A model computation of sky brightness around the 183 GHz water vapour line is shown in Fig. 2 for a range of total water vapour columns that is representative of typical conditions at the ALMA site. It can be seen that the conditions range from optically thin at the centre of the line to completely optically thick in a range of around 2 GHz around the centre of the line. This can also be seen Fig. 3, which shows the rate of change of sky brightness with respect to changes of the total water vapour column over the same frequency range as Fig. 2. Higher values of this rate of change mean that for the same magnitude of noise in the WVR receiver system, a smaller phase noise is achievable in the corrected data. It can therefore be seen from this plot that the optimum frequencies for measurement of water vapour fluctuations range from the centre of the line (under very dry conditions) to about to about 5 GHz away from the centre (for about 5 mm of water). In order to allow for a channel which measures primarily the continuum contribution, the IF bandwidth selected was 0.5 GHz to 8.0 GHz divided into four channels. The final design of the filter centres and bandwidths is illustrated in Fig. 4, together with a model computation of sky brightness of the 183 GHz water vapour line.
 |
Fig. 2 Model brightness of the atmosphere at frequencies around the 183 GHz water vapour line for six values of PWV along the line of sight: 0.3, 0.6, 1, 2, 3 and 5 mm (from lowest red line to highest blue line). The model was computed using the ATM program by Pardo et al. (2001), using the source code the model as used by ALMA (this is available for public download at http://www.mrao.cam.ac.uk/~bn204/alma/atmomodel.html). |
 |
Fig. 3 Differential of brightness of the atmosphere with respect to the total line of sight precipitable water vapour (c), computed for the same six values of total PWV as in Fig. 2. |
 |
Fig. 4 Design band-passes of the four channels of ALMA WVRs, together with a plot model brightness temperature for 1 mm of PWV. |
 |
Fig. 5 Relative change in the model phase correction coefficients for a 5% shift in the centre frequency of each filter versus the total column of water vapour in mm. Red to blue lines (following the spectrum) are channels 1 to 4. |
Since mass-production of WVRs with frequency responses that are very uniform is difficult, ALMA adopted a manufacturing specification with a 5% tolerance on the centre frequency and bandwidth of the response of the entire system. To obtain the required phase-correction performance it is however necessary to have better knowledge than this of the actual response. This is illustrated by Fig. 5 which shows a model computation of the change of the constant of proportionality between sky brightness fluctuations and path fluctuations for a 5% change in the channel centre frequency. It can be seen in this figure that a mis-characterisation of the centre frequency of that magnitude can easily lead to errors of a few to 10 per cent in the phase correction coefficients, which will typically lead to similar errors in the derived path correction. Such errors would be significant when compared to the specification shown in Eq. (1). For this reason the frequency response of each ALMA WVRs was characterised by the manufacturer after final assembly to better than 1 percent accuracy in the centre frequency and bandwidth of each channel.
 |
Fig. 6 Model phase correction coefficients versus the total column of water vapour. Red to blue lines (following the spectrum) are channels 1 to 4, i.e., innermost to outermost channel. Note that the units of the ordinate are Kelvin per millimetre of extra path in contrast to Fig. 3 which has units of Kelvin per mm of precipitable water vapour. |
3.2. Sensitivity requirements
A basic limit on the accuracy of phase correction arises from the white-spectrum
thermal-like noise arising in the mixer and amplifier of the WVR receivers. The magnitude
of the errors introduced by this thermal-like noise depends on the atmospheric conditions
(primarily the total water vapour column), the integration time used and the way in which
the signals for the four channels of the WVRs are combined. The thermal-like noise
fluctuation in the measured sky brightness is given by: 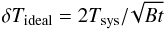 (2)where:
(2)where:
-
T
ideal
is the fluctuation, labelled “ideal” because it does not take intoaccount effect the gain fluctuations discussed inSect. 3.3;
-
B
is the bandwidth;
-
t
is the total integration time;
-
T
sys
is the system noise temperature (and is of the order of 1000 K for ALMA production systems).
The factor of two in Eq. (2) arises because the radiometers measure the
sky for only about half of the time while the calibration loads are measured in the other
half (this gives a factor of 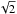 );
and, because the final measurement is derived approximately from the difference
of measurements on the sky and the calibration loads (giving another factor of
);
and, because the final measurement is derived approximately from the difference
of measurements on the sky and the calibration loads (giving another factor of
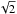 ).
A lower-noise design is possible by having two separate receivers arranged so that one is
observing the calibration loads while the other is observing the sky and vice versa. This
was implemented on the prototype WVRs but was not adopted for the production requirements
for reasons of cost and complexity.
).
A lower-noise design is possible by having two separate receivers arranged so that one is
observing the calibration loads while the other is observing the sky and vice versa. This
was implemented on the prototype WVRs but was not adopted for the production requirements
for reasons of cost and complexity.
The relationship between a small change in sky brightness and the consequent change in the electrical path to the antenna is given by “phase-correction coefficients” which we denote by dL/dTB. Plots of phase-correction coefficients computed from models for the four channels of the production WVRs and for a wide range water vapour columns are shown in Fig. 6. The critical region of PWV for sensitivity is around 2 mm of PWV where the line begins to saturate and the effective sensitivity of the central channel begins to decrease rapidly. The phase correction coefficients at around 2 mm PWV are around 4–6 K mm-1 while the specification in Eq. (1) calls for a path error of 0.03 mm. This calculation indicates that if the noise in measuring the sky brightness can be held to of order 0.1 K, the specification can be met in this critical region while still using data from only one channel. A more detailed analysis of this topic is given by Stirling et al. (2005).
3.3. Gain and absolute calibration
In order to achieve a high effective sensitivity, the WVRs must be calibrated frequently enough to remove the effect of gain fluctuations. These fluctuations in gain usually have a 1/f spectrum. Additionally, WVRs for ALMA need to have a good absolute calibration, since the total power of sky emission is used infer the water vapour column and other atmospheric parameters. They also need good stability in time and with respect to small motions in the antenna.
For a standard Dicke radiometer, an estimate of the effective noise including the effect
of gain fluctuations is: ![\begin{equation} \delta T_{\rm src}= \sqrt{\delta T_{\rm ideal}^2 + \left[(T_{\rm src}-T_{\rm ref})\frac{\delta G}{G} \right]^2} \end{equation}](/articles/aa/full_html/2013/04/aa20987-12/aa20987-12-eq24.png) (3)where:
(3)where:
-
δ
T
ideal
is the fluctuation of an “ideal” radiometer as discussed inSect. 3.2;
-
T
src
is the effective temperature of the source being measured, i.e. the sky brightness;
-
T
ref
is the effective temperature of reference, i.e. the calibration load or loads;
-
G
is the gain of the radiometer;
-
δG
is the fluctuation in the gain.
Normally a Dicke-switched radiometer is designed so that Tref is close to Tsrc and therefore the contribution of gain fluctuations to the uncertainty of measurement is minimised. This is however hard to achieve in the case of ALMA’s 183 GHz WVRs because:
-
1.
The sky brightness varies strongly as a function atmospheric conditions, frequency and airmass, with the range corresponding to brightness temperatures from 25 K to about 260 K. Therefore no single reference load temperature can be suitable for all observations.
-
2.
It is considerably cheaper and more reliable to have reference loads near the ambient temperature, whereas the sky brightness is always smaller than these ambient temperatures.
For these reasons the ALMA WVRs operate as unbalanced Dicke radiometers where the differencing scheme removes some but not all of the effects of gain fluctuations, and some form of frequent calibration for gain fluctuation must be used. This is implemented by observing two calibration loads, at different temperatures, Tcold (about 280 K for the ALMA production WVRs) and Thot (about 360 K).
The gain is estimated as: 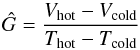 (4)where
Vcold is the signal when observing the cold load and
Vhot is the signal when observing the hot load. Therefore:
(4)where
Vcold is the signal when observing the cold load and
Vhot is the signal when observing the hot load. Therefore:
 but
Ĝ now includes fluctuations due to measurement error of
Vhot and Vcold. In fact unless
(Thot − Tcold) is much greater
than (Tsrc − Tref) then
Ĝ must be smoothed. If the gain is not smoothed, then even without any
gain fluctuations the effective noise will be dominated by the errors in the gain estimate
rather than the gain fluctuations themself. An approximate relationship is:
but
Ĝ now includes fluctuations due to measurement error of
Vhot and Vcold. In fact unless
(Thot − Tcold) is much greater
than (Tsrc − Tref) then
Ĝ must be smoothed. If the gain is not smoothed, then even without any
gain fluctuations the effective noise will be dominated by the errors in the gain estimate
rather than the gain fluctuations themself. An approximate relationship is:
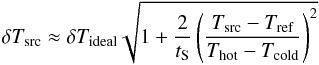 (8)where
the factor of two arises because the calibration loads are each observed for only half of
the time that the sky is observed and tS is the smoothing
factor, which is the ratio of the time over which the gain is smoothed to the integration
time used for the measurement of the sky brightness temperature. For the case of ALMA
WVRs, a smoothing factor of at least 60 is required to ensure that the errors in the gain
estimate are not dominant.
(8)where
the factor of two arises because the calibration loads are each observed for only half of
the time that the sky is observed and tS is the smoothing
factor, which is the ratio of the time over which the gain is smoothed to the integration
time used for the measurement of the sky brightness temperature. For the case of ALMA
WVRs, a smoothing factor of at least 60 is required to ensure that the errors in the gain
estimate are not dominant.
In fact, for unbalanced Dicke-switched radiometers like this, an alternative gain estimation scheme is possible which makes use of the facts that:
-
1.
The receiver noise temperature and any additive post-detectionoffsets are relatively stable in time.
-
2.
The total signal when observing a calibration load can then be used to calibrate the gain, i.e.:
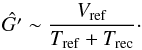 (9)
(9) -
3.
Longer time scale changes in the gain and receiver temperature/offset can be estimated from two-load observations using ample smoothing.
This has the advantage that, as denominator Tref + Trec is large, the significance of measurement fluctuations of Vref is small and no smoothing on gain needs to be employed, enabling correction of shorter timescale gain fluctuations. This scheme was explored for the use on the ALMA WVRs but was found not to be necessary.
The overall absolute calibration of the WVRs is fixed by observing external ambient and liquid nitrogen calibration loads during the in-factory characterisation of the units. The absolute calibration is important as the absolute sky brightness is used to fit an atmospheric model and to estimate the quantities needed for translation of WVR fluctuations into path changes.
3.4. Optical design
To ensure accurate phase correction it is important that the radiometer and astronomical beams overlap closely so that the radiometer is measuring the emission from the same water vapour which is delaying the astronomical radiation. This was achieved at ALMA by mounting the WVRs in the focal plane of the antennas so that they use the same primary and secondary mirror optics as the astronomical receiver. In fact the WVR beam corresponds to the bore-sight of the telescope, with the four astronomical beams closest to it being the highest frequency astronomical receivers (Bands 7, 8, 9 and 10) since these are the ones for which the phase correction is most important. The angular separation between the WVR beam and astronomical beams is between 3.5 and 9 arcmin, corresponding to a divergence of between 1 and 3 m at 1000 m above ground level. At this distance from the antennas the beams are still of order 12 m across, so this separation corresponds to about 10%–30% of the beam width. The quantitative impact of this beam divergence is investigated by Nikolic et al. (2007). Fixed relative pointing between astronomical and WVR beams is guaranteed by rigid mounting of the radiometer on the Front-End Support Structure that also supports the astronomical receivers.
The sensitivity of the WVRs is high enough that they can be quite sensitive to spill-over radiation, especially if it depends on time or the pointing of the antenna. For example, a 0.1 percent change in the spill-over onto the ground will lead to about a 0.3 K change in the observed signal, which is more than 3 times higher than the thermal noise in a one-second integration time. Such changes in spill-over would be confused with real changes of sky brightness and therefore be translated into inaccurate corrections of the phase of the astronomical signal.
The magnitude of the spill-over for ALMA WVRs is minimised by under-illuminating the optics. The overall antenna gain of the WVR system is not important for WVR operation since, to first order, the system needs only to measure the surface brightness of sky emission along the boresight of the antenna. Therefore the WVR system was designed to illuminate the primary reflector with an edge taper of − 16 dB and a maximum of 2% spill-over past the secondary. The under-illumination, together with adequate sizes for the relay optics between the WVR and the secondary mirror, means that the overall forward efficiency of the system is over 95%. The under-illumination does mean that the volume of the atmosphere that affects the astronomical signal is a little larger than that measured by the radiometer but this is expected to have only a small effect on the final results (see Nikolic et al. 2007).
4. Data processing
As described above, the WVR measurements are calibrated internally in the radiometer and are output as sky brightness in units of Kelvin. The subsequent data processing uses these measurements to correct the astronomical data for the effects of the atmosphere. ALMA has two software implementations of this processing: an on-line system which applies the phase correction, in the software associated with the correlator, before the visibilities are stored; and an off-line system which phase-rotates the visibilities during the standard interferometric data reduction. The on-line system is part of the overall on-line telescope calibration system “TelCal” described by Broguière et al. (2011), while the off-line system is the separate program “wvrgcal” described by Nikolic et al. (2012) and which is now incorporated into the CASA1 distribution. The principles of the two data processing implementations are broadly similar but where they are different the description below is of the off-line system.
At frequencies around 183 GHz the relationship between sky brightness and water vapour column (and therefore excess path) is highly non-linear because the water vapour line is close to saturation even in very dry conditions. This is in contrast to the situation at 22 GHz, where the line is relatively weak and therefore not saturated, but where other effects such as variable spill-over and cloud can become very important. This non-linearity, together with the dependence of the water vapour line on temperature and pressure of the atmosphere, means that a multi-dimensional non-linear model must be fitted to the observed sky brightness to determine the total excess path.
For ALMA phase-correction we are however primarily interested in the change of the
electrical path to the antenna over small changes of direction on sky and for small periods
of time. For small enough changes, the path can be linearised so that
δL ≈ (dL/dTB,k)δTB,k
where δTB,k is the fluctuation
in the kth radiometer channel and each channel produces an independent
estimate of the path fluctuation. These independent path estimates can then be combined to
obtain a single best estimate: 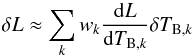 (10)where
wk is the weight assigned to each channel.
The sum of the weights is unity.
(10)where
wk is the weight assigned to each channel.
The sum of the weights is unity.
The data processing steps consist of:
-
1.
estimating the phase-correction coefficients dL/dTB,k;
-
2.
choosing how to combine the four channels, i.e., choosing a set of weights wk;
-
3.
optionally filtering the observed fluctuations δTB,k to reduce the effect of noise in radiometers;
-
4.
applying the phase correction to the observed visibilities.
In the present implementation of phase correction software, the coefficients dL/dTB,k are estimated by taking the values of the observed sky brightness in the four WVR channels for one integration time in the middle of the astronomical observation, and fitting a model for the atmospheric emission. The model used is a relatively simple, thin single-layer model with pressure, temperature and column density of the water vapour all treated as free parameters constrained to a range of feasible values. The model and the procedure used to fit it to the observations are described in detail by Nikolic (2009) and Nikolic et al. (2012). The same model, together with the inferred atmospheric parameters, is then used to estimate the phase correction coefficients. We show in Sect. 5 that this estimate of the phase correction coefficients is sufficiently good for the longest baseline lengths that we have been able to test so far (Bmax ~ 600 m). A fit to observations from just one antenna is used to calculate the phase correction coefficients for the entire array. We find that this is an adequate approximation for the relatively short baselines used with ALMA so far, but a more exact treatment may be needed when longer baselines come into operation.
In principle, there is a significant amount of freedom in selection of the weighting
factors for combining the path estimates from each channel (Stirling et al. 2004). The design work was based on assumption that they would be
chosen to minimise the expected path fluctuation due the random Gaussian-like noise
intrinsic to the radiometers and this is what the current software system implements. In
this case the weightings factors are simply: 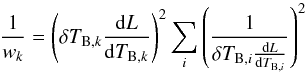 (11)where
δTB,k is the expected
intrinsic noise in the kth channel. Alternative strategies can provide
slightly better overall performance in certain conditions but at the cost of greater effect
of intrinsic noise. For example, in the case of relatively wet weather the centre of the
line is saturated and the measured sky brightness fluctuations then correspond not only to
water vapour column and intrinsic noise fluctuations but also to the fluctuations of the
physical temperature of the water vapour layer. In this case the measurement of path would
be improved by down-weighting the contribution of the central channel further than indicated
by Eq. (11). Such additional re-weightings
are a subject for further study and have not yet been implemented in the production
software.
(11)where
δTB,k is the expected
intrinsic noise in the kth channel. Alternative strategies can provide
slightly better overall performance in certain conditions but at the cost of greater effect
of intrinsic noise. For example, in the case of relatively wet weather the centre of the
line is saturated and the measured sky brightness fluctuations then correspond not only to
water vapour column and intrinsic noise fluctuations but also to the fluctuations of the
physical temperature of the water vapour layer. In this case the measurement of path would
be improved by down-weighting the contribution of the central channel further than indicated
by Eq. (11). Such additional re-weightings
are a subject for further study and have not yet been implemented in the production
software.
The results of phase correction can often be improved slightly by scaling down the entire
correction. The reason for this is that the intrinsic noise in the WVRs, and other sources
of error in the estimated phase correction, are usually not correlated with the true
atmospheric phase fluctuations. In more detail, the phase correction we estimate
 ,
for example according to Eq. (10), can be
decomposed into the “true” atmospheric phase change δL and an error term
E:
,
for example according to Eq. (10), can be
decomposed into the “true” atmospheric phase change δL and an error term
E: 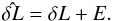 (12)If
this best estimate of atmospheric phase fluctuations is applied to correct the observed
data, then the residual will be E and the rms of the residual is simply:
(12)If
this best estimate of atmospheric phase fluctuations is applied to correct the observed
data, then the residual will be E and the rms of the residual is simply:
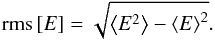 (13)Since
we are dealing with fluctuations and error terms we can drop the mean terms, i.e., we assume
in the following that ⟨E⟩ = 0 and ⟨δL⟩ = 0.
(13)Since
we are dealing with fluctuations and error terms we can drop the mean terms, i.e., we assume
in the following that ⟨E⟩ = 0 and ⟨δL⟩ = 0.
If, instead of correcting using the best estimate of atmospheric fluctuations, we scale our
estimate by a factor α before applying the correction, we find that the rms
of the residual is: 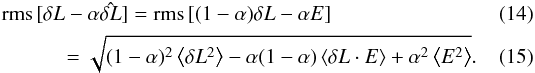 In
most cases, and especially when the error term is dominated by the intrinsic thermal-like
noise in the WVRs, the error term E is uncorrelated with the true
atmospheric error, and therefore ⟨δL·E⟩ ≡ 0. The residual
rms then reduces to:
In
most cases, and especially when the error term is dominated by the intrinsic thermal-like
noise in the WVRs, the error term E is uncorrelated with the true
atmospheric error, and therefore ⟨δL·E⟩ ≡ 0. The residual
rms then reduces to: 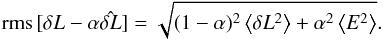 (16)This
expression, i.e., the residual phase fluctuation, has a minimum when
(16)This
expression, i.e., the residual phase fluctuation, has a minimum when
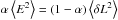 , i.e.:
, i.e.:
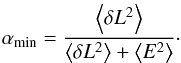 (17)It
can be seen from this expression that when the true atmospheric path fluctuations dominate
the noise term, δL ≫ E, it is best to apply essentially
the entire correction. However, when the two terms are approximately the same
δL ~ E, which is often the case on the very shortest
ALMA baselines, then it is optimal to apply only half of the best estimate
of the atmospheric path fluctuations. The optimum scaling therefore depends on the
configuration in which ALMA is observing and the atmospheric stability. Currently this
scaling is implemented as a simple user-tunable parameter.
(17)It
can be seen from this expression that when the true atmospheric path fluctuations dominate
the noise term, δL ≫ E, it is best to apply essentially
the entire correction. However, when the two terms are approximately the same
δL ~ E, which is often the case on the very shortest
ALMA baselines, then it is optimal to apply only half of the best estimate
of the atmospheric path fluctuations. The optimum scaling therefore depends on the
configuration in which ALMA is observing and the atmospheric stability. Currently this
scaling is implemented as a simple user-tunable parameter.
By default the ALMA WVRs integrate the sky observations for 1.152 s, resulting in noise well below 0.1 K rms in all of the channels. This is usually sufficiently low to ensure that the resulting contribution to the phase error is small. In very stable conditions and for short baselines it may be desirable to smooth the observed radiometer data somewhat, i.e. use a longer integration time, in particular if the integration period of the astronomical signal is also longer than 1.152 s.
4.1. Quality control and atmospheric conditions monitoring
It is useful to derive feedback on the likely quality of the WVR correction directly from the sky brightness temperature measurements since this avoids the need for longer specialised observations on quasars. We use two simple statistics to help identify any potential problems with WVRs or with the likely efficiency of the phase correction.
The first statistic is simply the root-mean-square fluctuation of the estimated path from each of the WVRs. This is computed by considering only data taken while the antennas were observing one object (usually the science source) within a scheduling block. Additionally, before computing the rms, the path is corrected for the changing airmass during the observation as the target object is tracked by the antenna. These steps ensure that the path rms is representative of the actual atmospheric stability or, potentially, of any problems within the WVR.
The second statistic that is computed is the difference between estimates of path fluctuations obtained independently from two channels of the WVR (the weighting and combining of channels is not done in this case). Since the optimum phase correction coefficients of the channels depend in a different way on the atmospheric properties, this statistic is useful for identifying errors in the phase correction coefficients due to wrong inference of atmospheric properties. This statistic is also useful because any fluctuation in sky brightness due to variable cloud cover will affect the channels in different ways, with the outer channels showing the largest effect in proportion to that of the water.
Although problems with ALMA radiometers have been rare so far, computing these quality control statistics is important because problems may not be apparent in astronomical data when they are processed.
4.2. Dealing with missing WVRs
ALMA will need to deal with antennas which do not have functioning WVRs. One of the reasons for this is that ALMA consists of two arrays of antennas: the “12 m Array” which will have 50 12 m-diameter antennas and the Atacama Compact Array (ACA) which will consist of four 12 m-diameter and twelve 7 m-diameter antennas. The ACA is designed to operate independently of the 12 m Array and with such short baselines it only needs basic phase correction. It is therefore not planned for the 7 m-diameter antennas to have their own WVRs but rather for them to use the data from nearby 12 m-diameter antennas. Other possible reasons for missing WVR data are faults in the hardware or problems in transmitting the data.
The simplest approach for dealing with missing data is to interpolate neighbouring antennas to compute a predicted WVR signal and use this predicted WVR signal throughout the remainder of the analysis. We have implemented interpolation as the weighted mean of signals from nearest three antennas, with the weighting factor proportional to inverse distance to the antenna. We find that this operates satisfactorily in the compact ALMA configurations since there are usually antennas with WVR measurements available that are reasonably close at hand.
5. Initial results of phase correction
The effectiveness of phase correction can be measured by observing known point-like sources (typically quasars) and comparing the measured phases to the expected values. For a point-like source at the phase tracking centre of the interferometer, the phase and amplitude of visibilities is expected to be constant for all baselines and therefore any fluctuation in phases is due to a combination of following effects:
-
1.
atmospheric phase fluctuations;
-
2.
instrumental effects;
-
3.
noise in the measurement of the astronomical visibility.
Here we summarise the results of initial measurements of effectiveness of radiometric phase correction, which were all made with ALMA in compact configurations, i.e. with baseline lengths between 15 and 650 m.
As shown in Eq. (10) the path (and therefore phase) correction for an antenna over short periods of time is described by a linearised relation with the changes in each of the WVR channels. Since the fluctuation in phase of visibility is proportional to the difference in path to the two antennas forming the baseline over which the visibility is measured, Eq. (10) implies that there should be proportionality between the phase fluctuations and the difference of readings of the WVRs on the two antennas.
 |
Fig. 7 Correlation between the atmospheric path error estimated from observations of a bright point-like object (horizontal axis) and the differenced WVR signal (vertical axis). Both the estimated path from astronomical visibilities and the WVR difference were filtered by removing the three minute running mean. Each plot is a two-dimensional histogram where the colour scale shows how many points fall in each bin. The four panels correspond to the four channels of the radiometers. |
A good way of visualising the potential efficiency of WVR phase correction is therefore to plot the correlation between these two quantities, i.e. the path fluctuation and the difference between WVR measurements, as a two dimensional histogram. We show these for a typical observation in Fig. 7. In this figure we analyse each channel of the WVR separately and so the figure contains four plots, one for each channel. In each plot, the difference between outputs of WVRs on the two antennas is used to place the data on the vertical axis while the phase of the visibility is converted to an apparent path fluctuation and used to place data on the horizontal axis. The density of points is shown by the colour. In order to concentrate on the changes in path over short timescales, both the observed path fluctuation and the WVR output differences were filtered to remove their running mean over 300 s.
It can be seen in Fig. 7 that the correlation between the WVR differences and the measured path fluctuations is very tight. A formal regression analysis shows that the adjusted R2 values are 0.82–0.9, depending on the channels, and the rms residuals in terms of brightness temperature differences are 0.13–0.19 K. This can be compared to expected rms residuals of 0.1–0.14 K due to thermal noise in the WVRs only. Furthermore it can be seen that there are no out-lying points which would be seen if there were spikes or glitches in either the WVR measurements or the interferometric phases.
The improvement in phase stability of astronomical visibility after WVR correction is illustrated in Figs. 8 and 9. The first figure (Fig. 8) shows the improvement in relatively humid conditions (PWV ~ 2.2 mm) during unstable daytime conditions on baseline which is about 650 m long. As can be seen the phase fluctuations are reduced by almost an order of magnitude (in terms of path rms from about 1 mm to 0.16 mm), meaning that they are reduced from a level which would almost completely decorrelate the signal to one which is adequate for interferometric imaging.
The results in the dry (PWV ~ 0.5 mm) and stable night-time conditions on a short baseline of ~20 m are shown in Fig. 9. In this example the path fluctuation (after removing the 3 min running mean) is reduced from 14 μm to 7 μm. Although the relative improvement is much smaller than that shown in Fig. 8, this example illustrates the very high absolute level of performance that can be achieved. Both examples also illustrate the good long-term stability of the WVRs with no noticeable drift.
The initial testing has confirmed the presence of some shortcomings which were, to some extent, anticipated during the design stage. The most obvious of these is the effect of cloud on the phase correction. Variable cloud cover causes fluctuations in sky brightness which do not have the same relation to the path fluctuation as those due to water vapour and this leads to erroneous phase correction. Even on relatively short baselines this effect has been found the be large enough to make the phases after correction worse than before correction on some occasions. While sky brightness measurements from the outermost channel have been useful in identifying when clouds are making a significant contribution to sky brightness, we have not yet found a way of using these measurements in a way that improves the phase correction in the presence of clouds.
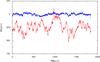 |
Fig. 8 Test observation at 90 GHz of a strong quasar on a ~650 m baseline with ALMA. The red line is the phase of the observed (complex) visibility on this baseline – note that for a quasar (or other point-like) source at the tracking centre of the interferometer we expect a constant phase in time. The blue line is the visibility phase after correction of the data based on the WVR signals and using the wvrgcal program. |
 |
Fig. 9 Test observation on a short (~25 m) baseline in excellent weather conditions. The phase of the uncorrected astronomical visibility is again in red while the phase after WVR correction is in blue. Note the much smaller range of the vertical axis compared to Fig. 8. |
The second shortcoming which has been identified is the presence of residual phase errors which are not correlated with the water vapour signal. The residual errors only become noticeable in quite dry conditions and their magnitude appears to increase with increasing length of the baseline. The origin of these residual errors has not yet been identified conclusively but it seems likely they are due to the fluctuations of refractive index of the dry component of the air, i.e. density fluctuations. Such density fluctuations will arise from temperature variations, especially in the daytime, but there may also be a component due to the dynamical pressure changes caused by the wind.
An important aspect of phase correction which we have not examined in this paper is the performance of the correction in combination with phase referencing. In this case the WVR corrections can first be applied to the whole sequence of data, consisting of interleaved observations of the astronomical source and the calibrator, and a further correction, based on the remaining phase variations seen in the calibrator, can then be applied to the astronomical data. This combination of the two corrections should result in better imaging quality than the application of either of the corrections on its own, since it addresses both the short-term atmospheric fluctuations and the somewhat longer-term phase drifts in the interferometer system. Phase referencing can however involve a significant change in telescope elevation. This might lead to instrumental effects in the WVRs which would cause errors in their readings. More significantly the changes in the observed sky brightness (due to change in airmass) may be quite large. Although the changes in brightness will be common for all the antennas in the array, small differences in the factors on the different WVRs that convert from sky brightness to excess path will produce errors in the phase corrections. Such elevation-dependent errors can mimic other sources of error, such as those due to inaccurately determined positions of the telescopes. We have not yet been able to make a proper assessment of the errors, where we can separate the various contributions, in the case of phase-referenced observations. In practice, the impact of such errors on ALMA observations can often be reduced by using self-calibration on timescales which are long enough to provide adequate signal to noise ratio but short enough to correct for the slowly changing elevation-dependent errors. Additionally, the sensitivity of ALMA is increasing as more telescopes are commissioned into the array and this means fainter (and therefore closer) phase calibrators can be used, which reduces any elevation-dependent errors. The accuracy of phase correction when combined with phase referencing is nevertheless an important topic which we hope to examine as part of future work.
6. Summary
We have described the design of the ALMA water-vapour radiometer phase-correction system. Compared to most previous systems, the ALMA system has the following advantages:
-
1.
it observes the very strong 183 GHz watervapour line which has a phase correction coefficient (i.e., therelationship between sky brightness change and electrical pathchange) as high as 40 K/mm;
-
2.
internal continuous two-load calibration;
-
3.
optical and mechanical design optimised during telescope design stages, giving low spill-over and rigid telescope mounting.
Additionally ALMA has the advantage that it is at a higher and dryer site, leading to intrinsically smaller water vapour fluctuations, and that its sensitivity is large, which means that phase calibration sources can often be found close to science targets.
The successes of this system to date include:
-
1.
initial tests of the phase correction system have shown that the radiometers have excellent sensitivity and stability;
-
2.
significant and often dramatic improvement in phase stability have been achieved under most conditions;
-
3.
phase correction is already in routine use for ALMA science observing.
The main limitations are erroneous phase corrections when there is thick cloud cover and the presence of some residual phase errors which may be due to air-density fluctuations.
Acknowledgments
This work was supported in part by the European Commission’s Sixth Framework Programme as part of the wider “Enhancement of Early ALMA Science” project. We would like to thank the referee Dr Robert Lucas for helpful and prompt suggestions for improving the paper.
References
- Asaki, Y., Saito, M., Kawabe, R., Morita, K.-I., & Sasao, T. 1996, Radio Science, 31, 1615 [NASA ADS] [CrossRef] [Google Scholar]
- Baars, J. 1967, Antennas and Propagation, IEEE Transactions on, 15, 582 [Google Scholar]
- Barrett, A. H., & Chung, V. K. 1962, J. Geophys. Res., 67, 4259 [NASA ADS] [CrossRef] [Google Scholar]
- Battat, J. B., Blundell, R., Moran, J. M., & Paine, S. 2004, ApJ, 616, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Bremer, M. 2002, in Astronomical Site Evaluation in the Visible and Radio Range, eds. J. Vernin, Z. Benkhaldoun, & C. Muñoz-Tuñón, ASP Conf. Ser., 266, 238 [Google Scholar]
- Bremer, M., Guilloteau, S., & Lucas, R. 1995, in IRAM Newsletter No. 24 (IRAM), 6 [Google Scholar]
- Broguière, D., Lucas, R., Pardo, J., & Roche, J.-C. 2011, in Astronomical Data Analysis Software and Systems XX, eds. I. N. Evans, A. Accomazzi, D. J. Mink, & A. H. Rots, ASP Conf. Ser., 442, 277 [Google Scholar]
- Carilli, C. L., & Holdaway, M. A. 1999, Radio Science, 34, 817 [Google Scholar]
- Cornwell, T., & Fomalont, E. B. 1999, in Synthesis Imaging in Radio Astronomy II, eds. G. B. Taylor, C. L. Carilli, & R. A. Perley, ASP Conf. Ser., 180, 187 [Google Scholar]
- Emrich, A., Andersson, S., Wannerbratt, M., et al. 2009, in 20th International Symposium on Space Terahertz Technology (National Radio Astronomy Observatory, Charlottesville, USA), available from http://www.nrao.edu/meetings/isstt/2009.shtml [Google Scholar]
- Evans, N., Richer, J. S., Sakamoto, S., et al. 2003, Site Properties and Stringency, ALMA Memo Series 471, The ALMA Project [Google Scholar]
- Hills, R. E. 2007, Optimization of the IF Filters for the ALMA Water Vapour Radiometers, ALMA Memo Series 568, The ALMA Project [Google Scholar]
- Hinder, R., & Ryle, M. 1971, MNRAS, 154, 229 [NASA ADS] [Google Scholar]
- Lay, O. P. 1997, A&AS, 122, 535 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nikolic, B. 2009, Inference of Coefficients for Use in Phase Correction I, ALMA Memo Series 587, The ALMA Project [Google Scholar]
- Nikolic, B., Hills, R. E., & Richer, J. S. 2007, Limits on Phase Correction Performance Due to Differences Between Astronomical and Water-Vapour Radiometer Beams, ALMA Memo Series 573, The ALMA Project [Google Scholar]
- Nikolic, B., Richer, J. S., & Hills, R. E. 2008, Simulating Atmospheric Phase Errors, Phase Correction and the Impact on ALMA Science, ALMA Memo Series 582, The ALMA Project [Google Scholar]
- Nikolic, B., Graves, S. F., Bolton, R. C., & Richer, J. S. 2012, Design and Implementation of the wvrgcal Program, ALMA Memo Series 593, The ALMA Project [Google Scholar]
- Pardo, J. R., Cernicharo, J., & Serabyn, E. 2001, Antennas and Propagation, IEEE Transactions on, 49, 1683 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, T. J., & Readhead, A. C. S. 1984, ARA&A, 22, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, L. M., Lamb, J. W., Woody, D. P., et al. 2010, ApJ, 724, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Roy, A. L., Rottmann, H., Teuber, U., & Keller, R. 2007 [arXiv:astroph/0703066] [Google Scholar]
- Schaper, L. W. J., Staelin, D. H., & Waters, J. H. 1970, in Proc. IEEE, 58, 272 [Google Scholar]
- Stirling, A., Hills, R., Richer, J., & Pardo, J. 2004, 183 GHz water vapour radiometers for ALMA: Estimation of phase errors under varying atmospheric conditions, ALMA Memo Series 496, The ALMA Project [Google Scholar]
- Stirling, A., Holdaway, M., Hills, R. E., & Richer, J. S. 2005, Calculation of Integration Times for WVR, ALMA Memo Series 515, The ALMA Project [Google Scholar]
- Toll, J. S. 1956, Phys. Rev., 104, 1760 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Wiedner, M. C., Hills, R. E., Carlstrom, J. E., & Lay, O. P. 2001, ApJ, 553, 1036 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, T. L., Rohlfs, K., & Hüttemeister, S. 2009, Tools of Radio Astronomy (Springer) [Google Scholar]
- Woody, D., Carpenter, J., & Scoville, N. 2000, in Imaging at Radio through Submillimeter Wavelengths, eds. J. G. Mangum, & S. J. E. Radford, ASP Conf. Ser., 217, 317 [Google Scholar]
- Zivanovic, S. S., Forster, J. R., & Welch, W. J. 1995, Radio Sci., 30, 877 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Conceptual design of the water vapour radiometers. |
| In the text | |
 |
Fig. 2 Model brightness of the atmosphere at frequencies around the 183 GHz water vapour line for six values of PWV along the line of sight: 0.3, 0.6, 1, 2, 3 and 5 mm (from lowest red line to highest blue line). The model was computed using the ATM program by Pardo et al. (2001), using the source code the model as used by ALMA (this is available for public download at http://www.mrao.cam.ac.uk/~bn204/alma/atmomodel.html). |
| In the text | |
 |
Fig. 3 Differential of brightness of the atmosphere with respect to the total line of sight precipitable water vapour (c), computed for the same six values of total PWV as in Fig. 2. |
| In the text | |
 |
Fig. 4 Design band-passes of the four channels of ALMA WVRs, together with a plot model brightness temperature for 1 mm of PWV. |
| In the text | |
 |
Fig. 5 Relative change in the model phase correction coefficients for a 5% shift in the centre frequency of each filter versus the total column of water vapour in mm. Red to blue lines (following the spectrum) are channels 1 to 4. |
| In the text | |
 |
Fig. 6 Model phase correction coefficients versus the total column of water vapour. Red to blue lines (following the spectrum) are channels 1 to 4, i.e., innermost to outermost channel. Note that the units of the ordinate are Kelvin per millimetre of extra path in contrast to Fig. 3 which has units of Kelvin per mm of precipitable water vapour. |
| In the text | |
 |
Fig. 7 Correlation between the atmospheric path error estimated from observations of a bright point-like object (horizontal axis) and the differenced WVR signal (vertical axis). Both the estimated path from astronomical visibilities and the WVR difference were filtered by removing the three minute running mean. Each plot is a two-dimensional histogram where the colour scale shows how many points fall in each bin. The four panels correspond to the four channels of the radiometers. |
| In the text | |
 |
Fig. 8 Test observation at 90 GHz of a strong quasar on a ~650 m baseline with ALMA. The red line is the phase of the observed (complex) visibility on this baseline – note that for a quasar (or other point-like) source at the tracking centre of the interferometer we expect a constant phase in time. The blue line is the visibility phase after correction of the data based on the WVR signals and using the wvrgcal program. |
| In the text | |
 |
Fig. 9 Test observation on a short (~25 m) baseline in excellent weather conditions. The phase of the uncorrected astronomical visibility is again in red while the phase after WVR correction is in blue. Note the much smaller range of the vertical axis compared to Fig. 8. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


