| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A59 | |
| Number of page(s) | 6 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220876 | |
| Published online | 25 March 2013 | |
Research Note
Parameters of rotating neutron stars with and without hyperons
N. Copernicus Astronomical Center, Bartycka 18,
00-716
Warsaw,
Poland
e-mail:
bejger@camk.edu.pl
Received:
10
December
2012
Accepted:
15
February
2013
Context. The discovery of a 2 M⊙ neutron star provided a robust constraint for the theory of exotic dense matter, bringing into question the existence of strange baryons in the interiors of neutron stars. Although many theories fail to reproduce this observational result, several equations of state containing hyperons are consistent with it.
Aims. We study global properties of stars using equations of state containing hyperons, and compare them to those without hyperons to find similarities, differences, and limits that can be compared with the astrophysical observations.
Methods. Rotating, axisymmetric, and stationary stellar configurations in general relativity are obtained, and their global parameters are studied.
Results. Approximate formulæ describing the behavior of the maximum and minimum stellar mass, compactness, surface redshifts, and moments of inertia as functions of spin frequency are provided. We also study the thin disk accretion and compare the spin-up evolution of stars with different moments of inertia.
Key words: stars: neutron / equation of state / stars: rotation / dense matter
© ESO, 2013
1. Introduction
The discovery of a 2M⊙ neutron star (NS; Demorest et al. 2010) provides a strong motivation for (the community of) dense-matter physicists to understand the role of exotic phases in the interior of neutron stars. The appearance of new particles (in general, new phases of matter) typically results in the softening of matter, since the contribution to pressure from energetic nucleons is replaced by that of slowly-moving, massive particles; the pressure increases less steeply with the density in the equation of state (EOS), which in turn lowers the NS maximum allowable mass (for a review concerning dense matter EOSs, see Haensel et al. 2007). The state of the dense matter in the NS cores is very different from the state known at the energies and densities reached by the terrestrial experiments; notably, stable strange matter may appear in the interiors of NSs at densities a few times the nuclear saturation density, with strange baryons (hyperons) being a very probable result.
We study a set of selected EOSs, representing current theoretical approaches to the description of the dense matter, that are consistent with the robust constraint put forward by the observers. If we assume that hyperons do exist in the interiors of massive NSs, then based on our present knowledge it seems necessary for such objects to be composed of sufficiently stiff matter (at lower densities) to sustain the softening that is introduced by the appearance of hyperons. In other words, substantial stiffness of the EOS of nucleonic (non-strange) matter is a necessary condition for the existence of hyperons in the core of a massive NS. Consequently, stellar configurations that contain hyperons will, at least partly, differ from those without hyperons. We therefore seek similarities and differences between them, as well as limits that can be applied to astrophysical observations.
This Note is composed as follows: Sect. 2 contains the description of methods and EOSs used; Sect. 3 presents the results for the gravitational mass, surface redshift, moment of inertia and accretion tracks; Sect. 4 contains the conclusions and summary.
2. Equations of state
The following selection of nucleonic EOSs is used: the APR EOS (Akmal et al. 1998, model A18 + δv + UIX⋆) is a variational, non-relativistic many-body solution with relativistic corrections; the DH EOS (Douchin & Haensel 2001) is constructed using a non-relativistic energy density functional based on the SLy4 effective nuclear interaction, designed to describe both crust and core in a unified way; the BSK20 EOS (moderate stiffness EOS by Goriely et al. 2010) is also based on the nuclear energy-density functional theory, using the generalized Skyrme forces fitted to experimental nuclear data and reproducing properties of infinite nuclear matter from the calculations of many-body interactions.
Realistic microscopic dense-matter theories (the Brueckner-Hartree-Fock approach) predict maximum masses of NSs with hyperons much below the observed ≃2 M⊙ (see e.g., Schulze et al. 2006; Burgio et al. 2011, and references therein). This may be caused by a limited knowledge of hyperon-hyperon and hyperon-nucleon three-body forces; see, however, a recent investigation of Vidaña et al. (2011), who estimated the effect of three-body forces in the hyperonic sector on the NS maximum mass. Assuming that hyperon interactions are weaker than the pure nucleonic interactions, the resulting non-rotating NS maximum mass is located in the 1.27−1.6 M⊙ range. The problematic feature of low Mmax is usually remedied by providing stronger repulsion between the hyperons and/or letting them appear only at very high densities. Below, we list a selection of EOSs with hyperons, derived from theories that successfully deal with the problem of a massive NS: the DS08 EOS (Dexheimer & Schramm 2008) uses an effective hadronic SU(3) chiral model including the baryon octet and fourth-order self-interaction terms of the ω, ρ, and φ vector mesons; the GM1Z0 EOS (Weissenborn et al. 2012) is based on a relativistic mean field model which allows the study of the departure from a vector meson-hyperon couplings stemming from the SU(6) quark model to a more general SU(3) prescription; the GM1 model with the ratio between the meson octet and the singlet coupling constant z = g8/g1 = 0 (all the baryon-meson couplings are equal) was used, which makes it the stiffest in our sample. The BM165 EOS (Bednarek et al. 2011) was also derived from a relativistic mean field model, with a non-linear Lagrangian that includes quatric terms in the meson fields, and two additional hidden-strangeness mesons σ∗ and φ that couple to hyperons only. The TM1C EOS (Gusakov et al., priv. comm.) employs a prescription similar to the BM165 EOS for purely nucleonic matter, and also introduces scalar σ∗ and vector φ mesons in the description of hyperon interaction, with an additional Λ−Λ hyperon attraction. The SU(6) symmetry breaking applied in the model amounts to z = 0.2.
Selected parameters of static configurations.
3. Results
The following subsections contain the results for constant spin frequency tracks (sequences of configurations) of rotating stars. The frequency range spans an astrophysically-relevant range from f = 0 Hz (static configurations, see Table 1 for their representative parameters) up to f = 1200 Hz (i.e., much above the frequency of 716 Hz of the most rapid pulsar to date, PSR J1748-2446ad of Hessels et al. 2006). Rigidly-rotating, stationary, and axisymmetric stellar configurations were obtained by means of the numerical library LORENE1, nrotstar code, using the formulation of Bonazzola et al. (1993), with the accuracy checked by a 2D virial theorem (Bonazzola & Gourgoulhon 1994). The sequences are limited by the following conditions: from the low central density end, they terminate at the so-called mass-shedding limit, when the orbital frequency of a test particle at the star’s equator equals the stellar spin frequency f. The high central density limit is marked by the onset of the axisymmetric perturbation instability described by the condition ∂M/∂λ|J = 0, where M is the gravitational mass and λ a suitable parametrization of the sequence of configurations (e.g., the central density; see Friedman et al. 1988 for details). We define the moment of inertia as I = J/Ω, where J is the total stellar angular momentum and Ω is the angular frequency, Ω = 2πf (for the definitions of M and J, see Bonazzola et al. 1993). For non-rotating configurations, I is calculated using the slow-rotation approximation (Hartle 1967).
Parameters of the approximate formulæ presented below were obtained by the χ2 fitting, yielding a typical accuracy of the order of one per cent.
3.1. Gravitational mass
Figure 1 shows how the mass-central baryon density M(nb) relation changes with f for the selected EOSs. A strong reduction of the available mass and the central density range for a large f is characteristic of hyperonic EOSs; moreover, configurations near the mass-shedding limit (left sides of curves) may be more massive than those near the axisymmetric perturbation instability limit (right sides).
 |
Fig. 1 Gravitational mass-central baryon density M − nb relations for selected spin frequencies f, for stars composed of the BSK20 EOS (dashed red lines) and four hyperonic EOSs: DS08 (solid green), BM165 (dash-dotted black), GM1Z0 EOS (dashed blue) and TM1C (solid red lines). High- and low-density ends correspond to the axisymmetric instability and the mass-shedding limits, respectively. From bottom to top for each EOS, f equals 0, 900, 1000, 1100 and 1200 Hz. (Color online.) |
 |
Fig. 2 Range of allowable gravitational masses as a function of spin frequency f. The vertical line indicates 716 Hz frequency (spin frequency of the most-rapidly rotating NS to date). (Color online.) |
 |
Fig. 3 Maximum mass Mmax (left panel) and minimum mass Mmin (right panel) of rotating NSs as a function of the spin frequency f. Values are scaled by the parameters of non-rotating configurations. (Color online.) |
Figure 2 shows the range of available masses as a
function of spin frequency f; we note that the mass of a hyperonic EOS
star is already strongly constrained by the existence of 716 Hz pulsar (Hessels et al. 2006). Detection of a
f ≃ 800 Hz pulsar would mean that such a stiff EOS cannot yield a star
with M < 1.4 M⊙. (In
the case of the TM1C EOS this minimum mass is already approached for 716 Hz). The growth
of the maximum mass Mmax, normalized by the maximum mass of
the static configuration 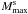 can be
approximated by
can be
approximated by 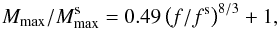 (1)where
(1)where
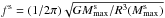 is the frequency scaling factor2 formed of a static
star maximum-mass parameters, gravitational mass
is the frequency scaling factor2 formed of a static
star maximum-mass parameters, gravitational mass 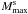 and
corresponding radius
and
corresponding radius 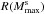 . In the case of minimum mass
Mmin, one can obtain a similar (although somewhat cruder)
approximation to the one for the Mmax,
. In the case of minimum mass
Mmin, one can obtain a similar (although somewhat cruder)
approximation to the one for the Mmax,
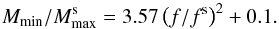 (2)The
above relation underestimates the
(2)The
above relation underestimates the 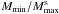 for BM165 EOS
stars for a given frequency, because the maximum-mass radius
R(Mmax) is smaller than for other hyperonic
EOSs, resulting in a larger fs.
for BM165 EOS
stars for a given frequency, because the maximum-mass radius
R(Mmax) is smaller than for other hyperonic
EOSs, resulting in a larger fs.
3.2. Surface redshifts
Surface redshift may provide important information about the spacetime in the vicinity of the NS. In the case of a rotating star, one considers the redshift zp of photons coming from the pole, as well as two equatorial redshifts for photons, emitted tangentially in and opposite the direction of rotation (forward zf and backward zb redshift, respectively; for definitions, see e.g., Gourgoulhon 2010, Sect. 4.6). The left panel in Fig. 4 shows the relations for z for the minimum compactness (M/Req)min, i.e., configurations at the mass-shedding limit, that bear some resemblance to the configurations during the photospheric radius expansion burst (Steiner et al. 2010 and references therein); Req denotes the equatorial radius. These relations may be regarded as upper limits on the compactness parameter for a measured z. We approximate zp and zb by a(M/R)3/2 + b, where a = 9.62 and b = 0.023 for zp, and a = 25.11 and b = 0.18 for zb; zf is approximated by − 0.68(M/R)0.4.
The right panel shows redshift functions for the maximum-compactness (M/Req)max configuration along the line corresponding to the axisymmetric perturbation instability limit. For spin frequencies under consideration, it may be also treated as an approximate lower limit on the stellar mass.
 |
Fig. 4 Surface redshifts for rotating configurations. Left panel: equatorial backward (top curve) and forward (bottom curve) redshifts zb and zf, and the polar redshift zp for configurations with the minimal mass, as functions of the compactness (M/Req)min. Right panel: functions of the three redshifts for rotating, maximally-compact configurations. (Color online.) |
We propose parametrizing these relations as follows: for
ζ = (zb − zf)/zp,
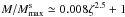 ; for
ζ = 1 − zf/zp,
; for
ζ = 1 − zf/zp,
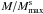 is
approximated by 0.06ζ2.5 + 1. In the case of the third
function, we chose
ζ = 1 − zf/zb,
and
is
approximated by 0.06ζ2.5 + 1. In the case of the third
function, we chose
ζ = 1 − zf/zb,
and 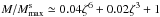 .
.
 |
Fig. 5 Maximal compactness vs. equatorial redshifts zf and zb for different rotation rates; for zf, f increases to the left of the bigger symbol that denotes the static configuration; for zb, f increases to the right. Points correspond to frequencies from 0 to 1200 Hz. (Color online.) |
The value of zb − zf quantifies the redshift effect on the maximal line broadening coming from the equator of a rotating star. Figure 5 presents the maximal compactness for such stars against the two equatorial redshifts. The (M/Req)max stays remarkably constant with rotation, and could be used to distinguish between the two sets of models.
3.3. Moment of inertia
A potentially interesting NS parameter is the moment of inertia I (in principle measurable using the spin-orbit coupling, Lattimer & Schutz 2005). Figure 6 shows the behavior of the gravitational mass M as a function of the moment of inertia I for static configurations. The curves in the left panel may be approximated by a straight line, I(M) = aIM + bI. For nucleonic EOSs, aI = 1.22 and bI = −0.34, for hyperonic EOSs aI = 1.51. In the right panel we plot the value of I/R6 as a function of M; this value enters the estimation of the minimum magnetic dipole field at the pulsar surface, B > (I/R6)1/2(3c3ṖP/8π2)1/2, where P = 2π/f denotes the spin period3. Figure 7 presents how the available range of the moments of inertia changes with rotation. For the frequencies f ≥ 800 Hz the moment of inertia tend to be already quite constrained. The minimum value of I for sub-millisecond rotation coincides with the high-density end of the track, while the mass-shedding limit is characterized by a large I (because of a strong equatorial radius dependence, the effect is much more pronounced than for the gravitational mass, Fig. 2).
 |
Fig. 6 Left panel: moment of inertia I as a function of gravitational mass M for static solutions. Right panel: moment of inertia I divided by R6 (as used in the estimation of the minimum surface magnetic field of a pulsar) for static stars. Vertical lines correspond to a fiducial model of I = 1045 g cm2 and 10 km. (Color online.) |
 |
Fig. 7 Top panels: the behavior of I(M) for rotating stars (from left to right f equals 0, 900, 1000, 1100 and 1200 Hz) for hyperonic EOSs and DH EOS for comparison. Bottom panels: allowable range of the moment of inertia for purely nucleonic stars (left) and hyperonic stars (right). Thin (thick) lines correspond to the minimum (maximum) of I that a stable configuration can attain at a given frequency. (Color online). |
 |
Fig. 8 Left panel: relation between I/MR2 and the compactness parameter M/R for static configurations (grey) and those rotating at 1200 Hz, in which case R ≡ Req. Right panel: minimal M/Req ratio (value corresponding to the mass-shedding configuration) as a function of rotational frequency. (Color online.) |
As many softer EOSs are now ruled out by observations, we reproduce the formula suggested
by Lattimer & Prakash (2001) in the form of
Bejger & Haensel (2002), with slightly
different coefficients in the static case. For an astrophysically relevant range of masses
M > 0.5 M⊙ we have
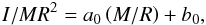 (3)with
a0 = 1.40 and b0 = 0.19 (left
panel in Fig. 8). This approximation is generally
valid for the static results in our sample. A more universal formula, which takes rotation
into account, will depend on the spin frequency f; the compactness
M/R must be re-defined as the
gravitational mass M to the circumferential radius
Req ratio. For EOSs without hyperons, we propose the
following approximation:
(3)with
a0 = 1.40 and b0 = 0.19 (left
panel in Fig. 8). This approximation is generally
valid for the static results in our sample. A more universal formula, which takes rotation
into account, will depend on the spin frequency f; the compactness
M/R must be re-defined as the
gravitational mass M to the circumferential radius
Req ratio. For EOSs without hyperons, we propose the
following approximation: 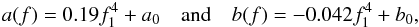 (4)where
f1 = f/(1 kHz). Since
the rotation influences hyperonic stars in a different way, we produce an analogous
approximation for a subset of hyperonic EOSs only. In the static case we obtain
a0h = 1.14 and
b0h = 0.22, and for rotating
configurations
(4)where
f1 = f/(1 kHz). Since
the rotation influences hyperonic stars in a different way, we produce an analogous
approximation for a subset of hyperonic EOSs only. In the static case we obtain
a0h = 1.14 and
b0h = 0.22, and for rotating
configurations 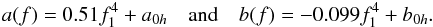 (5)In
order to estimate the moment of inertia, one needs to know the minimum
value of the compactness parameter
M/Req for a given spin
frequency (right panel in Fig. 8). It can be
described by
(5)In
order to estimate the moment of inertia, one needs to know the minimum
value of the compactness parameter
M/Req for a given spin
frequency (right panel in Fig. 8). It can be
described by 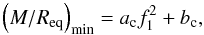 (6)where
bc = 0.005, and ac depends on
the type of the EOS. For EOSs without hyperons ac = 0.074,
otherwise ac = 0.099. Thanks to their stiffness, hyperonic
EOSs produce larger radii near the mass-shedding limit, but the minimum mass for a given
f is also higher in comparison to nucleonic EOSs (see Fig. 2), which results in higher
(M/Req)min.
(6)where
bc = 0.005, and ac depends on
the type of the EOS. For EOSs without hyperons ac = 0.074,
otherwise ac = 0.099. Thanks to their stiffness, hyperonic
EOSs produce larger radii near the mass-shedding limit, but the minimum mass for a given
f is also higher in comparison to nucleonic EOSs (see Fig. 2), which results in higher
(M/Req)min.
3.4. Spin-up by disk accretion
A process in which the moment of inertia is relevant is the so-called recycling of
pulsars to millisecond periods. To study the relation of spin-up to the EOS we use the
model described in Bejger et al. (2011a), a magnetic
torque in the form given by Kluźniak & Rappaport
(2007), updated to include the marginally-stable orbit and the magnetic field
decay proportional to the amount of accreted mass. The evolution of the total stellar
angular momentum in the process of accretion is 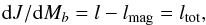 (7)where
l is the orbital angular momentum of a particle in the disk per unit
baryon mass, and lmag is the contribution from the braking
magnetic torque, resulting from the magnetosphere-disk interaction.
(7)where
l is the orbital angular momentum of a particle in the disk per unit
baryon mass, and lmag is the contribution from the braking
magnetic torque, resulting from the magnetosphere-disk interaction.
For comparison with the realistic EOSs, we employ a useful fiducial model4: I45, a star with a constant radius R = 10 km, and a constant moment of inertia I = 1045 g cm2.
 |
Fig. 9 Spin evolution of an accreting star as a function of the accreted mass (accretion rate is Ṁ = 10-9 M⊙/yr, the horizontal axes correspond to accretion time tacc in Gyr) with initial mass Mini = 1.4 M⊙. Left panel: accretion with the magnetic field decay and Bini = 1012 G. Right panel: accretion without B = 0 (from the marginally-stable orbit). (Color online.) |
To compare the effect of the EOS on the recycling process, Fig. 9 shows the evolution of spin frequency f for a chosen
accretion rate,
Ṁ = 10-9 M⊙/yr
and initial magnetic field B = 1012 G (left panel). As
anticipated, stars with larger moments of inertia gain f less rapidly.
With the above parameters, a hyperonic star has to accrete almost twice as much matter as
a nucleonic EOS star to reach given f (see also Bejger et al. 2011a). For comparison, the right panel shows the
importance of the magnetic torque. When it is neglected (B = 0), the
amount of mass needed to spin up the star to a given f is much smaller
(lines end at the mass-shedding limit). By rewriting Eq. (7) for J = IΩ, 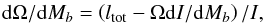 (8)one
deduces that both large I and its growth with M decrease
the spin-up rate (to be compared with the fiducial I45 configuration; see also the
top-left panel in Fig. 6 where we compare the BSK20
and DS08 EOSs). We also note that, contrary to intuition, more massive stars are spinning
up faster, as shown in Fig. 10 for
Mini = 1.2 M⊙ and
Mini = 1.9 M⊙. This feature
results from the fact that ltot is larger for larger
M. In the general case, the expression for
ltot(M) is rather complicated (see Bejger et al. 2011a for details); however, for
B = 0 in the Schwarzschild case,
(8)one
deduces that both large I and its growth with M decrease
the spin-up rate (to be compared with the fiducial I45 configuration; see also the
top-left panel in Fig. 6 where we compare the BSK20
and DS08 EOSs). We also note that, contrary to intuition, more massive stars are spinning
up faster, as shown in Fig. 10 for
Mini = 1.2 M⊙ and
Mini = 1.9 M⊙. This feature
results from the fact that ltot is larger for larger
M. In the general case, the expression for
ltot(M) is rather complicated (see Bejger et al. 2011a for details); however, for
B = 0 in the Schwarzschild case,
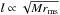 ,
and rms, the radius of the innermost stable circular orbit,
depends linearly on M. This effect is independent of the change of
I, as shown for the I = const. tracks
with different Mini. The change of
dI/dMb
for realistic EOSs, related to the I(M) behavior near
the Mmax, is visible as a slight change of slope in the right
panel of Fig. 10, just before the accretion ends at
the instability limit.
,
and rms, the radius of the innermost stable circular orbit,
depends linearly on M. This effect is independent of the change of
I, as shown for the I = const. tracks
with different Mini. The change of
dI/dMb
for realistic EOSs, related to the I(M) behavior near
the Mmax, is visible as a slight change of slope in the right
panel of Fig. 10, just before the accretion ends at
the instability limit.
3.5. Comparison with stiff nucleonic EOS
To be consistent with the 2 M⊙ NS mass measurement, the
hyperonic EOSs are necessarily stiff for densities lower than the hyperon appearance
threshold. This requirement is not essential for nucleonic EOSs, and is directly reflected
in higher compactnesses, smaller radii and smaller moments of inertia of associated
stellar models. The nucleonic EOS may however be stiff; to investigate
the imprint of hyperons, we construct a purely nucleonic BMN EOS by suppressing hyperons
in the BM165 EOS (see Bednarek et al. 2011 for
details, where the BMN EOS is called EOS.N). Compared to the BM165 EOS, it yields a
moderately higher non-rotating maximum mass, 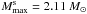 and larger
and larger
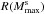 , 11.96 km. The lack of hyperons
results in available central density ranges that are shifted towards lower values for a
given spin frequency, as well as higher moments of inertia (see Fig. 11, in which the left and right panels correspond to Figs. 1 and 7).
, 11.96 km. The lack of hyperons
results in available central density ranges that are shifted towards lower values for a
given spin frequency, as well as higher moments of inertia (see Fig. 11, in which the left and right panels correspond to Figs. 1 and 7).
 |
Fig. 10 As in the left panel of Fig. 9, but for Mini = 1.2 M⊙ (left panel) and Mini = 1.9 M⊙ (right panel). (Color online.) |
Because of the considerable freedom in choosing EOS parameters, the discrimination between a given hyperonic EOS and another stiff, but purely nucleonic EOS is notably hindered, mostly because they give similar values of the stellar radius that affects potentially-measurable parameters. For relations presented in Figs. 1–10, the BMN EOS results resemble those of the DS08 EOS (e.g., in Fig. 5 the central value of (M/Req)max equals 0.177).
One can thus, in principle, construct a nucleonic EOS that will result in stellar parameters similar to hyperonic models; the reverse statement is, at least up to the current state of the art, not true.
 |
Fig. 11 Gravitational mass-central baryon density M − nb and the moment of inertia–mass I(M) relations for BM165 (dashed black), BMN (solid blue), and DS08 EOS (dash-dotted green lines). (Color online.) |
4. Summary and conclusions
We have studied a set of recent EOSs that contain hyperons and yield static NSs consistent with a robust observational constraint, a 2 M⊙ NS mass measured by Demorest et al. (2010). Stars constructed using hyperonic EOSs were compared with those using a minimalistic approach, i.e., containing nucleons only. Their global parameters, gravitational mass, compactness, surface redshift, and moments of inertia were calculated for a broad range of spin frequencies (0–1200 Hz). We have focused on the extreme values of these parameters and find that the minimum mass for hyperonic EOSs increases much faster with rotation than in the case of the representative set of nucleonic EOSs described in Sect. 2. For frequencies just slightly larger than 716 Hz the minimum mass approaches 1.4 M⊙. In the case of the compactness parameter M/Req, its minimal value is substantially larger than for nucleonic EOSs at a given f (Fig. 8). We also note that the sub-millisecond rotation confines the mass into a narrow interval (a feature that is present for softer EOS stars for much higher frequencies, see Bejger et al. 2007). However, as shown in Sect. 3.5, stellar models based on a sufficiently stiff nucleonic EOS may be confused with hyperonic EOS models; in view of the measurement of Demorest et al. (2010), an observation of a compact NS (i.e., suggesting a softer nucleonic EOS) with a mass far below 2 M⊙ would make the existence of hyperons at higher densities less plausible.
A number of approximate formulæ describing the whole set of EOSs is provided. We approximate the relations between the Mmax, Mmin, (M/Req)min, and functions of surface redshift for minimal and maximal compactness configurations for a range of studied frequencies. We find that the maximal compactness configuration has M/Req that changes little with rotation.
Because of their stiffness, hyperonic stars have comparatively large moments of inertia that increase with rotation to
values significantly larger than the usual 1045 g cm2. We extend the parametrization of Bejger & Haensel 2002 by supplying an approximate I/(MR2) vs. M/R relation for rotating stars. A large moment of inertia is also one of the parameters in the process of recycling a millisecond pulsar that hinders the spin-up. If hyperons exist in the interior of NSs (i.e., the nucleonic matter is sufficiently stiff), it may be one of the reasons high frequencies are not observed.
In general, the changes of stellar parameters relate to each other as dM = ΩdJ + μdMb, where μ = 1/ut is the chemical potential per unit mass, transfered onto the star by the accreting particle, ut being the time component of the particle four-velocity. In the case of B = 0, μ = e − Ωl, where e is the specific energy of a particle infalling onto the star (Sibgatullin & Sunyaev 2000; Zdunik et al. 2002), the gravitational mass growth of such a star is therefore dM = edMb; we adopt this prescription for B ≠ 0 too (we also correct a misprint in Eqs. (4) and (5) of Bejger et al. 2011a: instead of ut, it should read 1/ut).
Acknowledgments
I thank N. Chamel, D. Chatterjee, V. Dexheimer, and M. E. Gusakov for providing their tabulated EOSs, and P. Haensel, J. L. Zdunik, and an anonymous referee for comments. This work was partially supported by the Polish MNiSW research grants No. 2011/01/B/ST9/04838, N N203 512838 and completed using free and open software (LORENE, gnuplot, matplotlib, numpy and scipy).
References
- Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Bednarek, I., Haensel, P., Zdunik, J. L., et al. 2012, A&A, 543, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bejger, M., & Haensel, P. 2002, A&A, 396, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bejger, M., Haensel, P., & Zdunik, J. L. 2007, A&A, 464, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bejger, M., Zdunik, J. L., & Haensel, P. 2010, A&A, 520, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bejger, M., Fortin, M., Haensel, P., & Zdunik, J. L. 2011a A&A, 536, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bejger, M., Haensel, P., Zdunik, J. L., & Fortin, M. 2011b A&A, 536, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonazzola, S., & Gourgoulhon, E. 1994, CQG, 11, 1775 [NASA ADS] [CrossRef] [Google Scholar]
- Bonazzola, S., Gourgoulhon, E., Salgado, M., & Marck, J. A. 1993, A&A, 278, 421 [NASA ADS] [Google Scholar]
- Burgio, G. F., Schulze, H.-J., & Li, A. 2011, Phys. Rev. C, 83, 025804 [NASA ADS] [CrossRef] [Google Scholar]
- Demorest, P. B., Pennucci, T., Ransom, S. M., et al. 2010, Nature, 467, 1081 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dexheimer, V., & Schramm, S. 2008, ApJ, 683, 943 [Google Scholar]
- Douchin, F., & Haensel, P. 2001, A&A, 380, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Friedman, J. L., Ipser, J. R., & Sorkin, R. D. 1988, ApJ, 325, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Goriely, S., Chamel, N., & Pearson, J. M. 2010, Phys. Rev. C, 82, 035804 [NASA ADS] [CrossRef] [Google Scholar]
- Gourgoulhon, E. 2010 [arXiv:1003.5015] [Google Scholar]
- Haensel, P., Potekhin, A. Y., & Yakovlev, D. G. 2007, Neutron Stars 1: Equation of State and Structure (New York: Springer) [Google Scholar]
- Hartle, J. B. 1967, ApJ, 150, 1005 [Google Scholar]
- Hessels, J. W. T., Ransom, S. M., Stairs, I. H., et al. 2006, Science, 311, 1901 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kluźniak, W., & Rappaport, S. 2007, ApJ, 671, 1990 [NASA ADS] [CrossRef] [Google Scholar]
- Lattimer, J. M., & Prakash, M. 2001, ApJ, 550, 426 [Google Scholar]
- Lattimer, J. M., & Schutz, B. F. 2005, ApJ, 629, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Schulze, H.-J., Polls, A., Ramos, A., & Vidaña, I. 2006, Phys. Rev. C, 73, 058801 [NASA ADS] [CrossRef] [Google Scholar]
- Sibgatullin, N. R., & Sunyaev, R. A. 2000, Astron. Lett., 26, 772 [Google Scholar]
- Steiner, A. W., Lattimer, J. M., & Brown, E. F. 2010, ApJ, 722, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Vidaña, I., Logoteta, D., Providência, C., et al. 2011, EPL, 94, 11002 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weissenborn, S., Chatterjee, D., & Schaffner-Bielich, J. 2012, Phys. Rev. C, 85, 065802 [NASA ADS] [CrossRef] [Google Scholar]
- Zdunik, J. L., Haensel, P., & Gourgoulhon, E. 2002, A&A, 381, 933 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Gravitational mass-central baryon density M − nb relations for selected spin frequencies f, for stars composed of the BSK20 EOS (dashed red lines) and four hyperonic EOSs: DS08 (solid green), BM165 (dash-dotted black), GM1Z0 EOS (dashed blue) and TM1C (solid red lines). High- and low-density ends correspond to the axisymmetric instability and the mass-shedding limits, respectively. From bottom to top for each EOS, f equals 0, 900, 1000, 1100 and 1200 Hz. (Color online.) |
| In the text | |
 |
Fig. 2 Range of allowable gravitational masses as a function of spin frequency f. The vertical line indicates 716 Hz frequency (spin frequency of the most-rapidly rotating NS to date). (Color online.) |
| In the text | |
 |
Fig. 3 Maximum mass Mmax (left panel) and minimum mass Mmin (right panel) of rotating NSs as a function of the spin frequency f. Values are scaled by the parameters of non-rotating configurations. (Color online.) |
| In the text | |
 |
Fig. 4 Surface redshifts for rotating configurations. Left panel: equatorial backward (top curve) and forward (bottom curve) redshifts zb and zf, and the polar redshift zp for configurations with the minimal mass, as functions of the compactness (M/Req)min. Right panel: functions of the three redshifts for rotating, maximally-compact configurations. (Color online.) |
| In the text | |
 |
Fig. 5 Maximal compactness vs. equatorial redshifts zf and zb for different rotation rates; for zf, f increases to the left of the bigger symbol that denotes the static configuration; for zb, f increases to the right. Points correspond to frequencies from 0 to 1200 Hz. (Color online.) |
| In the text | |
 |
Fig. 6 Left panel: moment of inertia I as a function of gravitational mass M for static solutions. Right panel: moment of inertia I divided by R6 (as used in the estimation of the minimum surface magnetic field of a pulsar) for static stars. Vertical lines correspond to a fiducial model of I = 1045 g cm2 and 10 km. (Color online.) |
| In the text | |
 |
Fig. 7 Top panels: the behavior of I(M) for rotating stars (from left to right f equals 0, 900, 1000, 1100 and 1200 Hz) for hyperonic EOSs and DH EOS for comparison. Bottom panels: allowable range of the moment of inertia for purely nucleonic stars (left) and hyperonic stars (right). Thin (thick) lines correspond to the minimum (maximum) of I that a stable configuration can attain at a given frequency. (Color online). |
| In the text | |
 |
Fig. 8 Left panel: relation between I/MR2 and the compactness parameter M/R for static configurations (grey) and those rotating at 1200 Hz, in which case R ≡ Req. Right panel: minimal M/Req ratio (value corresponding to the mass-shedding configuration) as a function of rotational frequency. (Color online.) |
| In the text | |
 |
Fig. 9 Spin evolution of an accreting star as a function of the accreted mass (accretion rate is Ṁ = 10-9 M⊙/yr, the horizontal axes correspond to accretion time tacc in Gyr) with initial mass Mini = 1.4 M⊙. Left panel: accretion with the magnetic field decay and Bini = 1012 G. Right panel: accretion without B = 0 (from the marginally-stable orbit). (Color online.) |
| In the text | |
 |
Fig. 10 As in the left panel of Fig. 9, but for Mini = 1.2 M⊙ (left panel) and Mini = 1.9 M⊙ (right panel). (Color online.) |
| In the text | |
 |
Fig. 11 Gravitational mass-central baryon density M − nb and the moment of inertia–mass I(M) relations for BM165 (dashed black), BMN (solid blue), and DS08 EOS (dash-dotted green lines). (Color online.) |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


