| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 6 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201220396 | |
| Published online | 04 April 2013 | |
The central density of R136 in 30 Doradus
European Southern Observatory,
Alonso de Cordova 3107 Vitacura Casilla
7630355
Santiago,
Chile
e-mail:
fselman@eso.org
Received:
18
September
2012
Accepted:
13
February
2013
The central density, ρ0, of a stellar cluster is an important physical parameter for determining its evolutionary and dynamical state. How much mass segregation there is or whether the cluster has undergone core collapse both depend on ρ0. We reanalyze the results of a previous paper that gives the mass density profile of R136 and combine them with both a conservative upper limit for the core parameter and a more uncertain recent measurement. We thus place a lower limit on ρ0 under reasonable and defensible assumptions about the IMF, finding ρ0 ≥ 1.5 × 104 M⊙/pc3 for the conservative assumption a < 0.4 pc for the cluster core parameter. If we use the lower, but more uncertain value a = 0.025 pc, the central density estimate becomes greater than 107 M⊙/pc3. A mechanism based on the destruction of a large number of circumstellar disks is posited to explain the hitherto unexplained increase in reddening presented in that same work.
Key words: circumstellar matter / galaxies: clusters: individual: R 136 / stars: luminosity function, mass function / Magellanic Clouds / dust, extinction
© ESO, 2013
1. Introduction
Owing to its nearness and extreme nature, Radcliffe 136 (Feast et al. 1960) has been not only a template for other more extreme and distant starburst clusters, but also a good example of how a typical galactic globular cluster might have looked soon after its birth. To obtain its physical characteristics in a way firmly rooted in observations has been an important goal as the many studies of this interesting object attest (Melnick 1985; Weigelt & Baier 1985; Campbell et al. 1992; Parker & Garmany 1993; Malumuth & Heap 1994; Hunter et al. 1995; Brandl et al. 1996; Hunter et al. 1996; Walborn & Blades 1997; Massey & Hunter 1998; Andersen et al. 2009; Bosch et al. 2009; Campbell et al. 2010; Crowther et al. 2010; de Marchi et al. 2011; Hénault-Brunet et al. 2012, and the whole series of VLT-FLAMES Tarantula Survey papers; Sabbi et al. 2012). Selman et al. (1999b, henceforth SMBT) studied the IMF of R136 and provided several of its physically relevant parameters, including the mass density profile of the cluster. Three very important results of that paper gave insight into the age structure of the cluster, the normal nature of its IMF, and the scale-free character of the mass density profile between 0.4 and 10 pc.
The cuspy profile and the small core radius has been used to posit a post-core-collapse (PCC) state for this cluster (Campbell et al. 1992; but see opposite views by Malumuth & Heap 1994; Brandl et al. 1996; Mackey & Gilmore 2003). PCC clusters are characterized by a high central density and a density profile that can be modeled by a normal King profile, which shows a break and turns into a power law near the center. High central density means, in this context, that the relaxation time is shorter than the age of the system. Observations of Galactic globular clusters show that they can be separated into “core-collapsed” and non-core-collapsed depending on whether their photometric profile turns into a power law near the center (Harris 1996; McLaughlin & van der Marel 2005; Chatterjee et al. 2013, and references therein). The cluster R136 has been claimed to have the characteristics of a PCC cluster: a cuspy density profile (Mackey & Gilmore 2003), and a large number of runaway stars (see Fujii et al. (2012) and references therein). Nevertheless, the time scale for core collapse is too long if we believe the value of 3 × 104 M⊙/pc3 determined by Mackey & Gilmore (2003) for the central density. Fujii et al. (2012) invoke the fact that smaller clusters evolve faster, thereby speeding up the evolution via hierarchical merging of smaller substructures. This idea has been backed up by the recent work of Sabbi et al. (2012). Using theoretical isochrones for MS and PMS evolution, and Hubble Space Telescope (HST) optical and NIR photometry, they find that the central part of the cluster is very young with ages below 1 My, while an overdensity ~5.4 pc to the northeast of the center is closer to 2.5 My. This led them to propose that R136 is a double cluster that is currently interacting. Similar ages were found in SMBT, but with fits to the Geneva tracks in the upper part of the HR diagram. That similar age structure is found by using these two sets of tracks give credibility to both of these results.
Such a complex age structure is quite a complication when modeling to convert magnitudes and colors into masses. If the average age of the stellar population depends on radius, this will result in systematic errors in our estimates of physical parameters unless variable ages are allowed in the modeling. Most work on R136 so far assume simple stellar populations. The only work that we are aware of that does not is SMBT, which also considers variable reddening determined in a star-by-star basis, and does a full completeness analysis, which is fundamental when working in the optical bands.
Using ground-based observations in combination with the HST work of Hunter et al. (1995; 1996), SMBT determined the density profile of the cluster showing that between 0.4–10 pc it is represented well by a single power law, giving explicit expressions. Although a lower limit to the central density of the cluster can be derived from those numbers, it was not given explicitly in the paper. In this work we give the explicit results. If we use the same core parameter as used by Mackey & Gilmore (2003) we find a striking similarity between our result and that of those authors. Furthermore, using the recent estimates of the core parameter by Campbell et al. (2010), we find that the central density is considerably higher than the previous estimate, making core collapse a virtual certainty for this cluster, or an indication that the latter estimate of the core parameter is wrong.
2. Radial profile, central density, and total mass in R136
SMBT give the following relation for the stellar number density normalized to 1 pc, derived
counting stars with masses between
10 M⊙ < M < 40 M⊙:
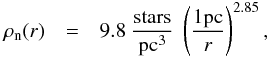 (1)where
\begin{lxirformule}$r$\end{lxirformule} is the distance to the cluster center in parsecs. As
previously noted, a strong effort was made by SMBT to correct for incompleteness, and
although the work was based on optical data, Eq. (1) should not be affected by differential reddening and should be complete in the
specified mass range.
(1)where
\begin{lxirformule}$r$\end{lxirformule} is the distance to the cluster center in parsecs. As
previously noted, a strong effort was made by SMBT to correct for incompleteness, and
although the work was based on optical data, Eq. (1) should not be affected by differential reddening and should be complete in the
specified mass range.
A form often used to parametrize the stellar density of a star cluster was given by Elson
et al. (1987): 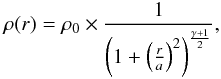 (2)where
a is the core parameter1, and
ρ0 is the central density. This form is suitable for clusters
that are young enough not to exhibit tidal truncation. We note that the core parameter
a is usually obtained by fits to the 2D profile, but if the fit is a good
one, then the value thus obtained is the same as for the cluster 3D density profile. Given a
core parameter, then and only then can we calculate ρ0. If we
only have valid measurements in the power-law region, where
r ≫ a, we can only obtain a lower limit to
ρ0. Thus, the challenge in determining the central density is
really a challenge in determining the core parameter. There are basically two methods of
determining this parameter: fits to star counts, and fits to the integrated light profile.
Brandl et al. (1996) cautions that determining the
core parameter using surface brightness profiles is not reliable, since the light can be
dominated by a few very bright stars (as is indeed the case near the center of R136), and
mimic a power-law cusp. A similar caveat can be found in Mackey & Gilmore (2003).
(2)where
a is the core parameter1, and
ρ0 is the central density. This form is suitable for clusters
that are young enough not to exhibit tidal truncation. We note that the core parameter
a is usually obtained by fits to the 2D profile, but if the fit is a good
one, then the value thus obtained is the same as for the cluster 3D density profile. Given a
core parameter, then and only then can we calculate ρ0. If we
only have valid measurements in the power-law region, where
r ≫ a, we can only obtain a lower limit to
ρ0. Thus, the challenge in determining the central density is
really a challenge in determining the core parameter. There are basically two methods of
determining this parameter: fits to star counts, and fits to the integrated light profile.
Brandl et al. (1996) cautions that determining the
core parameter using surface brightness profiles is not reliable, since the light can be
dominated by a few very bright stars (as is indeed the case near the center of R136), and
mimic a power-law cusp. A similar caveat can be found in Mackey & Gilmore (2003).
We can write the results for the stellar volume density found in SMBT using the Elson et
al. (1987) form for an arbitrary value of
a but fitting the SMBT power-law data: 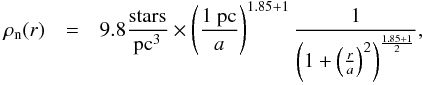 (3)showing
a clear power law of slope γ = 1.85, without signs of a core between 0.4–10
pc. Figure 1 reproduces Fig. 13 from SMBT, which gives
a profile totally determined counting stars in mass bins. The innermost
point suffers from strong incompleteness.
(3)showing
a clear power law of slope γ = 1.85, without signs of a core between 0.4–10
pc. Figure 1 reproduces Fig. 13 from SMBT, which gives
a profile totally determined counting stars in mass bins. The innermost
point suffers from strong incompleteness.
 |
Fig. 1 Radial density profile for the stars with 10 M⊙ < M < 40 M⊙. For the innermost bins we have calculated the points using the Hunter et al. (1995) data following the procedure described in SMBT. The line is a power law with exponent –1.85. The point at the smallest radius is strongly affected by incompleteness. Reproduced with permission from SMBT. |
Using the value a = 0.4 pc as an upper limit we can write the previous
result as 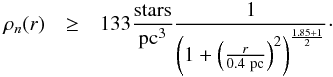 (4)This
expression is valid for stars with M in the range
10 M⊙ < M < 40 M⊙.
To convert this number density profile to a mass profile, we need the spectrum of stellar
masses to extrapolate the density from the given mass range to the full mass range. We
choose to use the spectrum of masses at birth, i.e. the IMF, instead of the present-day mass
function, although it does not make much of a difference given the young age of the central
parts of R136. At 1.2 My the most massive stars have lost less than 4% of their mass and at
2 My this figure is still only 20%. The lowest mass for which an IMF has been given for R136
so far is 1 M⊙ (Andersen et al. 2009). These authors found consistency with a Salpeter slope down to this mass
limit. We used this result as a check that the IMF does not show a break down to this mass
limit but used the SMBT IMF slope extrapolated down to this mass, because it was determined
in a rigorous and self-consistent way. We thus use a Kroupa IMF (Kroupa 2002) modified in the high mass range to have the slope
determined in SMBT (Γ = 1.17),
(4)This
expression is valid for stars with M in the range
10 M⊙ < M < 40 M⊙.
To convert this number density profile to a mass profile, we need the spectrum of stellar
masses to extrapolate the density from the given mass range to the full mass range. We
choose to use the spectrum of masses at birth, i.e. the IMF, instead of the present-day mass
function, although it does not make much of a difference given the young age of the central
parts of R136. At 1.2 My the most massive stars have lost less than 4% of their mass and at
2 My this figure is still only 20%. The lowest mass for which an IMF has been given for R136
so far is 1 M⊙ (Andersen et al. 2009). These authors found consistency with a Salpeter slope down to this mass
limit. We used this result as a check that the IMF does not show a break down to this mass
limit but used the SMBT IMF slope extrapolated down to this mass, because it was determined
in a rigorous and self-consistent way. We thus use a Kroupa IMF (Kroupa 2002) modified in the high mass range to have the slope
determined in SMBT (Γ = 1.17), 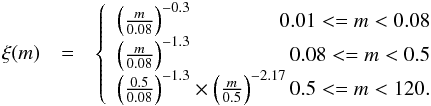 (5)With
this IMF the fraction of stars with masses between
10 M⊙ < M < 40 M⊙
is 0.3967%. The fraction in the mass range
1 M⊙ < M < 120 M⊙
is 7.286%, and the average mass is 3.85 M⊙. Thus, if we choose
to integrate only down to 1 M⊙, we estimate the central mass
density limit,
(5)With
this IMF the fraction of stars with masses between
10 M⊙ < M < 40 M⊙
is 0.3967%. The fraction in the mass range
1 M⊙ < M < 120 M⊙
is 7.286%, and the average mass is 3.85 M⊙. Thus, if we choose
to integrate only down to 1 M⊙, we estimate the central mass
density limit, 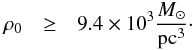 (6)The
result in Eq. (6) has been derived almost
directly from observations. There are modeling uncertainties, and an extrapolation from 10
M⊙ down to 1 M⊙, but the latter
supported by observations. To extend the result to even lower masses where the mass function
has not been determined observationally is somewhat risky. Depending on the actual dynamical
state of the cluster, we could have the effects of mass segregation invalidating the result.
The mass density profile we obtain with this extrapolation of the IMF to the full
0.01 M⊙ < M < 120 M⊙
range where the average mass is 0.46 M⊙ is given by
(6)The
result in Eq. (6) has been derived almost
directly from observations. There are modeling uncertainties, and an extrapolation from 10
M⊙ down to 1 M⊙, but the latter
supported by observations. To extend the result to even lower masses where the mass function
has not been determined observationally is somewhat risky. Depending on the actual dynamical
state of the cluster, we could have the effects of mass segregation invalidating the result.
The mass density profile we obtain with this extrapolation of the IMF to the full
0.01 M⊙ < M < 120 M⊙
range where the average mass is 0.46 M⊙ is given by
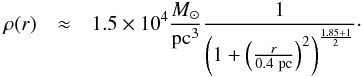 (7)Mackey
& Gilmore (2003) determine an upper limit to
the core parameter of a < 0.32 pc, and with this
value we can estimate a lower limit to the central density of
2.8 × 104 M⊙/pc3, in
excellent agreement with the value of
3 × 104 M⊙/pc3 given
by those authors. Because of the IMF extrapolation we have not preserved the inequality sign
in this equation, which was quite certain for Eq. (6).
(7)Mackey
& Gilmore (2003) determine an upper limit to
the core parameter of a < 0.32 pc, and with this
value we can estimate a lower limit to the central density of
2.8 × 104 M⊙/pc3, in
excellent agreement with the value of
3 × 104 M⊙/pc3 given
by those authors. Because of the IMF extrapolation we have not preserved the inequality sign
in this equation, which was quite certain for Eq. (6).
These numbers can also be used to determine a total mass. The complication here is that the
slope of the density profile results in an ever increasing total mass as one goes to larger
radii. Here we choose to cut the integration at a radius of 10 pc, the distance at which the
star counts become noisier due to the presence of a number of substructures. The same slope
value that diverges for large radii ensures convergence when integrating from the center.
Thus, we will give our estimates of the mass of the cluster as a range where the lower total
mass limit is given by the upper limit of the core parameter, and the upper total mass limit
is given for a power law all the way to the center. With these assumptions we can then write
 (8)where
we have defined
(8)where
we have defined 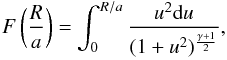 (9)and
in what follows we integrate numerically. We note that for
γ > 2 the integral converges in the limit
R/a → ∞. For γ = 2
it diverges logarithmically.
(9)and
in what follows we integrate numerically. We note that for
γ > 2 the integral converges in the limit
R/a → ∞. For γ = 2
it diverges logarithmically.
With these definitions the constraint to the total mass becomes
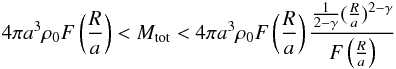 (10)and
for R136 using a < 0.4 pc,
(10)and
for R136 using a < 0.4 pc,
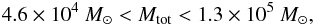 (11)or
in terms of total number of stars Ntot,
(11)or
in terms of total number of stars Ntot,
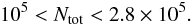 (12)
(12)
3. Discussion
As noted in the previous section, the estimate of the central mass density depends very strongly on the limits put on the core parameter. Because it was determined by star counts, we feel that the limit given in SMBT is a very conservative one. Other authors have placed a much more stringent constraint by analyzing the light profile (e.g. Campbell et al. 1992; Andersen et al. 2009). One of the latest such studies, and one that reaches similar conclusions to other studies that use the surface brightness method, is that of Campbell et al. (2010). They used the multiconjugate adaptive optics instrument (MAD) at ESO’s Melipal 8-m telescope to perform star counts and surface photometry in H and K, on frames with typical Strehl ratios in K of 15–25%. Although there is little leverage for disentangling masses and ages in the infrared bands, they are less affected by reddening so with proper care a good estimate of the radial profile can be obtained in the case of a simple stellar population. These bands are also separate from the peak emission for very massive stars so the cluster’s light profile is less affected by the presence of a few very massive stars. The magnitude limit of the MAD data corresponds to approximately 5 M⊙. Within approximately r < 2 pc they use the light profile integrated in annuli, while for r > 0.7 pc they use star counts. They merge the two profiles into a single one using the area of overlap to normalize the two sets. They find γ = −1.6 ± 0.1, and a = 0.025 pc. Because of the presence of radially dependent stellar populations with multiple ages, we only use their value for the core radius, while for the slope we use the value determined in SMBT where allowance has been made for multiple epochs of star formation.
The issues complicating the determination of the core parameter using integrated light profiles are not addressed at all by Campbell et al. (2010), but are fundamental in these kinds of studies. Their Fig. 20 shows that the power-law slope is virtually the same for the segment derived with star counts and the segment derived by the surface brightness fit. This might indicate that the surface brightness is a good proxy for mass surface density. Nevertheless, we must point out that the very bright central sources could give a similar signal due to scattering of light in the optical elements of the instrument. It has been known for a long time that the profile of a stellar image contains a kernel and a power-law part of index ~− 2 (de Vaucouleurs 1958; King 1971). The origin of this power-law halo has been ascribed to optics imperfections and dust. According to Kormendy (1973) the slope is flatter at ~− 1.54. This index is close to the –1.6 index determined with MAD so scattered light might mimic the cluster light profile. This shallow-slope power law is expected to dominate a few seeing radii away from the core of the PSF. Nevertheless, between the core of the PSF and this radius, we expect a much steeper uncompensated halo that falls off with a Moffat β ~ 11/3, approximately as r-3.7 (Moffat 1969; Roddier 1995; Racine 1999).
The results of Campbell et al. of a = 0.025 pc, imply moderately larger
bounds for the total mass and number of stars given by 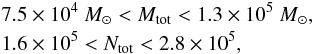 (13)and
central density of
(13)and
central density of 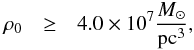 (14)which
is much higher than any other estimates of the R136 central density.
(14)which
is much higher than any other estimates of the R136 central density.
Is R136 a PCC cluster? If we take the MAD data at face value, the cluster must be in a PCC state since the relaxation time for a cluster with such a central density is only ~8 × 103 y, and the time to core collapse is approximately 15 times this value (using Binney & Tremaine 1987, as presented in Eq. (8) by Mackey & Gilmore 2003), or ~1 × 105 y, considerably below the current estimate of 106 y for the age of the cluster.
Two other subtleties related to relaxation and core collapse must be pointed out. First, the identification of “core-collapsed” clusters in the galaxy rests in identifying a break in the inner part of the light profile. When properly studied, that is by star counts, R136 shows a scale-free distribution from 10 pc all the way down to at least 0.4 pc. Second, the relaxation times used in the literature assume a single mass component, while for this very young cluster we have a spectrum of masses spanning at least three orders of magnitude. In such a case the relaxation time is diminished by the ratio of the lowest mass to the highest mass star. We do not delve deeper in this subject because the physics of core-collapse is beyond the scope of this work.
 |
Fig. 2 a) Radial profile of color excess, as determined in Selman et al. (1999a). b) Color excess versus selective extinction parameter S. Reproduced with permission from Selman et al. (1999a). |
A central density as high as implied by Eq. (14) would have other consequences. Selman et al. (1999a), the first paper of the series and dedicated in part to the study of the reddening distribution in R136, found a puzzling trend in reddening increasing toward the center of the cluster. Their Fig. 6a, reproduced here as Fig. 2 shows clearly that trend. The figure shows that in the inner regions most of the stars show a somewhat limited amount of variable extinction that increases toward the center. In the outer parts more than half of the stars follow the same trend, while another group, probably associated with the nebulosity that surrounds the cluster, show a much higher variation of extinction. The amount of dust associated with the inner component was estimated at 30–60 M⊙ within 15 pc, and its origin was a mystery.
The details of the calculation were not given in SMBT, so we give them in Appendix A. From Fig. 2 we see that the extinction increases from values near 0.2–0.3 at 80′′ from the center reaching values slightly in excess of 0.5 near the center. We assume that the former values sum the contributions from the Milky Way, the LMC and the larger 30 Doradus environment, and we assume the values above 0.2–0.3 to come from a component associated to R136 itself. Thus, using EB − V ≈ 0.1−0.2 for the extinction associated with R136, we find Mdust ~ 40−80 M⊙ within 15 pc from the cluster center, or Mdust ~ 18−36 M⊙ within 10 pc from the cluster center.
In SMBT, we stated our surprise to see dust in such an extreme environment. Any dust particle near the center of the cluster would, if not destroyed, be removed very rapidly. Thus, a source of dust is needed to replenish it. A natural source of matter is the mass loss from the massive stars. It is only the stars with masses above 15 M⊙ that lose significant amounts of mass, and the total amount of mass loss depends strongly on the age of the system as the rate increases rapidly with age. According to SMBT the central cluster stars belong to the first burst with ages below 1.5 My. A more recent estimate of the age of the central stars of the cluster is given by Crowther et al. (2010). These authors used rotating models and UV and IR spectroscopic observations of the central WN stars to constraint the age to 1.7 ± 0.2 My. We use for our estimate an upper limit of 2 My with the evolutionary models without rotation of Meynet et al. (1994). These authors doubled the mass loss rates of de Jaeger et al. (1988). With this artificial increase in the mass loss rate, these authors were able to explain the number ratio of WR stars to O stars, which otherwise would have come too low. With the current state of the art rotating models they are able to produce WR stars even if there is no wind! The new models use the mass loss rates for O stars by Vink et al. (2000), and for WR stars by Nugis & Lamers (2000) that have mostly revised the rates downward (Maeder & Meynet 2012). Thus, using the Meynet et al. (1994) 2 My isochrone for Z = 0.008, weighted by the IMF in Eq. (5) we can calculate an upper limit to the total mass loss due to stellar evolution that is 0.35%. If we set the total mass of the cluster to 105 M⊙, then the total mass loss corresponds to 350 M⊙. Although a natural source of matter is the mass loss from the massive stars, it is not clear that they are a natural source of dust. To convert this to an amount of dust, we need the uncertain gas-to-dust ratio in the wind of such hot stars. The amount of gas from mass loss, if it were to have the gas-to-dust ratio of 347 found by Pei (1992) for the LMC would correspond to only 1.0 M⊙, more than an order of magnitude below what we see. Using 100 for the gas-to-dust ratio results in only 3.5 M⊙ of dust. Thus, in SMBT we realized that we needed a different source of dust. Dust around massive stars, B-types, and WR had been found in the past (Geisel 1970; Allen & Swings 1972), which was later ascribed to colliding winds (Usov 1991), so we speculated that this dust could be produced in colliding winds of massive stars. Some work has been done in colliding winds since that time, and it has become clear that to produce dust we need a binary with a WC star as a member (Crowther 2003). There is only one WC star near the center of R136 in projection, Brey 83 (Breysacher 1981). This star is found at approximately 3 pc from the cluster center, and given the age structure of the cluster, it is probably farther away from the center. Even so, one star is not enough to explain the large amount of dust found. We would like to point out another possibility here.
If the IMF is normal, which it appears to be down to the lowest masses studied, we can assume that the star formation mechanism must also be normal, and we can expect the presence of circumstellar disks. The observational results are somewhat difficult to interpret. Rubio et al. (1998) used JHKs photometry to detect infrared excess sources around the 30 Doradus nebula. Most of the sources with excess are more than 5 pc away from the central cluster. These authors interpret this emission as coming from YSOs whose formation was triggered by the central cluster. Maercker & Burton (2005) use L-band observations with the 60-cm South Pole InfraRed Explorer (SPIREX) Telescope to detect L-band excess sources that they interpret as possessing circumstellar disks. They find a disk fraction of 42%. These observations are limited to the brightest sources, and the resolution does not permit studying the central regions of the cluster. It is likely that these sources are very bright YSOs that are still embedded in their dust shells. Stolte et al. (2010) studied the galactic star-burst Arches cluster near the center of the galaxy using L-band excess to find candidate disk sources. In addition they confirm the disk nature of these excess sources using SINFONI VLT observations to detect the signature of rotation in the CO bandhead emission (Bik & Thi 2004). They find that the disk fraction in Arches increases from 2.7% ± 1.8% in the cluster core (within 0.16 pc from the center), to 5.4% ± 2.6% for 0.16 pc < r < 0.3 pc, reaching 9.7% ± 3.7% outside. The overall disk fraction for the B stars in the Arches cluster is 6%, much lower than what would expect from the disk fraction age relation (Haisch et al. 2001). They explain the decrease in disk fraction toward the center by either UV radiation destruction, winds, or the tidal destruction mechanism of Olczak et al. (2012) that has the important characteristic, in the context of this work, of destroying the disk without destroying the dust.
In a recent series of papers, Olczak et al. (2012, and references therein) have proposed, based upon numerical simulations, that in an environment as dense as the core of the Arches cluster, where the density is expected to be >105 M⊙/pc3, encounters can destroy up to one third of the circumstellar disks. Olczak et al. (2010) posit a number density of 105 pc-3 as the threshold above which disk destruction occurs rapidly. If Eq. (14) represents the physical state of the cluster, then the disk destruction process might be responsible, at least in part, for the inner extinction that we have measured. According to recent studies, disks are formed in all environments, varying only the lifetimes of the disks, which are much shorter for massive stars where they are destroyed by photo-evaporation (see Williams & Cieza 2011, and references therein). There is a loose linear relation between disk mass and stellar mass. The median disk mass is approximately 1% of the parent star mass, and the variation is approximately ±0.5 dex. For our estimate we need the arithmetic mean, which for stellar masses between 0.015–4 M⊙ has been found to vary between 2% to 5% of the parent stellar mass for different galactic star forming regions studied (Andrews et al. 2010; Scholz et al. 2006; Manning & Sargent 2000). Thus, if we assume a total mass of 105 M⊙ for the cluster, we expect the total mass in disks to be 2000–5000 M⊙. Using a gas-to-dust ratio of 100 implies 20–50 M⊙ of dust, while using the gas-to-dust ratio of the 30 Doradus region of the LMC results in 6–15 M⊙. Thus, to explain the inner reddening of R136 with dust coming from the destruction of circumstellar disks requires (1) that most of these disks were destroyed recently, within a few 105 y or else the gas would have been removed from the central region; and (2) the gas-to-dust ratio must be closer to 100 than to the value of 347 measured elsewhere in the 30 Doradus region. If both of these conditions are not met, then an alternative origin must be sought.
4. Conclusions
In this work we estimate a conservative limit to the central mass density of R136 of
1.5 × 104 M⊙/pc3 for
a < 0.4 pc. From this we estimate that the total
mass of the cluster enclosed within 10 pc must be in the range
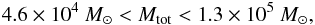 or
in terms of total number of stars Ntot,
or
in terms of total number of stars Ntot,
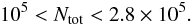 In
this case the observed scale-free profile must be in place at the moment of formation
because relaxation and core collapse have not had time to act in this young object.
In
this case the observed scale-free profile must be in place at the moment of formation
because relaxation and core collapse have not had time to act in this young object.
On the other hand, if we use the recent estimate of the core parameter by Campbell et al.
(2010), we get the moderately larger bound for the
total mass 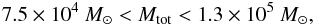 and
the more extreme constraint for the central density
and
the more extreme constraint for the central density 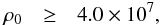 which
would imply that core collapse becomes a certainty.
which
would imply that core collapse becomes a certainty.
Such high central density can have other effects. We have shown that it is unlikely that the reddening distribution, observed by SMBT to increase toward the inner parts of the cluster, could come from normal mass loss from massive stars. It is posited in this work that a sizeable fraction of this dust could come from the recent destruction of most of the circumstellar disks in R136.
The core parameter in the Elson, Fall and Freeman form is related to the King profile
core radius by 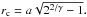 This
formula is incorrectly quoted in Campbell et al. (2010), but correctly given in Mackey & Gilmore (2003). We also note that rc is equivalent
to the r0 in the King (1962) model only when it is much smaller than the tidal radius. This is not
valid for low-concentration clusters, but certainly valid for R136.
This
formula is incorrectly quoted in Campbell et al. (2010), but correctly given in Mackey & Gilmore (2003). We also note that rc is equivalent
to the r0 in the King (1962) model only when it is much smaller than the tidal radius. This is not
valid for low-concentration clusters, but certainly valid for R136.
Acknowledgments
The authors would like to thank C. Olczak for the estimate of the number of disks needed to be destroyed to explain the total mass of dust implied in Selman et al. (1999a). The speculation that the color excess seen in the inner parts of R136 is due to such a process lies only with the authors. C. Olczak also pointed out to us the effect that a spectrum of masses can have on the relaxation time of a stellar system. We would also like to thank the anonymous referee, whose constructive criticism helped improve the paper. We would also like to thank Dave Jones and the language editor for help with the English.
References
- Allen, D. A., & Swings, P. 1972, Astophys. Lett., 10, 83 [Google Scholar]
- Andersen, M., Zinnecker, H., Moneti, A., et al. 2009, ApJ, 707, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Hughes, A. M., Qi, C., & Dullemond, C. P. 2010, ApJ, 723, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Bik, A., & Thi, W. F. 2004, A&A, 427, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binney, J., & Tremaine, S. 1987, Galactic Dynamics, Princeton Series in Astrophysics (Princeton: Princeton University Press) [Google Scholar]
- Brandl, B., Sams, B. J., Bertoldi, F., et al. 1996, ApJ, 466, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Breysacher, J. 1981, A&AS, 43, 203 [NASA ADS] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 291 [Google Scholar]
- Bosch, G., Terlevich, E., & Terlevich, R. 2009, AJ, 137, 3437 [NASA ADS] [CrossRef] [Google Scholar]
- Bouchet, P., Lequeux, J., Maurice, E., Prévot, L., & Prévot-Burnichon, M. L. 1985, A&A, 149, 330 [NASA ADS] [Google Scholar]
- Campbell, B., Hunter, D. A., Holtzman, J. A., et al. 1992, AJ, 104, 1721 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, M. A., Evans, C. J., Mackey, A. D., et al. 2010, MNRAS, 405, 421 [NASA ADS] [Google Scholar]
- Chatterjee, S., Umbreit, S., Fregeau, J. M., & Rasio, F. A. 2013, MNRAS, 429, 2881 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. 2003, APSS, 285, 677 [NASA ADS] [Google Scholar]
- Crowther, P., Schnurr, O., Hirschi, R., et al. 2010, MNRAS, 408, 731 [NASA ADS] [CrossRef] [Google Scholar]
- de Jager, C., Nieuwenhuijzen, H., & van der Hucht, K. A. 1988, A&AS, 72, 259 [NASA ADS] [Google Scholar]
- de Marchi, G., Paresce, F., Panagia, N., et al. 2011, ApJ, 739, 27 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G. 1958, ApJ, 128, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [Google Scholar]
- Elson, R. A. W., Fall, S. M., & Freeman, K. C. 1987, ApJ, 323, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Feast, M. W., Thackeray, A. D., & Wesselink, A. J. 1960, MNRAS, 121, 25 [Google Scholar]
- Fitzpatrick, E. 1985, ApJ, 299, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, P. C., Dorschner, J. M., Geiss, J., et al. 1999, ApJ, 525, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Fujii, M. S., Saitoh, T. R., & Portegies Zwart, S. F. 2012, ApJ, 753, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Geisel, S. L. 1970, ApJ, 161, L105 [Google Scholar]
- Haisch, K. E., Lada, E. A., & Lada, C. J. 2001, ApJ, 553, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Hénault-Brunet, V., Evans, C. J., Sana, H., et al. 2012, A&A, 546, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, D., Shaya, E. J., Holtzman, J. A., et al. 1995, ApJ, 448, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, D., O’Neil, E. J., Lynds, R., et al. 1996, ApJ, 459, L27 [NASA ADS] [CrossRef] [Google Scholar]
- King, I. 1962, AJ, 67, 471 [NASA ADS] [CrossRef] [Google Scholar]
- King, I. 1971, PASP, 83, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J. 1973, AJ, 78, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2002, Science, 295, 82 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mackey, A. D., & Gilmore, G. F. 2003, MNRAS, 338, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., & Meynet, G. 2012, RvMP, 84, 25 [Google Scholar]
- Maercker, M., & Burton, M. G. 2005, A&A, 438, 663 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malumuth, E., & Heap, S. 1994, AJ, 107, 1054 [NASA ADS] [CrossRef] [Google Scholar]
- Manning, V., & Sargent, A. I. 2000, ApJ, 529, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Massey, P., & Hunter, D. 1998, ApJ, 493, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, D. E., & van der Marel, R. P. 2005, ApJS, 161, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Melnick, J. 1985, A&A, 153, 235 [NASA ADS] [Google Scholar]
- Meynet, G., Maeder, A., Schaller, G., Schaerer, D., & Charbonnel, C. 1994, A&AS, 103, 97 [NASA ADS] [Google Scholar]
- Moffat, A. F. J. 1969, A&A, 3, 455 [NASA ADS] [Google Scholar]
- Nugis, T., & Lamers, H. J. G. L. M. 2000, A&A, 360, 227 [NASA ADS] [Google Scholar]
- Olczak, C., Pfalzner, S., & Eckart, A. 2010, A&A, 509, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olczak, C., Kaczmarek, T., Harfst, S., Pfalzner, S., & Portegies Zwart, S. 2012, ApJ, 756, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, J. W., & Garmany, C. D. 1993, AJ, 106, 1471 [NASA ADS] [CrossRef] [Google Scholar]
- Pei, Y. C. 1992, ApJ, 395, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Purcell, E. M. 1969, ApJ, 158, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Racine, R. 1996, PASP, 108, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Racine, R. 1999, PASP, 111, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Roddier, F. 1995, A&AS, 223, 109 [Google Scholar]
- Rubio, M., Barbá, R. H., Walborn, N. R., et al. 1998, AJ, 116, 1708 [NASA ADS] [CrossRef] [Google Scholar]
- Sabbi, E., Lennon, D. J., Gieles, M., et al. 2012, ApJ, 754, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Selman, F. J., Melnick, J., Bosch, G., & Terlevich, R. 1999a, A&A, 341, 98 [NASA ADS] [Google Scholar]
- Selman, F. J., Melnick, J., Bosch, G., & Terlevich, R. 1999b, A&A, 347, 532 [NASA ADS] [Google Scholar]
- Scholz, A., Jayawardhana, R., & Wood, K. 2006 ApJ, 645, 1498 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L. 1978, Physical Processes in the Interstellar Medium (John Wiley and Sons), 162 [Google Scholar]
- Stolte, A., Morris, M. R., Ghez, A. M., et al. 2010, ApJ, 718, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Usov, V. V. 1991, MNRAS, 252, 49 [NASA ADS] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2000, A&A, 362, 295 [NASA ADS] [Google Scholar]
- Walborn, N. R., & Blades, J. C. 1997, ApJS, 112, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Weigelt, G., & Baier, G. 1985, A&A, 150, L18 [NASA ADS] [Google Scholar]
- Williams, J. P., & Cieza, L. A. 2011, ARA&A, 49, 67 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: The total mass of dust from the observed E(B – V)
For our estimates we follow Purcell (1969), Spitzer (1978), and Pei (1992). This last author is interested in the gas-to-dust ratio, and all his derivations were done in terms of that parameter. However, the extinction can be directly converted into a mass column density of dust based solely on the assumed dust model. Spitzer (1978) gives an expression for the mass of dust as a function of E(B − V), but valid only for the Milky Way and in terms of the average extinction per kpc. We therefore redo the more modern Pei (1992) calculation to directly get the dust column density implied by the observed E(B − V).
The extinction optical depth at wavelength λ,
τ(λ), is given by
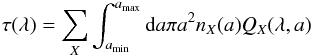 (A.1)where
the sum is over species X, graphite, and silicate; a is
the size of a grain; nX(a)
is the distribution of grain sizes of type X; amin and
amax are the lowest and largest grain sizes; and
QX(λ,a) is the extinction
efficiency factor for grains of type X. The distribution of grain sizes is that of Mathis
et al. (1977)2:
(A.1)where
the sum is over species X, graphite, and silicate; a is
the size of a grain; nX(a)
is the distribution of grain sizes of type X; amin and
amax are the lowest and largest grain sizes; and
QX(λ,a) is the extinction
efficiency factor for grains of type X. The distribution of grain sizes is that of Mathis
et al. (1977)2: ![\appendix \setcounter{section}{1} \begin{eqnarray} n_X(a){\rm d}a = \left\{ \begin{array}{ll} N_X (a/a_V)^{-\beta}{\rm d}(a/a_V) & {\rm if} a_{\rm min} < a < a_{\rm max};\\[1mm] 0 & \mbox{otherwise}, \end{array} \right. \end{eqnarray}](/articles/aa/full_html/2013/04/aa20396-12/aa20396-12-eq85.png) (A.2)with
β = 3.5, amin = 0.005 μm,
and amax = 0.25 μm. Then,
aV is given by
(A.2)with
β = 3.5, amin = 0.005 μm,
and amax = 0.25 μm. Then,
aV is given by
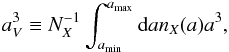 (A.3)which
for this grain size distribution results in
aV = 0.737 μm. With these
definitions they write
(A.3)which
for this grain size distribution results in
aV = 0.737 μm. With these
definitions they write 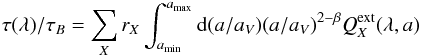 (A.4)where
(A.4)where
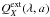 is the extinction efficiency
factor of grains of type X given by Draine & Lee (1984). They have defined
is the extinction efficiency
factor of grains of type X given by Draine & Lee (1984). They have defined 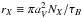 . They use this
expression, together with a dust grain model, to fit the extinction data to the Milky Way,
the LMC, and the SMC to find the value of rX
that fits the data. With these definitions the column density of dust, Σd, is
given by
. They use this
expression, together with a dust grain model, to fit the extinction data to the Milky Way,
the LMC, and the SMC to find the value of rX
that fits the data. With these definitions the column density of dust, Σd, is
given by 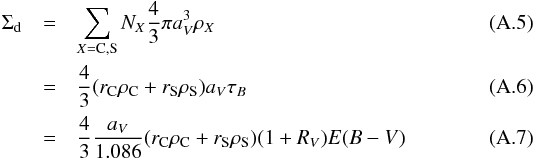 where
ρC = 2.26 g cm-3 and
ρS = 3.3 g cm-3 are the mass density of the
graphite and silicate grains, and RV is the
total-to-selective extinction parameter, which has the value 3.16 for the LMC. For the LMC
the extinction curve is best fit with rX
values given by rC = 0.018 and
rS = 0.083. The values for the Milky Way and the SMC are
somewhat different and can be found in Pei (1992),
and can be used to finally obtain
where
ρC = 2.26 g cm-3 and
ρS = 3.3 g cm-3 are the mass density of the
graphite and silicate grains, and RV is the
total-to-selective extinction parameter, which has the value 3.16 for the LMC. For the LMC
the extinction curve is best fit with rX
values given by rC = 0.018 and
rS = 0.083. The values for the Milky Way and the SMC are
somewhat different and can be found in Pei (1992),
and can be used to finally obtain
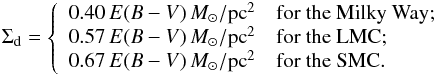 (A.8)Thus,
an average value E(B − V) ~ 0.1−0.2
implies, in the LMC, a total mass of 40–80 M⊙ within 15 pc,
and 18–36 M⊙ within 10 pc.
(A.8)Thus,
an average value E(B − V) ~ 0.1−0.2
implies, in the LMC, a total mass of 40–80 M⊙ within 15 pc,
and 18–36 M⊙ within 10 pc.
All Figures
 |
Fig. 1 Radial density profile for the stars with 10 M⊙ < M < 40 M⊙. For the innermost bins we have calculated the points using the Hunter et al. (1995) data following the procedure described in SMBT. The line is a power law with exponent –1.85. The point at the smallest radius is strongly affected by incompleteness. Reproduced with permission from SMBT. |
| In the text | |
 |
Fig. 2 a) Radial profile of color excess, as determined in Selman et al. (1999a). b) Color excess versus selective extinction parameter S. Reproduced with permission from Selman et al. (1999a). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


