| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 8 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201220372 | |
| Published online | 08 April 2013 | |
Possible survival of simple amino acids to X-ray irradiation in ice: the case of glycine
1
UPMC Univ. Paris 6 – CNRS UMR 7616, Laboratoire de Chimie Théorique
(LCT),
75005
Paris,
France
e-mail:
pauzat@lct.jussieu.fr
2
Synchrotron SOLEIL, L’Orme des Merisiers, Saint Aubin-BP48,
91192
Gif-sur-Yvette Cedex,
France
3
UPMC Univ. Paris 6 – CNRS UMR 7614, Laboratoire de
Chimie-Physique, Matière et
Rayonnement (LCPMR), 75005
Paris,
France
4
Present address:
CINaM, CNRS, Aix-Marseille Université, Campus de Lumigny, 13288
Marseille Cedex 9,
France
e-mail:
laffon@cinam.univ-mrs.fr
Received:
12
September
2012
Accepted:
18
February
2013
Context. Glycine, the simplest of amino acids, has been found in several carbonaceous meteorites collected on Earth, though its presence in the interstellar medium (ISM) has never been confirmed as of today. It is now considered that its synthesis took place in the icy mantles of interstellar grains, but it remains unclear how glycine, once synthesized and trapped in interplanetary particles, survives during the transfer to the Earth.
Aims. Assuming that glycine was effectively formed in the ice, we address the question of its resistance to a solar-like radiation field and look for the possible molecular remnants that would be useful tracers of its former existence.
Methods. The search was conducted using an interdisciplinary approach that mixes, on the one hand, irradiations in ultra high vacuum at 30 K on the TEMPO beam line of the synchrotron SOLEIL, simultaneously with near-edge X-ray absorption spectroscopy (NEXAFS) measurements, and on the other hand, quantum calculations to determine the energetics of the fragmentations and the relative stability of the different byproducts. The last points were addressed by means of density functional theory (DFT) simulations followed by high-level post Hartree-Fock calculations when more accurate relative energies were necessary. The constraints of an icy environment deserved special attention and the ice was modeled by a polarizable continuum medium that relies on the dielectric constant of water ice at 10–50 K.
Results. Destruction of glycine is observed in the first seconds of irradiation, and carbon dioxide (CO2) and methylamine (CH3NH2) are formed. Carbon monoxide (CO), methanimine (CH2NH) and hydrogen cyanide (HCN) are also produced in secondary reactions. The amino acid destruction is the same for pure glycine and glycine in ice, indicating that the OH radicals released by the water matrix is barely involved in the photolytic process; however, these radicals are involved in the production of the secondary byproducts through dehydrogenation reactions as shown by ab initio quantum chemical simulation presented in this article along with the experimental results.
Conclusions. The experiments show that glycine is only partially destroyed. Its abundance is found to stay at a level of ~30% of the initial concentration, for an irradiation dose equivalent to three years of solar radiation (at a distance of one astronomical unit). This result supports the hypothesis that, if trapped in protected icy environments and/or in the interior of interplanetary particles and meteorites, glycine may partly resist the radiation field to which it is submitted and, accordingly, survives its journey to the Earth.
Key words: ISM: molecules / astrobiology
© ESO, 2013
1. Introduction
It has been known for twenty years now that the presence of amino acids is not restricted to the Earth. Although none has been identified in the interstellar medium (ISM), they are known to be present in the organic matter of numerous carbonaceous chondrites (for a review, see e.g. Sephton 2002). The most striking example comes from analyzing the Murchison meteorite in which 70 amino acids have been identified, including 8 out of the 22 standard amino acids of living organisms (Cooper et al. 1992). Glycine, the simplest of them, is one of the most abundant (Botta et al. 2002).
Recently, it has been shown that several amino acids can be formed in the laboratory by UV irradiation of interstellar ice analogues containing H2O, CH3OH, NH3, CO, and CO2 (Bernstein et al. 2002; Muñoz-Caro et al. 2002). Bombardment by energetic particle yields N-methyl carbamic acid rather than glycine (Holtom et al. 2005; Bossa et al. 2008), and only successive UV irradiation would lead to glycine (Bossa et al. 2009). The most recent communication on the subject reports identifying twenty-six acids including six diamino acids in an artificial comet (Meinert et al. 2012). Nonetheless, one main question remains unsettled, namely, that of the survival of these amino acids embedded in the ice along their journey to the Earth.
The key issue of the resistance of amino acids to the radiation field in space has been addressed via several experimental approaches. For instance, it has been shown that the structure of pure condensed amino acids can be severely affected by photon irradiation (see e.g. Zubavichus et al. 2004a,b; Wilks et al. 2009), and the rôle of environment has been probed by IR spectroscopy (Ehrenfreund et al. 2001, 2002). In the case of glycine, the main fragments detected are HCN and CO2, in agreement with the results of the near-edge X-ray absorption spectroscopy (NEXAFS) study at the O K-edge that we reported earlier (Lattelais et al. 2011a).
In a recent theoretical study we have shown that glycine may not exist under the unique form of a neutral species, NH2CH2COOH, depending on the environment (Lattelais et al. 2011b). The possible fragmentations of glycine were investigated accordingly under different forms in order to cover all possibilities, namely, ionized, doubly ionized, protonated, and zwitterionic, which potentially exist in one or another interstellar environment.
Assuming that glycine stays embedded in the ice, both experimental and theoretical studies
have been focused on the zwitterionic structure NH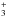 CH2COO−
that is known to be the most stable in the presence of water. A plausible scenario,
consistent with our experimental results, is that the glycine zwitterion is
photodecarboxylated. Such a mechanism would leave behind carbon dioxide (CO2) and
methylamine (CH3NH2), the former remaining as it is, the latter
resulting in HCN after further hydrogen abstractions by the OH radical created by the
irradiation of the surrounding ice. The formation of CO2 and amines has also been
reported recently (Gerakines et al. 2012) under
radiolytic destruction of amino acids under irradiation at low temperature with 0.8 MeV
protons. The experimental approach and NEXAFS results carried out at the Synchrotron SOLEIL
(Saint Aubin, France) on the TEMPO beam line are presented in Sect. 2. The theoretical part
is presented in Sect. 3. The model used is briefly summarized, and the results of the
reported calculations are centered on the role played by the icy environment in the fate of
glycine and the resulting fragments in relation to the experiments. Comparison of
experimental measurements with theoretical findings is done in Sects. 4, and 5 summarizes
the conclusions of this coupled approach to the survival of glycine.
CH2COO−
that is known to be the most stable in the presence of water. A plausible scenario,
consistent with our experimental results, is that the glycine zwitterion is
photodecarboxylated. Such a mechanism would leave behind carbon dioxide (CO2) and
methylamine (CH3NH2), the former remaining as it is, the latter
resulting in HCN after further hydrogen abstractions by the OH radical created by the
irradiation of the surrounding ice. The formation of CO2 and amines has also been
reported recently (Gerakines et al. 2012) under
radiolytic destruction of amino acids under irradiation at low temperature with 0.8 MeV
protons. The experimental approach and NEXAFS results carried out at the Synchrotron SOLEIL
(Saint Aubin, France) on the TEMPO beam line are presented in Sect. 2. The theoretical part
is presented in Sect. 3. The model used is briefly summarized, and the results of the
reported calculations are centered on the role played by the icy environment in the fate of
glycine and the resulting fragments in relation to the experiments. Comparison of
experimental measurements with theoretical findings is done in Sects. 4, and 5 summarizes
the conclusions of this coupled approach to the survival of glycine.
2. Experimental approach
2.1. Experimental setup at the synchrotron SOLEIL
The NEXAFS measurements of solid glycine and of glycine diluted into H2O ice were performed at the oxygen and nitrogen K-edges on the TEMPO beam line of the synchrotron SOLEIL (Saint-Aubin, France). The photon source uses an Apple II ondulator whose linear polarized beam is monochromatized and focused (500 μm2 spot) on the sample. This delivered high beam density produces an instant degradation of glycine, and therefore, we used the photon beam for in-situ irradiation at 30 K, which means it simultaneous with the NEXAFS recordings. To reduce the photon flux, in such way as to access to the kinetics, the ondulator gap was detuned. It also adjusts with the photon energy scan so that the flux remains constant all over the absorption range. In these experimental conditions, glycine damages are already perceptible in a few seconds. A submicrometer translation table makes it possible to move the sample in order to expose a fresh zone at each point of measure. This allows us to obtain the non-irradiated solid glycine NEXAFS spectra that are in perfect agreement with those published previously on the N1s and O1s edges (Gordon et al. 2003; Cooper et al. 2004).
All the experiments were made in the UHV chamber of the TEMPO setup connected to the beamline. Ice samples were deposited at 30 K on the copper finger of an He liquid cryostat from the vapor pressure of the components, either pure glycine or an appropriate mixture of the gas phase. In the latter case, the water pressure was adjusted to obtain a 15% glycine dilution (in molecular percent). Evaporation of glycine was achieved using a Knudsen cell held at 400 K. The deposition rates were about 0.02 and 0.1 Langmuir s-1 for the pure glycine and the glycine diluted in ice, respectively. It took one hour to prepare the solid glycine film and about ten minutes for the mixture. The total thickness of the films is estimated to be around 400 Å. The disappearance of the XPS copper lines ensures that the sample thickness is high enough so that the substrate does not influence the NEXAFS measurements.
Prior to the synchrotron experiments, this deposition method was checked at 140 K in our
laboratory using X-ray photoelectron spectroscopy and Fourier transform infrared
spectroscopy in reflection absorption mode. It confirms that glycine remains intact in the
evaporation stage and that its chemical form, when condensed pure or diluted in water ice,
is the 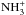 CH2COO−
zwitterion (Takeda et al. 1958; Fischer et al. 2005). However, neutral glycine is
observed with infrared spectroscopy for lower temperature deposits (Maté et al. 2012; Gerakines et al.
2012), although zwitterionic-to-neutral ratios have not been determined
unequivocally and may depend on the evaporation conditions (Maté et al. 2012); Maté et al. also assume that the zwitterion
prevails. As we see in Sect. 2.2, our NEXAFS data in the O1s
→ π∗ range are dominated by a single component at 532.5 eV
assigned to the COO− moiety (Messer et al.
2005). Messer et al. report that the O1s
→ π∗ in the neutral COOH group is downshifted by 0.25 eV
with respect to the corresponding O1s
→ π∗(COO−) in the negative ion. Therefore,
neutral glycine should manifest in the NEXAFS spectra as an additional contribution on the
low-energy side (532.25 eV) of the transition at 532.5 eV, which is not observed. We
estimated that neutral glycine should become distinguishable in the NEXAFS data at
concentrations above 20–30%, which sets the upper limit of neutral glycine content of
films deposited at 30 K in this 20–30% range.
CH2COO−
zwitterion (Takeda et al. 1958; Fischer et al. 2005). However, neutral glycine is
observed with infrared spectroscopy for lower temperature deposits (Maté et al. 2012; Gerakines et al.
2012), although zwitterionic-to-neutral ratios have not been determined
unequivocally and may depend on the evaporation conditions (Maté et al. 2012); Maté et al. also assume that the zwitterion
prevails. As we see in Sect. 2.2, our NEXAFS data in the O1s
→ π∗ range are dominated by a single component at 532.5 eV
assigned to the COO− moiety (Messer et al.
2005). Messer et al. report that the O1s
→ π∗ in the neutral COOH group is downshifted by 0.25 eV
with respect to the corresponding O1s
→ π∗(COO−) in the negative ion. Therefore,
neutral glycine should manifest in the NEXAFS spectra as an additional contribution on the
low-energy side (532.25 eV) of the transition at 532.5 eV, which is not observed. We
estimated that neutral glycine should become distinguishable in the NEXAFS data at
concentrations above 20–30%, which sets the upper limit of neutral glycine content of
films deposited at 30 K in this 20–30% range.
The NEXAFS spectra at the oxygen (530 eV) and nitrogen (400 eV) K-edges are recorded in partial electron yield (PEY) using a channeltron with an entrance-polarized grid suppressing the low-energy electrons. In these conditions we estimate that NEXAFS recordings probe about 40 Å of the topmost layers, which are a part of the total irradiated zone that extends several orders deeper (about 5000 Å). Although damage with the X-ray exposure could induce a loss of the mass sample (i.e. photodesorption), our PEY measurements guarantee we are always observing the topmost layers of the sample, regardless its composition or irradiation dose. For glycine in water ice and pure glycine samples, the temperature is maintained at 30 K to keep the volatile byproducts resulting from the destruction of the amino acid trapped. To help identify photoproducts, we also irradiated the pure glycine sample at 273 K. At this temperature the volatiles sublimate and only the solid residues remain in glycine.
The NEXAFS spectra are the ratio of the PEY signal of the sample to that of the photocurrent of semitransparent gold mesh that monitors the incident flux. The photon energy of the monochromator was calibrated using the 3a1 feature of water ice (Parent et al. 2002) at 535 eV for the O1s edge and to match the second peak of the N1s → π∗ vibrational resolved transition of N2 at 401.1 eV for the N1s edge (Chen et al. 1989). The photon irradiance is measured with a calibrated photodiode. It is 2.79 × 1015 and 5.17 × 1015 photons s-1 cm-2 at 530 and 406 eV, respectively. Each NEXAFS spectrum corresponds to 23 min of exposure, which is the duration of the data acquisition at the O and N K-edges. We convert the exposure to an equivalent time of solar irradiation taking the solar irradiance at one astronomical unit (AU) of 3 × 1013 photons s-1 cm-2 (Ehrenfreund et al. 2001). To correct for the photon energy, the flux is weighted with the ratio of the X-ray energy to that of the Lyα radiation (10.2 eV). In this approximation, each NEXAFS spectrum is then equivalent to an exposure to 2.57 and 3.66 months of solar irradiation at the O and N K-edges, respectively.
Alternatively, these exposures could be converted into absorbed energy dose, but it is difficult here because the irradiations are not monochromatic (or more precisely, they are monochromatic, but the energy is swept with time), and because the absorbed doses strongly vary below and above the O and N absorption K-edges. This makes it difficult to calculate the exact dose or to propose a relevant average value. One further obstacle, specific to X-ray, is that the dose is deposited in the material in a two step process. First, all the energy of the primary photon is released in at the absorption site (which primarily defines the absorbed energy dose). Second, electron cascade stem from the core-hole de-excitation, adding radiolysis to the damages induced by the primary photon. The number, energies, and interaction cross sections of these secondary electrons are poorly known, as well as their influence on the radiation damage. For these reasons exposures are preferable to absorbed doses calculated from the energy flux carried by the incident photon.
 |
Fig. 1 NEXAFS spectra at the oxygen K-edge of pure glycine (top), 15% glycine in water ice (bottom), before and at the end of the irradiation. On the right panels are shown the difference spectra (irradiated minus nonirradiated) at selected doses; pure glycine: 0.86; 1.79; 3.61 equivalent time of solar irradiation, in years (see text); 15% glycine dilution: 0.36; 1.0; 1.72 years. The red arrows indicate how the peaks grow when the irradiation proceeds. |
2.2. NEXAFS spectra
 |
Fig. 2 NEXAFS spectra at the nitrogen K-edge of pure glycine (top), 15% glycine in water ice (bottom), before and at the end of the irradiation. On the right panels are shown the difference spectra (irradiated minus non irradiated), at selected doses; pure glycine 0.30; 0.91; 1.52; 2.54 equivalent time of solar irradiation (year); 15% glycine dilution 0.36; 1.0; 1.72 years. The red arrows indicate how the peaks grow when the irradiation proceeds. |
Figure 1 (left panels) presents the oxygen K-edge NEXAFS spectra of pure glycine and 15% of glycine into 85% of water ice (hereafter referenced as 15:85). The right-hand panels in Fig. 1 show the difference spectra between the sample before irradiation and in the course of the irradiation, in selected doses. For the 15:85 sample, this difference allows removing the water ice contribution and reveals the glycine byproducts better. The spectra of pure glycine show an intense peak at 532.5 eV assigned to the O1s → π∗(COO−) transition of the carboxyl group of the zwitterion (Ehrenfreund et al. 2002). This spectral signature of glycine is used to determine the photodecomposition rates. In the 15:85 mixture, the spectra is dominated by the water ice features (Takeda et al. 1958) (i.e. 4a1 pre-edge at 535 eV and a broad band at around 540 eV), although the π∗(COO−) peak of glycine at 532.5 eV is very visible. Its energy position and peak shape, which is the same as in solid glycine, indicate that the charge state of the amino acid is also that of the zwitterion.
Under soft X-ray irradiation, the π∗(COO−) peak decreases in intensity as glycine is destroyed, while new peaks appear. As one can see in the difference spectra in Fig. 1, these new features are shared by the pure glycine and the water mixture, and they are identified as O1s excitation to the π∗ of CO and CO2. As the temperature of the sample is maintained at 30 K, these volatile species are not lost in the vapor phase but accumulate in the bulk as the irradiation goes on. These species come from the carboxylic group of the amino acid, which has been released after rupture of the -CH2-COO− bond. As shown Sect. 3, DFT calculations reveal that the primary bond rupture following the photoabsorption event proceeds exothermically and forms CO2, which agrees with the experiments. Nevertheless, the formation of CO from CO2 will require another bond rupture.
Figure 2 shows the nitrogen K-edge NEXAFS spectra of
the pure glycine and of 15:85 glycine in ice mixture samples with increasing X-ray
exposure. The spectra have been normalized to unity at 430 eV to correct for the dilution.
The N1s edge of nonirradiated solid zwitterionic glycine presents a unique and
strong asymmetric σ∗ band, labeled GLY, whose maximum is at
406.6 eV (Cooper et al. 2004). This resonance mainly
results from the electron scattering along the C-N bond. Under exposure to X-rays, pure
glycine and the mixture exhibit a decrease in the 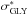 intensity,
accompagnied by a broadening and a shift of about –0.5 eV. We also observe two shoulders
appearing at 401.8 and 402.9 eV, labeled C-NH2. Such changes are expected when
the zwitterion is converted into methylamine, which forms simultaneously to
CO2. Indeed, Otero & Urquhart
(2006) also report pre-edge features around 402 eV in solid compounds where amine
is neutral, features that are not present when it is protonated. The
σ∗(C-N) features are also at a lower energy in the neutral
compounds, and the absorption cross section on the σ∗(C-N) is
also lower. This is consistent with ab initio quantum calculations performed on clusters
of methylamine and its chlorine salt (Otero &
Urquhart 2006), and with published results of amino acids in the solid phase
(Gordon et al. 2003; Messer et al. 2005). Zubavichus et al.
(2004a,b) report a difference of –2 eV
between the N1s binding energies of neutral and protonated amine. Such a
difference makes it possible to follow the photochemical production of C-NH2 on
various powdered amino acids at room temperature, on thin films of glycine at 110 K, and
on codeposited glycine water layers at 90 K (Tzvetkov
& Netzer 2010, 2011) .
intensity,
accompagnied by a broadening and a shift of about –0.5 eV. We also observe two shoulders
appearing at 401.8 and 402.9 eV, labeled C-NH2. Such changes are expected when
the zwitterion is converted into methylamine, which forms simultaneously to
CO2. Indeed, Otero & Urquhart
(2006) also report pre-edge features around 402 eV in solid compounds where amine
is neutral, features that are not present when it is protonated. The
σ∗(C-N) features are also at a lower energy in the neutral
compounds, and the absorption cross section on the σ∗(C-N) is
also lower. This is consistent with ab initio quantum calculations performed on clusters
of methylamine and its chlorine salt (Otero &
Urquhart 2006), and with published results of amino acids in the solid phase
(Gordon et al. 2003; Messer et al. 2005). Zubavichus et al.
(2004a,b) report a difference of –2 eV
between the N1s binding energies of neutral and protonated amine. Such a
difference makes it possible to follow the photochemical production of C-NH2 on
various powdered amino acids at room temperature, on thin films of glycine at 110 K, and
on codeposited glycine water layers at 90 K (Tzvetkov
& Netzer 2010, 2011) .
The photolysis also causes the appearance of several new peaks in the pre-edge region,
corresponding to N1s transitions to unoccupied p or
π∗ orbitals of several unsaturated nitrogen compounds.
Unlike the methylamine, which is a primary product of the C-C bond rupture of glycine,
these unsaturated species require several bonds breakings by photolysis, hydrogen
abstraction, or additional reactions between neigboring N-bearing fragments. Limited to
the region of interest (392–404 eV), the difference spectra (Fig. 2, right panels) show these features better. They are all common in pure
glycine (c) and in the mixture (d), which means that the very nature of the photoproducts
are unchanged in the presence of water, although their relative concentrations may change.
The peak at 401.1 eV, with its typical vibrational structure, is the N1s
excitation to the 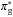 of
N2, showing that dinitrogen is produced in-situ. Its origin could be the same
as in the solid ammonia photolysis (Parent et al.
2009), where it forms via the unimolecular dissociation of hydrazine
(N2H4 → N2 +2H2). This is supported by the
observation of a very small amount of NH2 radicals at 395 eV, which are
precursors of hydrazine (NH2 + NH2 → N2H4).
of
N2, showing that dinitrogen is produced in-situ. Its origin could be the same
as in the solid ammonia photolysis (Parent et al.
2009), where it forms via the unimolecular dissociation of hydrazine
(N2H4 → N2 +2H2). This is supported by the
observation of a very small amount of NH2 radicals at 395 eV, which are
precursors of hydrazine (NH2 + NH2 → N2H4).
The other peaks are related to CN functional groups. The peak at 399.85 eV is assigned to the triply bonded cyano group –C ≡ N, whereas the imino group >C = N-H is present at 398.5 eV. When glycine is irradiated at 273 K(not shown), none of the species observed at 30 K are present, indicating that the species owning these C ≡ N and >C = N-H groups are volatile. Since methylamine is the primary N-bearing product, these species form through the hydrogen abstraction of methylamine, leading to methanimine (CH2 = NH) and hydrogen cyanide (HCN). These abstractions are either directly induced by the X-ray beam or might proceed via deshydrogenation channels through chemical reactions with OH radicals stemming from irradiated water (Laffon et al. 2010; Parent et al. 2011).
2.3. The role of water ice in the fate of glycine
 |
Fig. 3 a) Amount of glycine remaining in the samples (pure glycine and 15% glycine in water ice) as a function of the photon exposure at 530 eV converted into an equivalent time of solar irradiation at 1 AU. Fit to the data is obtained using Eq. (1) (see text). b) Evolution of CO and CO2 and (c) CH2NH and HCN quantities in pure glycine and in the 15:85 mixture as a function of the irradiation time. |
The loss in intensity of the glycine π∗(COO−)
resonance at 532.5 eV in the O K-edge spectra allows estimating the rate of destruction of
the amino acid with the irradiation time. It is presented in Fig. 3a (in % of the initial
amount to correct for the dilution), together with the productions of CO and
CO2 (b), and CH2NH and HCN (c) as the function of the equivalent
solar irradiation time at 1 AU. About 57% of glycine is destroyed during the first-year
equivalent. At later time, the destruction tends to slow, and a steady state is obtained
at about 70%, at three years of irradiation. As a result, ~30% of the initial amount of
glycine survives, regardless of the irradiation dose applied later. This steady state
results from an equilibrium between the destruction of glycine and its reformation
process. The concentration is a function of the irradiation time and it is expressed as
![\begin{eqnarray} [{\rm Glycine}]_t&=&[{\rm Glycine}]_{t=0}\Big\{(p_{\rm f}/(p_{\rm d} + p_{\rm f}))\nonumber \\ && + (1-( p_{\rm f}/(p_{\rm d} + p_{\rm f})) \exp (-(p_{\rm d} + p_{\rm f}) N.t)))\Big\} . \end{eqnarray}](/articles/aa/full_html/2013/04/aa20372-12/aa20372-12-eq29.png) (1)In
this equation, N is the number of photon impinging on the sample per
second (in photon s-1), i.e. the photon irradiance multiplied by the surface
defined as the intersection of the beam with the sample; and
pd and pf are the destruction
and reformation probabilities, respectively. The experimental data are correctly fitted
(Fig. 3a, full line) with pd = 0.08 and
pf = 0.035. These numbers indicate that reformation of
glycine from its fragments is about 2.3 times less probable than its destruction.
(1)In
this equation, N is the number of photon impinging on the sample per
second (in photon s-1), i.e. the photon irradiance multiplied by the surface
defined as the intersection of the beam with the sample; and
pd and pf are the destruction
and reformation probabilities, respectively. The experimental data are correctly fitted
(Fig. 3a, full line) with pd = 0.08 and
pf = 0.035. These numbers indicate that reformation of
glycine from its fragments is about 2.3 times less probable than its destruction.
As seen in Fig. 3a, the destruction is much the same for pure glycine and when diluted in ice. This means that the participation of the OH radicals in the glycine fragmentation is negligible compared to the direct photolysis (Laffon et al. 2010). The reaction of amino acids with OH has been theoretically studied in neutral glycine (Galano et al. 2001) and compared to that of alanine (Burgess et al. 2001; Owen et al. 2001). The calculations predict that hydrogen abstraction occurs on the α-alkyl and leads to the formation of a stable radical fragment, which could explain that the hydrogen abstraction by OH from glycine is not followed by its fragmentation. In contrast, the glycine radical can convert back to glycine either by reaction with H2O2 (Burgess et al. 2001; also present in irradiated water ice, Parent et al. 2002) or with an H atom issued from the water or glycine photolysis. Thus, the OH reaction with glycine is negligible compared with that of the direct photolysis, which is consistent with there being no enhancement of the destruction in presence of water ice.
Figure 3b and c show the evolution of the relative CO, CO2, CH2NH and HCN amounts with the irradiation time. These curves are determined from the π∗ intensities (peak area) of each species corrected from the final densities of states per excited atom. Indeed, HCN has a π∗ intensity that is twice that of the double bond in CH2 = NH because the number of π orbitals is twice. Similarly, CO has a density of final state of 2 (triple bond). CO2 owns two double bonds and two oxygen atoms. The density of π∗ state per oxygen atom is one, but per molecule it is two, which means that the intensities of the π∗ transitions of CO and CO2 are directly correlated to their relative molecular concentrations.
At low exposure, the intensity of these species increases conversely to the glycine degradation, then stabilizes at higher exposure. This is consistent with the glycine destruction below one year of exposure and a steady state regime at high dose. At low dose the molecular concentration of HCN is lower than that of the CH2NH, in agreement with a sequencial deshydrogenation event where the cyanide is formed from the imine. The production of CH2NH slows down as the glycine destruction proceeds, and also because it is itself destroyed to produce HCN.
In water ice at low dose (<one year), the production of imine and cyanide species is almost the same as in pure glycine, while at higher dose, imine species are favored in the mixture but not the cyanide. Assuming that it results from additional hydrogen abstractions by the OH radical, we can conclude that such reactions occur, and it appears to be easier to convert CH3NH2 in CH2NH than CH2NH into HCN. Such chemical reactions add to the direct photolysis process enhancing the formation of the imine species. Last, the evolution of the CO and CO2 species is very different in pure glycine and in the mixture. The formation of CO2 is favored in the presence of water, whereas that of CO is not. This is due to the additional OH reaction that is known to convert CO into CO2 + H (Laffon et al. 2010). It is very efficient in the water ice mixture because it increases the CO2/CO ratio by three in the water mixture compared to pure glycine (Lattelais et al. 2011b).
3. Theoretical approach
 |
Fig. 4 Schematic representation of the relative energies (kcal/mol) for the fragmentation channels of zwitterionic (top) and ionized zwitterionic (bottom) glycine. For clarity, ionic fragments are in italics and exothermic fragmentations (below the molecular backbone) are encapsulated in plain rectangles. |
The fragmentation of glycine upon irradiation in the ice is explored theoretically in order to better understand the results of the experimental investigation reported in the preceding section.
3.1. The ice model
Here, we have to compare all the forms of glycine that are generated by the irradiation in the ice and its fragments on an equal footing. In this context, the choice was to perform the calculations at the level of density functional theory (DFT) for the primary fragmentation involving large systems (Lattelais et al. 2011a). The B3LYP functional was used and associated with the extended cc-pVQZ basis set. For the secondary fragmentations, which involve much smaller systems, more precise post Hartree-Fock methods were employed. These calculations were based on a systematic increase in the levels of theory, allowing a better treatment of the electronic correlation using Moller-Plesset perturbation theory at the second and fourth orders (MP2, MP4), and coupled cluster developments (CCSD and CCSD(T). For a comprehensive presentation of DFT and post Hartree-Fock methods and their applicability, the reader may profitably refer to Koch & Holthausen (2001) and Szabo & Ostlund (1989).
The structures of all species were fully optimized and verified to be true minima by vibrational analysis. All the reported relative energies take zero point energy corrections into account. The 6-311++G** basis set was employed in all calculations, which were practically performed using the Gaussian03 program (Frisch et al. 2004).
In the ice, as in any polar medium, glycine should appear under a zwitterionic form. It
was verified experimentally in the present study for the pure condensate, as well as for
the glycine/water ice mixture. Theoretically, it has been shown that as few as two
H2O molecules, when properly positioned around glycine, are sufficient to
induce the proton transfer from the carboxylic group to the amino group leading to the
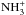 CH2COO−
zwitterion (Kassab et al. 2000). In the present
study, the icy environment is described as a homogeneous polarizable medium (PCM) (Tomasi & Persico 1994) characterized by its
ϵ dielectric constant. The value commonly used for water is 78.5, which
corresponds to the liquid state at room temperature. For the solid state, it has been
shown that ϵ increases sharply with decreasing temperatures (Johari & Jones 1976; Johari & Whalley 1981). A value of ϵ = 600 was
extrapolated from this comprehensive study for temperatures in the range of 10 to 50 K
corresponding to the conditions of both the experiments and the ISM.
CH2COO−
zwitterion (Kassab et al. 2000). In the present
study, the icy environment is described as a homogeneous polarizable medium (PCM) (Tomasi & Persico 1994) characterized by its
ϵ dielectric constant. The value commonly used for water is 78.5, which
corresponds to the liquid state at room temperature. For the solid state, it has been
shown that ϵ increases sharply with decreasing temperatures (Johari & Jones 1976; Johari & Whalley 1981). A value of ϵ = 600 was
extrapolated from this comprehensive study for temperatures in the range of 10 to 50 K
corresponding to the conditions of both the experiments and the ISM.
3.2. Fragmentation channels in the ice
Enthalpies of reaction (ΔH) and activation barriers (ΔE#) corrected for zero point vibrational energies (kcal/mol) of the successive hydrogen abstraction reactions starting from methylamine without (upper panel) and with (lower panel) participation of OH radicals.
When submitted to the strong synchrotron radiation field (~530 eV), zwitterionic glycine
may break in two ways, i.e., either directly, or after the ejection of the photoelectron,
which leads to the formation of a cation of the form
[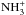 CH2COO−]+.
The energetics of these fragmentations are illustrated in Fig. 4.
CH2COO−]+.
The energetics of these fragmentations are illustrated in Fig. 4.
The lowest energy fragmentation of the zwitterion (endothermic by 3 kcal/mol) gives two
neutral fragments: CO2 and NH2CH3 (see top panel in Fig.
4). They are both issued from the neutralization of
the internal ion pair, the formation of the latter species being coupled to a molecular
rearrangement (hydrogen transfer). Such a destruction mechanism can be seen as a reverse
reaction of the synthesis of glycine, close to the mechanism proposed by Bossa et al.
(2009). The next fragmentation on the energy scale (at 27 kcal/mol) leads to
NH2CH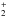 and HCOO− implying a hydrogen transfer without charge neutralization to form
the carboxylate ion.
and HCOO− implying a hydrogen transfer without charge neutralization to form
the carboxylate ion.
Ionization of the zwitterion removes an electron from the carboxylate end, resulting in
an N-protonated radical. It is remarkable that this structure breaks along two exothermic
channels (ΔH = −21 kcal/mol), both leading to CO2 and a
positive ion coming from hydrogen scrambling in the [CNH5]+ cation.
A third channel that needs almost no energy contribution (~0.3 kcal/mol) leads to
NH2CH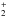 and HOCO.
and HOCO.
These results show that very little energy is needed to break glycine in the ice. The stable neutral fragments obtained in the end are CO2 and CH3NH2.
3.3. Secondary fragmentation channels
Starting from CH3NH2, the destruction process may continue
following two different paths, i.e., without or with direct participation of the OH
radicals created by irradiation of the ice, both ways leading to smaller products with
functional groups 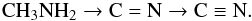 (2)A
large survey of the reaction possibilities was first performed at the DFT level. Then, the
energetics of the significant reaction schemes (reaction enthalpies and activation
barriers) were determined in a series of calculations based on a systematic increase in
the levels of theory. For clarity, only the highest two levels are reported here (Table
1). The CCSD(T) values corresponding to the embedded reactions have been estimated by
adding the PCM contribution at the CCSD level to the CCSD(T) gas phase energy differences.
(2)A
large survey of the reaction possibilities was first performed at the DFT level. Then, the
energetics of the significant reaction schemes (reaction enthalpies and activation
barriers) were determined in a series of calculations based on a systematic increase in
the levels of theory. For clarity, only the highest two levels are reported here (Table
1). The CCSD(T) values corresponding to the embedded reactions have been estimated by
adding the PCM contribution at the CCSD level to the CCSD(T) gas phase energy differences.
In the first case, i.e., without participation of OH radicals (upper panel in Table 1), all these chained reactions of hydrogen abstraction by unimolecular fragmentations are initiated by the radiation field. They are all endothermic and cannot proceed without the energy provided by the irradiation flux. That the fragmentation takes place embedded in the ice has a marginal influence (±2%) on the endothermicity. Activation barriers, at least equal to the endothermicity, are not relevant in this scheme. In the end two stable products are obtained, CH2 = NH and HC≡N.
In the second case, i.e., with active participation of the OH radicals from the surrounding ice, these OH radicals are able to react with the primary byproducts. The series of reactions is illustrated by the network in Fig. 5 whose energetics are given in Table 1 (lower panel). Starting from methylamine, the same two stable products are formed, namely methylene imine and hydrogen cyanide that possess the double and triple CN bonds, respectively. Their fingerprints have been observed in the NEXAFS experiments. The important difference is that all reactions become exothermic when they are initiated by OH instead of the radiation field. The role played by the confinement of the reactions in the ice has a marginal effect on the exothermicities, as well as on the height of the activation barriers for the radical-molecule processes. Radical-radical reactions are barrier free.
The endothermic formation of the CN radical with or without OH participation suggests that the CN triple bond observed is only due to the stable HCN.
4. Discussion
On the one hand, not detecting glycine in the ISM is consistent with the correlation found between the observations of various astrophysical objects and thorough computations of the relative stability of the isomers of a same generic chemical formula showing that the most abundant species observed were principally those of lower energies (Lattelais et al. 2009). Furthermore, the larger the energy differences between isomers, the higher their abundance ratios, in general. Glycine in the gas phase in the ISM is far from being the most stable isomer and has not been detected, in agreement with what is referred to as the minimum energy principle (Lattelais et al. 2009). It does not mean that glycine does not exist in the ISM. Several cases of high-energy isomers have indeed been found, such as HNC for HCN, cyc-C2H4O for CH3CHO, or CH2OHCHO for CH3COOH. It simply suggests that the glycine abundance should be very low and probably too small to be detected by the present instruments (Lattelais et al. 2011b). On the other hand, the identification of various amino acids in meteorites and the recent synthesis of prebiotic materials in artificial comets (Meinert et al. 2012) support the hypothesis of the formation of glycine in icy environments, which may apply to interstellar, as well as to outer solar system, conditions.
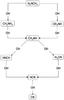 |
Fig. 5 Most important successive hydrogen abstractions by the OH radical. |
Our experimental results show that glycine is readily photo-decomposed in the solid phase, in agreement with previous studies (Wilks et al. 2009; Orzechowska et al. 2007). From our experimental conditions, the half life of glycine was extrapolated at ten months of equivalent UV solar irradiation at the Sun-to-Earth distance. Our experiments also show the puzzling result that zwitterionic glycine is almost equally destroyed when it is a pure condensate or diluted in water ice. Thus, one could conclude that water ice neither protects nor enhances the glycine photolysis.
However, when looking more closely at Fig. 4, it can be seen that all fragmentation routes
of the zwitterion but one require less energy than the 10.2 eV provided by
Lyman-α photons, which is far below the 530 eV energy of the synchrotron
photons, with the most energetically demanding fragmentation asking for ~15 eV. When an
ionizing photon is absorbed by glycine in our experiment, the process leaves a glycine
cation and a photoelectron ![\begin{eqnarray} {\rm NH_3^+CH_2COO^- + h\nu \rightarrow [NH_3^+CH_2COO^-]^+ + e^-}. \end{eqnarray}](/articles/aa/full_html/2013/04/aa20372-12/aa20372-12-eq55.png) (3)The
cation then dissociates directly into the fragments according to the fragmentation scheme in
Fig. 4 (bottom). In all the experimental studies that
we have performed so far, we observed only neutral fragments, indicating that the ionized
species are readily neutralized by attaching electrons flowing from the ionization process
around (Lacombe et al. 2009; Krim et al. 2009); it is what happens here to
[CNH5]+ ions. In fact, the cation breaks into two products,
releasing CO2, in agreement with our experiments where it is the main product
observed on the NEXAFS spectra at the oxygen K-edge.
(3)The
cation then dissociates directly into the fragments according to the fragmentation scheme in
Fig. 4 (bottom). In all the experimental studies that
we have performed so far, we observed only neutral fragments, indicating that the ionized
species are readily neutralized by attaching electrons flowing from the ionization process
around (Lacombe et al. 2009; Krim et al. 2009); it is what happens here to
[CNH5]+ ions. In fact, the cation breaks into two products,
releasing CO2, in agreement with our experiments where it is the main product
observed on the NEXAFS spectra at the oxygen K-edge.
![\begin{eqnarray} {\rm [NH_3^+CH_2COO^-]^+ \rightarrow NH_2CH_3^+ / NH_3CH_2^+ + CO_2}. \end{eqnarray}](/articles/aa/full_html/2013/04/aa20372-12/aa20372-12-eq56.png) (4)Following
the minimum energy principle, the neutralization of the [CNH5]+ leads
to methylamine, NH2CH3, which is the most stable species. The
signature of NH2CH3 is effectively observed on the NEXAFS spectra at
the nitrogen K-edge, together with those of its most stable decomposition products,
CH2NH and HCN, also obtained in the same irradiation conditions. It is also
worth mentioning that higher energy fragmentations may lead, after neutralization, to highly
energetic NH3, which is known to give N2 (Parent et al. 2009), whose signature is effectively observed as a major
feature in our experiment. When embedded in the ice, glycine should also react with the OH
radicals created by irradiation,
(4)Following
the minimum energy principle, the neutralization of the [CNH5]+ leads
to methylamine, NH2CH3, which is the most stable species. The
signature of NH2CH3 is effectively observed on the NEXAFS spectra at
the nitrogen K-edge, together with those of its most stable decomposition products,
CH2NH and HCN, also obtained in the same irradiation conditions. It is also
worth mentioning that higher energy fragmentations may lead, after neutralization, to highly
energetic NH3, which is known to give N2 (Parent et al. 2009), whose signature is effectively observed as a major
feature in our experiment. When embedded in the ice, glycine should also react with the OH
radicals created by irradiation, 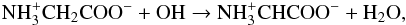 (5)where
the zwitterionic form of the radical is unambiguously identified by EPR spectroscopy in the
solid state (Ghosh & Whiffen 1959; Morton 1964; Neta
& Fessenden 1971). If this decomposition pathway (endothermic by ~1 eV) has
a significant rate, it should accelerate the glycine destruction in ice. But, as shown in
Fig. 3a, such a speed up is not observed. Thus, the role of the OH radical in the primary
fragmentation of molecular glycine seems negligible. This also establishes that, whether
glycine is pure or embedded in ice, its decomposition in our synchrotron experiment results
mostly from photolysis, i.e, a spontaneous internal process insensitive to the chemical
environment, which leaves no time for OH to react.
(5)where
the zwitterionic form of the radical is unambiguously identified by EPR spectroscopy in the
solid state (Ghosh & Whiffen 1959; Morton 1964; Neta
& Fessenden 1971). If this decomposition pathway (endothermic by ~1 eV) has
a significant rate, it should accelerate the glycine destruction in ice. But, as shown in
Fig. 3a, such a speed up is not observed. Thus, the role of the OH radical in the primary
fragmentation of molecular glycine seems negligible. This also establishes that, whether
glycine is pure or embedded in ice, its decomposition in our synchrotron experiment results
mostly from photolysis, i.e, a spontaneous internal process insensitive to the chemical
environment, which leaves no time for OH to react.
During its journey to the Earth, glycine is certainly not submitted continuously to a radiation flux of several hundreds of eV, but rather to intermittant radiations below the hydrogen ionization threshold. In these conditions, one may conjecture that the OH radicals could have enough time to react with the first fragmentation product, NH2CH3, according to the exothermic reaction chain of Fig. 5. Though exothermic, the abstractions of a hydrogen atom by OH are not free of activations barriers, but according to their magnitudes, it is reasonable to consider that they can be overpassed easily using the heating of the grain by the radiation field. In the end both mecanisms lead to the same stable products.
5. Conclusion
The important question of the stability of glycine during its transfer to the Earth under the interstellar radiation field, was modeled in our experiments using the SOLEIL synchrotron radiation of the TEMPO beam line for both irradiation and in situ NEXAFS experiments at the N1s and O1s edges. It was addressed in a joint approach by theoretical calculations of the fragmentation routes.
A systematic survey of the primary fragmentation products was made previously in which the rupture of the plausible forms under which glycine may be present in the ISM were considered. These calculations have shown (Lattelais et al. 2011a) that neutral glycine is able to survive a radiation field of ~3 eV, corresponding to a location deep inside interstellar clouds (Ehrenfreund et al. 2002).
Our present solid phase experiments are consistent with the fact that the decomposition of glycine occurs mainly because of its direct photolysis through an unstable ionized state. This internal process is insensitive to the matrix: the destruction rates are indeed the same in pure glycine and in water ice. The nature of the main byproducts detected at the oxygen K-edge is the same for pure glycine and for glycine in ice: CO and CO2. The signatures of the same N-bearing species are found at the nitrogen K-edge: CH3NH2, CH2NH, HCN. However, in water ice, the relative amounts of CH2NH is modified by the reaction with the OH radical produced by the water photolysis (Parent et al. 2011). Here we have shown that zwitterionic glycine breaks for much less than ~1 eV and that removal of an electron from the zwitterionic form of glycine leads to an exothermic destruction. In agreement with our experimental data, our calculations clearly show that the cation of the glycine zwitterion is unstable, and it releases CO2 and CH3NH2 in its dissociation. In addition, the OH radical persisting in the ice mantle leads to the other end products observed by successive hydrogen abstractions.
It is clear that glycine as a pure condensate is not relevant for modeling interstellar situations. However, that the evolution of the concentration of glycine under irradiation tends to a limit of ~30% of the initial load in the solid phase suggests a common mechanism at play in both cases. In view of the different chemical environments, it has to be a physical reason. Although not really protective, the role of the matrix appears to be that of a containment environment that allows the primary fragments to remain close, thus leading to some reformation of glycine in situ. Still, on a macroscopic scale, ice can provide a real protective layer to glycine, if the amino acid is buried at depths that are higher than the photon penetration (Laffon et al. 2010) (that was not the case in our study). Under these conditions, glycine could be incorporated into solar system bodies and be partially protected (but not entirely) during its journey to the Earth.
Acknowledgments
This work was supported by CNRS national programs PCMI (Physics and Chemistry of the Interstellar Medium), EPOV (Environment of Planets and Origins of Life) and COST Action CM0805 (The Chemical Cosmos). Part of the calculations were performed using HPC resources from GENCI-CINES (Grant 2011-085128).
References
- Bernstein, M. P., Dworkin, J., Sandford, S. A., Cooper, G. W., & Allamandola, L. J. 2002, Nature, 416, 401 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bossa, J.-B., Borget, F., Duvernay, F., Theulé, P., & Chiavassa, T. 2008, J. Phys. Chem. A, 112, 5113 [CrossRef] [PubMed] [Google Scholar]
- Bossa, J.-B., Duvernay, F., Theulé, P., et al. 2009, A&A, 506, 601 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Botta, O., Glavin, D. P., Kminek, G., & Bada, J. L. 2002, Origins of Life and Evolution of the Biosphere, 32, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Burgess, A.A., Easton, C. J., Hay, M. P., & Hay, M. P. 1989, J. Am. Chem. Soc., 111, 1047 [CrossRef] [Google Scholar]
- Chen, C. T., Ma, Y., & Sette, F. 1989, Phys. Rev. A, 40, 6737 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cooper, G. W., Onwo, W. M., & Cronin, J. R. 1992, Geochim. Cosmochim. Acta, 54, 4109 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, G., Gordon, M. L., Tulumello, D., et al. 2004, J. Electron Spectrosc., 137, 795 [CrossRef] [Google Scholar]
- Ehrenfreund, P., Bernstein, M. P., Dworkin, J., et al. 2001, ApJ, 550, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Ehrenfreund, P., Irvine, W., Becker, L., et al. 2002, Rep. Prog. Phys., 65, 1427 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, G., Cao, X., Cox, N., & Francis, M. 2005, Chem. Phys., 313, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, M., Trucks, G., & Schlegel, H. 2004, Gaussian 03, Rev.C.02, Gaussian Inc., Wallingford CT., 611, 605 [Google Scholar]
- Galano, A., Alvarez-Idaboy, J. R., Montero, L. A., & Vivier-Bunge, A. 2001, J. Comput. Chem., 22, 1138 [CrossRef] [Google Scholar]
- Gerakines, P. A., Hudson, R. L., Moore, M. H., & Belle, J. L. 2012, Icarus, 220, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, M. L., Cooper, G., Morin, C., et al. 2004, J. Phys. Chem. A, 107, 6144 [CrossRef] [Google Scholar]
- Ghosh, D. K., & Whiffen, V. H. 1959, Mol. Phys., 2, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Holtom, P. D., Bennett, C. J., Osamura, Y., Mason, N. J., & Kaiser, R. I. 2005, ApJ, 626, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Johari, G. P., & Jones, S. J. 1976, Proc. Roy. Soc., A, 349, 467 [Google Scholar]
- Johari, G. P., & Whalley, E. J. 1981, J. Chem. Phys., 75, 1333 [NASA ADS] [CrossRef] [Google Scholar]
- Kassab, E., Langlet, J., & Evleth, E. 2000, J. Mol. Struct. Theochem, 531, 267 [CrossRef] [Google Scholar]
- Koch, W., & Holthausen, M. C. 2001, A Chemist Guide to Density Functional Theory (Wiley-VCH, Weinheim, Germany (2nd edn.) [Google Scholar]
- Krim, L., Lasne, J., Laffon, C., & Parent, Ph. 2009, J. Phys. Chem. A, 113, 8979 [CrossRef] [Google Scholar]
- Lacombe, S., Bournel, F., Lasne, Laffon, C., & Parent, Ph. 2006, Angew. Chem. Int. Ed. Engl., 45, 4159 [CrossRef] [Google Scholar]
- Laffon, C., Lasne, J., Bournel, F., et al. 2010, Phys. Chem. Chem. Phys., 12, 10865 [CrossRef] [Google Scholar]
- Lattelais, M., Pauzat, F., Ellinger, Y., et al.. 2009, ApJ, 696, L133 [Google Scholar]
- Lattelais, M., Risset, O., Pilmé, J., et al. 2011a, Int. J. Quantum Chem., 111, 1163 [CrossRef] [Google Scholar]
- Lattelais, M., Pauzat, F., Pilmé, J., & Ellinger, Y. 2011b, A&A, 532, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maté, B., Rodriguez-Lazcano, Y., Galvez, O., Tanarro, I., & Escribano, R. 2012, Phys. Chem. Chem. Phys., 13, 12268 [CrossRef] [Google Scholar]
- Meinert, C., Filippi, J J., de Marcellus, P., d’Hendecourt, L., & Meierhenrich, U. J. 2011, Chem. Phys. Chem., February 29, on line [Google Scholar]
- Messer, B. M., Cappa, C D., Smith, J. D., et al., 2005, J. Phys. Chem., 109, 21640 [CrossRef] [Google Scholar]
- Morton, J. R. 1964, J. Am. Chem. Soc., 86, 2325 [CrossRef] [Google Scholar]
- Muñoz-Caro, G., Meierhenrich, U. J., Schutte, W. A., et al. 2002, Nature, 416, 403 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Neta, P., & Fessenden, R. W. 1971, J. Phys. Chem., 75, 2738 [CrossRef] [Google Scholar]
- Orzechowska, G. O., Goguen, J. D., Johnson, P., V., Tsapin, A., & Kanik, I. 2007, Icarus, 187, 584 [NASA ADS] [CrossRef] [Google Scholar]
- Otero, G. P., & Urquhart, E. J. 2006, J. Phys. Chem. A, 110, 12121 [CrossRef] [Google Scholar]
- Owen, M. C., Szori, M., Csizmadia, I. G., & Viskolcz, B. 2012, J. Phys. Chem. B, 116, 1143 [CrossRef] [Google Scholar]
- Parent, Ph., Laffon, C., Mangeney, C., Bournel, F., & Tronc, M. 2002, J. Chem. Phys., 117, 10842 [NASA ADS] [CrossRef] [Google Scholar]
- Parent, Ph., Bournel, F., Lasne, J., et al. 2009, J. Chem. Phys., 131, 154308 [NASA ADS] [CrossRef] [Google Scholar]
- Parent, Ph., Laffon, C., Lasne, J., Bournel, F., & Lacombe, S. 2011, J. Phys. Conf. Ser., 261, 12008 [NASA ADS] [CrossRef] [Google Scholar]
- Sephton, M. A. 2002, Nat. Prod. Rep., 19, 292 [CrossRef] [PubMed] [Google Scholar]
- Szabo, A., & Ostlund, N. 1989, In Modern Quantum Chemistry (New York: McGraw-Hill Inc.) [Google Scholar]
- Tomasi, J., & Persico, M. 1994, Chem. Rev., 94, 2027 [CrossRef] [Google Scholar]
- Takeda, M., Lavazzo, R. E. S., Garfinkel, D., Scheinberg, I. H., & Edsall, J. T. 1958, J. Am. Chem. Soc., 80, 3813 [CrossRef] [Google Scholar]
- Tzvetkov, G., & Netzer, F. P. 2010, J. Electron Spectrosc., 182, 41 [Google Scholar]
- Tzvetkov, G., & Netzer, F. P. 2011, J. Chem. Phys., 134, 204704 [NASA ADS] [CrossRef] [Google Scholar]
- Wilks, R. G., McNaughton, J. B., Kraats, H. B., et al. 2004b, J. Phys. Chem A, 113, 5360 [CrossRef] [Google Scholar]
- Zubavichus, Y., Fuchs, O., Weinhardt, L., et al. 2004a, Radiat. Res., 161, 346 [CrossRef] [PubMed] [Google Scholar]
- Zubavichus, Y., Zharnikov, M., Shaporenko, A., et al. 2004b, J. Phys. Chem A, 108, 4557 [Google Scholar]
All Tables
Enthalpies of reaction (ΔH) and activation barriers (ΔE#) corrected for zero point vibrational energies (kcal/mol) of the successive hydrogen abstraction reactions starting from methylamine without (upper panel) and with (lower panel) participation of OH radicals.
All Figures
 |
Fig. 1 NEXAFS spectra at the oxygen K-edge of pure glycine (top), 15% glycine in water ice (bottom), before and at the end of the irradiation. On the right panels are shown the difference spectra (irradiated minus nonirradiated) at selected doses; pure glycine: 0.86; 1.79; 3.61 equivalent time of solar irradiation, in years (see text); 15% glycine dilution: 0.36; 1.0; 1.72 years. The red arrows indicate how the peaks grow when the irradiation proceeds. |
| In the text | |
 |
Fig. 2 NEXAFS spectra at the nitrogen K-edge of pure glycine (top), 15% glycine in water ice (bottom), before and at the end of the irradiation. On the right panels are shown the difference spectra (irradiated minus non irradiated), at selected doses; pure glycine 0.30; 0.91; 1.52; 2.54 equivalent time of solar irradiation (year); 15% glycine dilution 0.36; 1.0; 1.72 years. The red arrows indicate how the peaks grow when the irradiation proceeds. |
| In the text | |
 |
Fig. 3 a) Amount of glycine remaining in the samples (pure glycine and 15% glycine in water ice) as a function of the photon exposure at 530 eV converted into an equivalent time of solar irradiation at 1 AU. Fit to the data is obtained using Eq. (1) (see text). b) Evolution of CO and CO2 and (c) CH2NH and HCN quantities in pure glycine and in the 15:85 mixture as a function of the irradiation time. |
| In the text | |
 |
Fig. 4 Schematic representation of the relative energies (kcal/mol) for the fragmentation channels of zwitterionic (top) and ionized zwitterionic (bottom) glycine. For clarity, ionic fragments are in italics and exothermic fragmentations (below the molecular backbone) are encapsulated in plain rectangles. |
| In the text | |
 |
Fig. 5 Most important successive hydrogen abstractions by the OH radical. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


