EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 552 (April 2013) A&A, 552 (2013) A125 Full HTML
Free Access
Issue
A&A
Volume 552, April 2013
Article Number A125
Number of page(s) 8
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/201220178
Published online 12 April 2013

© ESO, 2013

1. Introduction

The last decade has established ultra-high-energy cosmic ray (UHECR) physics as a phenomenologically rich and experimentally mature science. Key observations related to the UHECR energy spectrum (HiRes 2008; Auger 2011a; Telescope Array 2012a), its composition (HiRes 2010a; Auger 2010a, 2011b; Telescope Array 2011), and its distribution over the sky (Auger 2010b; HiRes 2010b; Telescope Array 2012b) have clarified some open questions, notably the existence of a strong decrease in the UHECR flux above  ~60 EeV. These same observations have also raised new, unexpected questions. In particular, the question of composition has become central, due to both new observational results and a greater understanding of the interplay between composition and general UHECR phenomenology. This includes constraints on individual source spectra and power, maximum energy, and source evolution (Berezinskii & Grigor’eva 1988; Allard et al. 2007; Aloisio et al. 2007; Allard 2012, and refs. therein).

The absence of a clear signal of anisotropy or correlation with some classes of astrophysical objects, although in line with some indications of the presence of heavy nuclei among the UHECRs, has raised doubts about the utility of pursuing the quest for the highest energy particles in the universe. Because of this, it is legitimate to question the ability of present and future detectors to identify sources and to study their properties through the particle channel.

On the other hand, even though large deflections at ultra-high-energy may be a reality due to large particle charges or strong magnetic fields, individual sources could still be isolated in the sky if the UHECR flux is dominated by the contribution of a limited number of sources. The reduction of the horizon associated with the GZK effect in fact implies that fewer and fewer sources contribute to the flux at higher and higher energy. In this regard, the GZK effect can turn into a useful phenomenon, provided that the associated low statistics can be overcome in future experiments.

In this paper, we address this question quantitatively by studying the contribution of individual sources to the overall flux. To this end, we simulate several astrophysical scenarios with different source densities, source spectra, and compositions. We also study the “cosmic variance” associated with different possible realizations and explore the effect of a distribution of intrinsic source luminosities. We leave the study of particle deflections, which strongly depend on assumptions made regarding magnetic fields and source composition, to future work. Therefore, we do not attempt to draw realistic sky maps, but focus on the number of contributing sources as a function of energy. This is in contrast to some earlier studies of source statistics, which were developed in the context of UHECR clustering and multiplet analyses (e.g. Blasi & de Marco 2004; Harari et al. 2004; Younk 2009).

2. The method

As the energy of cosmic-ray particles increases, their propagation length decreases due to their interaction with the photon background. As a result, the contribution of far-away sources is attenuated with increasing energy. Therefore, fewer and fewer sources are visible in the UHECR sky, an effect known as the GZK effect (Greisen 1966; Zatsepin & Kuzmin 1966). At an energy of 1020 eV, the 90% horizon scale is reduced to H ~ 80 Mpc. As a consequence, the number of sources potentially contributing will be limited to Ns = ns × 4πH3/3 ≃ 21(ns/10-5 Mpc-3) × (H/80   Mpc)3 (on average), where ns is an effective source density.

Of course, the fraction of the flux actually contributed by each individual source at a given energy depends on its actual distance, intrinsic power, and precise attenuation due to the intervening interactions. To study the combination of these effects, we do Monte-Carlo simulations using a previously developed and well-tested propagation code (e.g. Allard et al. 2008; Allard 2012). This code can be applied to models with various source spectra, compositions, powers, spatial distributions, and cosmological evolutions.

We explore various combinations, with the requirement that the resulting propagated energy spectrum is compatible with current data. Among the possible models, we chose four that include both conservative and extreme cases: a pure proton model, a pure Fe model, a generic mixed composition model, and the so-called low proton Emax model (Allard et al. 2007, 2008), which accounts for a possible evolution towards a heavier composition above 10 EeV (Auger 2011b).

A set of parameters that have been found to fit the data for each model are shown in Table 1. The spectrum is assumed to be a power law of index x, with an exponential cutoff above energy Emax for protons, and Z × Emax for nuclei of charge Z. For models with a mixed composition, β is a heuristic parameter that implements a bias towards heavier nuclei (Allard 2012): the relative abundance of nucleus i in the source composition is given by αi=αGCR,i×Aiβ−1\hbox{$\alpha_{i} = \alpha_{\mathrm{GCR},i}\times A_{i}^{\beta - 1}$}, where αGCR,i is its relative abundance in low-energy Galactic cosmic rays Duvernois & Thayer (1996). For the pure Fe model, the maximum energy of the nuclei is actually 26 times the quoted value of Emax. The maximum Fe energy in the pure-Fe case is thus in fact 360 EeV.

Table 1

Parameters chosen for the different models used in the simulations, as described in the text.

The quoted values correspond to the parameters that best fit the Auger data. However, we also used somewhat different values obtained by fitting the HiRes data and found that this had no significant impact on the results regarding source statistics. The values obtained for Emax in the different scenarios are adjusted, together with the source spectral index and composition enhancement, to reproduce the observed cutoff in the UHECR spectrum without introducing unobserved features in the spectrum around the maximum proton energy. The choice of 1020.5 eV for the maximum proton energy in the mixed-composition model is arbitrary. Any value larger that this (i.e. well above the GZK cutoff) would produce essentially the same results.

In all cases, we assume that there is no evolution of the intrinsic source power (and/or density) as a function of redshift in order not to increase the number of free parameters. To investigate the influence of such an evolution, we add a model, corresponding to the mixed composition model with strong cosmological evolution, i.e. with the source power depending on redshift following either the star formation rate in galaxies (SFR model) or the evolution of Fanaroff-Riley Class II galaxies (FRII model). This implies a different source spectral index: x = 2.1 and 1.8 respectively.

thumbnail Fig. 1

Histograms of the flux contributed by the top source in each realization. A histogram is shown for each of the four models (as per Table 1) with a source density of ns    =    10-5   Mpc-3 and Emin = 100 EeV.

The contribution of each source to the total UHECR flux also depends on its particular luminosity. By default, we assume the sources to be standard candles, i.e. each with the same power. However, we also study the effect of a distribution of intrinsic source luminosities by considering the same models, but assigning each source a luminosity following a given probability distribution. We consider both a log 10-normal distribution with a σ of either 1 or 2 and a power law distribution with an index of –2.

For each model, we build three different scenarios corresponding to three typical choices of source density: ns = 10-4   Mpc-3, 10-5   Mpc-3, and 10-6   Mpc-3. The highest density is representative of the active galactic nuclei (AGN) density in the local universe, which is an upper limit for scenarios involving AGNs as UHECR sources. The lowest density corresponds to an average of  ~4 sources within 100 Mpc, a situation in which only a few extreme sources are able to accelerate UHECRs up to and beyond 100 EeV.

For each of these scenarios, we build a particular realization of the source configuration with the assumed density. To this effect, we draw a subsample of the galaxies in the flux-limited 2MRS catalog (Huchra et al. 2012) up to a limiting radius of Rlimit=(180/2π)ns−1/3≤700 Mpc\hbox{$R_{\mathrm{limit}} = \left(180/2\pi\right) n_{\mathrm{s}}^{-1/3} \leq 700~\mathrm{Mpc}$}, thereby mimicking the local source distribution. Beyond Rlimit we assume a continuous source distribution. In addition, in the case of a distribution of intrinsic source luminosities, we assign each source a random luminosity according to the chosen distribution.

We then propagate hundreds of thousands of UHECRs emitted by each of the sources according to their assumed spectrum and composition. The particles reaching Earth are collected into sufficiently large a data set to avoid Poissonian fluctuations. From this data set, we determine the fraction of events that comes from each source in the configuration. This fraction depends on the energy of the UHECRs, since fewer and fewer sources contribute at higher and higher energy. We thus study the evolution of this fraction as a function of energy by considering only UHECR events above a given minimum energy, Emin.

As the actual universe is a definite, but a priori unknown realization of the underlying astrophysical scenario, we must explore the cosmic variance associated with various choices of source distances. We therefore repeat the above procedure for 50 different source configurations with the same density within the same astrophysical model and analyze the distribution of results.

3. Results

A major goal of UHECR studies is to isolate sources in the sky and study their individual properties. Whether this can be achieved observationally depends i) on the apparent angular size of the sources, as seen from Earth after propagation through the intergalactic and interstellar magnetic fields; ii) on the number of sources visible in the sky and their respective weight; and iii) on the statistics collected by the detectors.

The goal of the present study is to address the second point quantitatively. To this end, we determine for each of the scenarios described in the previous section the fraction of UHECRs contributed by all the sources and sort them by apparent luminosity.

3.1. Fractional contribution of the brightest sources

In Fig. 1, we show histograms of the contribution of the brightest source in the sky for four chosen astrophysical scenarios as a fraction of the total flux. The relatively large spread corresponds to the above-mentioned cosmic variance, with the contribution of the brightest source in a given realization depending solely on the spatial configuration of the sources in that realization. It can be seen that, depending on the realization, the brightest source may contribute as much as 68% of the total flux above Emin = 100 EeV or as low as 10%, with a standard deviation of  ~15%.

In the following, we present the value of the median of the distributions as the typical value to be expected for a given scenario, so that the actual contribution of the source would be higher in half of the cases and lower in the other half. In addition, we determine a 68% probability interval around the median value.

thumbnail Fig. 2

Median flux as a percentage of the total for the three brightest sources in the sky, shown for the models of Table 1 and a source density of ns = 10-5   Mpc-3.

In Fig. 2, we show the evolution of the fractional contribution of the three brightest sources as a function of minimum energy, Emin, for the different models of Table 1, with source density ns = 10-5   Mpc-3. As expected, the contribution of the brightest sources increases with increasing energy, which is the direct consequence of the GZK effect.

thumbnail Fig. 3

Median flux as a percentage of the total for the three brightest sources in the sky, shown for the mixed-composition model (parameters given in Table 1) with source densities of ns = 10-4, 10-5,and   10-6   Mpc-3.

In Fig. 3, the same results are shown for the mixed composition model with three different densities: ns = 10-6, 10-5, and 10-4   Mpc-3. As can be seen, the fractional contribution of the second brightest source is typically a factor of 2–2.5 lower than that of the brightest source, and the contribution of the third brightest source is another factor of two lower. This hierarchy is clearly marked when looking at the median of the distributions, but two or three sources may contribute roughly equally to the UHECR flux in individual realizations, as suggested by the 68% spread in the plots.

thumbnail Fig. 4

Median flux as a percentage of the total for the brightest source in the sky, shown for all four models of Table 1 and for source densities of ns = 10-4, 10-5, and 10-6   Mpc-3.

To compare the variation of the fractional contribution of the brightest source between models and source densities, we plot the median for each scenario as a function of Emin in Fig. 4. At a given density, the difference between the contributions of the brightest source in the four models is relatively moderate, of the order of a 20% relative variation at Emin = 100 EeV. However, a large difference can be seen for each model between the three source densities. At Emin = 100 EeV, the typical fractional contribution is a factor of two larger at ns = 10-5   Mpc-3 than at ns = 10-4   Mpc-3, and another 50% more at ns = 10-6   Mpc-3.

As expected, the domination of a few sources in the UHECR flux increases as the source density decreases, due primarily to the fewer number of sources overall. But as can also be seen, this effect is reduced at low energy. This is because the contribution of the most nearby sources, for which the actual density makes a difference (compared to a continuous distribution of sources), is reduced as the GZK horizon recedes. At the lowest energies considered here,  ~30 EeV, the horizon scale is much larger than the distance between neighboring sources and larger than the radius Rlimit, beyond which a continuous source distribution is assumed. As a consequence, the increase of the fractional contribution of the brightest source with energy is stronger for lower densities.

3.2. Influence of a luminosity distribution

In Fig. 5, we show the same histogram as in Fig. 1(a), but with the source luminosity now distributed according to a log 10-normal distribution with a σ of 1. The resulting distribution shows a much larger cosmic variance, with contributions of the brightest source being larger than 50% in slightly more than one-third of the cases and reaching up to almost 100% of the flux in a few rare instances.

thumbnail Fig. 5

Histogram of the flux contributed by the brightest source in each realization for a mixed-composition model (see Table 1) with a source density of ns = 10-5   Mpc-3 and Emin = 100 EeV. In this case, the individual sources have been given an intrinsic luminosity according to a log 10-normal distribution with σ = 1.

thumbnail Fig. 6

Median flux fraction for the brightest source in the sky, shown for a mixed-composition model with a source density of ns = 10-5   Mpc-3. The median is shown for a uniform source luminosity and for source luminosities distributed according to either a log 10-normal distribution or a power law, as described in the text.

The influence of different luminosity distribution scenarios, as mentioned in Sect. 2, is shown in Fig. 6. We plot the evolution with energy of the median fractional contribution of the brightest source for a mixed composition model with ns = 10-5   Mpc-3. The contribution increases in every case, passing from 34% at 100 EeV in the case of standard candles to up to 47% for the log 10-normal, σ = 1, scenario. This is because upward fluctuations, where one of the most nearby sources happens to be brighter than average, extend the distribution towards higher fractional contributions. Downward fluctuations, however, are more limited, simply switching the ordering of the source brightnesses.

3.3. Influence of source evolution

The previous plots show the results obtained, assuming that there is no evolution of the intrinsic source power and/or density as a function of redshift, or in other words, time. Since the brightest sources are always nearby, within a few tens of Mpc (even at low energy, where the GZK horizon is further away), the intrinsic power of these sources should not be expected to be different in any significant way on the corresponding timescale, whatever the evolution scenario. However, in all the source evolution scenarios considered, the source power and/or density is higher at earlier times, so that more distant sources contribute more to the flux than in the case with no evolution. This enhances the cosmic ray flux at low energy with respect to high energy, resulting in a change of the propagated spectrum obtained from a given source spectrum. In order to fit the actual UHECR data, source evolution scenarios thus require harder source spectra.

Because this might a priori change the above results, we computed the fractional contribution of the brightest sources, assuming that the source power or number follows the evolution of the star formation rate (SFR, Hopkins & Beacom 2006) or that of the FRII radio galaxies (Wall et al. 2005). As can be seen in Fig. 7, the effect is negligible. This is because the relative contribution of the different sources is dictated by the GZK horizon structure, which is not modified by the source evolution. Our results, computed for a no-evolution scenario, are thus robust in this respect.

thumbnail Fig. 7

Median flux fraction of the brightest source, shown for the mixed-composition model with a source density of ns = 10-5   Mpc-3, for three source evolution models: no evolution with time, SFR-like evolution, and FRII-like evolution (see text).

3.4. Source number

In Figs. 2 and 3, we show the contribution of the three brightest sources for various models. It is also interesting to determine how many sources are expected to make up more than, say, 50% of the flux in each scenario. This number, denoted by N50%, is shown in Fig. 8 for the mixed composition model and three values of the source density, as well as for each of the models of Table 1 with a density ns = 10-5   Mpc-3.

The strongest influencing parameter is again source density. For ns = 10-5   Mpc-3, N50% is between three and four at E = 100 EeV. At 80 EeV, N50% moderately increases to between four and seven. However, below 80 EeV, it rapidly increases as a result of the quickly receding horizon to reach more than 20 sources needed to make up more than 50% of the flux. This is a direct demonstration of the GZK effect. The dramatic decrease in the overall UHECR spectrum above 60 EeV is indeed due to a dramatic reduction of the number of contributing sources in that energy range.

The source density influences N50% as expected: fewer sources contribute a large fraction of the flux at lower densities, and a handful of sources make up 50% of the flux down to 60 EeV for ns = 10-6   Mpc-3, instead of 80 EeV for ns = 10-5   Mpc-3. For source densities as high as ns = 10-4   Mpc-3, N50% is greater than ten even at 100 EeV.

Finally, for a given model, a distribution of source luminosities results in a lower value of N50% compared to the same scenario assuming standard candle sources, as is shown in Fig. 8(b). This is in line with our previous remark that a scenario with a distribution of luminosities is effectively similar to a standard-candle version of the same model with a lower source density.

4. Discussion

We have shown that above E > 3 × 1019   eV the number of sources that contribute to the UHECR flux can be expected to strongly decrease, down to only a few sources at the highest energies. This decrease is due to the energy loss length of protons and heavy nuclei during propagation from their sources to the Earth, i.e. the GZK effect. To quantify this effect, we have shown results for the fractional contribution of the brightest sources in the UHECR sky as a function of minimum threshold energy. Because the exact contribution is dependent on the spatial configuration of the closest sources, we reported the median value over a set of realizations and for three choices of source density. We considered several UHECR source scenarios with respect to composition and energy spectrum. The choice of source parameters was motivated by previous studies of UHECR propagation so as to fit the data.

For a mixed-composition model with a source density of ns = 10-5   Mpc-3, we find that above E = 100 EeV the brightest UHECR source in the sky can be expected to contribute 34-17+15%\hbox{$34^{+15}_{-17}\%$} of the total flux, and the brightest three sources contribute more than 50% of the total flux (actually 58% in this case). In the previous number, the value of 34% is the median of the values obtained for different realizations, and the quoted range (from 17% to 49%) contains 68% of all realizations. For lower source densities, the UHECR sky at the highest energies is dominated by even fewer sources. Scenarios with ns = 10-6   Mpc-3 typically result in three or four sources making up more than 50% of the flux down to 80 EeV, and can leave only one or two sources contributing half of the total flux above 100 EeV.

thumbnail Fig. 8

Number of sources (starting from the highest percentage contributor) that provide at least 50% of the total flux, N50%, as a function Emin, the minimum event energy. In panel a), N50% is shown for a mixed-composition model with source densities of ns = 10-4,10-5,and   10-6   Mpc-3. Panel b) shows N50% for a source density of ns = 10-5   Mpc-3 for each model and, in addition, a mixed-composition model with source luminosities distributed according to a log10-normal distribution with σ = 1. The shaded contours show the region in which 68% of all realizations lie; it is omitted in the second figure for clarity.

The results presented in this paper conservatively assume that the UHECR sources are standard candles. Whatever they may be, however, it is likely that they distribute over a range of intrinsic luminosities. This can only increase, on average, the weight of the most luminous sources in the overall UHECR sky and strengthen the effect investigated here. We quantified this effect for a representative choice of source luminosity distributions, finding that the contribution of the brightest source increases to 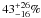43-16+26%\hbox{$43^{+26}_{-16}\%$} for a log-normal distribution with σ = 1 and a source density ns = 10-5   Mpc-3, at 100 EeV (the quoted range has the same interpretation as above). Thus, in such a scenario, two sources largely dominate the observed flux at this energy.

Such low numbers for the count of sources contributing at the highest energies justify the hope that individual sources can be isolated in the sky by future UHECR detectors. At an energy where less than a handful of sources are responsible for the observed flux, with negligible “background” from other, much less intense sources, distinct regions of the sky may be populated essentially by UHECR events coming from one single source. This will be the case even with relatively large deflections due to intervening magnetic fields if the deflections remain smaller than the angular distance between sources, which considerably increases (on average) when the source number is reduced to \hbox{$\mathcal{O}$}(1).

The results presented here illustrate the importance of concentrating on the highest energies, right inside the GZK cutoff, in order to take full advantage of the GZK effect and the associated reduction of the number of visible sources. In particular, Fig. 8 makes clear that a dramatic change in this number occurs between 50 EeV and 80 EeV. This suggests that a significant increase in the clustering signal can be expected if a new generation of detectors can be used to push the current statistics achieved at 50 or 60 EeV up to 80 or 100 EeV. Considering the very low number of contributing sources, one may loosely say that the sources somehow isolate themselves at 1020 eV, because the GZK horizon removes sources that would otherwise overlap due to magnetic deflections.

In a forthcoming work, we will make this qualitative statement quantitative through clustering analyses and anisotropy studies applied to simulated sky maps under generic assumptions regarding the Galactic and intergalactic magnetic fields. In the present paper, we focused on the source number and its evolution with energy. Given the low number of contributing sources suggested by this study, it is clear that any failure to detect a significant clustering signal at the highest energies will put strong constraints on the angular deflections of UHECRs and thus on the magnetic field and/or the UHECR composition. However, the present study clearly shows that the absence of a strong anisotropy signal and the inability of current detectors to isolate UHECR sources in the sky at 50 or 60 EeV does not imply that this will not be possible at 100 EeV.

Increasing the acceptance of the detectors sufficiently to gauge UHECRs deeply into the GZK cutoff is likely to require new observational set-ups, either by using space-based detectors, such as JEM-EUSO (JEM-EUSO 2012), or by exploring new observational techniques, such as radio detection. Since an order-of-magnitude gain in acceptance may be to the detriment of the precision of the measurements, it is important to investigate the effect of an imperfect energy resolution. With poor energy resolution, a cut in the UHECR energy, as assumed above, cannot be strictly applied. This is because some lower energy events will be (mis-)reconstructed at higher energy. These events will contaminate the energy range where very few sources contribute to the overall flux with UHECRs from additional sources within the more distant GZK horizon that prevails at lower energy. Since the UHECR spectrum rapidly decreases as energy increases, a small fraction of events reconstructed with an upward fluctuation of the estimated energy can represent a significant fraction of the events attributed to a higher energy bin.

thumbnail Fig. 9

Median flux fraction of the brightest source in the sky as a function of minimum reconstructed energy, shown for a mixed-composition model with a source density of ns = 10-5   Mpc-3. The top curve is the reference corresponding to a perfect energy reconstruction, and the other three curves correspond to detectors with an assumed Gaussian energy resolution of 10%, 20%, and 30%.

To illustrate this effect, we implemented a Gaussian detector response when binning each UHECR event with respect to Emin and performed the analysis with the effectively reconstructed energies, instead of the actual ones. The results are shown in Fig. 9 for a detector with 10%, 20%, and 30% energy resolution, overlaid with the results for a perfect detector. As expected, a deterioration of the energy resolution results in a smaller contribution of the brightest source to the UHECR events above any given energy. For our fiducial mixed-composition model with source density ns = 10-5   Mpc-3, this fraction goes from 24% for perfect resolution at 80 EeV to respectively 23%, 19%, and 17%, for a 10%, 20%, and 30% energy resolution. At 100 EeV, the reduction is from 34% to 32%, 28%, and 22%, respectively.

The ability of a given detector to actually isolate the brightest sources in the sky will thus depend on its energy resolution. The energy dependence of the detector acceptance will also play a role. For instance, for detectors with a larger acceptance at higher energy, the above effect will be reduced to some extent by the fact that lower energy events have a lower probability of being detected at all. This should thus be modeled for each experiment, given their individual performances.

In sum, regardless of magnetic deflections and experimental limitations, the existence of the GZK effect implies that only a handful of sources will contribute to the UHECR flux above 80 EeV or so. We thus argue that, even though the anisotropy patterns observed by current experiments at 60 EeV are not as enlightening as had long been hoped, the quest to understand UHECRs through anisotropy studies should not stop now, and that expanding our observational capabilities at 1020 eV should give us key information. The isolation of the first UHECR source in the sky would be an important achievement, allowing us to estimate currently unknown astrophysical parameters, such as source density, maximum energy at the source, individual source power, and UHECR energy budget, with corresponding constraints on the nature of the sources and acceleration mechanism.

References

  1. Abbasi, R. U., Abu-Zayyad, T., Al-Seady, M., et al. [HiRes collaboration] 2008, Phys. Rev. Lett., 100, 101101 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
  2. Abbasi, R. U., Abu-Zayyad, T., Al-Seady, M., et al. [HiRes Collaboration] 2010a, Phys. Rev. Lett., 104, id 199902 [NASA ADS] [Google Scholar]
  3. Abbasi, R. U., Abu-Zayyad, T., Allen, M., et al. [HiRes collaboration] 2010b, ApJ, 713, L64 [Google Scholar]
  4. Abu-Zayyad, T., Aida, R., Allen, M., et al. [Telescope Array Collaboration] 2012a, Astropart. Phys., 39, 109 [NASA ADS] [CrossRef] [Google Scholar]
  5. Abu-Zayyad, T., Aida, R., Allen, M., et al. [Telescope Array Collaboration] 2012b, ApJ, 757, 26 [Google Scholar]
  6. Allard, D. 2012, Astropart. Phys., 39, 33 [NASA ADS] [CrossRef] [Google Scholar]
  7. Allard, D., Parizot, E., & Olinto, A. V. 2007, Astrop. Phys., 27, 61 [Google Scholar]
  8. Allard, D., Busca, N. G., Decerprit, G., Olinto, A. V., & Parizot, E. 2008, JCAP, 10, 33 [Google Scholar]
  9. Aloisio, R., Berezinsky, V., Blasi, P., et al. 2007, Astropart. Phys., 27, 76 [NASA ADS] [CrossRef] [Google Scholar]
  10. Berezinskii, V. S., & Grigor’eva, S. I. 1988, A&A, 199, 1 [NASA ADS] [Google Scholar]
  11. Blasi, P., & de Marco, D. 2004, Astropart. Phys., 20, 559 [NASA ADS] [CrossRef] [Google Scholar]
  12. Duvernois, M. A., & Thayer, M. R. 1996, ApJ, 465, 982 [Google Scholar]
  13. Greisen, K. 1966, Phys. Rev. Lett., 16, 748 [Google Scholar]
  14. Harari, D., Mollerach, S., & Roulet, E. 2004, JCAP, 5, 10 [NASA ADS] [CrossRef] [Google Scholar]
  15. Hopkins, A. M., & Beacom, J. F. 2006, ApJ, 651, 142 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  16. Huchra, J. P., Macri, L. M., Masters, K. L., et al. 2012, ApJS, 199, 26 [NASA ADS] [CrossRef] [Google Scholar]
  17. Tameda, Y., et al. [Telescope Array Collaboration] 2011, Proc. of the 32nd ICRC, Beijing, China, 2, HE1.3, 246 [Google Scholar]
  18. The Pierre Auger Collaboration 2010a, Phys. Rev. Lett., 104, 091101 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
  19. The Pierre Auger Collaboration 2010b, Astropart. Phys., 34, 314 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  20. The Pierre Auger Collaboration 2011a, Nucl. Instruments Meth. Phys. Res. A, 630, 91 [NASA ADS] [CrossRef] [Google Scholar]
  21. The Pierre Auger Collaboration, Proc. of the 32nd ICRC, Beijing, China 2011b [arXiv:1107.4804v1] [Google Scholar]
  22. The JEM-EUSO Collaboration 2012 [arXiv:1204.5065] [Google Scholar]
  23. Wall, J. V., Jackson, C. A., Shaver, P. A., Hook, I. M., & Kellermann, K. I. 2005, A&A, 434, 133. [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Younk, P. W. 2009, ApJ, 696, L40 [NASA ADS] [CrossRef] [Google Scholar]
  25. Zatsepin, G. T., & Kuzmin, V. A., 1966 Sov. Phys. JETP Lett. 4, 78 [Google Scholar]

All Tables

Table 1

Parameters chosen for the different models used in the simulations, as described in the text.

In the text

All Figures

thumbnail Fig. 1

Histograms of the flux contributed by the top source in each realization. A histogram is shown for each of the four models (as per Table 1) with a source density of ns    =    10-5   Mpc-3 and Emin = 100 EeV.
In the text
thumbnail Fig. 2

Median flux as a percentage of the total for the three brightest sources in the sky, shown for the models of Table 1 and a source density of ns = 10-5   Mpc-3.
In the text
thumbnail Fig. 3

Median flux as a percentage of the total for the three brightest sources in the sky, shown for the mixed-composition model (parameters given in Table 1) with source densities of ns = 10-4, 10-5,and   10-6   Mpc-3.
In the text
thumbnail Fig. 4

Median flux as a percentage of the total for the brightest source in the sky, shown for all four models of Table 1 and for source densities of ns = 10-4, 10-5, and 10-6   Mpc-3.
In the text
thumbnail Fig. 5

Histogram of the flux contributed by the brightest source in each realization for a mixed-composition model (see Table 1) with a source density of ns = 10-5   Mpc-3 and Emin = 100 EeV. In this case, the individual sources have been given an intrinsic luminosity according to a log 10-normal distribution with σ = 1.
In the text
thumbnail Fig. 6

Median flux fraction for the brightest source in the sky, shown for a mixed-composition model with a source density of ns = 10-5   Mpc-3. The median is shown for a uniform source luminosity and for source luminosities distributed according to either a log 10-normal distribution or a power law, as described in the text.
In the text
thumbnail Fig. 7

Median flux fraction of the brightest source, shown for the mixed-composition model with a source density of ns = 10-5   Mpc-3, for three source evolution models: no evolution with time, SFR-like evolution, and FRII-like evolution (see text).
In the text
thumbnail Fig. 8

Number of sources (starting from the highest percentage contributor) that provide at least 50% of the total flux, N50%, as a function Emin, the minimum event energy. In panel a), N50% is shown for a mixed-composition model with source densities of ns = 10-4,10-5,and   10-6   Mpc-3. Panel b) shows N50% for a source density of ns = 10-5   Mpc-3 for each model and, in addition, a mixed-composition model with source luminosities distributed according to a log10-normal distribution with σ = 1. The shaded contours show the region in which 68% of all realizations lie; it is omitted in the second figure for clarity.
In the text
thumbnail Fig. 9

Median flux fraction of the brightest source in the sky as a function of minimum reconstructed energy, shown for a mixed-composition model with a source density of ns = 10-5   Mpc-3. The top curve is the reference corresponding to a perfect energy reconstruction, and the other three curves correspond to detectors with an assumed Gaussian energy resolution of 10%, 20%, and 30%.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.