| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A65 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201220946 | |
| Published online | 22 February 2013 | |
Bouncing behavior of microscopic dust aggregates
Institut für Astronomie and Astrophysik, Eberhard Karls Universität
Tübingen,
Auf der Morgenstelle 10c,
72076
Tübingen,
Germany
e-mail:
alexs@tat.physik.uni-tuebingen.de
Received: 18 December 2012
Accepted: 14 January 2013
Context. Bouncing collisions of dust aggregates within the protoplanetary disk may have a significant impact on the growth process of planetesimals. Yet, the conditions that result in bouncing are not very well understood. Existing simulations studying the bouncing behavior used aggregates with an artificial, very regular internal structure.
Aims. Here, we study the bouncing behavior of sub-mm dust aggregates that are constructed applying different sample preparation methods. We analyze how the internal structure of the aggregate alters the collisional outcome and we determine the influence of aggregate size, porosity, collision velocity, and impact parameter.
Methods. We use molecular dynamics simulations where the individual aggregates are treated as spheres that are made up of several hundred thousand individual monomers. The simulations are run on graphic cards (GPUs).
Results. Statistical bulk properties and thus bouncing behavior of sub-mm dust aggregates depend heavily on the preparation method. In particular, there is no unique relation between the average volume filling factor and the coordination number of the aggregate. Realistic aggregates bounce only if their volume filling factor exceeds 0.5 and collision velocities are below 0.1 ms-1.
Conclusions. For dust particles in the protoplanetary nebula we suggest that the bouncing barrier may not be such a strong handicap in the growth phase of dust agglomerates, at least in the size range of ≈100 μm.
Key words: planets and satellites: formation / methods: numerical / protoplanetary disks
© ESO, 2013
1. Introduction
For the planet formation process, the growth from micron-sized dust grains to kilometer-sized objects is a key ingredient of the core accretion scenario originally proposed by Pollack et al. (1996). Yet, the question remains unanswered how this process is accomplished in the face of various impediments. First of all, fast inward drift limits the time available to form planetesimals by successive collisions to less than 104 years (Weidenschilling 1977). The growth process itself heavily depends on two ingredients:
-
1.
the dynamical properties of the disk that determine the collisionrate as well as the parameters of a collision such as the impactvelocity;
-
2.
the mechanical behavior of the colliding aggregates that determines the outcome of the collision.
Since the information accessible through direct observations is limited, the first aspect is addressed mainly by theoretical work and computer simulations (Flaig et al. 2012). For an overview on the properties of protoplanetary disks, we refer to the following reviews by Dullemond et al. (2007) and Armitage (2011).
Various methods are employed to investigate the collision behavior of dust/icy aggregates. Depending on the size of the aggregates and the desired collision velocity, laboratory experiments are possible. As of today, laboratory experiments provide data of collisions ranging from millimeter- to decimeter-sized aggregates composed of different materials (mainly silicate/quartz and ice). A comprehensive summary of laboratory experiments is given by Blum & Wurm (2008). Computer simulations provide a second method to study the collisional behavior of dust or ice aggregates. Collisions of very small, micron-sized aggregates have been simulated using a molecular dynamics approach (e.g., Dominik & Tielens 1997; Paszun & Dominik 2009; Wada et al. 2007, 2009). For macroscopic aggregates different methods such as smoothed-particle hydrodynamics (SPH) are employed (e.g., Schäfer et al. 2007; Geretshauser et al. 2010).
More recent experiments showed that collisions of mm- to cm-sized aggregates often result in bouncing (e.g., Weidling et al. 2009; Heißelmann et al. 2010; Weidling et al. 2012; Jankowski et al. 2012). Extrapolating the results obtained from the various experiments, Güttler et al. (2010) devised a model describing the outcome of collision with respect to the collision velocity, and the mass and porosity of the colliding aggregates. Employing this model to simulate the evolution of a swarm of dust aggregates in a protoplanetary disk, the so called “bouncing barrier” emerged (Zsom et al. 2010). As the aggregates grow larger, their relative velocities increase. Because of the growing kinetic impact energy, aggregates get increasingly compacted during successive collisions. When the aggregates get too compact, their collisions do not result in sticking anymore. Instead, they bounce off each other and the growth process is stopped. This occurs in the size regime of centimeters.
A possible way to overcome the bouncing barrier has been recently suggested by Windmark et al. (2012a). Under the assumption of a few bigger aggregates that act as initial seeds, it is possible to grow 100 m-sized bodies on the timescale of 1 Myr. A possible origin of those seeds has been proposed by Windmark et al. (2012b). Taking into account a Maxwellian velocity distribution, they found that low velocity collisions can allow a few aggregates to grow considerably larger than the average of the simulated population.
Despite its significant influence on the growth process, bouncing still lacks theoretical understanding of its prerequisites on a microscopical scale. So far, molecular dynamics (MD) simulations result in bouncing only for compact aggregates (Wada et al. 2011; Schräpler et al. 2012). According to Wada et al. (2011) an average coordination number of 6 is required for aggregates to bounce off each other. However, in laboratory experiments bouncing was frequently observed in collisions of aggregates with lower filling factors/coordination numbers for which MD simulations clearly predict sticking. It has been speculated that this discrepancy could result from a size effect or a possible compaction of the outer shell during the handling process of the aggregates used in the laboratory experiments. However, the latter hypothesis has been refuted by recent experiments (Kothe et al. 2013).
The aim of this work is to study the influence of the internal structure on the bouncing behavior of sub-mm dust aggregates in greater detail. Using the enormous computing power provided by GPUs, we can simulate aggregates consisting of several hundreds of thousands of monomers and thus simulate aggregates in a size range from several microns up to ≈0.1 mm in diameter.
2. Interaction model
To simulate the behavior of dust aggregates we use a soft-sphere discrete element method (SSDEM) approach. The dust aggregates are composed of hundreds of thousands of micron-sized spherical grains (monomers). Our interaction model is based on the work of Dominik & Tielens (1997) who combined earlier theoretical work by Johnson et al. (1971); Dominik & Tielens (1995, 1996) into a detailed micro-mechanical model describing the interaction between two monomers. These monomers may establish adhesive contacts when touching each other and kinetic energy is dissipated upon deformation of these contacts. A few years later, Wada et al. (2007) presented a different approach when deriving nearly the same forces and torques from corresponding potentials.
When trying to reproduce the results of laboratory experiments performed by Güttler et al. (2009) on the compression of porous dust cakes, Seizinger et al. (2012) observed that the behavior predicted by the model of Dominik & Tielens (1997) was too soft. Since the samples used by Güttler et al. (2009) had been composed of micron-sized, spherical, monodisperse silicate grains their results constituted a perfect opportunity to calibrate the model. Introducing two free parameters mr and ms that modify the strength of the rolling and sliding interaction between two monomers, Seizinger et al. (2012) were able to obtain excellent agreement between the laboratory results and the computer simulations.
In this work we use the modified interaction model presented by Seizinger et al. (2012) with mr = 8 and ms = 2.5. The material parameters are listed in Table 1.
Material parameters of the individual monomers used in the simulations.
3. Sample generation
In this work we examine the conditions under which bouncing occurs. Apart from the external parameters describing the physics of collisions such as the impact parameter or velocity, we study the influence of the internal structure of the aggregate. Examples of such aggregates that have been generated by different methods are shown in Fig. 1.
To study the influence of the aggregate size, we use aggregates with diameters in the range of 30 to 100 μm. Unfortunately, simulations with larger aggregates are infeasible because of the required computational cost, at least for a wider range of parameters.
 |
Fig. 1 Examples of the different types of aggregates used in this work: a) hexagonal lattice φ = 0.59,nc = 9.93; b) ballistic aggregation with migration φ = 0.40,nc = 3.98; and c) static compaction φ = 0.49, nc = 3.50. All depicted spheres have a diameter of 60 μm. |
Typically, the volume filling factor φ and the average coordination number nc are used to classify aggregates. In general, the filling factor is given by 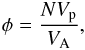 (1)where N denotes the number of monomers, Vp is the volume of a monomer, and VA is the total volume occupied by the aggregate. As we use spherical aggregates, VA can be calculated easily from the outer radius of the aggregate. For irregular-shaped aggregates there are different ways to define VA. For example Kozasa et al. (1992) determine the size of a porous aggregate based on its radius of gyration, whereas Ossenkopf (1993) uses the geometric cross section. It is important to keep this ambiguity in mind when comparing the porosities of fluffy aggregates to results presented by other papers.
(1)where N denotes the number of monomers, Vp is the volume of a monomer, and VA is the total volume occupied by the aggregate. As we use spherical aggregates, VA can be calculated easily from the outer radius of the aggregate. For irregular-shaped aggregates there are different ways to define VA. For example Kozasa et al. (1992) determine the size of a porous aggregate based on its radius of gyration, whereas Ossenkopf (1993) uses the geometric cross section. It is important to keep this ambiguity in mind when comparing the porosities of fluffy aggregates to results presented by other papers.
In molecular dynamics simulations, the coordination number of a monomer denotes the number of the neighbors it interacts with. Thus, the average coordination number nc is obtained by averaging the number of contacts of each particle.
In this work we use three different types of aggregates: Hexagonal lattice aggregates featuring a regular grid structure, aggregates produced by slowly compacting a porous dust cake, and aggregates generated by successively adding single monomers from randomly chosen directions. These choices were motivated by the fact that hexagonal lattice aggregates are easy to build and allow for comparison with earlier work by Wada et al. (2011), whereas the static compaction resembles the generation of samples used in laboratory results. The aggregates of the third type are generated algorithmically, but their structure remains comparable to the static-compaction type (see Sect. 3.4). Because the aggregates within the protoplanetary nebula grow through successive collisions one might expect that their internal structure lies somewhere in between the static-compression and the ballistic-aggregation cases.
3.1. Hexagonal lattice (CPE)
Hexagonal-lattice type aggregates, also referred to as hexagonal close packing with extraction (CPE), can be generated very easily. First, a hexagonal close-packing aggregate is generated which features a volume filling factor φ ≈ 0.74 and a coordination number nc ≈ 12 (because of surface effects nc equals 12 only for aggregates of infinite size). In the second step, a suitable number of randomly selected monomers will be removed to achieve the desired volume filling factor. As a result, a small number of monomers on the surface may become disconnected from the main aggregate and will be removed as well.
Wada et al. (2011) have already studied the bouncing behavior of these aggregates and found that bouncing will occur if the average coordination number is greater than 6. Schräpler et al. (2012) analyzed the relation between the coefficient of restitution and the collision velocity in experiments and simulations using CPE aggregates. Their results agreed well with a theoretical model by Thornton & Ning (1998).
3.2. Ballistic aggregation with migration (BAM)
The second type of aggregates was originally suggested by Shen et al. (2008) and also studied in the work of Wada et al. (2011). To generate a larger aggregate, single monomers are successively shot in from random directions onto the existing aggregate. When the monomer hits the aggregate it will either remain at the position where the first contact was established or it will migrate to a position close by where it establishes contacts with two or three monomers. Compared to Shen et al. (2008), we use three different methods to select the final position of the migrating particle:
-
1.
select the position closest to the spot where the monomerimpacts on the aggregate (referred to as “shortest migration”);
-
2.
select the position randomly from all available possibilities (referred to as “random migration”);
-
3.
select the position which is closest to the center of mass (referred to as “center migration”).
For a given coordination number, the resulting aggregates show a different filling factor depending on which selection mechanism is employed (see Fig. 2). The first method leads to the most porous aggregates since the monomers typically migrate to positions farther outward compared to the case of random migration. The resulting aggregates will become even more compact if monomers migrate to the most inward position available.
 |
Fig. 2 The relation between the volume filling factor φ and the average coordination number nc. All aggregates are spherical and have a diameter of 60 μm. |
Note that we do not claim that random and center migration are realistic growth processes that accurately describe the growth of dust aggregates in protoplanetary discs. Yet, they constitute a computationally very cheap approach to generate larger aggregates that do not suffer from the artificial lattice structure like the CPE aggregates described above. Compared to the static-compaction aggregates they offer the additional advantage of being perfectly relaxated. Since all monomers are at equilibrium distance from each other, there are no attractive or repulsive forces that could lead to a breakup of the aggregate.
3.3. Static compaction (SC)
The last type of aggregates used for our studies is the most computationally expensive. To generate a spherical aggregate of a certain diameter we start with a sufficiently large, cuboid-shaped dust cake generated by random ballistic deposition (RBD). Since RBD aggregates feature an initial volume filling factor of φ = 0.15, we first have to compact the aggregate until we reach the desired filling factor. For this purpose, the aggregate is put into a box with walls that can move toward each other. According to Seizinger et al. (2012) this compaction must be very slow to prevent inhomogeneities.
Even if the cake is compacted homogeneously for filling factors above ≈0.45, it will become elastically charged and expand when the compacting walls are removed. Therefore, the dust cake needs to be relaxated before removing the walls of the compaction box. For this purpose, we disturb the aggregate by modifying the position of the monomers randomly by a very small amount. We keep the disturbed aggregate in a box of fixed size and wait until the kinetic energy induced by the disturbance is damped away by the inelastic monomer interaction. To eliminate kinetic energy below the threshold where the inelastic regime is entered, we additionally enforce a viscous damping mechanism. For this purpose, the velocities and angular velocities of the monomers are multiplied by a factor of 1-κ in each time step, where κ denotes a damping coefficient. In this work we use κ = 0.0001.
It turns out that a maximum disturbance of a factor of 0.001 to the radius of a monomer is sufficient to stabilize the aggregate without altering its internal structure. Higher values may alter the coordination number significantly which could potentially change the collisional behavior of the aggregates and is therefore unwanted. For filling factors above φ = 0.58−0.59 this method no longer works because the compaction is too close to the random closest packing (φ ≈ 0.63) and no stable configuration can be reached without rearranging the monomers significantly.
After the aggregate has been relaxated the compaction box is removed and a spherical aggregate will be cut out of the compacted cake. As this procedure is computationally very expensive, it takes several days to generate larger (50 μm in diameter and above) aggregates of this type.
3.4. Comparison
Comparing the relation between φ and nc of the different types of aggregates described above shows very interesting features. As we can see in Fig. 2, the relation depends considerably on the preparation method. The different BAM generation methods have been described in Sect. 3.2.
From the work presented in this section two important conclusions can be drawn:
-
1.
the coordination number nc is not sufficient to describe the properties of an aggregate. Especially, there is no unambiguous relation φ(nc) between filling factor and coordination number;
-
2.
hexagonal lattice (CPE) aggregates have a distinct relation φ(nc) compared to the other two methods that produce aggregates with less artificial structures.
In laboratory experiments with aggregates composed of micron-sized dust grains, it is typically only possible to determine the filling factor but not the coordination number. Thus, one has to be very careful when comparing results from numerical simulations of CPE aggregates with results from laboratory experiments.
4. Results
In this section we present our results from various simulations in which we study the influence of the collision velocity, impact parameter, and aggregate size on the bouncing behavior. All simulations were performed on NVIDIA GPUs (GTX460, GTX570, Tesla C2070). Depending on the aggregate size and filling factor, each simulation took between less than an hour and half a day.
4.1. Growth factor
In the following bouncing maps the “growth factor” γ that is inspired by the four-population model suggested by Geretshauser et al. (2011) is depicted. It is defined by 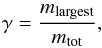 (2)where mlargest is the mass of the largest fragment and mtot the total mass of the colliding aggregates. For perfect sticking we obtain γ = 1, for total destruction γ → 0. In collisions of aggregates of equal size, a value γ = 0.5 indicates bouncing. However, during the transition from perfect sticking to fragmentation γ may also become 0.5. To distinguish between the two cases we consider the mass ratio γ2 of the second largest fragment. In the bouncing case γ = γ2 = 0.5 whereas in the fragmentation case the mass of the second largest fragment is much lower than 0.5 of the total mass as there are a lot of other smaller fragments.
(2)where mlargest is the mass of the largest fragment and mtot the total mass of the colliding aggregates. For perfect sticking we obtain γ = 1, for total destruction γ → 0. In collisions of aggregates of equal size, a value γ = 0.5 indicates bouncing. However, during the transition from perfect sticking to fragmentation γ may also become 0.5. To distinguish between the two cases we consider the mass ratio γ2 of the second largest fragment. In the bouncing case γ = γ2 = 0.5 whereas in the fragmentation case the mass of the second largest fragment is much lower than 0.5 of the total mass as there are a lot of other smaller fragments.
Thus, in the bouncing maps presented in this work the green areas indicate sticking, the upper left yellow areas bouncing, and the color gradient from green to yellow to red on the right marks the transition from sticking to fragmentation.
Note that γ = γ2 = 0.5 only applies in the case of “perfect bouncing”. In our simulations we often observe the loss of a few monomers (typically less than 100), which is negligible compared to the total number of monomers of 5 × 104 to 5 × 105. Thus, we also count collisions as bouncing events if γ and γ2 are slightly smaller than 0.5.
4.2. Hexagonal lattice
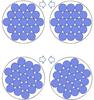 |
Fig. 3 Schematic view of the possible alignment of two CPE aggregates. In the upper case the aggregates are oriented with respect to their lattice structure. In the lower case the orientation is arbitrary. |
 |
Fig. 4 Growth factor γ (Eq. (2)) of the collision of two CPE aggregates with a diameter of 60 μm. Sticking occurs in the green area, whereas the yellow area in the upper left indicates bouncing. Left: orientation aligned to the lattice structure of the aggregates. Right: non-aligned orientation. |
 |
Fig. 5 Growth factor of the collision of two CPE aggregates of different size averaged over three different orientations. Left: aggregates of a diameter of 30 μm. Right: aggregates of a diameter of 60 μm. |
The outcome of head-on collisions of CPE aggregates has already been studied by Wada et al. (2011) who observed bouncing if the coordination number was greater than 6. However, their aggregates were much smaller (≈104 monomers). Since hexagonal-lattice aggregates feature a regular lattice structure, their orientation is likely to influence the collision behavior. Thus, we first examine the effect of the orientation by comparing the case where the aggregates are aligned to their lattice structure (see upper part of Fig. 3) with a random orientation (lower part of Fig. 3). As we can see in Fig. 4, the orientation of the aggregates is important especially for the transition from sticking to bouncing with increasing filling factor. Looking at the left panel of Fig. 4 and comparing the filling factor with the coordination number in Fig. 2 we can reproduce the nc ≥ 6-criterion proposed by Wada et al. (2011) for the aligned case. On the other hand, the bouncing map differs significantly for a non-aligned orientation (see right panel of Fig. 4).
In order to mitigate the effect of the orientation we averaged over three different orientations to investigate the size dependency of our results. Each map was generated using 12 different filling factors and 28 velocities. Thus, 3 × 336 = 1008 simulations had to be performed in total. Concerning bouncing, we could not observe a clear difference between aggregates with a diameter of 30 and 60 μm (see Fig. 5).
However, the velocity vs → f at which the transition from sticking to fragmentation occurs changes significantly. For the small aggregates we get vs → f ≈ 4 ms-1 (left panel of Fig. 5). For the bigger aggregates we observe that vs → f depends on the filling factor. For φ < 0.43 we find that vs → f ≈ 10 ms-1, whereas for φ > 0.43 vs → f ≈ 5 ms-1 (right panel of Fig. 5). This can be explained by the reduced capability of compact aggregates to dissipate kinetic energy by restructuring. Taking into account Fig. 2, we see that the transition occurs when the average coordination number nc exceeds a value of 6. A monomer with six or more contacts is fixated tightly and thus the aggregate can no longer change its internal structure as easily.
In summary, it can be said that for hexagonal lattice aggregates we regularly observe bouncing collisions for filling factors above 0.5 and for collision velocities up to roughly 0.2 ms-1.
4.3. Ballistic aggregation with migration
Wada et al. (2011) found that bouncing may occur if nc ≥ 6 independent of the type of aggregate they used. In Fig. 6 we show the outcome of collisions between two roughly 75 μm-sized BAM aggregates generated using the shortest migration method described in Sect. 3.2. The corresponding filling factor is between 0.36 and 0.39, however, we observed only two bouncing collisions. Since nc = 6 is the maximum value that can be achieved by two time migration, we could not investigate what happens at higher coordination numbers.
We repeated the shortest-migration setup described above, but this time for center migration case and we obtained similar results as for the shortest-migration case shown in Fig. 6. We observe hardly any bouncing events even for aggregates with nc = 6 (which corresponds to a filling factor of 0.49−0.5). This indicates that the bouncing behavior of BAM aggregates depends more on the filling factor than on the coordination number.
To achieve higher filling factors we switched to the center migration method (see Sect. 3.2). The corresponding bouncing maps are shown in Fig. 7. It is striking that the bouncing regime is much smaller compared to the CPE aggregates. As before, the transition from sticking to fragmentation occurs at higher velocities for larger aggregates.
4.4. Static compaction
The bouncing behavior of the aggregates generated by static compaction is quite similar to the bouncing behavior of BAM aggregates (see Fig. 8). Again, the bouncing regime is considerably smaller compared to the case of hexagonal lattice aggregates and bouncing is observed only in some cases for high filling factors above 0.5 and collision velocities below 0.1 ms-1.
As in the case of the other aggregate types, the transition velocity vs → f from sticking to fragmentation increases with increasing aggregate size. For the the small aggregates with d = 30 μm we observe vs → f ≈ 4 ms-1, whereas for d = 60 μm the transition velocity goes up to vs → f ≈ 12 ms-1.
4.5. Size dependency
To further examine the influence of the aggregate size we performed collisions of 100 μm-sized CPE and BAM aggregates (using the center migration method because it yields the BAM aggregates with the highest filling factors). For the CPE aggregates we observe slightly more bouncing for filling factors between 0.4 to 0.5 (see left panel of Fig. 9). However, for BAM aggregates there is no noticeable difference compared to the 60 μm aggregates (see right panel of Fig. 9).
Depending on the filling factor, the 100 μm aggregates consist of up to 350 000 monomers. In order to analyze the size dependency it would be desirable to simulate collisions of even larger aggregates. Unfortunately, this is rendered impossible by the lack of available computing power. Simulating a single collision of two 100 μm-sized aggregates took 10 to 20 h (owing to the different filling factors) on a GPU. Doubling the size would require computing times on the order of weeks for a single collision. For each orientation shown in Fig. 9, 48 collisions were performed.
4.6. Impact parameter
 |
Fig. 6 Growth factor of the collision of two BAM aggregates generated using the shortest migration method. For three different aggregates of a diameter of roughly 75 μm only two collisions at 1 cms-1 lead to bouncing. |
 |
Fig. 7 Growth factor of the collision of two BAM aggregates of different size generated using the center migration method. Left: diameter of 30 μm. Right: diameter of 60 μm. |
As a last step we examine the influence of the impact parameter b = 0.5. For the collisions, we used the same orientation as for the results shown in the right panel of Fig. 4. Contrary to our expectations, we do not observe a significant influence of the impact parameter on the bouncing behavior of CPE aggregates (see Fig. 10). However, fragmentation sets in at considerably lower velocities of vs → f ≈ 3 ms-1. In a head on collision the entire aggregate can dissipate the kinetic impact energy by internal restructuring which helps to prevent fragmentation. This does not apply to offset collisions where it is easier to tear away the outer layers without major restructuring of the core of the aggregates. However, comparing the growth map of the collisions between aggregates with a diameter of 30 and 60 μm we do not observe any significant increase of velocity vs → f where the transition from sticking to fragmentation occurs (see left and right panels of Fig. 10). As already pointed out by Wada et al. (2009) the increase of vs → f for larger aggregates is limited to the case of head-on collisions.
In contrast, for BAM aggregates we do observe bouncing in a larger regime compared to the case of head-on collisions (see Fig. 11). Again, the same samples and orientation as for the head-on collisions (right panel of Fig. 7) were used.
5. Requirements for bouncing
 |
Fig. 8 Growth factor of the collision of two static-compaction aggregates of different size. Left: diameter of 30 μm. Right: diameter of 60 μm. |
 |
Fig. 9 Growth factor of the collision of two aggregates with a diameter of 100 μm for three different orientations. The plot on the bottom right of both panels shows the values averaged over the three orientations. Left: CPE aggregtes. Right: BAM aggregates (center migration). |
 |
Fig. 10 Growth factor of the collision of two CPE aggregates with an impact parameter b = 0.5. Left: aggregates with a diameter of 30 μm. Right: aggregates with a diameter of 60 μm. |
 |
Fig. 11 Growth factor of the offset collisions of two 60 μm-sized BAM aggregates. Left: impact parameter b = 0.5. Right: impact parameter b = 0.75. |
 |
Fig. 12 Time evolution of the kinetic, potential, and dissipated energy during collisions of two aggregates with a diameter of 60 μm and filling factor φ ≈ 0.59. Left: a bouncing collision between two CPE aggregates. A sufficient amount of the impact energy is temporarily stored in the potential Unormal of the normal interaction. Right: during a sticking collision of two BAM aggregates most of the kinetic impact energy is dissipated. |
Compared to the aggregates generated by BAM or static compaction, the bouncing regime of CPE aggregates is significantly larger. A likely explanation for this discrepancy is given by the different structure of the aggregates. To gain a deeper insight into the physical processes leading to sticking or bouncing, it is worthwhile to have a closer look at a single collision.
Two aggregates can bounce off each other only if there is enough elastic energy left to break the contact area. Thus, a significant amount of the kinetic impact energy must be stored temporarily without being dissipated. If the colliding aggregates penetrate each other too deeply, the impact energy is dissipated upon internal restructuring in the area where the contact is established. In this case inelastic sliding and rolling constitute the main dissipation channels (Wada et al. 2011). Thus, the ratio of elastic to dissipated energy of colliding aggregates is the key parameter that determines whether sticking or bouncing will occur.
Being able to track the evolution of the different types of energies over time is the key advantage of the model presented by Wada et al. (2007). To address the different behavior of BAM and CPE aggregates we compare a bouncing collision of two CPE aggregates with a sticking collision of BAM aggregates. Both aggregates are 60 μm in diameter and have a filling factor φ ≈ 0.59. The time evolution of different types of energies and potentials for these collisions is shown in Fig. 12.
As expected, when sticking occurs most of the kinetic energy is dissipated by inelastic sliding and rolling (right panel of Fig. 12). Only a small percentage of the impact energy is stored in the elastic regime of the normal Unormal and sliding potential Uslide (since the elastic energy stored in the rolling and twisting potentials is negligible they are not shown in Fig. 12).
We observe an entirely different situation when bouncing occurs. As shown in the left panel of Fig. 12, only about one third of the impact energy is dissipated, while roughly half of the kinetic energy is temporarily converted into potential energy. This coincides well with our predictions above. The potential energy that is stored mainly in the normal and sliding interaction is converted back into kinetic energy and allows the colliding aggregates to separate again.
We can conclude that owing to their lattice structure, CPE aggregates can convert significantly more impact energy into elastic energy than BAM aggregates an. In a compact CPE aggregate the monomers are located in densely packed layers. When the outer monomer of such a layer hits the other aggregate it is pushed inwards and will compress the layer. In this way, kinetic energy is converted into potential energy without the occurrence of inelastic restructuring. This mechanism works well in the presence of a regular grid structure which is the case for CPE aggregates. However, the monomers of BAM aggregates are not arranged in any regular pattern. Thus, they are not likely to bounce unless they are very compact in which case energy dissipation by internal restructuring is hindered because the monomers are locked in their position.
It also offers an explanation for the lower impact velocity of BAM aggregates at which we observe the transition from bouncing to sticking. At impact velocities above 0.1 ms-1, the kinetic impact energy is sufficient to restructure the monomers in the contact area that had been locked at lower impact velocities. Since the lattice structure of CPE aggregates offers higher resistivity against restructuring, their transition velocity from bouncing to sticking is roughly 0.3 ms-1.
6. Conclusions
From the analysis of the statistical properties of the different samples presented in Sect. 3 we clearly see that the method of preparation plays a crucial role when studying the collisional behavior of microscopic dust aggregates. As the relation between the volume filling factor and the average coordination number strongly depends on the method of preparation, one must be careful when comparing results obtained from computer simulations with results obtained from laboratory work. In most laboratory experiments, only the volume filling factor can be measured, while the equally important coordination number remains unknown. Since the more compact aggregates used in laboratory experiments are typically produced by mechanical compression, we expect that their microscopic structure resembles the static compaction aggregates much more closely than the hexagonal lattice type aggregates.
For computer simulations, generating large, compact aggregates by static compaction is infeasible because of the additional computational effort. We suggest using BAM aggregates as an alternative. Their statistical properties are close to the aggregates produced by static compaction, yet they can be generated directly. Additionally, one does not run into problems caused by elastic charging as the generation procedure ensures that BAM aggregates are perfectly relaxated. At least in the various collision simulations performed in this work, BAM and static compaction aggregates show very similar behavior.
Based on the outcome of the simulations presented in this work, we can conclude that bouncing collisions of dust aggregates in the size regime below 0.1 mm are rare. Unless the aggregates feature a regular lattice structure, which is not likely to be the case for the aggregates in a protoplanetary disk, bouncing requires filling factors greater than 0.5 and collision velocities below 0.1 ms-1. Even if these prerequisites are met, bouncing does not occur very frequently. Additionally, laboratory experiments on dust growth show that the maximum filling factor that is achieved during the growth process is much lower than φ = 0.5 (e.g., Teiser et al. 2011). Therefore, the influence of bouncing on the growth process is limited in the sub-mm size regime.
Hence, from a microscopic view it remains unclear how cm-sized aggregates with filling factors considerably below 0.5 are able to bounce off each other. The idea of a compacted outer layer (also referred to as a hard shell) has been put forward as a possible explanation. Using SPH simulations, Geretshauser et al. (in prep.) observed that a hard shell can indeed lead to bouncing collisions between aggregates with a porous core. Wada et al. (2011) obtained similar results when performing molecular dynamics simulations of collisions of CPE aggregates featuring a hard sphere. Langkowski et al. (2008) found that molding an aggregate significantly alters the outcome of a collision experiment. However, Kothe et al. (2013) analyzed aggregates used in their collision experiments with X-ray computer tomography imaging and could not find any compacted outer layers.
In Sect. 4.6 we have shown that offset collisions result in bouncing somewhat more often than head-on collisions do. Depending on the experimental setup, head-on collisions will be rare, and in a setup featuring free collision with many particles head-on collisions will be rare as well (e.g., Weidling et al. 2012; Beitz et al. 2012). Thus, the impact parameter helps to resolve some of the discrepancies between numerical simulations and laboratory experiments.
Taking into account the different aggregate types we can only partially confirm the nc ≥ 6 criterion for bouncing proposed by Wada et al. (2011). It agrees well with our results from collisions of CPE aggregates. However, for BAM aggregates generated by the shortest migration method we observe very little bouncing at nc = 6 (see Sect. 4.3 and Fig. 6). Likewise, for static-compaction aggregates or BAM aggregates generated by the random or center migration method there are a few bouncing events where nc is considerably lower than 6. A volume filling factor of φ ≈ 0.5 appears to constitute a lower limit for bouncing. At the present time we do not have an explanation for what determines the exact value of the critical filling factor for the onset of bouncing. We have shown that it depends on the amount of energy that can be stored in the normal potential. The energy deposition is a continuous process, and it is to be expected that below a certain density sticking ensues. Numerically, we determined this value to be φ ≈ 0.5 in the sub-mm size regime.
Our simulations give insight into the fragmentation threshold as well. For small aggregates (30 μm) the fragmentation velocity is around 4 m/s. Upon increasing the projectile size the fragmentation threshold increases to about 10 m/s for the largest particle sizes we considered (60 μm), and this is independent of the sample generation method. This value is in very good agreement with the findings of SPH simulation for much larger objects (Geretshauser et al. 2011). The shift to a larger
fragmentation velocity is caused by the ability of larger particles to dissipate more kinetic energy. Upon increasing the filling factor, the fragmentation threshold decreases because the aggregates become much stiffer and cannot be deformed so easily. However, as shown in Sect. 4.6, this effect only applies to the case of head-on collisions.
With respect to the growth of small dust agglomerates in the protoplanetary nebula, our results indicate that for more realistic aggregates (BAM-type) bouncing only occurs for very small collision velocities (<0.1 m/s) and large filling factors >0.5. Thus, the bouncing barrier may not be such a strong handicap in the growth phase of dust agglomerates, at least in the size range of ≈100 μm. For larger, m-sized particles SPH results indicate bouncing up to 1 m/s.
Acknowledgments
A. Seizinger acknowledges the support through the German Research Foundation (DFG) grant KL 650/16. The authors acknowledge support through DFG grant KL 650/7 within the collaborative research group FOR 759 The formation of planets. We also thank the referee, Koji Wada, for his helpful comments that improved the quality of this paper. A part of the simulations were performed on the bwGRiD cluster, which is funded by the Ministry for Education, and Research of Germany and the Ministry for Science, Research and Arts of the state of Baden-Württemberg.
References
- Armitage, P. J. 2011, ARA&A, 49, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beitz, E., Güttler, C., Weidling, R., & Blum, J. 2012, Icarus, 218, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Blum, J., & Wurm, G. 2008, ARA&A, 46, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dominik, C., & Tielens, A. G. G. M. 1995, Philos. Mag., Part A, 72, 783 [Google Scholar]
- Dominik, C., & Tielens, A. G. G. M. 1996, Philos. Mag., Part A, 73, 1279 [Google Scholar]
- Dominik, C., & Tielens, A. G. G. M. 1997, ApJ, 480, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., Hollenbach, D., Kamp, I., & D’Alessio, P. 2007, Protostars and Planets V, 555 [Google Scholar]
- Flaig, M., Ruoff, P., Kley, W., & Kissmann, R. 2012, MNRAS, 420, 2419 [NASA ADS] [CrossRef] [Google Scholar]
- Geretshauser, R. J., Speith, R., Güttler, C., Krause, M., & Blum, J. 2010, A&A, 513, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geretshauser, R. J., Meru, F., Speith, R., & Kley, W. 2011, A&A, 531, A166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güttler, C., Krause, M., Geretshauser, R. J., Speith, R., & Blum, J. 2009, ApJ, 701, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Güttler, C., Blum, J., Zsom, A., Ormel, C. W., & Dullemond, C. P. 2010, A&A, 513, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heißelmann, D., Blum, J., Fraser, H. J., & Wolling, K. 2010, Icarus, 206, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Jankowski, T., Wurm, G., Kelling, T., et al. 2012, A&A, 542, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnson, K. L., Kendall, K., & Roberts, A. D. 1971, Roy. Soc. London Proc. Ser. A, 324, 301 [Google Scholar]
- Kothe, S., Blum, J., Weidling, R., & Güttler, C. 2013, Icarus, submitted [Google Scholar]
- Kozasa, T., Blum, J., & Mukai, T. 1992, A&A, 263, 423 [Google Scholar]
- Langkowski, D., Teiser, J., & Blum, J. 2008, ApJ, 675, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Ossenkopf, V. 1993, A&A, 280, 617 [NASA ADS] [Google Scholar]
- Paszun, D., & Dominik, C. 2009, A&A, 507, 1023 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Schäfer, C., Speith, R., & Kley, W. 2007, A&A, 470, 733 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schräpler, R., Blum, J., Seizinger, A., & Kley, W. 2012, ApJ, 758, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Seizinger, A., Speith, R., & Kley, W. 2012, A&A, 541, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shen, Y., Draine, B. T., & Johnson, E. T. 2008, ApJ, 689, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Teiser, J., Engelhardt, I., & Wurm, G. 2011, ApJ, 742, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Thornton, C., & Ning, Z. 1998, Powder Technol., 99, 154 [CrossRef] [Google Scholar]
- Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2007, ApJ, 661, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2009, ApJ, 702, 1490 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2011, ApJ, 737, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Weidling, R., Güttler, C., Blum, J., & Brauer, F. 2009, ApJ, 696, 2036 [NASA ADS] [CrossRef] [Google Scholar]
- Weidling, R., Güttler, C., & Blum, J. 2012, Icarus, 218, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Windmark, F., Birnstiel, T., Güttler, C. 2012a, A&A, 540, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Windmark, F., Birnstiel, T., Ormel, C. W., & Dullemond, C. P. 2012b, A&A, 544, L16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zsom, A., Ormel, C. W., Güttler, C., Blum, J., & Dullemond, C. P. 2010, A&A, 513, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Examples of the different types of aggregates used in this work: a) hexagonal lattice φ = 0.59,nc = 9.93; b) ballistic aggregation with migration φ = 0.40,nc = 3.98; and c) static compaction φ = 0.49, nc = 3.50. All depicted spheres have a diameter of 60 μm. |
| In the text | |
 |
Fig. 2 The relation between the volume filling factor φ and the average coordination number nc. All aggregates are spherical and have a diameter of 60 μm. |
| In the text | |
 |
Fig. 3 Schematic view of the possible alignment of two CPE aggregates. In the upper case the aggregates are oriented with respect to their lattice structure. In the lower case the orientation is arbitrary. |
| In the text | |
 |
Fig. 4 Growth factor γ (Eq. (2)) of the collision of two CPE aggregates with a diameter of 60 μm. Sticking occurs in the green area, whereas the yellow area in the upper left indicates bouncing. Left: orientation aligned to the lattice structure of the aggregates. Right: non-aligned orientation. |
| In the text | |
 |
Fig. 5 Growth factor of the collision of two CPE aggregates of different size averaged over three different orientations. Left: aggregates of a diameter of 30 μm. Right: aggregates of a diameter of 60 μm. |
| In the text | |
 |
Fig. 6 Growth factor of the collision of two BAM aggregates generated using the shortest migration method. For three different aggregates of a diameter of roughly 75 μm only two collisions at 1 cms-1 lead to bouncing. |
| In the text | |
 |
Fig. 7 Growth factor of the collision of two BAM aggregates of different size generated using the center migration method. Left: diameter of 30 μm. Right: diameter of 60 μm. |
| In the text | |
 |
Fig. 8 Growth factor of the collision of two static-compaction aggregates of different size. Left: diameter of 30 μm. Right: diameter of 60 μm. |
| In the text | |
 |
Fig. 9 Growth factor of the collision of two aggregates with a diameter of 100 μm for three different orientations. The plot on the bottom right of both panels shows the values averaged over the three orientations. Left: CPE aggregtes. Right: BAM aggregates (center migration). |
| In the text | |
 |
Fig. 10 Growth factor of the collision of two CPE aggregates with an impact parameter b = 0.5. Left: aggregates with a diameter of 30 μm. Right: aggregates with a diameter of 60 μm. |
| In the text | |
 |
Fig. 11 Growth factor of the offset collisions of two 60 μm-sized BAM aggregates. Left: impact parameter b = 0.5. Right: impact parameter b = 0.75. |
| In the text | |
 |
Fig. 12 Time evolution of the kinetic, potential, and dissipated energy during collisions of two aggregates with a diameter of 60 μm and filling factor φ ≈ 0.59. Left: a bouncing collision between two CPE aggregates. A sufficient amount of the impact energy is temporarily stored in the potential Unormal of the normal interaction. Right: during a sticking collision of two BAM aggregates most of the kinetic impact energy is dissipated. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


