| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A41 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201220845 | |
| Published online | 18 February 2013 | |
The fate of heavy elements in dwarf galaxies – the role of mass and geometry
Institute for Astrophysics, University of Vienna,
Türkenschanzstrasse 17,
1180
Vienna,
Austria
e-mail: simone.recchi@univie.ac.at; gerhard.hensler@univie.ac.at
Received: 4 December 2012
Accepted: 3 January 2013
Context. Energetic feedback from supernovae and stellar winds can drive galactic winds. Dwarf galaxies, due to their shallower potential wells, are assumed to be more vulnerable to this phenomenon. Metal loss through galactic winds is also commonly invoked to explain the low metal content of dwarf galaxies.
Aims. Our main aim in this paper is to show that galactic mass cannot be the only parameter determining the fraction of metals lost by a galaxy. In particular, the distribution of gas must play an equally important role.
Methods. We performed 2D chemo-dynamical simulations of galaxies characterized by different gas distributions, masses, and gas fractions.
Results. The gas distribution can change the fraction of lost metals through galactic winds by up to one order of magnitude. In particular, disk-like galaxies tend to lose metals more easily than roundish ones. Consequently, the final metallicities attained by models with the same mass but with different gas distributions can also vary by up to one dex. Confirming previous studies, we also show that the fate of gas and freshly produced metals strongly depends on the mass of the galaxy. Smaller galaxies (with shallower potential wells) more easily develop large-scale outflows, so that the fraction of lost metals tends to be higher.
Key words: galaxies: abundances / galaxies: dwarf / galaxies: evolution / galaxies: ISM / galaxies: jets
© ESO, 2013
1. Introduction
Theories of cold dark matter-dominated hierarchical growth of structures predict that dwarf galaxy- (DG-)sized objects are the building blocks for the formation of large galaxies. In spite of their relevance, the most important physical phenomena regulating the birth and evolution of DGs are still obscure. Star formation (SF) certainly plays a key role in shaping DGs and determining their fates. Since the binding energy of the interstellar medium (ISM) in early gas-rich DGs is very small (smaller than the explosion energy of just a few supernovae SNe) many authors speculated that a high SF rate in a DG would create a galactic wind and thus produce a transition from a dwarf irregular (dIrr) to a dwarf spheroidal (dSph) or dwarf elliptical (dE; see, e.g., Larson 1974; Vader 1986; Dekel & Silk 1986). From a chemical point of view, the occurrence of a galactic wind right after the formation of the first stars would imply a very limited interval of time during which the metals, restored by dying stars, can pollute the ISM and enrich the following stellar populations. If galactic winds preferentially occur in DGs, these objects (with low masses) will experience a limited chemical enrichment. Therefore, a correlation between stellar mass M (or luminosity L) and metallicity Z of DGs is expected. Indeed, this M-Z correlation among DGs exists (see, e.g., Skillman et al. 1989; Lee et al. 2006; Kirby et al. 2008; Zhao et al. 2010; Andrews & Martini 2012). The M-Z relation extends also to high redshifts (Erb et al. 2006; Maiolino et al. 2008; Laskar et al. 2011; Wuyts et al. 2012), although in this case, the galactic masses of the galaxies for which metallicity determinations are available are usually quite high (but see Mannucci et al. 2011). The M-Z relation among DGs corroborates the idea that SN-driven galactic winds play a dominant role in the evolution of these objects. More recently, a general relation between stellar mass, gas-phase metallicity and star formation rate (SFR) has been found (Mannucci et al. 2010; Lara-López et al. 2010).
However, detailed hydrodynamical simulations of DGs showed that the galactic winds, although often able to expel a large fraction of freshly produced metals, are unable to eject an equally large fraction of pristine (i.e., not processed) gas. This is mostly due to the fact that, if the initial DG gas distribution is flattened (as observed in dIrrs), there is then a direction with steeper pressure gradient. As a result, the galactic wind will preferentially expand along that direction. The transport of gas along the other directions is very limited (see, e.g., D’Ercole & Brighenti 1999; MacLow & Ferrara 1999, hereafter MF99; Recchi et al. 2001). This effect can be appreciated by inspecting Fig. 1, where the gas and oxygen distribution of a model galaxy experiencing a galactic wind (taken from the calculations of Recchi et al. 2006) is shown. Most of the disk gas (at least above R = 1 kpc) has not been affected by the galactic wind and will fall back towards the center of the galaxy once the energy source of the starburst is exhausted. On the other hand, the oxygen can be easily channeled along the funnel created by the galactic wind. Also very energetic (E ~ 1053 erg) hypernovae exploding in dwarf protogalaxies, although more disruptive than normal SNe, are able to expel only ~10 to 20% of the baryonic mass originally present in the galaxy (Vasiliev et al. 2008).
 |
Fig. 1 Gas (filled contours) and oxygen (black contour lines) distribution of a model galaxy (taken from Recchi et al. 2006) experiencing a galactic outflow. Brighter colors indicate larger gas densities. |
This result is widely accepted by the astrophysical community, although some authors (e.g., Tenorio-Tagle 1996; Silich & Tenorio-Tagle 1998) believe that low-density gaseous galactic halos can strongly affect the circulation of the metal-rich matter processed by the central starburst. Kiloparsec-scale bipolar outflows are created, but loss of pressure support and interaction with the diffuse halo later on slow down the expansion of the superbubble and the freshly produced metals can eventually fall back towards the center of the galaxy. Thus, according to this scenario, energetic events associated to a starburst can still create a large-scale outflow, but this outflow does not necessarily become a galactic wind (i.e., its velocity does not exceed the escape velocity of the galaxy).
While the chemical yields of exploding massive stars are very large (thus the metallicity of interiors of SN-driven bubbles is up to 40 times the solar value), abundances of the hot gas in galaxies experiencing large-scale outflows (determined from X-ray spectra) cover with high probability a range between only solar and twice solar (see, e.g., Martin et al. 2002 for NGC1569 or Ott et al. 2005 for a larger sample of galaxies). From this fact, it can be deduced that the hot SN ejecta becomes mass loaded (by a factor of up to ten) during its expansion, probably due to evaporative and turbulent mixing with colder interstellar clouds. Consequently, the hot gas loses not only momentum but also energy by enhanced cooling in addition to adiabatic expansion, so that the outbreak of the hot gas to a galactic wind could be hampered in many cases. This mass-loading effect is probably causing the discrepancy between the observed extent and temperature of the extremely cool superbubble in NGC 1705 and its analytic parameter correlation (Hensler et al. 1998).
Because of the gas density outside the SF region, the development of galactic outflows or galactic winds considerably depends on the degree of flattening (or on the rotation) of the parent galaxy, an aspect that has not been fully explored in the past (but see Silich & Tenorio-Tagle 2001; Michielsen et al. 2007; Schroyen et al. 2011. See also Strickland & Stevens 2000; Ferrara & Tolstoy 2000; Vasiliev et al. 2008; Recchi et al. 2009). While flat galaxies are supposed to lose a large fraction of metals as a consequence of bipolar galactic winds, roundish galaxies are not characterized by a direction along which the pressure gradient is significantly steeper and are thus more likely to retain much of the metals (Marcolini et al. 2006; Recchi et al. 2007). In the end, this difference in initial gas distribution could lead to a spread in the observed final metallicity of galaxies with the same mass. Such a spread is indeed observed in the M-Z relation of DGs (Lee et al. 2006; Kirby et al. 2008; Zhao et al. 2010) or in the same correlation at z ≃ 3.5 (Maiolino et al. 2008). In this paper, we explore in detail the effect of gas geometry on the development of galactic winds and on the fate of freshly produced metals. This work must be thus seen as a refined study along the lines of the MF99 work, in which variations in the initial distribution of gas in galaxies have not been considered. The second key parameter we consider in this study is the initial mass of the galaxy. As mentioned, small galaxies (with shallow potential wells) are expected to develop galactic winds more easily than larger galaxies. As a result, the mass is certainly a key parameter in determining the fate of pristine gas and freshly produced heavy elements.
The dynamical evolution of a galaxy is so complex that the fate of heavy elements cannot depend only on the mass and geometry of the parent galaxy. An obvious parameter that strongly affects the development of galactic winds is the luminosity (MF99). In turn, the luminosity depends on the SFR and on the star formation history (SFH), and it is known, at least in the Local Group, that very large galaxy-to-galaxy SFH variations exist (see, e.g., Monelli et al. 2010a,b; Hidalgo et al. 2011). Moreover, other details of the ISM structure (for instance, the presence of clouds or porosity) and of the feedback prescriptions (e.g., how the SN explosion energy is redistributed, where, on which timescales, and at which efficiency) can all play a role in determining the amount of metals carried out of a galaxy by galactic winds and eventually in the final global metallicity of the galaxy. Although the consequences of an inhomogeneous ISM on the development of galactic winds is analyzed in detail in Recchi & Hensler (2007, hereafter RH07), we have undertaken a comprehensive parameter study through detailed chemo-dynamical simulations, the results of which will be presented elsewhere. Here we focus mainly on 18 basic models, which are characterized by differences in geometries, total baryonic masses, and initial gas fractions.
The paper is organized as follows: Sect. 2 gives a short summary on the literature results concerning the fate of freshly produced metals. In Sect. 3 our numerical scheme is briefly reviewed and the set-up of the 18 basic models models described. In Sect. 4 the main results of these calculations are presented, underlying also the effect of some other key parameters not fully explored in this work. In Sect. 5 the results are discussed and some conclusions are drawn.
2. A brief overview of literature results
As mentioned in the Introduction, several papers in the literature have attempted to study the effect of galactic winds on the circulation and redistribution of metals in DGs. The main results of the often-cited work of MF99 are that, even in the presence of a strong galactic wind driven by SNeII, the ejection efficiency of unprocessed gas is always close to zero (with the exception of galaxies with initial baryonic mass ≤106 M⊙). On the other hand, the ejection efficiency of freshly produced heavy elements is always close to one (with the exception of galaxies with initial baryonic mass ≥ 109 M⊙). D’Ercole & Brighenti (1999) found results similar to the ones of MF99 in the sense that only minor fractions of ISM (but in some cases large fractions of metals) are expelled through galactic winds. However, they calculated the evolution of the galaxy for much longer times than MF99, discovering that the center of the galaxy can be replenished with cold gas in a timescale of ~100 Myr (see also Recchi & Hensler 2006). As previously stated, Silich & Tenorio-Tagle (1998) found instead that galactic winds do not develop in most of the models (mainly due to the presence of a hot gaseous halo surrounding the galaxy). Fragile et al. (2004) studied the effect of SN explosions that were not localized in the center of the galaxy (as MF99 did) but distributed over radii of up to 80% of the disk radius. They discovered that in this case radiative losses are more effective and the development of a large-scale outflow is hampered. Also very interesting is the work of Scannapieco & Brüggen (2010), who attempted to model turbulent velocities and turbulent length scales in DGs and to inject SN energy into supersonic turbulence. The wind efficiencies that they found are still quite low. Rodríguez-González et al. (2011) addressed the same problem (mass and metal ejection efficiencies in DGs), exploring a much more extended set of parameters (in particular, they covered a wide range of starburst and galactic gas masses). Their results are overall in agreement with the previously quoted works (with the exception of Silich & Tenorio-Tagle 1998). More recently, Schroyen et al. (2011) explored in detail the effect of rotation on the evolution of DGs. Their focus was to understand the origin of the dichotomy in radial stellar metallicity profiles of DGs and their “centrifugal barrier mechanism” helps to explain these observations. Because their models usually do not develop galactic winds (or develop only weak outflows), the determination of ejection efficiencies (of pristine gas and freshly produced metals) is not addressed in their paper. The same can be said about the detailed determination of the energy required to expel newly processed matter by Silich & Tenorio-Tagle (2001); their analytic model is in good agreement with the numerical results of MF99 and clearly shows the effect of geometry on the development of galactic winds and on the fate of metals if the intergalactic pressure is low. However, their inferred large intergalactic pressure hampers the development of galactic winds.
As this short summary indicates, the past literature focused mostly on the effect of mass and luminosity on the gas and metal ejection efficiencies from galaxies. The chemical evolution is usually not very detailed in these models. Recchi et al. (2001, 2002, 2004, 2006) provided detailed information on the ejection efficiencies of single chemical species produced by SNe (of both Type II and Type Ia) and by winds from intermediate-mass stars. RH07 added important information on the effect of clouds. The most significant results of these works can be summarized as follows:
-
Galactic-scale outflows carry out of the galaxy mostly the chemical elements produced by dying stars during the most recent episodes of SF, with large escape fraction of metals with delayed production (like Fe and N).
-
Models with very short burst(s) of SF can cool and mix the newly formed metals in a very short timescale. However, when the SFH is continuous and long-lasting, most of the metals are either directly ejected outside the galaxy through galactic winds or are confined in a hot medium. As a result, they cannot contribute to the chemical enrichment of the warm ionized medium observed by emission lines from the HII gas.
-
Models with complex and long-lasting SF episodes taken from the literature reproduce the chemical composition and abundance ratios observed in galaxies much better than models with bursting SF.
-
Clouds (if present) are able to increase the main density of the cavity created by the ongoing SF activity, provoking a reduction of the total thermal energy by ~20−40% compared to models without clouds.
-
The interaction clouds-supershell leads to strong structuring and piercing of the shell, allowing the venting out of metals in spite of the reduced thermal energy. The development of large-scale outflows is therefore generally delayed, but the ejection efficiency of metals remains unchanged.
-
Since the clouds are assumed to have a low metallicity, their mixing with the ISM tends to reduce the abundance of heavy elements of the galaxies. The models with infalling clouds thus have metallicities up to ~0.4 dex lower than corresponding models without clouds. The abundance ratios remain unaltered.
3. Description of the model
This work aims at studying in detail the dynamical and chemical evolution of DGs and the effect of key parameters (particularly baryonic mass, initial gas mass fraction, and degree of flattening) on the development of galactic winds and the fate of freshly produced metals. A follow-up study will extend the parameter space and concentrate on the details of the SFH and the effect of boundary conditions. The ultimate goal is to understand the main mechanisms determining the metallicity and abundance ratios in DGs and, at the same time, infer the degree of metal pollution of the inter-galactic and intra-cluster medium due to these objects.
3.1. The chemo-dynamical code
As chemo-dynamical code, we use basically the one of Recchi et al. (2007). We recall here the basic features of this code. It is a 2D code in cylindrical coordinates based on a second-order, MUSCL-type upwind scheme (the 1D version of this scheme is described in Bedogni & D’Ercole 1986). The chemical enrichment of the galaxy is followed in detail; the production (by SNe of Type II, Type Ia, and intermediate-mass stars) of eight chemical elements (H, He, C, N, O, Mg, Si, and Fe) is considered, and the advection of these elements is followed by means of passive scalar fields. For instantaneous bursts, this scheme is described in detail in Recchi et al. (2001) and its extension to more complex SFHs is explained in Recchi et al. (2004). Since the code keeps correct track of the evolution of the metallicity in each computational cell, the detailed metallicity-dependent cooling function of Böhringer & Hensler (1989) can be implemented. The heat transport equation is also solved by means of the Crank-Nicolson method (see D’Ercole & Brighenti 1999 for details) using the classical Spitzer-Härm thermal conductivity (Spitzer & Härm 1953; Spitzer 1956). A saturated heat flux (Cowie & McKee 1977) is adopted if the mean free path of electrons is larger than the temperature scale length. Some improvements of this code are described in Recchi et al. (2007). In particular, metallicity-dependent stellar winds from massive and intermediate-mass stars have been considered, and primary and secondary nucleosynthetic production by stars of any age and any metallicity has been carefully calculated. Recchi et al. (2007) also describe an implementation of SF recipes. We do not adopt the self-consistent SF module in this work, where, in analogy with many previous studies (MF99, for instance), the SFH (or the luminosity) is an input of the model and not the result of the galactic evolution. In a work in preparation, models with a self-consistent SFH will be shown and discussed. Moreover, although in Recchi et al. (2007) a self-gravity solver (based on Rieschick & Hensler 2003) has been implemented, we decided not to adopt it in this study. The main reason for this decision is that we neglect self-gravity in building the initial equilibrium configuration (see next subsection). A parallel line of research (Vorobyov et al. 2012, and in prep.) analyzes in detail DG models with a consistent implementation of the gas self-gravity. The inclusion of self-gravity in the code would imply that the gas is initially out of equilibrium at the beginning of the simulation, even without sinks or sources of energy. This would establish an inward gas flow. Since our main aim in this paper is to study the effects of geometry and other parameters on the flow rate of gas and metals, we do not want gas infall to affect our results and want flows of gas (and metals) to be solely affected by feedback processes. Moreover, it is important to notice that most of the similar papers described in Sect. 2 (e.g., MF99, D’Ercole & Brighenti 1999; Strickland & Stevens 2000) also neglect self-gravity.
3.2. The set-up
We start with a reliable set-up of a DG, in which the gas is initially in isothermal equilibrium with a spherical DM halo and the centrifugal force. Analogous to what is done in many similar studies, we neglect self-gravity in building the initial equilibrium configuration. We point out here that this is in general not correct, even if most of the mass of the model galaxy is in the form of DM and the correct derivation of an equilibrium configuration is the one outlined by Vorobyov et al. (2012). However, the equilibrium configurations produced by Vorobyov et al. (2012) are quite complex (and also computationally demanding), and it is difficult to obtain two analogous equilibrium configurations that differ only in the degree of flattening of the initial gas distribution.
We consider three possible values for the initial baryonic mass of the galaxy (107, 108, and 109 M⊙) with a factor of ~10 more massive DM halos. The exact factor is deduced by the correlation between the DM-to-baryon ratio φ and the gas content as adopted by MF99, namely, 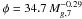 , where Mg,7 is the gaseous mass of the galaxy in units of 107 M⊙. This correlation is adapted from the work of Persic et al. (1996) and based on fitting procedures of observed rotation curves in local galaxies. However, it is not clear whether present-day DM-to-baryon ratios also correctly reflect the initial conditions of the galaxy. Nevertheless, we adopt this correlation in order to facilitate the comparison with the results of MF99. The virial radius of the DM halo is assumed to be
, where Mg,7 is the gaseous mass of the galaxy in units of 107 M⊙. This correlation is adapted from the work of Persic et al. (1996) and based on fitting procedures of observed rotation curves in local galaxies. However, it is not clear whether present-day DM-to-baryon ratios also correctly reflect the initial conditions of the galaxy. Nevertheless, we adopt this correlation in order to facilitate the comparison with the results of MF99. The virial radius of the DM halo is assumed to be 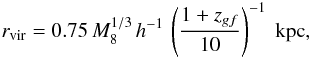 (1)(Madau et al. 2001; Mori et al. 2002). In this formula, M8 is the halo mass in units of 108M⊙ and zgf is the redshift of galaxy formation. Our reference value for zgf is 8. It is also important to stress that our initial distributions of gas are not artificially truncated at some cut-off radii as are the models of MF99. Therefore, without sources or sinks of energy, our models preserve their initial configurations (at variance with the models of MF99, which tend to expand). However, since our distribution of gas extends until the edges of the computational box, we need to establish a radius within which we calculate the mass of the galaxy. We take this to be half of the virial radius. Therefore, galaxies with the same nominal baryonic mass are normalized so that the total mass within 0.5rvir is the same, irrespective of the degree of flattening. This implies that flat galaxies have larger central densities than roundish ones (see below and Table 2).
(1)(Madau et al. 2001; Mori et al. 2002). In this formula, M8 is the halo mass in units of 108M⊙ and zgf is the redshift of galaxy formation. Our reference value for zgf is 8. It is also important to stress that our initial distributions of gas are not artificially truncated at some cut-off radii as are the models of MF99. Therefore, without sources or sinks of energy, our models preserve their initial configurations (at variance with the models of MF99, which tend to expand). However, since our distribution of gas extends until the edges of the computational box, we need to establish a radius within which we calculate the mass of the galaxy. We take this to be half of the virial radius. Therefore, galaxies with the same nominal baryonic mass are normalized so that the total mass within 0.5rvir is the same, irrespective of the degree of flattening. This implies that flat galaxies have larger central densities than roundish ones (see below and Table 2).
A small stellar disk is also initially present in the galaxy. Its density is such that a Miyamoto-Nagai potential 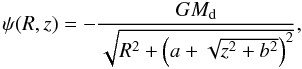 (2)(where Md is the mass of the stellar disk and R, z are the cylindrical radial and vertical coordinates, respectively) is reproduced. The ratio b/a between the scale lengths identifying the Miyamoto-Nagai potential is taken as one of the key parameters that we vary in our models. A small b/a corresponds to a flat model (for b/a → 0 the potential tends to the razor-thin Kuzmin model), whereas if b/a is very large, the galaxy tends to be rounder (for b/a → ∞ the potential tends to the Plummer’s spherical potential).
(2)(where Md is the mass of the stellar disk and R, z are the cylindrical radial and vertical coordinates, respectively) is reproduced. The ratio b/a between the scale lengths identifying the Miyamoto-Nagai potential is taken as one of the key parameters that we vary in our models. A small b/a corresponds to a flat model (for b/a → 0 the potential tends to the razor-thin Kuzmin model), whereas if b/a is very large, the galaxy tends to be rounder (for b/a → ∞ the potential tends to the Plummer’s spherical potential).
An initially flat distribution of gas is expected to results in an easier development of bipolar outflows, since the pressure gradient along the polar direction is much steeper than that along the galactic disk. As already discussed, a significant fraction of the matter processed in the central SF region can thus be channeled along the polar direction and eventually lost from the galaxy. On the other hand, if the galaxy is initially spherical (or almost spherical), no preferential propagation direction for the superbubble exists and the freshly produced metals are more likely to remain confined inside the galaxy. One of the aims of this work is to confirm this empirical assumption and quantitatively determine the fraction of gas and metal-rich stellar ejecta lost from a DG as a function of its degree of flattening. We consider three representative values for the ratio b/a: 0.2 (flat models, designated with the letter “F”); 1 (medium models or “M”) and 5 (roundish models or “R”). However, the mass of this pre-existing stellar disk cannot be established a priori. Therefore as another parameter, we vary the ratio between the mass of the Miyamoto-Nagai stellar disk and the total baryonic mass initially present in the galaxy. In particular, we consider two basic sets of models. For the first set (designated with “H”) the initial gas fraction is high (90% of the total baryonic mass of the galaxy), and the pre-existing stellar disk consequently represents a small fraction of the mass budget in the galaxy. The second set of models (designated with “L”) is characterized by a much smaller initial gas fraction (60% of the baryonic mass). Therefore, for instance, the model H7M represents a galaxy with high initial gas fraction, 107 M⊙ of initial baryonic mass and a medium degree of flattening (b/a = 1). We consider thus a total of 18 basic models, but we will discuss the dependence of our results on some key parameters in Sect. 4.2.
Other key parameters to be varied are the duration and intensity of the SF episode (as already mentioned, the analysis of models with self-consistent SFHs will be deferred to a future work). We assume here for simplicity that the SF is constant (with some pre-defined intensity ψ) for a period of time Δt. The two parameters ψ and Δt are allowed to vary, with the constraint that for models of equal mass the same final mass in stars is produced. In particular, we constrain the models “H” to produce, at the end of the SF period, a mass of newly formed stars that is twice as much as the mass of the initial stellar disk (namely, the fraction fN = M ∗ ,new/Md is set to be equal to 2). For the second set of models, designated with “L”, we set fN = 0.5, i.e., (since the pre-existing stellar disk is more massive for this set of models) we allow newly formed stars to be only 50% of the pre-existing disk at the end of the SF period. The resulting integrated luminosity of our models is not far from being constant (a constant luminosity has been assumed by MF99). Our reference models have Δt = 500 Myr and a SFR ψ such that, after Δt, the required fraction fN is obtained. Keeping the starburst duration Δt constant, it is obvious that a large starburst luminosity (i.e., a large ψ) produces a stronger outflow and thus in turn larger ejection efficiencies of gas and metals (see MF99). It is, however, not obvious if short, intense starbursts are more effective than long-lasting, milder SF episodes in getting rid of gas and processed matter. The answer to this question will be sought by considering the dependence of the ejection efficiencies in models with varying ψ and Δt but with constant ψ × Δt. In particular, a few models have been calculated in which Δt is a factor of ten smaller than the reference value (i.e., Δt = 50 Myr) and, consequently, the SFR is ten times more intense. Our reference value for Δt of 500 Myr is justified by observational studies indicating that the starbursts in DGs are not as short as previously thought, lasting on average a few hundred Myrs (see, e.g., McQuinn et al. 2010a,b).
The initial gas metallicity of our reference sets of model galaxies is zero. This is because we do not have a self-consistent evolution of the early phases of our model galaxies and can only suppose that the chemical enrichment of gas and stars in this early phase will be limited (particularly for the models “H”). Moreover, we do not expect it to be a fundamental parameter in determining the fate of metals, since the only way a different metallicity can affect the development of a galactic wind is through the cooling function and the difference between the zero-metal cooling curve and that of a modest metallicity (Z = 10-2 Z⊙ say) is negligible. We have nevertheless also considered models in which the initial metallicity of the stars (and gas!) is observationally determined (in particular, we make use of the M-Z relations observationally determined by Tremonti et al. 2004 for the local universe).
As done by Fragile et al. (2004) and Rodríguez-González et al. (2011), another important parameter in our study is the radius over which the feedback from dying stars is redistributed. If the “feedback radius” is very small, the density of the (metal-rich) ejected material is expected to be so high that radiative losses can be very significant and substantially increase the probability that the ejecta remain locked inside the galaxy (see, e.g., Tenorio-Tagle et al. 2007). It is unclear what happens if the feedback radius is larger, although, as already mentioned, the study of Fragile et al. (2004) suggests a reduction of ejection efficiencies (of both gas and starburst matter). Our reference feedback radius is RF = 200 pc, but models with RF = 50 pc and RF = 1000 pc have also been computed.
We have additionally considered the possibility (as we did in RH07) that the initial distribution of gas is characterized by inhomogeneities. However, for the sake of simplicity, we consider only a random perturbation of the initial galactic density distribution. Once an equilibrium configuration has been obtained, we modify the density ρ(i,j) in the grid (i,j) in this way: ![\begin{equation} \rho(i,j)=\rho(i,j) \left[1+\varepsilon R_{[-1,1]}\right], \label{eq:pert} \end{equation}](/articles/aa/full_html/2013/03/aa20845-12/aa20845-12-eq49.png) (3)where ε is a small number (corresponding to the largest possible amplitude of the perturbation) and R [−1,1] is a randomly generated number in the range [−1,1] . A more thorough (and self-consistent) treatment of inhomogeneities and a detailed study of the effect of boundary conditions (gravitational perturbations, external pressure, infall of clouds) is deferred to a future paper.
(3)where ε is a small number (corresponding to the largest possible amplitude of the perturbation) and R [−1,1] is a randomly generated number in the range [−1,1] . A more thorough (and self-consistent) treatment of inhomogeneities and a detailed study of the effect of boundary conditions (gravitational perturbations, external pressure, infall of clouds) is deferred to a future paper.
 |
Fig. 2 Initial gas distribution for three models (L8R – upper panel; L8M – central panel; L8F – lower panel) characterized by different degrees of flattening (see Table 2). The density scale (in g cm-3) is on the right-hand strip. |
Reference parameter values (common to all 18 basic models).
The central resolution of the simulations is 4 pc for the models with 108 and 109 M⊙ of initial baryonic mass and 2 pc for the models with 107 M⊙ of baryons. The resolution decreases outwards with a ratio between adjacent cells of 1.02. The reference values for some key parameters (common to all 18 basic models) are summarized in Table 1, whereas the specific parameter values distinguishing those models are presented in Table 2. In order to appreciate the distinction between models with different geometries, Fig. 2 shows the initial gas distribution of the models L8R (upper panel), L8M (central panel), and L8F (lower panel).
Parameter values for individual models and some representative results.
 |
Fig. 3 Gas density distribution for the 18 reference models (see Table 2) after 100 Myr of evolution. The nine panels on the left represent the models with high initial gas fraction (models “H”); the nine on the right are the corresponding models with low initial fraction of gas (models “L”). For each sequence of nine panels, the first column represents models with 107 M⊙ of initial baryonic mass, the middle column shows the gas distribution for models with mass 108M⊙, and the right-hand column displays the models with 109M⊙. The top rows of models are characterized by a roundish initial distribution (models “R”, with b/a = 5). The middle rows show models with b/a = 1 (models “M”), and the bottom rows are characterized by b/a = 0.2 (flat models or “F”). In the top-right corner of each panel, the model designation is also indicated. For each set of nine models, the left-hand strip shows the (logarithmic) density scale (in g cm-3). |
4. Results
4.1. The reference models
A snapshot of the evolution of all 18 reference models (see Table 2) is shown in Fig. 3 (after an evolutionary time of 100 Myr) and in Fig. 4 (after an evolutionary time of 200 Myr). The main features of our model results can be noticed from these two figures:
 |
Fig. 5 Distribution of oxygen mass density after 100 Myr of evolution for the nine models characterized by a small initial gas fraction (models “L” in Table 2). The oxygen density scale (in g cm-3) is on the left-hand strip. |
-
As expected, models characterized by a flat initial gas distribution (bottom rows) more easily develop a large-scale outflow. The roundish models (top rows) show very weak signs of outflows even at 200 Myr, irrespective of the baryonic mass.
-
For models characterized by the same geometry, the initial baryonic mass clearly plays a very important role, with much more prominent outflows in low-mass galaxies (left-most columns for each group of panels). This confirms the overall trend of gas ejection efficiency vs. mass shown by MF99, for instance.
-
If a large-scale outflow is formed, freshly produced metals can be easily lost from the galaxy (at an evolutionary time of 100 or 200 Myr, the SF is still ongoing). This is better seen in Fig. 5, where the distribution of oxygen (taken as a proxy of metals) is shown for the models with small initial gas fractions (models “L”), after 100 Myr. It is clear from this figure that in many model galaxies a large fraction of oxygen is leaving the parent galaxy. This will be quantified in detail below.
-
Outflows in models with high initial gas fraction (models “H”; the ones on the left of Figs. 3 and 4) are clearly less prominent compared to the corresponding outflows in low-gas models. This is due to the fact that the expansion of superbubbles is hampered by larger gas pressures in these models and to the fact that the SFRs are lower.
-
In roundish models, the ejected fractions of oxygen tend to be close or slightly smaller than the ejected fractions of pristine gas. This is because these models generally do not depart from their initial spherical symmetries. Under these circumstances, most of the metals remain confined inside the (almost spherical) superbubbles (the darker central regions in the upper rows of Figs. 3 and 4; see also Fig. 5). A large fraction of the pristine gas is swept up in a relatively dense shell surrounding the superbubble (the supershell), and occasionally a fraction of this gas can be located at distances from the galactic center greater than 0.5rvir.
-
In contrast, non-spherical models (models “M” and “F”) clearly show a tendency to retain pristine gas more easily than metals. This is in agreement with many previous studies already mentioned in the Introduction and in Sect. 2 (e.g., MF99; D’Ercole & Brighenti 1999; Recchi et al. 2001).
-
If we focus on models with the same initial gas distribution, we recover a clear trend of decreasing metal ejection efficiencies with increasing galactic baryonic mass, once again in agreement with the results of MF99. For instance, the oxygen ejection efficiencies at the end of the simulations (i.e., ϵO,500) for the “M” models are shown in Fig. 6. Oxygen ejection efficiencies are close to 1 for models with 107 M⊙ of baryonic mass and very low for models with Mb = 109 M⊙.

Fig. 6 Oxygen ejection efficiencies after 500 Myr of evolution for medium (b/a = 1) models as a function of the initial baryonic mass. Squares refer to models with initially low gas fractions and triangles to models with high fg.
-
As already noticed, models with a larger initial gas fraction are less effective in developing galactic winds. Consequently, the ejected fractions for these models are systematically lower than the corresponding “L” models (see also Fig. 6).
-
The effect of geometry on the development of galactic winds and on the fate of metals (and also on the fate of pristine gas) is quite evident from this table: models with the same baryonic mass can show very different retained fractions, depending on their degrees of flattening. Model L8R, for instance, retains almost all the oxygen at 200 Myr (ϵO,200 = 0.001), whereas model L8F, with the same baryonic mass but with a flat initial distribution, retains only 18.8% of oxygen, i.e., it expels 81.2% of the produced oxygen through galactic winds. If we look at the final ejection efficiencies, we notice again that the roundish model has the smallest oxygen ejection efficiency. The models L8F and L8M both have quite low retained oxygen fractions (therefore high oxygen ejection efficiencies), although ϵO,500 of model L8F is slightly smaller than the ejected fraction of L8M. The final retained gas fractions for all models depend very little on the degree of flattening. In contrast, focusing on the “H8” family of models, we notice again that the final ejection efficiencies of gas depend very little on b/a, whereas the final oxygen ejection efficiencies are 0.58, 0.375, and 0.061 for the models H8F, H8M, and H8R, respectively (see Col. 12 of Table 2), i.e., the metal ejection efficiencies can change by up to one order of magnitude depending on the geometry. Similar trends with the degree of flattening (little effect on the gas ejection efficiencies, large effect on the metal ejection efficiencies) can also be noticed for the families of models “L9”, “H9” and “H7”. The comparison of the final oxygen ejection efficiencies for the families of models “L9” and “H9” is shown in Fig. 7.
The last two columns of Table 2 show the oxygen abundance measured as 12+log(O/H) abundance ratio, where O/H is the abundance ratio in number of all model galaxies. This abundance ratio is a mass-weighted average of the abundance ratios in each computational cell lying within a sphere of radius 0.5rvir. Again, this is only an approximate measure of the galactic metallicity, and only relative abundance ratios between different model galaxies are relevant. In particular, the present grid of models is not aimed at reproducing the observed metallicities of individual DGs, and it can be noticed, e.g., that large galaxies do not always show larger O/H ratios compared to smaller galaxies (at variance with the observed M-Z relation; see Lee et al. 2006). It is also worth noticing that, unexpectedly, models with the highest metallicities experience the strongest galactic winds (models “L7”), at variance with the general idea that galactic winds can keep the metallicities of galaxies low (see the Introduction). This is because these model galaxies expel almost all pristine gas (see Table 2), so that the (continuously produced) oxygen is mixed with a very small fraction of unpolluted gas. The average metallicity of the galaxy is thus close to the (very large) metallicity of the stellar ejecta. However, this gas is destined to leave the parent galaxy and is anyway too hot to form star; it will thus not increase the average metallicity of the stellar populations in the galaxy. The models attaining the lowest metallicities are the ones (like H7F) that develop large-scale outflows but retain a large fraction of pristine gas bound to the galaxy. See also Sect. 5 for a more extended discussion on the connection between the results of our models and the M-Z relation.
 |
Fig. 7 Oxygen ejection efficiencies after 500 Myr of evolution for high-mass (Mb = 109 M⊙) models as a function of the degree of flattening b/a. Symbols as in Fig. 6. |
4.2. Widening the parameter space
As mentioned in Sect. 3.2, we have also considered models with different SFHs, different feedback radii, different initial metallicities, and with perturbed initial distributions of gas. We summarize in this subsection how these parameters affect our findings.
4.2.1. Dependence on the star formation history
We have re-run some models (specifically the ones for the family “L8”) in which the SFH, instead of being constant for 500 Myr as in the standard models, is different from zero only during the first 50 Myr, but the SFR is ten times more intense than in the standard models. A large-scale outflow quickly develops, even for the roundish model, sustained by the large rate of SNII explosions during the first ~80 Myr. At the end of this phase, energy is still supplied by Type Ia SNe and winds from intermediate-mass stars, but at a lower rate. This energy is still able to sustain the outflow for some time, but after a few times 108 yr, the gravitational pull prevails over the pressure gradient caused by the hot cavity of gas and some gas begins to recollapse towards the center of the galaxy (see Recchi & Hensler 2006 for a precise assessment of this phenomenon).
The result is that the calculated ejection efficiencies (of gas and metals) are larger at 100 or 200 Myr than at 500 Myr. In particular, the ejection efficiencies at 200 Myr are much larger than the ones in the standard models, tabulated in Table 2. Disk-like models (“F” and “M”) retain only a few percent of gas and metals, and the roundish model (“R”) is also able to expel more than 50% of the initial gas at distances larger than 0.5rvir. The large gas ejection efficiencies for these models are due to the fact that, at these high rates of energy release, the horizontal transport of gas can also be effective and some gas is pushed to large distances from the galactic center even along the disk. The disk-like “M” and “F” models again show metal ejection efficiencies (slightly) larger than gas ejection efficiencies. Consequently, the metallicities of these model galaxies are quite low during the SF episode.
However, as soon as the luminosity considerably reduces, this gas is pulled again within 0.5rvir (i.e., a fall back is occurring), whereas the material previously channeled along the galactic wind accelerates away from the galaxy due to the steep density gradient. Consequently, after 500 Myr of evolution, the retained gas fractions for these models tend to be larger (by a factor of ~1.5–2) than the corresponding fractions of the standard models (the ones reported in Col. 11 of Table 2), whereas the retained fraction of metals are only slightly larger.
4.2.2. Dependence on the feedback radius
We have considered (again for the family of models “L8”) a variation of the radius over which energy and metals are injected. As anticipated in Sect. 3.2, we have calculated models with RF = 50 pc and RF = 1000 pc instead of the reference value RF = 200 pc. The models with RF = 1000 show very large ejection efficiencies for both gas and metals. This is due to the unfortunate circumstance that 0.5rvir for this family of models is only slightly larger than 1000 pc, so that a moderate energy injection suffices to push a large fraction of gas at distances larger than 0.5rvir. The comparison with the ejection efficiencies of standard models thus makes little sense. We therefore calculated the ejection efficiencies of these models (and of the corresponding standard models) at r = rvir. These turn out to be ~10% smaller than the ones of corresponding reference models. We confirm therefore that, if the energy is redistributed over a large volume, radiative energy losses are more effective and the final ejection efficiencies are reduced, in agreement with the findings of Fragile et al. (2004). In addition the models with RF = 50 pc show slightly lower ejection efficiencies. In this case, the enhanced cooling efficiency is due to the fact that the gas within the feedback radius is now characterized by large densities and metallicities (see also Tenorio-Tagle et al. 2007). In this case, the effect of the feedback radius is quite limited, too (ejection efficiencies change by ~10−15%). As also shown by Rodríguez-González et al. (2011; see their Fig. 7), the dependence of the ejection efficiencies on the feedback radius is non-monotonic, although the dependence of our results on this particular parameter is quite limited.
4.2.3. Dependence on the initial metallicity
Since we consider models in which a stellar disk is already present at the beginning of the simulations, it seems unreasonable to start with a primordial metallicity. We studied therefore models in which the initial metallicity (of stars and gas) is regulated by the mass of the pre-existing disk: namely, according to the M-Z relation, the larger the disk mass, the larger the initial metallicity we must consider. In particular, if we take into account the correlation between mass and metallicity obtained by Tremonti et al. (2004), models of the “L8” family should have an initial metallicity of about one-tenth of solar. Of course, the final metallicities of these models will be much higher than the ones attained by models initially without metals. However, as already mentioned, the only dynamical effect of a different initial metallicity is to increase the radiative losses and thus reduce the amount of thermal energy of the galaxy. It turns out that this reduction is quite limited and, therefore, the ejection efficiencies do not change substantially (they are only a few percent lower than the ejection efficiencies of corresponding models initially without metals). For these models, the metal ejection efficiencies are calculated according only to the amount of freshly produced metals retained or ejected.
4.2.4. Models with random perturbation of the initial gas distribution
As described in Sect. 3.2, once an equilibrium initial configuration has been obtained, we perturbed it by means of Eq. (3). In particular, we perturbed the model L8R by amplitudes ε of 1% (mildly perturbed model) and 5% (largely perturbed model). The perturbation increases the turbulence of the model. Mixing between hot and cold regions is enhanced, and the net effect is an increase in the radiative energy losses, hence a reduced amount of energy available to drive galactic winds (in other words, the galactic winds become more mass loaded). Consequently, the retained gas fraction of the mildly perturbed model increases (from the final value of 0.442 of the model L8R, it increases to 0.547). However, the final retained fraction of freshly produced metals (slightly) decreases for this model (to 0.345 from the reference value of 0.401). This is because it is much more difficult to keep the model close to spherical symmetry if the initial gas distribution is perturbed. Regions of lower pressure can be created randomly within the computational box. The propagation of metals can deviate from isotropicity, and it is faster (and allows some venting out of metals) along (randomly oriented) directions with steep pressure gradients. This effect is similar to the one analyzed in great detail by RH07 (see also Sect. 2 for a short summary of the main results of this paper). In the largely perturbed model, the final metal ejection efficiency is similar to the one obtained in the mildly perturbed model. However, the venting out (along random directions) now also involves a non-negligible fraction of pristine gas, and the final gas-retained fraction is 0.443 (very similar to the gas-retained fraction of the reference model L8R). The piercing of the supershell along different directions and not just perpendicular to the disk of the galaxy can be appreciated by inspecting Fig. 8. It shows the gas and oxygen density distribution after 200 Myr of evolution of the largely perturbed model. Clearly, the perturbation of the initial gaseous distribution affects the ejection efficiencies of gas and metals in a non-linear (and sometimes non-predictable) way and deserves further study.
 |
Fig. 8 Distribution of gas (left panel) and oxygen (right panel) density for a model with large perturbation of the initial density distribution (see text), after 200 Myr of evolution. Brighter colors correspond to larger densities. |
It is important to stress that inhomogeneities represent rings of denser gas, due to the assumed symmetry and dimensionality of the code. It is not clear whether a realistic 3D distribution of inhomogeneities will produce the same results. Our group is currently running 3D chemo-dynamical simulations of DGs with inhomogeneities using the AMR code FLASH (Mitchell et al., in prep.). The results of these simulations can shed light on the reliability of our results.
5. Discussion and conclusions
In this paper we have studied the development of galactic outflows in DG models. Our main focus is to study the dependence of the ejected mass fractions of gas and freshly produced metals on the degree of flattening of the galaxy, a problem that has received little attention in the past. A very simple theoretical analysis leads to the conclusion that, in a very flat galaxy, the ejection efficiencies of freshly produced metals must be quite high. In fact, once the over-pressurized gas formed by SN explosions and stellar wind breaks out and forms a bipolar galactic wind, metals can be easily ejected out of the galaxy through this funnel. On the other hand, in a spherical (or almost spherical) galaxy, bipolar outflows cannot be formed because there is no preferential direction, along which the pressure gradient is steeper. Therefore, either the galaxy expels gas isotropically (but blow-away is very difficult in DGs; see, e.g., Hensler et al. 2004) or the superbubble of hot and metal-enriched gas remains confined inside the galaxy. Thus, the metal ejection efficiencies are very low. We considered three different degrees of flattening for our model galaxies: a roundish model (for which the ratio between the length scales a and b describing the Miyamoto-Nagai potential is b/a = 5), a thick-disk model (with b/a = 1), and a thin-disk model (with b/a = 0.2). Our study confirms the trend described above: ejection efficiencies in roundish galaxies are systematically lower than the ones in disk-like galaxies (see Table 2 or Fig. 7). On the other hand, for most of the analyzed models, transport of gas along the disk is quite limited. This is in agreement with many previous studies (e.g., MF99; D’Ercole & Brighenti 1999). Therefore, we can conclude that ejection efficiencies of gas are (at least for disk-like models) lower than ejection efficiencies of freshly produced metals.
We have also studied in detail the effect of galactic mass on the fate of gas and freshly produced metals, a problem that has received much more attention in the past (MF99; Rodríguez-González et al. 2011). We confirm that smaller DGs with shallower potential wells favor the development of large-scale outflows. As a result, the ejection efficiencies of gas and metals increase with decreasing galactic masses (see Table 2 or Fig. 6). The increase of metal ejection efficiencies through galactic winds has often been invoked to explain the observed M-Z relation in galaxies (see, e.g., Tremonti et al. 2004; Zhao et al. 2013). The dependence of the obtained metallicity (measured by means of 12+log (O/H)) of our model galaxies as a function of their initial masses is shown in Fig. 9 for the “H” set of models. For all three degrees of flattening, a trend of increasing metallicity as a function of mass is clearly visible. However, as outlined in Sect. 4.1, this trend is much less visible for the “L” set of models.
 |
Fig. 9 Oxygen abundances (in number) after 500 Myr of evolution for high gas fraction models (models “H”, with fg = 0.9), as a function of initial baryonic mass. Squares refer to flat models (models with b/a = 0.2); triangles show the results for intermediate models (b/a = 1) and rhombs correspond to roundish models (b/a = 5). |
It is important to notice that the abundances tabulated in Table 2 and plotted in Fig. 9 are mass-averaged means within the whole galactic region. However, two gas phases coexist within this region: a hot gas phase (the galactic wind and the starburst region) and a colder ISM. We expect the hot phase to have much higher metallicities than the cold phase. The metallicity of the galactic wind is not expected to play a role in the process of chemical enrichment of the galaxy (this gas is destined to leave the parent galaxy) but is important in the process of chemical enrichment of the intra-cluster medium. To have an idea on the oxygen abundances of these two phases, we distinguish grid points with temperatures above and below 2 × 104 K. Gas above this temperature threshold is supposed to be too hot to be detected by optical spectroscopy. The resulting values of 12+log(O/H) after 500 Myr of evolution for the “H” family of models is shown in Fig. 10 (red lines: cold phase; blue lines: hot phase). As expected, the abundances in the cold phase are much lower than the abundances in the hot phase. The cold phase abundances show the same trend of the total abundances displayed in Fig. 9, mainly because the calculated mean abundances are mass-weighted and most of the gas mass is colder than 2 × 104 K. For some models (particularly those with log M = 7), the cold phase abundances are significantly lower (~0.2 dex) than the total abundances. This is expected because the metal-rich hot gas (wind and starburst region) represents a significant fraction of the total gas in some models. On the other hand, models experiencing no, or very limited, galactic winds contain much less hot gas. As a result, the average total abundance is less affected by the metallicity of the hot phase and is much closer to the abundance of the cold gas (the differences are a few hundredths of dex).
In addition, the abundances of the hot phase tend to grow with mass (see the blue lines in Fig. 10). High-mass galaxies show higher hot-phase abundances because, for these models, much of the hot gas is in the starburst region and thus its metallicity is close to the very high metallicity of the stellar ejecta. On the other hand, galaxy models experiencing strong galactic winds show smaller hot-phase metallicities because the winds entrain more cold (and metal-poor) gas. This process is usually indicated as mass loading and is confirmed by many studies (both theoretical and observational) of galactic winds (see, e.g., Strickland & Stevens 2000; Tescari et al. 2009; Hopkins et al. 2012; Newman et al. 2012). Indeed, a clearer correlation can be shown between the ejected oxygen fraction after 500 Myr (12th Col. in Table 2) and the hot-phase oxygen abundance. This correlation is shown in Fig. 11. Models experiencing galactic winds (thus with high oxygen ejection efficiencies) also show mass loading, and thus dilution of the oxygen abundances in the hot phase. On the other hand, in models with weak or no galactic winds, most of the hot gas is concentrated in the starburst region, where the abundances closely resemble the very high abundances of the stellar ejecta.
 |
Fig. 10 Oxygen abundances (in number) after 500 Myr of evolution for “H” models as a function of initial baryonic mass. Symbols are as in Fig. 9. The abundances in the cold (T < 2 × 104 K) phase are shown in the lower set of points (connected by red lines). The abundances in the hot (T > 2 × 104 K) phase are shown in the upper set of points (connected by blue lines). |
 |
Fig. 11 Oxygen abundances in the hot phase plotted versus the oxygen ejection efficiencies (12th Col. in Table 2). Model designations are labeled close to each point. |
The processes of metal dispersal and mixing are very difficult to model. No hydrodynamical code is able to correctly resolve contact discontinuities that form between hot cavities and cold shells. Numerical diffusion tends to smear this discontinuity and create regions of intermediate temperature and densities, where metals can cool in a relatively short timescale and then mix with the surrounding shell. In spite of these uncertainties, we believe that 500 Myr is a sufficient time span to cool down most of the produced metals, if they are not channeled in a galactic wind. This is confirmed by some of our previous studies (see in particular Recchi et al. 2001; their Sect. 3.2) and also by other studies addressing the specific issue of metal mixing (e.g., de Avillez & MacLow 2002; Pan et al. 2012; Yang & Krumholz 2012), which confirm that a few hundred Myrs is a sufficient time to disperse and mix metallicity inhomogeneities. It is also important to stress that, in our results, cooling and mixing of stellar ejecta is mainly due to thermal conduction and to the formation of eddies and vortices. The presence of inhomogeneities (see Sect. 4.2.4) can facilitate both processes, and thus enhance the mass loading of the galactic winds.
One should also notice that the chosen temperature threshold separating the hot and the cold phase (2 × 104 K) is somewhat arbitrary and was taken in analogy with what was done in some of our previous publications (see in particular Recchi et al. 2006). A different and maybe better choice could be 4 × 104 K (the minimum of the cooling curve for low values of the metallicity; see Böhringer & Hensler 1989, their Fig. 1) or even 105 K. We have checked to what extent our results are affected by the choice of the temperature threshold. It turns out that the abundances in the cold phase are almost unaffected by this choice (for T = 4 × 104 K the abundances change negligibly whereas for T = 105 K the differences are 0.02 dex at most). This is due to the fact that a small fraction (in mass) of gas has temperatures in the range [2 × 104, 4 × 104] K or [2 × 104, 105] K. On the other hand, the variations in the hot phase abundances are more significant. They increase by up to 0.15–0.2 dex if the threshold is 105 K. However, the overall correlations shown in Figs. 10 and 11 remain.
The main aim of this paper was to show the effect that gas distribution can have on the development of galactic winds and hence on the fate of gas and freshly produced metals. We have not attempted to reproduce the observed M-Z relation (we focus on this task in a paper in preparation). For instance, all the models, irrespective of their masses, have the same SFRs per unit available gas mass (hence the same SF efficiencies). Models with initially 108 M⊙ of baryonic mass have SFRs ten times larger than models with Mb = 107 M⊙. The metal production rates are also ten times larger. However, these larger fractions of metals are mixed with ten times more pristine gas. Hence, if galactic winds do not play a significant role, the final metallicities of the models should be approximately independent of the galactic mass (see roundish models in Fig. 9). However, it is known from chemical evolution studies (e.g., Matteucci 1994; Pipino & Matteucci 2004) that SF efficiencies must increase with galactic masses in order to reproduce the observed chemical abundances and abundance ratios of galaxies. This is also consistent with the idea that SF efficiencies increase with pressure of the ambient diffuse gas, which increases with galactic mass (Elmegreen & Efremov 1997; Harfst et al. 2006; see also Leroy et al. 2008).
However, as we noticed in Sect. 4.2.1, metal ejection efficiencies of galaxies with higher SFRs are larger, although they produce the same mass in stars at the end of the simulation. Consequently, these galaxies tend to have lower metallicities during the SF episode. This qualitative trend is in agreement with the so-called fundamental metallicity relation (FMR: Mannucci et al. 2010), according to which the oxygen abundance in star forming galaxies correlates with the quantity μα = log (M ∗ ) − αlog (SFR), where α is a free parameter chosen to minimize the scatter in the FMR. Although the precise shape of the FMR is debated (for instance, the recent paper of Andrews & Martini 2012 find α = 0.66, more than twice the value of Mannucci et al.), the SFR undoubtedly plays a very important role in determining the gas-phase metallicity of a galaxy. Galaxies with the same stellar mass but with higher SFRs are characterized by lower metallicities (see, e.g., Fig. 11 of Andrews & Martini 2012). According to Andrews & Martini (2012), this is probably because galaxies with high SFRs are presently experiencing a merging. Major mergers drive in considerable amounts of low metallicity gas from large radii, which dilutes the metallicity of the galaxy and triggers a vigorous SF burst. Since most of the galaxies with large SFR already have large stellar masses, it seems unlikely that their gas components still have a low metallicity. It seems more likely to us that large SFRs drive large outflows, with a consequent significant metal loss, as our models show.
For models with the same mass and SFR, geometry plays a very significant role in determining the fate of freshly produced metals and, consequently, the final metallicity. An inspection of Table 2 shows that, for some models, ejection efficiencies of metals can change by up to an order of magnitude depending on the degree of flattening. The gas ejection efficiencies are instead quite independent of b/a. Consequently, the final metallicities of models with the same mass can vary up to 1 dex depending on the geometry (see Figs. 9 and 10). The large spread observed in the metallicity of DGs with the same masses (see, e.g., Lee et al. 2006, their Fig. 8) could be due to the effect of gas distribution. Although the parameter α is chosen to minimize the scatter in the FMR, galaxies with the same stellar mass and SFR still show a spread in the metal content (see, e.g., Figs. 11 and 12 of Andrews & Martini 2012). The gas distribution might be responsible for this spread.
A last comment related to the M-Z relation or the FMR concerns the correlation between mass and degree of flattening of DGs. Recent studies suggest that smaller DGs tend to have larger axial ratios (i.e., they tend to be rounder) than DGs with larger masses. This might complicate the interpretation of the M-Z and FMR relations according to our models. However, this effect seems to be quite limited. For instance, Sánchez-Janssen et al. (2010) show (their Fig. 1) that the average axial ratios change by at most ~20% between DGs with stellar masses of 107 and 109 M⊙ and that the spread in axial ratios is extremely large at all stellar masses. Moreover, Lisker et al. (2009) show that, at least for DGs in clusters, the axial ratio is more related to the DG velocity than to the mass.
Our main conclusions can be summarized as follows:
-
The gas distribution in a galaxy plays a very important role in determining the fate of freshly produced metals. Model galaxies with the same masses but with different degrees of flattening can have metal ejection efficiencies differing for one order of magnitude. In particular, flat galaxies easily develop bipolar outflows, through which a large fraction of metals can be lost.
-
On the other hand, the fate of pristine gas is less dependent on geometry than the fate of metals. Since some models with the same initial mass can have similar ejection efficiencies of pristine gas but very different ejection efficiencies of metals, the final attained metallicities can vary by up to one dex. The roundish models are characterized by larger final metallicities.
-
Models characterized by the same degree of flattening show a clear dependence of the metal ejection efficiencies on the galactic mass. Smaller galaxies (with shallower potential wells) more easily develop large-scale outflows, so that the fraction of lost metals tends to be higher.
-
Ejection efficiencies (of gas and freshly produced metals) also depend significantly on the star formation history of the galaxy and on the presence (or absence) of density perturbations.
-
The ejection efficiencies show instead a moderate dependence on the initial metallicity and on the size of the region in which the energetic and chemical feedback from supernovae and stellar winds is redistributed.
Acknowledgments
We thank the anonymous referee for very helpful comments and remarks and Masao Mori for very helpful discussions.
References
- Andrews, B. H., & Martini, P. 2012, ApJ, submitted [arXiv:1211.3418] [Google Scholar]
- Bedogni, R., & Dercole, A. 1986, A&A, 157, 101 [NASA ADS] [Google Scholar]
- Boehringer, H., & Hensler, G. 1989, A&A, 215, 147 [NASA ADS] [Google Scholar]
- Cowie, L. L., & McKee, C. F. 1977, ApJ, 211, 135 [NASA ADS] [CrossRef] [Google Scholar]
- de Avillez, M. A., & Mac Low, M.-M. 2002, ApJ, 581, 1047 [NASA ADS] [CrossRef] [Google Scholar]
- D’Ercole, A., & Brighenti, F. 1999, MNRAS, 309, 941 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., & Silk, J. 1986, ApJ, 303, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., & Efremov, Y. N. 1997, ApJ, 480, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Erb, D. K., Shapley, A. E., Pettini, M., et al. 2006, ApJ, 644, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrara, A., & Tolstoy, E. 2000, MNRAS, 313, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Fragile, P. C., Murray, S. D., & Lin, D. N. C. 2004, ApJ, 617, 1077 [NASA ADS] [CrossRef] [Google Scholar]
- Harfst, S., Theis, C., & Hensler, G. 2006, A&A, 449, 509 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hensler, G., Dickow, R., Junkes, N., & Gallagher, J. S. 1998, ApJ, 502, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Hensler, G., Theis, C., & Gallagher, J. S., III. 2004, A&A, 426, 25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hidalgo, S. L., Aparicio, A., Skillman, E., et al. 2011, ApJ, 730, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Quataert, E., & Murray, N. 2012, MNRAS, 421, 3522 [Google Scholar]
- Kirby, E. N., Simon, J. D., Geha, M., Guhathakurta, P., & Frebel, A. 2008, ApJ, 685, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Lara-López, M. A., Cepa, J., Bongiovanni, A., et al. 2010, A&A, 521, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larson, R. B. 1974, MNRAS, 169, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, T., Berger, E., & Chary, R.-R. 2011, ApJ, 739, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, H., Skillman, E. D., Cannon, J. M., et al. 2006, ApJ, 647, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [NASA ADS] [CrossRef] [Google Scholar]
- Lisker, T., Janz, J., Hensler, G., et al. 2009, ApJ, 706, L124 [NASA ADS] [CrossRef] [Google Scholar]
- Mac Low, M.-M., & Ferrara, A. 1999, ApJ, 513, 142 (MF99) [NASA ADS] [CrossRef] [Google Scholar]
- McQuinn, K. B. W., Skillman, E. D., Cannon, J. M., et al. 2010a, ApJ, 721, 297 [NASA ADS] [CrossRef] [Google Scholar]
- McQuinn, K. B. W., Skillman, E. D., Cannon, J. M., et al. 2010b, ApJ, 724, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., Ferrara, A., & Rees, M. J. 2001, ApJ, 555, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Nagao, T., Grazian, A., et al. 2008, A&A, 488, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., Marconi, A., & Gnerucci, A. 2010, MNRAS, 408, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- Mannucci, F., Salvaterra, R., & Campisi, M. A. 2011, MNRAS, 414, 1263 [NASA ADS] [CrossRef] [Google Scholar]
- Marcolini, A., D’Ercole, A., Brighenti, F., & Recchi, S. 2006, MNRAS, 371, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, C. L., Kobulnicky, H. A., & Heckman, T. M. 2002, ApJ, 574, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F. 1994, A&A, 288, 57 [NASA ADS] [Google Scholar]
- Michielsen, D., Valcke, S., & de Rijcke, S. 2007, EAS Pub. Ser., 24, 287 [CrossRef] [Google Scholar]
- Monelli, M., Gallart, C., Hidalgo, S. L., et al. 2010a, ApJ, 722, 1864 [NASA ADS] [CrossRef] [Google Scholar]
- Monelli, M., Hidalgo, S. L., Stetson, P. B., et al. 2010b, ApJ, 720, 1225 [NASA ADS] [CrossRef] [Google Scholar]
- Mori, M., Ferrara, A., & Madau, P. 2002, ApJ, 571, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, S. F., Genzel, R., Förster-Schreiber, N. M., et al. 2012, ApJ, 761, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Ott, J., Walter, F., & Brinks, E. 2005, MNRAS, 358, 1423 [NASA ADS] [CrossRef] [Google Scholar]
- Pan, L., Desch, S. J., Scannapieco, E., & Timmes, F. X. 2012, ApJ, 756, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Persic, M., Salucci, P., & Stel, F. 1996, MNRAS, 281, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Pipino, A., & Matteucci, F. 2004, MNRAS, 347, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Recchi, S., & Hensler, G. 2006, A&A, 445, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Recchi, S., & Hensler, G. 2007, A&A, 476, 841 (RH07) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Recchi, S., Matteucci, F., & D’Ercole, A. 2001, MNRAS, 322, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Recchi, S., Matteucci, F., D’Ercole, A., & Tosi, M. 2002, A&A, 384, 799 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Recchi, S., Matteucci, F., D’Ercole, A., & Tosi, M. 2004, A&A, 426, 37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Recchi, S., Hensler, G., Angeretti, L., & Matteucci, F. 2006, A&A, 445, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Recchi, S., Theis, C., Kroupa, P., & Hensler, G. 2007, A&A, 470, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Recchi, S., Hensler, G., & Anelli, D. 2009 [arXiv:0901.1976] [Google Scholar]
- Rieschick, A., & Hensler, G. 2003, Ap&SS, 284, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-González, A., Esquivel, A., Raga, A. C., & Colín, P. 2011, Rev. Mex. Astron. Astrofis. Conf. Ser., 40, 86 [NASA ADS] [Google Scholar]
- Sánchez-Janssen, R., Méndez-Abreu, J., & Aguerri, J. A. L. 2010, MNRAS, 406, L65 [NASA ADS] [Google Scholar]
- Scannapieco, E., & Brüggen, M. 2010, MNRAS, 405, 1634 [NASA ADS] [Google Scholar]
- Schroyen, J., de Rijcke, S., Valcke, S., Cloet-Osselaer, A., & Dejonghe, H. 2011, MNRAS, 416, 601 [NASA ADS] [Google Scholar]
- Silich, S. A., & Tenorio-Tagle, G. 1998, MNRAS, 299, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Silich, S., & Tenorio-Tagle, G. 2001, ApJ, 552, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Skillman, E. D., Kennicutt, R. C., & Hodge, P. W. 1989, ApJ, 347, 875 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L. 1956, Physics of Fully Ionized Gases (New York: Interscience Publishers) [Google Scholar]
- Spitzer, L., & Härm, R. 1953, Phys. Rev., 89, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Strickland, D. K., & Stevens, I. R. 2000, MNRAS, 314, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Tenorio-Tagle, G. 1996, AJ, 111, 1641 [NASA ADS] [CrossRef] [Google Scholar]
- Tenorio-Tagle, G., Wünsch, R., Silich, S., & Palouš, J. 2007, ApJ, 658, 1196 [NASA ADS] [CrossRef] [Google Scholar]
- Tescari, E., Viel, M., Tornatore, L., & Borgani, S. 2009, MNRAS, 397, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Vader, J. P. 1986, ApJ, 305, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Vasiliev, E. O., Vorobyov, E. I., & Shchekinov, Y. A. 2008, A&A, 489, 505 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vorobyov, E. I., Recchi, S., & Hensler, G. 2012, A&A, 543, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wuyts, E., Rigby, J. R., Sharon, K., & Gladders, M. D. 2012, ApJ, 755, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, C.-C., & Krumholz, M. 2012, ApJ, 758, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, Y., Gao, Y., & Gu, Q. 2010, ApJ, 710, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, Y., Gao, Y., & Gu, Q. 2013, ApJ, 764, 44 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Gas (filled contours) and oxygen (black contour lines) distribution of a model galaxy (taken from Recchi et al. 2006) experiencing a galactic outflow. Brighter colors indicate larger gas densities. |
| In the text | |
 |
Fig. 2 Initial gas distribution for three models (L8R – upper panel; L8M – central panel; L8F – lower panel) characterized by different degrees of flattening (see Table 2). The density scale (in g cm-3) is on the right-hand strip. |
| In the text | |
 |
Fig. 3 Gas density distribution for the 18 reference models (see Table 2) after 100 Myr of evolution. The nine panels on the left represent the models with high initial gas fraction (models “H”); the nine on the right are the corresponding models with low initial fraction of gas (models “L”). For each sequence of nine panels, the first column represents models with 107 M⊙ of initial baryonic mass, the middle column shows the gas distribution for models with mass 108M⊙, and the right-hand column displays the models with 109M⊙. The top rows of models are characterized by a roundish initial distribution (models “R”, with b/a = 5). The middle rows show models with b/a = 1 (models “M”), and the bottom rows are characterized by b/a = 0.2 (flat models or “F”). In the top-right corner of each panel, the model designation is also indicated. For each set of nine models, the left-hand strip shows the (logarithmic) density scale (in g cm-3). |
| In the text | |
 |
Fig. 4 Same as Fig. 3 but for snapshots taken after 200 Myr of galactic evolution. |
| In the text | |
 |
Fig. 5 Distribution of oxygen mass density after 100 Myr of evolution for the nine models characterized by a small initial gas fraction (models “L” in Table 2). The oxygen density scale (in g cm-3) is on the left-hand strip. |
| In the text | |
 |
Fig. 6 Oxygen ejection efficiencies after 500 Myr of evolution for medium (b/a = 1) models as a function of the initial baryonic mass. Squares refer to models with initially low gas fractions and triangles to models with high fg. |
| In the text | |
 |
Fig. 7 Oxygen ejection efficiencies after 500 Myr of evolution for high-mass (Mb = 109 M⊙) models as a function of the degree of flattening b/a. Symbols as in Fig. 6. |
| In the text | |
 |
Fig. 8 Distribution of gas (left panel) and oxygen (right panel) density for a model with large perturbation of the initial density distribution (see text), after 200 Myr of evolution. Brighter colors correspond to larger densities. |
| In the text | |
 |
Fig. 9 Oxygen abundances (in number) after 500 Myr of evolution for high gas fraction models (models “H”, with fg = 0.9), as a function of initial baryonic mass. Squares refer to flat models (models with b/a = 0.2); triangles show the results for intermediate models (b/a = 1) and rhombs correspond to roundish models (b/a = 5). |
| In the text | |
 |
Fig. 10 Oxygen abundances (in number) after 500 Myr of evolution for “H” models as a function of initial baryonic mass. Symbols are as in Fig. 9. The abundances in the cold (T < 2 × 104 K) phase are shown in the lower set of points (connected by red lines). The abundances in the hot (T > 2 × 104 K) phase are shown in the upper set of points (connected by blue lines). |
| In the text | |
 |
Fig. 11 Oxygen abundances in the hot phase plotted versus the oxygen ejection efficiencies (12th Col. in Table 2). Model designations are labeled close to each point. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


