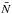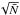| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A67 | |
| Number of page(s) | 16 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201220701 | |
| Published online | 22 February 2013 | |
Asteroids’ physical models from combined dense and sparse photometry and scaling of the YORP effect by the observed obliquity distribution ⋆
1 Astronomical Institute, Faculty of Mathematics and Physics, Charles University in Prague, V Holešovičkách 2, 18000 Prague, Czech Republic
e-mail: hanus.home@gmail.com
2 Astronomical Observatory Institute, Faculty of Physics, A. Mickiewicz University, Słoneczna 36, 60-286 Poznań, Poland
3 Palmer Divide Observatory, 17995 Bakers Farm Rd., Colorado Springs, CO 80908, USA
4 4438 Organ Mesa Loop, Las Cruces, NM 88011, USA
5 Goat Mountain Astronomical Research Station, 11355 Mount Johnson Court, Rancho Cucamonga, CA 91737, USA
6 Geneva Observatory, 1290 Sauverny, Switzerland
7 European Space Astronomy Centre, Spain, PO Box 78, 28691 Villanueva de la Cañada, Madrid, Spain
8 Astronomical Institute of the Academy of Sciences, Fričova 298, 25165 Ondřejov, Czech Republic
9 Observatoire de Bédoin, 47 rue Guillaume Puy, 84000 Avignon, France
10 Observatoire de Chinon, Mairie de Chinon, 37500 Chinon, France
11 Courbes de rotation d’astéroïdes et de comètes, CdR
12 Association T60, 14 avenue Édouard Belin, 31400 Toulouse, France
13 Harfleur, France
14 Observatoire des Engarouines, 84570 Mallemort-du-Comtat, France
15 Collonges Observatory, 90 allée des résidences, 74160 Collonges, France
16 Paris and Saint-Savinien, France
17 139 Antibes France
18 Via M. Rosa, 1, 00012 Colleverde di Guidonia, Rome, Italy
19 947 Saint-Sulpice, France
20 IMCCE – Paris Observatory – UMR 8028 CNRS, 77 Av. Denfert-Rochereau, 75014 Paris, France
21 A90 San Gervasi, Spain
22 l’Observatoire de Cabris, 408 chemin Saint Jean Pape, 06530 Cabris, France
23 929 Blackberry Observatory, USA
24 Plateau du Moulin à Vent, St-Michel l’Observatoire, France
25 J80 Saint-Hélène, France
26 B13 Tradate, Italy
27 138 Village-Neuf, France
28 TASS = The Amateur Sky Survey
29 Shed of Science Observatory, 5213 Washburn Ave. S, Minneapolis, MN 55410, USA
30 Association AstroQueyras, 05350 Saint-Véran, France
31 Association des Utilisateurs de Détecteurs Électroniques (AUDE), France
32 Observatoire du Bois de Bardon, 16110 Taponnat, France
33 Dark Cosmology Centre, Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej 30, 2100 Copenhagen, Denmark
34 Nordic Optical Telescope, Apartado 474, 38700 Santa Cruz de La Palma, Santa Cruz de Tenerife, Spain
35 Hamanowa Astronomical Observatory, Hikarigaoka 4–34, Motomiya, Fukushima, Japan
36 Institute of Planetary Research, German Aerospace Center, Rutherfordstrasse 2, 12489, Berlin, Germany
37 Hunters Hill Observatory, 7 Mawalan Street, Ngunnawal ACT 2913, Australia
38 056 Skalnaté Pleso, Slovakia
39 A83 Jakokoski, Finland
40 Astrophysics Division, Institute of Physics, Jan Kochanowski University, Świętokrzyska 15, 25–406 Kielce, Poland
41 Université de Toulouse, UPS-OMP, IRAP, 31400 Toulouse, France
42 CNRS, IRAP, 14 avenue Édouard Belin, 31400 Toulouse, France
43 980 Antelope Drive West, Bennett, CO 80102, USA
44 LESIA-Observatoire de Paris, CNRS, UPMC Univ. Paris 06, Univ. Paris-Diderot, 5 place Jules Janssen, 92195 Meudon, France
45 Stazione Astronomica di Sozzago, 28060 Sozzago, Italy
46 Forte Software, Os. Jagiełły 28/28 60-694 Poznań, Poland
47 SUPA (Scottish Universities Physics Alliance), Institute for Astronomy, University of Edinburgh, Royal Observatory, Edinburgh, EH9 3HJ, UK
48 Club d’Astronomie Lyon Ampère, 37 rue Paul Cazeneuve, 69008 Lyon, France
49 174 Nyrölä, Finland
50 Observatorio Montcabre, C/Jaume Balmes 24, 08348 Cabrils, Barcelona, Spain
51 Observatori Astronómico de Mallorca, Camí de l’Observatori, s/n 07144 Costitx, Mallorca, Spain
52 Kingsgrove, NSW, Australia
53 Mt. Suhora Observatory, Pedagogical University, Podchorążych 2, 30-084, Cracow, Poland
54 University of Helsinki, Department of Physics, PO Box 64, 00014 Helsinki
55 Department of Earth, Atmospheric, and Planetary Sciences, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
56 2 rue des Écoles, 34920 Le Crès, France
57 F.-X. Bagnoud Observatory, 3961 St.-Luc, Switzerland
58 Blauvac Observatory, 84570 St.-Estéve, France
59 Observatoire de la Côte d’Azur, BP 4229, 06304 Nice Cedex 4, France
60 Observatoire de Paris-Meudon, LESIA, 92190 Meudon, France
61 143 Gnosca, Switzerland
62 DeKalb Observatory, 2507 CR 60, Auburn, IN 46706, USA
63 181 Les Makes, la Réunion, France
64 CNRS-LKB-École Normale Supérieure – UMR 8552 – 24 rue Lhomond, 75005 Paris, France
65 ANS Collaboration, c/o Osservatorio Astronomico di Padova, Sede di Asiago, 36032 Asiago (VI), Italy
66 Institute of Astronomy, Karazin Kharkiv National University, Sums’ka 35, 61022 Kharkiv, Ukraine
67 Observatoire Francois-Xavier Bagnoud, 3961 St.-Luc, Switzerland
Received: 5 November 2012
Accepted: 15 January 2013
Context. The larger number of models of asteroid shapes and their rotational states derived by the lightcurve inversion give us better insight into both the nature of individual objects and the whole asteroid population. With a larger statistical sample we can study the physical properties of asteroid populations, such as main-belt asteroids or individual asteroid families, in more detail. Shape models can also be used in combination with other types of observational data (IR, adaptive optics images, stellar occultations), e.g., to determine sizes and thermal properties.
Aims. We use all available photometric data of asteroids to derive their physical models by the lightcurve inversion method and compare the observed pole latitude distributions of all asteroids with known convex shape models with the simulated pole latitude distributions.
Methods. We used classical dense photometric lightcurves from several sources (Uppsala Asteroid Photometric Catalogue, Palomar Transient Factory survey, and from individual observers) and sparse-in-time photometry from the U.S. Naval Observatory in Flagstaff, Catalina Sky Survey, and La Palma surveys (IAU codes 689, 703, 950) in the lightcurve inversion method to determine asteroid convex models and their rotational states. We also extended a simple dynamical model for the spin evolution of asteroids used in our previous paper.
Results. We present 119 new asteroid models derived from combined dense and sparse-in-time photometry. We discuss the reliability of asteroid shape models derived only from Catalina Sky Survey data (IAU code 703) and present 20 such models. By using different values for a scaling parameter cYORP (corresponds to the magnitude of the YORP momentum) in the dynamical model for the spin evolution and by comparing synthetic and observed pole-latitude distributions, we were able to constrain the typical values of the cYORP parameter as between 0.05 and 0.6.
Key words: minor planets, asteroids: general
Table 3 is available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
The lightcurve inversion method (LI) was developed by Kaasalainen & Torppa (2001) and Kaasalainen et al. (2001). This powerful tool allows us to derive physical models of asteroids (their rotational states and the shapes) from series of disk-integrated photometry.
Convex asteroid shape models can be derived from two different types of disk-integrated photometry: dense or sparse-in-time. Originally, only dense photometry was used. About 20 such dense lightcurves from at least four or five apparitions are necessary for a unique shape determination. By this approach, ~100 asteroid models have been derived (e.g., Kaasalainen et al. 2002; Michałowski et al. 2004; Ďurech et al. 2007; Marciniak et al. 2007, 2008). To significantly enlarge the number of asteroid models, sparse photometric data were studied and used in the LI. Ďurech et al. (2009) determined 24 asteroid models from a combination of dense data with sparse photometry from the U.S. Naval Observatory in Flagstaff (USNO-Flagstaff station, IAU code 689). Sparse data from seven astrometric surveys (including USNO-Flagstaff station) were used in the LI by Hanuš et al. (2011), who presented 80 asteroid models. Sixteen models were based only on sparse data, the rest on combined dense and sparse data.
Models of asteroids derived by the lightcurve inversion method are stored in the Database of Asteroid Models from Inversion Techniques (DAMIT1, Ďurech et al. 2010). In October 2012, models of 213 asteroids were included there.
A larger number of asteroids with derived models of their convex shapes and rotational states is important for further studies. Large statistical samples of physical parameters can tell us more about processes that take place in the asteroids’ populations (near-Earth asteroids, main-belt asteroids, or asteroids in individual families). For example, an anisotropy of spin-axis directions is present in the population of main-belt asteroids with diameters ≲30 km (Hanuš et al. 2011), where the YORP effect2, together with collisions and mass shedding, is believed to be responsible. There are similar effects on the rotational states of main-belt binaries (Pravec et al. 2012). Convex shape models were also used in combination with stellar occultations by asteroids where global nonconvexities can be detected, and the diameter can be estimated with a typical uncertainty of 10% (see Ďurech et al. 2011).
In Sect. 2, we describe the dense and sparse photometric data used in the lightcurve inversion method and present new asteroid models derived from combined photometric data sets or from the sparse-in-time data from the Catalina Sky Survey Observatory (IAU code 703) alone. The reliability tests for derived models are also described. In Sect. 3, we use a theoretical model of the latitude distribution of pole directions published in Hanuš et al. (2011) in a numerical simulation to constrain the free scaling parameter cYORP describing our uncertainty in the shape and the magnitude of the YORP momentum.
2. Asteroid models
We used four main sources of dense photometric lightcurves: (i) the Uppsala Asteroid Photometric Catalogue (UAPC3, Lagerkvist et al. 1987; Piironen et al. 2001), where lightcurves for about 1000 asteroids are stored; (ii) data from a group of individual observers provided via the Minor Planet Center in the Asteroid Lightcurve Data Exchange Format (ALCDEF4, Warner et al. 2009); (iii) data from another group of individual observers available online via Courbes de rotation d’astéroïdes et de comètes (CdR5); and (iv) data from the Palomar Transient Factory survey (PTF6, Rau et al. 2009). Polishook et al. (2012) recently analyzed a small fraction of PTF data and presented dense lightcurves for 624 asteroids. So far, only a fraction of photometric data from the PTF has been processed (four overlapping fields on four consecutive nights), which means that this source will become very important in the near future.
We downloaded sparse data from the AstDyS site (Asteroids – Dynamic Site7) and gathered sparse lightcurves from the USNO-Flagstaff station (IAU code 689) for ~1000 asteroids, from Roque de los Muchachos Observatory, La Palma (IAU code 950) for ~500 asteroids and ≳100 sparse data points from the Catalina Sky Survey Observatory (CSS for short, IAU code 703, Larson et al. 2003) for ~4000 asteroids. We present 119 asteroid models derived from combined dense and sparse data (Sect. 2.2) and 20 models based only on CSS data (Sect. 2.3).
During the model computation, a priori information about the rotational period of the asteroid was used, which significantly reduced the volume of the multidimensional parameter space that had to be searched, and saved computational time. Period values were taken from the regularly updated Minor Planet Lightcurve Database8 (Warner et al. 2009). If the period was unknown or insecure, we searched the model over all possible period values of 2–100 h (usually, when only sparse data are available).
2.1. Reliability tests
We carefully tested the reliability of derived models. If we had several dense lightcurves and sparse data from USNO-Flagstaff station for an asteroid, we considered a model as unique if: (i) the modeled sidereal rotational period was close to the synodic rotational period determined from a single apparition dense data set (synodic period values have usually been previously published and were available in the Minor Planet Lightcurve Database); (ii) the shape model rotated close to its axis with a maximum momentum of inertia (it was in a relaxed rotational state); and (iii) models with half and double period values gave significantly worse fits.
It was necessary to apply additional tests to models derived from sparse-in-time data alone. We used the tests presented in Hanuš et al. (2011, for more details, see Sect. 3.3 there), and they were sufficient if photometry from USNO-Flagstaff station was present. In Hanuš & Ďurech (2012), we have shown that reliable asteroid models can also be derived from the Catalina Sky Survey data alone, and we described a convenient procedure for how to proceed during the computation when the rotational period is unknown: the solution should be searched for all periods in an interval of 2–100 h, and the stability of the solution should be tested for at least two different shape parametrizations9. The correct solution had to be stable for both low (n = 3) and high (n = 6) shape resolutions. We followed these recommendations: we searched for the model in the multidimensional parameter space for shape resolutions n = 3 and n = 6 and checked that we derived solutions with similar rotational states. In Hanuš & Ďurech (2012), we tested values n = 2,3,4,5,6 for the shape resolution. Correct solutions (i.e., models from the CSS data were similar to the models based on different data sets) were reproduced for most values of n. On the other hand, incorrect solutions were derived only for values n = 6 and sometimes also for n = 4 or n = 5, but never for n = 2 or n = 3.
2.2. Models from combined dense and sparse data
The shape model determination scheme was very similar to the one used in Hanuš et al. (2011). 119 new asteroid models were derived because we gathered ~1000 new dense lightcurves from ALCDEF, another ~1000 lightcurves from PTF, ~300 from individual observers, and also additional sparse data observed by the CSS during the second half of the year 2010 and the first half of the year 2011. Derived rotational states with basic information about the photometry used for 119 asteroids are listed in Table 1. Out of them, 18 models are based only on combined sparse data from various sources, but in all cases, sparse data from USNO-Flagstaff station were present10. In Table 3, we list the references to the dense lightcurves we used for the new model determination.
Although the amount of photometric data from PTF was similar to that from ALCDEF, only two new shape models (for asteroids with numbers 52 820 and 57 394, see Table 1) were derived with their contribution. The first reason was a significantly worse quality of PTF data: only for 84 asteroids out of 624 were the data sufficient for determining a synodic period, while other lightcurves were noisy or burdened with systematic errors. In many cases they allowed only for an estimate of a lower limit for the lightcurve amplitude (presented in Polishook et al. 2012). The second reason was that PTF data alone were not sufficient for a unique model determination (they covered only one apparition), no other dense lightcurves were usually available, and sparse data were available for only fewer than a half of these asteroids. Many asteroids detected by the PTF survey were previously unknown.
There are previously published models available for 15 of the asteroids modeled here: (11) Parthenope, (79) Eurynome, (272) Antonia, (281) Lucretia, (351) Yrsa, (352) Gisela, (390) Alma, (787) Moskva, (852) Wladilena, (1089) Tama, (1188) Gothlandia, (1389) Onnie, (1572) Posnania, (1719) Jens, and (4954) Eric (see databases by Kryszczyńska et al. 2007; and Warner et al. 2009). As these models were usually based on limited datasets, our solutions differ from some of them substantially, while agreeing for some in the spin axis latitude or the sidereal period value. We fully confirmed previous models for six objects of that sample: the spin models of (79) Eurynome by Michałowski (1996), (787) Moskva by Svoren et al. (2009), and (1572) Posnania by Michałowski et al. (2001), as well as our preliminary solutions for (390) Alma, (1389) Onnie, and (1719) Jens obtained in Hanuš et al. (2011).
The shape models and their spin solutions can be found in the DAMIT database (Ďurech et al. 2010). We noticed that for the models based only on sparse data, their shapes tend to be very angular, with sharp edges and large planar areas, thus can be treated only as crude approximations of the real asteroid shapes. However, a substantial addition (≳10 lightcurves from ≳2 apparitions) of dense lightcurves smooths the shape models out, making them look more realistic, as confirmed by their better fit to occultation chords.
From observations of star occultations by asteroids, we can reconstruct asteroid projected silhouettes. These silhouettes can then be compared with the predicted contours of the convex shape models and used for the asteroid size determination by scaling the shape models to fit the occultation chords. A reasonable number of observations were available for three asteroids from our sample. By using the same methods as in Ďurech et al. (2011), we rejected mirror solutions for the asteroids (345) Tercidina and (578) Happelia, and also determined equivalent diameters (corresponding to spheres with the same volume as the scaled convex shape models): 96 ± 10 km for (345) Tercidina, 101 ± 5 km for (404) Arsinoe, and 70 ± 5 km for (578) Happelia. Two different stellar occultations are available for all three asteroids, and are plotted in Figs. 1–3.
During the apparition in 2004, the lightcurves of asteroid (1089) Tama have shown features typical of close binary systems (Behrend et al. 2004) and indeed, the system was later interpreted as a synchronous close binary (Behrend et al. 2006). Our brick-like convex shape model is strongly elongated with sharp edges and is similar to a convex shape model of a close binary system (90) Antiope. Such a shape appearance for close binaries was predicted from synthetic data (Ďurech & Kaasalainen 2003).
List of new asteroid models derived from combined dense and sparse data or from sparse data alone.
List of new asteroid models derived from the Catalina Sky Survey data alone.
 |
Fig. 1 Two observations of star occultations by asteroid (345) Tercidina. The solid contour corresponds to a scaled projected silhouette of the shape model with the pole (346°, −55°), each chord represents one occultation observation (solid lines are CCD, video, or photoelectric observations; dashed lines are visual observations, and dotted lines negative observations). Each plot also contains the time scale (lower left corner), the latitude of the sub-Earth point θ for the time of occultation (upper left corner), and the direction of the relative velocity (the arrow in the upper right corner). East points to the left and north up. |
 |
Fig. 2 Two observations of star occultations by asteroid (404) Arsinoe. The solid contour corresponds to a scaled projected silhouette of the shape model with the pole (25°,57°). See Fig. 1 for line types and symbols explanation. |
 |
Fig. 3 Two observations of star occultations by asteroid (578) Happelia. The solid contour corresponds to a scaled projected silhouette of the shape model with the pole (339°,62°). See Fig. 1 for line types and symbols explanation. |
2.3. Models based on data from the Catalina Sky Survey astrometric project
There are two different groups of asteroid models based on CSS data: (i) models with previously reported synodic periods determined from dense data (we did not have these dense data, so period values were taken from the literature, usually from the Minor Planet Lightcurve Database); and (ii) models with previously unknown rotational periods. In the first case, we could compare the published period value with the period value derived by the LI (see Table 2, Cols. 7 and 9). If both periods agreed within their uncertainties, we considered the solution reliable. This test could not be performed for the second group of models, so we had to use additional reliability tests (see Sect. 2.1).
In Table 2, we present 20 asteroid models based only on the CSS data. The previous period estimates were not available for 12 of them. All of these 20 models have higher uncertainties of the pole orientations and lower shape resolution than models based on combined data, and all are possible candidates for follow-up lightcurve observations for period confirmation and more detailed shape determination.
3. Semi-empirical scaling of the YORP effect
Our enlarged sample of physical parameters for ~330 asteroids11 validates our previous results based on a smaller asteroid sample (220 asteroids) presented in Hanuš et al. (2011). In Fig. 4, we show the observed debiased (i.e., we removed the systematic effect of the lightcurve inversion method caused by the method having a higher probability of deriving a unique solution for asteroids with larger pole latitudes. The debiasing procedure was based on a numerical simulation presented in Hanuš et al. 2011, see Sect. 4.3 there) latitude distributions of pole directions for main-belt asteroids with diameters D < 30 km and D > 60 km. The population of larger asteroids (D > 60 km) exhibits an excess of prograde rotators, probably of primordial origin (predicted also from numerical simulations by Johansen & Lacerda 2010). On the other hand, smaller asteroids (D < 30 km) have a clearly bimodal latitude distribution – most of the asteroids have ecliptic pole latitudes > 53°.
The debiased observed latitude distribution of the pole directions of MBAs represents fingerprints from the past evolution of this population. Direct comparison between the observed asteroid properties and predictions of theoretical models can validate/exclude some of the asteroid dynamical evolution theories or constrain specific free parameters.
 |
Fig. 4 Debiased observed latitude distribution of main-belt asteroids with diameters D > 60 km (left panel) and D < 30 km (right panel). The latitude bins are equidistant in sin β. The thin horizontal line corresponds to the average value |
In Hanuš et al. (2011), we introduced a simple dynamical model for the spin evolution of asteroids, where we included (i) the YORP thermal effect; (ii) random reorientations induced by noncatastrophic collisions; (iii) oscillations caused by gravitational torques and spin-orbital resonances; and also (iv) mass shedding when a critical rotational frequency is reached. Because we studied a large statistical sample of asteroids, the effect on the overall latitude distribution of pole directions caused by other processes (gravitational torques by the Sun, damping, or tumbling) was assumed to be only minor.
The model was based on the relations for the rate of the angular velocity ω (ω = 2π/P) and the obliquity ϵ (Euler equations) 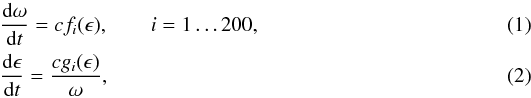 where f- and g-functions describing the YORP effect for a set of 200 shapes with the effective radius R0 = 1 km, the bulk density ρ0 = 2500 kg/m3, located on a circular orbit with the semi-major axis a0 = 2.5 AU, were calculated numerically by Čapek & Vokrouhlický (2004). We assigned one of the artificial shapes (denoted by the index i) for each individual asteroid from our sample12. The f- and g-functions were scaled by a factor
where f- and g-functions describing the YORP effect for a set of 200 shapes with the effective radius R0 = 1 km, the bulk density ρ0 = 2500 kg/m3, located on a circular orbit with the semi-major axis a0 = 2.5 AU, were calculated numerically by Čapek & Vokrouhlický (2004). We assigned one of the artificial shapes (denoted by the index i) for each individual asteroid from our sample12. The f- and g-functions were scaled by a factor  (3)where a, R, ρbulk denote the semi-major axis, the radius, and the density of the simulated body, respectively, and cYORP is a free scaling parameter reflecting our uncertainty in the shape models and the magnitude of the YORP torque, which dependents on small-sized surface features (even boulders, Statler 2009) and other simplifications in the modeling of the YORP torque.
(3)where a, R, ρbulk denote the semi-major axis, the radius, and the density of the simulated body, respectively, and cYORP is a free scaling parameter reflecting our uncertainty in the shape models and the magnitude of the YORP torque, which dependents on small-sized surface features (even boulders, Statler 2009) and other simplifications in the modeling of the YORP torque.
We enhanced the simulation of the spin evolution of asteroids presented in Hanuš et al. (2011), by testing different values of the free parameter cYORP and comparing the resulting synthetic latitude distributions with the observed debiased latitude distributions. Thanks to the new asteroid models, we had an updated observed spin vector distribution. We added 50% more observed asteroids, so we used 307 instead of 220 models for this comparison.
We used the following values of the parameter cYORP: 0.01, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.8. Values of cYORP ≳ 1 were already recognized as unrealistic.
For each value of cYORP, we ran 100 simulations with different random seeds to generate different initial ω and spin vector distributions. We integrated Eqs. (1) and (2) numerically. The time span was 4 Gyr with the time step of the explicit Euler scheme Δt = 10 Myr. As initial conditions, we assumed a Maxwellian distribution of angular velocities ω and isotropically distributed spin vectors. We also used K = 10-2 W/K/m, ρbulk = 2500 kg/m3.
Every time a critical angular velocity (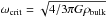 ) was reached for an asteroid, we assumed a mass shedding event, so that we reset the rotational period to a random value from an interval of 2.5, 9 h. We altered the assigned shape, but we kept the sense of the rotation and the orientation of the spin axis. We also included a simple Monte-Carlo model for the spin axis reorientations caused by collisions (with
) was reached for an asteroid, we assumed a mass shedding event, so that we reset the rotational period to a random value from an interval of 2.5, 9 h. We altered the assigned shape, but we kept the sense of the rotation and the orientation of the spin axis. We also included a simple Monte-Carlo model for the spin axis reorientations caused by collisions (with 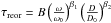 , where B = 84.5 kyr, β1 = 5/6, β2 = 4/3, D0 = 2 m, and ω0 corresponds to period P = 5 h, Farinella et al. 1998). After the collision, we reset the spin axis and period to random values (new period was from an interval of 2.5, 9 h). Collisional disruptions are not important in our case so they were not considered. We also accounted for spin-orbital resonances by adding a sinusoidal oscillation to β (to prograde rotators, only, Vokrouhlický et al. 2006b) with a random phase and an amplitude ≃ 40°.
, where B = 84.5 kyr, β1 = 5/6, β2 = 4/3, D0 = 2 m, and ω0 corresponds to period P = 5 h, Farinella et al. 1998). After the collision, we reset the spin axis and period to random values (new period was from an interval of 2.5, 9 h). Collisional disruptions are not important in our case so they were not considered. We also accounted for spin-orbital resonances by adding a sinusoidal oscillation to β (to prograde rotators, only, Vokrouhlický et al. 2006b) with a random phase and an amplitude ≃ 40°.
The spin states of our synthetic asteroids evolve during the simulation. At each time t of the simulation, we can construct a latitude distribution of the pole directions with the latitude values split into ten bins with a variable width corresponding to constant surface on the celestial sphere. Because we used ecliptic coordinates with the longitude λ and the latitude β, the bins were equidistant in sin β. To describe the temporal evolution of the simulated latitude distributions, we computed a χ2 metric between the simulated and the debiased observed latitude distributions of asteroids with diameters D < 60 km. The assumption of isotropically distributed initial spin vectors is not fulfilled for larger asteroids (D > 60 km), because this population has an excess of prograde rotators (see Fig. 4), which is believed to have a primordial origin (Johansen & Lacerda 2010). The second reason we rejected asteroids with D > 60 km from latitude comparison is that their evolution is rather slow compared to the simulation time span.
For each time t within the simulation run j (j = 1...100), the corresponding chi-square value 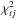 is defined by
is defined by 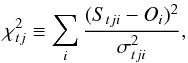 (4)where Stji denotes the number of synthetic bodies with latitudes in bin i, Oi the number of observed latitudes in bin i, and
(4)where Stji denotes the number of synthetic bodies with latitudes in bin i, Oi the number of observed latitudes in bin i, and 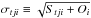 corresponds to the uncertainty estimate.
corresponds to the uncertainty estimate.
 |
Fig. 5 Temporal evolution of the χ2 that corresponds to the difference between the simulated latitude distributions, averaged over all 100 runs, and the debiased observed latitude distribution (i.e., |
In Fig. 5, we show the temporal evolution of the average chi-square 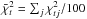 in the course of our numerical simulations for different cYORP values. As we see in Fig. 5, the average synthetic latitude distribution evolves in course of the time (while the debiased observed latitude distribution is fixed). We can distinguish three basic cases of the temporal evolution:
in the course of our numerical simulations for different cYORP values. As we see in Fig. 5, the average synthetic latitude distribution evolves in course of the time (while the debiased observed latitude distribution is fixed). We can distinguish three basic cases of the temporal evolution:
-
When the YORP effect is weak(cYORP ≲ 0.1), the synthetic latitude distribution only evolves slowly and is never similar to the observed latitude distribution, even at the end of the simulation, because
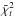 is still large (for N = 9, a statistically significant probability value of 5% corresponds to χ2 = 16.92).
is still large (for N = 9, a statistically significant probability value of 5% corresponds to χ2 = 16.92). -
A steady state (i.e., the state when the synthetic latitude distribution does not significantly evolve in time, and thus the
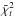 is approximately constant) is only reached for cYORP values close to 0.2.
is approximately constant) is only reached for cYORP values close to 0.2. -
For values cYORP ≳ 0.3, the synthetic latitude distribution evolves faster and, at a certain time, is most similar to the observed latitude distribution (i.e., the minimum of
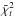 ). After that, the
). After that, the 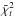 grows, because the YORP significantly develops also larger asteroids, and thus the bins with low latitudes are depopulated more than is observed.
grows, because the YORP significantly develops also larger asteroids, and thus the bins with low latitudes are depopulated more than is observed.
Vertical histograms on the righthand side of Fig. 5 represent the distributions of 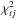 at the time t = 4 Gy for all 100 runs. The average chi-square
at the time t = 4 Gy for all 100 runs. The average chi-square 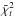 of the model with cYORP = 0.05 is substantially higher than 16.92, so this model can be considered wrong. However, from the distributions of
of the model with cYORP = 0.05 is substantially higher than 16.92, so this model can be considered wrong. However, from the distributions of 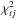 we can see that about 25% of individual runs have
we can see that about 25% of individual runs have 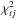 lower than 16.92. To avoid rejecting those cYORP values that are partially compatible with the observations, we should instead use a more representative value of χ2 than the average
lower than 16.92. To avoid rejecting those cYORP values that are partially compatible with the observations, we should instead use a more representative value of χ2 than the average 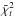 , namely a value
, namely a value  , for which 10% runs have lower
, for which 10% runs have lower 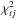 (see Fig. 6). Based on the
(see Fig. 6). Based on the  , the most probable values of the cYORP parameter are between 0.05 and 0.6.
, the most probable values of the cYORP parameter are between 0.05 and 0.6.
 |
Fig. 6 Dependence of |
4. Discusion and conclusions
Our preferred interpretation of the optimal cYORP value being much lower than one is that small-scale features (boulders) tend to decrease the YORP torque. This hypothesis is supported by the independent modeling of Rozitis & Green (2012), who estimate, by including rough surface thermal-infrared beaming effects in their long-term spin evolution model, that the surface roughness is on average responsible for damping the magnitude of the YORP effect typically by half of the smooth surface predictions. This would correspond to cYORP = 0.5 in our notation. The YORP effect is sensitive to the sizes of the boulders and can vary tens of percent, so the results of Rozitis & Green (2012) agree with our model.
As an important application, we mention that the constraint for the value of cYORP can be used in simulations of the long-term dynamical evolution of asteroid families. So far, cYORP has been used as a free parameter (e.g., in the method presented by Vokrouhlický et al. 2006a). Constraining cYORP therefore removes one free parameter from the simulations and should thus lead to a better determination of the ages of asteroid families.
Finally, the results of this paper can be briefly summarized as follows.
-
For 119 asteroids, we derived the convex shape models androtational states from their combined disk-integrated dense andsparse photometric data. This effort was achieved with the help of ~100 individual observers who were willing to share their lightcurves. The typical uncertainty of the sidereal rotational period is ~10-5 h and of the pole direction 10–20°. All new models are now included in the DAMIT database.
-
We also derived 20 asteroid models based purely on sparse-in-time photometry from the Catalina Sky Survey Observatory. The reliability of these models is supported by the fact that for eight of them, we obtained similar rotational period values that were previously reported in the literature and derived from an independent data set (dense photometry). We do not have any previous information about the rotational periods for the 12 other asteroids. Due to relatively larger uncertainties of the CSS sparse data, the typical uncertainty of the sidereal rotational period is ~10-4−10-5 h and of the pole direction 20–40°.
-
By combining observations of stellar occultations by asteroids with derived convex shape models, we determined equivalent diameters for the asteroids (345) Tercidina, (404) Arcinoe, and (578) Happelia to 96 ± 10 km, 101 ± 5 km, and 70 ± 5 km, respectively.
-
We updated a simple dynamical model for the spin evolution of asteroids and compared the synthetic pole latitude distributions to the debiased observed latitude distributions of 307 asteroids. By using several values of the scaling parameter cYORP defined by Eq. (3) (from 0.01 to 0.8), we constrained its value to cYORP ∈ [0.05,0.6]. We interpreted the low value of cYORP as a result of the surface roughness.
Online material
Observations used for the successful model determinations that are not included in the UAPC.
Yarkovsky–O’Keefe–Radzievskii–Paddack effect, a torque caused by the recoil force from anisotropic thermal emission, which can alter the rotational periods and orientation of spin axes, see e.g., Rubincam (2000), Vokrouhlický et al. (2003).
Models based only on data from the Catalina Sky Survey are described later in Sect. 2.3.
According to the asteroid size distribution function of Davis et al. (2002), we have in our sample ~30% of all asteroids with D > 100 km, ~15% asteroids with 60 km < D < 100 km, and ~14% asteroids with 30 km < D < 60 km.
We did not use the convex-hull shape models derived in this work because the two samples of shapes are believed to be statistically equivalent, and moreover, the YORP effect seems sensitive to small-scale surface structure (Scheeres & Mirrahimi 2007), which cannot be caught by our shape models.
Acknowledgments
The work of JH has been supported by grant GA UK 134710 of the Grant agency of the Charles University and by the project SVV 265301 of the Charles University in Prague. The work of J.H. and J.Ď. has been supported by grants GACR 209/10/0537 and P209/12/0229 of the Czech Science Foundation, the work of J.D. and M.B. by the Research Program MSM0021620860 of the Czech Ministry of Education, and the work of MB also by the grant GACR 13-01308S of the Grant Agency of the Czech Republic. The work of TSR was carried out through the Gaia Research for European Astronomy Training (GREAT-ITN) network. He has received funding from the European Union Seventh Framework Program (FP7/2007-2013) under grant agreement no. 264895. This work is partially based on observations made at the South African Astronomical Observatory (SAAO). It was based on observations made with the Nordic Optical Telescope, operated on the island of La Palma jointly by Denmark, Finland, Iceland, Norway, and Sweden, in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofisica de Canarias. This work is partially based on observations carried out with the Pic du Midi Observatory 0.6 m telescope, a facility operated by the Observatoire Midi-Pyrénées and Association T60, an amateur association. The calculations were performed on the computational cluster Tiger at the Astronomical Institute of Charles University in Prague (http://sirrah.troja.mff.cuni.cz/tiger).
References
- Baker, R. E., Pilcher, F., & Klinglesmith III, D. A. 2012, Minor Planet Bulletin, 39, 60 [NASA ADS] [Google Scholar]
- Behrend, R., Roy, R., Rinner, C., et al. 2004, IAU Circ., 8265, 2 [NASA ADS] [Google Scholar]
- Behrend, R., Bernasconi, L., Roy, R., et al. 2006, A&A, 446, 1177 [Google Scholar]
- Bembrick, C., & Bolt, G. 2003, Minor Planet Bulletin, 30, 42 [NASA ADS] [Google Scholar]
- Bembrick, C., Crawford, G., Oey, J., & Allen, B. 2007, Minor Planet Bulletin, 34, 67 [NASA ADS] [Google Scholar]
- Brinsfield, J. W. 2008a, Minor Planet Bulletin, 35, 179 [NASA ADS] [Google Scholar]
- Brinsfield, J. W. 2008b, Minor Planet Bulletin, 35, 86 [NASA ADS] [Google Scholar]
- Brinsfield, J. W. 2009, Minor Planet Bulletin, 36, 169 [NASA ADS] [Google Scholar]
- Buchheim, R. K. 2005, Minor Planet Bulletin, 32, 35 [NASA ADS] [Google Scholar]
- Buchheim, R. K. 2007, Minor Planet Bulletin, 34, 68 [Google Scholar]
- Buchheim, R. K. 2010, Minor Planet Bulletin, 37, 41 [Google Scholar]
- Buchheim, R. K., Conjat, M., Roy, R., Baudoin, P., & Behrend, R. 2004, Minor Planet Bulletin, 31, 90 [NASA ADS] [Google Scholar]
- Čapek, D., & Vokrouhlický, D. 2004, Icarus, 172, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Carbo, L., Kragh, K., Krotz, J., et al. 2009, Minor Planet Bulletin, 36, 91 [NASA ADS] [Google Scholar]
- Davis, D. R., Durda, D. D., Marzari, F., Campo Bagatin, A., & Gil-Hutton, R. 2002, Asteroids III, 545 [Google Scholar]
- Ditteon, R., Bixby, A. R., Sarros, A. M., & Waters, C. T. 2002, Minor Planet Bulletin, 29, 69 [NASA ADS] [Google Scholar]
- Ďurech, J., & Kaasalainen, M. 2003, A&A, 404, 709 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ďurech, J., Scheirich, P., Kaasalainen, M., et al. 2007, in IAU Symp., 236, eds. G. B. Valsecchi, D. Vokrouhlický, & A. Milani, 191 [Google Scholar]
- Ďurech, J., Kaasalainen, M., Warner, B. D., et al. 2009, A&A, 493, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ďurech, J., Sidorin, V., & Kaasalainen, M. 2010, A&A, 513, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ďurech, J., Kaasalainen, M., Herald, D., et al. 2011, Icarus, 214, 652 [NASA ADS] [CrossRef] [Google Scholar]
- Farinella, P., Vokrouhlicky, D., & Hartmann, W. K. 1998, Icarus, 132, 378 [NASA ADS] [CrossRef] [Google Scholar]
- Galad, A. 2008, Minor Planet Bulletin, 35, 128 [NASA ADS] [Google Scholar]
- Hanuš, J., & Ďurech, J. 2012, Planet. Space Sci., 73, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Hanuš, J., Ďurech, J., Brož, M., et al. 2011, A&A, 530, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Higgins, D. 2008, Minor Planet Bulletin, 35, 30 [NASA ADS] [Google Scholar]
- Higgins, D., & Goncalves, R. M. D. 2007, Minor Planet Bulletin, 34, 16 [NASA ADS] [Google Scholar]
- Higgins, D., & Warner, B. D. 2009, Minor Planet Bulletin, 36, 159 [NASA ADS] [Google Scholar]
- Higgins, D., Pravec, P., Kusnirak, P., et al. 2006, Minor Planet Bulletin, 33, 89 [NASA ADS] [Google Scholar]
- Higgins, D., Pravec, P., Kusnirak, P., et al. 2008, Minor Planet Bulletin, 35, 123 [NASA ADS] [Google Scholar]
- Johansen, A., & Lacerda, P. 2010, MNRAS, 404, 475 [NASA ADS] [Google Scholar]
- Kaasalainen, M., & Torppa, J. 2001, Icarus, 153, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., Torppa, J., & Muinonen, K. 2001, Icarus, 153, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., Torppa, J., & Piironen, J. 2002, Icarus, 159, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Koff, R. A., & Brincat, S. M. 2000, Minor Planet Bulletin, 27, 49 [NASA ADS] [Google Scholar]
- Kryszczyńska, A., La Spina, A., Paolicchi, P., et al. 2007, Icarus, 192, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Lagerkvist, C., Barucci, M. A., Capria, M. T., et al. 1987, Asteroid photometric catalogue, eds. C.-I. Lagerkvist, M. A. Barucci, M. T. Capria, et al. [Google Scholar]
- Larson, S., Beshore, E., Hill, R., et al. 2003, in BAAS, 35, AAS/Division for Planetary Sciences Meeting Abstracts #35, 982 [Google Scholar]
- López-González, M. J., & Rodríguez, E. 2000, A&AS, 145, 255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maleszewski, C., & Clark, M. 2004, Minor Planet Bulletin, 31, 93 [NASA ADS] [Google Scholar]
- Marciniak, A., Michałowski, T., Kaasalainen, M., et al. 2007, A&A, 473, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marciniak, A., Michałowski, T., Kaasalainen, M., et al. 2008, A&A, 478, 559 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michałowski, T. 1996, Icarus, 123, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Michałowski, T., Pych, W., Kwiatkowski, T., et al. 2001, A&A, 371, 748 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michałowski, T., Kwiatkowski, T., Kaasalainen, M., et al. 2004, A&A, 416, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molnar, L. A., Haegert, J. M., Beaumont, C. N., et al. 2008, Minor Planet Bulletin, 35, 9 [NASA ADS] [Google Scholar]
- Oey, J. 2008, Minor Planet Bulletin, 35, 132 [NASA ADS] [Google Scholar]
- Oey, J. 2009, Minor Planet Bulletin, 36, 4 [NASA ADS] [Google Scholar]
- Oey, J., & Krajewski, R. 2008, Minor Planet Bulletin, 35, 47 [NASA ADS] [Google Scholar]
- Oey, J., Behrend, R., Pravec, P., et al. 2007, Minor Planet Bulletin, 34, 2 [NASA ADS] [Google Scholar]
- Piironen, J., Lagerkvist, C., Torppa, J., Kaasalainen, M., & Warner, B. 2001, in BAAS, 33, 1562 [Google Scholar]
- Pilcher, F. 2008, Minor Planet Bulletin, 35, 135 [NASA ADS] [Google Scholar]
- Pilcher, F. 2009a, Minor Planet Bulletin, 36, 133 [Google Scholar]
- Pilcher, F. 2009b, Minor Planet Bulletin, 36, 25 [NASA ADS] [Google Scholar]
- Pilcher, F. 2009c, Minor Planet Bulletin, 36, 100 [NASA ADS] [Google Scholar]
- Pilcher, F. 2010, Minor Planet Bulletin, 37, 119 [NASA ADS] [Google Scholar]
- Pilcher, F. 2011a, Minor Planet Bulletin, 38, 183 [NASA ADS] [Google Scholar]
- Pilcher, F. 2011b, Minor Planet Bulletin, 38, 76 [NASA ADS] [Google Scholar]
- Pilcher, F., & Brinsfield, J. W. 2011, Minor Planet Bulletin, 38, 206 [NASA ADS] [Google Scholar]
- Pilcher, F., Benishek, V., & Oey, J. 2009, Minor Planet Bulletin, 36, 68 [NASA ADS] [Google Scholar]
- Polishook, D. 2012, Minor Planet Bulletin, 39, 242 [NASA ADS] [Google Scholar]
- Polishook, D., & Brosch, N. 2008, Icarus, 194, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Polishook, D., & Brosch, N. 2009, Icarus, 199, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Polishook, D., Ofek, E. O., Waszczak, A., et al. 2012, MNRAS, 421, 2094 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Scheirich, P., Vokrouhlický, D., et al. 2012, Icarus, 218, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Rau, A., Kulkarni, S. R., Law, N. M., et al. 2009, PASP, 121, 1334 [NASA ADS] [CrossRef] [Google Scholar]
- Rozitis, B., & Green, S. F. 2012, MNRAS, 423, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Rubincam, D. P. 2000, Icarus, 148, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Ruthroff, J. C. 2010, Minor Planet Bulletin, 37, 102 [NASA ADS] [Google Scholar]
- Scheeres, D. J., & Mirrahimi, S. 2007, in BAAS, 38, 416 [Google Scholar]
- Statler, T. S. 2009, Icarus, 202, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Stephens, R. D. 2005a, Minor Planet Bulletin, 32, 82 [NASA ADS] [Google Scholar]
- Stephens, R. D. 2005b, Minor Planet Bulletin, 32, 2 [NASA ADS] [Google Scholar]
- Stephens, R. D. 2008, Minor Planet Bulletin, 35, 126 [NASA ADS] [Google Scholar]
- Stephens, R. D. 2009a, Minor Planet Bulletin, 36, 59 [NASA ADS] [Google Scholar]
- Stephens, R. D. 2009b, Minor Planet Bulletin, 36, 18 [NASA ADS] [Google Scholar]
- Svoren, J., Husarik, M., Ambroz, J., Drbohlav, J., & Medek, J. 2009, Earth Moon and Planets, 105, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., Brož, M., Morbidelli, A., et al. 2006a, Icarus, 182, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., Nesvorný, D., & Bottke, W. F. 2003, Nature, 425, 147 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Vokrouhlický, D., Nesvorný, D., & Bottke, W. F. 2006b, Icarus, 184, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B. D. 2004, Minor Planet Bulletin, 31, 85 [NASA ADS] [Google Scholar]
- Warner, B. D. 2005a, Minor Planet Bulletin, 32, 90 [NASA ADS] [Google Scholar]
- Warner, B. D. 2005b, Minor Planet Bulletin, 32, 4 [NASA ADS] [Google Scholar]
- Warner, B. D. 2006a, Minor Planet Bulletin, 33, 58 [NASA ADS] [Google Scholar]
- Warner, B. D. 2006b, Minor Planet Bulletin, 33, 35 [NASA ADS] [Google Scholar]
- Warner, B. D. 2007, Minor Planet Bulletin, 34, 72 [NASA ADS] [Google Scholar]
- Warner, B. D. 2008a, Minor Planet Bulletin, 35, 56 [NASA ADS] [Google Scholar]
- Warner, B. D. 2008b, Minor Planet Bulletin, 35, 163 [NASA ADS] [Google Scholar]
- Warner, B. D. 2009a, Minor Planet Bulletin, 36, 109 [NASA ADS] [Google Scholar]
- Warner, B. D. 2009b, Minor Planet Bulletin, 36, 172 [NASA ADS] [Google Scholar]
- Warner, B. D. 2011a, Minor Planet Bulletin, 38, 52 [NASA ADS] [Google Scholar]
- Warner, B. D. 2011b, Minor Planet Bulletin, 38, 63 [NASA ADS] [Google Scholar]
- Warner, B. D. 2011c, Minor Planet Bulletin, 38, 96 [NASA ADS] [Google Scholar]
- Warner, B. D., Harris, A. W., & Pravec, P. 2009, Icarus, 202, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Yeung, K. W. 2006, Minor Planet Bulletin, 33, 49 [NASA ADS] [Google Scholar]
- Yoshida, F., Dermawan, B., Nakamura, T., et al. 2005, Abstr. IAU Symp., 229, 82 [Google Scholar]
All Tables
List of new asteroid models derived from combined dense and sparse data or from sparse data alone.
Observations used for the successful model determinations that are not included in the UAPC.
All Figures
 |
Fig. 1 Two observations of star occultations by asteroid (345) Tercidina. The solid contour corresponds to a scaled projected silhouette of the shape model with the pole (346°, −55°), each chord represents one occultation observation (solid lines are CCD, video, or photoelectric observations; dashed lines are visual observations, and dotted lines negative observations). Each plot also contains the time scale (lower left corner), the latitude of the sub-Earth point θ for the time of occultation (upper left corner), and the direction of the relative velocity (the arrow in the upper right corner). East points to the left and north up. |
| In the text | |
 |
Fig. 2 Two observations of star occultations by asteroid (404) Arsinoe. The solid contour corresponds to a scaled projected silhouette of the shape model with the pole (25°,57°). See Fig. 1 for line types and symbols explanation. |
| In the text | |
 |
Fig. 3 Two observations of star occultations by asteroid (578) Happelia. The solid contour corresponds to a scaled projected silhouette of the shape model with the pole (339°,62°). See Fig. 1 for line types and symbols explanation. |
| In the text | |
 |
Fig. 4 Debiased observed latitude distribution of main-belt asteroids with diameters D > 60 km (left panel) and D < 30 km (right panel). The latitude bins are equidistant in sin β. The thin horizontal line corresponds to the average value |
| In the text | |
 |
Fig. 5 Temporal evolution of the χ2 that corresponds to the difference between the simulated latitude distributions, averaged over all 100 runs, and the debiased observed latitude distribution (i.e., |
| In the text | |
 |
Fig. 6 Dependence of |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.