| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A36 | |
| Number of page(s) | 17 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201220574 | |
| Published online | 15 February 2013 | |
Metallicity of M dwarfs
III. Planet-metallicity and planet-stellar mass correlations of the HARPS GTO M dwarf sample⋆,⋆⋆
1
Centro de Astrofísica, Universidade do Porto,
Rua das Estrelas,
4150-762
Porto,
Portugal
e-mail: vasco.neves@astro.ua.pt
2
UJF-Grenoble 1/CNRS-INSU, Institut de Planétologie et
d’Astrophysique de Grenoble (IPAG) UMR 5274, 38041
Grenoble,
France
3
Departamento de Física e Astronomia, Faculdade de Ciências,
Universidade do Porto, Rua do Campo
Alegre, 4169-007
Porto,
Portugal
4
Centre de Recherche Astrophysique de Lyon, UMR 5574: CNRS,
Université de Lyon, École Normale
Supérieure de Lyon, 46 allée d’Italie, 69364
Lyon Cedex 07,
France
5
Observatoire de Genève, Université de Genève,
51 chemin des
Maillettes, 1290
Sauverny,
Switzerland
Received: 15 October 2012
Accepted: 13 December 2012
Aims. The aim of this work is the study of the planet-metallicity and the planet-stellar mass correlations for M dwarfs from the HARPS GTO M dwarf subsample.
Methods. We use a new method that takes advantage of the HARPS high-resolution spectra to increase the precision of metallicity, using previous photometric calibrations of [Fe/H] and effective temperature as starting values.
Results. In this work we use our new calibration (rms = 0.08 dex) to study the planet-metallicity relation of our sample. The well-known correlation for giant planet FGKM hosts with metallicity is present. Regarding Neptunians and smaller hosts no correlation is found but there is a hint that an anti-correlation with [Fe/H] may exist. We combined our sample with the California Planet Survey late-K and M-type dwarf sample to increase our statistics but found no new trends.
We fitted a power law to the frequency histogram of the Jovian hosts for our sample and for the combined sample, fp = C10α [Fe/H] , using two different approaches: a direct bin fitting and a Bayesian fitting procedure. We obtained a value for C between 0.02 and 0.04 and for α between 1.26 and 2.94.
Regarding stellar mass, an hypothetical correlation with planets was discovered, but was found to be the result of a detection bias.
Key words: stars: fundamental parameters / stars: late-type / stars: low-mass / stars: atmospheres / planetary systems
Based on observations made with the HARPS instrument on the ESO 3.6-m telescope at La Silla Observatory under programme ID 072.C-0488.
Tables 2, 8, and Appendix A are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Stellar mass and metallicity are two important observables directly connected to the formation and evolution of planetary systems. These quantities play an important role in core-accretion models of formation and evolution of planets, as shown by numerous works studying the relationship of both quantities with planet formation (e.g. Ida & Lin 2005; Kornet et al. 2006; Kennedy & Kenyon 2008; Thommes et al. 2008; Alibert et al. 2011; Mordasini et al. 2012).
The initial conditions of planet formation (e.g. disk mass, temperature and density profiles, gravity, gas-dissipation and migration timescales) all change with stellar mass (e.g. Ida & Lin 2005; Kornet et al. 2006; Kennedy & Kenyon 2008; Alibert et al. 2011). Metallicity also plays a major role in the efficiency of the formation of giant planets for FGK dwarfs, as shown by both models (e.g. Ida & Lin 2004; Mordasini et al. 2009, 2012) and observational data in the form of a planet-metallicity correlation (e.g. Gonzalez 1997; Santos et al. 2004; Fischer & Valenti 2005; Sousa et al. 2011; Mayor et al. 2011), that seems to partially vanish for Neptunian and smaller planet hosts (Sousa et al. 2008; Bouchy et al. 2009; Ghezzi et al. 2010; Sousa et al. 2011; Buchhave et al. 2012).
According to Thommes et al. (2008) and Mordasini et al. (2012), a lower metallicity can be compensated by a higher disk mass to allow giant planet formation (and vice-versa – the so called “compensation effect”). This result implies that M dwarfs, which are expected to have a lower disk mass (e.g. Vorobyov & Basu 2008; Alibert et al. 2011) can form giant planets, but only if they have high metallicities, thus suggesting an even stronger giant planet-metallicity correlation compared to FGK dwarfs.
Disk instability models (e.g. Boss 1997), on the other hand, do not predict, in general, the dependence of the planet formation on metallicity (Boss 2002) and they also don’t seem to depend strongly on stellar mass, at least in the case of M dwarfs (Boss 2006). Contrary to the core-accretion paradigm (Pollack et al. 1996), the formation of planets does not originate from the collisional accretion of planetesimals, but from the collapse of an unstable part of the protoplanetary disk, forming in a timescale of thousands of years when compared to a timescale of Myrs for core-accretion models. Observational evidence, however, has shown that there is a dependence between planet occurrence and both stellar mass and metallicity over a wide range of dwarf types (AFGKM – e.g. Laws et al. 2003; Bonfils et al. 2007; Lovis & Mayor 2007; Johnson et al. 2007, 2010a), thus favoring the core-accretion scenario as the primary mechanism of planet formation, at least for closer-in planets.
In this context, the “pollution” scenario (e.g. Gonzalez 1997; Murray et al. 2002), defends that the observed enhanced metallicity is only at the surface of the photosphere, and that the formation of planets occurs at all metallicities, thus supporting disk instability models. Observationally, this would translate, for M dwarfs into a non-detection of the planet-metallicity correlation, as M dwarfs have very deep convective layers and are expected to be fully convective at masses below 0.4 M⊙.
Recent observational works for M dwarfs are in line with a planet-metallicity correlation (e.g. Bonfils et al. 2007; Johnson & Apps 2009; Schlaufman & Laughlin 2010; Rojas-Ayala et al. 2012; Terrien et al. 2012). However, more detections of planets around M dwarfs and a more precise metallicity determination are needed to achieve higher confidence levels that remain low, below the ~3σ level (Bonfils et al. 2007; Schlaufman & Laughlin 2010). In this context it is important to use a volume-limited sample of stars, as several planet-hunting programs targeting FGK dwarfs have metallicity-biased samples (e.g. Baranne et al. 1996; Fischer et al. 2005; Melo et al. 2007).
In the course of this paper we implement a new method to derive the metallicities of a volume-limited sample of 102 M dwarfs from the HARPS GTO programme. This method uses the high-resolution spectra of HARPS to achieve a [Fe/H] precision of 0.08 dex and is described in the Appendix. Then, we search for correlations between the frequency of planets with stellar mass and metallicity. In Sect. 2, we describe our M dwarf sample and observations using the HARPS spectrograph. Then, in Sect. 3, we investigate the stellar mass/metallicity correlations with the frequency of planets. In Sect. 4 we explore the metallicity-planet relation from the joined HARPS+California planet search samples. Finally, we discuss our results in Sect. 5.
2. Sample and observations
Our sample of 102 M dwarfs is described in detail in Sect. 2 of Bonfils et al. (2013). It is a volume limited (11 pc) sample, containing stars with a declination δ < +20°, with V magnitudes brighter than 14 mag, and including only stars with a projected rotational velocity vsini ≤ 6.5 km s-1. All known spectroscopic binaries and visual pairs with separation lower than 5 arcsec, as well as previously unknown fast rotators were removed a priori or a posteriori from the original sample.
The observations were gathered using the HARPS instrument (Mayor et al. 2003; Pepe et al. 2004), installed at the ESO 3.6-m telescope at the La Silla observatory in Chile. It is a high resolution (R ~ 115 000) spectrograph in the visible, covering a region between 380 and 690 nm. During the time of the GTO program, from 11th February 2003 to the 1st of April 2009, a total of 1965 spectra were recorded. The aim of the HARPS M dwarf programme is to achieve a ~1 m/s RV precision per exposure for the brightest targets. The chosen recording mode during this period was single fiber mode, that relies only on a single calibration but gives enough precision to reach the aim of the programme. Using single fiber mode has the advantage of obtaining non-contaminated spectra that can be used to perform studies other than measuring the star’s RV, such as measuring activity diagnostics, using Ca II H and K lines, and calculating stellar parameters and abundances. A more detailed description of the observations is given in Sect. 3 of Bonfils et al. (2013).
From the 102 M dwarf stars, a total of 15 planets are currently detected, in 8 systems, from which 3 have more than one planet. Table 1 shows the planet hosts, planets, and planetary mass and period taken from Bonfils et al. (2013), except in the case of Gl 876e (Rivera et al. 2010). We refer to Table 1 of Bonfils et al. (2013) for the full planet parameters and respective references.
Planet host stars in the sample, along with the planetary mass and period.
The stellar masses were calculated using the empirical mass-luminosity relationship of Delfosse et al. (2000), using stellar parallaxes, taken mostly from the Hipparcos catalogue (van Leeuwen 2007), but also from van Altena et al. (1995); Jahreiß & Wielen (1997); Hawley et al. (1997); Henry et al. (2006). The V band magnitudes were taken from the Sinbad database1, and the infrared Ks magnitudes from 2MASS (Skrutskie et al. 2006). The stellar mass values range from 0.09 to 0.60 M⊙, with a mean and median values of 0.32 and 0.29 M⊙ respectively. We note that, Gl 803, a young (~20 Myr) M dwarf star in our sample, with a circumstellar disk (Kalas et al. 2004), has a derived stellar mass value of 0.75, too high for a M dwarf. Therefore, the stellar mass calibration being used may not be adequate for the youngest M dwarfs.
The metallicities were first calculated with the photometric calibration provided by Neves et al. (2012), using stellar parallaxes, and V and Ks magnitudes. To improve on precedent photometric calibrations, we try to root the metallicity effect in the high-resolution HARPS spectra, using the measurements of the equivalent widths of the lines and features of the 26 red orders (533−690 nm region) of the HARPS spectra. The new calibration is detailed in the Appendix. We achieve a better precision with the new calibration reaching a [Fe/H] dispersion of the order of 0.08 dex. The metallicity values range from −0.88 to 0.32 dex, with a mean and median values of −0.13 and −0.11 dex respectively. We note that there is a slight offset towards lower metallicities when compared with the 582 FGK dwarfs from the HARPS-2 volume-limited sample (Sousa et al. 2011) with mean and median values of −0.10 and −0.08 dex respectively.
Table 2 depicts the sample used in this paper, where Cols. 2 and 3 list the right ascension and declination respectively, Col. 4 the parallaxes and their respective uncertainties, Col. 5 the source of the parallax, Col. 6 the spectral type of the M dwarf, and Cols. 7 and 8 the V- and Ks-band magnitudes respectively. Finally, Cols. 9 and 10 contain the calculated stellar mass and metallicity.
3. Stellar mass, metallicity, and planets from the HARPS study
In this section we use the new metallicity values (see the Appendix) as well as the stellar mass determinations from the HARPS M dwarf GTO sample to study the possible correlations of these quantities with the presence of planets. In this paper we consider Jovian hosts as stars having any planet with Mp > 30 M⊕ and Neptunian/smaller planet hosts as stars having all planets with masses below 30 M⊕.
 |
Fig. 1 Stellar mass distribution of the sample. The blue solid and dashed vertical lines represent the mean and the median of the stellar mass of the sample respectively. The black vertical lines locate the systems with planet detections. |
3.1. The stellar mass-planet correlation bias
Figure 1 shows the histogram of the stellar mass distribution of the whole sample. The solid blue and dashed vertical lines represent the mean and the median of the stellar mass of the sample respectively. The black vertical lines locate the systems with planet detections.
We can see that the planet detections are all on one side of the median of our sample distribution with stellar mass (all detected planets are around the more massive stars), as previously shown by Bonfils et al. (2013). This is also true for the V magnitude distribution (all detected planets are around the brighter stars). Therefore, any result regarding stellar mass will be checked, because its distribution may be subject to detection biases: on the one hand the reflex motion induced by a planetary companion is higher in lower mass stars, meaning a higher radial velocity (RV) signal, but on the other hand, the lower mass stars are on average fainter, thus having higher measurement uncertainties, which makes smaller planets harder to detect.
A lower star count in the [0.35−0.40] M⊙ bin of Fig. 1 is observed. To check whether this feature is real or due to a small number statistical fluctuation we did a simple monte-carlo simulation by generating 100.000 virtual samples containing 102 stars in the [0.05−0.65] M⊙ region, using an uniform distribution generator. Then, for each sample, we searched for a bin, in the [0.15−0.5] region, where the count difference with both adjacent bins was the same or higher than in the observed stellar mass distribution. To this end we chose a count difference of 6, 7, and 8, obtaining a frequency of 10.6, 5.1, and 2.2% respectively. We thus attribute the low number of stars with a mass between 0.35 and 0.4 M⊙ to a small number statistical fluctuation.
To check if there is any statistically significative bias due to the detection limits in the stellar mass distribution, we will first investigate the reason why all planet detections of our sample are located in the brightest and more massive halves of the two distributions, as it was seen in Fig. 1, for the stellar mass. We will then confirm or deny the existence of a stellar mass-planet correlation in our sample, as shown in Table 3, where we can observe a significative difference between the difference of averages and medians of giant planet and non-planet hosts.
Difference of averages and medians of stellar mass between planet host and non-planet host distributions.
In order to do this, we divided the sample into two stellar mass ranges at the median value (0.29 M⊙). We note that we removed the star Gl803 from the sample, due to the fact that the mass for this star may have not been adequately calculated, as explained in Sect. 2. Then, we calculated the frequency of stars with planets, using only the most massive planet in stars with multiple planets, and the frequency of planets. For both cases, we take into account the detection limits of our sample for different regions of the mass-period diagram following the procedure described in Sect. 7 of Bonfils et al. (2013).
In short, for each region, we calculate the frequency f = Nd/N⋆,eff, where Nd is the number of planet detections (or stars with planets), and N⋆,eff is the number of stars whose detection limits exclude planets with similar mass and period at the 99% confidence level. The N⋆,eff is evaluated with Monte-Carlo sampling as described in Bonfils et al. (2013): we draw random mass and period within each region of study, assuming a log-uniform probability for both quantities. Then, we evaluate if the draw falls above or below the detection limit of each star. If it sits above the detection limit we include the star in the N⋆,eff. The final value of N⋆,eff will be the average of 10.000 trials. The confidence intervals are calculated using a Poissonian distribution to calculate the 1σ Gaussian-equivalent area of the probability distribution, as shown for the binomial distribution in Sect. 3.2.
The results for the two halves of the stellar mass distribution can be seen in Table 4 for the frequency of planet-hosts (N = 8), and in Table 5 for the occurrence of planets (N = 15). We observe that, in the planet-host case, all values between the upper limits for M⋆ ≤ 0.29 M⊙ and the frequency values for M⋆ > 0.29 M⊙ are compatible with each other for all regions of planetary mass and period, except in the three regions with period between 10 and 104 days, and mass between 1 and 10 M⊕, where we cannot compare the values due to a low Neff number. We observe the same regarding the results of the occurrence of planets.
a) Upper limits for the occurrence of planet-hosts for M⋆ ≤ 0.29 M⊙ (N⋆ = 52); b) frequencies and upper limits for the occurrence of planet-hosts for M⋆ > 0.29 M⊙ (N⋆ = 49).
a) Upper limits for the occurrence of planets for M⋆ ≤ 0.29 M⊙ (N⋆=52); b) frequencies and upper limits for the occurrence of planets for M⋆ > 0.29 M⊙ (N⋆ = 49).
The fact that we do not observe a statistically significative (>2σ) difference in any region of the mass-period diagram between the two stellar mass sub-samples indicate that the observed accumulation of planet hosts in the higher half of the stellar mass distribution is due to a stellar mass detection bias. Therefore, we will not study the stellar mass-planet relation any further for our HARPS sample.
We got similar results for the V magnitude distribution, as the brightness and stellar mass have similar effects regarding the precision of the RV measurements.
 |
Fig. 2 Histograms of stars without planets (solid red), with Jovian planets (filled dashed blue), and with Neptunians/smaller planets (dotted black) for metallicity. The vertical solid red, filled dashed blue, and dotted black lines above the histograms represent the mean of the [Fe/H] distribution. |
3.2. The metallicity-planet correlation
Figure 2 shows the histogram of metallicity of our sample. The solid red histogram represent the stars without planets, while the filled dashed blue histogram the stars with Jovians planets, and the dotted black histogram the stars with Neptunians/smaller planets only. The vertical solid red, dashed blue, and dotted black lines above each histogram depict the value of the mean of the distribution. We note here that we assume that metallicity is not influenced by detection biases, due to the fact that we are using a volume-limited sample.
We can observe in Table 6 that the difference of the averages (medians resp.) of the full sample between planet and non-planet host distributions is small (0.01 and −0.07 dex, respectively).
Difference of averages and medians of [Fe/H] between planet host and non-planet host distributions.
If we only take into account the three planet host stars with Jupiter-type planets, the difference of the averages and the medians of the [Fe/H] between stars with and without planets is higher (0.20 and 0.26 dex respectively). On the other hand, if we remove the 3 systems with Jupiters, we obtain a mean and median of −0.10 dex. The correlation we find between [Fe/H] and planet ocurrence agrees with previous studies focused on giant planets around M dwarfs (e.g. Bonfils et al. 2007; Johnson & Apps 2009; Johnson et al. 2010a; Schlaufman & Laughlin 2010; Rojas-Ayala et al. 2010; Rojas-Ayala et al. 2012; Terrien et al. 2012). We confirm also, with better statistics, that such correlation is vanishing for Neptunian and smaller planet hosts (e.g. Rojas-Ayala et al. 2012; Terrien et al. 2012). In fact our result hints at a anti-correlation between [Fe/H] and planets though the difference (−0.10 dex) is at the limit of our measurement precision. Despite that, the results hint a different type of planet formation mechanism for giant and Neptunian/super Earth-type planets (e.g. Mordasini et al. 2012).
We performed a Kolmogorov-Smirnov (KS) test to check the probability of the sub-samples of stars with and without planets of belonging to the same parent distribution. All KS tests show that we cannot discard the possibility that the three sub-samples with planets belong to the same distribution of the stars without planets. We obtain a value of 0.195 for the Jovians hosts, but we do not have enough hosts (N = 3) to calculate the KS test properly.
In order to explore the star-planet relation further, we divided the metallicity range in three bins and performed a frequency analysis for Jovian hosts and Neptunian/smaller planet hosts separately, as shown in Figs. 3 and 4. The upper panels of all figures are the same as in Fig. 2, but this time with only three bins.
 |
Fig. 3 Upper panel: histogram of metallicity with 3 bins for stars without planets (solid red) and stars with giant planets (dashed blue); lower panel: frequency of stars with giant planets. |
 |
Fig. 4 Upper panel: histogram of metallicity with 3 bins for stars without planets (solid red) and stars with Neptunians and smaller planets only (dashed blue); lower panel: frequency of stars with Neptunians and smaller planets only. |
The lower panels depict the relative frequency of the stars with planets. The solid red line corresponds to a direct least squares bin fitting, while the dashed black line is a Bayesian bin-independent parametric fitting, explained in Sect. 3.3. Both fits use the functional form f = C10α [Fe/H] , following previous works for FGK dwarfs (Valenti & Fischer 2005; Udry & Santos 2007; Sousa et al. 2011). The coefficients C and α of both methods and respective uncertainties are shown in Table 7. The errors in the frequency of each bin are calculated using the binomial distribution, 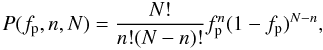 (1)following the procedure outlined in, e.g., Burgasser et al. (2003); McCarthy & Zuckerman (2004); Endl et al. (2006), and Sozzetti et al. (2009). In short we calculate how many n detections we have in a bin of size N, as a function of the planet frequency fp, of each bin. The upper errors, lower errors and upper limits of each bin are calculated by measuring the 68.2% of the integrated area around the peak of the binomial probability distribution function, that corresponds to the 1σ limit for a Gaussian distribution. An example is shown in Fig. 5, depicting a normalized binomial probability distribution function with n = 2, N = 20, and fp = 0.1.
(1)following the procedure outlined in, e.g., Burgasser et al. (2003); McCarthy & Zuckerman (2004); Endl et al. (2006), and Sozzetti et al. (2009). In short we calculate how many n detections we have in a bin of size N, as a function of the planet frequency fp, of each bin. The upper errors, lower errors and upper limits of each bin are calculated by measuring the 68.2% of the integrated area around the peak of the binomial probability distribution function, that corresponds to the 1σ limit for a Gaussian distribution. An example is shown in Fig. 5, depicting a normalized binomial probability distribution function with n = 2, N = 20, and fp = 0.1.
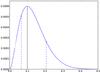 |
Fig. 5 Normalized binomial probability distribution function for n = 2, N = 20, and fp = 0.1.The solid vertical line depicts the observed frequency. The dashed lines show the 68.2% (1σ) limits around the maximum of the function. |
From Figs. 3 and 4 it can be observed that there is a small statistical difference between the frequency bins for both Jovian-hosts and Neptunian and smaller planet hosts, as the uncertainties of each bin are high. The first bin of Fig. 3 ([−0.9,0.47] dex) has an upper limit of 13.3%, with no planet detection, while the second and third bins ([−0.47, −0.03] and [−0.03,0.4] dex, resp.) have values of 1.9% and 5.6% respectively. Regarding Fig. 4, we observe the frequencies of 12.5, 5.4, and 2.9% for the same bins.
We can observe a correlation with [Fe/H] for Jovian hosts and a hint of an anti-correlation for Neptunian and smaller planets only hosts. Interestingly, the later anti-correlation for smaller planet hosts is predicted by recent studies using core-accretion models (Mordasini et al. 2012), but we note that we only consider Neptunian hosts as stars with Neptunians and smaller planets only: if a multi-planet system has a Jovian and one or more smaller planets, for instance, we count the system as being a Jupiter host, not a Neptunian-host. Therefore, it is expected that the number of Neptunians and smaller planets will be higher at lower metallicities.
3.3. Bayesian approach
To test the metallicity results we performed a parametric and bin-independent fitting of the data based on Bayesian inference. We followed the Johnson et al. (2010a) approach, using two functional forms for the planet frequency, fp1 = C and fp2 = C10α [Fe/H] , and choosing uniformly distributed priors for the parameters C and α. The choice of a power law for the functional form was based on previous works of [Fe/H] of FGK dwarfs (Valenti & Fischer 2005; Udry & Santos 2007; Sousa et al. 2011).
Table 7 summarizes and compares the results of the Bayesian fitting to the ones obtained with the bin fitting. Column 1 shows the functional forms used and respective parameters, Col. 2 the uniform prior range, Col. 3 the most likely value for the fit parameters, along with the 1σ Gaussian uncertainties and Col. 4 the fit parameters of the least squares bin fitting.
Parameters of the Bayesian and fit from binning models for the HARPS sample.
From Table 7 we can see that the Bayesian fit values are, in general, compatible with the bin fitting values. However, we observe that the α values obtained for the planet-host frequencies with the Bayesian method are higher than the same values using the bin fitting. This translates into a higher giant-host frequency values with [Fe/H] and a lower Neptunian/smaller planet host frequencies as a function of metallicity. We also note that the α values calculated by the Bayesian method have large uncertainties in both scenarios. In the case of Neptunian-hosts, the α value can easily accommodate both positive or negative values.
3.4. Comparison with the California Planet Survey late-K and M-type dwarf sample
Our aim here is to compare our results to a similar sample regarding the difference between planet hosts and non-planet hosts only. The California Planet Survey (CPS) late-K and M-type dwarf sample (Rauscher & Marcy 2006; Johnson et al. 2010b) was chosen for this goal. It is a 152 star sample where 18 planets (7 Jovians and 11 Neptunian/smaller planets) are already detected around 11 hosts. Most of the jovian detections come from the CPS sample while almost all detections of Neptunians and smaller planets were made with HARPS. The metallicities and stellar masses were calculated using the Johnson & Apps (2009) and the Delfosse et al. (2000) calibration, respectively. We note that the Johnson & Apps (2009) [Fe/H] calibration has a dispersion around ~0.2 dex and a systematic offset towards higher [Fe/H], as shown in Neves et al. (2012). The offset amounts to 0.13 dex when we compare the [Fe/H] of the CPS sample computed from the Johnson & Apps (2009) calibration with the Neves et al. (2012) calibration.
Table 8 depicts the CPS sample used in this paper, where Cols. 2 and 3 list the right ascension and declination respectively, Col. 4 the parallaxes and their respective uncertainties, Col. 5 the source of the parallax, Col. 6 the spectral type of the star, and Cols. 7 and 8 the V- and Ks-band magnitudes respectively. Column 9 lists the stellar mass. Finally, Cols. 10 and 11 contain the calculated metallicity using the Johnson & Apps (2009) and the Neves et al. (2012) photometric calibrations respectively.
We calculated the difference of averages and medians between planet hosts and non-planet hosts in the same way as we did for our sample, as shown in Table 6. Table 9 shows the results. For metallicity, we observe a much higher difference of averages and medians when compared to our sample, but as we noted before there is an offset when calculating the metallicity with different calibrations. The difference of averages and medians for Jupiter-type planets is higher than in our sample but is compatible with our results. For Neptunian-type hosts the difference of averages and medians are indistinguishable from the non-planet host sample.
We also performed a KS test for [Fe/H] between the three planet-host subsamples and the stars without planets, taking advantage of the higher number of stars with planets of the CPS sample, as shown in the forth column of Table 9. It can be seen that there is a very low probability (~0.2%) that the Jovian hosts and the stars without planets belong to the same distribution. For the case of Neptunian-hosts, however, the KS p-value is high (~98%). Again, this result is expected from previous works on FGK dwarfs (e.g. Sousa et al. 2011) and M dwarfs (e.g. Rojas-Ayala et al. 2012).
Regarding stellar mass, we do not see any trend. The difference of averages and medians between planet hosts and non-planet hosts is negligible. This result agrees with the findings of the HARPS sample as the trend we observe with stellar mass is biased.
Difference of averages and medians between planet host and non-planet host distributions for the CPS late-K and M-type dwarf sample.
4. Metallicity-planet relation from the HARPS+CPS joined sample
To improve our statistics and study the planet-metallicity correlation in more detail, we joined our HARPS sample with the CPS M dwarf sample. The [Fe/H] for the CPS sample was recalculated with the Neves et al. (2012) calibration, which has the same scale and accuracy of our new calibration, shown in the appendix. We kept the values of the [Fe/H] using our new spectroscopic calibration for the 49 stars in common. The joined sample has 205 stars, with 13 stars hosting 20 planets. Seven hosts have Jovian-type planets around them while six of them only have Neptunians and smaller planets.
Table 10 shows the results for the joined sample, and is similar to Table 9. We did not calculate the correlation between planet occurence and stellar mass, because as discussed in Sect. 3.1 such relation is biased. The joined sample results are similar to both our sample and the CPS sample: the difference of averages and medians between Jovian hosts and non-planet hosts show a correlation with [Fe/H], while the same quantities for Neptunians and smaller hosts do not show this trend. The tentative hint of an anti-correlation with [Fe/H] for the Neptunians/smaller hosts of the HARPS sample, in Table 6 is observed but is smaller than the one observed for the HARPS sample. However, we must note that the CPS sample is not as sensitive as the HARPS sample in the detection of Neptunian and smaller planets. Therefore we consider that in this paper the reference is the HARPS sample regarding the Neptunian-host metallicity relation.
 |
Fig. 6 Upper panel: histogram of metallicity of the joined sample with 3 bins for stars without planets (solid red) and stars with giant planets (dashed blue); Lower panel: frequency of stars with giant planets. |
Difference of averages and medians between planet host and non-planet host distributions for the joined sample.
The KS test results are similar to the ones performed for the CPS sample, in Table 9. However we must note the higher value in the case of the Jovian hosts, just above the 1% p-value.
We now proceed to the frequency analysis of the stars with Jovians and Neptunians/smaller planets. Figures 6 and 7 show, in their upper panel, the histograms of stars with Jovian planets and stars with only Neptunians and smaller planets, respectively, depicted by a dashed blue line. The histogram of the non-host stars of the joined sample are depicted by a solid red line. The lower panels show the frequency of planets of each bin. The solid red and the dashed black lines represent the fit of the binned values and the fit given by a Bayesian model (see Sect. 3.3) respectively. The values of the coefficients for both fits are shown in Table 11 and will be discussed together in Sect. 4.1.
 |
Fig. 7 Upper panel: histogram of metallicity of the joined sample with 3 bins for stars without planets (solid red) and stars with Neptunians and smaller planets only (dashed blue); lower panel: frequency of stars with Neptunians and smaller planets only. |
From both figures we can observe that the results are similar to the ones obtained with our sample (see Figs. 3 and 4), but with lower uncertainties. The correlation of Jovian-hosts and metallicity is now stronger, but the anti-correlation for Neptunians is weaker. The first bin of Fig. 6, ranging from −0.9 to −0.47 dex has an upper limit of 9.1%, with no planet detection, while the second and third bins ([−0.47, −0.03] and [−0.03,0.4] dex, resp.) have values of 1.6% and 8.2% respectively. Regarding Fig. 7, we observe the frequencies of 8.3, 2.3, and 3.4% for the same bins.
4.1. Bayesian approach for the joined sample
Here we perform the same Bayesian inference approach as done in Sect. 3.3 but this time for the joined sample. Table 11 summarizes and compares the results of the Bayesian fitting to the ones obtained with the bin fitting. The columns are the same as in Table 7.
Parameters of the two Bayesian and fit from binning models for the HARPS+CPS sample.
From Table 11 we can see that both the direct bin fitting and the Bayesian fitting values are compatible with the ones obtained with the HARPS sample. As we have seen in Sect. 3.3, the α values are higher than the same values using the bin fitting, translating into a higher giant-host frequency and a lower Neptunian/smaller planet host frequency. Again, the α values calculated by the Bayesian method have large uncertainties, and the α value, for the Neptunian and smaller planet hosts case, may easily have positive or negative values.
We can now compare the values for giant planets obtained with both fitting methods to previous works. Valenti & Fischer (2005), Udry & Santos (2007), and Sousa et al. (2011) all use a similar power law to the one used in this work for the frequency of giants around FGK dwarfs and obtained α values of 2.0, 2.04, and 2.58 respectively through direct bin fitting. Our α results from the bin fitting (1.26 ± 0.30 from the HARPS sample and 1.72 ± 0.18 from the joined sample) are lower than those works, which might suggest a less efficient planet-formation process around M dwarfs. However, the α values obtained from the Bayesian fit for the HARPS sample are very similar to the ones obtained for FGK dwarfs: 1.97 ± 1.25, despite the high uncertainty. Regarding the combined sample we obtain a higher value of 2.94 ± 1.03 from the Bayesian fitting, suggesting a more efficient process of planet-formation around M dwarfs. Therefore, our quantification of the α parameter for giant planets around M dwarfs, taking into account the large uncertainties involved, are compatible with the values found in FGK studies.
In order to check if the more complex power law functional form is preferred over the constant one, we used a method of Bayesian model comparison, following Kass & Raftery (1995). First, we calculate for both functional forms the total probability of the model conditioned on the data (the evidence) by integrating over the full parameter space. Computationally, in the case of uniformly distributed priors, we can calculate the evidence as 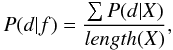 (2)where the P(d|X) is the likelihood, or the probability of observing the data d given the parameters X, and length(X) is the length of the full parameter space. Then, we calculate the Bayes factor that is just the ratio of the evidence of both functional forms,
(2)where the P(d|X) is the likelihood, or the probability of observing the data d given the parameters X, and length(X) is the length of the full parameter space. Then, we calculate the Bayes factor that is just the ratio of the evidence of both functional forms, 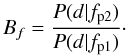 (3)According to Kass & Raftery (1995) a Bf value over 20 gives a strong evidence that the model fp2 is better at fitting the data than the fp1 model.
(3)According to Kass & Raftery (1995) a Bf value over 20 gives a strong evidence that the model fp2 is better at fitting the data than the fp1 model.
For the Jovian hosts case, we obtained a Bayes factor of 2.07 and 66.04 for the HARPS and the joined sample respectively. This means that, in the case of the HARPS sample, the more complex model cannot explain much better the data than the constant model. On the other hand, the combined sample achieves a high Bayes factor, meaning that there is a strong evidence that the more complex model does a better fit than the constant model, supporting the planet-metallicity correlation for giant planets.
Regarding the Neptunian hosts, we obtain values lower than the unity, which means that the constant model explain the data better than the more complex power model. Therefore, it is impossible at this moment to confirm the hypothetical anti-correlation observed for low [Fe/H] values. Despite this, we must note that our HARPS sample is much more sensitive in probing the Neptunian/super-Earth mass regime than the CPS sample. Therefore the frequency parametrization of the HARPS sample for the Neptunian/super-Earth mass range, and shown in detail in Sect. 3.2, is preferred over the joined one.
5. Discussion
In this paper we investigate the metallicity and stellar mass correlations with planets. We use a new method, described in the Appendix, to refine the precision of the metallicities of the HARPS GTO M dwarf sample calculated with the calibration of Neves et al. (2012). We use the established calibration of Delfosse et al. (2000) to calculate the stellar masses of our sample.
We confirm the trend of metallicity with the presence of giant planets in our sample, as shown by previous studies on FGK dwarfs (e.g. Gonzalez 1997; Santos et al. 2004; Sousa et al. 2011; Mayor et al. 2011) and M dwarfs (Bonfils et al. 2007; Johnson & Apps 2009; Schlaufman & Laughlin 2010; Rojas-Ayala et al. 2012; Terrien et al. 2012). For Neptunian and smaller planet hosts there is a hint that an anti-correlation may exist but our current statistic supports a flat relation, in concordance with previous results for FGK dwarfs (e.g. Sousa et al. 2008; Bouchy et al. 2009; Sousa et al. 2011) and M dwarfs (Rojas-Ayala et al. 2012). We calculate the difference of the averages and medians between planet and non-planet hosts, and most importantly the frequencies in three different bins, as well as a parametrization to both Jovian and Neptunian hosts.
We combined the HARPS sample with the California Planet Survey (CPS) late-K and M-type dwarf sample to improve our statistics, increasing the number of stars from 102 to 205 and the number of planet hosts from 8 to 13 (7 Jovian-hosts and 6 Neptunian/smaller planet hosts). The [Fe/H] of the CPS sample was calculated using the photometric calibration of Neves et al. (2012). The previous trend for Jovian-hosts is confirmed and reinforced, but the existence of an anti-correlation of Neptunian-hosts with [Fe/H] is inconclusive. The CPS sample is not as sensitive as the HARPS sample regarding the detection of Neptunian and smaller planets. Therefore the HARPS sample is the reference in this work regarding the Neptunian-host-metallicity relation.
Quantitatively, the difference of the averages and the medians between stars with and without planets for Jupiter-type hosts is 0.20 and 0.26 dex for the HARPS sample and 0.20 and 0.19 dex for the joined sample. Regarding the Neptunian and smaller planet hosts, the observed difference of the averages and the medians is −0.10 dex for the HARPS sample.
Regarding the frequency of giant hosts, we have no detection in the [−0.9, −0.47] dex bin for both HARPS and the joined sample. For the [−0.47, −0.03] bin we obtained a frequency of 1.9% and 1.6%, and between −0.03 and 0.4 we have a frequency of 5.6% and 8.2% for the HARPS and the joined sample respectively. Regarding Neptunian hosts, we obtained, for the same samples and bins, the values of 12.5%, and 8.3% for the first bin, 5.4% and 2.3% for the second bin and 2.9% and 3.4% for the last [Fe/H] bin. As noted, the frequencies obtained using the joined sample for the Neptunian-hosts are not as precise as in the HARPS sample due to a lower sensitivity of the CPS sample to Neptunian and smaller planets.
The parametrization of the planet-metallicity relation was based on bin fit and Bayesian fit models, following a functional form of the type fp = C10α [Fe/H] used in previous works for FGK dwarfs (Valenti & Fischer 2005; Udry & Santos 2007; Sousa et al. 2011). The results for the parameters C and α using the functional forms calculated by direct bin fitting or by using the Bayesian fitting are compatible with each other. However, we note a high uncertainty on the determination of the α parameter using the Bayesian fitting. Therefore the results for this parameter for giant planets vary a lot, between 1.26 ± 0.30 and 1.97 ± 1.25, using the bin fitting or the Bayesian fitting respectively, for the HARPS sample, and between 1.72 ± 0.18 to 2.94 ± 1.03 for the combined sample. At the actual statistical level, the α parameter we determine is compatible with the value found for FGK dwarfs in previous studies (Fischer & Valenti 2005; Udry & Santos 2007; Sousa et al. 2011). Regarding Neptunian-hosts, we obtain an α value, for the HARPS sample, between −0.79 ± 0.06 and −0.57 ± 0.71, using the bin fit or the bayes fit model respectively. This result configures an anti-correlation for Neptunian hosts with [Fe/H], but with an insufficient statistical confidence level.
We therefore conclude that the power law functional form works best for giant hosts, and that a constant functional form is preferred, for now, for Neptunian/smaller planet hosts. We also reject the possibility of a correlation for Neptunian-hosts of the same order of magnitude of that for Jupiter-hosts. In fact we suspect that an anti-correlation might exist but we lack the statistics to confirm it.
Regarding stellar mass, we detect a positive trend in planet detections towards higher masses. However, when we take the detection limits into account, we do not find any significant difference. Therefore, the trend of the frequency of planets with the stellar mass is due to a detection bias in our sample, stressing the importance of taking into account the planet detection biases in stellar mass studies.
Online material
HARPS M dwarf sample, sorted by right ascension.
California Planet Survey (CPS) sample, sorted by right ascension.
Appendix A: A new M dwarf metallicity and effective temperature calibration based on line and feature measurements of HARPS M dwarf spectra
Here we briefly explain the method that we developed to estimate the metallicity and effective temperature of M dwarfs. A paper regarding the full details of this calibration is in preparation (Neves et al., in prep.).
The method is based on the measurement of “peak-to-peak” equivalent widths (EW) of lines and features from the spectra of our volume-limited M dwarf HARPS sample and uses existing photometric calibrations for metallicity (Neves et al. 2012) and effective temperature (Casagrande et al. 2008), as starting values. Our method achieves an increase in precision of the metallicity and effective temperature but the accuracy of the new scale is tied to the accuracy of the photometric calibrations.
A.1. Calibration sample
From the initial 102 M dwarf star spectra of the Bonfils et al. (2013) sample we initially chose 62 stars with S/N greater than 100. Seven stars (Gl191, Gl285, Gl388, Gl699, Gl729, Gl803, GJ1125) were then discarded a posteriori, due to a bad correlation of the line measurements with either the reference metallicity or temperature scales, that can be attributed to high activity/rotation (Gl191, Gl285, Gl388, Gl729, Gl803) or to a bad value of the radial velocity (GJ1125). We ended up with a sample of 55 stars, shown in Table A.1 in which we based our calibration. Column 1 shows the star designation, Col. 2 the initial photometric [Fe/H] from Neves et al. (2012), Col. 3 the calibrated [Fe/H] value, Col. 4 the initial photometric effective temperature, and Col. 5 the calibrated Teff value.
Calibration sample.
A.2. Method
From our calibration sample we first measured “peak-to-peak” equivalent widths (EWs) of lines and features using the 26 redder orders of median normalized HARPS spectra, in the region between 530 to 690 nm. Here we consider features as blended lines. We define the “peak-to-peak” equivalent widths as 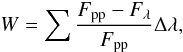 (A.1)where Fpp is the value of the flux between the peaks of the line/feature at each integration step and Fλ the flux of the line/feature. The measurement of the EWs is illustrated in Fig. A.1, where the “peak-to-peak” flux corresponds to the red dotted lines, and the black line is the flux of the reference spectra. The EW is thus measured between the red dotted line and the solid black line. We used the very high S/N (~1430 @ 550 nm) spectral orders of the star Gl 205 as a reference from where the line/feature regions are going to be measured for all other stars. We rejected lines/features with EW < 8 mÅ and very steep lines/features.
(A.1)where Fpp is the value of the flux between the peaks of the line/feature at each integration step and Fλ the flux of the line/feature. The measurement of the EWs is illustrated in Fig. A.1, where the “peak-to-peak” flux corresponds to the red dotted lines, and the black line is the flux of the reference spectra. The EW is thus measured between the red dotted line and the solid black line. We used the very high S/N (~1430 @ 550 nm) spectral orders of the star Gl 205 as a reference from where the line/feature regions are going to be measured for all other stars. We rejected lines/features with EW < 8 mÅ and very steep lines/features.
 |
Fig. A.1 Small region of the Gl 205 spectra illustrating the “peak to peak” equivalent width line measurement. The red dotted line represents the “peak-to-peak” flux. |
We investigated the correlations and partial correlations of [Fe/H] and Teff with the line/feature EWs. Figure A.2 shows the histograms of the partial correlation values of [Fe/H] with Teff kept constant (solid blue histogram) and the partial correlation values of Teff with [Fe/H] kept constant (dashed green histogram). We observe that a significant number of lines have a good correlation with the parameters.
 |
Fig. A.2 Histograms of the partial correlations of [Fe/H] (solid blue histogram) and Teff (dashed green histogram). |
Then we calculated a linear fit of the EWs with the metallicity (taken from Neves et al. 2012) and effective temperature (taken from Casagrande et al. 2008), using a least squares approach. For each EW i and for each star m we have, ![\appendix \setcounter{section}{1} \begin{equation} W_{i,m} = \alpha_{i}[{\rm Fe/H}]_{m}^{\rm T} + \beta_{i}T_{{\rm eff} m}^{\rm T} + \gamma_{i}, \label{first} \end{equation}](/articles/aa/full_html/2013/03/aa20574-12/aa20574-12-eq726.png) (A.2)where Wi,m is a i × m matrix containing the EWs, and both [Fe/H]m, and Teffm are 1 × m vectors. The α and the β are the coefficients related to metallicity and effective temperature, respectively, while γ is an independent coefficient.
(A.2)where Wi,m is a i × m matrix containing the EWs, and both [Fe/H]m, and Teffm are 1 × m vectors. The α and the β are the coefficients related to metallicity and effective temperature, respectively, while γ is an independent coefficient.
The error of each coefficient is calculated as 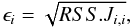 (A.3)where RSS is the residual sum of squares, expressed as
(A.3)where RSS is the residual sum of squares, expressed as 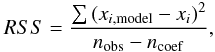 (A.4)and Ji,i is the diagonal of the estimate of the jacobian matrix around the solution. The xi,model, xi, nobs, and ncoef from Eq. (A.3) are, respectively, the predicted value of the data, xi, by the regression model, the data values, the number of data points, and the number of coefficients.
(A.4)and Ji,i is the diagonal of the estimate of the jacobian matrix around the solution. The xi,model, xi, nobs, and ncoef from Eq. (A.3) are, respectively, the predicted value of the data, xi, by the regression model, the data values, the number of data points, and the number of coefficients.
The total error of the coefficients can then be written as 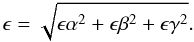 (A.5)Here we assume that both [Fe/H] and temperature are independent and do not correlate with each other.
(A.5)Here we assume that both [Fe/H] and temperature are independent and do not correlate with each other.
Our aim is to increase the metallicity precision using the photometric calibration as reference. In order to do this, we want to recover the values of the metallicity and temperature by doing a weighted least squares refit. To calculate the weights for the least squares refit we just invert the squared errors of the coefficients, and normalize the expression, 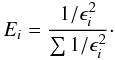 (A.6)To invert the fit of Eq. (A.2) we first take the calculated coefficients from the first fit and define the coefficient matrix as
(A.6)To invert the fit of Eq. (A.2) we first take the calculated coefficients from the first fit and define the coefficient matrix as ![\appendix \setcounter{section}{1} \begin{equation} C_{i,3} = \left[\begin{array}{ccc} \alpha_{1,1} & \beta_{1,2} & \gamma_{1,3} \\ \alpha_{2,1} & \beta_{2,2} & \gamma_{2,3} \\... & ... & ...\\ \alpha_{i,1} & \beta_{i,2} & \gamma_{i,3} \end{array}\right]\cdot \end{equation}](/articles/aa/full_html/2013/03/aa20574-12/aa20574-12-eq743.png) (A.7)Then we invert Eq. (A.2). After some operations we have
(A.7)Then we invert Eq. (A.2). After some operations we have ![\appendix \setcounter{section}{1} \begin{equation} [[{\rm Fe/H}],T_{\rm eff},Ind]_{3,m} = (C^{\rm T}_{3,i}C_{i,3})^{-1}C^{\rm T}_{3,i}W_{i,m}, \label{refit} \end{equation}](/articles/aa/full_html/2013/03/aa20574-12/aa20574-12-eq744.png) (A.8)where CT is the transpose of C and Ind is the value of the independent parameter.
(A.8)where CT is the transpose of C and Ind is the value of the independent parameter.
Finally, we use a levenberg-marquardt algorithm and apply the weights (Eq. (A.6) to Eq. (A.8)), recovering one value of metallicity and effective temperature for each star.
 |
Fig. A.3 [Fe/H] comparison between this work and the photometric calibration of Neves et al. (2012). |
 |
Fig. A.4 Teff comparison between this work and the photometric calibration of Casagrande et al. (2008). |
We also tried other methods, such as choosing groups of lines with a high correlation or partial correlation coefficients and then applying the same method as described in this Appendix. However, the weighted least squares method using all 4441 lines performed best at minimizing the uncertainties of both metallicity and effective temperature.
Using this method, we get a dispersion of metallicity and effective temperature of 0.08 dex and 80 K respectively. Figures A.3 and A.4 show the comparison between the values obtained in this work and the reference calibrations for metallicity and effective temperature, respectively. We emphasize that we only get an improvement of the precision. The accuracy of the calibration, as well as systematic errors, are tied to the original determinations of both [Fe/H] and temperature.
Acknowledgments
We would like to thank Annelies Mortier for useful discussions. We would also like to thank John Asher Johnson and Kevin Apps for kindly providing the CPS M dwarf sample. We acknowledge the support by the European Research Council/European Community under the FP7 through Starting Grant agreement number 239953. The financial support from the “Programme National de Planétologie” (PNP) of CNRS/INSU, France, is gratefully acknowledged. N.C.S. and V.N. also acknowledges the support from Fundação para a Ciência e a Tecnologia (FCT) through program Ciência 2007 funded by FCT/MCTES (Portugal) and POPH/FSE (EC), and in the form of grant reference PTDC/CTE-AST/098528/2008. V.N. would also like to acknowledge the support from the FCT in the form of the fellowship SFRH/BD/60688/2009. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France, and of the Extrasolar Planet Encyclopaedia at exoplanet.eu. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.
References
- Alibert, Y., Mordasini, C., & Benz, W. 2011, A&A, 526, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anglada-Escudé, G., Boss, A. P., Weinberger, A. J., et al. 2012, ApJ, 746, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benedict, G. F., McArthur, B., Chappell, D. W., et al. 1999, AJ, 118, 1086 [NASA ADS] [CrossRef] [Google Scholar]
- Benedict, G. F., McArthur, B. E., Forveille, T., et al. 2002, ApJ, 581, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Bonfils, X., Mayor, M., Delfosse, X., et al. 2007, A&A, 474, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2013, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boss, A. P. 1997, Science, 276, 1836 [NASA ADS] [CrossRef] [Google Scholar]
- Boss, A. P. 2002, ApJ, 567, L149 [Google Scholar]
- Boss, A. P. 2006, ApJ, 643, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Bouchy, F., Mayor, M., Lovis, C., et al. 2009, A&A, 496, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buchhave, L. A., Latham, D. W., Johansen, A., et al. 2012, Nature, 486, 375 [NASA ADS] [Google Scholar]
- Burgasser, A. J., Kirkpatrick, J. D., Reid, I. N., et al. 2003, ApJ, 586, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Flynn, C., & Bessell, M. 2008, MNRAS, 389, 585 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Correia, A. C. M., Couetdic, J., Laskar, J., et al. 2010, A&A, 511, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delfosse, X., Forveille, T., Ségransan, D., et al. 2000, A&A, 364, 217 [NASA ADS] [Google Scholar]
- Endl, M., Cochran, W. D., Kürster, M., et al. 2006, ApJ, 649, 436 [Google Scholar]
- Fabricius, C., & Makarov, V. V. 2000, AAPS, 144, 45 [Google Scholar]
- Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, D. A., Laughlin, G., Butler, P., et al. 2005, ApJ, 620, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Gatewood, G. 2008, AJ, 136, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Gatewood, G., Kiewiet de Jonge, J., & Persinger, T. 1998, AJ, 116, 1501 [NASA ADS] [CrossRef] [Google Scholar]
- Ghezzi, L., Cunha, K., Smith, V. V., et al. 2010, ApJ, 720, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, G. 1997, MNRAS, 285, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, S. L., Gizis, J. E., & Reid, N. I. 1997, AJ, 113, 1458 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, T. J., Jao, W.-C., Subasavage, J. P., et al. 2006, AJ, 132, 2360 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., & Lin, D. N. C. 2004, ApJ, 616, 567 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ida, S., & Lin, D. N. C. 2005, ApJ, 626, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Jahreiß, H., & Wielen, R. 1997, in Hipparcos – Venice ’97, eds. R. M. Bonnet, E. Høg, P. L. Bernacca, et al., ESA SP, 402, 675 [Google Scholar]
- Jao, W.-C., Henry, T. J., Subasavage, J. P., et al. 2005, AJ, 129, 1954 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., & Apps, K. 2009, ApJ, 699, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Butler, R. P., Marcy, G. W., et al. 2007, ApJ, 670, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Aller, K. M., Howard, A. W., & Crepp, J. R. 2010a, PASP, 122, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Howard, A. W., Marcy, G. W., et al. 2010b, PASP, 122, 149 [NASA ADS] [Google Scholar]
- Kalas, P., Liu, M. C., & Matthews, B. C. 2004, Science, 303, 1990 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kass, R. E., & Raftery, A. E. 1995, J. Am. Statist. Association, 90, 773 [Google Scholar]
- Kennedy, G. M., & Kenyon, S. J. 2008, ApJ, 673, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Kornet, K., Wolf, S., & Różyczka, M. 2006, A&A, 458, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laws, C., Gonzalez, G., Walker, K. M., et al. 2003, AJ, 125, 2664 [NASA ADS] [CrossRef] [Google Scholar]
- Lovis, C., & Mayor, M. 2007, A&A, 472, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011, A&A, submitted [arXiv:1109.2497] [Google Scholar]
- McCarthy, C., & Zuckerman, B. 2004, AJ, 127, 2871 [NASA ADS] [CrossRef] [Google Scholar]
- Melo, C., Santos, N. C., Gieren, W., et al. 2007, A&A, 467, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Alibert, Y., & Benz, W. 2009, A&A, 501, 1139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Alibert, Y., Benz, W., Klahr, H., & Henning, T. 2012, A&A, 541, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murray, N., Paskowitz, M., & Holman, M. 2002, ApJ, 565, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Neves, V., Bonfils, X., Santos, N. C., et al. 2012, A&A, 538, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pepe, F., Mayor, M., Queloz, D., et al. 2004, A&A, 423, 385 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pollack, J., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Rauscher, E., & Marcy, G. W. 2006, PASP, 118, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, I. N., Hawley, S. L., & Gizis, J. E. 1995, AJ, 110, 1838 [NASA ADS] [CrossRef] [Google Scholar]
- Rivera, E. J., Laughlin, G., Butler, R. P., et al. 2010, ApJ, 719, 890 [Google Scholar]
- Rojas-Ayala, B., Covey, K. R., Muirhead, P. S., & Lloyd, J. P. 2010, ApJ, 720, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Rojas-Ayala, B., Covey, K. R., Muirhead, P. S., & Lloyd, J. P. 2012, ApJ, 748, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2004, A&A, 415, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlaufman, K. C., & Laughlin, G. 2010, A&A, 519, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Söderhjelm, S. 1999, A&A, 341, 121 [Google Scholar]
- Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Udry, S. 2011, A&A, 533, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sozzetti, A., Torres, G., Latham, D. W., et al. 2009, ApJ, 697, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Terrien, R. C., Mahadevan, S., Bender, C. F., et al. 2012, ApJ, 747, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Thommes, E. W., Matsumura, S., & Rasio, F. A. 2008, Science, 321, 814 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Udry, S., & Santos, N. 2007, ARA&A, 45, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- van Altena, W. F., Lee, J. T., & Hoffleit, E. D. 1995, The general catalogue of trigonometric [stellar] parallaxes, eds. W. F. van Altena, J. T. Lee, & E. D. Hoffleit [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2008, ApJ, 676, L139 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Difference of averages and medians of stellar mass between planet host and non-planet host distributions.
a) Upper limits for the occurrence of planet-hosts for M⋆ ≤ 0.29 M⊙ (N⋆ = 52); b) frequencies and upper limits for the occurrence of planet-hosts for M⋆ > 0.29 M⊙ (N⋆ = 49).
a) Upper limits for the occurrence of planets for M⋆ ≤ 0.29 M⊙ (N⋆=52); b) frequencies and upper limits for the occurrence of planets for M⋆ > 0.29 M⊙ (N⋆ = 49).
Difference of averages and medians of [Fe/H] between planet host and non-planet host distributions.
Difference of averages and medians between planet host and non-planet host distributions for the CPS late-K and M-type dwarf sample.
Difference of averages and medians between planet host and non-planet host distributions for the joined sample.
Parameters of the two Bayesian and fit from binning models for the HARPS+CPS sample.
All Figures
 |
Fig. 1 Stellar mass distribution of the sample. The blue solid and dashed vertical lines represent the mean and the median of the stellar mass of the sample respectively. The black vertical lines locate the systems with planet detections. |
| In the text | |
 |
Fig. 2 Histograms of stars without planets (solid red), with Jovian planets (filled dashed blue), and with Neptunians/smaller planets (dotted black) for metallicity. The vertical solid red, filled dashed blue, and dotted black lines above the histograms represent the mean of the [Fe/H] distribution. |
| In the text | |
 |
Fig. 3 Upper panel: histogram of metallicity with 3 bins for stars without planets (solid red) and stars with giant planets (dashed blue); lower panel: frequency of stars with giant planets. |
| In the text | |
 |
Fig. 4 Upper panel: histogram of metallicity with 3 bins for stars without planets (solid red) and stars with Neptunians and smaller planets only (dashed blue); lower panel: frequency of stars with Neptunians and smaller planets only. |
| In the text | |
 |
Fig. 5 Normalized binomial probability distribution function for n = 2, N = 20, and fp = 0.1.The solid vertical line depicts the observed frequency. The dashed lines show the 68.2% (1σ) limits around the maximum of the function. |
| In the text | |
 |
Fig. 6 Upper panel: histogram of metallicity of the joined sample with 3 bins for stars without planets (solid red) and stars with giant planets (dashed blue); Lower panel: frequency of stars with giant planets. |
| In the text | |
 |
Fig. 7 Upper panel: histogram of metallicity of the joined sample with 3 bins for stars without planets (solid red) and stars with Neptunians and smaller planets only (dashed blue); lower panel: frequency of stars with Neptunians and smaller planets only. |
| In the text | |
 |
Fig. A.1 Small region of the Gl 205 spectra illustrating the “peak to peak” equivalent width line measurement. The red dotted line represents the “peak-to-peak” flux. |
| In the text | |
 |
Fig. A.2 Histograms of the partial correlations of [Fe/H] (solid blue histogram) and Teff (dashed green histogram). |
| In the text | |
 |
Fig. A.3 [Fe/H] comparison between this work and the photometric calibration of Neves et al. (2012). |
| In the text | |
 |
Fig. A.4 Teff comparison between this work and the photometric calibration of Casagrande et al. (2008). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


