| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A73 | |
| Number of page(s) | 17 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201220520 | |
| Published online | 25 February 2013 | |
WASP-54b, WASP-56b, and WASP-57b: Three new sub-Jupiter mass planets from SuperWASP⋆,⋆⋆
1
Department of PhysicsUniversity of Warwick, Coventry, CV4 7AL
UK
e-mail: f.faedi@warwick.ac.uk
2
Astrophysics Research Centre, School of Mathematics and Physics,
Queen’s University Belfast, University Road, Belfast
BT7 1NN,
UK
3
Aix Marseille Universit, CNRS, LAM (Laboratoire d’Astrophysique de
Marseille) UMR 7326, 13388
Marseille,
France
4
School of Physics and Astronomy, University of St.
Andrews, St.
Andrews, Fife
KY16 9SS,
UK
5
Astrophysics Group, Keele University, Staffordshire, ST5 5BG, UK
6
Université de Liège, Allée du 6 août 17, Sart Tilman, Liège 1,
Belgium
7
Physics and Astronomy Department, Vanderbilt
University, Nashville, Tennessee, USA
8
Institut d’Astrophysique de Paris, UMR7095 CNRS, Université Pierre
& Marie Curie, France
9
Observatoire de Haute-Provence, CNRS/OAMP,
04870
St Michel l’Observatoire,
France
10
Observatoire astronomique de l’Université de Genève,
51 ch. des Maillettes,
1290
Sauverny,
Switzerland
11
Department of Physics and Astronomy, University of
Leicester, Leicester,
LE1 7RH,
UK
12
Qatar Foundation, PO Box 5825, Doha, Qatar
13
Department of Physical Sciences, The Open
University, Milton
Keynes, MK7
6AA, UK
14
Argelander-Institut für Astronomie der Universität
Bonn, Auf dem Hgel
71, 53121
Bonn,
Germany
15
Isaac Newton Group of Telescopes, Apartado de Correos 321, 38700
Santa Cruz de Palma,
Spain
Received:
8
October
2012
Accepted:
23
December
2012
We present three newly discovered sub-Jupiter mass planets from the SuperWASP survey: WASP-54b is a heavily bloated planet of mass 0.636+0.025-0.024MJ and radius 1.653+0.090-0.083RJ. It orbits a F9 star, evolving off the main sequence, every 3.69 days. Our MCMC fit of the system yields a slightly eccentric orbit (e = 0.067+0.033-0.025) for WASP-54b. We investigated further the veracity of our detection of the eccentric orbit for WASP-54b, and we find that it could be real. However, given the brightness of WASP-54 V = 10.42 mag, we encourage observations of a secondary eclipse to draw robust conclusions on both the orbital eccentricity and the thermal structure of the planet. WASP-56b and WASP-57b have masses of 0.571+0.034-0.035MJ and 0.672+0.049-0.046MJ, respectively; and radii of 1.092+0.035-0.033RJ for WASP-56b and 0.916+0.017-0.014RJ for WASP-57b. They orbit main sequence stars of spectral type G6 every 4.67 and 2.84 days, respectively. WASP-56b and WASP-57b show no radius anomaly and a high density possibly implying a large core of heavy elements; possibly as high as ~50 M⊕ in the case of WASP-57b. However,the composition of the deep interior of exoplanets remains still undetermined. Thus, more exoplanet discoveries such as the ones presented in this paper, are needed to understand and constrain giant planets’ physical properties.
Key words: techniques: photometric / techniques: radial velocities / stars: individual: WASP-54 / stars: individual: WASP-56 / stars: individual: WASP-57
RV data (Tables 6–9) are available in electronic form at http://www.aanda.org
Photometric data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr(130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/551/A73
© ESO, 2013
1. Introduction
To date the number of extrasolar planets for which precise measurements of masses and radii are available amounts to more than a hundred. Although these systems are mostly Jupiter-like gas giants they have revealed an extraordinary variety of physical and dynamical properties that have had a profound impact on our knowledge of planetary structure, formation and evolution and unveiled the complexity of these processes (see Baraffe et al. 2010, and references there in). Transit surveys such as SuperWASP (Pollacco et al. 2006) have been extremely successful in providing great insight into the properties of extrasolar planets and their host stars (see e.g., Baraffe et al. 2010). Ground-based surveys excel in discovering systems with peculiar/exotic characteristics. Subtle differences in their observing strategies can yield unexpected selection effects impacting the emerging distributions of planetary and stellar properties such as orbital periods, planetary radii and stellar metallicity (see e.g., Cameron 2011 for a discussion). For example WASP-17b (Anderson et al. 2010) is a highly inflated (Rpl = 1.99RJ), very low density planet in a tilted/retrograde orbit, HAT-P-32b (Hartman et al. 2011) could be close to filling its Roche Lobe Rpl = 2.05 RJ (if the best fit eccentric orbit is adopted1), thus possibly losing its gaseous envelope, and the heavily irradiated and bloated WASP-12b (Hebb et al. 2009), has a Carbon rich atmosphere (Kopparapu et al. 2012; Fossati et al. 2010), and is undergoing atmospheric evaporation (Llama et al. 2011; Lecavelier Des Etangs 2010) losing mass to its host star at a rate ~10-7MJ yr-1 (Li et al. 2010). On the opposite side of the spectrum of planetary parameters, the highly dense Saturn-mass planet HD 149026b is thought to have a core of heavy elements with ~70 M⊕, needed to explain its small radius (e.g., Sato et al. 2005, and Carter et al. 2009), and the massive WASP-18b (Mpl = 10 MJ, Hellier et al. 2009), is in an orbit so close to its host star with period of ~0.94 d and eccentricity e = 0.02, that it might induce significant tidal effects probably spinning up its host star (Brown et al. 2011). Observations revealed that some planets are larger than expected from standard coreless models (e.g., Fortney et al. 2007; Baraffe et al. 2008) and that the planetary radius is correlated with the planet equilibrium temperature and anti-correlated with stellar metallicity (see Guillot et al. 2006; Laughlin et al. 2011; Enoch et al. 2011; Faedi et al. 2011). For these systems different theoretical explanations have been proposed for example, tidal heating due to unseen companions pumping up the eccentricity (Bodenheimer et al. 2001, and 2003), kinetic heating due to the breaking of atmospheric waves (Guillot & Showman 2002), enhanced atmospheric opacity (Burrows et al. 2007), semi convection (Chabrier & Baraffe 2007), and finally ohmic heating (Batygin et al. 2011, 2010; and Perna et al. 2012). While each individual mechanism would presumably affect all hot Jupiters to some extent, they can not explain the entirety of the observed radii (Fortney & Nettelmann 2010; Leconte et al. 2010; Perna et al. 2012). More complex thermal evolution models are necessary to fully understand their cooling history.
Recently, the Kepler satellite mission released a large number of planet candidates (>2000) and showed that Neptune-size candidates and Super-Earths (>76% of Kepler planet candidates) are common around solar-type stars (e.g., Borucki et al. 2011; and Batalha et al. 2012). Although these discoveries are fundamental for a statistically significant study of planetary populations and structure in the low-mass regime, the majority of these candidates orbit stars that are intrinsically faint (V > 13.5 for ~78% of the sample of Borucki et al. 2011) compared to those observed from ground-based transit surveys, making exoplanet confirmation and characterisation extremely challenging if not impossible. Thus, more bright examples of transiting planets are needed to extend the currently known parameter space in order to provide observation constraints to test theoretical models of exoplanet structure, formation and evolution. Additionally, bright gas giant planets also allow study of their atmospheres via transmission and emission spectroscopy, and thus provide interesting candidates for future characterisation studies from the ground (e.g. VLT and e-ELT) and from space (e.g. PLATO, JWST, EChO, and FINESSE).
Here we describe the properties of three newly discovered transiting exoplanets from the WASP survey: WASP-54b, WASP-56b, and WASP-57b. The paper is structured as follows: in Sect. 2 we describe the observations, including the WASP discovery data and follow up photometric and spectroscopic observations which establish the planetary nature of the transiting objects. In Sect. 3 we present our results for the derived system parameters for the three planets, as well as the individual stellar and planetary properties. Finally, in Sect. 4 we discuss the implication of these discoveries, their physical properties and how they add information to the currently explored mass-radius parameter space.
2. Observations
The stars 1SWASP J134149.02-000741.0 (2MASS J13414903-0007410) hereafter WASP-54; 1SWASP J121327.90+230320.2 (2MASS J12132790+2303205) hereafter WASP-56; and 1SWASP J145516.84-020327.5 (2MASS J14551682-0203275) hereafter WASP-57; have been identified in several northern sky catalogues which provide broad-band optical (Zacharias et al. 2005) and infra-red 2MASS magnitudes (Skrutskie et al. 2006) as well as proper motion information. Coordinates, broad-band magnitudes and proper motion of the stars are from the NOMAD 1.0 catalogue and are given in Table 1.
2.1. SuperWASP observations
The WASP North and South telescopes are located in La Palma (ORM – Canary Islands) and Sutherland (SAAO – South Africa), respectively. Each telescope consists of 8 Canon 200 mm f/1.8 focal lenses coupled to e2v 2048 × 2048 pixel CCDs, which yield a field of view of 7.8 × 7.8 square degrees, and a pixel scale of 13.7′′ (Pollacco et al. 2006).
WASP-56 (V = 11.5) is located in the northern hemisphere with Declination δ ~ + 23h and thus it is only observed by the SuperWASP-North telescope; WASP-54 and WASP-57 (V = 10.42 and V = 13.04, respectively) are located in an equatorial region of sky monitored by both WASP instruments, however only WASP-54 has been observed simultaneously by both telescopes, with a significantly increased observing coverage on the target. In January 2009 the SuperWASP-N telescope underwent a system upgrade that improved our control over the main sources of red noise, such as temperature-dependent focus changes (Barros et al. 2011; Faedi et al. 2011). This upgrade resulted in better quality data and increased the number of planet detections.
Photometric properties of the stars WASP-54, WASP-56, and WASP-57.
All WASP data for the three new planet-hosting stars were processed with the custom-built reduction pipeline described in Pollacco et al. (2006). The resulting light curves were analysed using our implementation of the Box Least-Squares fitting and SysRem de-trending algorithms (see Collier Cameron et al. 2006; Kovács et al. 2002; Tamuz et al. 2005), to search for signatures of planetary transits. Once the candidate planets were flagged, a series of multi-season, multi-camera analyses were performed to strengthen the candidate detection. In addition different de-trending algorithms (e.g., TFA, Kovács et al. 2005) were used on one season and multi-season light curves to confirm the transit signal and the physical parameters of the planet candidate. These additional tests allow a more thorough analysis of the stellar and planetary parameters derived solely from the WASP data thus helping in the identification of the best candidates, as well as to reject possible spurious detections.
 |
Fig. 1 Upper panel: discovery light curve of WASP-54b phase folded on the ephemeris given in Table 4. Lower panel: binned WASP-54b light curve. Black-solid line, is the best-fit transit model estimated using the formalism from Mandel & Agol (2002). |
-
WASP-54 was first observed in 2008, February 19. The same field was observed again in 2009, 2010 and 2011 by both WASP telescopes. This resulted in a total of 29938 photometric data points, of which 1661 are during transit. A total of 58 partial or full transits were observed with an improvement in χ2 of the box-shaped model over the flat light curve of Δχ2 = −701, and signal-to-red noise value (Collier Cameron et al. 2006) of SNred = −13.02. When combined, the WASP data of WASP-54, showed a characteristic periodic dip with a period of P = 3.69 days, duration T14 ~ 270 min, and a depth ~11.5 mmag. Figure 1 shows the discovery photometry of WASP-54b phase folded on the period above, and the binned phased light curve.
-
WASP-56 was first observed during our pilot survey in May 2004 by SuperWASP-North. The same field was also observed in 2006 and 2007 yielding a total of 16441 individual photometric observations. SuperWASP first began operating in the northern hemisphere in 2004, observing in white light with the spectral transmission defined by the optics, detectors, and atmosphere. During the 2004 season the phase coverage for WASP-56b was too sparse to yield a robust detection with only ~10 points falling during the transit phase. Later in 2006 a broad-band filter (400−700 nm) was introduced and with more data available multi-season runs confirmed the transit detection. Over the three seasons a total of 14 partial or full transits were observed, yielding 300 observations in transit, with a Δχ2 = −213 improvement over the flat light curve, and SNred = −7.02. The combined WASP light curves, plotted in Fig. 2, show the detected transit signal of period = 4.61 days, depth = ~13 mmag, and duration T14 ~ 214 min.
-
WASP-57b was first observed in March 2008 and subsequently in Spring 2010. A total of 30 172 points were taken of which about 855 were during transit. About 65 full or partial transits were observed overall with a Δχ2 = −151, and SNred = −6.20. Figure 3-upper panel shows the combined WASP light curves folded on the detected orbital period of 2.84 days. Additionally, for WASP-57b there is photometric coverage from the Qatar Exoplanet Survey (QES, Alsubai et al. 2011) and the phase folded QES light curve is shown in Fig. 3-middle panel. In both WASP and QES light curves the transit signal was identified with a period ~2.84 days, duration T14 ~ 138 min, and transit depth of ~17 mmag.
 |
Fig. 2 Upper panel: discovery light curve of WASP-56b phase folded on the ephemeris given in Table 5. Lower panel: binned WASP-56b light curve. Black-solid line, is the best-fit transit model estimated using the formalism from Mandel & Agol (2002). |
 |
Fig. 3 Upper panel: discovery WASP light curve of WASP-57b phase folded on the ephemeris given in Table 5. Middle panel: QES light curve of WASP-57b. Lower panel: binned WASP light curve of WASP-57b. Black-solid line, is the best-fit transit model estimated using the formalism from Mandel & Agol (2002). |
2.2. Low S/N photometry
Several observing facilities are available to the WASP consortium and are generally used to obtain multi-band low-resolution photometry to confirm the presence of the transit signal detected in the WASP light curves. This is particularly useful in case of unreliable ephemerides, and in case the transit period is such that follow up from a particular site is more challenging. Small-to-medium sized telescopes such as the remote-controlled 17-inch PIRATE telescope in the Observatori Astronomic de Mallorca (Holmes et al. 2011), together with the James Gregory 0.94 m telescope (JGT) at the University of St. Andrews, provide higher precision, higher spatial resolution photometry as compared to WASP, and thus have an important role as a link in the planet-finding chain, reducing the amount of large telescope time spent on false-positives. Observations of WASP-56 were obtained with both PIRATE and JGT, while observations of WASP-54 were obtained only with PIRATE.
Multiple Markov-chain Monte Carlo (MCMC) chains have been obtained for both systems to assess the significance of adding the PIRATE and JGT light curves to the corresponding dataset in determining the transit model, in particular the impact parameter, the transit duration, and a/R⋆. We conclude that for WASP-54 the effect is not significant, never the less, the PIRATE light curves were included in our final analysis presented in Sect. 3.2. In the case of WASP-56 instead, because we only have a partial TRAPPIST light curve (see Sect. 2.4), the full JGT light curve, although of lower quality, is crucial to better constrain the transit ingress/egress time, impact parameter and a/R⋆, allowing us to relax the main sequence mass-radius constraint.
2.3. Spectroscopic follow up
WASP-54, 56 and 57 were observed during our follow up campaign in Spring 2011 with the SOPHIE spectrograph mounted at the 1.93 m telescope (Perruchot et al. 2008; Bouchy et al. 2009) at Observatoire de Haute-Provence (OHP), and the CORALIE spectrograph mounted at the 1.2 m Euler-Swiss telescope at La Silla, Chile (Baranne et al. 1996; Queloz et al. 2000; Pepe et al. 2002). We used SOPHIE in high efficiency mode (R = 40 000) and obtained observations with very similar signal-to-noise ratio (S/N ~30), in order to minimise systematic errors (e.g., the Charge Transfer Inefficiency effect of the CCD, Bouchy et al. 2009). Wavelength calibration with a Thorium-Argon lamp was performed every ~2 h, allowing the interpolation of the spectral drift of SOPHIE (<3 m s-1 per hour; see Boisse et al. 2010). Two 3″ diameter optical fibers were used; the first centred on the target and the second on the sky to simultaneously measure the background to remove contamination from scattered moonlight. During SOPHIE observations of WASP-54, 56 and 57 the contribution from scattered moonlight was negligible as it was well shifted from the targets’ radial velocities. The CORALIE observations of WASP-54 and WASP-57 were obtained during dark/grey time to minimise moonlight contamination. The data were processed with the SOPHIE and CORALIE standard data reduction pipelines, respectively. The radial velocity uncertainties were evaluated including known systematics such as guiding and centring errors (Boisse et al. 2010), and wavelength calibration uncertainties. All spectra were single-lined.
For each planetary system the radial velocities were computed from a weighted cross-correlation of each spectrum with a numerical mask of spectral type G2, as described in Baranne et al. (1996) and Pepe et al. (2002). To test for possible stellar impostors we performed the cross-correlation with masks of different stellar spectral types (e.g. F0, K5 and M5). For each mask we obtained similar radial velocity variations, thus rejecting a blended eclipsing system of stars with unequal masses as a possible cause of the variation.
We present in Tables 6–8 the spectroscopic measurements of WASP-54, 56 and 57 together with their line bisectors (Vspan). In each Table we list the Barycentric Julian date (BJD), the stellar radial velocities (RVs), their uncertainties, the bisector span measurements, and the instrument used. In Col. 6, we list the radial velocity measurements after subtracting the zero point offset to CORALIE and SOPHIE data respectively (the zero-point offsets are listed in Tables 4, and 5 respectively). In Col. 7 we also give the line bisectors after subtracting the mean value for SOPHIE and CORALIE respectively, and finally, in Col. 8, the radial velocity residuals to the best-fit Keplerian model. The root-mean-square (rms) of the residuals to the best-fit Keplerian models are as follow: rms = 18.9 m s-1 for WASP-54, rms = 19.5 m s-1 for WASP-56, and rms = 24.4 m s-1 for WASP-57.
For all figures presented in the paper we adopted the convention for which SOPHIE data are always represented as filled circles and CORALIE data are represented as open squares. In Figs. 4 to 9 we present the RVs, Vspan, and the residuals O−C diagrams for the three systems. Both CORALIE and SOPHIE data sets are offset with respect to the radial velocity zero point, γSOPHIE and γCORALIE, respectively (see Tables 4 and 5). We examined Vspan to search for asymmetries in spectral line profiles that could result from unresolved binarity or indeed stellar activity. Such effects would cause the bisector spans to vary in phase with radial velocity. For the three systems no significant correlation is observed between the radial velocity and the line bisector, or the bisector and the time at which observation were taken. This supports each signal’s origin as being planetary, rather than due to a blended eclipsing binary system, or to stellar activity (see Queloz et al. 2001).
 |
Fig. 4 Upper panel: phase folded radial velocity measurements of WASP-54 obtained combining data from SOPHIE (filled-circles) and CORALIE (open-squares) spectrographs. Superimposed is the best-fit model RV curve with parameters from Table 4. The centre-of-mass velocity for each data set was subtracted from the RVs (γSOPHIE = −3.1109 km s-1 and γCORALIE = −3.1335 km s-1). Lower panel: residuals from the RV orbital fit plotted against time. |
 |
Fig. 5 Upper panel: the bisector span measurements of WASP-54 as a function of radial velocity, values are shifted to a zero-mean (⟨ Vspan ⟩ SOPHIE = −29 m s-1, ⟨ Vspan ⟩ CORALIE = 48 m s-1). Lower panel: the bisector span measurements as a function of time (BJD – 2 450 000.0). The bisector span shows no significant variation nor correlation with the RVs, suggesting that the signal is mainly due to Doppler shifts of the stellar lines rather than stellar profile variations due to stellar activity or a blended eclipsing binary. |
-
WASP-54’s follow up spectroscopy was obtained from both the SOPHIE and CORALIE spectrographs (see Figs. 4 and 5). The rms for SOPHIE and CORALIE radial velocity residuals to the best-fit model are rmsSOPHIE = 33.6 m s-1 and rmsCORALIE = 8.2 m s-1. Typical internal errors for CORALIE and SOPHIE are of 10–15 m s-1. The significantly higher rms of the SOPHIE residuals is mostly due to one observation (RV = 134 m s-1). Removing this measurement results in a rmsSOPHIE = 18 m s-1, which is comparable to the quoted internal error. We investigated the reasons of the particularly large error bar associated with the measurement above (55 m s-1) and we found that it is due to a shorter exposure time, cloud absorption, and Moon pollution. The specific observation was obtained during grey time at a Moon distance of 57°. To estimate and remove the sky contamination we used the method described in Pollacco et al. (2008) and Hébrard et al. (2008), however, the RV shift induced by the Moon was high (310 m s-1) and the relative low S/N resulted in a less accurate measurement (1.3-σ away from the residuals).

Fig. 6 Upper panel: similar to Fig. 4, the phase folded radial velocity measurements of WASP-56. The centre-of-mass velocity for the SOPHIE data was subtracted from the RVs (γSOPHIE = −4.6816 km s-1). Lower panel: residuals from the RV orbital fit plotted against time.

Fig. 7 Upper panel: the bisector span measurements for WASP-56 as a function of radial velocity, values are shifted to a zero-mean (⟨ Vspan ⟩ SOPHIE = −40 m s-1). Lower panel: the bisector span measurements as a function of time (BJD – 2 450 000.0). No correlation with radial velocity and time is observed suggesting that the Doppler signal is induced by the planet.

Fig. 8 Upper panel: similar to Figs. 4 and 6 for WASP-57. The centre-of-mass velocity for each data set was subtracted from the RVs (γSOPHIE = −23.214 km s-1 and γCORALIE = −23.228 km s-1). Lower panel: residuals from the RV orbital fit plotted against time.

Fig. 9 Upper panel: same as Figs. 5 and 7 we show the bisector span measurements for WASP-57 as a function of radial velocity, values are shifted to a zero-mean (⟨ Vspan ⟩ SOPHIE = −2 m s-1, ⟨ Vspan ⟩ CORALIE = 22 m s-1). Lower panel: the bisector span measurements as a function of time (BJD – 2 450 000.0). No correlation with radial velocity and time is observed suggesting that the Doppler signal is induced by the planet.
-
WASP-56 has radial velocity data only from SOPHIE (see Figs. 6 and 7). The rms of the RV residuals to the best-fit model is 19.4 m s-1. When removing the only discrepant RV value at phase 0.5 (RV = −61 m s-1) the overall rms reduces to 12 m s-1, comparable to SOPHIE internal error.
-
Finally, for WASP-57 the rms of the SOPHIE and CORALIE radial velocity residuals to the best-fit model are rmsSOPHIE = 22.3 m s-1 and rmsCORALIE = 26.5 m s-1, respectively (see Figs. 8 and 9). These become 14 m s-1 and 17.4 m s-1 respectively for SOPHIE and CORALIE data sets when ignoring the two measurements with the largest errors.
2.4. follow up multi-band photometry
To allow more accurate light curve modelling of the three new WASP planets and tightly constrain their parameters, in-transit high-precision photometry was obtained with the TRAPPIST and Euler telescopes located at ESO La Silla Observatory in Chile. The TRAPPIST telescope and its characteristics are described in Jehin et al. (2011) and Gillon et al. (2011). A detailed description of the physical characteristics and instrumental details of EulerCam can be found in Lendl et al. (2012).
Photometry for WASP-54, WASP-56, and WASP-57.
 |
Fig. 10 Euler r-band and TRAPPIST “I + z”-band follow up high signal-to-noise photometry of WASP-54 during the transit (see Table 2). The TRAPPIST light curve has been offset from zero by an arbitrary amount for clarity. The data are phase-folded on the ephemeris from Table 4. Superimposed (black-solid line) is our best-fit transit model estimated using the formalism from Mandel & Agol (2002). Residuals from the fit are displayed underneath. |
 |
Fig. 11 TRAPPIST “I + z”-band and JGT R-band follow up high signal-to-noise photometry of WASP-56 during the transit (see Table 2). The JGT light curve has been offset from zero by an arbitrary amount for clarity. The The data are phase-folded on the ephemeris from Table 5. Superimposed (black-solid line) is our best-fit transit model estimated using the formalism from Mandel & Agol (2002). Residuals from the fit are displayed underneath. |
 |
Fig. 12 Euler r-band and TRAPPIST “I + z”-band follow up high signal-to-noise photometry of WASP-57 during the transit (see Table 2). The TRAPPIST light curves have been offset from zero by an arbitrary amount for clarity. The data are phase-folded on the ephemeris from Table 5. Superimposed (black-solid lines) are the best-fit transit models estimated using the formalism from Mandel & Agol (2002). The residuals from each fit are displayed underneath the relative light curves. |
All photometric data presented here are available from the NStED database2. One full and one partial transits of WASP-54b have been observed by EulerCam in 2011 April 6 and TRAPPIST in 2012 February 26, respectively. Only a partial transit of WASP-56b was observed by TRAPPIST in 2011 May 16, and a full transit was observed by JGT in 2012 March 11. A partial and a full transit of WASP-57b were captured by TRAPPIST on the nights of 2011 May 5 and June 10 respectively, while a full transit of WASP-57b was observed with EulerCam in 2011 June 10. A summary of these observations is given in Table 2.
We show in Figs. 10–12 the high S/N follow up photometry (EulerCam and TRAPPIST) for WASP-54b, WASP-56b and WASP-57b respectively. In each plot we show the differential magnitude versus orbital phase, along with the residual to the best-fit model. The data are phase folded on the ephemerides derived by our analysis of each individual object (see Sect. 3.2). In Figs. 10 and 12 some of the light curves are assigned an arbitrary magnitude offset for clarity.
2.5. TRAPPIST “I + z”–band photometry
TRAPPIST photometry was obtained using a readout mode of 2 × 2 MHz with 1 × 1 binning, resulting in a readout time of 6.1 s and readout noise 13.5 e− pix-1, respectively. A slight defocus was applied to the telescope to optimise the observation efficiency and to minimise pixel to pixel effects. TRAPPIST uses a special “I + z” filter that has a transmittance >90% from 750 nm to beyond 1100 nm. The positions of the stars on the chip were maintained to within a few pixels thanks to the “software guiding” system that regularly derives an astrometric solution to the most recently acquired image and sends pointing corrections to the mount, if needed (see e.g., Gillon et al. 2011 for more details). A standard pre-reduction (bias, dark, flat field correction), was carried out and the stellar fluxes were extracted from the images using the IRAF/DAOPHOT3 aperture photometry software Stetson (1987). After a careful selection of reference stars differential photometry was then obtained.
2.6. Euler r-band photometry
Observations with the Euler-Swiss telescope were obtained in the Gunn r filter. The Euler telescope employs an absolute tracking system which keeps the star on the same pixel during the observation, by matching the point sources in each image with a catalogue, and adjusting the telescope pointing between exposures to compensate for drifts (Lendl et al. 2012). WASP-54b’s observations were carried out with a 0.2 mm defocus and one-port readout with exposure time of 30 s. All images were corrected for bias and flat field effects and transit light curve were obtained by performing relative aperture photometry of the target and optimal bright reference stars. For WASP-57b no defocus was applied, and observations were performed with four-port readout, and 60 s exposures. Six reference stars were used to perform relative aperture photometry to obtain the final light curve.
3. Results
3.1. Stellar parameters
For all the three systems the same stellar spectral analysis has been performed, co-adding individual CORALIE and SOPHIE spectra with a typical final S/N of ~80:1. The standard pipeline reduction products were used in the analysis, and the analysis was performed using the methods given in Gillon et al. (2009). The Hα line was used to determine the effective temperature (Teff). The surface gravity (log g) was determined from the Ca i lines at 6122 Å, 6162 Å and 6439 Å along with the Na i D and Mg i b lines. The elemental abundances were determined from equivalent width measurements of several clean and unblended lines. A value for micro-turbulence (ξt) was determined from Fe i using the method of Magain (1984). The quoted error estimates include that given by the uncertainties in Teff, log g and ξt, as well as the scatter due to measurement and atomic data uncertainties. The projected stellar rotation velocity (vsini⋆) was determined by fitting the profiles of several unblended Fe i lines. For each system a value for macro-turbulence (vmac) was assumed based on the tabulation by Bruntt et al. (2010), and we used the telluric lines around 6300 Å to determine the instrumental full width at half maximum (FWHM). The values for the vmac and the instrumental FWHM are given in Table 3. There are no emission peaks evident in the Ca H+K lines in the spectra of the three planet host stars. For each stellar host the parameters obtained from the analysis are listed in Table 3 and discussed below:
Stellar parameters of WASP-54, WASP-56, and WASP-57 from spectroscopic analysis.
-
WASP-54: our spectral analysis yields the following results: Teff = 6100 ± 100 K, log g = 4.2 ± 0.1 (cgs), and [Fe/H] = −0.27 ± 0.08 dex, from which we estimate a spectral type F9. WASP-54’s stellar mass and radius were estimated using the calibration of Torres et al. (2010). We find no significant detection of lithium in the spectrum of WASP-54, with an equivalent width upper limit of 0.4 mÅ, corresponding to an abundance upper limit of log A(Li) < 0.4 ± 0.08. The non-detection of lithium together with the low rotation rate obtained from vsini⋆(Prot = 17.60 ± 4.38 d), assuming i⋆ is perpendicular to the line of sight (thus vsini⋆ = Vequatorial), and the lack of stellar activity (shown by the absence of Ca ii H and K emission), all indicate that the star is relatively old. From the estimated vsini⋆ we derived the stellar rotation rates, and we used the expected spin-down timescale (Barnes 2007) to obtain a value of the stellar age through gyrochronology. We estimate an age of
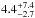 Gyr, This value also suggest the
system is old. Although we point out that in the case of WASP-54 using
gyrochoronlogy to constrain the age of the system could be inappropriate as the
planet could have affected the stellar rotation velocity via tidal interaction (see
Sect. 4.1 for more details). However, we note that the gyrochronological age we
obtain is in agreement with that from theoretical evolutionary models discussed
below, which imply that WASP-54 has evolved off the main sequence.
Gyr, This value also suggest the
system is old. Although we point out that in the case of WASP-54 using
gyrochoronlogy to constrain the age of the system could be inappropriate as the
planet could have affected the stellar rotation velocity via tidal interaction (see
Sect. 4.1 for more details). However, we note that the gyrochronological age we
obtain is in agreement with that from theoretical evolutionary models discussed
below, which imply that WASP-54 has evolved off the main sequence. -
WASP-56 and WASP-57: both stellar hosts are of spectral type G6V. From our spectral analysis we obtain the following parameters: Teff = 5600 ± 100 K, and log g = 4.45 ± 0.1 (cgs) for WASP-56, Teff = 5600 ± 100 K, and log g = 4.2 ± 0.1 (cgs) for WASP-57. As before the stellar masses and radii are estimated using the Torres et al. (2010) calibration. With a metallicity of [Fe/H] = 0.12 dex WASP-56 is more metal rich than the sun, while our spectral synthesis results for WASP-57 show that it is a metal poor star ([Fe/H] = −0.25 dex). For both stars the quoted lithium abundances take account non-local thermodynamic equilibrium corrections (Carlsson et al. 1994). The values for the lithium abundances if these corrections are neglected are as follows: log A(Li) = 1.32 and log A(Li) = 1.82 for WASP-56 and WASP-57, respectively. These values imply an age of ≳5 Gyr for the former and an age of ≳2 Gyr for the latter (Sestito & Randich 2005). From vsini⋆ we derived the stellar rotation period Prot = 32.58 ± 18.51 d for WASP-56, implying a gyrochronological age (Barnes 2007) for the system of ~
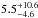 Gyr. Unfortunately, the
gyrochronological age can only provide a weak constraint on the age of WASP-56. For
WASP-57 we obtain a rotation period of
Prot = 18.20 ± 6.40 d corresponding to an age of
~
Gyr. Unfortunately, the
gyrochronological age can only provide a weak constraint on the age of WASP-56. For
WASP-57 we obtain a rotation period of
Prot = 18.20 ± 6.40 d corresponding to an age of
~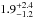 Gyr. Both the above results are in
agreement with the stellar ages obtained from theoretical evolution models (see
below) and suggest that WASP-56 is quite old, while WASP-57 is a relatively young
system.
Gyr. Both the above results are in
agreement with the stellar ages obtained from theoretical evolution models (see
below) and suggest that WASP-56 is quite old, while WASP-57 is a relatively young
system.
 |
Fig. 13 Isochrone tracks from Marigo et al. (2008) and Girardi et al. (2010) for WASP-54 using the metallicity [Fe/H] = −0.27 dex from our spectral analysis and the best-fit stellar density 0.2 ρ⊙. From left to right the solid lines are for isochrones of: 1.0, 1.3, 1.6, 2.0, 2.5, 3.2, 4.0, 5.0, 6.3, 7.9, 10.0 and 12.6 Gyr. From left to right, dashed lines are for mass tracks of: 1.4, 1.3, 1.2, 1.1 and 1.0 M⊙. |
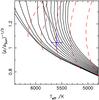 |
Fig. 14 Isochrone tracks from Demarque et al. (2004) for WASP-56 using the metallicity [Fe/H] = 0.12 dex from our spectral analysis and the best-fit stellar density 0.88 ρ⊙. From left to right the solid lines are for isochrones of: 1.8, 2.0, 2.5, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0, 11.0, 12.0, 13.0 and 14.0 Gyr. From left to right, dashed lines are for mass tracks of: 1.2, 1.1, 1.0, 0.9 and 0.8 M⊙. |
The stellar masses of planet host stars are usually derived by comparing measurable
stellar properties to theoretical evolutionary models, or from empirical calibrations. Of
the latter, the most widely used is the Torres et al.
(2010) calibration, which is derived from eclipsing binary stars, and relates
log g and Teff to the stellar mass and
radius. However, while Teff can be determined with high
precision, log g is usually poorly constrained, and thus stellar masses
derived from the spectroscopic log g can have large uncertainties and can
suffer from systematics. For example the masses of 1000 single stars, derived by Valenti et al. (1998) via spectral analysis, were
found to be systematically 10% larger than those derived from theoretical isochrones. A
similar discrepancy was also found in the analysis of the stellar parameters of WASP-37
(Simpson et al. 2011), WASP-39 (Faedi et al. 2011), and WASP-21 (Bouchy et al. 2010). Additionally, different sets of theoretical models
might not perfectly agree with each other (Southworth
2010), and moreover at younger ages isochrones are closely packed and a small
change in Teff or
ρ⋆ can have a significant effect on the
derived stellar age. For each planet host star we show a plot with one set of stellar
tracks and isochrones, while we give a comprehensive list of the four models’ results in
Table 9. Using the metallicity of [Fe/H] = −0.27
dex our best-fit stellar properties from the Padova isochrones (Marigo et al. 2008 and Girardi et al.
2010) for WASP-54 yield a mass of 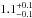 M⊙ and a
stellar age of
M⊙ and a
stellar age of  Gyr, in agreement with the
gyrochronological age and a more accurate estimate. The Padova isochrones together with
the stellar mass tracks and WASP-54 results are shown in Fig. 13. According to the stellar models, a late-F star with [Fe/H] = −0.27
dex, of this radius and mass has evolved off the zero-age main sequence and is in the
shell hydrogen burning phase of evolution with an age of
Gyr, in agreement with the
gyrochronological age and a more accurate estimate. The Padova isochrones together with
the stellar mass tracks and WASP-54 results are shown in Fig. 13. According to the stellar models, a late-F star with [Fe/H] = −0.27
dex, of this radius and mass has evolved off the zero-age main sequence and is in the
shell hydrogen burning phase of evolution with an age of
 Gyr. The best-fit stellar ages from the
other sets of stellar models of WASP-54 also agree with our conclusion. In Fig. 13 the large uncertainty on the minimum stellar mass
estimated from interpolation of the Padova isochrones is likely due to the proximity to
the end of the main sequence kink. The Padova evolutionary models were selected
nevertheless, because they show clearly the evolved status of WASP-54.
Gyr. The best-fit stellar ages from the
other sets of stellar models of WASP-54 also agree with our conclusion. In Fig. 13 the large uncertainty on the minimum stellar mass
estimated from interpolation of the Padova isochrones is likely due to the proximity to
the end of the main sequence kink. The Padova evolutionary models were selected
nevertheless, because they show clearly the evolved status of WASP-54.
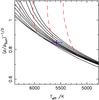 |
Fig. 15 Isochrone tracks from Demarque et al. (2004) for WASP-57 using the metallicity [Fe/H] = −0.25 dex from our spectral analysis and the best-fit stellar density 1.638 ρ⊙. From left to right the solid lines are for isochrones of: 0.1, 0.6, 1.0, 1.6, 2.0, 2.5, 3.0, 4.0, 5.0 and 6.0 Gyr. From left to right, dashed lines are for mass tracks of: 1.1, 1.0, 0.9 and 0.8 M⊙. |
In Figs. 14, and 15 we show the best-fit Yonsei-Yale stellar evolution models and mass tracks
(Demarque et al. 2004) for the planet host stars
WASP-56 and WASP-57, respectively. Using the metallicity of [Fe/H] = 0.12 dex for WASP-56
our fit of the YY-isochrones gives a stellar mass of
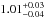 M⊙ and a
stellar age of
M⊙ and a
stellar age of 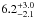 Gyr. This is in agreement with the Li
abundance measured in the spectral synthesis (see Table 3), and supports the conclusion that WASP-56 is indeed an old system. Using the
metallicity of [Fe/H] = −0.25 dex derived from our spectral analysis of WASP-57, we
interpolate the YY-models and we obtain a best-fit stellar mass of
Gyr. This is in agreement with the Li
abundance measured in the spectral synthesis (see Table 3), and supports the conclusion that WASP-56 is indeed an old system. Using the
metallicity of [Fe/H] = −0.25 dex derived from our spectral analysis of WASP-57, we
interpolate the YY-models and we obtain a best-fit stellar mass of
 M⊙ and age of
M⊙ and age of
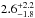 Gyr. These results also agree with our
results from spectral synthesis and shows that WASP-57 is a relatively young system. For
each system the uncertainties in the derived stellar densities, temperatures and
metallicities were included in the error calculations for the stellar ages and masses,
however systematic errors due to differences between various evolutionary models were not
considered.
Gyr. These results also agree with our
results from spectral synthesis and shows that WASP-57 is a relatively young system. For
each system the uncertainties in the derived stellar densities, temperatures and
metallicities were included in the error calculations for the stellar ages and masses,
however systematic errors due to differences between various evolutionary models were not
considered.
3.2. Planetary parameters
The planetary properties were determined using a simultaneous MCMC analysis including the
WASP photometry, the follow up TRAPPIST and Euler photometry, together with SOPHIE and
CORALIE radial velocity measurements (as appropriate see Tables 2 and 6–8). A detailed description of the method is given in Collier Cameron et al. (2007) and Pollacco et al. (2008). Our iterative fitting method uses the following
parameters: the epoch of mid transit T0, the orbital period
P, the fractional change of flux proportional to the ratio of stellar
to planet surface areas 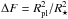 , the transit duration
T14, the impact parameter b, the radial
velocity semi-amplitude K1, the stellar effective temperature
Teff and metallicity [Fe/H], the Lagrangian elements
, the transit duration
T14, the impact parameter b, the radial
velocity semi-amplitude K1, the stellar effective temperature
Teff and metallicity [Fe/H], the Lagrangian elements
 and
and
 (where e is the
eccentricity and ω the longitude of periastron), and the systematic
offset velocity γ. For WASP-54 and WASP-57 we fitted the two systematic
velocities γCORALIE and γSOPHIE to
allow for instrumental offsets between the two data sets. The sum of the
χ2 for all input data curves with respect to the models was
used as the goodness-of-fit statistic. For each planetary system four different sets of
solutions were considered: with and without the main-sequence mass-radius constraint in
the case of circular orbits and orbits with floating eccentricity.
(where e is the
eccentricity and ω the longitude of periastron), and the systematic
offset velocity γ. For WASP-54 and WASP-57 we fitted the two systematic
velocities γCORALIE and γSOPHIE to
allow for instrumental offsets between the two data sets. The sum of the
χ2 for all input data curves with respect to the models was
used as the goodness-of-fit statistic. For each planetary system four different sets of
solutions were considered: with and without the main-sequence mass-radius constraint in
the case of circular orbits and orbits with floating eccentricity.
An initial MCMC solution with a linear trend in the systemic velocity as a free parameter, was explored for the three planetary systems, however no significant variation was found. For the treatment of the stellar limb-darkening, the models of Claret (2000, 2004) were used in the r-band, for both WASP and Euler photometry, and in the z-band for TRAPPIST photometry.
From the parameters mentioned above, we calculate the mass M, radius R, density ρ, and surface gravity log g of the star (which we denote with subscript ⋆) and the planet (which we denote with subscript pl), as well as the equilibrium temperature of the planet assuming it to be a black-body (Tpl, A = 0) and that energy is efficiently redistributed from the planet’s day-side to its night-side. We also calculate the transit ingress/egress times T12/T34, and the orbital semi-major axis a. These calculated values and their 1-σ uncertainties from our MCMC analysis are presented in Tables 4 and 5 for WASP-54, WASP-56 and WASP-57. The corresponding best-fitting transit light curves are shown in Figs. 1–3 and in Figs. 10–12. The best-fitting RV curves are presented in Figs. 4, 6, and 8.
-
For WASP-54 the MCMC solution imposing the main sequence mass-radius constraint gives unrealistic values for the best-fit stellar temperature and metallicity, as we expected for an evolved star. We then relaxed the main sequence constraint and explored two solutions: one for a circular and one for an eccentric orbit. In the case of a non-circular orbit we obtain a best-fit value for e of
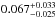 . This is less than a
3-σ detection, and as suggested by Lucy & Sweeney (1971), Eq. (22), it could be spurious. From
our analysis we obtain a best-fit χ2 statistic of
. This is less than a
3-σ detection, and as suggested by Lucy & Sweeney (1971), Eq. (22), it could be spurious. From
our analysis we obtain a best-fit χ2 statistic of
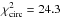 for a circular orbit, and
for a circular orbit, and
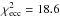 for an eccentric orbit. The circular
model is parameterised by three parameters: K, γSOPHIE
and γCORALIE, while the eccentric model additionally
constrains ecosω and
esinω. We used the 23 RV measurements available
and we performed the Lucy & Sweeney F-test (Eq. (27) of Lucy & Sweeney 1971), to investigate the probability of a
truly eccentric orbit for WASP-54b. We obtained a probability of 9% that the
improvement in the fit produced by the best-fitting eccentricity could have arisen
by chance if the orbit were real circular. Lucy
& Sweeney (1971) suggest a 5% probability threshold for the
eccentricity to be significant. From our MCMC analysis we obtain a best-fit value
for
for an eccentric orbit. The circular
model is parameterised by three parameters: K, γSOPHIE
and γCORALIE, while the eccentric model additionally
constrains ecosω and
esinω. We used the 23 RV measurements available
and we performed the Lucy & Sweeney F-test (Eq. (27) of Lucy & Sweeney 1971), to investigate the probability of a
truly eccentric orbit for WASP-54b. We obtained a probability of 9% that the
improvement in the fit produced by the best-fitting eccentricity could have arisen
by chance if the orbit were real circular. Lucy
& Sweeney (1971) suggest a 5% probability threshold for the
eccentricity to be significant. From our MCMC analysis we obtain a best-fit value
for 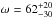 degree, this differs from 90° or
270° values expected from an eccentric fit of a truly circular orbit (see Laughlin et al. 2005). We decided to investigate
further our chances to detect a truly eccentric orbit which we discuss in Sect.
3.3. Table 4 shows our best-fit MCMC solutions for WASP-54b for a forced circular
orbit, and for an orbit with floating eccentricity. However, based on our analysis
in Sect. 3.3, we adopted the eccentric
solution. Table 4
degree, this differs from 90° or
270° values expected from an eccentric fit of a truly circular orbit (see Laughlin et al. 2005). We decided to investigate
further our chances to detect a truly eccentric orbit which we discuss in Sect.
3.3. Table 4 shows our best-fit MCMC solutions for WASP-54b for a forced circular
orbit, and for an orbit with floating eccentricity. However, based on our analysis
in Sect. 3.3, we adopted the eccentric
solution. Table 4System parameters of WASP-54.
-
For WASP-56b the available follow up spectroscopic and photometric data do not offer convincing evidence for an eccentric orbit. The free-eccentricity MCMC solution yields a value of e = 0.098 ± 0.048. The Lucy & Sweeney (1971) F-test, indicates that there is a 42% probability that the improvement in the fit could have arisen by chance if the orbit were truly circular. With only a partial high S/N follow up light curve it is more difficult to precisely constrain the stellar and planetary parameters (e.g., the time of ingress/egress, the impact parameter b, and a/R⋆), however the full, although noisy, low S/N GJT light curve (see Fig. 11), allows us to better constrain the parameters mentioned above. Therefore we decided to relax the main-sequence constrain on the stellar mass and radius and we adopt a circular orbit.
-
For WASP-57b the follow up photometry and radial velocity data allowed us to relax the main-sequence mass-radius constrain and perform an MCMC analysis leaving the eccentricity as free parameter. However, our results do not show evidence for an eccentric orbit, and the Lucy & Sweeney test yields a 100% probability that the orbit is circular. Moreover, we find that imposing the main-sequence constraint has little effect on the MCMC global solution. Thus, we decided to adopt no main sequence prior and a circular orbit.
System parameters of WASP-56 and WASP-57.
3.3. Eccentricity of WASP-54b
Here we investigate possible biases in the detection of the eccentricity of WASP-54b, and we explore the possibility that the eccentricity arises from the radial velocity measurements alone. It is well known that eccentricity measurements for a planet in a circular orbit can only overestimate the true zero eccentricity (Ford 2006). We want to quantify whether using only the radial velocity measurements at hand we can find a significant difference in the best-fit model of truly circular orbit compared to that of a real eccentric orbit with e = 0.067, as suggested by our free-floating eccentric solution. Indeed, the best-fit eccentricity depends on the signal-to-noise of the data, on gaps in the phase coverage, on the number of orbital periods covered by the data set, and the number of observations (see e.g., Zakamska et al. 2011).
We use the uncertainty of the CORALIE and SOPHIE radial velocity measurements of WASP-54,
the MCMC best-fit orbital period, velocity semi-amplitude K, and epoch of
the transit T0 as initial parameters, to compute synthetic
stellar radial velocities at each epoch of the actual WASP-54 RV data set. We generated
synthetic radial velocity data using the Keplerian model of Murray & Dermott (1999), for the two input eccentricities,
e = 0 and e = 0.067. We then added Gaussian noise
deviates to the synthetic RV at each epoch, corresponding to the original RV uncertainties
added in quadrature with 3.5 m s-1 accounting for stellar jitter. In this way
at each observation time the simulated velocity is a random variable normally distributed
around a value
v(ti) + γ,
with dispersion 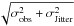 , where γ is the centre of
mass velocity. In this manner the simulated data have similar properties to the real
WASP-54 velocities but with the advantage of having a known underlying eccentricity and
orbital properties.
, where γ is the centre of
mass velocity. In this manner the simulated data have similar properties to the real
WASP-54 velocities but with the advantage of having a known underlying eccentricity and
orbital properties.
 |
Fig. 16 Histograms of the output eccentricity distributions for the input e = 0 (grey solid line), and for the input eccentricity of 0.067 (black dashed line). |
 |
Fig. 17 Cumulative Distribution Function for the two sets of best-fit eccentricities. We show in grey the CDFs for the simulated data sets with underline circular orbits, and in black the CDFs for the eccentric ones. |
We generated 1000 synthetic data sets for each input eccentricity and found the best-fit values for e. In Fig. 16 we show the output eccentricity distributions for the input e = 0 (grey solid line), and for the input eccentricity of 0.067 (black dashed line). Clearly, the one-dimensional distribution of the output eccentricity is highly asymmetric. Because e is always a positive parameter, the best-fit eccentricities are always positive values. We used the 1000 output best-fit values of e of the two samples of synthetic data sets to perform the Kolmogorov-Smirnov (KS) test to asses our ability to distinguish between the two underlying distributions. In Fig. 17 we show the Cumulative Distribution Function (CDFs) of the 1000 mock best-fit eccentricities for the two cases. We show in grey the CDFs for the simulated data sets with underlying circular orbits, and in black the CDFs for the eccentric case. We calculated D, the absolute value of the maximum difference between the CDFs of the two samples, and we used tabulated values for the KS test. We are able to reject the hypothesis that the two samples have the same underlying distribution with a confidence of 99.999%. We then conclude that the detected eccentricity of WASP-54b could indeed be real. We point out however, that time-correlated noise could potentially yield a spurious eccentricity detection. This is difficult to asses with the limited number of radial velocity observations at hand; more data and photometric monitoring during transit and secondary eclipses are needed to better constrain the orbital parameters of WASP-54b. In the following, we adopt the eccentric MCMC model for WASP-54b.
4. Discussion
We report the discovery of three new transiting extra-solar planets from the WASP survey, WASP-54b, WASP-56b and WASP-57b. In the following we discuss the implications of these new planet discoveries.
4.1. WASP-54b
From our best-fit eccentric model we obtain a planetary mass of
 MJ and a radius
of
MJ and a radius
of  RJ which yields
a planetary density of
RJ which yields
a planetary density of 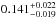 ρJ. Thus,
WASP-54b is among the least dense, most heavily bloated exoplanets and shares similarities
with low-density planets such as WASP-17b (Anderson et al.
2010), WASP-31b (Anderson et al. 2011), and
WASP-12b (Hebb et al. 2010). These exoplanets have
short orbital periods, orbit F-type host stars and therefore are highly irradiated. Using
standard coreless models from Fortney et al. (2007)
and Baraffe et al. (2008), we find that WASP-54b has
a radius more than 50% larger than the maximum planetary radius predicted for a slightly
more massive 0.68MJ coreless planet, orbiting at 0.045 AU from
a 5 Gyr solar-type star (Rexpected = 1.105
RJ). However, WASP-54 is an F-type star and therefore hotter
than the Sun, implying that WASP-54b is more strongly irradiated. The low stellar
metallicity ([Fe/H] = −0.27 ± 0.08) of WASP-54 supports the expected low planetary
core-mass thus favouring radius inflation. Different mechanisms have been proposed to
explain the observed anomalously large planetary radii such as tidal heating (Bodenheimer et al. 2001, 2003), kinetic heating (Guillot &
Showman 2002), enhanced atmospheric opacity (Burrows et al. 2007), and semi-convection (Chabrier & Baraffe 2007). While each individual mechanism would presumably
affect all hot Jupiters to some degree – for example the detected non-zero eccentricity of
WASP-54b and the strong stellar irradiation are contributing to the radius inflation –
they cannot explain the entirety of the observed radii (Fortney & Nettelmann 2010; Baraffe et al.
2010), and additional mechanisms are needed to explain the inflated radius of
WASP-54b. More recently, Batygin et al. (2011) and
Perna et al. (2010) showed that the ohmic heating
mechanism (dependent on the planet’s magnetic field and atmospheric heavy element
content), could provide a universal explanation of the currently measured radius anomalies
(see also Laughlin et al. 2011). However, according
to Wu & Lithwick (2012) Eq. (6), the maximum
expected radius for WASP-54b, including ohmic heating, is 1.61
RJ. This value for the radius is calculated assuming a
system’s age of 1 Gyr and that ohmic heating has acted since the planet’s birth.
Therefore, if we regard this value as an upper limit for the expected radius of WASP-54b
at 6 Gyr, it appears more difficult to reconcile the observed anomalously large radius of
WASP-54b (although the value is within 1-σ) even when ohmic heating is
considered, similarly to the case of WASP-17b (Anderson
et al. 2011), and HAT-P-32b (Hartman et al.
2011), as discussed by Wu & Lithwick
(2012). Additionally, Huang & Cumming
(2012) find that the efficacy of ohmic heating is reduced at high
Teff and that it is difficult to explain the observed radii
of many hot Jupiters with ohmic heating under the influence of magnetic drag. The ability
of ohmic heating in inflating planetary radii depends on how much power it can generate
and at what depth, with deeper heating able to have a stronger effect on the planet’s
evolution (Rauscher & Menou 2013; Guillot & Showman 2002). Huang & Cumming (2012) models predict a smaller radius for WASP-54b
(see their Fig. 12).
ρJ. Thus,
WASP-54b is among the least dense, most heavily bloated exoplanets and shares similarities
with low-density planets such as WASP-17b (Anderson et al.
2010), WASP-31b (Anderson et al. 2011), and
WASP-12b (Hebb et al. 2010). These exoplanets have
short orbital periods, orbit F-type host stars and therefore are highly irradiated. Using
standard coreless models from Fortney et al. (2007)
and Baraffe et al. (2008), we find that WASP-54b has
a radius more than 50% larger than the maximum planetary radius predicted for a slightly
more massive 0.68MJ coreless planet, orbiting at 0.045 AU from
a 5 Gyr solar-type star (Rexpected = 1.105
RJ). However, WASP-54 is an F-type star and therefore hotter
than the Sun, implying that WASP-54b is more strongly irradiated. The low stellar
metallicity ([Fe/H] = −0.27 ± 0.08) of WASP-54 supports the expected low planetary
core-mass thus favouring radius inflation. Different mechanisms have been proposed to
explain the observed anomalously large planetary radii such as tidal heating (Bodenheimer et al. 2001, 2003), kinetic heating (Guillot &
Showman 2002), enhanced atmospheric opacity (Burrows et al. 2007), and semi-convection (Chabrier & Baraffe 2007). While each individual mechanism would presumably
affect all hot Jupiters to some degree – for example the detected non-zero eccentricity of
WASP-54b and the strong stellar irradiation are contributing to the radius inflation –
they cannot explain the entirety of the observed radii (Fortney & Nettelmann 2010; Baraffe et al.
2010), and additional mechanisms are needed to explain the inflated radius of
WASP-54b. More recently, Batygin et al. (2011) and
Perna et al. (2010) showed that the ohmic heating
mechanism (dependent on the planet’s magnetic field and atmospheric heavy element
content), could provide a universal explanation of the currently measured radius anomalies
(see also Laughlin et al. 2011). However, according
to Wu & Lithwick (2012) Eq. (6), the maximum
expected radius for WASP-54b, including ohmic heating, is 1.61
RJ. This value for the radius is calculated assuming a
system’s age of 1 Gyr and that ohmic heating has acted since the planet’s birth.
Therefore, if we regard this value as an upper limit for the expected radius of WASP-54b
at 6 Gyr, it appears more difficult to reconcile the observed anomalously large radius of
WASP-54b (although the value is within 1-σ) even when ohmic heating is
considered, similarly to the case of WASP-17b (Anderson
et al. 2011), and HAT-P-32b (Hartman et al.
2011), as discussed by Wu & Lithwick
(2012). Additionally, Huang & Cumming
(2012) find that the efficacy of ohmic heating is reduced at high
Teff and that it is difficult to explain the observed radii
of many hot Jupiters with ohmic heating under the influence of magnetic drag. The ability
of ohmic heating in inflating planetary radii depends on how much power it can generate
and at what depth, with deeper heating able to have a stronger effect on the planet’s
evolution (Rauscher & Menou 2013; Guillot & Showman 2002). Huang & Cumming (2012) models predict a smaller radius for WASP-54b
(see their Fig. 12).
 |
Fig. 18 We plot the degree of (mis)alignment, ηRM, versus the radius anomaly ℛ and the stellar effective temperature for known planets (see text for details). The black dashed line separates aligned from mis-aligned systems following our description. The black solid line indicates ℛ = 0. Known planetary systems with characteristics across the parameter space are indicated as follows: W for WASP, H for HatNet, C for CoRoT, K for Kepler, and others by their full name. Our three new discoveries are indicated by fuchsia square symbols. We note that no RM measurement is yet available for WASP-54b, WASP-56b, WASP-57b. |
 |
Fig. 19 Planetary radius versus stellar metallicity [Fe/H] (dex) (left panel), and as a function of planet equilibrium temperature Teq (K) (right panel). Black points indicate known planets, planets in the mass range 0.2 < Mpl < 0.7 MJ are indicated by Turquoise points. Black and turquoise dashed lines are a simple linear regression to the two samples. Data were taken from the exoplanet encyclopaedia. Known planetary systems with characteristics across the parameter space are indicated as in Fig. 18. Our three new discoveries are indicated by fuchsia filled circles. |
However, the discrepancy between observations and the ohmic heating models in particular in the planetary low-mass regime (e.g. Batygin et al. 2011), shows that more understanding of planets’ internal structure, chemical composition and evolution is required to remove assumptions limiting current theoretical models. Moreover, Wu & Lithwick (2012) suggest that ohmic heating can only suspend the cooling contraction of hot–Jupiters; planets that have contracted before becoming subject to strong irradiation, can not be re-inflated. Following this scenario, the observed planetary radii could be relics of their past dynamical histories. If this is true, we could expect planets migrating via planet–planet scattering and/or Kozai mechanisms, which can become important at later stages of planetary formation compared to disc migration (Fabrycky & Tremaine 2007; Nagasawa et al. 2008), to show a smaller radius anomaly and large misalignments. This interesting possibility can be tested by planets with Rossiter-McLaughlin (RM) measurements of the spin-orbit alignment (Holt 1893; Rossiter 1924; McLaughlin 1924; Winn et al. 2006). We use all systems from the RM-encyclopedia4 to estimate the degree of spin-orbit (mis)alignment. We consider aligned every system with | λ| < 30° (a 3-σ detection from zero degrees; Winn et al. 2010), and define ηRM = (| λ| − 30°)/30° as the measure of the degree of (mis)alignment of each system. This has the advantage to show all aligned systems in the region −1 < ηRM ≤ 0. In Fig. 18 we show ηRM versus the radius anomaly and the stellar temperature Teff (as a colour gradient) for planets with RM measurements. We have calculated the radius anomaly, ℛ, as follows (Robs − Rexp)/Rexp, see also Laughlin et al. (2011). We find it difficult to identify any correlation (see also Jackson et al. 2012, and their Fig. 11). We want to stress here that the uncertainty in the timescales of planet-planet scattering and Kozai migration mechanism relative to disc migration remain still large and thus any robust conclusion can not be drawn until all the underlying physic of migration is understood. Moreover, Albrecht et al. (2012) suggest that the Kozai mechanism is responsible for the migration of the majority, if not all, hot Jupiters, those mis-aligned as well as the aligned ones, and finally, that tidal interaction plays a central role. Additionally, measurements of spin-orbit obliquities could bear information about the processes involved in star formation and disc evolution rather than on the planet migration. For example Bate et al. (2010) have recently proposed that stellar discs could become inclined as results of dynamics in their environments (e.g. in stellar clusters), and Lai et al. (2011) suggest that discs could be primordially mis-aligned respect to the star, although Watson et al. (2011) could find no evidence of disc mis-alignment. Last but not least we note that not many planets showing the radius anomaly have measured RM effects and that more observations are needed to constrain theoretical models before any robust conclusion can be drawn.
We investigate the radius anomaly of WASP-54b with respect to the full sample of known exoplanets and respect to the sample of Saturn-mass planets including the latest discoveries and the planets presented in this work (for an updated list see the extra-solar planet encyclopaedia)5. In Fig. 19 we plot the planetary radius versus the stellar metallicity (left panel), and as a function of the planet equilibrium temperature Teq (right panel). WASP-54b is indicated with a filled fuchsia circle. We highlight the sample of Saturn mass planets in turquoise; the black and turquoise dashed lines show a simple linear regression for the full exoplanet and the Saturn mass sample respectively.
 |
Fig. 20 Radius anomaly, ℛ versus [Fe/H] (dex) (left panel), and as a function of Teq (K) (right panel). The radius anomaly is calculated using the Enoch et al. (2012) empirical relation for planetary radii. Symbols are like in Fig. 19. Our three new discoveries are indicated by fuchsia filled circles. |
WASP-54b appears to strengthen the correlation between planets’ inflated radii and stellar temperature, and the anti-correlation with metallicity. With an irradiation temperature of ~2470 K, WASP-54b is in the temperature region, identified by Perna et al. (2012), with Tirr > 2000 K (Tirr as defined by Heng et al. 2012), in which planets are expected to show large day-night flux contrast and possibly temperature inversion, in which case the ohmic power has its maximum effect. With more gas giant planet detections we can start to shed some light on which mechanism might be more efficient and in which circumstances. For example, in the case of WASP-39b (Faedi et al. 2011), and WASP-13b (Skillen et al. 2009; Barros et al. 2011), two Saturn-mass planets with similar density to WASP-54b, but much less irradiated (Teq = 1116 K, and Teq = 1417 K, respectively) ohmic heating could play a less significant role (see for example Perna et al. 2012). However, many unknowns still remain in their model (e.g., internal structure, magnetic field strength, atmospheric composition). We selected all the exoplanets in the mass range between 0.1 < Mpl < 12MJ, and we used the empirical calibrations for planetary radii derived by Enoch et al. (2012) to calculate the expected planetary radius Rexp. We then used these values to derive again the Radius Anomaly. We plot the results of radius anomaly versus stellar metallicity [Fe/H] and as a function of Teq in Fig. 20. Colours and symbols are like in Fig. 19, the dotted line indicates a zero radius anomaly. The Enoch et al. (2012) relations take into account the dependence of the planetary radius from planet Teq, [Fe/H], and also tidal heating and semi-major axis. However, we note that even including this dependence, there remained significant scatter in the observed radii in particular for systems such as WASP-17b, WASP-21b and also WASP-54b, WASP-56b and WASP-57b.
Thus, more gas giant planet discoveries and their accurate characterisation are needed to
compare planetary physical properties, in order to understand their thermal structure and
distinguish between various theoretical models. With a magnitude of
V = 10.42 WASP-54 is a bright target and thus its spectroscopic and
photometric characterisation is readily feasible. Given the detected non-zero eccentricity
we encourage secondary eclipse observations in the IR. These observations will allow
precise measurement of the system’s eccentricity as well as provide fundamental
information on the thermal structure of the planet. However, we note that even in the case
of a circular orbit our MCMC solution for WASP-54 yields a very similar, inflated,
planetary radius 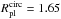 RJ, see Table
4.
RJ, see Table
4.
Finally, WASP-54 is an old (>6 Gyr) F9 star which has evolved off the main sequence and is now in the Hydrogen shell-burning phase of stellar evolution (see Fig. 13). This implies that recently in its life WASP-54 has increased its radius by more than 60%, and thus it is ascending the red giant branch (RGB). WASP-54b thus could be experiencing drag forces, both gravitational and tidal, which will affect its orbital radius. Two main factors contribute to the change of the planetary orbit: 1) the host-star can lose mass via stellar wind which could be accreted by the planet resulting in an increase of the orbital radius; and 2) the planet’s orbital angular momentum decreases due to the tidal drag, leading to a decrease of the orbital radius. This is expressed by ȧpl = ȧtide + ȧmass loss (Zahn 1977, 1989). While the second term is negligible for Jupiter-like planets (Duncan & Lissauer 1998), the term due to tides can become important as it is proportional to (R⋆/a(r))8, where a(r) is the decreasing orbital radius. This could re-set the clock of WASP-54b making it appear younger, and maybe contributing to the planet radius inflation. Finally, any planet within the reach of the star’s radius during RGB and asymptotic giant branch (AGB) phases (about 1 AU for a Solar-type star) will spiral-in and eventually merge with the star or evaporate (Villaver & Livio 2007; Livio & Soker 1984).
4.2. WASP-56b and WASP-57b
Our modelling of the WASP-56 system yields a planet mass of
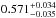 MJ and radius
of
MJ and radius
of 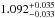 RJ which in
turn give a planet density of
RJ which in
turn give a planet density of 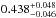 ρJ. Hence
WASP-56b belongs to the class of Saturn-mass planets and does not show a radius anomaly
(Laughlin et al. 2011). Figure 19 shows that the radius of WASP-56b is not inflated.
With a metallicity of [Fe/H] = +0.12 dex WASP-56 is more metal rich than the Sun, and with
an age of ~6.3 Gyr standard planetary evolutionary models from Fortney et al. (2007) and Baraffe et al.
(2008), show that WASP-56b has a core of approximately >10
M⊕ of heavy material. Moreover, WASP-56b orbits a main
sequence G6 star, thus it is subject to less stellar irradiation than WASP-54b. Our
best-fit MCMC model for the WASP-57 system yields a planetary mass of 0.672
MJ and a radius of 0.916 RJ.
Similarly to WASP-56b, we find that WASP-57b has a high density
(ρpl = 0.873 ρJ) and small
radius. As our analysis suggests that WASP-57b may be relatively young (~2.6 Gyr), it
may posses a significant core-mass of more than 50 M⊕, as
derived from standard evolutionary models (Fortney et al.
2007). Figure 19 shows that WASP-56 and
WASP-57 systems have different physical properties, for example the radius of WASP-57b
appears to depart from the observed trend with stellar metallicity, and the planet
possibly shares more similarities with the giant planet in the HAT-P-12 system (Hartman et al. 2009). The derived radii of WASP-56b and
WASP-57b are also consistent with more recent planetary models that include ohmic heating.
Models from Batygin et al. (2011), Wu & Lithwick (2012), and Huang & Cumming (2012), all agree in that planets with lower
effective temperatures have smaller radii, and that Jupiter-mass planets with
Teff< 1400 K experience no significant radius inflation
at all (Miller & Fortney 2011; and Fig. 6 by
Batygin et al. 2011). However, despite all
available information, we are still far from knowing the composition of the deep interior
of exoplanets. For example the very existence of planetary cores, their masses, as well as
the amount and distribution of heavy elements in the planets’ core or in their envelopes,
remain undetermined. Recently, Wilson & Militzer
(2012) suggested that planetary cores, mostly composed of rock and ices, can be
eroded and/or dissolve (depending on their mass) into the metallic H/He layers above, and
thus be redistributed in the planetary envelope (see also Umemoto et al. 2006). This can have significant implications for giant planets’
thermal evolution, their radius contraction, and overall structure.
ρJ. Hence
WASP-56b belongs to the class of Saturn-mass planets and does not show a radius anomaly
(Laughlin et al. 2011). Figure 19 shows that the radius of WASP-56b is not inflated.
With a metallicity of [Fe/H] = +0.12 dex WASP-56 is more metal rich than the Sun, and with
an age of ~6.3 Gyr standard planetary evolutionary models from Fortney et al. (2007) and Baraffe et al.
(2008), show that WASP-56b has a core of approximately >10
M⊕ of heavy material. Moreover, WASP-56b orbits a main
sequence G6 star, thus it is subject to less stellar irradiation than WASP-54b. Our
best-fit MCMC model for the WASP-57 system yields a planetary mass of 0.672
MJ and a radius of 0.916 RJ.
Similarly to WASP-56b, we find that WASP-57b has a high density
(ρpl = 0.873 ρJ) and small
radius. As our analysis suggests that WASP-57b may be relatively young (~2.6 Gyr), it
may posses a significant core-mass of more than 50 M⊕, as
derived from standard evolutionary models (Fortney et al.
2007). Figure 19 shows that WASP-56 and
WASP-57 systems have different physical properties, for example the radius of WASP-57b
appears to depart from the observed trend with stellar metallicity, and the planet
possibly shares more similarities with the giant planet in the HAT-P-12 system (Hartman et al. 2009). The derived radii of WASP-56b and
WASP-57b are also consistent with more recent planetary models that include ohmic heating.
Models from Batygin et al. (2011), Wu & Lithwick (2012), and Huang & Cumming (2012), all agree in that planets with lower
effective temperatures have smaller radii, and that Jupiter-mass planets with
Teff< 1400 K experience no significant radius inflation
at all (Miller & Fortney 2011; and Fig. 6 by
Batygin et al. 2011). However, despite all
available information, we are still far from knowing the composition of the deep interior
of exoplanets. For example the very existence of planetary cores, their masses, as well as
the amount and distribution of heavy elements in the planets’ core or in their envelopes,
remain undetermined. Recently, Wilson & Militzer
(2012) suggested that planetary cores, mostly composed of rock and ices, can be
eroded and/or dissolve (depending on their mass) into the metallic H/He layers above, and
thus be redistributed in the planetary envelope (see also Umemoto et al. 2006). This can have significant implications for giant planets’
thermal evolution, their radius contraction, and overall structure.
In conclusion, it is clear that continued exoplanet discoveries are needed to provide stronger constraints on theoretical models of close in giant planets and hence their physical properties.
Online material
Radial velocity and line bisector span measurements of WASP-54.
Radial velocity and line bisector span measurements of WASP-56.
Radial velocity and line bisector span measurements of WASP-57.
Theoretical evolutionary models for WASP-54, WASP-56 and WASP-57.
Acknowledgments
The SuperWASP Consortium consists of astronomers primarily from Queens University Belfast, St Andrews, Keele, Leicester, The Open University, Warwick, Isaac Newton Group La Palma and Instituto de Astrofsica de Canarias. The SuperWASP-N camera is hosted by the Issac Newton Group on La Palma and WASPSouth is hosted by SAAO. We are grateful for their support and assistance. Funding for WASP comes from consortium universities and from the UK’s Science and Technology Facilities Council. Spectroscopic observations were made with SOPHIE spectrograph mounted on the 1.9-m telescope at Observatoire de Haute-Provence (CNRS), France and at the ESO La Silla Observatory (Chile) with the CORALIE Echelle spectrograph mounted on the Swiss telescope.TRAPPIST is funded by the Belgian Fund for Scientific Research (Fonds National de la Recherche Scientifique, FNRS) under the grant FRFC 2.5.594.09.F, with the participation of the Swiss National Science Fundation (SNF). M. Gillon and E. Jehin are FNRS Research Associates. The research leading to these results has received funding from the European Community’s Seventh Framework Programme (FP7/2007−2013) under grant agreement number RG226604 (OPTICON). FF is grateful to the anonymous referee for useful comments significantly improving the paper.
References
- Albrecht, S., Winn, J. N., Johnson, J. A., et al. 2012, ApJ, 757, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Alsubai, K. A., Parley, N. R., Bramich, D. M., et al. 2011, MNRAS, 417, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, D. R., Hellier, C., Gillon, M., et al. 2010, ApJ, 709, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, D. R., Collier Cameron, A., Hellier, C., et al. 2011, A&A, 531, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Chabrier, G., & Barman, T. 2008, A&A, 482, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Chabrier, G., & Barman, T. 2010, Rep. Prog. Phys., 73, 016901 [NASA ADS] [CrossRef] [Google Scholar]
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barnes, S. A. 2007, ApJ, 669, 1167 [NASA ADS] [CrossRef] [Google Scholar]
- Barros, S. C. C., Faedi, F., Collier Cameron, A., et al. 2011, A&A, 525, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Batalha, N. M., Rowe, J. F., Bryson, S. T., et al. 2012, ApJS, 204, 24 [Google Scholar]
- Bate, M. R., Lodato, G., & Pringle, J. E. 2010, MNRAS, 401, 1505 [NASA ADS] [CrossRef] [Google Scholar]
- Batygin, K., Stevenson, D. J., & Bodenheimer, P. H. 2011, ApJ, 738, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bodenheimer, P., Lin, D. N. C., & Mardling, R. A. 2001, ApJ, 548, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Bodenheimer, P., Laughlin, G., & Lin, D. N. C. 2003, ApJ, 592, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Boisse, I., Eggenberger, A., Santos, N. C., et al. 2010, A&A, 523, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D. G., Basri, G., et al. 2011, ApJ, 736, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Bouchy, F., Hébrard, G., Udry, S., et al. 2009, A&A, 505, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Hebb, L., Skillen, I., et al. 2010, A&A, 519, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, D. J. A., Collier Cameron, A., Hall, C., Hebb, L., & Smalley, B. 2011, MNRAS, 415, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Bruntt, H., Bedding, T. R., Quirion, P.-O., et al. 2010, MNRAS, 405, 1907 [NASA ADS] [Google Scholar]
- Burrows, A., Hubeny, I., Budaj, J., & Hubbard, W. B. 2007, ApJ, 661, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, A. C. 2011, in IAU Symp. 276, eds. A. Sozzetti, M. G. Lattanzi, & A. P. Boss, 129 [Google Scholar]
- Carlsson, M., Rutten, R. J., Bruls, J. H. M. J., & Shchukina, N. G. 1994, A&A, 288, 860 [NASA ADS] [Google Scholar]
- Carter, J. A., Winn, J. N., Gilliland, R., & Holman, M. J. 2009, ApJ, 696, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., & Baraffe, I. 2007, ApJ, 661, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Claret, A. 2004, A&A, 428, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collier Cameron, A., Pollacco, D., Street, R. A., et al. 2006, MNRAS, 373, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Collier Cameron, A., Wilson, D. M., West, R. G., et al. 2007, MNRAS, 380, 1230 [NASA ADS] [CrossRef] [Google Scholar]
- Demarque, P., Woo, J., Kim, Y., & Yi, S. K. 2004, ApJ, 155, 667 [Google Scholar]
- Duncan, M. J., & Lissauer, J. J. 1998, Icarus, 134, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, B., Cameron, A. C., Anderson, D. R., et al. 2011, MNRAS, 410, 1631 [NASA ADS] [Google Scholar]
- Enoch, B., Collier Cameron, A., & Horne, K. 2012, A&A, 540, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabrycky, D., & Tremaine, S. 2007, ApJ, 669, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Faedi, F., Barros, S. C. C., Anderson, D. R., et al. 2011, A&A, 531, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ford, E. B. 2006, ApJ, 642, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., & Nettelmann, N. 2010, Space Sci. Rev., 152, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Marley, M. S., & Barnes, J. W. 2007, ApJ, 659, 1661 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, L., Haswell, C. A., Froning, C. S., et al. 2010, ApJ, 714, L222 [NASA ADS] [CrossRef] [Google Scholar]
- Gillon, M., Smalley, B., Hebb, L., et al. 2009, A&A, 496, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Jehin, E., Magain, P., et al. 2011, Detection and Dynamics of Transiting Exoplanets, St. Michel l’Observatoire, France, eds. F. Bouchy, R. Díaz, & C. Moutou, EPJ Web of Conferences, Vol. 11, id. 06002, 11, 6002 [Google Scholar]
- Girardi, L., Williams, B. F., Gilbert, K. M., et al. 2010, ApJ, 724, 1030 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F. 2008, The Observation and Analysis of Stellar Photospheres [Google Scholar]
- Guillot, T., & Showman, A. P. 2002, A&A, 385, 156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillot, T., Santos, N. C., Pont, F., et al. 2006, A&A, 453, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Torres, G., et al. 2009, ApJ, 706, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Torres, G., et al. 2011, ApJ, 742, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Hebb, L., Collier-Cameron, A., Loeillet, B., et al. 2009, ApJ, 693, 1920 [NASA ADS] [CrossRef] [Google Scholar]
- Hebb, L., Collier-Cameron, A., Triand, A. H. M. J., et al. 2010, ApJ, 708, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Hébrard, G., Bouchy, F., Pont, F., et al. 2008, A&A, 488, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hellier, C., Anderson, D. R., Collier Cameron, A., et al. 2009, Nature, 460, 1098 [NASA ADS] [CrossRef] [Google Scholar]
- Heng, K., Hayek, W., Pont, F., & Sing, D. K. 2012, MNRAS, 420, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Holmes, S., Kolb, U., Haswell, C. A., et al. 2011, PASP, 123, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Holt, J. R. 1893, A&A, 12, 646 [Google Scholar]
- Huang, X., & Cumming, A. 2012, ApJ, 757, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, A. P., Davis, T. A., & Wheatley, P. J. 2012, MNRAS, 422, 2024 [NASA ADS] [CrossRef] [Google Scholar]
- Jehin, E., Gillon, M., Queloz, D., et al. 2011, The Messenger, 145, 2 [NASA ADS] [Google Scholar]
- Kopparapu, R.k., Kasting, J. F., & Zahnle, K. J. 2012, ApJ, 745, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Kovács, G., Zucker, S., & Mazeh, T. 2002, A&A, 391, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kovács, G., Bakos, G., & Noyes, R. W. 2005, MNRAS, 356, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Lai, D., Foucart, F., & Lin, D. N. C. 2011, MNRAS, 412, 2790 [NASA ADS] [CrossRef] [Google Scholar]
- Laughlin, G., Marcy, G. W., Vogt, S. S., Fischer, D. A., & Butler, R. P. 2005, ApJ, 629, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Laughlin, G., Crismani, M., & Adams, F. C. 2011, ApJ, 729, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Lecavelier Des Etangs, A. 2010, Bull. Astron. Soc. India, 38, 137 [NASA ADS] [Google Scholar]
- Leconte, J., Chabrier, G., Baraffe, I., & Levrard, B. 2010, A&A, 516, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lendl, M., Anderson, D. R., Collier-Cameron, A., et al. 2012, A&A, 544, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, S.-L., Miller, N., Lin, D. N. C., & Fortney, J. J. 2010, Nature, 463, 1054 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Livio, M., & Soker, N. 1984, MNRAS, 208, 783 [NASA ADS] [Google Scholar]
- Llama, J., Wood, K., Jardine, M., et al. 2011, MNRAS, 416, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B., & Sweeney, M. A. 1971, AJ, 76, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Magain, P. 1984, A&A, 134, 189 [NASA ADS] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLaughlin, D. B. 1924, ApJ, 60, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, N., & Fortney, J. J. 2011, ApJ, 736, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, C. D., & Dermott, S. F. 1999, Solar system dynamics (Princeton University Lib.) [Google Scholar]
- Nagasawa, M., Ida, S., & Bessho, T. 2008, ApJ, 678, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perna, R., Menou, K., & Rauscher, E. 2010, ApJ, 724, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Perna, R., Heng, K., & Pont, F. 2012, ApJ, 751, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Perruchot, S., et al. 2008, in SPIE Conf. Ser., 7014 [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Pollacco, D. L., Skillen, I., Collier Cameron, A., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Pollacco, D., Skillen, I., Collier Cameron, A., et al. 2008, MNRAS, 385, 1576 [NASA ADS] [CrossRef] [Google Scholar]
- Queloz, D., Eggenberger, A., Mayor, M., et al. 2000, A&A, 359, L13 [NASA ADS] [Google Scholar]
- Queloz, D., Henry, G. W., Sivan, J. P., et al. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauscher, E., & Menou, K. 2013, ApJ, 764, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Rossiter, R. A. 1924, ApJ, 60, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, B., Fischer, D. A., Henry, G. W., et al. 2005, ApJ, 633, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Seager, S., & Mallén-Ornelas, G. 2003, ApJ, 585, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Sestito, P., & Randich, S. 2005, A&A, 442, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simpson, E. K., Faedi, F., Barros, S. C. C., et al. 2011, AJ, 141, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Skillen, I., Pollacco, D., Collier Cameron, A., et al. 2009, A&A, 502, 391 [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J. 2010, MNRAS, 408, 1689 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Tamuz, O., Mazeh, T., & Zucker, S. 2005, MNRAS, 356, 1466 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- Umemoto, K., Wentzcovitch, R. M., & Allen, P. B. 2006, Science, 311, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, J. A., Piskunov, N., & Johns-Krull, C. M. 1998, ApJ, 498, 851 [Google Scholar]
- VandenBerg, D. A., Bergbusch, P. A., & Dowler, P. D. 2006, ApJ, 162, 375 [Google Scholar]
- Villaver, E., & Livio, M. 2007, ApJ, 661, 1192 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, C. A., Littlefair, S. P., Diamond, C., et al. 2011, MNRAS, 413, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, H. F., & Militzer, B. 2012, ApJ, 745, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Johnson, J. A., Marcy, G. W., et al. 2006, ApJ, 653, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Fabrycky, D., Albrecht, S., & Johnson, J. A. 2010, ApJ, 718, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., & Lithwick, Y. 2012, ApJ, submitted [arXiv:1210.7810] [Google Scholar]
- Zacharias, N., Monet, D. G., Levine, S. E., et al. 2005, VizieR Online Data Catalog: I/297 [Google Scholar]
- Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]
- Zahn, J.-P. 1989, A&A, 220, 112 [NASA ADS] [Google Scholar]
- Zakamska, N. L., Pan, M., & Ford, E. B. 2011, MNRAS, 410, 1895 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Upper panel: discovery light curve of WASP-54b phase folded on the ephemeris given in Table 4. Lower panel: binned WASP-54b light curve. Black-solid line, is the best-fit transit model estimated using the formalism from Mandel & Agol (2002). |
| In the text | |
 |
Fig. 2 Upper panel: discovery light curve of WASP-56b phase folded on the ephemeris given in Table 5. Lower panel: binned WASP-56b light curve. Black-solid line, is the best-fit transit model estimated using the formalism from Mandel & Agol (2002). |
| In the text | |
 |
Fig. 3 Upper panel: discovery WASP light curve of WASP-57b phase folded on the ephemeris given in Table 5. Middle panel: QES light curve of WASP-57b. Lower panel: binned WASP light curve of WASP-57b. Black-solid line, is the best-fit transit model estimated using the formalism from Mandel & Agol (2002). |
| In the text | |
 |
Fig. 4 Upper panel: phase folded radial velocity measurements of WASP-54 obtained combining data from SOPHIE (filled-circles) and CORALIE (open-squares) spectrographs. Superimposed is the best-fit model RV curve with parameters from Table 4. The centre-of-mass velocity for each data set was subtracted from the RVs (γSOPHIE = −3.1109 km s-1 and γCORALIE = −3.1335 km s-1). Lower panel: residuals from the RV orbital fit plotted against time. |
| In the text | |
 |
Fig. 5 Upper panel: the bisector span measurements of WASP-54 as a function of radial velocity, values are shifted to a zero-mean (⟨ Vspan ⟩ SOPHIE = −29 m s-1, ⟨ Vspan ⟩ CORALIE = 48 m s-1). Lower panel: the bisector span measurements as a function of time (BJD – 2 450 000.0). The bisector span shows no significant variation nor correlation with the RVs, suggesting that the signal is mainly due to Doppler shifts of the stellar lines rather than stellar profile variations due to stellar activity or a blended eclipsing binary. |
| In the text | |
 |
Fig. 6 Upper panel: similar to Fig. 4, the phase folded radial velocity measurements of WASP-56. The centre-of-mass velocity for the SOPHIE data was subtracted from the RVs (γSOPHIE = −4.6816 km s-1). Lower panel: residuals from the RV orbital fit plotted against time. |
| In the text | |
 |
Fig. 7 Upper panel: the bisector span measurements for WASP-56 as a function of radial velocity, values are shifted to a zero-mean (⟨ Vspan ⟩ SOPHIE = −40 m s-1). Lower panel: the bisector span measurements as a function of time (BJD – 2 450 000.0). No correlation with radial velocity and time is observed suggesting that the Doppler signal is induced by the planet. |
| In the text | |
 |
Fig. 8 Upper panel: similar to Figs. 4 and 6 for WASP-57. The centre-of-mass velocity for each data set was subtracted from the RVs (γSOPHIE = −23.214 km s-1 and γCORALIE = −23.228 km s-1). Lower panel: residuals from the RV orbital fit plotted against time. |
| In the text | |
 |
Fig. 9 Upper panel: same as Figs. 5 and 7 we show the bisector span measurements for WASP-57 as a function of radial velocity, values are shifted to a zero-mean (⟨ Vspan ⟩ SOPHIE = −2 m s-1, ⟨ Vspan ⟩ CORALIE = 22 m s-1). Lower panel: the bisector span measurements as a function of time (BJD – 2 450 000.0). No correlation with radial velocity and time is observed suggesting that the Doppler signal is induced by the planet. |
| In the text | |
 |
Fig. 10 Euler r-band and TRAPPIST “I + z”-band follow up high signal-to-noise photometry of WASP-54 during the transit (see Table 2). The TRAPPIST light curve has been offset from zero by an arbitrary amount for clarity. The data are phase-folded on the ephemeris from Table 4. Superimposed (black-solid line) is our best-fit transit model estimated using the formalism from Mandel & Agol (2002). Residuals from the fit are displayed underneath. |
| In the text | |
 |
Fig. 11 TRAPPIST “I + z”-band and JGT R-band follow up high signal-to-noise photometry of WASP-56 during the transit (see Table 2). The JGT light curve has been offset from zero by an arbitrary amount for clarity. The The data are phase-folded on the ephemeris from Table 5. Superimposed (black-solid line) is our best-fit transit model estimated using the formalism from Mandel & Agol (2002). Residuals from the fit are displayed underneath. |
| In the text | |
 |
Fig. 12 Euler r-band and TRAPPIST “I + z”-band follow up high signal-to-noise photometry of WASP-57 during the transit (see Table 2). The TRAPPIST light curves have been offset from zero by an arbitrary amount for clarity. The data are phase-folded on the ephemeris from Table 5. Superimposed (black-solid lines) are the best-fit transit models estimated using the formalism from Mandel & Agol (2002). The residuals from each fit are displayed underneath the relative light curves. |
| In the text | |
 |
Fig. 13 Isochrone tracks from Marigo et al. (2008) and Girardi et al. (2010) for WASP-54 using the metallicity [Fe/H] = −0.27 dex from our spectral analysis and the best-fit stellar density 0.2 ρ⊙. From left to right the solid lines are for isochrones of: 1.0, 1.3, 1.6, 2.0, 2.5, 3.2, 4.0, 5.0, 6.3, 7.9, 10.0 and 12.6 Gyr. From left to right, dashed lines are for mass tracks of: 1.4, 1.3, 1.2, 1.1 and 1.0 M⊙. |
| In the text | |
 |
Fig. 14 Isochrone tracks from Demarque et al. (2004) for WASP-56 using the metallicity [Fe/H] = 0.12 dex from our spectral analysis and the best-fit stellar density 0.88 ρ⊙. From left to right the solid lines are for isochrones of: 1.8, 2.0, 2.5, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0, 11.0, 12.0, 13.0 and 14.0 Gyr. From left to right, dashed lines are for mass tracks of: 1.2, 1.1, 1.0, 0.9 and 0.8 M⊙. |
| In the text | |
 |
Fig. 15 Isochrone tracks from Demarque et al. (2004) for WASP-57 using the metallicity [Fe/H] = −0.25 dex from our spectral analysis and the best-fit stellar density 1.638 ρ⊙. From left to right the solid lines are for isochrones of: 0.1, 0.6, 1.0, 1.6, 2.0, 2.5, 3.0, 4.0, 5.0 and 6.0 Gyr. From left to right, dashed lines are for mass tracks of: 1.1, 1.0, 0.9 and 0.8 M⊙. |
| In the text | |
 |
Fig. 16 Histograms of the output eccentricity distributions for the input e = 0 (grey solid line), and for the input eccentricity of 0.067 (black dashed line). |
| In the text | |
 |
Fig. 17 Cumulative Distribution Function for the two sets of best-fit eccentricities. We show in grey the CDFs for the simulated data sets with underline circular orbits, and in black the CDFs for the eccentric ones. |
| In the text | |
 |
Fig. 18 We plot the degree of (mis)alignment, ηRM, versus the radius anomaly ℛ and the stellar effective temperature for known planets (see text for details). The black dashed line separates aligned from mis-aligned systems following our description. The black solid line indicates ℛ = 0. Known planetary systems with characteristics across the parameter space are indicated as follows: W for WASP, H for HatNet, C for CoRoT, K for Kepler, and others by their full name. Our three new discoveries are indicated by fuchsia square symbols. We note that no RM measurement is yet available for WASP-54b, WASP-56b, WASP-57b. |
| In the text | |
 |
Fig. 19 Planetary radius versus stellar metallicity [Fe/H] (dex) (left panel), and as a function of planet equilibrium temperature Teq (K) (right panel). Black points indicate known planets, planets in the mass range 0.2 < Mpl < 0.7 MJ are indicated by Turquoise points. Black and turquoise dashed lines are a simple linear regression to the two samples. Data were taken from the exoplanet encyclopaedia. Known planetary systems with characteristics across the parameter space are indicated as in Fig. 18. Our three new discoveries are indicated by fuchsia filled circles. |
| In the text | |
 |
Fig. 20 Radius anomaly, ℛ versus [Fe/H] (dex) (left panel), and as a function of Teq (K) (right panel). The radius anomaly is calculated using the Enoch et al. (2012) empirical relation for planetary radii. Symbols are like in Fig. 19. Our three new discoveries are indicated by fuchsia filled circles. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


