| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A111 | |
| Number of page(s) | 14 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201220409 | |
| Published online | 04 March 2013 | |
On the shape of the mass-function of dense clumps in the Hi-GAL fields
I. Spectral energy distribution determination and global properties of the mass-functions
1
INAF, Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125
Firenze, Italy
e-mail: olmi.luca@gmail.com
2
University of Puerto Rico, Rio Piedras Campus, Physics
Dept., Box 23343,
UPR station, San Juan,
Puerto Rico,
USA
3
Department of Physics, University of Arizona,
1118 E. 4th Street,
Tucson, AZ
85721,
USA
4
Istituto di Fisica dello Spazio Interplanetario –
INAF, via Fosso del Cavaliere
100, 00133
Roma,
Italy
5
Centre d’Étude Spatiale des rayonnements, CNRS-UPS,
31028
Toulouse,
France
6
Laboratoire d’Astrophysique de Marseille (UMR 6110 CNRS and
Université de Provence), 38 rue F.
Joliot-Curie, 13388
Marseille Cedex 13,
France
7
School of Physical Sciences, Ingram Building, University of
Kent, Canterbury,
Kent, CT2 7NH, UK
8
ESO, Karl-Schwarzschild-Str. 2, 85748
Garching bei Mnchen,
Germany
9
Centre for Astrophysics Research, University of
Hertfordshire, College
Lane, Hatfield,
AL10 9AB,
UK
Received:
19
September
2012
Accepted:
8
January
2013
Context. Stars form in dense, dusty clumps of molecular clouds, but little is known about their origin and evolution. In particular, the relationship between the mass distribution of these clumps (also known as the clump mass function or CMF) and the stellar initial mass function (IMF), is still poorly understood.
Aims. To discern the “true” shape of the CMF and to better understand how the CMF may evolve toward the IMF, large samples of bona-fide pre- and proto-stellar clumps are required. The sensitive observations of the Herschel Space Observatory (HSO) are now allowing us to look at large clump populations in various clouds with different physical conditions.
Methods. We analyze two fields in the Galactic plane mapped by HSO during its science demonstration phase (SDP), as part of the more complete and unbiased Herschel infrared GALactic Plane Survey (Hi-GAL). These fields underwent a source-extraction and flux-estimation pipeline, which allowed us to obtain a sample with thousands of clumps. Starless and proto-stellar clumps were separated using both color and positional criteria to find those coincident with MIPS 24 μm sources. We describe the probability density functions of the power-law and lognormal models that were used to fit the CMFs. For the lognormal model we applied several statistical techniques to the data and compared their results.
Results. The CMFs of the two SDP fields show very similar shapes, but very different mass scales. This similarity is confirmed by the values of the best-fit parameters of either the power-law or lognormal model. The power-law model leads to almost identical CMF slopes, whereas the lognormal model shows that the CMFs have similar widths.
Conclusions. The similar CMF shape but different mass scale represents an evidence that the overall process of star formation in the two regions is very different. When comparing with the IMF, we find that the width of the IMF is narrower than the measured widths of the CMF in the two SDP fields. This may suggest that an additional mass selection occurs in later stages of gravitational collapse.
Key words: stars: formation / stars: pre-main sequence / ISM: clouds / ISM: structure
© ESO, 2013
1. Introduction
Stars form in dense, dusty clumps of molecular clouds, but little is known about their origin and evolution (sometimes the term core is also used, see Sect. 3.2.1). In particular, the relationship between the mass distribution of these clumps (also known as the clump mass function or CMF) and the stellar initial mass function (IMF), is poorly understood (McKee & Ostriker 2007). One of the reasons for this lack of understanding, at least from the observational point of view, has been so far the difficulty in selecting a statistically significant sample of truly pre- and proto-stellar clumps from an otherwise unremarkable collection of high column density features.
Starless (or pre-stellar, if gravitationally bound) clumps represent a very early stage of the star formation (SF) process, before collapse results in the formation of a central protostar, and the physical properties of these clumps can reveal important clues about their nature: mass, spatial distributions and lifetime are important diagnostics of the main physical processes leading to the formation of the clumps from the parent molecular cloud. In addition, a comparison of the CMF to the IMF may help to understand what processes are responsible for further fragmentation of the clumps, thus determining stellar masses. Therefore, large samples of bona-fide starless clumps are important for comparison of observations with various SF models and scenarios.
Previous studies from datasets obtained with ground facilities (e.g., Testi & Sargent 1998; Motte et al. 1998; Nutter & Ward-Thompson 2006; Enoch et al. 2008; Alves et al. 2008; and Sadavoy et al. 2010) have revealed that CMFs can roughly follow either power-law or lognormal shapes, which in some cases closely resemble the observed stellar IMF. Unfortunately, these works have also emphasized the difficulty in discerning the form of the CMF (Swift & Beaumont 2010). In fact, in some cases relatively small regions within larger clouds were examined or, even when the observations produced surveys over larger areas, they were carried out at a single wavelength (e.g., 850 μm, 1.1 mm) and used different set of conditions to identify “clumps” in molecular clouds.
This scenario changed recently thanks to submillimeter continuum surveys based on telescopes placed on (sub)orbital platforms, namely the Balloon-borne Large Aperture Submillimeter Telescope (BLAST; Pascale et al. 2008) and the Herschel Space Observatory (HSO). BLAST carried out simultaneous observations at λ = 250, 350, and 500 μm of several Galactic star forming regions (SFRs; Chapin et al. 2008; Netterfield et al. 2009; Olmi et al. 2009; Roy et al. 2011). The even more sensitive and higher-angular resolutions observations of HSO are now allowing us to look at large clump populations in various clouds with different physical conditions, while using a self-consistent analysis to derive their physical parameters. For example, the first results from the Herschel Gould Belt Survey confirm that the shape of the pre-stellar CMF resembles the stellar IMF (André et al. 2010; Könyves et al. 2010).
In this first paper we analyze two fields in the Galactic plane mapped by HSO during its science demonstration phase (SDP). The two fields observed represent a sample of the more complete and unbiased Herschel infrared GALactic Plane Survey (Hi-GAL). Hi-GAL is a key program of HSO to carry out a 5-band photometric imaging survey at 70, 160, 250, 350, and 500 μm of a | b| ≤ 1°-wide strip of the Milky Way Galactic plane, originally planned for the longitude range −60° ≤ l ≤ 60° (Molinari et al. 2010b), and then extended in subsequent proposals to the whole Galactic plane.
The two SDP fields have been thoroughly analyzed and have also been used to test various methods of source extraction. In addition, they have different global properties that make them interesting for the purposes of this work. Here we use these two regions as a test bed for methods of analysis that will be later applied to the rest of the Hi-GAL survey. Therefore, the conclusions of this work should be considered preliminary and specific for the SDP fields.
The outline of the paper is the following: in Sect. 2, we give a general description of the Hi-GAL data. In Sect. 3, we describe the source extraction technique and the photometry specifically adopted in this work, while we describe how the spectral energy distributions (SEDs) were assembled in Sect. 4. The statistical analysis of the CMFs is carried out in Sects. 5 and 6. We discuss our results in Sect. 7 and draw our conclusions in Sect. 8.
2. Observations
The observations were carried out by HSO during the SDP that took place in November 2009. Five wavebands were simultaneously observed: the SPIRE instrument (Griffin et al. 2010) at λ = 250, 350, and 500 μm, and the PACS instrument (Poglitsch et al. 2010) at λ = 70 and 160 μm, were used (see Table 1). The two observed fields were centered at l = 30° and l = 59° and the final maps spanned ≃2° in both Galactic longitude and latitude.
The detailed description of the observation settings and scanning strategy adopted as well as the map generation procedure is given in Molinari et al. (2010a,b). Images of the SDP fields can be found in Molinari et al. (2010a) and an analysis of various general properties of these regions can be found in Battersby et al. (2011), Billot et al. (2010) and Elia et al. (2010). Here we summarize the most relevant SFRs known in both regions.
2.1. The ℓ = 30° region
The ℓ = 30° region that has been analyzed is approximately 4 deg2 in size and is dominated by the SRBY 162 (named after Solomon et al. 1987; see also Mooney et al. 1995; also called W43-main, see Nguyen Luong et al. 2011) and SRBY 171 (also called W43-south) SFRs, with a total mass of several times 106 M⊙. The clump of W43-main harbors a well-known giant Hii region powered by a very luminous (~3.5 × 106 L⊙, Blum et al. 1999 and references therein) cluster of Wolf-Rayet and OB stars. W43-south corresponds to a less extreme cloud, which also harbors a smaller Hii region, the well-known ultra-compact Hii region G29.96−0.02 (Cesaroni et al. 1998).
Recent analysis of the W43-main region, also in the context of the Hi-GAL project, revealed a complex structure that could be resolved into a dense cluster of protostars, infrared dark clouds, and ridges of warm dust heated by high-mass stars, thus confirming its efficiency in forming massive stars (Bally et al. 2010). While the two SDP fields seem to have similar clustering properties (Billot et al. 2011), Battersby et al. (2011) show that the median temperatures and the column densities, for all the pixels in the source masks considered, are higher in the ℓ = 30° field than in ℓ = 59°. In addition, Battersby et al. (2011) also speculate that the fact that the fraction of pixels with absorption at 8 μm in the ℓ = 59° field is so much lower than that in the ℓ = 30° field, could suggest that there is a lower fraction of cold, high-column density clouds in the ℓ = 59° field.
Finally, the richness of the ℓ = 30° region in young massive stars has also been associated with it being approximately located at the interaction region between one end of the Galactic bar and the Scutum spiral arm (Garzon et al. 1997).
PACS/SPIRE wavebands and beam FWHM.
2.2. The ℓ = 59° region
Contrary to the ℓ = 30° region, the ℓ = 59° field is not located at the tip of the Galactic bar, but belongs mostly to the Sagittarius (and, to a lesser extent, Perseus) spiral arm (Russeil et al. 2011).This region covers approximately 5 deg2 and it is prominent in images of thermal dust emission as well as in the radio and the optical (see, e.g., Chapin et al. 2008; Billot et al. 2010). The most active SFR is the Vulpecula OB association which hosts the star cluster NGC 6823 and three bright H ii regions, Sh2-86, 87 and 88. The stellar HR diagram for NGC 6823 has been examined by Massey et al. (1995). They find an age of 5–7 Myr for the bulk of the stars.
The far-infrared (60 and 100 μm) emission in this region is dominated by several luminous high-mass SFRs. Three of these have been studied by Beltrán et al. (2006) and Zhang et al. (2005) and are associated with the IRAS sources 19368+2239, 19374+2352, and 19388+2357. A further four IRAS regions (19403+2258, 19410+2336, 19411+2306, and 19413+2332) have been studied extensively by Beuther et al. (2002), using CS multi-line, multi-isotopologue observations and the 1.2 mm dust continuum.
3. Source photometry and identification of compact sources
There is no standard terminology to identify the compact sources extracted in bolometer maps by various existing algorithms. However, while “core” usually refers to a smaller-scale object (≲0.1 pc), possibly corresponding to a later stage of fragmentation, the term “clump” is generally used for a somewhat larger (≳1 pc), unresolved object, possibly composed of several cores (Williams et al. 2000). Our maps are likely a collection of both cores and clumps; however, given the distances of the two fields being analyzed here (see Sect. 4 and Russeil et al. 2011), we think the term clump is more appropriate to refer to the compact objects extracted in the SDP fields. We also note that since we are constructing the clump (and not core) mass functions, with the clumps likely being composed of smaller fragments, no attempt will be made here to separate the gravitationally bound and unbound sources.
3.1. Source and flux extraction in the SPIRE/PACS maps
As we mentioned in the introduction, the SDP fields have been useful test beds for various methods of source extraction and brightness estimation. However, for the purposes of this work it was also necessary to adopt a method that in the end would be able to determine source masses, and thus the CMF, with a better accuracy compared to the original source extraction and brightness estimation pipeline described by Elia et al. (2010) and Molinari et al. (2011). This is achieved in two ways: first, the method outlined here defines in a consistent manner the region of emission of the same volume of gas/dust at different wavelengths, thus differing from the source grouping and band-merging procedures described by Molinari et al. (2011) and Elia et al. (2010). In addition, the SED fitting procedure is more accurate compared to that described by (Elia et al. 2010, see Sect. 4).
The source extraction and brightness estimation techniques applied to the Hi-GAL maps in this work are similar to the methods used during analysis of the BLAST05 (Chapin et al. 2008) and BLAST06 data (Netterfield et al. 2009; Olmi et al. 2009). However, important modifications have been applied to adapt the technique to the SPIRE/PACS maps, as described below.
Candidate sources are identified by finding peaks after a Mexican Hat Wavelet type convolution (MHW, hereafter; see, e.g., Barnard et al. 2004) is applied to all five SPIRE/PACS maps. Initial candidate lists from 70, 160 and 250 μm are then found and fluxes at all three bands extracted by fitting a compact Gaussian profile to the source. Sources are not identified at 350 and 500 μm due to the greater source-source and source-background confusion resulting from the lower resolution, and also because these two SPIRE wavebands are in general more distant from the peak of the source SED. The Gaussian-fitted sources are then selected based on their FWHM, which is allowed to vary from 80% of the beam (to allow for pixelization effects on point sources) to 90 arcsec.
Number of sources selected in the two SDP fields.
Each temporary source list at 70, 160 and 250 μm is then purged of overlapping sources, by comparing the positions of nearby sources at a given wavelength using their estimated FWHM: if two sources are nearer than one-half of the sum of their respective FWHMs, they are taken as being the same object. Purged lists at 70 and 160 μm are then merged, and nearby 70 and 160 μm positions are treated as before. This merged 70/160 μm catalog is then compared with the (already purged) 250 μm source list, and the same procedure is repeated for identifying overlapping objects and merge the two catalogs. Finally, these sources are selected based on their integrated flux (which cannot be lower than 0.5, 1.5 and 1.2 Jy at 70, 160 and 250 μm, respectively).Thus, a final source catalog is generated that contains well separated objects detected from all three 70, 160 and 250 μm wavebands.
In the next stage, Gaussian profiles are fitted again to all SPIRE/PACS maps, including the 350 and 500 μm wavebands, using the size and location parameters determined at the shorter wavelengths during the previous steps (the size of the Gaussian is convolved to account for the differing beam sizes). The center of the new Gaussian fit is allowed to move at most by ≃5 arcsec relative to the candidate source location, to allow for morphological differences at 350 and 500 μm, and for fitting one single Gaussian profile at those locations where more than one candidate source had been identified during the previous steps. Then, before writing the final catalog, sources are again selected using their final FWHM.Using this technique, 5851 and 2595 selected compact clumps were identified in the ℓ = 59° and ℓ = 30° fields, respectively. The number of sources effectively used in the subsequent analysis was further reduced during the SED fitting process to 3402 and 1950 sources, respectively (see Sect. 4 and Table 2). The difference in the number of sources selected for the two regions is likely a consequence of the larger area mapped toward the ℓ = 59° field and its closer proximity, which allows us to be more sensitive to the more numerous less massive clumps1.
Monte Carlo simulations are then used to determine the completeness of this process. Following the method outlined by Netterfield et al. (2009), fake sources are added to the 160 and 250 μm maps and are then processed through the same source extraction pipeline. To generate these fake sources, we randomly select a fraction (~20−30%) of the sources in the final catalog, we convolve them with the measured beam in each band and insert them back into the original maps. The locations of these new sources are chosen to be at least 2 arcmin from their original location, but not more than 4 arcmin, so that the fake sources will reside in a similar background environment to their original location. These added sources are not allowed to overlap each other, but are not prevented from overlapping sources originally present in the map so that the simulation will account for errors due to confusion. Therefore, the sample of fake sources approximately reproduces the distributions in intensity and size of the original catalog.
The resulting set of maps, with both original and fake sources, is run through the source extraction pipeline and the extracted source parameters are compared to the simulation input. The simulations are performed using smaller (≃0.2 deg2) maps, extracted from the original maps of the ℓ = 59° and ℓ = 30° fields (containing a few hundreds sources), in order to be able to run the source extraction pipeline multiple times, thus achieving a statistical average for the mass completeness limits (estimated from the 160 μm maps, at the 80% confidence level), which are listed in Table 3. These values have been estimated for the median distances of each field, also listed in the same table, and typical values of T = 20 K and β = 2 (the dust emissivity index, see Sect. 4) have been used to convert the flux completeness limit into a mass completeness limit.
3.2. Separating starless and proto-stellar clumps
3.2.1. Color criteria
The catalogs of sources compiled with the technique described in Sect. 3.1 do not attempt to separate starless and proto-stellar clumps. These populations must be separated using independent methods, to ensure that they can be accurately characterized. Various criteria can be found in the literature (see, e.g., De Luca et al. 2007; Enoch et al. 2009; Netterfield et al. 2009; Olmi et al. 2009), that use both proximity criteria to infrared objects and temperature criteria. The different approaches may differ in their operational definition of the positional criteria and the identification of proto-stellar phases based on SED shape and/or other color criteria.
In this work we combine color and positional criteria. This approach has the advantage of being less computationally expensive, and least biased to particular models or model parameters, as compared to a full SED approach (e.g., Robitaille et al. 2006). Given the range of spatial resolutions and spectral coverage within the SPIRE/PACS wavebands, this combined approach should also be least biased as compared to positional criteria applied to data sets with single resolutions and limited spectral coverage.
Young protostars still embedded in dense clumps should peak in the far-infrared due to the absorption and reprocessing of light to longer wavelengths by envelopes. Several recent studies have identified these sources using IRAC and MIPS colors (e.g., Harvey et al. 2006; Jørgensen et al. 2006, 2007, 2008). Here, however, we also include the somewhat more restrictive criteria of Sadavoy et al. (2010). In fact, since embedded protostars peak in the far-infrared, we also require that proto-stellar clumps have strong detections at 24 and 70 μm and rising-red colors. The red colors will exclude stellar sources, which have flat colors in the infrared regime, but not extragalactic sources. Extragalactic contamination must be excluded separately, for example following the color criteria of Gutermuth et al. (2008). IRAC and MIPS colors were assigned to the Hi-GAL sources using the MIPSGAL catalog (Shenoy et al. 2012) and according to positional criteria (see Sect. 3.2.2). Our sensitivity and color criteria for identifying proto-stellar objects are thus as follows (see also Sadavoy et al. 2010):
-
(A) The source flux at 24 μm has a signal-to-noise ratio (S/N) ≥ 3 and the source 70 μm flux is higher than 0.1 Jy.
-
(B) Source colors are dissimilar to those of star-forming galaxies (see Gutermuth et al. 2008), i.e.,
![\begin{eqnarray*} \left [4.5\right ] - \left [5.8\right ] & < & \frac{1.05}{1.20} ~ (\left [5.8\right ] - \left [8.0\right ] - 1), \,\,\, {\rm and} \\ \left [4.5\right ] - \left [5.8\right ] & > & 1.05, \,\,\, {\rm and} \\ \left [5.8\right ] - \left [8.0\right ] & > & 1. \end{eqnarray*}](/articles/aa/full_html/2013/03/aa20409-12/aa20409-12-eq34.png)
-
(C2) If the source is not detected at 24 μm (i.e., due to the lower sensitivity), then the IRAC bands are used,
![\begin{eqnarray*} \left [3.6 \right ] - \left [5.8 \right ] & > & 1.25, \,\,\, {\rm and} \\ \left [4.5 \right ] - \left [8.0 \right ] & > & 1.4. \end{eqnarray*}](/articles/aa/full_html/2013/03/aa20409-12/aa20409-12-eq36.png)
Thus, for a clump to be classified as proto-stellar, conditions (A), (B) and (C1) (or (C2) if the source is not detected at 24 μm) must be simultaneously fulfilled. It should be noted that the higher spatial resolution of IRAC data makes it more likely to have chance associations.In addition, sources with no 24 μm detection, and possibly even those with no 70 μm counterpart, cannot be definitively classified as starless, at least in a low-mass clump (see Chen et al. 2010). These kind of sources may in fact represent a stage intermediate between a gravitationally-bound starless clump (i.e., pre-stellar) and a Class 0 protostar, and are difficult to identify. However, apart from these elusive objects, our color-criteria should be able to efficiently separate starless and proto-stellar clumps on a statistical basis. Separating gravitationally bound and unbound clumps is beyond the scopes of this work.
Median values of mass, temperature, distance and completeness limits toward the ℓ = 30° and ℓ = 30° fields.
3.2.2. Positional criteria
The positional criteria to associate a MIPSGAL counterpart to the Hi-GAL sources could make the usual assumption that a given clump is to be considered proto-stellar only if a young stellar object (YSO) candidate is found in the region of a clump where the intensity of emission is higher, which is generally associated with the peak submillimeter flux. However, this simple scenario may become more complicated in confused regions, where several clumps are blended together, at which point the peak value could be off-center with respect to the volume occupied by the individual clumps.
The search for YSO candidates near a given submillimeter clump is further complicated by the fact that clumps can be irregular in shape. In these cases, a circular approximation of the clump extent, by using the radius obtained with a 2D Gaussian fit to the clump intensity distribution, could lead the search algorithm to actually probe regions beyond the “real” boundaries of the clump. On the other hand, a fixed angular tolerance could clearly lead to either underestimate or overestimate the number of YSO counterparts to the submillimeter clumps.
An alternative algorithm to ensure that the observed size and shape of the clump is considered, has been suggested by Sadavoy et al. (2010), in which the object location is compared to a percentage of the difference between the peak submillimeter intensity and the boundary intensity. Sadavoy et al. (2010) use a constant value for the boundary intensity, but in the case of the SPIRE/PACS maps, where the clump shape and intensity has to be defined with respect to the local background, we used a different approach.
First, a 1 arcmin box is extracted from the PACS 160 μm flux density map, centered around each catalog clump. To the purpose of this procedure, we think the 160 μm map constitutes the best trade-off between sensitivity and angular resolution. An average, local background level is then estimated and subtracted from the map. Intensity at the nominal position of the clump is evaluated in this background-subtracted map; the algorithm also examines the nearby pixels in case the (local) peak submillimeter intensity is off-center from the clump nominal location. The search area for coincidence with YSO candidates is then defined as all those pixels interior to the contour corresponding to a fraction f = 0.7 of the peak intensity value found in the previous step (see Fig. 1).
The fraction f = 0.7 has been determined by trial-and-error, and thus there were always several cases where identifying unique YSO candidates within the specified contour was not always clear, particularly in crowded regions or when a dim clump was found near a much more intense source. In these cases, the search area could result in an elongated or quite irregular shape, and we thus introduced further constraints; for example, the YSO candidate must be located within a maximum angular distance from the center of the clump, which is a function of the clump FWHM. We note that the arbitrarity of the f = 0.7 value may lead to some cross-contamination of the starless and proto-stellar samples, but it should be statistically comparable in the two SDP fields.
The presence of a Mid-Infrared source near a Hi-GAL clump was checked in two different ways. First, the MIPSGAL catalog was used (Shenoy et al. 2012). To complement this catalog, we also decided to apply the source extraction algorithm described in Sect. 3.1 to the mosaicked 24 μm MIPS maps (MIPS24, hereafter) of the ℓ = 59° and ℓ = 30° fields (hereafter, we will refer to these MIPS24 sources as MHW24 objects). This approach had the advantage of being able to detect MIPS24 sources that could have been missed by the point response function fitting applied by the MIPSGAL team (Carey et al. 2009). The application of the MHW method also ensured that MIPS24 sources were extracted in a similar and uniform fashion to the SPIRE/PACS maps.
Thus, for each Hi-GAL clump, once the contour defined by f = 0.7 was determined, the presence of both MIPSGAL and MHW24 sources within this contour was checked. If a MIPSGAL source satisfies the coincidence criterion, and if in addition its colors satisfy the criteria described in Sect. 3.2.1, then this object is assumed to be an embedded YSO and its associated Hi-GAL clump is considered to be proto-stellar. If a MHW24 source satisfies the coincidence criterion, and if it also satisfies the sensitivity criterion (A) above, then this object is equally assumed to be an embedded YSO and its associated Hi-GAL clump proto-stellar. Thus, if either a MIPSGAL or MHW24 source satisfies the color and coincidence criteria, then the associated Hi-GAL clump is considered proto-stellar.
On the other hand, if no MIPSGAL and no MHW24 counterpart is found, or a 24 μm counterpart is found but one or more of the criteria (A), (B) and (C) of Sect. 3.2.1 is not fulfilled, then the Hi-GAL clump is assumed to be pre-stellar. In the latter case, the catalog of pre-stellar cores could be contaminated by for example, star forming galaxies and planetary nebulae. However, only very few galaxies are likely to be detected in the two SDP fields (Russeil et al. 2011). In addition, we have checked for contamination of our catalogs by planetary nebulae, using the color criteria described by Anderson et al. (2012), and found it also negligible.
4. Submillimeter-MIR SEDs
As discussed by Olmi et al. (2009), our goal here is to use a simple, single-temperature SED model to fit the sparsely sampled photometry described in Sect. 3.1, which will allow us to infer the main physical parameters of each clump: mass, temperature and luminosity. These quantities must be interpreted as a parameterization of a more complex distribution of temperature and density in the clump and the equally complex response of each instrument to these physical conditions.
In this work we mainly follow the method described by Olmi et al. (2009, and references
therein). Contrary to these authors, however, we do not assume
optically-thin emission and use a general isothermal modified blackbody (or gray-body)
emission of the type (see, e.g., Mezger et al. 1990),
![\begin{equation} S_{\nu} = \Omega_{\rm s} B_{\nu}(T) \, \left [ 1 - \exp ( - \tau_{d} ) \right ], \label{eq:sed} \end{equation}](/articles/aa/full_html/2013/03/aa20409-12/aa20409-12-eq45.png) (1)where
τd, the dust optical depth, can be written
as:
(1)where
τd, the dust optical depth, can be written
as: 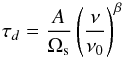 (2)where A is a constant,
Bν(T) is the Planck
function, β is the dust emissivity index, Ωs is the solid angle
subtended by the source and the emissivity factor is normalized at a fixed frequency
ν0. We then write the factor A in terms of a
total (gas + dust) clump mass, M, the dust mass absorption coefficient
κ0 (evaluated at ν0), and the
distance to the object, d:
(2)where A is a constant,
Bν(T) is the Planck
function, β is the dust emissivity index, Ωs is the solid angle
subtended by the source and the emissivity factor is normalized at a fixed frequency
ν0. We then write the factor A in terms of a
total (gas + dust) clump mass, M, the dust mass absorption coefficient
κ0 (evaluated at ν0), and the
distance to the object, d: 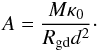 (3)The distance to individual clumps was taken
from the catalog of Russeil et al. (2011), if an
object of known distance is found within a radius of 5 arcmin, and otherwise set to the
median value (see Table 3). Since
κ0 refers to a dust mass, the gas-to-dust mass ratio,
Rgd, is required in the denominator to infer total masses. We
adopt κ0 = 11 cm2 g-1, evaluated at
ν0 = c/250 μm, and
Rgd ≃ 100 (Martin et al.
2012).
(3)The distance to individual clumps was taken
from the catalog of Russeil et al. (2011), if an
object of known distance is found within a radius of 5 arcmin, and otherwise set to the
median value (see Table 3). Since
κ0 refers to a dust mass, the gas-to-dust mass ratio,
Rgd, is required in the denominator to infer total masses. We
adopt κ0 = 11 cm2 g-1, evaluated at
ν0 = c/250 μm, and
Rgd ≃ 100 (Martin et al.
2012).
Equation (1) is fit to all of the five SPIRE/PACS fluxes (with the PACS 70 μm flux used as upper-limit, see below), using χ2 optimization. Color correction of the SPIRE/PACS flux densities is performed using the filter profiles, and color-corrected fluxes are thus used in all subsequent applications. Besides to A and T, also β and Ωs are allowed to vary during the χ2 optimization, for a total of four free parameters.
 |
Fig. 1 Top. Example of a Hi-GAL starless clump (nominal position represented with a yellow “+” sign) with an irregular shape (shown by the black area, against the gray-scale background, representing the 160 μm emission). No MIPSGAL or other source found with the Mexican Hat Wavelet algorithm, also named as MHW24 source (see Sect. 3.1),(shown with the “∗” and “diamond” symbols, respectively) is falling within the black area and thus they cannot be associated with the Hi-GAL source. Bottom. Example of a proto-stellar Hi-GAL clump. One MHW24 source is associated with the submillimeter clump, but no MIPSGAL source satisfies the coincidence and color criteria. |
 |
Fig. 2 Top. SED of a source in the ℓ = 30° field. The upper limit at 70 μm is shown and black line shows the best-fit modified blackbody, whereas gray lines show the 68% confidence envelope of modified blackbody models from Monte Carlo simulations. Also shown are the best-fit parameters from the SED fit: temperature, T, total luminosity, L, dust mass, Mdust, dust emissivity index, β, and dust optical depth, τ.Bottom. Another Hi-GAL clump with a more peculiar shape of the SED, due to the use of Eq. (1) instead of the optically-thin approximation. |
As far as the parameter Ωs is concerned, the SED fit will generally result in a different value of the source size as compared to that obtained during the source extraction procedure described in Sect. 3.1. This is because the source extraction procedure yields a source size mainly based on the source shape; however, the source size delivered by the χ2 optimization of the SED depends solely on the source photometry. In general, we find that the latter method tends to underestimate the source size obtained during the source extraction procedure.
Uncertainties for all model parameters are obtained from Monte Carlo simulations (see Chapin et al. 2008). Mock data sets are generated from realizations of Gaussian noise. The χ2 minimization process is repeated for each data set, and the resulting parameters are placed in histograms. Means and 68% confidence intervals are then measured from the relevant histograms. Figure 2 shows example SEDs obtained with this procedure; the black line consists of the best-fit modified blackbody at wavelengths >70 μm and the solid gray lines indicate the 68% confidence envelope of modified blackbodies that fit the SPIRE and PACS data.
The 70 μm flux is always treated as an upper-limit, because it would otherwise cause systematic deviations from a single-temperature gray-body fit. In fact, a non-negligible fraction of the flux at this wavelength is emitted by the warmer proto-stellar object, either formed or in advanced stage of formation at the center of the clump, while most of the emission at λ ≥ 160 μm originates in the colder envelope of the clump (Elia et al. 2010). We adopt “survival analysis” to properly include the upper-limit in the calculation of χ2 (see the discussion in Chapin et al. 2008). A threshold value has been chosen for χ2 in order to select the final sample of sources used in the next sections (see Table 2).
5. Description of models used to fit the CMF
The goal of our analysis is to find the best fit parameters for some selected models given the data. In the following sub-sections we give a general description of the mathematical functions used in this analysis, whereas in the Appendices we outline the details of the numerical implementation, where all procedures were written in the Interactive Data Language2.
5.1. Definitions
For the sake of mathematical convenience we will approximate discrete power-law and
lognormal behavior with their continuous counterparts. Therefore, if
dN represents the number of objects of mass M lying
between M and M + dM, the number
density distribution per mass interval (or CMF),
ξ(M) = dN/dM, is
defined through the relation (e.g., Chabrier 2003):
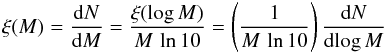 (4)thus,
ξ(M)dM represents the number of
objects with mass M lying in the interval
[M,M + dM]. The probability of a mass falling in the
interval [M,M + dM] can be written for a continuous
distribution as p(M)dM, where
p(M) represents the mass probability density function
(PDF). The PDF and CMF must obey the following normalization conditions:
(4)thus,
ξ(M)dM represents the number of
objects with mass M lying in the interval
[M,M + dM]. The probability of a mass falling in the
interval [M,M + dM] can be written for a continuous
distribution as p(M)dM, where
p(M) represents the mass probability density function
(PDF). The PDF and CMF must obey the following normalization conditions: 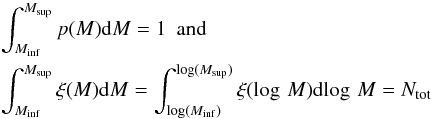 (5)where Ntot is a
normalization constant which, for the case of discrete data, can be interpreted as the
total number of objects being considered in the sample. From Eq. (5) p(M) can
also be written as
p(M) = ξ(M)/Ntot.
(5)where Ntot is a
normalization constant which, for the case of discrete data, can be interpreted as the
total number of objects being considered in the sample. From Eq. (5) p(M) can
also be written as
p(M) = ξ(M)/Ntot.
Minf and Msup denote respectively the inferior and superior limits of the mass range for the objects in the sample, beyond which the distribution does not follow the behavior specified by the PDF or CMF. For example, the power-law density (see Sect. 5.1.1) diverges as M → 0 so its formal distribution cannot hold for all M ≥ 0; there must be some lower bound to the power-law behavior, which we denote by Minf. More in general, Minf and Msup should give us a more quantitative estimate of the mass range where the assigned PDF gives a better description of the data.
In the following, we will also make use of the complementary cumulative
distribution function (CCDF), which we denote
Pc(M) and which is defined as the
probability of the mass to fall in the interval ![\hbox{$\left[M, M_{\rm sup} \right]$}](/articles/aa/full_html/2013/03/aa20409-12/aa20409-12-eq86.png) , i.e.:
, i.e.: 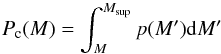 (6)
(6)
5.1.1. Power-law form
The most widely used functional form for the CMF is the power-law: 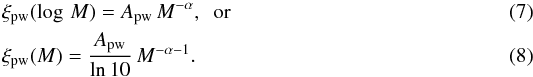 where Apw is
the normalization constant. The original Salpeter value for the IMF is
α = 1.35 (Salpeter 1955).
where Apw is
the normalization constant. The original Salpeter value for the IMF is
α = 1.35 (Salpeter 1955).
The PDF of a power-law (continuous) distribution is given by (e.g., Clauset et al. 2009): 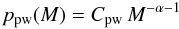 (9)where the normalization constant can be
determined by applying the condition in Eq. (5), yielding:
(9)where the normalization constant can be
determined by applying the condition in Eq. (5), yielding: 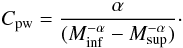 (10)For α > 0 and
Msup ≫ Minf one can use the
approximation
(10)For α > 0 and
Msup ≫ Minf one can use the
approximation 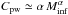 as in Clauset et al. (2009) and Swift &
Beaumont (2010, when the proper
adjustments for the different definition of the power-law exponent in Eq. (8) are done).
as in Clauset et al. (2009) and Swift &
Beaumont (2010, when the proper
adjustments for the different definition of the power-law exponent in Eq. (8) are done).
According to Elmegreen (1985) power-laws tend to arise when only the fragments can fragment, and lognormals arise when both the fragments and the interfragment gas can fragment during a hierarchical process of star formation. However, the power-law functional form is also widely used because of its versatility. Past surveys of SFRs (see for example Swift & Beaumont 2010, and references therein) have shown a variety of values for α, and the same dataset can be typically fit by one or more power-laws with different slopes. In particular, the power-law behavior does not extend to very low masses, where it displays a turnover or break below typically a few M⊙.
5.1.2. Lognormal form
Another widely used functional form for the CMF is the lognormal,
which can be rigorously justified because the central limit theorem applied to
isothermal turbulence naturally produces a lognormal PDF in density. A CMF consistent
with a lognormal form has also been observed in recent surveys of nearby SFRs (see,
e.g., Enoch 2006). The continuous lognormal CMF
can be written (e.g., Chabrier 2003):
![\begin{eqnarray} \xi_{\rm ln}(\ln\,M) = \frac{A_{\rm ln}}{\sqrt{2\pi} \, \sigma} \, \exp \left[ - \frac{(\ln M - \mu)^2}{2 \sigma^2} \right] \label{eq:logn} \end{eqnarray}](/articles/aa/full_html/2013/03/aa20409-12/aa20409-12-eq97.png) (11)where μ and
σ2 = ⟨ (lnM − ⟨ lnM ⟩ )2 ⟩
denote respectively the mean mass and the variance in units of lnM.
Aln represents a normalization constant which is evaluated
in Appendix A.
(11)where μ and
σ2 = ⟨ (lnM − ⟨ lnM ⟩ )2 ⟩
denote respectively the mean mass and the variance in units of lnM.
Aln represents a normalization constant which is evaluated
in Appendix A.
The PDF of a continuous lognormal distribution can be written as (e.g., Clauset et al. 2009): ![\begin{eqnarray} p_{\rm ln}(M) & = & \frac{C_{\rm ln}}{M} \, \exp \left[ - \frac{(\ln M - \mu)^2}{2 \sigma^2} \right] = \frac{C_{\rm ln}}{M} \, \exp \left[ - x^2 \right]. \label{eq:PDFln} \end{eqnarray}](/articles/aa/full_html/2013/03/aa20409-12/aa20409-12-eq101.png) (12)Again, by applying the normalization
condition, Eq. (5), we find:
(12)Again, by applying the normalization
condition, Eq. (5), we find:
![\begin{equation} C_{\rm ln} = \sqrt{\frac{2}{\pi \sigma^2} } \, \times \left[ {\rm erfc}(x_{\rm inf}) - {\rm erfc}(x_{\rm sup}) \right]^{-1} \end{equation}](/articles/aa/full_html/2013/03/aa20409-12/aa20409-12-eq102.png) (13)where the variables x,
xinf and xsup are defined in
Appendix A, and we note that the parameters
Minf and Msup are not
necessarily the same as those determined for the power-law distribution. As we already
mentioned in Sect. 5.1.1, if the condition
Msup ≫ Minf holds, then we can
write:
(13)where the variables x,
xinf and xsup are defined in
Appendix A, and we note that the parameters
Minf and Msup are not
necessarily the same as those determined for the power-law distribution. As we already
mentioned in Sect. 5.1.1, if the condition
Msup ≫ Minf holds, then we can
write: ![\begin{equation} C_{\rm ln} \simeq \sqrt{\frac{2}{\pi \sigma^2} } \, \times \left[ {\rm erfc}(x_{\rm inf}) \right]^{-1}. \end{equation}](/articles/aa/full_html/2013/03/aa20409-12/aa20409-12-eq106.png) (14)Then, by using the definition of PDF given
in Sect. 5.1 and the relations for the erf and
erfc functions shown in Appendix A, the CCDF for
the lognormal distribution,
(14)Then, by using the definition of PDF given
in Sect. 5.1 and the relations for the erf and
erfc functions shown in Appendix A, the CCDF for
the lognormal distribution, 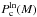 , can be written as:
, can be written as: ![\begin{equation} P_{\rm c}^{\rm ln}(M) = \left[ \frac{ {\rm erfc}(x) - {\rm erfc}(x_{\rm sup}) } { {\rm erfc}(x_{\rm inf}) - {\rm erfc}(x_{\rm sup}) } \right]\cdot \label{eq:CCDFerf} \end{equation}](/articles/aa/full_html/2013/03/aa20409-12/aa20409-12-eq108.png) (15)
(15)
 |
Fig. 3 Left panels. Log–log histograms showing the distribution of M for all (black), starless (red) and proto-stellar (blue) clumps in the ℓ = 30° (top) and ℓ = 59° (bottom) fields. The bin width has been chosen according to the Freedman and Diaconis’ rule (see Sect. 6.3). The dashed lines represent the results of fit to the data using the procedure PLFIT. The vertical dashed line corresponds to the value of Minf, whereas the solid vertical line shows the 80% completeness limits (see Sect. 3.1 and Table 3). Vertical bars show Poisson errors. Right panels. Histograms showing the distribution of clump temperature (color codes are as in the left panels) in the ℓ = 30° (top) and ℓ = 59° (bottom) fields. The bin width has also been chosen according to the Freedman and Diaconis’ rule. Line styles are as before. |
Best-fit parameters (from PLFIT) to the CMF of the ℓ = 30° and ℓ = 59° fields, for the power-law distribution.
6. Fitting the data
6.1. Evaluating the global CMF
In this section we apply several statistical methods to analyze the CMF of the two regions, and find the best-fit parameters for power-law and lognormal models. An important question is whether the source sample for which the CMF is constructed should undergo more specific selection criteria, such as distance, cloud or cluster location, etc. The two SDP fields may be divided into smaller sub-regions, each containing clumps in various stages of evolution as well as already formed stars. Each sub-region is in turn characterized by locally different mass distributions, which may be functions of the radial distance from the region’s center (see, e.g., Dib et al. 2010). The mass function of clumps in an entire SDP field is thus the sum of all the sub-regions and “local” distributions.
The analysis of the effects of all these local distributions on the CMF of a larger (several sq. degrees) region is out of the scopes of this work. We do not attempt to separate the complete source sample of a given SDP region into somewhat smaller sub-samples. Here we limit ourselves to address the differences, if any, between the global CMF of the two regions and postpone the study of the aforementioned effects to future work. To minimize the effects that distance uncertainties may have on the determination of the CMF of each SDP region, each source has been assigned a specific distance, by searching for the nearest counterpart (within a 5 arcmin radius) from the catalog of Russeil et al. (2011). If no counterpart of known distance is found for a given source, then it is assigned the median distance.
On the other hand, when evaluating the distance effects between the two SDP fields we only consider the median distance of each region (see Sect. 7.3.1). Clearly, this also means that the CMF will be affected by distance-dependent sensitivity and completeness effects. However, this approach will allow us to determine if there are any significant differences with previous surveys, where the source sample is usually smaller and confined to a single cloud.
6.2. Fitting the power-law form with the method of maximum likelihood
Various methods exist to fit a parametric model to an astronomical dataset (see, e.g., Babu & Feigelson 2006). One of the most popular methods to analyze the mass spectra of the starless and proto-stellar clump populations, consists of placing the masses of individual clumps in logarithmically spaced bins, with a lower limit on the error estimated from the Poisson uncertainty for each bin. The resulting CMF can then be fitted with either a power-law or a lognormal function. Then, the resulting best-fit slope, α, and the parameters of the lognormal function, μ and σ, usually depend somewhat on the histogram binning, and the selected mass range, particularly when “small” samples of sources are used.
Alternatively, we have considered a method described by Babu & Feigelson (2006) and more in details by Clauset et al. (2009), that consists of a statistically principled set of techniques that allow for the validation and quantification of power-laws. According to Clauset et al. (2009), this method should be quite immune to the significant systematic errors that may affect the histogram technique, including those uncertainties associated with the histogram binning. Clauset et al. (2009) have described a procedure that implements both the discrete and continuous maximum likelihood estimator (MLE) for fitting the power-law distribution to data, along with a goodness-of-fit based approach to estimating the lower cutoff of the data. Hereafter, we will refer to this procedure simply as “PLFIT”, from the name of the main MATLAB3 function performing the aforementioned statistical operations. The results of the PLFIT method are shown in Fig. 3 and Table 4, and are discussed in Sect. 7.
6.3. Fitting the lognormal form
Like Sect. 6.2, also in the case of the lognormal distribution we want to avoid the uncertainties inherent in fitting data using regression models arising from data binning. The first method we describe here is thus based on Bayesian regression techniques. In particular we have used WinBUGS4, a programing language based software that is used to generate a random sample (using Markov chain Monte Carlo, or MCMC, methods) from the posterior distribution of the parameters of a Bayesian model. As it is customary in Bayesian regression techniques (e.g., Gregory 2005), once the posterior distributions of the parameters of interest have been generated, they can be analyzed using various descriptive measures. In Table 5 we show the mean values obtained for the μ and σ parameters from 10 000 samples MCMC runs in WinBUGS. We note that the procedure implemented in WinBUGS does not currently allow to estimate the Minf and Msup parameters. In the left panels of Fig. 4 we also show the histograms of the ln(M) values, with the solid lines representing Guassian fits to the histograms obtained with a standard regression technique. Both histograms and fits are shown for graphical purposes only.
 |
Fig. 4 Left panels. Histograms showing the distribution of ln(M) for all (black), starless (red) and proto-stellar (blue) clumps in the ℓ = 30° (top) and ℓ = 59° (bottom) fields. The solid lines represent the results of Gaussian fits to the histograms. The vertical solid lines represent the completeness limits as in Fig. 3. Vertical bars show Poisson errors. Right panels. PDFs of the mass distribution (black solid line) and best-fit (red dashed line), in the ℓ = 30° (top) and ℓ = 59° (bottom) fields. |
Mean values, obtained using WinBUGS, from the posterior distributions of the μ and σ parameters of the lognormal distribution, shown separately for the ℓ = 30° and ℓ = 59° fields.
While we consider the results from the Bayesian regression technique our baseline results, we also want to compare them with two alternative methods. The first one is based on the computation of the PDF of the mass distribution, and is actually dependent on data binning. To compute the PDF, we plot in the right panels of Fig. 4 the normalized counts, i.e., the count per bin divided by the product of the total number of data points in the sample, N, and the (linear) bin width. For this normalization, the area under the histogram is equal to one, as described in Sect. 5.1. From a probabilistic point of view, this normalization results in a relative histogram that is most akin to the PDF. In addition, the bin width, W, has been chosen according to the Freedman and Diaconis’ rule (Freedman & Diaconis 1981) W = 2(IQR)N−1/s3, where IQR represents the inter-quartile range. The best-fit results to the PDF from standard regression techniques are then listed in Table 6.
The final method we describe here to fit the CMF with a lognormal distribution, consists of implementing a MLE method for the lognormal function, similar to the one described in Sect. 6.2 for the power-law distribution. Therefore, we have numerically maximized the likelihood of the distribution in Eq. (12) as a function of σ and μ, using Powell’s method (e.g., Press et al. 2002), while Minf and Msup were arbitrarily fixed to constant values.The results of this method are also listed in Table 6 (4th and 5th column).
Best-fit parameters to the CMF of the ℓ = 30° and ℓ = 59° fields, for the lognormal distribution and the PDF and MLE methods.
A modification of the MLE method can also allow the computation of the Minf and Msup parameters. These parameters can then be found by minimizing the Kolmogorov-Smirnov (KS) statistic between the best fit model and the data as a function of Minf and Msup (see Appendix B). These latter results are listed in the columns 6–9 of Table 6.
7. Discussion
7.1. ℓ = 30° field
As shown in Sect. 6.2, because of our large sample of sources, we were able to apply the PLFIT procedure not only to the whole sample of clumps detected toward the ℓ = 30° field, but also to the starless and proto-stellar clump samples, separately. Irrespectively of the specific sample used, we obtained α ≃ 1.1 (see Fig. 3 and Table 4). For Minf, which represents the break or turnover below which the distribution does not follow power-law behavior, we find Minf ~ 200 M⊙, except for the sample of proto-stellar clumps where Minf = 138 M⊙ but it has a large uncertainty. As previously stated, we estimate the distance of each source by finding the nearest counterpart from the catalog of Russeil et al. (2011). One may thus be concerned about the effects that sources with assigned the median distance may have on the results shown in Table 4. This is not an issue for the ℓ = 30° field, where only a few percent of the sources cannot be assigned a counterpart from the catalog of Russeil et al. (2011). However, this is not the case for the ℓ = 59° field (see Sect. 7.2).
Compared to the observations of the ℓ = 30° region by Eden et al. (2012), the values of our power-law slopes are higher than the corresponding values found by these authors. We note, however, that the region mapped by Eden et al. (2012) is not exactly coincident with the Hi-GAL map, and that different methods for source extraction and mass estimation have been used. Assigning distances to the individual sources and fitting the CMF also followed different procedures.
In comparing our results with previous surveys of regions other than the ℓ = 30° and ℓ = 59° fields, we prefer to use the results of Swift & Beaumont (2010), who applied similar statistical techniques to various (smaller) datasets from the literature. In particular, for the power-law functional form, we prefer not to compare our best-fit parameters with corresponding parameters obtained using regression models depending on data binning, which are subject to large uncertainties, especially when the sample is relatively small (a few hundred sources or less).
Thus, in terms of the power-law functional form, the estimated value of α agrees very well with the typical values(α + 1 ~ 1.7 to 4.1 with typical errors ~5 to 25%)found by Swift & Beaumont (2010)5, for both low- and high-mass SFRs. On the other hand, the estimated value of Minf ~ 200 M⊙, is higher compared to the values estimated by Swift & Beaumont (2010) for intermediate- and high-mass SFRs. We also note the similar values of α and (to a lesser extent) Minf for the starless and proto-stellar clump samples.
As far as the lognormal fits are concerned, Table 5 shows that the starless population in ℓ = 30° has a slightly higher (lower) value of μ (σ) compared to the proto-stellar population. More Hi-GAL fields need to be observed to determine whether this is a general property. In terms of the other statistical methods, in Table 6 we note that while the results of the MLE and PDF methods yield μ values quite similar to the Bayesian results, the values of σ can differ significantly (by almost a factor of 2). We also note the relatively small value of Msup, compared to the whole range of masses in the ℓ = 30° field.
It is worth noting that the completeness limit of the ℓ = 30° field (see Table 3) is lower than the Minf value. Therefore, the peak of the ln(M) distribution in Fig. 4 is real, though barely constrained. Likewise, the turnover or break in the CMF of Fig. 3 is also effectively observed. However, the fact that the turnover is not better constrained may render all later comparisons between the power-law and lognormal distributions problematic.
7.2. ℓ = 59° field
As shown in Table 4 (see also Fig. 3) we find that the values of α in the ℓ = 59° field are also approximately equal for the whole sample and the starless clumps. These values are consistent, within the errors, with those found in the ℓ = 30° field, as discussed in Sect. 7.3.1. However, the α value for the proto-stellar clumps is indeed lower than that for the starless sample. Apart from statistical uncertainty, given the much smaller number of proto-stellar clumps in the ℓ = 59° field, we also investigated distance effects as a possible explanation for this discrepancy. In fact, about 30% of the clumps in the ℓ = 59° field do not have a counterpart from the catalog of Russeil et al. (2011), and thus were assigned the median distance.
Therefore, we run the PLFIT procedure again without including in the sample the sources that were initially assigned the median distance. The values obtained for both α and Minf were then consistent with those of Table 4, except for the proto-stellar sample, where we get α = 1.44 ± 0.39 and Minf = 9.9 ± 4.0 M⊙. Although these values of α and Minf are now consistent, within the errors, with the other samples listed in Table 4, this simple test strongly suggests that differences between starless and proto-stellar samples, as well as distance effects, will need to be carefully analyzed in all subsequent Hi-GAL fields.
Interestingly, the value of Minf estimated in the ℓ = 59° region is much lower than that of the ℓ = 30° field, as expected given that the ℓ = 59° field is mostly a low- to intermediate-mass SFR. However, contrary to the ℓ = 30° region, our estimated value of Minf is comparable to the values estimated by Swift & Beaumont (2010) for low-mass SFRs. On the other hand, while Swift & Beaumont (2010) report a wide range of CMF slopes (corresponding to α ~ 0.7−3.1), our estimated values of α do not appreciably vary from the ℓ = 30° to the ℓ = 59° field.
In terms of the lognormal functional form of the CMF toward the ℓ = 59° field, the results shown in Fig. 4 and Tables 5 and 6 confirm that the mass range in the two SDP fields are quite different (see Table 3). As in the ℓ = 30° region, Table 6 shows that the values of σ obtained through the MLE and PDF methods can significantly differ from the Bayesian results. We have yet to determine if this is a feature associated with the different methods.
Finally, the completeness limit of the ℓ = 59° region is quite lower than its corresponding Minf value. Therefore, the peak of the ln(M) distribution in Fig. 4 is at least partially resolved, and the detection of a turnover in the CMF is more reliable than it is in the ℓ = 30° field.
 |
Fig. 5 Top. Histogram profiles from Fig. 4, with solid and dashed lines representing the ℓ = 30° and ℓ = 59° fields, respectively. The dash-dotted line represents the distribution obtained for the ℓ = 59° field traslated to the distance of ℓ = 30° (see text). Bottom. CMF profiles from Fig. 3; line styles are as before. The vertical lines mark the completeness limits listed in Table 3 for the ℓ = 30° (solid line) and ℓ = 59° (dashed line) fields. |
7.3. Comparing the two SDP fields
7.3.1. Distance effects
Comparing now the results for the ℓ = 30° and ℓ = 59° fields, we have already noted how the values of α are similar for the two regions. Therefore, if the evolution toward the IMF of high-mass clumps (ℓ = 30°) is different from those of low- and intermediate-mass clumps (ℓ = 59°), it leaves no trace on the shape of the CMF of these two regions. This conclusion, however, is critically dependent on the correcteness of the distance estimates, and in any case it is the result of a survey over a large collection of different SFRs. In fact, our findings in the ℓ = 30° field are different from those of Netterfield et al. (2009) who found a different slope of the CMF for the cold and warm populations of clumps in the Vela-C region, which is a less heterogeneous region compared to our field.
We have also seen that the values of μ and Minf are clearly different for the two regions (see Tables 5 and 6). However, and despite the uncertainty on the absolute value of σ, when comparing the results obtained with the same regression technique in the two SDP fields, we find that the values of σ are remarkably similar. We can also estimate the average values from all four methods used, and we find ⟨ σ ⟩ = 2.0 ± 0.8 and 1.8 ± 0.6 [ln M⊙] for ℓ = 30° and ℓ = 59°, respectively. These average values are also consistent with the range of σ found by Swift & Beaumont (2010), ~0.7 to 3.4, who also found the variation in the values of μ (~−5.4 to 2.7) larger compared to that of σ. Therefore, the histograms representing the distribution of the ln(M) values in the two SDP fields (Fig. 4) are characterized by decidedly different mass scales, but are quite similar in shape, as it can be noted in the left panels of Fig. 4.
This similarity can be noted even more clearly in the top panel of Fig. 5, where the histogram profiles from Fig. 4, for the ℓ = 30° and ℓ = 59° fields, are shown side by side. We also compare the CMFs in the bottom panel of Fig. 5. Apart from differences due to binning, one can clearly see that the mass distributions are very similar, although this similarity should be taken as far as the completeness limits actually allow to.
Thus, although a full comparison of the mass spectra, including the mass range below the peak of the ln(M) distribution, will require higher sensitivities than those achieved in the two SDP fields, the existence of a mass scale difference between the two regions is clear. It seems unlikely that the different mass scales could be due entirely to differences in the median distance (see Table 3), since this could account for a factor ~4 at most in mass sensitivity.
To test this issue more quantitatively, we have performed a simulation where the ℓ = 59° field is traslated to the same distance as the ℓ = 30° region. In this procedure, the angular resolution in all of the original maps is first degraded by convolving with a beam in each band enlarged for the increased distance, and then the maps are re-binned accordingly (Facchini, priv. comm.). The resulting maps are run through the source extraction and SED-fitting pipelines, and the extracted SED parameters are estimated by scaling the distance of each source by the ratio of the median distances in the ℓ = 30° and ℓ = 59° fields.
Our test thus shows that the mass of the sources in the traslated maps can increase due to the larger distance and, to a lesser extent, due to the “merging” of sources that are detected as separate objects in the original maps of the ℓ = 59° region. The new mass distribution is shown in Fig. 5, where we can clearly see that the CMF for the traslated ℓ = 59° region lies between the original CMFs of the ℓ = 59° and ℓ = 30° fields. This appears to confirm our earlier assumption that distance effects alone cannot explain the overall difference in mass scales between these two specific SFRs. This difference could be explained by different evolutionary stages, if the sources in the ℓ = 59° field were in a more advanced state of fragmentation compared to those in the ℓ = 30° region. However, we do not have any additional evidence of this systematic evolutionary difference between the two fields. We thus think that this mass scale effect is more likely evidence that the overall process of star formation in the two regions must be radically different.
7.3.2. Clump formation efficiency
It is too early to speculate about the physical origins of the differences described in the previous section. In fact, we have exploited only a few percent of the Hi-GAL survey in the present analysis. With more and more regions being analyzed we expect to find statistically significant indications that there may indeed exist different Galactic star-forming regimes, as stated in the Hi-GAL scientific goals. For the present analysis, the prominence of the ℓ = 30° region in star-forming indicators, compared to ℓ = 59° (Battersby et al. 2011), including the (triggered) W43 “mini-starburst” complex (Bally et al. 2010), and the mass scale difference we found between the two regions, could all be related with the ℓ = 30° field being located near the interaction region between one end of the Galactic bar and the Scutum spiral arm, where high concentrations of shocked gas are more likely to be found (Garzon et al. 1997; López-Corredoira et al. 1999).
To further test this scenario, we have estimated an additional figure of merit, the
clump formation efficiency (CFE), that we define as:
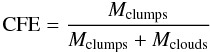 (16)where Mclumps
represents the total mass of the clumps (above completeness limit) and
Mclouds is the mass of the ambient gas. Given that the two
SDP fields represent a collection of regions, possibly at different distances, rather
than being a single molecular cloud at a single distance, two obvious problems must be
considered. First off, we have to select a method to map the total column density,
without being limited by threshold, opacity and temperature variations in the ambient
gas/dust. Second, the distance to separate parcels of gas must be estimated.
(16)where Mclumps
represents the total mass of the clumps (above completeness limit) and
Mclouds is the mass of the ambient gas. Given that the two
SDP fields represent a collection of regions, possibly at different distances, rather
than being a single molecular cloud at a single distance, two obvious problems must be
considered. First off, we have to select a method to map the total column density,
without being limited by threshold, opacity and temperature variations in the ambient
gas/dust. Second, the distance to separate parcels of gas must be estimated.
Goodman et al. (2009) have discussed and
compared several methods for measuring column density in molecular clouds and they
conclude that dust extinction is likely the best probe. Therefore, we have downloaded
the Av extinction maps6 obtained by Rowles & Froebrich
(2009) and Froebrich & Rowles (2010)
and used them to estimate the total column density in the two SDP regions. Specifically,
we have selected only those pixels with Av > 1 mag and
we have assigned them a distance based on the closest (within a 3 arcmin radius) Hi-GAL
clump previously identified. Then, the extinction in each pixel has been converted to
column density using the conversion factor
NH = βv Av cm-2
where
βv = 2 × 1021 cm-2 mag-1
(Savage & Mathis 1979). Therefore, the
total mass in the clouds has been calculated as:
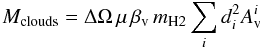 (17)where ΔΩ is the solid angle subtended by
each pixel in the extinction maps, μ = 1.38 takes into account the
cosmic He abundance, mH2 is the mass of molecular hydrogen,
and di and
(17)where ΔΩ is the solid angle subtended by
each pixel in the extinction maps, μ = 1.38 takes into account the
cosmic He abundance, mH2 is the mass of molecular hydrogen,
and di and
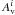 represent the distance and visual
extinction toward the i-th pixel.
represent the distance and visual
extinction toward the i-th pixel.
Our estimated CFE thus amounts to ≃2.4% and ≃0.7% for the l = 30° and l = 59° regions, respectively. We note that both values are quite lower compared to the CFE estimated by Eden et al. (2012) and Nguyen Luong et al. (2011) toward the l = 30° field.However, although the determination of the absolute values of the CFE is subject to several uncertainties (mainly due to the estimate of the distance and the mass of the ambient gas), the relative comparison between the two SDP fields indicates that clumps may indeed form more efficiently in the l = 30° rather than in the l = 59° field. However, since the relationship of the CFE with the star formation efficiency (SFE) is not known, our present analysis is not yet conclusive that the SFE is also higher in the l = 30° field.
7.4. Comparing the CMF to the IMF
The qualitative similarity, observed in past studies, between the CMF and the IMF offers support for the accepted idea that stars form from dense clumps, and thus comparing the two distributions should allow us to learn how observed samples of clumps evolve into stars. This comparison is actually a complex task because CMFs are often different but the IMF appears to be quite universal. In addition, it is difficult to understand whether the CMFs of different regions are intrinsically different, or to what degree systematic differences in each dataset (either observational or from post-processing) may contribute to the variations seen from dataset to dataset.
Swift & Williams (2008) have shown that different evolutionary pathways from clumps to stars produce variations in the form of the resultant IMF. They also showed that while the power-law slope is robustly determined, the width of the lognormal distribution is a more sensitive indicator of clump evolution. As we showed earlier, the average value of σ in the two SDP fields is ~1.9 [ln M⊙], consistent with the range of σ found by Swift & Beaumont (2010), and with an uncertainty of as much as 40%. However, the width of the IMF has been measured to be narrower, between 0.3 and 0.7 [ln M⊙] (e.g., Chabrier 2003). As already suggested by Swift & Beaumont (2010) this would appear to indicate that an additional mass selection occurs in later stages of gravitational collapse.
8. Conclusions
We have analyzed two fields mapped by the SPIRE and PACS instruments of HSO during its science demonstration phase. The two fields, which are part of the Herschel infrared GALactic Plane Survey, were centered at l = 30° and l = 59° and the final maps covered almost 10 deg2 of galactic plane.
The two regions underwent a source-extraction and flux-estimation pipeline, which allowed us to obtain a sample with thousands of clumps. The mass of the clumps was obtained from a gray-body fit to the SED of each source, with the distance estimated using the catalog of Russeil et al. (2011).We then applied several statistical methods to analyze the resulting CMFs, and found the best-fit parameters for power-law and lognormal models. No attempt was made to select more uniform sub-samples, except for starless and proto-stellar clumps. Our main conclusions are the following:
-
Our best-fit parameters for the power-law distribution show a well defined slope (α ≃ 1.2, with a ~15% uncertainty) when comparing the two SDP fields. In contrast, we find a very different value of the parameter Minf for the two regions analyzed. We find that Minf is higher than the completeness limit in each region and is thus well defined.
-
We have used several statistical techniques to estimate the best-fit parameters of the lognormal functional form. For each separate method, the values of the width, σ, in the two SDP fields are remarkably similar. The average values, ⟨ σ ⟩ = 1.9 ± 0.8 and 1.8 ± 0.6 [ln M⊙] for ℓ = 30° and ℓ = 59°, respectively, are also very similar. Like Minf, the value of the characteristic mass, μ, is very different in the two regions.
-
The similarity of α and σ on one side, and the difference of Minf and μ on the other, show that the CMFs of the two SDP fields have very similar shapes but different mass scales which, according to our simulations, cannot be explained by distance effects alone. This represents an evidence that the overall process of star formation in the two regions is very different.
-
The similarity of the shape of the CMF in the two SDP regions suggests that if the evolution toward the IMF of high-mass clumps (ℓ = 30°) is different from those of low- and intermediate-mass clumps (ℓ = 59°), it leaves no trace on the shape of the CMF.
-
The width of the IMF is narrower than the measured values of σ in the two SDP fields. This suggests that an additional mass selection occurs in later stages of gravitational collapse.
Acknowledgments
We thank S. Carey for making the 24 μm catalog avialable to us prior to its official release.
References
- Alves, J., Lombardi, M., & Lada, C. J. 2008, A&A, 462, L17 [Google Scholar]
- Anderson, L. D., Zavagno, A., Barlow, M. J., García-Lario, P., & Noriega-Crespo, A. 2012, A&A, 537, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Babu, G. J., & Feigelson, E. D. 2006, in Astronomical Data Analysis Software and Systems XV, eds. C. Gabriel, C. Arviset, D. Ponz, & S. Enrique, ASP Conf. Ser., 351, 127 [Google Scholar]
- Bally, J., Anderson, L. D., Battersby, C., et al. 2010, A&A, 518, L90 [Google Scholar]
- Barnard, V. E., Vielva, P., Pierce-Price, D. P. I., et al. 2004, MNRAS, 352, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Battersby, C., Bally, J., Ginsburg, A., et al. 2011, A&A, 535, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beltrán, M. T., Brand, J., Cesaroni, R., et al. 2006, A&A, 447, 221 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Beuther, H., Schilke, P., Menten, K. M., et al. 2002, ApJ, 566, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Billot, N., Noriega-Crespo, A., Carey, S., et al. 2010, ApJ, 712, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Billot, N., Schisano, E., Pestalozzi, M., et al. 2011, ApJ, 735, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Blum, R. D., Damineli, A., & Conti, P. S. 1999, AJ, 117, 1392 [NASA ADS] [CrossRef] [Google Scholar]
- Carey, S. J., Noriega-Crespo, A., Mizuno, D. R., et al. 2009, PASP, 121, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Cesaroni, R., Hofner, P., Walmsley, C. M., & Churchwell, E. 1998, A&A, 331, 709 [NASA ADS] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Chapin, E., Ade, P. A. R., Bock, J. J., et al. 2008, ApJ, 681, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., Arce, H. G., Zhang, Q., et al. 2010, ApJ, 715, 1344 [Google Scholar]
- Clauset, A., Shalizi, C. R., & Newman, M. E. J. 2009, SIAM Rev., 51, 661 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- De Luca, M., Giannini, T., Lorenzetti, D., et al. 2007, A&A, 474, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dib, S., Shadmehri, M., Padoan, P., et al. 2010, MNRAS, 405, 401 [NASA ADS] [Google Scholar]
- Eden, D. J., Moore, T. J. T., Plume, R., & Morgan, L. K. 2012, MNRAS, 422, 3178 [NASA ADS] [CrossRef] [Google Scholar]
- Elia, D., Schisano, E., Molinari, S., et al. 2010, A&A, 518, L97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elmegreen, B. G. 1985, in Birth and Infancy of Stars, eds. R. Lucas, A. Omont, & R. Stora, 257 [Google Scholar]
- Enoch, M. L., Young, K. E., Glenn, J., et al. 2006, ApJ, 638, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, M. L., Evans, II, N. J., Sargent, A. I., et al. 2008, ApJ, 684, 1240 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, M. L., Evans, II, N. J., Sargent, A. I., & Glenn, J. 2009, ApJ, 692, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, D., & Diaconis, P. 1981, Probability Theory and Related Fields, 57, 453 [Google Scholar]
- Froebrich, D., & Rowles, J. 2010, MNRAS, 406, 1350 [NASA ADS] [Google Scholar]
- Garzon, F., Lopez-Corredoira, M., Hammersley, P., et al. 1997, ApJ, 491, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, A. A., Pineda, J. E., & Schnee, S. L. 2009, ApJ, 692, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, P. C. 2005, Bayesian Logical Data Analysis for the Physical Sciences: A Comparative Approach with Mathematica Support (Cambridge University Press) [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Gutermuth, R. A., Myers, P. C., Megeath, S. T., et al. 2008, ApJ, 674, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, P. M., Chapman, N., Lai, S.-P., et al. 2006, ApJ, 644, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, J. K., Harvey, P. M., Evans, II, N. J., et al. 2006, ApJ, 645, 1246 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, J. K., Johnstone, D., Kirk, H., & Myers, P. C. 2007, ApJ, 656, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, J. K., Johnstone, D., Kirk, H., et al. 2008, ApJ, 683, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Könyves, V., André, P., Men’shchikov, A., et al. 2010, A&A, 518, L106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Corredoira, M., Garzón, F., Beckman, J. E., et al. 1999, AJ, 118, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, P. G., Roy, A., Bontemps, S., et al. 2012, ApJ, 751, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Massey, P., Johnson, K. E., & Degioia-Eastwood, K. 1995, ApJ, 454, 151 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Ostriker, E. C. 2007, ARA&A, 45, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Mezger, P. G., Zylka, R., & Wink, J. E. 1990, A&A, 228, 95 [NASA ADS] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010a, A&A, 518, L100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010b, PASP, 122, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Schisano, E., Faustini, F., et al. 2011, A&A, 530, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mooney, T., Sievers, A., Mezger, P. G., et al. 1995, A&A, 299, 869 [NASA ADS] [Google Scholar]
- Motte, F., Andre, P., & Neri, R. 1998, A&A, 336, 150 [NASA ADS] [Google Scholar]
- Netterfield, C. B., Ade, P. A. R., Bock, J. J., et al. 2009, ApJ, 707, 1824 [NASA ADS] [CrossRef] [Google Scholar]
- Nguyen Luong, Q., Motte, F., Schuller, F., et al. 2011, A&A, 529, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nutter, D., & Ward-Thompson, D. 2006, MNRAS, 368, 1833 [NASA ADS] [CrossRef] [Google Scholar]
- Olmi, L., Ade, P. A. R., Anglés-Alcázar, D., et al. 2009, ApJ, 707, 1836 [NASA ADS] [CrossRef] [Google Scholar]
- Pascale, E., Ade, P. A. R., Bock, J. J., et al. 2008, ApJ, 681, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2002, Numerical recipes in C++ : the art of scientific computing, eds. W. H., Press, S. A., Teukolsky, W. T., Vetterling, & B. P., Flannery [Google Scholar]
- Robitaille, T. P., Whitney, B. A., Indebetouw, R., Wood, K., & Denzmore, P. 2006, ApJS, 167, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Rowles, J., & Froebrich, D. 2009, MNRAS, 395, 1640 [NASA ADS] [CrossRef] [Google Scholar]
- Roy, A., Ade, P. A. R., Bock, J. J., et al. 2011, ApJ, 727, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Russeil, D., Pestalozzi, M., Mottram, J. C., et al. 2011, A&A, 526, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sadavoy, S. I., Di Francesco, J., Bontemps, S., et al. 2010, ApJ, 710, 1247 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Savage, B. D., & Mathis, J. S. 1979, ARA&A, 17, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Shenoy, S. S., Carey, S. J., Noriega-Crespo, A., et al. 2012, ApJ, submitted [Google Scholar]
- Solomon, P. M., Rivolo, A. R., Barrett, J., & Yahil, A. 1987, ApJ, 319, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Swift, J. J., & Beaumont, C. N. 2010, PASP, 122, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Swift, J. J., & Williams, J. P. 2008, ApJ, 679, 552 [NASA ADS] [CrossRef] [Google Scholar]
- Testi, L., & Sargent, A. I. 1998, ApJ, 508, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., Blitz, L., & McKee, C. F. 2000, Protostars and Planets IV, 97 [Google Scholar]
- Zhang, Q., Hunter, T. R., Brand, J., et al. 2005, ApJ, 625, 864 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Normalization of the lognormal mass function
By applying the normalization condition (5) to the lognormal MF in Eq. (11), we get: ![\appendix \setcounter{section}{1} \begin{eqnarray*} \int_{\ln(M_{\rm inf})}^{\ln(M_{\rm sup})} \frac{A_{\ln}}{\sqrt{2\pi}\sigma} \, \exp \left [ - \frac{(\ln M - \mu)^2}{2 \sigma^2} \right ] {\rm d}\!\ln\,M = N_{\rm tot} \end{eqnarray*}](/articles/aa/full_html/2013/03/aa20409-12/aa20409-12-eq182.png) which by changing the variable of integration
can be easily transformed into:
which by changing the variable of integration
can be easily transformed into: 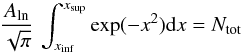 (A.1)where we have defined the variable
(A.1)where we have defined the variable
 , and
xinf = x(Minf)
and
xsup = x(Msup).
Then, by using the following relation
, and
xinf = x(Minf)
and
xsup = x(Msup).
Then, by using the following relation 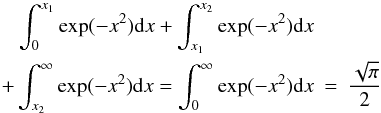 which converts into:
which converts into: ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{eq:Aln2} \int_{x_1}^{x_2} \exp(-x^2) {\rm d} x & = & \frac{\sqrt{\pi}}{2} \left[ 1 - {\rm erf}(x_1) - {\rm erfc}(x_2) \right] \\ \nonumber & =& \frac{\sqrt{\pi}}{2} \left[ {\rm erfc}(x_1) - {\rm erfc}(x_2) \right] \end{eqnarray}](/articles/aa/full_html/2013/03/aa20409-12/aa20409-12-eq188.png) (A.2)we can write Eq. (A.1) as:
(A.2)we can write Eq. (A.1) as: ![\appendix \setcounter{section}{1} \begin{equation} \frac{A_{\rm ln}}{2} \, \left[ 1 - {\rm erf}(x_{\rm inf}) - {\rm erfc}(x_{\rm sup}) \right] = N_{\rm tot} \label{eq:Aln3} \end{equation}](/articles/aa/full_html/2013/03/aa20409-12/aa20409-12-eq189.png) (A.3)where the erf and erfc are defined as:
(A.3)where the erf and erfc are defined as:
![\appendix \setcounter{section}{1} \begin{eqnarray*} && {\rm erf}(x) = \frac{2}{\sqrt{\pi}} \int_{0}^{x} \exp(-t^2) {\rm d} t \,\,\, {\rm and} \\[-1mm] && {\rm erfc}(x) = 1 - {\rm erf}(x) = \frac{2}{\sqrt{\pi}} \int_{x}^{\infty} \exp(-t^2) {\rm d} t . \end{eqnarray*}](/articles/aa/full_html/2013/03/aa20409-12/aa20409-12-eq192.png) Finally, we can write the normalization
constant, Aln, as:
Finally, we can write the normalization
constant, Aln, as: ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{eq:Aln} A_{\rm ln} &&= 2 N_{\rm tot} \\ &&\quad \times\left[ {\rm erfc} \left( \frac{(\ln M_{\rm inf} - \mu)^2}{2 \sigma^2} \right) - {\rm erfc} \left( \frac{(\ln M_{\rm sup} - \mu)^2}{2 \sigma^2} \right) \right]^{-1} \cdot \nonumber \end{eqnarray}](/articles/aa/full_html/2013/03/aa20409-12/aa20409-12-eq193.png) (A.4)
(A.4)
Appendix B: Estimating the Minf and Msup parameters
The most common and easiest ways of choosing the Minf and
Msup parameters (for both the power-law and lognormal
functional forms) are either to take the minimum (above the completeness limit) and
maximum values of the mass range in the dataset, or to plot a histogram of
M and choose Minf and
Msup based on a (arbitrary) threshold occupancy for the
bins. A more robust approach is desirable. In the method we use here, we choose the values
of Minf and Msup that make the
probability distributions of the observed data and the best-fit lognormal model as similar
as possible in the range ![\hbox{$\left [ {M}_{\rm inf}, {M}_{\rm sup} \right]$}](/articles/aa/full_html/2013/03/aa20409-12/aa20409-12-eq198.png) (Clauset
et al. 2009).
(Clauset
et al. 2009).
There are a variety of measures for quantifying the distance between two probability
distributions, and following Clauset et al. (2009)
we choose the Kolmogorov-Smirnov (or KS) statistics, which is simply the maximum distance
between the CCDFs (see Sect. 5.1) of the observed
data, 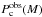 , and the fitted model,
, and the fitted model,
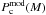 :
: ![\appendix \setcounter{section}{2} \begin{equation} D = {\rm max}_{_{ \left[ M_{\rm inf} \leq M \leq M_{\rm sup} \right ] } } | P_{\rm c}^{\rm obs}(M) - P_{\rm c}^{\rm mod}(M) |. \label{eq:ks} \end{equation}](/articles/aa/full_html/2013/03/aa20409-12/aa20409-12-eq201.png) (B.1)The procedure that implements this method
thus follows four basic steps:
(B.1)The procedure that implements this method
thus follows four basic steps:
-
(1) choose Minf and Msup from selected (arbitrary) intervals;
-
(2) calculate the MLE values of μ and σ using Powell’s method;
-
(3) apply the KS statistic to the interval
![\hbox{$\left [ {M}_{\rm inf}, {M}_{\rm sup} \right]$}](/articles/aa/full_html/2013/03/aa20409-12/aa20409-12-eq198.png) and estimate D;
and estimate D;
-
(4) go back to step (1) and keep exploring the (Minf,Msup) space.
At the end of this procedure, we choose the values of μ,
σ, Minf and
Msup that minimizes D.
Ntot is thus the total number of objects with mass in the
range ![\hbox{$\left [ {M}_{\rm inf}, {M}_{\rm sup} \right]$}](/articles/aa/full_html/2013/03/aa20409-12/aa20409-12-eq198.png) .
.
All Tables
Median values of mass, temperature, distance and completeness limits toward the ℓ = 30° and ℓ = 30° fields.
Best-fit parameters (from PLFIT) to the CMF of the ℓ = 30° and ℓ = 59° fields, for the power-law distribution.
Mean values, obtained using WinBUGS, from the posterior distributions of the μ and σ parameters of the lognormal distribution, shown separately for the ℓ = 30° and ℓ = 59° fields.
Best-fit parameters to the CMF of the ℓ = 30° and ℓ = 59° fields, for the lognormal distribution and the PDF and MLE methods.
All Figures
 |
Fig. 1 Top. Example of a Hi-GAL starless clump (nominal position represented with a yellow “+” sign) with an irregular shape (shown by the black area, against the gray-scale background, representing the 160 μm emission). No MIPSGAL or other source found with the Mexican Hat Wavelet algorithm, also named as MHW24 source (see Sect. 3.1),(shown with the “∗” and “diamond” symbols, respectively) is falling within the black area and thus they cannot be associated with the Hi-GAL source. Bottom. Example of a proto-stellar Hi-GAL clump. One MHW24 source is associated with the submillimeter clump, but no MIPSGAL source satisfies the coincidence and color criteria. |
| In the text | |
 |
Fig. 2 Top. SED of a source in the ℓ = 30° field. The upper limit at 70 μm is shown and black line shows the best-fit modified blackbody, whereas gray lines show the 68% confidence envelope of modified blackbody models from Monte Carlo simulations. Also shown are the best-fit parameters from the SED fit: temperature, T, total luminosity, L, dust mass, Mdust, dust emissivity index, β, and dust optical depth, τ.Bottom. Another Hi-GAL clump with a more peculiar shape of the SED, due to the use of Eq. (1) instead of the optically-thin approximation. |
| In the text | |
 |
Fig. 3 Left panels. Log–log histograms showing the distribution of M for all (black), starless (red) and proto-stellar (blue) clumps in the ℓ = 30° (top) and ℓ = 59° (bottom) fields. The bin width has been chosen according to the Freedman and Diaconis’ rule (see Sect. 6.3). The dashed lines represent the results of fit to the data using the procedure PLFIT. The vertical dashed line corresponds to the value of Minf, whereas the solid vertical line shows the 80% completeness limits (see Sect. 3.1 and Table 3). Vertical bars show Poisson errors. Right panels. Histograms showing the distribution of clump temperature (color codes are as in the left panels) in the ℓ = 30° (top) and ℓ = 59° (bottom) fields. The bin width has also been chosen according to the Freedman and Diaconis’ rule. Line styles are as before. |
| In the text | |
 |
Fig. 4 Left panels. Histograms showing the distribution of ln(M) for all (black), starless (red) and proto-stellar (blue) clumps in the ℓ = 30° (top) and ℓ = 59° (bottom) fields. The solid lines represent the results of Gaussian fits to the histograms. The vertical solid lines represent the completeness limits as in Fig. 3. Vertical bars show Poisson errors. Right panels. PDFs of the mass distribution (black solid line) and best-fit (red dashed line), in the ℓ = 30° (top) and ℓ = 59° (bottom) fields. |
| In the text | |
 |
Fig. 5 Top. Histogram profiles from Fig. 4, with solid and dashed lines representing the ℓ = 30° and ℓ = 59° fields, respectively. The dash-dotted line represents the distribution obtained for the ℓ = 59° field traslated to the distance of ℓ = 30° (see text). Bottom. CMF profiles from Fig. 3; line styles are as before. The vertical lines mark the completeness limits listed in Table 3 for the ℓ = 30° (solid line) and ℓ = 59° (dashed line) fields. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{eqnarray*} \left [8.0 \right ] - \left [24 \right ] & > & 2.25, \,\,\, {\rm and} \\ \left [3.6 \right ] - \left [5.8 \right ] & > & -0.28 \, (\left [8.0 \right ] - \left [24 \right ]) + 1.88. \end{eqnarray*}](/articles/aa/full_html/2013/03/aa20409-12/aa20409-12-eq35.png)