| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A135 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201220304 | |
| Published online | 07 March 2013 | |
Implications for electron acceleration and transport from non-thermal electron rates at looptop and footpoint sources in solar flares
SUPA, School of Physics and Astronomy, University of Glasgow, G12 8QQ, UK
e-mail: paulo.simoes@glasgow.ac.uk
Received: 29 August 2012
Accepted: 30 January 2013
The interrelation of hard X-ray (HXR) emitting sources and the underlying physics of electron acceleration and transport presents one of the major questions in high-energy solar flare physics. Spatially resolved observations of solar flares often demonstrate the presence of well-separated sources of bremsstrahlung emission, so-called coronal and footpoint sources. Using spatially resolved X-ray observations by the Reuven Ramaty High Energy Solar Spectroscopic Imager (RHESSI) and recently improved imaging techniques, we investigate in detail the spatially resolved electron distributions in a few well-observed solar flares. The selected flares can be interpreted as having a standard geometry with chromospheric HXR footpoint sources related to thick-target X-ray emission and the coronal sources characterised by a combination of thermal and thin-target bremsstrahlung. Using imaging spectroscopy techniques, we deduce the characteristic electron rates and spectral indices required to explain the coronal and footpoint X-ray sources. We found that, during the impulsive phase, the electron rate at the looptop is several times (a factor of 1.7−8) higher than at the footpoints. The results suggest that a sufficient number of electrons accelerated in the looptop explain the precipitation into the footpoints and imply that electrons accumulate in the looptop. We discuss these results in terms of magnetic trapping, pitch-angle scattering, and injection properties. Our conclusion is that the accelerated electrons must be subject to magnetic trapping and/or pitch-angle scattering, keeping a fraction of the population trapped inside the coronal loops. These findings put strong constraints on the particle transport in the coronal source and provide quantitative limits on deka-keV electron trapping/scattering in the coronal source.
Key words: Sun: flares / Sun: particle emission / Sun: X-rays, gamma rays
© ESO, 2013
1. Introduction
The X-ray images of solar flares with spectral capabilities taken by the Hard X-ray Telescope (HXT) onboard of Yohkoh (Kosugi et al. 1991) and Reuven Ramaty High Energy Solar Spectroscopic Imager (RHESSI, Lin et al. 2002) have revealed a wealth of information on spatially resolved distributions of energetic electrons in solar flares (see e.g. Dennis et al. 2011; Holman et al. 2011; Kontar et al. 2011a, as recent reviews). These spatially resolved observations indicate appearances of distinct coronal and footpoint X-ray sources. Hard X-ray (HXR) footpoint sources are usually described in terms of collisional thick-target models (Dubov 1963; Elliot 1969; Arnoldy et al. 1968; Lingenfelter 1969; Brown 1971; Syrovatskii & Shmeleva 1972; Brown 1973a; Lin & Hudson 1976), where the electrons accelerated in the corona travel downwards inside magnetic loops marking footpoint sources in dense chromospheric plasma by emission in X-rays, EUV, and white-light emissions (Phillips et al. 2008). The observations show that the HXR source height in the chromosphere decreases with increasing X-ray energy (Matsushita et al. 1992; Aschwanden et al. 2002; Kontar et al. 2008; Saint-Hilaire et al. 2010; Battaglia & Kontar 2011a) as anticipated from downward propagating electron beams. In addition, the characteristic sizes of HXR sources decrease with increasing energy, which is consistent with collisional electron transport along converging magnetic flux tubes (Kontar et al. 2008; Battaglia & Kontar 2011a; Fedun et al. 2011; Battaglia et al. 2012; Xu et al. 2012). Coronal X-ray sources are prominently visible at and below ~10−30 keV and are usually due to thermal and non-thermal bremsstrahlung, which indicates plasma heating and the presence of non-thermal electron populations (e.g. Emslie et al. 2003). Spectroscopically, there is no clear boundary between the two processes, with the spectrum transiting smoothly from thin-target emission in the corona to thick-target emission within the range 10−30 keV. The looptop sources are believed to be connected to the process of energy release in flares (e.g. Priest & Forbes 2002; Holman et al. 2011). Some models place the magnetic reconnection at the looptop, where the X-ray emission is a consequence of the plasma heating and particle acceleration (Jakimiec et al. 1998; Petrosian & Donaghy 1999; Bastian et al. 2007; Kontar et al. 2011b; Guo et al. 2012). Other models propose that the X-point is placed higher in the corona, and the looptop X-ray source shows that the interaction between a downward reconnection flow and plasma fills a soft X-ray loop (Tsuneta et al. 1997). The recent observations of energy-dependent HXR source sizes inside the dense coronal loops (Xu et al. 2008; Kontar et al. 2011b; Bian et al. 2011; Guo et al. 2012; Torre et al. 2012) also suggest within-the-loop electron acceleration and transport.
Petrosian et al. (2002) presented a comprehensive analysis of 18 Yohkoh events, finding that the spectral index of the looptop source is softer than the footpoints on the average by about 1, although this result is limited by the poor energy resolution of the Yohkoh images, with only four energy ranges (Kosugi et al. 1991). With the launch of RHESSI, detailed imaging spectroscopy with energy resolution ~1 keV has become widely available (e.g. Emslie et al. 2003; Battaglia & Benz 2006; Piana et al. 2007; Kundu et al. 2009). Thus, Emslie et al. (2003) found that for the GOES X-class 2002 July 23 flare the coronal source is consistent with the thermal source of around 4 × 107 K and the footpoint-like sources that have power-law spectra with different spectral indices. Battaglia & Benz (2006) presented a systematic study of the relation between looptop and footpoint sources for a few flares observed by RHESSI. They found soft-hard-soft behaviour in both the coronal source and the footpoints. Assuming the scenario where the same electron population produces the coronal source by thin-target bremsstrahlung and the chromospheric source by thick-target bremsstrahlung, one would expect a difference of ≃2 between the two photon spectral indices. They found that the average of all mean differences is ≃1.8. However, the difference is considerably larger than 2 for two out of five events, and smaller than 2 for the other three events analyzed. The coronal source is nearly always softer than the footpoints. The footpoint spectra differ significantly only in one event out of five. While the observations are consistent with acceleration in the coronal source and a subsequent propagation into the chromosphere, their result excludes the simplest scenario of electrons free-streaming from the acceleration region towards the footpoints, which indicates that other transport processes must be considered, e.g. wave-particle interaction can account for spectral differences larger than 2 (Hannah & Kontar 2011). Tomczak & Ciborski (2007) used HXT/Yohkoh data of 117 flares to investigate the ratio of photon counts from looptop to footpoint sources, finding a correlation between this ratio and height and attributing the effect of loop convergence in 80% of the flare sample to inferred mirror ratios lower than 2.1. Coronal trapping is a natural consequence of the expected convergence of the magnetic field between the corona and the chromosphere. Trap-plus-precipitation models have been proposed and developed (Takakura & Kai 1966; Melrose & Brown 1976; Leach & Petrosian 1981; Alexander 1990; Leach & Petrosian 1983; MacKinnon 1988; McClements 1990; MacKinnon 1991; Fletcher 1997; Fletcher & Martens 1998; Park & Fleishman 2010). Also, considerable observational evidence of trapping has been provided (Ramaty et al. 1994; Alexander & Metcalf 1997; Aschwanden et al. 1998, 1999; Metcalf & Alexander 1999; Lee et al. 2000; Lee & Gary 2000; Lee et al. 2002; Alexander & Metcalf 2002; Melnikov et al. 2002; Fleishman et al. 2011; Huang & Li 2011). Analysing microwave brightness maps, Melnikov et al. (2002) applied a collisionless adiabatic trap model to explain looptop sources at 17 and 34 GHz observed in four flares. They concluded that the electron distribution along the loops must be highly inhomogeneous, with the energetic electrons concentrated at the upper part of the loop. On the other hand, microwave loop-like brightness structures of different flares could only be reconciled with models of uniform magnetic field and homogeneous spatial distribution of non-thermal electrons (Kundu et al. 2001). Nindos et al. (2000) successfully reproduced the main spatial morphology of 5 and 15 GHz brightness maps of a weak flare using a non-uniform magnetic field model and uniform distribution of electrons, in agreement with model simulations (Alissandrakis & Preka-Papadema 1984; Klein & Trottet 1984; Simões & Costa 2006, 2010). Those examples evidence how trapping conditions can change from flare to flare, influencing the electron distribution along flaring loops. Moreover, it seems that the microwave emission maps indirectly show the trapped population, as the emission also depends strongly on the magnetic strength. However, HXR images will mainly show the precipitated population as footpoint sources, only eventually showing a non-thermal HXR coronal source. As the collisions are energy-dependent, one can expect that deka-kev HXR-producing electrons and MeV microwave-producing electrons will evolve in slightly different ways during a solar flare (e.g. Lee et al. 2002; Giménez deCastro et al. 2012).
Importantly, electron scattering (often strong) is required to achieve efficient acceleration of particles (e.g. Miller et al. 1997; Miller 1998; Petrosian 1999; Bian et al. 2012) and to explain the lack of strong HXR anisotropy in observations, while the transport of particles affects how the particles are accelerated (see e.g. Bykov & Fleishman 2009; Bian et al. 2012; Petrosian 2012).
Despite the importance of comparative studies between the coronal sources and footpoints, there were no systematic comparisons of the number of electrons in the footpoints and the coronal sources for the events with visible footpoints. We emphasize that the inference of imaging spectroscopy parameters relies strongly on the precise knowledge of the X-ray source area, which was only developed fairly recently (e.g. Schmahl et al. 2007; Kontar et al. 2008; Dennis & Pernak 2009; Kontar et al. 2010). In addition, the full Spectral Response Matrix (SRM) of RHESSI detectors (including non-diagonal terms) for imaging spectroscopy became available relatively recently, since 2006 February.
We present a comparative analysis of the electron distributions in footpoints and coronal sources for four well-observed flares. We find for the first time the electron rate required to explain the coronal and chromospheric X-ray emissions. In Sect. 2 we present the observations and in Sect. 3 the methodology to retrieve the electron rates from imaging spectroscopy. Our results are presented in Sect. 4 and discussed in Sect. 5. The work is summarized in Sect. 6.
2. Observational data
We selected four well-observed events in which the common loop structure could be identified: two footpoint sources at higher photon energies and a looptop source at lower energies. We avoided events where looptops and footpoints overlap due to the projection of the loop geometry. Also, we only selected flares where a non-thermal source at the looptop could be resolved. The flare list with details is presented in Table 1. Different aspects of the selected flares were previously investigated by other authors: 2002 July 23 (Emslie et al. 2003), 2003 November 02 (Silva et al. 2007), 2011 February 24 (Battaglia & Kontar 2011b).
Selected solar flares.
3. Methodology
3.1. Imaging spectroscopy
For each of the four flares, we constructed CLEAN images (Hurford et al. 2002) with a pixel size of 1′′, using front detectors 3 to 8, for 19 logarithmically binned energy bands from 10 to 100 keV. Since we rely on the source sizes taken from the reconstructed images, we verified the best CLEAN beam width for each flare. Dennis & Pernak (2009) and Kontar et al. (2010) have pointed out that CLEAN images usually have systematically larger sizes than other algorithms when using the default beam width factor of 1.0. To ensure the best possible determination of the source sizes using CLEAN images, we applied the visibility forward-fitting procedure (Schmahl et al. 2007) on the footpoints of each flare, adjusted the CLEAN beam size, and re-calculated the images until the FWHM of the footpoint from both algorithms had the same size. The integration time interval during the impulsive phase and the CLEAN beam used for each event are presented in Table 1. The CLEAN beam factor found for these flares lay in the range 1.9−2.4, suggesting the optimum value is ≃2 (Dennis & Pernak 2009; Kontar et al. 2010), instead of the default value of 1. Figure 1 shows CLEAN maps for the four flares at lowest (10−11.3 keV) and highest (88.6−100 keV) energy bins.
 |
Fig. 1 CLEAN maps for each flare: a) 2002 July 23; b) 2003 November 02; c) 2011 February 24; and d) 2011 September 24, showing the emission at 10−11.3 keV (black contours) and 88.6−100 keV (blue contours) at 30, 50, 70, 90% of maximum of each energy bin. The ROIs for the imaging spectroscopy are defined in gray lines: footpoints (continuous lines) and looptop (dashed lines). Integration times are shown in each frame and in Table 1. The CLEAN beam width factor used to construct each map according to the best agreement with visibility forward-fitting is also presented in Table 1. For each, a total of 19 maps were made with energy bins logarithmically spaced between 10 and 100 keV. |
3.1.1. Regions of interest selection
Within each image, we selected regions of interest (ROI) which capture looptop (LT) and footpoint (FP) sources for further imaging spectroscopy using OSPEX (Schwartz et al. 2002). For the flares considered here, two footpoints can be easily identified and noted in the literature, e.g. Emslie et al. (2003), Silva et al. (2007), and Battaglia & Kontar (2011b) for flares A, B, and C, respectively. The looptop ROI was chosen to include the main emitting regions at low energies, but without being too large, to avoid contribution from the FPs. The looptop and footpoint ROIs for each flare are shown in Fig. 1. The background was estimated taking the sum of pixels outside the ROIs in each image, then normalized for the area of each ROI, similar to an approach applied by Battaglia & Benz (2006). This method probably overestimates the background noise, especially at lower energies; nevertheless, it is useful to identify the reliable energy ranges for the fitting procedure.
3.1.2. Spectral fitting
While the detailed analysis of HXR spectrum in some events, e.g. 2002 July 23 flare, demonstrated that the actual spectrum does contain deviations from a simple power-law (Piana et al. 2003; Kontar et al. 2011a), we assume a single power-law in the electron spectrum for the purposes of our analysis. For each flare, the looptop source was fitted with a thin-target model and the footpoint sources were fitted using a thick-target model (see Kontar et al. 2011a, for details). Assuming looptop source is a thin-target emission, the photon flux detected at the Earth is the convolution of the electron distribution and the bremsstrahlung cross-section.
Following Brown (1971) and Brown et al. (2003), we define the mean target proton density  , where n(r) is the plasma density, V is the volume of the LT emitting region. We can then write the photon spectrum at distance the Earth as
, where n(r) is the plasma density, V is the volume of the LT emitting region. We can then write the photon spectrum at distance the Earth as  (1)where the bremsstrahlung cross-section Q(ϵ,E) following (Haug 1997) and
(1)where the bremsstrahlung cross-section Q(ϵ,E) following (Haug 1997) and 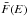 is the mean electron flux spectrum defined by
is the mean electron flux spectrum defined by  (2)From the OSPEX (Schwartz et al. 2002) fit of the photon flux from looptop ROI with the model given by Eq. (1), one finds
(2)From the OSPEX (Schwartz et al. 2002) fit of the photon flux from looptop ROI with the model given by Eq. (1), one finds  without any additional assumptions, where
without any additional assumptions, where  (3)normalised to
(3)normalised to  (electrons cm-2 s-1), which is the product of the mean target density
(electrons cm-2 s-1), which is the product of the mean target density  and the energy-integrated (above the low energy cut-off E0) mean electron flux
and the energy-integrated (above the low energy cut-off E0) mean electron flux  in the volume V. The energy-integrated electron rate ṄLT [electrons s-1] required to explain the observed thin target emission in the looptop is simply
in the volume V. The energy-integrated electron rate ṄLT [electrons s-1] required to explain the observed thin target emission in the looptop is simply  (4)where S is the cross-section area of the loop. We can estimate
(4)where S is the cross-section area of the loop. We can estimate  by
by  (5)where L is the length of the looptop source in the direction along the loop (hence V = LS). Substituting Eq. (5) into Eq. (4) we have
(5)where L is the length of the looptop source in the direction along the loop (hence V = LS). Substituting Eq. (5) into Eq. (4) we have  (6)The thermal plasma density
(6)The thermal plasma density  and the size L are obtained from observation data (see Sect. 3.1.3).
and the size L are obtained from observation data (see Sect. 3.1.3).
For the footpoint emission, we assume a thick-target model, so that the observed photon flux at the distance R is given:  (7)where ṄFP is the electron precipitation rate at footpoints (electrons s-1), and K = 2πe4Λ, e is the electronic charge and Λ is the Coulomb logarithm (assumed ≃22.7 for fully ionized chromosphere and 7.1 for neutral chromosphere, see Sect. 4.1). Here we emphasize that δFP and ṄFP are the spectral index and the electron precipitation rate of the electrons entering into the footpoints. If the electrons are unaffected by the transport within the loop, this spectral index should match δLT and the electron rate that of looptop source ṄLT. Both fits included a thermal component, using full CHIANTI model (Dere et al. 2009), with continuum and spectral lines. A spatially integrated spectrum was also made for each flare using the same time intervals and fitted with a thermal plus thick-target component. The thick-target model was set as a single power-law. The fitting results (Eqs. (1) and (7)) for the imaging and spatially integrated spectroscopy are presented in Table 1. The photon spectra of the LT, FP, and spatially integrated sources are plotted in Figs. 2 to 5 for each flare, respectively, showing the fitting components (thermal and non-thermal) and fitting residuals.
(7)where ṄFP is the electron precipitation rate at footpoints (electrons s-1), and K = 2πe4Λ, e is the electronic charge and Λ is the Coulomb logarithm (assumed ≃22.7 for fully ionized chromosphere and 7.1 for neutral chromosphere, see Sect. 4.1). Here we emphasize that δFP and ṄFP are the spectral index and the electron precipitation rate of the electrons entering into the footpoints. If the electrons are unaffected by the transport within the loop, this spectral index should match δLT and the electron rate that of looptop source ṄLT. Both fits included a thermal component, using full CHIANTI model (Dere et al. 2009), with continuum and spectral lines. A spatially integrated spectrum was also made for each flare using the same time intervals and fitted with a thermal plus thick-target component. The thick-target model was set as a single power-law. The fitting results (Eqs. (1) and (7)) for the imaging and spatially integrated spectroscopy are presented in Table 1. The photon spectra of the LT, FP, and spatially integrated sources are plotted in Figs. 2 to 5 for each flare, respectively, showing the fitting components (thermal and non-thermal) and fitting residuals.
 |
Fig. 2 Looptop (a), footpoint (b) sources and spatially integrated (c) HXR spectra (black) of flare A, 2002 July 23, estimated background (gray), and fitting result (red) and its components: thermal (green) and non-thermal (blue). For the looptop spectrum, the non-thermal is a thin-target model; for the footpoint and integrated spectra, it is a thick-target model. |
3.1.3. Image-derived parameters
The overall geometry of the selected flares can be interpreted as a single loop-like magnetic structure with two footpoints and a coronal source at the apex of the loop. We defined a loop baseline as the line connecting the two footpoints, which is used as a reference to measure the sizes of the sources at the looptop. The thermal plasma density can be calculated using the observations of thermal X-ray emission. The isothermal fit to the spatially integrated RHESSI spectrum (right-hand frames in Figs. 2 to 5) gives emission measure  , where the volume of the thermal source can be estimated as Vth = AD, A is the area of the source, D is the cross-section diameter of the source, and assuming uniform plasma density
, where the volume of the thermal source can be estimated as Vth = AD, A is the area of the source, D is the cross-section diameter of the source, and assuming uniform plasma density  within the volume Vth. Using the emission maps at 10−11.3 keV, D was estimated by measuring the length of this source at 50% level in the direction orthogonal to the baseline and A as the source area at 50% level of the maximum emission. Using those measurements, the plasma density is then obtained by
within the volume Vth. Using the emission maps at 10−11.3 keV, D was estimated by measuring the length of this source at 50% level in the direction orthogonal to the baseline and A as the source area at 50% level of the maximum emission. Using those measurements, the plasma density is then obtained by  and directly inserted into Eq. (6), resulting in
and directly inserted into Eq. (6), resulting in  (8)Similar results for EM are obtained using the imaging spectroscopy and selecting looptop regions only (left-hand frames of Figs. 2 to 5), but the imaging spectroscopy gives larger uncertainties. The values found for the plasma density
(8)Similar results for EM are obtained using the imaging spectroscopy and selecting looptop regions only (left-hand frames of Figs. 2 to 5), but the imaging spectroscopy gives larger uncertainties. The values found for the plasma density  cm-3 are 2.7, 1.5, 0.6, and 1.9 for flares A, B, C, and D, respectively. The geometry aspects of the flares and plasma density values inferred are presented in Table 1.
cm-3 are 2.7, 1.5, 0.6, and 1.9 for flares A, B, C, and D, respectively. The geometry aspects of the flares and plasma density values inferred are presented in Table 1.
 |
Fig. 6 CLEAN maps for the four flares, evidencing thermal emission at 10−11.3 keV (red), footpoints at 61.6−69.5 keV (blue contours, at 50% of the maximum of each map), and non-thermal looptop sources (green solid) at 42.8−48.3 keV (50%) for flares A and B, 20.7−23.4 keV (40%) for flare C, and 29.8−33.6 keV (50%) for flare D. The countour levels of 30% and 70% at those energies (green dashed lines) are also shown. The thick yellow line indicates the length L. Date and integration times are indicated in each map. |
We define the length L of the non-thermal source at the looptop as the size (at 50% of maximum emission) in the direction parallel to the footpoint baseline and crossing the point with the maximum emission. L is measured at a sufficiently high energy, where the contribution from thermal emission is not significant and where the source is spatially resolved. The non-thermal looptop sources can be easily identified at 42.8 − 48.3 keV, 42.8 − 48.3 keV, 20.7 − 23.4 keV, and 29.8 − 33.6 keV for each flare, respectively (Fig. 6); the measured lengths L for each flare are presented in Table 1.
4. Observational results and analysis
Using Eq. (8) with the values found above, the electron rate at the looptop ṄLT can be calculated and is summarized in Table 1, along with the electron rate at the footpoints obtained using thick-target forward fit for the photon flux spectrum.
Spectral index analysis of these four flares reveals that all flares have a similar footpoint spectral index, which is close to 3.9 (see Table 1). The differences between the spectral index are δLT − δFP = −0.3 ± 0.2, − 1.0 ± 0.1, − 0.5 ± 0.2, and − 0.2 ± 0.4 for each flare. This appears consistent with previous findings, e.g. Emslie et al. (2003) reported that the photon spectral index difference is less than 2 for the 2002 July 23 flare and Battaglia & Benz (2006) reports a fairly broad range of spectral index differences between footpoints and coronal sources.
In general, our results suggest that in all flares the precipitation rate into footpoints is smaller than the electron rate required to explain the coronal HXR emission, i.e. ṄLT/ṄFP > 1. Assuming fully ionized chromospheric footpoints and no albedo, ṄLT/ṄFP for the four flares appears around 1.6, which is slightly larger than unity. This is expected in an idealized model, where non-thermal electrons propagate without interaction, so that ṄLT ≃ ṄFP. However, as discussed in the next section, the effects of neutral chromosphere and albedo can increase this ratio by a factor of ~2−6.
4.1. Effects of photospheric albedo and neutral chromosphere
The solar atmosphere above the regions where the X-ray bremsstrahlung is produced during flares is optically thin, while the dense photospheric layers below those regions are optically thick to X-ray photons. As a consequence, photons emitted downwards can be efficiently Compton backscattered by atomic electrons in the photosphere (Tomblin 1972; Santangelo et al. 1973; Bai & Ramaty 1978; Magdziarz & Zdziarski 1995). The observed X-ray spectrum from flares is then a combination of the primary and albedo photons. The reflectivity is dependent both on the primary photon spectrum and the flare position on the Sun relative to the observer, or more precisely, the heliocentric angle of the source. The backscattered radiation can be significant and modify the primary X-ray spectrum. More importantly for our analysis here, when the albedo contribution is taken into account, the number of electrons required to explain the observed photon flux changes (Alexander & Brown 2002; Kontar et al. 2006). New fittings taking the albedo correction (Kontar et al. 2006) into account give expectedly lower numbers for the electron rate at footpoints ṄFP/1035 electrons s-1: 18 ± 3, 69 ± 5, 0.9 ± 0.1, 2.1 ± 0.5, or factors of 1.8, 2.2, 1.2, 2.5 lower than the electron rate found without considering the albedo photons. The effect is more pronounced for flares closer to the centre of the solar disk, while less significant for limb flares (only 20% for flare C), as expected. Similar results are found for the full (spatially integrated) spectrum.
The partially ionized or fully neutral chromosphere is a more efficient thick-target bremsstrahlung emitter (e.g. Hayakawa & Kitao 1956; Brown 1973a; Emslie 1978), which can increase HXR flux by a factor of ~3 in comparison with fully ionized atmosphere. The decrease in the ionization of the target reduces the collisional energy loss of the non-thermal electrons, thus enhancing the efficiency of the HXR bremsstrahlung. Applying the thick-target model with a neutral target for the footpoint emission, we found the electron rates ṄFP/1035 electrons s-1 for each flare, respectively, 13 ± 2, 60 ± 4, 0.4 ± 0.1, 2.0 ± 0.5, which are a factor of ~2.5 smaller than the values found for a fully ionized target. Similar results are found for the spatially integrated spectrum.
Considering the thick-target model with both the albedo component and a neutral target, the values for ṄFP for each flare are 6 ± 1, 27 ± 2, 0.4 ± 0.1, 0.8 ± 0.2 in units of 1035 electrons s-1. With ṄLT found in the previous section, the values for the ratio ṄLT/ṄFP are 9.3 ± 3.0, 10.1 ± 2.3, 4.5 ± 1.4, 7.8 ± 5.2, with an average 7.9.
5. Discussion
The value ṄLT/ṄFP > 1 found for the flares suggests either (i) the emissivity per unit of length in coronal sources that is more efficient than free propagation or (ii) additional energy losses in the footpoint region. These electron rates also imply that the main acceleration/injection region is near the looptop, at least for these flares. We would possibly expect to find ṄLT/ṄFP ≤ 1 if the acceleration region is not near the looptop or even if the electrons are accelerated along the loop, due either to stochastic electric fields (e.g. Vlahos et al. 2004; Turkmani et al. 2006; Bian & Browning 2008; Gordovskyy et al. 2010) or to re-acceleration by beam-generated Langmuir waves (Kontar et al. 2012). We now discuss the result of ṄLT/ṄFP > 1 in terms of magnetic trapping, injection properties, and pitch-angle scattering.
5.1. Magnetic trapping
The simplest scenario which can be involved to explain the excess of electrons in the looptop area is magnetic trapping due to adiabatic mirroring in a converging magnetic field. The convergence of the magnetic field, characterized by its mirror ratio σ = BFP/BLT and losscone angle α0 = cos-1(μ0) = sin-1(σ− 1/2), and the conservation of the magnetic moment of the fast electrons divide the injected particle population I in a trapped fraction T, where the pitch-angle α > α0, while the other precipitating fraction P (with α < α0) escapes the trap and precipitates into the dense chromosphere. Defining ξ as the fraction of the injected population that remains trapped, we have  relating this scenario to our results:
relating this scenario to our results:
 where
where  (15)where the footpoint electron rate ṄFP indicates the precipitated fraction P, while ṄLT indicates the fraction of electrons that pass through the looptop, i.e. both the trapped fraction and the electrons that precipitate directly.
(15)where the footpoint electron rate ṄFP indicates the precipitated fraction P, while ṄLT indicates the fraction of electrons that pass through the looptop, i.e. both the trapped fraction and the electrons that precipitate directly.
Let us consider two typical pitch-angle distributions of energetic electrons: (i) isotropic f(μ) = constant and (ii) beamed f(μ), defined as a Gaussian distribution centred along the loop with spread Δμ = 0.1. For these two models, one finds the following relations  Eqs. (16) and (17) can be solved for the losscone value μ0, and hence σ. For the isotropic case, Eqs. (16) and (17) reduce to T/I = μ0 = ξ and P/I = (1 − μ0) = (1 − ξ). Solving these equations using the observed values of ṄLT and ṄFP, we find the values for ξ and σ, which are presented in Table 2. Here, we stress that this simple model is meant as a way to divide the injected population in terms of the losscone, representing an upper limit for the derived mirror ratio values, since the accumulation of electrons is not considered in the model.
Eqs. (16) and (17) can be solved for the losscone value μ0, and hence σ. For the isotropic case, Eqs. (16) and (17) reduce to T/I = μ0 = ξ and P/I = (1 − μ0) = (1 − ξ). Solving these equations using the observed values of ṄLT and ṄFP, we find the values for ξ and σ, which are presented in Table 2. Here, we stress that this simple model is meant as a way to divide the injected population in terms of the losscone, representing an upper limit for the derived mirror ratio values, since the accumulation of electrons is not considered in the model.
Under the assumption of an isotropic injection, σ values are small (σ ≳ 1) and in agreement with values found by Aschwanden et al. (1999) and Tomczak & Ciborski (2007). In the case of the narrow beam, we found that σ ≳ 5, which is higher than the range of mirror ratios found by Costa & Rosal (2005) for microwave data, without assuming a particular pitch-angle distribution, although their determination is biased by a higher weight of the loop-leg source and offers only a lower limit of the mirror ratio. When considering our results for the case with albedo and neutral target, we found 2.5 ≤ σ ≤ 5 for the isotropic case and σ ≳ 17 − 42, for the beamed injection case. As mentioned above, the values for the required mirror ratio are just upper bounds. The observations could be explained by lower mirror ratios and sustained injection which cause accumulation of electrons at the looptop.
Estimated values for trapping fraction ξ and mirror ratio σ.
5.2. Pitch-angle scattering
The accelerated electrons in the flaring loop are usually assumed to be trapped within an adiabatic magnetic trap. Two approaches can be used to describe their dynamics and spectra, namely Coulomb collisions (Melrose & Brown 1976; MacKinnon et al. 1985) and interactions between electrons and waves in the plasma (Wentzel 1976; Bespalov et al. 1987; Stepanov & Tsap 2002). Observed energy-dependent time delays of the 20−200 keV HXR emission favour the Coulomb collision hypothesis (Aschwanden 2005). The time delays of 1−10 s for smoothed components of the emission follow the law ϵ3/2 (ϵ is photon energy) and can be explained by Coulomb scattering of non-thermal electrons by dense background plasma (Aschwanden et al. 1997). However, these observed time delays can also be explained by a magnetic trap plus pitch-angle scattering by plasma turbulence (Stepanov & Tsap 1999).
Bespalov et al. (1987), following Kennel & Petschek (1966), describe three diffusion regimes of pitch-angle diffusion: weak diffusion regime, moderate diffusion regime, and strong diffusion regime. The three regimes of pitch-angle diffusion are characterised by the mean time of pitch-angle scattering td, flight time through the loop tc = L/v, where v is the particle speed, and mirror ratio σ = BFP/BLT: weak (td > σtc), intermediate, or strong in Kennel & Petschek (1966) description, (tc < td < σtc), and strong (td < tc). In terms of pitch-angle distribution, the weak regime generally means that the electrons are weakly (Coulomb) scattered in a timescale of the bounce period and that the losscone is empty. In the intermediate regime, the electrons can travel through the loop and are scattered into the losscone, which can be considered full, and the pitch-angle distribution is nearly isotropic. The strong regime means that a electron can change its direction many times during one bounce period. This regime can only take place by wave-particle interactions, as a strong collisional diffusion also means that the fast electrons will quickly lose their energy and thermalize.
To explain the observations in a scenario without magnetic trapping, i.e. no coronal convergence of the magnetic field, the pitch angle scattering should be strong  , with the values of 0.1 < td/tc < 0.7. Let us consider that the HXR-producing electrons are magnetically trapped only at the looptop where the emission appears, i.e. the mirror points are high in the coronal field. In this case, it is reasonable to expect that σ would not be much higher than 2. This scenario can be justified because there is no emission detected along the loop legs, which would be expected if the electrons were to bounce between the mirrorpoints near the footpoints. From our results of the trapping analysis in Table 2, we find σ > 2, except when an isotropic injection and an ionized target are considered. Assuming that at the looptop 1 < σ < 2 but a higher value of σ is required to trap the electrons, efficient scattering is needed at the looptop to change the pitch-angle distribution and allow the electrons to be magnetically trapped. Also, the isotropic injection implies strong scattering in the acceleration process. Although the electron accumulation at the looptop can be explained by a trap-plus-precipitation model with modest mirror ratios σ < 2, we concluded that the pitch-angle distribution must be wide enough to be divided by the losscone, or else it will result in either a fully trapped (as proposed by Melnikov et al. (2002) due to an anisotropic pitch-angle distribution orthogonal do the magnetic field, the so-called pancake distribution) or fully precipitated scenario (as in the classical thick-target model). This requirement can be fulfilled by moderate/strong pitch-angle scattering processes. The presence of strong pitch-angle scattering is particularly important for stochastic acceleration models, where the transport of electrons strongly influences the acceleration rate of particles (see Bian et al. 2012, as a recent review).
, with the values of 0.1 < td/tc < 0.7. Let us consider that the HXR-producing electrons are magnetically trapped only at the looptop where the emission appears, i.e. the mirror points are high in the coronal field. In this case, it is reasonable to expect that σ would not be much higher than 2. This scenario can be justified because there is no emission detected along the loop legs, which would be expected if the electrons were to bounce between the mirrorpoints near the footpoints. From our results of the trapping analysis in Table 2, we find σ > 2, except when an isotropic injection and an ionized target are considered. Assuming that at the looptop 1 < σ < 2 but a higher value of σ is required to trap the electrons, efficient scattering is needed at the looptop to change the pitch-angle distribution and allow the electrons to be magnetically trapped. Also, the isotropic injection implies strong scattering in the acceleration process. Although the electron accumulation at the looptop can be explained by a trap-plus-precipitation model with modest mirror ratios σ < 2, we concluded that the pitch-angle distribution must be wide enough to be divided by the losscone, or else it will result in either a fully trapped (as proposed by Melnikov et al. (2002) due to an anisotropic pitch-angle distribution orthogonal do the magnetic field, the so-called pancake distribution) or fully precipitated scenario (as in the classical thick-target model). This requirement can be fulfilled by moderate/strong pitch-angle scattering processes. The presence of strong pitch-angle scattering is particularly important for stochastic acceleration models, where the transport of electrons strongly influences the acceleration rate of particles (see Bian et al. 2012, as a recent review).
5.3. Instrumental effects
Because the events we selected for this analysis are GOES M and X class flares, it is important to check for pileup (Smith et al. 2002). This effect, depending on attenuator state, is usually stronger in the range 20−50 keV, which is the range where the looptop sources were identified. We tested the importance of pileup, comparing the ratio of the corrected and uncorrected count rate spectra of each flare. These spectra and their ratio are presented in Fig. 7, taken for the time intervals presented in Table 1. Presently, it is not possible to correct for pileup in imaging spectroscopy; however, we can assess its effects in the spatially integrated spectrum and estimate the errors in the looptop and footpoint spectra. Taking the minimum of the ratio between corrected and uncorrected count rate spectra as the maximum error due to pileup, we find the values of 14% and 20% (both around 40 keV) for flares 2002 July 23 and 2003 November 02, while errors due to pileup are lower than 2% for flares 2011 February 24 and 2011 September 24. These errors are much smaller than the errors from the fittings propagated to the final ratio ṄLT/ṄFP: 35%, 24%, 27%, and 64%. Consequently, pileup effects do not seem to be significant in our findings.
 |
Fig. 7 Pileup effect in the count spectra for flares A, B, C, and D (time intervals in Table 1 and noted in each frame). Top row: corrected (gray) and uncorrected (black) count spectra. Bottom row: the ratio of pileup corrected and uncorrected count spectra for each flare. |
6. Summary
We presented an analysis of the electron distribution in footpoints and coronal sources for four well-observed solar flares and, for the first time, found the electron rate required to explain the coronal and chromospheric X-ray emissions. Using imaging spectroscopy techniques, the X-ray spectra of the coronal and footpoint sources are obtained and fitted with thin- and thick-target models, respectively. The thick-target model directly provides the electron rate ṄFP necessary to explain the observed footpoint emission. To obtain the electron rate ṄLT at the looptop source from the thin-target model, it is also necessary to find the length of the source L and the thermal plasma density n (Eq. (6)). The length L was measured for each flare in CLEAN maps in an energy range where the coronal source was resolved at 50% of the maximum of the image and thermal contribution can be safely neglected, while the plasma density n was deduced from the emission measure EM (from spectral fittings) and source volume estimated from ~10 keV source size.
Assuming no albedo and a fully ionized target, we found an average ṄLT/ṄFP of 1.6. The ratio ṄLT/ṄFP is further enhanced when considering the Compton back-scattered photons, i.e. albedo (e.g. Kontar et al. 2006), and a neutral target in the chromosphere (e.g. Brown 1973b). Both processes reduce the required electron rate to match the observed HXR photon flux, effectively reducing ṄFP. Under these considerations, the average ratio found is ~8. The ratio ṄLT/ṄFP> 1 could suggest that the acceleration/injection region is near the looptop, at least for these flares. In previous studies using microwave emission maps, homogeneous electron distribution along the loop (Kundu et al. 2001) or high accumulation of electrons at the looptop (Melnikov et al. 2002) were proposed to explain the loop-like morphology of the 17 and 34 GHz emission. Melnikov et al. (2002) concluded that a ratio of electrons at the looptop to footpoint in the range ~10−100 is required to reproduce the observations of the four flares considered in their study. We note, however, that those results only account for the trapped population, without considering the number of precipitated electrons required to produce HXR at chromospheric footpoints. In fact, their solution requires a pancake pitch-angle distribution at the looptop, which would produce very weak HXR chromospheric emission (if any at all) due to the lack of direct precipitation. Moreover, there is extensive evidence of microwave sources associated with HXR footpoint emission (e.g. Kundu et al. 1995, 2006, 2009; Nishio et al. 1997; Lee et al. 2000; Schmahl et al. 2006), indicating that the trapping conditions vary strongly from flare to flare, as one might expect. In fact, evidence for how trapping conditions are different for each flare is presented by Mel’Nikov (1994), showing that the ratio between the number of trapped high-energy electrons (i.e. produce microwave emission) and precipitated low-energy electrons (i.e. electrons that produce HXR emission) can vary by three orders of magnitude, depending on the electron lifetime value inside the trap and duration of the injection. We note that all those works compared two different electron energy ranges, while in this paper our results are presented for electrons in the deka-keV energy range.
We considered a collisionless magnetic trapping to explain the electron rates found (for fully ionized target and no albedo) and found that the required mirror ratios are in the range 1.1 ≲ σ ≲ 6, while for a neutral chromospheric target and accounting for albedo photons, 2.5 ≲ σ ≲ 17 − 42. These values reflect an upper boundary for the mirror ratio, as our simple model does not account for electron accumulation over a sustained injection. Therefore, the observations can possibly be explained considering a trap-plus-precipitation scenario with modest mirror ratio values. However, we note that the pitch-angle distribution must be wide enough to be divided into trapped and precipitated fractions by the trap losscone. This requirement indicates that moderate/strong pitch-angle scattering must take place in the acceleration site or during the transport along the loop.
If we consider a scenario without significative convergence of the coronal field towards the chromosphere, i.e. no efficient magnetic trapping, the pitch-angle scattering time required to explain the observations appears to be in the range 0.1−0.7 of the time required for an electron to cross the length of the loop. The observations do not support very strong scattering with values smaller than 0.1, which is sometimes required for efficient stochastic acceleration. This conclusion indicates that the observed coronal source is not the acceleration region, which could be in a smaller or larger portion of the loop. Hence the coronal HXR source is mainly due to transport processes. Equally, it can also mean that the stochastic acceleration models with strong pitch-angle scattering are not the dominant mechanism for electron acceleration at these energies. Conclusions in favour of the trap-plus-precipitation model are given by other studies (e.g. Aschwanden et al. 1999; Tomczak & Ciborski 2007). Nevertheless, the effect of moderate/strong scattering can possibly explain the formation of the HXR looptop source or at least enhance the effect of the magnetic trapping. It is our impression that the scattering cannot be neglected and should be investigated with the trap-plus-precipitation model for the deka-keV energy range in more detail.
In conclusion, our results suggest that the accelerated electrons must be subject to magnetic trapping and/or moderate or strong pitch-angle scattering, keeping a fraction of the population trapped inside the coronal loops. This is in full agreement with the trap-plus-precipitation models first proposed by Takakura & Kai (1966) and further developed by many other authors.
Acknowledgments
Financial support by the European Commission through HESPE (FP7-SPACE-2010-263086) (PJAS, EPK), the “Radiosun” (PEOPLE-2011-IRSES-295272) Networks (EPK), and by the STFC rolling grant is gratefully acknowledged.
References
- Alexander, D. 1990, A&A, 235, 431 [NASA ADS] [Google Scholar]
- Alexander, D., & Metcalf, T. R. 1997, ApJ, 489, 442 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, D., & Metcalf, T. R. 2002, Sol. Phys., 210, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, R. C., & Brown, J. C. 2002, Sol. Phys., 210, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Alissandrakis, C. E., & Preka-Papadema, P. 1984, A&A, 139, 507 [NASA ADS] [Google Scholar]
- Arnoldy, R. L., Kane, S. R., & Winckler, J. R. 1968, ApJ, 151, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J. 2005, Physics of the Solar Corona. An Introduction with Problems and Solutions, 2nd edn. (Pour la Science) [Google Scholar]
- Aschwanden, M. J., Bynum, R. M., Kosugi, T., Hudson, H. S., & Schwartz, R. A. 1997, ApJ, 487, 936 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Schwartz, R. A., & Dennis, B. R. 1998, ApJ, 502, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Fletcher, L., Sakao, T., Kosugi, T., & Hudson, H. 1999, ApJ, 517, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Brown, J. C., & Kontar, E. P. 2002, Sol. Phys., 210, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, T., & Ramaty, R. 1978, ApJ, 219, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, T. S., Fleishman, G. D., & Gary, D. E. 2007, ApJ, 666, 1256 [NASA ADS] [CrossRef] [Google Scholar]
- Battaglia, M., & Benz, A. O. 2006, A&A, 456, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Battaglia, M., & Kontar, E. P. 2011a, ApJ, 735, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Battaglia, M., & Kontar, E. P. 2011b, A&A, 533, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Battaglia, M., Kontar, E. P., Fletcher, L., & MacKinnon, A. L. 2012, ApJ, 752, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Bespalov, P. A., Zaitsev, V. V., & Stepanov, A. V. 1987, Sol. Phys., 114, 127 [NASA ADS] [Google Scholar]
- Bian, N. H., & Browning, P. K. 2008, ApJ, 687, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Bian, N. H., Kontar, E. P., & MacKinnon, A. L. 2011, A&A, 535, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bian, N., Emslie, A. G., & Kontar, E. P. 2012, ApJ, 754, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C. 1971, Sol. Phys., 18, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C. 1973a, Sol. Phys., 31, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C. 1973b, Sol. Phys., 28, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., Emslie, A. G., & Kontar, E. P. 2003, ApJ, 595, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Bykov, A. M., & Fleishman, G. D. 2009, ApJ, 692, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Costa, J. E. R., & Rosal, A. C. 2005, A&A, 436, 347 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dennis, B. R., & Pernak, R. L. 2009, ApJ, 698, 2131 [NASA ADS] [CrossRef] [Google Scholar]
- Dennis, B. R., Emslie, A. G., & Hudson, H. S. 2011, Space Sci. Rev., 159, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Dere, K. P., Landi, E., Young, P. R., et al. 2009, A&A, 498, 915 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubov, É. E. 1963, Soviet Physics Doklady, 8, 543 [NASA ADS] [Google Scholar]
- Elliot, H. 1969, in Solar Flares and Space Research, eds. C. de Jager, & Z. Svestka, 356 [Google Scholar]
- Emslie, A. G. 1978, ApJ, 224, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Emslie, A. G., Kontar, E. P., Krucker, S., & Lin, R. P. 2003, ApJ, 595, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Fedun, V., Verth, G., Jess, D. B., & Erdélyi, R. 2011, ApJ, 740, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Fleishman, G. D., Kontar, E. P., Nita, G. M., & Gary, D. E. 2011, ApJ, 731, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, L. 1997, A&A, 326, 1259 [NASA ADS] [Google Scholar]
- Fletcher, L., & Martens, P. C. H. 1998, ApJ, 505, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Giménez de Castro, C. G., Cristiani, G. D., Simões, P. J. A., et al. 2012, Sol. Phys., 296 [Google Scholar]
- Gordovskyy, M., Browning, P. K., & Vekstein, G. E. 2010, ApJ, 720, 1603 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, J., Emslie, A. G., Kontar, E. P., et al. 2012, A&A, 543, A53 [Google Scholar]
- Hannah, I. G., & Kontar, E. P. 2011, A&A, 529, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haug, E. 1997, A&A, 326, 417 [NASA ADS] [Google Scholar]
- Hayakawa, S., & Kitao, K. 1956, Progr. Theor. Phys., 16, 139 [Google Scholar]
- Holman, G. D., Aschwanden, M. J., Aurass, H., et al. 2011, Space Sci. Rev., 159, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, G., & Li, J. 2011, ApJ, 740, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Hurford, G. J., Schmahl, E. J., Schwartz, R. A., et al. 2002, Sol. Phys., 210, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Jakimiec, J., Tomczak, M., Falewicz, R., Phillips, K. J. H., & Fludra, A. 1998, A&A, 334, 1112 [NASA ADS] [Google Scholar]
- Kennel, C. F., & Petschek, H. E. 1966, J. Geophys. Res., 71, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, K.-L., & Trottet, G. 1984, A&A, 141, 67 [NASA ADS] [Google Scholar]
- Kontar, E. P., MacKinnon, A. L., Schwartz, R. A., & Brown, J. C. 2006, A&A, 446, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kontar, E. P., Hannah, I. G., & MacKinnon, A. L. 2008, A&A, 489, L57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kontar, E. P., Hannah, I. G., Jeffrey, N. L. S., & Battaglia, M. 2010, ApJ, 717, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Kontar, E. P., Brown, J. C., Emslie, A. G., et al. 2011a, Space Sci. Rev., 159, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Kontar, E. P., Hannah, I. G., & Bian, N. H. 2011b, ApJ, 730, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Kontar, E. P., Ratcliffe, H., & Bian, N. H. 2012, A&A, 539, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kosugi, T., Masuda, S., Makishima, K., et al. 1991, Sol. Phys., 136, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Kundu, M. R., Nitta, N., White, S. M., et al. 1995, ApJ, 454, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Kundu, M. R., Nindos, A., White, S. M., & Grechnev, V. V. 2001, ApJ, 557, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Kundu, M. R., Schmahl, E. J., & White, S. M. 2006, in Solar Activity and its Magnetic Origin, eds. V. Bothmer, & A. A. Hady, IAU Symp., 233, 334 [Google Scholar]
- Kundu, M. R., Grechnev, V. V., White, S. M., et al. 2009, Sol. Phys., 260, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Leach, J., & Petrosian, V. 1981, ApJ, 251, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Leach, J., & Petrosian, V. 1983, ApJ, 269, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J., & Gary, D. E. 2000, ApJ, 543, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J., Gary, D. E., & Shibasaki, K. 2000, ApJ, 531, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J., Gary, D. E., Qiu, J., & Gallagher, P. T. 2002, ApJ, 572, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, R. P., & Hudson, H. S. 1976, Sol. Phys., 50, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, R. P., Dennis, B. R., Hurford, G. J., et al. 2002, Sol. Phys., 210, 3 [Google Scholar]
- Lingenfelter, R. E. 1969, Sol. Phys., 8, 341 [NASA ADS] [CrossRef] [Google Scholar]
- MacKinnon, A. L. 1988, A&A, 194, 279 [NASA ADS] [Google Scholar]
- MacKinnon, A. L. 1991, A&A, 242, 256 [NASA ADS] [Google Scholar]
- MacKinnon, A. L., Brown, J. C., & Hayward, J. 1985, Sol. Phys., 99, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Magdziarz, P., & Zdziarski, A. A. 1995, MNRAS, 273, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Matsushita, K., Masuda, S., Kosugi, T., Inda, M., & Yaji, K. 1992, PASJ, 44, L89 [NASA ADS] [Google Scholar]
- McClements, K. G. 1990, A&A, 234, 487 [NASA ADS] [Google Scholar]
- Mel’Nikov, V. F. 1994, Radiophysics and Quantum Electronics, 37, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Melnikov, V. F., Shibasaki, K., & Reznikova, V. E. 2002, ApJ, 580, L185 [NASA ADS] [CrossRef] [Google Scholar]
- Melrose, D. B., & Brown, J. C. 1976, MNRAS, 176, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Metcalf, T. R., & Alexander, D. 1999, ApJ, 522, 1108 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. A. 1998, Space Sci. Rev., 86, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. A., Cargill, P. J., Emslie, A. G., et al. 1997, J. Geophys. Res., 102, 14631 [NASA ADS] [CrossRef] [Google Scholar]
- Nindos, A., White, S. M., Kundu, M. R., & Gary, D. E. 2000, ApJ, 533, 1053 [NASA ADS] [CrossRef] [Google Scholar]
- Nishio, M., Yaji, K., Kosugi, T., Nakajima, H., & Sakurai, T. 1997, ApJ, 489, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Park, S.-H., & Fleishman, G. D. 2010, Sol. Phys., 266, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Petrosian, V. 1999, in Plasma Turbulence and Energetic Particles in Astrophysics, eds. M. Ostrowski, & R. Schlickeiser, 135 [Google Scholar]
- Petrosian, V. 2012, Space Sci. Rev., 49 [Google Scholar]
- Petrosian, V., & Donaghy, T. Q. 1999, ApJ, 527, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Petrosian, V., Donaghy, T. Q., & McTiernan, J. M. 2002, ApJ, 569, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, K. J. H., Feldman, U., & Landi, E. 2008, Ultraviolet and X-ray Spectroscopy of the Solar Atmosphere, eds. K. J. H. Phillips, U. Feldman, & E. Landi (Cambridge University Press) [Google Scholar]
- Piana, M., Massone, A. M., Kontar, E. P., et al. 2003, ApJ, 595, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Piana, M., Massone, A. M., Hurford, G. J., et al. 2007, ApJ, 665, 846 [Google Scholar]
- Priest, E. R., & Forbes, T. G. 2002, A&ARv, 10, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Ramaty, R., Schwartz, R. A., Enome, S., & Nakajima, H. 1994, ApJ, 436, 941 [NASA ADS] [CrossRef] [Google Scholar]
- Saint-Hilaire, P., Krucker, S., & Lin, R. P. 2010, ApJ, 721, 1933 [NASA ADS] [CrossRef] [Google Scholar]
- Santangelo, N., Horstman, H., & Horstman-Moretti, E. 1973, Sol. Phys., 29, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Schmahl, E. J., Kundu, M. R., & Garaimov, V. I. 2006, ApJ, 643, 1271 [NASA ADS] [CrossRef] [Google Scholar]
- Schmahl, E. J., Pernak, R. L., Hurford, G. J., Lee, J., & Bong, S. 2007, Sol. Phys., 240, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Schwartz, R. A., Csillaghy, A., Tolbert, A. K., et al. 2002, Sol. Phys., 210, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Silva, A. V. R., Share, G. H., Murphy, R. J., et al. 2007, Sol. Phys., 245, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Simões, P. J. A., & Costa, J. E. R. 2006, A&A, 453, 729 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simões, P. J. A., & Costa, J. E. R. 2010, Sol. Phys., 266, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D. M., Lin, R. P., Turin, P., et al. 2002, Sol. Phys., 210, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Stepanov, A. V., & Tsap, Y. T. 1999, Astron. Rep., 43, 838 [NASA ADS] [Google Scholar]
- Stepanov, A. V., & Tsap, Y. T. 2002, Sol. Phys., 211, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Syrovatskii, S. I., & Shmeleva, O. P. 1972, Soviet Astron., 16, 273 [Google Scholar]
- Takakura, T., & Kai, K. 1966, PASJ, 18, 57 [NASA ADS] [Google Scholar]
- Tomblin, F. F. 1972, ApJ, 171, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Tomczak, M., & Ciborski, T. 2007, A&A, 461, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Torre, G., Pinamonti, N., Emslie, A. G., et al. 2012, ApJ, 751, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuneta, S., Masuda, S., Kosugi, T., & Sato, J. 1997, ApJ, 478, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Turkmani, R., Cargill, P. J., Galsgaard, K., Vlahos, L., & Isliker, H. 2006, A&A, 449, 749 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vlahos, L., Isliker, H., & Lepreti, F. 2004, ApJ, 608, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Wentzel, D. G. 1976, ApJ, 208, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, Y., Emslie, A. G., & Hurford, G. J. 2008, ApJ, 673, 576 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, Y., Cao, W., Jing, J., & Wang, H. 2012, ApJ, 750, L7 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 CLEAN maps for each flare: a) 2002 July 23; b) 2003 November 02; c) 2011 February 24; and d) 2011 September 24, showing the emission at 10−11.3 keV (black contours) and 88.6−100 keV (blue contours) at 30, 50, 70, 90% of maximum of each energy bin. The ROIs for the imaging spectroscopy are defined in gray lines: footpoints (continuous lines) and looptop (dashed lines). Integration times are shown in each frame and in Table 1. The CLEAN beam width factor used to construct each map according to the best agreement with visibility forward-fitting is also presented in Table 1. For each, a total of 19 maps were made with energy bins logarithmically spaced between 10 and 100 keV. |
| In the text | |
 |
Fig. 2 Looptop (a), footpoint (b) sources and spatially integrated (c) HXR spectra (black) of flare A, 2002 July 23, estimated background (gray), and fitting result (red) and its components: thermal (green) and non-thermal (blue). For the looptop spectrum, the non-thermal is a thin-target model; for the footpoint and integrated spectra, it is a thick-target model. |
| In the text | |
 |
Fig. 3 Same as Fig. 2, for flare B, 2003 November 02. |
| In the text | |
 |
Fig. 4 Same as Fig. 2, for flare C, 2011 February 24. |
| In the text | |
 |
Fig. 5 Same as Fig. 2, for flare D, 2011 September 24. |
| In the text | |
 |
Fig. 6 CLEAN maps for the four flares, evidencing thermal emission at 10−11.3 keV (red), footpoints at 61.6−69.5 keV (blue contours, at 50% of the maximum of each map), and non-thermal looptop sources (green solid) at 42.8−48.3 keV (50%) for flares A and B, 20.7−23.4 keV (40%) for flare C, and 29.8−33.6 keV (50%) for flare D. The countour levels of 30% and 70% at those energies (green dashed lines) are also shown. The thick yellow line indicates the length L. Date and integration times are indicated in each map. |
| In the text | |
 |
Fig. 7 Pileup effect in the count spectra for flares A, B, C, and D (time intervals in Table 1 and noted in each frame). Top row: corrected (gray) and uncorrected (black) count spectra. Bottom row: the ratio of pileup corrected and uncorrected count spectra for each flare. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


