| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A35 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201219874 | |
| Published online | 15 February 2013 | |
A peek behind the dusty curtain: KS-band polarization photometry and bow shock models of the Galactic center source IRS 8⋆
1
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Str. 77,
50937
Köln,
Germany
e-mail: rauch@ph1.uni-koeln.de; eckart@ph1.uni-koeln.de; buchholz@ph1.uni-koeln.de;
maca@ph1.uni-koeln.de, sabha@ph1.uni-koeln.de; cstraubm@ph1.uni-koeln.de; mvalencias@ph1.uni-koeln.de;
syazici@ph1.uni-koeln.de
2
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
3
European Southern Observatory, Alonso de Córdova 3107, Casilla 19, 19001
Santiago,
Chile
e-mail:
kmuzic@eso.org
Received:
22
June
2012
Accepted:
3
December
2012
Context. IRS 8 offers the possibility to study unique bow shock properties and polarization features in the dusty environment at the Galactic center.
Aims. We aim to gain insight into the properties of the surrounding material of the bow shock source IRS 8, based on the measured polarization distribution along its extended feature. Bow shock models enable a relative positioning of its central star with respect to the northern arm and Sagittarius A*.
Methods. The analysis is based on polarimetric KS-band and nonpolarimetric L′- and N-band data obtained with the adaptive-optics assisted instrument NAOS/CONICA (KS- and L′-band) and the mid-infrared imager/spectrograph VISIR (N-band) at the ESO Very Large Telescope. A polarization map covering an area of ~31.9′′ × 8.2′′ at the position of IRS 8 was obtained using high-precision photometric methods, together with a polarimetric calibration specified for NACO. In addition, simulated L′-band bow shock models are presented, which allow a positioning of IRS 8 with respect to the interaction medium of the northern arm.
Results. This work presents interstellar dust properties for the northern arm in the vicinity of a bow shock, as well as a three-dimensional positioning of IRS 8 with respect to the northern arm and Sagittarius A*. The presented polarization maps for the Galactic center source IRS 8 show a total intrinsic polarization degree of 3.3% at 13° east of north, measured on nondeconvolved images, and 4.3% at 19° on Lucy-Richardson deconvolved images. Analysis of the polarization distribution along the bow shock reveals a polarization pattern as it would be produced by absorption on aligned grains and shows a decreasing polarization degree towards the apex of the bow shock. Current literature provides a mean electron density for IRS 8. The comparison of this value with properties of simulated polarization maps in a circumstellar environment, which are capable of multiple scattering, leads to the conclusion that multiple scattering events reduce the degree of polarization at the apex of the bow shock. Additionally, bow shock models that allow relative positioning of IRS 8 with respect to the northern arm and Sagittarius A* are presented. The results indicate that its central star is located closer towards the observer than the northern arm.
Key words: polarization / scattering / methods: data analysis / techniques: polarimetric / ISM: general / infrared: ISM
FITS files of the reduced polarimetric images are available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/551/A35
© ESO, 2013
1. Introduction
The Milky Way is an SBb galaxy, following the Hubble classification. It contains a super-massive black hole at its center with a mass of ~4.0 × 106 M⊙ at a solar distance of ~8.0 kpc (Eckart et al. 2002; Schödel et al. 2002, 2003; Ghez et al. 2003, 2008; Gillessen et al. 2009). This gravitational center attracts stars, as well as dust and gas. Radio observations and studies of the provided hydrogen recombination lines have led to the discovery of complex structures of ionized gas called the mini-spiral (Schwarz et al. 1989; Roberts & Goss 1993; Roberts et al. 1996). Although the complete dynamics of these structures still remain unknown, the best-fitting model is provided by gas orbiting Sagittarius A* (Sgr A*) on three major streamers called the northern, eastern, and western arms (Schwarz et al. 1989; Sanders 1998; Vollmer & Duschl 2000; Liszt 2003; Paumard et al. 2004; Mužić et al. 2007; Zhao et al. 2009, 2010).
Stars with high proper motions and stellar winds cut across these features and interact with the gaseous and dusty medium. If a supersonic wind originating in a hot star impinges on its surrounding material, the wind is abruptly decelerated and shocked. This causes the medium to be illuminated and compressed into relatively thin and dense shells that are driven into the ambient medium, producing a bow shock. The orientation and shape of the bow shock depends on the relative velocity of the surrounding dust and gas with respect to the interacting star. Other defining parameters are the density of this material and its distribution within the interaction region. Nonaxisymmetric bow shocks are produced by an anisotropic wind originating in the star or by the surrounding material having a density gradient along the interaction zone (Wilkin 2000). These properties define all observable parameters of a bow shock, such as the stand-off distance between the central star and the apex, its three-dimensional angular orientation, and the shape of the bow.
In this work polarimetric data for the Galactic center (GC) source IRS 8 are presented. There are several effects that cause polarization, which are considered as either intrinsic to the source itself or as foreground effects caused by grains along the line-of-sight. These effects are the scattering on spherical and/or aligned grains, (re-)emission from heated nonspherical particles, and dichroic extinction by nonspherical and aligned grains. Only scattering and (re-)emission are considered to be intrinsic polarization features. For sources embedded in optically thick material, dichroic extinction can also contribute a significant amount of polarization, which is an effect of grain alignment averaged along the line-of-sight (Whitney & Wolff 2002).
These effects can be observed in the GC, as Capps & Knacke (1976) and Knacke & Capps (1977) showed by observing ten sources in K-, L-, and N-bands within ≤2 pc of the GC. They found uniform polarization degrees and angles of ~4% at ~15° east of north for all four observed K-band sources. This polarization is almost parallel to the projection of the Galactic plane, which has a position angle of ~31.4° at the location of Sgr A* (Reid et al. 2004). This effect was interpreted as caused by aligned dust grains located in the Galactic spiral arms along the line-of-sight. In addition, almost perpendicular polarization vectors for the same sources observed at N-band were found. This led to the conclusion that this polarization must be caused by the sources themselves, and therefore, these values were classified as intrinsic. Polarimetric L-band observations have shown an intermediate polarization between the orientation of the aforementioned K- and N-band polarization vectors. This can be explained as a superposition of intrinsic and foreground polarization. Observations of more than ~160 sources in H-, K-, L′, and M-band support this wavelength dependency of the measured polarization (Kobayashi et al. 1980; Lebofsky et al. 1982; Bailey et al. 1984; Eckart et al. 1995; Ott et al. 1999). More recently, Buchholz et al. (2011) report a foreground polarization of (4.6 ± 0.6)% at (26 ± 6)° for KS-band and (9.3 ± 1.3)% at (20 ± 6)° for H-band at the GC. These results indicate higher polarization degrees and steeper polarization angles for higher separation from the GC (KS-band: (7.5 ± 1.0)% at 11° ± 6°; H-band: (12.1 ± 2.1)% at (13 ± 6)°). A difference in polarization degree and angle from this uniform foreground polarization is interpreted as intrinsic.
Although there is no solely accepted scenario for intrinsic polarization, the most likely ones are (Mie-)scattering on dust grains and absorption/emission from magnetically aligned particles. These processes depend on the dust attributes in the interaction region of a bow shock. Thus, polarization measurements are a revealing method to investigate the dust properties in these areas. The strongest thermal emission occurs at 12.5 μm (Aitken et al. 1998) and is assumed to be negligible at shorter wavelengths. Thus, emission can be neglected for the presented KS-band observations of this work.
Many sources located at the projected position of the northern arm (NA) lacked a completely accepted classification for almost three decades. Recent high angular resolution observations have revealed complex bow shock structures for many of these sources and led to the explanation that these features were veiled at lower resolutions by the dusty and gaseous material of the surrounding medium. There are several bow shock sources associated with the NA, the most prominent ones being IRS 1W, 5, 10W, 21, and IRS 8 (e.g. Tanner et al. 2002, 2005).
Because of its relatively isolated location (1.112′′ E and 29.088′′ N of Sgr A*, corresponding to a projected distance of about 1.13 pc, assuming a galactocentric distance of 8 kpc, Schödel et al. 2010), IRS 8 was not observed until 1975 using a 2.5′′ circular aperture of the Hale 5 m telescope at 2.2 μm (Becklin & Neugebauer 1975). The source is observable at near- and mid-infrared wavelengths, while radio observations just show its extended component. The luminosity of IRS 8 has been determined to be L = 105.6±0.2 L⊙ from a derived Teff = 36 000 ± 2000 K and the observed K-band magnitude of 10.1 mag at 2.2 μm (Becklin et al. 1978; Geballe et al. 2006). Its true shape consisting of a bow shock and a central star (in the following referred to as IRS 8*) remained unknown until adaptive optics measurements could be acquired (Rigaut et al. 2003; Geballe et al. 2004).
Geballe et al. (2004) obtained high-resolution H- and K-band images using the Gemini North telescope, which revealed a central point-like source embedded in a bow shock with an apex ~0.2′′ northeast of IRS 8*. They conclude that the extended feature is in fact a bow shock caused by the interaction of a high-velocity wind originating from a hot star with dense interstellar gas. Geballe et al. (2006) were able to classify IRS 8* as an O5-6.5 star with III-If ranges. The fact that Lacy et al. (1991) observed a blueshifted NeII component led Geballe et al. (2006) to the conclusion that IRS 8* lies well in front or behind the NA, assuming this component is associated with IRS 8*.
This work aims towards a better understanding of the properties of the surrounding material and of the positioning of the central star IRS 8* with respect to the interaction medium of the NA. To achieve this goal, polarization maps of IRS 8 and several sources in its vicinity are presented along with bow shock models based on known and observable properties.
 |
Fig. 1 KS-band FOV for one Wollaston channel covering an area of 31.9′′ × 8.2′′. The white box marks the area used for the presented polarization maps. |
2. Observations and data reduction
2.1. Polarization data
The polarimetric KS-band datasets of this work were obtained in March 2011 at the ESO VLT unit telescope 4 (Yepun) on Mt. Cerro Paranal in Chile using the NACO (NAOS/CONICA) instrument (program 086.C-0049(A)). The adaptive optics feedback loop was closed targeting IRS 7 as the guide star, using the infrared wavefront sensor provided by NAOS.
Two datasets were obtained on 18 and 20 March 2011. The dataset taken on 18 March 2011 between 8:26:52 and 8:45:08 UT (in the following referred to as dataset 1) suffers from bad and variable seeing conditions during the observation time (ranging from 1.57′′ to 2.14′′, DIMM-Seeing provided by ESO Observatories Ambient Conditions Database), while the data obtained on 20 March 2011 between 06:12:06 and 06:40:15 UT (dataset 2) benefited from better, but still poor, conditions (DIMM seeing: 0.57′′−1.17′′).
Sky subtraction, flat-fielding, and dead/hot-pixel correction were applied to all images, using the software DPUSER. The sky background was determined targeting an area, devoid of resolved sources, located at 266.191331 (RA), −29.10391 (Dec).
The Wollaston prism installed at NACO provides two channels corresponding to an ordinary beam (0°) and an extraordinary beam (90°). A rotatable half-wave-plate (HWP) that can be inserted in the beam yields two additional channels (45° and 135°) at a rotated HWP-angle of 22.5°. These four channels were taken consecutively to avoid a significant change in the observing conditions between the individual images.
It is crucial to obtain the flat-field using the Wollaston prism, because inclined mirrors and different transmissivity of the channels have a significant impact on the calibration. Not using the Wollaston prism for flat-field calibration can produce offsets of up to 2% and 10° (Buchholz et al. 2011; Witzel et al. 2011). All images contained in the datasets were cut into stripes with a dimension of 27.8′′ × 6.1′′. These images were shifted and added to four mosaics (see Fig. 1) covering a field of view (FOV) of 31.9′′ × 8.2′′, which corresponds to 1.24 × 0.32 pc. All photometry was performed on these mosaics. The linear polarization was obtained by measuring the fluxes of these four different polarization channels, making it possible to derive polarization degrees and angles. In addition to bad seeing conditions, anisoplanatic effects caused by the loss of AO performance due to the high angular separation from the guide star (23.34 ′′ to IRS 8) become significant.
The bright star located east of IRS 8, which is contained in most of the images, was used to determine an accurate 80 × 80 pixel point-spread-function (PSF), using the PSF extraction feature of the StarFinder-IDL-Code (Diolaiti et al. 2000). Unfortunately, the automatic secondary source removal feature failed to extract the star contaminating the eastern area of the PSF. This star was extracted manually by cutting out a circular region and filling the gap with a patch cut out of a mirrored image of the PSF source itself.
The source’s complex morphology prevented an accurate PSF fitting of its components. To properly map the distribution of polarization of IRS 8 by placing apertures along the bow shock and the central source without including flux of the other component, it was necessary to increase the spatial resolution of the image. This was done by applying Lucy-Richardson deconvolution. According to Ott et al. (1999), this method of deconvolution is flux-sustaining for stars brighter than mK = 13 mag, such as IRS 8.
The central source of the Lucy-Richardson deconvolved images contributes 16% of the total extended source flux. Applying Lucy-Richardson deconvolution to an extended bow shock structure leads to uncertainties in the determination of the polarization degree and angle because of its tendency to suck up flux into more illuminated regions. Buchholz et al. (2011) present an estimation for the error induced by Lucy-Richardson deconvolution on an artificial image of an extended bow shock source in a crowded field. They show that the maximum deviation in polarization amounts to 2.6% at 5° for the central star and 1.5−2% at 5−7° for the bow shock feature.
 |
Fig. 2 Polarization map of IRS 8 and its surrounding sources. Polarization was measured on nondeconvolved images using the techniques described in Sect. 2. The images were not corrected for background flux or foreground and instrumental polarization. |
2.2. Polarimetry and calibration
The bow shock was mapped with eight overlapping apertures of 0.32 ′′, while the central source was covered by a single aperture of the same size. Measuring the fluxes in these regions provides four intensities, each corresponding to a Wollaston channel (0°, 45°, 90°, 135°).
The polarization degree and angle for each source, as well as the distribution of
polarization along the bow shock, can be obtained using the Stokes formalism. In this
formalism all information about the polarization can be described by four Stokes
parameters (I, Q, U,
V). These parameters can be written as a single Stokes vector
S: 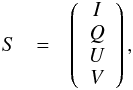 (1)where
I is the Stokes parameter representing the total measured flux, which
is usually normalized to I = 1.
(1)where
I is the Stokes parameter representing the total measured flux, which
is usually normalized to I = 1.
The linear polarization in the horizontal plane is described by the Stokes parameter
Q, while U describes the amount of linear polarization
in a plane rotated by 45° east of north, with f0,
f45, f90, and
f135 being the fluxes for different polarization angles.
Q and U are given by
 The
Stokes parameter V yields information about the amount of circular
polarization. NACO does not provide a
The
Stokes parameter V yields information about the amount of circular
polarization. NACO does not provide a 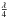 -plate to
measure this quantity, so V is assumed to be 0. This is reasonable,
because the degree of circular polarization at the GC is considered to be very low (Bailey et al. 1984).
-plate to
measure this quantity, so V is assumed to be 0. This is reasonable,
because the degree of circular polarization at the GC is considered to be very low (Bailey et al. 1984).
Using this formalism, the polarization degree P and angle θ can be
calculated by using the following equations:  Because
NACO was not designed to obtain polarimetric data, the optical elements (e.g. mirrors and
the HWP) inside the telescope itself affect the measured polarization. Therefore, there is
an instrumental polarization superposing the original signal (Witzel et al. 2011). In the Stokes formalism, all optical effects can
be described by Müller matrices. Witzel et al.
(2011) derived matrices for the optical components of NACO that are capable of
describing reflection, transmission, polarization, and other effects for each optical
element. If these matrices are known for each component of the telescope, the offset
induced by instrumental polarization can be corrected by simply multiplying a combination
of these matrices with the measured Stokes vectors. Correcting the instrumental
polarization keeps the uncertainties at ~1% in polarization degree and ~5° in
polarization angle (Witzel et al. 2011).
Because
NACO was not designed to obtain polarimetric data, the optical elements (e.g. mirrors and
the HWP) inside the telescope itself affect the measured polarization. Therefore, there is
an instrumental polarization superposing the original signal (Witzel et al. 2011). In the Stokes formalism, all optical effects can
be described by Müller matrices. Witzel et al.
(2011) derived matrices for the optical components of NACO that are capable of
describing reflection, transmission, polarization, and other effects for each optical
element. If these matrices are known for each component of the telescope, the offset
induced by instrumental polarization can be corrected by simply multiplying a combination
of these matrices with the measured Stokes vectors. Correcting the instrumental
polarization keeps the uncertainties at ~1% in polarization degree and ~5° in
polarization angle (Witzel et al. 2011).
2.3. Background calibration
The measured fluxes of each pixel are a superposition of the flux of sources at the pixel position and a background flux produced by general emission of the targets environment, induced flux along the line-of-sight, and uncorrected residues of the detector chip at the pixel position. A mean background flux for the presented mosaic was determined by measuring the flux of ~40 apertures at areas devoid of resolved sources, dividing the measured flux by the number of pixels in these apertures and averaging the outcome. To subtract the background flux from the apertures used to obtain polarization degrees and angles, the mean background flux per pixel was multiplied by the number of pixels contained in each aperture and subtracted from their total flux.
2.4. Foreground polarization
The foreground polarization is assumed to be a linear polarization with a polarization
degree Pfg at an angle of
θfg, as it would be produced by dust
forming a large-scale wiregrid, which induces an additional polarization along the
line-of-sight. This effect, just like the instrumental polarization, can be described by
Müller matrices:  (6)where
Sobs is the observed Stokes vector and
Sint the Stokes vector of the intrinsic polarization. The
matrices Mlin and Mrot represent
the Müller matrix of a linear polarizer with its maximum at N-S-axis and the rotation
matrix.
(6)where
Sobs is the observed Stokes vector and
Sint the Stokes vector of the intrinsic polarization. The
matrices Mlin and Mrot represent
the Müller matrix of a linear polarizer with its maximum at N-S-axis and the rotation
matrix.
To be able to apply the foreground matrix to the Stokes vector, it has to be rotated to
the proper angle by a rotation matrix Mrot:
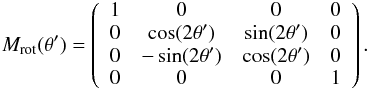 (7)The
angle used in the Müller matrix describing the linear polarizer is the angle of maximum
absorption, while the polarization angle is defined as the angle of measured maximum flux.
Therefore,
θ′ = 90° + θfg
has to be used for the rotation matrix instead of
θfg. The angle
θfg can be determined by using the mean
value of the polarization parameters of surrounding sources. The uncorrected polarization
vectors for IRS 8 and other sources in the FOV are shown in Fig. 2. To subtract the foreground polarization the Müller matrix has to be
inverted and the calibrated Stokes vector has to be multiplied with it. This method was
used to obtain the intrinsic polarization of the surrounding sources, as well as IRS 8*
and the polarization distribution of its bow shock. A polarization map corrected for
background, foreground, and instrumental polarization, with polarization vectors scaled to
twice the size of the vectors in Fig. 2 is shown in
Fig. 3.
(7)The
angle used in the Müller matrix describing the linear polarizer is the angle of maximum
absorption, while the polarization angle is defined as the angle of measured maximum flux.
Therefore,
θ′ = 90° + θfg
has to be used for the rotation matrix instead of
θfg. The angle
θfg can be determined by using the mean
value of the polarization parameters of surrounding sources. The uncorrected polarization
vectors for IRS 8 and other sources in the FOV are shown in Fig. 2. To subtract the foreground polarization the Müller matrix has to be
inverted and the calibrated Stokes vector has to be multiplied with it. This method was
used to obtain the intrinsic polarization of the surrounding sources, as well as IRS 8*
and the polarization distribution of its bow shock. A polarization map corrected for
background, foreground, and instrumental polarization, with polarization vectors scaled to
twice the size of the vectors in Fig. 2 is shown in
Fig. 3.
2.5. N-band data
A 13.04 μm VISIR image from the program 085.C-0047(A) taken on 15 October 2010 at the ESO VLT UT3 is shown in Fig. 4. The data was obtained using the standard mode of the mid-infrared imager/spectrograph VISIR. In this mode the camera electronics averages several tens of exposures to a single image. The standard nodding (~270° east of north) and chopping technique (chop throw ~30′′) was used. The resulting image was sky-subtracted and corrected for bad pixels. The presented FOV covers an area of 26.3′′ × 32.1′′ at a pixel scale of 0.127 ′′ pixel-1. Two negative flux areas in the northern part of the NA were masked by a circular patch with an average flux of the surrounding pixels. This image was used to derive the dimensions of the NA and its relative position with respect to IRS 8.
 |
Fig. 3 Polarization map of IRS 8 and its surrounding sources. Polarization was measured on nondeconvolved images and corrected for background, foreground, and instrumental polarization. Polarization vectors were determined with the techniques mentioned in Sect. 2 and are scaled to twice the size of the vectors in Fig. 2. The surrounding sources show approximately no residual intrinsic polarization, indicating a proper calibration and subtraction of the foreground polarization. This calibrated map is used for Lucy-Richardson deconvolution. |
2.6. L′-band imaging
The bow shock of IRS 8 was modeled based on L′-band data taken on 6 August 2009 at the ESO VLT UT4 (program: 083.B-0390(A), see Fig. 5). The NACO L27 camera used for these images provides a pixel scale of 0.02719 ′′ pixel-1. IRS 7 served as a guide star for AO correction. DIMM seeing was stable during the observations and around 1′′. The sky was sampled on a dark field located ~60 ′′ northeast of Sgr A*. Jittered sky frames were median-combined for sky reconstruction. The obtained science data were flat-fielded, sky-subtracted, and corrected for bad pixels using our own IDL routines. Individual frames were finally combined to a mosaic using the jitter algorithm of the ESO eclipse software package. The intensity contours of IRS 8, used for bow shock modeling, were extracted from this mosaic.
3. Results
3.1. Density of the bow shock
The magnetic field at the position of IRS 8 is considered to be parallel to the north-south axis (Aitken et al. 1998; Morris 1998; LaRosa et al. 2000; Glasse et al. 2003). The presented polarization maps show polarization vectors parallel to the magnetic field of the NA as they would be produced by absorptive scattering on dust grains, aligned by Davis-Greenstein alignment (Davis & Greenstein 1951). The asymmetric bow shock is brighter towards the east, indicating an increasing density towards this direction.
For IRS 8 a total intrinsic polarization degree of 3.3% at 13° east of north was determined on nondeconvolved images and 4.3% at 19° on Lucy-Richardson deconvolved images, using the data reduction techniques described in Sect. 2. The nondeconvolved polarization map of the bow shock (Fig. 6a) shows increasing polarization degrees towards its western edge ranging from 2.2% at 21° at the eastern part of the bow shock to up to 3.3% at 12° in the west. The polarization degree of the Lucy-Richardson deconvolved bow shock (Fig. 6b) reaches its minimum of 0.7% at the position of the apex and has a maximum value of 5.2% at the western edge of the bow shock at angles around 19°.
The uncertainties of the corrected nondeconvolved polarization measurements amount to 1% and 5° (Witzel et al. 2011). In the case of the Lucy-Richardson deconvolved images, these errors rise to 2.8%, 7.1° for the central source and 2.3%, 8.7° for the bow shock feature (Witzel et al. 2011; Buchholz et al. 2011). Even if these maximum uncertainties induced by Lucy-Richardson deconvolution are considered, the aforementioned drop in polarization degree towards the apex in the deconvolved images is still present.
While the nondeconvolved image just shows a smooth trend of lower polarization towards the eastern part of the bow shock’s lobe, the Lucy-Richardson deconvolved image has a significant loss of polarization at the position of the apex. In this region the matter is highly compressed by the wind originating in the central source. This suggests that lower polarization degrees might be connected to high-density areas.
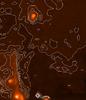 |
Fig. 4 Smoothed VISIR image of IRS 8 and the NA taken at 13.04 μm. The FOV covers an area of 26.3′′ × 32.1′′. The overlaid contours range from 0.68 Jy to 0.84 Jy in steps of 0.04 Jy. |
 |
Fig. 5 L′-band image of IRS 8. This image was used to extract the intensity contours of IRS 8 (see Fig. 8). The bow shock modeling was performed using these contours. |
 |
Fig. 6 Intrinsic KS-band polarization map of the bow shock surrounding IRS 8*. The bow shock was covered with 8 apertures to map the polarization distribution along this feature. |
An explanation for this pattern could be multiple scattering events. In a turbulent particle environment, like a bow shock’s interaction region, grains will have a random alignment. If a photon is scattered several times on these nonaligned grains, the information of each previous scattering event is lost, which results in a loss of polarization degree. Multiple scattering presumably occurs in a dense particle environment, such as the apex of a bow shock. The following sections will show that the density in this region is high enough to produce a significant amount of multiple scattering events.
Fischer et al. (1994, 1996) simulated polarization maps in a circumstellar environment for pre-main sequence objects. The maps were calculated for three different midplane densities of ρF = (1,3,10) × 10-18 g cm-3 at three wavelengths (1.25 μm, 1.65 μm, and 2.2 μm) and applied to different accretion disk types (see Lazareff 1990 or Table 1 in Fischer et al. 1996). To cover a wide field of properties for circumstellar dust, which are quite uncertain, two different grain populations were introduced for their simulation: a small grain population with radii a = 0.005−0.25 μm and a population consisting of larger grains with radii a = 0.1−1.0 μm. The modeled material is a compound of astronomical silicate (62.5%) and graphite (37.5%). Fischer et al. (1994, 1996) find multiple scattering events for many of their simulated polarization maps. The number of scattering events rises for larger grains and higher densities (see Fig. 8 in Fischer et al. 1996). At 2.2 μm, multiple scattering on large grains occurs for every accretion disk type except for a massive (self-gravitating) disk with a rigid body and a massive (self-gravitating) disk with an infinite isothermal slab. When excluding these two accretion disk types, the simulations show multiple scattering events for all particles and densities at 2.2 μm. Assuming that these polarization maps describe the same properties that we find at the position of IRS 8, we can derive a particle density for which multiple scattering can occur.
Looking at the model parameters used by Fischer et al.
(1994, 1996), the mean mass of a particle
(mF) can be calculated by assuming a mean density for the
mixture of astronomical silicate (“as”) and graphite (“g”) of
ρas + g = 2 g cm-3:
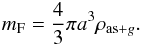 (8)The
particle density used in the model (nF) can be obtained by
dividing the midplane density of their model
(ρF) by this mass:
(8)The
particle density used in the model (nF) can be obtained by
dividing the midplane density of their model
(ρF) by this mass: 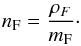 (9)Zhao et al. (2009), on the other hand, derived a mean
electron density of
ne = 6 × 103 cm-3
from the H92α line in the emission spectrum of IRS 8, assuming it is
optically thin. To attain a particle density from this value it has to be considered that
emission line spectra only show ionized particles. The definition of an ionization factor
I as the ratio of ionized to nonionized particles provides the proton
density of the medium. An ionization degree of 100% is described by
I = 1. Assuming the material solely consists of atomic hydrogen particles
the proton density (np) is calculated by
(9)Zhao et al. (2009), on the other hand, derived a mean
electron density of
ne = 6 × 103 cm-3
from the H92α line in the emission spectrum of IRS 8, assuming it is
optically thin. To attain a particle density from this value it has to be considered that
emission line spectra only show ionized particles. The definition of an ionization factor
I as the ratio of ionized to nonionized particles provides the proton
density of the medium. An ionization degree of 100% is described by
I = 1. Assuming the material solely consists of atomic hydrogen particles
the proton density (np) is calculated by
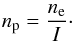 (10)The
mass density of all atomic particles in 1 cm3
(ρz,a) is
(10)The
mass density of all atomic particles in 1 cm3
(ρz,a) is
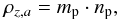 (11)with
mp = 1.67 × 10-24 g being the proton mass. The
ambient medium consists of gas and dust. From a dust-to-gas ratio R, a
dust density (ρz,d) can be obtained by
(11)with
mp = 1.67 × 10-24 g being the proton mass. The
ambient medium consists of gas and dust. From a dust-to-gas ratio R, a
dust density (ρz,d) can be obtained by
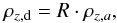 (12)where
R = 1 corresponds to 100% of the mass being dust. The ambient material
does not solely consist of single hydrogen particles but is a mixture of H, H2,
and He particles. Taking this into account, the density of dust consisting of H,
H2, and He can be derived by
(12)where
R = 1 corresponds to 100% of the mass being dust. The ambient material
does not solely consist of single hydrogen particles but is a mixture of H, H2,
and He particles. Taking this into account, the density of dust consisting of H,
H2, and He can be derived by
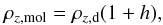 (13)where
h is the ratio of H2+He to H (h = 1
corresponds to 100% H2+He).
(13)where
h is the ratio of H2+He to H (h = 1
corresponds to 100% H2+He).
The mass of a single grain (m1p) is needed to determine the particle density. This work adopts the DL-MRN interstellar grain model that was derived by fitting the observed extinction at several wavelengths with different spherical graphite particles (Mathis et al. 1977; Draine & Lee 1984). Since the observed extinction shows a uniform wavelength dependence over the whole sky (Bless & Savage 1972; York et al. 1973; Nandy et al. 1975, 1976), it is reasonable to assume that the same grain population is present in the NA.
Fischer et al. (1994, 1996) utilize the same interstellar grain model for their simulations
of protostellar envelopes. Therfore, the mass of a single particle can be calculated by
using a mean mass density of
ρas + g = 2 g cm-3 for this
mixture of astronomical silicate and graphite, together with the grain radius
(a) of their simulations:
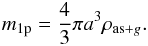 (14)The
particle density nz derived from Zhao et al. (2009) can now be calculated by dividing
the density of dust by the mass of a single particle:
(14)The
particle density nz derived from Zhao et al. (2009) can now be calculated by dividing
the density of dust by the mass of a single particle:
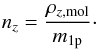 (15)Thus,
the particle density is given by
(15)Thus,
the particle density is given by 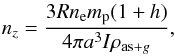 (16)while,
as described earlier, the particle density used in the models from Fischer et al. (1994, 1996) can
be calculated from Eq. (9):
(16)while,
as described earlier, the particle density used in the models from Fischer et al. (1994, 1996) can
be calculated from Eq. (9):
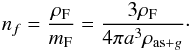 (17)Ferrière (2012) state that the interstellar gas in the
central cavity around Sgr A* is a composition of warm ionized gas and atomic gas with
roughly equal amounts. Assuming the same properties as occur in the vicinity of IRS 8, an
ionization degree of ~40% can be adopted.
(17)Ferrière (2012) state that the interstellar gas in the
central cavity around Sgr A* is a composition of warm ionized gas and atomic gas with
roughly equal amounts. Assuming the same properties as occur in the vicinity of IRS 8, an
ionization degree of ~40% can be adopted.
The ambient medium of IRS 8 consists of swept-up material of the NA (Geballe et al. 2006; Tanner et al. 2002). Tanner et al. (2002) derived a gas density for the NA of nH = 3 × 104 cm-3 (see also Tanner et al. 2005). Assuming that the gaseous medium of the NA mainly consists of atomic hydrogen, this corresponds to a mass density of ρH = nHmp ~ 10-19 g cm-3. This gas is compressed into a much denser shell at the position of the bow shock. Thus, assuming a factor 100, or even more, between the gas density in the NA and in the bow shock can be justified. This leads to a mass density of ρH ~ 10-17 g cm-3 for the gas at the apex of the bow shock. Tanner et al. (2002) show that the best-fitting model for IRS 21 is a bow shock model with a dust density of ρd = 2.3 × 10-17 g cm-3. IRS 21 was classified as a WC9 Wolf-Rayet star (Tanner et al. 2002). Thus, this star provides a general estimate for gas densities in a bow shock of a mass-losing star with strong stellar winds located in the NA, such as IRS 8. Supposing similar properties for the dust surrounding IRS 8, a dust-to-gas mass ratio in the bow shock of R ~ 0.5 can be derived.
Broadbent et al. (1988) report that 60% of the mass in the central 10 kpc of the galaxy consists of molecular hydrogen. This leads to a ratio of H2 to H particles of about 0.5. According to Zhao et al. (2010), the ratio of He to H atoms in the NA amounts to 0.08, which provides a total ratio of H2+He to H of h ~ 0.6.
Assuming that 40% of the dusty and gaseous material is ionized (I = 0.4), 50% of the material mass consisting of dust (R = 0.5), and 60% of the particles being either H2 or He (h = 0.6), particle densities for the two grain populations can be derived, as they were used in Fischer et al. (1994, 1996). Applying a mean particle radius a = 0.13 μm (small grain population) and a = 0.55 μm (large grain population) to the measured electron density from Zhao et al. (2009) leads to particle densities of
-
small grains: nz = 1.09 × 10-6 cm-3,
-
large grains: nz = 1.44 × 10-8 cm-3.
This is in good agreement with the particle densities of ~10-6−10-7 cm-3Cox et al. (2012) find for modeled bow shocks.
While the particle densities derived from the models of Fischer et al. (1994, 1996), using ρas + g = 2 g cm-3 and ρF = 1 × 10-18 g cm-3, amount to
-
small grains: nF = 5.43 × 10-5 cm-3,
-
large grains: nF = 7.17 × 10-7 cm-3.
The particle densities derived from Zhao et al. (2009) differ by about one magnitude from the values used in the Fischer models. The electron density measured by Zhao et al. (2009) is a mean density obtained for the total extended source IRS 8 (IRS 8* + bow shock) and is directly proportional to the derived mass densities. Assuming a density gradient, as used for the best-fitting bow shock models (see Sect.3.2.1), the density in the bow shock is much higher than ne = 6 × 103 cm-3, especially at the apex. This assumption closes the gap of one magnitude between the derived densities from Zhao et al. (2009) and Fischer et al. (1994, 1996). Therefore, it can be concluded that the particle density for the presented dust parameters reaches values capable of producing a significant amount of multiple scattering events at the position of the apex that lead to a loss of polarization degree.
 |
Fig. 7 Example solutions for different behaviors of the ambient medium density. The solid line shows the symmetric solution assuming the uniform density (Wilkin 1996). The two nonaxisymmetric solutions arise from the stratified ambient medium with the density gradient in the direction of the arrow (Wilkin 2000). The density of the medium follows the law ρ = ρ0(1 + a1x + a2x2), for x ≥ 0. |
3.2. Bow shock modeling
The following section presents a determination of the actual position of the central star IRS 8* with respect to its surrounding material based on bow shock models of L′-band contours and N-band images of the NA and IRS 8.
3.2.1. Description of the model
In Mužić et al. (2010) we developed a
three-dimensional bow shock model, based on the analytic two-dimensional solution for a
mass-losing star moving through a medium of uniform density (Wilkin 1996). The appearance of IRS 8’s bow shock on the plane of the
sky is clearly asymmetric and cannot be well fit by the axisymmetric bow shock model.
Nonaxisymmetric stellar wind bow shocks occur when a star with an anisotropic wind moves
supersonically with respect to the local medium, or if the star has an isotropic wind
but moves in an ambient medium containing a transverse density gradient (Wilkin 2000). We have no a priori reason to assume
that the wind of the star IRS 8 is anisotropic. Furthermore, IRS 8 seems to be
interacting with the NA (e.g. Tanner et al. 2005;
Zhao et al. 2009), and is clearly not located
in its densest part. Therefore it is reasonable to assume that the asymmetry of the bow
shock is caused by the motion of the massive star IRS 8 through a nonuniform medium.
Wilkin (2000) presented the solution for the
shape of a bow shock due to a star moving supersonically with respect to an ambient
medium with a density gradient perpendicular to the stellar velocity. We tested the case
in which the stratification of the medium follows a polynomial density law, and
considered the linear and quadratic solutions. In Fig. 7 we compare the symmetric analytic solution (solid line; Wilkin 1996) with two asymmetric solutions arising
from the density gradient law
ρ = ρ0(1 + a1x + a2x2),
where ρ0 is the value of the ambient density along the
z-axis at x = 0. The axes are in the units of
standoff distance R0, given by 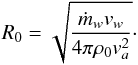 (18)Here
ṁw is the stellar mass-loss rate,
vw the terminal velocity of the stellar
wind, ρ0 the ambient medium mass density, and
va is the velocity at which the star
moves through the medium (i.e. the relative velocity of the ambient medium and the star
velocity in case that the ambient medium is not stationary). The effect that introducing
the density gradient has on the bow shock’s shape is demonstrated in Fig. 7. The solutions shown with dashed and dash-dotted
lines are clearly nonaxisymmetric, and are also “narrower” than the axisymmetric
solutions in the plane parallel to the direction of the density gradient. There are
three angles with which we can describe the orientation of the bow shock shell in space:
(18)Here
ṁw is the stellar mass-loss rate,
vw the terminal velocity of the stellar
wind, ρ0 the ambient medium mass density, and
va is the velocity at which the star
moves through the medium (i.e. the relative velocity of the ambient medium and the star
velocity in case that the ambient medium is not stationary). The effect that introducing
the density gradient has on the bow shock’s shape is demonstrated in Fig. 7. The solutions shown with dashed and dash-dotted
lines are clearly nonaxisymmetric, and are also “narrower” than the axisymmetric
solutions in the plane parallel to the direction of the density gradient. There are
three angles with which we can describe the orientation of the bow shock shell in space:
-
(1)
i – inclination to the line-of-sight; for the observer looking directly at the apex of the bow shock we define i = 0 (the bow shock appears circularly symmetric in this case); for 0° < i < 90° the apex of the bow shock is oriented towards the observer, while the apex points away from the observer for 90° < i < 180° (see Fig. 3 in Mužić et al. 2010).
-
(2)
PA – position angle in the plane parallel to the plane of the sky measured east of north.
-
(3)
α – rotation angle in the plane perpendicular to the plane of the sky (i.e. xy-plane in the coordinate system shown in Fig. 7). While α has no effect on the symmetric bow shock, in the nonaxisymmetric case it will depend on the direction of the density gradient. For α = 0, the density gradient vector is pointing along the line-of-sight towards the observer. For 0° < α < 180°, the x-component of the gradient vector is in the direction of positive x-axis, and for 180° < α < 360° it is in the direction of negative x-axis (i.e. the positive RA). To generate a simulated observation, we start with the bow shock grid calculated following the solution from Wilkin (2000) for a set of polynomial coefficients in the ambient medium density law. We give a shell a certain thickness, by using two solutions with the standoff distances of 0.95R0 and 1.05R0. We then rotate the three-dimensional grid by the angles α, i and PA. To generate the emission maps we use the method described in Mužić et al. (2010), taking only the thermal emission from the dust grains in the shell, in the L′-band into account. To calculate the temperature of the dust grains in the shell we assume the central star with luminosity log (L/L⊙) = 5.6 (Geballe et al. 2006).
3.3. Constraints from the observations
The orientation of a bow shock in space is determined by the relative velocity between the velocity of the star and the ambient medium. The proper motion of the star IRS 8* is (vα, vδ) = (42.4 ± 4.7,59.8 ± 26.0) km s-1 (Schödel et al. 2009). From the observations in the NeII line, Lacy et al. (1991) identified two velocity components, one at −10 km s-1 localized at IRS 8 and the other centered at +110 km s-1 associated with the NA. Although the K-band spectrum of IRS 8* from Geballe et al. (2006) does not allow for accurate determination of the radial velocity, the authors report the average radial velocity from three different lines to be about −10 km s-1, in good agreement with Lacy et al. (1991). From the VLA observations of the mini-spiral, Zhao et al. (2009) report two velocity components in this region, at (− 12 ± 6) km s-1 and (93 ± 28) km s-1. The slightly blueshifted component is consistent with the radial velocity of IRS 8*, while the other one can be attributed to the NA. Zhao et al. (2009) determined the three-dimensional velocity distribution of Sgr A West. They model the mini-spiral with three bundles of Keplerian orbits around Sgr A*. From their Fig. 21c we read proper motions of the NA at the approximate position of IRS 8 to be (vα, vδ) ≈ (45 ± 22, −65 ± 36) km s-1. While there are no nominal uncertainties associated with the NA proper motions from the model, here we adopt the average uncertainties of the proper motions measurements from the 1.3 cm maps, to get the flavor of the uncertainties associated with the quantities we want to derive. The position angle in the plane of the sky (PA) is determined by the relative proper motion of the star and the NA. From the values listed above, we obtain PA = (0 ± 10)°, consistent with the value in Tanner et al. (2005). The inclination to the line-of-sight (i) is determined with the relative transversal velocity and the relative radial velocity. The relative vr will have the negative sign, thus we expect the bow shock to point towards the observer. We obtain i = (50 ± 13)°.
 |
Fig. 8 L′-band contour model to determine the χ2 of the bow shock models in Fig. 9. The axes show relative RA (abscissa) and relative Dec (ordinate) with respect to the central star in units of pixels, with one pixel corresponding to 0.027′′. |
 |
Fig. 9 Bow shock models with corresponding χ2-values for six different rotation angles α under five different inclination angles i. All models were simulated for a constant stand-off distance R0 = 3.5 × 1016 cm with a constant position angle PA = 10°. Black lines represent intensity contours derived from L′-band images. Red lines correspond to simulated bow shock model intensity contours. The best-fitting plots are marked by the blue box. The axes of each model show the relative RA and Dec with respect to the central star in units of pixels, with one pixel corresponding to 0.027′′. |
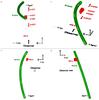 |
Fig. 10 Relative position of IRS 8*, the NA, and Sgr A*, depending on the rotation angle α as it would be seen from different angles of view. We derived the projected NA positions between 0.27 pc and 0.82 pc north of Sgr A* from the N-band image (Fig. 4) with an accuracy of ±0.015 pc in te east-west direction, while the other parts of the NA are based on its curvature and Fig. 21 in Zhao et al. (2009). Radial distances of the NA with respect to Sgr A* were obtained from Fig. 21 in Zhao et al. (2009) at an accuracy of ± 0.1 pc. We determined a mean thickness for the NA of 0.07 ± 0.02 pc from the 0.68 Jy contours of the presented N-band image (Fig. 4). Because no radial dimension of the NA can be derived it is pictured as a circle. Light green arrows indicate the flowing direction of its material. Rotation angles smaller than 270°, as for the best-fitting models, correspond to IRS 8* being well in front of the NA. The thin red line marks the position of IRS 8* along the line-of-sight. Our best-fitting bow shock models indicate α is between 240° and 270°. The corresponding relative position of IRS 8 is marked by the red 3d model. |
3.4. Results of the bow shock modeling
To support our qualitative impression of the bow shock model fitting, we employed a quantitative χ2 approach covering essential parameters of the fitting procedure. For this purpose five points along the L′-band contours, four angles that these points generate (see Fig. 8), and the derived inclination of i = (50 ± 13)° were compared to their modeled values. Positions 1 and 2 correspond to the eastern and western tip positions of the bow shock. Positions 3, 4, and 5 are on a straight line. With positions 4 and 5 located on the outer contour, this line is defined by the central apex (intensity peak of the L′-band contours, position 3) and the position closest to the central apex (position 4) on the outermost contour between positions 1 and 2.
The modeling algorithm has the tendency to elongate the tips of the extended feature. Therefore, positions 3, 4, and 5 were weighted twice the amount of the tip-positions (positions 1 and 2). The sums of all angles and positions, as well as the inclination, were equally weighted to derive the χ2-value.
The results of the bow shock modeling are shown in Fig. 9. The best-fitting plots are produced by rotation angles ranging from 240° to 270° at an inclination of 60°. Angles smaller than 270° correspond to IRS 8* being closer to the observer than the NA. This leads to the conclusion that IRS 8* is in fact well in front of the NA.
The relative position of IRS 8 with respect to the NA and Sgr A* is shown in Fig. 10. The projected positions in the plane of the sky at elevations between 0.27 pc and 0.82 pc north of Sgr A* are derived from the N-band image contours presented in this work (see Fig. 4) with an accuracy of ±0.015 pc in the east-west direction resulting from the uncertainties in defining the center of the NA. A mean thickness of 0.07 ± 0.02 pc for the NA was determined from the 0.68 Jy contour. Because no radial information about its thickness can be achieved, the NA is modeled in a circular symmetric shape. Positions above 0.82 pc and below 0.27 pc are extrapolated from Fig. 21 in Zhao et al. (2009) and the curvature of the NA. These positions can be consistently connected to the dimensions derived from the presented N-band image. Zhao et al. (2009) (Fig. 21) also provide the radial distances for the NA with respect to Sgr A* with an accuracy of ±0.1 pc.
4. Summary and conclusions
We presented the results showing polarization features for ten of the observed stars in the vicinity of the bow shock source IRS 8. While most of the stars do not show a significant polarization after subtracting the foreground, instrumental polarization, and the background flux, IRS 8 has an intrinsic polarization of 3.3% at 13° east of north measured on nondeconvolved images and 4.3% at 19° for Lucy-Richardson deconvolved images. The uncertainties amount to ~1% and ~5° for polarization measurements on nondeconvolved images. In the case of deconvolved images, the errors add up to 2.8%, 7.1° for the central source and to 2.3%, 8.7° for the bow shock. A closer look at the polarization distribution along the bow shock reveals a decrease in polarization towards high-density regions (Figs. 6a, 6b).
Light passing through high-density regions has an increased probability of scattering events compared to lower density regions. In a turbulent particle environment, such as a bow shock’s apex, dust grains will be randomly aligned. Therefore, with each scattering event the information about the preceding event is lost, so the degree of the resulting polarization is lowered. This leads to the conclusion that multiple scattering is the most feasible explanation for the loss of polarization towards the higher density regions of IRS 8.
Particle densities in the bow shock were derived and compared to densities that produce multiple scattering in simulated polarization maps. Assuming an increasing density gradient towards the NA leads to the conclusion that the particle density at the apex of the bow shock reaches values high enough to produce a significant loss of polarization due to multiple scattering events. Thus, the presented set of parameters is able to fit the assumption of multiple scattering in the bow shock of IRS 8 into a consistent picture. These parameters satisfy the electron densities of IRS 8 derived from the H92α measurements (Zhao et al. 2009) and densities of simulated circumstellar polarization maps capable of multiple scattering (Fischer et al. 1994, 1996).
To determine the relative position of IRS 8 with respect to the NA, bow shock models are presented that explain the observed asymmetry in the plane of the sky by the motion of a mass-losing star through a nonuniform ambient medium. The best-fitting models indicate that IRS 8 lies most probably within ~0.1 pc in front of the NA’s center.
The derived dust properties for the NA in the presence of a bow shock indicate which values are typical in the dynamic environment close to Sgr A*.
Valuable information can be gained from the fact that the presented bow shock modeling algorithm yields information about the usually inaccessible relative radial position and can therefore be used to position bow shock sources with respect to their interacting medium. This can be utilized to improve the three-dimensional image of the central parsec region of the Galactic center.
Acknowledgments
The German federal department for education and research (BMBF) supported M. García-Marín under project number 50OS1101. N. Sabha is a member of the Bonn Cologne Graduate School (BCGS) for Physics and Astronomy, which is supported by the Deutsche Forschungsgemeinschaft. M. Valencia-S. was supported by the Max Planck Society as a member of the International Max-Planck Research School (IMPRS) for Astronomy and Astrophysics at the University of Bonn and Cologne. Part of this work was supported by fruitful discussions with members of the European Union funded COST Actions MP0905 “Black Holes in a Violent Universe” and MP1104 “Polarization as a tool to study the Solar System and beyond”.
References
- Aitken, D., Smith, C., Moore, T., & Roche, P. 1998, MNRAS, 299, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Bailey, J., Hough, J. H., & Axon, D. J. 1984, MNRAS, 208, 661 [NASA ADS] [Google Scholar]
- Becklin, E. E., & Neugebauer, G. 1975, ApJ, 200, 71 [Google Scholar]
- Becklin, E. E., Matthews, K., Neugebauer, G., & Willner, S. P. 1978, ApJ, 220, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Bless, R. C., & Savage, B. D. 1972, ApJ, 171, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Broadbent, A., MacLaren, I., & Wolfendale, A. W. 1988, in Dust in the universe, Proc. Conf., Manchester, England, Dec. 14−18, 1987 (Cambridge and New York: Cambridge University Press), 435 [Google Scholar]
- Buchholz, R. M., Witzel, G., Schödel, R., et al. 2011, A&A, 534, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capps, R. W., & Knacke, R. F. 1976, ApJ, 210, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, N-. L. J., Kerschbaum, F., van Marle, A.-J., et al. 2012, A&A, 537, A35; Erratum: 543, C1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davis, L. Jr., & Greenstein, J. L. 1951, ApJ, 114, 206 [Google Scholar]
- Diolaiti, E., Bendinelli, O., Bonaccini, D., et al. 2000, Proc. SPIE, 4007, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [Google Scholar]
- Eckart, A., Genzel, R., Hofmann, R., Sams, B. J., & Tacconi-Garman, L. E. 1995, ApJ, 445, 23 [Google Scholar]
- Eckart, A., Genzel, R., Ott, T., & Schödel, R. 2002, MNRAS, 331, 917 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrière, K. 2012, A&A, 540, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fischer, O., Henning, Th., & Yorke, H. W. 1994, A&A, 284, 187 [NASA ADS] [Google Scholar]
- Fischer, O., Henning, Th., & Yorke, H. W. 1996, A&A, 308, 863 [NASA ADS] [Google Scholar]
- Geballe, T. R., Rigaut, F., Roy, J.-R., & Draine, B. T. 2004, ApJ, 602, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Geballe, T. R., Najarro, F., Rigaut, F., & Roy, J.-R. 2006, ApJ, 652, 370 [NASA ADS] [CrossRef] [Google Scholar]
- Ghez, A. M., Duchêne, G., Matthews, K., et al. 2003, ApJ, 586, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Ghez, A. M., Salim, S., Weinberg, N. N., et al. 2008, ApJ, 689, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Gillessen, S., Eisenhauer, F., Trippe, S., et al. 2009, ApJ, 692, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Glasse, A. C. H., Aitken, D. K., & Roche, P. F. 2003, AN, 324, 563 [Google Scholar]
- Knacke, R. F., & Capps, R. W. 1977, ApJ, 216, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, Y., Kawara, K., Kozasa, T., Sato, S., & Okuda, H. 1980, Publ. Astron. Soc. Japan, 32, 291 [NASA ADS] [Google Scholar]
- Lacy, J. H., Achtermann, J. M., & Serabyn, E. 1991, ApJ, 380, L71 [NASA ADS] [CrossRef] [Google Scholar]
- LaRosa, T. N., Kassim, N. E., Lazio, T. J., & Hyman, S. D. 2000, AJ, 119, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Lazareff, B., Pudritz, R. E., & Monin, J.-L. 1990, ApJ, 358, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Lebofsky, M. J., Rieke, G. H., Deshpande, M. R., & Kemp, J. C. 1982, ApJ, 263, 672 [NASA ADS] [CrossRef] [Google Scholar]
- Liszt, H. S. 2003, A&A, 408, 1009 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Morris, M. 1998, in The Central Regions of the Galaxy and Galaxies, ed. Y. Sofue (Dordrecht: Kluwer), IAU Symp. 184, 331 [Google Scholar]
- Mužić, K., Eckart, A., Schödel, R., Meyer, L., & Zensus, A. 2007, A&A, 469, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mužić, K., Eckart, A., Schödel, R., et al. 2010, A&A, 521, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nandy, K., Thompson, G. I., Jamar, C., Monfils, A., & Wilson, R. 1975, A&A, 44, 195 [NASA ADS] [Google Scholar]
- Nandy, K., Thompson, G. I., Jamar, C., Monfils, A., & Wilson, R. 1976, A&A, 51, 63 [NASA ADS] [Google Scholar]
- Ott, T., Eckart, A., & Genzel, R. 1999, ApJ, 523, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Paumard, T., Maillard, J.-P., & Morris, M. 2004, A&A, 426, 81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, M. J., & Brunthaler, A. 2004, ApJ, 616, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Rigaut, F., Geballe, T. R., Roy, J.-R., & Draine, B. T. 2003, AN, 324, 551 [Google Scholar]
- Roberts, D. A., & Goss, W. M. 1993, ApJ, 86, 133 [Google Scholar]
- Roberts, D. A., Yusef-Zadeh, F., & Goss, W. M. 1996, ApJ, 459, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, R. H. 1998, MNRAS, 294, 35 [Google Scholar]
- Schödel, R., Ott, T., Genzel, R., et al. 2002, Nature, 419, 694 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schödel, R., Ott, T., Genzel, R., et al. 2003, ApJ, 596, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Schödel, R., Merritt, D., & Eckart, A. 2009, A&A, 502, 91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schödel, R., Najarro, F., Mužić, K., & Eckart, A. 2010, A&A, 511, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwarz, U. J., Bregman, J. D., & Gorkom, J. H. 1989, A&A, 215, 33 [NASA ADS] [Google Scholar]
- Tanner, A., Ghez, A. M., Morris, M., et al. 2002, ApJ, 575, 860 [NASA ADS] [CrossRef] [Google Scholar]
- Tanner, A., Ghez, A. M., Morris, M., & Christou, J. C. 2005, ApJ, 624, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Vollmer, B., Duschl, W. J. 2000, NA, 4, 581 [Google Scholar]
- Whitney, B. A., & Wolff, M. J. 2002, ApJ, 574, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkin, F. P. 1996, Ph.D. Thesis, University of California, Berkeley [Google Scholar]
- Wilkin, F. P. 2000, ApJ, 532, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Witzel, G., Eckart, A., Buchholz, R. M., et al. 2011, A&A, 525, 130 [Google Scholar]
- York, D. G., Drake, J. F., Jenkins, E. B., et al. 1973, ApJ, 182, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, J.-H., Morris, M. R., Goss, W. M., & An, Tao 2009, ApJ, 699, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, J.-H., Blundell, R., Moran, J. M., et al. 2010, ApJ, 723, 1097 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 KS-band FOV for one Wollaston channel covering an area of 31.9′′ × 8.2′′. The white box marks the area used for the presented polarization maps. |
| In the text | |
 |
Fig. 2 Polarization map of IRS 8 and its surrounding sources. Polarization was measured on nondeconvolved images using the techniques described in Sect. 2. The images were not corrected for background flux or foreground and instrumental polarization. |
| In the text | |
 |
Fig. 3 Polarization map of IRS 8 and its surrounding sources. Polarization was measured on nondeconvolved images and corrected for background, foreground, and instrumental polarization. Polarization vectors were determined with the techniques mentioned in Sect. 2 and are scaled to twice the size of the vectors in Fig. 2. The surrounding sources show approximately no residual intrinsic polarization, indicating a proper calibration and subtraction of the foreground polarization. This calibrated map is used for Lucy-Richardson deconvolution. |
| In the text | |
 |
Fig. 4 Smoothed VISIR image of IRS 8 and the NA taken at 13.04 μm. The FOV covers an area of 26.3′′ × 32.1′′. The overlaid contours range from 0.68 Jy to 0.84 Jy in steps of 0.04 Jy. |
| In the text | |
 |
Fig. 5 L′-band image of IRS 8. This image was used to extract the intensity contours of IRS 8 (see Fig. 8). The bow shock modeling was performed using these contours. |
| In the text | |
 |
Fig. 6 Intrinsic KS-band polarization map of the bow shock surrounding IRS 8*. The bow shock was covered with 8 apertures to map the polarization distribution along this feature. |
| In the text | |
 |
Fig. 7 Example solutions for different behaviors of the ambient medium density. The solid line shows the symmetric solution assuming the uniform density (Wilkin 1996). The two nonaxisymmetric solutions arise from the stratified ambient medium with the density gradient in the direction of the arrow (Wilkin 2000). The density of the medium follows the law ρ = ρ0(1 + a1x + a2x2), for x ≥ 0. |
| In the text | |
 |
Fig. 8 L′-band contour model to determine the χ2 of the bow shock models in Fig. 9. The axes show relative RA (abscissa) and relative Dec (ordinate) with respect to the central star in units of pixels, with one pixel corresponding to 0.027′′. |
| In the text | |
 |
Fig. 9 Bow shock models with corresponding χ2-values for six different rotation angles α under five different inclination angles i. All models were simulated for a constant stand-off distance R0 = 3.5 × 1016 cm with a constant position angle PA = 10°. Black lines represent intensity contours derived from L′-band images. Red lines correspond to simulated bow shock model intensity contours. The best-fitting plots are marked by the blue box. The axes of each model show the relative RA and Dec with respect to the central star in units of pixels, with one pixel corresponding to 0.027′′. |
| In the text | |
 |
Fig. 10 Relative position of IRS 8*, the NA, and Sgr A*, depending on the rotation angle α as it would be seen from different angles of view. We derived the projected NA positions between 0.27 pc and 0.82 pc north of Sgr A* from the N-band image (Fig. 4) with an accuracy of ±0.015 pc in te east-west direction, while the other parts of the NA are based on its curvature and Fig. 21 in Zhao et al. (2009). Radial distances of the NA with respect to Sgr A* were obtained from Fig. 21 in Zhao et al. (2009) at an accuracy of ± 0.1 pc. We determined a mean thickness for the NA of 0.07 ± 0.02 pc from the 0.68 Jy contours of the presented N-band image (Fig. 4). Because no radial dimension of the NA can be derived it is pictured as a circle. Light green arrows indicate the flowing direction of its material. Rotation angles smaller than 270°, as for the best-fitting models, correspond to IRS 8* being well in front of the NA. The thin red line marks the position of IRS 8* along the line-of-sight. Our best-fitting bow shock models indicate α is between 240° and 270°. The corresponding relative position of IRS 8 is marked by the red 3d model. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


