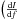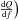| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | L12 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201219854 | |
| Published online | 05 March 2013 | |
Improved mm-wave photometry for kinetic inductance detectors
1
Institut Néel, CNRS & Université Joseph Fourier,
BP 166, 38042
Grenoble, France
e-mail: martino.calvo@grenoble.cnrs.fr
2
Institut de RadioAstronomie Millimétrique,
300 rue de la Piscine, 38406 Saint-Martin
d’ Hères,
France
3
IPAG, Observatoire de Grenoble, BP 53, 38041
Grenoble,
France
4 Cardiff School of Physics and Astronomy, Cardiff University,
CF24 3AA, UK
5
LPSC, UJF Grenoble 1, CNRS/IN2P3, INPG, 53 rue des Martyrs, 38026
Grenoble Cedex,
France
6
Università di Roma La Sapienza, 00185
Roma,
Italy
7
Dept. of Physics and SESE, Arizona State University,
Tempe, Arizona, 85287, USA
Received:
3
December
2012
Accepted:
7
February
2013
Context. We have developed a dual-band (140 and 220 GHz) mm-wave imaging camera based on superconducting kinetic inductance detector (KID) arrays. Each array contains 132 superconducting resonators whose resonant frequencies are shifted by mm-wave photons absorption. The read out is achieved with a single electronics chain per band, taking advantage of the intrinsic KID frequency-domain multiplexability. The arrays are easily scalable and well adapted for future large format focal plane instruments. NIKA (formerly Néel IRAM KID Array, now New IRAM KID Array) has been specifically designed for the IRAM 30 m telescope at Pico Veleta, and is one of the first instruments using KIDs to have made measurements of astronomical sources.
Aims. In this Letter we describe the solutions adopted to improve the calibration accuracy and the sensitivity of the instrument, and we report on the outcome of the 3rd NIKA observing run of October, 2011.
Methods. We use a fast electronic modulation of the readout tone for each KID pixel in order to linearize the instrument calibration, which we track with measurements of planets. We also adopt a new design of the KIDs, sensitive to both polarizations, to increase the amount of radiation absorbed and thus the optical efficiency of the system.
Results. We measured an average sensitivity on the sky of 21 mJys0.5 per beam at 140 GHz and 140 mJys0.5 at 220 GHz in the best observing conditions (τ220 ≃ 0.2) after atmospheric noise decorrelation. The sensitivity at 220 GHz was limited by the atmospheric attenuation and loading as well as a reduction in the spectral bandwidth due to a misplaced filter. We found the repeatability in the photometry over the entire observing run to be better than 10% in both bands, thus demonstrating a significant improvement over the previous runs. We also find good agreement between NIKA measurements of faint astronomical sources and previous measurements of the same sources.
Key words: instrumentation: detectors / methods: observational / telescopes / techniques: photometric
© ESO, 2013
1. Introduction
Kinetic inductance detectors (KIDs) are superconducting resonators usually fabricated from thin metal films that change their electromagnetic properties in response to incoming radiation. KIDs represent an alternative detector technology to bolometers for future mm and sub-mm large format array instruments. In a bolometer, the incoming optical power is first converted into thermal phonons (heat) in a thermally isolated absorber and the resulting temperature change is measured by a suitable thermometer (Richards 2006). In a KID, on the other hand, incoming photons absorbed by the superconducting film alter the ratio of paired to unpaired charge carriers. This modifies the surface impedance of the superconducting strip which can be parameterized by a complex conductance with an inductive and a resistive component. The change in the so-called kinetic inductance together with the change in residual resistive losses in the superconductor modifies the resonant frequency and quality factor of the KID. A crucial point in favour of KIDs for large format arrays is that they are intrisically suited for frequency domain multiplexing, since the low resistive loss of the superconducting films leads to high resonator quality factors, Qres, and therefore high multiplexing ratios (Day et al. 2003).
The New IRAM KID Array (NIKA) is a dual-band imaging camera operating at frequencies of 140 and 220 GHz with 132 KID pixels per band. In the first two observing runs at the IRAM 30 m telescope NIKA demonstrated sensitivities within a factor two of state-of-the-art instruments based on well-established bolometers technology (Monfardini et al. 2010, 2011). However, in these runs NIKA was not able to measure the brightness of sources with good repeatability from pixel to pixel due to the large changes in responsivity of the KIDs under changes in optical loading. In the next section we describe an innovative modulated readout scheme which enables the optical power absorbed by a KID to be continuously monitored and leads to a large improvement in the consistency of the photometric calibration. In Sect. 3 we present the new dual-polarization KID design adopted. In Sect. 4, we show results obtained during the third NIKA observing run (October, 2011). Variable weather during the run allowed us to test the performance of the KIDs in a broad range of conditions.
2. Modulated readout for kinetic inductance detectors
The resonant frequency, f0, of a KID is determined by the geometry of the resonator and the surface impedance of the superconducting film. In NIKA the KID resonant frequencies are from 1−1.5 GHz. Because the surface impedance is sensitive to variations in the density of superconducting carriers, photons with high enough energy to break apart superconducting Cooper pairs will induce a shift in the resonant frequency. For thin films, the relationship between the shift, δf0, of the resonant frequency and the incoming optical power, Popt, is linear for small variations in Popt (Swenson et al. 2010).
Each KID is weakly coupled to a nearby microwave transmission line which carries a readout
tone signal close to the resonant frequency of every detector in an array. The amplitude and
phase of each transmitted and reflected signal is affected by the corresponding KID. Near
resonance the ratio of the transmitted signal to the input signal is given by:
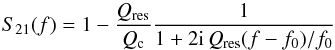 (1)where
Qc is the coupling quality factor (Zmuidzinas 2012). It is possible to reconstruct the changes in
S21(t), and thus in
f0(t), by monitoring the time-varying
in-phase (I(t)) and in quadrature (Q(t)) components of the
transmitted signal corresponding to a given input tone signal sent into the cryostat, as
I and Q are directly related to the real and imaginary
components of S21.
(1)where
Qc is the coupling quality factor (Zmuidzinas 2012). It is possible to reconstruct the changes in
S21(t), and thus in
f0(t), by monitoring the time-varying
in-phase (I(t)) and in quadrature (Q(t)) components of the
transmitted signal corresponding to a given input tone signal sent into the cryostat, as
I and Q are directly related to the real and imaginary
components of S21.
The multiplexing electronics used for the KID readout is described in Bourrion et al. (2011), and is based around an FPGA which synthesizes a bias signal containing a set of tone frequencies in the range of 0−250 MHz that are used to excite each of the resonators in an array. These tones are up and down converted by mixing them with a local oscillator carrier signal (LO) of frequency fLO (fLO = 1.312 GHz in our setup).
One of the challenges of operating a KID compared to a device with a dissipative readout
like a bolometer is converting the observed (I(t),
Q(t)) values to an absorbed optical power or shift in
resonant frequency as a function of time,
δf0(t) ∝ δPopt(t).
In the previous NIKA observing runs this was accomplished by making a frequency sweep before
starting a scan, roughly every few minutes. For each detector it was then possible to
determine the center of the resonance circle and the phase
φ(f) of a point in the (I,Q) plane as a
function of frequency. Assuming that the change in phase for a shift in the resonant
frequency is linear for small variations of φ this can be used to estimate
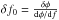 .
If a resonance is not perfectly symmetric then the factor,
.
If a resonance is not perfectly symmetric then the factor,
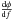 is not constant for fairly small changes in Popt. In principle
this can be corrected using the details of the shape of each resonant feature.
is not constant for fairly small changes in Popt. In principle
this can be corrected using the details of the shape of each resonant feature.
However, in practice, this approach led to poor photometric reproducibility of approximately 30%.
 |
Fig. 1 Typical KID resonance circle in raw A/D units at the input of the FPGA. The line (red
online) represents the (I, Q) data of the frequency
sweep around the resonance, and the arrows are the
|
To address this problem we have developed a system to constantly monitor the rate of change
of the signal, 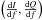 using a known frequency shift, that we artificially create by modulating
the frequency of the LO by a fixed quantity,
δfLO
(δfLO = 2 kHz in our case). The LO
frequency is modulated synchronously to the FPGA data acquisition rate at about 1 kHz, so
that the values of (I,Q) sampled by the FPGA correspond to frequencies
alternating between
using a known frequency shift, that we artificially create by modulating
the frequency of the LO by a fixed quantity,
δfLO
(δfLO = 2 kHz in our case). The LO
frequency is modulated synchronously to the FPGA data acquisition rate at about 1 kHz, so
that the values of (I,Q) sampled by the FPGA correspond to frequencies
alternating between 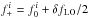 and at
and at
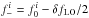 . The time ordered data values
(I(t),Q(t))i
from detector i are given by:
. The time ordered data values
(I(t),Q(t))i
from detector i are given by:
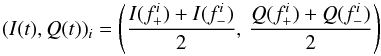 (2)and
the corresponding differential values are:
(2)and
the corresponding differential values are:
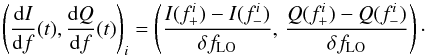 (3)A preliminary sweep around
the resonance, such as the one in Fig. 1, is still
necessary in order to correctly place the excitation tones, but is not required for
calibration. During a scan, the value of δf0
for each pixel, i, is obtained comparing the difference
(ΔI(t),ΔQ(t))i
between successive
(I(t),Q(t))i
points with the gradient
(3)A preliminary sweep around
the resonance, such as the one in Fig. 1, is still
necessary in order to correctly place the excitation tones, but is not required for
calibration. During a scan, the value of δf0
for each pixel, i, is obtained comparing the difference
(ΔI(t),ΔQ(t))i
between successive
(I(t),Q(t))i
points with the gradient 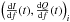 used as a
reference. This is achieved by projecting
(ΔI(t),ΔQ(t))i
along the gradient itself.
used as a
reference. This is achieved by projecting
(ΔI(t),ΔQ(t))i
along the gradient itself.
The total frequency shift of a resonator between times t1 and t2 is Δf0(t2 − t1) which is proportional to the difference in the absorbed power ΔP(t2 − t1) and is given by the integral of δf0(t) from t1 to t2. Using this scheme, as the observing conditions vary, the coefficient linking (ΔI, ΔQ) to δf0 is automatically updated, making the measurements much less sensitive to background fluctuations.
This method of determining absorbed optical power in a KID is simple and convenient but
still affected by some systematic uncertainty. Indeed, the instantaneous differential value
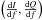 is calculated by modulating the LO frequency, and is therefore tangent to the
(I,Q) circle for a fixed background optical power (see
Fig. 1). On the other hand, the actual variation
(ΔI, ΔQ) occurs for a fixed excitation frequency and is
due to a difference in the optical power, which includes a change in the
(I,Q) circle radius. This is physically related to the fact that an
increase in the quasiparticle density leads to a larger kinetic inductance value as well as
more loss in the superconductor. The observed (I,Q) trajectory is therefore
not exactly parallel to the direction given by
is calculated by modulating the LO frequency, and is therefore tangent to the
(I,Q) circle for a fixed background optical power (see
Fig. 1). On the other hand, the actual variation
(ΔI, ΔQ) occurs for a fixed excitation frequency and is
due to a difference in the optical power, which includes a change in the
(I,Q) circle radius. This is physically related to the fact that an
increase in the quasiparticle density leads to a larger kinetic inductance value as well as
more loss in the superconductor. The observed (I,Q) trajectory is therefore
not exactly parallel to the direction given by 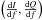 ,
but typically different by less than 10°, so that the estimated error introduced
by the projection method is less than 2% for faint sources.
,
but typically different by less than 10°, so that the estimated error introduced
by the projection method is less than 2% for faint sources.
For bright sources such as Mars the change in optical load can shift the resonances far
from their excitation frequency, and lead to distortions in the (I,Q)
plane. To address this we assume a polynomial relationship between the
(I,Q) point and the frequency f of the form
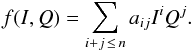 (4)From this formula,
it is possible to evaluate the expected variation of (I,Q) for a known
variation of f, and then to fit the
aij coefficients so as to make the
theoretical values and the observed
(4)From this formula,
it is possible to evaluate the expected variation of (I,Q) for a known
variation of f, and then to fit the
aij coefficients so as to make the
theoretical values and the observed 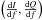 values match over a scan. Once the aij are
determined by matrix inversion this method yields a relation between the observed
(I,Q) values and the resonant frequency of each pixel. For
n = 3, the value of
Δf0(t2 − t1)
given by the projection method and the one found using the polynomial approach is almost
identical in all but the extreme situations (i.e. very strong sources). In this case
Δf0 can be calculated only after the end of the scan, and we
find consistently higher values of absorbed power with the polynomial fit than with the
simple projection.
values match over a scan. Once the aij are
determined by matrix inversion this method yields a relation between the observed
(I,Q) values and the resonant frequency of each pixel. For
n = 3, the value of
Δf0(t2 − t1)
given by the projection method and the one found using the polynomial approach is almost
identical in all but the extreme situations (i.e. very strong sources). In this case
Δf0 can be calculated only after the end of the scan, and we
find consistently higher values of absorbed power with the polynomial fit than with the
simple projection.
3. Dual-polarization detectors design
A lumped element KID (Doyle et al. 2008) is a planar resonator which consists of an interdigital capacitor and a meandering inductor shaped to directly absorb the incoming radiation. The classical design (Monfardini et al. 2010) is only sensitive to radiation polarized parallel to the main lines of the inductor. For a purely imaging experiment, like NIKA, this results in reduced overall quantum efficiency. We therefore adopted a new design, in which the inductance is based on a Hilbert curve of 3rd order (Roesch et al. 2012). This fractal pattern can absorb both polarizations. To take full advantage of the new design, we replaced the grid polarizer splitter used in previous runs with a 45° dichroic. This allows to effectively double the optical efficiency of the 140 GHz band, which is now around 30%. The improvement was lower at 220 GHz as a consequence of a misplaced filter in the optical chain. The filters used had an effective transmission band of 200−240 GHz, whereas the atmospheric window of interest is 200−280 GHz. For a thermal continuum spectrum, that translates in a loss of over 50% of the available optical power, without affecting the performances of the readout chain, which is the main noise source. The resulting sensitivity is thus degraded by more than a factor two. The noise spectrum of the detectors, after sky-noise subtraction, is relatively flat down to 0.1 Hz in good weather conditions.
We adopted the same geometry for both arrays, each consisting of 132 pixels with a pitch of 2.3 mm, giving an effective focal plane sampling of approximately 0.75Fλ at 140 GHz and 1.25Fλ at 220 GHz. Out of the 132 pixels, we found 103 (116) valid resonances for the 140 GHz (220 GHz) band. Taking out the 12 (12) overlapping resonances and the 24 (15) showing instable or doubtful behaviour, we have a total of 67 (89) valid pixels, in the two bands.
4. Results
To show the effectiveness of the improved calibration technique we present results from a small set of primary and secondary calibrators. For this analysis we rely on the polynomial fitting approach to estimate the observed frequency shift.
As a primary calibrator we use Mars, assumed to be a 202 K blackbody source which during the run had a diameter of 5.6 arcsec. To span the whole array, the typical map size is about 6 arcmin wide. The point-source flux is then obtained with a fixed-width Gaussian fitting technique with a full width at half maximum of 18 arcsec (16 arcsec) for the 140 GHz (220 GHz) channels respectively. To be able to compare results from different maps, we used the same approach to reduce the data on other sources like Uranus, Neptune and the Galactic source MWC349, used as secondary calibrators. We first use a map of Mars to extract the response of each KID to a known source (primary calibrator). This gives us a Hz/Jy conversion factor per detector. Then we make a map of a secondary calibrator, and measure the flux we observe on each KID using the conversion factor we found. The dispersion of the fluxes from pixel to pixel around the mean value gives us a measure of the repeatability of the calibration.
Figure 2 shows the normalized distribution of calibrated flux for all of the useful KIDs of the two channels from one observation of Uranus. The dispersion among the valid detectors around the mean value is 7% (9%) for the 140 GHz (220 GHz) channels. While the signal-to-noise ratio of each measurement by individual pixels is much larger than 100, some of the dispersion in a single measurement can be attributed to variations in sky opacity during a scan, variations in the baseline due to filtering or common mode subtraction of sky noise, and variations in the beam shapes due to focus or pointing errors. Overall, we find a good consistency between the flux measured by the valid detectors, especially if we consider that the observations of Mars and Uranus were performed 10 h apart, that the background was different, and that we retuned the excitation tones many times between the two maps. Similar results have been obtained with all the secondary calibrators used. The repeatability of the photometry achieved with the new method allows now, for the first time, deeper integrations.
 |
Fig. 2 Histogram of the normalized signals observed on Uranus with the arrays at 140 GHz (full line) and 220 GHz (dashed line). |
We correct for the attenuation of the astronomical sources due to non-zero atmospheric
opacity, τ, by correlating this with the average resonant frequencies of
the detectors. As the atmosphere becomes more opaque, its emission also increases leading to
an increase in the background load and lowering the resonant frequencies of the KIDs. It is
therefore possible to find a function 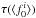 by
relating the average resonance position
by
relating the average resonance position 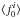 to the external measurement of
τ read by a tipping 225 GHz taumeter. Through this function we are able
to extrapolate the atmospheric opacity during a scan with an uncertainty of
<10%.
to the external measurement of
τ read by a tipping 225 GHz taumeter. Through this function we are able
to extrapolate the atmospheric opacity during a scan with an uncertainty of
<10%.
We compare the flux measured by NIKA from 8 bright millimetre quasars with that obtained by the Plateau de Bure interferometer. The 140 GHz NIKA fluxes are on average 93% the PdB fluxes, within the 10% absolute uncertainty of PdB data.
To estimate the sensitivity of our arrays we also observed several faint point sources. Here we show the measurements of 4C05.19 (MG J0414+0534) and APM08279+5255. The data are binned in sky coordinates after a sky-noise decorrelation procedure based on a common-mode linear subtraction.
 |
Fig. 3 Map of quasar 4C05.19 at 140 GHz. The data have been smoothed with a 5 arcsec Gaussian filter. |
 |
Fig. 4 (sub)mm spectrum of the quasar 4C05.19. The black circle is the value obtained here in the third NIKA run, whereas other data are taken from Barvainis & Ivison (2002) and Kellermann & Pauliny-Toth (1973). Absolute photometric uncertainties have not been included. The spectral energy distribution fit includes a power-law synchrotron component (dotted line) and a contribution from dust emission (dashed line). |
4C05.19 is a gravitationally lensed quasar at a redshift of 2.64. We made 7 consecutive on-the-fly maps of the source during a ~1500 s observation with a zenith opacity of 0.09 at 140 GHz. Because the size of the scan was larger than the array size, the on-source integration time was approximately 700 s. From the 140 GHz map in Fig. 3 we measure a flux of 27.1 ± 1.4 mJy. This value is consistent with the measurements at longer and shorter wavelengths reported in literature (Fig. 4). At 220 GHz we get a marginal detection with a flux of 23 ± 9 mJy.
APM08279+5255 is another gravitationally lensed quasar at a redshift of 3.91. Its spectral energy distribution is shown in Fig. 5. The measured 140 GHz flux of 6.6 ± 1.3 mJy was obtained in a 3000 s observation with a zenith opacity of 0.11 at 140 GHz and an on-source integration time of ≃1000 s. The flux of 17 ± 7 mJy observed at 220 GHz is less precise compared to previous measurements. As in the case of 4C05.19, however, it is compatible with literature data.
Accounting for the effective time spent by all detectors on the source, the noise equivalent flux density (NEFD) measured in several blank sky observations averaged over the array is 21 mJy s0.5 per beam at 140 GHz and 140 mJy s0.5 per beam at 220 GHz. These figures have been obtained in the best opacity conditions experienced during the run (τ220 = 0.2, stable atmosphere). On the other hand, the observations presented previously have been carried out in average weather. This explains the reduced effective sensitivity, in particular for the 220 GHz band, more affected by the atmospheric absorption and sky noise.
 |
Fig. 5 (sub)mm spectrum of the quasar APM08279+5255. The black circle is the value obtained here in the third NIKA run, whereas other data are taken from Beelen et al. (2006), Garcia-Burillo et al. (2006), Wagg et al. (2006), Krips et al. (2007) and Riechers et al. (2009). The spectral energy distribution model by Beelen et al. (2006) is shown as the black line. It includes a dust component (dashed line) and a synchrotron component (dotted line). |
5. Conclusions and perspectives
We have developed a modulated readout scheme that allows continuous simultaneous tracking of multiple KID resonant frequencies which change proportionally to the absorbed optical power. With this readout, we demonstrate photometric reproducibility
with the NIKA instrument of around 7% and 9% for the 140 GHz and 220 GHz channel respectively. A first attempt at using total power as a measurement of opacity gives an absolute photometric accuracy of about 10%. To further reduce the systematic uncertainty to the level of 2% required by the next generation instruments an additional internal optical calibrator is being designed for the larger field-of-view (6.5 arcmin) NIKA2 camera.
In addition, we demonstrate an improved sensitivity of the KID arrays: a conservative estimate of the NEFDs is 21 mJy s0.5 per beam at 140 GHz and 140 mJy s0.5 per beam at 220 GHz. A misplaced filter and poor weather conditions partially explain the 220 GHz figure. Laboratory measurements on newly designed 220 GHz arrays have shown highly encouraging results.
NIKA is now permanently installed at the Pico Veleta telescope, and will remain on site until 2014, when it will be replaced by the new NIKA2 kilopixel instrument.
Acknowledgments
We thank Santiago Navarro, Juan Peñalvez, Carsten Kramer and the whole IRAM staff for the outstanding support during the preparation, installation and the observations. Part of this work was supported by the French National Research Agency Grant No. ANR-09-JCJC-0021-01 and by the STFC Bridging Grant No. ST/J001449/1.
References
- Barvainis, R., & Ivison, R. 2002, ApJ, 571, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Beelen, A., Cox, P., Benford, D. J., et al. 2006, ApJ, 642, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Bourrion, O., Bideaud, A., Benoit, A., et al. 2011, JINST, 6, P06012 [Google Scholar]
- Day, P. K., Leduc, H. G., Mazin, B. A. et al. 2003, Nature, 425, 817 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Doyle, S., Mauskopf, P., Naylon, J., et al. 2008, J. Low Temp. Phys., 151, 530 [Google Scholar]
- Garcia-Burillo, S., Gracia-Carpio, J., Guelin, M., et al. 2006, ApJ, 645, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Kellermann, K. I., & Pauliny-Toth, I. I. K. 1973, AJ, 78, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Krips, M., Peck, A. B., Sakamoto, G. B., et al. 2007, ApJ, 671, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Mazin, B. 2004, Ph.D. Thesis, California Institute of Technology, USA [Google Scholar]
- Monfardini, A., Swenson, L. J., Bideaud, A., et al. 2010, A&A, 521, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monfardini, A., Benoit, A., Bideaud, A., et al. 2011, ApJ, 194, 24 [Google Scholar]
- Richards, P. L. 1994, J. Appl. Phys., 76, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Riechers, D., Walter, F., Carilli, C. L., & Lewis, G. F. 2009, ApJ, 690, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Roesch, M., Benoit, A., Bideand, A., et al. 2011, Proc. of the ISSTT2011 workshop [arXiv:1212.4585] [Google Scholar]
- Swenson, L. J., Cruciani, A., Benoit, A., et al. 2010, APL, 96, 263511 [Google Scholar]
- Wagg, J., Wilner, D. J., Neri, R., et al. 2006, ApJ, 651, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Yorke, H. W. 1980, A&A, 86, 286 [NASA ADS] [Google Scholar]
- Zmuidzinas, J. 2012, Annu. Rev. Cond. Mat. Phys., 3, 169 [Google Scholar]
All Figures
 |
Fig. 1 Typical KID resonance circle in raw A/D units at the input of the FPGA. The line (red
online) represents the (I, Q) data of the frequency
sweep around the resonance, and the arrows are the
|
| In the text | |
 |
Fig. 2 Histogram of the normalized signals observed on Uranus with the arrays at 140 GHz (full line) and 220 GHz (dashed line). |
| In the text | |
 |
Fig. 3 Map of quasar 4C05.19 at 140 GHz. The data have been smoothed with a 5 arcsec Gaussian filter. |
| In the text | |
 |
Fig. 4 (sub)mm spectrum of the quasar 4C05.19. The black circle is the value obtained here in the third NIKA run, whereas other data are taken from Barvainis & Ivison (2002) and Kellermann & Pauliny-Toth (1973). Absolute photometric uncertainties have not been included. The spectral energy distribution fit includes a power-law synchrotron component (dotted line) and a contribution from dust emission (dashed line). |
| In the text | |
 |
Fig. 5 (sub)mm spectrum of the quasar APM08279+5255. The black circle is the value obtained here in the third NIKA run, whereas other data are taken from Beelen et al. (2006), Garcia-Burillo et al. (2006), Wagg et al. (2006), Krips et al. (2007) and Riechers et al. (2009). The spectral energy distribution model by Beelen et al. (2006) is shown as the black line. It includes a dust component (dashed line) and a synchrotron component (dotted line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.