| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A31 | |
| Number of page(s) | 12 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201219433 | |
| Published online | 14 February 2013 | |
An MK-like system of spectral classification for hot subdwarfs⋆
1 Department of Physics and Astronomy, Louisiana State University, Baton Rouge, LA 70803, USA
e-mail: johndrilling@comcast.net
2 Armagh Observatory, College Hill, Armagh BT61 9DG, Northern Ireland
e-mail: csj@arm.ac.uk
3 Dr. Remeis Sternwarte, Universität Erlangen-Nürnberg, 96049 Bamberg, Germany
e-mail: Ulrich.Heber@sternwarte.uni-erlangen.de
4 European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching, Germany
e-mail: smoehler@eso.org
5 Centre for Astrophysics Research, University of Hertfordshire, College Lane, Hatfield AL10 9AB, UK
e-mail: r.napiwotzki@gmail.com
Received: 17 April 2012
Accepted: 27 November 2012
An MK (Morgan-Keenan)-like system of spectral classification for hot subdwarfs is presented. We find that a three-dimensional spectral type, consisting of a “spectral” class, a “luminosity” class, and a “helium” class, is necessary to classify the sdO (subdwarf O) and sdB (subdwarf B) stars. In addition, the helium-strong stars appear to form two parallel spectral sequences: one showing strong lines of CII, CIII, or CIV, and the other with these same lines weak or absent. We also give a preliminary calibration of the new spectral types in terms of effective temperature, surface gravity, and surface helium-to-hydrogen abundance ratio, and show the relation between the new spectral types and the natural groups defined by the Palomar-Green (PG) survey.
Key words: stars: early-type / subdwarfs / stars: atmospheres
The normalized, unsmoothed spectra used in this paper are available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/551/A31
© ESO, 2013
1. Introduction
We begin with a few words about spectral classification and its role with respect to the fine analysis of stellar spectra. Nobody will deny the importance of classifying astronomical objects on the basis of observable characteristics. What is not always appreciated, however, is the significance of exploiting the classification process to its full potential, as it is in the MK system of spectral classification (Morgan et al. 1943; Walborn 1971; Keenan 1987). As an example, consider the visual comparison of two spectra. One can tell very quickly from visual inspection if the two spectra are identical, to within the errors of observation, and one can predict the outcome of a fine analysis of the second spectrum if one has already been performed on the first (i.e. there will be no significant difference between the results of the two analyses). Furthermore, one normally does not need spectra of as high a resolution as that required to do a fine analysis to come to this conclusion, as blended lines are nearly as useful as unblended ones in determining whether the two spectra are identical, whereas blended lines are nearly useless in performing a fine analysis (although this problem can in principle be solved through the use of synthetic spectra). Finally, one can conclude that the atmospheres of two stars which have slightly different line strengths differ only slightly in their atmospheric properties, since the number of spectral lines is usually much greater than the number of physical parameters characterizing the atmosphere.
Since the spectral resolution of the MK system (2 Å) is sufficient to determine whether the atmospheres of “normal” stars have similar effective temperatures, surface gravities, and chemical compositions, and the differences in the physical parameters characterizing adjacent spectral types are of the same order as the random errors in the determination of these quantities by the fine analysis of 2 Å resolution spectra, an MK spectral type of a “normal” star is, in a sense, equivalent to a fine analysis of a 2 Å resolution spectrum. That this is self-evident is seen by considering that the fine analyses would be done most efficiently by fitting to a model atmosphere grid where the differences in the line strengths of adjacent models were comparable to the random errors in the line strengths, which is also the case with adjacent MK spectral types. For the same reason, fitting to the model grid is, in a sense, equivalent to classifying the spectra using the models as standard spectra. Moreover, because the method of fine analysis depends on the theory of stellar atmospheres, and on the physics underlying it, a fine analysis needs to be redone whenever there are significant advances in the theory, whereas the MK spectral type, which is defined by standard stars, does not change as long as the star itself does not change. Of course, the calibration of the spectral types in terms of physical quantities must be redone whenever there are significant advances in the theory, but this is much easier than redoing the fine analysis for every star. Finally, because spectral classification is independent of the theory of stellar atmospheres, it provides a test of the theory and its underlying physics. Explaining the small changes in line strength as we move between adjacent classes in the MK system is just as valid a test of the theory of stellar atmospheres as explaining the line-to-line variations in the spectrum of a single star. In fact, the MK system itself may be considered to be a kind of hyper-spectrum, which contains within it the spectroscopic constraints to the theory of stellar evolution for “normal” stars (main-sequence stars, giants, and supergiants with atmospheric composition similar to the sun).
It is also of interest that there are similarities in the methodology of both the fine analysis of a spectrum and spectral classification. One does not base a fine analysis on a computer program which blindly matches up local minima in the energy distribution with the wavelengths of all known spectral lines, but rather demands consistency between the strengths of all lines used in the analysis and the results of the analysis, i.e. that all of the strongest lines be present in a given multiplet, and in other multiplets of similar excitation energy for the same ion, and that the effective temperatures, surface gravities, and abundances derived from different lines be in agreement. In classifying the spectrum, we also demand this global consistency: the spectral class must be consistent with all of the lines present in the spectrum, and all of the line strengths must agree with those of the standard to within the observational errors.
It is this last criterion which gives spectral classification one of its most important characteristics: its ability to separate out stars which do not have “normal” spectra, i.e. stars which are not identical to one of the MK standards to within the errors of observation. We are then able to use the method of fine analysis to try to explain how the atmospheres of these “peculiar” stars are different physically from the MK standards. Eventually, it may happen that the number of stars with a given peculiarity becomes so large that it is necessary to set up a new system of spectral classification which incorporates them. The development of new systems of spectral classification which supplement the MK system in this way is an example of the MK process (Morgan 1984).
The hot subdwarfs do not at present fall within the framework of the MK system, i.e. they are “peculiar” stars, and all advances in the understanding of their atmospheres to date have come from model-atmosphere analyses. Green et al. (1986) defined a system of eight classes based on the two dimensions of the HeI/HeII and H/He line strengths. Because the differences in the physical characteristics of adjacent classes were large compared to the errors in the determination of these quantities by fine analysis, and because the number of known hot subdwarfs (more than 3000 at present) was much larger than the number of spectral classes, Drilling (1996) pointed out the need for an MK-like system for the classification of hot subdwarf spectra, and outlined how such a system might be set up. Jeffery et al. (1997) used a preliminary version of this system to classify spectra of one of the eight classes described above (sdOD). In this paper, we attempt to define the system, which has been greatly refined and expanded using a much larger sample of stars distributed over all eight of the Green et al. classes.
2. Observations
The sample of stellar spectra which we consider here is described in detail in a series of papers (Moehler et al. 1990a,b, 1994; Dreizler et al. 1990; and Theissen et al. 1993, 1995) where many of them have been analyzed using model atmospheres. Most of the stars observed were selected from the sample of Green et al. (1986) and may be considered to be a more-or-less representative sample of the Green et al. hot subdwarfs and blue horizontal-branch stars. Most of these spectra cover the wavelength region from 4050 to 4900 Å at a resolution of 2.5 Å. In addition, spectra of nearly all stars classified by Green et al. as sdOD have been included using the similar spectra described by Jeffery et al. (1997). Spectra contaminated with lines from a cooler companion have been eliminated from the sample. All spectra were normalized to the continuum, shifted in wavelength to zero radial velocity, and smoothed to the lowest instrumental resolution used (2.5 Å).
3. Standards and spectral classification
It has been said many times that a system of spectral classification should be defined by the spectra of standard stars, because the system will then be completely independent of the theory of stellar atmospheres and the laws of physics, and can thus serve as a check and a guide to the theory. Indeed, one of the great triumphs of the theory of stellar atmospheres was its success in explaining the gradual variations in line strength as we move through the MK spectral and luminosity sequences. The classification of a star on the MK system is accomplished by comparing its spectrum with those of standard stars. Since the MK system was set up using photographic plates as detectors, it was necessary to obtain spectrograms of all stars, including the standards, with the same equipment and at similar exposure level and air mass in order to do accurate classification. In fact, the classifier needs to use the spectra of as many of the standard stars as possible in determining the spectral type of a given star in order to (a) take into account random errors in the line strengths; (b) ascertain the relative importance of the lines in determining the spectral type; and (c) determine whether or not the spectrum contains any significant peculiarities. It is for these reasons that spectral classification is very difficult to program a computer to do, although this is going to have to be done in order to analyze the very large number of spectra being obtained in current surveys. Encouraging progress along these lines is being made by Winter et al. (2004, 2006). The best classification is not obtained by picking the standard which the star matches most closely, but rather by comparing the strengths of all of the lines in the spectrum of the star to the strengths of all of the lines in all of the standard spectra. A numerical analog of this process is the interpolation of a tabulated quantity using a scheme which makes use of all of the entries in the table.
 |
Fig. 1 Spectra of He-normal stars for which hydrogen is dominant and either helium lines of both ionization states or metallic lines are visible. The lines marked are H + HeII λλ 4101, 4340, 4861; HeII λλ 4200, 4541, 4686; NV λ 4604–20; OIV λ 4632; CIV λ 4658 blend; SiIII λ 4552–68; HeI λλ 4144, 4387, 4471, 4713; SiII λ 4128–30; MgII λ 4481; and λλ 4360, 4369, 4772 emission. |
Since the introduction of linear detectors, it has been possible to do a pretty good job of classifying by comparing spectra taken with different instruments at different locations but with the same resolution and signal-to-noise, although optical or detector differences may still affect the overall appearance or individual features, and continuum normalization and different rebinning/smoothing algorithms can alter the line ratios. The advantage of digital data, in addition to sky subtraction, is the capability of adjusting resolution, line broadening, S/N, and continuum gradients to improve the matching. Therefore, the digital atlas published by Walborn & Fitzpatrick (1990) and the MK standard spectra available on Richard Gray’s website1 proved to be very useful in attempting to interface the hot subdwarf classification described below with the MK system.
The actual procedure to be followed in classifying stellar spectra is not well described in the literature, but we have found it useful to arrange all of the spectra, including the standards, in sequences according to the line strengths, and to then assign a class based on the position of the star in this sequence. This procedure can also be used to set up a new system of classification, and it is greatly facilitated by the ability to display large numbers of spectra simultaneously on a computer screen. As a starting point, we arranged all of the spectra according to the increasing line depths of the Balmer lines (which was historically the starting point for the MK system). When we did this, the other lines did not vary in a gradual manner, presumably due to the fact that the spectral lines are affected by more than one physical parameter in the atmospheres of hot subdwarfs. After much experimentation, it became clear that the spectra could be arranged into sequences where the lines did vary in a gradual manner if the spectra were broken into the following four categories:
-
1.
He-normal: spectra dominated by hydrogen lines in whichmetallic lines or lines due to both HeI and HeII are visible.
-
2.
He-weak: spectra containing only hydrogen lines or hydrogen plus either HeI or HeII (but not both). Metallic lines are very weak or absent.
-
3.
He-strong C: spectra dominated by helium lines in which carbon lines are present.
-
4.
He-strong: spectra dominated by helium lines in which carbon lines are very weak or absent.
We then chose a number of stars from each of these four sequences which we felt best represented the changes within each sequence to serve as standards for the new system. These spectra are displayed in Figs. 1–9, and the apparent B magnitudes, equatorial coordinates and spectral types (from this paper) of all of the standards are given in Table 1. Note that the PG designations used in Table 1 and elsewhere in this paper are those given on the finding charts of Green et al. (1986), i.e. with the coordinates given by Green et al. (1986) truncated after minutes of right ascension and rounded off to the nearest tenth of a degree in declination. The J2000 coordinates and B magnitudes given in Table 1 were taken from the database described by Østensen (2006) whenever possible, or from SIMBAD. A colon after the B magnitude indicates that it is the value given by Green et al. (1986). Emission lines are marked in Figs. 1–9 if they appear in more than one spectrum of the same star. With the exception of the CIII λ 4650 blend, we have not been able to identify these lines from published high-resolution spectra of similar stars, and studies at much higher resolution will be required to identify them.
 |
Fig. 2 Spectra of He-weak stars for which hydrogen is dominant and helium lines of only one ionization state may be visible. Metallic lines are very weak or absent. Note that PG1708+602 fits this definition even though the helium class is much higher than those of the other stars. The lines marked are H + HeII λλ 4101, 4340, 4861; and HeII λλ 4200, 4541, 4686. |
 |
Fig. 3 Spectra of He-strong C stars for which helium is dominant and carbon present. The lines marked are HeII λλ 4100, 4200, 4338, 4541, 4686, 4859; CIV λλ 4442, 4647, 4658; CIII λ 4650 blend; NIII λλ 4379, 4511–15, 4640 blend ; HeI λλ 4121, 4144, 4387, 4471, 4713; CII λλ 4267, 4619; H λλ 4340, 4861; and λλ 4326, 4510–11, 4599−4600, 4615, 4776 emission. |
 |
Fig. 4 Spectra of He-strong stars for which helium is dominant and carbon is very weak or absent. NIII may be present. The lines marked are HeII λλ 4100, 4200, 4338, 4541, 4686, 4859; NIII λλ 4379, 4511–15, 4640 blend ; HeI λλ 4121, 4144, 4387, 4471, 4713; H λλ 4340, 4861; and λλ 4324, 4509, 4637, 4774 emission. |
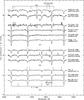 |
Fig. 5 Luminosity effects for a) H-strong sdO2 stars; b) He-strong sdO2 stars; c) H-strong sdO8 stars; and d) He-strong sdO7 stars. The lines marked are HeI λλ 4121, 4144, 4387, 4471, 4713; CIII/CIV/NIII λ 4630 broad absorption feature; NV λ 4604-20; OIV λ 4632; CIV λ 4658 blend; H + HeII λλ 4101, 4340, 4861; HeII λλ 4200, 4541, 4686; and λλ 4325–9, 4365, 4510–11, 4599–4601, 4615, 4651, 4705, 4776, 4828 emission. |
 |
Fig. 6 a) Luminosity effects at sdO9; b) abundance effects at sdO9 – sdB0. The lines marked are HeI λλ 4121, 4144, 4387, 4471, 4713; NIII λλ 4379, 4511–15, 4640 blend; CIII λ 4650 blend; H + HeII λλ 4101, 4340, 4861; and HeII λλ 4200, 4541, 4686. |
 |
Fig. 7 a) Luminosity effects at sdB0.5; b) abundance effects at sdB0.2 – sdB0.5. The lines marked are the same as in Fig. 6. |
 |
Fig. 8 a) Luminosity effects at sdB1; b) abundance effects at sdB1 – sdB2. The lines marked are the same as in Fig. 6. |
Since the variations which occur within each sequence are similar to those which occur in MK standards of spectral classes O and B, we use the MK spectral subclasses to identify the subclasses within each sequence. We have attempted to match the new subclasses with the MK subclasses in such a way that the new system merges smoothly with the MK system, so that the two systems can in the future be combined into a single system. Note that this was done before the recent revisions to the MK system by Sota et al. (2011). Note also that a new subclass, O1, has been created in order to accomplish this end. For the time being, the distinction between the new system and the MK system is denoted by using “sdO” and “sdB” instead of “O” and “B” to denote the spectral class, even though a number of stars classified are not subdwarfs, but related objects such as blue horizontal-branch stars. We identify to which of the above sequences a given star belongs with an “He” designation following the spectral class, here an integer from 0 to 40 denoting the strengths of the helium lines relative to the Balmer lines of hydrogen. The helium class is roughly equal to the following function of the line depths:
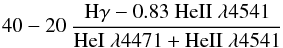 for helium classes 20–40. The term − 0.83 HeII λ4541 is an empirical correction for the contribution of the Pickering series of HeII to the depth of Hγ. We denote spectra from the third group by including the letter “C” in the spectral class to identify them as spectra showing strong carbon lines. Finally, we note that the hydrogen and helium line widths seem to vary smoothly throughout each sequence, so we have appended “luminosity” class “VII” to most of the hot subdwarfs. If the lines are significantly narrower than average (but still significantly wider than for MK class “V” stars), we append luminosity class “VI” instead, and if the lines are significantly wider than the average, we use luminosity class “VIII”. Because most of the hot subdwarfs follow the average trend (luminosity class VII), we do not feel that a more detailed “luminosity” classification for them is is justified at the present time. Stars given luminosity classes I–V were classified using MK standards. Note that the term luminosity class is something of a misnomer, as the physical quantity upon which the luminosity class is dependent is the surface gravity, and not the luminosity. This point is discussed further in Sect. 4. A detailed description of the standard spectra displayed in Figs. 1–9 follows:
for helium classes 20–40. The term − 0.83 HeII λ4541 is an empirical correction for the contribution of the Pickering series of HeII to the depth of Hγ. We denote spectra from the third group by including the letter “C” in the spectral class to identify them as spectra showing strong carbon lines. Finally, we note that the hydrogen and helium line widths seem to vary smoothly throughout each sequence, so we have appended “luminosity” class “VII” to most of the hot subdwarfs. If the lines are significantly narrower than average (but still significantly wider than for MK class “V” stars), we append luminosity class “VI” instead, and if the lines are significantly wider than the average, we use luminosity class “VIII”. Because most of the hot subdwarfs follow the average trend (luminosity class VII), we do not feel that a more detailed “luminosity” classification for them is is justified at the present time. Stars given luminosity classes I–V were classified using MK standards. Note that the term luminosity class is something of a misnomer, as the physical quantity upon which the luminosity class is dependent is the surface gravity, and not the luminosity. This point is discussed further in Sect. 4. A detailed description of the standard spectra displayed in Figs. 1–9 follows:
 |
Fig. 9 Luminosity effects at a) sdB3; b) sdB5; c) sdB7-B8; d) sdB8; and e) sdB9-A0. The lines marked are HeI λλ 4121, 4144, 4387, 4471, 4713; SiII λ 4128-30; CII λ 4267; MgII λ 4481; and λλ 4358, 4772 emission. |
-
1.
-
He-normal (strong hydrogen, metallic lines or both HeI andHeII present): it is for the stellar spectra shown inFig. 1 that we see variations very similar to thosefor MK luminosity class V. Wechose BD+28 4211 as the standard for spectralclass sdO2, since it shows weak lines of NV, OIVand CIV, but no trace of HeI at this resolution, which is consistentwith the definition of spectral class O2 given byWalborn et al. (2002). From O2 through B1, theprincipal criterion for the spectral class isHeI λ 4471/HeII λ 4541. Because of the weakness of the Pickering series in subdwarfs of these spectral classes, we use HeI λ 4471/HeII λ 4686, which is affected somewhat by the luminosity class, as a secondary criterion. From O8 to B1, HeI λ 4713/HeII λ 4686 can also be used. From B0.5 through A0, the primary criteria are SiIII/HeI, MgII/HeI and SiII/HeI. Again, these criteria have been adjusted so that the line ratios defining each spectral class are roughly the same as they are in normal stars of the same MK spectral class at luminosity class V. Note that the depths of the Balmer lines increase downwards through the sequence. This is of critical importance, since we are going to be forced to use the depths of the Balmer lines as the primary indicator of spectral class in the next sequence.
Table 1Standard stars defining the new system.
-
2.
He-weak (strong hydrogen, lines of HeI and HeII not simultaneously present, metallic lines very weak or absent): in Fig. 2, the spectra are arranged in the order of increasing depths of the Balmer lines. This is the only indicator of spectral class, and the classes are assigned such that stars which have the same Balmer line depths in Figs. 1 and 2 have the same spectral class.
-
3.
He-strong C (helium dominant, carbon present): in Fig. 3, we see that from OC1 through OC2, lines due to CIV and the HeII Pickering series are all strong and decrease in strength. HeI λ 4471 is very weak, as it is in MK class O3 as defined by Walborn and Fitzpatrick (1990). One must bear in mind, however, that this line would be invisible if helium were as weak in these spectra as in normal main-sequence stars. From OC2 to BC1, we take the ratio of the line depths of HeI λ 4471 and HeII λ 4541 as the principal criterion for the spectral class, with the correspondence between that line ratio and spectral class being roughly the same as that for normal stars of MK luminosity class V. Secondary criteria are HeI λ 4713/HeII λ 4541, CIV/CIII (for spectral classes OC2 through OC9), CII/CIII (for spectral classes OC9 through BC1), and the absolute strengths of the NIII lines (for spectral classes OC6.5 through BC1). The similarity of these variations to the MK temperature sequence suggests that the variations in the helium, carbon, and nitrogen lines are primarily due to a decrease in the effective temperatures of the corresponding stellar atmospheres as we move from the top to the bottom of the sequence. This point is discussed further in Sect. 4.
-
4.
He-strong (helium dominant, carbon weak or absent): in Fig. 4, we see that spectra of stars of a given spectral class appear to be identical to stars of the same spectral class in Fig. 3, except for the carbon lines, which are weak or absent. This would suggest that these stars have a carbon abundance significantly lower than stars of the same spectral class in Fig. 3, which are designated by a “C” in the spectral class. If CIII is weak or absent and NIII is visible, we use sdBN in the spectral class in order to be consistent with the definition of OBN stars given by Walborn (1976).
In Fig. 5, we show luminosity and abundance effects for stars earlier than spectral class sdO9. These stars tend to be either H-strong (helium class less than 15) or extremely He-strong (helium class 40). Note the increased broadening of the H and He lines and the increase in the HeII λ 4686 line depth relative to the Pickering series of HeII as we move from luminosity class V to luminosity class VIII at spectral class sdO2-sdO8. Note also the emission reversal of the CIII λ 4650 blend at luminosity class VI for the sdOC2 stars. We may be seeing here, and in some of the other emission features marked, the same type of NLTE effects seen in the O supergiants and in main-sequence stars near spectral class O4 (see Walborn & Fitzpatrick 1990; Walborn et al. 2010) in these even hotter O-type subdwarfs. At sdO7, luminosity class VIII is distinguished from luminosity class VII in the He-strong stars by the increased strength of HeII λ 4686 relative to the other helium lines and by the broad feature centered near λ 4630, which is due to CIII, CIV, and NIII (Dreizler, priv. comm.).
Similar effects are present at spectral class sdO9, as shown in Fig. 6. We have included a spectrum of the post-EAGB star PG2120+062 (Moehler et al. 1994) to show how it fits into this scheme, and of the very narrow-lined extreme helium star HD160641 (Bidelman 1952) to show how these stars may be considered to be the low surface-gravity counterparts of the extremely He-strong subdwarfs. We also show a series of sdO9VII – sdB0VII stars of increasing helium class in Fig. 6. Notice that unlike the sdO stars, the intermediate helium classes for the sdB0 stars are now starting to fill in at He35 (PG0921+311) and He28 (HZ 44). These intermediate helium classes continue to fill in from sdB0.2 to sdB2, as shown in Figs. 7 and 8. We also show luminosity effects for sdB0.5 and sdB1.
The broadening of the Balmer lines with increasing luminosity class is shown for the H-strong sdB3 stars in Fig. 9. At later spectral types we find only blue horizontal-branch stars, which we have essentially classified using MK standards (except for the helium class).
Finally, we use the standard spectra listed in Table 1 and shown in Figs. 1–9 to classify all of the spectra in our sample. The results are given in Table 2. A “p” is appended to the spectral type to indicate a peculiarity described in the remarks to Table 2, and an “e” is appended if emission features were present in more than one spectrum of the same star. Note that the emission features have been clipped at 15 percent above the continuum in Figs. 1–9. The mean errors of classification, as estimated from the results for stars for which we have more than one spectrum, are ±0.4 spectral classes, ±0.2 luminosity classes, and ±1.1 helium classes.
Spectral types for all stars in our sample.
4. Calibrations
As mentioned earlier, model-atmosphere analyses have been carried out for a large number of these spectra (in fact, this was the primary reason for obtaining the spectra used for the spectral classification). We have not used the results of Moehler et al. (1990b) or Theissen et al. (1993) in the calibrations, as colors were used in these analyses to determine the effective temperatures, and the effective temperature versus color calibration used (Lester et al. 1986) is not valid for O and B subdwarfs (Napiwotzki et al. 1993). We also did not use the results of Saffer et al. (1994) in the calibrations because they are based on spectra of a much lower (and variable) resolution and because the analyses did not account for metallic line blanketing. The spectral classification itself proved to be a very useful tool in deciding which results to use in the calibrations, as the spectral types can be used to compare the results of different workers even though they have no stars in common, and plots of the atmospheric parameters versus spectral type revealed significant systematic differences between our final calibrations and the results cited above. The results upon which our final calibrations are based are given in Table 3, and there appear to be no significant systematic differences between them.
 |
Fig. 10 Effective temperature versus spectral class for helium class 0–28 and luminosity class V–VIII. |
 |
Fig. 11 Effective temperature versus spectral class for helium class 35–40 and luminosity class V–VIII and for helium class 0–11 and luminosity class I–IV. The large cross is the average given in the text. |
The scheme of spectral classification which we have just set up in an empirical fashion, completely independent of the theory of stellar atmospheres, suggests that the sequences which we have identified are temperature sequences which differ primarily in the H/He and C/He abundance ratios. This is supported by the calibrations given in Figs. 10 and 11, in which the effective temperatures from Table 3 are plotted against spectral class. The straight line fit shown in Fig. 10,
![$$ T_\mathrm{eff}[\mathrm{K}]=74\,900-4030\,{s}, $$](/articles/aa/full_html/2013/03/aa19433-12/aa19433-12-eq11.png) where s is the spectral subclass for sdO stars and 10 plus the spectral subclass for sdB stars, yields the effective temperatures for hot subdwarfs of spectral class O9–B3, helium class 0–28, and luminosity class V–VIII to a mean error of ±1700 K. There appears to be no correlation of the effective temperature with either helium class or luminosity class within these ranges, although only 5 of the 23 stars plotted have He classes greater than 13. Straight line fits in effective temperature versus spectral class also seem to be adequate for hot subdwarfs of spectral class O7–B1, helium class 35–40, and luminosity class V–VIII,
where s is the spectral subclass for sdO stars and 10 plus the spectral subclass for sdB stars, yields the effective temperatures for hot subdwarfs of spectral class O9–B3, helium class 0–28, and luminosity class V–VIII to a mean error of ±1700 K. There appears to be no correlation of the effective temperature with either helium class or luminosity class within these ranges, although only 5 of the 23 stars plotted have He classes greater than 13. Straight line fits in effective temperature versus spectral class also seem to be adequate for hot subdwarfs of spectral class O7–B1, helium class 35–40, and luminosity class V–VIII,
to a mean error of ±1600 K, and for stars of luminosity class I–IV, spectral class B2.5–B8, and helium class 0–11,
![$$ T_\mathrm{eff}[\mathrm{K}]=28\,700-841~{s}, $$](/articles/aa/full_html/2013/03/aa19433-12/aa19433-12-eq14.png) to a mean error of ±1900 K (see Fig. 11). Again, within the ranges given, there appears to be no correlation of the effective temperature with either helium class or luminosity class. The O2 stars of helium class 36–40 have been calibrated separately from the other types and yield a mean effective temperature of 66 000 K with a mean error of ±2600 K.
to a mean error of ±1900 K (see Fig. 11). Again, within the ranges given, there appears to be no correlation of the effective temperature with either helium class or luminosity class. The O2 stars of helium class 36–40 have been calibrated separately from the other types and yield a mean effective temperature of 66 000 K with a mean error of ±2600 K.
That He-weak stars have low helium abundances, He-normal stars, more nearly solar helium abundances, and He-strong stars, high helium abundances is supported by the calibrations given in Figs. 12 and 13, where the helium abundances given in Table 3 are plotted against helium class. In Fig. 12, the quadratic fit,
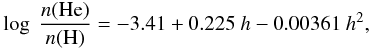 where h is the helium class, is seen to be adequate for sdB (sdB0–sdB3 V–VIII) stars with 1 < h < 29 with a mean error in log [n(He)/n(H)] of ±0.21. For 34 < h < 40, n(H)/n(He) is 0.01 with a mean error less than 0.01. The reason for this is that the Hβ line is clearly visible at these spectral classes if even this trace amount of hydrogen is present. For h = 0, log [n(He)/n(H)] < − 4. Also in Fig. 12, the straight line fit,
where h is the helium class, is seen to be adequate for sdB (sdB0–sdB3 V–VIII) stars with 1 < h < 29 with a mean error in log [n(He)/n(H)] of ±0.21. For 34 < h < 40, n(H)/n(He) is 0.01 with a mean error less than 0.01. The reason for this is that the Hβ line is clearly visible at these spectral classes if even this trace amount of hydrogen is present. For h = 0, log [n(He)/n(H)] < − 4. Also in Fig. 12, the straight line fit,
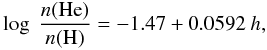 is seen to be adequate for sdB2.5-sdB8 I–IV stars with h < 12, with a mean error of ±0.18. Figure 12 shows that there is a dependence of the helium abundance on luminosity class, and for this reason we have only included stars of luminosity class VII in the sdB calibration.
is seen to be adequate for sdB2.5-sdB8 I–IV stars with h < 12, with a mean error of ±0.18. Figure 12 shows that there is a dependence of the helium abundance on luminosity class, and for this reason we have only included stars of luminosity class VII in the sdB calibration.
The situation is much less clear for the sdO stars, as shown in Fig. 13. All but 2 of the stars for which helium abundances are given in Table 3 have h > 35, and these are either rather uncertain upper limits (n(He)/n(H) less than 10 or 20) or have very large mean errors. The reason for this is the blending of the Balmer lines with the Pickering series of HeII in the sdO stars, which makes the determination of n(He)/n(H) difficult.
 |
Fig. 12 Helium to hydrogen abundance ratio (by numbers of atoms) versus helium class for sdB0-sdB3 V–VIII and sdB2.5-sdB8 I–IV. |
Atmospheric parameters used in the calibrations.
Finally, we plot the surface gravities given in Table 3 against luminosity class in Fig. 14 (helium classes 0–18) and Fig. 15 (helium classes 24–40). The resulting calibrations are given in Tables 4 and 5, respectively. There appears to be no significant dependence of these calibrations on either spectral class or helium class within the ranges given, although it is seen from the figures that the distribution of the points with spectral class is far from uniform, and only 5 of the 50 stars plotted have helium classes of 14–34. We do not consider the calibrations for luminosity classes I–V to be significantly different from those given for “normal” stars by Drilling and Landolt (1999), even though the stars in the present paper probably have much lower masses and luminosities.
 |
Fig. 13 Helium to hydrogen abundance ratio (by numbers of atoms) versus helium class for sdO stars. |
 |
Fig. 14 Surface gravity versus luminosity class for helium class 0–18. The large crosses are the averages given in Table 4. |
Surface gravity calibration for helium class 0–18.
 |
Fig. 15 Surface gravity versus luminosity class for helium class 24–40. The large crosses are the averages given in Table 5. |
5. Comparison with other systems
In Fig. 16, we compare the Green et al. (1986) classifications with the system that we have just defined. It is seen that the Green et al. classes sdOC, sdOB, and sdOD isolate He-strong stars of progressively later spectral class, from early O for class sdOC to early B for class sdOD, although there is a great deal of overlap in spectral class between these three Green et al. classes. Both C-strong and C-weak spectra are included in each of the three classes. The Green et al. classes sdB, sdB-O, sdOA, and sdOD isolate early B-type stars of progressively higher helium class, from a median of He3 for class sdB to He37 for sdOD, but again there is a large scatter in both spectral class and helium class, and a lot of overlap in helium class, as would be expected from the much lower resolution spectra on which the Green et al. classes are based. The other Green et al. class represented here, HBB, tends to isolate late B-type stars of luminosity class III–V, but there is seen to be some overlap in Fig. 16 between the earlier HBB stars and the Green et al. types sdB and sdB-O. One sees from these figures that despite statements which have been made to the contrary (Jeffery et al. 1997), the Green et al. classes do define “natural” groups in the spectral class – helium class – luminosity class space defined by this paper.
Surface gravity calibration for helium class 24–40.
 |
Fig. 16 Comparison of the new spectral and helium classes with the PG classes. The points have been given small random shifts to resolve overlap. |
6. Conclusions
We have defined with standards an MK-like system for classifying hot subdwarfs which merges smoothly with the MK system itself in the following respects:
- 1.
The spectral types of helium-normal stars have been definedsuch that all line ratios are roughly the same as they are forMK standards of the same spectral class (andluminosity class for luminosity classes I–V).
- 2.
The spectral types of helium-strong stars have been defined such that all line ratios for different ions of the same element are roughly the same as they are for MK standards of the same spectral class.
- 3.
The spectral types of helium-weak stars have been defined such that the Balmer-line widths and depths are roughly the same as they are for helium-normal stars of the same spectral type.
- 4.
The spectra of the blue horizontal-branch stars and other stars which are not hot subdwarfs have essentially been classified using MK standards (except for the helium class).
Acknowledgments
We gratefully acknowledge the ESO and Calar Alto Observatories. This research made use of the SIMBAD database, operated at CDS, Strasbourg, France, and was supported in part by National Science Foundation grant AST-9819835. We thank Chris Copperwheat for providing us with his spectra of PG1432+004, PG1644+404 and PG2314+076. We especially wish to thank the referee, N.R. Walborn, whose many comments and suggestions greatly improved both the science and the readability of the paper.
References
- Ahmad, A., & Jeffery, C. S. 2003, A&A, 402, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bidelman, W. P. 1952, ApJ, 116, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Conlon, E. S., Theissen, A., & Moehler, S. 1993, A&A, 269, L1 [NASA ADS] [Google Scholar]
- Copperwheat, C. M., Morales-Rueda, L., Marsh, T. R., Maxted, P. F. L., & Heber, U. 2011, MNRAS, 415, 1381 [NASA ADS] [CrossRef] [Google Scholar]
- Dreizler, S., Heber, U., Werner, K., Moehler, S., & de Boer, K. S. 1990, A&A, 235, 234 [NASA ADS] [Google Scholar]
- Drilling, J. S. 1996, in Hydrogen-Deficient Stars, eds. C. S. Jeffery, & U. Heber (San Francisco: ASP), 461 [Google Scholar]
- Drilling, J. S., & Landolt, A. U. 1999, in Allen’s Astrophysical Quantities, ed. A. N. Cox (New York: Springer Verlag), 381 [Google Scholar]
- Green, R. F., Schmidt, M., & Liebert, J. 1986, ApJS, 61, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Hirsch, H. A. 2009, Ph.D. Thesis, Universität Erlangen-Nürnberg [Google Scholar]
- Jeffery, C. S., Drilling, J. S., Harrison, P. M., Heber, U., & Moehler, S. 1997, A&AS, 125, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keenan, P. C. 1987, PASP, 99, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Lester, J. B., Gray, R. O., & Kurucz, R. L. 1986, ApJS, 61, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Maxted, P. F. L., Heber, U., Marsh, T. R., & North, R. C. 2001, MNRAS, 326, 1391 [NASA ADS] [CrossRef] [Google Scholar]
- Moehler, S., & Heber, U. 1998, A&A, 335, 985 [NASA ADS] [Google Scholar]
- Moehler, S., Richtler, T., de Boer, K. S., Dettmar, R. J., & Heber, U. 1990a, A&AS, 86, 53 [NASA ADS] [Google Scholar]
- Moehler, S., Heber, U., & de Boer, K. S. 1990b, A&A, 239, 265 [NASA ADS] [Google Scholar]
- Moehler, S., Heber, U., & Dreizler, S. 1994, A&A, 282, L29 [NASA ADS] [Google Scholar]
- Morales-Rueda, L., Maxted, P. F. L., Marsh, T. R., North, R. C., & Heber, U. 2003, MNRAS, 338, 752 [Google Scholar]
- Morgan, W. W. 1984, in The MK Process and Stellar Classification, ed. R. F. Garrison (Toronto: David Dunlap Obs.), 18 [Google Scholar]
- Morgan, W. W., Keenan, P. C., & Kellman, E. 1943, An Atlas of Stellar Spectra (Chicago: University of Chicago Press) [Google Scholar]
- Napiwotzki, R. 1993, Acta Astron., 43, 343 [NASA ADS] [Google Scholar]
- Napiwotzki, R., Schönberner, D., & Wenske, V. 1993, A&A, 268, 653 [NASA ADS] [Google Scholar]
- Østensen, R. H. 2006, Baltic Astron., 15, 85 [Google Scholar]
- Ramspeck, M., Heber, U., & Edelmann, H. 2001, A&A, 379, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saffer, R. A., Bergeron, P., Koester, D., & Liebert, J. 1994, ApJ, 432, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Salomon, Z. 2003, Diploma thesis, Universität Erlangen-Nürnberg [Google Scholar]
- Schmidt, J. H. K. 1996, Ph.D. Thesis, Universität Bonn [Google Scholar]
- Sota, A., Maiz Apellániz, J., Walborn, N. R., et al. 2011, ApJS, 193, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Theissen, A., Moehler, S., Heber, U., & de Boer, K. S. 1993, A&A, 273, 524 [NASA ADS] [Google Scholar]
- Theissen, A., Moehler, S., Heber, U., Schmidt, J. H. K., & de Boer, K. S. 1995, A&A, 298, 577 [NASA ADS] [Google Scholar]
- Walborn, N. R., 1971 ApJS, 23, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R. 1976, ApJ, 205, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R., & Fitzpatrick, E. L. 1990, PASP, 102, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R., Howarth, I. D., Lennon, D. J., et al. 2002, AJ, 123, 2754 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R., Sota, A., Maiz Apellániz, J., et al. 2010, ApJ, 711, L143 [NASA ADS] [CrossRef] [Google Scholar]
- Winter, C., Jeffery, C. S., & Drilling, J. S. 2004, Astrophys. Space Sci., 291, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Winter, C., Jeffery, C. S., Ahmad, A., & Morgan, D. R. 2006, Baltic Astron., 15, 69 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Spectra of He-normal stars for which hydrogen is dominant and either helium lines of both ionization states or metallic lines are visible. The lines marked are H + HeII λλ 4101, 4340, 4861; HeII λλ 4200, 4541, 4686; NV λ 4604–20; OIV λ 4632; CIV λ 4658 blend; SiIII λ 4552–68; HeI λλ 4144, 4387, 4471, 4713; SiII λ 4128–30; MgII λ 4481; and λλ 4360, 4369, 4772 emission. |
| In the text | |
 |
Fig. 2 Spectra of He-weak stars for which hydrogen is dominant and helium lines of only one ionization state may be visible. Metallic lines are very weak or absent. Note that PG1708+602 fits this definition even though the helium class is much higher than those of the other stars. The lines marked are H + HeII λλ 4101, 4340, 4861; and HeII λλ 4200, 4541, 4686. |
| In the text | |
 |
Fig. 3 Spectra of He-strong C stars for which helium is dominant and carbon present. The lines marked are HeII λλ 4100, 4200, 4338, 4541, 4686, 4859; CIV λλ 4442, 4647, 4658; CIII λ 4650 blend; NIII λλ 4379, 4511–15, 4640 blend ; HeI λλ 4121, 4144, 4387, 4471, 4713; CII λλ 4267, 4619; H λλ 4340, 4861; and λλ 4326, 4510–11, 4599−4600, 4615, 4776 emission. |
| In the text | |
 |
Fig. 4 Spectra of He-strong stars for which helium is dominant and carbon is very weak or absent. NIII may be present. The lines marked are HeII λλ 4100, 4200, 4338, 4541, 4686, 4859; NIII λλ 4379, 4511–15, 4640 blend ; HeI λλ 4121, 4144, 4387, 4471, 4713; H λλ 4340, 4861; and λλ 4324, 4509, 4637, 4774 emission. |
| In the text | |
 |
Fig. 5 Luminosity effects for a) H-strong sdO2 stars; b) He-strong sdO2 stars; c) H-strong sdO8 stars; and d) He-strong sdO7 stars. The lines marked are HeI λλ 4121, 4144, 4387, 4471, 4713; CIII/CIV/NIII λ 4630 broad absorption feature; NV λ 4604-20; OIV λ 4632; CIV λ 4658 blend; H + HeII λλ 4101, 4340, 4861; HeII λλ 4200, 4541, 4686; and λλ 4325–9, 4365, 4510–11, 4599–4601, 4615, 4651, 4705, 4776, 4828 emission. |
| In the text | |
 |
Fig. 6 a) Luminosity effects at sdO9; b) abundance effects at sdO9 – sdB0. The lines marked are HeI λλ 4121, 4144, 4387, 4471, 4713; NIII λλ 4379, 4511–15, 4640 blend; CIII λ 4650 blend; H + HeII λλ 4101, 4340, 4861; and HeII λλ 4200, 4541, 4686. |
| In the text | |
 |
Fig. 7 a) Luminosity effects at sdB0.5; b) abundance effects at sdB0.2 – sdB0.5. The lines marked are the same as in Fig. 6. |
| In the text | |
 |
Fig. 8 a) Luminosity effects at sdB1; b) abundance effects at sdB1 – sdB2. The lines marked are the same as in Fig. 6. |
| In the text | |
 |
Fig. 9 Luminosity effects at a) sdB3; b) sdB5; c) sdB7-B8; d) sdB8; and e) sdB9-A0. The lines marked are HeI λλ 4121, 4144, 4387, 4471, 4713; SiII λ 4128-30; CII λ 4267; MgII λ 4481; and λλ 4358, 4772 emission. |
| In the text | |
 |
Fig. 10 Effective temperature versus spectral class for helium class 0–28 and luminosity class V–VIII. |
| In the text | |
 |
Fig. 11 Effective temperature versus spectral class for helium class 35–40 and luminosity class V–VIII and for helium class 0–11 and luminosity class I–IV. The large cross is the average given in the text. |
| In the text | |
 |
Fig. 12 Helium to hydrogen abundance ratio (by numbers of atoms) versus helium class for sdB0-sdB3 V–VIII and sdB2.5-sdB8 I–IV. |
| In the text | |
 |
Fig. 13 Helium to hydrogen abundance ratio (by numbers of atoms) versus helium class for sdO stars. |
| In the text | |
 |
Fig. 14 Surface gravity versus luminosity class for helium class 0–18. The large crosses are the averages given in Table 4. |
| In the text | |
 |
Fig. 15 Surface gravity versus luminosity class for helium class 24–40. The large crosses are the averages given in Table 5. |
| In the text | |
 |
Fig. 16 Comparison of the new spectral and helium classes with the PG classes. The points have been given small random shifts to resolve overlap. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



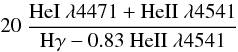
![$$ T_\mathrm{eff}[\mathrm{K}]=63\,200-2520~{s}, $$](/articles/aa/full_html/2013/03/aa19433-12/aa19433-12-eq13.png)