| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A50 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201219430 | |
| Published online | 20 February 2013 | |
Eccentricity-pumping in post-AGB stars with circumbinary discs
1
Argelander-institut für Astronomie, University of Bonn,
Auf dem Hügel 71,
53121
Bonn,
Germany
e-mail: tdermine@gmail.com
2 Institut d’Astronomie et d’Astrophysique, Université Libre de
Bruxelles, Belgium
3
Instituut voor Sterrenkunde, K.U. Leuven,
Belgium
Received: 17 April 2012
Accepted: 7 December 2012
Circumbinary discs are commonly observed around post-asymptotic giant branch (post-AGB) systems and are known to play an important role in their evolution. Several studies have pointed out that a circumbinary disc interacts through resonances with the central binary and leads to angular momentum transfer from the central binary orbit to the disc. This interaction may be responsible for a substantial increase in the binary eccentricity. We investigate whether this disc eccentricity-pumping mechanism can be responsible for the high eccentricities commonly found in post-AGB binary systems.
Key words: binaries: general / stars: AGB and post-AGB / stars: chemically peculiar / Galaxy: stellar content
© ESO, 2013
1. Introduction
Post-asymptotic giant branch (AGB) stars just left the AGB phase and evolve rapidly to hotter effective temperatures at constant luminosity but they are not yet hot enough to ionise circumstellar material ejected during the AGB phase. Some post-AGB stars also show near-infrared emission due to thermal radiation of hot circumstellar dust. The colour temperature of the dust is a good indication that there must be circumstellar dust close to the star and this spectral energy distribution (SED) feature is always related to binarity (van Winckel et al. 2009, and references therein). The extremely narrow CO emission lines (a few km s-1 width, e.g. Jura et al. 1995), the presence of large (sub-micron) grains (Gielen et al. 2011) and the detection of oxygen-rich crystalline silicates (Waters et al. 1998) are distinct characteristics best explained by the long-term processing of dust in a stable circumbinary (CB) disc.
A key problem still remains regarding the inability of population-synthesis models to reproduce the observed large eccentricities of post-AGB stars, similarly observed in barium stars (Pols et al. 2003; Izzard et al. 2010). In the previous evolutionary phase (i.e. the AGB), the very large stellar radii lead to efficient circularisation of the binary orbit by tides (Zahn 1977). Systems too close to accommodate an AGB star undergo Roche-lobe-overflow (RLOF), in most cases in an unstable regime which leads the system into a common envelope (CE). Due to friction between the stellar cores and the CE, the envelope may be ejected, and the orbit shrunk and circularised (Iben & Livio 1993). Post-AGB binaries with orbital periods shorter then about 1000 d are expected to be circular. Observations reveal, however, that this is clearly not the case and many of the systems with periods below 1000 d are highly eccentric. A mechanism that increases the binary eccentricity is therefore required.
If tides are as efficient as predicted (Zahn 1977), a mechanism to increase the eccentricity must take place during the AGB or post-AGB phase. Different mechanisms have been investigated such as enhanced mass-transfer at periastron (i.e. differential mass loss during an orbital period; Soker 2000), eccentricity pumping induced by a wind-RLOF hybrid mass transfer (Bonačić Marinović et al. 2008) and a kick to the newly-born white dwarf (Izzard et al. 2010).
In this paper we investigate the possibility that CB discs cause the large eccentricities observed in some post-AGB systems. The current knowledge of CB discs is summarised in Sect. 2. In Sect. 3 we describe our model of eccentricity-pumping. In Sect. 4 we present our results and compare them to observed post-AGB periods and eccentricities. Section 5 discusses successes and potential problems of our model. Conclusions are drawn in Sect. 6.
2. Circumbinary discs
In this section we list the classes of stars known or suspected to be binaries that possess dust discs.
2.1. Observed disc properties
Dust discs are observed in very different classes of stars known to be binaries (Chesneau et al. 2011). Stable discs are observed around most known post-AGB binaries (van Winckel 2003; de Ruyter et al. 2006; Van Winckel et al. 2006). About half of the objects classified as good post-AGB candidates of the Large Magellanic Cloud, show a SED that is indicative of a disc rather than an expanding wind and cooling AGB remnant (van Aarle et al. 2011). Like in the Galaxy, these disc sources are likely associated with binary evolution but this remains to be proven observationally. Dust discs are increasingly being identified around the central stars of planetary nebulae, e.g. NGC 2346 for which eclipses from a dusty disc have been detected (Costero et al. 1986; Miszalski et al. 2011), as well as in some symbiotic stars (Angeloni et al. 2007) and hydrogen-deficient binary (Netolický et al. 2009). Around some silicate J-type stars the disc is resolved (Deroo et al. 2007), but only one system shows evidence for binarity (Izumiura et al. 2008). Some AGB stars (e.g. X Her; Kahane & Jura 1996) have a very slowly expanding wind (a few km s-1), however none is a confirmed binary system. Keplerian discs are also observed in B[e] stars (Meilland et al. 2007); but only a few B[e] stars are confirmed binaries and it remains unclear whether the B[e] behaviour is related to binarity (Lamers et al. 1998). Finally, discs have been discovered around white dwarfs (e.g. Gänsicke et al. 2006). Surveys for such discs around the oldest white dwarfs have been unsuccessful (Kilic et al. 2009), but around 15% of local white dwarfs show metal-rich material in their photosphere, indicative of accretion from a residual dust reservoir (Sion et al. 2009), although this reservoir may not necessarily originate from binary interaction.
The variety of classes of objects that host CB discs and the wide range of orbital periods of the central stars (from 115.9 d for SAO 173329 – van Winckel et al. 2000 – to 2597 d for U Mon; Pollard & Cottrell 1995) show that they are very common around binary systems and easily formed in late-type mass-transfer systems. The structure of discs surrounding young stellar objects and post-AGB stars is somewhat similar (de Ruyter et al. 2006), which is rather remarkable because of their (possibly) very different formation mechanism.
The stable nature of the dust disc in post-AGB systems can be inferred from the observation that none of them shows evidence for a current dusty mass loss while the dust excess starts near the dust-sublimation radius. The near-IR emitting material must then be gravitationally bound in the system. In addition, post-AGB systems show depletion patterns, i.e. the gas in the disc is separated from the dust and subsequently re-accreted onto the star (Waters et al. 1992; Maas et al. 2005). This re-accretion process occurs more efficiently if circumstellar gas and dust are trapped in a stable disc (Van Winckel et al. 2006; de Ruyter et al. 2006; Gielen et al. 2008). Furthermore the presence of near-IR (from about 5 to 20 μm) excesses indicates that in all systems the circumstellar shell is not freely expanding but stored in a disc. The detection of cool (from about 100 to 150 K) oxygen-rich crystalline silicate dust grains (Waters et al. 1998) as well as the presence of large (sub-micron) grains are other indications of the long-lived nature of these discs (e.g. Angeloni et al. 2007; Gielen et al. 2008). In some cases, Keplerian rotation is detected at least in the inner disc region (Bujarrabal et al. 2005).
2.2. Formation
The formation of CB discs and their impact on the central star is not well understood. Most likely, CB discs in post-AGB stars remain from CE ejection or form during mass-transfer events in a binary system. The former case is supported by population synthesis models which show that most post-AGB systems that possess a CB disc are post CE systems. The possibility of forming a CB disc from a fraction of the ejected CE has already been suggested from detailed CE models (Sandquist et al. 1998; Nordhaus & Blackman 2006; Kashi & Soker 2011). It turns out that the CE is not necessarily completely ejected, so some gas remains around the system. While CE evolution is expected to lead systems to orbital periods of hours to hundreds of days, no disc has been observed around systems with periods shorter than a hundred days.
On the other hand, many studies have investigated the possibility that matter flows through the second Lagrangian point L2 during RLOF (e.g. Podsiadlowski et al. 1992; Frankowski & Jorissen 2007; van Rensbergen et al. 2011), possibly because of radiation pressure which could reshape the Roche equipotentials by a reduction of the effective gravity of the mass-losing star (Schuerman 1972; Frankowski & Tylenda 2001; Dermine et al. 2009). Hydrodynamical simulations have shown that this can lead to the formation of a CB disc in a close binary system (Sytov et al. 2009). However, the disc may not be stable and may disappear as soon as the mass transfer stops. Two-dimensional hydrodynamical simulations show that, for a typical slow and massive wind from an AGB star, the flow pattern is similar to Roche lobe overflow, and that a small fraction of the mass transferred to the companion flows through L2 (de Val-Borro et al. 2009; Mohamed & Podsiadlowski 2010). The companion focuses the ejected material into the equatorial plane of the system (Theuns & Jorissen 1993; Theuns et al. 1996; Mastrodemos & Morris 1998). However, the possibility of forming a stable CB disc from a mass-losing giant star has not yet been confirmed by simulations.
2.3. Evolution
Surveys performed at wavelengths as long as 100 μm show that none of the post-AGB systems with a disc is surrounded by an outflow remaining from the AGB phase (Gielen et al. 2011). This means that the observed post-AGBs have left the AGB phase long enough ago for the last ejecta of the AGB star to reach a distance at which the emission at 100 μm cannot be detected. A lower limit of the disc lifetime can then be inferred. Using the code DUSTY (Ivezic & Elitzur 1997) for a post-AGB star with an effective temperature of 4000 K, a luminosity of 5000 L⊙ and a wind composed only of silicate grains, we deduce a distance of about 0.4 pc. Assuming a typical wind velocity of 15 km s-1, this timescale is approximately 2.5 × 104 yr.
It is known that the CB-disc mass decreases during the post-AGB and planetary nebula (PN) phases because material flows away from the outer part of the disc and re-accretes on the central stars from its inner edge. Gesicki et al. (2010) pointed out the sharp decrease in CB-disc mass as the star ages. Finally, the discs observed around cooling white dwarfs have very low masses because all the gas was probably expelled and only the dust remains. An upper limit of the disc lifetime can then be estimated from the time since the mass transfer stopped, i.e. the end of the AGB phase, given by the timescale to cross the post-AGB and PN phases. While it has been estimated for single stars (of the order of 1000–10 000 yr; Bloecker 1995), this timescale is very uncertain for binaries. The evolution of post-AGB stars is governed by mass loss that expels the thin envelope remaining from the AGB and reveals its core, i.e. a young hot white dwarf. The post-AGB phase ends when the temperature of the post-AGB star reaches 30 000 K and circumstellar material ejected during the AGB phase is ionised and becomes a PN. Therefore, if re-accretion occurs, e.g. from a CB disc, the envelope ejection could take much longer and extend the post-AGB lifetime. From the observed strongly depleted post-AGB stars in the LMC (Reyniers & van Winckel 2007; Gielen et al. 2009), we can infer a dilution of their envelopes by a factor of about 10. As the envelope mass is about 10-3 M⊙ (Bloecker 1995), assuming a fully convective envelope, 10-2 M⊙ must have been accreted from a CB disc. With a typical mass-loss rate of 10-7 M⊙ yr-1, the accreted mass therefore extends the post-AGB lifetime by about 105 yr. However, this estimate strongly depends on the fraction of envelope which is convective, the composition of re-accreted material and the mass-loss rate on the post-AGB, which are all very uncertain.
The disc lifetime is determined by two competing mechanisms: (i) disc accretion (Hartmann et al. 1998); and (ii) photoevaporation of the surface layer of the gas disc due to far- and extreme-ultraviolet radiation from the central star (Hollenbach et al. 2000). For comparison, pre-main-sequence disc lifetimes are thought to be 5–10 Myr (Yasui et al. 2010).
Once the star is on the white-dwarf cooling track, any further dissipation is set by the Poynting-Robertson drag (Weidenschilling & Jackson 1993), with a time scale of the order of 107 yr. The disc may remain detectable for about 108 yr, long after any sign of the planetary nebula has disappeared.
3. Resonant interactions between a binary star and its circumbinary disc
Goldreich & Tremaine (1979) and Artymowicz & Lubow (1994) describe the resonant and nonresonant interactions between a binary system and its CB disc using a linear perturbation theory and assuming (i) the disc is thin (0.01 < H/R < 0.1, where H and R are the thickness and the half angular momentum radius of the disc respectively); and (ii) the nonaxisymmetric potential perturbations are small around the average binary potential. The binary potential is expanded in a series as ![\begin{equation} \Phi(r,\theta,t)=\sum_{m,l}\phi_{m,l}(r)\, \exp\left[i\; m\left(\theta-(l/m)\Omega_{b}t\right)\right], \end{equation}](/articles/aa/full_html/2013/03/aa19430-12/aa19430-12-eq15.png) (1)of which only the real part is relevant, and l and m are integers. Ωb is the orbital angular frequency which, in an inertial frame, is
(1)of which only the real part is relevant, and l and m are integers. Ωb is the orbital angular frequency which, in an inertial frame, is 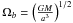 , where a is the semi-major axis of the system, and M its total mass. The individual potential harmonics φm,l(r) rotate uniformly with pattern speed
, where a is the semi-major axis of the system, and M its total mass. The individual potential harmonics φm,l(r) rotate uniformly with pattern speed 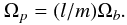 (2)A resonance occurs in the disc when the pulsation κ of radial motion of a disc particle (on an epicyclic orbit with azimuthal pulsation Ω) is commensurate with the angular frequency (Ω−Ωp) in the frame rotating with component (l,m) of the perturber,
(2)A resonance occurs in the disc when the pulsation κ of radial motion of a disc particle (on an epicyclic orbit with azimuthal pulsation Ω) is commensurate with the angular frequency (Ω−Ωp) in the frame rotating with component (l,m) of the perturber, 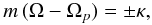 (3)where the positive/negative sign corresponds to the outer/inner Lindblad resonance (LR) respectively. A corotation resonance (CR) occurs when Ω = Ωp. These resonant interactions result in the excitation of density waves located at radii
(3)where the positive/negative sign corresponds to the outer/inner Lindblad resonance (LR) respectively. A corotation resonance (CR) occurs when Ω = Ωp. These resonant interactions result in the excitation of density waves located at radii 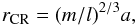 (4)and
(4)and ![\begin{equation} r_{{\rm LR}}=[(m\pm1)/l]^{2/3}a.\label{Eq:LR} \end{equation}](/articles/aa/full_html/2013/03/aa19430-12/aa19430-12-eq31.png) (5)Many studies have investigated whether these resonances increase the orbital eccentricity (Artymowicz et al. 1991; Artymowicz & Lubow 1994; Frankowski & Jorissen 2007). We apply the model of Lubow & Artymowicz (1996) for small and moderate eccentricities (e ≲ 0.2). This model is based on results of smooth particle hydrodynamics (SPH) simulations which show that for a disc in which the kinematic viscosity, ν, is independent of the density, the torque is independent of resonance strength and width. The resonant torque can then be estimated from the rate of change of the disc angular momentum. The viscous torques within the disc balance the gravitational torque generated by resonances in the inner part of the disc and redistribute mass and angular momentum throughout the disc. The viscous torque is
(5)Many studies have investigated whether these resonances increase the orbital eccentricity (Artymowicz et al. 1991; Artymowicz & Lubow 1994; Frankowski & Jorissen 2007). We apply the model of Lubow & Artymowicz (1996) for small and moderate eccentricities (e ≲ 0.2). This model is based on results of smooth particle hydrodynamics (SPH) simulations which show that for a disc in which the kinematic viscosity, ν, is independent of the density, the torque is independent of resonance strength and width. The resonant torque can then be estimated from the rate of change of the disc angular momentum. The viscous torques within the disc balance the gravitational torque generated by resonances in the inner part of the disc and redistribute mass and angular momentum throughout the disc. The viscous torque is 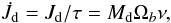 (6)where the viscous timescale τ = R2/ν = α-1(H/R)-2Ω-1 gives the timescale on which matter diffuses through the disc under the effect of the viscous torque and is of the order of 105 yr. Md, ν and α are the mass, kinematic viscosity and the viscosity parameter of the disc respectively. The viscosity parameter is typically α ≈ 0.1.
(6)where the viscous timescale τ = R2/ν = α-1(H/R)-2Ω-1 gives the timescale on which matter diffuses through the disc under the effect of the viscous torque and is of the order of 105 yr. Md, ν and α are the mass, kinematic viscosity and the viscosity parameter of the disc respectively. The viscosity parameter is typically α ≈ 0.1.
The variation of the orbital separation due to the resonant interaction between the binary and the CB disc is given by (Lubow & Artymowicz 1996) 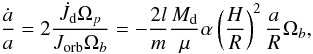 (7)where Jorb is the orbital angular momentum and μ is the reduced mass of the binary system. The increase of the eccentricity due to resonances can be given as a function of ȧ/a and depends on the binary eccentricity. At very small eccentricities (e ≤ 0.1α1/2), the resonances weakly drive the eccentricity so the inner radius of the CB disc is maintained by the m = l resonances that take place close to the binary at r/a ≲ 1.7. The eccentricity pumping in that regime increases with e and is estimated (Lubow & Artymowicz 1996) to proceed as
(7)where Jorb is the orbital angular momentum and μ is the reduced mass of the binary system. The increase of the eccentricity due to resonances can be given as a function of ȧ/a and depends on the binary eccentricity. At very small eccentricities (e ≤ 0.1α1/2), the resonances weakly drive the eccentricity so the inner radius of the CB disc is maintained by the m = l resonances that take place close to the binary at r/a ≲ 1.7. The eccentricity pumping in that regime increases with e and is estimated (Lubow & Artymowicz 1996) to proceed as 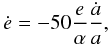 (8)up to a maximum of ė = 5α−1/2ȧ/a at e ≃ 0.1α1/2. At larger eccentricities (0.1α1/2 ≲ e ≲ 0.2), the m = 2, l = 1 resonance is the strongest contribution to the eccentricity driving and the disc is progressively pushed away as the binary eccentricity increases. In that regime, ė decreases as 1/e. The eccentricity pumping diminishes as 1/e until e ≃ 0.5−0.7, at which point resonances that damp the eccentricity begin to dominate (e.g. Roedig et al. 2011). To include this effect, we assume the e-pumping to be inefficient (ė = 0) for e ≥ 0.7 (note however that ȧ is not necessarily 0). The e-pumping efficiency for very small and moderate eccentricities (i.e. for e ≲ 0.2) is shown in Fig. 1 and is given by (see Lubow & Artymowicz 1996, 2000)
(8)up to a maximum of ė = 5α−1/2ȧ/a at e ≃ 0.1α1/2. At larger eccentricities (0.1α1/2 ≲ e ≲ 0.2), the m = 2, l = 1 resonance is the strongest contribution to the eccentricity driving and the disc is progressively pushed away as the binary eccentricity increases. In that regime, ė decreases as 1/e. The eccentricity pumping diminishes as 1/e until e ≃ 0.5−0.7, at which point resonances that damp the eccentricity begin to dominate (e.g. Roedig et al. 2011). To include this effect, we assume the e-pumping to be inefficient (ė = 0) for e ≥ 0.7 (note however that ȧ is not necessarily 0). The e-pumping efficiency for very small and moderate eccentricities (i.e. for e ≲ 0.2) is shown in Fig. 1 and is given by (see Lubow & Artymowicz 1996, 2000) 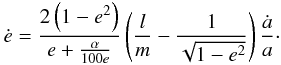 (9)The inner radius of the disc, rin, is determined by the condition that the resonant torque, which tends to push the disc away, overcomes the viscous torque which acts to fill the inner region. Artymowicz & Lubow (1994) estimate from SPH simulations the disc inner radius at different binary eccentricities and for different Reynolds number of the disc gas, ℛ = (H/R)-2α-1 (see Fig. 3 of Artymowicz & Lubow 1994) which we fit with
(9)The inner radius of the disc, rin, is determined by the condition that the resonant torque, which tends to push the disc away, overcomes the viscous torque which acts to fill the inner region. Artymowicz & Lubow (1994) estimate from SPH simulations the disc inner radius at different binary eccentricities and for different Reynolds number of the disc gas, ℛ = (H/R)-2α-1 (see Fig. 3 of Artymowicz & Lubow 1994) which we fit with 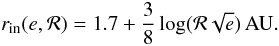 (10)Finally, the variation of the orbital angular momentum in the centre-of-mass frame is given by
(10)Finally, the variation of the orbital angular momentum in the centre-of-mass frame is given by 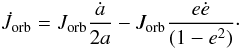 (11)Our model is in reasonable (within a factor two) agreement with the SPH results of Artymowicz et al. (1991), who give ȧ/a ≃ −4.3 × 10-4ΩbMd/Mb and ėe ≃ 1.9 × 10-3ΩbMd/Mb at e = 0.1, for μ = 0.3, α = 0.1, ℛ = 103, with a CB disc extending from r = 1.7a to r = 6a, with a surface density distribution σ ∝ r-1. Our model gives ȧ/a ≃ −2.8 × 10-4ΩbMd/Mb and ėe ≃ 2.5 × 10-3ΩbMd/Mb.
(11)Our model is in reasonable (within a factor two) agreement with the SPH results of Artymowicz et al. (1991), who give ȧ/a ≃ −4.3 × 10-4ΩbMd/Mb and ėe ≃ 1.9 × 10-3ΩbMd/Mb at e = 0.1, for μ = 0.3, α = 0.1, ℛ = 103, with a CB disc extending from r = 1.7a to r = 6a, with a surface density distribution σ ∝ r-1. Our model gives ȧ/a ≃ −2.8 × 10-4ΩbMd/Mb and ėe ≃ 2.5 × 10-3ΩbMd/Mb.
 |
Fig. 1 de/dt in units of dlna/dt as a function of e (Eq. (9)) based on the model of Lubow & Artymowicz (1996, 2000), for a circumbinary disc with a viscosity parameter α = 0.1. The curve is divided in three regions. For eccentricities from 0 to 0.2, our model is strictly valid (red solid curve). For eccentricities from 0.2 to 0.7, the model is extrapolated outside its validity range according to an efficiency decreasing as 1/e (black dotted curve). At higher eccentricities, resonances that damp the eccentricity dominate, so de/dt = 0 (blue dashed curve). |
3.1. Eccentricity gap
Pre-main sequence (MS) and MS systems lack nearly circular orbits at long periods (called the eccentricity gap; see Mathieu 1992, 1994), whereas short-period systems are circularised by tides. Although the eccentricity distribution of pre-MS and MS systems is likely the result of numerous processes such as binary formation, stellar encounters and tides, interaction with a CB disc certainly occurs as well. Discs commonly observed in pre-MS systems are similar to those observed around post-AGB stars (de Ruyter et al. 2006), with masses from 0.004 to 0.3 M⊙. Artymowicz et al. (1991), Artymowicz & Lubow (1994), Mathieu et al. (1995) and Lubow & Artymowicz (1996) suggest that they pump the binary eccentricity, which explains the eccentricity gap. Note however the surprising exception of GW Orionis, a system still embedded in a disc of Md ≈ 0.3 M⊙, with a period of 242 d and an unexpected low eccentricity of e ≈ 0.04 ± 0.06 (Mathieu et al. 1991). Following the evolution of pre-MS with disc-binary interaction is however beyond the scope of this paper.
Note that an eccentricity gap seems also present in post-AGB binaries (see discussion in Sect. 5.2).
4. Modelling post-AGB binaries with circumbinary discs
We introduce the CB-disc properties and apply our model of Sect. 3 to derive the evolution of post-AGB systems in the period-eccentricity plane.
4.1. Circumbinary disc model
 |
Fig. 2 Disc geometry as described in Dullemond et al. (2001). L1, L2 and L3 are the Lagrangian points. rin, R and H are the inner radius, the half angular-momentum radius and the thickness of the disc, respectively. The given radii are indicative. |
Post-AGB disc properties can be derived from SED modelling in the near-IR. Observed disc masses range from about 10-4 to 10-2 M⊙ (Gielen et al. 2007). The relative thickness near the inner edge is H/R = 0.1−0.25 (Dullemond et al. 2001). However, as our model is only valid for thin discs, we assume H/R = 0.1. SED fitting shows that the location of the inner disc edge is very dependent on the opacities used in the radiative transfer calculations. A small difference in e.g. the iron content of dust species or even a contribution of metallic iron strongly impacts on the opacity and hence on the model dimensions needed to fit the observed SEDs (Gielen et al. 2011). So, depending on the adopted abundance of iron, the SED can be fitted with different disc inner radii ranging from about 2 to 10 AU. These values are in good agreement with our predicted inner radius (Eq. (10)) assuming typical separations of post-AGB systems from about 0.5 to 5 AU. The outer radius ranges from about 100 to a few thousand AU (de Ruyter et al. 2006; Gielen et al. 2011) and is taken to be rout = 500 AU. The surface density distribution decreases with distance from the centre of the disc, σ(r) ∝ rδ, with −2 ≲ δ ≲ −1 (de Ruyter et al. 2006). In our model, we choose σ(r) ∝ r-2 such that the half-angular-momentum radius is 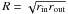 .
.
Since when e = 0 the pumping of the eccentricity is ineffective (ė = 0), we assume that perturbations of the orbit, e.g. due to the CB disc or to stellar pulsation, lead to a minimum eccentricity of 10-3.
4.2. Post-AGB evolution in the e-log P plane with CB disc interaction
Possible range and adopted values of the parameters.
 |
Fig. 3 Evolutionary tracks during the post-AGB phase (black lines) in the e − log P plane including the interaction with a circumbinary disc as described by Eqs. (7) and (9) (see also Fig. 1) with the adopted circumbinary-disc properties of Table 1. The ⋄ symbols are observed post-AGB systems. The blue dashed lines show the final eccentricity corresponding to eccentricity-pumping as given by Eq. (9), modulated by the labelled values (1 corresponds to the adopted parameters). The timescale needed to pump the eccentricity can be estimated from Eq. (12). |
In Fig. 3 we show four evolutionary tracks in the e − log P plane of post-AGB systems, with periods of 100 d, 300 d, 1000 d and 3000 d at the start of the post-AGB, which interact with a CB disc with properties as given in Col. 3 of Table 1. The binary systems are characterised by a reduced mass μ = 0.3 M⊙. Their orbits are initially nearly circular because tides are very efficient during the AGB phase and circularise all systems with P ≲ 2000 d. Longer-period systems can remain eccentric at the start of the post-AGB phase.
The mass and lifetime of the disc are Md = 10-2 M⊙ and td = 2.5 × 104 yr, respectively, which correspond to the highest mass observed and to a lower limit of the disc lifetime. As expected from Eqs. (7) and (9), the e-pumping decreases with increasing period because of the dependence of ė on the orbital period, i.e. ė ∝ aΩb ∝ P−1/3. However, this trend is not observed among the post-AGB stars (see discussion in Sect. 5.2). Nevertheless, our simulations may explain the observed eccentricities of post-AGB systems, except for the three systems with P > 103 d and e > 0.4. Moreover, all the systems are not equally evolved on the post-AGB phase, so some systems may have interacted longer with their CB disc leading to a more eccentric orbit. When extending the disc lifetime to 105 yr, its expected maximum lifetime, our model predicts systems with e = 0.7 at P ~ 103 d (Eq. (12)).
5. Discussion
In this section we discuss the factors which influence the eccentricity-pumping efficiency in our model and the agreement between the predicted and observed eccentricities of post-AGB binaries.
5.1. Parameter study
The time to pump the binary eccentricity from 0 to ef is given by 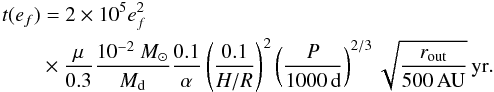 (12)Regarding the possible range of the disc parameters (i.e. Md, td, α, H/R and rout) given in Table 1, the eccentricity-pumping efficiency can be increased by a factor 36 or decreased by a factor 2000 compared to the adopted values. The blue dashed lines in Fig. 3 indicate the final binary eccentricity due to eccentricity-pumping as given by Eqs. (7) and (9) for different disc properties. Each line corresponds to pumping modulated by the labelled value. For example, the line labelled 0.5 corresponds to the case where ė is decreased by a factor 2 compared to our adopted case (labelled 1). It shows that for an efficiency decreased by a factor more than 100, the CB disc has no significant effect on the binary eccentricity any more.
(12)Regarding the possible range of the disc parameters (i.e. Md, td, α, H/R and rout) given in Table 1, the eccentricity-pumping efficiency can be increased by a factor 36 or decreased by a factor 2000 compared to the adopted values. The blue dashed lines in Fig. 3 indicate the final binary eccentricity due to eccentricity-pumping as given by Eqs. (7) and (9) for different disc properties. Each line corresponds to pumping modulated by the labelled value. For example, the line labelled 0.5 corresponds to the case where ė is decreased by a factor 2 compared to our adopted case (labelled 1). It shows that for an efficiency decreased by a factor more than 100, the CB disc has no significant effect on the binary eccentricity any more.
There is a large discrepancy between the values of the viscosity parameter α obtained from magnetohydrodynamic simulations, α ≤ 0.01, and those required to model the observed mass and size of the disc and accretion rate (King et al. 2007, and references therein). Protostellar discs require a small viscosity parameter of α ~ 0.01 because they are cool enough that they are not fully ionised so that magnetorotational instability, which is thought to drive the viscosity mechanism, is significantly suppressed (Gammie 1996). In fully ionised discs such as cataclysmic variables or X-ray binaries, models require higher viscosity, α ~ 0.1−0.4. In our model the viscosity parameter is taken to be α = 0.1. A smaller value of α, e.g. α = 0.01, in better agreement with theoretical models of non-ionised discs, thus decreases the eccentricity-pumping efficiency by a factor 10.
5.2. Our eccentricity-pumping model
Our model can explain the orbits of post-AGB binaries except for the three systems at P > 103 d and e > 0.4 (Fig. 3). Extending the disc lifetime to 105 yr, the expected upper limit, gives enough time for the CB disc to increase the system eccentricity to the observed value. Systems with periods longer than about 2000 d are not efficiently circularised during the AGB phase, so they can start the post-AGB phase in an eccentric orbit. Moreover, as the CB disc is formed during the AGB phase, eccentricity pumping starts before the post-AGB phase. This leads to an underestimate of the binary eccentricity at P ≳ 2000 d. At shorter periods, binary systems enter a CE which circularises the orbit before the system starts its evolution on the post-AGB phase.
These very eccentric systems may initially have been triple systems in which dynamical instabilities led to the collision between two stars or the ejection of one component and to the formation of eccentric binaries (Perets & Kratter 2012).
An eccentricity gap, i.e. a lack of circular systems at long periods, seems present in observed post-AGB binaries with periods longer than 103 d (see Fig. 3) in which tides are inefficient. This gap may remain from the interaction with a CB disc during the pre-MS phase which increased the binary eccentricity (see Sect. 3.1).
There is an important discrepancy between the expected and observed distributions of post-AGB systems in the period-eccentricity plane. Our model predicts systems with eccentricities that decrease with increasing periods while the observed distribution shows the opposite. As discussed before, this discrepancy may partly be explained by an underestimate in our model of the eccentricity at long orbital periods. Tides are also efficient for post-AGB systems with periods shorter than a few hundred days. This would counteract the eccentricity-pumping due to resonances with a CB disc. Moreover, when member of a binary system, kicks applied on the white dwarf at its birth can significantly change the orbital eccentricity. Such kicks are supported by independent observational evidence from globular clusters (Heyl 2008; Fregeau et al. 2009), in which young white dwarfs display higher velocity dispersion than old white dwarfs and main-sequence stars. Izzard et al. (2010) show that a kick can significantly increase the binary eccentricity at the start of the post-AGB phase, especially in long period systems which have smaller orbital velocities so that the effect of kicks on the orbit is larger. Another hypothesis to explain this discrepancy is that the properties of the disc and the binary are correlated in such a way that e-pumping is more efficient in longer-period systems. It would be a surprise if discs that form through wind mass-transfer or remaining from CE ejection are similar. However, our understanding of disc formation is poor, so no a priori correlation can be suggested. None of the observed disc properties are correlated with the binary properties. Nevertheless, it is surprising that no post-AGB stars with a disc are observed in systems with orbital periods shorter than 100 d. From binary evolutionary models, such systems are predicted to exist as post-CE systems and are expected to have periods from a few hours to hundreds of days. As none are observed, CB discs may be very short-lived or unstable at periods shorter than about 100 d.
In our model we do not consider accretion of matter onto the central stars or outflow from the disc. While the effects of such re-accretion are observed in some post-AGB stars (Waters et al. 1992), the disc mass is assumed constant for simplicity. However, as discussed in Sect. 2.3, post-AGB systems are observed at least 104 yr after they left the AGB phase. The inferred disc masses thus represent a lower limit of their initial masses. Note that the most important effect of re-accretion is to slow down the evolution along the post-AGB phase. It then takes longer for the central star to become hot enough to efficiently evaporate the disc gas due to ultraviolet radiation compared to single star evolution where no accretion takes place. Another consequence of re-accretion is the presence of gas in the gap between the binary system and the disc, near the corotation region with the binary. Corotational resonances strongly damp the eccentricity (Artymowicz 1993). However, it is difficult to evaluate this effect on the eccentricity pumping. Regarding the very low density of gas streams that penetrate the gap compared to the density at the inner edge of the disc, the damping effect is expected to be small. Further investigations through SPH simulations are required to confirm this assumption.
The conclusions reached in this paper not only concern post-AGB systems, but a variety of classes of post-mass transfer systems such as barium stars, S stars, subgiant CH and carbon-enriched metal-poor (CEMP) binaries, which we observe long after mass transfer finished. If CB discs play an important role in the evolution of post-AGB systems, they are also relevant for these classes of stars. Their periods and eccentricities similar to post-AGB stars support an identical eccentricity-pumping mechanism.
6. Conclusions
We evaluate in this paper the resonant interaction between a circumbinary disc and its central binary. Stable dust discs are detected in a large fraction of post-AGB stars and are known to be closely related to binarity. Circumbinary discs are thought to strongly alter the evolution of the binary system because of resonant interactions and re-accretion from the circumbinary disc. Resonant interactions with a circumbinary disc transfer angular momentum from the binary orbit to the disc and increase the binary eccentricity. We use the model described by Lubow & Artymowicz (1996) with the disc properties derived from the observed SED of post-AGB stars. Re-accretion of gas deficient in refractory elements, because they condense in grains maintained in the disc by radiation pressure, is responsible for the depletion patterns observed at the surface of numerous post-AGB systems and slows the evolution of the post-AGB star.
We estimate binary post-AGB lifetimes to range from 2.5 × 104 yr to 105 yr which are long compared to single-star models that predict only 103 to 104 yr. Even on these short timescales, the interaction with a circumbinary disc can significantly increase the eccentricity of post-AGB binary stars. Although the disc lifetime represents the major uncertainty, our model can explain the eccentricities of post-AGB systems even for the lower limit of the disc lifetime. Three long-period systems show higher eccentricities than expected and require more efficient eccentricity-pumping. However, extending the disc lifetime to its expected maximum lifetime of 105 yr solves the problem. On the other hand, our model underestimates the eccentricities of long-period post-AGB stars because we assume all systems to have initially circular orbits while systems with periods longer than 2000 d are not efficiently circularised by tides during the AGB phase. Moreover, the circumbinary disc is formed during the AGB phase so that eccentricity-pumping already operates on the AGB. We conclude that our model and parameter study indicates that disc-binary resonant interaction is a very viable process which can pump-up the eccentricities of post-AGB stars to observed values.
Finally, Ba, S, CH and CEMP stars experience a similar evolution than post-AGB stars and show similar period and eccentricity distributions. This suggests that interaction with a circumbinary disc is also a key mechanism in the evolution of Ba, S, CH and CEMP stars.
Acknowledgments
T.D. would like to thank Thomas Masseron, Sophie Van Eck, Philipp Podsiadlowski, Clio Gielen, Nadya Gorlova and Steve Lubow for many useful discussions. Warm thanks are addressed to Adam Frankowski for his highlights while starting this project. Finally, T.D. thanks Pawel Artymowicz, the referee of this paper, who helped improve its quality. This work has been partially funded by an Action de Recherche Concertée from the Direction générale de l’enseignement non obligatoire et de la Recherche Scientifique – Direction de la Recherche Scientifique – Communauté Française de Belgique.
References
- Angeloni, R., Contini, M., Ciroi, S., & Rafanelli, P. 2007, A&A, 472, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Artymowicz, P. 1993, ApJ, 419, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Artymowicz, P., Clarke, C. J., Lubow, S. H., & Pringle, J. E. 1991, ApJ, 370, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Bloecker, T. 1995, A&A, 299, 755 [NASA ADS] [Google Scholar]
- Bonačić Marinović, A. A., Glebbeek, E., & Pols, O. R. 2008, A&A, 480, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bujarrabal, V., Castro-Carrizo, A., Alcolea, J., & Neri, R. 2005, A&A, 441, 1031 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chesneau, O., Meilland, A., Banerjee, D. P. K., et al. 2011, A&A, 534, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Costero, R., Tapia, M., Méndez, R. H., et al. 1986, Rev. Mex. Astron. Astrofis., 13, 149 [NASA ADS] [Google Scholar]
- de Ruyter, S., van Winckel, H., Maas, T., et al. 2006, A&A, 448, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Val-Borro, M., Karovska, M., & Sasselov, D. 2009, ApJ, 700, 1148 [NASA ADS] [CrossRef] [Google Scholar]
- Dermine, T., Jorissen, A., Siess, L., & Frankowski, A. 2009, A&A, 507, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deroo, P., Acke, B., Verhoelst, T., et al. 2007, A&A, 474, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Frankowski, A., & Jorissen, A. 2007, Balt. Astron., 16, 104 [NASA ADS] [Google Scholar]
- Frankowski, A., & Tylenda, R. 2001, A&A, 367, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fregeau, J. M., Richer, H. B., Rasio, F. A., & Hurley, J. R. 2009, ApJ, 695, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Gammie, C. F. 1996, ApJ, 457, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Gänsicke, B. T., Marsh, T. R., Southworth, J., & Rebassa-Mansergas, A. 2006, Science, 314, 1908 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gesicki, K., Zijlstra, A. A., Szyszka, C., et al. 2010, A&A, 514, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gielen, C., van Winckel, H., Waters, L. B. F. M., Min, M., & Dominik, C. 2007, A&A, 475, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gielen, C., van Winckel, H., Min, M., Waters, L. B. F. M., & Lloyd Evans, T. 2008, A&A, 490, 725 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gielen, C., van Winckel, H., Reyniers, M., et al. 2009, A&A, 508, 1391 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gielen, C., Bouwman, J., van Winckel, H., et al. 2011, A&A, 533, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldreich, P., & Tremaine, S. 1979, ApJ, 233, 857 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Heyl, J. S. 2008, MNRAS, 385, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenbach, D. J., Yorke, H. W., & Johnstone, D. 2000, Protostars and Planets IV, 401 [Google Scholar]
- Iben, Jr., I., & Livio, M. 1993, PASP, 105, 1373 [Google Scholar]
- Ivezic, Z., & Elitzur, M. 1997, MNRAS, 287, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Izumiura, H., Noguchi, K., Aoki, W., et al. 2008, ApJ, 682, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Izzard, R. G., Dermine, T., & Church, R. P. 2010, A&A, 523, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jura, M., Balm, S. P., & Kahane, C. 1995, ApJ, 453, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Kahane, C., & Jura, M. 1996, A&A, 310, 952 [NASA ADS] [Google Scholar]
- Kashi, A., & Soker, N. 2011, MNRAS, 417, 1466 [NASA ADS] [CrossRef] [Google Scholar]
- Kilic, M., Kowalski, P. M., Reach, W. T., & von Hippel, T. 2009, ApJ, 696, 2094 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R., Pringle, J. E., & Livio, M. 2007, MNRAS, 376, 1740 [NASA ADS] [CrossRef] [Google Scholar]
- Lamers, H. J. G. L. M., Zickgraf, F.-J., de Winter, D., Houziaux, L., & Zorec, J. 1998, A&A, 340, 117 [NASA ADS] [Google Scholar]
- Lubow, S. H., & Artymowicz, P. 1996, in NATO ASIC Proc. 477: Evolutionary Processes in Binary Stars, eds. R. A. M. J. Wijers, M. B. Davies, & C. A. Tout, 53 [Google Scholar]
- Lubow, S. H., & Artymowicz, P. 2000, Protostars and Planets IV, 731 [Google Scholar]
- Maas, T., Van Winckel, H., & Lloyd Evans, T. 2005, A&A, 429, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mastrodemos, N., & Morris, M. 1998, ApJ, 497, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Mathieu, R. D. 1992, in Binaries as Tracers of Star Formation, eds. A. Duquennoy, & M. Mayor, 155 [Google Scholar]
- Mathieu, R. D. 1994, ARA&A, 32, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Mathieu, R. D., Adams, F. C., & Latham, D. W. 1991, AJ, 101, 2184 [NASA ADS] [CrossRef] [Google Scholar]
- Mathieu, R. D., Adams, F. C., Fuller, G. A., et al. 1995, AJ, 109, 2655 [NASA ADS] [CrossRef] [Google Scholar]
- Meilland, A., Stee, P., Vannier, M., et al. 2007, A&A, 464, 59 [Google Scholar]
- Miszalski, B., Mikołajewska, J., Köppen, J., et al. 2011, A&A, 528, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mohamed, S., & Podsiadlowski, P. 2010, in Amer. Inst. Phys. Conf. Ser., eds. V. Kologera, & M. van der Sluys, Conf. Ser., 1314, 51 [Google Scholar]
- Netolický, M., Bonneau, D., Chesneau, O., et al. 2009, A&A, 499, 827 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nordhaus, J., & Blackman, E. G. 2006, MNRAS, 370, 2004 [NASA ADS] [CrossRef] [Google Scholar]
- Perets, H. B., & Kratter, K. M. 2012, ApJ, 760, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Joss, P. C., & Hsu, J. J. L. 1992, ApJ, 391, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Pollard, K. H., & Cottrell, P. L. 1995, in Astrophysical Applications of Stellar Pulsation, eds. R. S. Stobie, & P. A. Whitelock, IAU Colloq., 155, ASP Conf. Ser., 83, 409 [Google Scholar]
- Pols, O. R., Karakas, A. I., Lattanzio, J. C., & Tout, C. A. 2003, in ASP Conf. Ser., eds. R. L. M. Corradi, J. Mikolajewska, & T. J. Mahoney, 303, 290 [Google Scholar]
- Reyniers, M., & van Winckel, H. 2007, A&A, 463, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roedig, C., Dotti, M., Sesana, A., Cuadra, J., & Colpi, M. 2011, MNRAS, 415, 3033 [NASA ADS] [CrossRef] [Google Scholar]
- Sandquist, E. L., Taam, R. E., Chen, X., Bodenheimer, P., & Burkert, A. 1998, ApJ, 500, 909 [NASA ADS] [CrossRef] [Google Scholar]
- Schuerman, D. W. 1972, Ap&SS, 19, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Sion, E. M., Holberg, J. B., Oswalt, T. D., McCook, G. P., & Wasatonic, R. 2009, AJ, 138, 1681 [NASA ADS] [CrossRef] [Google Scholar]
- Soker, N. 2000, A&A, 357, 557 [NASA ADS] [Google Scholar]
- Sytov, A. Y., Bisikalo, D. V., Kaigorodov, P. V., & Boyarchuk, A. A. 2009, Astron. Rep., 53, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Theuns, T., & Jorissen, A. 1993, MNRAS, 265, 946 [NASA ADS] [CrossRef] [Google Scholar]
- Theuns, T., Boffin, H. M. J., & Jorissen, A. 1996, MNRAS, 280, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- van Aarle, E., van Winckel, H., Lloyd Evans, T., et al. 2011, A&A, 530, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Rensbergen, W., de Greve, J. P., Mennekens, N., Jansen, K., & de Loore, C. 2011, A&A, 528, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Winckel, H. 2003, ARA&A, 41, 391 [NASA ADS] [CrossRef] [Google Scholar]
- van Winckel, H., Waelkens, C., & Waters, L. B. F. M. 2000, in The Carbon Star Phenomenon, ed. R. F. Wing, IAU Symp., 177, 285 [Google Scholar]
- Van Winckel, H., Lloyd Evans, T., Reyniers, M., Deroo, P., & Gielen, C. 2006, Mem. Soc. Astron. Italiana, 77, 943 [Google Scholar]
- van Winckel, H., Lloyd Evans, T., Briquet, M., et al. 2009, A&A, 505, 1221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Waters, L. B. F. M., Trams, N. R., & Waelkens, C. 1992, A&A, 262, L37 [NASA ADS] [Google Scholar]
- Waters, L. B. F. M., Beintema, D. A., Zijlstra, A. A., et al. 1998, A&A, 331, L61 [NASA ADS] [Google Scholar]
- Weidenschilling, S. J., & Jackson, A. A. 1993, Icarus, 104, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Yasui, C., Kobayashi, N., Tokunaga, A. T., Saito, M., & Tokoku, C. 2010, ApJ, 723, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 de/dt in units of dlna/dt as a function of e (Eq. (9)) based on the model of Lubow & Artymowicz (1996, 2000), for a circumbinary disc with a viscosity parameter α = 0.1. The curve is divided in three regions. For eccentricities from 0 to 0.2, our model is strictly valid (red solid curve). For eccentricities from 0.2 to 0.7, the model is extrapolated outside its validity range according to an efficiency decreasing as 1/e (black dotted curve). At higher eccentricities, resonances that damp the eccentricity dominate, so de/dt = 0 (blue dashed curve). |
| In the text | |
 |
Fig. 2 Disc geometry as described in Dullemond et al. (2001). L1, L2 and L3 are the Lagrangian points. rin, R and H are the inner radius, the half angular-momentum radius and the thickness of the disc, respectively. The given radii are indicative. |
| In the text | |
 |
Fig. 3 Evolutionary tracks during the post-AGB phase (black lines) in the e − log P plane including the interaction with a circumbinary disc as described by Eqs. (7) and (9) (see also Fig. 1) with the adopted circumbinary-disc properties of Table 1. The ⋄ symbols are observed post-AGB systems. The blue dashed lines show the final eccentricity corresponding to eccentricity-pumping as given by Eq. (9), modulated by the labelled values (1 corresponds to the adopted parameters). The timescale needed to pump the eccentricity can be estimated from Eq. (12). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


