EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 550 (February 2013) A&A, 550 (2013) A28 Full HTML
Free Access
Issue
A&A
Volume 550, February 2013
Article Number A28
Number of page(s) 5
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/201220761
Published online 21 January 2013

© ESO, 2013

1. Introduction

Magnesium plays an important role in studies of cool stars. It affects atmospheric structure by donating free electrons and with a significant contribution of Mg i photoionization to the ultraviolet (UV) opacity. Magnesium is a key element for studying the history of α-process nucleosynthesis in the Universe. The Mg/Fe abundance ratio of metal-poor (MP) stars carries information on the initial mass function and star formation rate in our Galaxy, dwarf galaxies of the Local Group, and distant galaxies (see Tolstoy et al. 2009, for references). Magnesium is one of the best observed elements in A to late-type stars, though it is represented by only a few lines of neutral atoms in the visual spectral range. The Mg ib lines at 5167, 5172, and 5183 Å can be measured over a wide range of metallicity from super-solar values down to [Fe/H]1 = –5.5 (Frebel et al. 2005) and over a wide range of effective temperature from 3000 K up to 12 000–13 000 K (Przybilla et al. 2001). In stellar atmospheres with Teff > 4500 K, neutral magnesium is a minority species, and its statistical equilibrium (SE) can easily deviate from thermodynamic equilibrium due to deviations in the mean intensity of ionizing radiation from the Planck function. Since the end of the 1960s, the problem of nonlocal thermodynamic equilibrium (NLTE) line formation for Mg i in stellar atmospheres was considered in many studies. The model atoms of Mg i have been created by Athay & Canfield (1969), Lemke & Holweger (1987), Mauas et al. (1988), Gigas (1988), Carlsson et al. (1992), Mashonkina et al. (1996), Zhao et al. (1998), Gratton et al. (1999), Idiart & Thévenin (2000), Przybilla et al. (2001), Mishenina et al. (2004), and Merle et al. (2011).

This study was motivated by the recent detailed quantum mechanical calculations of Barklem et al. (2012, hereafter, BBSGF) for inelastic Mg+H collisions. The role of inelastic collisions with neutral hydrogen atoms in establishing the SE of atoms in cool stars has been debated for decades. Steenbock & Holweger (1984) implemented the classical Drawin (1968, 1969) formula to calculate H i collision rates, and it suggests that their influence is comparable to electron impacts. Up recent times, laboratory measurements and/or detailed quantum mechanical calculations of collisions with H i atoms have only been available for Na i and Li i (see Barklem et al. 2011, for references). Based on these data, the Drawin formalism has been criticized for not providing a realistic description of the physics involved and overestimating the collision rates. Interestingly, spectroscopic studies of Na i also suggest that Drawin’s formula strongly overestimates the Na+H collision rates. For example, Allende Prieto et al. (2004) has reproduced the center-to-limb variation of the solar Na i 6160Å line with pure electronic collisions. At the same time, the need for a thermalizing process not involving electrons in the atmospheres of, in particular, very metal-poor stars, has been indicated by many NLTE line-formation studies (see Mashonkina et al. 2011, and references therein).

The main goal of this paper is to investigate how the use of recent data of BBSGF on Mg+H collisions influences the NLTE results for Mg i. We started from an analysis of the solar Mg i lines, for which the departures from LTE are small, and the derived abundances are not influenced by H i collision treatment. It was found that the two lines Mg i 4703 Å and Mg i 5528 Å give significantly lower abundance compared with that from the Mg ib lines and also compared with the meteoritic value. To understand the source of discrepancies and to differentiate the effects of oscillator strengths and van der Waals broadening, we moved to the hotter A-type stars.

The paper is organized as follows. All our results are based on the NLTE line formation for Mg i. The model atom of magnesium and the used atomic data are described in Sect. 2. In Sect. 3, we derive abundances from individual Mg i lines in the solar spectrum and in the spectra of four well studied A-type stars. Section 4 investigates the effect of Mg+H collisions on the SE of magnesium and NLTE abundances for the two very metal-poor ([Fe/H]  < −2, VMP) stars. We compare the NLTE results from calculations using Mg+H collision data of BBSGF and using the classical Drawinian rates. The NLTE abundance corrections are presented for lines of Mg i in the grid of metal-poor model atmospheres. Our conclusions are given in Sect. 5.

2. Method of NLTE calculations for magnesium

This study uses a comprehensive model atom that includes 85 levels of Mg i, 2 levels of Mg ii, and the ground state of Mg iii. For Mg i, we rely on the model atom produced by Zhao et al. (1998), who carefully investigated atomic data on the energy levels, transition probabilities, and photoionization cross sections. In this study, the calculation of collisional rates was updated. For electron-impact excitation, we used rate coefficients of Mauas et al. (1988), where available, and the same recipes as in Zhao et al. (1998) for the remaining transitions. Ionization by electronic collisions was calculated from the Seaton (1962) formula with a mean Gaunt factor set equal to 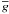= 0.1 for Mg i and to 0.2 for Mg ii. For H i impact excitations and charge transfer processes Mg i + H i  ↔  Mg ii + H−, rate coefficients were taken from the detailed quantum mechanical calculations of BBSGF.

Singly ionized magnesium is represented in our model atom by the two levels 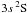and 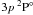. Their energies and gf-value of the resonance transition were taken from the NIST database2 (Ralchenko et al. 2008). Photoionization is treated by utilizing Opacity Project cross-sections as available through the TOPBASE database3.

To solve the coupled radiative transfer and statistical equilibrium equations, we used a revised version of the DETAIL program (Butler & Giddings 1985). The update was described by Przybilla et al. (2011). Calculations were performed with plane-parallel (1D), LTE, and blanketed model atmospheres computed for given stellar parameters. These are the MAFAGS-OS models by Grupp et al. (2009) for the Sun and VMP stars, the LLMODELS models (Shulyak et al. 2004) by D. Shulyak for the three A-type stars, and the model by R. Kurucz4 for Sirius.

Table 1 lists the lines of Mg i used in abundance analyses for MP stars, together with the adopted line data. Oscillator strengths were taken from the laboratory measurements of Aldenius et al. (2007) for the Mg ib lines, calculations of Chang & Tang (1990) for Mg i 4703 Å and 5528 Å, and calculations of Tachiev & Froese Fischer for Mg i 4571 Å as presented in the NIST database. An accuracy of predicted gf-values can only be estimated for the Mg ib lines, where the difference between calculations of Chang & Tang (1990) and measurements of Aldenius et al. (2007) amounts to 0.06 dex. The van der Waals broadening constants Γ6 were computed with cross-sections and velocity parameters from Anstee & O’Mara (1995) and Barklem & O’Mara (1997). Hereafter, these papers by Anstee, Barklem, and O’Mara are referred to as the ABO theory. The quadratic Stark effect broadening constants Γ4 were taken from Dimitrijevic & Sahal-Brechot (1996), except for Mg i 4571 Å, with Γ4 from the VALD database (Kupka et al. 1999).

Table 1

Mg i line data.

Table 2

Magnesium NLTE and LTE abundances log AMg of the Sun and hot stars.

3. Mg i lines in the Sun and A-type stars

In the galactic chemical evolution studies, the stellar sample covers, as a rule, a range of metallicities of more than 3 dex. The lines Mg i 4703 and 5528 Å are favorites for abundance determinations of mildly MP ([Fe/H]  >  −2) stars; however, these lines cannot be measured in hyper metal-poor stars, with [Fe/H]  <  −4.5, where one relies on the Mg ib lines. One needs, therefore, to prove that the use of different Mg i lines does not produce a systematic shift in derived abundance between various metallicity stars. In the beginning, we checked whether the lines listed in Table 1 give consistent abundances for the Sun, when employing the most up-to-date theoretical and experimental atomic data available so far. The observed solar spectrum was taken from the Kitt Peak Solar Flux Atlas (Kurucz et al. 1984). We used the MAFAGS-OS solar model atmosphere with Teff/log    g/[Fe/H] = 5780/4.44/0. Microturbulence velocity was fixed at Vmic = 0.9 km s-1. Element abundances from individual lines were determined from line-profile fitting using the code SIU (Reetz 1991). The obtained results are presented in Table 2. We find that (i) the NLTE effects are minor for each investigated line; (ii) abundances derived from the Mg ib and Mg i 4571 Å lines are consistent with the meteoritic value log AMg,met5  =  −4.45 (Lodders et al. 2009); and (iii) Mg i 4703 and 5528 Å give significantly lower abundances, by 0.24 dex and 0.15 dex, respectively. These discrepancies can arise from the uncertainty in either gf-values or/and Γ6 values. The influence of atmospheric inhomogeneities on derived solar Mg abundance was evaluated by Asplund (2005) as −0.03 dex.

To test gf-values, we chose the three well studied stars Sirius, Vega, and 21 Peg (Table 3), where the Mg i lines are insensitive to Γ6 variation. The departures from LTE are expected to be greater in hot atmospheres than in the solar one. Thus, analysis of the Mg i lines in the A-type stars also tests our NLTE method. For each star, its stellar parameters and observed equivalent widths indicated in Table 2 and used to determine element abundances were taken from a common source cited in Table 3. We find that, for each star, (i) the NLTE effects are minor for Mg i 4703 Å and 5528 Å; (ii) abundances from these two lines are consistent within 0.02 dex, in contrast to the solar case; (iii) departures from LTE for the Mg ib lines are significant, so that the NLTE abundance correction ΔNLTE = log εNLTE − log εLTE ranges between −0.14 dex and −0.22 dex for different stars; and (iv) the difference in NLTE abundance between the Mg ib and Mg i 4703, 5528 Å lines is smaller compared to that for the Sun. It is worth noting that it does not exceed 0.05 dex when applying gf-values from a single source (Chang & Tang 1990) for all the investigated lines.

Table 3

Stellar parameters of selected stars.

Once we return to the Sun, the abundance discrepancies found between different solar lines of Mg i can only be caused by the van der Waals damping treatment, and they are removed by reducing the Γ6(ABO) values by 0.3 dex and 0.2 dex for Mg i 4703 Å and Mg i 5528 Å, respectively. The use of such corrections was justified by analysis of the Mg i lines in the cool subdwarf star HD 103095 (Table 3). We obtained the difference (Mg i 4703, 5528 – Mg ib) = −0.18 dex, when using Γ6(ABO), and a significantly lower value of  + 0.02 dex, with the above corrections. Table 2 presents Mg abundances of the late A-type star HD 32115, where Mg i 4703 Å and 5528 Å are less sensitive to Γ6 variation. Both lines give identical abundances at log AMg =  −4.51, and the difference (Mg i 4703, 5528 – Mg ib) reduces to −0.07 dex, when employing the corrected Γ6-values.

4. Influence of Mg+H collisions on the NLTE results for metal-poor stars

thumbnail Fig. 1

Departure coefficients for selected levels of Mg i as a function of log τ5000 in the model atmosphere 4600/1.60/−2.56 from the calculations with pure electronic collisions (top panel) and with H i collisions taken into account following BBSGF (bottom panel). Tick marks indicate the locations of line center optical depth unity for the Mg i lines 5172 Å (1) and 5528 Å (2).
Open with DEXTER

The departures from LTE for Mg i grow toward lower metallicity due to the decreasing number of electrons donated by metals, which results in decreasing collision rates and also due to decreasing the UV opacity, which results in increasing photoionization rates. The largest uncertainties in NLTE results are caused by the uncertainties in collisional data. Here, we apply for the first time Mg+H collision data of Barklem et al. (2012) to calculate the SE of magnesium in two well studied VMP stars. HD 84937 represents the hot end of the stars that evolve on time scales comparable to the Galaxy lifetime. HD 122563, in contrast, is a cool giant (Table 3).

Figure 1 shows the departure coefficients 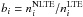for the Mg i levels in the model atmosphere 4600/1.60/−2.56 from calculations with two different treatments of collisional rates. Here, 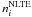and 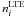are the SE and thermal (Saha-Boltzmann) number densities, respectively. In the line-formation layers, the Mg i levels have fewer populations compared with the thermal ones, independent of collision treatment; however, the magnitude of departures from LTE is significantly smaller in the case of included Mg+H collisions than for the case of pure electronic collisions. The main NLTE mechanism is overionization caused by the superthermal radiation of a nonlocal origin below the thresholds of the and levels. When taking Mg+H collisions into account, the charge transfer processes Mg i + H i  ↔  Mg ii + H− establish close collisional coupling of excited terms of Mg i to the ground state of Mg ii and reduce their underpopulation. This effect is redistributed to the lower excitation levels via the bound-bound transitions, including the H i impact excitation and de-excitation processes.

Table 4

Magnesium LTE and NLTE abundances of HD 84937 and HD 122563 from calculations with different treatments of H i collisions.

Table 4 presents abundances determined from individual lines of Mg i under different assumptions for line formation. It is worth noting that results for Mg i 4703 Å and 5528 Å do not depend on the van der Waals damping treatment because both lines are weak. For each star, NLTE leads to depleted absorption in the lines at 4571, 4703, and 5528 Å due to overall overionization of Mg i in the atmospheric layers, where they form. As expected, including Mg+H collisions leads to weaker NLTE effects compared with that for pure electronic collisions, such that ΔNLTE reduces by 0.06–0.23 dex for different lines. For HD 122563, the NLTE effects have different signs for Mg i 4703 Å and Mg i 5528 Å, resulting in a remarkable consistency of abundances derived from these two lines.

thumbnail Fig. 2

Best NLTE (continuous curve) and LTE (dotted curve) fits of the Mg i 5172 Å line in HD 122563 (bold dots). The NLTE calculations were performed with log AMg =  −6.95, while the LTE ones with a 0.02 dex higher value. Mg+H collisions are treated following BBSGF. Our theoretical flux profiles were convolved with a profile that combines instrumental broadening with a Gaussian profile and broadening by macroturbulence with a radial-tangential profile. The macroturbulence values are 4.7 km s-1 for the NLTE and 3.8 km s-1 for the LTE fits.
Open with DEXTER

Despite the low Mg abundance, the Mg ib lines are fairly strong in both VMP stars. For each line, its core forms in the layers, where the departure coefficient of the upper level 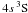drops rapidly (Fig. 1) due to photon escape from the Mg ib triplet lines themselves, resulting in dropping the line source function below the Planck function and enhanced absorption in the line core (Fig. 2). In contrast, in the line wings, absorption is weaker compared with the LTE case due to overall overionization in deep atmospheric layers. The combined effect is that the obtained NLTE abundances are lower than the corresponding LTE ones and lower than those from the other lines, independent of collisional rate treatment. The difference Δlog ε(Mg i 4703, 5528 – Mg ib) is less in the case of Mg+H collisions included than in the case of pure electronic collisions and amounts to 0.09 dex for HD 84937 and 0.12 dex for HD 122563. For LTE abundances from the Mg ib lines, we used EWs, because their profiles cannot be fitted at the LTE assumption. Despite this fact, the obtained LTE abundances are consistent within 0.05 dex with those from the other lines.

Our calculations show that inelastic collisions with H i atoms as treated by BBSGF produce significant thermalization effect on the SE of Mg i in the atmospheres of VMP stars and improve Mg abundance determinations compared with the case of pure electronic collisions. To understand the remaining discrepancies between different lines, one probably needs to go beyond the 1D analysis. The models based on hydrodynamical calculations (3D models) show, on average, lower temperatures outside log τ5000 =  −1 compared with those in the corresponding 1D model, for example, by 1000 K at log τ5000 =  −2 in the 4858/2.2/−3 model, according to Collet et al. (2007). For VMP giants, these are exactly the layers where the line core of the Mg ib lines forms.

Table 5

NLTE abundance corrections (dex) for lines of Mg i from calculations with Mg+H collision rates of BBSGF and with the Drawinian rates scaled by a factor of SH = 0.1 (D0.1).

For most atoms, the formalism of Drawin (1968, 1969) is still widely applied to simulate an additional source of thermalization in the atmospheres of cool stars by parametrized H i collisions. For Mg i, Barklem et al. (2012) compared in their Fig. 1 the quantum scattering rate coefficients at T = 6000 K with the results of the Drawin formula for five common bound-bound transitions. The Drawin/BBSGF rate ratio is close to unity for the – transition, but the Drawinian rates are one to four orders of magnitude higher for the remaining transitions. However, relatively high rates compared to those for excitation were obtained by BBSGF for the charge transfer processes. We find that they are higher than the Drawinian rates for ionization from the excited levels above , especially from the state, where the difference is about four orders of magnitude at T = 6000 K. It is worth noting that the Drawin/BBSGF rate ratios are only weakly sensitive to temperature variation.

We employed the Drawinian rates scaled by a factor of SH = 0.1 to determine the magnesium abundances of the investigated stars (Table 4). The changes in collisional rates result in different effects for different lines in different stars. For example, using accurate Mg+H collision data and scaled Drawinian rates leads to very similar results for Mg i 4571, 4703, and 5528 Å in the model 6350/4.09/−2.08. For the cool giant model, the departures from LTE are greater when applying the BBSGF rates. However, nowhere does the difference between using these two recipes exceed 0.1 dex. This is smaller than or similar to a line-to-line scatter for stellar abundance determinations including the present one.

The NLTE calculations were performed for a small grid of model atmospheres with hydrogenic collisions taken into account following BBSGF and Drawin (1968, 1969). The obtained NLTE corrections are presented in Table 5. Their inspection will help the user decide whether the Mg abundances determined earlier using the Drawinian rates should be revised. This depends on which spectral lines were employed in the analysis and what the range of stellar parameters was.

5. Conclusions

For each of four investigated A-type stars, using gf-values of Chang & Tang (1990) leads to consistency within 0.05 dex between NLTE abundances from Mg i 4703 Å, 5528 Å, and Mg ib. The difference between different lines increases up to 0.11 dex, when employing experimental gf-values of Aldenius et al. (2007) for the Mg ib lines. We recommend applying the corrections Δlog Γ6 =  −0.3 and −0.2 for Mg i 4703 Å and 5528 Å, respectively, to the ABO van der Waals damping constants, to remove the abundance discrepancy between different solar Mg i lines.

Inelastic collisions with H i atoms as treated by Barklem et al. (2012) serve as an efficient thermalizing process for the SE of Mg i in the atmospheres of metal-poor stars. The use of new collisional data improves Mg abundance determinations for HD 84937 and HD 122563, though it does not completely remove the difference in abundance between different lines.

1

In the classical notation, where [X/H] = log    (NX/NH)star − log    (NX/NH)Sun.

5

log AA = log NA/NH.

Acknowledgments

L.M. thanks Paul Barklem for initiating this study and providing the Γ6 value for Mg i 4571 Å. This study is supported by the Ministry of education and science of Russian Federation, project 8529 and the RF President with a Leading Scientific Schools grant 3602.2012.2.

References

  1. Aldenius, M., Tanner, J. D., Johansson, S., Lundberg, H., & Ryan, S. G. 2007, A&A, 461, 767 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Allende Prieto, C., Asplund, M., & Fabiani Bendicho, P. 2004, A&A, 423, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Anstee, S. D., & O’Mara, B. J. 1995, MNRAS, 276, 859 [NASA ADS] [CrossRef] [Google Scholar]
  4. Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
  5. Athay, R. G., & Canfield, R. C. 1969, ApJ, 156, 695 [NASA ADS] [CrossRef] [Google Scholar]
  6. Barklem, P. S., & O’Mara, B. J. 1997, MNRAS, 290, 102 [NASA ADS] [CrossRef] [Google Scholar]
  7. Barklem, P. S., Belyaev, A. K., Guitou, M., et al. 2011, A&A, 530, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Barklem, P. S., Belyaev, A. K., Spielfiedel, A., Guitou, M., & Feautrier, N. 2012, A&A, 541, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Butler, K., & Giddings, J. 1985, Newsletter on the analysis of astronomical spectra, No. 9, University of London [Google Scholar]
  10. Carlsson, M., Rutten, R. J., & Shchukina, N. G. 1992, A&A, 253, 567 [NASA ADS] [Google Scholar]
  11. Chang, T. N., & Tang, X. 1990, J. Quant. Spec. Radiat. Transf., 43, 207 [NASA ADS] [CrossRef] [Google Scholar]
  12. Collet, R., Asplund, M., & Trampedach, R. 2007, A&A, 469, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Dimitrijevic, M. S., & Sahal-Brechot, S. 1996, A&AS, 117, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Drawin, H.-W. 1968, Z. Phys., 211, 404 [Google Scholar]
  15. Drawin, H. W. 1969, Z. Phys., 225, 483 [Google Scholar]
  16. Fossati, L., Ryabchikova, T., Bagnulo, S., et al. 2009, A&A, 503, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Fossati, L., Ryabchikova, T., Shulyak, D. V., et al. 2011, MNRAS, 417, 495 [NASA ADS] [CrossRef] [Google Scholar]
  18. Frebel, A., Aoki, W., Christlieb, N., et al. 2005, Nature, 434, 871 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  19. Gigas, D. 1988, A&A, 192, 264 [NASA ADS] [Google Scholar]
  20. Gratton, R. G., Carretta, E., Eriksson, K., & Gustafsson, B. 1999, A&A, 350, 955 [NASA ADS] [Google Scholar]
  21. Grupp, F., Kurucz, R. L., & Tan, K. 2009, A&A, 503, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Idiart, T., & Thévenin, F. 2000, ApJ, 541, 207 [NASA ADS] [CrossRef] [Google Scholar]
  23. Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
  24. Kurucz, R. L., Furenlid, I., Brault, J., & Testerman, L. 1984, Solar flux atlas from 296 to 1300 nm (New Mexico: National Solar Observatory) [Google Scholar]
  25. Lemke, M., & Holweger, H. 1987, A&A, 173, 375 [NASA ADS] [Google Scholar]
  26. Lodders, K., Plame, H., & Gail, H.-P. 2009, in Landolt-Börnstein – Group VI Astronomy and Astrophysics Numerical Data and Functional Relationships in Science and Technology Volume 4B: Solar System, ed. J. E. Trümper, 44 [Google Scholar]
  27. Mashonkina, L. I., Shimanskaya, N. N., & Sakhibullin, N. A. 1996, Astron. Rep., 40, 187 [NASA ADS] [Google Scholar]
  28. Mashonkina, L., Korn, A. J., & Przybilla, N. 2007, A&A, 461, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Mashonkina, L., Gehren, T., Shi, J.-R., Korn, A. J., & Grupp, F. 2011, A&A, 528, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Mauas, P. J., Avrett, E. H., & Loeser, R. 1988, ApJ, 330, 1008 [NASA ADS] [CrossRef] [Google Scholar]
  31. Merle, T., Thévenin, F., Pichon, B., & Bigot, L. 2011, MNRAS, 418, 863 [NASA ADS] [CrossRef] [Google Scholar]
  32. Mishenina, T. V., Soubiran, C., Kovtyukh, V. V., & Korotin, S. A. 2004, A&A, 418, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Przybilla, N., Butler, K., Becker, S. R., & Kudritzki, R. P. 2001, A&A, 369, 1009 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Przybilla, N., Nieva, M.-F., & Butler, K. 2011, J. Phys. Conf. Ser., 328, 012015 [NASA ADS] [CrossRef] [Google Scholar]
  35. Ralchenko, Y. A., Kramida, E., Reader, J., & Team, N. A. 2008, NIST Atomic Spectra Database (version 3.1.5) (USA) [Google Scholar]
  36. Reetz, J. K. 1991, Diploma Thesis, Universität München [Google Scholar]
  37. Seaton, M. J. 1962, Atomic and Molecular Processes (New York: Academic Press) [Google Scholar]
  38. Shulyak, D., Tsymbal, V., Ryabchikova, T., Stütz, C., & Weiss, W. W. 2004, A&A, 428, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Sitnova, T. M., Mashonkina, L. I., & Ryabchikova, T. A. 2013, Astron. Lett., 38, in press [Google Scholar]
  40. Steenbock, W., & Holweger, H. 1984, A&A, 130, 319 [NASA ADS] [Google Scholar]
  41. Tolstoy, E., Hill, V., & Tosi, M. 2009, ARA&A, 47, 371 [NASA ADS] [CrossRef] [Google Scholar]
  42. Zhao, G., Butler, K., & Gehren, T. 1998, A&A, 333, 219 [NASA ADS] [Google Scholar]

All Tables

Table 1

Mg i line data.

In the text
Table 2

Magnesium NLTE and LTE abundances log AMg of the Sun and hot stars.

In the text
Table 3

Stellar parameters of selected stars.

In the text
Table 4

Magnesium LTE and NLTE abundances of HD 84937 and HD 122563 from calculations with different treatments of H i collisions.

In the text
Table 5

NLTE abundance corrections (dex) for lines of Mg i from calculations with Mg+H collision rates of BBSGF and with the Drawinian rates scaled by a factor of SH = 0.1 (D0.1).

In the text

All Figures

thumbnail Fig. 1

Departure coefficients for selected levels of Mg i as a function of log τ5000 in the model atmosphere 4600/1.60/−2.56 from the calculations with pure electronic collisions (top panel) and with H i collisions taken into account following BBSGF (bottom panel). Tick marks indicate the locations of line center optical depth unity for the Mg i lines 5172 Å (1) and 5528 Å (2).
Open with DEXTER
In the text
thumbnail Fig. 2

Best NLTE (continuous curve) and LTE (dotted curve) fits of the Mg i 5172 Å line in HD 122563 (bold dots). The NLTE calculations were performed with log AMg =  −6.95, while the LTE ones with a 0.02 dex higher value. Mg+H collisions are treated following BBSGF. Our theoretical flux profiles were convolved with a profile that combines instrumental broadening with a Gaussian profile and broadening by macroturbulence with a radial-tangential profile. The macroturbulence values are 4.7 km s-1 for the NLTE and 3.8 km s-1 for the LTE fits.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.