| Issue |
A&A
Volume 550, February 2013
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220483 | |
| Published online | 04 February 2013 | |
Deflagration-to-detonation transition by amplification of acoustic waves in type Ia supernovae
1
CEA, IRFU, SAp,
91191
Gif-sur-Yvette,
France
e-mail:
camille.charignon@cea.fr
2
AIM – Unité Mixte de Recherche CEA, CNRS, Université Paris VII,
UMR
7158,
France
Received:
2
October
2012
Accepted:
21
December
2012
Aims. We study a new mechanism for deflagration-to-detonation transition in thermonuclear supernovae (SNe Ia), based on the formation of shocks by amplification of sound waves in the steep density gradients of white dwarfs envelopes. We characterise, in terms of wavelength and amplitude, the perturbations which will ignite a detonation after their amplification.
Methods. This study was performed using the well tested HERACLES code, a conservative hydrodynamical code, validated in the present specific application by an analytical description of the propagation of sound waves in white dwarfs. Thermonuclear combustion of the carbon oxygen fuel was treated with the α-chain nuclear reactions network.
Results. In planar geometry we found the critical parameter to be the height of shock formation. When it occurs in the inner dense regions (ρ > 106 g cm-3) detonation is inevitable but can take an arbitrarily long time. We found that ignition can be achieved for perturbation as low as Mach number: M ~ 0.005, with heating times compatible with typical explosion time scale (a few seconds). On the opposite no ignition occurs when shocks initiated by small amplitude or large wavelength form further away in less dense regions. We show finally that ignition is also achieved in a spherical self-gravitating spherical model of cold C+O white dwarf of 1.430 M⊙, but due to the spherical damping of sound waves it necessitates stronger perturbation (M ~ 0.02). Small perturbations (M ~ 0.003) could still trigger detonation if a small helium layer is considered. In the context of SNe Ia, one has to consider further the initial expansion of the white dwarf, triggered by the deflagration, prior to the transition to detonation. As the star expands, gradients get flatter and ignition requires increasingly strong perturbations.
Key words: shock waves / supernovae: general / white dwarfs
© ESO, 2013
1. Introduction
Type Ia supernovae are thought to result from the thermonuclear explosion of a carbon oxygen white dwarf. Presently two main families of models are proposed: in the single degenerate scenario (Whelan & Iben 1973) explosion is triggered by continuous accretion of the hydrogen or helium rich envelop of a non-degenerate companion until Chandrasekhar mass is reached; in the double degenerate scenario (Iben & Tutukov 1984) the explosion results of the merging of two C+O white dwarfs. In the latter mechanism, only the detonation mode of combustion can release enough energy to prevent a collapse and produce a healthy explosion. Furthermore ignition is not so easy and require violent mergers (Pakmor et al. 2012), that might not be frequent enough to explain the SN Ia rates. In the former scenario pure detonation and pure deflagration fail to reproduce light curves and nucleosynthesis. Detonation models (Arnett 1969) incinerate the whole star at high density producing mostly 56Ni and resulting in wrong nucleosynthesis. On the other hand pure deflagration is very subsonic and gives time for expansion so that burning also occurs at lower density and produce the intermediate elements needed for spectra, but those models are under-energetics (Röpke et al. 2007). Accordingly the delayed detonation scenario has been proposed (Khokhlov 1991a) to combine the advantages of both combustion modes. In this model a flame born as a subsonic deflagration is accelerated by turbulence and transitions at some point to a detonation. The initial phase allow the star to expand so that IME are produced in the final detonation stage.
However, after many years of studies the mechanism of deflagration-to-detonation transition (DDT) is still unclear. It has been shown by 3D simulations (Gamezo et al. 2005) that this mechanism was the most promising path for single degenerate models to reasonably account for observables, however due to the lack of theoretical understanding of this transition, the turning point between deflagration and detonation still relies on educated guesses (Woosley et al. 2009) or is adjusted in order to best reproduces nucleosynthesis of normal type Ia supernovae (Jackson et al. 2010). On earth, DDT has been observed in confined media, for which Ivanov et al. (2010) provided numerical evidence that the transition may occur through shock-flame interactions, see also Khokhlov et al. (1999) and Oran & Gamezo (2007) for more details on shock-flame interaction in DDT. See also Ciccarelli & Dorofeev (2008) for a review of DDT mechanisms in typical terrestrial systems. However in unconfined media, terrestrial experiments showed that a turbulent flame is rather stable against DDT. Thus it has been proposed that the transition should occur through the gradient mechanism (Khokhlov 1991b), where a suitable gradient of the reactions induction time is created and maintained over a time long enough for a coherent burning wave to build up pressure and create a self-sustained detonation. It has been suggested that the turning point from turbulent deflagration to detonation might be the creation of such a flat gradient at the transition between the flamelet and the distributed combustion regimes, for which the flame changes in nature. However it is not clear if the turbulence level necessary for the distributed regime to occur is achieved during the explosion, even at the late stages. More recently, through numerical studies Poludnenko et al. (2011) claimed that intense enough turbulence could directly initiate DDT, without relying on this induction time gradient. Other mechanisms able to ignite a delayed detonation from a turbulent deflagration have also been proposed: creation of hot spot, or shock convergence in the turbulent flame brush (Kushnir et al. 2012). Thus in the context of supernova where the plasma is fully unconfined but where high level of turbulence should be present, the question is still debated.
Here we examine a new mechanism by which pressure perturbations, created by flame turbulence, are amplified during their propagation ahead of the flame in the steep density gradient where they turn into shocks, which can be strong enough to ignite a detonation. It is known since Lighthill (1955) that compressible turbulence can produce sound waves, even with small rms Mach number turbulence. Moreover the turbulent combustion is likely to enhance sound production. It is also known that sound waves propagating through steep density gradients get amplified, and given a large enough density jump they result in strong shocks and substantial heating. The mechanism of formation of strong shocks in density gradient has been proposed, for example, for the heating of the solar chromosphere (see Ulmschneider 1970, for a review).
In this paper, we analyse the propagation properties of finite amplitude pressure waves in C+O degenerate matter, first in terms of the density gradient and then in a more realistic spherical WD model. We determine the frequencies and amplitudes which lead to a successful detonation. We postpone to a following paper the study of the actual source of pressure perturbations. Our paper is constructed as follows: in the first part we present our numerical methods and the physics included. In the second part we derive an approximate equation for shock formation and amplification in density gradients in C+O degenerate matter and compare numerical results obtained for the planar models to validate the numerical simulations. Then we apply this to spherical models closer to the reality: first a cold and dense white dwarf and then a set of pre-expanded structures. Finally we briefly discuss the applicability of this mechanism to thermonuclear supernovae.
2. Numerical methods and physical input
We will consider the dense plasma of WD interiors composed of carbon-oxygen mixture. At these densities the plasma is degenerate and needs special treatment. Section 2.1 describes the method used to simulate gas hydrodynamic in the dense plasma with the HERACLES code1 (González et al. 2007). Section 2.2 describes the implementation of the degenerate equation of state (EoS) within the code. Finally Sect. 2.4 presents the implementation of the thermonuclear reaction network.
2.1. The code: HERACLES
The simulations are performed using the HERACLES code. It is a grid-based conservative
compressible hydro code, with a second order Godunov scheme, which solves the usual Euler
fluid equations: ![\begin{eqnarray} &&\frac{\partial \rho}{\partial t} + \vec{\nabla}(\rho \vec{u}) = 0 \nonumber \\ && \frac{\partial \rho \vec{u}}{\partial t} + \vec{\nabla}(\rho \vec{u}\otimes\vec{u} + P) = -\rho\vec{g} \nonumber \\ && \frac{\partial E}{\partial t} + \vec{\nabla}[(E+P)\vec{u}] = \epsilon_{\rm nuc}, \end{eqnarray}](/articles/aa/full_html/2013/02/aa20483-12/aa20483-12-eq9.png) (1)where
g is the acceleration of gravity, ϵnuc is the
energy release due to thermonuclear reactions and
E = E0 + Eth + 0.5ρu2
is the total energy including respectively degeneracy, thermal and kinetic energy. The
fluxes between cells are computed through a Riemann solver adapted to our degenerate EoS.
It also include gravity implemented as a Cranck-Nicholson step decoupled from the hydro
step. Since we made only 1D calculations, the gravitational acceleration is either
constant in the planar geometry or is computed self-consistently at every radius
r as the acceleration of gravity due to the enclosed mass:
(1)where
g is the acceleration of gravity, ϵnuc is the
energy release due to thermonuclear reactions and
E = E0 + Eth + 0.5ρu2
is the total energy including respectively degeneracy, thermal and kinetic energy. The
fluxes between cells are computed through a Riemann solver adapted to our degenerate EoS.
It also include gravity implemented as a Cranck-Nicholson step decoupled from the hydro
step. Since we made only 1D calculations, the gravitational acceleration is either
constant in the planar geometry or is computed self-consistently at every radius
r as the acceleration of gravity due to the enclosed mass:
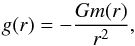 where
where
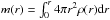 is the
enclosed mass in the sphere of radius r and G is gravitational constant.
is the
enclosed mass in the sphere of radius r and G is gravitational constant.
2.2. Equation of state
In a white dwarf, the electron gas is degenerate and ions form an almost perfect gas.
Depending on the temperature and density, electrons have various degrees of degeneracy.
Thus a general EoS is used to described the plasma including a perfect gas of ions,
photons in local thermal equilibrium and electrons at all degrees of degeneracy and
relativity (Timmes & Swesty 2000). To solve
the Riemann problem for a general EoS we use the solver described by Colella & Glaz (1985) as implemented in the FLASH code (Fryxell et al. 2000). But in some cases it was not
accurate enough to follow precisely the temperature. Indeed in the density and temperature
conditions relevant here, the main contribution to the pressure and energy of the gas is
from the degenerate electrons and is essentially independent of the temperature. The
thermal contribution, defined as
Eth(ρ,T) = Ein(ρ,T) − Ein(ρ,T = 0 K)
represents often less than 0.1% of the internal energy (Ein).
Since a conservative code computes only the total energy:
E = E0 + Eth + 0.5ρu2,
direct inversion to obtain the temperature is sometimes inaccurate. Thus, in order to
accurately follow the temperature of the plasma, an equation of evolution for the thermal
energy is derived and used when necessary: 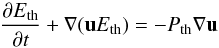 where
Pth is the thermal pressure defined as
Pth(ρ,T) = P(ρ,T) − P(ρ,T = 0 K).
where
Pth is the thermal pressure defined as
Pth(ρ,T) = P(ρ,T) − P(ρ,T = 0 K).
2.3. Numerical dissipation and waves propagation
To resolve sound waves with minimum numerical dissipation, there must be enough points per wavelength and the time step must be much smaller than the period. To check the ability of our code to propagate sound waves without too much dissipation, we initiate waves of different frequencies at a given amplitude and measure the amplitude at the opposite side. With a 1500 points grid the numerical losses are only 5% for a wavelength of 1/30 of the computational box length , which correspond to 50 points per period. For larger wavelength the losses are smaller (2% at 1/20 and less than 1% at more than 1/10). As will be shown latter, spatial frequencies higher than 1/20 are not relevant to the problem considered here, thus the code is actually well suited for the present study.
2.4. Nuclear network and detonations
Since we are not concerned here with the details of nuclear burning, we adopt the classical α chain network, composed of 13 nuclei from 12C to 56Ni plus 4He. This time saving network is sufficient to describe the energetics of the C+O combustion (Timmes 1999). For the reaction rates we use the NACRE compilation. The implementation of nuclear reactions in the hydro code HERACLES, uses a decoupled combustion step with multiple local nuclear time steps. To check this implementation we compare forced detonations with a high resolution adaptive mesh code, which can nicely resolve flames and detonations (ASTROLABE code, developed by one of us: Chièze). This is visible in Fig. 1, where the cells from ASTROLABE are plotted in blue dots along the Rayleigh line for mass and momentum conservation, the Rankine-Hugoniot curve for energy conservation and the Crussard curve (the Crussard curve is the non-adiabatic Rankine-Hugoniot curve, modified by the energy released by the combustion). We can see, according to the ZND model, that the detonation results of a primary shock which heats up and compresses the plasma, pushing it on the Hugoniot. Then, combustion on scales much larger than the shock thickness, will expand the plasma and reach the intersection of the Crussard curve and the Rayleigh line. For the same set up, we plotted the simulation cells for the HERACLES code. Due to lower resolution, the initial state at v = 2 × 10-8cm3g-1 goes almost directly to the final state where the combustion is complete. But even without resolving the combustion zone, the final state corresponds nicely with the high resolution simulation. Then we compare several detonations from HERACLES and found detonation speeds agreeing within less than 1%. Finally we consider the effect of resolution on detonation initiation. The mechanism described later is self-consistent and rely only on compression and heating by shocks. There is no artificial criteria or threshold for ignition. Usually only one cell runs away, when the density and temperature of the cell are sufficient so that heating due to combustion is faster than the cooling following the shock. In those conditions the cell reaches sufficiently high pressure to compress the neighbouring cells, propagating the detonation. This means that the ignition scale is not resolved. But since density and temperature are averaged over the cell, the under-resolved ignition conditions are a lower estimate. Indeed, ignition occurs in the region of decompression following the shock, where temperature and density decrease almost linearly from the post shock state. Thus inside the detonating cell, the unresolved region of maximum density and temperature would runaway faster than the whole cell, with averaged density and temperature.
 |
Fig. 1 Pressure (P)-specific volume (V) diagram of a forced detonation in a plasma of density ρ0 = 5 × 107 gcm-3. The Hugoniot curve represents the energy conservation through a shock, the Rayleigh line is the line of mass and momentum conservation and the Crussard curve corresponds to the energy conservation after the nuclear burning is complete. Each blue point is the (P,V) value of a simulation cell from the high resolution code, ASTROLABE. This simulation resolves the reaction zone following the leading shock, while the crosses representing the simulation cells of the code HERACLES, jump directly to the final state. This demonstrates that even without resolving the combustion zone, this code reproduces the correct energetics and dynamics. |
3. Shock formation and heating mechanisms
In this section we analyse the propagation and the amplification of sound waves in slab geometry. We consider a vertical column, with h measuring the height from the base (h = 0) to the top (h = L). The gravity points towards the base. By an analogy to spherical geometry, we speak there of inner boundary and upper density, while the top of the column would correspond to the outer boundary and lower densities. We adopt this simplifying assumption in order to derive a simple analytical description which is then compared to numerical simulations of hydrodynamics to validate them.
3.1. Analytical description
The Poynting flux of a wave of velocity amplitude u is
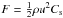 . This corresponds to
the energy flux carried by the wave in the linear regime. This flux is conserved in the
absence of dissipation. If the perturbation originates from a region with density
ρ0 and sound speed
Cs,0, its amplitude at any height
h reads as:
. This corresponds to
the energy flux carried by the wave in the linear regime. This flux is conserved in the
absence of dissipation. If the perturbation originates from a region with density
ρ0 and sound speed
Cs,0, its amplitude at any height
h reads as: 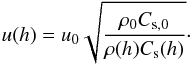 (2)In degenerate matter the
sound speed depends mainly on the density. Thus a wave travelling outward will slow down,
so that the perturbation amplitude will grow to conserve the flux. And this, until a shock
forms and dissipates kinetic energy. A good way of estimating the height of shock
formation, Hsh, is to follow the hills of the wave until they
catch up the valleys. The hills move with respect to the wave at
+ u(h) while the valleys at
− u(h) and they will merge when they have travelled
their initial separation of λ0/2. For a
perturbation initiated at h = 0, this reads as:
(2)In degenerate matter the
sound speed depends mainly on the density. Thus a wave travelling outward will slow down,
so that the perturbation amplitude will grow to conserve the flux. And this, until a shock
forms and dissipates kinetic energy. A good way of estimating the height of shock
formation, Hsh, is to follow the hills of the wave until they
catch up the valleys. The hills move with respect to the wave at
+ u(h) while the valleys at
− u(h) and they will merge when they have travelled
their initial separation of λ0/2. For a
perturbation initiated at h = 0, this reads as: 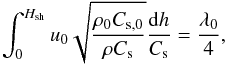 (3)The height of shock
formation is calculated for a barometric structure with an upper density of
ρ0 = 5 × 109 gcm-3 decreasing to a
density of 104 gcm-3, over a length of L = 5260 km.
The choice of the lower density is a limit where thermonuclear ignition would no longer be
possible. The constant gravity acceleration is:
g = GM⊙/(1500 km)2
and the sound speed at h = 0 is
Cs,0 = 10 500 kms-1.
Equation (3) for this gradient is plotted
versus the frequency in Fig. 2. It provides a quite
good estimate of the height at which a perturbation starts to dissipate and heat up the
medium, due to the formation of shocks. There are two trends: the longer the wavelengths
the farther they start dissipating and for a given wavelength
λ0, stronger initial perturbation starts dissipating
earlier. Hsh determines if heating will occur in regions where
densities are sufficient for ignition to occur, when
Hsh < L. In that
case the heating rate is increasing with the perturbation amplitude u and
the detonation initiation only necessitates a sufficient number of shocks to reach
ignition temperature. On the other hand when
Hsh > L, shocks
form too late in regions of low densities, where detonation is not possible whatever the
number of shocks.
(3)The height of shock
formation is calculated for a barometric structure with an upper density of
ρ0 = 5 × 109 gcm-3 decreasing to a
density of 104 gcm-3, over a length of L = 5260 km.
The choice of the lower density is a limit where thermonuclear ignition would no longer be
possible. The constant gravity acceleration is:
g = GM⊙/(1500 km)2
and the sound speed at h = 0 is
Cs,0 = 10 500 kms-1.
Equation (3) for this gradient is plotted
versus the frequency in Fig. 2. It provides a quite
good estimate of the height at which a perturbation starts to dissipate and heat up the
medium, due to the formation of shocks. There are two trends: the longer the wavelengths
the farther they start dissipating and for a given wavelength
λ0, stronger initial perturbation starts dissipating
earlier. Hsh determines if heating will occur in regions where
densities are sufficient for ignition to occur, when
Hsh < L. In that
case the heating rate is increasing with the perturbation amplitude u and
the detonation initiation only necessitates a sufficient number of shocks to reach
ignition temperature. On the other hand when
Hsh > L, shocks
form too late in regions of low densities, where detonation is not possible whatever the
number of shocks.
 |
Fig. 2 Height of shock formation versus the initial wavelength of the perturbation normalised to the size of the box: λ0/L in the planar and spherical cases. |
The amount of energy dissipated by a shock depends on its strength defined as
η = (ρ∗ − ρ)/ρ,
with ρ∗ and ρ the shocked and pre-shock
densities respectively. To estimate the shock strength we follow Ulmschneider (1967) and Ulmschneider
(1970). Since we consider very weak perturbations the resulting shocks are never
strong (η ~ 1), this implies they will be of the sawtooth type (Landau & Lifshitz 1959, Sect. 102, p. 385). For
this shape the energy carried by the wave is: 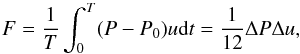 where
ΔP and Δu are the jumps in pressure and velocity
across the shock front and T is the period. Assuming weak shocks,
Δu = ηCs and
where
ΔP and Δu are the jumps in pressure and velocity
across the shock front and T is the period. Assuming weak shocks,
Δu = ηCs and
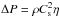 and using the adiabatic index
γ = 1 + P/E and
and using the adiabatic index
γ = 1 + P/E and
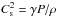 , this
formula reduces to:
, this
formula reduces to: 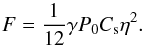 (4)On the other
hand, shocks dissipate kinetic energy into internal energy. The corresponding rate can be
estimated following Landau & Lifshitz
(1959) for weak shocks, or for arbitrary strong shocks as in Brinkley & Kirkwood (1947):
(4)On the other
hand, shocks dissipate kinetic energy into internal energy. The corresponding rate can be
estimated following Landau & Lifshitz
(1959) for weak shocks, or for arbitrary strong shocks as in Brinkley & Kirkwood (1947): 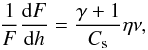 (5)where
ν = 1/T is the frequency. Then
deriving Eq. (4) and equating it to
dissipation losses, we get the shock strength equation:
(5)where
ν = 1/T is the frequency. Then
deriving Eq. (4) and equating it to
dissipation losses, we get the shock strength equation: 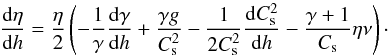 (6)Osterbrock (1961) showed that for weak shock the
conserved quantity is actually
(6)Osterbrock (1961) showed that for weak shock the
conserved quantity is actually 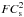 . The inclusion of
this refraction effect adds an additional factor
. The inclusion of
this refraction effect adds an additional factor 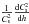 .
Equation (6) can then be integrated to get
shock strengths η(h) given the position of formation and
an initial shock strength η0. We note that the pressure term,
.
Equation (6) can then be integrated to get
shock strengths η(h) given the position of formation and
an initial shock strength η0. We note that the pressure term,
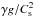 , and the
energy dissipation rate,
(γ + 1)ην/Cs,
dominate the RHS of Eq. (6), so that an
asymptotic behaviour of the shock strength can be approximated by equating these two terms
to obtain:
, and the
energy dissipation rate,
(γ + 1)ην/Cs,
dominate the RHS of Eq. (6), so that an
asymptotic behaviour of the shock strength can be approximated by equating these two terms
to obtain: 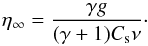 (7)This relation is plotted
as solid lines in Fig. 3 for different frequencies or
equivalently initial wavelengths. It can be noticed that the asymptotic value depends only
on the frequency of the perturbation. Accordingly perturbations of given wavelength with
different amplitudes tend to a common asymptotic behaviour:
η∞,ν(h).
(7)This relation is plotted
as solid lines in Fig. 3 for different frequencies or
equivalently initial wavelengths. It can be noticed that the asymptotic value depends only
on the frequency of the perturbation. Accordingly perturbations of given wavelength with
different amplitudes tend to a common asymptotic behaviour:
η∞,ν(h).
3.2. Numerical description and validation
Here we use (6) to validate the numerical
code used in the following section, which will be devoted to ignition. In our simulations,
to create the initial sound waves we impose oscillating density and momentum perturbations
at the inner eulerian boundary, h = 0: 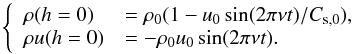 (8)The
velocity perturbation (u0) and the wavelength
(λ0 = Cs,0/ν)
are the free parameters of our study. For the outer boundary we constructed a transmitting
boundary condition, which allows matter carried by the shocks to leave the box. Figure
3 summarises our validation results and shows that
the HERACLES code nicely reproduce the results of Eqs. (6) and (7). These
calculations have been performed for a set of 3 initial wavelength ranging from
L/4 to L/20, where L is the length of
the computational domain, each one with three different initial velocity amplitudes (200,
100 and 50 kms-1).
(8)The
velocity perturbation (u0) and the wavelength
(λ0 = Cs,0/ν)
are the free parameters of our study. For the outer boundary we constructed a transmitting
boundary condition, which allows matter carried by the shocks to leave the box. Figure
3 summarises our validation results and shows that
the HERACLES code nicely reproduce the results of Eqs. (6) and (7). These
calculations have been performed for a set of 3 initial wavelength ranging from
L/4 to L/20, where L is the length of
the computational domain, each one with three different initial velocity amplitudes (200,
100 and 50 kms-1).
 |
Fig. 3 Profiles of shock strength. Dots represent the measurements from our numerical simulations: three different amplitudes (200, 100, 50 kms-1) in magenta, green and blue respectively for each wavelength families represented by their common asymptote Eq. (7) for the three wavelengths (λ0 = 0.05 L, 0.1 L, 0.2 L in solid lines in red, magenta and black respectively). Also plotted are the predictions from Eq. (6) in black dashed lines. |
4. Ignition conditions
The analytical results from the previous section can predict quite accurately the shock strength and the dissipation at any position in the degenerate carbon oxygen matter of a white dwarf. But, ignition by itself depends on the thermonuclear properties of the plasma. Hereinafter we consider numerical simulation including the nuclear network described in Sect. 2.4, both planar and spherical geometry will be discuss.
4.1. Slab geometry
We showed that the perturbation wavelength plays a major role regarding the ignition process. Indeed, short wavelength perturbations generate a train of small amplitude shocks whose cumulative dissipation brings the temperature up to ignition, at some point in the profile. Conversely a large wavelength perturbation can trigger ignition through dissipation across one single shock. To show this, we adopted an initial small Mach number perturbation, M = 0.01, corresponding to a velocity amplitude of u0 = 100 kms-1 and we varied the wavelength by one order of magnitude.
 |
Fig. 4 Propagation and amplification of a 100 kms-1 or M = 0.01 perturbation in the planar density gradient. In blue the velocity from the numerical simulation, compared to the amplification of Eq. (2) in the absence of dissipation. They separate when the shocks kinetic energy is dissipated. This is stressed by the temperature at three subsequent times plotted in black. |
We consider first the short wavelength perturbation with λ0 = 0.05 L = 263 km, corresponding to a frequency of 40 Hz. Transition to a shock occurs at the height of about 2500 km as predicted by Eq. (2). This is the point where the velocity from the simulation, in blue in Fig. 4, diverges from the prediction of Eq. (2) in red, since it enters the dissipation dominated regime. At that point the wave begins to heat up the plasma by dissipating kinetic energy. This is illustrated by the three black curves representing the temperature at three subsequent times. In that case, heating occurs through many successive weak shocks each one contributing to a small net temperature increase. This quasi-continuous dissipation process is governed by the evolution of the shock strength in Eq. (5), nicely predicted by Eq. (6) (see Fig. 3). For the α-chain thermonuclear network the runaway temperature is reached after 6.9 s (250 periods).
We turn now to the case of larger perturbation wavelength λ0 = 0.5 L, with the same initial amplitude, in Fig. 5. Detonation is triggered by dissipation of a single shock, before decompression occurs. The shock forms at about h = 4500 km, which again is close to the predictions of Eq. (2). Due to a longer travel across the steep gradient, the perturbation is more amplified, according to Eq. (2), before dissipation inhibits its growth. This leads to a much stronger shock, Δu = 4000 kms-1, and thus a very strong dissipation. In Fig. 5, when the shock forms, the post shock temperature is greater than 109 K. But contrary to the short wavelength case it is immediately followed by drastic cooling in the decompression region. For ignition to occur, the post-shock induction time should be smaller than the cooling time behind the shock, which requires higher post shock temperatures. Since these single shocks are strong, this regime is not predictable by Eq. (6), but due to long wavelength it is more easily simulated.
 |
Fig. 5 Propagation and amplification of the same initial perturbation in the same gradient. Here the shock is formed latter and the numerical velocity (in blue) sticks to the dissipationless prediction (in red) much longer. This results in strong dissipation as soon as the shock forms and a detonation is triggered before decompression can occur. |
Whatever the mechanism to reach ignition temperature at the hot spot, the runaway creates a strong overpressure sufficient to propagate a double detonation both upward and downward. Figure 6 illustrates such a successful ignition of a detonation.
 |
Fig. 6 Ignition and propagation of a detonation in the large wavelength case (λ0 = 0.5 L and u = 100 km s-1). Temperature and pressure profiles in black and red respectively are plotted at four successive times. |
We analyse now the results of the parametric study. The number of shocks needed to ignite
a detonation is presented in Table 1, for 7
different frequencies and amplitudes varied from 200 kms-1 to 30
kms-1, corresponding to Mach number from 0.02 to 0.003. As discussed above
increasing the initial amplitude, u0, has two opposite
effects. It increases the acoustic energy flux, which depends on
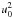 , leading to
stronger shocks but dissipation occurs earlier preventing further amplification. Regarding
detonation ignition, the stronger the perturbation the faster the ignition. Also at some
point, when decreasing the amplitude, Hsh enters region where
the density is too low for ignition to be possible, this corresponds to the dash symbols
in 1.
, leading to
stronger shocks but dissipation occurs earlier preventing further amplification. Regarding
detonation ignition, the stronger the perturbation the faster the ignition. Also at some
point, when decreasing the amplitude, Hsh enters region where
the density is too low for ignition to be possible, this corresponds to the dash symbols
in 1.
The wavelengths of the perturbations has a drastic effect as seen by comparison of the
two cases described before. Although it has no effects on the energy flux
(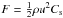 ), it has a strong
effect on the height of shock formation: higher frequency or shorter wavelength
perturbations will start dissipating earlier leading to less amplification and weaker
shocks. The energy flux being independent of the frequency, the same energy will diluted
and deposited over wider area. On the other hand it makes it possible for weaker
perturbations to trigger a detonation given more time by reducing the shock formation
height and bringing it back in denser region where ignition is possible. For example a 30
kms-1 initial perturbation, would not detonate with a wavelength of
λ0 = 0.5 L, because the shocks would form too late, but a
smaller wavelength makes ignition possible after many weak shocks.
), it has a strong
effect on the height of shock formation: higher frequency or shorter wavelength
perturbations will start dissipating earlier leading to less amplification and weaker
shocks. The energy flux being independent of the frequency, the same energy will diluted
and deposited over wider area. On the other hand it makes it possible for weaker
perturbations to trigger a detonation given more time by reducing the shock formation
height and bringing it back in denser region where ignition is possible. For example a 30
kms-1 initial perturbation, would not detonate with a wavelength of
λ0 = 0.5 L, because the shocks would form too late, but a
smaller wavelength makes ignition possible after many weak shocks.
Last, the density gradient has no effect in normalised units. The parameter determining the gradient is the acceleration of gravity: g. If g is increased by a factor 10 (as is done in the lower part of Table 1), the same density gradient will shrink to 10 times smaller box. Taking accordingly smaller wavelength the shock strengths and height formations are the same. The frequency is thus higher by a factor 10, leading to a higher rates of dissipation. But in term of dissipation per shock, it is also the same. Thus ignition of a detonation needs almost the same number of shocks. The small difference is due to smaller region at maximum temperature just after the shock. It shortens the time where reactions can run away before decompression.
Parametric study of the parameter space λosc × u0 with the conservative code HERACLES, for the case of a shallow gradient over 5000 km with g0 = GM⊙/(1500 km)2 and a steeper gradient with ten times the gravity.
4.2. Spherical structure
We apply this ignition mechanism to white dwarf structures. In spherical geometry the
flux is still conserved but since the surface of the spherical wave grows as
r2 the perturbation growth is weakened. The conservation
equation now reads: 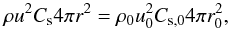 which
gives for the velocity perturbation at any radii:
which
gives for the velocity perturbation at any radii: 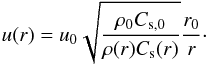 (9)Thus the
amplification has to be stronger than the spherical damping
r0/r. This introduces a
new parameter: the position r0 of the perturbation emitter.
The dependence on r0 of the amplification through Eq. (9), is shown in Fig. 7. At small r0 geometrical damping is strong
and reduce the final amplification, whereas at large radius, the variations in density and
sound speed are smaller, leading to weaker amplification. The maximum of
(9)Thus the
amplification has to be stronger than the spherical damping
r0/r. This introduces a
new parameter: the position r0 of the perturbation emitter.
The dependence on r0 of the amplification through Eq. (9), is shown in Fig. 7. At small r0 geometrical damping is strong
and reduce the final amplification, whereas at large radius, the variations in density and
sound speed are smaller, leading to weaker amplification. The maximum of
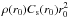 is the
optimum position between these two opposite effects, and it lies around 350 km from the
centre for the structure of the 1.43 M⊙ cold C+O white dwarf
used here.
is the
optimum position between these two opposite effects, and it lies around 350 km from the
centre for the structure of the 1.43 M⊙ cold C+O white dwarf
used here.
 |
Fig. 7 ρCsr2 versus the initial perturbation position r0, the maximum of this curve is the position where a perturbation will be most amplified. |
The first model of supernova progenitor chosen is a cold (T = 107 K) self-gravitating sphere of carbon and oxygen (XO = XC = 0.5). Two different models are constructed with a total mass of 1.43 M⊙, with the same fixed outer pressure (Pext = 1,7 × 1021 ergcm-3) which correspond to a density of ρ ~ 105 gcm-3, but one with only carbon and oxygen and the other with a thin helium layer at the surface. The central density is ρc = 7,5 × 109 gcm-3 and sound speed: Cs = 12 000 kms-1 with a radius of RWD = 1400 km. We choose such a dense structure because it presents a very strong density gradient, best emphasising the amplification mechanism. We will study more realistic structures of pre-expanded white dwarfs in next section. To initiate perturbation on this spherical model, the radius r0, of the oscillating pressure prescription, generating the initial perturbation is chosen. This could correspond to the position of the turbulent flame which would create pressure perturbations. At the optimal radius of 350 km the density is 2 × 109 gcm-3 and the sound speed is Cs = 10 000 kms-1.
 |
Fig. 8 Propagation of a 500 kms-1 perturbation of period 36 ms initiated at a r0 = 100 km. The period corresponds to a wavelength of λ0 = 0.25RWD at the optimal radius: r0 = 350 km. Initially geometry dampens the wave but then the gradient steepens and it is amplified. We compare the theoretical formula (9) for a dissipationless case to the simulation. |
In Fig. 8, the result for an initial perturbation of 500 kms-1 (M ~ 0.05) originating close to the centre (r0 = 100 km) is shown to emphasise the geometrical effect in the central region. Our simulation, in blue, is compared to the predictions of formula (9) in red. Initially where the curvature effect is strong, the damping is more important than the amplification due to the relatively flat gradient in the central region, and the amplitude of the perturbation cannot grow. But then, the gradient steepens while the effect of growing wave surface becomes smaller and the waves are amplified.
As in the planar case, we studied the possibility of detonation ignition for initial perturbations of different wavelengths and amplitudes. Here we consider the period of the waves, because the wavelength is varying with the position r0. The results are shown in Table 2 and we observe the same trends. However, due to spherical damping the amplification is reduced, so that the formation of shocks strong enough to ignite a detonation necessitates larger amplitudes. In the end a quite large initial perturbation is needed: u0 = 200 kms-1, corresponding to a Mach number of M0 = 0.02. We show in the following that if an helium layer is considered, the initial perturbation may be reduced to 30 kms-1 or M0 = 0.003.
Parametric study of the parameter space Tosc × u0 with the conservative code HERACLES, for the case of a cold C+O white dwarf (upper table) and 0.01 M⊙ helium layer (lower table).
 |
Fig. 9 Initial structures of the three pre-expanded white dwarfs. The solid lines represent the temperature profiles while the dashed lines are the density profiles of these white dwarfs. |
Helium Layer:
the presence of an helium layer at the top of the C+O core favours a detonation. This layer is small so as to keep the explosion undisturbed. According to Woosley & Kasen (2011), the presence of an helium shell above the C+O core would lead to unobserved peculiar light curves and spectra if the shell is larger than ~0.05 M⊙. Thus a very thin helium layer of MHe = 0.01 M⊙ is considered. Since Helium combustion is strongly exothermic this layer detonates with weaker shocks. Once ignited, when they reach the C+O core these He-detonations are then strong enough to initiate C+O-detonations. The set-up here is different from the double detonation scenario, where an accretion induced detonation is initiated at the base of the helium layer and where the transmission of the detonation to the core may need to wait for the He-detonation induced shocks to convergence inside the core and ignite the carbon. Indeed helium either ignites above the core/envelope boundary, which leave time for the inward propagating detonation to build up large enough pressure to directly trigger the C+O-detonation or ignition occurs at the transition with sufficiently compressed and heated carbon so as to ignite an He-outward moving detonation and an inward C+O-detonation. And even if this fails under some conditions, the usually invoked shock convergence (Fink et al. 2010) could still trigger the C+O-detonation, with some additional delay. The results of the simulations with an helium layer are summarised in the lower part of Table 2. Now, the ignition of detonation necessitates a smaller perturbation of 30 kms-1 or M0 = 0.003.
Pre-expanded structures:
however, observations of the SN Ia nucleosynthetic yield of intermediate mass elements require that DDT should occur in a pre-expanded WD, typically 1 to 1.5 s after the initial thermonuclear runaway. Ideally, the previous calculations should be applied to a dynamically expanding white dwarf, with the perturbation moving with the flame front. However, the HERACLES code is presently unable to follow dynamically the expanding structure. Thus we postpone calculations with dynamic expansion for further studies. Nevertheless, as a first approach of the behaviour of the present mechanism in an expanding star, we consider three pre-expanded WD structures with densities at the flame front of ρfl = 9 × 108, 3 × 108 and 108 gcm-3, respectively. They are obtained with the ASTROLABE code, using its moving mesh capabilities, together with an ADR flame (Khokhlov 1995), to follow the whole star expansion, starting from ignition. These three structures used in the following are shown in Fig. 9, where the temperature and density profiles are displayed. Since the densities at the perturbations initiation positions are different in these three cases, we have to consider the Mach number of the perturbations.
Parametric study of the parameter space M × Tosc, for the three cases of expanded C+O white dwarfs with an 0.01 M⊙ helium layer.
Due to expansion, density gradients steadily decrease, resulting in weaker and weaker amplification of perturbations. Consequently, at later times, quite stronger perturbations are required to trigger sufficiently prompt DDT. Here we only consider detonation ignition occurring in less than 1.5 s, thus excluding weak perturbations. Indeed, weak perturbations must be treated in a dynamical set up, allowing for repeated shock heating from the start. Table 3 summarises the results for the three pre-expanded white dwarfs. For those structures the sound velocities at the flame front are Cs = 8023, 6720 and 5880 kms-1 respectively. To get an idea of the wavelengths of the perturbations we consider, we give the period corresponding to a wavelength of half the star radius: T0.5 = 0.14, 0.21 and 0.28 s respectively. We find again the same trends, longer period and smaller amplitude perturbations turn to shocks farther away, so that at some point shocks form in the outer envelope, with too low density for ignition to be possible. On the opposite, shorter period and stronger perturbations start to dissipate closer to the flame, leading to ignition in the carbon-oxygen core rather than in the helium shell. These cases are marked with a letter c in the Table 3. In this case, corresponding to high frequency perturbations, the energy is deposited mainly in the carbon-oxygen mixture and the presence of an helium layer is of no relevance. Only the strongest perturbations, reaching at least 10% of the pressure, can trigger a timely detonation. Moreover, due to the short distance between the flame, where perturbations are generated, and the locus of shock formation, where the energy is dissipated, the ignition doesn’t really rely on amplification by the density gradient, since density does not significantly change over such a short distance. In fact, it relies mainly upon the natural evolution of any perturbation to steepen into shocks, so that the ignition times are almost independent of the structure. However, since the energy is deposited close to the flame, the fact that the flame is actually moving, may prevent the temperature to reach ignition conditions. But in any case, the preheating of fuel due to shocks will have strong effects on the flame when it reaches this pre-heated region. Conversely long period perturbations with smaller amplitudes could trigger a detonation in the helium shell, due to a longer delay for shock formation. As the star expands, the minimum amplitude to detonate the helium layer increases, due to less and less amplification through a flatter and flatter gradient. From M = 0.003 in the cold and dense initial white dwarf, the required triggering pressure perturbation, δP/P, are respectively 0.02, 0.03 and finally 0.05.
Comparison of the acoustic flux needed for detonation ignition to the nuclear energy generation of the corresponding laminar flame in the three pre-expanded white dwarfs studied previously.
5. Discussion
Finally we can estimate the energy flux needed for a cold white dwarf with a thin helium
layer to detonate through the amplification mechanism as:
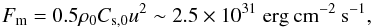 with
ρ0 = 2 × 109g cm-3,
Cs,0 = 10 000kms-1 and a
perturbation amplitude of M = 0.005
(u = 50kms-1). The question is then to find how and where this
flux could be produced. An estimate of the energy flux generated by the thermonuclear
combustion during the initial deflagration phase at the density
ρ0, is:
with
ρ0 = 2 × 109g cm-3,
Cs,0 = 10 000kms-1 and a
perturbation amplitude of M = 0.005
(u = 50kms-1). The question is then to find how and where this
flux could be produced. An estimate of the energy flux generated by the thermonuclear
combustion during the initial deflagration phase at the density
ρ0, is: 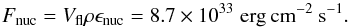 The
laminar flame velocity used here is: Vfl = 75kms-1 in
agreement with Timmes & Woosley (1992) and
the nuclear energy released is: ϵnuc = 5.81017
ergg-1, corresponding to the combustion of the
XO = XC = 0.5 mixture. The laminar
deflagration speed is used as a lower limit since it should be greatly enhanced by
turbulence. But even considering this limit, only 0.3% of the generated energy injected into
sound waves would be sufficient for a successful ignition in the cold initial white dwarf.
In Table 4 the same comparison is made for the
pre-expanded white dwarfs. For these structures the required energy represents a more and
more substantial part of the available nuclear energy: 6%, 19% and finally almost all the
energy generated by a laminar flame. Accordingly, only fast turbulent flames could generate,
at late times, enough energy for this mechanism.
The
laminar flame velocity used here is: Vfl = 75kms-1 in
agreement with Timmes & Woosley (1992) and
the nuclear energy released is: ϵnuc = 5.81017
ergg-1, corresponding to the combustion of the
XO = XC = 0.5 mixture. The laminar
deflagration speed is used as a lower limit since it should be greatly enhanced by
turbulence. But even considering this limit, only 0.3% of the generated energy injected into
sound waves would be sufficient for a successful ignition in the cold initial white dwarf.
In Table 4 the same comparison is made for the
pre-expanded white dwarfs. For these structures the required energy represents a more and
more substantial part of the available nuclear energy: 6%, 19% and finally almost all the
energy generated by a laminar flame. Accordingly, only fast turbulent flames could generate,
at late times, enough energy for this mechanism.
As stressed in the previous section, a strong constraint on perturbations frequencies and amplitudes would be the time scale over which the transition to detonation has to occur. In the context of the delayed detonation model of SNe Ia, the detonation has to be triggered after an initial phase of expansion driven by the energy released by the deflagration. Thus, it should not be too fast at the early stage of flame propagation, so that an early detonation is avoided. But it should be fast enough, so that the detonation can be triggered before the expansion gets too large. In the classical local DDT, many studies agree to say the detonation has to occur when the flame reaches densities of about 2 × 107 gcm-3. In this paper the DDT mechanism is non local, with a shift in space and time between the deflagration, producing the perturbations, and the position where they trigger a detonation. Thus the critical density, derived from usual DDT, is not directly relevant to this mechanism. Taking the delay due to wave propagation and shock heating accumulation into account, we have considered white dwarfs where the flame is still at densities above the classical critical density, so that during the shock heating period, the star will further expand and detonation will be initiated when the flame encompasses regions with approximately the critical density. Obviously a serious drawback of this study is to consider a static flame position, in a structure devoid of previous shock formation. Indeed, shock heating should occur right from the beginning, with evolving characteristics as the flame travel across the white dwarf. The final heating will thus be a complex interplay between the moving flame and the history of shocks formation and dissipation. Thus, the next step after this preliminary study, will be to take properly into account the expansion of the star, along with a moving perturbation generator.
Finally, we found that there are two kinds of perturbations that could successfully trigger a non-local DDT. Either long period and small amplitude perturbations, corresponding to large combustion scale, like Rayleigh-Taylor mushrooms. Those perturbations will heat up the outer helium layer, igniting an helium detonation, given the right shock heating history. Or, conversely, high frequency and large amplitude perturbations, corresponding to repeated strong pressure perturbations, which could be associated with small scale turbulent combustion. In that case, it is unlikely that there will be enough time for shock heating to reach ignition temperature, since shocks will form not so far from the flame. But in case of detonation ignition failure, the fuel would have been efficiently pre-heated, which would have a positive feedback on the flame.
In the classical DDT through the gradient mechanism of Khokhlov (1991b), pressure perturbation has to build up directly to detonation pressure, and this necessitate over 10 km. In our case a failed build up to only a fraction of that pressure would
be enough, if sufficiently repeated. Moreover, in an attempt to get direct transition to detonation, Poludnenko (priv. comm.) obtained strong pressure pulses of about 30% of the unperturbed pressure, repeated every eddy turn-over time. This perturbation corresponds to Col. 2 of Table 3 and might detonate, given the right conditions. To conclude, we propose a promising possibility for the revival of failed local DDT, as non-local DDT induced by density gradient amplification.
References
- Arnett, W. D. 1969, Ap&SS, 5, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Brinkley, S. R., & Kirkwood, J. G. 1947, Phys. Rev., 72, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Ciccarelli, G., & Dorofeev, S. 2008, Progr. Energy Combust. Sci., 34, 499 [CrossRef] [Google Scholar]
- Colella, P., & Glaz, H. M. 1985, J. Comput. Phys., 59, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Fink, M., Röpke, F. K., Hillebrandt, W., et al. 2010, A&A, 514, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fryxell, B., Olson, K., Ricker, P., et al. 2000, ApJS, 131, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Gamezo, V. N., Khokhlov, A. M., & Oran, E. S. 2005, ApJ, 623, 337 [NASA ADS] [CrossRef] [Google Scholar]
- González, M., Audit, E., & Huynh, P. 2007, A&A, 464, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iben, Jr., I., & Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanov, M. F., Kiverin, A. D., Liberman, M. A., & Fortov, V. E. 2010, Physics - Doklady, 55, 480 [Google Scholar]
- Jackson, A. P., Calder, A. C., Townsley, D. M., et al. 2010, ApJ, 720, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Khokhlov, A. M. 1991a, A&A, 245, 114 [NASA ADS] [Google Scholar]
- Khokhlov, A. M. 1991b, A&A, 246, 383 [NASA ADS] [Google Scholar]
- Khokhlov, A. M. 1995, ApJ, 449, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Khokhlov, A., Oran, E., & Thomas, G. 1999, Combustion and Flame, 117, 323 [CrossRef] [Google Scholar]
- Kushnir, D., Livne, E., & Waxman, E. 2012, ApJ, 752, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Landau, L. D., & Lifshitz, E. M. 1959, Fluid mechanics (Pergamon Press) [Google Scholar]
- Lighthill, M. J. 1955, in Gas Dynamics of Cosmic Clouds, IAU Symp., 2, 121 [Google Scholar]
- Oran, E. S., & Gamezo, V. N. 2007, Combustion and Flame, 148, 4 [CrossRef] [Google Scholar]
- Osterbrock, D. E. 1961, ApJ, 134, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Pakmor, R., Kromer, M., Taubenberger, S., et al. 2012, ApJ, 747, L10 [Google Scholar]
- Poludnenko, A. Y., Gardiner, T. A., & Oran, E. S. 2011, Phys. Rev. Lett., 107, 054501 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Röpke, F. K., Hillebrandt, W., Schmidt, W., et al. 2007, ApJ, 668, 1132 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X. 1999, ApJS, 124, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., & Swesty, F. D. 2000, ApJS, 126, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., & Woosley, S. E. 1992, ApJ, 396, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Ulmschneider, P. 1967, ZAp, 67, 193 [NASA ADS] [Google Scholar]
- Ulmschneider, P. 1970, Sol. Phys., 12, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Whelan, J., & Iben, Jr., I. 1973, ApJ, 186, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Kasen, D. 2011, ApJ, 734, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Kerstein, A. R., Sankaran, V., Aspden, A. J., & Röpke, F. K. 2009, ApJ, 704, 255 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Parametric study of the parameter space λosc × u0 with the conservative code HERACLES, for the case of a shallow gradient over 5000 km with g0 = GM⊙/(1500 km)2 and a steeper gradient with ten times the gravity.
Parametric study of the parameter space Tosc × u0 with the conservative code HERACLES, for the case of a cold C+O white dwarf (upper table) and 0.01 M⊙ helium layer (lower table).
Parametric study of the parameter space M × Tosc, for the three cases of expanded C+O white dwarfs with an 0.01 M⊙ helium layer.
Comparison of the acoustic flux needed for detonation ignition to the nuclear energy generation of the corresponding laminar flame in the three pre-expanded white dwarfs studied previously.
All Figures
 |
Fig. 1 Pressure (P)-specific volume (V) diagram of a forced detonation in a plasma of density ρ0 = 5 × 107 gcm-3. The Hugoniot curve represents the energy conservation through a shock, the Rayleigh line is the line of mass and momentum conservation and the Crussard curve corresponds to the energy conservation after the nuclear burning is complete. Each blue point is the (P,V) value of a simulation cell from the high resolution code, ASTROLABE. This simulation resolves the reaction zone following the leading shock, while the crosses representing the simulation cells of the code HERACLES, jump directly to the final state. This demonstrates that even without resolving the combustion zone, this code reproduces the correct energetics and dynamics. |
| In the text | |
 |
Fig. 2 Height of shock formation versus the initial wavelength of the perturbation normalised to the size of the box: λ0/L in the planar and spherical cases. |
| In the text | |
 |
Fig. 3 Profiles of shock strength. Dots represent the measurements from our numerical simulations: three different amplitudes (200, 100, 50 kms-1) in magenta, green and blue respectively for each wavelength families represented by their common asymptote Eq. (7) for the three wavelengths (λ0 = 0.05 L, 0.1 L, 0.2 L in solid lines in red, magenta and black respectively). Also plotted are the predictions from Eq. (6) in black dashed lines. |
| In the text | |
 |
Fig. 4 Propagation and amplification of a 100 kms-1 or M = 0.01 perturbation in the planar density gradient. In blue the velocity from the numerical simulation, compared to the amplification of Eq. (2) in the absence of dissipation. They separate when the shocks kinetic energy is dissipated. This is stressed by the temperature at three subsequent times plotted in black. |
| In the text | |
 |
Fig. 5 Propagation and amplification of the same initial perturbation in the same gradient. Here the shock is formed latter and the numerical velocity (in blue) sticks to the dissipationless prediction (in red) much longer. This results in strong dissipation as soon as the shock forms and a detonation is triggered before decompression can occur. |
| In the text | |
 |
Fig. 6 Ignition and propagation of a detonation in the large wavelength case (λ0 = 0.5 L and u = 100 km s-1). Temperature and pressure profiles in black and red respectively are plotted at four successive times. |
| In the text | |
 |
Fig. 7 ρCsr2 versus the initial perturbation position r0, the maximum of this curve is the position where a perturbation will be most amplified. |
| In the text | |
 |
Fig. 8 Propagation of a 500 kms-1 perturbation of period 36 ms initiated at a r0 = 100 km. The period corresponds to a wavelength of λ0 = 0.25RWD at the optimal radius: r0 = 350 km. Initially geometry dampens the wave but then the gradient steepens and it is amplified. We compare the theoretical formula (9) for a dissipationless case to the simulation. |
| In the text | |
 |
Fig. 9 Initial structures of the three pre-expanded white dwarfs. The solid lines represent the temperature profiles while the dashed lines are the density profiles of these white dwarfs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


