| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 12 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201220387 | |
| Published online | 21 December 2012 | |
A simple prescription for simulating and characterizing gravitational arcs
1
Departamento de AstronomiaUniversidade Federal do Rio Grande do
Sul,
Av. Bento Gonçalves, 9500, RS,
91501-970
Porto Alegre,
Brazil
e-mail: furlanetto.cristina@gmail.com
2
Laboratório Interinstitucional de e-Astronomia, Rua Gen. José
Cristino, 77, RJ, 20921-400
Rio de Janeiro,
Brazil
3
Centro Brasileiro de Pesquisas Físicas, Rua Dr. Xavier Sigaud 150,
RJ, 22290-180
Rio de Janeiro,
Brazil
4
Laboratório Nacional de Computação Científica, Av. Getúlio Vargas,
333, RJ, 25651-075
Petrópolis,
Brazil
5
Departamento de Física, Universidade Federal do Rio Grande do
Norte, Campus Universitário, RN,
59072-970
Natal,
Brazil
6
Observatório Nacional, Rua Gen. José Cristino, 77, RJ
20921-400
Rio de Janeiro,
Brazil
Received:
14
September
2012
Accepted:
5
November
2012
Simple models of gravitational arcs are crucial for simulating large samples of these objects with full control of the input parameters. These models also provide approximate and automated estimates of the shape and structure of the arcs, which are necessary for detecting and characterizing these objects on massive wide-area imaging surveys. We here present and explore the ArcEllipse, a simple prescription for creating objects with a shape similar to gravitational arcs. We also present PaintArcs, which is a code that couples this geometrical form with a brightness distribution and adds the resulting object to images. Finally, we introduce ArcFitting, which is a tool that fits ArcEllipses to images of real gravitational arcs. We validate this fitting technique using simulated arcs and apply it to CFHTLS and HST images of tangential arcs around clusters of galaxies. Our simple ArcEllipse model for the arc, associated to a Sérsic profile for the source, recovers the total signal in real images typically within 10%−30%. The ArcEllipse+Sérsic models also automatically recover visual estimates of length-to-width ratios of real arcs. Residual maps between data and model images reveal the incidence of arc substructure. They may thus be used as a diagnostic for arcs formed by the merging of multiple images. The incidence of these substructures is the main factor that prevents ArcEllipse models from accurately describing real lensed systems.
Key words: gravitational lensing: strong / methods: analytical
© ESO, 2012
1. Introduction
Gravitational lensing is an important tool for a variety of astrophysical applications. In particular, gravitationally lensed arcs produced by massive galaxy clusters can provide information on their total inner mass distribution (Hattori et al. 1999; Guzik & Seljak 2002; Mandelbaum & Seljak 2006; Treu 2010; Kneib & Natarajan 2011). Statistical analyses of gravitational arcs provide constraints on the evolution of structure with cosmic time and on the cosmological parameters (Hilbert et al. 2007; Vuissoz et al. 2007; Kochanek et al. 2006; Meneghetti et al. 2004; Golse et al. 2002; Bartelmann et al. 1998; Estrada et al.(2007)Estrada Annis; Hennawi et al. 2008; Kausch et al. 2010; More et al. 2012). Because of the flux amplification associated to gravitational lensing, these arcs are also a probe for the high-redshift universe, which is unaccessible through unlensed sources.
On the other hand, gravitational arcs are very rare objects, since each square degree of the sky contains approximately one galaxy cluster massive enough to produce arcs by gravitational lensing (Gladders & Yee 2005). So far an order of hundreds of these objects were detected (Luppino et al. 1999; Zaritsky & Gonzalez 2003; Gladders et al. 2003; Sand et al. 2005; Cabanac et al. 2007; Bolton et al. 2008). Future wide-field surveys with sub-arcsecond seeing, such as the Dark Energy Survey (DES)1, will provide large samples of gravitational arc systems that will enable numerous statistical studies. Because of the large area, it will be virtually impossible to visually inspect the whole survey to look for gravitationally lensed sources. Therefore, automated detection methods are ultimately needed.
 |
Fig. 1 Geometrical figures produced by the ArcEllipse. Left panel: symmetric ArcEllipse created with e = 1 − b/a = 0.9, b = 1 pixels, rc = 15 pixels, and θ0 = 45°. Right panel: asymmetric ArcEllipse created with e1 = 0.9,e2 = 0.75, with the remaining parameters as in the left panel. |
There are a few proposals for automated detection algorithms in the literature, although none of them is considered as the default algorithm (e.g., Lenzen et al. 2004; Horesh et al. 2005; Seidel & Bartelmann 2007; Cabanac et al. 2007; More et al. 2012; Bom et al. 2012). Moreover, most of these algorithms are not fully characterized in the sense that they do not have a determined efficiency and contamination. These quantities could be quantified by using samples of images with simulated arcs, which would act as truth tables for this type of study. Furthermore, simulated arc images are useful to test in controlled studies arc measurement tools and image pre-processing algorithms used to enhance their detectability.
Currently, the literature lacks sufficiently detailed works related to the fast simulation and characterization of gravitational arcs. Arc simulations have mostly been based on ray-tracing techniques given a distribution of source and lens properties. The common practice is to measure the arc’s length L, width W, and its distance to the center of the lens. Few authors have tried to constrain their shapes and orientation. Miralda-Escude (1993) introduced the idea of measuring L by fitting a circle arc through the arc center and its extremes. Bartelmann & Weiss (1994) have pioneered the idea of approximating gravitational arcs as an ellipse whose major axis is equal to L (the so-called ellipse fitting). However, we are not aware of any preceding study that has introduced a surface brightness distribution to simulate and characterize gravitational arcs.
Motivated by these questions, we developed a code called PaintArcs which draws geometric figures that mimic arcs and adds them to images. It currently uses the prescription of an ArcEllipse, which is an analytical expression for the deformation of an ellipse such that one of its main axis becomes a circle segment. Only a handful of fully controllable parameters go into this simple prescription. We use the ArcEllipse in conjunction with a Sérsic profile to take into account the surface brightness distribution of the simulated arc. We also present ArcFitting, which is a code that uses the ArcEllipse+Sérsic model to estimate the morphological and structural parameters of real arcs.
The prescriptions that we adopt here for the shape and structure of arcs are certainly a simplification of real gravitational arcs, which are often formed by the merging of individual multiple images of a source. One such situation are the giant arcs formed when a source is close to the cusp of a caustics. Particularly when real arcs are imaged in high resolution, the ArcEllipse shape with a Sérsic profile will not accommodate their substructures. Our goal here is to exactly quantify the observed discrepancies from a simple model and, as a result, assess which improvements are most promising and to what extent these simple models can be used in controlled experiments for automatic arc detection algorithms.
This paper is organized as follows. In Sect. 2 we present the ArcEllipse, including the addition of a surface brightness profile and asymmetry. In Sect. 3 we describe the PaintArcs code, accounting for image pixelation, and including seeing effects and Poisson noise in the simulated image. The ArcFitting methods are presented in Sect. 4 and their application to fit real images are presented in Sect. 5. Finally, in Sect. 6, we discuss the results and future work.
2. ArcEllipse
The ArcEllipse consists of a simple idea to analytically express arc shapes as the distortion of an ellipse such that one of its main axes is bent into an arc of a circle. The resulting geometrical figure can be used to create a surface brightness map that mimics a gravitational arc.
An ordinary ellipse is formed by the set of points whose distances to the
x and y axes, weighted by the semi-axes,
a and b, satisfy 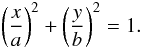 (1)Following the same idea,
we can define the ArcEllipse as the set of points whose distances from a point on the
circumference along the tangential direction
(rc Δθ) and along the radial direction
(Δr) satisfy
(1)Following the same idea,
we can define the ArcEllipse as the set of points whose distances from a point on the
circumference along the tangential direction
(rc Δθ) and along the radial direction
(Δr) satisfy 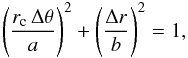 (2)where
rc is the radius of curvature of the circle (and thus the
curvature radius of the arc).
(2)where
rc is the radius of curvature of the circle (and thus the
curvature radius of the arc).
This simple expression indeed gives a shape that resembles an arc, as we can see in the left panel of Fig. 1. We define the length of an ArcEllipse as the length of the arc segment between the two extreme points where Δr = 0. This leads to L = 2a. The width at Δθ = 0 is given by W = 2b. Therefore, the length-to-width ratio of the ArcEllipse is simply given as L/W = a/b.
In polar coordinates, if the origin of the coordinate system corresponds to the center
of curvature of the ArcEllipse, we have
Δr = r − rc and
Δθ = θ − θ0, where
θ0 is the position angle of the ArcEllipse center, such that
![\begin{equation} r_{\pm} = r_{\rm c} \pm b \sqrt{1-\left[\frac{r_{\rm c} \left(\theta_0 - \theta \right)}{a} \right]^2}\cdot \label{r_arcellipse} \end{equation}](/articles/aa/full_html/2013/01/aa20387-12/aa20387-12-eq26.png) (3)The ArcEllipse is therefore
defined by four parameters: the length 2a, the width 2b, the curvature radius
rc, and the position angle θ0.
(3)The ArcEllipse is therefore
defined by four parameters: the length 2a, the width 2b, the curvature radius
rc, and the position angle θ0.
From the solution above, it is simple to show that the area of the ArcEllipse is given by
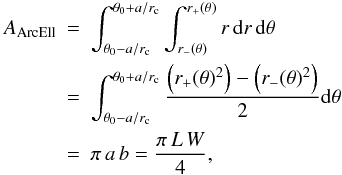 (4)i.e.,
identical to that of an ellipse with semi-axes a and b.
(4)i.e.,
identical to that of an ellipse with semi-axes a and b.
In order to represent an arc, we must impose some limits on the ArcEllipse parameters such as b < rc, to ensure the arc shape, and a < 2πrc, to avoid closing the ArcEllipse into a ring.
2.1. Surface brightness profile for ArcEllipses
To create a surface brightness map with ArcEllipse isophotes, from a given radial
profile, we need to simply replace the argument in a radial profile by the function
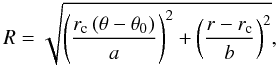 (5)which is constant over
ArcEllipses. Notice that in this case the ArcEllipse must be centered at the origin
(center of curvature). We can rewrite this expression as
(5)which is constant over
ArcEllipses. Notice that in this case the ArcEllipse must be centered at the origin
(center of curvature). We can rewrite this expression as ![\begin{equation} R = \frac{1}{b} \sqrt{[r_{\rm c} \left(\theta-\theta_0 \right) (1-e) ]^2+(r-r_{\rm c})^2}=\frac{1}{b}R_{{\rm prof}}, \label{new_profile} \end{equation}](/articles/aa/full_html/2013/01/aa20387-12/aa20387-12-eq31.png) (6)where
e = 1 − b/a is the
ellipticity.
(6)where
e = 1 − b/a is the
ellipticity.
2.2. Asymmetric ArcEllipse
Since the gravitational arcs in general are not symmetric, we can also add some asymmetry
to the ArcEllipse model. The simplest way to implement that is to consider two different
values for the semi-major axis, a1 and
a2, preserving the semi-minor axis as b; in
other words, two ArcEllipses with different a matched at
θ0. Points whose angle θ are larger that
θ0 will therefore have ellipticity 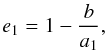 (7)whereas points whose
angle θ are smaller that θ0 will have
(7)whereas points whose
angle θ are smaller that θ0 will have
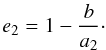 (8)Now the length is
given by
(8)Now the length is
given by 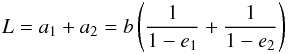 (9)and
Eq. (4) still holds.
(9)and
Eq. (4) still holds.
In the right panel of Fig. 1 we show an example of an asymmetric ArcEllipse. It has the same values of rc and θ0 as the symmetric arc shown on the left panel. But now we set e1 = 0.9 and e2 = 0.75.
3. PaintArcs: an implementation of ArcEllipse
PaintArcs is a code written in Python that implements a model to simulate objects with arc morphology and adds them to astronomical images. It performs the digitalization of the surface brightness profile whose radial argument is given by the Eq. (6). It also performs point spread function (PSF) convolution, to add the effect of the atmosphere and instrument, and adds the effect of Poisson fluctuations on the image counts. The code makes use of functions from SLtools2, a library for image processing, catalog manipulation, and strong-lensing applications.
PaintArcs is currently set to use the ArcEllipse model to mimic gravitational arc shapes.
But it is built in a modular way that can accommodate other prescriptions. The surface
brightness distribution currently uses the Sérsic
(1968) model, for which the intensity profile is given by ![\begin{equation} I_{\rm S}(r)=I_{\rm e} \exp \left\{-b_n\left[\left(\frac{r}{r_{\rm e}} \right)^{1/n} - 1 \right]\right\}, \label{sersic} \end{equation}](/articles/aa/full_html/2013/01/aa20387-12/aa20387-12-eq41.png) (10)where
Ie is the intensity at the effective radius
re that encloses half of the total light from the model. The
constant bn is defined in terms of the
parameter n, which describes the shape of the profile. The value
of bn can be computed numerically or obtained
using analytical expressions that approximate its value. In this work we use the
approximation of Ciotti & Bertin (1999),
given by
(10)where
Ie is the intensity at the effective radius
re that encloses half of the total light from the model. The
constant bn is defined in terms of the
parameter n, which describes the shape of the profile. The value
of bn can be computed numerically or obtained
using analytical expressions that approximate its value. In this work we use the
approximation of Ciotti & Bertin (1999),
given by 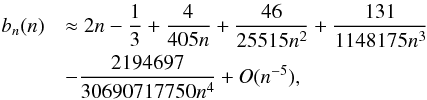 which
is better than one part in ≈ 10-4 for
n > 0.36. Note that if
re is defined in a different way, the expression for
bn will be different.
which
is better than one part in ≈ 10-4 for
n > 0.36. Note that if
re is defined in a different way, the expression for
bn will be different.
For an arc created with ArcEllipse we choose b = re. In other words, we distort the circular profile only in the tangential direction, preserving its effective size (re) in the radial direction. In this case, the ArcEllipse with Sérsic profile is given by
We need to normalize the intensity of the ArcEllipse
I(r,θ) such that the total signal of the arc, given by
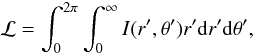 (12)is equal to the total
signal of the arc in the image, which is given by
(12)is equal to the total
signal of the arc in the image, which is given by 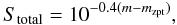 (13)where
m and mzpt are the total magnitude of the arc
to be simulated and the zero point of the magnitude scale of the image. Therefore, the
constant I0 can be found as
(13)where
m and mzpt are the total magnitude of the arc
to be simulated and the zero point of the magnitude scale of the image. Therefore, the
constant I0 can be found as ![\begin{equation} I_0= \frac{10^{-0.4 (m - m_{\rm zpt})}}{\int_0^{2\pi}\int_0^{\infty}\exp \left\{-b_n\left[\frac{\sqrt{[r_{\rm c} \left(\theta'-\theta_0 \right) (1-e) ]^2+(r'-r_{\rm c})^2}}{r_{\rm e}} \right]^{1/n} \right\} r'{\rm d}r'{\rm d}\theta'}\cdot \label{integral_I_0} \end{equation}](/articles/aa/full_html/2013/01/aa20387-12/aa20387-12-eq59.png) (14)For asymmetric ArcEllipses,
the denominator of Eq. (14) should be
replaced by a sum of two integrals, associated to the two values of ellipticity
(e1 and e2, see Sect. 2.2), each one on either side
of θ0.
(14)For asymmetric ArcEllipses,
the denominator of Eq. (14) should be
replaced by a sum of two integrals, associated to the two values of ellipticity
(e1 and e2, see Sect. 2.2), each one on either side
of θ0.
To illustrate the method presented above, we show an arc created following the process described above in the left panel of Fig. 2.
 |
Fig. 2 Example of an ArcEllipse created by PaintArcs using a Sérsic profile. The left panel shows the pure arc, created using rc = 17′′, re = 0.6′′, θ0 = 40°, n = 1, e1 = 0.85, e2 = 0.75, m = 21, and mzpt = 31.83. The pixel scale of the image is 0.154′′. The middle panel shows the application of a Gaussian convolution (FWHM = 1.1′′) on the pure arc image. The right panel shows the effect of adding Poisson noise to the convolved arc. |
3.1. Pixelation
To create a digitized image from a continuous intensity model, we need to integrate the
object signal over a discrete number of pixels. We thus need to control the change in
signal caused by the pixelation and try to keep it lower than some tolerance value,
ϵ. In a typical position in our image, close to the Sérsic effective
radius re, the profile intensity is expected to vary by
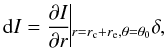 (15)where
δ is the linear size of the pixel. Therefore, the fractional error in
the pixel intensity is
(15)where
δ is the linear size of the pixel. Therefore, the fractional error in
the pixel intensity is 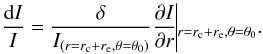 (16)We keep this error
within a tolerance limit by estimating the intensity at a number of subpixels. We can find
the number of subpixels np by imposing
dI/I = ϵ as
follows
(16)We keep this error
within a tolerance limit by estimating the intensity at a number of subpixels. We can find
the number of subpixels np by imposing
dI/I = ϵ as
follows 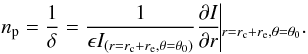 (17)The number
np represents the minimum integer number of subdivisions
of a pixel required to make the error on the pixelation less than ϵ.
(17)The number
np represents the minimum integer number of subdivisions
of a pixel required to make the error on the pixelation less than ϵ.
In the example of Fig. 2, we used ϵ = 0.1 as the upper limit for the error on the digitalization of the arc signal. In this case, np = 4, which means that each pixel was subdivided into 16 parts. The exact value of the digitalization error, computed afterwards by comparing the total signal to be simulated (Stotal, see Eq. (13)) with the signal that was effectively distributed, is on the order of 10-3. This value is much lower than the adopted ϵ, attesting that the criterium given by Eq. (17) is based on a profile region where the variation in the arc intensity is stronger than average, while the exact value of the error is computed using all pixels. Therefore the actual pixelation error is much smaller than ϵ.
3.2. Adding the seeing effect
To add the seeing effect to a simulated image created with PaintArcs, we convolve it with
a 2D normalized Gaussian PSF, given by ![\begin{equation} {\it PSF} = g(x,y)= \frac{\exp \left\{-\left[\frac{x^2}{2\sigma_x^2}+\frac{y^2}{2\sigma_y^2}\right]\right\}}{\int{\int{ \exp \left\{-\left[\frac{x^2}{2\sigma_x^2}+\frac{y^2}{2\sigma_y^2}\right]\right\}{\rm d}x {\rm d}y}}}, \label{gaussiana} \end{equation}](/articles/aa/full_html/2013/01/aa20387-12/aa20387-12-eq84.png) (18)where
σx and
σy are the standard deviation in
x and y directions. The option
σx ≠ σy
allows an elliptical Gaussian.
(18)where
σx and
σy are the standard deviation in
x and y directions. The option
σx ≠ σy
allows an elliptical Gaussian.
Assuming a circular Gaussian
(σ = σx = σy),
the standard deviation can be obtained from the full width at half maximum (FWHM) of an
actual image through 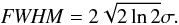 (19)We implemented a
Python module to convolve images with a Gaussian kernel whose size is a multiple of the
standard deviation (nσ).
(19)We implemented a
Python module to convolve images with a Gaussian kernel whose size is a multiple of the
standard deviation (nσ).
In the middle panel of Fig. 2 we show the result of the Gaussian convolution on the arc image previously presented (arc in the left panel of this figure), where we use a seeing FWHM of 1.1′′, which corresponds to σ = 0.47′′, and nσ = 4.
Attesting the code’s flexibility and modularity, new implementations of PaintArcs are being developed to use alternative seeing kernels, such as a 2D Moffat function.
3.3. Adding Poisson noise
In a quantum detector such as a CCD the photon counts follow a Poisson distribution,
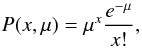 (20)where
μ is the mean of the distribution.
(20)where
μ is the mean of the distribution.
We add Poisson noise to an ArcEllipse produced by PaintArcs by randomly picking values from the distribution given by Eq. (20) with the mean equal to the signal in each pixel of the simulated image after convolution with the PSF. This is done with a separate module that generates random numbers from a Poisson distribution.
In the right panel of Fig. 2 we show the result of adding Poisson noise to the arc of the middle panel of the same figure.
3.4. Applying PaintArcs
After the pixelation of the surface brightness profile of the arc created with PaintArcs with a Sérsic profile and adding seeing and Poisson noise to its image, PaintArcs can paste this simulated arc onto a real image (for example one containing a galaxy cluster), which can be specified in its input configuration file. In this case, PaintArcs adds the arc model parameters to the image header for bookkeeping purposes.
Figure 3 shows an example of an arc simulated with PaintArcs. It was added to the image of the galaxy cluster SOGRAS0328+0044, which was imaged by the SOAR Gravitational Arc Survey (SOGRAS, Furlanetto et al. 2012).Two real arc candidates are also found around the cluster’s brightest galaxy (indicated by arrows), and may serve as a visual guideline for the accuracy of the PaintArcs outputs. The simulated ArcEllipse is circled in the figure and was generated with the parameters m = 21.5,e1 = 0.9,e2 = 0.8,rc = 7.7′′,θ0 = 40°,n = 3, and re = 0.8′′. It was convolved with a Gaussian PSF whose FWHM was obtained from the image (FWHM = 0.7′′). The origin of the coordinate system of the arc coincides with the center of the cluster’s brightest galaxy. The pixel size of this image is 0.154′′.
 |
Fig. 3 Example of the application of PaintArcs on a real image: the circled arc was created by the code using an ArcEllipse+Sérsic model with m = 21.5,e1 = 0.9,e2 = 0.8,rc = 7.7′′,θ0 = 40°,n = 3, re = 0.8′′,FWHM = 0.7′′ and was added to the image of the galaxy cluster SOGRAS0328+0044, where two real arc candidates (indicated by arrows) were found. |
4. ArcFitting
Motivated by the need for tools for measuring arc parameters, such as its length, width, curvature, and surface brightness, we also developed a tool that fits these properties to real (or realistically simulated) gravitational arcs. We named it ArcFitting.
Currently, ArcFitting is based on the ArcEllipse model with a Sérsic profile. Therefore, it performs measurements on actual arc images that lead to estimates of the ArcEllipse parameters. Similarly to PaintArcs, ArcFitting is also a Python-based code that was designed in a modular way to allow different shape- and profile models to be adopted in the future.
In Sect. 2 we showed that the ArcEllipse depends on the following parameters (see Eq. (6))
-
x0: x position of the point where the arc is centered (pixel);
-
y0: y position of the point where the arc is centered (pixel);
-
rc: distance of the arc center relative to (x0,y0) (pixel);
-
θ0: orientation of the arc center relative to the x axis (radians);
-
e1 and e2: ellipticities of the arc;
-
b: minor semi-axes of the arc (pixel).
If the surface brightness distribution of the arc follows a Sérsic profile, we add three more parameters to the fitting:
-
re: radius that encloses half of the total luminosity of the Sérsic profile (pixel);
-
n: index that describes the shape of the Sérsic profile;
-
I0: intensity of the Sérsic profile at the center of the arc (r = 0).
4.1. Creating an arc image to be fitted
The ArcFitting code works on a postage stamp image of an observed arc (i.e., an image where the pixels not belonging to the arc are set to zero), which we call the arc image. To create the arc image we first run SExtractor 2.8.6 (Bertin & Arnouts 1996) on the original image that contains the arc. SExtractor then creates a segmentation image, which assigns a single value (corresponding to the sequential number of the object in the output image catalog) to all pixels that it associates to the object. The arc image is then created by copying all arc pixels defined by the segmentation image, but using their values as in the original image. All other pixels in the arc image are assigned a zero value. The size of the arc image in the x and y directions are multiples of the arc’s major and minor axis values as found by SExtractor. The procedure described above to create the arc image makes use of functions from SLtools.
4.2. Parameter determination from the arc image
In the following we describe the measurements performed by ArcFitting to find the ArcEllipse parameters. But the ArcFitting is not only restricted to the model parameters, which currently are the nine ArcEllipse+Sérsic parameters listed above. It also attempts to measure other commonly used arc parameters, such as its length L and width W.
4.2.1. Determining the ArcEllipse parameters
First, ArcFitting finds the two farthest points of the arc image, p1 and p2. For that, it uses any reference point to find the first extreme as the farthest point from the reference one. It then finds the farthest point from this first extreme through the farthest-of-farthest method. The code then names the extreme point whose angle is larger (smaller) than θ0 (see Eq. (22) below) as p1 (p2).
After that, ArcFitting obtains the points along the bisectrix between p1 and p2. This line is perpendicular to the line segment that connects these two extreme points. It then finds p3, which is the mean point of the arc along the b direction.
This process is repeated twice to obtain the points p4 and
p5. p4 is the mean arc
position along the bisectrix line between p1 and
p3, whereas p5 is the mean arc
position along the bisectrix line between p2 and
p3. This method is an application of the Mediatrix method
(Bom et al. 2012) for
nb = 2, where nb is the number
of bisections. The length (L) of the arc is then computed as the sum
of the line segments connecting the five points 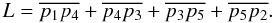 (21)
(21)
 |
Fig. 4 Illustration of the process of tracing a real arc in its image. The left panel shows the five p points used to compute the arc length. The right panel shows the high-intensity m points (dashed circles) used to find pmax for the same arc. The center and radius of curvature are determined as the circle containing the points p1,p2, and pmax = m2. The width is based on the line through the central point p3, whereas the asymmetric major-axes a1 and a2 are the lengths of the segments connecting m2 = pmax to the arc extremes p1 and p2. |
In the left panel of Fig. 4, we illustrate this process of tracing the arc image and determining its length. The five points pi,i = 1,5 are shown along the arc image. The image used as an example in the figure is taken from an HST arc sample that will be presented in Sect. 7.
The ArcEllipse parameters x0,
y0 and rc are found by
determining the unique circle that passes through the extreme points,
p1 and p2, and through the
point with maximum intensity, pmax. The latter point is
found as the arc point with maximum intensity among those that lie within
0.5σb from the line segments of Eq. (21), where σb is
the dispersion of the points along the bisectrix line containing
p3. This procedure is intended to eliminate arc image
pixels located far away from the traced arc, which may be associated to a cosmic ray, or
to a residual from the process of object segmentation and deblending, as these pixels
would bias the pmax estimate. The determination
of pmax is depicted in the right panel of Fig. 4. The pixel of maximum intensity in the entire image,
m1, failed to satisfy the
0.5σb distance criterion, in this case measured from the
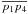 segment. The second maximum, m2, however, is well-placed
along the observed arc.
segment. The second maximum, m2, however, is well-placed
along the observed arc.
The width of the arc is taken as W = 4σb. The ArcEllipse semi-minor axis b is then taken as half of the width (b = W/ 2 = 2σb).
The angle θ0 is obtained using the expression 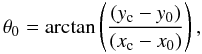 (22)where
(xc,yc) are
the coordinates of the pmax point.
(22)where
(xc,yc) are
the coordinates of the pmax point.
The asymmetric ArcEllipse ellipticities e1 and
e2 are obtained using Eqs. (7) and (8),
respectively, where a1 is the size of the line segment
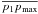 and a2 is the size of the line
segment
and a2 is the size of the line
segment 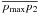 .
.
The procedure outlined above is different compared to previous works. Some studies, particularly of observed arcs, quote L, L/W, or other arc parameters, without clearly mentioning how they are determined. Other sources use no more than three points to infer L, either using a sum of arc segments, as in Eq. (21), or fitting a circular arc through them (Oguri 2002; Dalal et al. 2004; Li et al. 2005; Sand et al. 2005; Horesh et al. 2005; Meneghetti et al. 2008; Horesh et al. 2010; More et al. 2012). Lenzen et al. (2004) and Kausch et al. (2010) measured momenta over arc images to derive their sizes.
Width measurements are usually based on the area of the arc divided by its length assuming some arc geometry, usually a rectangle. Meneghetti et al. (2008), however, measured widths at several different positions along the arc length and assumed a median value. Some authors also account for seeing effects when measuring W (Meneghetti et al. 2008; Zaritsky & Gonzalez 2003).
Arc orientation and curvature are not as common to find. One such reference is Luppino et al. (1999), who used the chord length from the arc extremes and its sagittal depth to estimate rc. Estimates of θ0 can also be found in Oguri (2002) and Miralda-Escude (1993).
We are unaware of previous studies that accommodate a possible asymmetry in the arc’s shape. Finally, another element lacking in previous attempts to measure arc properties is the surface brightness distribution. This is the topic of the next subsection.
4.2.2. Determining the Sérsic parameters
We use χ2 minimization to determine the Sérsic profile parameters, I0, n and re. This χ2 minimization works as follows.
We consider a data set that represents the information of N pixels in
an arc image. We denote Iimg(j) as the
count of the jth pixel of the arc image and
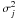 as its
associated uncertainty, where j = (1,N). We also
denote p as the theoretical count of the jth pixel from ArcEllipse with
a Sérsic profile. This theoretical intensity depends on the pixel position and on the
set of parameters p. Except for I0, n and
re, whose values are unknown, the other parameters are
fixed by the procedure described in Sect. 4.2.1.
Assuming that the pixel counts Iimg(j) are
independent from each other, we must minimize the quantity
as its
associated uncertainty, where j = (1,N). We also
denote p as the theoretical count of the jth pixel from ArcEllipse with
a Sérsic profile. This theoretical intensity depends on the pixel position and on the
set of parameters p. Except for I0, n and
re, whose values are unknown, the other parameters are
fixed by the procedure described in Sect. 4.2.1.
Assuming that the pixel counts Iimg(j) are
independent from each other, we must minimize the quantity 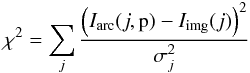 (23)to
estimate the remaining parameters that provide the best fit to the data.
(23)to
estimate the remaining parameters that provide the best fit to the data.
In general, we use the reduced χ2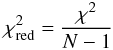 (24)as
a measure of the concordance between the model and the data. If this value is much
higher than unity, the model is not considered a good description of the data.
(24)as
a measure of the concordance between the model and the data. If this value is much
higher than unity, the model is not considered a good description of the data.
We assume that the pixel counts follow a Poisson distribution, such that 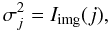 (25)and Eq. (24) becomes
(25)and Eq. (24) becomes 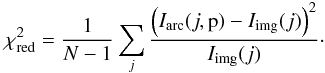 (26)The
(26)The
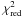 function
minimization is carried out with Pyminuit3, which
is an extension for Python modules of the Minuit4
functions.
function
minimization is carried out with Pyminuit3, which
is an extension for Python modules of the Minuit4
functions.
The initial guesses for I0 and
re are determined through measurements on the arc image.
We consider the intensity of the point pmax as the initial
estimate for I0. The semi-minor axis b,
whose estimate was described above, is the initial guess for
re. Given the lack of a direct method to estimate the
parameter n from the image, the initial guess of this parameters is
found by using the algorith Scan from Pyminuit, which calculates
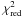 for a range
of n values keeping all other parameters in the p set fixed, i.e.,
the morphological parameters as determined in the previous subsection, and
I0 and re fixed at their
initial guesses.
for a range
of n values keeping all other parameters in the p set fixed, i.e.,
the morphological parameters as determined in the previous subsection, and
I0 and re fixed at their
initial guesses.
After determining the initial guesses for I0,
n and re, we use the Pyminuit algorithm
Migrad, which is an optimized gradient-based minimum search algorithm, to perform the
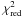 minimization and to find the best-fitting values for these parameters.
minimization and to find the best-fitting values for these parameters.
The approach outlined here to estimate the shape parameters directly from the image and
to apply a χ2 minimization to the Sérsic profile proved to
be the most effective. We tried other alternatives, such as
χ2 minimization (using Migrad) of all shape- and Sérsic
parameters, or an iterative method that combines Migrad for some parameters and brute
force (Scan) for others. In many of the cases we tried, these methods did not converge,
or resulted in a final 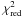 much larger
than unity. These failures are probably caused by a combination of strong degeneracies
among the ArcEllipse and Sérsic model parameters and by the limited degrees of freedom
when considering the number of available pixels in the arc image.
much larger
than unity. These failures are probably caused by a combination of strong degeneracies
among the ArcEllipse and Sérsic model parameters and by the limited degrees of freedom
when considering the number of available pixels in the arc image.
4.3. Testing the ArcFitting algorithm
To test and validate the ArcFitting code, we applied it to images of pure arcs (noiseless and with no seeing convolution) produced with PaintArcs, using the ArcEllipse+Sérsic model.
As an example, we considered an arc with true parameters as shown in the middle column of Table 1. The values recovered by ArcFitting are displayed in the right column, showing an excellent agreement with the input values used by PaintArcs. This situation is typical of the validation tests. Indeed, ArcFitting was very successful in recovering the ArcEllipse and Sérsic parameters in this idealized case. This is expected since both PaintArcs and ArcFitting use the same analytical expression for the arc shape and surface brightness profile, but demonstrates the validity of the whole process of determining the morphological parameters and using the initial guesses for scanning and fitting the Sérsic parameters.
Input and fitted ArcEllipse and Sérsic parameters for an arc created with PaintArcs using the ArcEllipse prescription and a Sérsic surface brightness profile.
5. ArcFitting application to real and simulated arcs
We applied the ArcFitting code to three different sets of arcs. The first one consists of realistically simulated arcs. The other two sets are of real arcs, one from ground-based images and the other from HST images.
We used the residual signal contrast
ΔS/S, defined as 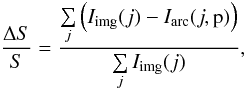 (27)and the reduced
χ2, given by Eq. (26), as metrics for the concordance between the ArcEllipse+Sérsic model, resulting
from ArcFitting, and the data. Both quantities are computed using only the pixels that
belong to the arc as described in Sect. 4.1.
(27)and the reduced
χ2, given by Eq. (26), as metrics for the concordance between the ArcEllipse+Sérsic model, resulting
from ArcFitting, and the data. Both quantities are computed using only the pixels that
belong to the arc as described in Sect. 4.1.
 |
Fig. 5 ArcFitting results for AddArcs arcs. Left panels: original arc; middle panels: arc reproduced with PaintArcs using the parameters provided by the application of ArcFitting on original arcs; right panels: difference between original and reproduced arcs. |
 |
Fig. 6 Distribution of residual signal contrast
ΔS/S (left
panel) and of |
5.1. Applying ArcFitting on arcs simulated with AddArcs
For this first application we used a set of arcs simulated with the AddArcs code (Brandt et al., in prep.), which was originally designed for Dark Energy Survey image simulations. The code uses as basic inputs a catalog of lenses, a catalog of sources, the cosmological parameters, and the properties of the images on which the arcs will be simulated (e.g., pixel scale, magnitude zero points, etc.). For the simulations used in this work, the input lens catalogs were given by the Carmen Las Damas N-body cosmological simulation5 (McBride et al. 2011) and the lenses are modeled as a projected Navarro-Frenk-White (Navarro et al. 1996, 1997, hereafter NFW) profile with elliptical mass distribution. The redshift and mass of each lens are taken from the catalog, but the NFW concentration parameter is taken from the fits of Neto et al. (2007), since the simulations do not have sufficient precision to determine it accurately. The sources are modeled as elliptical Sérsic brightness distributions whose parameters are obtained from fits to galaxies in the Hubble Ultra-Deep Field (UDF) given by Coe et al. (2006), which provides the input source catalog. This same catalog contains the photometric redshift information from multi-waveband data on the UDF.
The sources are divided into redshift bins whose spatial distribution is uniform in each bin. For each lens (i.e., dark matter halo) in the catalog, a number of sources is lensed using the Gravlens (Keeton 2001) software. The number of sources to be lensed is obtained from the surface density distribution of the input source catalog. A first selection of sources is made using the local magnification computed with Gravlens and then the same code is used to produce a full brightness distribution by lensing finite Sérsic sources from the UDF catalog. Finally, images are identified and are dimensionally estimated by SExtractor, and only elongated images are selected by the code. We selected a subset of nine arcs generated from these simulations to have a similar sample size as the two other samples.
We ran ArcFitting on the arcs produced with AddArcs to infer their ArcEllipse+Sérsic parameters and recreate them with PaintArcs. In Fig. 5 we show some examples of this application of the ArcFitting code. In the left panels we show the original simulated arcs (noiseless and without seeing convolution) from AddArcs. In the middle panel we show the ArcEllipse derived from ArcFitting and reproduced with PaintArcs. In the right panel we show the residual image resulting from the difference between the two previous ones. All panels use the same grayscale. Some substructures are visible in these latter images, indicating the limitations of the ArcEllipse prescription. But the residuals are much less intense than the fitted arcs.
We computed the residual signal contrast
ΔS/S, as given in Eq. (27), between each AddArcs simulation and its
fitted ArcEllipse+Sérsic. In the left panel of Fig. 6
we show the resulting distribution
of ΔS/S values. The median
ΔS/S value is −0.09, indicating
that the ArcFitting process based on the ArcEllipse+Sérsic model typically reproduces 91%
of the signal of the input arc image. In the right panel of Fig. 6 we present the distribution of 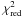 resulting
from the application of ArcFitting on arcs simulated with AddArcs, whose median is
resulting
from the application of ArcFitting on arcs simulated with AddArcs, whose median is
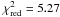 .
.
5.2. Applying ArcFitting on arcs observed with the HST
We here test the reconstruction of HST arcs using the ArcFitting code based on the ArcEllipse+Sérsic model. A sample of HST arcs was selected from the work by Smith et al. (2005). We chose bright and isolated arcs with spectroscopic redshift measurements that confirm their nature as lensed sources. A total of 12 arcs were selected. We use the same notation here as the original authors. The arcs are C4, C8, and C12 from the Abell 68 galaxy cluster; H0, H1, H2, and H3 from Abell 963; B0/B1/B4 from Abell 383; M1 and M3 from Abell 2218; and P0 and P2 from Abell 2219. Arc properties such as magnitude, L/W, and distance to the BCG of these arcs are presented in Sand et al. (2005).
 |
Fig. 7 Selected ArcFitting results for HST arcs. Left panels: original arc; middle panels: arc created with PaintArcs using the parameters derived from ArcFitting applied to the original arcs; right panels: difference between original and reproduced arcs. From top to bottom: arc C8 found in Abell 68; arc H0 of Abell 963; arc M3 of Abell 2218, and arc B0/B1/B4 of Abell 383. |
In Fig. 7 we present some results of the application of ArcFitting to our selected HST arcs. The panels of Fig. 7 are similar to those of Fig. 5. The left panels show the original HST arc image, the middle panels show the fitted ArcEllipse+Sérsic model arc, which was reproduced with PaintArcs, and the right panels show residual images.
From the middle panels we can see that ArcFitting is efficient in recovering arc curvature and orientation. In some cases, as for the second and third arc in the figure, apart from the efficiency in recovering the arc shape, ArcFitting is also efficient in reproducing the arc brightness distributions, so that the residual images contain only little substructure and noise. However, for arcs with many substructures, such as the first and the last of that figure, ArcFitting cannot effectively reproduce the arc brightness profiles.
We again used the residual signal contrast
ΔS/S, given by Eq. (27), and the
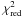 , given by
Eq. (26), to assess the agreement
between model and data. The distribution
of ΔS/S values for all 12 arcs in
our HST sample is shown in the left panel of Fig. 8,
while the distribution of
, given by
Eq. (26), to assess the agreement
between model and data. The distribution
of ΔS/S values for all 12 arcs in
our HST sample is shown in the left panel of Fig. 8,
while the distribution of 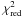 is shown in
the right panel of the same figure. The median of the
ΔS/S distribution is −0.13, but
values as high as −0.32 are found. The median
is shown in
the right panel of the same figure. The median of the
ΔS/S distribution is −0.13, but
values as high as −0.32 are found. The median 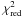 is 18.39, but
the distribution has a long tails toward much higher values. These results clearly attest
that there is a stronger discrepancy between model and HST data than for the simulated
AddArcs images. For all arcs, ΔS is negative, which means that ArcFitting
is overestimating the arc signal. High values in both distributions correspond to the arcs
that present many substructures (example: last arc of Fig. 7, which has ΔS/S = −0.32
and
is 18.39, but
the distribution has a long tails toward much higher values. These results clearly attest
that there is a stronger discrepancy between model and HST data than for the simulated
AddArcs images. For all arcs, ΔS is negative, which means that ArcFitting
is overestimating the arc signal. High values in both distributions correspond to the arcs
that present many substructures (example: last arc of Fig. 7, which has ΔS/S = −0.32
and 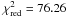 ).
).
 |
Fig. 8 Residual signal contrast
(ΔS/S) distribution
(left panel) and |
In Fig. 9 we show a comparison of the L/W values measured by Sand et al. (2005) to those obtained with ArcFitting. Since the arcs H1, H2, and H3 from Abell 963 are considered as a single object in Sand et al. (2005), these arcs are not included in this comparison. No strong systematics is seen, which shows that ArcFitting provides a robust and automatic measure of L/W ratio in real gravitational arcs.
5.3. Applying ArcFitting on arcs observed from the ground
We also ran the ArcFitting code to reconstruct arcs observed from the ground. We selected bright and isolated arcs in cluster and galaxy group lenses from the CFHTLS Strong Lensing Legacy Survey (SL2S), presented in the work by Cabanac et al. (2007). Following the notation of the original authors, the seven selected arcs that compose our CFHTLS sample are SL2SJ021416-050315, SL2SJ021807-051536, SL2SJ085446- 012137, SL2SJ141912+532612, SL2SJ142258+512440, SL2SJ143001+554647, and SL2SJ143140+553323.
The results of applying ArcFitting on three arcs of our CFHTLS sample are shown in Fig. 10. As in the previous comparisons, the left panels show the original arc images, the middle panels show the fitted ArcEllipse+Sérsic model reproduced with PaintArcs, and the right panels show residual images resulting from the difference between the previous two. We can see that ArcFitting is efficient in recovering arc shape and brightness distributions.
In the left panel of Fig. 11 we present the
residual signal contrast distribution for the selected CFHTLS arc sample. As in the HST
arcs, we can see that ArcFitting overestimates the arc signal, since
ΔS < 0 for all arcs of this sample. The median
of the ΔS/S distribution is −0.11
and ΔS/S = −0.20 in the worst case.
In the rigth panel of the same figure, we show the distribution
of 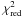 , whose median is
10.76. In contrast to the HST arcs, no high
, whose median is
10.76. In contrast to the HST arcs, no high 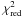 tail is seen;
the only outlier in the
tail is seen;
the only outlier in the 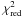 distribution
corresponds to the arc SL2SJ085446-012137, the same arc that presents the highest value in
the ΔS/S distribution. The
improvement in ArcFitting of CFHTLS arcs with respect to HST arcs is likely caused by the
smearing of the arc substructures caused by seeing effects on the ground-based set.
distribution
corresponds to the arc SL2SJ085446-012137, the same arc that presents the highest value in
the ΔS/S distribution. The
improvement in ArcFitting of CFHTLS arcs with respect to HST arcs is likely caused by the
smearing of the arc substructures caused by seeing effects on the ground-based set.
6. Conclusions and future perspectives
We have presented and explored in detail the ArcEllipse, which is a simple analytical model that approximately reproduces the shape of real gravitational arcs. ArcEllipses are ordinary ellipses whose major axes are bent along an arc of a circle and which therefore mimic the shape of tangential arcs. They are fully characterized by a limited number of parameters that quantify their curvature, length and width, degree of deformation, and orientation. We also devised a simple prescription to incorporate asymmetries to their shapes. This description of arc morphology is more comprehensive than previously found in the literature. We also incorporated a Sérsic light profile distribution to the ArcEllipses in an attempt to explore a rough structural model for lensed galaxies.
We also implemented PaintArcs, which is a tool that currently generates simulated ArcEllipse images, and ArcFitting, which is a code that derives model parameters from images of real arcs. Both are Python codes built in a modular way, thus allowing flexibility. PaintArcs, for instance, incorporates the effects of pixelation, atmospheric seeing, and Poisson noise to the simulated ArcEllipse images, where the latter two can be turned on and off. ArcFitting is capable of deriving the model parameters using different techniques that vary from simple and direct estimates applied on an image to statistical inference methods. Even though both codes currently adopt the ArcEllipse shapes and Sérsic profiles for the arcs, other more complex models can be added to their capabilities in the future.
 |
Fig. 9 Comparison between the L/W measurements presented in Sand et al. (2005) and those obtained with ArcFitting. The solid line represents the identity function. |
We applied the ArcFitting code to different types of gravitational arcs. Realistic arc simulations based on ray-tracing techniques applied to physical models of lens and source, such as those generated with Gravlens, have their general features and total signal reasonably well fit by an ArcEllipse+Sérsic model. The resulting model from ArcFitting typically amounts to more than 90% of the original signal from the arc. Typical reduced χ2 values are on the order of 5.
 |
Fig. 10 ArcFitting results for CFHTLS arcs. Left panels: original arc; middle panels: ArcEllipse+Sérsic image reproduced with PaintArcs using the parameters resulting from ArcFitting; right panels: difference between the previous two panels. From top to bottom: arcs SL2SJ141912+532612, SL2SJ143140+553323, and SL2SJ021807-051536. |
 |
Fig. 11 Residual signal contrast (ΔS/S)
distribution (left panel) and |
For real gravitational arcs around galaxy clusters, either imaged from the ground or using the HST, the total signals are reproduced within 10−20% for ground-based images and within 10−30% for HST images. Comparing the L/W values inferred from ArcFitting to those published for HST data shows that ArcFitting successfully quantifies their axial ratio. We attribute the poorer fitting results from HST images to the presence of substructure in the arcs. This opens up the possibility of using ArcEllipse models to enhance these substructures, helping in identifying giant arcs formed from merging of multiple images. Extending this reasoning, the ArcEllipse shape coupled with a single Sérsic profile might in fact be used as a discriminator to filter out contaminanting elongated galaxies from a sample of arc candidates. Alternatively, gravitational arcs formed from multiple merged images of the same source may be fit by more than one ArcEllipse+Sérsic component to improve their structural modeling.
Attempts to apply a full χ2 minimization fail in general, given the relatively small number of degrees of freedom in the limited arc images available. Our results also indicate that the ArcEllipse prescription is too simplistic to yield significant improvement in the models based on formal statistical inference. We thus reached a compromise set-up in ArcFitting by which statistical inference is applied only to the structural Sérsic parameters, while the shape ArcEllipse parameters are based on measurements over the arc images. The algorithm was succesfully validated in this way by fitting a pure ArcEllipse+Sérsic object with high precision.
The usefulness of the ArcEllipse+Sérsic prescription should not be underestimated. ArcEllipses of varying magnitudes, lenghts, L/W, and radii of curvature can be speedily generated by PaintArcs and used in a number of arc studies, taking advantage of the full control we have on the input arc parameters. The Dark Energy Survey (DES) simulations have already included a sizable sample of arcs generated by PaintArcs by the DES strong lensing working group. Simulated objects using PaintArcs allow an efficient testing of arcfinders, which are codes meant to automatically detect gravitational arcs (Furlanetto et al., in prep.). In a 5000 sq. deg survey such as DES, usage of automated arcfinders is unavoidable, since their large areas preclude visual image inspection.
The ArcEllipse also allows an approximate initial characterization of observed gravitational arcs. Even such rough morphological and structural parameters of observed gravitational arcs are not commonly found in the literature. Our approach is thus providing both a qualitative and quantitative improvement on the amount of information extracted from observed gravitational arcs. The efficiency of ArcFitting is also an important aspect. For large samples of arcs that contain perhaps thousands of them, as in the case of the DES, an efficient first pass on arc parameters is a necessary tool associated to the arcfinders themselves.
The SLtools library is available at http://che.cbpf.br/sltools/
Acknowledgments
We thank the anonymous referee for useful comments. We acknowledge the support of the Laboratório Interinstitucional de e-Astronomia (LIneA) operated jointly by Centro Brasileiro de Pesquisas Físicas (CBPF), Laboratório Nacional de Computação Científica (LNCC), and Observatório Nacional (ON) and funded by the Ministério da Ciência, Tecnologia e Inovação (MCTI) da República Federativa do Brasil. The authors are supported by grants from the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES). M.M. is also partially supported by FAPERJ (grant E-26/110.516/2012). M.M. acknowledges the hospitality of Instituto Balseiro at Centro Atomico Bariloche where part of this work was done. This paper makes use of observations obtained at the Southern Astrophysical Research (SOAR) telescope, which is a joint project of MCTI, the US National Optical Astronomy Observatory (NOAO), the University of North Carolina at Chapel Hill (UNC), and Michigan State University (MSU); observations made with the NASA/ESA Hubble Space Telescope, obtained from the ESO/ST-ECF Science Archive Facility; and observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council (NRC) of Canada, the Institut National des Science de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This work is based in part on data products produced at TERAPIX and the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS.
References
- Bartelmann, M., & Weiss, A. 1994, A&A, 287, 1 [NASA ADS] [Google Scholar]
- Bartelmann, M., Huss, A., Colberg, J. M., Jenkins, A., & Pearce, F. R. 1998, A&A, 330, 1 [NASA ADS] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolton, A. S., Burles, S., Koopmans, L. V. E., et al. 2008, ApJ, 682, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Bom, C. R., Makler, M., & Albuquerque, M. P. 2012 [arXiv:1212.1799] [Google Scholar]
- Cabanac, R. A., Alard, C., Dantel-Fort, M., et al. 2007, A&A, 461, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ciotti, L., & Bertin, G. 1999, A&A, 352, 447 [NASA ADS] [Google Scholar]
- Coe, D., Benítez, N., Sánchez, S. F., et al. 2006, AJ, 132, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Dalal, N., Holder, G., & Hennawi, J. F. 2004, ApJ, 609, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Estrada, J., Annis, J., Diehl, H. T., et al. 2007, ApJ, 660, 1176 [NASA ADS] [CrossRef] [Google Scholar]
- Furlanetto, C., Santiago, B. X., Makler, M., et al. 2012, MNRAS, submitted [arXiv:1210.4136] [Google Scholar]
- Gladders, M. D., & Yee, H. K. C. 2005, ApJS, 157, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Gladders, M. D., Hoekstra, H., Yee, H. K. C., Hall, P. B., & Barrientos, L. F. 2003, ApJ, 593, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Golse, G., Kneib, J.-P., & Soucail, G. 2002, A&A, 387, 788 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guzik, J., & Seljak, U. 2002, MNRAS, 335, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Hattori, M., Kneib, J., & Makino, N. 1999, Progress Theoret. Phys. Suppl., 133, 1 [Google Scholar]
- Hennawi, J. F., Gladders, M. D., Oguri, M., et al. 2008, AJ, 135, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Hilbert, S., White, S. D. M., Hartlap, J., & Schneider, P. 2007, MNRAS, 382, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Horesh, A., Ofek, E. O., Maoz, D., et al. 2005, ApJ, 633, 768 [NASA ADS] [CrossRef] [Google Scholar]
- Horesh, A., Maoz, D., Ebeling, H., Seidel, G., & Bartelmann, M. 2010, MNRAS, 406, 1318 [NASA ADS] [Google Scholar]
- Kausch, W., Schindler, S., Erben, T., Wambsganss, J., & Schwope, A. 2010, A&A, 513, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keeton, C. R. 2001 [arXiv:astro-ph/0102340] [Google Scholar]
- Kneib, J.-P., & Natarajan, P. 2011, A&ARv, 19, 47 [Google Scholar]
- Kochanek, C. S., Morgan, N. D., Falco, E. E., et al. 2006, ApJ, 640, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Lenzen, F., Schindler, S., & Scherzer, O. 2004, A&A, 416, 391 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, G.-L., Mao, S., Jing, Y. P., et al. 2005, ApJ, 635, 795 [NASA ADS] [CrossRef] [Google Scholar]
- Luppino, G. A., Gioia, I. M., Hammer, F., Le Fèvre, O., & Annis, J. A. 1999, A&AS, 136, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mandelbaum, R., & Seljak, U. 2006, in Am. Astron. Soc. Meet. Abstracts #208, BAAS 38, 148 [Google Scholar]
- McBride, C., Berlind, A. A., Scoccimarro, R., et al. 2011, in Am. Astron. Soc. Meet. Abstracts #217, BAAS 43, 249.07 [Google Scholar]
- Meneghetti, M., Dolag, K., Tormen, G., et al. 2004, Mod. Phys. Lett. A, 19, 1083 [NASA ADS] [CrossRef] [Google Scholar]
- Meneghetti, M., Melchior, P., Grazian, A., et al. 2008, A&A, 482, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miralda-Escude, J. 1993, ApJ, 403, 509 [NASA ADS] [CrossRef] [Google Scholar]
- More, A., Cabanac, R., More, S., et al. 2012, ApJ, 749, 38 [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Neto, A. F., Gao, L., Bett, P., et al. 2007, MNRAS, 381, 1450 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M. 2002, ApJ, 573, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Sand, D. J., Treu, T., Ellis, R. S., & Smith, G. P. 2005, ApJ, 627, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Seidel, G., & Bartelmann, M. 2007, A&A, 472, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sérsic, J. L. 1968, Atlas de galaxias australes (Cordoba, Argentina: Observatorio Astronomico) [Google Scholar]
- Smith, G. P., Kneib, J.-P., Smail, I., et al. 2005, MNRAS, 359, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Treu, T. 2010, ARA&A, 48, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Vuissoz, C., Courbin, F., Sluse, D., et al. 2007, A&A, 464, 845 [Google Scholar]
- Zaritsky, D., & Gonzalez, A. H. 2003, ApJ, 584, 691 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Input and fitted ArcEllipse and Sérsic parameters for an arc created with PaintArcs using the ArcEllipse prescription and a Sérsic surface brightness profile.
All Figures
 |
Fig. 1 Geometrical figures produced by the ArcEllipse. Left panel: symmetric ArcEllipse created with e = 1 − b/a = 0.9, b = 1 pixels, rc = 15 pixels, and θ0 = 45°. Right panel: asymmetric ArcEllipse created with e1 = 0.9,e2 = 0.75, with the remaining parameters as in the left panel. |
| In the text | |
 |
Fig. 2 Example of an ArcEllipse created by PaintArcs using a Sérsic profile. The left panel shows the pure arc, created using rc = 17′′, re = 0.6′′, θ0 = 40°, n = 1, e1 = 0.85, e2 = 0.75, m = 21, and mzpt = 31.83. The pixel scale of the image is 0.154′′. The middle panel shows the application of a Gaussian convolution (FWHM = 1.1′′) on the pure arc image. The right panel shows the effect of adding Poisson noise to the convolved arc. |
| In the text | |
 |
Fig. 3 Example of the application of PaintArcs on a real image: the circled arc was created by the code using an ArcEllipse+Sérsic model with m = 21.5,e1 = 0.9,e2 = 0.8,rc = 7.7′′,θ0 = 40°,n = 3, re = 0.8′′,FWHM = 0.7′′ and was added to the image of the galaxy cluster SOGRAS0328+0044, where two real arc candidates (indicated by arrows) were found. |
| In the text | |
 |
Fig. 4 Illustration of the process of tracing a real arc in its image. The left panel shows the five p points used to compute the arc length. The right panel shows the high-intensity m points (dashed circles) used to find pmax for the same arc. The center and radius of curvature are determined as the circle containing the points p1,p2, and pmax = m2. The width is based on the line through the central point p3, whereas the asymmetric major-axes a1 and a2 are the lengths of the segments connecting m2 = pmax to the arc extremes p1 and p2. |
| In the text | |
 |
Fig. 5 ArcFitting results for AddArcs arcs. Left panels: original arc; middle panels: arc reproduced with PaintArcs using the parameters provided by the application of ArcFitting on original arcs; right panels: difference between original and reproduced arcs. |
| In the text | |
 |
Fig. 6 Distribution of residual signal contrast
ΔS/S (left
panel) and of |
| In the text | |
 |
Fig. 7 Selected ArcFitting results for HST arcs. Left panels: original arc; middle panels: arc created with PaintArcs using the parameters derived from ArcFitting applied to the original arcs; right panels: difference between original and reproduced arcs. From top to bottom: arc C8 found in Abell 68; arc H0 of Abell 963; arc M3 of Abell 2218, and arc B0/B1/B4 of Abell 383. |
| In the text | |
 |
Fig. 8 Residual signal contrast
(ΔS/S) distribution
(left panel) and |
| In the text | |
 |
Fig. 9 Comparison between the L/W measurements presented in Sand et al. (2005) and those obtained with ArcFitting. The solid line represents the identity function. |
| In the text | |
 |
Fig. 10 ArcFitting results for CFHTLS arcs. Left panels: original arc; middle panels: ArcEllipse+Sérsic image reproduced with PaintArcs using the parameters resulting from ArcFitting; right panels: difference between the previous two panels. From top to bottom: arcs SL2SJ141912+532612, SL2SJ143140+553323, and SL2SJ021807-051536. |
| In the text | |
 |
Fig. 11 Residual signal contrast (ΔS/S)
distribution (left panel) and |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{eqnarray} \label{sersic_arcellipse} I(r,\theta)&=&I_{\rm S}\left(R_{{\rm prof}}(r,\theta)\right)\nonumber \\ &=& I_0\exp \left\{\!-b_n\left[\frac{\sqrt{[r_{\rm c} \left(\theta-\theta_0 \right) (1\!-\!e) ]^2\!+\!(r\!-\!r_{\rm c})^2}}{r_{\rm e}} \right]^{1/n} \!\right\}, \end{eqnarray}](/articles/aa/full_html/2013/01/aa20387-12/aa20387-12-eq51.png)