| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A82 | |
| Number of page(s) | 9 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201218792 | |
| Published online | 21 December 2012 | |
Early evolution of the birth cluster of the solar system
1 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
2 Kavli Institute of Theoretical Physics, Kohn Hall, University of California, Santa Barbara, CA 93106-4030, USA
e-mail: spfalzner@mpifr-bonn.mpg.de
Received: 9 January 2012
Accepted: 30 October 2012
Context. The solar system was most likely born in a star cluster containing at least 1000 stars. It is highly probable that this cluster environment influenced various properties of the solar system such as its chemical composition, size, and the orbital parameters of some of its constituting bodies.
Aims. In the Milky Way, clusters with more than 2000 stars only form in two types – starburst clusters and leaky clusters –, each following a unique temporal development in the mass-radius plane. The aim is here to determine the encounter probability in the range relevant to solar system formation for starburst or leaky cluster environments as a function of cluster age.
Methods.N-body methods were used to investigate the cluster dynamics and the effect of gravitational interactions between cluster members on young solar-type stars surrounded by discs.
Results. Using the now available knowledge of the cluster density at a given cluster age we demonstrate that in starburst clusters the central densities over the first 5 Myr are so high (initially > 105 M⊙ pc-3) that hardly any discs with solar system building potential would survive this phase. This makes starburst clusters an unlikely environment for the formation of our solar system. Instead it is highly probable that the solar system formed in a leaky cluster (often classified as OB association). We demonstrate that an encounter determining the characteristic properties existing in our solar systems most likely happened very early on (<2 Myr) in its formation history and that after 5 Myr the likelihood of a solar-type star experiencing such an encounter in a leaky cluster is negligible even if it was still part of the bound remnant. This explains why the solar system could develop and maintain its high circularity later in its development.
Key words: planets and satellites: formation / planetary systems / open clusters and associations: general / galaxies: star formation / Sun: general
© ESO, 2012
1. Introduction
The average stellar density in the solar neighbourhood is 0.112 stars pc-3, meaning that the Sun resides in relative isolation. This may not have been the case at the time of its formation. Most stars form within groups or clusters of stars (Lada & Lada 2003; Porras et al. 2003; Evans et al. 2009). The majority of these clusters and associations dissolve within some tens of Myr (Lada 2006; Portegies Zwart et al. 2010). Even the long-lived open clusters do not exceed a lifetime of some hundreds of Myr. At the current epoch the solar system is about 4.6 Gyr old. This means that if the Sun formed in a cluster environment, the solar birth cluster would have dissipated a long time ago (Portegies Zwart 2009).
Several characteristics of the today’s solar system give clues to the early formation process. These are
-
the outer boundary of the planetary system at 30 AU and innerboundary of the Kuiper belt at ~45 AU;
-
the much higher eccentricities and inclination angles of the Kuiper belt objects, as a group, compared to the planetary orbits;
-
the presence of precursors to the short-lived radioactive isotopes 60Fe and 26Al in meteorites.
These properties strongly indicate that the birthplace of the sun is likely to have been a cluster environment (Gaidos 1995; Fernandez 1997; Adams 2010). Perhaps the strongest constraint comes from the presence of the short-lived radioactive isotopes 60Fe and 26Al inferred from their precursor products in meteorites (Wasserburg et al. 2006; Thrane et al. 2006; Wadhwa et al. 2007; Duprat & Tatischeff 2008; Dauphas & Chaussidon 2011; Gritschneider et al. 2012). These isotopes have half-lives of 2.62 Myr and 0.717 Myr, respectively. Because they decay so quickly, their presence in meteorites means that they must have been incorporated into the early solar system very soon after they were produced.
A supernova is the most likely source for these short-lived radioactive isotopes; in particular the isotope 60Fe is extremely difficult to produce otherwise than by stellar nucleosynthesis (Looney et al. 2006; Williams & Gaidos 2007; Gounelle et al. 2009). A range of supernovae progenitor masses Msp are possible, and no mass scale produces perfect abundances. However, these studies suggest that stars with Msp ≈ 25 M⊙ provide the best fit to the ensemble of short-lived radioactive nuclei (Adams 2010, and references therein). Stars of this high mass usually form only in relatively massive clusters. External enrichment of short-lived radio-isotopes suggests a cluster with at least N > 4000 to have a reasonable chance of producing a star with Msp = 25 M⊙ (Lee et al. 2008).
The relatively high concentration of these short-lived nuclei means not only that they should have been formed just after the formation of the Sun but also fairly close to it. If not, the cross-section of the solar protoplanetary disc would have been too small to account for the amount of material. Several authors have estimated the maximum distance of the solar system when this supernova exploded, obtaining values between 0.2 and 2 pc (for a discussion, see Adams 2010).
The outer boundary of our planetary system (30 AU) and inner boundary of the Kuiper belt at 45 AU are likely significant for the early history of the solar system, too. This outer edge is relatively sharp – as best illustrated by the low mass contained in the total of the large number of Kuiper belt objects, which is only ~ 0.01–0.1 times the mass of the Earth (Bernstein et al. 2004). The protoplanetary disc from which the solar system eventually formed was most likely considerably larger at the time of planet formation. Possible processes that could have led to the truncation of the disc include gravitational interactions with other cluster members (Ida et al. 2000; Kobayashi & Ida 2001; Pfalzner et al. 2005; Kenyon & Bromley 2004; Spurzem et al. 2009), photo-evaporation by nearby massive stars (Adams et al. 2006; Owen et al. 2010; Mitchell & Stewart 2011) or the supernova explosion itself (Chevalier 2000). Each of these scenarios requires a cluster environment of relatively high stellar density.
An alternative explanation for the sharp edge in the mass distribution in the solar system would be the Nice model (Gomes et al. 2005), which suggests that the migration of the giant planets caused a planetesimal clearing event, leading to a late heavy bombardment (LHB) at 880 Myr. However, Booth et al. (2009) found that collisional processes are important in the solar system before the LHB and that parameters for weak Kuiper belt objects are inconsistent with the Nice model interpretation of the LHB.
The much higher eccentricities and inclination angles of the Kuiper belt objects as a group compared to the planetary orbits also point to an encounter as the most likely cause. The most prominent example is Sedna with a periastron of 76 AU, an apastron of 937 AU and an eccentricity of 0.8527. It is well beyond the reach of the gas giants and could not be scattered into this highly eccentric orbit from interactions with Neptune alone (Gomes et al. 2005). The most straightforward explanation for these high eccentricities would be some type of dynamical interactions (Morbidelli & Levison 2004) – either a close single encounter, or a wide binary solar companion (Matese et al. 2005).
If an encounter is responsible for the disc cut-off and the Sedna orbit, then it must have taken place when the stellar density was still relatively high. It is generally assumed that clusters expand significantly after gas expulsion, which is accompanied by a dramatic drop in stellar densities. The time scale of this cluster expansion was not well known until recently. The encounter must have occurred early on in the history of the solar system (Malhotra 2008) because otherwise the dynamical interactions due to passing stars would have not only lead to the truncation of the disc and the high eccentricities in the Kuiper belt objects, but would also have perturbed the orbits of the planets, stripped the comets away and led to portions of the Inner Oort Cloud becoming unstable (Gaidos 1995; Adams & Laughlin 2001). That all planetary orbits are nearly in the same plane (inclination angles < 3.5°) as well as their low orbital eccentricities (<0.2) and the presence of the Inner Oort Cloud all point to a lack of severe disruption after the solar system was fully formed. This provided an upper limit on the stellar density in the solar birth cluster for ages > 30 Myr.
Recently several authors tried to translate constraints derived from the meteorite composition, the disc cut-off, and the Sedna orbit into properties of the solar birth environment. These are basically limitations on the number of stars N in the solar birth cluster and its central density ρc. For a summary of their results see Table 1. These conditions do not necessarily need to be fulfilled over a long period of time. Therefore the condition on N based on the chemical composition needs only to be fullfilled before the supernova explodes, whereas the upper limit based on the radiation field needs to be fulfilled after gas expulsion from the cluster – before a gas expulsion photo evaporation is much less efficient – until about 5 Myr, when discs are anyway largely dispersed (Hernandez et al. 2007). The conditions on the cluster density must only be fulfilled at the instant of the encounter.
Constraints on the properties of the solar birth cluster.
Most investigations conclude that a membership of N ≈ 103 to several 104 is the most likely scenario for the solar birth cluster. The lower limit of this estimate is based on the demand that the solar birth cluster should have contained enough stars to make it reasonably likely that it hosted the required supernova progenitor (for details see Adams 2010). Chemical considerations also suggest that the Sun formed in the presence of strong far-ultraviolet radiation fields, where rough estimates indicate a birth cluster with N > 4000 (Lee et al. 2008). Very massive clusters with N > 105 have been also considered as the birth place of the solar system (Williams & Gaidos 2007; Hester et al. 2004). However, the radiation fields provided by these massive young clusters are potentially disruptive. Nevertheless, the early solar nebula could survive in clusters with N ~ several 104 provided that it spends enough time in the outer cluster regions (Scally & Clarke 2001; Mann & Williams 2009).
The cut-off radius of the disc is also used to constrain the membership of the solar birth cluster. The basic method here is to determine the required periastron distance rperi of the Sun with respect to the star encountered to obtain a cut-off in the disc. In a second step this is related to a certain cluster membership. The lower limit of rperi is derived from the results of Hall et al. (1996) and Kobayashi & Ida (2001), which state that parabolic, prograde encounters with solar-type stars lead to a reduction of the disc size to approximately 1/2–1/3 of the periastron distance. Assuming a typical disc size of 100 AU, the cut-off radius translates into a periastron distance of rperi ≈ 100 AU to a grazing encounter. Here a number of simplifying assumptions (parabolic, solar-type star) are made that may require reconsidering (Olczak et al. 2008, 2010). Other authors (Morbidelli & Levison 2004; Looney et al. 2006) come to somewhat different periastron values. To cover the entire parameter range, we therefore consider periastra from 100 AU to 1000 AU to be potentially solar-system-forming encounter events. This translates into a solar birth cluster in the approximate range N = 103 − 104 (Adams 2010).
To summarise, the abundances of short-lived radioactive isotopes and the cut-off at 30 AU both strongly hint at a solar birth cluster size in the range of 4000 < N < 105. Assuming that the stellar masses in the cluster follow the initial mass function (IMF) with an average stellar mass of mav = 0.5 M⊙, this is equivalent to a total cluster mass mcl of 2000 M⊙ < mcl < 0.5 × 105 M⊙.
What about the stellar densities in these clusters? The density of the solar system birth cluster is so far mainly constrained by considering what types of encounters are necessary to result in a Sedna-like orbit. It is a point of debate whether there is an encounter scenario that can account for both features – cut-off and the Sedna orbit – resulting from a single encounter, or whether two separate encounters are necessary.
Investigating the origin of Sedna’s orbit, Brasser et al. (2006) required central cluster densities higher than 103 M⊙ pc-3, whereas Schwamb et al. (2010) ruled out central densities ≥ 105 M⊙ pc-3. Both authors worked with somewhat different periastri than Adams (2010), which can be summarised in that an encounter between 100–1000 AU was required to result in the high eccentricities of the Kuiper belt objects. Brasser et al. (2006) and Schwamb et al. (2010) give limits to the central, and not the mean density of the cluster, because due to mass segregation the most massive stars of a cluster are usually located close to the cluster centre. Because the solar system must have formed close to a supernova that had a massive star as progenitor, the Sun most likely resided close to the cluster centre.
In summary, the presence of short-lived isotopes, the fall-off of the mass distribution of the solar system, and the orbit of Sedna all combine to constrain the solar birth cluster to a membership of a few thousands to ten thousands of stars with a central density of 103 ≤ ρc ≤ 105 M⊙ pc-3.
Recently it was found that massive clusters evolve in specific ways after gas expulsion (Pfalzner 2009). In this paper we investigate how this knowledge can be applied to deduce the birth environment of the solar system. Section 2 summarises the temporal development of massive clusters. In Sect. 3 we show by means of simple approximations that the solar system is unlikely to have developed in a starburst cluster. Section 4 shows the results of detailed modelling of the temporal developement of solar type star-disc systems in leaky clusters. The limitations and consequences of these results are discussed in Sect. 5.
2. Cluster environments
The requirement of the mass of the solar system birth cluster that needs to be in the range 2000 M⊙ < mcl < 5 × 104 M⊙ puts it in the class of massive clusters. In the Milky Way massive young star clusters (tc < 20 Myr, Mc > 103 M⊙) are observed to have mean densities ranging from less than 0.01 to several 105 M⊙ pc-3 and radii from 0.1 pc to several tens of pc. This means that clusters with properties, in terms of mass and density, as demanded for the solar birth cluster exist also at the present time in the Milky Way.
 |
Fig. 1 Observed cluster mass (filled symbols) and derived density (open symbols) as a function of cluster size for clusters more massive than 103 M⊙ as published by Pfalzner (2011). The values were taken from Figer (2008), Wolff (2007) and Borissova et al. (2008) and references therein. |
Recently we demonstrated that these massive clusters evolve in time only along one of two well-defined density-radius tracks – strongly suggesting a bi-modal cluster formation (see Fig. 1) (Pfalzner 2009). The two cluster groups differ considerably in their properties: one group, termed starburst clusters, comprises young compact clusters that develop from a radius Rc of ~ 0.1 pc at 1 Myr to about 1–3 pc at 20 Myr. Simultaneously, the density drops from the initially very high mean stellar density of ≥ 1005 M⊙ pc-3 to 10 M⊙ pc-3 during that timespan. All these starburst clusters are born with the same mean cluster mass, radius, and density and then simply diffuse as 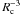 while more or less retaining their mass. The expansion basically proceeds linearly in time, i.e. as Rc ∝ tc with an expansion velocity of 0.1–0.2 pc/Myr.
while more or less retaining their mass. The expansion basically proceeds linearly in time, i.e. as Rc ∝ tc with an expansion velocity of 0.1–0.2 pc/Myr.
The other group, termed leaky clusters, contains many clusters that are usually termed OB associations. This group consists of clusters covering the same age span, but having on average larger radii and lower mean cluster densities (<1–103 M⊙ pc-3). Starting with cluster radii of ~ 2 pc at 1 Myr, they also expand on a time sequence, but here the cluster density decreases as 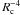 rather than
rather than 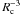 . In these clusters the clusters lose mass, in addition to diffusion. The cluster size does not increase linearly with time, but approximately as
. In these clusters the clusters lose mass, in addition to diffusion. The cluster size does not increase linearly with time, but approximately as 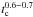 and reaches about 25 pc at 20 Myr.
and reaches about 25 pc at 20 Myr.
This restriction of the development of clusters more massive than 103 M⊙ along only two possible developmental tracks has profound consequences on the formation history of our solar sytem: the solar system inevitably developed either in a starburst or a leaky cluster. The now available knowledge of how the average cluster density ρc changes with cluster age tc in these two environments reduces the scenarios of the solar birth cluster to only two possible developmental paths. It now remains to determine which of the two environments – starburst cluster or leaky cluster – is the more likely origin of the solar system.
3. Solar system in a starburst cluster?
Starburst clusters more or less retain their complete mass over the first 20 Myr. They are likely to remain a bound entity until the galactic tidal field disrupts them. This probably only happens for ages tsb > 100 Myr. A statistical argument against starburst clusters as solar birth hosts would be that probably only ~10% of the stellar population is born within systems that remain gravitationally bound over timescales longer than 100 Myr (e.g., Battinelli & Capuzzo-Dolcetta 1991; Adams & Myers 2001). Most stars are born within clusters that dissolve quickly, after only a few tens of Myr (Lada & Lada 2003; Porras et al. 2003).
 |
Fig. 2 Mean cluster density as function of the cluster age for starburst (circles – observed values and dashed line – interpolation as in Pfalzner 2009) and leaky clusters (triangles and solid line, observations and interpolation, respectively). The red box shows the density requirement for solar-system-forming encounters to be likely. The open squares show the parameters of the clusters modelled in Sect. 4. The thin dashed line shows a fit through the data case where the Arches cluster is excluded from the starburst cluster sequence. Here only the errors in cluster age are given, the errors in cluster densities can be found in Fig. 2 of Pfalzner (2009). |
However, the strongest argument against starburst clusters is their very high initial density of 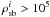 M⊙ pc-3, combined with the high number of massive stars. From the density-size and size-age relations derived in Pfalzner (2009), it follows that the development of the mean stellar density ρsb in a starburst cluster environment can be approximated by (see also dashed line in Fig. 2)
M⊙ pc-3, combined with the high number of massive stars. From the density-size and size-age relations derived in Pfalzner (2009), it follows that the development of the mean stellar density ρsb in a starburst cluster environment can be approximated by (see also dashed line in Fig. 2) ![\begin{eqnarray} \rho_{\rm sb} \approx 5\times 10^5 t_{\rm c}^{-3 \pm 0.3}~\left[\Msun~\mbox{pc}^{-3}\right], \end{eqnarray}](/articles/aa/full_html/2013/01/aa18792-12/aa18792-12-eq44.png) (1)where in the following tc is in units of Myr. Before comparing this density development in starburst clusters with the requirements derived by Brasser et al. (2006) and Schwamb et al. (2010) for the solar birth cluster, one has to correct for the fact that the values by Brasser et al. and Schwamb et al. are central densities, whereas Eq. (1) describes the mean density. The reason why these authors considered central cluster densities is that many star clusters exhibit mass segregation at early ages (<1 Myr) with the most massive stars preferrentially being located close to the cluster centre. From that it follows that most likely the Sun was located near the cluster centre because otherwise it could not have been in close vicinity to the exploding supernova.
(1)where in the following tc is in units of Myr. Before comparing this density development in starburst clusters with the requirements derived by Brasser et al. (2006) and Schwamb et al. (2010) for the solar birth cluster, one has to correct for the fact that the values by Brasser et al. and Schwamb et al. are central densities, whereas Eq. (1) describes the mean density. The reason why these authors considered central cluster densities is that many star clusters exhibit mass segregation at early ages (<1 Myr) with the most massive stars preferrentially being located close to the cluster centre. From that it follows that most likely the Sun was located near the cluster centre because otherwise it could not have been in close vicinity to the exploding supernova.
The mass density values quoted in Pfalzner (2009) are obtained by dividing the cluster mass by its volume – implying an average density. The stellar density in a cluster is in fact a strong function of the radial distance to the cluster centre. Consequently, the central density of a cluster is usually much higher than its mean density. For model clusters of the Orion Nebula Cluster (details of the simulation method can be found in Olczak et al. 2010) we find – depending on the definition of “central” – that the central cluster density ranges from a factor 5–100 times higher than the average stellar density obtained at the half-mass radius. Observations confirm this fact at least for low-mass clusters: for example, Guthermuth et al. (2003) found that in all of the three embedded clusters that they observed, the mean volume densities were of the order of 102–103 M⊙ pc-3, whereas their peak volume densities ranged from 104–105 M⊙ pc-3. Whether this holds also for high-mass clusters needs further investigation.
Accordingly, the requirement by Brasser et al. (2006) and Schwamb et al. (2010) that the central density in the solar system birth cluster should lie in the range 103 M⊙ pc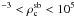 M⊙ pc-3 translates into a mean density of 10 M⊙ pc
M⊙ pc-3 translates into a mean density of 10 M⊙ pc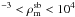 M⊙ pc-3. In Fig. 2 this area is depicted by a red box. It can be seen that the density requirement for the solar birth cluster overlaps with the development of starburst clusters at ages tc > 4 Myr.
M⊙ pc-3. In Fig. 2 this area is depicted by a red box. It can be seen that the density requirement for the solar birth cluster overlaps with the development of starburst clusters at ages tc > 4 Myr.
However, at younger ages starburst clusters have densities up to 102 times higher. At these high densities many of the stars would be completely stripped of their discs by gravitational interactions (Olczak et al. 2010).
 |
Fig. 3 Probability for encounters closer than 100 AU taking place as function of cluster age. The solid and the dashed lines show the estimates for starburst and leaky clusters, respectively. The thick and thin lines distinguish between the entire cluster and the central area only. |
The average time τenc until a star undergoes an encounter with a certain periastron distance rperi can be approximated by (Davies 2011). 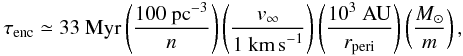 (2)where n is the stellar number density in pc-3, v∞ the mean relative velocity at infinity of the cluster stars and m the mass of the considered star in M⊙. With the cluster mass Mc ≈ 0.5 Nc M⊙, where Nc is the number of cluster members, it follows that ρ [M⊙ pc-3] ≈ 0.5n. Therefore the encounter probability in a star burst cluster can be approximated by
(2)where n is the stellar number density in pc-3, v∞ the mean relative velocity at infinity of the cluster stars and m the mass of the considered star in M⊙. With the cluster mass Mc ≈ 0.5 Nc M⊙, where Nc is the number of cluster members, it follows that ρ [M⊙ pc-3] ≈ 0.5n. Therefore the encounter probability in a star burst cluster can be approximated by 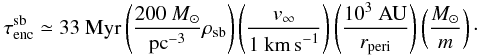 (3)In a simplified picture an encounter closer than 100 AU would lead to a truncation of the disc to rdisc < 30 AU (Adams 2010). This deprives the disc of the material necessary to form the outer planets, that is the resulting planetary system would no longer resemble our solar system. Equation (3) can be used to estimate the likelihood of such a destructive encounter to occur in a starburst environment. Figure 3 (solid lines) shows the likelihood of a destructive encounter (rperi < 100 AU) in a starburst cluster as a function of cluster age using the density development given by Eq. (1). The thin line shows the probability for such an encounter to happen in the entire cluster and the thick line the result for the cluster center, assuming the density there to be on average about 20 times denser then the mean cluster density. Here disc destruction is assumed if each star is likely to experiences at least one encounter closer than 100 AU during a time interval of 1 Myr. Or in other words, the destruction probability is 1, if
(3)In a simplified picture an encounter closer than 100 AU would lead to a truncation of the disc to rdisc < 30 AU (Adams 2010). This deprives the disc of the material necessary to form the outer planets, that is the resulting planetary system would no longer resemble our solar system. Equation (3) can be used to estimate the likelihood of such a destructive encounter to occur in a starburst environment. Figure 3 (solid lines) shows the likelihood of a destructive encounter (rperi < 100 AU) in a starburst cluster as a function of cluster age using the density development given by Eq. (1). The thin line shows the probability for such an encounter to happen in the entire cluster and the thick line the result for the cluster center, assuming the density there to be on average about 20 times denser then the mean cluster density. Here disc destruction is assumed if each star is likely to experiences at least one encounter closer than 100 AU during a time interval of 1 Myr. Or in other words, the destruction probability is 1, if 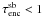 Myr and 1/
Myr and 1/![\hbox{$\tau^{\rm sb}_{\rm enc}[{\rm Myr}]$}](/articles/aa/full_html/2013/01/aa18792-12/aa18792-12-eq62.png) for
for 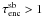 Myr. This definition does not include repeated encounters, so in reality meaning that disc destruction would be even higher than indicated in Fig. 3.
Myr. This definition does not include repeated encounters, so in reality meaning that disc destruction would be even higher than indicated in Fig. 3.
In both cases the cluster environment is extremely collisional and encounters closer than 100 AU are very common. For the outskirts of the cluster this changes after 3 Myr, but for the central area it continues up to 7–8 Myr. Disc destruction happens on fairly short timescales. For example, for a solar-type star in a cluster with ρc > 105 M⊙ pc-3, which is typical for starburst cluster environments younger than < 2 Myr, an encounter closer than 100 AU can be expected already after 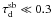 Myr. The disc destruction happens on such short timescales (<1 Myr) that it would be difficult to form a planetary system before the disc is destroyed. Though one cannot completely exclude the possibility that the solar system may have developed in a starburst cluster environment, it seems rather unlikely. Moreover, photo-evaporation (Adams 2010), which has not been included in this estimate, would lead to additional disc destruction.
Myr. The disc destruction happens on such short timescales (<1 Myr) that it would be difficult to form a planetary system before the disc is destroyed. Though one cannot completely exclude the possibility that the solar system may have developed in a starburst cluster environment, it seems rather unlikely. Moreover, photo-evaporation (Adams 2010), which has not been included in this estimate, would lead to additional disc destruction.
Recent observations by Stolte et al. (2010) suggest that there exist discs around some of the stars in the starburst cluster Arches, but the vast majority is devoid of inner discs. These authors only found discs around B-type stars with a frequency of 6% ± 2%. For solar-type stars the likelihood of retaining a disc would be even lower (Pfalzner et al. 2006). Assuming for a moment that the solar system happened to develop in one of these rare cases of its disc surviving the first Myr, the chances of discs surviving even longer would indeed increase, because starburst clusters become much less dense as they age. Nonetheless, at an age of 20 Myr the average stellar density would still be several 100 M⊙ pc-3. This is such a high density that, even if one assumes that some discs in a starburst environment survive long enough to form a planetary system, it would inevitably lead to a strong perturbation when the planetary system is close to being completed. Interactions with other cluster members would inevitably lead to disturbances destroying the near circularity and co-planarity of the solar systems.
The only way that our solar system could have formed as part of a starburst cluster would be if it had formed at the outer edge of this cluster, always remained there and never transversed the cluster center. A rough estimate using Eq. (2) would result in the requirement that the solar system would then have to have been located at 4–5 times the half-mass radius at the time of cluster formation.
It has been suggested that Arches might be exceptional for Milky Way clusters as it is thought to evolve quite differently from the clusters in the disk because of the unusually strong tidal fields (only ~30 pc away from the Galactic center). If we exclude this cluster from our investigation, this means that the size of the cluster at the time of gas expulsion could be larger than anticipated by including it. The thin dashed line in Fig. 2 shows the density developemnt excluding Arches. The cluster expansion starts at lower densities on the developmental track in Fig. 1. However, even in this case the cluster would go through a phase of 3–4 Myr where basically every star in the cluster center undergoes at least one encounter closer than 100 AU in every 1 Myr timespan. Consequently it still holds that nearly all discs are likely destroyed in the cluster center. However, there is an increased change that discs could survive in the cluster outskirts. The requirement reduces to the condition that the solar system would then have to have been located at 2–4 times the half-mass radius at the time of cluster formation.
However, at the same time a massive star would have to have been at these outskirts of the cluster to account for the observed chemical composition. Although this scenario cannot be excluded, it seems fairly unlikely. In the following we will see that it is much more likely that the solar system developed in a leaky cluster environment.
4. Solar system in a leaky cluster
For the leaky clusters the age-dependence of the average cluster density ρl can be approximated by (Pfalzner 2009) ![\begin{eqnarray} \rho_{\rm l} \> = 150 t_{\rm c}^{-2.6 \pm 0.2}~\left[\Msun~\mbox{pc}^{-3}\right] \hspace{1cm} \mbox{for } t~{\ge}~1~\mbox{Myr}, \end{eqnarray}](/articles/aa/full_html/2013/01/aa18792-12/aa18792-12-eq68.png) (4)where tc is in units of Myr. This is illustrated by the solid line in Fig. 2. Early on in the cluster development the mean cluster density will be approximately a few times 10 M⊙/pc3 to 100 M⊙/pc3 and will rapidly decrease over the following 20 Myr. Looking again at Fig. 3 (dashed lines), one sees that disc destruction approximated from
(4)where tc is in units of Myr. This is illustrated by the solid line in Fig. 2. Early on in the cluster development the mean cluster density will be approximately a few times 10 M⊙/pc3 to 100 M⊙/pc3 and will rapidly decrease over the following 20 Myr. Looking again at Fig. 3 (dashed lines), one sees that disc destruction approximated from 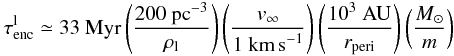 (5)is not an issue in the leaky cluster environment. Even early on in the cluster development, less than 10% of the stars in the cluster center are likely to undergo encounters closer than 100 AU and in the entire cluster it is < 1% of solar-type stars that are affected.
(5)is not an issue in the leaky cluster environment. Even early on in the cluster development, less than 10% of the stars in the cluster center are likely to undergo encounters closer than 100 AU and in the entire cluster it is < 1% of solar-type stars that are affected.
Figure 2 shows that the density requirement for the solar birth cluster overlaps with the development of leaky clusters for ages tc < 4 Myr. At later times the cluster density is considerably lower, making a solar-system-forming encounter unlikely. This is the central result of this study: with a very high probability, the solar system developed in a leaky cluster.
This development of the stellar density in such leaky clusters also neatly solves the seemingly contradictory situation that a dense birth cluster is required to provide for the nuclear enrichment and explain Sedna’s orbit, but at the same time, a less interactive environment is needed to avoid disruptive dynamical interactions with the formed solar system.
In the following we aim to go beyond the simple estimates of Eqs. (2)–(4) and determine what the development of the solar system in a leaky cluster means in terms of its history by performing numerical simulations of its encounter dynamics.
4.1. Numerical method and initial conditions
The clusters identified in Fig. 1 as part of the leaky cluster sequence are all exposed clusters, where the gas has been expelled from the cluster. Although gas expulsion seems to be a vital ingredient for the cluster expanding in the observed way, there are currently many unknowns setting the course of the following cluster dynamics and mass loss in the leaky cluster sequence. These uncertainites concern the time scales of the gas expulsion, the dynamical state – equilibrium, sub- or supervirial – before gas expulsion and to the degree to which early substructuring plays a role.
Therefore, instead of trying to include these unknown processes here, existing simulations (Olczak et al. 2010) of clusters in virial equilibrium at different densities are used to obtain a first estimate of the dynamics of the early solar environment as a function of cluster age. The densities of the modelled clusters are indicated in Fig. 2 as open squares. The densities of these model clusters decrease very slightly over the considered timespan of 1 Myr. This means that the observed cluster density development is replaced by snapshots of clusters of fairly constant density. The actual numerical method and the model set-up is described in detail in Olczak et al. (2010).
The main aspects of the model can be summarised in the following way: all simulations were performed using the direct many-body code Nbody6++ (Aarseth 2003; Spurzem 1999). For simplicity we assumed that all stars are initially single and no primordial binaries are considered. This seems to be justified, as Adams et al. (2006) and Brasser et al. (2006) found in their investigation of potential solar system environments that binary scattering events do not influence the results significantly. The effect of stellar evolution was not included. This is justified by us modelling only the first 5 Myr of the cluster development in detail, where stellar evolution plays a minor role.
The stellar masses in the cluster were sampled from the initial mass function given by Kroupa (2001). The cluster members cover the mass range from the lower mass end of 0.08 M⊙ to the currently accepted upper mass limit of 150 M⊙ (Koen 2006; Oey & Clarke 2005; Maíz Apellániz et al. 2007; Zinnecker & Yorke 2007; Weidner & Kroupa 2006; Figer 2005). The velocity distribution is Maxwellian and the cluster is assumed to be in virial equilibrium. In reality leaky clusters at that phase of their development are supervirial because the cluster still adjusts after the gas explusion process. Bastian & Goodwin (2006) found for somewhat larger clusters than we study here and with star formation efficiencies of ≈ 30% that it takes several 107 years until the clusters reach their new equilibrium state. However, not really knowing the gas expulsion dynamics and star formation efficencies in leaky clusters in detail, we resort to the easiest assumption, namely, treating the virial equilibrium case. We discuss below to which degree this might influence our results.
Cluster models, resulting mean cluster densities and age, at which these densities are reached in the leaky cluster development.
The cluster density profile was chosen in such a way that it resembles the observed Orion Nebula Cluster (ONC) profile (McCaughrean et al. 2002) after 1 Myr of simulation. We chose an ONC-like density profile because it is the best-known massive cluster just before gas expulsion. Because we model the early stages of exposed clusters, we assume that the shape of the density profile does not alter significantly (at least in the central areas) over the timespan of the first ≈ 5 Myr. Much older open and globular clusters are known to have less centrally condensed Plummer-type profiles, but this development happens on timesclaes of > 100 Myr to Gyr.
Owing to the adopted stellar number density distribution, which is roughly represented by ρ = ρ0r-2, the density of the models scales as the stellar number, 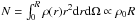 . Different initial stellar densities are obtained by varying the stellar numbers to 1000, 2000, 4000 (ONC), 8000, 16 000, and 32 000 (see Table 2). These density-scaled cluster models were simulated with the same initial size of R = 2.5 pc corresponding to the size of the ONC. The central density in the different models covers the range of ≈ 1–42 × 104 pc-3.
. Different initial stellar densities are obtained by varying the stellar numbers to 1000, 2000, 4000 (ONC), 8000, 16 000, and 32 000 (see Table 2). These density-scaled cluster models were simulated with the same initial size of R = 2.5 pc corresponding to the size of the ONC. The central density in the different models covers the range of ≈ 1–42 × 104 pc-3.
For each cluster model a set of simulations was performed with varying random configurations of positions, velocities, and masses, according to the given distributions, to minimise the effect of statistical uncertainties. For the clusters with 1000, 2000, 4000, 8000, 16 000, and 32 000 particles, a number of 200, 100, 100, 50, 20, and 20 simulations were performed to ensure statistical robustness. Due to the relatively high particle number in the simulation the encounter statistics of the stars close the center is not influenced by the change in simulation particles (see Olczak et al. 2010). Therefore we can treat the obtained encounter probabilities as the direct function of the cluster densities.
In contrast to previous studies we do not consider the simulation of clusters of different densities as different possible solar system birth environments, but as consecutive stages in the development of a leaky cluster environment that we can assign to certain cluster ages. In the following this is described in more detail.
 |
Fig. 4 Percentage of solar-type stars (0.8 M⊙ < Ms < 1.2 M⊙) located within 0.7 pc (solid line) or 0.5 pc (dashed line) from the cluster center at the moment of the encounter, which has a periastron in the range 100–1000 AU during the first Myr of the cluster development as a function of mean cluster density. The mean density is the spatial and temporale mean during this 1 Myr timespan. The dotted line shows the percentage of stars that have an encounter closer than 100 AU. |
4.2. Encounter statistics
While simulating the stellar dynamics of the above described clusters, for solar-type stars the parameters (mass ratio, periastron, eccentricity) of every encounter closer 1000 AU is recorded. Here we define solar-type stars as stars in the mass-range 0.8–1.2 M⊙.
The Sun must have been close to a massive star that exploded as a supernova and enriched the solar system with 60Fe and 26Al. To consider this we again take the ONC as a guide for the typical cluster environment. Here the result of mass segregation is that most massive stars are located within 0.5 pc of the cluster center. To model the early history of the solar system we therefore considered only stars within 0.5 pc and 0.7 pc form the cluster center. The latter denotes the central cluster area of 0.5 pc plus the estimated distance of the Sun to the supernova of 0.2 pc.
 |
Fig. 5 Dots: simulation results of the percentage of solar-type stars (0.8 M⊙ < Ms < 1.2 M⊙) located within 0.5 pc from the cluster center that have a single encounter with a periastron in the range 100–1000 AU as a function of cluster age for leaky cluster environments. The triangles shows the percentage of encounters closer than 100 AU. The solid and dashed lines show the equivalent estimates according to Eq. (2). |
Figure 4 shows the probability of a solar-type star located within 0.5 pc (solid line) and 0.7 pc (dashed line) from the cluster center to have an encounter between 100 AU and 1000 AU during 1 Myr of cluster developement as a function of the cluster density. Stars that have additional encounters closer than 100 AU before or after are excluded, because such encounters would truncate the disc to such a degree that they would be too small to develop into a solar-type planetary system. As expected, the likelihood of encounters between 100 and 1000 AU increases considerably with higher cluster density. However, so does the value of encounters closer than 100 AU – the proportion of “destroyed” discs (dotted line in Fig. 4). Therefore, in very dense clusters (ρ > 2 × 104) the likelihood of a solar-system-forming encounter decreases again, because an increasing number of discs have an encounter closer than 100 AU that makes it unsuitable for developing into a solar system.
Given the encounter likelihood at different central densities, we can now deduce the encounter statistcs during the development in a leaky cluster with age using Eq. (3). Table 2 shows how the different densities correspond to ages in the leaky cluster sequence. No densities above ~5 × 103 M⊙ pc-3 are reached in the leaky cluster sequence. However, this does not necessarily mean that the cluster never went through a phase of higher stellar density. Such a situation might have existed in the earlier embedded phase while the cluster was still in its formation process. However, little information about the stellar densities in forming massive clusters exists and existing knowledge can be interpreted very differently (for different views see for example Pfalzner 2011; and Parmentier & Pfalzner 2012). Therefore we restrain this study to the exposed phase only.
Figure 5 shows the probability for an encounter at a distance of 100 AU to 1000 AU in such an evolving leaky cluster. Here Table 2 and Eq. (4) were used to equate a given density to a cluster age. The encounter rate is obtained as an average over 0.5 Myr. During that time interval the cluster density decreases faster in the leaky cluster development than in the simulated systems, which are in virial equilibrium. Therefore the encounter rates have to be regarded as upper limits, which is reflected by the larger error bars towards lower encounter rates.
Figure 5 shows that in a leaky cluster environment solar-type stars have a probability of ~30% of experiencing a potentially solar-system-forming encounter early on in the development. As the cluster density decreases with cluster age, so does the encounter probability. This plot demonstrates that the highest likelihood for a solar-system-forming encounter is early on in the cluster development (<2 Myr). After 5 Myr of cluster development, encounters below 1000 AU become extremely rare because the density in the cluster has decreased so much.
It can be seen that the encounter rate measured in the N-body simulations (circles) is higher than the one expected from the simple estimate of Eq. (5) (solid line). This is because there is gravitational focusing around the massive stars, which themselves are concentrated in the cluster center (Pfalzner et al. 2006; Fujii & Portegies Zwart 2011), which in turn leads to a significantly higher number of encounters. The combination of gravitational focussing and mass segregation is not considered in the estimate of Eq. (5).
These more detailed studies support the idea that disc destruction is less of a problem in leaky clusters. Although the simulation value of disc destruction (triangles) is higher than the estimated one (dashed line), still very few solar-type stars have an encounter that is closer than the threshold of 100 AU.
 |
Fig. 6 Distribution of the perturber mass of the encounters between 100 AU and 1000 AU for solar-type stars in leaky clusters at 1.8 (dashed line) and 2.8 Myr (solid line). |
Figure 6 shows the mass distribution of the encounter partners in a timespan of 1 Myr in these encounters between 100 AU and 1000 AU at a cluster age of 1.8 Myr and 2.8 Myr, respectively. Evidently, there are two maxima in this distribution – one for low-mass and one for high-mass perturbers. Most encounters are with low-mass stars (m2 < 0.8 M⊙), this is simply because they are the most common in the cluster. However, a considerable amount of encounters take also place with the highest mass stars (>10 M⊙) of the cluster. As Fig. 6 shows, indeed it is just as likely for the Sun to have had an encounter between 100 AU and 1000 AU with a solar-type star as with a high-mass star despite low number of the latter. The reason is gravitational focusing. This is most pronounced later in the cluster development when the cluster density is lower. This result shows that the often applied assumption that the perturber was also a solar-type star has to be reconsidered in future work. These new results do not even exclude that the supernova progenitor itself might have been the encounter partner that led to the shape of the solar system.
 |
Fig. 7 Eccentricity distribution of the encounters between 100 AU and 1000 AU for solar-type stars in leaky clusters at 1.8 (dashed line) and 2.8 Myr (solid line). |
There is another point about the solar-system-forming encounter that might require revision: the eccentricity. Figure 7 shows the distribution of the eccentricities of the encounters for two different cluster ages as the leaky cluster environment develops. In the early cluster development strongly hyperbolic encounters are more likely. Hyperbolic encounters lead to considerably less mass loss in the disc than the equivalent do parabolic ones because the interaction time for disc mass removal is much shorter (see, for example, Pfalzner 2004; Pfalzner et al. 2005; Olczak et al. 2010). Only at ages > 2 Myr do parabolic encounters start to happen more often.
The fact that highly hyperbolic encounters dominate in dense cluster environments might increase the chance that the solar system formed in a starburst cluster environment because the disc destruction timescale in these environments might increase. First indications that this might be the case were found by Olczak et al. (2012). However, the problem of the strong radiation field in starburst clusters remains.
In summary, it can be said that it is highly questionable that the perturber that formed the shape of the solar system was a solar-type star on a parabolic orbit (see as well Dukes & Krumholz 2012). Future investigations will have to take the entire mass spectrum and a much wider eccentricity range into account to narrow down the encounter sceanrio that leads to the formation of the solar system.
5. Discussion and conclusions
Previous work puts the cluster population limit of the birth environment of the Sun at 103 to 105 members. Recently it was shown that these massive clusters only develop along one of two existing tracks in the density-radius plane – as either starburst clusters or leaky clusters (OB associations). As a consequence, the solar system must have developed in one of these two environments. Using the now known temporal density development of starburst clusters, we demonstrated here that in starburst clusters the high initial central stellar density (>105 M⊙/pc3) leads almost inevitably to disc truncation over the first 5–10 Myr despite its rapid decline. The resulting discs are often too small to account for the geometry of the solar system. In addition, the high concentration of massive – and therefore very luminous – stars drives additional disc destruction. The combination of both effects makes it unlikely that the solar system formed in a starburst cluster.
Our central results are:
-
The solar system most likely formed in a leaky clusterenvironment.
-
As a consequence, the solar birth cluster dispersed to a higher degree over timescales of ~20 Myr, where the cluster radius increased approximately like
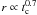 and the density in the cluster diminished as
and the density in the cluster diminished as ![\hbox{$ \rho_{\rm l} [\Msun~{\rm pc}^{-3}] = 150~t_{\rm c}^{-2.6 \pm 0.2}$}](/articles/aa/full_html/2013/01/aa18792-12/aa18792-12-eq83.png) , leaving behind a cluster that only has 10–20% at most of its initial mass.
, leaving behind a cluster that only has 10–20% at most of its initial mass. -
owing to the rapid decrease in density in the solar birth cluster, encounters played a role in shaping the solar system only very early on in the cluster development. At 1.8 Myr the probability for an encounter at an distance of 100 to 1000 AU is ≈ 30%. The encounter most likely took place when the cluster was less than 5 Myr old, because by then the likelihood for such an encounter dropped well below 10%. If the development to less concentrated profiles happens on timescales <10 Myr, we would overestimate the encounter frequency in the central parts at the later stages (>3 Myr) in our simulations. Therefore our results at >3 Myr can be regarded as upper limits. This means that a cluster older than 5 Myr would be even less likely to experience a solar-system-destroying encounter.
-
Hyperbolic encounters with low-mass stars and parabolic encounters with high-mass stars are the most common events for solar-type stars in solar system birth clusters. The former mostly happen in the very early stages (<2 Myr), the latter preferrentially in the timespan of 2–4 Myr.
Perturbation of the already formed planetary system (Malmberg et al. 2007, 2011; Lestrade et al. 2011; Parker & Quanz 2011) by encounters did not take place, because having formed in a leaky cluster, the encounter probability for the solar system rapidly dropped as the cluster density decreased precipitately with cluster age. Even if the solar system was part of the remnant cluster after gas expulsion, the stellar density would be <1 M⊙ pc-3, far too low to make a close encounter likely.
For the same reason, the presence of so many massive stars (10–100) in the solar birth cluster did not lead to its destruction. Although the most massive stars only need 3–5 Myr from their formation to their explosion, the rapid cluster expansion of the cluster can account for the solar system being spared additional disruption by supernovae at later times, even if these supernovae were closely packed at the start of the cluster development due to mass segregation.
The encounters investigated here within the distance range of 100 to 1000 AU lead not only to a cut-off in the disc but also to a steepening of the mass distribution inside the remaining disc. Steinhausen et al. (2012) showed that this could result in an r2.2-dependence as required for the minimum mass solar nebula (Desch 2007).
In the still embedded phase the stellar density in leaky clusters was still perhaps somewhat higher (Pfalzner 2011, for an alternative view see Parmentier & Pfalzner 2012). If this were the case, the encounter frequency in the embedded phase could possibly have been higher than in the exposed phase. However, star formation proceeds most likely in an accelerated way with most stars forming just before gas expulsion. In this stage the stellar density is only slightly higher than at the start of the exposed phase, therefore the sun most likely spent only a short time in this slightly denser environment.
In this study we took the earlier results of the most likely periastron of the solar-system-forming encounter to have been between 100 and 1000 AU at face value. These previous studies often considered only encounters between two solar-type stars and/or parabolic orbits. However, the results obtained here strongly suggest that these assumptions are not necessarily justified. Future work should also consider hyperbolic encounters and include the entire mass spectrum of encounter partners. This may be especially important in evaluating the likelihood of the solar system to have formed in a starburst cluster.
In the current study we included the cluster density development in a simplified way, by looking at simulations of clusters of different densities in virial equilibrium. Obviously, leaky clusters at that stage in their development are not in virial equilibrium, most prominently illustrated by their mass loss. Accordingly, it will be essential in future studies to include the gas expulsion phase to treat the cluster expansion in an appropriate way.
We have recently modelled the cluster expansion of starburst and leaky clusters after gas expulsion. Preliminary results seem to show that the observational data are surprisingly well reproduced by the simulations (Pfalzner & Kacmarek, in prep.). However, that bound and unbound stars, which latter have a preferrential direction, occupy the same space might influence the encounter statistics. This needs to be investigated in future work. In addition, we find indications that the leaky cluster sequence might only be representative for the development of the most massive clusters in the Galaxy ( ≥ 104 M⊙). Lower mass clusters, although starting with approximately the same cluster size, develop along a slightly different path, quickly decreasing so much in density that they fall below the detection limit. If these results are confirmed, the cluster mass range 2–10 × 103 M⊙ would require to be re-investigated in the light of these new results. However, because of the fast decrease in density in these lower mass clusters, the time span of a high encounter probability is extremely short – probably in the range of 1 Myr or even shorter.
Acknowledgments
We would like to thank the referee for the very constructive comments. This research was supported in part by the National Science Foundation under Grant No. NSF PHY05-51164.
References
- Aarseth, S. J. 2003, Gravitational N-Body Simulations (UK: Cambridge University Press) [Google Scholar]
- Adams, F. C. 2010, ARA&A, 48, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Adams, F. C., & Laughlin, G. 2001, Icarus, 150, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Adams, F. C., & Myers, P. C. 2001, ApJ, 553, 744 [NASA ADS] [CrossRef] [Google Scholar]
- Adams, F. C., Proszkow, E. M., Fatuzzo, M., & Myers, P. C. 2006, ApJ, 641, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N., & Goodwin, S. P. 2006, MNRAS, 369, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Battinelli, P., & Capuzzo-Dolcetta, R. 1991, MNRAS, 249, 76 [NASA ADS] [Google Scholar]
- Bernstein, G. M., Trilling, D. E., Allen, R. L., et al. 2004, AJ, 128, 1364 [NASA ADS] [CrossRef] [Google Scholar]
- Booth, M., Wyatt, M. C., Morbidelli, A., Moro-Martín, A., & Levison, H. F. 2009, MNRAS, 399, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Borissova, J., Ivanov, V. D., Hanson, M. M., et al. 2008, A&A, 488, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brasser, R., Duncan, M. J., & Levison, H. F. 2006, Icarus, 184, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A. 2000, ApJ, 538, L151 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dauphas, N., & Chaussidon, M. 2011, AREPS, 39, 351 [Google Scholar]
- Davies, M. B. 2011, IAU Symp., 276, 304 [NASA ADS] [Google Scholar]
- Desch, S. J. 2007, ApJ, 671, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Dukes, D., & Krumholz, M. R. 2012, ApJ, 754, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Duprat, J., & Tatischeff, V. 2008, New A Rev., 52, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., & Clemens, C. 1985, ApJ, 294, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, N. J., II, Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Fernandez, J. A. 1997, Icarus, 129, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Figer, D. F. 2005, Nature, 434, 192 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Figer, D. F. 2008, IAU Symp., 250, 247 [NASA ADS] [Google Scholar]
- Fujii, M., & Portegies Zwart, S. 2011, Science, 334, 1380 [NASA ADS] [CrossRef] [Google Scholar]
- Gaidos, E. J. 1995, Icarus, 114, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Gomes, R. S., Gallardo, T., Fernández, J. A., & Brunini, A. 2005, Cel. Mech. Dyn. Astron., 91, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Gounelle, M., Meibom, A., Hennebelle, P., & Inutsuka, S.-I. 2009, ApJ, 694, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Gritschneder, M., Lin, D. N. C., Murray, S. D., Yin, Q.-Z., & Gong, M.-N. 2012, ApJ, 745, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Gutermuth, R. A., Megeath, S. T., Pipher, J. L., et al. 2005, ApJ, 632, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Hall, S. M., Clarke, C. J., & Pringle, J. E. 1996, MNRAS, 278, 303 [NASA ADS] [Google Scholar]
- Hester, J. J., Desch, S. J., Healy, K. R., & Leshin, L. A. 2004, Science, 304, 1116 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ida, S., Larwood, J., & Burkert, A. 2000, ApJ, 528, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J., & Bromley, B. C. 2004, Nature, 432, 598 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kobayashi, H., & Ida, S. 2001, Icarus, 153, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Koen, C. 2006, MNRAS, 365, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Aarseth, S., & Hurley, J. 2001, MNRAS, 321, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J. 2006, ApJ, 640, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J.-E., Bergin, E. A., & Lyons, J. R. 2008, Meteor. Planet. Sci., 43, 1351 [NASA ADS] [CrossRef] [Google Scholar]
- Lestrade, J.-F., Morey, E., Lassus, A., & Phou, N. 2011, A&A, 532, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Looney, L. W., Tobin, J. J., & Fields, B. D. 2006, ApJ, 652, 1755 [NASA ADS] [CrossRef] [Google Scholar]
- McCaughrean, M., Zinnecker, H., Andersen, M., Meeus, G., & Lodieu, N. 2002, The Messenger, 109, 28 [NASA ADS] [Google Scholar]
- Maíz Apellániz, J., Walborn, N. R., Morrell, N. I., Niemela, V. S., & Nelan, E. P. 2007, ApJ, 660, 1480 [NASA ADS] [CrossRef] [Google Scholar]
- Malhotra, R. 2008, BAAS, 40, 464 [NASA ADS] [Google Scholar]
- Malmberg, D., de Angeli, F., Davies, M. B., et al. 2007, MNRAS, 378, 1207 [NASA ADS] [CrossRef] [Google Scholar]
- Malmberg, D., Davies, M. B., & Heggie, D. C. 2011, MNRAS, 411, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Mann, R. K., & Williams, J. P. 2009, ApJ, 694, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Matese, J. J., Whitmire, D. P., & Lissauer, J. J. 2005, Earth Moon and Planets, 97, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Mitchell, T. R., & Stewart, G. R. 2011, AJ, 142, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., & Levison, H. F. 2004, AJ, 128, 2564 [NASA ADS] [CrossRef] [Google Scholar]
- Oey, M. S., & Clarke, C. J. 2005, ApJ, 620, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Olczak, C., Pfalzner, S., & Eckart, A. 2008, A&A, 488, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olczak, C., Pfalzner, S., & Eckart, A. 2010, A&A, 509, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olczak, C., Kaczmarek, T., Harfst, S., Pfalzner, S., & Portegies Zwart, S. 2012, ApJ, 756, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, J. E., Ercolano, B., Clarke, C. J., & Alexander, R. D. 2010, MNRAS, 401, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, R. J., & Quanz, S. P. 2011, MNRAS, 1760 [Google Scholar]
- Parmentier, G., & Pfalzner, S. 2012, A&A, in press, DOI: 10.1051/0004-6361/201219648 [Google Scholar]
- Pfalzner, S. 2004, ApJ, 602, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Pfalzner, S. 2009, A&A, 498, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pfalzner, S. 2011, A&A, 536, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pfalzner, S., Vogel, P., Scharwächter, J., & Olczak, C. 2005, A&A, 437, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pfalzner, S., Olczak, C., & Eckart, A. 2006, A&A, 454, 811 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Porras, A., Christopher, M., Allen, L., et al. 2003, Sun. AJ, 126, 1916 [NASA ADS] [Google Scholar]
- Portegies Zwart, S. F. 2009, ApJ, 696, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Portegies Zwart, S. F., McMillan, S. L. W., & Gieles, M. 2010, ARA&A, 48, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Scally, A., & Clarke, C. 2001, MNRAS, 325, 449 [Google Scholar]
- Schwamb, M. E., Brown, M. E., Rabinowitz, D. L., & Ragozzine, D. 2010, ApJ, 720, 1691 [NASA ADS] [CrossRef] [Google Scholar]
- Spurzem, R., Giersz, M., Heggie, D. C., & Lin, D. N. C. 2009, ApJ, 697, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Steinhausen, M., Olczak, C., & Pfalzner, S. 2012, A&A, 538, 10 [Google Scholar]
- Stolte, A., Morris, M. R., Ghez, A. M., et al. 2010, ApJ, 718, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Thrane, K., Bizzarro, M., & Baker, J. A. 2006, ApJ, 646, L159 [NASA ADS] [CrossRef] [Google Scholar]
- Wadhwa, M., Amelin, Y., Davis, A. M., et al. 2007, Protostars and Planets V, 835 [Google Scholar]
- Wasserburg, G. J., Busso, M., Gallino, R., & Nollett, K. M. 2006, Nucl. Phys. A, 777, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., & Kroupa, P. 2006, MNRAS, 365, 1333 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., & Gaidos, E. 2007, ApJ, 663, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Wolff, S. C., Strom, S. E., Dror, D., Lanz, L., & Venn, K. 2006, AJ, 132, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Zinnecker, H., & Yorke, H. W. 2007, ARA&A, 45, 481 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Cluster models, resulting mean cluster densities and age, at which these densities are reached in the leaky cluster development.
All Figures
 |
Fig. 1 Observed cluster mass (filled symbols) and derived density (open symbols) as a function of cluster size for clusters more massive than 103 M⊙ as published by Pfalzner (2011). The values were taken from Figer (2008), Wolff (2007) and Borissova et al. (2008) and references therein. |
| In the text | |
 |
Fig. 2 Mean cluster density as function of the cluster age for starburst (circles – observed values and dashed line – interpolation as in Pfalzner 2009) and leaky clusters (triangles and solid line, observations and interpolation, respectively). The red box shows the density requirement for solar-system-forming encounters to be likely. The open squares show the parameters of the clusters modelled in Sect. 4. The thin dashed line shows a fit through the data case where the Arches cluster is excluded from the starburst cluster sequence. Here only the errors in cluster age are given, the errors in cluster densities can be found in Fig. 2 of Pfalzner (2009). |
| In the text | |
 |
Fig. 3 Probability for encounters closer than 100 AU taking place as function of cluster age. The solid and the dashed lines show the estimates for starburst and leaky clusters, respectively. The thick and thin lines distinguish between the entire cluster and the central area only. |
| In the text | |
 |
Fig. 4 Percentage of solar-type stars (0.8 M⊙ < Ms < 1.2 M⊙) located within 0.7 pc (solid line) or 0.5 pc (dashed line) from the cluster center at the moment of the encounter, which has a periastron in the range 100–1000 AU during the first Myr of the cluster development as a function of mean cluster density. The mean density is the spatial and temporale mean during this 1 Myr timespan. The dotted line shows the percentage of stars that have an encounter closer than 100 AU. |
| In the text | |
 |
Fig. 5 Dots: simulation results of the percentage of solar-type stars (0.8 M⊙ < Ms < 1.2 M⊙) located within 0.5 pc from the cluster center that have a single encounter with a periastron in the range 100–1000 AU as a function of cluster age for leaky cluster environments. The triangles shows the percentage of encounters closer than 100 AU. The solid and dashed lines show the equivalent estimates according to Eq. (2). |
| In the text | |
 |
Fig. 6 Distribution of the perturber mass of the encounters between 100 AU and 1000 AU for solar-type stars in leaky clusters at 1.8 (dashed line) and 2.8 Myr (solid line). |
| In the text | |
 |
Fig. 7 Eccentricity distribution of the encounters between 100 AU and 1000 AU for solar-type stars in leaky clusters at 1.8 (dashed line) and 2.8 Myr (solid line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


