| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A46 | |
| Number of page(s) | 16 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201015444 | |
| Published online | 14 December 2012 | |
AGN host galaxies at redshift z ≈ 0.7: peculiar or not?
1 Institute for Astro- and Particle Physics, University of Innsbruck, Technikerstr. 25/8, 6020 Innsbruck, Austria
e-mail: Asmus.Boehm@uibk.ac.at
2 Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
3 University of Michigan, Department of Astronomy, 830 Dennison Building, 500 Church Street, Ann Arbor, MI 48105, USA
4 Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
5 Department of Physics, Denys Wilkinson Building, University of Oxford, Keble Road, Oxford, OX1 3RH, UK
6 Institute of Cosmology and Gravitation, University of Portsmouth, Hampshire Terrace, Portsmouth, PO1 2EG, UK
7 School of Physics and Astronomy, The University of Nottingham, University Park, Nottingham NG7 2RD, UK
8 Department of Anthropology, University of Waterloo, Waterloo, Ontario, N2L 3G1, Canada
9 Department of Astronomy, University of Texas at Austin, 1 University Station, C1400 Austin, TX 78712-0259, USA
10 Department of Physics, University of Missouri-Kansas City, Kansas City, MO 64110, USA
11 Giant Magellan Telescope Organization, 251 South Lake Avenue, Pasadena, CA 91101, USA
12 Institut de Ciéncies del Cosmos, University of Barcelona, 08028 Barcelona, Spain
13 Department of Physics and Astronomy, University Of Waterloo, Waterloo, Ontario, N2L 3G1, Canada
14 Department of Physics, University of Basel, Klingelbergstrasse 82, 4056 Basel, Switzerland
15 University of Texas, McDonald Observatory, Fort Davis, TX 79734, USA
16 Institute for Astronomy, University of Edinburgh, Blackford Hill, Edinburgh, EH9 3HJ, UK
17 European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching bei München, Germany
18 Centro Hispano Aleman de Calar Alto, C/Jesus Durban Remon 2-2, 04004 Almeria, Spain
19 Purple Mountain Observatory, National Astronomical Observatories, Chinese Academy of Sciences, 210008 Nanjing, PR China
Received: 21 July 2010
Accepted: 19 October 2012
Aims. We perform a quantitative morphological comparison between the hosts of active galactic nuclei (AGN) and quiescent galaxies at intermediate redshifts (z ≈ 0.7). The imaging data are taken from the large HST/ACS mosaics of the GEMS and STAGES surveys. Our main aim is to test whether nuclear activity at this cosmic epoch is triggered by major mergers.
Methods. Using images of quiescent galaxies and stars, we created synthetic AGN images to investigate the impact of an optical nucleus on the morphological analysis of AGN hosts. Galaxy morphologies are parameterized using the asymmetry index A, the concentration index C, the Gini coefficient G, and the M20 index. A sample of ~200 synthetic AGN was matched to 21 real AGN in terms of redshift, host brightness, and host-to-nucleus ratio to ensure a reliable comparison between active and quiescent galaxies.
Results. The optical nuclei strongly affect the morphological parameters of the underlying host galaxy. Taking these effects into account, we find that the morphologies of the AGN hosts are clearly distinct from galaxies undergoing violent gravitational interactions. Indeed, the host galaxy distributions in morphological descriptor space are more similar to undisturbed galaxies than to major mergers.
Conclusions. Intermediate-luminosity (LX ≲ 1044 erg/s) AGN hosts at z ≈ 0.7 show morphologies similar to the general population of massive galaxies with significant bulges at the same redshifts. If major mergers are the driver of nuclear activity at this epoch, the signatures of gravitational interactions fade rapidly before the optical AGN phase starts, making them undetectable on single-orbit HST images, at least with usual morphological descriptors. This could be investigated in future synthetic observations created from numerical simulations of galaxy-galaxy interactions.
Key words: galaxies: active / galaxies: interactions / galaxies: evolution
© ESO, 2012
1. Introduction
For a long time, active galactic nuclei (AGN) were considered a very special class of objects, characterized by an accreting supermassive black hole (SMBH) in their center. Only during the past decade, an SMBH has been found in practically all galaxies that are sufficiently close to determine the stellar kinematics in the center at high spatial resolution and that have a significant bulge component. It also became evident that the properties of SMBHs and their host galaxies are coupled. The mass of the SMBH for instance is observed to be correlated with the luminosity (e.g. Marconi & Hunt 2003), velocity dispersion (e.g. Gebhardt et al. 2000; Ferrarese & Merritt 2000), and mass (e.g. Häring & Rix 2004) of the spheroidal component of its host galaxy. These correlations probably point towards a fundamental link between the formation and evolution of galaxies and their central black holes (e.g., Hopkins et al. 2008). However, some authors have demonstrated that the correlations might also arise from galaxy mergers without any physically coupled growth of black holes and galaxies (e.g. Peng 2007; Jahnke & Maccio 2011).
The main mechanism that turns a quiescent SMBH into an AGN is still under debate. Candidates for this are secular processes such as bar-driven gas inflows, gravitational interactions, or galaxy mergers (for reviews, see Martini 2004; Jogee 2006). It is likely that the main triggering process will depend on the luminosity regime and/or the cosmic epoch under investigation.
One possible approach for identifying this process is to compare the morphological properties of AGN host galaxies and quiescent (non-AGN) galaxies. To this end, some previous studies have used descriptors such as CAS (Conselice et al. 2000). Grogin et al. (2005) for example found no difference between active and inactive galaxies at 0.4 < z < 1.3 in the Chandra Deep Fields North and South. Similarly, Pierce et al. (2007) used the Gini coefficient G and the M20 index (Lotz et al. 2004) to quantify the morphologies of X-ray selected AGN at 0.2 < z < 1.2 in the DEEP2 survey and concluded that the majority of the AGN reside in nonpeculiar early-type hosts. These studies could be taken as evidence that signs of gravitational interactions in AGN at intermediate redshifts are scarce. However, it should be noted that these analyses did not include a decomposition of the AGN images into the nucleus and host components. Although an X-ray selection yields a high fraction of absorbed or so-called optically dull AGN, it is not clear whether optical nuclei had an impact on these results.
In a different approach, some AGN studies focused on the environment. Serber et al. (2006) have found for instance that the galaxy density around quasars at z < 0.4 is enhanced with respect to inactive L ∗ galaxies. The reported density excess is highest for the brightest quasars and separations R < 100 kpc. Hennawi et al. (2006) derived the autocorrelation function of quasars at 0.5 < z < 3 and showed an order-of-magnitude excess at R < 40 h-1 kpc in comparison to the expectation from large scales R > 3 h-1 Mpc. Myers et al. (2007) found a lower, albeit significant enhancement in the range 0.4 < z < 2.3. Silverman et al. (2011) compared galaxies at 0.3 < z < 1.1 with and without a companion galaxy at less than 75 kpc separation and showed an enhanced AGN fraction (by a factor of 2.6) in close pairs. According to a study by Ellison et al. (2011) based on > 105 galaxies from the Sloan survey, this result also holds in the local universe. Although there is some disagreement on the magnitude of the density enhancement around AGN, these findings favor gravitational interactions or mergers as a triggering mechanism.
An active nucleus with significant contributions to the total flux will bias any morphological analysis of the host galaxy in the sense that it appears too bulge-dominated (e.g., Pierce et al. 2010). Several studies have investigated ways to correct for the effect of a central point source (Sanchez et al. 2004; Simmons & Urry 2008; Kim et al. 2008; Gabor et al. 2009; Cisternas et al. 2011). Performing a decomposition into the host and nucleus components, Sanchez et al. (2004) found that 12 out of 15 AGN at 0.5 < z < 1.1 reside in early-type galaxies, with roughly one third of the hosts showing signs of gravitational interactions. Moreover, the rest-frame U − V colors of the majority of the early-type hosts were significantly bluer than those of non-AGN early-types, indicating recent or ongoing star formation. The same has been found at similar redshifts for X-ray selected AGN in the Extended Chandra Deep Field South (Böhm et al. 2007; Silverman et al. 2008). Rafferty et al. (2011) covered the wide redshift range 0.3 < z < 3.0 and showed evidence for a correlation between star formation rate and AGN fraction, which reaches 30% for galaxies forming stars at ψ ≈ 1000 M⊙/yr. These findings could be understood in a scenario where some mechanism triggers star formation and, potentially with some delay, AGN activity, which eventually suppresses star formation via feedback processes (e.g. Schawinski et al. 2007; Hopkins 2012).
Recent studies presented evidence against major mergers being the main triggering process: Cisternas et al. (2011) for instance found no strong distortions in > 85% of their sample of AGN hosts at 0.3 < z < 1.0. Schawinski et al. (2011) showed that, even at much earlier cosmic epochs up to z ≈ 3, some 80% of moderate-luminosity AGN (with LX < 1044 erg/s) reside in disk-like hosts, making a recent similar-mass merger very unlikely.
In our analysis, we aim to further investigate the question whether AGN activity is connected to strong tidal interactions. Our sample covers intermediate redshifts (0.5 < z < 1.1) and X-ray luminosities (1042 erg/s ≲ LX ≲ 1044 erg/s). We will for the first time use real galaxy images for the simulation of AGN images and use these for a quantitative morphological comparison between quiescent and active galaxies at intermediate redshifts. At variance with previous studies, our sample is not X-ray but optically selected for AGN with broad emission lines (→ type-1).
The paper is organized as follows: In Sect. 2, we introduce the surveys we used and Sect. 3 describes the selection of the AGN sample. The construction of the non-AGN comparison sample and the simulated AGN images is outlined in Sect. 4. We perform the morphological analysis of both samples and discuss our results in Sect. 5; Sect. 6 will give a short summary. Throughout the paper, we assume a flat concordance cosmology with ΩΛ = 0.7, Ωm = 0.3 and H0 = 70 km s-1 Mpc-1. Unless stated otherwise, all magnitudes are given in the AB system.
2. Data sets
Our morphological analysis relies on HST/ACS imaging data taken from the GEMS survey (Rix et al. 2004) and the STAGES survey (Gray et al. 2009).
GEMS is a survey in the F606W and F850LP bands (similar to V and z), consisting of 78 ACS pointings. It covers a continuous field of 28′ × 28′ in the extended Chandra Deep Field South. Details on the data reduction are given in Caldwell et al. (2008). The STAGES survey extends over a slightly larger area (30′ × 30′) centered on the A901/2 multiple cluster system at z = 0.165. With 80 tiles of imaging through the F606W filter, STAGES forms one of the largest mosaics ever taken with the HST. Details on the data reduction can be found in Gray et al. (2009).
In brief, the data reduction comprised the standard steps (bias subtraction, flat-fielding, flux calibration), drizzling of the data from the original 0.05 arcsec/pixel to a final scale of 0.03 arcsec/pixel, background estimation and variance determination for each pixel. For both data sets, the individual exposures were multi-drizzled with a Gaussian kernel1. For the purpose of this analysis, we used only the F606W images of GEMS, to allow a combination with STAGES in a homogeneous data set.
Both the STAGES and GEMS areas are covered by COMBO-17 (Wolf et al. 2003), a photometric redshift survey based on imaging in 12 medium- and 5 broad-band filters with the Wide Field Imager at the MPG/ESO 2.2 m telescope on La Silla, Chile. COMBO-17 provides the estimated redshifts and spectral energy distribution (SED) classifications of several 104 objects. For galaxies brighter than R = 23 (Vega), the error on the photometric redshifts is typically σz ~ 0.02(1 + z), (Wolf et al. 2008). For non-AGN galaxies, stellar mass estimates M∗ are also available (Wolf et al. 2004; Borch et al. 2006).
3. AGN sample
3.1. Local point spread function
The analysis of the underlying host galaxy in AGN images is a challenging task, particularly in cases of low flux contrasts between the host and nucleus. The key issue for accurately removing the central point source and determining the host properties is a good knowledge of the point spread function (PSF). Its width and shape depend on the filter, the CCD position, the observation date, and the spectral shape of the source. Tests on GEMS data showed that the temporal variations are negligible compared to the spatial variations (see Sanchez et al. 2004).
Owing to the variations of the PSF shape across the CCD (with pixel-to-pixel flux variations of up to 20%), it is mandatory to construct individual, local PSFs for each AGN. These local PSFs were determined by normalizing and averaging the nearest 35 stars from all tiles (only using stars from GEMS for GEMS AGN and from STAGES for STAGES AGN) around a given AGN position on the CCD. Very faint (V > 24) or saturated stars were rejected. The typical maximum distance between the AGN and the stars that were included was ~40 arcsec for GEMS and ~25 arcsec for the STAGES data.
A small fraction of the STAGES images (8 tiles out of 80) were obtained ~6 months later than the main block, which spreads over only three weeks. The tiles with delayed imaging (nos. 29, 46, 75 ...80; see Heymans et al. 2008 for details) show significant deviations of their PSFs from those of the data taken earlier and were therefore neglected in our analysis. To construct local PSFs just from these tiles was no option, it would have produced PSFs with a much lower S/N.
3.2. Definition of AGN sample
Within the COMBO-17 catalog, there are 278 objects classified as AGN for which ACS imaging from STAGES or GEMS is available. We restricted our analysis to AGN in the redshift range 0.5 < z < 1.1. The lower limit was chosen simply due to the lack of AGN identified with COMBO-17 at lower redshifts. The upper limit is mainly motivated by the shift of the F606W filter’s wavelength range into the rest-frame UV, which would strongly affect the morphological appearance and limit the comparability to objects at lower redshifts. Moreover, there is a dearth of quiescent galaxies in COMBO-17 at redshifts z > 1.1 usable as a comparison sample. Because of the SED-based selection technique, the vast majority of the COMBO-17 AGN are type-1, i.e. they show broad emission lines and a prominent nucleus in optical images. We introduced a cut at R < 24 Vega mag for SED and redshift reliability. Finally, we rejected objects that were either located close to the edges of the tiles or observed during the delayed STAGES observations (see previous section). This sample comprised 28 AGN with robust photometric redshifts and good ACS imaging data at 0.5 < z < 1.1.
As a final constraint, we checked which of the AGN have a detectable host galaxy. To this end, the local PSF of each AGN was normalized to the AGN’s flux within an annulus of a two-pixel radius and then subtracted from the AGN image. By definition, this approach is an oversubtraction of the nucleus because the normalization to the central flux includes the contribution of the host galaxy. In other words, a scaled PSF subtraction provides a conservative lower limit on the host-to-nucleus flux ratio H/N. Only objects showing a flux residual of more than 10% of the total flux were included in our final sample. This resulted in 21 AGN with a median redshift of ⟨ z ⟩ = 0.71.
3.3. Decomposition of AGN images
We determined the H/N and the structural properties of the AGN host galaxies using the GALFIT package (Peng et al. 2002). GALFIT allows multi-component fitting of galaxy images in a χ2 minimization approach. To decompose the AGN images, the individually constructed local PSF was used as a model for the unresolved nucleus of the AGN, and a Sérsic profile (Sérsic 1968) as a model for the host galaxy. This model can be used to approximate various types of surface brightness profiles with a Sérsic index n = 1 being equivalent to an exponential disk and n = 4 to a de Vaucouleurs profile.
The two-component GALFIT modeling introduces a total of ten free parameters. For the Sérsic component, these were the position xs, ys, total brightness vhost, effective radius reff, Sérsic index n, position angle θ, and axis ratio q. For the nucleus model, only position xn, yn and brightness vnuc were free parameters. The user has to define initial guesses for all parameters, which GALFIT uses to start the fitting process. These initial guess values of ms, xs, ys, reff, θ, mn, xn, yn were determined with Source Extractor (Bertin & Arnouts 1996). The flux ratio between host and nucleus was set according to the estimate from scaled PSF subtraction. The initial guess value of the Sérsic index was n = 2.5, representing an intermediate type between an n = 1 exponential disk and a de Vaucouleurs profile. Fits were performed on thumbnails of size 256 × 256 pixel2, corresponding to 7.68 × 7.68 arcsec2. Neighboring objects and bad pixels were masked.
GALFIT allows one to set constraint intervals on the free fitting parameters. We required the relative positions Δx = xs − xn and Δy = ys − yn to be within five pixels, constrained the Sérsic index to 0.25 ≤ n ≤ 8 and the effective radius to 0.1 arcsec ≤ reff ≤ 3 arcsec. All fits were visually checked, in particular for the fit residuals. For a few objects, it was necessary to set additional constraints, e.g. on the position of the components, to acquire the best fitting results.
We find median values of ⟨ vhost ⟩ = 23.05, ⟨ H/N ⟩ = 0.63, ⟨ n ⟩ = 1.51 and ⟨ reff ⟩ = 0.22 arcsec corresponding to 1.6 kpc at the average redshift ⟨ z ⟩ = 0.71 of the sample. Host parameter distributions and a test of their reliability are discussed in the following section.
3.4. X-ray luminosities
Our spectrophotometric classification rests on the COMBO-17 data. By definition, all objects identified as AGN in this survey (in the rest-frame UV/optical) are type-1, i.e. unabsorbed AGN. It is not clear whether our sample covers the same range in X-ray luminosities as X-ray-selected samples at similar redshifts. Nuclear activity of different luminosity regimes might be triggered by different processes (e.g. secular evolution vs. gravitational interactions), and this could complicate a comparison between our study and others. This section presents an estimate of the X-ray luminosities for our sample.
Ten objects in our sample are covered by the Chandra Deep Field South (CDFS) point source catalog (Lehmer et al. 2005). Their hardness ratios between the 0.5−2 keV and the 2 − 8 keV band (HR = (H − S)/(H + S), where H and S represent the hard and soft bands, respectively) cover the range −0.64 < HR < −0.40, confirming that they are unabsorbed. Adopting an X-ray power law slope of Γ = 2, we derived the X-ray luminosity at 2−8 keV. They span values between LX = 1.7 × 1042 erg/s and LX = 3.2 × 1044 erg/s with a median of ⟨ LX ⟩ = 2.1 × 1043 erg/s. For the other 11 objects, we had to apply an indirect estimate. Using the AGN template by Berk et al. (2001), we transformed the observed v-band nuclear brightnesses into the rest-frame B-band luminosities. These, in turn, were computed into X-ray luminosities following Hopkins et al. (2007). They cover the range 5.9 × 1041 erg/s < LX < 6.3 × 1043 erg/s with a median of ⟨ LX ⟩ = 7.2 × 1042 erg/s. We hence find that, even though the sample consists of optically selected type-1 AGN with prominent nuclear sources, most of their X-ray luminosities are in the intermediate range. Only 3 out of 21 are powerful AGN with LX > 1044 erg/s. As a test, we used the approach of Hopkins et al. also to estimate the luminosities of the ten AGN covered by the CDFS. The indirectly computed X-ray luminosities differ from the CDFS-based ones by only ~0.22 dex on average.
We now compare the luminosity range of our sample to X-ray-selected studies at similar cosmic epochs. Grogin et al. (2005) only gave a lower limit of LX > 1042 erg/s at the high-redshift end of their 0.4 < z < 1.3 sample. The data sets of Pierce et al. (2007, 0.2 < z < 1.2), Gabor et al. (2009, 0.3 < z < 1.0), and Cisternas et al. (2011, 0.3 < z < 1.0) span the ranges 1041 erg/s ≲ LX ≲ 1044 erg/s, 1042 erg/s ≲ LX ≲ 4 × 1044 erg/s and 2 × 1042 erg/s ≲ LX ≲ 3 × 1044 erg/s, respectively. Despite of the differences in selection, our sample hence covers similar luminosities as these previous studies.
4. Comparison sample
In contrast to many previous studies we aim to take into account the impact of the optical nucleus on the quantitative AGN host galaxy properties. Thus we have constructed a special kind of comparison sample in three main steps.
First, we defined a set of non-AGN galaxies that is matched to the redshifts and magnitudes of our sample of 21 AGN hosts. Secondly, we created synthetic AGN images from these quiescent galaxies that cover the same H/N as the real AGN (Sect. 4.3). Finally, the synthetic AGN images were decomposed into the host and nucleus components using GALFIT in the same way as the real AGN. After subtracting the model nucleus from the AGN image, the recovered host galaxies of the synthetic AGN were combined with the host galaxies of the real AGN and analyzed in concentration, asymmetry, Gini and M20 index (see Sect. 5).
4.1. Selection
The basis for the selection of the comparison sample was the COMBO-17 catalog of the GEMS field. For the pre-selection, the following constraints were used:
-
1.
Apparent Vega magnitude R < 24. In this magnitude regime, we can rely on photometric redshifts accurate to within 3 − 4% and robust SED classifications from COMBO-17 (Wolf et al. 2003).
-
2.
Source classified as a “galaxy” on the basis of its SED (but not as an AGN).
-
3.
No X-ray counterpart in the point source catalog of the Extended Chandra Deep Field South (Lehmer et al. 2005). This criterion was applied to exclude absorbed or “optically dull” AGN.
-
4.
Sérsic index n > 1.5 (derived on the F850LP images, i.e. z-band, by Häussler et al. 2007). This constraint was set to restrict the sample to galaxies with significant bulge components. According to the relation between bulge mass and SMBH mass, host galaxies with small bulges or even without a bulge are not expected to be present in the AGN sample.
These criteria were fulfilled by 3536 galaxies with GEMS data. In the next step, ten quiescent counterparts were selected for each of the 21 AGN hosts within a bin Δz/z ≤ 0.025 of the AGN redshift and within Δvhost ≤ 0.05 mag of the total brightness of the host as determined with the GALFIT decomposition. When less than 10 non-AGN were found in the catalog within these limits, the limits were slightly relaxed and the search repeated iteratively until ten counterparts could be selected. After visual inspection of all 210 objects in the resulting sample, seven galaxies had to be rejected because they were unresolved. The final non-AGN sample hence contained 203 galaxies.
The COMBO photometric redshift distributions of the 21 AGN hosts and the 203 quiescent galaxies are shown in Fig. 1. The z-distribution of the AGN was normalized to a total of 203 objects to allow a direct comparison between the two samples. The median photometric redshift of the AGN sample is ⟨ z ⟩ = 0.71, virtually identical to the ⟨ z ⟩ = 0.70 of the quiescent sample. Figure 2 displays the distributions in total apparent V magnitude of the AGN hosts (from GALFIT) and the quiescent comparison sample (Source Extractor MAG_AUTO values). Again, both samples’ distributions are normalized to the same number of objects. The median total magnitudes of the two samples are ⟨ vhost ⟩ = 23.05 (AGN) and ⟨ vhost ⟩ = 23.33 (comparison sample). The slight difference can be explained with the relaxation of the constraints partly necessary during the selection of the comparison sample.
 |
Fig. 1 Comparison between the redshifts of the AGN (dashed) and the sample of quiescent galaxies (solid). The histograms are normalized to the same total number of objects. |
 |
Fig. 2 Distribution of the AGN host galaxy magnitudes derived with GALFIT (dashed) compared to the quiescent sample (solid). The histograms are normalized to the same total number of objects. |
4.2. Visual classification
To calibrate the following quantitative morphological analysis, we performed a visual classification of all galaxies in the quiescent sample. We decided to use a very plain scheme.Its main purpose is to test whether major mergers are the triggering mechanism of AGN at redshifts 0.5 < z < 1.1. To this end, we distinguished between three morphological classes:
-
1.
Major mergers: galaxies that are heavily distorted (“train-wrecks”), show two nuclei of similar luminosity, or two pronounced tidal tails of equal length.
-
2.
Undisturbed galaxies: no signs of recent or ongoing gravitational interactions.
-
3.
Unclear cases: all other objects, including minor mergers, ambiguous major merger candidates, or morphologies on the edge between undisturbed and mildly disturbed.
Using this simple scheme, all 203 galaxies in the comparison sample were visually inspected and classified by eight of the authors (AB, DB, MaB, MG, GH, SJ, DM, AR). Comparing the individual classifications, agreement was found between four classifiers or more in 88% of the cases; between five or more in 84% of the cases; between six or more in 67% of the cases, and between seven or more in 48% of the cases.
 |
Fig. 3 HST/ACS v-band images of galaxies from the non-AGN comparison sample. Each row displays six examples of the three different morphological types that were denoted via visual classification (with at least four out of eight classifiers agreeing). The bar in each image has a length of one arcsec, corresponding to ~6 kpc at z = 0.5 or ~8 kpc at z = 1. |
The classifications were merged with a constraint of at least four classifiers agreeing on a certain type. Cases with less than four identical classifications were considered unclear. If an object was classified as a major merger four times and as unclear four times, it was also defined as unclear. We refer to the criterion of at least four identical classifications per object as the 4/8 sample. Examples are presented in Fig. 3. Similarly, a scheme 5/8 requires that five or more classifiers agree (or else, the given object is unclear); and equivalently for the 6/8 and 7/8 samples. The respective number of major mergers, undisturbed, and unclear objects are summarized in Table 1.
Visual classifications of the 203 quiescent comparison galaxies.
We tested how well the various combined classifications distinguish between undisturbed galaxies and major mergers on the basis of morphological descriptors such as concentration C and asymmetry A, to choose a scheme for our final analysis. This is described in Sect. 5.2.
4.3. Synthetic AGN images
The modifications of the quiescent galaxy ACS images described in the following constitute the backbone of our analysis. The same kind of residuals that occur after subtracting the nucleus in the central part of an AGN host were introduced in the quiescent galaxy images. This ensures a direct comparability of the morphologies of AGN hosts and non-AGN galaxies. We achieved this by adding a synthetic nucleus to a given quiescent galaxy, constructing its local PSF and finally decomposing it into the host and nucleus component with GALFIT. Thus, we analyzed synthetic and real AGN in exactly the same way. For the synthetic nuclei, we used real stellar images from GEMS. It is hence ensured that the deviations between the light profile shape of a nucleus and the corresponding local PSF will be statistically the same as in the case of the real AGN, and the residuals of the nucleus in simulated AGN and real AGN images – after subtracting the best-fit model nucleus – will have the same noise properties.
The stars we used as synthetic nuclei were selected from the GEMS catalog, constrained to the v-band magnitude range of the nuclei of the real AGN, 19.6 < v < 25.3. Since the PSF shape is sensitive to the SED of a source and the nuclei of AGN have very blue colors, we set color cuts of (B − V) < 0.6 and (V − R) < 0.6 (both Vega magnitudes). Five stars were rejected because they showed cosmics or bad pixels close to the central peak. The final list for creating synthetic nuclei consisted of 58 stars with median colors of ⟨ B − V ⟩ ≈ 0.44 and ⟨ V − R ⟩ ≈ 0.43 (Vega magnitudes).
For each of the quiescent galaxies, a star was selected from this list such that the flux ratio between galaxy and star was the same as the H/N of the AGN to which the quiescent galaxy initially was assigned in the construction of the comparison sample. Small normalizations of about a few percent were applied to the stellar fluxes to achieve exactly the same flux ratios between a galaxy and the star on the one hand and AGN host and nucleus on the other. After normalization, the quiescent galaxy (synthetic host) and stellar image (synthetic nucleus) were simply co-added with the star positioned at the galaxy’s central coordinates according to the GALFIT modeling on the initial image. The variance frames of the two components were also combined to use them in the subsequent GALFIT decomposition.
The local PSF for each synthetic AGN was created based on the CCD position of the star that was used as a synthetic nucleus. The 35 nearest stars around the CCD position of a given synthetic nucleus were normalized and averaged. Local PSFs for the synthetic AGN hence have the same quality as those of the real AGN. Finally, using GALFIT, all synthetic AGN were decomposed into nucleus and Sérsic host with the same configuration as described for the real AGN (Sect. 3.3). The main steps of the creation and decomposition of the synthetic AGN are illustrated in Fig. 4.
 |
Fig. 4 Illustration of the AGN simulation procedure. Upper left: original quiescent galaxy at redshift z = 0.52, apparent brightness v = 23.27. Upper middle: star of brightness v = 21.46 used as a synthetic nucleus. Upper right: simulated AGN (co-added galaxy and star) with a host-to-nucleus ratio of H/N = 0.18. Lower left: GALFIT model of the host galaxy (from fitting a nucleus + host model to the simulated AGN). Lower middle: recovered host galaxy after subtracting the GALFIT model of the nucleus from the simulated AGN image. Lower right: residual after subtracting the combined galaxy + nucleus model from the simulated AGN image. Each image is ~ 2 arcsec on the side. |
 |
Fig. 5 Distribution of the host-to-nucleus ratios H/N of the real AGN (dashed) compared to the simulated AGN (solid). The histograms are normalized to the same total number of objects. |
The H/N values of the real AGN and the synthetic AGN are compared to each other in Fig. 5. As in the case of the redshifts and host magnitudes, the two samples differ only slightly in H/N, with median values of ⟨ H/N ⟩ = 0.57 and ⟨ H/N ⟩ = 0.63 for the simulated AGN and real AGN, respectively. These deviations do not stem from the selection process itself but from the limited accuracy of the GALFIT decomposition; we discuss this in detail in the next section.
The visual classifications described in the previous section were also applied to the real AGN sample after subtracting the best-fit models of the nuclear point sources from the images. These classifications were made as a blind test with all nucleus-subtracted real AGN and all nucleus-subtracted simulated AGN randomly mixed. We present an overview in Table 2. It is striking that none of the real AGN is classified as a major merger. This is discussed in more detail in Sect. 5.4, in combination with the results from our quantitative morphological analysis. All real AGN and their respective visual classes (based on the 4/8 criterion) are shown in Fig. 6.
 |
Fig. 6 Visual classifications of the nucleus-subtracted real AGN sample (with subtracted model nucleus from two-component modeling as described in Sect.3.3). The bar in each image has a length of one arcsec. |
Visual classifications of the 21 real AGN hosts.
4.4. Stability of the AGN decomposition
Our synthetic AGN images can be used to test the GALFIT recovery of the main host galaxy parameters such as total brightness, effective radius, and Sérsic index for a broad range of H/N. Similar tests have been carried out by Sanchez et al. (2004), Kim et al. (2008), and Gabor et al. (2009); but in these studies, no real galaxy images but simulated, perfectly symmetric hosts have been used. Only Simmons & Urry (2008) used observed data for part of their tests.
Even though studying the robustness of AGN host galaxy parameters derived with GALFIT is not the raison d’être of our analysis, it is an interesting byproduct. The plots in Figs. 7 and 8 compare the initial host parameters (with suffix ini), as derived on the images prior to adding a synthetic nucleus, and the recovered host parameters (suffix sim) from simultaneous fitting of galaxy and synthetic nucleus.
 |
Fig. 7 GALFIT recovery of host galaxy parameters for the simulated AGN sample. a) Deviations between input host magnitude vhost, ini and recovered host magnitude as a function of input host magnitude. b) Deviations between original host magnitude and recovered host magnitude vhost, sim as a function of input H/Nini. c) Deviations between input effective radius reff, ini and recovered effective radius reff, sim as a function of input effective radius. d) Deviations between input effective radius and recovered effective radius as a function of input H/N. e) Deviations between input Sérsic index nini and recovered Sérsic index nsim as a function of input host magnitude. f) Deviations between input Sérsic index nini and recovered Sérsic index nsim as a function of input H/N. |
In Fig. 7a, we show the total brightness vhost, ini of the quiescent galaxies (single Sérsic modeling on the original images, before the addition of synthetic nuclei) plotted against the deviations Δvhost = vhost, ini − vhost, sim between the initial brightness vhost, ini and the brightness vhost, sim determined from two-component GALFIT modeling after adding the synthetic nucleus. The values of Δvhost are basically distributed around zero with a scatter of ~0.25 mag. The scatter is mostly independent of the galaxy magnitude except for objects brighter than vhost,ini ≈ 21.3. It is surprising that most of these galaxies have high positive values of Δvhost, meaning that the fluxes of these objects are overestimated when they are fitted simultaneously with a synthetic nucleus. It is quite obvious that this occurs because the fitting algorithm attributes part of the nucleus flux to the host, because the Sérsic indices of most of these galaxies are overestimated, too – this leads to low values of the fraction nini/nsim between Sérsic index in the original image and the simulated AGN, depicted by filled green circles; see also panel e).
Figure 7b shows the deviations between original host magnitude and recovered host magnitude as a function of input H/Nini. The scatter in Δvhost strongly increases toward low values of H/Nini, as expected. Moreover, in the regime H/Nini < 1, i.e. in cases where the nucleus outshines the host, the recovered host magnitudes vhost,sim tend to be too bright. This trend indicates that part of the bright nucleus flux is attributed to the host component by the fitting algorithm. A similar results has been found by Kim et al. (2008). These authors argued that mismatches between the nucleus profile and the input local PSF cause this systematic effect.
 |
Fig. 8 GALFIT recovery of host galaxy parameters for the simulated AGN sample. a) Deviations between input host magnitude vhost,ini and recovered host magnitude vhost, sim as a function of the deviations between input Sérsic index nini and recovered Sérsic index nsim. b) Deviations between input H/Nini and the recovered H/Nsim as a function of the deviations between original host magnitude and recovered host magnitude. c) Deviations between input H/Nini and the recovered H/Nsim as a function of input H/N. d) Deviations between input H/Nini and the recovered H/Nsim as a function of input host magnitude. |
Figure 7c shows the input effective radii reff, ini determined on the original images plotted against the deviations between input effective radius reff, ini and recovered effective radius reff, sim. This parameter is accurate to within less than 30% for 3/4 of the objects. Figure 7d shows the deviations between input and recovered effective radius as a function of input H/Nini. Like the host brightnesses, the effective radii have a larger scatter toward low H/N.
In Fig. 7e, the ratio Δn = log (nini/nsim) between original and recovered Sérsic index is plotted as a function of input total host magnitude vhost, ini. Evidently, n is a parameter that is much harder to determine than the brightness or effective radius of the host galaxy. Toward fainter host magnitudes, the Sérsic indices are systematically underestimated in a decomposition into nucleus and host component. For the distribution in H/N considered here (the median for our AGN sample is ⟨ H/N ⟩ = 0.63), this effect starts to kick in at host magnitudes fainter than vhost, ini ≈ 23. Owing to this systematic effect and the very large scatter in Δn, it is impossible to use the best-fit Sérsic index to determine the morphological type of an AGN host. A similar trend has been found e.g. by Sanchez et al. (2004) on the basis of simulated host galaxies and nuclei. Those simulations used symmetric single-component host galaxies (Sérsic profiles with either n = 1 or n = 4). In contrast to this, many of the host galaxies in our sample consist of two or more components (bulge, disk, potentially spiral structure, etc.). This higher complexity of the host profiles leads to a much larger uncertainty in the recovered Sérsic indices than found by Sanchez et al. A comparison to the results of Simmons & Urry (2008) is difficult because the authors did not use constraints on the Sérsic index in their fits.
Figure 7f displays the ratio Δn = log (nini/nsim) between original and recovered Sérsic index as a function of the input H/N. At low H/N, the scatter in Δn is approximately 0.4 dex.
Figure 8a shows the host magnitude deviations Δvhost plotted as a function of the Sérsic index deviations Δn. Not surprisingly, there is an anti-correlation of these two parameters. A too faint model profile for the host galaxy (Δvhost < 0) is accompanied by an underestimated Sérsic index, because a fraction of the host galaxies’ flux is assigned to the model nucleus. Since this effect occurs at small galactocentric radii, the host model profile becomes too shallow (vice versa for an overestimated host flux). A false host model flux results in a wrong value of the model H/N (see Fig. 8b, displaying ΔH/N as a function of the host magnitude deviations Δvhost). Figure 8c shows the ratio between the input H/Nini and the recovered value H/Nsim, plotted as a function of H/Nini. The H/N is slightly underestimated for low input values and slightly overestimated for high input values, which partly is a consequence of the systematic error on vhost at low H/N. In Fig. 8d, the ratio between the input and recovered H/N is plotted against the original total host magnitude vhost, ini. In general, H/N is overestimated for very bright hosts – which is induced by the frequently overestimated host fluxes in this regime (cf. Fig. 7a).
The comparisons between single-component light profile modeling of quiescent galaxies and two-component modeling of these galaxies with added synthetic nuclei provides a systematic error in the decomposition of AGN images using GALFIT. Ignoring extreme outliers and taking only the best 95% of the fits into account, host fluxes, H/N, effective radii and Sérsic indices are recovered to within fractional errors of σvhost = 0.23, σH/N = 0.34, and σreff = 0.50, σn = 0.90, respectively. Since the scatter in host magnitude, effective radius and Sérsic index is dominated by objects with low H/N (cf. Figs. 7b, d and f), we repeated this test by rejecting objects with H/N < 0.4. We then find respective fractional errors of σvhost = 0.18, σH/N = 0.46, and σreff = 0.22, σn = 0.82. In particular for the effective radius, these values are more representative for an AGN decomposition with not too faint hosts. The numbers also show that the Sérsic indices of distant type-1 AGN hosts are very hard to recover.
5. Morphological analysis and discussion
Prior to the following analysis, the best-fit model nuclei from the GALFIT decomposition were subtracted from all synthetic and real AGN images.
We define a galaxy’s outer contours using the segmentation maps from Source Extractor because they determine which pixels of an image are assigned to a given galaxy. All these maps were visually inspected. In a few cases, e.g. when the deblending of multiple galaxies was not satisfying, Source Extractor was re-run with different input parameters until the segmentation maps were accurate. In our approach, major merger candidates were not deblended into the individual sub-components but analyzed as one single object. In the SExtractor configuration used here, the flux at the outermost isophotes of a given galaxy corresponds to the 1σ sky noise level.
5.1. Definition of morphological descriptors
We here rely on two parameter spaces that have been frequently used in the literature, in particular for distant galaxies. These are the concentration index C and asymmetry index A (Conselice et al. 2000), the Gini coefficient G and the M20 index (Lotz et al. 2004).
The asymmetry parameter A is measured by subtracting a galaxy image rotated by 180° from the original image: 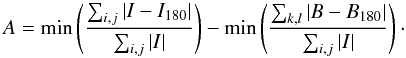 (1)Here, I is the original image, I180 is the image rotated by 180° about the galaxy’s center, and B and B180 are the background and rotated background. This latter contribution to A due to the background noise is estimated from blank sky regions in the vicinity of the object under investigation. The sums are computed over all pixels within the 1σ isophotes of the galaxy; B covers the same number of pixels as I. The minimization is computed by shifting the galaxy image on an integer pixel grid, with a maximum shift of eight pixels for our data sets.
(1)Here, I is the original image, I180 is the image rotated by 180° about the galaxy’s center, and B and B180 are the background and rotated background. This latter contribution to A due to the background noise is estimated from blank sky regions in the vicinity of the object under investigation. The sums are computed over all pixels within the 1σ isophotes of the galaxy; B covers the same number of pixels as I. The minimization is computed by shifting the galaxy image on an integer pixel grid, with a maximum shift of eight pixels for our data sets.
There are various definitions of the concentration index C in the literature that only have slight differences to each other. We adopted C as the ratio between two fluxes in elliptical areas G1 and G2, which have the same axis ratio and position angle but a different major axis with a2 = 0.3 a1 (Abraham et al. 1996): 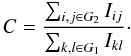 (2)Here, Iij is the flux at the pixel (i,j) within the inner isophotal region G2 and Ikl is the flux at the pixel (k,l) within the larger isophotal region G1.
(2)Here, Iij is the flux at the pixel (i,j) within the inner isophotal region G2 and Ikl is the flux at the pixel (k,l) within the larger isophotal region G1.
The Gini coefficient has originally been developed for applications in social sciences. When computed for galaxy images, it is a measure of the concentration of an object’s light profile, similar to C, but insensitive to the definition of a central pixel. We adopted the Gini coefficient as given in Lotz et al. (2004): 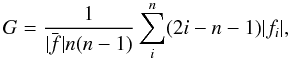 (3)where | fi | are the absolute flux values of the ith pixel (ranked in increasing order) and
(3)where | fi | are the absolute flux values of the ith pixel (ranked in increasing order) and 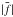 is the mean of the absolute flux values of all n pixels assigned to an object.
is the mean of the absolute flux values of all n pixels assigned to an object.
The M20 index is based on the total second-order moment Mtot, which is the flux in each pixel fi multiplied by the squared distance to the center of the galaxy, summed over all pixels of a given object: 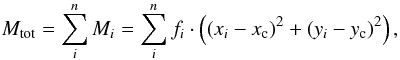 (4)where xc,yc is the galaxy’s center. The center is computed by finding xc,yc such that Mtot is minimized. M20 then is defined as the normalized second-order moment of the brightest 20% of the galaxy’s flux. To compute M20, the pixels are rank-ordered by flux, and Mi is summed over the brightest pixels until the sum of the brightest pixels amounts to 20% of the total galaxy flux, followed by a normalization to Mtot (Lotz et al. 2004):
(4)where xc,yc is the galaxy’s center. The center is computed by finding xc,yc such that Mtot is minimized. M20 then is defined as the normalized second-order moment of the brightest 20% of the galaxy’s flux. To compute M20, the pixels are rank-ordered by flux, and Mi is summed over the brightest pixels until the sum of the brightest pixels amounts to 20% of the total galaxy flux, followed by a normalization to Mtot (Lotz et al. 2004): 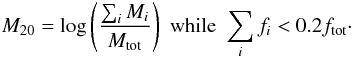 (5)Here, ftot is the total flux of a galaxy and fi are the fluxes for each pixel i, ordered according to their flux values such that f1 is the brightest pixel, f2 the second brightest, etc. Basically, M20 traces the spatial distribution of bright features such as off-center star-forming regions.
(5)Here, ftot is the total flux of a galaxy and fi are the fluxes for each pixel i, ordered according to their flux values such that f1 is the brightest pixel, f2 the second brightest, etc. Basically, M20 traces the spatial distribution of bright features such as off-center star-forming regions.
5.2. Quantitative morphological comparison of AGN hosts and quiescent galaxies
Our visual classifications of the comparison sample will be used as a calibration in the C/A and G/M20 parameter spaces. Since these classifications were carried out prior to including a synthetic optical nucleus, they are much more robust than the nucleus-subtracted host galaxy images of the real AGN that are affected by the nucleus residuals in the center of the images (cf. Fig. 7).
First we defined when to call a visual classification reliable. Eight team members visually inspected the galaxies in the non-AGN comparison sample and classified them as a major merger, undisturbed, or unclear. Combining the various classifications for each object, we constructed various samples (as described in Sect. 4.2). Only using cases with at least four identical classifications, we obtained a sample 4/8, five or more identical classifications define a sample 5/8, etc. We used a two-dimensional Kolmogorov-Smirnov test to quantify the distinguishability between major merger candidates and undisturbed galaxies in the parameter spaces C/A and G/M20. Table 3 shows the respective probabilities P that both samples are drawn from the same parent distribution. The probability P increases with the minimum number of agreeing classifications. This mainly is an effect of the sample sizes. As a test, we restricted all samples to the size of the 7/8 scheme (by randomly selecting subsets from the other larger samples) and recomputed the KS test. The probabilities then are comparable between the four different schemes. However, since a larger sample offers more robust statistics, we decided to use scheme 4/8 in the following.
 |
Fig. 9 Distribution of the quiescent galaxies in concentration index C versus asymmetry A (left) and in Gini coefficient G versus M20 (right). Tiny open symbols depict ambiguous cases, large open symbols show undisturbed galaxies, large filled symbols are classified as major mergers. Galaxies have highly concentrated light profiles toward the right-hand side of the graphs and become more asymmetric/show more substructure toward the upper part of the graphs. |
 |
Fig. 10 Distribution of the simulated AGN (i.e. a quiescent galaxy with an additional synthetic nucleus (before subtraction), depicted here as circles) and real AGN host galaxies (open diamonds), in concentration index C versus asymmetry A (left) and in Gini coefficient G versus M20 (right). Tiny open symbols depict ambiguous cases, large open symbols show undisturbed galaxies, large filled symbols are classified as major mergers. With respect to the original galaxy images (the distributions of which are shown in Fig. 9), the distinguishability between different morphological types is degraded. |
Our main morphological analysis is based on galaxy images with removed central point sources (cf. Fig. 4). For this reason we tested the distinguishability between major mergers and undisturbed galaxies also with the images of the nucleus-subtracted simulated AGN. As shown in Table 4, the contrast between the two morphologies is degraded with respect to the original images, because of the residuals in the galaxy centers after the point-source subtraction (just for completeness, we give the KS test results for all four classification schemes).
Two-dimensional KS test comparing major mergers and undisturbed galaxies in the quiescent comparison sample.
Two-dimensional KS test comparing major mergers and undisturbed galaxies in the simulated AGN sample (after removal of the central point sources).
In Fig. 9 (left-hand plot), we show the distribution of the quiescent galaxies in terms of C vs. A. Major merger candidates have systematically higher asymmetry indices A and lower concentration C than undisturbed galaxies. This is well-known from observations as well as from synthetic images created from numerical simulations (e.g. Lotz et al. 2008). The galaxies with unclear morphology are located between major mergers and undisturbed galaxies, showing substantial overlap with the former. A number of galaxies that could not be clearly characterized visually might thus be major mergers. Still, the KS test probability that major mergers and unclear objects stem from the same parent distribution is low: P = 0.004.
In G/M20 space (right-hand plot of Fig. 9), the situation is similar: major mergers populate a region of high M20 values (i.e. bright off-center features) and lower G indices compared to the undisturbed galaxies. The distinction between the two classes seems slightly worse than in C/A space; this indeed is reflected in the higher KS test P values for G/M20 with respect to C/A (Table 3).
 |
Fig. 11 Distribution of the simulated and real AGN host galaxies after subtracting the best-fit model nucleus in concentration index C versus asymmetry A (left) and in Gini coefficient G versus M20 (right). Tiny open symbols depict ambiguous cases, large open symbols show undisturbed galaxies, large filled symbols are classified as major mergers. Major mergers and undisturbed galaxies are better separated than before subtracting the nuclei (Fig. 10). |
The distributions in C/A and G/M20 are completely different in the presence of an optical nucleus. In Fig. 10, we show simulated AGN (quiescent galaxies plus synthetic nucleus) and real AGN (including their optical nuclei). Note that the displayed range in M20 is slightly different from Fig. 9. Compared to the original quiescent galaxies, the synthetic AGN have much higher concentration indices and Gini coefficients, which is an obvious effect of the nuclear point source. The M20 indices become lower, indicating the loss of structure because the combined light profile of host + nucleus is smoother than that of the host alone. The mean asymmetry of all types (median value ⟨ A ⟩ sim = 0.3) is almost unchanged with respect to the original galaxy images (⟨A ⟩ orig = 0.27). This is somewhat surprising because the nuclear point sources should result in a less elliptical combined light profile. However, the synthetic nucleus is usually not perfectly centered on the pixel grid; just like the nucleus in an observed real AGN. Since the asymmetry index is minimized on an integer pixel shift basis, even an almost symmetric light profile can therefore yield an untypically high value for A. One other net effect of the nuclei was that the distribution in A became narrower. The distinguishability between the morphological classes of the simulated AGN hosts is, when compared to the initial distributions in Fig. 9, clearly degraded. Repeating the KS test to quantify how well undisturbed and major mergers are separated, we find P = 0.001 in C/A and P = 0.004 in G/M20. Simulated and real AGN cover similar regions in the parameter spaces. Before we perform a quantitative comparison, we go one step further.
For the next computation of C, A, G, and M20, the best-fit nuclei from two-component modeling with GALFIT were subtracted from the simulated and real AGN. The resulting distributions are shown in Fig. 11. In C/A space, mergers and undisturbed objects are better separated than before subtracting the nucleus (cf. Fig. 10). However, there clearly is a stronger overlap between these two types than there was based on the original images (cf. Fig. 9). This is reflected in an increase of the KS test probability when comparing merging and undisturbed galaxies: values increase from P = 10-6 to P ≈ 10-3 in C/A and from P ≈ 10-5 to P ≈ 10-3 in G/M20, as given in Tables 3 and 4. Some objects feature asymmetry indices above unity, which in the case of normal galaxy images would be impossible. This effect indicates additional noise in the center of the images that is not related to the sky background but residuals from the nucleus subtraction. As we discuss below, this particularly affects objects with low H/N.
We will now use the KS test to determine which subsample of the quiescent galaxies is most similar to the AGN hosts. Or, more precisely, which subsample of the nucleus-subtracted synthetic AGN hosts is most similar to the real AGN hosts. Comparing the AGN to major mergers, undisturbed, and unclear objects in C/A space, we find Pmm = 0.015, Pundis = 0.32 and Puncl = 0.034, respectively. The distribution of the AGN hosts in asymmetry and concentration is by far best matched by the undisturbed galaxies, while unclear cases show the second highest – albeit much lower – probability. The same comparison in G/M20 space yields Pmm = 0.040, Pundis = 0.22 and Puncl = 0.033, respectively. Again, the distribution of undisturbed galaxies is most similar to the AGN hosts, while major mergers are much less likely to stem from the same parent distribution.
We also compared the AGN hosts to the whole quiescent sample. The KS test then yields Pall = 0.20 in C/A or Pall = 0.12 in G/M20. In both parameter spaces, these probabilities are slightly lower than those comparing between AGN hosts and undisturbed galaxies. This indicates that the AGN hosts comprise a mix of morphological classes that is slightly different from the comparison sample, in the sense that the former contain a higher fraction of undisturbed galaxies than the latter.
These numbers argue against a significant fraction of major mergers among the AGN hosts. Frequent minor mergers, on the other hand, cannot be ruled out. The unclear category is a mixed bag, containing minor mergers as well as ambiguous cases that might partly be major mergers. If major mergers are not the main triggering mechanism, these ambiguous cases will result in a relatively low KS test probability, just like we have found. We tested an alternative visual classification scheme that distinguishes between minor and major mergers. To do this on an object-by-object basis is of course a challenging task. The usage of this alternate scheme confirmed our results, albeit at lower statistical significance, on the basis of KS statistics. This is why we here adopted a simple scheme with only three different morphological types, as a straightforward test of the major merger scenario.
 |
Fig. 12 Illustration of the impact of a subtracted nucleus on the quantitative morphologies of the simulated AGN galaxies in concentration index C (upper left), asymmetry A (upper right), Gini coefficient G (bottom left), and M20 (bottom right). As a function of H/N, all plots show the initial parameter value before (index ini) and after addition & subtraction of a synthetic nucleus (index sim), normalized to the initial value. See text for details. |
 |
Fig. 13 Illustration of the impact of an unsubtracted nucleus on the quantitative morphologies of the simulated AGN galaxies in concentration index C (upper left), asymmetry A (upper right), Gini coefficient G (bottom left), and M20 (bottom right). As a function of H/N, both plots show the initial value before (index ini) and after the addition of a synthetic nucleus (index unsub), normalized to the initial value. See text for a discussion. |
The presented distributions in the parameter spaces spanned by C, A, G, and M20 already gave some insight into the effects of an optical nucleus in the morphological analysis. We now investigate this in more detail for each of the four descriptors in Fig. 12. In the upper left plot, Cini is the initial concentration index of a non-AGN galaxy before adding a synthetic nucleus, Csim gives the index after addition and subtraction of a synthetic nucleus. The difference between the two is normalized to the absolute initial value via ΔC = (Cini − Csim/ | Cini | ). This parameterization allows us to distinguish between systematic trends, showing up as changes in the average value of ΔC, and a loss of information leading to an increased scatter in ΔC. We show ΔC as a function of H/N.
After subtracting the synthetic nucleus, the concentration indices Csim are on average slightly underestimated for high H/N values, corresponding to ΔC > 0. This trend is the equivalent of the underestimated Sérsic indices nsim in Fig. 7e. When decomposing the AGN into host and nucleus, some part of the host’s flux is systematically attributed to the central point source. However, this approach introduces fewer systematic effects than leaving the nucleus unaccounted for, as we will show below. The scatter in ΔC becomes larger toward lower H/N, independent of morphological disturbances. This explains why the C/A diagram of nucleus-subtracted AGN hosts is more noisy than that of quiescent galaxies, and the effect is stronger for objects with lower H/N.
The asymmetry index (Fig. 12b) is the only descriptor that shows a clear systematic effect: toward lower H/N, Asim is increased, probably because of the artificial noise from the residuals after subtracting the nucleus. The scatter in ΔA (hence, the noise in the C/A diagram) also increases with decreasing H/N. This trend is much weaker for major mergers, however – mainly due to their high Aini values – than for undisturbed galaxies. Since we are particularly interested in correctly identifying major mergers, this supports our results.
The Gini coefficient (Fig. 12c) shows a trend similar to C, with slightly underestimated values of G at H/N ≳ 0.5 and increasing noise toward lower H/N. The scatter is slightly smaller for major merger candidates. The M20 index (Fig. 12d) is slightly overestimated for high H/N and underestimated for low H/N; the noise increases with decreasing host–to–nucleus contrast, independent of the morphology.
Figure 13 demonstrates how the morphological descriptors are affected when an optical nucleus is not accounted for. Again, we computed the difference between the initial value (index ini) and that after the addition of a synthetic nucleus (index unsub) for C, A, G, and M20. Unsurprisingly, the concentration index (upper left graph) becomes systematically higher due to the central point source, resulting in high negative values of ΔCu. This effect becomes stronger toward weaker host-to-nucleus contrasts and affects major mergers stronger than undisturbed galaxies. The upper right plot shows the change in asymmetry index A. Particularly interesting here is the morphological dependence: while A on average becomes larger for undisturbed galaxies after the addition of a nucleus (ΔAu < 0), the asymmetry of major mergers is slightly underestimated. Overestimated asymmetry indices probably are caused by nuclei that are not perfectly symmetrical but show a more complex shape of the PSF. The Gini coefficient shows the same trend as C, but without a noticeable dependence on morphology. M20 is systematically underestimated (i.e. overestimated in absolute values), and this effect is slightly stronger for major mergers. The central point sources probably mask out bright structures that are off-center but still relatively close to the hosts’ centers.
To summarize, we find that an unsubtracted nucleus has a strong systematic effect on all four morphological parameters considered here. In contrast, subtracting the central point source systematically only affects the asymmetry index A. This implies that comparisons between quiescent galaxies and AGN with non-negligible nuclei will be biased if the impact of the nuclei is ignored. Similar results have been found e.g. by Sanchez et al. (2004) or Gabor et al. (2009).
5.3. AGN host colors
We constructed our quiescent galaxy sample in such a way that a fair comparison to the real AGN hosts is feasible: they are matched in their redshift and apparent magnitude distributions. A lower limit on the Sérsic index was applied to reject bulgeless disks among the non-AGN. The initial selection criteria did not use any information on spectral type, except that galaxies classified as AGN within the COMBO-17 survey did not enter the comparison sample.
For testing purposes, we used the observed color as an additional constraint for the definition of the non-AGN sample. This analysis is restricted to the GEMS part of our sample, which offers v- and z-band HST/ACS imaging, while the STAGES survey only comprises v-band data from HST. Note that the nucleus-subtracted HST images are our only option to derive host colors – the ground-based COMBO-17 data have a totally insufficient resolution for a host-nucleus decomposition.
Our sample holds 12 real AGN hosts with available GEMS data. Their colors span the range 0.86 ≤ (v − z) ≤ 2.4. Matching the comparison sample to this color distribution reduces it to a total of 62 galaxies.
We repeated the KS tests using this new non-AGN sample matched in redshifts, magnitudes, and colors. Comparing the AGN to major mergers, undisturbed, and unclear objects in C/A space, we now find Pmm = 0.04, Pundis = 0.24 and Puncl = 0.03, respectively. As in our initial analysis, undisturbed galaxies show the highest probability of stemming from the same parent distribution as the real AGN hosts. In G/M20 space, the respective probabilities are Pmm = 0.29, Pundis = 0.59 and Puncl = 0.18. Again, undisturbed galaxies are most similar to the real AGN hosts. Compared to the initial results without a color selection, the difference in probability between undisturbed and major merger cases is reduced.
We emphasize that, because of small number statistics, these results are not as robust as our initial analysis. The additional color criterion shrinks the comparison sample of major mergers from 15 objects to just six. In particular, four very blue major mergers with colors (v − z) < 0.9 are excluded from the quiescent sample. A visual inspection of these galaxies does not reveal obvious morphological differences to the rest of the major merger cases. But the very blue ones show relatively low absolute M20 values and excluding them slightly affects the KS test results in G/M20 space (by increasing the value of Pmm).
Nevertheless, the reanalysis with a color-constrained comparison sample confirms our initial results. The fact that major mergers have much bluer average colors ( ⟨ (v − z) ⟩ = 0.95) than the real AGN hosts ( ⟨ (v − z) ⟩ = 1.65) can be taken as some spectrophotometric evidence that major mergers are scarce among the host galaxies. This agrees with previous findings by, e.g., Sanchez et al. (2004) or Schawinski et al. (2007): at least up to redshifts z ≈ 1, AGN hosts show intermediate – but not very blue – colors.
5.4. Discussion
Our quantitative morphological analysis shows that the majority of 21 AGN in our sample reside in only mildly disturbed or even undisturbed galaxies. The same result is found in a visual classification of the nucleus-subtracted images (see Table 2): Ten of them (48%) have an undisturbed morphology, 11 (52%) are unclear cases, but none has been classified as a major merger. For comparison, the quiescent sample comprises 15 (7%) major mergers, 95 (47%) undisturbed and 93 (46%) unclear objects.
Hence, neither with a quantitative analysis nor by visual inspection we find evidence that a significant fraction of the AGN hosts are undergoing major mergers. This is at variance with a naive expectation for a connection between major mergers and AGN. In principle, there are three possible explanations for this:
-
1.
Morphological descriptors like C/A or G/M20 might miss a significant fraction of strong gravitational interactions on single-orbit ACS data of intermediate-redshift galaxies;
-
2.
there might be a delay between a major merger and the onset of the optical AGN phase: the merger signatures could fade and become undetectable (or very hard to detect) before the nuclear accretion starts, or
-
3.
violent gravitational interactions might not be the main triggering mechanism of nuclear activity in the redshift regime considered here, which corresponds to look-back times between ~5 and ~8 Gyr.
Regarding the first of these possibilities, our analysis shows that major mergers should be detectable at a high success rate, even in the presence of residuals from a subtracted nucleus. This is what we conclude from the KS tests between undisturbed and strongly interacting galaxies (probability P = 8.6 × 10-4 using C/A or P = 1.1 × 10-3 using G/M20, cf. Fig. 11 and Table 4) as well as from the discussion of the trends in Fig. 12. However, even if major mergers are triggering the nuclear activity for a significant fraction of our sample, it is not necessarily the case that the morphological imprint of the merger is still detectable by the time the AGN phase has started. The start of the SMBH accretion and the time of the strongest morphological perturbations (hence the best “detectability” of the merger) might not occur simultaneously.
This brings us to the second option listed above. Observational evidence for a delay between a merger and the onset of an AGN phase has been found e.g. by Schawinski et al. (2007) and Bennert et al. (2008). Synthetic observations to estimate the time during which a major merger could be identified have been carried out by Conselice (2006; using the CAS space) and Lotz et al. (2008; based on CAS and G/M20). The involved time scales depend on very many parameters, such as the mass ratios, gas and dust content, or the geometry and sense of rotation of the merging galaxies. According to these authors, the phase of the strongest perturbation occurs at the earliest a few 100 Myr and at the latest ≳ 1 Gyr after the first encounter. However, these analyses did not attempt to estimate the time when the nuclear gas accretion starts, nor did they include the impact of an AGN’s optical nucleus on the image analysis.
Using numerical simulations, Hopkins et al. (2008) have investigated the various evolutionary stages of merger-induced nuclear activity. The encounter and major merger phases are followed by the coalescence and start of the SMBH accretion. By the time the object would be observed as an AGN at rest-frame optical wavelengths, the tidal features might have faded. For distant objects, the merger signatures could be only detectable with very deep observations, but not with single-orbit ACS data such as those from GEMS or STAGES.
Concerning the third hypothesis, it can be argued that at least at higher redshifts and luminosities, there is evidence both from observations and numerical simulations for a connection between major mergers and AGN phases. Ultraluminous infrared galaxies (ULIRGs), e.g., which are mostly found in merging systems (e.g. Sanders & Mirabel 1996), have a much higher AGN fraction than the overall population of luminous galaxies (e.g. Canalizo & Stockton 2001). Simulations were used to show that major mergers can efficiently transport gas to the central parts of the merger remnant to feed the central SMBH (e.g. Di Matteo et al. 2005). At later stages, the feedback by the AGN can terminate the star formation; this scenario might be a necessity to produce the “red and dead” ellipticals observed in the present-day universe (e.g. Khalatyan et al. 2008).
Studies using very large samples drawn from the Sloan Digital Sky Survey, on the other hand, did not find an increased fraction of interacting galaxies among AGN hosts at low z (e.g. Kauffmann et al. 2003, Li et al. 2008). It has to be noted that these local studies on average cover much lower AGN luminosities than intermediate-redshift samples like our own. A straightforward comparison is thus not feasible. The observational results at differing redshifts are diverse but indicate that a possible connection between major mergers and nuclear activity seems to weaken toward lower redshifts and lower AGN luminosities.
Our results are consistent with weak gravitational interactions (fly-bys, minor mergers) playing an important role in AGN triggering at z ≈ 0.7. This would also agree with the increased galaxy density in the vicinity of quasars (e.g. Hennawi et al. 2006) and the enhanced AGN fraction in galaxy pairs at low (e.g. Ellison et al. 2011) and intermediate redshifts (e.g. Silverman et al. 2011). Tidal interactions or minor mergers can induce the transport of gas with low angular momentum to the central parts of the host to (re-)start SMBH accretion (e.g. Hernquist & Mihos 1995); the host morphology would be much less affected than in a major merger event. Indeed we find that the AGN hosts are most similar to undisturbed galaxies, in the sense of highest KS test probability (P = 0.32 or P = 0.22, depending on which pair of descriptors is used). Our visually derived fraction of undisturbed AGN hosts is 48%, and it is likely that more objects with only weak tidal features are among the remaining 52% of unclear cases (Table 2).
The lack of signatures for frequent strong interactions is consistent with the findings at similar redshifts by Grogin et al. (2005), Pierce et al. (2007), Gabor et al. (2009), and Cisternas et al. (2011). One major difference between the first two of these and our analysis is that they did not account for the potential influence of an optical nucleus. The first three of the above samples mainly comprise type-2 AGN since they are X-ray selected (Gabor et al. give a type-1 AGN fraction of ~10%). Only the data set by Cisternas et al. (2011) mainly consists of type-1 AGN (contributing 60%); our own sample is made up entirely of type-1 AGN. Despite these differences in the type mix, our results and these previous studies agree qualitatively. This is to be expected in the context of the classical unification scheme of AGN (e.g. Urry & Padovani 1995), where the distinction between type 1 and type 2 is assumed to be an observational effect and not an intrinsic property.
To further interpret the observational findings, it would be highly desirable to create synthetic images based on numerical simulations. With simulations that include galaxy interactions and mergers in various configurations and a prescription for AGN activity (as, e.g., Di Matteo et al. 2005), sets of synthetic observations would have to be generated to investigate, for a given data quality, the detectability of interaction signatures during the AGN phase. Such an approach is, however, beyond the scope of this paper. In the future, we will also aim at developing a morphological descriptor scheme that is better capable of tracing weak interaction signatures than those we currently have at our disposal.
6. Summary
We carried out a quantitative comparison between the morphologies of the host galaxies of AGN and quiescent galaxies at redshifts 0.5 < z < 1.1. The imaging data were taken from the large HST/ACS mosaics of the GEMS and STAGES surveys. Our main aim was to test whether the AGN host galaxy population shows an increased fraction of morphological perturbations with respect to non-AGN. We created synthetic images to investigate the impact of an optical nucleus on the morphological analysis of AGN host galaxies. To quantify galaxy morphologies, we used the asymmetry index A, the concentration index C, the Gini coefficient G, and the M20 index. A sample of ~200 synthetic AGN was matched to 21 real AGN in terms of redshift, host brightness and host-to-nucleus ratio to ensure a reliable comparison between active and quiescent galaxies. The optical nuclei of type-1 AGN strongly affect the quantitative morphological properties of the underlying host galaxy. When these effects are accounted for, active and inactive galaxies show similar distributions in C/A and G/M20 space. The morphologies of the AGN hosts are clearly distinct from galaxies undergoing strong gravitational interactions. This is at variance with a naive expectation for a connection between major mergers and AGN. However, the signatures of gravitational interactions might be too weak to be detected by the commonly used descriptors like C/A due to a delay between the strongest morphological perturbation and the onset of the AGN phase.
Acknowledgments
We thank the anonymous referee for many suggestions that helped to improve the manuscript. AB acknowledges funding by the Deutsches Zentrum für Luft- und Raumfahrt (50 OR 0404) and by the Austrian Science Foundation FWF (grants P19300-N16 and P23946-N16); M.B. and E.v.K. acknowledge support by the FWF under grant P18416; M.E.G. and C.W. are supported by STFC Advanced Fellowships; CH by an European Commission Programme 6th framework Marie Cure Outgoing International Fellowship under contract MOIF-CT-2006-21891, and a CITA National fellowship; B.H. is grateful for support from the Science and Technology Facilities Council (STFC). K.J. is supported by the Emmy Noether Programme of the Deutsche Forschungsgemeinschaft; S.J. by NASA under LTSA Grant NAG5-13063, NSF grant AST-0607748 and HST grant GO-11082 from STScI, which is operated by AURA, Inc., for NASA, under NAS5-26555; D.H.M. by NASA under LTSA Grant NAG5-13102; C.Y.P. by STScI and NRC-HIA Fellowship programs; S.F.S. by the Spanish MEC grants AYA2005-09413-C02-02 and the P.A.I. of the Junta de Andalucía as research group FQM322. Support for STAGES was provided by NASA through GO-10395 from STScI operated by AURA under NAS5-26555.
References
- Abraham, R. G., Tanvir, N. R., Santiago, B. X., et al. 1996, MNRAS, 279, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Bennert, N., Canalizo, G., Jungwiert, B., et al. 2008, ApJ, 677, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhm, A., Wisotzki, L., & GEMS team 2007, ASP Conf. Ser. 379, eds. N. Metcalfe, & T. Shanks, 185 [Google Scholar]
- Borch, A., Meisenheimer, K., Bell, E. F., et al. 2006, A&A, 453, 869 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caldwell, J. A. R., McIntosh, D. H., Rix, H.-W., et al. 2008, ApJS, 174, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Canalizo, G., & Stockton, A. 2001, ApJ, 555, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Cisternas, M., Jahnke, K., Inskip, K. J., et al. 2011, ApJ, 726, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J. 2006, ApJ, 638, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J., Bershady, M. A., & Jangren, A. 2000, ApJ, 529, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Di Matteo, T., Springel, V., & Hernquist, L. 2005, Nature, 433, 604 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ellison, S. L., Patton, D. R., Mendel, J. T., & Scudder, J. M. 2011, MNRAS, 418, 2043 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrarese, L., & Merritt, D. 2000, ApJ, 539, 9 [Google Scholar]
- Gabor, J. M., Impey, K., Jahnke, K., et al. 2009, ApJ, 691, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Gebhardt, K., Bender, R., Bower, G., et al. 2000, ApJ, 539, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Grogin, N. A., Conselice, C. J., Chatzichristou, E., et al. 2005, ApJ, 627, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, M. E., Wolf, C., Barden, M., et al. 2009, MNRAS, 393, 1275 [NASA ADS] [CrossRef] [Google Scholar]
- Häring, N., & Rix, H.-W. 2004, ApJ, 604, 89 [Google Scholar]
- Häussler, B., McIntosh, D. H., Barden, M., et al. 2007, ApJS, 172, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennawi, J. F., Strauss, M. A., Oguri, M., et al. 2006, AJ, 131, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Hernquist, L., & Mihos, C. J., 1995, ApJ, 448, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Heymans, C., Gray, M. E., Peng, C. Y., et al. 2008, MNRAS, 385, 1431 [Google Scholar]
- Hopkins, P. F. 2012, MNRAS, 420, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Richards, G. T., & Hernquist, L. 2007, ApJ, 654, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., & Keres, D. 2008, ApJS, 175, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Jahnke, K., & Maccio, A. 2011, ApJ, 734, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Jahnke, K., Sanchez, S. F., Wisotzki, L., et al. 2004, ApJ, 614, 568 [NASA ADS] [CrossRef] [Google Scholar]
- Jogee, S. 2006, AGN Physics on All Scales, eds. D. Alloin, R. Johnson, & P. Lira, Lecture Notes in Physics, 93, 143 [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
- Khalatyan, A., Cattaneo, A., Schramm, M., et al. 2008, MNRAS, 387, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, M., Ho, L. C., Peng, C. Y., Barth, A. J., & Im, M. 2008, ApJS, 179, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Lehmer, B., Brandt, W. N., Alexander, D. M., et al. 2005, ApJS, 161, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Li, C., Kauffmann, G., Heckman, T. M., White, S. D. M., & Jing, Y. P. 2008, MNRAS, 385, 1915 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, J., Primack, J., & Madau, P. 2004, AJ, 128, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, J., Jonsson, P., Cox, T. J., & Primack, J. 2008, MNRAS, 391, 1137 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, A., & Hunt, L. K. 2003, ApJ, 589, 21 [Google Scholar]
- Martini, P. 2004, in The Interplay Among Black Holes, Stars and ISM in Galactic Nuclei, eds. T. Storchi-Bergmann, L. C. Ho, & H. R. Schmitt (Cambridge: Cambridge Univ. Press), IAU Symp., 222, 235 [Google Scholar]
- Myers, A. D., Brunner, R. J., Richards, G. T., et al. 2007, ApJ, 658, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y. 2007, ApJ, 671, 1098; AJ, 124, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Pierce, C. M., Lotz, J. M., Laird, E. S., et al. 2007, ApJ, 660, 19 [Google Scholar]
- Pierce, C. M., Lotz, J. M., Primack, J. R., et al. 2010, MNRAS, 405, 718 [NASA ADS] [Google Scholar]
- Rafferty, D. A., Brandt, W. N., Alexander, D. M., et al. 2011, ApJ, 742, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Rix, H.-W., Barden, M., Beckwith, S. V. W., et al. 2004, ApJS, 152, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchez, S. F., Jahnke, K., Wisotzki, L., et al. 2004, ApJ, 614, 586 [NASA ADS] [CrossRef] [Google Scholar]
- Schawinski, K., Thomas, D., Sarzi, M., et al. 2007, MNRAS, 382, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Schawinski, K., Treister, E., Urry, C. M., et al. 2011, ApJ, 727, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Serber, W., Bahcall, N., Menard, B., & Richards, G. 2006, ApJ, 643, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Sérsic, J. L. 1968, Atlas de Galaxias Australes (Córdoba: Obs. Astron. Uni. Nacional Cordoba), 1 [Google Scholar]
- Silverman, J. D., Mainieri, V., Lehmer, B. D., et al. 2008, ApJ, 675, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Silverman, J. D., Kampczyk, P., Jahnke, K., et al. 2011, ApJ, 743, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Simmons, B. D., & Urry, C. M. 2008, ApJ, 683, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Van den Berk, D. E., Richards, G. T., Bauer, A., et al. 2001, AJ, 122, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, C., Meisenheimer, K., Rix, H.-W., et al. 2003, A&A, 401, 73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolf, C., Meisenheimer, K., Kleinheinrich, M., et al. 2004, A&A, 421, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolf, C., Hildebrandt, H., Taylor, E. N., & Meisenheimer, K. 2008, A&A, 492, 933 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Two-dimensional KS test comparing major mergers and undisturbed galaxies in the quiescent comparison sample.
Two-dimensional KS test comparing major mergers and undisturbed galaxies in the simulated AGN sample (after removal of the central point sources).
All Figures
 |
Fig. 1 Comparison between the redshifts of the AGN (dashed) and the sample of quiescent galaxies (solid). The histograms are normalized to the same total number of objects. |
| In the text | |
 |
Fig. 2 Distribution of the AGN host galaxy magnitudes derived with GALFIT (dashed) compared to the quiescent sample (solid). The histograms are normalized to the same total number of objects. |
| In the text | |
 |
Fig. 3 HST/ACS v-band images of galaxies from the non-AGN comparison sample. Each row displays six examples of the three different morphological types that were denoted via visual classification (with at least four out of eight classifiers agreeing). The bar in each image has a length of one arcsec, corresponding to ~6 kpc at z = 0.5 or ~8 kpc at z = 1. |
| In the text | |
 |
Fig. 4 Illustration of the AGN simulation procedure. Upper left: original quiescent galaxy at redshift z = 0.52, apparent brightness v = 23.27. Upper middle: star of brightness v = 21.46 used as a synthetic nucleus. Upper right: simulated AGN (co-added galaxy and star) with a host-to-nucleus ratio of H/N = 0.18. Lower left: GALFIT model of the host galaxy (from fitting a nucleus + host model to the simulated AGN). Lower middle: recovered host galaxy after subtracting the GALFIT model of the nucleus from the simulated AGN image. Lower right: residual after subtracting the combined galaxy + nucleus model from the simulated AGN image. Each image is ~ 2 arcsec on the side. |
| In the text | |
 |
Fig. 5 Distribution of the host-to-nucleus ratios H/N of the real AGN (dashed) compared to the simulated AGN (solid). The histograms are normalized to the same total number of objects. |
| In the text | |
 |
Fig. 6 Visual classifications of the nucleus-subtracted real AGN sample (with subtracted model nucleus from two-component modeling as described in Sect.3.3). The bar in each image has a length of one arcsec. |
| In the text | |
 |
Fig. 7 GALFIT recovery of host galaxy parameters for the simulated AGN sample. a) Deviations between input host magnitude vhost, ini and recovered host magnitude as a function of input host magnitude. b) Deviations between original host magnitude and recovered host magnitude vhost, sim as a function of input H/Nini. c) Deviations between input effective radius reff, ini and recovered effective radius reff, sim as a function of input effective radius. d) Deviations between input effective radius and recovered effective radius as a function of input H/N. e) Deviations between input Sérsic index nini and recovered Sérsic index nsim as a function of input host magnitude. f) Deviations between input Sérsic index nini and recovered Sérsic index nsim as a function of input H/N. |
| In the text | |
 |
Fig. 8 GALFIT recovery of host galaxy parameters for the simulated AGN sample. a) Deviations between input host magnitude vhost,ini and recovered host magnitude vhost, sim as a function of the deviations between input Sérsic index nini and recovered Sérsic index nsim. b) Deviations between input H/Nini and the recovered H/Nsim as a function of the deviations between original host magnitude and recovered host magnitude. c) Deviations between input H/Nini and the recovered H/Nsim as a function of input H/N. d) Deviations between input H/Nini and the recovered H/Nsim as a function of input host magnitude. |
| In the text | |
 |
Fig. 9 Distribution of the quiescent galaxies in concentration index C versus asymmetry A (left) and in Gini coefficient G versus M20 (right). Tiny open symbols depict ambiguous cases, large open symbols show undisturbed galaxies, large filled symbols are classified as major mergers. Galaxies have highly concentrated light profiles toward the right-hand side of the graphs and become more asymmetric/show more substructure toward the upper part of the graphs. |
| In the text | |
 |
Fig. 10 Distribution of the simulated AGN (i.e. a quiescent galaxy with an additional synthetic nucleus (before subtraction), depicted here as circles) and real AGN host galaxies (open diamonds), in concentration index C versus asymmetry A (left) and in Gini coefficient G versus M20 (right). Tiny open symbols depict ambiguous cases, large open symbols show undisturbed galaxies, large filled symbols are classified as major mergers. With respect to the original galaxy images (the distributions of which are shown in Fig. 9), the distinguishability between different morphological types is degraded. |
| In the text | |
 |
Fig. 11 Distribution of the simulated and real AGN host galaxies after subtracting the best-fit model nucleus in concentration index C versus asymmetry A (left) and in Gini coefficient G versus M20 (right). Tiny open symbols depict ambiguous cases, large open symbols show undisturbed galaxies, large filled symbols are classified as major mergers. Major mergers and undisturbed galaxies are better separated than before subtracting the nuclei (Fig. 10). |
| In the text | |
 |
Fig. 12 Illustration of the impact of a subtracted nucleus on the quantitative morphologies of the simulated AGN galaxies in concentration index C (upper left), asymmetry A (upper right), Gini coefficient G (bottom left), and M20 (bottom right). As a function of H/N, all plots show the initial parameter value before (index ini) and after addition & subtraction of a synthetic nucleus (index sim), normalized to the initial value. See text for details. |
| In the text | |
 |
Fig. 13 Illustration of the impact of an unsubtracted nucleus on the quantitative morphologies of the simulated AGN galaxies in concentration index C (upper left), asymmetry A (upper right), Gini coefficient G (bottom left), and M20 (bottom right). As a function of H/N, both plots show the initial value before (index ini) and after the addition of a synthetic nucleus (index unsub), normalized to the initial value. See text for a discussion. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


