| Issue |
A&A
Volume 548, December 2012
|
|
|---|---|---|
| Article Number | A73 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201220365 | |
| Published online | 23 November 2012 | |
The impact of atmospheric circulation on the chemistry of the hot Jupiter HD 209458b
1 Univ. Bordeaux, LAB, UMR 5804, 33270 Floirac, France
e-mail: Marcelino.Agundez@obs.u-bordeaux1.fr
2 CNRS, LAB, UMR 5804, 33270 Floirac, France
3 Astrophysics Group, Keele University, Keele, Staffordshire, ST5 5BG, UK
Received: 11 September 2012
Accepted: 23 October 2012
We investigate the effects of atmospheric circulation on the chemistry of the hot Jupiter HD 209458b. We use a simplified dynamical model and a robust chemical network, as opposed to previous studies, which have used a three-dimensional circulation model coupled to a simple chemical kinetics scheme. The temperature structure and distribution of the main atmospheric constituents are calculated in the limit of an atmosphere that rotates as a solid body with an equatorial rotation rate of 1 km s-1. Such motion mimics a uniform zonal wind, which resembles the equatorial superrotation structure found by three-dimensional circulation models. The uneven heating of this tidally locked planet causes, even in the presence of such a strong zonal wind, large temperature contrasts, up to 800 K, between the dayside and nightside. This would result in important longitudinal variations of some molecular abundances if the atmosphere were at chemical equilibrium. The zonal wind, however, acts as a powerful disequilibrium process. We identify the existence of a pressure level of transition between two regimes, which may be located between 100 and 0.1 mbar depending on the molecule. Below this transition layer, chemical equilibrium holds. Above it, however, the zonal wind tends to homogenise the chemical composition of the atmosphere, bringing molecular abundances in the limb and nightside regions close to chemical equilibrium values characteristic of the dayside, i.e. producing a horizontal quenching effect in the abundances. Reasoning based on timescale arguments indicates that horizontal and vertical mixing are likely to compete in HD 209458b’s atmosphere, producing a complex distribution where molecular abundances are quenched horizontally to dayside values and vertically to chemical equilibrium values characteristic of deep layers. Either assuming pure horizontal mixing or pure vertical mixing, we find substantial variations in the molecular abundances at the evening and morning limbs, up to one order of magnitude for CH4. This may have consequences for the interpretation of transmission spectra that sample the planet’s terminator of hot Jupiters.
Key words: astrochemistry / planets and satellites: atmospheres / planets and satellites: individual: HD 209458b
© ESO, 2012
1. Introduction
Gas giant planets that orbit close to their star, the so-called hot Jupiters, are not the most common type of extrasolar planets (Batalha et al. 2012), although they are the easiest to observe due to their short orbital distance and large mass. The first planets discovered around main sequence stars other than the Sun are, in fact, hot Jupiters, such as 51 Pegasi b, the first such object found (Mayor & Queloz 1995), and HD 209458b, the first exoplanet caught transiting its star (Charbonneau et al. 2000; Henry et al. 2000). Moreover, hot Jupiters are nearly the only ones among extrasolar planets for which constraints on their atmospheric composition have been obtained from observations. Transiting exoplanets offer the opportunity to get transmission and emission spectra of the atmosphere by observing at different wavelengths during the primary transit and secondary eclipse, respectively. The interpretation of such spectra, although difficult and sometimes contradictory, allows to identify the main atmospheric constituents and to derive their abundances (Charbonneau et al. 2002; Tinetti et al. 2007; Swain et al. 2008, 2009; Grillmair et al. 2008; Sing et al. 2009; Madhusudhan et al. 2011; Beaulieu et al. 2011). Incoming missions such as FINESSE, James Webb Space Telescope, and EChO will in the near future allow the observation of the atmospheres of transiting exoplanets down to the size of rocky planets, although to date hot Jupiters offer the best and almost unique chance to get access to the atmospheric composition of extrasolar planets.
The characterization of hot Jupiter atmospheres has motivated the development of one-dimensional models that include thermochemical kinetics, diffusion, and photochemistry, and that aim at describing the chemical behaviour and composition of such atmospheres in the vertical direction (Zahnle et al. 2009; Line et al. 2010; Moses et al. 2011; Kopparapu et al. 2012; Venot et al. 2012). These models indicate that chemical equilibrium is attained deep in the atmosphere, although the chemical composition of the layers typically sampled by transit observations, in the 1 bar to 0.01 mbar pressure regime, is maintained out of equilibrium due to two major disequilibrium processes. On the one hand, the intense ultraviolet radiation received from the star on top of the atmosphere drives an active photochemistry, which may extend down to the 1 mbar layer. On the other, vertical mixing processes tend to homogenise the chemical composition above a certain height as a consequence of the rapid transport of material from deep and hot layers to higher and cooler altitudes, where chemical kinetics is much slower.
Hot Jupiters are, according to theory (see e.g. Guillot et al. 1996), tidally locked to their star and thus receive stellar light on one hemisphere only. Therefore, in the absence of atmospheric winds, there would be an extremely high temperature contrast between the dayside and the nightside. General circulation models, however, predict the presence of strong winds, with velocities up to a few km s-1, that would efficiently redistribute the energy from the dayside to the nightside (Guillot & Showman 2002; Cho et al. 2003, 2008; Cooper & Showman 2005; Showman et al. 2008, 2009; Menou & Rauscher 2009; Heng et al. 2011; Miller-Ricci Kempton & Rauscher 2012; Dobbs-Dixon et al. 2012). Moreover, observational evidence of such winds has been tentatively found by Snellen et al. (2010). These authors have observed a 2 km s-1 blueshift of carbon monoxide absorption lines in the transmission spectrum of HD 209458b at the 2σ confidence level, which they have interpreted as an evidence of day-to-night winds occurring in the 0.01–0.1 mbar pressure regime.
Winds transport material between different locations in the atmosphere and therefore may have an impact on the distribution of the atmospheric constituents. In a study that investigated this phenomenon, Cooper & Showman (2006) coupled a simplified kinetics scheme for the conversion between CO and CH4 to a three-dimensional circulation model of HD 209458b. These authors showed that dynamics driven by uneven heating of the planet act as a strong disequilibrium process and homogenise the mixing ratios of CO and CH4 in the 1 bar to 1 mbar pressure range, even in the presence of strong temperature gradients. It is, however, difficult to disentangle from such complex circulation models, whether vertical or horizontal transport is the dominant disequilibrium process. In their study, Cooper & Showman (2006) argue in terms of timescale estimates and conclude that horizontal transport is not important compared to vertical mixing.
Here we adopt a different approach to studying the impact of horizontal winds on the distribution of the atmospheric constituents of HD 209458b. We use a time-dependent radiative model to calculate the temperature structure of an atmosphere that rotates as a solid body, mimicking a uniform zonal1 wind. Afterwards, the chemical evolution is computed at various pressure levels with a robust chemical kinetics network to obtain the chemical composition as a function of longitude and height.
2. The model
2.1. The radiative model
A detailed description of the adopted physical model is given in Iro et al. (2005). Briefly, we consider a planet tidally locked to its star, i.e. in synchronous rotation, with a radius of 1.38 RJ and a mass of 0.714 MJ, as derived for the hot Jupiter HD 209458b (Southworth 2010). We consider that the atmosphere rotates as a solid body, with respect to the synchronously rotating frame, at a constant angular velocity corresponding to an equatorial linear velocity of 1 km s-1 at the 1 bar pressure level. Such motion of the atmosphere mimics a uniform zonal wind independent of height, where layers remain static with respect to each other. Under this assumption, the evolution of the vertical temperature profile is given by 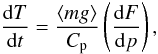 (1)where T is the temperature, t the time, ⟨ mg ⟩ the mean molecular weight, Cp the specific heat, F the radiative net flux, and p the pressure. The incoming stellar flux is computed adopting a Kurucz spectrum for HD 2094582 (Teff = 6100 K and log g = 4.38), a stellar radius of 1.2 R⊙ (Mazeh et al. 2000), and an orbital distance of 0.047 AU (Southworth 2010). The longitude-dependent insolation pattern is calculated for a latitude of 30°, which corresponds approximately to the flux averaged over latitude, i.e. along a meridian (see details in Iro et al. 2005). The sources of atmospheric opacity included are Rayleigh scattering, absorption from H2–H2 and H2–He pairs, H− bound-free, H
(1)where T is the temperature, t the time, ⟨ mg ⟩ the mean molecular weight, Cp the specific heat, F the radiative net flux, and p the pressure. The incoming stellar flux is computed adopting a Kurucz spectrum for HD 2094582 (Teff = 6100 K and log g = 4.38), a stellar radius of 1.2 R⊙ (Mazeh et al. 2000), and an orbital distance of 0.047 AU (Southworth 2010). The longitude-dependent insolation pattern is calculated for a latitude of 30°, which corresponds approximately to the flux averaged over latitude, i.e. along a meridian (see details in Iro et al. 2005). The sources of atmospheric opacity included are Rayleigh scattering, absorption from H2–H2 and H2–He pairs, H− bound-free, H free-free absorption, ro-vibrational lines of the molecules CO, H2O, CH4, CO2, NH3, and TiO, and resonance lines of the alkali atoms Na and K. The sources of the opacity data used are described in Iro et al. (2005), except for NH3 and CO2, whose spectroscopic data were taken from HITRAN 2008 and HITEMP, respectively (Rothman et al. 2009, 2010). In the current model, 45 layers are included, with pressures ranging from 100 to 10-6 bar. We adopt as initial condition a vertical temperature profile computed at radiative equilibrium with a one-dimensional radiative-convective model under planet-averaged insolation conditions. The abundances of the species that provide opacity are calculated at chemical equilibrium, adopting solar elemental abundances and the radiative equilibrium temperature profile. They are assumed to remain constant with time and therefore with longitude (see Iro et al. 2005, for more details). The thermal structure and chemical composition could be calculated self-consistently by iterating between the radiative and chemical models. In the case of HD 209458b, our approach is, however, justified by the fact that the main species that provide opacity and affect the thermal structure are H2O and CO, whose abundances, as shown in Sect. 3, are very close to the chemical equilibrium values and remain uniform with longitude. The thermal structure of the atmosphere (temperature as a function of longitude and height) is evaluated by integrating Eq. (1) during several rotation cycles until the temperature reaches a periodic state in each layer. We note that below the 10 bar level the temperature does not completely reach a periodic state due to the very long radiative timescale. These deep layers have, however, little interest to study the variation with longitude of the chemical composition since the temperature is nearly uniform with longitude.
free-free absorption, ro-vibrational lines of the molecules CO, H2O, CH4, CO2, NH3, and TiO, and resonance lines of the alkali atoms Na and K. The sources of the opacity data used are described in Iro et al. (2005), except for NH3 and CO2, whose spectroscopic data were taken from HITRAN 2008 and HITEMP, respectively (Rothman et al. 2009, 2010). In the current model, 45 layers are included, with pressures ranging from 100 to 10-6 bar. We adopt as initial condition a vertical temperature profile computed at radiative equilibrium with a one-dimensional radiative-convective model under planet-averaged insolation conditions. The abundances of the species that provide opacity are calculated at chemical equilibrium, adopting solar elemental abundances and the radiative equilibrium temperature profile. They are assumed to remain constant with time and therefore with longitude (see Iro et al. 2005, for more details). The thermal structure and chemical composition could be calculated self-consistently by iterating between the radiative and chemical models. In the case of HD 209458b, our approach is, however, justified by the fact that the main species that provide opacity and affect the thermal structure are H2O and CO, whose abundances, as shown in Sect. 3, are very close to the chemical equilibrium values and remain uniform with longitude. The thermal structure of the atmosphere (temperature as a function of longitude and height) is evaluated by integrating Eq. (1) during several rotation cycles until the temperature reaches a periodic state in each layer. We note that below the 10 bar level the temperature does not completely reach a periodic state due to the very long radiative timescale. These deep layers have, however, little interest to study the variation with longitude of the chemical composition since the temperature is nearly uniform with longitude.
 |
Fig. 1 Thermal atmospheric structure of HD 209458b. The top panel shows the temperature distribution as a function of longitude and pressure, while the middle panel shows the temperature as a function of longitude at selected pressure levels. The bottom panel shows the vertical temperature profiles at the substellar and antistellar meridians and at the morning and evening limbs. |
The resulting temperature distribution is shown in three different ways in Fig. 1. The increase in the radiative timescale, or thermal inertia, with increasing depth produces a couple of interesting effects. First, the maximum of temperature is shifted in longitude with respect to the substellar meridian by an amount that increases with depth (see top and middle panels of Fig. 1 in the 1–10-2 bar pressure regime). This is a simple consequence of the eastward transport of heat. An eastward jet and the resulting shift of the thermal emission peak was predicted by Showman & Guillot (2002) to be a common phenomenon in hot Jupiter atmospheres. The shift was later observed in the thermal phase curve of HD 189733b by Knutson et al. (2007). In the same vein, we find that the temperature is not homogeneous in the nightside (which would be the case in the absence of winds), but rather inhomogeneous, with the coldest regions located close to the morning limb (see mid and bottom panels of Fig. 1). A second effect worth noting is that the longitudinal profile of temperature is markedly different in the deep and high regions of the atmosphere. Below the 1 bar pressure level, the temperature remains nearly uniform (see bottom panel of Fig. 1), while above this level large temperature contrasts, up to 800 K, exist (see middle panel of Fig. 1).
Our time-dependent radiative model provides an accurate treatment of the radiative processes, although the atmospheric dynamics is somewhat simplified. In the limit of a solid-body rotating atmosphere, the dynamics is restricted to a uniform zonal wind. Meridional winds are, therefore, neglected as well as vertical transport processes (layers are radiatively coupled but dynamically decoupled). Focusing on horizontal advection (winds), three-dimensional circulation models of hot Jupiters (e.g. Cooper & Showman 2005, 2006; Showman et al. 2008, 2009; Heng et al. 2011) find that the atmospheric circulation is dominated by a fast eastward (superrotating) jet stream that develops at low latitudes and may reach wind speeds up to a few km s-1. Equatorial superrotation dominates the dynamics of the atmosphere in the deep regions, but as we move towards higher altitudes the circulation pattern changes. Three-dimensional circulation models of HD 209458b (see e.g. Showman et al. 2009, 2012) indicate that above the 1–0.1 mbar level zonal winds are no longer superrotating and strong substellar-to-antistellar zonal and meridional winds dominate the atmospheric dynamics. Our assumption of a uniform zonal wind with an equatorial velocity of 1 km s-1 also ignores variations of the zonal wind speed with altitude, which may be significant (wind speeds generally increase with height) according to circulation models (e.g. Showman et al. 2009). With the above limitations, our approach should still offer a realistic approximation of the atmospheric dynamics of HD 209458b in the 1–10-4 bar pressure range, where equatorial superrotation holds. This is in fact the most interesting region to study the disequilibrium effects caused by atmospheric circulation, as will be shown hereafter.
2.2. The chemical model
Still under the assumption of a solid-body rotating atmosphere, the evolution in the chemical composition of the different atmospheric layers as they cycle around the planet is calculated by solving a system of differential equations of the type 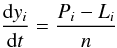 (2)where yi is the mole fraction of the species i, Pi and Li are the rates of production and loss of species i due to chemical reactions (with cgs units of cm-3 s-1), and n is the total volume density of particles (with cgs units of cm-3), which is related to the pressure p and temperature T through the ideal gas law. The system of chemical equations is integrated, independently for each layer, during several rotation cycles until the abundances of the major species reach a periodic state. During the integration, the pressure remains constant in each layer, and the temperature varies according to the longitude-dependent profiles calculated with the radiative model. We start the integration at the substellar meridian with a chemical composition calculated at chemical equilibrium with solar elemental abundances (Asplund et al. 2009) and the (T,p) profile shown in the bottom panel of Fig. 1. The chemical equilibrium calculations are done with a code that minimizes the Gibbs energy following the algorithm of Gordon & McBride (1994). The choice of the initial composition at the chemical equilibrium values of hot regions, such as the substellar meridian, is very convenient as it accelerates considerably the convergence towards a periodic state. The reasons for that are discussed in Sect. 3.1.
(2)where yi is the mole fraction of the species i, Pi and Li are the rates of production and loss of species i due to chemical reactions (with cgs units of cm-3 s-1), and n is the total volume density of particles (with cgs units of cm-3), which is related to the pressure p and temperature T through the ideal gas law. The system of chemical equations is integrated, independently for each layer, during several rotation cycles until the abundances of the major species reach a periodic state. During the integration, the pressure remains constant in each layer, and the temperature varies according to the longitude-dependent profiles calculated with the radiative model. We start the integration at the substellar meridian with a chemical composition calculated at chemical equilibrium with solar elemental abundances (Asplund et al. 2009) and the (T,p) profile shown in the bottom panel of Fig. 1. The chemical equilibrium calculations are done with a code that minimizes the Gibbs energy following the algorithm of Gordon & McBride (1994). The choice of the initial composition at the chemical equilibrium values of hot regions, such as the substellar meridian, is very convenient as it accelerates considerably the convergence towards a periodic state. The reasons for that are discussed in Sect. 3.1.
The adopted chemical network, available from the KIDA database3 (Wakelam et al. 2012), is described in detail in Venot et al. (2012). Here we use their nominal mechanism, which consists of 102 neutral species composed of C, H, O, and N (He is just a non-reactive collider in some reactions) linked by 1882 chemical reactions of three main types: bimolecular disproportionation, three-body association, and thermal decomposition. The full set of reactions consists, in fact, of 941 reversible reactions written in the forward and backward directions. For most of them, the rate constant of the backward reaction is calculated applying the principle of detailed balance and using the rate constant of the forward process and thermochemical data of the species involved. This chemical network ensures that the chemical composition will evolve towards a chemical equilibrium state (see Venot et al. 2012). The set of rate constants and thermochemical data of our mechanism comes from combustion chemistry. More specifically, it consists of a C/H/O reaction base developed for industrial applications (Fournet et al. 1999; Bounaceur et al. 2010), which has been validated for species containing up to two carbon atoms and a nitrogen base constructed to deal with NOx compounds and other nitrogen-containing species (Coppens et al. 2007; Konnov 2009). The mechanism has been validated against numerous combustion experiments over a wide range of temperature (300–2500 K) and pressure (0.01–100 bar) and been found suitable to model the atmospheric chemistry of hot Jupiters (Venot et al. 2012).
There are two main differences with respect to the original nominal mechanism used in Venot et al. (2012). First, in this study we also model the nightside of HD 209458b, whose upper atmospheric layers may have temperatures lower than 300 K, i.e. outside the temperature range of validation of the chemical network. At these low temperatures, the rate constants of a few reactions (mostly backward ones whose rate constant is calculated applying detailed balance) reach too large values. For these few reactions, we have either adopted a different rate constant expression from the literature or imposed a maximum rate constant (2 × 10-9 cm3 s-1 and 10-28 cm6 s-1 for bimolecular and termolecular reactions, respectively) to get reasonable values down to temperatures lower than 300 K. The impact of these modifications on the abundances of the major species is nonetheless negligible. A second difference is that in this study we have not considered photochemical processes, so that the excited states of oxygen and nitrogen atoms, O(1D) and N(2D), have not been included, as they are mainly produced by photodissociation of various molecules. Previous studies have found that photochemistry has a very minor impact on the atmospheric composition of the dayside of HD 209458b, due to the high temperatures that help to maintain chemical equilibrium (Moses et al. 2011; Venot et al. 2012). The vertical temperature profiles adopted by these authors are mainly based on the results of the three-dimensional circulation model of Showman et al. (2009), which results in dayside temperatures higher than those found with our time-dependent radiative model. We therefore note that the lower temperatures we find are likely to increase the impact of photochemistry, as compared to the studies of Moses et al. (2011) and Venot et al. (2012), on the abundances of some species, noticeably HCN, CO2, CH4, and NH3, in the upper (above the 10-4–10-5 bar layer) dayside atmosphere of HD 209458b. At these altitudes, horizontal winds are anyway substellar to antistellar rather than superrotating.
Some of the limitations of our current chemical modelling approach, where layers are assumed to be independent from each other (they are neither radiatively coupled through the transfer of ultraviolet photons nor dynamically coupled by vertical mixing), will be addressed in a future study.
3. Results and discussion
3.1. Zonal wind: effects on the chemistry
The impact of a uniform zonal wind mimicking an equatorial superrotation on the atmospheric chemistry of a hot Jupiter such as HD 209458b may be understood in terms of timescales. On the one hand, we have the chemical timescale of the different chemical transformations that take place as the wind moves material between the hot dayside and the cooler nightside. On the other hand, there is the dynamical timescale related to the zonal wind motion.
 |
Fig. 2 Longitudinal distributions of the mole fractions of CH4, CO, and CO2 for selected pressure levels, as calculated by the chemical kinetics model with a uniform zonal wind of 1 km s-1 (solid lines) and by chemical equilibrium adopting the longitudinal temperature profile of each pressure level (dotted lines). |
If the atmosphere were at chemical equilibrium everywhere, we would expect important differences in the chemical composition of the dayside and nightside due to the high temperature contrast between both planet sides. For example, at chemical equilibrium most of the carbon is in the form of CO at high temperatures and as CH4 at temperatures below ~1000 K. This is illustrated in Fig. 2, where chemical equilibrium abundances of a few molecules (CH4, CO, and CO2), as computed along the longitudinal temperature profile of each pressure level, are shown (as dotted lines) as a function of longitude for selected pressures. It is seen that for p ≤ 10-2 bar methane has a low abundance in the dayside, where most of carbon is in the form of CO, but becomes very abundant in the nightside at the expense of carbon monoxide.
The presence of a zonal wind, however, produces significant departures from chemical equilibrium. In Fig. 2 we also show (as solid lines) the mole fractions of CH4, CO, and CO2 resulting from the chemical kinetics model after ten rotation cycles, when the abundances of the major species have already reached a periodic state. We can identify two major types of regimes. In the hot and dense bottom layers of the atmosphere, chemical timescales are short and chemical equilibrium is attained (see e.g. the case of CH4 at 1 bar). At higher altitudes, however, temperatures and pressures decrease and chemical timescales become longer than the dynamical timescale, producing a quenching effect on the abundances (see e.g. the case of CH4 at 10-2 and 10-3 bar). In these upper layers, species tend to reach an abundance uniform with longitude, close to the chemical equilibrium values of the hottest dayside regions. This latter fact makes it very convenient to start the integration with the chemical equilibrium composition at the substellar meridian because the initial abundances are already close to the final quenched values and so the convergence is considerably accelerated. We verified the non-dependence of our results on the initial chemical composition by starting with chemical equilibrium compositions at other longitudes, such as the antistellar meridian. We find that the same periodic state is reached for the abundances of the major species, although at much longer integration times, especially in low-pressure layers.
 |
Fig. 3 Vertical distributions of the major species, after H2 and He, at four longitudes: substellar meridian, evening limb, antistellar meridian, and morning limb. We show the mole fractions given by the zonal wind thermochemical kinetics model (solid lines), by a one-dimensional model in the vertical direction including thermochemical kinetics and vertical eddy diffusion (dashed lines), and by chemical equilibrium adopting the (p,T) vertical profile at each longitude (dotted lines). Note that abundances above the 10-4–10-5 bar level may not be reliable due to the lack of photochemistry in our model and, in the case of the zonal wind model, to a likely change in the circulation pattern. |
In the layers of transition between these two regimes, the behaviour of the chemical composition with longitude is such that abundances are close to the chemical equilibrium values in the hot dayside, where chemical kinetics proceeds faster, and remain somewhat quenched in the cooler nightside, where chemical kinetics is slower (see e.g. the case of CH4 at 10-1 bar). Each species has its own chemical timescale of formation and destruction, and so the transition between the chemical equilibrium and quenching regimes is located at a different pressure level for each species. For CH4 and CO, the quenching region is found above the 10-1 bar level (see Fig. 2), so that the large day-to-night abundance variations predicted by chemical equilibrium for these two molecules at p ≤ 10-2 bar are not effectively attained. This result was also found by Cooper & Showman (2006) using a simple conversion scheme for CO and CH4. For other molecules with shorter chemical timescales, the quenching level is located at higher altitudes (above the 10-3–10-4 bar level for CO2; see Fig. 2).
We adopted an equatorial wind velocity of 1 km s-1, although three-dimensional circulation models of HD 209458b find equatorial wind velocities in the range 0.1–10 km s-1 (Showman et al. 2009; Heng et al. 2011; Miller-Ricci Kempton & Rauscher 2012). The wind velocity affects the distribution of the abundances in two ways. On the one hand, it has an impact on the longitudinal temperature profile: the slower the wind velocity, the higher the day-to-night temperature contrast (see Iro et al. 2005). It therefore affects the chemical equilibrium composition attained in the bottom atmospheric layers, which depend on the local temperature. On the other hand, the wind velocity determines the horizontal dynamical timescale and therefore the quenching level, which is shifted upwards with slower wind velocities. Although our results depend to some extent on the adopted wind velocity, overall the qualitative behaviour of the distribution of the abundances remains the same.
The zonal wind, therefore, tends to homogenise the chemical composition of the atmosphere, bringing species abundances in the nightside close to those prevailing in the dayside. In the upper atmospheric layers, above the 0.1–10-4 bar level depending on the species, abundances are quenched to chemical equilibrium values of the hottest dayside longitudes. Below this quenching level, where chemical timescales become comparable or shorter than horizontal dynamical timescales, abundances can experience significant variations with longitude induced by the longitudinal temperature gradients. At these pressure levels, the abundances of some molecules can be quite different in the two meridians of the planet’s terminator (the morning and evening limbs), with consequences for the interpretation of transmission spectra (see below). Deeper in the atmosphere, below the 1 bar level, temperatures are high and uniform with longitude, so that the chemical composition is also uniform with longitude and given by chemical equilibrium.
At high enough levels, horizontal quenching makes the chemical composition homogeneous with longitude, which allows the application of retrieval methods based on a single vertical chemical profile when interpreting transmission spectra. At these chemically homogeneous levels, the molecular composition of the limbs is nearly independent of the local temperature and is mainly determined by the substellar temperature. This raises an interesting question: can the abundances measured at the limbs be used as a thermometer for the substellar region? Although they can indeed provide constraints on the hottest temperatures experienced by the gas, quenching occurs at a different temperature for each species. Therefore, the observed mixture is in disequilibrium not only with the local temperature but also with any temperature. For instance, at the 10-4 bar level, the sunrise and sunset limbs are at 510 and 820 K, respectively, and they both exhibit the same abundances for CO, CH4, CO2, N2, and NH3. The CH4/CO and NH3/N2 abundance ratios both correspond to a chemical equilibrium composition at 1300 K, which is nearly the temperature of the substellar region. However, the CO2/CO abundance ratio corresponds to an equilibrium composition of a cooler mixture (at 1145 K). Of course, these quenching temperatures depend on the elemental composition and the wind velocity, and are derived from a rather simple circulation pattern. In addition, composition may vary significantly between the equator and the poles. We come back to this point at the end of Sect. 3.2.
3.2. Horizontal vs. vertical quenching
In the limit of a solid-body rotating atmosphere, where dynamics is restricted to a uniform zonal wind, molecular abundances are quenched above a certain pressure level to chemical equilibrium dayside values. The distribution of the chemical composition computed in this way is, however, likely to be unrealistic due to the existence of vertical transport processes, which tend to quench abundances vertically above a certain height to chemical equilibrium values characteristic of hot deep regions (Moses et al. 2011; Venot et al. 2012).
In order to compare the predictions of our zonal wind model with a model where dynamics is restricted to vertical mixing, we constructed a one-dimensional model in the vertical direction that includes thermochemical kinetics and vertical eddy diffusion, which we apply to various longitudes. Photochemistry was not included to allow for a proper comparison with the zonal wind model. We used a code that is based on the same principles as that used by Dobrijevic et al. (2010) and Venot et al. (2012). We adopted the temperature-pressure vertical profiles calculated at each longitude with the time-dependent radiative model (see bottom panel of Fig. 1) and the chemical network described in Sect. 2.2. The dayside-averaged eddy diffusion coefficient profile estimated by Moses et al. (2011) from the three-dimensional circulation model of Showman et al. (2009) was adopted, for simplicity, at every longitude.
In Fig. 3 we show the vertical distribution of the major species at the substellar meridian, evening limb, antistellar meridian, and morning limb, as computed by the zonal wind model (solid lines), by the vertical mixing model (dashed lines), and by chemical equilibrium (dotted lines). Both the zonal wind and vertical mixing models predict important departures from chemical equilibrium, especially in the cool nightside regions (see e.g. CO and CH4 at the antistellar meridian). The vertical distribution of the abundances predicted by the zonal wind model is similar at the four longitudes and is essentially given by the chemical equilibrium composition calculated at the substellar meridian. There are a few differences in the vertical abundance profile of some molecules when moving from one longitude to another (see e.g. CO2 and CH4 at the substellar and antistellar meridians), although the main effect of the zonal wind is to homogenise the chemical composition at the limbs and nightside to chemical equilibrium dayside values. The vertical mixing model shows a quite different picture, where abundances remain at chemical equilibrium in the deep atmosphere and are quenched above the 1–0.01 bar pressure level, depending on the molecule, to the chemical equilibrium values characteristic of this quenching level. Since the vertical temperature profile is different at each longitude, the value at which the abundance of a given molecule is quenched can also vary from one longitude to another (see e.g. CH4 at the substellar and antistellar meridians). We note that photochemistry may play an important role above the 10-4–10-5 bar level, so that the abundances calculated by the zonal wind and vertical mixing models above this layer may not be very reliable.
Therefore, in the limit of a zonal wind, abundances are quenched horizontally (above the 0.1–10-4 bar level) to chemical equilibrium dayside values, while in the limit where dynamics is restricted to vertical mixing, abundances are quenched vertically (above the 1–0.01 bar level) to chemical equilibrium values characteristic of the hot deep layers. We can get a rough idea of the relative importance of horizontal and vertical quenching from timescale arguments. The dynamical timescale of horizontal mixing τdyn,h may be roughly estimated as πRp/u, where Rp is the radius of the planet, u is the zonal wind speed, and where the distance between substellar and antistellar points has been adopted as length scale. For our zonal wind speed of 1 km s-1, we get τdyn,h ~ 3 × 105 s. Similarly, a rough estimate of the dynamical timescale of vertical mixing τdyn,v may be obtained as H2/Kzz, where H is the atmospheric scale height and Kzz is the eddy diffusion coefficient. Adopting values for H and Kzz in the 1 bar to 1 mbar pressure range of HD 209458b’s atmosphere (H = 300–700 km, Kzz = 1010–1011 cm2 s-1), we find that τdyn,v takes values between 104 and 5 × 105 s. We must keep in mind that the above timescale values are just a crude estimation. On the one hand, the zonal wind speed may span a broad range of values up to 10 km s-1 depending on height and latitude, according to three-dimensional circulation models of HD 209458b (Showman et al. 2009; Heng et al. 2011; Miller-Ricci Kempton & Rauscher 2012). On the other hand, the use of the atmospheric scale height to estimate the dynamical timescale for vertical mixing may not be an accurate choice, as discussed by Smith (1998). Finally, the values of the eddy diffusion coefficient adopted, which are estimated by Moses et al. (2001) from the three-dimensional circulation model of Showman et al. (2009) as the horizontally averaged global rms vertical velocity times the height scale, may be quite different if they are more properly estimated through, e.g., the diffusive behaviour of a passive tracer included in the circulation model. Moreover, dynamical timescales are expected to experience important variations as a function of longitude, latitude, and height. Taking into account all these limitations, we may just conclude that the dynamical timescales for horizontal and vertical mixing have the same order of magnitude. It is, therefore, very likely that both horizontal and vertical quenching are simultaneously at work in the atmosphere of HD 209458b, which may result in a complex atmospheric distribution of the abundances of some species. Our timescale estimates are similar to those found by Cooper & Showman (2006) for HD 209458b, although these authors conclude that horizontal quenching is not important. Cooper & Showman (2006) argue that chemical timescales exceed the horizontal dynamical timescale above the 3 bar level, where abundances have already been quenched by vertical mixing. It is, nevertheless, the comparison between the dynamical timescales for horizontal and vertical mixing, τdyn,h and τdyn,v, which allows one to decide whether horizontal or vertical quenching dominates, whenever τchem remains longer than any dynamical timescale.
As shown in Fig. 3, the molecules CO, H2O, and N2 (as well as H2, which is not shown) show a uniform abundance with height and longitude, either adopting the zonal wind model or the vertical mixing model. For these molecules it is therefore of no relevance whether horizontal or vertical quenching dominates. The vertical abundance profile of the other major molecules CH4, NH3, CO2, and HCN shows important differences when calculated with the zonal wind model or with the vertical mixing one. Moreover, when either of the two models is used, some abundance variations with longitude are found. These molecules therefore may have different abundances in the evening and morning limbs, which would have consequences for the interpretation of transmission spectra. In Fig. 4 we compare the vertical distribution of the abundances of CH4, NH3, CO2, and HCN at the evening and morning limbs, as computed with the zonal wind model and the vertical mixing model. In the case of CH4, we see that abundance differences up to one order of magnitude are found between the two limbs, either in the 1–0.1 bar pressure regime (if horizontal mixing dominates) or at every height above the 1 bar level (if vertical mixing dominates). NH3 and HCN show a similar behaviour, with very small abundance differences in the 1–0.1 bar pressure range, as predicted by the zonal wind model, and a difference of a factor of 2–3 above the 1 bar level, according to the vertical mixing model. Finally, in the case of CO2, it is predicted that a moderate abundance difference between the two limbs would be found if horizontal mixing dominates, while no difference would be observed if vertical mixing dominates. Methane thus seems to be the species that could show the most important abundance differences between the evening and morning limbs.
 |
Fig. 4 Vertical distributions of the abundances of CH4, NH3, CO2, and HCN at the evening (solid lines) and morning (dashed lines) limbs, as calculated by the zonal wind model (thick lines) and by the vertical mixing model (thin lines). Note that abundances above the 10-4–10-5 bar level may not be reliable due to the lack of photochemistry in our model and, in the case of the zonal wind model, to a likely change in the circulation pattern. |
The retrieval of atmospheric properties and composition from primary transits implies the comparison of the observed transmission spectrum with a synthetic one obtained with an atmosphere model. Ideally, this model would be a detailed three-dimensional model coupling dynamics, radiative transfer, and chemistry, so that the only parameters to be adjusted would be the elemental abundances. This is unfortunately not doable at this time and one-dimensional models are currently used for this purpose. Our study shows that the one-dimensional approach is acceptable because of the longitudinal homogenisation produced by zonal circulation. On the other hand, transmission spectra generally probe simultaneously both west and east limbs4, which have very different temperatures. Since transmission spectroscopy is very sensitive to the temperature via the scale height (Tinetti et al. 2007), retrieval should include the contribution of (at least) two different vertical temperature profiles. Transmission spectra also probe latitudes from the equator to the poles, and therefore latitudinal temperature variations are an additional complication.
Another important matter of debate is the lack of self-consistency between chemical and temperature vertical profiles used by one-dimensional retrieval models. It would be tempting to use one-dimensional profiles in which molecular abundances and temperature are computed consistently in order to limit the dimensions of the parameter space that has to be explored when the model is not self-consistent and any composition is allowed (e.g. Tinetti et al. 2007; Swain et al. 2008; Beaulieu et al. 2011). We have shown, however, that the temperature variations experienced by the gas in the zonal flow affect the composition so that abundances above the 1 bar layer are determined by a mixture of temperatures, which are close to those of the hottest regions encountered rather than to the local temperature. Because this effect competes with the chemical quenching produced by vertical mixing, a minimum self-consistent approach would imply calculation of the limb vertical structure and composition with a time dependent model that accounts for both the vertical mixing and the horizontal circulation (an additional complication would be to account for latitudinal chemical gradients). This will be the next upgrade of our model. To our knowledge, such a model has never been used to interpret spectra, although it may help to shed light on some unexplained observations and contradictory analyses.
4. Summary
In this study we have carried out an attempt to understand the impact of atmospheric circulation on the distribution of the atmospheric constituents of a tidally locked hot Jupiter, such as HD 209458b. The temperature structure and the distribution of the chemical composition as a function of longitude and height were computed in the limit of a solid-body rotating atmosphere, which mimics a uniform zonal wind. Adopting an equatorial wind speed of 1 km s-1, we find that chemical equilibrium is attained below the 0.1–10-4 bar pressure level, depending on the molecule. Above this transition layer, however, molecular abundances are quenched to chemical equilibrium values characteristic of the hottest dayside regions. Reasoning based on timescale arguments indicate that such horizontal quenching is likely to compete in HD 209458b’s atmosphere with the vertical quenching induced by eddy diffusion processes. This implies that in some atmospheric regions molecular abundances are quenched horizontally to dayside values, while in other regions abundances are quenched vertically to chemical equilibrium values characteristic of deep layers. Moderate abundance variations between the evening and morning limbs are found for some molecules, up to one order of magnitude in the case of CH4, assuming that dynamics is either restricted to a zonal wind or to vertical mixing. This may have consequences for the interpretation of transmission spectra obtained during primary transits.
Ideally, a realistic distribution of the molecular abundances throughout the whole planetary atmosphere could be obtained by coupling a three-dimensional circulation model to a robust chemical network. Such an approach is, however, a complicated task for numerical reasons. For the moment, insights into the influence of atmospheric dynamics on the chemistry must be addressed either by coupling a three-dimensional circulation model to a simple chemical kinetics scheme, as done by Cooper & Showman (2006), or by using a simplified dynamical model and a robust chemical network, as done in this work. In a future study we plan to overcome some of the limitations of our current modelling approach, which does not consider photochemistry or the coupling between horizontal and vertical mixing.
Acknowledgments
M.A., O.V., F.S., and E.H. acknowledge support from the European Research Council (ERC Grant 209622: E3ARTHs). Computer time for this study was provided by the computing facilities MCIA (Mésocentre de Calcul Intensif Aquitain) of the Université de Bordeaux and of the Université de Pau et des Pays de l’Adour. We thank the anonymous referee for a constructive report that helped to improve this manuscript.
References
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Batalha, N. M., Rowe, J. F., Bryson, S. T., et al. 2012, ApJS, submitted [arXiv:1202.5852] [Google Scholar]
- Beaulieu, J.-P., Tinetti, G., Kipping, D. M., et al. 2011, ApJ, 731, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Bounaceur, R., Herbinet, O., Fournet, R., et al. 2010, SAE Technical Paper 2010-01-0546 [Google Scholar]
- Charbonneau, D., Brown, T. M., Latham, D. W., & Mayor, M. 2000, ApJ, 529, L45 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Charbonneau, D., Brown, T. M., Noyes, R. W., & Gilliland, R. L. 2002, ApJ, 568, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Cho, J. Y.-K., Menou, K., Hansen, B. M. S., & Seager, S. 2003, ApJ, 587, 117 [Google Scholar]
- Cho, J. Y.-K., Menou, K., Hansen, B. M. S., & Seager, S. 2008, ApJ, 675, 817 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, C. S., & Showman, A. P. 2005, ApJ, 629, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, C. S., & Showman, A. P. 2006, ApJ, 649, 1048 [NASA ADS] [CrossRef] [Google Scholar]
- Coppens, F. H. V., De Ruyck, J., Konnov, A. A. 2007, Combustion and Flame, 149, 409 [CrossRef] [Google Scholar]
- Dobbs-Dixon, I., Agol, E., & Burrows, A. 2012, ApJ, 751, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Dobrijevic, M., Cavalié, T., Hébrard, E., et al. 2010, Planet. Space Sci., 58, 1555 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, S., & McBride, B. J. 1994, NASA Reference Publication, 1311, I [Google Scholar]
- Fournet, R., Baugé, J. C., & Battin-Leclerc, F. 1999, Int. J. Chem. Kinet., 31, 361 [CrossRef] [Google Scholar]
- Grillmair, C. J., Burrows, A., Charbonneau, D., et al. 2008, Nature, 456, 767 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Guillot, T., Burrows, A., Hubbard, W. B., et al. 1996, ApJ, 459, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T., & Showman, A. P. 2002, A&A, 385, 156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heng, K., Menou, K., & Phillips, P. J. 2011, MNRAS, 413, 2380 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, G. W., Marcy, G. W., Butler, R. P., & Vogt, S. S. 2000, ApJ, 529, L41 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Iro, N., Bézard, B., & Guillot, T. 2005, A&A, 436, 719 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knutson, H. A., Charbonneau, D., Allen, L. E., et al. 2007, Nature, 447, 183 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Konnov, A. A. 2009, Combustion and Flame, 156, 2093 [CrossRef] [Google Scholar]
- Kopparapu, R. K., Kasting, J. F., & Zahnle, K. J. 2012, ApJ, 745, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Line, M. R., Liang, M. C., & Yung, Y. L. 2010, ApJ, 717, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Madhusudhan, N., Harrington, J., Stevenson, K. B., et al. 2011, Nature, 469, 64 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Mazeh, T., Naef, D., Torres, G., et al. 2000, ApJ, 532, L55 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Menou, K., & Rascher, E. 2009, ApJ, 700, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Miller-Ricci Kempton, E., & Rauscher, E. 2012, ApJ, 751, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Moses, J. I., Visscher, C., Fortney, J. J., et al. 2011, ApJ, 737, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Rothman, L. S., Gordon, I. E., Barbe, A., et al. 2009, J. Quant. Spec. Radiat. Transf., 110, 533 [Google Scholar]
- Rothman, L. S., Gordon, I. E., Barber, R. J., et al. 2010, J. Quant. Spec. Radiat. Transf., 111, 2139 [Google Scholar]
- Showman, A. P., & Guillot, T. 2002, A&A, 385, 166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Showman, A. P., Cooper, C. S., Fortney, J. J., & Marley, M. S. 2008, ApJ, 682, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A. P., Fortney, J. J., Lian, Y., et al. 2009, ApJ, 699, 564 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A. P., Fortney, J. J., Lewis, N. K., & Shabram, M. 2012, ApJ, submitted [arXiv:1207.5639] [Google Scholar]
- Sing, D. K., Désert, J.-M., Lecavelier des Etangs, A., et al. 2009, A&A, 505, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, M. D. 1998, Icarus, 132, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Snellen, I. A. G., de Kok, R. J., de Mooij, E. J. W., & Albrecht, S. 2010, Nature, 465, 1049 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Southworth, J. 2010, MNRAS, 408, 1689 [NASA ADS] [CrossRef] [Google Scholar]
- Swain, M. R., Vasisht, G., Tinetti, G., et al. 2008, Nature, 452, 329 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Swain, M. R., Tinetti, G., Vasisht, G., et al. 2009, ApJ, 704, 1616 [NASA ADS] [CrossRef] [Google Scholar]
- Tinetti, G., Vidal-Madjar, A., Liang, M.-C., et al. 2007, Nature, 448, 169 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Venot, O., Hébrard, E., Agúndez, M., et al. 2012, A&A, 546, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., Herbst, E., Loison, J.-C., et al. 2012, ApJS, 199, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Zahnle, K., Marley, M. S., Freedman, R. S., et al. 2009, ApJ, 701, L20 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Thermal atmospheric structure of HD 209458b. The top panel shows the temperature distribution as a function of longitude and pressure, while the middle panel shows the temperature as a function of longitude at selected pressure levels. The bottom panel shows the vertical temperature profiles at the substellar and antistellar meridians and at the morning and evening limbs. |
| In the text | |
 |
Fig. 2 Longitudinal distributions of the mole fractions of CH4, CO, and CO2 for selected pressure levels, as calculated by the chemical kinetics model with a uniform zonal wind of 1 km s-1 (solid lines) and by chemical equilibrium adopting the longitudinal temperature profile of each pressure level (dotted lines). |
| In the text | |
 |
Fig. 3 Vertical distributions of the major species, after H2 and He, at four longitudes: substellar meridian, evening limb, antistellar meridian, and morning limb. We show the mole fractions given by the zonal wind thermochemical kinetics model (solid lines), by a one-dimensional model in the vertical direction including thermochemical kinetics and vertical eddy diffusion (dashed lines), and by chemical equilibrium adopting the (p,T) vertical profile at each longitude (dotted lines). Note that abundances above the 10-4–10-5 bar level may not be reliable due to the lack of photochemistry in our model and, in the case of the zonal wind model, to a likely change in the circulation pattern. |
| In the text | |
 |
Fig. 4 Vertical distributions of the abundances of CH4, NH3, CO2, and HCN at the evening (solid lines) and morning (dashed lines) limbs, as calculated by the zonal wind model (thick lines) and by the vertical mixing model (thin lines). Note that abundances above the 10-4–10-5 bar level may not be reliable due to the lack of photochemistry in our model and, in the case of the zonal wind model, to a likely change in the circulation pattern. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


