| Issue |
A&A
Volume 548, December 2012
|
|
|---|---|---|
| Article Number | A68 | |
| Number of page(s) | 8 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201220062 | |
| Published online | 23 November 2012 | |
The IRAM-30 m line survey of the Horsehead PDR
II. First detection of the l-C3H+ hydrocarbon cation⋆
1 IRAM, 300 rue de la Piscine, 38406 Saint Martin d’Hères France
e-mail: pety@iram.fr; gratier@iram.fr; guzman@iram.fr; bardeau@iram.fr
2 LERMA, UMR 8112, CNRS and Observatoire de Paris, 61 avenue de l’Observatoire, 75014 Paris, France
e-mail: maryvonne.gerin@lra.ens.fr
3 LUTH, UMR 8102, CNRS and Observatoire de Paris, Place J. Janssen, 92195 Meudon Cedex, France
e-mail: evelyne.roueff@obspm.fr
4 Centro de Astrobiología. CSIC-INTA. Carretera de Ajalvir, Km 4. Torrejón de Ardoz, 28850 Madrid, Spain
e-mail: jr.goicoechea@cab.inta-csic.es
5 IRAM, 7 Avenida Pastora, Granada Spain
e-mail: sievers@iram.es
6 Max-Planck Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: belloche@mpifr-bonn.mpg.de
7 LUPM, UMR 5299, Université Montpellier 2, Place Eugène Bataillon, 34095 Montpellier Cedex 05, France
e-mail: dahbia.talbi@univ-montp2.fr
Received: 19 July 2012
Accepted: 11 October 2012
Context. Pure gas-phase chemistry models do not succeed in reproducing the measured abundances of small hydrocarbons in the interstellar medium. Information on key gas-phase progenitors of these molecules sheds light on this problem.
Aims. We aim to constrain the chemical content of the Horsehead mane with a millimeter unbiased line survey at two positions, namely the photo-dissociation region (PDR) and the nearby shielded core. This project revealed a consistent set of eight unidentified lines toward the PDR position. We associate them to the l-C3H+ hydrocarbon cation, which enables us to constrain the chemistry of small hydrocarbons. We observed the lowest detectable J line in the millimeter domain along a cut toward the illuminating direction to constrain the spatial distribution of the l-C3H+ emission perpendicular to the photo-dissociation front.
Methods. We simultaneously fit 1) the rotational and centrifugal distortion constants of a linear rotor; and 2) the Gaussian line shapes located at the eight predicted frequencies. A rotational diagram is then used to infer the excitation temperature and the column density. We finally compare the abundance to the results of the Meudon PDR photochemical model.
Results. Six out of the eight unidentified lines observable in the millimeter bands are detected with a signal-to-noise ratio from 6 to 19 toward the Horsehead PDR, while the two last ones are tentatively detected. Mostly noise appears at the same frequency toward the dense core, located less than 40′′ away. Moreover, the spatial distribution of the species integrated emission has a shape similar to radical species such as HCO, and small hydrocarbons such as C2H, which show enhanced abundances toward the PDR. The observed lines can be accurately fitted with a linear rotor model, implying a 1Σ ground electronic state. The deduced rotational constant value is B = 11 244.9512 ± 0.0015 MHz, close to that of l-C3H.
Conclusions. This is the first detection of the l-C3H+ hydrocarbon in the interstellar medium. Laboratory spectroscopy is underway to confirm these results. Interferometric imaging is needed to firmly constrain the small hydrocarbon chemistry in the Horsehead.
Key words: surveys / photon-dominated region (PDR) / ISM: lines and bands / ISM: individual objects: Horsehead nebula / line: identification
© ESO, 2012
1. Introduction
Molecular ions play an important role in the physics and chemistry of the insterstellar medium. They trace the gas physical conditions, e.g., its ionization rate and its ionization fraction (see for example Goicoechea et al. 2009), and they participate in the coupling of the gas with the magnetic field. Moreover, molecular ions are key species in the gas phase synthesis of molecules because ion-molecule reactions most often have no activation barrier.
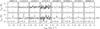 |
Fig. 1 Millimeter lines attributed to the l-C3H+ cation in the PDR (lower panels) and the dense core (upper panels) positions. The numbers above each panel are the line rest frequencies in MHz. The spectra and the Gaussian fits are shown as black histograms and green curves, respectively. The inferred rest frequencies are displayed as vertical dotted black lines for vlsr = 10.7 km s-1 and ± 3σ noise levels as horizontal dotted red lines. |
Simple hydrocarbon molecules, such as C2H, C3H, and C3H2 have been detected in a wide variety of sources from diffuse (e.g. Lucas & Liszt 2000) to dark clouds (e.g. Wootten et al. 1980; Mangum & Wootten 1990). The high abundances found at the UV-illuminated edges of molecular clouds or photo-dissociation regions (PDRs) cannot be reproduced by current pure gas-phase models (Fuente et al. 2003; Teyssier et al. 2004). Pety et al. (2005) proposed another chemical route, namely the photo-erosion of Polycyclic Aromatic Hydrocarbons (PAHs) and small carbon grains to produce these hydrocarbons. Rimmer et al. (2012) showed that using a column-dependent cosmic ray ionization rate slightly improves the agreement between models and observations in the Horsehead PDR. Ion-molecule reactions with the C2H+ and C3H+ cations are thought to be the most important gas-phase channels to form small hydrocarbons (Turner et al. 2000; Wakelam et al. 2010), but they have not yet been observed in the interstellar medium. Constraining the abundances of these intermediate hydrocarbon cations will shed light on the formation routes of hydrocarbons.
In this paper, we report the first detection in the interstellar medium of the l-C3H+ hydrocarbon cation toward the Horsehead PDR (more precisely, at the peak of the HCO emission, Gerin et al. 2009). Section 2 describes the observations. Sections 3 and 4 explain how we inferred the spectroscopic parameters associated with the set of unidentified lines, and why we attribute these to l-C3H+. Section 5 discusses the determination of the l-C3H+ abundance and its chemistry.
2. Observations
The Horsehead WHISPER project (Wideband High-resolution Iram-30 m Surveys at two Positions with Emir Receivers, PI: J. Pety) is a complete unbiased line survey of the 3, 2, and 1 mm bands that is being completed at the IRAM-30 m telescope. Two positions are observed: 1) the “HCO peak” (RA = 5h40m53.936s, Dec = −2°28′00′′, J2000), which is characteristic of the photo-dissociation region at the surface of the Horsehead nebula (Gerin et al. 2009); and 2) the “DCO+ peak” (RA = 5h40m55.61s, Dec = −2°27′38′′, J2000), which belongs to a cold and shielded condensation located less than 40′′ away from the PDR edge, where HCO+ is highly deuterated (Pety et al. 2007). The combination of the new EMIR receivers and Fourier transform spectrometers at the IRAM-30 m telescope yields a spectral survey with unprecedented combination of bandwidth (36 GHz at 3 mm, 19 GHz at 2 mm, and 76 GHz at 1 mm), spectral resolution (49 kHz at 3 and 2 mm; and 195 kHz at 1 mm), and sensitivity (median noise 8.1 mK, 18.5 mK, and 8.3 mK, respectively). A detailed presentation of the observing strategy and data reduction process will be given in another paper. In short, any frequency was observed with two different frequency tunings and the Horsehead PDR and dense core positions were alternatively observed every 15 min. The total observing time amounted to one hour per frequency setup and position.
Results for the simultaneous fit of the l-C3H+ line parameters (bottom) and the associated spectroscopic modeling (top).
In the analysis of the survey, we found an 89 mK line peak around 89.957 GHz, that could not be associated to any transition listed in the common public catalogs: CDMS1 (Müller et al. 2001), JPL2 (Pickett et al. 1998), and splatalogue3. The observing strategy allowed us to rule out that the detected line is a ghost line incompletely rejected from a strong line in the image side band (the typical rejection of the EMIR sideband separating mixers is 13 dB). Our search for an identification started with the simplest assumption, i.e., the associated species is a linear rigid rotor. The frequency of the transition (J + 1 → J) is then given by 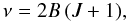 (1)where B is the rotational constant. In this simple model, the ratio of line frequencies depends only on the ratio of J + 1 values. We thus could predict different sets of frequencies to search for companion lines associated to the same species, each set associating a given J + 1 → J transition to the frequency of the detected unidentified line, i.e., ~89.957 GHz. The only set of frequencies that consistently brings five other detected lines and two more tentative detections less than 1 MHz from the frequency predictions was the one which associates the 89.957 GHz unidentified line to the J = 4 → 3 transition of a linear rigid rotor. Using the WEEDS extension (Maret et al. 2011) of the GILDAS/CLASS software4 (Pety 2005), we quickly ruled out the assignment of any of the detected unidentified lines to other possible species because the potential candidate species were complex molecules for which many other expected transitions were not detected in the survey.
(1)where B is the rotational constant. In this simple model, the ratio of line frequencies depends only on the ratio of J + 1 values. We thus could predict different sets of frequencies to search for companion lines associated to the same species, each set associating a given J + 1 → J transition to the frequency of the detected unidentified line, i.e., ~89.957 GHz. The only set of frequencies that consistently brings five other detected lines and two more tentative detections less than 1 MHz from the frequency predictions was the one which associates the 89.957 GHz unidentified line to the J = 4 → 3 transition of a linear rigid rotor. Using the WEEDS extension (Maret et al. 2011) of the GILDAS/CLASS software4 (Pety 2005), we quickly ruled out the assignment of any of the detected unidentified lines to other possible species because the potential candidate species were complex molecules for which many other expected transitions were not detected in the survey.
Figure 1 displays the spectra at the Horsehead PDR and dense core positions of the consistent set of eight unidentified lines, which lie in the millimeter frequency bands. Even though the weather conditions, the pointing and focus corrections, and the tuning setups were shared for the two observed positions, the unidentified lines were detected with a profile, integrated signal-to-noise ratio between 3 and 19 at the PDR position, while only two-sigma upper limits of typically 25 mK km s-1 for a 0.8 km s-1 linewidth could be derived at the dense core position. The only exception is the J = 4−3 line, which is tentatively detected toward the dense core. Assuming that the emission arises from a Gaussian filament of 12′′ full width at half maximum centered on the PDR (see Gerin et al. 2009), 27% of the emission detected at the core position is explained by beam pickup from the PDR. The remaining emission could arise in the lower density skin of the dense core, already detected in HCO (Gerin et al. 2009) and CF+ (Guzmán et al. 2012a,b). In summary, the eight (tentatively) detected lines in the PDR are unlikely to be observing artifacts.
3. Associated spectroscopic constants
To compute the spectroscopic parameters associated with the set of unidentified lines, we used higher order improvements to the simple model of a linear rotor. The second and third order corrections, which include the effect of the centrifugal distortion, predict that the frequency of the J + 1 → J transition is ![\begin{eqnarray} \nu &=& 2 \Be (\J+1) - 4 \De (\J+1)^3, \quad \mbox{and} \\[3mm] \nu &=& 2 \Be (\J+1) - 4 \De (\J+1)^3 + \He (\J+1)^3 [(\J+2)^3 - \J^3], \end{eqnarray}](/articles/aa/full_html/2012/12/aa20062-12/aa20062-12-eq92.png) where D and H are the centrifugal distortion constants to the second and third order, respectively.
where D and H are the centrifugal distortion constants to the second and third order, respectively.
Using these expressions, it is possible to generate the sum of 1) Gaussian white noise; 2) a baseline offset; and 3) Gaussian line profiles at the eight predicted frequencies of arbitrary areas and line widths. This allows us to simultaneously fit the noise level, a residual baseline offset, and the Gaussian parameters (areas and line widths) as well as the rotational and centrifugal distortion constants associated with these models. In practice, it is very difficult to make the fit converge with the eight lines because of the limited signal-to-noise ratio of some of them. We therefore assume that the eight lines have the same line width. This is likely for two reasons. First, the line width is dominated by the turbulent velocity field and the lines are probably emitted from the same gas cells because the range of energy probed by the eight transitions is relatively narrow (from 10 to 80 K). Second, the velocity gradient in the plane of the sky is shallow, ensuring that the line width does not evolve significantly when the beam size changes with frequency. This assumption enables a quick fit convergence when we start the fit with the following initial values: B = 11.2 GHz, D = 5 kHz, H = 1 Hz, zero offsets, 10 mK noise levels, and 1 km s-1 common linewidth. Appendix A discusses why the third order model gives the best fit to the data and Table 1 gives the results of the fits (both the Gaussian line parameters and the spectroscopic constants).
Because laboratory measurements are not available, the only unambiguous frequency available is the one measured in the local standard of rest (LSR) frame, νlsr. The frequency given in the source frame, νsou, assumes an LSR systemic velocity of the source, vlsr. These frequencies are linked through νsou = νlsr [1 − (vlsr/c)], where c is the speed of light. The systemic velocity may vary from species to species because of different coupling between the gas kinematics and its chemistry and/or line-shape variations due to optical-depth effects. The analysis of the unambiguously attributed detected lines in the survey shows that the possible range of LSR systemic velocities in the Horsehead PDR is quite narrow, ~0.2 km s-1 around 10.7 km s-1 (see Fig. A.1 which displays different lines of several hydrocarbons). All frequencies quoted here accordingly assume an LSR velocity of 10.7 km s-1. The derived spectroscopic parameters may therefore need to be slightly linearly scaled.
 |
Fig. 2 High angular resolution maps of the integrated intensity of H13CO+, HCO, C2H, and c-C3H2, and the 7.7 μm PAH emission. Maps are rotated by 14° counter-clockwise around the projection center, located at (δx,δy) = (20′′,0′′), to bring the illuminated star direction in the horizontal direction. The horizontal zero is set at the PDR edge. The emission of all lines is integrated between 10.1 and 11.1 km s-1. Displayed integrated intensities are expressed in the main beam temperature scale. Contour levels are shown in the grey-scale lookup tables. The red vertical line shows the PDR edge and the blue and green crosses show the dense core and PDR positions, respectively. |
4. Attribution of the lines to the l-C3H+ cation
 |
Fig. 3 Integrated intensity profiles across the PDR photo-dissociation front of the l-C3H+, HCO, H13CO+, and C2H species (IRAM-30 m). The cut would appear horizontal at δy = 0′′ in Fig. 2. The observed lines are summarized in Table 2. |
The unidentified lines were all detected at the PDR position, but not at the dense core position. We thus complemented these data with a cut from the Hii region into the molecular cloud along the direction of the exciting star, σ Ori, i.e., perpendicular to the photo-dissociation front. Figure 3 displays the integrated intensity emission of the J = 4−3 unidentified line as a function of the angular distance from the photo-dissociation front, along with the emission of HCO, H13CO+, and C2H species (Table 2 defines the observed lines). All these lines were observed simultaneously with the IRAM-30 m telescope during 4 h of mild summer weather (typically 11 mm of precipitable water vapor), but they all were well-detected nevertheless. At 29′′ resolution, it is clear that the unidentified species cut peaks in the UV-illuminated part of the Horsehead mane in the same way as HCO and C2H, while H13CO+ peaks in the dense core, shielded from the UV field. This led us to conclude that the species is a reactive molecule with a spatial distribution similar to small hydrocarbon chains. For reference, Fig. 2 displays the integrated intensity emission of the same lines, imaged at ~6′′ with the Plateau de Bure Interferometer (Pety et al. 2007; Gerin et al. 2009; Pety et al. 2005), plus the 7.7 μm PAH emission imaged at ~6′′ with ISO (Abergel et al. 2003).
The quality of the spectroscopic fit suggests that the molecule is a linear rotor with a 1Σ electronic ground state, i.e., with a closed electronic shell. The rotational constant is B ~ 11.24 GHz, which implies the presence of several heavy atoms in the species. According to the literature, the most probable canditate is the l-C3H+ cation. Indeed, ab initio calculation implies that 1) the linear structure is the most stable; 2) it has the right electronic state; and 3) the computed rotational constant value is about 11.1 GHz (Radom et al. 1976; Wilson & Green 1980, 1982; Cooper & Murphy 1988; Ikuta 1997). Experimental spectroscopic confirmation for this cation is being performed at the PhLAM laboratory in Lille (Bailleux & Margules, priv. comm.).
Wilson & Green (1980) estimated the dipole moment of this cation to be 2.6 Debye, but this is a rather old value. We therefore computed it again with more sophisticated ab initio techniques of quantum chemistry, as implemented in the MOLPRO suite of programs5. We used the CASSCF-MRCI level of theory with the correlation-consistent aug-cc-pVQZ basis sets of Woon & Dunning (1993) for all atoms. The active space of the CASSCF included the n = 2 orbitals of carbon and the 1S orbital of H. The geometry was first optimized at the CASSCF level, leading to bond distances for l-C3H+ (1.090 Å, 1.246 Å, 1.355 Å) that perfectly match the results obtained in Ikuta (1997). The dipole moment was then computed at the center of mass of the molecule for the CASSCF optimized geometry. The resulting dipole moment of l-C3H+ is 3 Debye at the CASSCF-MRCI level of theory, i.e., close to the initial value of Wilson & Green (1980). We used the new value to compute the column density of l-C3H+.
Comparison of the measured and modeled abundances with respect to the number of protons at three different positions across the PDR front.
5. l-C3H+ abundance and chemistry
We used the formalism of the rotational diagram to estimate the column density of l-C3H+. Goldsmith & Langer (1999) give the expressions for the level energies, the quantum level degeneracies, the Einstein coefficients, and the partition function Z(T) for a rigid rotor of dipole moment, μ. For instance, the Einstein coefficients are given by 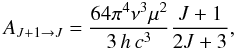 (4)where h and c are the Planck constant and the light speed, respectively. Using these formula, we are able to compute the rotational diagram, assuming 1) that the lines are optically thin (τ < 1); and 2) that the l-C3H+ emission is co-spatial with the illuminated filament of the C2H emission, i.e., it approximately fills as a Gaussian filament of ~12′′ width in the δx direction, infinite size in the δy direction, and centered at the HCO peak (see Fig. 2). The filling factors are 0.4, 0.6, and 0.8 at 90, 157, and 270 GHz, respectively. Figure 4 displays the diagram for μ0 = 3 Debye (this work). The rotational temperature inferred from the observations is independent of the dipole moment because it scales with the slope of the rotational diagram, while the column density scales as μ-2. The typical rotational temperature and column density thus are 14 ± 2 K and (μ0/μ)2 (4.8 ± 0.9) × 1011 cm-2, respectively.
(4)where h and c are the Planck constant and the light speed, respectively. Using these formula, we are able to compute the rotational diagram, assuming 1) that the lines are optically thin (τ < 1); and 2) that the l-C3H+ emission is co-spatial with the illuminated filament of the C2H emission, i.e., it approximately fills as a Gaussian filament of ~12′′ width in the δx direction, infinite size in the δy direction, and centered at the HCO peak (see Fig. 2). The filling factors are 0.4, 0.6, and 0.8 at 90, 157, and 270 GHz, respectively. Figure 4 displays the diagram for μ0 = 3 Debye (this work). The rotational temperature inferred from the observations is independent of the dipole moment because it scales with the slope of the rotational diagram, while the column density scales as μ-2. The typical rotational temperature and column density thus are 14 ± 2 K and (μ0/μ)2 (4.8 ± 0.9) × 1011 cm-2, respectively.
 |
Fig. 4 Rotational diagram of l-C3H+ at the PDR position. |
We took advantage of the Horsehead WHISPER survey to make a consistent summary of the small hydrocarbon detections in the Horsehead PDR. The spectra of the detected lines in the 3 mm band of C2H, c-C3H, l-C3H, c-C3H2, l-C3H2, and C4H are displayed in Fig. A.1 and their Gaussian fit results are summarized in Table A.1. The integrated intensities of the lines are consistent with the results published by Teyssier et al. (2004, 2005). We accordingly just summarized their column densities and abundances in Table 4. Pety et al. (2005) presented higher angular (typically 6′′) observations of C2H and c-C3H2 obtained with the Plateau de Bure Interferometer. The associated abundances at three different positions (the “IR peak” close to the usual “HCO peak”, one position named “cloud” representative of the UV-shielded material, and one position named “IR edge” closer to the Hii region) are summarized in Table 3. The comparison of Tables 3 and 4 indicates that the C2H and c-C3H2 abundances measured at a typical resolution of 25−28′′ falls in the uncertainty range of abundances measured at a four times better resolution with PdBI. This means that their emission more or less fills the 25−28′′ beam, even though it is substructured into filaments (see Fig. 2). Indeed, if we had assumed that the l-C3H+ emission fills the beam at every measured frequency, the inferred l-C3H+ abundance would have only be reduced by a factor 2.
Column densities and abundances with respect to the number of protons, i.e., [X] = 0.5 N(X)/N(H2), toward the PDR position, from single-dish observations at resolutions between 25 and 28′′.
 |
Fig. 5 Photochemical model of the Horsehead PDR displayed at the full resolution of the model (left column) and convolved with a Gaussian of 6′′-FWHM (right column). Top: Horsehead density profile nH = n(H) + 2n(H2). Middle: predicted abundance of selected small hydrocarbons molecules and cations. Bottom: abundances of the same hydrocarbons relative to the abundance of C3H+. The illuminating star is positioned at the right of the plots. The symbols present the measured range of possible abundances for C2H (blue vertical segment), C3H2 (green vertical segment), and C3H+ (red filled rectangle), inferred at a typical resolution of 6′′. The legend at the bottom of the figure presents the line coding for the curves: C2H in plain blue, C2H+ in dashed blue, C3H in plain red, C3H+ in dashed red, and C3H2 in green. |
We finally compared the derived abundances with a one-dimensional, steady-state photochemical model (Meudon PDR model, Le Bourlot et al. 2012; Le Petit et al. 2006). The used version of the Meudon PDR code includes the Langmuir-Hinshelwood and Eley-Rideal mechanisms to describe the formation of H2 on grains (Le Bourlot et al. 2012), and surface reactions for other species (Le Bourlot et al., in prep.). The physical conditions in the Horsehead have already been constrained by our previous observational studies and we kept the same assumptions for the steep density gradient, radiation field (χ = 60 in Draine units, see Abergel et al. 2003), elemental gas-phase abundances (see Table 6 in Goicoechea et al. 2006) and cosmic ray primary ionization rate (ζ = 5 × 10-17 s-1 per H2 molecule, Goicoechea et al. 2009).
We used the Ohio State University (osu) pure gas-phase chemical network upgraded for photochemical studies. C3H+ is produced by reactions between C2H2 and C+. Then, C3H+ is thought to produce C3H2+, and C3H3+ through reactions with H2, which later recombines with electrons to form C3H and C3H2![\begin{equation*} \xymatrixrowsep{-0.1cm} \xymatrixcolsep{0.6cm} \hskip-9mm\xymatrix{ & & & \chem{C_3H^+_2} \ar[r]^{\tiny \chem{e^{-}}} & \CCCH\\ & \CCHH \ar[r]^{\tiny \Cp} & \CCCHp \ar[ru]^{\tiny \HH} \ar[rd]_{\tiny \HH} & & \\ & & & \CCCHHHp \ar[r]^{\tiny \chem{e^{-}}} & \CCCHH.} \end{equation*}](/articles/aa/full_html/2012/12/aa20062-12/aa20062-12-eq163.png) Hence these species are usually included in gas-phase chemical networks with reaction rate accuracies of a factor 2 or better. We can thus use them to compare models with observations.
Hence these species are usually included in gas-phase chemical networks with reaction rate accuracies of a factor 2 or better. We can thus use them to compare models with observations.
Figure 5 presents the results of the photochemical model for a few small hydrocarbon molecules and cations, namely C2H, C3H, C3H2, C2H+, and C3H+. From top to bottom, the figure shows the spatial profiles of the density, abundances relative to the number of hydrogen atoms, and the abundances relative to C3H+. The left column presents the profiles computed by the code, which samples the UV-illuminated gas on a finer spatial grid than the UV-shielded gas to correctly represent the steep physical and chemical gradients. The right column presents the profiles convolved with a Gaussian of 6′′ full width at half maximum to facilitate the comparison with the abundances inferred from PdBI observations at 6′′ angular resolution. The measured abundances are displayed with vertical segments for C2H, and c-C3H2, and with a filled rectangle for C3H+. Although the l-C3H+ abundance is only inferred from the IRAM-30 m single-dish telescope, we also show it here because we used a simple model of its emission based on the PdBI hydrocarbon data to correct for the beam dilution. Table 3 quantitatively compares the measured and modeled abundances at the PDR position (“IR peak” at Av ~ 1 mag), inside the molecular cloud at a position representative of the UV-shielded material “cloud” (Av ~ 8 mag), and closer to the Hii region (i.e., “IR edge” at Av ~ 0.01 mag).
We only consider the most stable isomers to compare the measured and modeled abundances. Table 4 indicates that the amount of C3H2 locked in the linear species is negligible, and that twice as much C3H is locked in the cyclic species compared to the linear species. Moreover, Table 1 of Mebel et al. (2007) indicates that the cyclic form of C3H2 and C3H are more stable than their linear form by 59.3 kJ mol-1 (or 0.61 eV), and 11 kJ mol-1 (or 0.11 eV), respectively. Finally, Savić et al. (2005) indicated that the cyclic form of C3H+ is less stable than the linear one by 220 kJ mol-1, or 2.28 eV. Given the large difference in energies, we here assume that the linear form is the main product in the gas phase.
While C2H has much brighter lines and a column density higher by two orders of magnitude compared to linear and cyclic C3H, we have no hint of a detection of bright lines associated to C2H+. This is due to a combination of two effects. First, the spectroscopic structure of C2H+ (which has a 3Π ground electronic state) is more complex than that of C3H+, implying that the emission is spread over more lines. The knowledge of the rotational spectrum of C2H+ would enable a deep search of this reactive molecular ion to check whether C2H+ is also present in the Horsehead PDR. Second, C2H+ is predicted to be less abundant than C3H+ (except when Av ≤ 0.1 mag), because it is efficiently destroyed by H2, independently of the temperature. In contrast, the detection of C3H+ at the warm PDR position corroborates that the destruction of C3H+ by H2 is much less efficient there than in the cold-core region, i.e., the C3H+ + H2 reaction is strongly dependent on the gas temperature (Savić & Gerlich 2005).
On one hand, the agreement between the interferometric abundances of C2H and C3H2 and the modeled curves improved at the “cloud” position by up to four orders of magnitude compared to the models of Pety et al. (2005, see their Fig. 10). This is the result of the recent addition of the chemistry on the grain surface to the Meudon PDR code. Indeed, the modeled and predicted abundances of c-C3H2 are consistent, while the modeled abundance of C2H is still one order of magnitude lower than the measured abundance (cf. Table 3). However, it is worth noting that the “cloud” position (δx = 24.9′′,δy = −5.3′′) does not fall, for historical reasons, on the dense core. Indeed, the C2H emission presents a dip at the DCO+ peak (δx = 44.7′′,δy = 16.5′′, blue cross in Fig. 2), while the c-C3H2 emission shows a bright filament there. These observational facts indicate that C2H probably depletes at a higher rate onto grains than C3H2.
On the other hand, the model results did not change significantly in the UV-illuminated part (IR peak and IR edge). The measured abundances are typically one and two orders of magnitude higher than the modeled abundances for C2H and C3H2. In contrast, the measured abundance of C3H+ is only about a factor 2 higher than the modeled abundance (cf. Table 3). If the assumptions used here are correct (the geometry of the l-C3H+ emission, and neglecting the amount of c-C3H+), this difference between the small hydrocarbon molecules and l-C3H+ would confirm that there is a non gas-phase chemical way in which small hydrocarbons are formed in UV-illuminated regions, e.g., the photo-erosion of PAHs (Pety et al. 2005). Interferometric observations of C3H and C3H+ are needed to confirm this result. Indeed, Fig. 6 shows the spatial profile of the modeled C3H+ abundance convolved by convolution at 6′′ and 27′′. Clearly, only interferometric observations can provide the high angular resolution needed to resolve the actual structure of the C3H+ emission, and potentially detect a spatial shift with respect to the millimeter wave emission of other small hydrocarbons and to the infrared imaging of PAHs and dust grains.
 |
Fig. 6 Spatial profiles of the predicted abundance of C3H+ cation. The modeled abundance profile was convolved along the x-axis with a Gaussian of 6′′-FWHM (red line), and 27′′-FWHM (blue line). |
6. Summary
We reported the first detection of l-C3H+ in the interstellar medium. Laboratory measurements of the l-C3H+ spectroscopy are needed to improve the spectroscopic characterization of this molecular ion. Interferometric imaging with either PdBI or ALMA is required to better constrain the small hydrocarbon chemistry.
See http://www.iram.fr/IRAMFR/GILDAS for more information about the GILDAS softwares.
Acknowledgments
This work was funded by grant ANR-09-BLAN-0231-01 from the French Agence Nationale de la Recherche as part of the SCHISM project. V.G. thanks the Chilean Government for support through the Becas Chile scholarship program. J.R.G. thanks the Spanish MICINN for his support through a Ramón y Cajal research contract and additional funding through grants AYA2009-07304 and CSD2009-00038. We thank H. S. Liszt for finding the neat acronym of this project, “Horsehead WHISPER”.
References
- Abergel, A., Teyssier, D., Bernard, J. P., et al. 2003, A&A, 410, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cooper, D. L., & Murphy, S. C. 1988, ApJ, 333, 482 [Google Scholar]
- Fuente, A., Rodríguez-Franco, A., García-Burillo, S., Martín-Pintado, J., & Black, J. H. 2003, A&A, 406, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerin, M., Goicoechea, J. R., Pety, J., & Hily-Blant, P. 2009, A&A, 494, 977 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goicoechea, J. R., Pety, J., Gerin, M., et al. 2006, A&A, 456, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goicoechea, J. R., Pety, J., Gerin, M., Hily-Blant, P., & Le Bourlot, J. 2009, A&A, 498, 771 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldsmith, P. F., & Langer, W. D. 1999, ApJ, 517, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Guzmán, V., Pety, J., Gratier, P., et al. 2012a, A&A, 543, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guzmán, V., Roueff, E., Gauss, J., et al. 2012b, A&A, in press, DOI: 10.1051/0004-6361/201220174 [Google Scholar]
- Ikuta, S. 1997, J. Chem. Phys., 106, 4536 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bourlot, J., Le Petit, F., Pinto, C., Roueff, E., & Roy, F. 2012, A&A, 541, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Petit, F., Nehmé, C., Le Bourlot, J., & Roueff, E. 2006, ApJS, 164, 506 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucas, R., & Liszt, H. S. 2000, A&A, 358, 1069 [NASA ADS] [Google Scholar]
- Mangum, J. G., & Wootten, A. 1990, A&A, 239, 319 [NASA ADS] [Google Scholar]
- Maret, S., Hily-Blant, P., Pety, J., Bardeau, S., & Reynier, E. 2011, A&A, 526, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mebel, A. M., Kislov, V. V., & Hayashi, M. 2007, J. Chem. Phys., 126, 204310 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pety, J. 2005, in SF2A-2005: Semaine de l’Astrophysique Française, eds. F. Casoli, T. Contini, J. M. Hameury, & L. Pagani, 721 [Google Scholar]
- Pety, J., Teyssier, D., Fossé, D., et al. 2005, A&A, 435, 885 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pety, J., Goicoechea, J. R., Hily-Blant, P., Gerin, M., & Teyssier, D. 2007, A&A, 464, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spec. Radiat. Transf., 60, 883 [Google Scholar]
- Radom, L., Hariharan, P. C., Pople, J. A., & Schleyer, P. R. 1976, J. Am. Chem. Soc., 98, 3436 [CrossRef] [Google Scholar]
- Rimmer, P. B., Herbst, E., Morata, O., & Roueff, E. 2012, A&A, 537, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savić, I., & Gerlich, D. 2005, Phys. Chemist. Chem. Phys. (Incorporating Faraday Transactions), 7, 1026 [Google Scholar]
- Savić, I., Schlemmer, S., & Gerlich, D. 2005, ApJ, 621, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, D., Fossé, D., Gerin, M., et al. 2004, A&A, 417, 135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teyssier, D., Hily-Blant, P., Gerin, M., et al. 2005, in ESA SP 577, ed. A. Wilson, 423 [Google Scholar]
- Turner, B. E., Herbst, E., & Terzieva, R. 2000, ApJS, 126, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Smith, I. W. M., Herbst, E., et al. 2010, Space Sci. Rev., 156, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, S., & Green, S. 1980, ApJ, 240, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, S., & Green, S. 1982, ApJ, 253, 989 [NASA ADS] [CrossRef] [Google Scholar]
- Woon, D. E., & Dunning, Jr., T. H. 1993, J. Chem. Phys., 98, 1358 [CrossRef] [Google Scholar]
- Wootten, A., Bozyan, E. P., Garrett, D. B., Loren, R. B., & Snell, R. L. 1980, ApJ, 239, 844 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Fit likelihood
 |
Fig. A.1 Hydrocarbon lines detected toward the Horsehead PDR at RA = 5h40m53.936s, Dec = −2°28′00′′ (J2000). Only lines in the 3 mm band, whose energy of the upper level is lower than 100 K and which have a higher signal-to-noise ratio than 8, are shown. The green lines are Gaussian fits. The vertical dashed lines mark 10.7 km s-1. |
Gaussian fit results for the lines of small hydrocarbons detected toward the Horsehead PDR at RA = 5h40m53.936s, Dec = −2°28′00′′ (J2000).
We wish to know to which development order we can significantly fit the frequency model to the observed data. Assuming that all intensity channels are independent measures with Gaussian noise, the likelihood, ℒ, of the fit of the model to the data is given by ![\appendix \setcounter{section}{1} \begin{equation} \likelihood = \prod_{i=1}^{N} \bracket{\frac{1}{\sqrt{2\pi\sigma_i}} \exp\paren{-\frac{[I^\emr{obs}_i-I^\emr{mod}_i(\theta)]^2}{2\sigma_i^2}}}, \end{equation}](/articles/aa/full_html/2012/12/aa20062-12/aa20062-12-eq209.png) (A.1)where i is the index over the N measured channel intensities, σi the noise of channel i, Iobs and Imod the observed and modeled intensities, and θ the set of model parameters. Taking the logarithm yields ln(ℒ) = K − 0.5χ2, where
(A.1)where i is the index over the N measured channel intensities, σi the noise of channel i, Iobs and Imod the observed and modeled intensities, and θ the set of model parameters. Taking the logarithm yields ln(ℒ) = K − 0.5χ2, where ![\begin{equation*} K = -\frac{1}{2}N\ln(2 \pi\sigma_{i}) \quad \mbox{and} \quad \chi^{2} = \sum_{i=1}^{N}\frac{[I^\emr{obs}_{i}-I^\emr{mod}_{i}(\theta)]^2}{\sigma_{i}^2}\cdot \end{equation*}](/articles/aa/full_html/2012/12/aa20062-12/aa20062-12-eq216.png) K is a constant and χ2 is the usual chi square measure of the fit quality. If we try to fit two models M1 and M2, which differs only by one parameter, to the same data, the comparison of the fits is said to have only one degree of freedom. The difference
K is a constant and χ2 is the usual chi square measure of the fit quality. If we try to fit two models M1 and M2, which differs only by one parameter, to the same data, the comparison of the fits is said to have only one degree of freedom. The difference  then follows the well known χ2 distribution with one degree of freedom. In our case, the difference of χ2 between the second and third order models is 9.2, which implies that the third-order model better reproduces the data than the second-order model with a probability ≥ 99.75%. In contrast, developing the centrifugal effect to the fourth order does not bring a significant improvement over the third order development. We therefore stopped the determination of the spectroscopic constants to the third order model.
then follows the well known χ2 distribution with one degree of freedom. In our case, the difference of χ2 between the second and third order models is 9.2, which implies that the third-order model better reproduces the data than the second-order model with a probability ≥ 99.75%. In contrast, developing the centrifugal effect to the fourth order does not bring a significant improvement over the third order development. We therefore stopped the determination of the spectroscopic constants to the third order model.
All Tables
Results for the simultaneous fit of the l-C3H+ line parameters (bottom) and the associated spectroscopic modeling (top).
Comparison of the measured and modeled abundances with respect to the number of protons at three different positions across the PDR front.
Column densities and abundances with respect to the number of protons, i.e., [X] = 0.5 N(X)/N(H2), toward the PDR position, from single-dish observations at resolutions between 25 and 28′′.
Gaussian fit results for the lines of small hydrocarbons detected toward the Horsehead PDR at RA = 5h40m53.936s, Dec = −2°28′00′′ (J2000).
All Figures
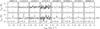 |
Fig. 1 Millimeter lines attributed to the l-C3H+ cation in the PDR (lower panels) and the dense core (upper panels) positions. The numbers above each panel are the line rest frequencies in MHz. The spectra and the Gaussian fits are shown as black histograms and green curves, respectively. The inferred rest frequencies are displayed as vertical dotted black lines for vlsr = 10.7 km s-1 and ± 3σ noise levels as horizontal dotted red lines. |
| In the text | |
 |
Fig. 2 High angular resolution maps of the integrated intensity of H13CO+, HCO, C2H, and c-C3H2, and the 7.7 μm PAH emission. Maps are rotated by 14° counter-clockwise around the projection center, located at (δx,δy) = (20′′,0′′), to bring the illuminated star direction in the horizontal direction. The horizontal zero is set at the PDR edge. The emission of all lines is integrated between 10.1 and 11.1 km s-1. Displayed integrated intensities are expressed in the main beam temperature scale. Contour levels are shown in the grey-scale lookup tables. The red vertical line shows the PDR edge and the blue and green crosses show the dense core and PDR positions, respectively. |
| In the text | |
 |
Fig. 3 Integrated intensity profiles across the PDR photo-dissociation front of the l-C3H+, HCO, H13CO+, and C2H species (IRAM-30 m). The cut would appear horizontal at δy = 0′′ in Fig. 2. The observed lines are summarized in Table 2. |
| In the text | |
 |
Fig. 4 Rotational diagram of l-C3H+ at the PDR position. |
| In the text | |
 |
Fig. 5 Photochemical model of the Horsehead PDR displayed at the full resolution of the model (left column) and convolved with a Gaussian of 6′′-FWHM (right column). Top: Horsehead density profile nH = n(H) + 2n(H2). Middle: predicted abundance of selected small hydrocarbons molecules and cations. Bottom: abundances of the same hydrocarbons relative to the abundance of C3H+. The illuminating star is positioned at the right of the plots. The symbols present the measured range of possible abundances for C2H (blue vertical segment), C3H2 (green vertical segment), and C3H+ (red filled rectangle), inferred at a typical resolution of 6′′. The legend at the bottom of the figure presents the line coding for the curves: C2H in plain blue, C2H+ in dashed blue, C3H in plain red, C3H+ in dashed red, and C3H2 in green. |
| In the text | |
 |
Fig. 6 Spatial profiles of the predicted abundance of C3H+ cation. The modeled abundance profile was convolved along the x-axis with a Gaussian of 6′′-FWHM (red line), and 27′′-FWHM (blue line). |
| In the text | |
 |
Fig. A.1 Hydrocarbon lines detected toward the Horsehead PDR at RA = 5h40m53.936s, Dec = −2°28′00′′ (J2000). Only lines in the 3 mm band, whose energy of the upper level is lower than 100 K and which have a higher signal-to-noise ratio than 8, are shown. The green lines are Gaussian fits. The vertical dashed lines mark 10.7 km s-1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


