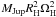| Issue |
A&A
Volume 548, December 2012
|
|
|---|---|---|
| Article Number | A116 | |
| Number of page(s) | 7 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201218879 | |
| Published online | 03 December 2012 | |
Circum-planetary discs as bottlenecks for gas accretion onto giant planets
1 Laboratoire Lagrange, UMR7293, Université de Nice Sophia-Antipolis/CNRS/Observatoire de la Côte d’Azur, BP 4229, 06304 Nice Cedex 4, France
e-mail: aurelien.crida@oca.eu
2 Formation Supaéro, Institut Supérieur de l’Aéronautique et de l’Espace, 10 Av. Edouard Belin, BP 94235, 31400 Toulouse Cedex 4, France
3 Laboratoire LERMA/Observatoire de Paris, 61 avenue de l’Observatoire, 75014 Paris, France
Received: 24 January 2012
Accepted: 29 October 2012
Context. With hundreds of exoplanets detected, it is necessary to revisit giant planets accretion models to explain their mass distribution. In particular, formation of sub-jovian planets remains unclear, given the short timescale for the runaway accretion of massive atmospheres. However, gas needs to pass through a circum-planetary disc. If the latter has a low viscosity (as expected if planets form in “dead zones”), it might act as a bottleneck for gas accretion.
Aims. We investigate what the minimum accretion rate is for a planet under the limit assumption that the circum-planetary disc is totally inviscid, and the transport of angular momentum occurs solely because of the gravitational perturbations from the star.
Methods. To estimate the accretion rate, we present a steady-state model of an inviscid circum-planetary disc, with vertical gas inflow and external torque from the star. Hydrodynamical simulations of a circum-planetary disc were conducted in 2D, in a planetocentric frame, with the star as an external perturber in order to measure the torque exerted by the star on the disc.
Results. The disc shows a two-armed spiral wave caused by stellar tides, propagating all the way in from the outer edge of the disc towards the planet. The stellar torque is small and corresponds to a doubling time for a Jupiter mass planet of the order of 5 Myr. Given the limit assumptions, this is clearly a lower bound of the real accretion rate.
Conclusions. This result shows that gas accretion onto a giant planet can be regulated by circum-planetary discs. This suggests that the diversity of masses of extra-solar planets may be the result of different viscosities in these discs.
Key words: accretion, accretion disks / planets and satellites: formation / protoplanetary disks / planet-disk interactions
© ESO, 2012
1. Introduction
The detection of exoplanets is probably one of the most striking discoveries of the past 50 years in astrophysics. Up to now, more than 700 exoplanets have been found. This constantly increasing number allows a statistical approach to the analysis of exoplanets. The resulting statistical distributions are then crucial benchmarks for planetary formation models. For an exoplanet, the two easiest parameters to determine are the mass and the semi-major axis of its orbit. Low mass planets are still hard to detect, but it seems that the mass distribution of planets more than 10 Earth masses is double-peaked, with a peak close to the mass of Neptune, and another peak close to the mass of Jupiter1. The first peak is probably an effect of observational biases as low-mass planets are still hard to detect, but the second peak seems to be real (Mayor et al. 2011).
The most popular model for giant planet formation is the core accretion model of Bodenheimer & Pollack (1986). In this model, a solid core grows, embedded in a gaseous proto-planetary disc. The gas within the Bondi radius (Bodenheimer et al. 2000) is gravitationally bound to the core, and forms an envelope. When the planet reaches a critical core mass of about 12–16 M⊕ (Pollack et al. 1996; Tajima & Nakagawa 1997), the envelope starts to contract quasi-statically and gas accretion rate increases, for an evolution timescale of a few million years. This long phase is followed by a runaway gas accretion stage occurring as soon as both core and envelope masses are approximately equal, during which quasi-static contraction and thus gas accretion rate dramatically increase. This leads to an exponential growth of the planet, in a few 105 yr, which proceeds as long as there is gas available.
This raises the question: what sets the terminal mass of a giant planet? When a planet becomes massive enough (typically a Saturn mass), it starts to open a gap in the disc around its orbit (Papaloizou & Lin 1984; Lin & Papaloizou 1986; Crida et al. 2006). However, gap opening does not necessarily imply that the gas flow onto the planet has ceased (Artymowicz & Lubow 1996) because the gap is not totally empty. Hydro-dynamical simulations (Bryden et al. 1999; Kley 1999; Lubow et al. 1999; Lubow & D’Angelo 2006) show that a Jupiter-mass planet keeps accreting gas almost as fast as if gap-opening had not occurred. Accretion stalls by gap-opening only once a mass in the range of 5–10 Jupiter masses is achieved. This is at odds with the masses of the giant planets in the solar system and of many of the extra-solar giant planets. In particular, the existence of Saturn-mass planets is a mystery in this scenario.
An often proposed solution (e.g.: Thommes et al. 2008) is that the giant planets form in “dead zones” – regions in the disc with very low viscosity – and, consequently, open gaps that are much wider and cleaner than previously thought. These gaps could inhibit accretion for planet masses of order of a Jupiter mass or less. However, this idea fails because, as demonstrated by Crida et al. (2006), the depth and width of a gap does not depend just on viscosity but also on the temperature (i.e. scale height) of the disc. Thus, even in a dead zone the gap opened by a Jupiter-mass planet should not inhibit significantly the accretion of gas into the planet’s Hill sphere. Thus, we believe that the question on the terminal mass of giant planets is still open.
We notice, however, that the Pollack et al. (1996) model considered an omnidirectional gas accretion towards the planet; yet, it is physically impossible to reach this state due to angular momentum conservation of the inflowing gas. In fact, gas must form a consistent circum-planetary disc (CPD) once the mass of the planet is higher than about a hundred Earth masses and the planetary atmosphere has shrunk well inside the planet’s Hill radius (Ward & Canup 2010). This has been confirmed by numerical simulations (e.g. Ayliffe & Bate 2009a,b). Once a CPD is formed, the accretion rate of the planet depends on the ability of gas to lose angular momentum, either by its re-distribution within the disc (through viscosity) or exchange with external perturbers (e.g. the star).
Most of the previous simulations considered a significant viscosity in the CPD, comparable to that of the active zones of the circum-stellar disc. In this case, angular momentum is redistributed very quickly and the accretion of gas from the CPD onto the planet is extremely fast, so that the role of the disc can generally be neglected as shown by Papaloizou & Nelson (2005) who assumed a viscosity about α = 10-3. However, it is possible that the CPD is in an MRI dead state as suggested by Turner et al. (2010), leading to vanishing turbulence and a very low viscosity. Indeed, if the circum-planetary disc has a very low viscosity, then the transport of angular momentum through this disc can be very inefficient and gas can only accrete onto the planet at the rate allowed by the removal of angular momentum by external perturbations, such as the stellar tide. Consequently, the CPD may act as a bottleneck for gas accretion and dramatically slow down the planet’s growth. If, as a result, the accretion of a planet does not enter the runaway phase but proceeds at a more regular pace on a timescale comparable to the circum-stellar disc lifetime (a few million years; Haisch et al. 2001; Hillenbrand et al. 2008) then the observed mass spectrum of the giant planets may be the consequence of the competition between gas accretion and gas dissipation.
To test whether the idea of a slow accretion rate through a low-viscosity disc is realistic, we study in this paper the effect of the stellar tides. We are aware that Reynolds stresses from waves driven from the circum-solar disc may allow angular momentum losses in the CPD as well. However, the accretion rate due solely to the solar tide provides a lower-bound to the real accretion rate for a CPD of vanishing viscosity. If the result is encouraging – i.e. the mass-doubling time for a Jupiter-mass planet from solar tides is longer than the proto-planetary disc lifetime – then the idea of a low-viscosity CPD as a regulator of the gas accretion rate onto a giant planet is promising. In this case, future work will have to evaluate in detail the gas accretion rate with realistic 3D hydro-dynamical simulations. Thus, our present paper should be considered as a first step in a long research plan.
The structure of the paper is the following. In Sect. 2 we elaborate an idealised semi-analytical model to evaluate the steady state accretion rate of a planet that is surrounded by an inviscid disc which undergoes vertical gas inflow and is submitted to a tidal torque from a distant star. Then we evaluate the two key parameters that enter in this model. The vertical gas influx rate is estimated in Sect. 3 from 3D simulations available in the literature. To compute the stellar torque, in Sect. 4 we perform 2D hydrodynamical simulations of a disc centred on a Jupiter-mass planet. The disc feels the gravitational perturbation from the star, assumed to be on a distant, circular orbit. We measure the torque due to the stellar tides, after a steady-state is reached. With these two values in hand, in Sect. 5 we estimate the planet accretion rate, expressed as a timescale for the doubling of the mass of a Jupiter-planet. Finally, we interpret these results and discuss their possible implications for giant planet formation theories in Sect. 6.
2. Model
The tidal torque and the accretion rate are not related in a trivial way in an inviscid disc. In this section, we present a simple model to derive an accretion rate on the planet from the tidal torque that we will measure in Sect. 5.
2.1. Depletion of the CPD
The torque exerted by the star on a ring of the disc is not entirely deposited locally in the disc. Only a fraction of the torque is deposited. This fraction depends on the disc viscosity and tends to zero for vanishing viscosity (Martin & Lubow 2011). The rest (i.e. the totality of the torque in the case of an inviscid disc) is passed to the adjacent rings through pressure effects (Crida et al. 2006, Appendix C). If no torque is deposited on a ring, then the gas in the ring does not lose angular momentum and does not move towards the central planet.
It would be incorrect, though, to expect that the wave raised by the star does not promote gas accretion from an inviscid disc. The torque is transmitted from each annulus of the disc to its internal neighbour by pressure all the way to the inner edge of the disc (at the boundary with the atmosphere). This inner annulus, not being supported by anything interior to it on a Keplerian motion, then loses angular momentum and falls onto the planet. Once the innermost annulus is emptied, the same fate occurs to the second innermost annulus and so forth. Thus, an inviscid disc is depleted from the inside out as gas is accreted onto the planet’s atmosphere.
More precisely, let us note X the radius of the region of the CPD that is emptied by the torque over a time t. The total orbital angular momentum of the gas present within r < X is given by: 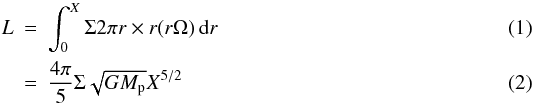 (assuming the surface density of the gas, Σ is independent of r). Here,
(assuming the surface density of the gas, Σ is independent of r). Here, 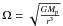 is the angular speed of the gas in Keplerian motion at a radius r, with Mp the mass of the planet.
is the angular speed of the gas in Keplerian motion at a radius r, with Mp the mass of the planet.
By definition of X, L should be exactly opposite to the total angular momentum taken by the star, which is the torque T, accumulated over time: T × t. This gives: 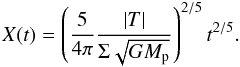 (3)We see that the radius X increases with time, as expected.
(3)We see that the radius X increases with time, as expected.
2.2. Infilling of the CPD
Here, we assume that the CPD is non-viscous. Thus, the CPD doesn’t spread radially, and any gas input at its outer edge just stays there. However, Machida et al. (2008) and Tanigawa et al. (2012) have shown that vertical inflow onto the CPD is the main source mass of the CPD. Let us call C this vertical mass flux per surface unit of the CPD.
Then, the surface density in an initially void region is Σ = Ct. Input into Eq. (3), this gives: 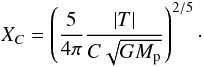 (4)This implies that there is a radius XC (independent of time) such that inside r < XC, depletion due to the stellar torque T and infilling due to the vertical inflow C exactly balance out. In an arbitrary time span, all the gas input within a circle of radius XC around the planet has exactly the orbital angular momentum taken by the stellar torque. As a consequence, the whole gas of this region falls onto the planet while the vertical inflow completely refills it in the same time. Thus, the region within XC reaches a steady-state density.
(4)This implies that there is a radius XC (independent of time) such that inside r < XC, depletion due to the stellar torque T and infilling due to the vertical inflow C exactly balance out. In an arbitrary time span, all the gas input within a circle of radius XC around the planet has exactly the orbital angular momentum taken by the stellar torque. As a consequence, the whole gas of this region falls onto the planet while the vertical inflow completely refills it in the same time. Thus, the region within XC reaches a steady-state density.
The disc outside XC, however, does not accrete and gas piles up. This issue will be discussed later in Sect. 2.4.
2.3. Accretion rate estimate
We can now write the planet accretion rate as a function of the torque. The mass flow on the planet is simply the mass flow inside r < XC: ![\begin{eqnarray} \dot M_{\rm p} & = & C \pi {X_C}^2 \nonumber \\[2mm] \dot M_{\rm p} & = & \pi \left(\frac{5}{4\pi \sqrt{G M_{\rm p}}}\right)^{4/5} T^{4/5} C^{1/5}. \label{accr-rate} \end{eqnarray}](/articles/aa/full_html/2012/12/aa18879-12/aa18879-12-eq21.png) (5)Note that the accretion rate depends weakly on the gas injection flux C, whereas it depends almost linearly on the torque exerted by the star T. This equation is central in this paper, as it links the stellar torque to the planetary accretion rate.
(5)Note that the accretion rate depends weakly on the gas injection flux C, whereas it depends almost linearly on the torque exerted by the star T. This equation is central in this paper, as it links the stellar torque to the planetary accretion rate.
2.4. The issue of gas-piling beyond XC
The model introduced in Sect. 2.2 raises the issue of gas-piling in the outer part of the disc. Indeed, if the density in the outer disc continued to increase, the total torque T exerted through the wave would increase as well, as it is proportional to Σ. This would imply an increase of the accretion radius X, and of the accretion rate Ṁp. Moreover, the density in the outer disc could reach the gravitational instability limit, changing completely the structure of the CPD and leading to outbursts of accretion, as suggested by Martin & Lubow (2011).
In reality, though, gas cannot pile-up indefinitely. If the density in the CPD becomes too large, gas is repelled by pressure and the inflow from the circum-stellar disc has to stop. Thus, in this section we estimate the density in the outer CPD, by imposing the pressure equilibrium between the CPD and the circum-stellar disc (CSD). Our approach is detailed below.
We assume the CSD is much thicker than the CPD. This, and the fact that the inflow from the CSD to the CPD is along the vertical direction (Tanigawa et al. 2012) suggests that the CSD “weights” on top of the surface of the CPD. Then, at equilibrium, the pressure in the CPD at a height HCPD has to be equal to the pressure of the CSD at the same height.
Let us now assume a standard Gaussian pressure profile in both discs: 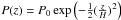 where P0 is the pressure at the mid-plane (denoted hereafter
where P0 is the pressure at the mid-plane (denoted hereafter 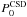 and
and 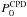 for the CSD and CPD respectively). At height HCPD, the pressure in the CSD is
for the CSD and CPD respectively). At height HCPD, the pressure in the CSD is 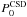 , given our assumption that HCSD ≫ HCPD. In the CPD,
, given our assumption that HCSD ≫ HCPD. In the CPD, 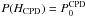 /
/ . P0 and Σ are linked by the equation of state
. P0 and Σ are linked by the equation of state 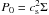 (where cs = HΩ is the sound speed). The equation PCPD(HCPD) = PCSD(0) can then be solved for the sole unknown of the problem:
(where cs = HΩ is the sound speed). The equation PCPD(HCPD) = PCSD(0) can then be solved for the sole unknown of the problem: 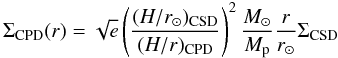 where M⊙ is the mass of the star and r⊙ the semi-major axis of the planet.
where M⊙ is the mass of the star and r⊙ the semi-major axis of the planet.
For (H/r⊙)CSD = 0.05 (Piétu et al. 2007), (H/r)CPD = 0.3 (Ayliffe & Bate 2009b), M⊙ = 103Mp, r⊙ = 14.4 RH (see simulation set-up in Sect. 4.1.1) and r = 0.3 RH which corresponds to the truncation radius of the CPD, as explained in Sect. 4.1.3, one gets HCSD = 8 × HCPD, justifying our assumption. This gives: 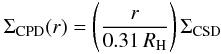 (6)with RH the Hill radius of the planet:
(6)with RH the Hill radius of the planet: 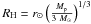 .
.
So, we estimate that the surface density of the CPD at 0.3 RH is about equal to the local surface density of the CSD, and can not exceed this value. This value of the density will be used in our simulations for tidal torque calculation in Sect. 4.1.2.
3. Gas inflow estimate
To apply the method outlined in Sect. 2, we need to estimate C: the flux per unit area of the gas injected onto the CPD. To do that, we use the results from Ayliffe & Bate (2009b). Those simulations give the flux of gas through the Hill sphere (MH, identified in that paper as the “planet accretion rate”). For a planet of mass Mp = 333 M⊕ (which is consistent with our choice of parameters) and a locally isothermal disc, Ayliffe & Bate (2009b) find ṀH = 8 × 10-5 MJup/yr. Given that almost all of this flux is vertical (Tanigawa et al. 2012), we can set 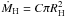 , which gives
, which gives 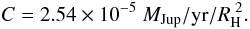 (7)
(7)
Simulation parameters and results.
4. Numerical simulations and Torque computation
The model introduced in Sect. 2 allows us to derive analytically an accretion rate onto the planet, given a gas inflow on the whole disc and an accurate knowledge of tidal effects from the star, i.e. an estimate of the stellar torque on the disc. Having evaluated the former in the previous section, here we describe how we compute the torque numerically. We start by reviewing the set-up of our simulations.
4.1. Simulation set-up
4.1.1. Code
To run simulations, we have used the code FARGO2 from Masset (2000a,b), which is a 2D Eulerian, non self-gravitating, isothermal code, with a polar grid. FARGO is very suitable for simulations of the interactions between planets and the proto-planetary disc. Here, we focus on the environment of the planet. Thus, we have slightly modified FARGO to adapt it to our case of study.
From now on, the central body will be the planet, while the star will be the orbiting body around the planet and its disc. Simulations take place in a planetocentric frame, corotating with the star. The orbit of the star is circular and fixed.
The mass unit is the mass of the central body: the planet, Mp. The distance unit is RH. The time unit is 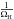 , where
, where 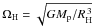 is the angular speed at r = RH. Note that the star’s angular speed is thus
is the angular speed at r = RH. Note that the star’s angular speed is thus 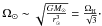
The mass of the star is taken to be M⊙ = 1000 Mp, which makes our system scaled like the Jupiter–Sun system. This gives r⊙ = 14.4 RH.
The star being out of the grid, we do not apply any smoothing in the computation of the force exerted by the star onto the disc. This is actually necessary for an accurate computation of the differential, tidal forces.
4.1.2. Gas parameters
In our simulations, we take an initial density profile 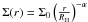 , with
, with 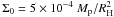 . This is in agreement with the global simulations from Ayliffe & Bate (2009a). Moreover, the surface density evaluated at 0.3 RH is ~
. This is in agreement with the global simulations from Ayliffe & Bate (2009a). Moreover, the surface density evaluated at 0.3 RH is ~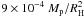 as α = 1/2 (see below). This should be compared to the surface density at the location of Jupiter:
as α = 1/2 (see below). This should be compared to the surface density at the location of Jupiter: 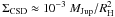 in the Minimum Mass Solar Nebula (Weidenschilling 1977; Hayashi 1981). Thus, our disc fulfils the condition of maximum pile-up, that we evaluated in Sect. 2.4.
in the Minimum Mass Solar Nebula (Weidenschilling 1977; Hayashi 1981). Thus, our disc fulfils the condition of maximum pile-up, that we evaluated in Sect. 2.4.
Due to numerical reasons, FARGO does not allow the modelling of a perfectly inviscid disc. Thus, we take a low but non-zero kinematic viscosity 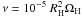 , unless specified otherwise and adopt a surface density profile α = 1/2 so that the viscous torque between adjacent annuli is zero. Notice, moreover, that our method to compute the gas accretion onto the planet does not use the actual flow of the gas, but only the shape of the spiral wave generated by the star (whose structure is detailed in Sect. 5.1). Thus, our results should not be significantly affected by our choice of ν, as we will check in Sect. 5.2.
, unless specified otherwise and adopt a surface density profile α = 1/2 so that the viscous torque between adjacent annuli is zero. Notice, moreover, that our method to compute the gas accretion onto the planet does not use the actual flow of the gas, but only the shape of the spiral wave generated by the star (whose structure is detailed in Sect. 5.1). Thus, our results should not be significantly affected by our choice of ν, as we will check in Sect. 5.2.
The Equation Of State in FARGO is locally isothermal, with P = cs2 Σ, where cs is the sound speed and cs = HΩ. The aspect ratio, H/r, is constant in all of our simulations and independent of r.
The H/r of the CPD has been measured to be 0.3 − 0.4 in Ayliffe & Bate (2009a). Unfortunately, the code FARGO is not stable for values of the scale height that are so large. Thus, we have run simulations with H/r values ranging from 0.05 to 0.2, in order to extrapolate the results to H/r = 0.4. Fortunately, as we will see below, the cumulated torque at the inner edge of the disc turns out to be independent of the H/r value, which makes the extrapolation trivial.
4.1.3. Numerical parameters
In several previous studies, simulations have shown that the disc reaches an equilibrium distribution with a sharp truncation at its outer edge (Ayliffe & Bate 2009a,b; Martin & Lubow 2011). This truncation radius is about 0.3–0.4 RH and is likely set by tidal truncation effects as outlined by Martin & Lubow (2011). Indeed, we observed ourselves such a truncation radius in simulations with a grid extended to the Hill radius.
Outside the truncation radius, the motion of the gas relative to the planet is strongly non-Keplerian, as noticed by Ayliffe & Bate (2009a). The interaction between this region and the CPD is not clearly understood. Therefore, as we just want to measure the effect of stellar tides on the CPD, we consider in this paper a limit case where the CPD is completely isolated and we truncate the grid at Rout = 0.3 RH. The inner border radius is Rin = 0.01 RH; for a Jupiter mass planet at 5.2 AU, it corresponds to about 540 000 km, which is smaller than the semi-major axis of Europa.
We choose a logarithmic radial spacing for the grid (the width of a ring δr is proportional to its radius r), which is suitable to have an accurate resolution very close to the planet. The resolution is taken such that δθ = δr/r < H/5r (see Table 1). This resolution is appropriate to resolve the pressure density wave exerted by the star, as H is the typical pressure scale length.
4.1.4. Boundary conditions
We use a non-reflecting boundary condition for both the inner and the outer borders of the disc. This prevents density waves from reflecting at the border of the grid. It is important for an accurate evaluation of the torque onto the disc through the wave. It also does not allow gas inflow or outflow and keeps the mean density on the first and last rings constant with time, which is consistent with our model of an isolated disc.
4.2. Torque computation
The gravitational torque exerted by the star on each ring of the CPD is computed as follows (see Martin & Lubow 2011). First, it is computed on each grid-cell. To the direct torque Tg, we have to subtract an indirect torque Ti due to the acceleration of the frame (i.e. of the planet).
Denoting by r = (xc,yc) the coordinates of a cell of mass mcell, by r⊙ = (x⊙,y⊙) the coordinates of the star and by d = r − r⊙ = (xd,yd) the mutual distance vector, the direct and indirect forces exerted by the star on the cell write: ![\begin{eqnarray*} \vec f_{\rm g} &=& -\frac{G M_{\odot} m_{\rm cell}}{d^2} \, \frac{\vec d}{\Vert \vec d \Vert} \\[3mm] \vec f_{\rm i} &=& -\frac{G M_{\odot} m_{\rm cell}}{r_\odot^2} \, \frac{\vec r_\odot}{\Vert \vec r_\odot \Vert} \end{eqnarray*}](/articles/aa/full_html/2012/12/aa18879-12/aa18879-12-eq122.png) thus, the gravitational torque exerted from the star on one cell is:
thus, the gravitational torque exerted from the star on one cell is: ![\begin{eqnarray*} \Vert \vec T \Vert & = &\Vert \vec T_{\rm g} - \vec T_{\rm i} \Vert \\[3mm] & = & \Vert \vec r \wedge (\vec f_{\rm g} - \vec f_{\rm i}) \Vert \\[3mm] & = & - [x_{\rm c} (f_{\rm g} y_{\rm d} - f_{\rm i} y_\odot) - y_{\rm c} (f_{\rm g} x_{\rm d} - f_{\rm i} x_\odot)]. \end{eqnarray*}](/articles/aa/full_html/2012/12/aa18879-12/aa18879-12-eq123.png) Then, we compute the azimuthal sum over all the cells of an annulus, to obtain the gravitational torque felt by one ring. Finally, the total torque on the disc is the sum of the torques felt by the individual rings. Thus, it is useful to introduce the notion of cumulative torque, which is the sum of the torques felt from the first ring to the ring in consideration. The total torque is therefore the cumulative torque at the last ring. For our purposes in this paper we consider the outermost ring to be the first and the innermost one the last (unlike Martin & Lubow (2011), who adopted the opposite convention).
Then, we compute the azimuthal sum over all the cells of an annulus, to obtain the gravitational torque felt by one ring. Finally, the total torque on the disc is the sum of the torques felt by the individual rings. Thus, it is useful to introduce the notion of cumulative torque, which is the sum of the torques felt from the first ring to the ring in consideration. The total torque is therefore the cumulative torque at the last ring. For our purposes in this paper we consider the outermost ring to be the first and the innermost one the last (unlike Martin & Lubow (2011), who adopted the opposite convention).
5. Results
In this section, we describe the results of numerical simulations on the structure of the CPD and present our estimate of the stellar torque. Then, we derive results for the accretion rate according to our analytical model.
5.1. Disc structure
As expected, we see a two-armed spiral density wave, created by the tides of the star. The wave propagates radially inwards with the speed of sound. As cs = HΩ, its radial velocity is H/r times its azimuthal velocity. Thus, the wave has the shape of a logarithmic spiral, with its pitch angle given by H/r. This is clearly seen in Fig. 1.
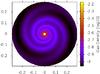 |
Fig. 1 Density map for an aspect ratio of 0.15. The disc is extended from r = 0.01 to 0.3 RH. |
5.2. Torque
We measure the torques after the simulations have reached a steady-state (after 150 orbits at 0.3 RH). Martin & Lubow (2011) showed that the total torque is negative and that most of it is exerted on the outer region of the disc (which represents less than 10% of the disc mass). Therefore, the variations of the cumulative torque in the inner part of the disc (r ≤ 0.1 RH) are negligible , as can be seen in Fig. 2. This figure shows the cumulative torques for various H/r, after 250 orbits at r = 0.3 RH. They oscillate from r = 0.3 to 0.1 RH. As explained by Martin & Lubow (2011), the disc can be divided in four quadrants, starting from the line connecting the planet to the star, rotating in the anti-clockwise direction. When the two-arm wave is in the first and third radiant, the torque is negative; when it is in the second and fourth one, the torque is positive. Thus, the oscillations of the torque correspond to the passage of the wave from even to odd quadrants and vice versa, due to its spiral shape. The wave-length of these pseudo-periodic oscillations is the radial propagation of the wave during half a revolution around the planet, that is π r (H/r).
 |
Fig. 2 Cumulated torques (in |
Notice that, although the radial profile of the cumulative torque is different from simulation to simulation given that the wavelength of its oscillation is a function of H/r, the limit value at the inner edge of the disc is remarkably insensitive on H/r. Thus we can safely assume that the total cumulative torque for a H/r = 0.3−0.4 disc (the realistic value of the scale height according to Ayliffe & Bate 2009a is also ~4 × 10-8.
We can now check whether our choice of the disc viscosity ν impacts significantly the total torque that we measure. For this purpose, Table 1 shows the torques measured in simulations with various viscosities. Some differences are visible, which is a sign that our simulations are not dominated by numerical viscosity. However, the total torques are very similar to each other (within 10% for an order of magnitude change in ν). This gives confidence that the total torque that we estimate is valid also in the limit of an inviscid disc.
5.3. Accretion rate
In Sect. 3, we obtained a value for the influx of gas onto the CPD C. Then, thanks to numerical simulations, we measured the stellar torque for different aspect ratios and low viscosities and obtained its order of magnitude in Sect. 5.2. Given these values, we can derive analytically the planet accretion rate Ṁ from Eq. (5). The resulting values are listed in Table 1, along with results on the torques and the corresponding steady-state radius XC. We find that XC is of the order of ~0.05 RH, approximately 50 times the current physical radius of Jupiter.
As can be seen in Table 1, the accretion rate hardly depends on the aspect ratio, and only increases by about 5% when H/r doubles. This is because, as we said above, the total cumulative torque is insensitive to the H/r value of the disc. The viscosity of the gas in the simulation also has very little influence on the measured torque. In all the cases, we find that the accretion rate is of the order of: 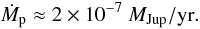 This accretion rate is low, making Jupiter double its mass in 5 million years. The torque that we measure is of course proportional to the surface density of the CPD in the simulations, but we have shown that the adopted value is realistic, and could hardly be larger. The parameter C may be poorly constrained, but the dependence of Ṁp on C is such that two orders of magnitude difference in C would only change Ṁp by a factor 3. Therefore, this order-of-magnitude estimate of the accretion rate in an inviscid CPD solely perturbed by the star, is robust. As a consequence, the accretion of giant planets could be much slower than expected, thus preventing the runaway accretion phase of the planet.
This accretion rate is low, making Jupiter double its mass in 5 million years. The torque that we measure is of course proportional to the surface density of the CPD in the simulations, but we have shown that the adopted value is realistic, and could hardly be larger. The parameter C may be poorly constrained, but the dependence of Ṁp on C is such that two orders of magnitude difference in C would only change Ṁp by a factor 3. Therefore, this order-of-magnitude estimate of the accretion rate in an inviscid CPD solely perturbed by the star, is robust. As a consequence, the accretion of giant planets could be much slower than expected, thus preventing the runaway accretion phase of the planet.
6. Conclusion
The classic model for giant planet formation (Pollack et al. 1996) predicts that the final phase of gas accretion occurs in a very fast runaway mode. Consequently, planets should keep accreting gas until they are so massive they open very wide gaps in the disc, which occurs when they reach a mass equal to multiple times the mass of Jupiter (Bryden et al. 1999; Kley 1999; Lubow et al. 1999; Lubow & D’Angelo 2006).
In this paper we considered that, during the alleged runaway growth phase, a planet should be surrounded by a circum-planetary disc (CPD) due to angular momentum conservation of the gas global flow. Thus, most of the gas that it accretes should have passed through this disc. The viscosity in the CPD may be very low, if the planet is located in a dead zone. Therefore, we have investigated whether a non-viscous CPD could act as a bottleneck for gas accretion. If, consequently, the gas accretion timescale can become comparable to the timescale of gas removal from the proto-planetary nebula, the observed large spread in giant planet masses could stem from the competitions between these two timescales.
Considering that there is no radial drift in a non-viscous disc, we have developed a model for a steady-state non-viscous CPD. The disc is fed by a vertical gas inflow from the surrounding environment (as previously observed in 3D numerical simulations, see Machida et al. 2008; Tanigawa et al. 2012; Ayliffe & Bate 2012), until a pressure equilibrium is reached. The surface density of the CPD is thus analytically determined and found in agreement with previous numerical simulations (Ayliffe & Bate 2009a).
However, the CPD is perturbed by the star. This results in the formation of a two-armed logarithmic spiral density wave, that propagates all the way inwards down to the inner edge of our disc. As a consequence, a negative torque from the star is deposited in the very inner regions of the disc, where gas consequently falls onto the planet. We find that the planetary accretion rate depends almost linearly on the cumulated stellar torque, and weakly on the vertical gas inflow (Eq. (5)).
Running 2D simulations of an isolated disc, in a planetocentric frame, extended to 0.3 Hill radius, we have studied the effect of the star on the disc, and measured the torque. We find that the torque is negative and basically independent on the disc’s aspect ratio. This allowed us to derive the accretion rate of a giant planet surrounded by a non-viscous CPD perturbed by the star. We find that the mass doubling time for a Jupiter-mass planet is about 5 Myr. This timescale is much longer than that in the runaway accretion mode of Pollack et al. (1996). However, such a low accretion rate is valid in the limit condition of an inviscid disc. In reality, even in a dead zone the viscosity is not null, though it is still extremely hard to estimate quantitatively its value. Furthermore, viscosity, if related to ionisation, can increase with time as the disc becomes less optically thick (Turner et al. 2010). As a consequence, the broad mass range of observed exoplanets may come from a range of viscosities (or viscosity evolutions) in their original CPDs.
Moreover, we have only studied the effect of the star on gas accretion inside the CPD. Several other effects may intervene to make the CPD lose angular momentum, which need to be investigated in the near future. In particular, interaction with the gas beyond 0.3 RH from the planet and outside the Hill sphere may perturb the flow in the CPD. The study of such interactions would require further investigations in global simulations and is beyond the scope of this paper.
In conclusion, it emerges from this paper that the accretion history for planets more massive than Saturn (the mass beyond which a CPD forms Ayliffe & Bate 2009b) may be dominated by the viscous evolution of the CPD. We speculate that planets with masses between Saturn’s and a few times Jupiter’s may have formed in “dead zones” with different levels of low viscosity in their CPDs. Instead, very massive planets (5–10 Jupiter masses), which reached the mass limit of the runaway growth process imposed by gap opening in the disc, should have formed in active zones, where CPDs did not act as bottlenecks to accretion.
Acknowledgments
G.R. and Y.B.’s internships at O.C.A. were funded by the PPF OPERA. We thank the CRIMSON team, who manages the mesocentre SIGAMM of the O.C.A., on which most simulations were performed.
References
- Artymowicz, P., & Lubow, S. H. 1996, ApJ, 467, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Ayliffe, B. A., & Bate, M. R. 2009a, MNRAS, 397, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Ayliffe, B. A., & Bate, M. R. 2009b, MNRAS, 393, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Ayliffe, B. A., & Bate, M. R. 2012, MNRAS, accepted [arXiv:1208.5513] [Google Scholar]
- Bodenheimer, P., & Pollack, J. B. 1986, Icarus, 67, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Bodenheimer, P., Burkert, A., Klein, R. I., & Boss, A. P. 2000, Protostars and Planets IV, 675 [Google Scholar]
- Bryden, G., Chen, X., Lin, D. N. C., Nelson, R. P., & Papaloizou, J. C. B. 1999, ApJ, 514, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Crida, A., Morbidelli, A., & Masset, F. 2006, Icarus, 181, 587 [Google Scholar]
- Haisch, Jr., K. E., Lada, E. A., & Lada, C. J. 2001, ApJ, 553, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, C. 1981, Prog. Theor. Phys. Suppl., 70, 35 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hillenbrand, L. A., Bauermeister, A., & White, R. J. 2008, in 14th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, ed. G. van Belle, ASP Conf. Ser., 384, 200 [Google Scholar]
- Kley, W. 1999, MNRAS, 303, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. 1986, ApJ, 309, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Lubow, S. H., & D’Angelo, G. 2006, ApJ, 641, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Lubow, S. H., Seibert, M., & Artymowicz, P. 1999, ApJ, 526, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, M. N., Kokubo, E., Inutsuka, S.-I., & Matsumoto, T. 2008, ApJ, 685, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, R. G., & Lubow, S. H. 2011, MNRAS, 413, 1447 [NASA ADS] [CrossRef] [Google Scholar]
- Masset, F. 2000a, A&AS, 141, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masset, F. S. 2000b, in Disks, Planetesimals, and Planets, eds. G. Garzón, C. Eiroa, D. de Winter, & T. J. Mahoney, ASP Conf. Ser., 219, 75 [Google Scholar]
- Mayor, M., Lovis, C., Segransan, D., et al. 2011, AAS, ESS Meeting, 2, 102 [Google Scholar]
- Papaloizou, J., & Lin, D. N. C. 1984, ApJ, 285, 818 [NASA ADS] [CrossRef] [Google Scholar]
- Papaloizou, J. C. B., & Nelson, R. P. 2005, A&A, 433, 247 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piétu, V., Dutrey, A., & Guilloteau, S. 2007, A&A, 467, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Tajima, N., & Nakagawa, Y. 1997, Icarus, 126, 282 [NASA ADS] [CrossRef] [Google Scholar]
- Tanigawa, T., Ohtsuki, K., & Machida, M. N. 2012, ApJ, 747, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Thommes, E. W., Matsumura, S., & Rasio, F. A. 2008, Science, 321, 814 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Turner, N. J., Lee, M. H., & Sano, T. 2010, in BAAS 42, AAS/Division for Planetary Sciences Meeting Abstracts, 959 [Google Scholar]
- Ward, W. R., & Canup, R. M. 2010, AJ, 140, 1168 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J. 1977, Ap&SS, 51, 153 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Density map for an aspect ratio of 0.15. The disc is extended from r = 0.01 to 0.3 RH. |
| In the text | |
 |
Fig. 2 Cumulated torques (in |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.