| Issue |
A&A
Volume 548, December 2012
|
|
|---|---|---|
| Article Number | A34 | |
| Number of page(s) | 34 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201015615 | |
| Published online | 15 November 2012 | |
Elemental abundances and classification of carbon-enhanced metal-poor stars⋆,⋆⋆
1
Instituto de Astronomia, Geofísica e Ciências Atmosféricas, Universidade de
São Paulo, rua do Matão
1226, 05508-900
São Paulo, Brazil
e-mail: dimallen@astro.iag.usp.br; rossi@astro.iag.usp.br
2
Centre for Astrophysics Research, STRI and School of Physics,
Astronomy and Mathematics, University of Hertfordshire, Hatfield, UK
e-mail: s.g.ryan@herts.ac.uk
3
National Optical Astronomy Observatory,
950 N. Cherry Avenue,
Tucson, AZ
85719,
USA
e-mail: beers@noao.edu
Received:
19
August
2010
Accepted:
24
August
2012
We present a detailed study of carbon-enhanced metal-poor (CEMP) stars, based on high-resolution spectroscopic observations of a sample of 18 stars. The stellar spectra for this sample were obtained at the 4.2 m William Herschel Telescope in 2001 and 2002, using the Utrecht Echelle Spectrograph, at a resolving power R ~ 52 000 and S/N ~ 40, covering the wavelength range λλ3700−5700 Å. The atmospheric parameters determined for this sample indicate temperatures ranging from 4750 K to 7100 K, log g from 1.5 to 4.3, and metallicities −3.0 ≤ [Fe/H] ≤ −1.7. Elemental abundances for C, Na, Mg, Sc, Ti, Cr, Cu, Zn, Sr, Y, Zr, Ba, La, Ce, Nd, Sm, Eu, Gd, Dy are determined. Abundances for an additional 109 stars were taken from the literature and combined with the data of our sample. The literature sample reveals a lack of reliable abundance estimates for species that might be associated with the r-process elements for about 67% of CEMP stars, preventing a complete understanding of this class of stars, since [Ba/Eu] ratios are used to classify them. Although eight stars in our observed sample are also found in the literature sample, Eu abundances or limits are determined for four of these stars for the first time. From the observed correlations between C, Ba, and Eu, we argue that the CEMP-r/s class has the same astronomical origin as CEMP-s stars, highlighting the need for a more complete understanding of Eu production.
Key words: stars: abundances / stars: atmospheres / stars: chemically peculiar / stars: carbon
Full Tables 2, 5, and 7 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/548/A34
Current address: Escola de Artes, Ciências e Humanidades, USP, Av. Arlindo Bettio, 1000, 03828-000 São Paulo, SP, Brazil.
© ESO, 2012
1. Introduction
Over the course of the past few decades, several groups have actively studied stars identified as very metal poor by two major objective-prism surveys, the HK Survey of Beers and colleagues (Beers et al. 1992, 1985) and the Hamburg/ESO survey of Christlieb and colleagues (Christlieb et al. 2008). A large fraction, at least 20%, of stars with metallicities [Fe/H] < −2.0 have been shown to exhibit large over-abundances of carbon relative to iron, [C/Fe] > +1.0 (Rossi et al. 1999; Lucatello et al. 2006; Marsteller et al. 2009; Carollo et al. 2012). The fraction of so-called carbon-enhanced metal-poor (CEMP) stars rises to 30% for [Fe/H] < −3.0, 40% for [Fe/H] < −3.5, and 75% for [Fe/H] < −4.0 (Christlieb et al. 2002; Beers & Christlieb 2005; Frebel et al. 2005; Norris et al. 2007; Carollo et al. 2012). The CEMP fraction for ultra metal-poor stars with [Fe/H] < −4.0 was 100% until the recent report by Caffau et al. (2011) of a new hyper metal-poor star (SDSS J102915+172927, with [Fe/H] = −5.0) that differs from the other three known ultra and hyper metal-poor stars in that it does not exhibit carbon enhancement.
The diversity of chemical compositions seen among the CEMP stars, together with their very low metallicities, provides insights into the early stages of Galactic star formation, stellar evolution, and galaxy formation. Several scenarios have been proposed to explain the likely multiple origins of the high carbon enhancements shown by these stars, but uncertainties remain. Observations of the neutron-capture elements (those produced by the s-process and r-process) can help shed light on these questions, given that their production is related to different timescales, and almost certainly different astrophysical sites. In this regard, it is of importance that Hansen et al. (2011) have recently reported the results of a four-year radial velocity monitoring project for moderately and highly r-process-enhanced metal-poor stars (classes r-I and r-II according to the nomenclature of Beers & Christlieb 2005), and demonstrated that the binary fraction of these stars is no different than found for other low-metallicity halo stars (about 20%). In comparison, s-process-enhanced CEMP stars possess elevated binary fractions, possibly 100%, (Lucatello et al. 2005). This result immediately suggests that the r-process enhancement phenomenon does not apparently require pollution from a companion star, and underscores the likelihood that the astrophysical sites of the r-process and s-process are decoupled from one another.
Barium and europium are often taken as representatives of the s- and the r-processes, respectively, according to the dominance of these processes on their production in Solar System material. According to Arlandini et al. (1999), in the Solar System, the main component of the s-process contributes ≈ 82% of the Ba, whereas ≈ 18% is due to the r-process. By way of contrast, while 6% of Eu in solar-composition material results from the s-process, the r-process accounts for the production of essentially all the rest (94%). Barium abundances are easily measured for very metal-poor stars, since its strongest lines are unsaturated, which is often not the case for stars with higher metallicities. Although the lines of Eu are weaker than those of Ba, Eu abundances nevertheless are often readily measurable in optical spectra of metal-poor stars. Hence, Ba and Eu are useful and accessible indicators of the s- and r-processes.
The r-process is believed to occur in the final evolutionary stages of massive stars (M > 8 M⊙), whereas the main component of the s-process is believed to occur in thermally-pulsing asymptotic giant-branch (TP-AGB) stars of low (1−3 M⊙) to intermediate (4−8 M⊙) masses (e.g., Herwig 2005). As the timescale for stars to reach the SN II (type II supernova) stage (t < 108 yr) is less than that for stars to reach the AGB phase, it is usual to investigate the s-process contribution by analyzing the [Ba/Eu] abundance ratio. A value of [Ba/Eu] ~−0.70, found in metal-poor stars, indicates Ba production only by the r-process (Mashonkina & Gehren 2001). When the s-process begins to produce Ba, an increase in its abundance relative to Eu can be seen, ultimately reaching values compatible with the solar [Ba/Eu] ratio (Travaglio et al. 1999).
Beers & Christlieb (2005) have used the Ba and Eu abundance signatures to classify CEMP stars into several broad categories: CEMP-s, stars that exhibit large over-abundances of s-process elements, with [Ba/Fe] > +1 and [Ba/Eu] > +0.5, and account for some 80% of all studied CEMP stars according to Aoki et al. (2007); CEMP-r, stars exhibiting over-abundances of r-process elements and [Ba/Eu] < 0 (McWilliam et al. 1995; Norris et al. 1997; Sneden et al. 2003; Honda et al. 2004; Barklem et al. 2005; Cohen et al. 2006); CEMP-r/s, stars with 0 < [Ba/Eu] ≲ +0.5, and exhibiting both r- and s-process enhancements (Hill et al. 2000; Wanajo et al. 2006); and CEMP-no, stars that exhibit no over-abundances of neutron-capture elements ([Ba/Fe] < 0; e.g., Aoki et al. 2007; Ito et al. 2009).
There has been some discussion in the literature concerning the relationship of the CEMP-r/s class to the CEMP-s class. Tsangarides (2005) pointed out that the [Ba/Eu] ratios for some stars classified previously as CEMP-s are similar to those for stars classified as CEMP-r/s, and called into question whether the hybrid r/s classification is strictly necessary. He also speculated that the progenitors of the CEMP-s and CEMP-r/s class may even be one and the same (TP-AGB stars). Unfortunately, for many known CEMP stars, measurements of Eu abundances are not available, and instead Ba is sometimes used as an r-process indicator, even though it is produced in both the r- and s-processes. For further discussion of these issues, see the recent paper by Bisterzo et al. (2010).
In this paper we seek a better understanding of the possible differences between stars classified as CEMP-s and CEMP-r/s, by expanding the numbers of CEMP stars with available Eu abundance measurements. We also reconsider the interpretation of previously published high-resolution abundance determinations for CEMP stars. The paper is organized as follows. Section 2 presents the data and describes the determination of the stellar atmospheric parameters. Section 3 describes the abundance and uncertainty determinations. In Sect. 4 our results are discussed, as well as those obtained from inspection of data from the literature. Our conclusions are drawn in Sect. 5.
2. Observations and stellar parameters
Twenty-six candidate CEMP stars, listed in Table 1, were selected from the HK survey of Beers et al. (1985), and from more recent unpublished follow-up medium-resolution extensions of that programme, according to two criteria: an HK-survey metallicity estimate [Fe/H] ≲ −1.5, and a carbon-enhancement index CEN ≳ 0.5, implying a CH G-band strength more than 1.5 × the median value at that temperature and metallicity. The CEN index is defined as (GP∗ – GPM)/GPM, where GP is the Beers et al. (1985, their Table 1 CH G-band index, and the subscripts “*” and “M” refer to a particular star and the median for stars of that temperature and metallicity. The notes column identifies stars which our analysis ultimately showed were not genuine CEMP stars (Sect. 3.1).
Twenty-three stellar spectra were observed by SAT1 and SGR2 at the 4.2 m William Herschel Telescope (WHT) in August 2001 and April 2002, using the Utrecht Echelle Spectrograph (UES), with a resolving power of R ~ 52 000 and signal-to-noise ratio (S/N) ~ 40 per 0.026 Å pixel. The spectra cover the wavelength range λλ3500−5700 Å. Three additional high-resolution spectra were obtained by SGR and John Norris on the 3.9 m Anglo-Australian Telescope in September 2000, using the UCL Echelle Spectrograph (UCLES). The spectra were reduced by SAT with IRAF3, using standard procedures. Because of the large number of spectra taken, the reduced data were analysed in two subgroups, one by DMA4 (12 stars) and the other by SAT (14 stars). The approaches were similar in concept, although they differed slightly in the details.
Photometric UBVRI observations of stars from the SAT subsample (see Table 1) were obtained by TCB5 on the Wisconsin-Indiana-Yale-NOAO (WIYN) Observatory 0.9 m telescope on Kitt Peak, and at the ESO/Danish 1.5 m telescope at La Silla (Chile), and by TCB and Don Terndrup on the MDM Observatory 2.5 m telescope, also on Kitt Peak (Beers et al. 1994, 2007). Near-IR JHK photometry was taken for the 26 objects from the interim data release of the 2MASS point source catalogue (2MASS 2003; Skrutskie et al. 1997).
Calculation of even a single model atmosphere is a computationally intensive task. Stellar parameters, such as effective temperature (Teff), surface gravity (log g), and metallicity ([Fe/H]), are usually required a priori. However, these are quantities to be determined using the model atmosphere during the analysis;thus, we can only arrive at an appropriate set of parameters and model atmosphere by iteration. This procedure is impractical if a fresh model is to be obtained at every step, given the computational demands of its calculation. Hence, most groups evaluate a grid of several model atmospheres to begin with, in which each model possesses a different set of input atmospheric parameters. One then interpolates between models of this grid, in order to more quickly compute new models at a desired set of atmospheric parameters. Inherent in this interpolation is the assumption that the physics of each grid model can be scaled to nearby atmospheric parameters.
2.1. The DMA subsample
The adopted model atmospheres were computed with the latest version of the ATLAS9 code, initially developed by Kurucz (1992, 1993), and subsequently updated by Castelli et al. (1997) and Castelli & Kurucz (2004), with enhanced α-element abundances, but no C- or N-enhancement. The current version uses an improved opacity distribution function, where the solar abundances, TiO lines, and some atomic and molecular constants were replaced.
Before determining the photometric temperatures, an initial value for interstellar
reddening was estimated. Since there are no available Hipparcos parallaxes for the stars
in our sample, the first values for the absolute
magnitude (MV) of each star were taken
from the colour−magnitude diagrams (CMDs,
MV) vs.
B − V) given by Green
et al. (1987) and Lejeune et al. (1998).
These diagrams usually provide two MV values
for each B − V, according to the evolutionary state of
the star, so the first value to be used was chosen arbitrarily. This absolute magnitude
was then used to estimate the first value for the distance; that, together with the
Galactic coordinates in Table 1, were used to
calculate the first value for the visual
extinction, AV, following Hakkila et al. (1997). Then, the photometric
temperatures were calculated using the colour−temperature calibrations of Alonso et al. (1996a, 1999), considering [Fe/H] = −1.5, −2, and −2.5. These authors use accurate
stellar-diameter effective temperatures from the literature to calculate temperatures for
objects with observed multiple pass-band colours, using the infrared flux-method (IRFM).
Alonso et al. (1996a, 1999) use the Johnson system for UBVRI and TCS
(Telescopio Carlos Sánchez) for JHKLMN, so before determining the
temperatures, the colours were transformed according to Bessell (1979), Alonso et al. (1998), and
Carpenter (2001). The mean value for the
temperature derived from B − V,
V − R, V − I, and
colours derived from 2MASS magnitudes is the first value for the temperature used to
create the model atmosphere. For some stars, such as BS 16077-077, temperatures derived
from the B − V and
V − K colours are very low compared to those from
other colours, so they were neglected. Bolometric
corrections BC(V) were determined according to Alonso et al. (1995) or Alonso et al. (1999), depending on the more probable evolutionary stage of the
star, as estimated from the CMD. With the initial values of temperature and
extinction-corrected (B − V)o, the first
input for the mass was taken from the Yonsei-Yale isochrones (Y2), described by
Yi et al. (2001), Kim et al. (2002), Yi et al.
(2003) and Demarque et al. (2004). Then,
the first estimate for log g (and its error) were taken from
the relations: 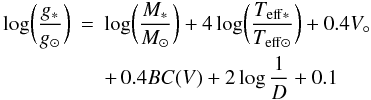 (1)
(1)![\begin{eqnarray} \sigma_{\log g}&= & \biggl[\biggl({\sigma_M\over {M\ln(10)}}\biggr)^2+\biggl({4\sigma_{T_{\rm eff\ast}}\over{T_{\rm eff\ast}\ln(10)}}\biggr)^2+\biggl({4\sigma_{T_{\rm eff\odot}}\over {T_{\rm eff\odot}\ln(10)}}\biggr)^2 \nonumber \\ &&+ \, \sigma_{\log g\odot}^{2}+(0.4\sigma_{V\circ})^2+(0.4\sigma_{BC})^2+\biggl({2\sigma_\pi\over{\pi\ln(10)}}\biggr)^2\biggr]^{0.5} \end{eqnarray}](/articles/aa/full_html/2012/12/aa15615-10/aa15615-10-eq41.png) (2)where M∗ is the
stellar mass, V° is the extinction-corrected magnitude, and
D is the distance. For the Sun, we have adopted
Teff ⊙ = 5781 K (Bessell
et al. 1998); log g⊙ = 4.44;
Mbol ⊙ = 4.75 (Cram
1999).
(2)where M∗ is the
stellar mass, V° is the extinction-corrected magnitude, and
D is the distance. For the Sun, we have adopted
Teff ⊙ = 5781 K (Bessell
et al. 1998); log g⊙ = 4.44;
Mbol ⊙ = 4.75 (Cram
1999).
Iron lines for the DMA subsample.
With the first estimates for Teff and log g, the Fe i and Fe ii abundances were calculated using the code WIDTH9 (Castelli 2004), which derives abundances from the equivalent widths (EW) of atomic lines. Table 2 shows the Fe i and Fe ii lines, with the respective atomic constants and EW for each star of the DMA subsample. As indicated in Table 2, the main source of oscillator strengths and excitation potential for Fe i lines was the library of the National Institute of Standards and Technology (NIST; Martin et al. 1988, 2002); for Fe ii, values by Fuhr & Wiese (2006) were adopted. A significant number of Fe i lines were used, ranging from 12 to 124. For two stars, less than 20 Fe i lines were available. Concerning Fe ii, most stars had more than 10 lines available. After running WIDTH9, we have the first estimates for the Fe i and Fe ii abundances. Iron lines whose abundances were beyond 1σ from the overall mean value were discarded for the next iteration.
An isochrone for a given age changes if the metallicity changes, so we have to look for new MV and mass estimates at the isochrone of metallicity closest to that obtained from the WIDTH9 analysis; the process must then be restarted with this new MV, so that new photometric temperatures can be derived. In this first iteration, it is not unusual that the abundance of Fe i is very different from that of Fe ii. One possible cause for this discrepancy is the inadequacy of the initial choice of MV. This means that the value corresponding to the (B − V) with opposite evolutionary state to the first choice is the more suitable MV value to be used. Indeed, if [Fe ii/H] is higher than [Fe i/H], log g must decrease in order to decrease [Fe ii/H]. In such a case, the more suitable MV is lower than the first choice. Then, the process must be restarted using the new MV and new parameters derived. When the difference between log ϵ(Fe i) and log ϵ(Fe ii) obtained with WIDTH9 is below 0.2 dex, and close to those used in the previous iteration, fine tuning adjustments are made. WIDTH9 provides fits for abundance vs. excitation potencial (χex) and vs. EW, and analysing their slopes for each iteration it is possible to seek the best set of parameters. The temperatures were changed in the atmosphere model depending on whether the χ slope was positive or negative. When there is no trend between the abundances, χex, and EW we have obtained our desired excitation temperature (Tex), and the microturbulent velocity (ξ).
Summarizing, the entire process is iterated until convergence is obtained to a consistent set of parameters. The uncertainties on Tex and ξ were estimated directly from this iterative process, taking into account the slopes of the best fits. We had many iron lines, hence the random uncertainties on Fe i and Fe ii abundances were taken to be the standard error of the mean. The various photometric temperatures derived with the final Fe i and Fe ii abundances are shown in Table 3, and all final parameters are listed in Table 4. Photometric temperatures vary considerably – by up to a few hundred K – for different colour indices, which suggests a need for better photometry and/or transformations. It is worth noting that the Alonso et al. effective temperatures were fairly accurate for [Fe/H] ≳ −2.5 to −2.0, but become non-physical for metallicities smaller than −3.0, due to the small number of stars with [Fe/H] ≲ −2.5 available in the literature at the time the calibration was undertaken. For this reason, we adopted Tex as the temperatures for our sample of stars in the DMA analysis.
Other stellar parameters and their uncertainties shown in Table 4 are derived through application of the equations below. Uncertainties
on BC(V) are estimated by computing how the
uncertainties on Tex modify their values. From Eqs. (3) to (9), one obtains the absolute
magnitude MV, the bolometric
magnitude Mbol,
luminosity (L∗/L⊙), and
radius (R∗/R⊙), providing as
inputs for the distance D(pc),
AV, V,
and log g: ![\begin{eqnarray} \label{magab} && M_v = V-5\log D+5-A_v \\[1mm] && \sigma_{M_v}=\biggl[({\sigma_V)^2+\biggl({5\sigma_D\over D\ln(10)}\biggr)^2+\sigma_{A_v}^2}\biggr]^{0.5} \\[1mm] \label{magbol} && M_{\rm bol\ast} = M_v+BC(V) \\[1mm] && \sigma_{M_{\rm bol\ast}}=\biggl({\sigma_{M_v}^2+\sigma_{BC}^2}\biggr)^{0.5} \\[1mm] \label{lumin} && L_\ast = 10^{-0.4(M_{\rm bol\ast}-M_{\rm bol\odot})}L_\odot \\[1mm] && \sigma_L=L0.4\ln(10)\biggl({\sigma_{M_{\rm bol\ast}}^2+\sigma_{M_{\rm bol\odot}}^2}\biggr)^{0.5} \\[1mm] && R_\ast = \left({L_\ast T_{\rm eff\odot}^4\over L_\odot T_{\rm eff\ast}^4}\right)^{0.5}R_\odot \label{raio} \\[1mm] && \sigma_R=R\biggl[{\biggl({\sigma_L\over 2L}\biggr)^2+\biggl({2\sigma_{T_{\rm eff\odot}}\over T_{\rm eff\odot}}\biggr)^2+\biggl({2\sigma_{T_{\rm eff\ast}}\over T_{\rm eff\ast}}\biggr)^2}\biggr]^{0.5}\cdot \end{eqnarray}](/articles/aa/full_html/2012/12/aa15615-10/aa15615-10-eq64.png)
Atomic lines for the SAT subsample with atomic constants and EW measurements.
2.2. The SAT subsample
The SAT analysis is fully described in Tsangarides (2005). For completeness, we present here a short description of his procedure. The grid of model atmospheres was taken from Bell et al. (1976) and Bell (1983, priv. comm.). The former work tabulates model atmospheres for (early-G to early K-type) giants in the parameter space 3750 K ≤ Teff ≤ 6000 K, 0.75 ≤ log g ≤ 3.0 and −3.0 ≤ [Fe/H] ≤ 0.0. The latter supplements this parameter space to include dwarfs, main-sequence turnoff stars and subgiants; i.e., it extends the upper limits of effective temperature and surface gravity to 6500 K and 5.0, respectively. Both works calculate the grid models by scaling the solar abundance ratios of all naturally occurring elements by each model’s desired metallicitty.
Atmospheric parameters and abundances for HD 140283 obtained by SAT and DMA.
For the SAT subsample, an earlier version of the code WIDTH9 was used, WIDTH6 (Kurucz & Furenlid 1979). Table 5 shows the lines, as well as the atomic constants and the EW used as input for the code. As for the DMA subsample, a large number of Fe i were used, ranging from 44 to 105. For Fe ii, the number of lines ranges from 7 to 17. SAT used two models for HD 140283. In the first, model A, the temperature, gravity, microturbulence, and iron abundance were all derived from the spectral analysis (requiring ionisation balance). This resulted in a rather low gravity (see Table 6), at odds with the value obtained from Hipparcos parallax measurements. Consequently, SAT calculated a second model, model B, in which the temperature was determined from IRFM-calibrated colours (using Alonso et al. 1996b), and the gravity was fixed at the parallax value. This created a disparity in the abundances inferred from neutral and ionised Fe lines, suggestive of overionisation. Model B is preferred, but serves as a reminder that for stars without trigonometric parallaxes the results could have greater uncertainties. In order to compare the SAT and DMA procedures, the latter determined atmospheric parameters and abundances of Ti ii and C for the star HD 140283. Table 6 shows that both procedures are in good agreement, although the [C/Fe] abundance varies considerably between SAT (Model B) and the DMA analysis, despite the similarity between the adopted parameters. The initial model atmosphere for the WIDTH6 calculation was adopted by estimating the metallicity and surface gravity of each target and calculating its effective temperature from the observed colours. SAT estimated the line-of-sight reddening E(B − V) of the targets’ observed colours using the dust maps of Schlegel et al. (1998), as shown in Table 1. Then, dereddened colours were used in deriving the initial effective temperatures. These were calculated using the semi-empirical calibrations of Alonso et al. (1996a) for dwarfs and Alonso et al. (1999) for giants. The initial surface gravity of the candidate CEMP stars was estimated based on the approximate evolutionary stage of each target. For stars with colours near the main-sequence turnoff (BS 16080-175, BS 16090-048, BS 17451-031, CS 22171-009, CS 22887-048, and CS 22898-027), SAT initially adopted log g = 4.0, and for objects with colours on the giant branch (including BS 17436-058, CS 22174-007, CS 22183-015, and CS 29502-092), log g = 2.5. An incorrect initial gravity implied longer computation times for the abundances of Fe i and Fe ii to converge, but since the final adopted log g was set using the Fe ionisation balance, it was not affected by the starting value. The metallicity of the model has the smallest effect on the derived abundances among these three atmospheric parameters, which was illustrated by a posterior error analysis. Therefore, [Fe/H] = −1.5 for all the initial models were adopted, which is the mean Population II metallicity (Laird et al. 1988). All photometric temperatures and final parameters adopted for the SAT subsample are shown in Tables 3 and 4.
3. Abundances and uncertainties
3.1. Effectiveness of the selection method
The stellar parameters and [Fe/H] values derived in Sect. 2 enable us to examine the effectiveness of the selection criteria used for the CEMP stars. The majority of these CEMP candidates are confirmed as metal-poor stars. The five exceptions are as follows. BS 17451-031 has two disparate B − V colours, provided in Table 1. The excitation temperature (5800 K) is consistent with the more recent, bluer colour. We infer that because of the older and presumably erroneous colour, viz. B − V = 0.711, this Sun-like dwarf was originally mistaken as a cool giant and, being weak lined compared to genuine giants, was misclassified as metal-poor but, as with other Sun-like dwarfs, having a prominent G-band. BS 16086-022 and CS 22169-002 were found to have extremely broad Hγ, Hϵ and λ4324 features, which reveal them to be white dwarfs. The only narrow lines in these spectral regions are the Ca ii H and K lines, which are likely of interstellar origin. For this reason, these two white dwarfs were misclassified as metal-poor candidates in the HK-survey objective-prism selection. The spectra also exhibit a broad, shallow depression of flux around 4310 Å. The broad 4310 Å and 4324 Å depressions coincide with the CH G-band, and suggest these stars to be C-rich (DQ) white dwarfs. BS 16542-052 was listed amongst the emission line candidates of Beers et al. (1994). Our spectrum showed it to be strong lined, with a preliminary analysis indicating [Fe/H] ~ −0.8. This star is unlikely to be a CEMP star, and is more likely a mildly metal-poor star with a normal G-band. The Ca ii H and K lines did not appear in emission at the time of our observation. We chose not to analyse it further. Our spectrum of BS 16088-104 showed this star to be quite strong lined, with a preliminary analysis (conducted by A. Hosford) indicating [Fe/H] ~ −0.3. As it was almost certainly misclassified as a CEMP star; we did not analyse it further.
We have found five misclassified stars in our echelle observations of 26 CEMP candidates, corresponding to a false-positive rate of 19% in the original sample selection. We do not consider these stars further.
3.2. Other elemental abundances
For the elements other than Fe, abundances were derived through 1D LTE spectrum synthesis, using the code SYNTHE created by R. Kurucz, or in the case of the SAT analysis, the synthesis code ATLAS by Cottrell & Norris (1978). Abundances of carbon were derived using molecular synthesis of the G-band (CH A3Δ – X3π) at λλ4290−4315 Å. Atomic lines were used to calculate the abundances of Na, Mg, Sc, Ti, Cr, Cu, Zn, Sr, Y, Zr, Ba, La, Ce, Nd, Sm, Eu, Gd, Dy by DMA, and Ti, Zn, Sr, Y, Zr, Ba, La, Eu, Pb by SAT. Table 5 shows the lines used for the SAT subsample; Table 7 lists the abundances line by line, along with the respective atomic constants for the DMA subsample.
The oscillator strengths for elements other than Fe, and their respective sources, are shown in Table 7. For the α- and iron-peak elements, most values are from NIST; a few data are from VALD (Piskunov et al. 1995; Ryabchikova et al. 1997; Kupka et al. 1999, 2000). Laboratory values, where available, were given preference over theoretical values. For the lines of Cu i, Eu ii, La ii, and Ba ii the hyperfine structure (hfs) was taken into account, employing a code made available by A. McWilliam, following the calculations described by Prochaska et al. (2000). The hfs constants were taken from Rutten (1978) for Ba ii, Lawler et al. (2001a) for La ii, and Lawler et al. (2001b) for Eu ii. The final hfs components were determined by using the solar isotopic mix by Lodders (2003) and the total log gf values from laboratory measurements. For copper, the hfs from Biehl (1976) was used, with isotopic fractions of 0.69 for 63Cu and 0.31 for 65Cu. In this case, small corrections were applied such that the total log gf equals the gf value adopted in this work. The lines for which hfs were used were tested by creating a sinthetic solar spectrum to compare to the solar observed spectrum by Kurucz et al. (1984).
Tables 8 and 9 show the average abundance for the elements in each star, for the DMA and remaining SAT subsamples, respectively. For most elements, the solar abundances used were extracted from Grevesse & Sauval (1998); full references are indicated in Table 8. The usual notations log ϵ(A) = log (NA/NH) + 12 and [A/B] = log (NA/NB)∗ − log (NA/NB)⊙ were adopted.
Uncertainties in the abundances were evaluated by consideration of the degree to which a variation of 1σ in the atmospheric parameters and S/N affected the output value of the synthesis routine. For details of the error calculations, see Appendix A.
Lines, equivalent widths, and abundances for the DMA subsample.
Although the errors in the atmospheric parameters are usually the dominant source of the total error on the abundance estimates, observational sources can be more significant at a S/N around 40. A change of 50 K in Teff leads to a change of typically 0.03 dex in [X/Fe], with the largest change being 0.10 dex for some elements. Changes of 0.10 dex in log g result in alterations of [X/Fe] of up to 0.04 dex. Changes of 0.10 km s-1 in ξ lead to [X/Fe] changes up to 0.03 dex. For the present sample, the major contribution to the uncertainties on [X/Fe] is the S/N achieved in the spectra. For example, for BS 16077-077 (the star in our sample with the highest S/N) the contribution of error due to S/N ranges typically from 0.07 dex to 0.15 dex, reaching, for some elements with very weak lines, as high as 0.40 dex. For stars with S/N around 30, the contribution to the uncertainties is even higher, ranging typically from 0.10 dex to 0.30 dex, reaching 0.50 dex for some elements. Uncertainties are listed in Table 8.
4. Discussion
In order to study the distributions of elemental abundances for as many known CEMP stars as possible, an extensive search for abundances available in the literature has been performed. Elemental abundances for C, N, O, Na, Mg, Al, Si, Ca, Sc, Ti, V, Cr, Mn, Co, Ni, Zn, Sr, Y, Zr, Ba, La, Ce, Pr, Nd, Sm, Eu, Dy, and Pb (see Tables B.1 to B.4) are shown in the figures, together with abundances for our sample stars. The following criteria were applied to the literature data:
-
only data with resolving power R > 30 000 were used;
-
if two works belong essentially to the same group of scientists, the more recent value was adopted;
-
the average abundance was taken for the same star studied by different groups;
-
an upper limit was used only when there was no other value available.
One difficulty in combining data from the literature is that we no longer have a homogeneous abundance analysis, since different authors employ different procedures which could involve different line lists, atomic data for the lines used, adopted solar abundances, model atmospheres, and spectrum synthesis codes. All of these could contribute to an increase in the scatter in the patterns of observed abundances.
Eight stars from our observational program are in common with other works from the literature meeting the criteria above, as shown in Table 10. However, among those, only four had an Eu abundance determined elsewhere. For the others, Eu abundances were determined here for the first time. We have chosen not to average our measurements with others from the literature.
Stars with anomalously high abundances of O, Na, Mg, Al, or Si compared with Ca. For elements other than Ca, there are many values around or above [X/Fe] = +1.4.
4.1. C-rich stars: selection and classification
Carbon abundances for the 21 stars for which we have analysed C (Tables 8 and 9) are in the range +0.25 ≤ [C/Fe] ≤ +2.76. Of these, only three (BS 16033-081, BS 16090-048, and CS 22174-007) have [C/Fe] < +1.0, falling below the formal threshold for classification as a CEMP star (the usual definition for CEMP objects is [C/Fe] > +1.0; Beers & Christlieb 2005), although even two of these have [C/Fe] > +0.6, i.e. four times the solar ratio. In addition, the star CS 22171-009 has an upper limit of [C/Fe] < +1.03, so it may not be C-rich.
At face value, this suggests a further 14% misclassification (false positives) in the CEMP-star selection, or overall a ~70% success rate in identifying genuine CEMP objects. However, according to Aoki et al. (2007), some stars with [C/Fe] < +1.0 could still be CEMP stars, depending on their evolutionary stage, since the surface carbon abundance is expected to decrease after first dredge-up. Following their criteria, CS 30322-023 was classified by them as CEMP star, although it has [C/Fe] = +0.56. This is one of the stars from the literature represented by open triangles in Fig. 1. Other stars from the literature with low [C/Fe] that could still be considered CEMP stars are shown in Fig. 1: CS 22885-096 with [C/Fe] = +0.60 (cross, Norris et al. 2001), CS 30314-067 with [C/Fe] = +0.50 (cross, Aoki et al. 2002a), BS 17435-532 with [C/Fe] = +0.68 (filled square, Roederer et al. 2008). Applying the Aoki et al. criteria for stars of this work, BS 16033-081 with [C/Fe] = +0.77 also can be considered C-rich. Consequently, 18 among 21 stars of our sample are C-rich.
Large over-abundances of C and N in CEMP stars are usually explained by one of three mechanisms: mass transfer from a companion AGB star in a binary system (environmental); self-enrichment of the star in these elements (internal); or from the star having been born from a reviously-enriched cloud (congenital). Mechanisms to produce such large amounts of C and N in population III stars have been studied by, e.g., Fujimoto et al. (2000) and Siess et al. (2002), who claim that if mixing is efficient during the He-flash in the core when the star reaches the tip of the red-giant branch, C and N abundances can be significantly enhanced. However, that mechanism cannot be the origin of internal C and N enrichment in stars that have not reached this evolutionary stage, as can be seen from log g in Table B.1. For example, if the evolutionary stage of the very C- and N-rich star HE 1327-2326 is a dwarf or subgiant (present evidence suggests a subgiant classification; Korn et al. 2009), this mechanism cannot be applied, and the source of these elements must be extrinsic (environmental or congenital). Very massive stars (e.g., Wolf-Rayet stars) undergo significant mass loss during the red supergiant stage, releasing C and N to the interstellar medium. Hirschi (2007) claim that the CNO abundances of HE 1327-2326 can be reproduced by the winds of their rotating massive-star models. Umeda & Nomoto (2003) have simulated the supernova explosion of population III progenitors from 20 to 130 M⊙ and calculated the expected nucleosynthesis yields. In their 25 M⊙ model, CNO are produced during the pre-supernovae phase, in He shell burning, and although N is underproduced in this stage, it could have already been produced through the C-N cycle, and brought up to the surface during the first dredge-up stage. In this model, only a small amount of the heavier elements such as Mg, Ca, and the iron-peak elements are produced. Umeda & Nomoto claim that the elemental abundances for this model are in good agreement with the abundances of HE 0107-5240 by Christlieb et al. (2002, 2004), characterized by very large [C/Fe] and [N/Fe] ratios, while the abundances of elements heavier than Mg are normal.
Because of the relation between the r-process and massive star evolution (Truran 1981; Woosley & Weaver 1995), the expectation is that there might be evidence of element production from the r-process in the early Galaxy. In contrast, due to the secondary nature of the s-process, the naive expectation is that evidence of this source in metal-deficient stars should be scarce (Truran 1981; Travaglio et al. 1999). However, many CEMP stars have been found to exhibit clear s-process signatures (Norris et al. 1997). Given that Ba and Eu are significant representatives of the s- and r-processes in Solar System material, CEMP-star classifications emerged to reflect their neutron-capture element compositions. Beers & Christlieb (2005) defined subclasses of CEMP stars as follows:
CEMP-r: [Eu/Fe] > +1.0
CEMP-s: [Ba/Fe] > +1.0 and [Ba/Eu] > +0.5
CEMP-r/s: 0 < [Ba/Eu] < +0.5
CEMP-no: [Ba/Fe] < 0.
Aoki et al. (2002b) obtained large over-abundances of C, N, Mg and Si from their analysis of CS 29498-043, and suggested a new class of CEMP stars – CEMP-α.
The [Ba/Eu] ratio for the stars from the literature was determined (see Table B.1). Then, following the Beers & Christlieb definition, we found that 19 stars in the literature sample are CEMP-s, 2 are CEMP-r, 15 are CEMP-r/s, and 15 might be CEMP-no, although among the latter only one has had its Eu abundance determined, 7 have only an upper limit, and 7 have no Eu abundance estimated; such stars are represented by different symbols in Figs. 1−6, and their stellar classifications are indicated in Table B.1. Five stars among the 109 stars cannot be classified yet, since they have no published Ba or Eu abundance.
4.2. The α- and iron-peak elements
Figure 1 shows that the runs of [X/Fe] vs. [Fe/H] for most of the CEMP stars follow the canonical trend of metal-poor stars for O, Na, Mg, Al, Si, and Ca (Tsangarides 2005 did not compute abundances for Na, nor for V, Mn, Co, or Ni). The Mg abundance for the CEMP stars in Fig. 1 remains around [Mg/Fe] = +0.5, according to the canonical α-element behaviour, except for six stars with [Fe/H] < −2.40, for which very high Mg abundances are found, [Mg/Fe] > +1.4 (see Table 11): CS 22949-037, CS 29498-043, CS 29528-028, HE 1447+0102, HE 1327-2326, and HE 1012-1540. These six stars are outlined in Fig. 1 by large open squares, where they are seen to also have [Na/Fe] ≳ +1.2. In addition, most of the Mg-rich stars also have high [Al/Fe] ratios (Fig. 1), so the CEMP-α class would appear to be enriched in a wider set of elements including Na, Mg and Al, implying that a “CEMP-light” classification might be more appropriate than CEMP-α. In fact, both of these suggested sub-classes are also CEMP-no stars, so the nomenclature should be revisted.
The stars CS 22942-019, CS 29497-034, SDSS 1707+58, CS 22958-042, shown in Table 11, also have [Na/Fe] ≥ +1.4, although their [Mg/Fe] ranges from +0.3 to +1.1. The star with a high Na abundance represented by a filled triangle in Fig. 1 without a big open square surrounding it is SDSS 1707+58, for which Aoki et al. (2008) determined [Na/Fe] = +2.71 and [Mg/Fe] = +1.13. One star of the present sample, BS 15621-047, also has a high Na abundance, with [Na/Fe] = +1.35 and [Mg/Fe] = +0.85 (see Table 8).
As seen in Table 11, some CEMP stars exhibit large over-abundances of the lighter elements N, O, Na, Mg, and Si, in particular among the lowest metallicity stars (Aoki et al. 2007). This table suggests that all CEMP stars with high [Mg/Fe] and [Na/Fe] are also oxygen-rich, with [O/Fe] ≳ +1.0. Unfortunately, some of these stars have no oxygen abundance available in the literature to confirm this point. It is worth noting that other stars in Table 11, CS 29497-030, CS 29528-041, CS 31080-095, and HE 0557-4840 are O-rich, but are not Na- or Mg-rich. Three of the stars in Table 11 with high Mg abundances have also the highest Si abundances, with [Si/Fe] ranging from +0.8 to +1.1. However, the last two stars, CS 30314-067 and CS 29502-092, have [Si/Fe] in this range, but their Mg, Na and O abundances are low. In contrast to O and Na, C and N seem to have no correlation with the high over-abundance of Mg. Figure 5c makes the pattern of [Mg/Fe] vs. [C/Fe] clearer, where one can see that stars with the highest Mg abundance are spread over the range +1.0 ≲ [C/Fe] ≲ +3.8.
 |
Fig. 1 [X/Fe] for CEMP stars of this work and from the literature. Symbols – starred circles: this work; filled squares: 0 < [Ba/Eu] ≲ 0.5 (CEMP-r/s); open squares: [Ba/Eu] > 0.5 (CEMP-s); crosses: [Ba/Fe] < 0 (CEMP-no); filled triangles: [Ba/Fe] > +1 but there is no available Eu abundance (s or r/s?); open triangles: 0 < [Ba/Fe] < +1 but there is no available Eu abundance (r?); filled circles: [Ba/Eu] < 0 (r); dashes: upper limit for Ba and Eu; big open squares involving four crosses, two filled triangles and one dash indicate high over-abundance of Mg, [Mg/Fe] > +1.4. The dotted lines indicate where [X/Fe] = 1. See text for an explanations concering stars with [C/Fe] < +1. |
 |
Fig. 2 [X/Fe] for CEMP stars of this work and from the literature. Symbols are the same as in Fig. 1. |
The [Ca/Fe] ratios for all of these stars are not as high as [O/Fe], [Na/Fe], and [Mg/Fe], and the Ca abundance has no relationship with a high Mg abundance. Figure 1 shows that [Ca/Fe] vs. [Fe/H] follows a flat pattern, and Fig. 2 shows that the same occurs for the abundances of elements lighter than Zn for different classes of CEMP stars, with only a few exceptions. HE 1327-2326 has only upper limits for V, Zn, Mn, and Co. For other elements, the CEMP star abundances follow the general trend formed by other stars. Table 11 also indicates that there is no segregation among stars with high over-abundance of the α-elements according to the class of CEMP star, since one can find several classes of CEMP stars with this characteristic.
Large over-abundances relative to iron for these intermediate-mass elements cannot be explained by (environmental) mass transfer from a companion AGB star. Turatto et al. (1998) and Zampieri et al. (2003) used the fallback supposition to explain the observed low Fe abundance for SN 1997D and SN 1999br, respectively, and claim that similar SNe may be the origin of the abundance pattern of stars with high abundances of Na, Mg, or Si relative to iron-peak elements. These supernovae, characterized by relatively small Fe ejection, are massive, but less energetic, and very underluminous (Woosley & Weaver 1995), the so-called “faint supernovae”. In this view, extremely metal-poor stars without enhancements of C and N correspond to the abundance patterns from energetic supernovae (Umeda & Nomoto 2003). CEMP stars with large over-abundances of intermediate-mass elements may have similarly formed, in a congenital scenario, from gas enriched by SN experiencing partial fallback of heavier material onto the collapsed remnant. In this case, Ca, Fe, as well as other Fe-group elements such as Cr, Mn, Co, and Ni produced in the deep interior, would fall back onto the nascent neutron star. In contrast, lighter elements synthesized in the outer layers of the star would be ejected and be excluded from any fallback. As a result, lighter elements are significantly enhanced with respect to Fe-group elements. Aoki et al. (2004) and Cohen et al. (2008) claim that the observed elemental abundance patterns of CS 29498-043 and CS 22949-037, respectively, exhibit characteristics that fit this explanation. The high redshift (z = 2.3), extremely metal-poor Damped Lyman-α (DLA) system recently reported by Cooke et al. (2011, [Fe/H] ~ −3.0 exhibits an enhanced carbon-to-iron ratio ([C/Fe] = +1.5) and other elemental abundance signatures that Kobayashi et al. (2011) associate with production by faint supernovae which experienced mixing and fallback.
Another possible progenitor for this class is massive, rapidly rotating, mega metal-poor ([Fe/H] < −6.0) stars, which models suggest have greatly enhanced abundances of CNO due to distinctive internal burning and mixing episodes, followed by strong mass loss (Hirschi et al. 2006; Meynet et al. 2006, 2010a,b). It is also of interest that Matsuoka et al. (2011) have reported evidence for strong carbon production in the early universe, based on their analysis of the optical spectrum of the most distant known radio galaxy, TN J0924-2201, with z = 5.19. There is the exciting possibility that the same or similar progenitors, likely associated with the very first generations of stars, are responsible for the distinctive abundance patterns in both the CEMP-no stars and the high-redshift gas and galaxies.
4.3. Neutron-capture elements
4.3.1. Abundances
The behaviour of the neutron-capture-element abundances shown in Figs. 3 and 4 is remarkably different from the behaviour seen in Figs. 1 and 2 for the lighter elements. While in Figs. 1 and 2 all symbols are mixed together, the scatter is much higher in Figs. 3 and 4. However, if one considers only data with the same symbol (excluding data of this work), the scatter is lower than when considering all data. Given that the different symbols are defined according to Ba and Eu abundances, this separation is most likely a consequence of the contribution of the r- and s-processes, which increase the abundances of neutron-capture elements in different degrees for each class of star. It is worth recalling that the difference among the procedures adopted by different authors might increase the scatter observed in the reported abundance patterns.
 |
Fig. 3 [X/Fe] for CEMP stars of this work and from the literature. Symbols are the same as in Fig. 1. |
 |
Fig. 4 [X/Fe] for CEMP stars of this work and from the literature. Symbols are the same as in Fig. 1. |
The pattern of abundances of the neutron-capture elements for the stars with large over-abundances of Mg (large open squares involving other symbols) is not as clear as for the lighter elements. The stars CS 22949-037, CS 29498-043, and HE 1012-1540 have [Ba/Fe] < 0, whereas CS 29528-028, HE 1447+0102 and HE 1327-2326 have very high barium abundances, with [Ba/Fe] = +3.27 (+2.49 in this work6), +2.70, and +1.40, respectively. Three of these stars, CS 22949-037, HE 1012-1540, and HE 1327-2326 have only upper limits for [Eu/Fe] published (<+0.57, <+1.62, <+4.64, respectively), and the three remaining have no published Eu abundance. The lack of accurate abundances for [Eu/Fe] prevents a more meaningful analysis of the possible relationship between the α-elements and the r-process elements.
Figure 5 exhibits an increasing trend for [Ba/Fe] vs. [C/Fe]. While not all C-enhanced stars are Ba enhanced, those that are lie on or below the envelope at [Ba/C] = 0; a fiducial line with [Ba/C] = 0 is drawn to guide the eye. This behaviour of Ba – a spread in [Ba/C] with an upper bound at constant [Ba/C] (where C is presumably 12C) – might be understood as the consequence of the primary production of 12C in He burning and up to but not exceeding an equilibrium amount of 13C (the latter in hydrogen-ingestion via 12C(p, γ)13N(β+νe)13C), and the production of Ba proportionately to 13C through the 13C(α, n)16O source, in a TP-AGB star whose wind is then transferred to its lower-mass companion forming the CEMP-s and CEMP-r/s binary stars.
As noted by Tsangarides (2005), [Eu/Fe] vs. [C/Fe] exhibits a similar increasing trend (though many stars are missing in this panel compared to the upper one for Ba because they have no Eu abundance available). The upper envelope to [Eu/C] may be interpreted in the same way as the maximal s-process Eu production, alongside Ba, for a given level of 12C. There are also many stars known with r-process enhancements but no C-enhancement; the origin of genuine r-process enhancements might well be independent of the process responsible for carbon and nitrogen excesses (e.g., Aoki et al. 2002a; Hansen et al. 2011).
4.3.2. An upper limit on [C/H]
In order for this scenario to have merit, we require primary production of C in TP-AGB stars, and require this signature to remain even after transfer onto a lower mass companion in an environmental CEMP-star production event. Such evidence already exists, as it has been noted already by Ryan (2003) that the [C/Fe] vs. [Fe/H] relation of CEMP stars likewise exhibits an upper envelope consistent with [C/H] = const., close to zero. This implies that TP-AGB stars may produce up to, but not in excess of, this level of C irrespective of metallicity across the full metallicity range of halo stars. Precisely this behaviour is seen in the yields of TP-AGB models of Karakas (2002). Specifically, Karakas’ carbon yields show that the ejected carbon mass, while strongly dependent on progenitor mass – minimal for stars below 1.5 M⊙ and peaking for stars around 3 to 4 M⊙ – are almost independent of metallicity. Karakas presents calculations for Z = 0.020, 0.008, 0.004, i.e. over a range of a factor of five, and shows that while the progenitor mass at which the ejected carbon mass peaks does shift slightly – but most importantly – the level does not change markedly; in other words ejected carbon is produced as a primary element independent of metallicity. Although these AGB models have a higher metallicity than genuine halo stars, the lack of metallicity sensitivity over this broad range makes it plausible that the carbon is produced in a primary fashion even as metallicity reduces further. In the environmental enrichment scenarios for the production of CEMP stars, the progenitor-mass dependence of ejected carbon mass and the various accretion geometries will ensure that recipient stars achieve a range of accreted carbon masses, and hence a range of [C/Fe] values, but the metallicity independence of the ejected carbon mass, and the presumed metallicity independence of the accretion mass, will ensure there is no metallicity dependence of [C/H], thus providing an explanation for the upper envelope for [C/H] seen in the population of CEMP stars. A prediction coming from this interpretation, which may be testable given larger samples in the future, is that CEMP stars formed by other, non-AGB, mechanisms need not be restricted by this limit.
 |
Fig. 5 [Mg, Eu, Ba/Fe] vs. [C/Fe] for CEMP stars of this work and from the literature. Fiducial lines [Ba, Eu, Mg/C] = 0 are drawn for convenience. Symbols are the same as in Fig. 1. The arrows toward left indicate upper limit for [C/Fe]. |
 |
Fig. 6 CEMP stars from the literature and this work with the same symbols as in Fig. 1. a) [Ba/Eu] vs. [Fe/H]. The dotted lines are the limits of the range for CEMP-r/s and the dashed line is the limit for the r-process only, [Ba/Eu] = −0.7. The arrows up and down indicate upper limit for [Eu/Fe] and [Ba/Fe], respectively. b) [Ba/Fe] vs. [Eu/Fe]. Dashed line indicates [Ba/Eu] = −0.7, and dotted lines indicate where [Ba/Fe] = 0 and [Eu/Fe] = 0; CEMP-s and CEMP-r/s share instinctively the limits [Ba/Fe] > 0 and [Ba/Fe] = [Eu/Fe], whereas CEMP-no are inside the limits [Ba/Fe] and [Eu/Fe] < 0 and CEMP-r inside [Eu/Fe] > 0 and [Ba/Fe] = [Eu/Fe]. The arrows toward left and down indicate upper limit for [Eu/Fe] and [Ba/Fe], respectively. |
 |
Fig. 7 The behaviour of Mg, Ba and Eu abundances for CEMP stars of this work and from the literature. Symbols are the same as in Fig. 1. |
4.3.3. Classification of CEMP-s stars
Figures 6a and b show the relationship between Fe, Ba and Eu. Figure 6b indicates the conventional CEMP classification boundaries. CEMP stars exhibiting large over-abundances of the s-process elements, with [Ba/Fe] > +1 and [Ba/Eu] > +0.5, are CEMP-s, and are represented by the open squares in Figs. 1 to 4. The environmental scenario suggested for their neutron-capture element enrichment involves mass transfer in a binary system. The initially more massive star evolves first and enters the TP-AGB phase, where it convectively enriches its atmosphere with s-process products. After a phase of strong mass loss through a stellar wind, it becomes a white dwarf, and now the former secondary presents in its atmosphere vestiges of the nucleosynthesis of the previous TP-AGB star. Nineteen stars from the literature were found in our search to be in this class. Two stars of our sample (BS 16077-077 and CS 29512-073) might be CEMP-s (Fig. 6a). Although the Ba abundance of BS 16077-077 is not so high ([Ba/Fe] = +0.75), the low Eu abundance ([Eu/Fe] = −0.01) increases the ratio [Ba/Eu]. This star is close to the line [Eu/Fe] ~ 0 in panel (b).
4.3.4. Classification of CEMP-r and CEMP-no stars
The CEMP stars that exhibit [Ba/Eu] < 0 are referred to as CEMP-r. As an example, the mean values for the star CS 22892-052 (McWilliam et al. 1995; Norris et al. 1997; Sneden et al. 2003; Honda et al. 2004; Barklem et al. 2005) are: [Eu/Fe] = +1.54 and [Ba/Fe] = +0.96, resulting in [Ba/Eu] = −0.59 (see Tables B.3 and B.4). Cohen et al. (2006) reported a very high value of the Eu abundance for the star HE 1410-0004, so this star is likely the second CEMP-r star found in the literature. It is worth noting, however, that their high Eu abundance is only an upper limit ([Eu/Fe] < +2.40), and therefore, only a lower limit in [Ba/Eu] > −1.34, can be inferred. These two stars are represented by circles in the figures.
Results from Hansen et al. (2011) support the hypothesis that r-process enhancement is not coupled with the presence of a binary companion, and suggests that where it is found to occur, it must have originated in separate pollution events of the natal molecular clouds from which CEMP-r stars formed. It is worth noting that CS 22892-052 is included in the sample of r-process enhanced stars that received extensive radial-velocity monitoring in the work of Hansen et al. (2011). They report that this star appears not to be a binary, despite the earlier suggestion by Preston & Sneden (2001), indicating that its C content was not produced by a companion. Thus, membership in a binary system appears to be decoupled from details associated with these particular abundance variations.
The CEMP stars with [Ba/Fe] < 0 were called CEMP-no by Ryan et al. (2005). However, some of the stars in the literature with [Ba/Fe] < 0 might be CEMP-r, rather than CEMP-no, if [Eu/Fe] > +1. Since some of them have no Eu abundance available, they could not be classified accordingly.
Five stars of this work have [Ba/Eu] < 0, the region of CEMP-no and CEMP-r, where two of them are below the dashed line in Fig. 6a, which represents the production of Ba only through the r-process, [Ba/Eu] ~ −0.7 (Mashonkina & Gehren 2001). One of them (BS 16033-081), might be called CEMP-no, since its [Ba/Fe] < 0, whereas the other (BS 16929-005) might be CEMP-r, since [Ba/Fe] ~ 07 and [Eu/Fe] > +1. If no Eu abundance is given, one may classify this star as CEMP-no. Two stars with [Ba/Fe] ~ +0.35 (BS 15621-047, BS 16543-097) might be CEMP-r, since [Ba/Eu] < 0 for both and [Eu/Fe] ~ +1. The last star, CS 31070-073, has the highest value of [Eu/Fe], even higher than the ones from the literature referred to as CEMP-r (see filled circles in Fig. 6b). [Ba/Eu] is very low, even though [Eu/Fe] and [Ba/Fe] are high, suggesting that it might be CEMP-r/s.
4.3.5. Classification of CEMP-r/s stars
For CEMP stars with 0 < [Ba/Eu] ≲ +0.5, both r-process and s-process enhancements have been inferred (Hill et al. 2000; Wanajo et al. 2006). Fifteen CEMP stars corresponding to this description were found in the literature so far, and are referred to as CEMP-r/s (or variations). Cohen et al. (2003) was the first group to propose that the origin of CEMP-r/s stars includes two mass transfers – the first one would result in the enrichment of s-process (from an AGB member of a binary system), while the second would involve a so-called accretion-induced collapse (AIC), as proposed by Qian & Wasserburg (2003), at which time the r-process enrichment would occur. After those events, the survivor star would be observed as a CEMP-r/s star. Qian & Wasserburg (2001) commented on the possibility that stars like CS 31082-001, which is r-process rich (but not C-rich), has survived the SN II explosion of its companion and now has a compact companion, most likely a black hole.
Three stars in the present work have ratios in the range 0 < [Ba/Eu] < +0.5, the CEMP-r/s zone represented in Fig. 6b: CS 29503-010, CS 29526-110, and CS 29528-028. One of them, CS 29526-110, was similarly classified as CEMP-r/s by Aoki et al. (2002d), but the other two are being classified for the first time, since Aoki and collaborators did not determine their Eu abundances (see Table 10).
Ivans et al. (2005) have derived abundances for CS 29497-030, and compared their results to theoretical models of neutron-capture processes at low metallicity, both with and without pre-enrichment of the initial abundances. In the pre-enrichment in r-elements case, the heavy-element isotopes act as strong poisons for the neutron exposure, competing with Fe and decreasing s-process efficiency.
Ivans et al. (2005) claim that CS 29497-030 could be classified as CEMP-r/s, since their abundance ratios are best fitted by a pre-enrichment of r-process material out of which the binary system formed. However, Ivans et al. (2005) derived values 0.15 dex and 0.55 dex higher than Sivarani et al. (2004) for [Ba/Fe] and [Eu/Fe], respectively. The Sivarani et al. [Eu/Fe] is better fitted by the model without pre-enrichment in Fig. 2 of Ivans et al. Therefore, Sivarani et al. (2004) would classify as CEMP-s; the same situation pertains if the classification comes from the average of the two works, as shown in Table B.1.
Although the CEMP-r/s classification has been widely used, we suggest (following Tsangarides 2005) that it is a superfluous class, and that there is no physical distinction between CEMP-s and CEMP-r/s stars, other than the arbitrary choice of the [Ba/Eu] boundary. The r/s classification was motivated by a belief that the high [Eu/Fe] values and intermediate [Ba/Eu] values must signify Eu production by the r-process in a site distinct from the one where Ba was produced via the s-process. However, CEMP-s stars are able to produce quite high [Eu/Fe] values, easily up to +2.0 (see Table B.4). The reasonable conclusion is that Eu production, although r-process dominated in the Solar System, is readily achievable by the s-process alone. Three further arguments strengthen this view. First, if Eu production and Ba production in CEMP-r/s stars is genuinely decoupled into separate r- and s-processes, it is astonishing how remarkably tight the correlation between [Ba/Fe] and [Eu/Fe] for CEMP-s and CEMP-r/s stars appears in Fig. 6b. Two separate processes would naturally be expected to provide more diverse outcomes. Secondly, Fig. 5 shows that the upper envelope of [Eu/Fe] in CEMP stars closely corresponds to [Eu/C] = 0. That is, irrespective of the degree of the C over-abundance in CEMP stars, Eu production is coupled to that value, at least as an upper bound. The r-process, occurring presumably in the final stage of evolution of these stars’ progenitors, should not be expected to follow the C abundance so closely. Thirdly, we note that high Eu abundances are found in Pop. I Ba stars, where the r-process is not believed to be active at all (Allen & Barbuy 2006). For the CEMP stars, a more reasonable view (and certainly the view more consistent with Occam’s razor) is that only one process is responsible for the production of both Ba and Eu in lockstep with C, and that process is the s-process, not a tuned balance between s- and r-processes under widely different physical conditions and at different phases of stellar evolution.
4.3.6. Eu detections
Our search for data from the literature reveals that the nucleosynthetic record is seriously incomplete, particularly with respect to elements associated with the r-process. About 67% of CEMP stars have no measured Eu abundance (or only an upper limit); this makes the abundance pattern of many stars unclear. The lack of Eu abundances becomes clear in Fig. 7 through the open and filled triangles, which represent stars for which there is no published abundance for Eu. The missing crosses from one panel to another in Fig. 7 also illustrate the lack of Eu for CEMP stars with [Ba/Fe] < 0. For some stars, only an upper limit was published either for Eu and Ba; these stars are represented by dashes in Figs. 1 to 6. This work has provided Eu abundances for fifteen stars, only four of which had a previous determination (see Table 10). For two stars of our sample it was not possible to determine a Eu abundance, and for one, only an upper limit could be estimated. Masseron et al. (2010) compiled abundances from analyses of high-resolution spectra of metal-poor stars, including C-rich stars. However, their suggestions of classifications for CEMP stars was hampered due to the absence of Eu detection for many stars. The difficulty in determining Eu abundances resides in the fact that its lines in CEMP stars are very weak, so higher-quality spectra than have been obtained to date are required (which in turn require long exposure times on large telescopes). So, more research programs dedicated to the investigation of Eu in CEMP stars, using new high-resolution spectrographs on large telescopes, are needed to make further progress in understanding the nucleosynthetic processes that took place in the early Galaxy.
5. Conclusions
We have presented a detailed analysis of the elemental abundances for a sample of 18 CEMP stars, based on high-resolution spectroscopic data, and together with data from the literature, examined the behaviour of their abundance ratios. Some stars exhibit large over-abundances of O, Na, Mg, and Si: 3 stars are Si-rich; these 3 plus an additional 4 stars are Mg-rich; these 7 plus 4 additional stars are Na-rich. Ten stars, including some of these 11 Na-rich stars for which oxygen abundances were available, are O-rich. These results are in agreement with the fallback hypothesis (Turatto et al. 1998; Zampieri et al. 2003). However, stronger conclusions must await suitable data from which O abundances for all of these stars can be derived.
This work has shown that the lack of accurate Eu abundances has made the abundance pattern of many CEMP stars quite unclear. Once we have better available data, it will be possible to perform an accurate detailed analysis, allowing an improvement in our understanding of the astrophysical origins of the different classes of CEMP stars. Observing lines of Eu and other elements usually associated with the r-process would indicate the true extent of the r-process. Notwithstanding the relative paucity of Eu data, we contend on the basis of available C, Ba, and Eu abundances that the hybrid CEMP-r/s class is superfluous, and arises because of incomplete knowledge of Eu production by the s-process at low metallicity. As a result, stars labeled as CEMP-r/s have the same origin as CEMP-s stars. On the other hand, the presence of r-process elements CEMP-r stars may well be due to previous pollution of the molecular clouds from which they formed.
Online material
Colours and magnitudes of our program stars before dereddening.
Temperatures derived from photometric data by using the final metallicity found for each star.
Results for the stellar parameters, for the DMA (upper portion) and SAT (lower portion) subsamples.
Average of abundances for the DMA subsample of CEMP stars, and solar abundances used as reference, as well as their sources.
Average of abundances for the SAT subsample of CEMP stars.
Comparison between results from this work and from the literature.
Diference between the output value of the synthesis program (log Ap) and the output value with 1σ of diference in temperature (ΔT), log g (Δlg), metallicity (Δfeh), velocity of microturbulent (Δξ), observational (ΔObs), and macroturbulence Δmu.
Appendix C: Data from the literature
Abundances [X/Fe] of light elements for CEMP stars.
Abundances [X/Fe] of iron-peak elements for CEMP stars.
Abundances [X/Fe] of heavy elements for CEMP stars.
Abundances [X/Fe] of heavy elements for CEMP stars.
The origin of the large difference between the Ba abundance of this star obtained in this work and Aoki et al. (2007) might be the significant difference in atmospheric parameters (see Table 10) adopted by these works.
Honda et al. (2004) and Aoki et al. (2007) determined a very low value of [Ba/Fe] for BS 16929-005, as can be seen in Table 10.
Acknowledgments
D.M.A. acknowledges the University of Hertfordshire, where part of this work was developed. D.M.A. also acknowledges a CAPES post-doctoral fellowship No. BEX 3448/06-1, as well as FAPESP, for the post-doctoral fellowship No. 2008/01265-0, and CNPq, for the post-doctoral fellowship No. 150370/2012-1. We are gratefull to Fiorella Castelli for her prompt help concerning the codes ATLAS9, WIDTH9 and SYNTHE. T.C.B. acknowledges partial funding of this work from grants PHY 02-16783 and PHY 08-22648: Physics Frontier Center/Joint Institute for Nuclear Astrophysics (JINA), awarded by the US National Science Foundation. S.R. thanks the partial support from FAPESP, CNPq, and CAPES. We acknowledge the anonymous referee for help in improving the error analysis.
References
- Akerman, C. J., Carigi, L., Nissen, P. E., Pettini, M., & Asplund, M. 2004, A&A, 414, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen, D. M., & Barbuy, B. 2006, A&A, 454, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1995, A&A, 297, 197 [NASA ADS] [Google Scholar]
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1996a, A&A, 313, 873 [NASA ADS] [Google Scholar]
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1996b, A&AS, 117, 227 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1998, A&AS, 131, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1999, A&AS, 140, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aoki, W., Norris, J. E., Ryan, S. G., Beers, T. C., & Ando, H. 2000, ApJ, 536, L97 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aoki, W., Ryan, S. G., Norris, J. E., et al. 2001, ApJ, 561, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W., Norris, J. E., Ryan, S. G., Beers, T. C., & Ando, H. 2002a, ApJ, 567, 1166 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W., Norris, J. E., Ryan, S. G., Beers, T. C., & Ando, H. 2002b, ApJ, 576, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W., Norris, J. E., Ryan, S. G., Beers, T. C., & Ando, H. 2002c, PASJ, 54, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W., Ryan, S. G., Norris, J. E., et al. 2002d, ApJ, 580, 1149 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W., Ando, H., Honda, S., et al. 2002e, PASJ, 54, 427 [NASA ADS] [Google Scholar]
- Aoki, W., Norris, J. E., Ryan, S. G., et al. 2004, ApJ, 608, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W., Bisterzo, S., Gallino, R., et al. 2006a, ApJ, 650, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W., Frebel, A., Christlieb, N., et al. 2006b, ApJ, 639, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W., Beers, T. C., Christlieb, N., et al. 2007, ApJ, 655, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Aoki, W., Beers, T. C., Sivarani, T., et al. 2008, ApJ, 678, 1351 [NASA ADS] [CrossRef] [Google Scholar]
- Arlandini, C., Käppeler, F., & Wisshak, K. 1999, ApJ, 525, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Barbuy, B., Spite, M., Spite, F., et al. 2005, A&A, 429, 1031 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barklem, P. S., Christlieb, N., Beers, T. C., et al. 2005, A&A, 439, 129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beers, T. C., & Christlieb, N. 2005, ARA&A, 43, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T. C., Preston, G. W., & Shectman, S. A. 1985, AJ, 90, 2089 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T. C., Preston, G. W., & Shectman, S. A. 1992, AJ, 103, 1987 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T. C., Bestman, W., & Wilhelm, R. 1994, AJ, 108, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T. C., Sivarani, T., Marsteller, B., et al. 2007, AJ, 133, 1193 [NASA ADS] [CrossRef] [Google Scholar]
- Behara, N. T., Bonifacio, P., Ludwig, H.-G., et al. 2010, A&A, 513, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, R. A., Eriksson, K., Gustafsson, B., & Nordlund, A. 1976, A&AS, 23, 37 [NASA ADS] [Google Scholar]
- Bergstrom, H., Biémont, E., Lundberg, H., & Persson, A. 1988, A&A, 192, 337 [Google Scholar]
- Bessell, M. S. 1979, PASP, 91, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Bessell, M. S., Castelli, F., & Plez, B. 1998, A&A, 333, 231 [NASA ADS] [Google Scholar]
- Biehl, D. 1976, Ph.D. Thesis, Kiel University [Google Scholar]
- Bielski, A. 1975, JQSRT, 15, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Biémont, E., & Godefroid, M. 1980, A&A, 84, 361 [NASA ADS] [Google Scholar]
- Biémont, E., & Lowe, R. M. 1993, A&A, 273, 665 [NASA ADS] [Google Scholar]
- Biémont, E., Grevesse, N., Hannaford, P., & Lowe, R. M. 1981, ApJ, 248, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Biémont, E., Grevesse, N., Hannaford, P., & Lowe, R. M. 1989, A&A, 222, 307 [NASA ADS] [Google Scholar]
- Bisterzo, S., Gallino, R., Straniero, O., Cristallo, S., & Käppeler, F. 2010, MNRAS, 404, 1529 [NASA ADS] [Google Scholar]
- Caffau, E., Bonifacio, P., François, P., et al. 2011, nature, 477, 67 [Google Scholar]
- Carollo, D., Beers, T. C., Bovy, J., et al. 2012, ApJ, 744, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Carpenter, J. M. 2001, AJ, 121, 2851 [NASA ADS] [CrossRef] [Google Scholar]
- Castelli, F. 2004, Mem. S. A. It, 1, 1 [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2004 [arXiv:astro-ph/0405087v1] [Google Scholar]
- Castelli, F., Gratton, R. G., & Kurucz, R. L. 1997, A&A, 318, 841 [NASA ADS] [Google Scholar]
- Christlieb, N., Bessell, M. S., Beers, T. C., et al. 2002, Nature, 419, 904 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Christlieb, N., Gustafsson, B., Korn, A. J., et al. 2004, ApJ, 603, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Christlieb, N., Schörck, T., Frebel, A., et al. 2008, A&A, 484, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cohen, J. G., Christlieb, N., Qian, Y.-Z., & Wasserburg, G. J. 2003, ApJ, 588, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., McWilliam, A., Shectman, S., et al. 2006, AJ, 132, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., Christlieb, N., McWilliam, A., et al. 2008, AJ, 672, 320 [Google Scholar]
- Cooke, R., Pettini, M., Steidel, C. C., Rudie, G. C., & Nissen, P. E. 2011, MNRAS, 417, 1534 [NASA ADS] [CrossRef] [Google Scholar]
- Corliss, C. H., & Bozman, W. R. 1962, Experimental Transition Probabilities for Spectral Lines of Seventy Elements, NBS Monograph 32 (Washington: GPO) [Google Scholar]
- Cottrell, P. L., & Norris, J. 1978, ApJ, 221, 893 [NASA ADS] [CrossRef] [Google Scholar]
- Cram, L. 1999, Transactions of the International Astronomical Union, Vol. XXIIIB, ed. J. Andersen, 141 [Google Scholar]
- Demarque, P., Woo, J.-H., Kim, Y., & Yi, S. K. 2004, ApJS, 155, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Depagne, E., Hill, V., Spite, M., et al. 2002, A&A, 390, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frebel, A., Aoki, W., Christlieb, N., et al. 2005, Nature, 434, 871 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Frebel, A., Norris, J. E., Aoki, W., et al. 2007, ApJ, 658, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Frebel, A., Collet, R., Eriksson, K., Christlieb, N., & Aoki, W. 2008, ApJ, 684, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhr, J. R., & Wiese, W. L. 2006, J. Phys. Chem. Ref. D., 35, 4 [Google Scholar]
- Fuhr, J. R., Martin, G. A., & Wiese, W. L. 1988, J. Phys. Chem. Ref. Data, 17, Supplement 4 (Washington: US Government Printing Office) [Google Scholar]
- Fuhrmann, K., Axer, M., & Gehren, T. 1995, A&A, 301, 492 [NASA ADS] [Google Scholar]
- Fujimoto, M. Y., Ikeda, Y., & Iben, I. Jr. 2000, ApJ, 529, L25 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Giridhar, S., Lambert, D. L., Gonzalez, G., & Pandey, G. 2001, PASP, 113, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Goswami, A., & Aoki, W. 2010, MNRAS, 404, 253 [NASA ADS] [Google Scholar]
- Goswami, A., Aoki, W., Beers, T. C., et al. 2006, MNRAS, 372, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R. G., & Sneden, C. 1994, A&A, 287, 927 [NASA ADS] [Google Scholar]
- Green, E. M., Demarque, P., & King, C. R. 1987, in The revised Yale isochrones and luminosity functions (New Haven: Yale Observatory) [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Hakkila, J., Myers, J. M., Stidham, B. J., & Hartmann, D. H. 1997, AJ, 114, 2043 [NASA ADS] [CrossRef] [Google Scholar]
- Hannaford, P., & Lowe, R. M. 1983, Opt. Eng., 22, 532 [CrossRef] [Google Scholar]
- Hannaford, P., Lowe, R. M., Grevesse, N., Biémont, E., & Whaling, W. 1982, ApJ, 261, 736 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, T., Andersen, J., Nordström, B., Buchave, L. A., & Beers, T. C. 2011, ApJ, 743, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Hartog, E. A. D., Lawler, J. E., Sneden, C., & Cowan, J. J. 2003, ApJS, 148, 543 [Google Scholar]
- Herwig, F. 2005, ARA&A, 43, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, V., Barbuy, B., Spite, M., et al. 2000, A&A, 353, 557 [NASA ADS] [Google Scholar]
- Hirschi, R. 2007, A&A, 461, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirschi, R., et al. 2006, RvMA, 19, 101 [Google Scholar]
- Honda, S., Aoki, W., Kajino, T., et al. 2004, ApJ, 607, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Ito, H., Aoki, W., Honda, S., & Beers, T. C. 2009, ApJ, 698, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Ivans, I. I., Sneden, C., Gallino, R., Cowan, J. J., & Preston, G. W. 2005, ApJ, 627, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A. 2002, ApJS, 139, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., & Bolte, M. 2002, ApJ, 579, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., & Bolte, M. 2004, ApJ, 605, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Jonsell, K., Barklem, P. S., Gustafsson, B., et al. 2006, A&A, 451, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karakas, A. I. 2002, Ph.D. Thesis, Monash University [Google Scholar]
- Kim, Y., Demarque, P., Yi, S. K., & Alexander, D. R. 2002, ApJS, 143, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Kipper, T., & Jorgensen, U. G. 1994, A&A, 290, 148 [NASA ADS] [Google Scholar]
- Kobayashi, C., Tominaga, N., & Nomoto, K. 2011, ApJ, 730, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Korn, A. J., Richard, O., Mashonkina, L., et al. 2009, ApJ, 698, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Kupka, F., Piskunov, N. E., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Kupka, F., Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., & Weiss, W. W. 2000, Balt. Astron., 9, 590 [NASA ADS] [Google Scholar]
- Kurucz, R. L. 1992, IAUS, 149, 225 [Google Scholar]
- Kurucz, R. L. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km s-1 grid, Kurucz CD-ROM No. 13 [Google Scholar]
- Kurucz, R. L., & Furenlid, I. 1979, SAO Special Report 387 Sample Spectral Atlas for Sirius [Google Scholar]
- Kurucz, R. L., & Peytremann, E. 1975, SAO Special Report 362 (Cambridge: Smithsonian Institution) [Google Scholar]
- Kurucz, R. L., Furenlid, I., & Brault, J. 1984, Solar flux atlas from 296 to 1300 nm, National Solar Observatory Atlas, Sunspot (New Mexico: National Solar Observatory) [Google Scholar]
- Kusz, J. 1992, A&AS, 92, 517 [NASA ADS] [Google Scholar]
- Laird, J. B., Carney, B. W., Rupen, M. P., & Latham, D. W. 1988, AJ, 96, 1908 [NASA ADS] [CrossRef] [Google Scholar]
- Lawler, J. E., Bonvallet, G., & Sneden, C. 2001a, ApJ, 556, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Lawler, J. E., Wickliffe, M. E., & Hartog, A. D. 2001b, ApJ, 563, 1075 [CrossRef] [Google Scholar]
- Lejeune, T., Cuisinier, F., & Buser, R. 1998, A&AS, 130, 65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Lucatello, S., Gratton, R., Cohen, J. G., et al. 2003, AJ, 125, 875 [NASA ADS] [CrossRef] [Google Scholar]
- Lucatello, S., Tsangarides, S., Gratton, R. G., et al. 2005, ApJ, 625, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Lucatello, S., Beers, T. C., Christlieb, N., et al. 2006, ApJ, 652, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Maier, R. S., & Whaling, W. 1977, JQSRT, 18, 501 [Google Scholar]
- Marsteller, B., Beers, T. C., Thirupathi, S., et al. 2009, AJ, 138, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, G. A., Fuhr, J. R., & Weise, W. L. 1988, J. Phys. Chem. Ref. D, 17, 3 [Google Scholar]
- Martin, W. C., Fuhr, J. R., Kelleher, D. E., et al. 2002, NIST Atomic Database, version 2.0, National Institute of Standards and Technology, Gaithersburg, MD, http://physics.nist.gov/asd [Google Scholar]
- Mashonkina, L., & Gehren, T. 2001, A&A, 376, 232 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masseron, T., Johnson, J. A., Plez, B., et al. 2010, A&A, 509, 93 [Google Scholar]
- Matsuoka, K., Nagao, T., Maiolino, R., Marconi, A., & Taniguchi, Y. 2011, A&A, 532, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McWilliam, A. 1998, AJ, 115, 1640 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A., Preston, G. W., Sneden, C., & Searle, L. 1995, AJ, 109, 2757 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., Ekström, S., & Maeder, A. 2006, A&A, 447, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., Hirschi, R., Ekstrom, S., et al. 2010a, IAUS, 265, 98 [NASA ADS] [Google Scholar]
- Meynet, G., Hirschi, R., Ekstrom, S., et al. 2010b, A&A, 521, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Norris, J. E., Ryan, S. G., & Beers, T. C. 1997, ApJ, 488, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. E., Ryan, S. G., & Beers, T. C. 2001, ApJ, 561, 1034 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. E., Ryan, S. G., Beers, T. C., Aoki, W., & Ando, H. 2002, ApJ, 569, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, J. E., Christlieb, N., Korn, A. J., et al. 2007, ApJ, 670, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Palmeri, P., Quinet, P., Wyart, J. F., & Biémont, E. 2000, Physica Scripta, 61, 323 [Google Scholar]
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [NASA ADS] [Google Scholar]
- Plez, B., & Cohen, J. G. 2005, A&A, 434, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Preston, G. W., & Sneden, C. 2001, AJ, 122, 1545 [NASA ADS] [CrossRef] [Google Scholar]
- Prochaska, J. X., Naumov, S. O., Carney, B. W., McWilliam, A., & Wolfe, A. M. 2000, AJ, 120, 2513 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, Y.-Z., & Wasserburg, G. J. 2001, ApJ, 552, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, Y.-Z., & Wasserburg, G. J. 2003, ApJ, 588, 1099 [NASA ADS] [CrossRef] [Google Scholar]
- Roederer, I. U., Frebel, A., Shetrone, M. D., et al. 2008, ApJ, 679, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Rossi, S., Beers, T. C., & Sneden, C. 1999, ASPC, 165, 264 [Google Scholar]
- Rutten, R. J. 1978, Sol. Phys., 56, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Ryabchikova, T. A., Piskunov, N. E., Kupka, F., & Weiss, W. W. 1997, Balt. Astron., 6, 244 [NASA ADS] [Google Scholar]
- Ryan, S. G. 2003, ASP Conf. Ser., 304, 128 [NASA ADS] [Google Scholar]
- Ryan, S. G., & Lambert, D. L. 1995, AJ, 109, 2068 [NASA ADS] [CrossRef] [Google Scholar]
- Ryan, S. G., Aoki, W., Norris, J. E., & Beers, T. C. 2005, ApJ, 635, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L., Livio, M., & Lattanzio, J. 2002, ApJ, 570, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Sivarani, T., Bonifacio, P., Molaro, P., et al. 2004, A&A, 413, 1073 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sivarani, T., Beers, T. C., Bonifacio, P., et al. 2006, A&A, 459, 125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sneden, C., McWilliam, A., Preston, G. W., et al. 1996, ApJ, 467, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C., Cowan, J. J., Lawler, J. E., et al. 2003, ApJ, 591, 936 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Schneider, S. E., Stiening, R., et al. 1997, ASSL, 210, 25 [NASA ADS] [Google Scholar]
- Thévenin, F. 1989, A&AS, 77, 137 [NASA ADS] [Google Scholar]
- Thompson, I. B., Ivans, I. I., Bisterzo, S., et al. 2008, ApJ, 677, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Tomkin, J., Lemke, M., Lambert, D. L., & Sneden, C. 1992, AJ, 14, 1568 [NASA ADS] [CrossRef] [Google Scholar]
- Travaglio, C., Galli, D., Gallino, R., et al. 1999, ApJ, 521, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Truran, J. W. 1981, A&A, 97, 391 [NASA ADS] [Google Scholar]
- Tsangarides, S. A. 2005, PhD. Thesis, The Open University-UK [Google Scholar]
- Turatto, M., Mazzali, P. A., Young, T. R., et al. 1998, ApJ, 498, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Umeda, H., & Nomoto, K. 2003, Nature, 422, 871 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Van Eck, S., Goriely, S., Jorissen, A., & Plez, B. 2003, A&A, 404, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wanajo, S., Nomoto, K., Iwamoto, N., Ishimaru, Y., & Beers, T. C. 2006, ApJ, 636, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Yi, S., Demarque, P., Kim, Y.-C., et al. 2001, ApJS, 136, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Yi, S. K., Kim, Y.-C., & Demarque, P. 2003, ApJS, 144, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Zampieri, L., Pastorello, A., Turatto, M., et al. 2003, MNRAS, 338, 711 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Uncertainty calculations
Uncertainties on abundances were evaluated by consideration of the degree to which a variation of 1σ in the atmospheric parameters (including macroturbulence for the SAT subsample) and the S/N (only for the DMA subsample) affects the output value of the synthesis routine. Table A.1 shows the systematic effects that estimated errors in the adopted atmospheric parameters have on abundances (log ϵ(X)).
For the DMA subsample, the star BS 16543-097 was used as a reference to calculate uncertainties, since it has a similar temperature as many of the other stars. One line of each element was chosen to calculate the effects that errors on atmospheric parameters have on our derived abundances; these were then extended to all other lines of the same element.
Extending the results on uncertainties computed for one line to the other lines of the same element is not actually the best procedure. Different lines (i.e., lines with different EPs, strengths, etc.) may have different dependences on the stellar parameters. In fact, the ideal procedure would be to compute all variations for all lines. However, it is impractical using spectrum synthesis, due to the very long time that it would take, since each variation requires the complete “ritual” of the full spectrum synthesis. However, if one chooses a suitable line as a proxy for the remaining lines, it is valid to estimate the variations due the atmospheric and experimental parameters for this line, and to assume that this variation is representative for all other lines of the same element. The profile of this line must to be as well-defined as possible – not too strong, not too weak, in order to make the line representative.
To determine the uncertainties on abundances, we followed Johnson (2002); a portion of this procedure and formulae are rewritten below.
Then, the variance in log ϵ(X) can be written as ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{errlogEp} && \sigma_{\log\epsilon}^2 = \sigma_{\rm rand}^2+ {\left(\partial\log\epsilon \over\partial T\right)}^2\sigma_T^2+ {\left(\partial\log\epsilon \over\partial \log g\right)}^2\sigma_{\log g}^2 + {\left(\partial\log\epsilon \over\partial \xi\right)}^2\sigma_{\xi}^2 \nonumber \\ &&\quad + \, 2{\left[ {\left(\partial\log\epsilon \over\partial T\right)}{\left(\partial\log\epsilon \over\partial \log g\right)}\sigma_{T\log g}\right]} + 2{\left[ {\left(\partial\log\epsilon \over\partial \xi\right)}{\left(\partial\log\epsilon \over\partial \log g\right)}\sigma_{\log g \xi} \right]}\nonumber \\ &&\quad + \, 2{\left[ {\left(\partial\log\epsilon \over\partial \xi\right)}{\left(\partial\log\epsilon \over\partial T\right)\sigma_{\xi T}} \right]} \end{eqnarray}](/articles/aa/full_html/2012/12/aa15615-10/aa15615-10-eq99.png) (A.1)where
(A.1)where 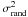 is the difference between the determined
abundance for one line found through the best fit and that found after
adding (S/N)-1 to it. The term (S/N)-1 comes from the inverse
relation between S/N and the difference of the observed fluxes and the synthetic spectrum
used to determine the abundance of a line. The S/N shown in Table 3 were measured in a window around λ4500 Å. The partial
derivatives (∂log ϵ/∂T),
(∂log ϵ/∂log g), and
(∂log ϵ/∂ξ) were determined by
varying 1σ on the model atmosphere for the star BS 16543-097,
as explained above.
is the difference between the determined
abundance for one line found through the best fit and that found after
adding (S/N)-1 to it. The term (S/N)-1 comes from the inverse
relation between S/N and the difference of the observed fluxes and the synthetic spectrum
used to determine the abundance of a line. The S/N shown in Table 3 were measured in a window around λ4500 Å. The partial
derivatives (∂log ϵ/∂T),
(∂log ϵ/∂log g), and
(∂log ϵ/∂ξ) were determined by
varying 1σ on the model atmosphere for the star BS 16543-097,
as explained above.
The covariances σTlog g,
σlog gξ, and
σξT also were determined using the star
BS 16543-097. We picked 11 values for temperature from −1σ
to +1σ, and created model atmospheres with several values
of log g to force ionization balance. Then, the covariance
between T and log g is
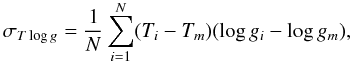 (A.2)where
Tm and
log gm are the adopted temperature
and log g for the star. The correlation coefficient is defined as
(A.2)where
Tm and
log gm are the adopted temperature
and log g for the star. The correlation coefficient is defined as
 (A.3)where in this case,
σT and
σlog g are the standard deviation
for T and log g, taking into account the 11 values
mentioned above. We found
σTlog g = 3.06 and
ρ(T,log g) = 1.02, indicating a
strong correlation between T and log g. We performed a
similar calculation to determine
σlog gξ = −0.00062 and correlation
ρ(log gξ) = −0.8197, indicating
that log g and ξ are highly correlated, although less
so than for T and log g. Similarly to Johnson (2002),
σξT was found to be negligible,
and σTlog g, the
strongest correlation.
(A.3)where in this case,
σT and
σlog g are the standard deviation
for T and log g, taking into account the 11 values
mentioned above. We found
σTlog g = 3.06 and
ρ(T,log g) = 1.02, indicating a
strong correlation between T and log g. We performed a
similar calculation to determine
σlog gξ = −0.00062 and correlation
ρ(log gξ) = −0.8197, indicating
that log g and ξ are highly correlated, although less
so than for T and log g. Similarly to Johnson (2002),
σξT was found to be negligible,
and σTlog g, the
strongest correlation.
Considering the ratio of two elements A and B, its error is
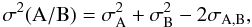 (A.4)where the covariance between two abundances
is given by
(A.4)where the covariance between two abundances
is given by ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{errAB} && \sigma_{\rm A,B}= {\left(\partial\log\epsilon_{\rm A} \over\partial T\right)}{\left(\partial\log\epsilon_{\rm B} \over\partial T\right)}\sigma_T^2 + {\left(\partial\log\epsilon_{\rm A} \over\partial \log g\right)}{\left(\partial\log\epsilon_{\rm B} \over\partial \log g\right)}\sigma_{\log g}^2\nonumber \\ &&\quad \;\; + \, {\left(\partial\log\epsilon_{\rm A} \over\partial \xi\right)}{\left(\partial\log\epsilon_{\rm B} \over\partial \xi\right)}\sigma_\xi^2 \nonumber \\ &&\quad \;\; + \, {\left[ {\left(\partial\log\epsilon_{\rm A} \over\partial T\right)}{\left(\partial\log\epsilon_{\rm B} \over\partial \log g\right)} + {\left(\partial\log\epsilon_{\rm A} \over\partial \log g\right)}{\left(\partial\log\epsilon_{\rm B} \over\partial T\right)} \right]}\sigma_{T\log g} \nonumber \\ &&\quad \;\; + \, {\left[ {\left(\partial\log\epsilon_{\rm A} \over\partial \xi\right)}{\left(\partial\log\epsilon_{\rm B} \over\partial \log g\right)} + {\left(\partial\log\epsilon_{\rm A} \over\partial \log g\right)}{\left(\partial\log\epsilon_{\rm B} \over\partial \xi\right)} \right]}\sigma_{\log g \xi} \end{eqnarray}](/articles/aa/full_html/2012/12/aa15615-10/aa15615-10-eq120.png) (A.5)Table 8 includes uncertainties on DMA subsample, while the last column in Table A.1 shows the estimate uncertainties for the
SAT subsample.
(A.5)Table 8 includes uncertainties on DMA subsample, while the last column in Table A.1 shows the estimate uncertainties for the
SAT subsample.
All Tables
Stars with anomalously high abundances of O, Na, Mg, Al, or Si compared with Ca. For elements other than Ca, there are many values around or above [X/Fe] = +1.4.
Temperatures derived from photometric data by using the final metallicity found for each star.
Results for the stellar parameters, for the DMA (upper portion) and SAT (lower portion) subsamples.
Average of abundances for the DMA subsample of CEMP stars, and solar abundances used as reference, as well as their sources.
Diference between the output value of the synthesis program (log Ap) and the output value with 1σ of diference in temperature (ΔT), log g (Δlg), metallicity (Δfeh), velocity of microturbulent (Δξ), observational (ΔObs), and macroturbulence Δmu.
All Figures
 |
Fig. 1 [X/Fe] for CEMP stars of this work and from the literature. Symbols – starred circles: this work; filled squares: 0 < [Ba/Eu] ≲ 0.5 (CEMP-r/s); open squares: [Ba/Eu] > 0.5 (CEMP-s); crosses: [Ba/Fe] < 0 (CEMP-no); filled triangles: [Ba/Fe] > +1 but there is no available Eu abundance (s or r/s?); open triangles: 0 < [Ba/Fe] < +1 but there is no available Eu abundance (r?); filled circles: [Ba/Eu] < 0 (r); dashes: upper limit for Ba and Eu; big open squares involving four crosses, two filled triangles and one dash indicate high over-abundance of Mg, [Mg/Fe] > +1.4. The dotted lines indicate where [X/Fe] = 1. See text for an explanations concering stars with [C/Fe] < +1. |
| In the text | |
 |
Fig. 2 [X/Fe] for CEMP stars of this work and from the literature. Symbols are the same as in Fig. 1. |
| In the text | |
 |
Fig. 3 [X/Fe] for CEMP stars of this work and from the literature. Symbols are the same as in Fig. 1. |
| In the text | |
 |
Fig. 4 [X/Fe] for CEMP stars of this work and from the literature. Symbols are the same as in Fig. 1. |
| In the text | |
 |
Fig. 5 [Mg, Eu, Ba/Fe] vs. [C/Fe] for CEMP stars of this work and from the literature. Fiducial lines [Ba, Eu, Mg/C] = 0 are drawn for convenience. Symbols are the same as in Fig. 1. The arrows toward left indicate upper limit for [C/Fe]. |
| In the text | |
 |
Fig. 6 CEMP stars from the literature and this work with the same symbols as in Fig. 1. a) [Ba/Eu] vs. [Fe/H]. The dotted lines are the limits of the range for CEMP-r/s and the dashed line is the limit for the r-process only, [Ba/Eu] = −0.7. The arrows up and down indicate upper limit for [Eu/Fe] and [Ba/Fe], respectively. b) [Ba/Fe] vs. [Eu/Fe]. Dashed line indicates [Ba/Eu] = −0.7, and dotted lines indicate where [Ba/Fe] = 0 and [Eu/Fe] = 0; CEMP-s and CEMP-r/s share instinctively the limits [Ba/Fe] > 0 and [Ba/Fe] = [Eu/Fe], whereas CEMP-no are inside the limits [Ba/Fe] and [Eu/Fe] < 0 and CEMP-r inside [Eu/Fe] > 0 and [Ba/Fe] = [Eu/Fe]. The arrows toward left and down indicate upper limit for [Eu/Fe] and [Ba/Fe], respectively. |
| In the text | |
 |
Fig. 7 The behaviour of Mg, Ba and Eu abundances for CEMP stars of this work and from the literature. Symbols are the same as in Fig. 1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


