| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | A113 | |
| Number of page(s) | 8 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201220124 | |
| Published online | 08 November 2012 | |
Signal detection for spectroscopy and polarimetry
Instituto de Astrofísica de Canarias, 38205 La Laguna, TenerifeSpain
Departamento de Astrofísica, Universidad de La Laguna,
38205 La Laguna,
Tenerife,
Spain
e-mail: aasensio@iac.es
Received: 30 July 2012
Accepted: 27 September 2012
The analysis of high spectral resolution spectroscopic and spectropolarimetric observations constitutes a very powerful way of inferring the dynamical, thermodynamical, and magnetic properties of distant objects. However, these techniques starve photons, making it difficult to use them for all purposes. A common problem is not being able to detect a signal because it is buried on the noise at the wavelength of some interesting spectral feature. This problem is especially relevant for spectropolarimetric observations, because only a small fraction of the received light is typically polarized. We present in this paper a Bayesian technique for detecting spectropolarimetric signals. The technique is based on applying the nonparametric relevance vector machine to the observations, which allows us to compute the evidence for the presence of the signal and compute the more probable signal. The method is suited for analyzing data from experimental instruments onboard space missions and rockets aiming at detecting spectropolarimetric signals in unexplored regions of the spectrum, such as the Chromospheric Lyman-Alpha Spectro-Polarimeter (CLASP) sounding rocket experiment.
Key words: methods: data analysis / techniques: polarimetric / methods: statistical / techniques: spectroscopic
© ESO, 2012
1. Introduction
Spectroscopy and spectropolarimetry are two of the most important techniques in the observational astrophysics toolbox. By recording the intensity and polarization state of light at each wavelength we get a complete1 characterization of the state of the light from the observed object, and from its analysis we may infer all the available information on the chemical, thermodynamical, and magnetic properties of the plasma that emitted that light. In some cases, even the mere detection of a given spectral or polarimetric feature may provide fundamental constraints on the observed object. For example, just the measurement of a linear polarization signal from an unresolved object may lead to strong constraints on its geometry (it cannot be spherically symmetric), the presence of an organized magnetic field, or both.
The main drawback of spectroscopy and spectropolarimetry is that they are often photon-starving techniques. Spectroscopic observations are characterized by the spectral resolution of the spectrograph R = λ/Δλ (Δλ is the wavelength interval within a resolution element observed at the wavelength λ), which in the optical and infrared, may typically range from R ~ 1000 to R ~ 1 000 000 (for low-resolution night-time spectrographs or solar spectrographs, respectively). On the other hand, the fraction of polarized photons P in a light beam is P ~ 1–10% for strongly polarized sources and, typically, P ≲ 10-3. Even worse, polarization is subject to cancellations, and P decreases rapidly for low-resolution observations. As a consequence, even with the largest telescopes and the most efficient instrumentation, the number of (polarized) photons finally reaching a resolution element of the detector may be very low and close to the noise levels (either the photon noise or the noise of the detection devices), rendering detection of the signal difficult. In those cases, the presence of a spectral pattern is often determined from heuristic or somehow subjective arguments. Typically, some kind of filtering is applied to the data to enhance the possible signal, which is then identified graphically by simple visual inspection or by fitting an appropriate parametric function. A quantitative assessment of the quality of the detection or an objective estimate of the confidence intervals is then lacking or impossible.
In this paper we apply a Bayesian nonparametric regression method for extracting spectroscopic and/or spectropolarimetric signals (or any other one-dimensional signal) from noisy observations. The method is based on relevance vector machines (RVM; Tipping 2000), a Bayesian version of the support vector machine machine-learning technique. It offers several fundamental advantages. First, we are able to quantify signal detection by computing the evidence ratio between two models: one that contains the signal of interest plus noise and one in which there is only noise. Second, the complexity of the signal is automatically adapted to the information present in the observations. Observations with low noise will facilitate the inference of minute details in the signal of interest, while very noisy observations will favor simpler (and typically smoother) signals. Finally, we obtain an estimation of the signal, together with error bars. We demonstrate the formalism with its application to synthetic and real data.
2. General considerations
Consider the detection of a spectroscopic signal I(λ) (equivalently for spectropolarimetric signals) in an observation perturbed with Gaussian noise with zero mean and variance σ2. In principle, two possibilities may be contemplated: one, which we term model ℳ1, that there is indeed a signal on the observations I(λ) and that it is corrupted with Gaussian noise; the other, model ℳ0, that there is not such a signal at all, only Gaussian noise. The two options give the following models for the observed signal:  where we make it explicit that the observed signal is sampled at a set of wavelength points
where we make it explicit that the observed signal is sampled at a set of wavelength points 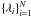 .
.
If a good parametric model that depends on the vector of parameters θ is available for the expected signal I(λ;θ), the most straightforward way to proceed in order to test for the presence of the signal in any given observation (that we represent by the vector d, built by stacking the observed fluxes at all observed wavelength points) is to compute likelihood ratio (Cox 2006) 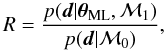 (2)where the likelihood for the model ℳ1 is given by
(2)where the likelihood for the model ℳ1 is given by ![\begin{equation} p({\vec d}|\thetabold,\mathcal{M}_1) = \prod_{i=1}^N (2\pi\sigma^2)^{-1/2} \exp \left[- \frac{\left[d(\lambda_i) - I(\lambda_i;\thetabold) \right]^2}{2\sigma^2} \right], \label{eq:likelihood} \end{equation}](/articles/aa/full_html/2012/11/aa20124-12/aa20124-12-eq21.png) (3)and it is evaluated at the parameters that maximize it. The likelihood is the product of N Gaussians because of the noise model we have chosen (uncorrelated noise with zero mean and variance σ2). Likewise, the likelihood for the model ℳ0 is
(3)and it is evaluated at the parameters that maximize it. The likelihood is the product of N Gaussians because of the noise model we have chosen (uncorrelated noise with zero mean and variance σ2). Likewise, the likelihood for the model ℳ0 is ![\begin{equation} p({\vec d}|\mathcal{M}_0) = \prod_{i=1}^N (2\pi\sigma^2)^{-1/2} \exp \left[- \frac{d(\lambda_i)^2}{2\sigma^2} \right]\cdot \label{eq:likelihood_nosignal} \end{equation}](/articles/aa/full_html/2012/11/aa20124-12/aa20124-12-eq24.png) (4)The decision about the presence of the signal is made in terms of the ratio at different confidence levels (see Cox 2006), and the signal obtained with parameters θML is the maximum likelihood signal.
(4)The decision about the presence of the signal is made in terms of the ratio at different confidence levels (see Cox 2006), and the signal obtained with parameters θML is the maximum likelihood signal.
In spite of its simplicity, there is a fundamental problem with the likelihood ratio. Using the maximum likelihood value of the parameters, one is not taking the uncertainty about θ into account. One of the consequences is that it is possible to promote complicated models if the number of parameters is sufficiently large, leading to overfitting. In other words, in complex models, we can fit the noise so that the signal is always detected. That is why model comparison (and, consequently, signal detection) is done in the Bayesian formalism through the evidence ratio (or Bayes ratio) (e.g., Jeffreys 1961; Kass & Raftery 1995; Gregory 2005; Trotta 2008; Asensio Ramos et al. 2012): 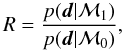 (5)which gives the ratio of the probability that the observed data has been generated by a model with a signal and the probability that the observed data is only compatible with pure noise. These ratios can be transformed into significance using the modified Jeffreys scale that has been presented by Jeffreys (1961), Kass & Raftery (1995), and Gordon & Trotta (2007).
(5)which gives the ratio of the probability that the observed data has been generated by a model with a signal and the probability that the observed data is only compatible with pure noise. These ratios can be transformed into significance using the modified Jeffreys scale that has been presented by Jeffreys (1961), Kass & Raftery (1995), and Gordon & Trotta (2007).
Two main differences appear between the evidence ratio and the likelihood ratio. The first one is that the model is compared with the evidence, after the parameters have been integrated: 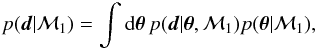 (6)so uncertainties in θ are taken into account. The second one is the standard inclusion of a prior distribution for the parameters, which works as a regularizing term.
(6)so uncertainties in θ are taken into account. The second one is the standard inclusion of a prior distribution for the parameters, which works as a regularizing term.
3. Bayesian signal detection with nonparametric models
Parametric models are appropriate when one is confident about the shape of the expected signal. For instance, it can be used to detect a spectral line that is known to have a Gaussian shape although the precise position, broadening, and amplitude are unknown. However, this is not often the case, for the following two reasons at least. First, many of the interesting cases are those in which the observed signal cannot be reproduced with our models, constituting a potential source of new phenomena (e.g., several velocity components in the spectral line generate a very complex pattern that is difficult to anticipate). Second, it might be that an observation is made with the aim of detecting a signal that has never been observed, making it difficult to propose a parametric model that can explain its exact shape.
To overcome the potential failure of parametric models, nonparametric regression models have also been developed in the recent years. Nonparametric regression relies on the application of a sufficiently general function that only depends on observed quantities and that is used to approximate the observations. The signal detection scheme we have developed is based on applying the RVM (Tipping 2000), a Bayesian update of the support vector machine machine learning technique (Vapnik 1995). In this case, the general function is just a linear combination of kernels, 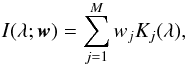 (7)where the Kj(λ) functions are arbitrary and defined in advance, and wj is the weight associated to the jth kernel function. This functional form is also known as a linear regressor. The parameters we infer from the data appear linearly in the model once the kernel functions are fixed. For instance, if the kernel functions are chosen to be polynomials, one ends up with a standard polynomial regression.
(7)where the Kj(λ) functions are arbitrary and defined in advance, and wj is the weight associated to the jth kernel function. This functional form is also known as a linear regressor. The parameters we infer from the data appear linearly in the model once the kernel functions are fixed. For instance, if the kernel functions are chosen to be polynomials, one ends up with a standard polynomial regression.
The main advantage of nonparametric regression is that the model automatically adapts to the observations. For this adaption to occur, the basis functions should ideally capture part of the behavior of the signal. Together with the fact that the number of basis functions that one can include in the linear regression can be arbitrarily large (even potentially infinite, in some cases), this constitutes a very powerful model for any unknown signal.
3.1. Hierarchical modeling
The linear regression problem is usually solved by computing the value of the weights wj that minimize the ℓ2-norm between the observations and the predictions (e.g., Press et al. 1986). In other words, the value of the wj are the solution to the least-squares problem. However, it is known that the least-squares solution leads to severe overfitting and renders the method useless. Tipping (2000) considered overcoming the overfitting by pursuing a hierarchical Bayesian solution to the linear regression problem. The aim is to use the available data to compute the posterior distribution function for the vector of weights w and the noise variance σ2 (will be estimated from the same data). Therefore, a direct application of the Bayes theorem will give 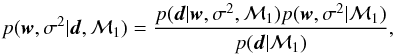 (8)where p(d|w,σ2,ℳ1) is the likelihood function given by Eq. (3), p(w,σ2|ℳ1) is the prior distribution for the parameters that we define now, and p(d|ℳ1) is the evidence which, like Eq. (6), is given by the integral over w and σ2 of the numerator of the right-hand side. To simplify the notation, we drop the conditioning on ℳ1 from then on because we are focusing on the model that assumes the presence of signal. Putting flat priors on w and σ2 (i.e., p(w,σ2) ∝ 1) is equivalent to the maximum-likelihood solution, which might lead to overfitting. To overcome this problem, Tipping (2000) used a hierarchical approach in which the prior for w is made to depend on a set of hyperparameters α, which are learnt from the data during the inference process. The final posterior distribution is, after following the standard procedure in Bayesian statistics of including a prior for the newly defined random variables, given by
(8)where p(d|w,σ2,ℳ1) is the likelihood function given by Eq. (3), p(w,σ2|ℳ1) is the prior distribution for the parameters that we define now, and p(d|ℳ1) is the evidence which, like Eq. (6), is given by the integral over w and σ2 of the numerator of the right-hand side. To simplify the notation, we drop the conditioning on ℳ1 from then on because we are focusing on the model that assumes the presence of signal. Putting flat priors on w and σ2 (i.e., p(w,σ2) ∝ 1) is equivalent to the maximum-likelihood solution, which might lead to overfitting. To overcome this problem, Tipping (2000) used a hierarchical approach in which the prior for w is made to depend on a set of hyperparameters α, which are learnt from the data during the inference process. The final posterior distribution is, after following the standard procedure in Bayesian statistics of including a prior for the newly defined random variables, given by 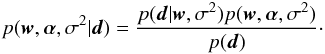 (9)The likelihood does depend directly on w and not on the election of α. Assuming that the priors for α and σ2 are independent and that the prior for w depends on the hyperparameters α, the previous equation can be trivially modified to read as
(9)The likelihood does depend directly on w and not on the election of α. Assuming that the priors for α and σ2 are independent and that the prior for w depends on the hyperparameters α, the previous equation can be trivially modified to read as 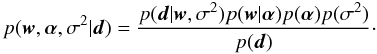 (10)The value of the evidence, or marginal posterior, is computed to ensure that the posterior is normalized to unit hyperarea:
(10)The value of the evidence, or marginal posterior, is computed to ensure that the posterior is normalized to unit hyperarea: 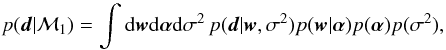 (11)where the priors p(w|α), p(α) and p(σ2) are still left undefined, and we have again made the conditioning on ℳ1 explicit for clarity.
(11)where the priors p(w|α), p(α) and p(σ2) are still left undefined, and we have again made the conditioning on ℳ1 explicit for clarity.
3.2. Sparsity prior
One of the fundamental ideas of RVMs is to regularize the regression problem by favoring the sparsest solutions, i.e., those that contain the least number of nonzero elements in w. For this reason, and to keep the analytical tractability, Tipping (2000) decided to use a product of Gaussian functions for p(w|α): 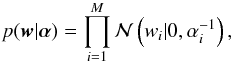 (12)where
(12)where 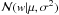 is a Gaussian distribution on the variable w with mean μ and variance σ2. Although not obvious, this prior favors low values of w when selecting an appropriate prior for α. The reason is that, in the hierarchical scheme, the final prior over w is given by the marginalization:
is a Gaussian distribution on the variable w with mean μ and variance σ2. Although not obvious, this prior favors low values of w when selecting an appropriate prior for α. The reason is that, in the hierarchical scheme, the final prior over w is given by the marginalization: 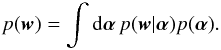 (13)If a Jeffreys prior is used for each αi so that
(13)If a Jeffreys prior is used for each αi so that 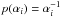 , we end up with p(wi) ∝ |wi|-1, which clearly favors low values of wi. In essence, the form of p(w|α) is such that, in the limiting case that αi tends to infinity, the marginal prior for wi is so peaked at zero that it is compatible with a Dirac delta. This means that this specific wi does not contribute to the model of Eq. (7) and can be dropped from the model without impact. This regularization proposed by Tipping (2000) leads to a sparse w vector, so an automatic relevance determination is implemented in the method.
, we end up with p(wi) ∝ |wi|-1, which clearly favors low values of wi. In essence, the form of p(w|α) is such that, in the limiting case that αi tends to infinity, the marginal prior for wi is so peaked at zero that it is compatible with a Dirac delta. This means that this specific wi does not contribute to the model of Eq. (7) and can be dropped from the model without impact. This regularization proposed by Tipping (2000) leads to a sparse w vector, so an automatic relevance determination is implemented in the method.
 |
Fig. 1 Example of the Bayesian signal detection scheme applied to a synthetic spectrum of the scattering polarization pattern across the Mg ii h and k lines obtained by Belluzzi & Trujillo Bueno (2012). The dots display the observations with increasingly higher Gaussian noise. To avoid cluttering, we only show one error bar. The solid (dotted) red curve is the mean (standard deviation) of the Gaussian predictive distribution and is computed using Eq. (18). The blue curves display the contribution of each individual kernel function, and the green curve is the original synthetic profile. The logarithm of the evidence ratio given in Eq. (5) is shown for each case. Additionally, we display Mactive, the number of active basis functions considered by the relevance vector machine algorithm. |
3.3. Type-II maximum likelihood
The computation of the evidence of Eq. (11) is intractable. Looking for an analytical solution, Tipping (2000) proceeded with a Type-II maximum likelihood approximation (also known as empirical Bayes, generalized maximum likelihood or evidence approximation; MacKay 1999). The idea is that, if the posterior for the hyperparameters α and the noise variance σ2 is fairly peaked, one can substitute their values by their modes and simplify the expressions. Therefore, if we make the substitutions p(α) = δ(α−αMP) and 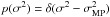 , where the subindex “MP” refers to the maximum a-posterior values, the evidence in Eq. (11) simplifies to
, where the subindex “MP” refers to the maximum a-posterior values, the evidence in Eq. (11) simplifies to  (14)which is now Gaussian with zero mean and covariance matrix,
(14)which is now Gaussian with zero mean and covariance matrix, 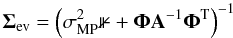 (15)where A = diag(α1,α2,...,αM) is a diagonal matrix with the αMP vector in the main diagonal, 1 is the identity matrix and Φ is the N × M matrix with elements Φij = Kj(λi). The strategy is then to compute the value of the elements of αMP (and
(15)where A = diag(α1,α2,...,αM) is a diagonal matrix with the αMP vector in the main diagonal, 1 is the identity matrix and Φ is the N × M matrix with elements Φij = Kj(λi). The strategy is then to compute the value of the elements of αMP (and 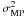 if one also wants the noise variance estimated from the data) that maximizes the evidence given by Eq. (14) and to fix them to the inferred values to proceed. The evidence is used afterwards for model comparison.
if one also wants the noise variance estimated from the data) that maximizes the evidence given by Eq. (14) and to fix them to the inferred values to proceed. The evidence is used afterwards for model comparison.
3.4. Predictive distribution
Given the information gained from the data about α, σ2 and w, the predicted value I ⋆ at an arbitrary wavelength λ ⋆ is a random variable. Its distribution, known as predictive distribution, is given by (e.g., Gregory 2005) 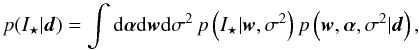 (16)which is just the integral of the likelihood for a new value I ⋆ associated with λ ⋆ weighted by the posterior distribution for all the parameters. Under the Type-II maximum likelihood approach that we applied before, the integral over α and σ2 can be carried out analytically so that
(16)which is just the integral of the likelihood for a new value I ⋆ associated with λ ⋆ weighted by the posterior distribution for all the parameters. Under the Type-II maximum likelihood approach that we applied before, the integral over α and σ2 can be carried out analytically so that 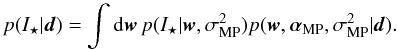 (17)The result of the integral turns out to be a Gaussian distribution with the following mean and variance:
(17)The result of the integral turns out to be a Gaussian distribution with the following mean and variance: 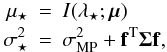 (18)where f = [K(λ ⋆ − λ1),...,K(λ ⋆ − λN)] T and
(18)where f = [K(λ ⋆ − λ1),...,K(λ ⋆ − λN)] T and 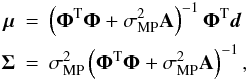 (19)with the A and Φ matrices defined above.
(19)with the A and Φ matrices defined above.
3.5. Summary
To summarize, one computes the values of αMP and 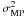 that maximize the evidence of Eq. (14) and uses these values to estimate the mean and variance of the predicted value at an arbitrary new point λ ⋆ using Eqs. (18). During the optimization of the evidence, the RVM algorithm devised by Tipping (2000) discards all the functions contributing to the regression function of Eq. (7), whose value of αi becomes very large. If αi becomes very large, this means that the kernel function associated to wi is not needed (thus the method automatically selects which basis functions are needed depending on the noise level)2.
that maximize the evidence of Eq. (14) and uses these values to estimate the mean and variance of the predicted value at an arbitrary new point λ ⋆ using Eqs. (18). During the optimization of the evidence, the RVM algorithm devised by Tipping (2000) discards all the functions contributing to the regression function of Eq. (7), whose value of αi becomes very large. If αi becomes very large, this means that the kernel function associated to wi is not needed (thus the method automatically selects which basis functions are needed depending on the noise level)2.
4. Applications
We present the characteristics of the method with applications to several signal detection examples. We start with some synthetic cases to verify the robustness of the method to different noise levels. Then, we apply it to a few realistic cases. Although the RVM method is able to infer the noise variance σ2 from the data, we prefer in this paper to give this as an input by setting 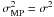 in order to show the ability of the method to extract the signal when the noise level is correctly estimated. In any case, we have tested in all cases that, if the value of
in order to show the ability of the method to extract the signal when the noise level is correctly estimated. In any case, we have tested in all cases that, if the value of 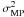 is inferred from the maximization of Eq. (14), its value is quite similar to the original noise variance introduced in the experiments.
is inferred from the maximization of Eq. (14), its value is quite similar to the original noise variance introduced in the experiments.
4.1. Synthetic data
4.1.1. Linear polarization of the Mg ii h and k lines
The linear polarization signal in the Mg ii h and k lines around 2800 Å produced by coherent scattering is expected to be strong given the large anisotropy of the ultraviolet (UV) radiation field in this spectral region. However, the observation of this UV window cannot be accomplished from the ground and one has to use space-borne observatories. Consequently, it is expected that detection of such signals in the future will be a technical challenge.
To test our signal detection procedure, we used the theoretical results of Belluzzi & Trujillo Bueno (2012) as a testbench. They synthesize the emergent Q/I across the h and k lines taking partial redistribution (PRD) and J-state interference effects into account in the FAL-C semiempirical atmosphere of Fontenla et al. (1993) for an observation at μ = 0.1, with μ the heliocentric angle. The synthetic curve is shown in green in Fig. 1. The calculations are done in an adaptive wavelength axis so that the sampling close to the line cores is finer than away from them. Since this will not be the case in real observations, we resample the profile at fixed intervals of 80 mÅ and add different noise levels characterized by their standard deviation, quoted in the lower right-hand corner of each panel. These figures are representative of instruments like IRIS (de Pontieu et al. 2009), which will observe these very same lines but without polarimetric capabilities.
The previous formalism is applied using a basis set consisting of Gaussian functions centered on each observed point and with widths ranging from 0.3 Å to 10 Å in 20 steps of 0.5 Å plus a constant function to allow for a continuum bias. The reason to allow for such a variety of basis functions is to simultaneously accommodate the large structure produced by the PRD and J-state interference effects and the fine structure in the cores of the lines (see Belluzzi & Trujillo Bueno 2012, for the details). Such a large flexibility facilitates the fits being done with a very sparse w vector. The results are shown in Fig. 1 for different noise levels parameterized with the standard deviation of the Gaussian noise indicated in the lower right-hand corner of each panel. The number of basis functions for each case, and their associated evidence ratio with respect to the no-signal model is shown in the upper part of each panel. The results indicate that the signal is nicely recovered with our method and that it strongly favors the presence of signal (relatively high evidence ratios) even for signal-to-noise (S/N) ratios in the range 1–3. The mean of the predictive distribution given by Eq. (18) shown with a red solid curve (with its associated standard deviation, shown in dashed red curves) is a very good representation of the underlying synthetic signal.
4.1.2. Linear polarization in the He I 10 830 Å multiplet
A second example showing the ability of our scheme to detect signals consists of a synthetic linear polarization profile calculated with Hazel (Asensio Ramos et al. 2008) for the 10 830 Å multiplet of neutral helium. The profiles are obtained at the solar disk center with a magnetic field that is parallel to the surface with a strength of 100 G. This is a typical configuration in which the Hanle effect generates linear polarization in the forward scattering geometry due to a symmetry-breaking effect (see Trujillo Bueno et al. 2002). The slab of He i atoms is assumed to be located at a height of ~6000 km and the optical depth measured in the red component of the multiplet (the one centered at ~10 830.5 Å) is 1.25. The width of the line is set to 8 km s-1. Synthetic observations are generated by adding different noises with standard deviations shown in the lower right-hand corner of each panel (the error bar is also shown on the lower left corner). The basis set chosen for the signal detection algorithm is made of Gaussian functions with widths between 0.3 and 1 Å in 20 steps. Since the amplitude of the Q/Ic signals (with Ic the intensity at the continuum nearby) is ~0.25% in the blue component and ~0.5% in the red component, the noises we have considered are equivalent to S/N between 1 and 5 in the red component and between 0.5 and 2.5 in the blue component. According to the results, displayed in Fig. 2, the nonparametric signal detection method gives an evidence ratio greater than 5 for the noisier case, strongly favoring the presence of a signal. The mean of the predictive distribution (in red) is very similar to the synthetic one (in green) using a very sparse solution with only two or three active basis functions.
4.2. Real data
4.2.1. Linear polarization of the Mg II h and k lines
Given the difficulty of operating a spectropolarimeter on space, the only measurement of the linear polarization in the Mg ii h and k lines was carried out by Henze & Stenflo (1987) using the UltraViolet Spectrometer and Polarimeter (UVSP) on the Solar Maximum Mission (SMM). The observations consisted of ten wavelength samples across the h and k lines of Mg ii spanning a range of 15 Å with a slit length of 180′′. They observed a region close to the solar limb and one at disk center. For symmetry reasons, the signal at disk center is expected to be zero (in the absence of a deterministic magnetic field in the resolution element), while it is expected to be non-negligible close to the limb. Figure 3 shows the observations extracted from a scanned version of Fig. 1 in Henze & Stenflo (1987), in the left panel for the observation at μ = 0.15 and in the right one for the observation at disk center. Each of the plotted points is calculated as an average over all the observations of Henze & Stenflo (1987) for a certain wavelength bin. The error bar is estimated to be σ = 0.009, which we consider fixed and do not introduce it in the inference process (so σMP = 0.009).
We apply the previous formalism using a basis set composed of Gaussian functions centered on each observed point and with widths ranging from 1 Å to 5 Å in 11 steps of 0.4 Å plus a constant function to allow for a continuum. Therefore, even though the number of observations is N = 10, the number of potentially active basis functions is M = 110. Overfitting does not occur in our case because of the Bayesian treatment. Computing the evidence ratio in the two cases, we find lnR = 7.1 for the profile close to the limb using only four active kernels and lnR = 0.4 at disk center using two active kernels. According to the standard Jeffreys scale, there is really strong evidence for the presence of signal in the observation close to the limb and inconclusive at disk center. Also the solution is very sparse, using only ~4% of the potential basis functions for the observation close to the limb and only ~2% for the observation at disk center.
 |
Fig. 2 Example of the Bayesian signal detection scheme applied to a synthetic spectrum of the He i 10 830 Å multiplet obtained with Hazel (Asensio Ramos et al. 2008). The dots display the observations with increasingly higher Gaussian noise. To avoid cluttering, we only show one error bar. The solid red curve is the mean of the predictive distribution, together with the error bars shown as red dotted lines. The blue curves display the contribution of each individual kernel function, and the green curve is the original profile. |
 |
Fig. 3 Application of the signal detection scheme to the linear polarization signals in the Mg ii h and k lines observed by Henze & Stenflo (1987). The dots display the observations, with their associated Gaussian error bars. The solid red curve is the mean of the predictive distribution, together with the error bars in red dotted lines. The blue curves display the contribution of each individual kernel function. |
 |
Fig. 4 Application to the linear polarization signals in the Ca ii H and K lines observed in the atlas of (Gandorfer 2002) resampled at 50 wavelength points and with different amounts of noise added for each row. The dots display the observations, with their associated Gaussian error bars (with their standard deviation indicated in the panels). Each column shows the results of the line detection using Gaussian functions of different widths as basis functions. The solid red curve is the mean of the predictive distribution, together with the range inside one standard deviation shown as red dotted lines. The blue curves display the contribution of each individual kernel function. Each panel also displays the evidence ratio and the number of active basis functions. |
 |
Fig. 5 Application of the signal detection scheme to the line-core linear polarization signals estimated for the CLASP rocket experiment by Trujillo Bueno et al. (2011). The dots display the observations, with their associated Gaussian error bars. The solid red curve is the mean of the predictive distribution, together with the error bars in red dotted lines. The blue curves display the contribution of each individual kernel function. |
4.2.2. Linear polarization of the Ca ii H and K lines
The second realistic example is the observation of the linear polarization signals of the H and K lines of Ca ii in the UV. These signals have been acquired by Gandorfer (2002) at an heliocentric angle of μ = 0.1 and display an enormous amount of spectral signals that are overlapped with the large-scale structure of the linear polarization of the two Ca ii lines produced by superinterferences. We have resampled the profile at a spectral resolution of ~2 Å to mimick a very low spectral resolution spectropolarimeter. The aim is to show that it is possible to detect the linear polarization signal even at such low spectral resolutions when there are strong noise contaminations.
We carried out the signal detection procedure for four different levels of Gaussian noise with different standard deviations, as shown in each row of Fig. 4. Given the original (resampled to low resolution) signals, we contaminate them with Gaussian noise so that the S/N in the amplitude peaks of Q/I ranges from 1 to 10, approximately. The signal detection is done with basis sets composed of Gaussian functions of different widths (each column). The results shown in Fig. 4 look very promising because, even for S/N as low as 1, we can reliably recover the original signal, even though the observed signal is almost unrecognizable. The mean of the predictive distribution is surprisingly similar to a smoothed version of the green curve, specially when the basis width is large, while many of the minute details of the signal can be estimated correctly if the noise is not too strong and the width of the Gaussian basis is small.
Concerning the evidence ratio, we find evidence of signals in all the cases. However, the signal detection algorithm points to moderate evidence of a signal for the case with S/N = 1. The number of active Gaussian functions is usually smaller when the width is larger, with an upper limit of ten for the smallest considered noise level and width. In any case, we find that the exact green curve is systematically inside one standard deviation of the predictive distribution.
4.2.3. Linear polarization of the Lyα line with CLASP
With the aim of investigating the magnetism of the upper chromosphere and transition region of the Sun, the Chromospheric Lyman-Alpha Spectro-Polarimeter (CLASP; Kobayashi et al. 2012) is a sounding rocket proposed to carry out the first measurement of the linear polarization produced by scattering processes in the Lyα ultraviolet resonance line. A recent investigation Trujillo Bueno et al. (2011) indicates that the Lyα line should show measurable line-core linear polarization either when observed at disk center or close to the solar limb. Additionally, the linear polarization signal is sensitive to the magnetic eld strengths that are expected in the upper chromosphere and transition region.
Because CLASP is mounted on a rocket, the total integration time is quite reduced. Consequently, the final expected standard deviation of the noise (when taking the whole duration of the mission of ~5 min into account) is expected to be about 0.03% in units of the monochromatic emission intensity of the line (see Kobayashi et al. 2012). To test the possibility of reliably detecting linear polarization signals with CLASP, we carried out the following experiment. We used the Q/I profiles computed by Trujillo Bueno et al. (2011) under the assumption of complete redistribution in frequency at two different positions in the solar disk and for four values of the strength of a horizontal magnetic field. The synthetic curves are shown in Fig. 5. The upper panel corresponds to an observation at disk center, while the lower panel corresponds to an observation at μ = 0.3. The observations were corrupted with Gaussian noise of several standard deviation, from 0.03% (the best expected observation) up to 0.1%. The signal detection was done with basis sets composed of Gaussian functions of widths between 0.1 and 0.3 Å in steps of 0.01 Å.
Given that the amplitude of the Q/I signal depends on the magnetic field strength, it is possible to find high and low evidence ratios for a fixed noise variance. This is the case for the first row of the lower panel. The signal is clearly detected (high value for the evidence ratio) up to fields below 50 G, but the case for 100 G gives no clear detection. In fact, the specific value of the evidence ratio might change for different noise realizations. When the standard deviation of the noise decreases, the method finds the signal in all the cases with a very reduced set of basis functions. The predicted signal, closely follows the synthetic one even in the cases with a reduced S/N. Concerning the results at disk center, it is interesting to focus on the nonmagnetic case. Given the symmetry of the problem, the synthetic signal is strictly equal to zero. Our evidence ratios give no special preference for the presence of a signal. From these results it seems that, if the Q/I signal emerging from the solar atmosphere is similar to the computed one, it is possible to detect it by relaxing the CLASP requirements.
It is clear that the ultimate objective when detecting and extracting a signal from spectropolarimetric observations is to infer the thermodynamic and magnetic properties of the plasma. To this end, the mean of the predictive distribution can be used as a statistically meaningful estimation of the signal. Together with the mean, one has to add the error bars obtained from the standard deviation of the predictive distribution. The main difficulty at this stage is to propose a suitable model for the polarimetric signal from which one infers the thermal and magnetic properties. This is exactly the reason we pursued a nonparametric scheme when we do not have a proper model for the expected signal of interest. A straightforward way to proceed is to fit a suitable parametric model to the extracted signal with any standard least-squares algorithm. Given that this mixture of Bayesian and non-Bayesian approaches surely does not make much sense, we are also in the process of studying a semiparametric (combination of parametric and non-parametric regressor) scheme that might give good results.
5. Conclusions
We have shown how a nonparametric Bayesian regression method can be applied to the problem of detecting a spectroscopic and/or spectropolarimetric signal that is buried in the noise. The method is specially suited to analyzing signals whose spectral shapes are not known in advance. The output of the method is the evidence ratio between the model that assumes a nonzero spectral signal and one that assumes no signal is present. Without any additional computational cost, the method also gives the predictive distribution, from where one can extract the most probable regression and the corresponding error bars. This technique is appropriate for relaxing the noise requirements of observations where the shape of the signal is not known in advance.
Our experiments in different spectral regions demonstrate that a signal corrupted with Gaussian noise whose S/N on the order of 1 (or even less in some cases) can be efficiently detected and extracted using the nonparametric RVM method. We propose that a signal is detected when log R ≳ 2.5, which according to the scale of Jeffreys (1961), corresponds to moderate evidence in favor of the presence of a signal. Once the signal has been detected, signal extraction is carried out by examining the mean of the predictive distribution and its associated standard deviation. The quality of the signal extraction is obviously better when the signal is less buried in the noise. Summarizing, S/N = 1 can be considered to be the lower limit for reliable signal detection and extraction.
Finally, we propose that this technique could be applied to the detection of the ultimate property of light, its orbital angular momentum, from astrophysical objects (Harwit 2003), whose detection, if present, is going to be challenging (Uribe-Patarroyo et al. 2011).
Or nearly so: see Harwit (2003) and Uribe-Patarroyo et al. (2011).
A signal detection code based on the routines of Tipping (2000) can be freely downloaded from http://www.iac.es/project/magnetism/signal_detection
Acknowledgments
We thank L. Belluzzi, J. Štěpán, and J. Trujillo Bueno for providing the synthetic profiles used in Figs. 1 and 5. Financial support by the Spanish Ministry of Economy and Competitiveness through projects AYA2010-18029 (Solar Magnetism and Astrophysical Spectropolarimetry) and Consolider-Ingenio 2010 CSD2009-00038 is gratefully acknowledged. A.A.R. also acknowledges financial support through the Ramón y Cajal fellowship. This research has benefited from discussions that were held at the International Space Science Institute (ISSI) in Bern (Switzerland) in February 2010 as part of the International Working group Extracting information from spectropolarimetric observations: comparison of inversion codes.
References
- Asensio Ramos, A., Trujillo Bueno, J., & Landi Degl’Innocenti, E. 2008, ApJ, 683, 542 [NASA ADS] [CrossRef] [Google Scholar]
- Asensio Ramos, A., Manso Sainz, R., Martínez González, M. J., et al. 2012, ApJ, 748, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Belluzzi, L., & Trujillo Bueno, J. 2012, ApJ, 750, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, D. R. 2006, Principles of Statistical Inference (Cambridge University Press) [Google Scholar]
- de Pontieu, B., Title, A. M., Schryver, C. J., et al. 2009, AGU Fall Meeting Abstracts, B1499 [Google Scholar]
- Fontenla, J. M., Avrett, E. H., & Loeser, R. 1993, ApJ, 406, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Gandorfer, A. 2002, The Second Solar Spectrum, Vol. II, 3910 Å to 4630 Å (Zurich: vdf) [Google Scholar]
- Gordon, C., & Trotta, R. 2007, MNRAS, 382, 1859 [Google Scholar]
- Gregory, P. C. 2005, Bayesian Logical Data Analysis for the Physical Sciences (Cambridge: Cambridge University Press) [Google Scholar]
- Harwit, M. 2003, ApJ, 597, 1266 [NASA ADS] [CrossRef] [Google Scholar]
- Henze, W., & Stenflo, J. O. 1987, Sol. Phys., 111, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffreys, H. 1961, Theory of Probability (Oxford: Oxford University Press) [Google Scholar]
- Kass, R., & Raftery, A. 1995, J. Am. Stat. Assoc., 90, 773 [Google Scholar]
- Kobayashi, K., Kano, R., Trujillo-Bueno, J., et al. 2012, in ASP Conf. Ser. 456, eds. L. Golub, I. De Moortel, & T. Shimizu, 233 [Google Scholar]
- MacKay, D. J. C. 1999, Neural Comput., 11, 1035 [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1986, Numerical Recipes (Cambridge: Cambridge University Press) [Google Scholar]
- Tipping, M. E. 2000, in Advances in Neural Information Processing Systems 12, eds. S. A. Solla, T. K. Leen, & K. R. Müller, 652 [Google Scholar]
- Trotta, R. 2008, Contemp. Phys., 49, 71 [Google Scholar]
- Trujillo Bueno, J., Landi Degl’Innocenti, E., Collados, M., Merenda, L., & Manso Sainz, R. 2002, Nature, 415, 403 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Trujillo Bueno, J., Štěpán, J., & Casini, R. 2011, ApJ, 738, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Uribe-Patarroyo, N., Alvarez-Herrero, A., López Ariste, A., et al. 2011, A&A, 526, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vapnik, V. N. 1995, The nature of statistical learning theory (New York: Springer) [Google Scholar]
All Figures
 |
Fig. 1 Example of the Bayesian signal detection scheme applied to a synthetic spectrum of the scattering polarization pattern across the Mg ii h and k lines obtained by Belluzzi & Trujillo Bueno (2012). The dots display the observations with increasingly higher Gaussian noise. To avoid cluttering, we only show one error bar. The solid (dotted) red curve is the mean (standard deviation) of the Gaussian predictive distribution and is computed using Eq. (18). The blue curves display the contribution of each individual kernel function, and the green curve is the original synthetic profile. The logarithm of the evidence ratio given in Eq. (5) is shown for each case. Additionally, we display Mactive, the number of active basis functions considered by the relevance vector machine algorithm. |
| In the text | |
 |
Fig. 2 Example of the Bayesian signal detection scheme applied to a synthetic spectrum of the He i 10 830 Å multiplet obtained with Hazel (Asensio Ramos et al. 2008). The dots display the observations with increasingly higher Gaussian noise. To avoid cluttering, we only show one error bar. The solid red curve is the mean of the predictive distribution, together with the error bars shown as red dotted lines. The blue curves display the contribution of each individual kernel function, and the green curve is the original profile. |
| In the text | |
 |
Fig. 3 Application of the signal detection scheme to the linear polarization signals in the Mg ii h and k lines observed by Henze & Stenflo (1987). The dots display the observations, with their associated Gaussian error bars. The solid red curve is the mean of the predictive distribution, together with the error bars in red dotted lines. The blue curves display the contribution of each individual kernel function. |
| In the text | |
 |
Fig. 4 Application to the linear polarization signals in the Ca ii H and K lines observed in the atlas of (Gandorfer 2002) resampled at 50 wavelength points and with different amounts of noise added for each row. The dots display the observations, with their associated Gaussian error bars (with their standard deviation indicated in the panels). Each column shows the results of the line detection using Gaussian functions of different widths as basis functions. The solid red curve is the mean of the predictive distribution, together with the range inside one standard deviation shown as red dotted lines. The blue curves display the contribution of each individual kernel function. Each panel also displays the evidence ratio and the number of active basis functions. |
| In the text | |
 |
Fig. 5 Application of the signal detection scheme to the line-core linear polarization signals estimated for the CLASP rocket experiment by Trujillo Bueno et al. (2011). The dots display the observations, with their associated Gaussian error bars. The solid red curve is the mean of the predictive distribution, together with the error bars in red dotted lines. The blue curves display the contribution of each individual kernel function. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


