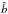| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | A31 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201219946 | |
| Published online | 23 October 2012 | |
The X-ray variability history of Markarian 3
1 European Space Astronomy Centre of ESA, PO Box 78, Villanueva de la Cañada, 28691 Madrid, Spain
e-mail: Matteo.Guainazzi@sciops.esa.int
2 INAF IASF Palermo, via Ugo La Malfa 153, 90146 Palermo, Italy
3 Centro de Astrobiologia (CSIC-INTA), Dep. de Astrofisica, ESA, PO Box 78, 28691, Villanueva de la Cañada, Madrid, Spain
Received: 4 July 2012
Accepted: 4 September 2012
Context. The unified scenario for active galactic nuclei (AGN) postulates that our orientation with respect to a parsec-scale azimuthally-symmetric gas and dust system causes the difference in their phenomenology in the optical/UV and X-ray bands. Only recently have high-resolution radio (VLBI) and IR interferometric observations provided direct constraints on the size and structure of this obscuring system (known historically as the “torus”). On the other hand, variability in optically-thick X-ray absorption and reprocessing in heavily obscured AGN often probe smaller scales, down to the broad line region and beyond.
Aims. We aim at constraining the geometry of the reprocessing matter in the nearby prototypical Seyfert 2 Galaxy Markarian 3 by studying the time evolution of the spectral components associated to the primary AGN emission and to its Compton-scattering.
Methods. We analyzed archival spectroscopic observations of Markarian 3 taken over the last ≃ 12 years with the XMM-Newton, Suzaku and Swift observatories, as well as data taken during a monitoring campaign activated by us in 2012.
Results. The timescale of the Compton-reflection component variability (originally discovered by ASCA in the mid-’90s) is ≲ 64 days. This upper limit improves by more than a factor of 15 on previous estimates of the Compton-reflection variability timescale for this source. When the light curve of the Compton-reflection continuum in the 4−5 keV band is correlated with the 15–150 keV Swift/BAT curve, a delay ≳1200 days is found. The cross-correlation results depend on the model used to fit the spectra, although the detection of the Compton-reflection component variability is independent of the range of models employed to fit the data. Reanalysis of an archival Chandra image of Markarian 3 indicates that the Compton-reflection and the Fe Kα emitting regions are extended to the north up to ≃300 pc. The combination of these findings suggests that the optically-thick reprocessor in Markarian 3 is clumpy.
Conclusions. There is mounting experimental evidence that the structure of the optically-thick gas and dust in the nuclear environment of nearby heavily obscured AGN is extended and complex. We discuss possible modifications to the standard unification scenarios encompassing this complexity. Markarian 3, which exhibits X-ray absorption and reprocessing on widely different spatial scales, is an ideal laboratory to test these models.
Key words: galaxies: active / galaxies: nuclei / galaxies: Seyfert / galaxies: groups: individual: Markarian 3 / X-rays: galaxies
© ESO, 2012
1. Optically thick reprocessing in AGN
Unified scenarios for radio-quiet active galactic nuclei (AGN) (Antonucci & Miller 1985; Antonucci 1993) postulate an azimuthally-symmetric distribution of optically-thick gas and dust surrounding the nucleus, as well as around the gas clouds responsible for optical broad ( ≳ 1000 km s-1) lines. This structure is commonly referred to as the “torus”. We adhere to this convention in this paper, as is customary in recent AGN literature, although one of the main astrophysical motivations of our study is to constrain the geometry of this absorbing system. Warm dust dominates the mid-IR emission in nearby AGN (see, e.g., Alonso-Herrero et al. 2011) The innermost regions of the dusty phase therefore have to be located beyond the sublimation radius (~0.4 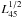 pc, where L45 is the ionizing luminosity in units of 1045 erg s-1; Barvainis 1987). This evidence suggests that one is dealing with a structure at a parsec-scale distance from the active nucleus.
pc, where L45 is the ionizing luminosity in units of 1045 erg s-1; Barvainis 1987). This evidence suggests that one is dealing with a structure at a parsec-scale distance from the active nucleus.
The unified scenarios have been shown to hold for as many as 97% of the AGN in X-ray selected samples (Mateos et al. 2010). Violations of its basic prediction (i.e.: a different classification from optical and X-ray spectroscopy) can be explained by the poor quality of the spectrum on which the classification was based, the variability in the AGN emission, the complexity of the absorber structure (Bianchi et al. 2012), or threshold effects on the AGN luminosity. For instance, a minimum Eddington ratio could be necessary for the broad line regions (BLR) to form (Nicastro 2000; Marinucci et al. 2012a).
It is crucial to validate the above structure model by constraining the geometry of the gas and dust in the AGN environment. Reverberation mapping of optical-UV lines against their ionizing continuum (Peterson et al. 2004) and monitoring changes in the column density covering highly obscured AGN (Maiolino et al. 2010, and references therein) constrain the location of the BLR clouds within a few lightdays in typical Seyfert-like objects (i.e., with total bolometric luminosity ≤ 1044 erg s-1). However, it is currently arguable whether X-ray obscuration can indeed be ascribed to BLR clouds in most obscured AGN, in particular in Compton-thick ones (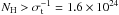 cm-1).
cm-1).
Recently, mid-IR interferometry has for the first time allowed for effectively “imaging” of the dusty component of the parsec-scale torus. In the three cases for which such measurements have been possible so far (NGC 1068, the Circinus Galaxy, and NGC 4151), the data are consistent with a two-temperature distribution of dust, with most of the obscuration occurring on scales smaller than 1 pc (Jaffe et al. 2004; Tristram et al. 2007; Burtscher et al. 2009).
The log of the observations analyzed in this paper.
Constraining the geometry of the X-ray reprocessing gas is currently possible only by studying the response of spectral components dominated by optically-thick reprocessing to variability of the primary continuum. These measurements are difficult, because they require simultaneous measurements of fluxes in at least two energy bands dominated by the AGN primary emission and by its reprocessing, respectively, on timesscales that are long enough to be able to detect the response of the latter to changes in the former. These timescales are likely to be months, at least. Dedicated monitoring campaigns of this kind are expensive, although the launch of the Swift satellite in 2004 (Gehrels et al. 2004), with its BAT X-ray transient monitoring instrument scanning continuously the high-energy sky in the 15–150 keV band, has opened a new window on this field.
In this paper we discuss flux variability in a Compton-reflection-dominated energy band on timescales of months to years in the nearby (z = 0.014) prototypical Seyfert 2 galaxy Markarian 3. Known since the dawn of X-ray astronomy, Markarian 3 hosts a heavily obscured AGN. The most prominent feature in its X-ray spectrum is a strong iron Kα fluorescent line (Awaki et al. 1991). The continuum in the 3 − 7 keV range is dominated by unabsorbed Compton-reflection (Georgantopoulos et al. 1999; Cappi et al. 1999). Iwasawa et al. (1994) discovered a variability in the hard (E > 4 keV) luminosity that is a factor of 3 in 3.6 years by comparing their ASCA observation in April 1993 with previous Ginga and BBXRT observations. The soft X-ray emission had remained constant over the previous 13 years.
The paper is organized as follows. In Sect. 2 we present the observations discussed in this paper and their data reduction. The spectral analysis is described in Sect. 3, where we also show light curves over the first decade of this century in energy bands dominated by different spectral components. We discuss the implication of our results in Sect. 4, focusing on three main aspects: the geometry of optically-thick reprocessing matter, the location of the iron Kα line emitting gas, and the variability of the soft X-ray emission. We summarize our main results in Sect. 5.
In this paper, energies are shown in the source’s rest reference frame, statistical errors are calculated at the 1σ confidence level for one interesting parameter, and the following cosmological parameters were used to calculate luminosities: H0 = 70 km s-1 Mpc-1, Λ0 = 0.73, and ΩM = 0.27 (Bennett et al. 2003). At the distance of Markarian 3, 1″ corresponds to 270 pc.
2. Data reduction
In this paper we analyze Markarian 3 spectra obtained with imaging CCD cameras on-board Swift and XMM-Newton. The longest XMM-Newton observation (October 2000) is discussed in Bianchi et al. (2005), and Pounds et al. (2005). The log of the observations discussed in this paper is shown in Table 1.
2.1. XMM-Newton/EPIC-pn
In this paper we discuss only those spectra extracted with the EPIC-pn camera (Strüder et al. 2001). Markarian 3 was observed seven times in the early phase of the XMM-Newton mission using the full frame mode. The March 2012 observation was instead performed in timing mode. Raw scientific telemetry (observation data files) was reduced using SAS Version 12 (Gabriel et al. 2003), and the calibration files available on June 1, 2012. Spectra were extracted from calibrated event lists generated with the task epchain. The timing mode event list energy scale was corrected for any rate-dependent effect, which is, however, likely to be negligible due to the source flux level.
For imaging modes, source spectra were extracted using circular regions of 40″ radius centered on Markarian 3 optical coordinates (α2000 = 93.9015194°; δ2000 = 71.0375254°); background spectra were extracted from circular regions free of serendipitous contaminating sources on the same CCD quadrant as the boresight position, and corresponding to RAWY positions close to where Markarian 3 is located on the EPIC-pn boresight CCD, to ensure that a similar charge transfer efficiency correction applies.
For the timing mode observation, source spectra were extracted from a box in detector coordinates centered on RAWX = 36 and with a radius of five pixels (each pixel in the EPIC-pn camera corresponds to 4.4″). No constraints were applied to the pseudo-spatial coordinate RAWY, which represents the elapsed time during the observation in this mode. Background spectra were extracted from a nearby box centered on RAWX = 50 to ensure that the background spectrum represent the true background underneath the source positiont as faithfully as possible. The background represents about 75% of the source level in the 4 − 10 keV energy band. The emission profile along the RAWX coordinate shows a gradual decrease (once the signal corresponding to Markarian 3 is removed) by about 5% between RAWX = 27 and RAWX=55. Through a linear interpolation to RAWX=36, we estimate that our background spectrum could underestimate the true background level underneath the source by about 3%. We have added this factor in the analysis of the timing mode spectrum.
Response files appropriate for each observation were generated with the SAS tasks rmfgen and arfgen. The EPIC-pn response is known to be stable within 3% (Sartore et al. 2012).
2.2. Swift/XRT
Swift/XRT (Burrows et al. 2005) observed Markarian 3 on nine occasions. However, as two observations have relatively short exposure time (2 ks and 55 s respectively), we consider here seven Swift XRT observations with exposure times longer than 5 ks. We extracted Swift XRT products from the cleaned photon counting event files following the procedures described in The Swift XRT Data reduction Guide V.1.21. Spectra of Markarian 3 were extracted from circular regions of radius 60″, while background spectra were obtained from larger (100″ in radius) source-free regions close to the source. We used the standard response files for the photon counting mode with grades 0 to 12, which are part of the current Swift XRT calibration database, taking the observation epoch into account. Ancillary files have instead been created for each observation using the xrtmkarf task for the specific source position. After checking that the individual spectra were consistent, we merged the spectra from ObsID 00035460002 and 00035460003 (3 days apart) and from ObsID 00035460004 and 00035460005 (1 day apart). As a result, five X-ray XRT spectra of of Markarian 3 are considered here.
2.3. Swift/BAT
The Swift-BAT (Barthelmy et al. 2005) data were processed with the Bat_Imager code (Segreto et al. 2010). The 15 − 150 keV light curve, as well as those in three energy bands of 15–30, 30 − 70, and 70 − 150 keV, were obtained producing a set of all-sky maps each covering 15 days, starting from December 2005 up to March 2012, and extracting the count rate and its error from the pixel corresponding to the source position in each of the maps.
3. Spectral analysis
All the EPIC-pn and XRT spectra were independently analyzed in the nominal 4–10 keV band, where Compton-reflection dominates (Iwasawa et al. 1994). However, the upper bound is observation-dependent (see Fig. A.1) as XRT dost not confidently detect the source up to 10 keV in most observations. Background-subtracted spectra were fitted using the Cash statistics (C; Cash 1976) for us to be able to use the natural instrumental spectral binning.
Our first goal was to measure the light curves of the fluxes of spectral components associated with reflection of the primary continuum by optically thick matter. We therefore fit the spectra with the following phenomenological model, Mpr (“pure reflection”):
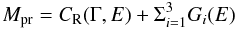 where CR is a Compton-reflection continuum component (Magdziarz & Zdziarski 1995), and the Gi are unresolved (i.e., intrinsic width assumed to be equal to 0) Gaussian emission lines. In the Compton-reflection component we assumed no high-energy cut-off of the primary continuum (as this will most likely fall outside the EPIC-pn and XRT sensitive bandpass: Dadina 2007), solar abundances (according to Anders & Grevesse 1983), and a 45° inclination angle between the normal to the plane of the Compton-reflecting slab and the line-of-sight. The only free parameter in this component, apart from its normalization, is therefore the photon index of the power-law primary continuum, Γ. The centroid energies of the Gaussian profiles were fixed to 6.4, 6.7, and 6.96 keV, respectively, corresponding to fluorescent emission from neutral or mildly ionized iron, the resonant component of the He-like triplet, and the H-like iron line, respectively. Sako et al. (2000) report an energy of 6.685 keV (without error) for the Heα from their analysis of the Chandra/HETG spectrum of Markarian 3. This energy is intermediate between that of the resonant, the intercombination (6.668–6.682 keV), and the forbidden (6.637 keV) components. Neither the EPIC-pn nor the Swift/XRT spectra can constrain this parameter. We have therefore opted for fixing the centroid energy to the laboratory value of the resonant component following the results after Bianchi et al. (2005), which rule out an important contribution from the forbidden component. The results presented in this paper are insensitive to this choice. The intensity of the He-like and H-like lines can only be constrained in the longest XMM-Newton observation: I6.7 = (7.0 ± 1.4) × 10-6 and I6.96 = (5.5 ± 1.4) × 10-6 photons cm-2 s-1, respectively. In the other observations, they were fixed to the above best-fit values. This assumption is astrophysically justified, because a substantial fraction of them is likely to produced in the X-ray narrow line regions, extended on scales of a few hundred parsecs (see Bianchi et al. 2006 for a quantitative discussion of this point).
where CR is a Compton-reflection continuum component (Magdziarz & Zdziarski 1995), and the Gi are unresolved (i.e., intrinsic width assumed to be equal to 0) Gaussian emission lines. In the Compton-reflection component we assumed no high-energy cut-off of the primary continuum (as this will most likely fall outside the EPIC-pn and XRT sensitive bandpass: Dadina 2007), solar abundances (according to Anders & Grevesse 1983), and a 45° inclination angle between the normal to the plane of the Compton-reflecting slab and the line-of-sight. The only free parameter in this component, apart from its normalization, is therefore the photon index of the power-law primary continuum, Γ. The centroid energies of the Gaussian profiles were fixed to 6.4, 6.7, and 6.96 keV, respectively, corresponding to fluorescent emission from neutral or mildly ionized iron, the resonant component of the He-like triplet, and the H-like iron line, respectively. Sako et al. (2000) report an energy of 6.685 keV (without error) for the Heα from their analysis of the Chandra/HETG spectrum of Markarian 3. This energy is intermediate between that of the resonant, the intercombination (6.668–6.682 keV), and the forbidden (6.637 keV) components. Neither the EPIC-pn nor the Swift/XRT spectra can constrain this parameter. We have therefore opted for fixing the centroid energy to the laboratory value of the resonant component following the results after Bianchi et al. (2005), which rule out an important contribution from the forbidden component. The results presented in this paper are insensitive to this choice. The intensity of the He-like and H-like lines can only be constrained in the longest XMM-Newton observation: I6.7 = (7.0 ± 1.4) × 10-6 and I6.96 = (5.5 ± 1.4) × 10-6 photons cm-2 s-1, respectively. In the other observations, they were fixed to the above best-fit values. This assumption is astrophysically justified, because a substantial fraction of them is likely to produced in the X-ray narrow line regions, extended on scales of a few hundred parsecs (see Bianchi et al. 2006 for a quantitative discussion of this point).
Best-fit values of the free parameters in Mpr (Γ, F4 − 5, I6.4, C/ν) and of the phenomenological model used to fit the 0.5–2 keV energy band (Γs, F0.5 − 1.5).
 |
Fig. 1 Light curves of the: observed flux in the 4–5 keV energy band (upper panel); intensity of the Fe Kα line (medium panel); observed flux in the 0.5–1.5 keV energy band (lower panel). The numbers in each panel indicate the chi-squared value for a fit against a constant versus the number of degrees of freedom. Filled circles: XMM-Newton/EPIC; empty circles: Swift/XRT; filled star: Suzaku. The scale on the y-axis in all panels corresponds to ± 50% of the mean level (dotted lines). |
Mpr does not leave unaccounted for residuals in any of the spectrum. The best-fit parameter values are reported in Table 2. Figure 1 (upper and medium panels) shows the light curves of the observed flux in the 4–5 keV band and of the intensity of the Kα fluorescent iron line. We have also added the results of the Suzaku pointed observation of Markarian 3 discussed by Awaki et al. (2008; Obs.#1000040010)2 We decided not to analyze the XIS spectra again, because they were reduced and published by a highly experienced team, and no significant change in the calibration has occurred above 3 keV since the time of the original data reduction in Awaki et al. (2008). The 4–10 keV energy band, chosen because it is dominated by emission-line free Compton-reflection, shows a variability dynamical range over 70%. Similar dynamical ranges are seen when comparing the XMM-Newton or Swift observations, ruling out cross-calibration effects (which should be anyhow at most 10%; Tsujimoto et al. 2011). The chi-squared for a fit against a constant, 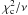 , is 199.9/13. On the other hand, the iron line light curve exhibits a lower variability dynamical range. The
, is 199.9/13. On the other hand, the iron line light curve exhibits a lower variability dynamical range. The 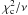 value is 34.1/13. The two quantities are very weakly correlated (Fig. 2). A linear fit
value is 34.1/13. The two quantities are very weakly correlated (Fig. 2). A linear fit 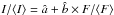 yields3: â = 0.7 ± 0.2 and
yields3: â = 0.7 ± 0.2 and 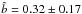 . The two-side significance of the Spearman’s rank correlation coefficient is only ≃ 31% only. This indicates that the equivalent width (EW) is not constant. However, care must be exercised in interpreting this result, as well as the low
. The two-side significance of the Spearman’s rank correlation coefficient is only ≃ 31% only. This indicates that the equivalent width (EW) is not constant. However, care must be exercised in interpreting this result, as well as the low 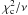 of the Fe Kα intensity light curve, because the statistical uncertainties on its measurements are a factor of 2–3 larger than those on the 4–5 keV Compton flux. To make a more quantitative assessment of the correlation likelihood (or lack thereof) between the observables in Fig. 2, we performed Monte-Carlo simulations of the Fe Kα intensity light curve, assuming that it follows the same relative trend (in units of ratio against the mean) as the measurements of the 4–5 keV flux. In astrophysical terms, the simulated scenario assumes that the continuum Compton-reflection and the Fe line intensity simultaneously respond to changes in the same primary continuum. For each observation, 104 realizations of a Gaussian distribution were drawn from a random sample, whose mean is the Fe line intensity aligned to the Compton-flux and whose standard deviation is the measured statistical uncertainty on the Fe line intensity. For each simulated light curve, we calculated the slope of the best linear fit between the Compton flux and the simulated Fe line intensity. In Fig. 3 we compare the distribution of the simulated slopes with the measured slope. The probability of getting a value of
of the Fe Kα intensity light curve, because the statistical uncertainties on its measurements are a factor of 2–3 larger than those on the 4–5 keV Compton flux. To make a more quantitative assessment of the correlation likelihood (or lack thereof) between the observables in Fig. 2, we performed Monte-Carlo simulations of the Fe Kα intensity light curve, assuming that it follows the same relative trend (in units of ratio against the mean) as the measurements of the 4–5 keV flux. In astrophysical terms, the simulated scenario assumes that the continuum Compton-reflection and the Fe line intensity simultaneously respond to changes in the same primary continuum. For each observation, 104 realizations of a Gaussian distribution were drawn from a random sample, whose mean is the Fe line intensity aligned to the Compton-flux and whose standard deviation is the measured statistical uncertainty on the Fe line intensity. For each simulated light curve, we calculated the slope of the best linear fit between the Compton flux and the simulated Fe line intensity. In Fig. 3 we compare the distribution of the simulated slopes with the measured slope. The probability of getting a value of 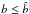 is ≤ 10-4.
is ≤ 10-4.
 |
Fig. 2 Intensity of the Fe Kα against the observed flux in the 4–5 keV energy band. The dotted line indicates the locus of constant line EW, normalized to the value measured during the deepest XMM-Newton observation (October 2000). The dashed line indicates the linear best fit, whereas the dot-dashed lines indicate the envelope corresponding to the 1σ uncertainties on the best-fit parameters. |
Variation in the flux in the 4–5 keV energy band could be due to a change in the Compton-reflected flux in this band, as well as to the emergence of different spectral components. It is in principle possible, for instance, that a reduction of the photoelectric column density covering the primary AGN emission brings a fraction of the primary emission into this energy band during some of the observations presented in Fig. 1. The intrinsic spectral indices yielded by Mpr are significantly flatter than typically observed in Seyfert galaxies (Bianchi et al. 2009a) and measured in X-ray broad-band observations of Markarian 3 (Cappi et al. 1999; Awaki et al. 2008). While we warn against interpreting Γ in Mpr as a reliable measurement of the photon index of the primary continuum on spectra with a small sensitive bandpass, the systematic flat spectral indices may indicate that a different spectral model is required to properly fit the data.
To test the impact that different origins for the spectral variability may have on our measurements of the Compton-reflection variability, we fit the EPIC-pn and XRT spectra with two alternative models. These models were applied to the EPIC-pn and XRT spectra discussed in this paper under the same conditions as Mpr. In particular, we fit the data in the same energy band: 4–10 keV. Because we want to address the flat spectral indices yielded by Mpr, in the remainder of this section we fix the value of this parameter to the one determined by Awaki et al. (2008; Γint ≡ 1.8) from their analysis of the Suzaku observation of Markarian 3, unless otherwise specified. This choice is justified by the fact that the spectral coverage of the scientific payload on board Suzaku up to several tens of keV allows one to better constrain the intrinsic shape of the primary continuum in such an obscured source.
 |
Fig. 3 Distribution of slopes of the best liner fit between the 4–5 keV Compton fluxes and Fe line intensities, when the latter are simulated assuming that they responded simultaneously to the same primary emission. The vertical line indicates the measured slope |
unobscured reflection plus obscured transmission. We assumed the full continuum model as discussed in Bianchi et al. (2005):
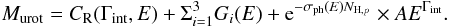 There is a strong correlation between the primary spectral index and the iron abundance of the Compton-reflection component (see, e.g., the discussion in Bianchi et al. 2005), primarily driven by the depth of the neutral iron photo-absorption edge. We therefore required ZFe to vary within the confidence interval as determined from the deepest XMM-Newton observation: ZFe = 0.43 ± 0.09 Z⊙. The photoelectric cross-section σph(E) is according to the Tübingen-Boulder model with the associated abundances (Wilms et al. 2000), and also includes the contribution from optically-thin Compton-scattering4. The typical column densities measured in the EPIC-pn spectra are NH,p ≃ 1.2 − 1.6 × 1024 cm-2. In the deepest EPIC-pn observations, NH,p = (1.19 ± 0.06) in October 2000 and
There is a strong correlation between the primary spectral index and the iron abundance of the Compton-reflection component (see, e.g., the discussion in Bianchi et al. 2005), primarily driven by the depth of the neutral iron photo-absorption edge. We therefore required ZFe to vary within the confidence interval as determined from the deepest XMM-Newton observation: ZFe = 0.43 ± 0.09 Z⊙. The photoelectric cross-section σph(E) is according to the Tübingen-Boulder model with the associated abundances (Wilms et al. 2000), and also includes the contribution from optically-thin Compton-scattering4. The typical column densities measured in the EPIC-pn spectra are NH,p ≃ 1.2 − 1.6 × 1024 cm-2. In the deepest EPIC-pn observations, NH,p = (1.19 ± 0.06) in October 2000 and 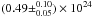 cm-2 in March 2012. Lower limits from the XRT spectra are in the range NH,p ≃ 0.6 − 1.4 × 1024 cm-2. We urge readers not to overinterpret the measurements of the absorber column density in this scenario. The column density of the absorber cannot be constrained by our data if the value of the photon index is left free to vary. Fixing the shape of the spectral index severely limits the size of the confidence interval parameter space.
cm-2 in March 2012. Lower limits from the XRT spectra are in the range NH,p ≃ 0.6 − 1.4 × 1024 cm-2. We urge readers not to overinterpret the measurements of the absorber column density in this scenario. The column density of the absorber cannot be constrained by our data if the value of the photon index is left free to vary. Fixing the shape of the spectral index severely limits the size of the confidence interval parameter space. -
obscured reflection. We added a photoelectric absorption component covering the Compton-reflection emission:
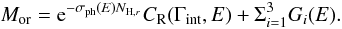 We again constrained ZFe = 0.43 ± 0.09 Z⊙. In astrophysical terms, Mor represents a scenario whereby the line-of-sight to the inner far side of the torus grazes the rim of its near side or crosses a dust lane in the host galaxy (Lamastra et al. 2008). Although gas from the torus rim is likely to be evaporated by the AGN radiation pressure, hence significantly ionized, we used in Mor a photoelectric model for cold matter, as the data do not require the ionization parameter as a further degree of freedom. We refrain from deriving any astrophysical inference from the measured column densities, due to the simplicity of the assumptions and to the statistical quality of most of the spectra analyzed in this paper. Not surprisingly, only the two deepest XMM-Newton observations require a column density that is significantly different from zero: Nh,r = 4.5 ± 0.6 in October 2000 and
We again constrained ZFe = 0.43 ± 0.09 Z⊙. In astrophysical terms, Mor represents a scenario whereby the line-of-sight to the inner far side of the torus grazes the rim of its near side or crosses a dust lane in the host galaxy (Lamastra et al. 2008). Although gas from the torus rim is likely to be evaporated by the AGN radiation pressure, hence significantly ionized, we used in Mor a photoelectric model for cold matter, as the data do not require the ionization parameter as a further degree of freedom. We refrain from deriving any astrophysical inference from the measured column densities, due to the simplicity of the assumptions and to the statistical quality of most of the spectra analyzed in this paper. Not surprisingly, only the two deepest XMM-Newton observations require a column density that is significantly different from zero: Nh,r = 4.5 ± 0.6 in October 2000 and 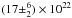 cm-2 in March 2012. In the other observations, the statistical quality of the spectra is the main driver behind upper limits in the range 1.7 − 6 × 1022 cm-2.
cm-2 in March 2012. In the other observations, the statistical quality of the spectra is the main driver behind upper limits in the range 1.7 − 6 × 1022 cm-2. 
Fig. 4 Spectrum of the October 2000 XMM-Newton observation (upper panel) and residuals in units of data/model ratio (lower panel) if a model of ionized reflection with Γint = 1.8 is applied.
-
ionized reflection. We replaced the Compton-reflection component in Mpr with a model that explicitly includes the ionization state of the reflector5, also producing the ionized iron lines that are empirically fit with Gaussian profiles in other models. This model is based on the calculation by Ross & Fabian (2005). If we assume Γint = 1.8, the model does not yield a good fit to the best-quality spectra (see, e.g., the results on the deepest XMM-Newton observation in Fig. 4). If left free to vary, the spectral index pegs to the minimum value allowed by the model (1.6), still leaving significant residuals. Even when applied to spectra with a lower statistical quality, where the formal quality of the fit is comparable to that yielded by Mpr, the model exhibits a) too broad an iron line profile and b) too shallow a photoelectric absorption edge with respect to the data. We therefore do not consider this model in this paper any longer.
 |
Fig. 5 Light-curve of the absorption-corrected 4–5 keV flux of the Compton-reflection component when models Mpr (upper panel; the same quantity as in the upper panel of Fig. 1), Mor (medium panel), and Murot (lower panel) are used. The units on the y-axis are the difference between the logarithm of the flux and its median. The dotted line indicates the median level. |
In summary, the flux associated to the Compton-reflection component varies does not depend on the spectral model used to fit the data analyzed in this paper (within the simple spectral models used). On the other hand, quantitative estimates of the variability pattern timescales do depend on the spectral modeling. The reader should bear in mind this important caveat over the rest of the paper. Long-term deeper monitoring of Markarian 3 would be required to break this degeneracy, where each individual spectrum has a statistical quality comparable to or better than the deepest EPIC-pn observation discussed in this paper.
Finally, in the lower panel of Fig. 1 we show the light curve in the 0.5–1.5 keV energy band. It was measured by fitting the spectra in the 0.5–2 keV with a phenomenological model constituted by a powerlaw (of photon index Γs) and seven unresolved Gaussian profiles, with energy and normalization fixed to the best-fit values obtained from the deepest XMM-Newton observations. We did not include the Suzaku measurement in this panel, because it is likely to be contaminated by the ROSAT source IXO30 (Bianchi et al. 2005; Awaki et al. 2008). Variability with a dynamical range of about ± 10% is also seen in this band (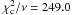 /12). Such a dynamical range is close to the systematic uncertainties in the cross-calibration among flying X-ray detectors in this energy range (Tsujimoto et al. 2011). This casts doubt on an astrophysical origin of these differences. We discuss this finding in more detail in Sect. 5.4 of this paper.
/12). Such a dynamical range is close to the systematic uncertainties in the cross-calibration among flying X-ray detectors in this energy range (Tsujimoto et al. 2011). This casts doubt on an astrophysical origin of these differences. We discuss this finding in more detail in Sect. 5.4 of this paper.
 |
Fig. 6 Light curve in the 4–5 keV energy band (filled circles) and the Swift/BAT light curve in the 15–150 keV energy band (empty squares). Both curves are normalized to their respective mean for direct comparison. |
4. Variability timescales in Markarian 3
In Fig. 6 we compare the 4–5 keV observed flux to the flux measured by the Swift/BAT in the 14-195 keV energy band. Both curves are normalized to their respective mean. The 4–5 keV points are calculated with the Mpr model.
The variability observed in the BAT light curve could be due either to true changes in the intrinsic nuclear flux or to changes in the column densities covering the source of the primary emission. In the latter case we should see different variability patterns in light curves extracted in different BAT energy ranges, with the light curve extracted from the hardest band tracing the primary continuum most closely. In Fig. 7 we show the Markarian 3 BAT light curves in three bands, 15 − 30 keV, 30 − 70 keV, and 70 − 150 keV, together with their hardness ratios. They exhibit a qualitatively similar pattern. The hardness ratios are consistent with being constant, with 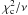 values of 19.7/43 and 22.3/41 for the 30–70/15–30 and the 70–150/30–70 keV hardness ratio, respectively.
values of 19.7/43 and 22.3/41 for the 30–70/15–30 and the 70–150/30–70 keV hardness ratio, respectively.
With the light curves shown in Figs. 6 and 7 we can estimate the following timescales:
-
The minimum variability timescale of the primary emission, τp. We define it from the shortest interval between two bins of the BAT light curve, which are inconsistent at the 95% confidence level. This quantity is basically constrained by the statistics of the BAT light curve. There are several consecutive bins, both in the full and in the energy-resolved BAT light curves, which are inconsistent at this statistical level. We conclude that τp ≲ 15 days. Significantly shorter (hours to days) timescales are common in Seyfert galaxies (Barr & Mushotzky 1986; McHardy et al. 2006), but they are basically inaccessible to us in such a heavily obscured source as Markarian 3.

Fig. 7 Swift/BAT Markarian 3 light curves in three bands, and their hardness ratios.
-
The maximum variability timescale of the Compton flux, τ. We define it as the minimum time interval between two bins of the Compton flux light curve differing at more than the 95% confidence level. It depends on the spectral model, owing to the larger statistical errors affecting the measurement of the Compton flux where more complex spectral models are used (Table 3).
The delay in the response of the Compton flux to variation in the primary continuum Δts We calculate the quantity
![$$ \chi^2 (\Delta t_{\rm s}) = \Sigma \left[ \left(F^n_{4-5}(\Delta t_{\rm s})-F^n_{14-195}\right)/\left(\sigma^2_{4-5}+\sigma^2_{14-195}\right) \right], $$](/articles/aa/full_html/2012/11/aa19946-12/aa19946-12-eq137.png) where
where 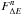 are the normalized fluxes in the ΔE energy range, σΔE are the corresponding statistical uncertainties, augmented by 5% to take possible systematic cross-calibration uncertainties into account, and Δts is a temporal shift applied only to the 4–5 keV flux data points. For this cross-correlation to be astrophysically meaningful (cf. Sect. 5.1), the BAT light curve must be binned with ΔtBAT > τ. We used the smallest integer multiple of 15 days fulfilling this relation.
are the normalized fluxes in the ΔE energy range, σΔE are the corresponding statistical uncertainties, augmented by 5% to take possible systematic cross-calibration uncertainties into account, and Δts is a temporal shift applied only to the 4–5 keV flux data points. For this cross-correlation to be astrophysically meaningful (cf. Sect. 5.1), the BAT light curve must be binned with ΔtBAT > τ. We used the smallest integer multiple of 15 days fulfilling this relation.
 |
Fig. 8 Probability of χ2(Δts) as a function of Δts for Mpr when ΔtBAT = 75 days. The dotted line indicates the 95% confidence level. |
Minimum variability timescale of the Compton-reflection component, τ, and delay in the response of the Compton-reflection to changes of the primary continuum, Δts.
In principle, the variable Compton-reflection component could contribute to the variability of the BAT light curves as well. While spectral decompositions in continuum components must been taken with a grain of salt when performed in spectral regions where the instrumental resolution is poor, the results of the Suzaku observation formally indicate that the Compton-reflection could contribute about one third of the total flux at 15 keV, and about 50% thereof above 30 keV (cf. Fig. 2 in Awaki et al. 2008). However, it is unlikely that the Compton-reflection contribute significantly to the variability above 15 keV on the following grounds: a) the short variability timescale of the BAT light curve; b) its energy invariance (Compton-reflection and primary continuum exhibit very different spectral shapes around the Compton peak at 30 keV); c) there is very little correlation between the 4–5 keV and the 15–150 keV light curves at zero time shift. The probability of χ2(Δts = 0) is ~6 × 10-4 for Mpr.
5. Discussion
5.1. Constraining the torus geometry through variability
In principle, the variability timescales determined in Sect. 4 can be used to constrain the location and geometry of the optically-thick reprocessor. We discuss in this section the method, its assumptions, and its limitations, as well as the results of its application to the monitoring campaign of Markarian 3 discussed in this paper.
If the primary continuum illuminating a slab of optically thick gas varies on a timescale τp, the variability of the primary emission can be fully diluted if the light crossing time across the reflecting part of the slab is more than τp. For all the spectral models discussed in this paper, τ ≫ τp (Table 3). Due to its finite size, the reprocessor will not respond to the instantaneous primary flux, but instead to an average over its own light-crossing time. This is why we impose the condition ΔtBAT > τ in our cross-correlation analysis (Sect. 4).
Under this condition, the delayed response of the reflected component to changes in the primary continuum can be used to constrain the distance between the AGN and the reflecting cloud, through simple light crossing-time arguments: Δl ~ cΔts, where Δl is the difference in optical path between the primary and the reflected radiation. If reflection occurs from the inner far side of the torus, d ~ Δl/2, where d is the distance between the reflecting cloud and the source of the illuminating continuum.
If reflection occurs in an individual cloud, the difference in optical-path length between photons coming from extreme regions of the cloud has to be smaller than its light-crossing cloud linear size. This puts a lower limit on its opening angle:
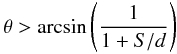 where S is the size of the reflecting cloud and d its distance from the primary source. For Mpr: S ≤ 0.05 pc, d ≳ 0.5 pc, θ ≳ 71°.
where S is the size of the reflecting cloud and d its distance from the primary source. For Mpr: S ≤ 0.05 pc, d ≳ 0.5 pc, θ ≳ 71°.
An independent estimate of the reflector opening angle can be derived from the opening angle of the ionization cone, θo. Capetti et al. (1995) derive θo > 55° from HST imaging of the NLR. This estimate is larger then previous estimates based on ground-based observations (Wilson & Tsvetanov 1994).
Ikeda et al. (2009) tried to constrain the geometry of the reflector by fitting the Suzaku time-averaged spectrum of Markarian 3 with Monte-Carlo simulations of the primary continuum emission by a Compton-thick accreting torus. The simultaneous measure of the reflected and the transmitted (above 10 keV) components may in principle allow the geometry to be constrained as well as the column density of the reflector (Murphy & Yaqoob 2009; Yaqoob 2012). Unfortunately, there is an intrinsic degeneracy between the opening angle and the inclination angle against the line-of-sight, which cannot be resolved even with the best-quality broad band spectral data available. Awaki et al. (2008) constrained the distance of the reflector within ≃ 1 pc due to the low-ionization and unresolved profile of the iron line. A similar analysis of the deepest EPIC-pn spectrum by Bianchi et al. (2005) has yielded an estimate of the inner size of the torus comprised between 0.3 and 0.5 pc.
While the formal geometrical constraints on the torus derived by our variability study are consistent with those obtained by other studies using different techniques, one might ask whether the implicit underlying picture of a single compact reflecting cloud with a size smaller than 0.05 pc is tenable. We present in the following further observational evidence that questions it.
5.2. The Kα iron line emission region
In the current picture of Compton-thick reprocessing in the AGN environment, the Compton-reflection continuum and the “narrow”6 iron Kα fluorescent line should be produced by the same reflecting gas. Indeed, these features almost invariably come together in the X-ray spectra of highly-obscured AGN. Existing exceptions (e.g., NGC 7213, Bianchi et al. 2008) are explained by reprocessing from Compton-thin gas in BLR clouds. If both components are produced by reprocessing the same emission, one may expect them to respond simultaneously to changes in the primary.
This does not seem to be the outcome of the X-ray spectroscopic campaign in Markarian 3. The intensity of the strong and ubiquitous iron Kα fluorescent line does not follow the variability of the Compton-reflected continuum (Fig. 2). This finding is puzzling. To explain it, one has to assume that the production of the line is decoupled from the underlying continuum. The line could be produced in Compton-thin clouds, while the Compton-reflection continuum could track Compton-thick clouds. Several mechanisms can be invoked to explain the lack of a strong iron emission line from Compton-thick material. Ionization can suppress the emission line via resonant trapping (Matt et al. 1993) or full electron stripping. However, the data with the best statistical quality rule out this explanation (cf. Fig. 4). Alternatively, the Compton-thick clouds could be iron deficient. It is, however, unclear why abundances of different gaseous systems in the environment of the same AGN should be largely different. Furthermore, this hypothesis is inconsistent with the deep photoelectric absorption edge, which is clearly visible in all spectra (see, e.g., Fig. A.1). More importantly, there is no other evidence of any Compton-thin clouds in X-ray spectroscopic observations of Markarian 3, although they could not be detected along the same line-of-sight of the Compton-thick absorber.
To investigate this point further, we reanalyzed the zeroth order image of the Chandra/HETG observation of Markarian 3 originally presented in Sako et al. (2000). As they showed (cf. the Fig.1 in their paper), the soft X-ray emission is extended in an approximate east-west direction (the elongation direction corresponds to an astronomical position angle of 356°.6). Intensity profiles in three different bands: 0.5–3 keV, 3–6 keV, and 6 − 7 keV are shown in Fig. 9. We confirm that emission is primarily extended in the softest energy band along the east-west direction up to ≃ 4″ on the east side and ≃ 2″ on the west side. In the hard band (E ≥ 3 keV) an excess by ± 1″ ( ≃ 270 pc) is visible in the hardest bands along the north direction only (i.e., perpendicular to the extension of the X-ray NLR). However, there is no statistical difference between the Compton continuum and the iron fluorescence line profiles.
 |
Fig. 9 Intensity profiles measured from the 0th order image taken during the Chandra/HETG observation of Markarian 3 (Sako et al. 2000). From top: E-W; bottom: N-S, Symbols indicate energy bands: empty circles: 0.5–3 keV; filled squares: 3–6 keV; filled triangles: 6–7 keV. The dotted lines indicate the point spread function. From the innermost to the outermost profiles in each panel: 0.5–3 keV, 3–6 keV, and 6 − 7 keV, respectively. |
Extended soft X-ray (E ≤ 2 keV) emission on scales ranging from a few hundred parsecs to a few thousand parsec has been commonly discovered in highly obscured nearby AGN, almost invariably in morphological agreement with the optical NLR (Bianchi et al. 2006 and references therein). Extension in the hard energy band is much less common. Young et al. (2001) report hard X-ray extended emission, together with a tentatively detected iron line, in NGC 1068 on scales of ≃ 20″ (2.2 kpc), alongside a low surface brightness component up to ≃50″ (5.5 kpc). More recently, Marinucci et al. (2012b) have reported a clumpy and flattened ~150 pc structure in the hard band Chandra/ACIS image of NGC 4945. Compact hard X-ray emission in the Circinus galaxy (Sambruna et al. 2001), constrains the size of the Compton reflector to within 8 pc. In bright, nearby obscured AGN, mir-IR interferometry allows constraining the location and size of the dusty torus within a few parsecs (Jaffe et al. 2004; Meisenheimer et al. 2007; Tristram et al. 2007). While the X-ray and IR studies indicate that dusty structures in the nuclear environment of AGN are extended on scales from a fraction to a hundred parsecs, we stress that the two techniques probe two different phases of the obscuring matter in the nuclear environment. X-ray direct imaging and variability are sensitive to the gaseous phase, whereas IR measurements probe the dust component.
5.3. Implications for the AGN structure model
The results presented in this paper favor a complex structure of the optically-thick absorber/reflector in Markarian 3. X-ray energy-dependent cross-correlation results favor a reflecting cloud at a distance of ≳0.5 pc. On the other hand, the variability of the Compton-reflection component on scales of ≲64−150 days (depending on the spectral model) suggests that the variability episodes presented in this paper might be dominated by small clouds, implying a large opening angle, i.e. a small covering factor. We discovered a puzzling lack of correlation between the Compton-reflection flux and the Fe Kα line intensity from our X-ray monitoring (Fig. 3; correlation probability ≲10-4). Furthermore, at least part of the reflection occurs on scales as large as 300 pc (Fig. 9). Indirect evidence for optically thick reprocessing of the primary radiation with a large covering fraction comes from the fact that Markarian 3 is a strong mid-IR emitter. It is one of the prototypical AGN-dominated Type 2 objects in mid-IR continuum (Deo et al. 2009). This also represents indirect evidence in favor of an extended structure reprocessing the AGN emission into the IR band.
In summary, we report various (and partly conflicting) evidence of optically-thick reprocessing of the AGN primary emission in Markarian 3 on a variety of different spatial scales, from a fraction to hundreds of parsecs.
Comparing these findings with other Compton-thick AGN in the local Universe unveils a similar variety, although detecting variability in the Compton-reflection component is difficult and therefore rare. In NGC 4945, the historical (Chandra, Suzaku and XMM-Newton) light curve of the reflected component remains constant within < 10% despite the strong intrinsic variability of the Swift/BAT light curve on time scales longer than one year (Marinucci et al. 2012b). The constant flux of the reflected components over a monitoring campaign covering almost a decade was reported in NGC 5506 (Guainazzi et al. 2010). On the other hand, a delayed response of the Kα iron line and Compton-reflection to a decrease in the primary flux by a factor ≃ 20 in 16 years constrained the torus to be located at about 3.2 pc from the AGN in NGC 2992 (Weaver et al. 1996). Variability by about 25% of the iron Kα line on timescales of about one year was reported by different authors in the unobscured Seyfert NGC 4151 (Perola et al. 1986; Takahashi et al. 2002; Zdziarski et al. 2002; Schurch et al. 2003), suggesting that the emitting region is about 0.03 pc from the nucleus.
One possible explanation for these apparently contradictory results is that the absorber is clumpy. Qualitatively, reflection on different spatial scales requires that absorption-free lines-of-sight to the active nucleus must exist for clouds located at various distances. The case for a clumpy torus was originally made by Krolik & Begelman (1998), and more recently fully developed in the calculations of Nenkova et al. (2002, 2008). While strong direct observational evidence exists for a clumpy absorber on scales of the BLR in several nearby AGN from X-ray variability studies (Elvis et al. 2004; Risaliti et al. 2005; Puccetti et al. 2007; Bianchi et al. 2009b; Maiolino et al. 2010; Risaliti et al. 2011), evidence of the torus clumpiness is mainly found by comparing between torus models and multiwavelength spectral energy distributions. A compact, pc-scale torus can hardly reproduce the multi-temperature IR emission (Pier & Krolik 1992). Large-scale dusty torii can reproduce the observations (Granato & Danese 1994), but they are no longer favored given the IR interferometric evidence of very compact warm dust structures surrounding nearby obscured AGN (see, however, NGC 4945; Marinucci et al. 2012b).
Recently, Eliztur (2012) has proposed that the complex structure of the absorber/reflecting matter in the AGN environment should lead us to revise our interpretation of the AGN unification scenario. Its strictest formulation postulates that the orientation with respect to an azimuthally symmetric obscuring structure is the only driving factor in the classification of an AGN. Elitzur suggests that this view should be replaced by a probabilistic interpretation, whereby the classification of a radio-quiet AGN would depend on the covering factor distribution of the obscuring matter. “Type 2” would be more likely identified in AGN surrounded by matter with a higher covering factor. A less extreme view, where the Poissonian fluctuations in the number of optically thick clouds on scales comparable to or lower than the BLR are superposed on the standard formulation of the unified scenario, is discussed by Matt (2000) and Bianchi et al. (2009a,b).
Markarian 3 is one of the few obscured AGNs in the local universe, where evidence of AGN primary emission reprocessing by optically thick gas on scales from a fraction of to several hundred parsecs have been reported. It may represent one of the best laboratories for testing these scenarios with future observations in X-rays as well as in other wavelengths. ALMA is expected to give a paramount contribution to our understanding of the circumnuclear dusty torus.
5.4. The variability in the soft X-ray band
The soft X-ray (E ≤ 3 keV) flux history in Markarian 3 also exhibits significant variations around a mean of ≃ 7 × 10-13 erg cm-2 cm-1. The dynamical range is around ± 10%. This is within the typical systematic uncertainties in the flux determination between the EPIC-pn and the XRT detector (Tsujimoto et al. 2011). Indeed, the variability pattern is mainly observed by comparing between the EPIC-pn and the XRT observations, although the difference (XRT yielding systematically lower fluxes) is the opposite of what Tsujimoto et al. (2011) measured. A 5% difference in the X-ray flux measured by XMM-Newton in 2000 − 2002 and in 2012 could be affected by uncertainties in the background subtraction in the most recent observation (see Sect. 2). While we stress that further higher quality measurements are required to confirm this finding, we discuss briefly in this section some of its possible implications.
Bianchi et al. (2006) estimate that about 10% of the emission in this band is unresolved in the Chandra/ACIS image. Variability by a factor ≃ 100% of this compact component (associated to the innermost region of the NLR) could account for the observed variability pattern. Alternatively, the observed variability could be due to primary emission transmitted through a partial covering absorber. In the Palermo BAT Catalogue (Cusumano et al. 2010), Markarian 3 is detected with a 15 − 150 keV flux of (1.18 ± 0.03) × 10-11 erg cm-2 cm-1 and a spectral index ΓBAT = 1.74. The extrapolation of this flux into the 0.5 − 1.5 keV energy band (assuming a simple power-law of photon index ΓBAT) is ≃ 4.4 × 10-11 erg cm-2 cm-1. The observed flux is about 1.5% of this extrapolation. Such a fraction is usual in Compton-thin AGN (Risaliti 2002). See also Paggi et al. (2012) for the detection of variability in the soft X-ray spectrum of Mkn 573.
6. Conclusions
The main conclusions of this paper can be summarized as follows.
-
We report on a study of the decade-long X-ray flux variability in Markarian 3 in the 4–10 keV energy band, dominated by Compton-reflection of the primary AGN emission. The shortest variability timescale is ≲ 64 days, as measured by the shortest interval between two statistically inconsistent measurements.
-
Assuming that the light curve of the Compton-reflection-dominated energy band and that of the 15–150 keV energy band are correlated, with the former lagging behind the latter, the minimum measured delay is ≳ 1200 days.
-
The intensity of the iron Kα emission line is uncorrelated to the flux in the Compton-reflection-dominated band. This suggests that the bulk of the iron line is emitted in a different, more extended structure. Energy-resolved analysis of existing Chandra data indicates a region of the extended emission of both the line-free Compton-reflection continuum and of the Fe Kα line up to ~300 pc to the north of the active nucleus
Still, the constraints on the geometry of the reprocessing matter in Markarian 3 depend on the details of the spectral modeling, owing to the coarse X-ray monitoring in the Compton-reflection-dominated energy band, as well as to the statistical quality of the available data. We intend to tighten them in the near future, by pursuing a specific observational monitoring program. The perspectives offered by the successful launch of NuSTAR (Harrison et al. 2010) are particularly promising. It is reasonable to assume that at least part of the material reflecting the intrinsic continuum is also responsible for the absorption along the line-of-sight. In this case the variability of the measured line-of-sight may provide additional constraints. These measurements are virtually impossible now, but may be possible thanks to the increased sensitivity of NuSTAR at higher energies than the photoelectric cut-off. Similar measurements may also be possible with Astro-H in the near future.
Markarian 3 was observed also by the Chandra/HETG in combination with ACIS-S exactly seven months before the first XMM-Newton observation. We downloaded the spectrum from the TGCat archive, and analyzed it using the same procedure and model as the EPIC-pn and XRT spectra. While the intensity of the iron Kα line is comparatively well constrained [I6.4 = (5.0 ± 0.5) × 10-5 erg cm2 s-1; Sako et al. 2000], the 4–5 keV Compton flux is not (log 10(F4 − 5) = −12.8 ± 0.7; cf. Table 2). We therefore do not discuss these data in our paper.
In this context we employed the implementation cabs in Xspec for comparison with previous works, despite the problems described in Murphy & Yaqoob (2009) which should discourage its use for Compton-thick absorbers. They primarily affect the determination of the absorption-corrected luminosity of the obscured primary, a measurements in which we are not interested within the scope of this paper.
We use the term “narrow” here to identify emission line features, whose profile is not broadened and skewed by relativistic effects in X-ray illuminated accretion disks a few gravitational radii from the black hole event horizon (Fabian et al. 1989).
Acknowledgments
Based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA. Financial support for this work was partly provided by the Spanish Ministry of Science and Innovation through grant AYA2010-21490-C02-02. We are grateful to the referee, Dr. Stefano Bianchi, whose careful revision of the manuscript led to a substantial change in the structure of the paper, as well as to a more careful assessment of the astrophysical implications of our results.
References
- Alonso-Herrero, A., Ramos-Almeida, C., Mason, R., et al. 2011, ApJ, 736, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
- Antonucci, R. R. J., & Miller, J. S. 1985, ApJ, 297, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Awaki, H., Koyama, K., Inoue, H., & Halpern, J. O. 1991, PASJ, 43, 195 [NASA ADS] [Google Scholar]
- Awaki, H., Anabuki, N., Fukazawa, Y., et al. 2008, PASJ, 60, S293 [NASA ADS] [CrossRef] [Google Scholar]
- Barr, P., & Mushotzky, R. F. 1986, Nature, 320, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Barthelmy, S. D., Barbier, L. M., Cummings, J. R., et al. 2005, SSR, 120, 143 [Google Scholar]
- Barvainis, R. 1987, ApJ, 320, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. L., et al. 2003, ApJS, 148, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, S., Miniutti, G., Fabian, A. C., & Iwasawa, K. 2005, MNRAS, 360, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, S., Guainazzi, M., & Chiaberge, M. 2006, A&A, 448, 499 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, S., La Franca, F., Matt, G., et al. 2008, MNRAS, 389, L52 [NASA ADS] [Google Scholar]
- Bianchi, S., Guainazzi, M., Matt, G., Fonseca Bonilla, N., & Ponti, G. 2009a, A&A, 495, 421 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, S., Piconcelli, E., Chiaberge, M., et al. 2009b, ApJ, 695, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, S., Maiolino, R., & Risaliti, G. 2012, AdAST, 2012, 17 [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, SSR, 120, 165 [Google Scholar]
- Burtscher, L., Jaffe, W., Röttgering, H., Meisenheimer, K., & Tristram, K. R. W. 2009, MNRAS, 394, 1325 [NASA ADS] [CrossRef] [Google Scholar]
- Capetti, A., Macchetto, F., Axon, D. J., Sparks, W. B., & Boksenberg, A. 1995, ApJ, 448, 600 [NASA ADS] [CrossRef] [Google Scholar]
- Cappi, M., et al. 1999, A&A, 344, 857 [NASA ADS] [Google Scholar]
- Cash, W. 1976, A&A, 52, 307 [NASA ADS] [Google Scholar]
- Cusumano, G., La Parola, V., Segreto, A., et al. 2010, A&A, 510, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dadina, M. 2007, A&A, 461, 1209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deo, R. P., Richards, T. G., Crenshaw, D. M., & Kraemer, S. B. 2009, ApJ, 705, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Elitzur, M. 2012, ApJ, 747, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M. 2000, ApJ, 545, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M., Risaliti, G., Nicastro, F., et al. 2004, ApJ, 615, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Rees, M. J., Stella, L., & White, N. E. 1989, MNRAS, 238, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Gabriel, C., Denby, M., Fyfe, D. J., Hoar, J., & Ibarra, A. 2003, in Astronomical Data Analysis Software and Systems XIII, eds. F. Ochsenbein, M. Allen, & D. Egret (San Francisco: ASP), ASP Conf. Ser., 314, 759 [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Georgantopoulos, I., Papadakis, I., Warwick, R. S., et al. 1999, MNRAS, 307, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Granato, G. L., & Danese, L. 1994, MNRAS, 268, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Guainazzi, M., Bianchi, S., Matt, G., et al. 2010, MNRAS, 406, 2013 [NASA ADS] [Google Scholar]
- Harrison, F. A., Boggs, S., Christensen, F., et al. 2010, SPIE, 7732, 21 [NASA ADS] [Google Scholar]
- Ikeda, S., Awaki, H., & Terashima, Y. 2009, ApJ, 692, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Iwasawa, K., Yaqoob, T., Awaki, H., & Ogasaka, Y. 1994, PASJ, 46, L167 [NASA ADS] [Google Scholar]
- Jaffe, W., Meisenheimer, K., Röttgering, H. J. A., et al. 2004, Nature, 429, 47 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Krolik, J. H., & Begelman, M. C. 1988, ApJ, 329, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Lamastra, A., Perola, G. C., & Matt, G. 2008, A&A, 487, 109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magdziarz, P., & Zdziarski, A. A. 1995, MNRAS, 273, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Risaliti, G., Salvati, M., et al. 2010, A&A, 517, 47 [Google Scholar]
- Marinucci, A., Bianchi, S., Nicastro, F., Matt, G., & Goulding, A. D. 2012a, ApJ, 748, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Marinucci, A., Risaliti, G., Wang, J., et al. 2012b, MNRAS, 423, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Mateos, S., Carrera, F. J., Page, M. J., et al. 2010, A&A, 510, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matt, G. 2000, A&A, 335, L31 [NASA ADS] [Google Scholar]
- Matt, G., Fabian, A. C., & Ross, R. R. 1993, MNRAS, 261, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, G., Guainazzi, M., & Maiolino, R. 2003, MNRAS, 342, 422 [NASA ADS] [CrossRef] [Google Scholar]
- McHardy, I., Koerding, E., Knigge, C., Uttley, P., & Fender, R. P. 2006, Nature, 444, 730 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Meisenheimer, K., Tristram, K. R. W., Jaffe, W., et al. 2007, A&A, 471, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, K., & Yaqoob, T. 2009, MNRAS, 397, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Nenkova, M., Ivezić, Z., & Elitzur, M. 2002, ApJ, 570, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Nenkova, M., Sirocky, M. M., Nikutta, R., Ivezić, Z., & Elitzur, M. 2008, 685, 160 [Google Scholar]
- Nicastro, F. 2000, ApJ, 530, L65 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Paggi, A., Wang, J., Fabbiano, G., Elvis, M., & Karvoska, M. 2012, ApJ, in press [arXiv:1203.1279] [Google Scholar]
- Perola, G. C., Piro, L., Altamore, A., et al. 1986, ApJ, 306, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Pier, E. A., & Krolik, J. H. 1992, ApJ, 399, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Pounds, K. A., & Page, K. L. 2005, MNRAS, 360, 1123 [NASA ADS] [CrossRef] [Google Scholar]
- Puccetti, S., Fiore, F., d’Elia, V., et al. 2007, MNRAS, 377, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G. 2002, A&A, 386, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Risaliti, G., Elvis, M., Fabbiano, G., Baldi, A., & Zezas, A. 2005, ApJ, 623, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., Nardini, E., Salvati, M., et al. 2011, MNRAS, 410, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, R. R., & Fabian, A. C. 2005, MNRAS, 358, 211 [Google Scholar]
- Sako, M., Kahn, S. M., Paerels, F., & Liedahl, D. A. 2000, ApJ, 543, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Sambruna, R., Netzer, H., Kaspi, S., et al. 2001, ApJ, 546, L13 A [NASA ADS] [CrossRef] [Google Scholar]
- Sartore, N., Tiengo, A., Mereghetti, S., et al. 2012, A&A, 541, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schurch, N. J., Warwick, R. S., Griffiths, R. E., & Sembay, S. 2003, MNRAS, 345, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Segreto, A., Cusumano, G., Ferrigno, C., et al. 2010, A&A, 510, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takahashi, K., Inoue, H., & Dotani, T. 2002, PASJ, 54, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Tristram, K. R. W., Meisenheimer, K., Jaffe, W., et al. 2007, A&A, 474, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsujimoto, M., Guainazzi, M., Plucinsky, P. P., et al. 2011, A&A, 525, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weave, K. A., Nousek, J., Yaqoob, T., et al. 1996, ApJ, 458, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, A. S., & Tsvetanov, Z. I. 1994, AJ, 107, 1227 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, A. S., & Ulvestad, J. S. 1983, ApJ, 275, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Yaqoob, T. 2012, MNRAS, 423, 3360 [NASA ADS] [CrossRef] [Google Scholar]
- Young, A. J., Wilson, A. S., & Shopbell, P. L. 2001, ApJ, 556, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Leighly, K. M., Matsuoka, M., Cappi, M., & Mihara, T. 2002, ApJ, 573, 505 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A
In Fig. A.1 we show the spectra (upper panels) and residuals in units of data/model ratio (lower panels) for all the observations analyzed in this paper.
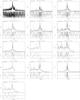 |
Fig. A.1 Spectra (upper panels) and residuals in units of data/model ratio (lower panels) when the baseline model is applied to the spectra of the observations discussed in this paper. The data were rebinned such that each data point corresponds to a sigma-to-noise ratio > 3 for visualization purposes only (the analysis was performed on the unbinned spectra). The spectrum of the deepest observation (October 2000; upper left) is shown with a coarser binning (minimum signal-to-noise ratio >10) in Fig. 4. |
All Tables
Best-fit values of the free parameters in Mpr (Γ, F4 − 5, I6.4, C/ν) and of the phenomenological model used to fit the 0.5–2 keV energy band (Γs, F0.5 − 1.5).
Minimum variability timescale of the Compton-reflection component, τ, and delay in the response of the Compton-reflection to changes of the primary continuum, Δts.
All Figures
 |
Fig. 1 Light curves of the: observed flux in the 4–5 keV energy band (upper panel); intensity of the Fe Kα line (medium panel); observed flux in the 0.5–1.5 keV energy band (lower panel). The numbers in each panel indicate the chi-squared value for a fit against a constant versus the number of degrees of freedom. Filled circles: XMM-Newton/EPIC; empty circles: Swift/XRT; filled star: Suzaku. The scale on the y-axis in all panels corresponds to ± 50% of the mean level (dotted lines). |
| In the text | |
 |
Fig. 2 Intensity of the Fe Kα against the observed flux in the 4–5 keV energy band. The dotted line indicates the locus of constant line EW, normalized to the value measured during the deepest XMM-Newton observation (October 2000). The dashed line indicates the linear best fit, whereas the dot-dashed lines indicate the envelope corresponding to the 1σ uncertainties on the best-fit parameters. |
| In the text | |
 |
Fig. 3 Distribution of slopes of the best liner fit between the 4–5 keV Compton fluxes and Fe line intensities, when the latter are simulated assuming that they responded simultaneously to the same primary emission. The vertical line indicates the measured slope |
| In the text | |
 |
Fig. 4 Spectrum of the October 2000 XMM-Newton observation (upper panel) and residuals in units of data/model ratio (lower panel) if a model of ionized reflection with Γint = 1.8 is applied. |
| In the text | |
 |
Fig. 5 Light-curve of the absorption-corrected 4–5 keV flux of the Compton-reflection component when models Mpr (upper panel; the same quantity as in the upper panel of Fig. 1), Mor (medium panel), and Murot (lower panel) are used. The units on the y-axis are the difference between the logarithm of the flux and its median. The dotted line indicates the median level. |
| In the text | |
 |
Fig. 6 Light curve in the 4–5 keV energy band (filled circles) and the Swift/BAT light curve in the 15–150 keV energy band (empty squares). Both curves are normalized to their respective mean for direct comparison. |
| In the text | |
 |
Fig. 7 Swift/BAT Markarian 3 light curves in three bands, and their hardness ratios. |
| In the text | |
 |
Fig. 8 Probability of χ2(Δts) as a function of Δts for Mpr when ΔtBAT = 75 days. The dotted line indicates the 95% confidence level. |
| In the text | |
 |
Fig. 9 Intensity profiles measured from the 0th order image taken during the Chandra/HETG observation of Markarian 3 (Sako et al. 2000). From top: E-W; bottom: N-S, Symbols indicate energy bands: empty circles: 0.5–3 keV; filled squares: 3–6 keV; filled triangles: 6–7 keV. The dotted lines indicate the point spread function. From the innermost to the outermost profiles in each panel: 0.5–3 keV, 3–6 keV, and 6 − 7 keV, respectively. |
| In the text | |
 |
Fig. A.1 Spectra (upper panels) and residuals in units of data/model ratio (lower panels) when the baseline model is applied to the spectra of the observations discussed in this paper. The data were rebinned such that each data point corresponds to a sigma-to-noise ratio > 3 for visualization purposes only (the analysis was performed on the unbinned spectra). The spectrum of the deepest observation (October 2000; upper left) is shown with a coarser binning (minimum signal-to-noise ratio >10) in Fig. 4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.