EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 547 (November 2012) A&A, 547 (2012) A94 Full HTML
Free Access
Issue
A&A
Volume 547, November 2012
Article Number A94
Number of page(s) 4
Section The Sun
DOI https://doi.org/10.1051/0004-6361/201219861
Published online 06 November 2012

© ESO, 2012

1. Introduction

The electromagnetic ion-cyclotron (EMIC) emissions are ubiquitous in the solar wind (Jian et al. 2009) and planetary magnetospheres (Nguyen et al. 2007). EMIC instability propagates nearly parallel (k ≃ k∥) to the large-scale magnetic field (B0) and is driven by an excess of transverse kinetic energy of ions, e.g., a temperature anisotropy T⊥ > T∥. These deviations from thermal equilibrium are usually enhanced by the suprathermal ion populations, i.e., the high-energy tails of the measured distributions (Christon et al. 1991; Collier et al. 1996; Fisk & Gloeckler 2006), which, overall, are properly described by the generalized power-law (Kappa) distribution functions (Pierrard & Lazar 2010; Lazar et al. 2012). The presence of suprathermal populations is therefore expected to change the EMIC instability conditions predicted by an idealized bi-Maxwellian model.

Studies are in general focused on the impact of suprathermal ion populations on the EMIC wave generation in magnetospheric plasma systems (Xue et al. 1993, 1996a,b; Chaston et al. 1997; Vega et al. 1998; Xiao et al. 2007; Mace et al. 2011), even though the observational data are poor (Christon et al. 1991) and not necessarily favorable to the existence of suprathermal ions in these environments. The growth rates Im(ω) ≡ γ (and their maximum values, γmax ≡ γm) exhibit two opposite behaviors with the increase of suprathermal population (i.e., decrease of the κ index), as they are either enhanced for plasmas with relatively low temperature anisotropies, or they are suppressed for higher anisotropies. 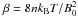This switch is not always at the same anisotropy, but seems to be dependent on the plasma beta (β=8nkBT/B02\hbox{$\beta = 8nk_{\rm B}T/B_0^2$}, kinetic energy reported to magnetic energy). An immediate conclusion is that a decrease of the power-index κ must lower the anisotropy thresholds corresponding to the lowest EMIC growth rates (marginal conditions of instability, γm → 0). But this evolution appears to disagree with the results of Xiao et al. 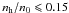(2007), which are restrained only to a particular (magnetopsheric) plasma model with a fractional composition of four (dominant) cold components (electrons, H+ (protons), He+, O+) and a minor hot population of protons (relative density \hbox{$n_{\rm h}/n_0 \leqslant 0.15$}) .

To clarify these properties, here I propose to refine the analysis describing the EMIC threshold conditions in close correlation with the evolution of the growth rates under the influence of suprathermal populations. The instability conditions are extended in the context of the solar wind, where the EMIC instability is enhanced selfconsistently by any excess of perpendicular temperature Tp,⊥ > Tp,∥ (Gary et al. 1997; Hellinger et al. 2006; Matteini et al. 2007). The mirror instability develops for the same conditions, and compressible magnetic field fluctuations are more visible in the observations (Bale et al. 2009), possibly because mirror modes are weakly propagating, i.e., Re(ω) ≡ ωr ≪ γ (Schlickeiser et al. 2011), whereas the EMIC instability in general grows faster (Gary et al. 1976), but also dissipates faster due to resonant cyclotron interactions with ions (ωr ≫ γ). For the same reason, the observed upper bounds of the solar wind plasma anisotropy seem to be better explained by the wave-particle scattering by mirror modes (Hellinger et al. 2006; Matteini et al. 2007).

According to the observations, the solar wind plasma is sufficiently hot (>105 K) and poor-collisional, and ion distributions are the best and overall fitted by the (anisotropic) Kappa distributions, which enclose both populations of the thermal (and less anisotropic) core and the highly anisotropic suprathermal halo (see Marsch 2006, and references therein). Thus, we assume a bi-Kappa distributed plasma, see the model distribution function in Eq. (3) from Lazar & Poedts (2009), and derive the anisotropy threshold conditions for the lowest EMIC growth rates.

Table 1

Proton temperature anisotropy fitting parameters from Eq. (5).

2. EMIC instability in bi-Kappa plasmas

Assuming the initially unperturbed plasma described by velocity distribution functions of bi-Kappa-type Fκ=1π3/2θ⊥2θ∥ Γ(κ+1)κ3/2Γ(κ−1/2) [1+v∥2κθ∥2+v⊥2κθ⊥2]−κ−1,∫d3v Fκ=1,\begin{eqnarray} \label{e0} F_{\kappa} && = {1 \over \pi^{3/2} \theta_{\perp}^2 \theta_{\parallel}} \, {\Gamma (\kappa + 1) \over \kappa^{3/2} \Gamma(\kappa -1/2)} \, \Biggl[1 + {v_{\parallel}^2 \over \kappa \theta_{\parallel}^2} + {v_{\perp}^2 \over \kappa \theta_{\perp}^2}\Biggr]^{-\kappa -1}, \notag \\ \int && {\rm d}^3v\, F_{\kappa} = 1, \end{eqnarray}(1)we start from the general dispersion relation for the electromagnetic (subluminal, ω2 ≪ k2c2) LH circularly polarized modes propagating along the regular magnetic field, e.g., Eq. 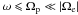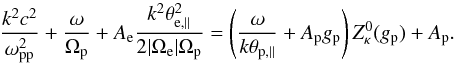(7) from Lazar & Poedts (2009), which, for small proton scales (\hbox{$\omega \leqslant \Omega_{\rm p} \ll |\Omega_{\rm e}|$}), reads k2c2ωpp2+ωΩp+Aek2θe,∥22|Ωe|Ωp=(ωkθp,∥+Apgp)Zκ0(gp)+Ap.\begin{eqnarray} {k^2c^2 \over \omega_{\rm pp}^2} + {\omega \over \Omega_{\rm p}} + A_{\rm e} {k^2 \theta_{\rm e,\parallel}^2 \over 2 |\Omega_{\rm e}|\Omega_{\rm p} } = \left( {\omega \over k \theta_{\rm p,\parallel}} + A_{\rm p} g_{\rm p} \right) Z^0_{\kappa} (g_{\rm p}) + A_{\rm p}. 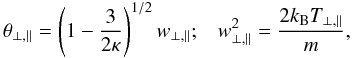\label{e1} \end{eqnarray}(2)Symbols used are for the generalized thermal velocities θ⊥,∥=(1−32κ)1/2w⊥,∥;w⊥,∥2=2kBT⊥,∥m,\begin{equation} \theta_{\perp,\parallel} = \left(1 -{3 \over 2 \kappa } \right)^{1/2} w_{\perp,\parallel} ; \;\;\; w_{\perp,\parallel}^2= {2k_{\rm B} T_{\perp,\parallel} \over m}, \label{e2} \end{equation}(3)temperature anisotropy Aa = Ta,⊥/Ta,∥, and Ωa = qaB0/(mac) and ωp,a = (4πnae2/ma)1/2 are, respectively, the gyrofrequency and the plasma frequency for electrons, a = e, and protons (or ions), a = p. The Kappa dispersion function 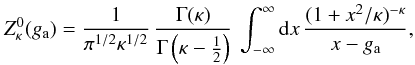Zκ0(ga)=1π1/2κ1/2 Γ(κ)Γ(κ−12) ∫−∞∞dx (1+x2/κ)−κx−ga,\begin{equation} Z^0_{\kappa}(g_{\rm a}) = {1 \over \pi^{1/2} \kappa^{1/2}} \, {\Gamma (\kappa) \over \Gamma \left( \kappa -{1 \over 2}\right)} \, \int_{-\infty}^{\infty} {\rm d}x \, {(1+x^2/\kappa)^{-\kappa } \over x - g_{\rm a}}, \label{e2bis} \end{equation}(4)

thumbnail Fig. 1

Effect of power-index κ = 2, 6, ∞ (Maxwellian) on the thresholds of the EMIC instability for three levels of the maximum growth rates γm/Ωp = 10-1 (top), 10-2 (middle) and 10-3 (bottom).

of the argument ga = (ω − Ωa)/(kθa,∥) with Im(ga) > 0, was introduced to describe a particular Kappa-Maxwellian plasma (Hellberg & Mace 2002), and to simplify in general the dispersion relations for the transverse modes (Lazar et al. 2008; Lazar & Poedts 2009). The electron influence is negligible at these time scales, and we consider isotropic (Ae = 1).

The EMIC instability thresholds are derived exactly numerically for the lowest levels of the maximum growth rates γm/Ωp = 10-4, 10-3, 10-2 and 10-1, which are the most relevant for the marginal instability condition (γ → 0). Values of the anisotropy thresholds are calculated for an extended range of the plasma beta parameter 0.01 ≤ βp,∥ ≤ 10, including the solar wind and magnetospheric plasma conditions. The inverse correlation law between temperature anisotropy, A = T⊥/T∥, and plasma beta, βp,∥, is obtained by fitting thresholds with (Gary & Lee 1994) 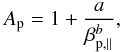Ap=1+aβp,∥b,\begin{eqnarray} A_{\rm p} = 1 + {a \over \beta_{\rm p,\parallel}^b}, \label{e4} \end{eqnarray}(5)where the fitting parameters a and b are shown in Table 1. Contours of the maximum growth rates (in units of Ωp) are displayed in Fig. 1.

The anisotropy thresholds decrease with plasma beta because for a hotter plasma we need lower anisotropies to ignite the EMIC instability. Moreover, the effect of suprathermal populations is not uniform as thresholds increase at high growth rates γm/Ωp = 10-1 (top), and decrease at lower growth rates γm/Ωp = 10-3 (bottom) and γ/Ωp = 10-4 (not displayed here). The switch between these two opposite behaviors is localized close to the level γm/Ωp = 10-2 (middle), where the anisotropy threshold does not change much with values of the power-index κ.

Growth rates of the EMIC instability are derived exactly numerically and are displayed in Figs. 2 and 3 for two different plasma beta conditions βp,∥ = 0.05 and βp,∥ = 1. One can recognize again the opposite effects of suprathermal populations suppressing the high growth rates (top panels) and enhancing the lower growth rates (bottom panels). To correlate with the instability threshold conditions, temperature anisotropies are chosen in the range of their threshold values in Fig. 1. Now it is clear that the lower thresholds (γm/Ωp = 10-3) close to the marginal instability conditions must decrease as the corresponding growth rates increase with an enhance of suprathermal populations (decrease of κ-index). A description of the growth rates close to the switch level (γm/Ωp = 10-2) is made in the middle panels of Figs. 2 and 3, where the influence of power index κ is again minimal. As was anticipated in the introduction, this threshold is not always the same but depends on plasma beta: for βp,∥ = 0.05 it is found to be about Ap = 3.2, while for βp,∥ = 1 it is found to be about Ap = 1.65. Over the switch level, growth rates of the EMIC instability are inhibited by the suprathermal ions, and the higher anisotropy thresholds (γm/Ωp = 10-1) must increase.

thumbnail Fig. 2

Effect of power-index κ = 2, 4, 6, 8, ∞ (Maxwellian) on the growth rates of the EMIC instability for βp,∥ = 0.05, and three values of the temperature anisotropies Ap = Tp,⊥/Tp,∥ = 5.0 (top), 3.2 (middle), 2.3 (bottom).

thumbnail Fig. 3

Effect of power-index κ =2, 4, 6, 8, ∞ (Maxwellian) on the growth rates of the EMIC instability for βp,∥ = 1.0, and three values of the temperature anisotropies Ap = Tp,⊥/Tp,∥ = 3.50 (top), 1.65 (middle), 1.50 (bottom).

The influence of suprathermals on the oscillatory frequency of the EMIC instability is shown in Fig. 4, with the remark that only for a sufficiently high anisotropy far from threshold conditions, the wave frequency decreases for lower values of the κ-index (top). Otherwise, there is not much influence on the wave frequency of growing modes (bottom) for low anisotropies close to thresholds.

The central conclusion is that marginal instability thresholds (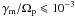\hbox{$\gamma_{\rm m} / \Omega_{\rm p} \leqslant 10^{-3}$}) are lowered by an increase of suprathermal populations leading to a maximum threshold for the ideal Maxwellian plasmas. This apparently disagrees with the previous results of Xiao et al. (2007), who found a uniform increase of the anisotropy thresholds (at γm/Ωp = 10-3, and 10-2) with the increase of suprathermal protons.

3. Influence of the cold (isotropic) populations

More investigations are needed, given the apparent disagreement between the new anisotropy thresholds found here and the results of Xiao et al. (2007), which suggest that a dominant cold ion population will temperate variations of the threshold conditions, leading to their uniform increasing. To clarify this question, one can use the model developed here, progressively decreasing the hot (suprathermal) proton fractional composition, and increasing the cold (heavier) ions composition. (The dispersion relation (2) changes accordingly.) This way enables one to approach the particular model of a dominantly cold plasma proposed in Xiao et al. (2007) for the outer magnetosphere near the the geostationary orbit, and follow step-by-step changes in the evolution of the instability thresholds.

Starting from the same model with two species, electrons and protons, but with two proton populations, one cold and dominant, and another one less dense and hot (suprathermal) with nh/n0 = 0.15 (where n0 is the electron density), the same effect of suprathermal populations lowering the EMIC instability thresholds and enhancing the growth rates in these regions is found. In the second step, heavier (cold) ions of He+ are added (nHe/n0 = 0.25) at the expense of cold protons (nc/n0 = 0.60, nh/n0 = 0.15), the effects of suprathermal protons on the anisotropy thresholds remain the same in the proton band, but it is reversed, increasing thresholds and suppressing growth rates in the He+ band. Finally, the exact model in Xiao et al. (2007) can be reproduced, adding heavier ions of O+ (nO/n0 = 0.05) at the expense of He+ (nHe/n0 = 0.20) and showing, indeed, an increase of thresholds in both EMIC bands of protons and He+. In this case the effect of suprathermals is minimized by a dominant presence of the heavier (cold) ions (O+), and does not agree with the new thresholds derived here for a bi-Kappa plasma.

thumbnail Fig. 4

Effect of power-index κ =2, 4, 6, 8, ∞ (Maxwellian) on the frequencies of the EMIC instability for βp,∥ = 0.05, and two values of the temperature anisotropies Ap = Tp,⊥/Tp,∥ = 3.50 (top), 1.50 (bottom).

4. Discussion and conclusions

The EMIC low-frequency wave fluctuations are regularly observed in the solar wind, and planetary magnetosphere as well as linear theory suggests that they are self-consistently driven by the kinetic anisotropy of ions. In response, these waves can easily dissipate, (re)accelerating and pitch-angle scattering the ions, which leads to the formation of suprathermal and highly anisotropic distributions. The energetic suprathermal protons (or heavier ions) are widely confirmed by observations, but their role in the EMIC wave generation or dissipation process is still unclear.

In this paper, the EMIC instability thresholds were described for a general bi-Kappa distributed plasma in close correlations with the growth rates, which exhibit a nonuniform dependence on the density of suprathermal populations and implicitly on the power-index κ. Consequently, the effect of suprathermal proton populations on the EMIC wave generation is found to be markedly dependent on the temperature anisotropy and the plasma beta. Thus, the lowest thresholds, 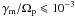\hbox{$\gamma_{\rm m} / \Omega_{\rm p} \leqslant 10^{-3}$}, close to the marginal stability conditions, decrease with the increase of suprathermal populations. This result is fully predicted by the enhanced fluctuations of this instability for sufficiently low temperature anisotropies, but apparently disagrees with the results in Xiao et al. (2007), which show a uniform increase of the thresholds. However, the model in Xiao et al. (2007) seems to underestimate the presence of Kappa protons by less than 15%, and overestimate to 25% the density of the heavier ions (H+, O+).

Distributions of ions, including protons, measured in the solar wind and magnetosphere exhibit a constant and finite thermal spread, and are overall better described by the Kappa distribution functions, which incorporate both the cooler core and the suprathermal halo. The same effect can be predicted for the RH-polarized branch of EMIC instabilities as was shown (Summers & Thorne 1992) from the increasing growth rate with decreasing of the power index κ > 2, for sufficiently low values of the plasma beta (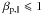\hbox{$\beta_{\rm p,\parallel} \leqslant 1$}) and the temperature anisotropy (Ap < 1). For high βp,∥ > 1, the increase of parallel temperature is constrained by the firehose instability (Lazar et al. 2011).

For higher anisotropies, far from threshold conditions, the presence of suprathermal protons has an opposite effect that suppresses the growth rates and increases the thresholds. This evolution does not apply to the marginal conditions of instability, but could be relevant in the context of an interplay with the mirror instability, which grows in the same conditions, but for which a classical bi-Maxwellian approach predicts growth rates lower than the EMIC instability. On the other hand, for very low power indices κ < 2, the effect on the growth rates (Mace et al. 2011), and, implicitly, on the thresholds can be opposite from the one outlined here, but this is not relevant for the solar wind and magnetospheric ions, which normally exhibit a power index κ > 2 (Collier et al. 1996).

Acknowledgments

The author acknowledges support by the Deutsche Forschungsgemeinschaft (DFG), grant Schl 201/21-1, and partial support from the EU Commission and Research Foundation Flanders (FWO) as FWO Pegasus Marie Curie Fellow (grant 1.2.070.13).

References

  1. Bale, S., Kasper, J. C., Howes, G. G., et al. 2009, Phys. Rev. Lett., 103, 211101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  2. Chaston, C. C., Hu, Y. D., & Fraser, B. J. 1997, Geophys. Res. Lett., 24, 2913 [NASA ADS] [CrossRef] [Google Scholar]
  3. Christon, S. P., Williams, D. J., Mitchell, D. G., et al. 1991, J. Geophys. Res., 96, 1 [NASA ADS] [CrossRef] [Google Scholar]
  4. Collier, M. R., Hamilton, D. C., Gloeckler, G., et al. 1996, Geophys. Res. Lett., 23, 1191 [NASA ADS] [CrossRef] [Google Scholar]
  5. Fisk, L. A., & Gloeckler, G. 2006, ApJ, 640, L79 [NASA ADS] [CrossRef] [Google Scholar]
  6. Gary, S. P., & Lee, M. A. 1994, J. Geophys. Res., 99, 11297 [NASA ADS] [CrossRef] [Google Scholar]
  7. Gary, S. P., Montgomery, M. D., Feldman, W. C., & Forslund, D. W. 1976, J. Geophys. Res., 81, 1241 [NASA ADS] [CrossRef] [Google Scholar]
  8. Gary, S. P., Wang, J., Winske, D., & Fuselier, S. A. 1997, J. Geophys. Res., 102, 27159 [NASA ADS] [CrossRef] [Google Scholar]
  9. Hellberg, M. A., & Mace, R. L. 2002, Phys. Plasmas, 9, 1495 [NASA ADS] [CrossRef] [Google Scholar]
  10. Hellinger, P., Travnicek, P., Kasper, J. C., & Lazarus, A. J. 2006, Geophys. Res. Lett., 33, L09101 [NASA ADS] [CrossRef] [Google Scholar]
  11. Jian, L. K., Russell, C. T., Luhmann, J. G., et al. 2009, ApJ, 701, L105 [Google Scholar]
  12. Kasper, J. C., Lazarus, A. J., & Gary, S. P. 2002, Geophys. Res. Lett., 29, 1839 [NASA ADS] [CrossRef] [Google Scholar]
  13. Lazar, M., & Poedts, S. 2009, A&A, 494, 311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Lazar, M., Schlickeiser, R., & Shukla, P. K. 2008, Phys. Plasmas, 15, 042103 [NASA ADS] [CrossRef] [Google Scholar]
  15. Lazar, M., Poedts, S., & Schlickeiser, R. 2011, A&A, 534, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Lazar, M., Schlickeiser, R., & Poedts, S. 2012, in Exploring the Solar Wind, InTech, ed. M. Lazar, 241 http://www.intechopen.com/books/exploring-the-solar-wind/ [Google Scholar]
  17. Mace, R. L., Sydora, R. D., & Silin, I. 2011, J. Geophys. Res., 116, A05206 [NASA ADS] [CrossRef] [Google Scholar]
  18. Marsch, E. 2006, Liv. Rev. Sol. Phys., 3, 1 [Google Scholar]
  19. Matteini, L., Landi, S., Hellinger, P., et al. 2007, Geophys. Res. Lett., 34, L20105 [NASA ADS] [CrossRef] [Google Scholar]
  20. Nguyen, S. T., Perez, J. D., & Fennell, J. F. 2007, J. Geophys. Res., 112, A12203 [NASA ADS] [CrossRef] [Google Scholar]
  21. Pierrard, V., & Lazar, M. 2010, Sol. Phys., 267, 153 [NASA ADS] [CrossRef] [Google Scholar]
  22. Schlickeiser, R., Lazar, M., & Skoda, T. 2011, Phys. Plasmas, 18, 012103 [NASA ADS] [CrossRef] [Google Scholar]
  23. Summers, D., & Thorne, R. M. 1991, Phys. Fluids B, 3, 1835 [NASA ADS] [CrossRef] [Google Scholar]
  24. Summers, D., & Thorne, R. M. 1992, J. Geophys. Res., 97, 16827 [NASA ADS] [CrossRef] [Google Scholar]
  25. Vega, P., Palma, L., & Elgueta, R. 1998, J. Plasma Phys., 60, 29 [NASA ADS] [CrossRef] [Google Scholar]
  26. Xiao, F., Zhou, Q., He, H., Zheng, H., & Wang, S. 2007, J. Geophys. Res., 112, A07219 [NASA ADS] [CrossRef] [Google Scholar]
  27. Xue, S., Thorne, R. M., & Summers, D., 1993, J. Geophys. Res., 98, 17475 [NASA ADS] [CrossRef] [Google Scholar]
  28. Xue, S., Thorne, R. M., & Summers, D., 1996a, J. Geophys. Res., 101, 15457 [Google Scholar]
  29. Xue, S., Thorne, R. M., & Summers, D., 1996b, J. Geophys. Res., 101, 15467 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Proton temperature anisotropy fitting parameters from Eq. (5).

In the text

All Figures

thumbnail Fig. 1

Effect of power-index κ = 2, 6, ∞ (Maxwellian) on the thresholds of the EMIC instability for three levels of the maximum growth rates γm/Ωp = 10-1 (top), 10-2 (middle) and 10-3 (bottom).
In the text
thumbnail Fig. 2

Effect of power-index κ = 2, 4, 6, 8, ∞ (Maxwellian) on the growth rates of the EMIC instability for βp,∥ = 0.05, and three values of the temperature anisotropies Ap = Tp,⊥/Tp,∥ = 5.0 (top), 3.2 (middle), 2.3 (bottom).
In the text
thumbnail Fig. 3

Effect of power-index κ =2, 4, 6, 8, ∞ (Maxwellian) on the growth rates of the EMIC instability for βp,∥ = 1.0, and three values of the temperature anisotropies Ap = Tp,⊥/Tp,∥ = 3.50 (top), 1.65 (middle), 1.50 (bottom).
In the text
thumbnail Fig. 4

Effect of power-index κ =2, 4, 6, 8, ∞ (Maxwellian) on the frequencies of the EMIC instability for βp,∥ = 0.05, and two values of the temperature anisotropies Ap = Tp,⊥/Tp,∥ = 3.50 (top), 1.50 (bottom).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.