| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | A95 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201016238 | |
| Published online | 06 November 2012 | |
Upper limits on the high-energy emission from gamma-ray bursts observed by AGILE-GRID⋆
1
Dip. di Fisica, Univ. di Trieste, via Valerio 2,
34127
Trieste,
Italy
e-mail: francesco.longo@ts.infn.it
2
INFN–Trieste, via Valerio 2, 34127
Trieste,
Italy
3
CIFS–Torino, c/o Dipartimento di Fisica, Univ. di Torino,
via Pietro Giuria
1, 10125
Torino,
Italy
4
Royal Institute of Technology (KTH), Stockholm, Sweden
5
The Oskar Klein Centre for Cosmoparticle Physics,
Stockholm,
Sweden
6
APC, Univ Paris Diderot, CNRS/IN2P3, CEA/Irfu, Obs de Paris, Sorbonne Paris Cité,
10 rue Domon
et Duquet, 75205
Paris,
France
7
Dept. of Physics and Astronomy, Uppsala University,
Box 516, 75120
Uppsala,
Sweden
8
Fakultät für Physik und Astronomie, Ruhr-Universität
Bochum, 44780
Bochum,
Germany
9
INAF/IAPS, via del Fosso del Cavaliere 100,
00133
Roma,
Italy
10
INFN–Pavia, via Bassi 6, 27100
Pavia,
Italy
11
INAF/IASF–Bologna, via Gobetti 101, 40129
Bologna,
Italy
12
INAF/IASF–Milano, via E. Bassini 15, 20133
Milano,
Italy
13 ASI Science Data Center (ASDC), ESRIN, 00044 Frascati ( RM),
Italy
14
INAF – Osservatorio Astron. di Roma, via di Frascati
33, 00040,
Monte Porzio Catone,
Italy
15
Dip. di Fisica, Univ. “Tor Vergata”, via della Ricerca Scientifica
1, 00133
Roma,
Italy
16
Dip. di Fisica, Univ. di Perugia, via Alessandro
Pascoli, 06123
Perugia,
Italia
17
Dip. di Fisica Generale “A. Avogadro”, via Pietro Giuria 1, Univ.
di Torino, 10125
Torino,
Italy
18
ENEA, via Martiri di Monte Sole 4, 40129
Bologna,
Italy
19
INFN–Roma “La Sapienza”, Piazzale A. Moro 2,
00185
Roma,
Italy
20
INFN–Roma “Tor Vergata”, via della Ricerca Scientifica
1, 00133
Roma,
Italy
21
INAF – Osservatorio Astronomico di Cagliari, localita’ Poggio dei
Pini, strada 54, 09012
Capoterra,
Italy
22
NASTRON, the Netherlands Institute for Radio
Astronomy, Postbus
2, 7990 AA,
Dwingeloo, The
Netherlands
23
Dip. di Fisica, Univ. dell’Insubria, via Valleggio
11, 22100
Como,
Italy
24
INFN–Milano Bicocca, Piazza della Scienza 3,
20126
Milano,
Italy
25 ENEA–Frascati, via E. Fermi 45, 00044 Frascati ( Roma),
Italy
26
INAF-IASF-Palermo, via U. La Malfa 153,
90146
Palermo,
Italy
27
Wits University, 1 Jan Smuts Avenue Braamfontein 2000,
Johannesburg, South
Africa
28
ASI, Viale Liegi 26, 00198
Roma,
Italy
Received: 30 November 2010
Accepted: 25 August 2012
Context. The detection and the characterization of the highenergy emission component from individual gamma-ray bursts (GRBs) is one of the key science objectives of the currently operating gamma-ray satellite AGILE, launched in April 2007. In its first two years of operation AGILE detected three GRBs with photons of energy larger than 30 MeV. One more GRB was detected in AGILE third operation year, while operating in spinning mode.
Aims. For the 64 other GRBs localized during the period July 2007 to October 2009 in the field of view of the AGILE Gamma-Ray Imaging Detector (GRID), but not detected by this instrument, we estimate the count and flux upper limits on the GRB high energy emission in the AGILE-GRID energy band (30 MeV−3 GeV).
Methods. To calculate the count upper limits, we adopted a Bayesian approach. The flux upper limits are derived using several assumptions on the high-energy spectral behavior. For 28 GRBs with available prompt spectral information, a flux upper limit and the comparison with the expected flux estimated from spectral extrapolation of the Band spectrum to the 30 MeV−3 GeV band are provided. Moreover, upper limits on the flux under the assumption of an extra power law component dominating the 30 MeV−3 GeV band are calculated for all GRBs and considering four different values for the spectral photon index. Finally, we performed a likelihood upper limit on the possible delayed emission up to 1 h after the GRB.
Results. The estimated flux upper limits range between 1 × 10-4 and ~2 × 10-2 photons cm-2 s-1 and generally lie above the flux estimated from the extrapolation of the prompt emission in the 30 MeV−3 GeV band. A notable case is GRB 080721, where the AGILE-GRID upper limit suggests a steeper spectral index or the presence of a cut-off in the high energy part of the Band prompt spectrum. The four GRBs detected by AGILE-GRID show high-energy (30 MeV−3 GeV) to low-energy (1 keV−10 MeV) fluence ratios similar to those estimated in this paper for the 64 GRBs without GRID detection, favoring the possibility that AGILE-GRID detected only high-fluence, hard GRBs. From the flux upper limits derived in this work we put some constraint on high-energy radiation from the afterglow emission and from synchrotron self Compton emission in internal shocks.
Key words: gamma-ray burst: general
© ESO, 2012
1. Introduction
A relatively small number of gamma-ray bursts (GRBs) have been detected so far at ~100 MeV−few GeV energies. Energetic photons between 200 MeV and 20 GeV were detected with the EGRET spark chamber on board the Compton Gamma Ray Observatory (CGRO) from only a few GRBs (see e.g. Dingus 2001). A larger sample of high-energy photons from GRBs was collected using the large calorimeter of the EGRET instrument that provided GRB light curves and spectra in the 1−200 MeV energy range, thus extending the spectral coverage of the brightest GRBs seen at lower energy with the Burst And Transient Source Experiment (BATSE) (Kaneko et al. 2008).
The slow temporal decay of the high-energy flux of GRB 941017 (González et al. 2003), as well as the delayed (up to 1.3 h) detection of very energetic gamma rays from GRB 940217 (Hurley et al. 1994), have pointed to the existence of emission mechanisms that are different from the one generating (prompt) photons at lower energies. These observations show there are a few GRBs with very hard spectra, peak energies up to 170 MeV, and high-energy “excesses”, i.e. emissions above 100 MeV, that are not compatible with simple extrapolations of the corresponding low-energy spectra. To explain the origin and the temporal evolution of such spectral components, distinct from the common Band function fit (Band et al. 1993), leptonic and hadronic models have both been proposed (consider e.g. Zhang & Mészáros 2001).
Two factors that affected the study of GRBs at high energy are intrinsic to pair production telescopes of the old generation, based on spark chamber trackers: the relatively small field of view, which limits the sample of observed GRBs, and the significant instrumental dead time, which reduces the number of detected photons in the brightest emission episodes of the GRBs, thus preventing a reliable measure of their peak fluxes and fluences in the prompt phase. Both limitations are overcome by new gamma-ray satellites equipped with self-triggering trackers based on silicon microstrip technology, such as AGILE (Tavani et al. 2009) and Fermi-LAT (Atwood et al. 2009).
Indeed in only a few years, the number of GRBs detected by pair production telescopes is already larger by almost a factor of three with respect to those detected by EGRET (e.g. Omodei 2010) and some of the spectral and temporal features detected by EGRET are present in the AGILE and Fermi GRBs, too. A few examples are the temporally extended high-energy tail seen in the short GRB 090510 (Giuliani et al. 2010; Ghirlanda et al. 2010; Ackermann et al. 2010; De Pasquale et al. 2010; Kumar & Barniol Duran 2010), the presence of a distinct high energy spectral component in the long GRB 090902B (Abdo et al. 2009a) and the long delayed components observed in several GRB by Fermi-LAT. Notably in the case of 080916C, this component extends up to a thousand seconds after the trigger and is consistent with an extrapolation of the spectral fit at low energy (Abdo et al. 2009b).
The detection of GRBs by AGILE and Fermi has given rise to several other models explaining the high-energy emission from GRBs, with its key peculiar observational characteristics, i.e. the delayed onset and the extended duration, the typical Fν spectral shape ~ν-1, and the long-lasting flux decay obeying a power law decline ~t-1.5 (e.g., Ghisellini et al. 2010, for a detailed description), among them, the synchrotron/self-synchrotron Compton (Zou et al. 2009) or the afterglow synchrotron model (Ghirlanda et al. 2010; Ghisellini et al. 2010; Kumar & Barniol Duran 2009, 2010).
Moreover, the number of GRB detections is well below the prelaunch expectations (for both AGILE and Fermi-LAT) based on the assumption of the ubiquitous presence of high-energy emission in GRBs (Thompson 2008). As long as AGILE is considered, we predicted almost 1 GRB per month (Longo et al. 2007). Preliminary estimates by the Fermi Collaboration expected about 50 GRBs per year (Omodei et al. 2007). Updated and correct rates for Fermi-LAT detections were calculated by the Fermi Collaboration, when adopting the spectral parameters of bright GRBs in the BATSE sample (Band et al. 2009). A systematic study of upper limits on GRB high-energy emission using Fermi-LAT data was performed by several authors (Guetta et al. 2011; Beniamini et al. 2011; The Fermi-LAT Collaboration & The Fermi-GBM Collaboration 2012).
To understand the discrepancy between our earlier predictions and the actual rate, we searched for prompt high-energy emission components in the spectra of all the GRBs occurring in the AGILE-GRID field of view. The presence of such a component could not be ruled out if considering EGRET data alone (Thompson 2008), and upper limits in the AGILE-GRID energy range would be important for constraining the models. We also try to reconsider the prelaunch predictions based on the rates of observed GRBs.
We report the analysis of all the GRBs that occurred in the AGILE-GRID field of view from the launch up to October 2009 without being detected by AGILE-GRID. The sample is described in Sect. 2. For most of them a count upper limit is provided using a Bayesian approach, described in Sect. 3. Section 4 provides and discusses flux upper limits on GRB whose spectral information are available from other space missions. A brief discussion of the likelihood upper limits on the delayed emission is considered in Sect. 5. Section 6 presents some theoretical considerations based on the data obtained in this paper. The revision of the prelaunch expectations and a general discussion of the upper limits obtained in this paper are presented in Sect. 7.
The large statistical sample of GRBs considered in this paper allows drawing some preliminary conclusions on the conditions needed for the presence of high-energy components in GRB emission spectra. In particular, the fluence ratios seem to indicate that high-fluence emission in the low-energy band favors the emission of high-energy photons.
2. The GRB sample
The AGILE satellite (Tavani et al. 2009), launched on 23 April 2007, is an Italian space mission dedicated to high-energy astrophysics. Its main instrument, the GRID (Gamma-ray Imaging Detector), is a pair conversion telescope (Prest et al. 2003) operating in the 30 MeV−50 GeV energy band. It is characterized by a large field of view (~2.5 sr), a point spread function of ~0.1° at 1 GeV, a very short deadtime (~200 μs), and a relatively low particle background (~1 Hz after the ground reconstruction cuts). For comparison, EGRET had a field of view of ~0.5 sr and a dead time of ~200 ms.
The two other instruments onboard the AGILE mission are able to trigger on GRBs and study their emission in different energy ranges. SuperAGILE (Feroci et al. 2007) operates in the 20−60 keV energy band, with a field of view of about 1 sr. The Mini-Calorimeter (MCAL) (Labanti et al. 2009) is an all-sky monitor sensitive to photons in the 350 keV−100 MeV energy range (Marisaldi et al. 2008).
After two years of operations, three GRBs were detected by AGILE-GRID: GRB 080514B (Giuliani et al. 2008), GRB 090401B (Moretti et al. 2009), and GRB 090510 (Longo et al. 2009; Giuliani et al. 2010). A fourth GRB, GRB 100724B (Del Monte et al. 2011) was detected in the third year of AGILE’s operation.
This contrasts with the rough estimate of 1 GRB/month that AGILE was expected to observe, based on the previous EGRET detections (Longo et al. 2007). Indeed, GRB emission at MeV−GeV energies appears to be quite a rare phenomenon, typically associated with the brightest events, as also confirmed by the relative paucity of the recent Fermi detections (Guetta & Pian 2009; Guetta et al. 2011; Beniamini et al. 2011; The Fermi-LAT Collaboration & The Fermi-GBM Collaboration 2012).
The GRBs studied in this paper were localized and detected by other satellites (Swift, INTEGRAL, Konus, Suzaku-WAM, Fermi-GBM, the Interplanetary Network) or by SuperAGILE within the AGILE-GRID field of view. The count upper limit was properly derived for all the events that did not show evidence of a high-energy component. Selected events fall in the time window between July 2007, when AGILE-GRID observations started, and October 2009, when AGILE switched from a fixed pointing mode to spinning mode due to a problem in the reaction wheel. The selection criteria required locating the GRB to be within the AGILE-GRID field of view (with the angle θ from the pointing direction ≤ 60°) and the distance of the GRB from the center of the Earth to be greater than 90° to avoid occultation and/or residual contamination by albedo gamma rays. No cuts based on brightness or spectral hardness were applied. The 64 GRBs that satisfy all the criteria are listed in Table 1, with the corresponding GCN reporting trigger time, location and spectral parameters when available. The spectral information is provided by Konus/WIND (KW, Aptekar et al. 1995), Wide-band All-sky Monitor (WAM, Yamaoka et al. 2009) on board the Suzaku satellite, Gamma-Ray Burst Monitor (GBM, Meegan et al. 2009) on board the Fermi satellite and Burst Alert Telescope (BAT) on board the Swift satellite (Gehrels et al. 2004). Table 1 includes the GCNs issued by AGILE-GRID containing the results of a “quick-look” analysis. A comparison of the properties of the four GRBs detected by AGILE-GRID with those of the sample has been already preliminarily discussed (Del Monte et al. 2010) and will be the subject of further analysis.
3. Upper limit calculation
The purpose of this paper is to derive upper limits (UL) on fluxes of GRBs observed by other satellites and located in the AGILE-GRID field of view. For such a task, we adopt the method proposed by Helene (1983, 1984). It follows a Bayesian approach where an “a-priori” knowledge or estimate of the signal is needed. In the frequentist calculation of upper limits, the physical source flux limits are not taken into account in the first step. This means that the confidence level interval can contain negative fluxes. Only in a second step is the confidence level interval cut according to the physical limits on the studied quantity (e.g. Feldman & Cousins 1998; Wittek et al. 2007).
We indicate with S the mean of the counts received from a source within the time interval tobs and with N the total number of counts detected in tobs. If a background with average counts B is also present, the Poisson distribution for N is
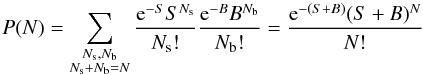 (1)with Nb and Ns counts from background and source respectively. Here, the mean value of the background counts, B, is very well known. In fact it is sampled over a pre-trigger time window that is at least ten times longer than tobs.
(1)with Nb and Ns counts from background and source respectively. Here, the mean value of the background counts, B, is very well known. In fact it is sampled over a pre-trigger time window that is at least ten times longer than tobs.
From the Bayes theorem the posterior probability for the parameter S as a function of the observables N and B is 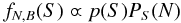 (2)where PS(N) is the Poisson distribution (1) for S + B. The function p(S) is the so-called prior, which contains all the prior knowledge on S one wants to put into the estimate.
(2)where PS(N) is the Poisson distribution (1) for S + B. The function p(S) is the so-called prior, which contains all the prior knowledge on S one wants to put into the estimate.
The subjective information contained in p(S) is often debated because of its influence on the final probability. In the Helene method, however, the prior includes the physical bound of non-negative flux from the source and is defined as a constant. Its physical meaning is therefore that all the source fluxes have the same emission probability. It is shown that the final result depends weakly on the prior (Kraft et al. 1991). Other priors that disfavor large fluxes give similar upper limits.
The posterior probability in the Helene method is 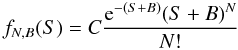 (3)where C is a constant that incorporates the prior constant and the normalization of the Poisson distribution of S + B with respect to S (Kraft et al. 1991)
(3)where C is a constant that incorporates the prior constant and the normalization of the Poisson distribution of S + B with respect to S (Kraft et al. 1991) ![\begin{equation} C = \biggl[\int_0^{\infty}{{\rm d}S \frac{{\rm e}^{-(S+B)} (S+B)^{N}}{N!}}\biggr]^{-1} = \biggl(\sum_{n=0}^N {\frac{{\rm e}^{-B}B^n}{n!}}\biggr)^{-1}\cdot \label{e:helenenorma} \end{equation}](/articles/aa/full_html/2012/11/aa16238-10/aa16238-10-eq34.png) (4)The difference between the frequentist and the Bayesian approaches is reflected in the difference between Eqs. (1) and (3). The last one gives the probability for a source to have a flux S, given B and the observed N counts. The confidence level is defined as the integral of fN,B(S) in the interval [Smin,Smax]
(4)The difference between the frequentist and the Bayesian approaches is reflected in the difference between Eqs. (1) and (3). The last one gives the probability for a source to have a flux S, given B and the observed N counts. The confidence level is defined as the integral of fN,B(S) in the interval [Smin,Smax] 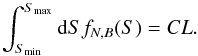 (5)The interval Smax−Smin is minimized for a given confidence level as shown by Kraft et al. (1991).
(5)The interval Smax−Smin is minimized for a given confidence level as shown by Kraft et al. (1991).
In the upper limit calculation, an accurate estimate of the background is crucial for defining the quantity B within tobs. Two requirements have to be fulfilled for a correct estimate of the background rate. First the satellite on-flight data parameters have to be correctly estimated (i.e. GPS information, star sensors, and pointing information). Second the events need to be completely reconstructed off-line and properly classified by the background filter. Background studies over the same 15° region around the GRB position are made before the GRB trigger time to avoid signal contamination.
Data taken during Earth occultation and the passage over the South Atlantic Anomaly are excluded when sampling the background. The time interval, over which the background rate is calculated, needs to be at least ten times longer than the tobs. This last condition assures that the mean B has a negligible error. Finally, the interval selected for the background evaluation is the nearest to the trigger time, among those that share all the above characteristics.
Checks were performed on the trend of the background, particularly in some interesting cases. The rate of events in the background interval closest in time to the signal, has been compared with the background rate in intervals with the same characteristics, but farther from the signal interval. A 10% variation is observed, thus not affecting significantly the estimate of the upper limits.
As for the background, similar requirements are made when searching for a signal S. The events must be completely reconstructed with good flight parameters. Because of the lack of signal in the sample, the upper limit on high-energy emission during the prompt GRB phase is calculated over the GRB duration, as shown in Table 2. In some cases the temporal search was extended with respect to the reported T901, as measured by the satellite that observed the GRB, due to possible further emission episodes reported by other satellites. An angular region of 15° around each GRB is chosen to allow for acceptance of events detected at lower energies and therefore characterized by a larger point spread function.
Duration of the search, the total observed counts, the expected background counts in the same region and time period, the source count upper limit, the photon flux, energy flux upper limits (in the 30 MeV−3 GeV energy range), and the measured spectral index.
While the background rate B is estimated over a time period that is not occulted, in case the signal region is partially occulted by the Earth, the value of B is multiplied by the fraction of the unocculted field of view, in order to be compatible with S. Figure 1 shows the results of this search for an individual GRB, in this case GRB 080721.
 |
Fig. 1 Example of a particular background selection for evaluating the upper limit on a single GRB. The “Bkg” events are those detected by the GRID, the “not complete” events are those for which the off-line reconstruction or the satellite information were not fully available. The “Events in the selected region” are those in the 15° region around the GRB position. The particular GRB taken as example is GRB 080721. |
The confidence level of the derived counts upper limits is 99.7% (corresponding to a ~3 Gaussian σ). The confidence interval defined in Eq. (5) can be obtained by integrating Eq. (3) numerically starting from its most probable value and integrating in both directions, always choosing to add the side with the higher probability to the integral, until the desired confidence level is reached (Kraft et al. 1991). If the lower limit of this interval is 0, the source flux is then compatible with 0 and an upper limit is provided. Table 2 shows the upper limits, calculated according to the Helene method applied to all the GRBs in our sample (Col. 5).
4. Results
Given an upper limit on the counts, it is necessary to introduce the AGILE-GRID effective area to determine the corresponding flux upper limit. The effective area is obtained using the well-known Vela spectrum in the energy range between 30 MeV and 20 GeV. We first divide the known spectrum into 15 energy bins. The photon counts detected from Vela in each bin are then divided by the corresponding known Vela flux to obtain the instrument effective area in that energy range.
The total effective area is therefore obtained by taking the convolution of the source spectrum with the areas estimated above in different energy bins. For an E−β spectrum, for example, the total effective area is given by 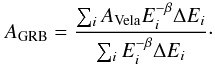 (6)This calculation is needed to estimate the expected flux. Indeed, since the effective area is energy dependent, similar count rate upper limits correspond to different flux upper limits if different assumptions on the high-energy spectrum are made.
(6)This calculation is needed to estimate the expected flux. Indeed, since the effective area is energy dependent, similar count rate upper limits correspond to different flux upper limits if different assumptions on the high-energy spectrum are made.
First, we assume that the low-energy spectrum extends to the high-energy regime as observed for example in the case of GRB 080916C by Fermi (Abdo et al. 2009b). Photon and energy flux limits derived under this assumption are reported in the last two columns of Table 2. For the high-energy spectral index, the value 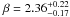 is adopted for all 64 GRBs in the sample. This value corresponds to the average value derived from the spectral analysis of BATSE GRBs (Kaneko et al. 2008).
is adopted for all 64 GRBs in the sample. This value corresponds to the average value derived from the spectral analysis of BATSE GRBs (Kaneko et al. 2008).
In some cases, the high-energy spectral index β of the Band prompt spectrum has been directly measured from spectral analysis. In these cases, as reported in Table 3, we estimated the upper limits on the photon and energy fluxes by adopting the measured β preliminary reported by GCN (first set of values in the table) or calculated by Nava et al. (second set) and Bissaldi et al. (third set).
Figure 2 shows the histogram of the calculated UL flux both for the complete sample, where the average β was used, and for the small subsample for which the measured high-energy spectral index was used.
 |
Fig. 2 Distribution of the flux upper limits (in units of erg/cm2/s) estimated in the energy range 30 MeV−3 GeV by assuming that the high-energy emission is the extrapolation at high energies of the prompt spectrum detected in the keV−MeV range. A spectral index β = 2.36 is assumed for all bursts in our sample (64 events-gray filled histogram). Values are reported in Table 2. The red shaded histogram instead shows those bursts in our sample (10 events) for which the β value has been estimated from the spectral fit of the keV−MeV component reported in the GCN (see Table 3). |
For 28 GRBs in our sample, the shape of the prompt spectra is well known, and it is described either by the Band function (Band et al. 1993) or by an exponential cutoff. The extrapolation of this spectrum at higher energies (30 MeV−3 GeV) allows the flux expected in the GRID energy range to be derived. We performed this estimate for the 28 events for which the preliminary spectral parameters are reported in the GCN Circular system2. In cases where an exponential cutoff is seen, the derivation of the 30 MeV−3 GeV expected flux is performed by considering a high-energy power law spectral index β = 2.36. The expected flux is then compared to the flux upper limit estimated from the GRID non-detection (as shown in Fig. 4 for GRB 080721). Results are presented in Table 5 and in Fig. 3. Errors on the expected flux are calculated by varying the β value within its error, provided by the GCN notices. GRBs fitted with Band functions are listed at the beginning of the table. For GRBs whose spectra are described by a power law with a high-energy exponential cutoff the minimum and maximum values of β are taken from the distribution measured by BATSE (respectively βmin = 2.58, βmax = 2.19).
From Table 5, the upper limit marginally constrains the value of the expected flux only for three GRBs, namely GRB 080721, GRB 081224, and GRB 090904B. The case of GRB 081224 is not particularly interesting since the extrapolation at high energy in this case is based on the assumption of the presence of a power law consistent with BATSE average value, not reported by the GCN (Hayashi et al. 2008). AGILE-GRID limit in this case confirms the absence of such a component.
 |
Fig. 3 Comparison between the flux expected in the 30 MeV−3 GeV energy range (from the extrapolation of the keV−MeV spectral component) and the flux upper limit estimated in the same energy range. The sample is composed of the 28 GRBs for which it has been possible to estimate the peak energy of the prompt component from the spectral analysis. Preliminary spectral results from the GCN are considered: in 10 cases the spectrum is well fit by a BAND model (filled circles), while in 18 cases the best-fit model is a power law with an exponential cutoff (filled stars). Open gray symbols show the same comparison when spectral parameters are taken from Nava et al. (2011) and Bissaldi et al. (2011). |
 |
Fig. 4 High-energy spectral extrapolation of the GRB 080721. The blue horizontal line shows the derived expectation for the GRB flux in the band 30 MeV−3 GeV, adopting a spectral index β = 2.43, while the red line is the UL flux estimated with the Helene method. Since the UL is slightly below the expectations a steeper spectral index is expected. |
The upper limits for GRB 080721 and GRB 090904B lie below the expected flux so they can constrain the β index measured by other satellites. A refined calculation was performed using the updated spectral analyses reported by Nava et al. (2011) and Bissaldi et al. (2011) (see Table 6 and Fig. 3). We note that GRB 090904B is now better fit with a power law with an exponential cutoff, so it is no more significant in the AGILE-GRID energy band. Even when adopting the most favorable conditions, the spectral extrapolation lies well below the AGILE UL. Figure 4 shows the flux of GRB 080721 extrapolated at high energies (30 MeV−3 GeV) adopting a spectral index β = −2.43.
The AGILE-GRID upper limit for GRB 080721 could be used, for example, to derive a different spectral shape at high energy. Our calculations seem to indicate, in this GRB, the presence of a spectral break (between the MeV and the GeV range) towards a steeper spectral index, thus contributing to predict a smaller number of GRBs detectable at high energy, with respect to calculations that make use of simple extrapolations. The change in β index, Δβ = −0.007, is not significant, however, considering that the upper limit ranges within the error bars on the flux extrapolating the spectral shape reported by Konus-WIND (Golenetskii et al. 2008).
Comparison of the derived upper limit with the estimated photon flux derived using the publicly available spectral information preliminarily reported by GCN Circulars.
 |
Fig. 5 High-energy spectral extrapolation of the GRB 090618. The blue horizontal line shows the derived expectation for the GRB flux in the band 30 MeV−3 GeV, adopting a spectral index β = 2.50, while the red line is the UL flux estimated with the Helene method. In this case the UL flux is still consistent with the extrapolation of the low-energy spectral shape. |
The other interesting case is represented by GRB 090618 (Fig. 5). It is the brightest event detected by MCAL and SuperAGILE. It has a peak flux of 1.6 × 10-5 erg cm-2 s-1 in the energy range 20 keV−2 MeV (Golenetskii et al. 2009). Despite such a bright peak, GRB 090618 was not detected by the AGILE-GRID. This GRB therefore provides evidence of a class of bright GRBs that lack significant emission above 30 MeV. Using the newer spectral measurements reported in Table 6, the upper limit put by AGILE on GRB 090618 is indeed now marginally constraining the presence of an high-energy component consistent with an extrapolation of the low-energy Band spectrum at high energies. This GRB was studied in detail by Page et al. (2011). The gamma-ray spectrum is confirmed to be fit by a power law with an exponential cutoff. The authors find the evidence of a thermal X-ray component interpreted as a Supernova shock breakout.
Finally, we derive flux upper limits in the GRID energy range by considering a different scenario, in which the high-energy emission is dominated by an extra component, spectrally distinct from the sub-MeV prompt spectrum. This analysis is justified since in some cases of high-energy detection an additional spectral energy component has been found. For this reason, we now assume that the high-energy spectrum has a different spectral behavior as compared to the sub-MeV spectrum and calculate the corresponding flux upper limit. In particular, we calculate the upper limits derived from AGILE observations assuming the emission in the GRID band (30 MeV−3 GeV) can only be attributed to a high-energy spectral extra component as in the case of GRB 941017 (β = 1.1) (González et al. 2003), GRB 980923 (β = 1.3) (González et al. 2009), GRB 090510 (β = 1.6) (De Pasquale et al. 2010), GRB 090902B (β = 1.8) (Abdo et al. 2009a). The results are reported in Table 4 and shown in Fig. 6 for the two extreme cases β = 1.1 and β = 1.8.
Comparison of the derived upper limit with the estimated photon flux derived using the publicly available spectral information reported by Nava et al. (2011) – upper rows – and by Bissaldi et al. (2011) – lower rows.
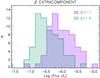 |
Fig. 6 Distribution of the flux upper limits (in units of erg/cm2/s) estimated in the energy range 30 MeV−3 GeV by assuming that the high-energy emission represents a distinct extra component as compared to the keV−MeV spectral component. The filled purple (shaded green) histogram shows the distribution when a spectral index β = 1.1 (β = 1.8) is assumed for all bursts in our sample (64 events). |
The importance of the upper limits measured by AGILE-GRID, in the energy range 30 MeV−3 GeV, can be estimated by calculating the ratio of the UL fluence and the fluence calculated in the energy range (1 keV−10 MeV) using the publicly available spectral information. The calculated values range between a factor of ~0.05 and a factor of ~5. This is similar to the calculation reported by Beniamini et al. (2011). The ratio was also performed for the UL fluence assuming the energy emission in the GRID energy range as only due to the spectral extra component in addition to the low-energy Band spectrum. We calculated the same ratios for those GRBs, detected by Fermi-GBM, for which a complete spectral analysis was available (Nava et al. 2011; Bissaldi et al. 2011)3. The results are reported in Table 7 for the UL calculated using the measured beta values and in Tables 8 and 9 for the UL assuming the high-energy emission due to the spectral extra component and shown in Fig. 7. We note that the ratios range in this case between a factor of ~0.05 and a factor of ~30. Figure 7 also shows the high-energy and low-energy fluence for those bursts detected by GRID, calculated using spectral information reported by Giuliani et al. (2008), Moretti et al. (2009), Giuliani et al. (2010), Del Monte et al. (2011) and listed at the bottom of Table 7. On average, the ratio is ~0.1 (with the exception of GRB 090510, for which the two fluences are comparable), in agreement with results from Fermi-LAT detected bursts. GRBs without GRID detection considered in this work, instead, lie in the region of the plane characterized by higher ratios. This suggests that the presence of high-energy emission is not a common property of GRBs or that the fluence of the possible high-energy component lies well below the upper limit that is possible to derive with the GRID instrument.
 |
Fig. 7 Comparison between the prompt fluence measured in the 1 keV−10 MeV energy range and the upper limit to the 30 MeV−3 GeV fluence for the 28 events with well known prompt spectral properties. The fluence upper limit is derived under different assumptions: i) extrapolation of the prompt spectrum (yellow circles); ii) power law extra component with spectral index β = 1.8 (blue stars); and iii) power law extra component with spectral index β = 1.1 (green squares). The red diamonds are the four GRB detected by AGILE GRID. |
5. Search for delayed components
The aim of the analysis performed so far in the paper was to constrain the detection of the high-energy emission by GRBs during the prompt phase with AGILE-GRID. GRBs are known to emit for a longer duration in the high-energy band (E > 100 MeV) with respect to the typical low-energy GRB energy range (1 keV−10 MeV). Two typical examples are GRB 090323 and GRB 090328 (McEnery 2010) for which the high energy emission extended up to few ks after the trigger.
A preliminary likelihood analysis of the delayed high-energy emission from GRBs was performed on all the GRBs in the sample. The AGILE-GRID data were analyzed by adopting the optimal gamma-ray filter technique (filter FM3.119). For each GRB, counts, exposure, and gas maps were created centered on the GRB position, in a time window ranging from 100 to 3700 s after the GRB time. The likelihood analysis was done using a script developed for an extensive search of counterparts to AGILE sources (Rappoldi et al. 2011). All the sources from EGRET (Hartman et al. 1999), AGILE (Pittori et al. 2009), and Fermi-LAT (Abdo et al. 2010) within 10° of the GRB position were included in the source model.
Due to very low count statistics, the likelihood analysis gets meaningful results only for a subsample of 26 GRBs. Results are presented in Table 10. Values with square root of the test statistics (TS) (e.g. Mattox et al. 1996) more than 5 sigma are considered as a detection. A detailed analysis of the possible extended emission from the three GRBs detected by AGILE in its first two years is in progress.
Estimation of the upper limits of flux above 100 MeV up to one hour after the GRB trigger.
6. Theoretical implications
In this section we discuss two different models that predict high-energy emission from GRBs. The non-detection of such emission and the flux upper limits derived in this work allow us to put some constraint on the parameters of both models.
In the first case we constrain the presence of high-energy synchrotron emission from relativistic electrons accelerated in external shocks (afterglow scenario). This scenario is particularly interesting since the spectral and temporal behavior of several GRBs with detection of high-energy emission seems to be consistent with expectations from the afterglow model (Ghisellini et al. 2010). Fireballs with large Lorentz factors are expected to decelerate early, producing bright afterglow emission at high frequencies. When instead the Lorentz factor is lower, the emission peaks at later times and is fainter. The low rate of GRBs with detected high-energy emission suggests that this is the case for most bursts. Within this scenario we can then estimate an upper limit on the bulk Lorentz factor Γ0: higher values of Γ0 would have implied a high-energy emission detectable by GRID in the considered time interval (which in our analysis coincide more or less with the prompt duration).
The second considered scenario is synchrotron self Compton (SSC) emission in internal shocks, i.e. inverse-Compton scattering of synchrotron radiation by the same relativistic electrons (accelerated in internal shocks) that produced the synchrotron radiation. This model is not favored for explaining high-energy emission detected by AGILE and Fermi-LAT, since some common temporal and spectral properties often characterizing this emission (as the temporal delay and the long lasting extended emission detected in several cases) can hardly be explained within this scenario. The study of this model is however interesting to derive some information about the radiation mechanism producing prompt radiation: if prompt radiation is synchrotron emission from electrons accelerated in internal shocks, an inverse Compton component produced by the same electrons is naturally expected. The non-detection of such a component in the GRID energy range can be explained in several ways. In particular, if the peak of the SSC component lies outside the GRID energy range and/or the flux is suppressed by the Klein-Nishina limit, no detectable emission is expected. In both cases, the flux upper limits derived in this work allow deriving interesting constraints on the Compton parameter Y and on the microphysical parameters ϵe and ϵB.
6.1. Testing the external shock scenario
Several authors (Kumar & Barniol Duran 2010; Ghisellini et al. 2010; Ghirlanda et al. 2010) have suggested that the MeV−GeV radiation detected in several GRBs is emitted by electrons accelerated in ultrarelativistic shocks with the interstellar medium, i.e., has the same origin as the X-ray and optical afterglow emission. Both synchrotron and SSC have been proposed as viable emission mechanisms to explain the observed high-energy radiation. The peak time of the afterglow light curve (which marks the start of the blast wave deceleration) depends on the initial bulk Lorentz factor Γ0 (with faster fireballs decelerating earlier) and on the total energy E0 of the fireball (after the end of the internal shock phase), which is estimated from the isotropic prompt energy Eiso (E0 = Eiso/η, where η is the efficiency of the prompt emission). For very high Lorentz factors (Γ0 ~ 103) the afterglow light curve is expected to peak a few seconds after the onset of the prompt emission. Under the assumption that the MeV−GeV emission is due to afterglow radiation, the upper limits derived in this work on the GRID flux can be translated into upper limits on Γ0. From our sample of 64 GRBs we select those with measured spectral peak energy and compute the prompt fluence in the observed energy range 1 keV−10 MeV. For GRBs with measured redshift we estimate the isotropic equivalent energy Eiso and compute the peak time of the afterglow lightcurve, by assuming a given value for Γ0. For GRBs without measured redshift, we vary z from 0.01 to 10 and repeat the estimate for each z. To estimate the peak time we adopt the modeling of the afterglow emission presented by Ghirlanda et al. (2012). From their equations we also estimate the expected afterglow luminosity before and after the peak time and integrate it in the same time interval where upper limits on the GRID flux are estimated. We finally estimate the expected average flux from afterglow emission and compare its value to the GRID upper limit. The expected average flux depends on the value of Γ0 that we choose: by equating the estimated afterglow flux and the GRID flux upper limit we derive an upper limit on Γ0. This method requires several assumptions. First of all, we restrict ourselves to the case of a homogeneous density of the interstellar medium, with the typical value n = 3 cm-3. For the efficiency of the prompt emission we use η = 0.2, and for ϵe (the fraction of dissipated energy gained by the electrons) we use ϵe = 0.1 (Panaitescu & Kumar 2001). Moreover, for the GRID upper limits we use the values derived under the assumption of and extra component with spectral index β = 1.8. Our results are shown in Fig. 8. We can estimate upper limits on Γ0 only for bursts with measured redshift. For the other events, we derive the upper limits on Γ0 by varying z from 0.01 to 10. As a general rule, when the prompt average flux is larger, stronger upper limits on Γ0 can be derived, since a brightest afterglow is expected (Fig. 8). Figure 8 also shows that when the redshift is high it is not possible to put strong constraints on Γ0: high-z bursts will produce low-flux afterglow emission (below the GRID detection threshold) even when the Γ0 is large, due to the large distance. At high redshift, then, very weak constraints on Γ0 can be derived.
 |
Fig. 8 Upper limits on the initial bulk Lorentz factor (as a function of the redshift) derived under the assumption of a leptonic external shock origin of the high-energy emission. Red triangles mark GRBs with measured redshift. For the other events a redshift ranging between 0.01 and 10 is assumed. Higher flux GRBs are marked with lighter curves. The orange region shows the Γ0 distribution derived by Ghirlanda et al. (2012) for a sample of GRBs with afterglow peak time measured from optical data. |
By investigating a sample of bursts with the afterglow peak time detected in the optical light curve, Ghirlanda et al. (2012) show that, when homogeneous density is assumed, the Γ0 distribution peaks around ~140 and ranges between 30 and 400 (see Fig. 8). From the comparison of our results with the distribution of measured Γ0 we conclude that the most constraining values are derived for GRBs at low redshift (z ≤ 1). Our results confirm that, if the leptonic external shock scenario is the correct interpretation for bursts with a high-energy extra component, bursts with GeV detection correspond to those with the largest Lorentz factor (Γ ~ 103); otherwise, GRID should have detected high-energy emission from at least some of the bursts in our sample.
6.2. Testing SSC emission in the internal shock scenario
In the internal shock scenario, the prompt emission is commonly interpreted as synchrotron emission from electrons accelerated in the mildly-relativistic shocks. According to this scenario, another radiative mechanism might play an important role: SSC, where the same population of relativistic electrons scatters the synchrotron radiation.
Several authors (Guetta & Granot 2003; Finke et al. 2008) have investigated the possibility of detecting SSC emission in the MeV−GeV energy range. The non-detection of high-energy emission by GRID and the upper limits on the flux estimated in this work allow us to put some constraints on the SSC emission. To predict the contribution of SSC emission in the GRID energy range and compare it to our flux upper limits, we model SSC emission by following Guetta & Granot (2003).
There are two simple ways to explain non-detection of the SSC component by GRID: i) the inverse Compton process proceeds in the Klein-Nishina regime; and the flux is suppressed and ii) the peak of this component falls outside the energy range of sensitivity of GRID (in this case the bulk of the emission is missed and the expected flux in the GRID energy range is low). The first case occurs when γeEpeak > Γmec2, where γe is the typical random Lorentz factor of the accelerated electrons, Epeak the peak energy of the synchrotron component, Γ the bulk Lorentz factor, and me the electron mass. This condition can be easily verified for quite slow fireballs (for example, ϵe > 0.08 is sufficient for fireballs with Γ = 50 and typical peak energies Epeak = 250 keV). The second case (spectral peak of the SSC component outside the GRID energy range) occurs when γe is particularly high (which implies high values of ϵe – in this case a few hundred GeV can be reached) or when it is particularly low (ϵe < 10-2). This last case, however, is not favored because, as shown by Ghisellini et al. (2000), the typical energies of the synchrotron peak can hardly be explained for low values of the microphysical parameters.
When the SSC process is governed by Thompson scattering and the bulk of the emission falls within the GRID energy range (30 MeV−3 GeV), some interesting results can be drawn from the flux upper limits derived in this work. From the request that the SSC spectral peak lies well inside the range of sensitivity (at ~300 MeV), we can estimate, for each burst in our sample, the typical random Lorentz factor γe of the electrons accelerated by the shock, and then the parameter ϵe. This estimate requires the knowledge of Epeak and β. When β is not constrained from the spectral analysis we use the fixed value β = 2.36, as elsewhere in this work. The ratio between the flux upper limits and the synchrotron flux gives an upper limit on the Compton parameter Y. Putting together the upper limit on Y and the estimate of ϵe, a lower limit on ϵB can be derived. Results are shown in Fig. 9.
While for the external shocks some hints about the typical values of the microphysical parameters can be derived from modeling the afterglow light curves (Panaitescu & Kumar 2001), it is more difficult to infer these values for internal shocks. Our analysis suggests a rather clustered value for ϵe, ranging between 3 × 10-2 and 10-1, and a wider range for the lower limits on ϵB, in agreement with the results found by Panaitescu & Kumar (2001) for the external shock emission.
 |
Fig. 9 Upper limit for the Compton parameter Y, the estimate of ϵe, and the lower limits for ϵB as a function of the prompt flux for the sample of GRBs with measured Epeak. When β cannot be constrained from the spectral analysis, a value of β = 2.36 is assumed (red stars). In the other cases the value derived from the spectral fit is adopted (blue circles). |
7. Discussion
The analysis performed on the GRB in the AGILE-GRID field of view allows reaching the following preliminary conclusions. The inferred ULs are consistent with the extrapolation of the low-energy Band spectrum to the GeV range in the vast majority of cases. The only exception is GRB 080721, which suggests the existence of a spectral steepening at high energy. The spectral component in addition to the Band spectrum (if any) contributes to less than a few percent of the low-energy fluence.
The expected high-energy flux is, apart from a few cases, systematically lower than the AGILE-GRID upper limit. However, using the spectral parameters publicly distributed by GCNs, a simple comparison of the prompt emission properties of the four GRBs detected by AGILE-GRID, and their measured fluences in the GRID band was performed. Ratios of the measured fluences in the AGILE-GRID band and the one calculated in the band 1 keV−10 MeV, reported in the bottom part of Table 7, are very similar to the one calculated using the upper limits reported in this paper and lie in the range ~4 × 10-2 for GRB 080514B to ~1.5 for GRB 090510. Considering that their fluence is similar to other GRBs not detected by AGILE-GRID, this seems to indicate that the low-energy fluence is not the crucial parameter for being considered to predict the emission at high energy. A preliminary analysis indeed showed that AGILE-GRID detected only the brightest events so far, those characterized by the highest peak flux (Del Monte et al. 2010).
High-energy photons are preferably associated with GRBs whose spectra are either described by harder indexes or show evidence of distinct components, so far well fitted by simple power laws up to tens of GeV (e.g. Abdo et al. 2009a). Those components are possibly associated with different emission mechanisms and characterized by emission episodes with high peak fluxes. Detailed temporal analyses of the events of our sample might be important to derive further conclusions.
AGILE pre-launch expectations were derived using the ratio between the fields of view of EGRET and AGILE-GRID. From this simple consideration, it was stated that AGILE-GRID was expected to detect about 1 GRB per month (Longo et al. 2007). We update here those predictions for two reasons. First, EGRET field of view was shown to be only five times smaller than the AGILE-GRID field of view (e.g. Dingus 1995), instead of the assumed factor of ten (Longo et al. 2007), thus reducing the rate predicted by AGILE to one GRB every two months. Second, as future analysis will show, the number of GRBs potentially detected by AGILE was not as high as if AGILE had an on-board all-sky trigger detector like BATSE. In our sample 26 and 34 GRBs were detected during the first and the second years respectively. Only three of them were statistically significant. Nevertheless, the majority of the events that occurred within the AGILE-GRID field of view were detected by Swift-BAT and showed both lower peak fluxes and softer spectra. Therefore AGILE detected about 1 GRB every 20 that occurred within its field of view, as many as the GRBs seen by EGRET, estimating a total of 300 GRB yr-1 triggered by BATSE and considering a field of view of 1/25 of the sky for EGRET and a partial occultation factor of 50%. We thus conclude that AGILE and EGRET observed almost the same population of GRBs (the brightest and hardest ones) with approximatively the same statistics (Kaneko et al. 2008; González et al. 2009). More untriggered events could have been seen by AGILE, and a dedicated analysis will be presented in a future work. The analysis performed by Le & Dermer (2009) indeed predicted a rate of around 20 GRBs full-sky per year potentially detectable by AGILE with more than five photons with energy greater than 30 MeV. This agrees with the measured ratio when considering the field of view and the occultation factor.
Owing to the limited sensitivity of AGILE, the upper limits derived here do not allow distinguishing among different theoretical models that explain the emission at high photon energies. Both leptonic and hadronic models predict the production of very energetic (MeV−GeV) photons, and different mechanisms within the internal shock scenario, such as inverse Compton, synchrotron emission from protons, and decay of neutral pions (reviewed in e.g. Mészáros 2006; Gupta & Zhang 2007; Fan & Piran 2008), are able to reproduce the observed spectral features in the GeV energy band. Observations with higher sensitivities, such as those reported by Fermi-LAT (The Fermi-LAT Collaboration & The Fermi-GBM Collaboration 2012), are needed to settle the debate. Indeed many of the current models predict an emission in the range of a few × 10-3 counts cm-2 s-1 (e.g. Bošnjak et al. 2009). Similarly Fan (2009) shows that the non ubiquitous presence of high-energy emission from GRBs observed by Fermi might be explained by IC emission, provided some specific values of the microphysical parameters at play in the fireball evolution are given. Even if no conclusions can be derived from GRID upper limits about the origin of the high-energy emission detected in some cases by GRID and by Fermi-LAT, we showed how upper limits can be used to constrain some parameters of different models predicting high-energy emission during the prompt phase. In particular we investigated early afterglow emission and inverse Compton emission on synchrotron prompt radiation. In the first case we derived upper limits on the bulk Lorentz factor Γ0. Even if the majority of bursts in our sample do not allow interesting constraints to be put on this parameter, the brightest events in our sample constrain Γ0 to below a few hundred (for typical redshift z ~ 2), in agreement with the Γ0 distribution derived by Ghirlanda et al. (2012) (Fig. 8). In the second case (SSC scenario), we discussed that under typical conditions the SSC component should fall within the GRID energy range and the upper limits derived in this work allow us to estimate the fraction of energy gained by electrons in external shocks ϵe ~ 10-1, upper limits on the Compton parameter Y and, consequently, lower limits on the fraction of energy gained by the magnetic field ϵB (Fig. 9).
Even considering the sensitivity of AGILE, the analysis of the sample presented here confirms the results by EGRET-TASC (Total Absorbtion Shower Counter). The presence of high-energy components, with a fluence ratio of ~0.5−10, distinct from the Band function, is ruled out in most cases (see also González et al. 2009). Fermi detections are also consistent with such a conclusion (Toma et al. 2011).
AGILE-GRID upper limits in the GRB prompt phase were compared with those from Cherenkov telescopes. In particular, limits provided by the MAGIC collaboration (Albert et al. 2007) are consistent with ours, when the low-energy spectral shape is extrapolated up to very high energy. Air shower detectors instead provided upper limits at higher values (Abdo et al. 2007; Aielli et al. 2009), considering the same power law extending up to their energy range. Upper limits from H.E.S.S. (Aharonian et al. 2009) and VERITAS (Galante & for the VERITAS Collaboration 2009; Acciari et al. 2011) were released only for afterglow and flare searches.
This paper presents an analysis of extended emission in gamma rays for a large sample of GRBs. The extended emission photon flux detected by Fermi-LAT for GRB 080916c (Abdo et al. 2009b), GRB 090323 and GRB 090328 (McEnery 2010), GRB 090902B (Abdo et al. 2009a) is in the range of 10-5−10-6 cm-2 s-1. Preliminary analysis of the extended emission from GRBs presented in this paper shows that this component is not present with similar flux rates, in all GRBs, particularly for those that do not show strong prompt gamma-ray emission. This favors different spectral models for the prompt soft phase and the extended high-energy emission phase (e.g. Kumar & Barniol Duran 2009; Ghisellini et al. 2010).
8. Conclusions
During the first two years of observations the AGILE satellite was able to detect photons from GRBs over an energy range that spans more than six orders of magnitude with the X-ray monitor, the mini calorimeter, and the pair production telescope. When detections within the field of view are considered, the AGILE-GRID telescope detected in two years of operation, only three out of 60 GRBs above 30 MeV, with the highest peak flux and harder spectral index. For non detections within the field of view, a statistically robust upper limit has been calculated. Due to the limited sensitivity of AGILE-GRID this result does not yet rule out the existence of the high-energy spectral components described by an extrapolation in the MeV region of the spectral shape at lower energies. Previous results from EGRET are confirmed here. In particular, we stress that high-energy emission is not a ubiquitous property of GRBs. A detailed temporally resolved spectral analysis of this sample might shed new light on the physics that lies behind of GRBs.
Online material
Sample of 64 GRBs selected for the upper limit calculation.
Duration of the search, the total observed counts, the expected background counts in the same region and time period, the source count upper limit, the photon flux, and energy flux upper limits (in the 30 MeV−3 GeV energy range) for each GRB.
Upper limits table reporting the photon and energy flux upper limits derived under the assumption of a high-energy power law extra component; four different values of the photon spectral index are considered.
Ratios of the calculated UL fluence (30 MeV−3 GeV) and the measured fluence (1 keV−10 MeV), calculated using the preliminary spectral parameters values as reported by GCN circulars (top table), and with values calculated by Nava et al. (2011) and by Bissaldi et al. (2011) (second and third tables). Bottom table: measured fluence for the four GRBs detected by AGILE GRID.
Ratios of the calculated UL fluences in the 30 MeV−3 GeV band using different high energy spectral indexes with that calculated in the 1 keV−10 MeV range, calculated using the preliminary spectral parameters values as reported by GCN circulars; fluences and errors are in units of (× 10-6) erg cm-2.
Ratios of the calculated UL fluences in the 30 MeV−3 GeV band using different high energy spectral indexes with that calculated in the 1 keV−10 MeV range, calculated using the preliminary spectral parameters values as reported by Nava et al. (2011) – top table, and by Bissaldi et al. (2011) – bottom table; fluences and errors are in units of (× 10-6) erg cm-2.
The analysis performed in this paper was completed before the final GBM spectral catalog (Goldstein et al. 2012) was published.
Acknowledgments
The AGILE Mission is funded by the Italian Space Agency (ASI) with scientific and program participation by the Italian Institute of Astrophysics (INAF) and the Italian Institute of Nuclear Physics (INFN).
References
- Abdo, A. A., Allen, B. T., Berley, D., et al. 2007, ApJ, 666, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009a, ApJ, 706, L138 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Arimoto, M., et al. 2009b, Science, 323, 1688 [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJS, 188, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Acciari, V. A., Aliu, E., Arlen, T., et al. 2011, ApJ, 743, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Asano, K., Atwood, W. B., et al. 2010, ApJ, 716, 1178 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Barres de Almeida, U., et al. 2009, A&A, 495, 505 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aielli, G., Bacci, C., Bartoli, B., et al. 2009, Astropart. Phys., 32, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2007, ApJ, 667, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Aptekar, R. L., Frederiks, D. D., Golenetskii, S. V., et al. 1995, Space Sci. Rev., 71, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Band, D., Matteson, J., Ford, L., et al. 1993, ApJ, 413, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Band, D. L., Axelsson, M., Baldini, L., et al. 2009, ApJ, 701, 1673 [NASA ADS] [CrossRef] [Google Scholar]
- Beniamini, P., Guetta, D., Nakar, E., & Piran, T. 2011, MNRAS, 416, 3089 [NASA ADS] [CrossRef] [Google Scholar]
- Bissaldi, E., von Kienlin, A., Kouveliotou, C., et al. 2011, ApJ, 733, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Bošnjak, Ž., Daigne, F., & Dubus, G. 2009, A&A, 498, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Pasquale, M., Schady, P., Kuin, N. P. M., et al. 2010, ApJ, 709, L146 [NASA ADS] [CrossRef] [Google Scholar]
- Del Monte, E., Barbiellini, G., Fuschino, F., et al. 2010, in The Shocking Universe – Gamma Ray Bursts and High Energy Shock Phenomena, eds. G. Chincarini, P. D’Avanzo, R. Margutti, & R. Salvaterra, Ital. Phys. Soc. Conf. Proc., 102, 103 [Google Scholar]
- Del Monte, E., Barbiellini, G., Donnarumma, I., et al. 2011, A&A, 535, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dingus, B. L. 1995, Ap&SS, 231, 187 [Google Scholar]
- Dingus, B. L. 2001, in High Energy Gamma-Ray Astronomy: Int. Symp., eds. F. A. Aharonian, & H. J. Völk, AIP Conf. Ser., 558, 383 [Google Scholar]
- Fan, Y. 2009, MNRAS, 397, 1539 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y., & Piran, T. 2008, Frontiers of Physics in China, 3, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Feldman, G. J., & Cousins, R. D. 1998, Phys. Rev. D, 57, 3873 [Google Scholar]
- Feroci, M., Costa, E., Soffitta, P., et al. 2007, Nucl. Instr. Meth. Phys. Res. A, 581, 728 [Google Scholar]
- Finke, J. D., Dermer, C. D., & Böttcher, M. 2008, in AIP Conf. Ser. 1000, eds. M. Galassi, D. Palmer, & E. Fenimore, 385 [Google Scholar]
- Galante, N., & VERITAS Collaboration 2009 [arXiv:0907.4997] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Ghirlanda, G., Ghisellini, G., & Nava, L. 2010, A&A, 510, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghirlanda, G., Nava, L., Ghisellini, G., et al. 2012, MNRAS, 420, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Celotti, A., & Lazzati, D. 2000, MNRAS, 313, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Ghirlanda, G., Nava, L., & Celotti, A. 2010, MNRAS, 403, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Giuliani, A., Mereghetti, S., Fornari, F., et al. 2008, A&A, 491, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giuliani, A., Fuschino, F., Vianello, G., et al. 2010, ApJ, 708, L84 [NASA ADS] [CrossRef] [Google Scholar]
- Goldstein, A., Burgess, J. M., Preece, R. D., et al. 2012, ApJS, 199, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Golenetskii, S., Aptekar, R., Mazets, E., et al. 2008, GRB Coordinates Network, 7995, 1 [NASA ADS] [Google Scholar]
- Golenetskii, S., Aptekar, R., Mazets, E., et al. 2009, GRB Coordinates Network, 9553, 1 [NASA ADS] [Google Scholar]
- González, M. M., Dingus, B. L., Kaneko, Y., et al. 2003, Nature, 424, 749 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- González, M. M., Carrillo-Barragán, M., Dingus, B. L., et al. 2009, ApJ, 696, 2155 [NASA ADS] [CrossRef] [Google Scholar]
- Guetta, D., & Granot, J. 2003, ApJ, 585, 885 [NASA ADS] [CrossRef] [Google Scholar]
- Guetta, D., & Pian, E. 2009 [arXiv:0910.2134] [Google Scholar]
- Guetta, D., Pian, E., & Waxman, E. 2011, A&A, 525, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gupta, N., & Zhang, B. 2007, MNRAS, 380, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, R. C., Bertsch, D. L., Bloom, S. D., et al. 1999, ApJS, 123, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, E., Sonoda, H., Yamauchi, M., et al. 2008, GRB Coordinates Network, 8739, 1 [NASA ADS] [Google Scholar]
- Helene, O. 1983, Nucl. Instr. Meth. Phys. Res., 212, 319 [Google Scholar]
- Helene, O. 1984, Nucl. Instr. Meth. Phys. Res. A, 228, 120 [Google Scholar]
- Hurley, K., Dingus, B. L., Mukherjee, R., et al. 1994, Nature, 372, 652 [NASA ADS] [CrossRef] [Google Scholar]
- Kaneko, Y., González, M. M., Preece, R. D., Dingus, B. L., & Briggs, M. S. 2008, ApJ, 677, 1168 [NASA ADS] [CrossRef] [Google Scholar]
- Kraft, R. P., Burrows, D. N., & Nousek, J. A. 1991, ApJ, 374, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, P., & Barniol Duran, R. 2009, MNRAS, 400, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, P., & Barniol Duran, R. 2010, MNRAS, 409, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Labanti, C., Marisaldi, M., Fuschino, F., et al. 2009, Nucl. Instr. Meth. Phys. Res. A, 598, 470 [Google Scholar]
- Le, T., & Dermer, C. D. 2009, ApJ, 700, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Longo, F., Tavani, M., Barbiellini, G., et al. 2007, in Gamma-Ray Bursts: Prospects for GLAST, eds. M. Axelsson, & F. Ryde, AIP Conf. Ser., 906, 147 [Google Scholar]
- Longo, F., Moretti, E., Barbiellini, G., et al. 2009, GRB Coordinates Network, 9343, 1 [NASA ADS] [Google Scholar]
- Marisaldi, M., Labanti, C., Fuschino, F., et al. 2008, A&A, 490, 1151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mattox, J. R., Bertsch, D. L., Chiang, J., et al. 1996, ApJ, 461, 396 [NASA ADS] [CrossRef] [Google Scholar]
- McEnery, J. E. 2010, in Am. Astron. Soc. Meet. Abstracts, 215, 207.03 [Google Scholar]
- Meegan, C., Lichti, G., Bhat, P. N., et al. 2009, ApJ, 702, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Mészáros, P. 2006, Rep. Prog. Phys., 69, 2259 [NASA ADS] [CrossRef] [Google Scholar]
- Moretti, E., Longo, F., Barbiellini, G., et al. 2009, GRB Coordinates Network, 9069, 1 [NASA ADS] [Google Scholar]
- Nava, L., Ghirlanda, G., Ghisellini, G., & Celotti, A. 2011, A&A, 530, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Omodei, N. 2010, in The Shocking Universe - Gamma Ray Bursts and High Energy Shock Phenomena, eds. G. Chincarini, P. D’Avanzo, R. Margutti, & R. Salvaterra, Ital. Phys. Soc. Conf. Proc., 102, 155 [Google Scholar]
- Omodei, N., Battelino, M., Komin, N., et al. 2007, in Gamma-Ray Bursts: Prospects for GLAST, eds. M. Axelsson, & F. Ryde, Am. Inst. Phys. Conf. Ser., 906, 1 [Google Scholar]
- Page, K. L., Starling, R. L. C., Fitzpatrick, G., et al. 2011, MNRAS, 416, 2078 [NASA ADS] [CrossRef] [Google Scholar]
- Panaitescu, A., & Kumar, P. 2001, ApJ, 560, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Pittori, C., Verrecchia, F., Chen, A. W., et al. 2009, A&A, 506, 1563 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prest, M., Barbiellini, G., Bordignon, G., et al. 2003, Nucl. Instr. Meth. Phys. Res. A, 501, 280 [Google Scholar]
- Rappoldi, A., Longo, F., Argan, A., et al. 2011, Nucl. Instr. Meth. Phys. Res. A, 630, 202 [Google Scholar]
- Tavani, M., Barbiellini, G., Argan, A., et al. 2009, A&A, 502, 995 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- The Fermi-LAT Collaboration, & The Fermi-GBM Collaboration 2012, ApJ, 754, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, D. J. 2008, Rep. Prog. Phys., 71, 116901 [NASA ADS] [CrossRef] [Google Scholar]
- Toma, K., Wu, X.-F., & Mészáros, P. 2011, MNRAS, 415, 1663 [NASA ADS] [CrossRef] [Google Scholar]
- Wittek, W., Bartko, H., Galante, N., & Schweizer, T. 2007 [arXiv:0706.3622] [Google Scholar]
- Yamaoka, K., Endo, A., Enoto, T., et al. 2009, PASJ, 61, 35 [Google Scholar]
- Zhang, B., & Mészáros, P. 2001, ApJ, 559, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Zou, Y.-C., Fan, Y.-Z., & Piran, T. 2009, MNRAS, 396, 1163 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Duration of the search, the total observed counts, the expected background counts in the same region and time period, the source count upper limit, the photon flux, energy flux upper limits (in the 30 MeV−3 GeV energy range), and the measured spectral index.
Comparison of the derived upper limit with the estimated photon flux derived using the publicly available spectral information preliminarily reported by GCN Circulars.
Comparison of the derived upper limit with the estimated photon flux derived using the publicly available spectral information reported by Nava et al. (2011) – upper rows – and by Bissaldi et al. (2011) – lower rows.
Estimation of the upper limits of flux above 100 MeV up to one hour after the GRB trigger.
Duration of the search, the total observed counts, the expected background counts in the same region and time period, the source count upper limit, the photon flux, and energy flux upper limits (in the 30 MeV−3 GeV energy range) for each GRB.
Upper limits table reporting the photon and energy flux upper limits derived under the assumption of a high-energy power law extra component; four different values of the photon spectral index are considered.
Ratios of the calculated UL fluence (30 MeV−3 GeV) and the measured fluence (1 keV−10 MeV), calculated using the preliminary spectral parameters values as reported by GCN circulars (top table), and with values calculated by Nava et al. (2011) and by Bissaldi et al. (2011) (second and third tables). Bottom table: measured fluence for the four GRBs detected by AGILE GRID.
Ratios of the calculated UL fluences in the 30 MeV−3 GeV band using different high energy spectral indexes with that calculated in the 1 keV−10 MeV range, calculated using the preliminary spectral parameters values as reported by GCN circulars; fluences and errors are in units of (× 10-6) erg cm-2.
Ratios of the calculated UL fluences in the 30 MeV−3 GeV band using different high energy spectral indexes with that calculated in the 1 keV−10 MeV range, calculated using the preliminary spectral parameters values as reported by Nava et al. (2011) – top table, and by Bissaldi et al. (2011) – bottom table; fluences and errors are in units of (× 10-6) erg cm-2.
All Figures
 |
Fig. 1 Example of a particular background selection for evaluating the upper limit on a single GRB. The “Bkg” events are those detected by the GRID, the “not complete” events are those for which the off-line reconstruction or the satellite information were not fully available. The “Events in the selected region” are those in the 15° region around the GRB position. The particular GRB taken as example is GRB 080721. |
| In the text | |
 |
Fig. 2 Distribution of the flux upper limits (in units of erg/cm2/s) estimated in the energy range 30 MeV−3 GeV by assuming that the high-energy emission is the extrapolation at high energies of the prompt spectrum detected in the keV−MeV range. A spectral index β = 2.36 is assumed for all bursts in our sample (64 events-gray filled histogram). Values are reported in Table 2. The red shaded histogram instead shows those bursts in our sample (10 events) for which the β value has been estimated from the spectral fit of the keV−MeV component reported in the GCN (see Table 3). |
| In the text | |
 |
Fig. 3 Comparison between the flux expected in the 30 MeV−3 GeV energy range (from the extrapolation of the keV−MeV spectral component) and the flux upper limit estimated in the same energy range. The sample is composed of the 28 GRBs for which it has been possible to estimate the peak energy of the prompt component from the spectral analysis. Preliminary spectral results from the GCN are considered: in 10 cases the spectrum is well fit by a BAND model (filled circles), while in 18 cases the best-fit model is a power law with an exponential cutoff (filled stars). Open gray symbols show the same comparison when spectral parameters are taken from Nava et al. (2011) and Bissaldi et al. (2011). |
| In the text | |
 |
Fig. 4 High-energy spectral extrapolation of the GRB 080721. The blue horizontal line shows the derived expectation for the GRB flux in the band 30 MeV−3 GeV, adopting a spectral index β = 2.43, while the red line is the UL flux estimated with the Helene method. Since the UL is slightly below the expectations a steeper spectral index is expected. |
| In the text | |
 |
Fig. 5 High-energy spectral extrapolation of the GRB 090618. The blue horizontal line shows the derived expectation for the GRB flux in the band 30 MeV−3 GeV, adopting a spectral index β = 2.50, while the red line is the UL flux estimated with the Helene method. In this case the UL flux is still consistent with the extrapolation of the low-energy spectral shape. |
| In the text | |
 |
Fig. 6 Distribution of the flux upper limits (in units of erg/cm2/s) estimated in the energy range 30 MeV−3 GeV by assuming that the high-energy emission represents a distinct extra component as compared to the keV−MeV spectral component. The filled purple (shaded green) histogram shows the distribution when a spectral index β = 1.1 (β = 1.8) is assumed for all bursts in our sample (64 events). |
| In the text | |
 |
Fig. 7 Comparison between the prompt fluence measured in the 1 keV−10 MeV energy range and the upper limit to the 30 MeV−3 GeV fluence for the 28 events with well known prompt spectral properties. The fluence upper limit is derived under different assumptions: i) extrapolation of the prompt spectrum (yellow circles); ii) power law extra component with spectral index β = 1.8 (blue stars); and iii) power law extra component with spectral index β = 1.1 (green squares). The red diamonds are the four GRB detected by AGILE GRID. |
| In the text | |
 |
Fig. 8 Upper limits on the initial bulk Lorentz factor (as a function of the redshift) derived under the assumption of a leptonic external shock origin of the high-energy emission. Red triangles mark GRBs with measured redshift. For the other events a redshift ranging between 0.01 and 10 is assumed. Higher flux GRBs are marked with lighter curves. The orange region shows the Γ0 distribution derived by Ghirlanda et al. (2012) for a sample of GRBs with afterglow peak time measured from optical data. |
| In the text | |
 |
Fig. 9 Upper limit for the Compton parameter Y, the estimate of ϵe, and the lower limits for ϵB as a function of the prompt flux for the sample of GRBs with measured Epeak. When β cannot be constrained from the spectral analysis, a value of β = 2.36 is assumed (red stars). In the other cases the value derived from the spectral fit is adopted (blue circles). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


