| Issue |
A&A
Volume 546, October 2012
|
|
|---|---|---|
| Article Number | A78 | |
| Number of page(s) | 5 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201219637 | |
| Published online | 08 October 2012 | |
Research Note
Uncovering the magnetic environment of our solar system
1
UPMC Univ Paris 06, UMR7095, Institut d’Astrophysique de
Paris,
75014
Paris,
France
e-mail: bjaffel@iap.fr
2
CNRS, UMR7095, Institut d’Astrophysique de Paris,
75014
Paris,
France
3
Institute of Aviation, Warsaw, Poland
4
Space Research Center, Polish Academy of Sciences,
Warsaw,
Poland
e-mail: roma@cbk.waw.pl
Received: 21 May 2012
Accepted: 11 August 2012
Since its formation 4.6 billion years ago, our solar system has most likely crossed numerous magnetized interstellar clouds and bubbles of different sizes and contents on its path through the Milky Way. Having a reference model for how the heliosphere and interstellar winds interact is critical for understanding our current Galactic environment, and it requires untangling the roles of two major actors: the time-variable solar wind and the local interstellar magnetic field. Numerical simulations predict a distortion of the heliosphere caused by both solar wind anisotropy and interstellar magnetic field orientation. However, model comparison to deep space probes’ measurements led to contradictory reports by Voyager 1 and Voyager 2 of both several crossings of the solar wind’s termination shock and of the strength of the local interstellar field, with values ranging from 1.8 to 5.7 μG. Here, we show that Voyager 1 and 2 plasma, fields, and Lyman-α sky background measurements, as well as space observations of high-energy particles of heliospheric origin, may all be explained by a rather weak interstellar field 2.2 ± 0.1 μG pointing from Galactic coordinates (l,b) ~ (28,52) ± 3°. For the 2000 epoch Ulysses-based helium parameters assumed thus far, the interstellar bow shock must exist. By contrast, using the 2010 epoch IBEX-based He parameters and a stronger magnetic field leads to a plasma configuration that is not consistent with the Voyagers TS crossings. For the newly proposed interstellar He parameters, more simulations are required before one may determine whether the interstellar bow shock truly does disappear under those assumptions.
Key words: solar wind / Sun: heliosphere / ISM: magnetic fields / solar neighborhood / magnetohydrodynamics (MHD)
© ESO, 2012
1. Introduction
The supersonic, expanding solar wind (SW) slows through the termination shock (TS) to adjust to the outer conditions and then carves a cavity into the local interstellar medium (LISM), which is called the heliosphere. While the asymmetry of the heliosphere caused by the local interstellar magnetic field (ISMF) was first predicted by the Newtonian approximation (Fahr et al. 1988), it was not confirmed until 10 years later by full 3D magnetohydrodynamic (MHD) theoretical models (e.g., Ratkiewicz et al. 1998). Since then, modelers quickly realized that the observation/modelling of such asymmetry may constrain the direction of the ISMF and act as an interstellar magnetic compass. Before MHD models were employed, the first attempt to uncover the ISMF vector was made using observations of an asymmetry in the spatial distribution of the Lyman-α emission far from the Sun (Ben-Jaffel et al. 2000). Assuming the observed Lyman-α glow of heliospheric origin, the simple Newtonian approximation showed that the ISMF vector points ~40° away from the LISM flow direction with a strength of ~1.8 μG. These results were later confirmed by MHD 3D simulations, providing an independent estimation of the ISMF direction pointing from Galactic coordinates (37 ± 14°,49.5 ± 8.5°) (Ratkiewicz et al. 2008).
Apart from the Lyman-α radiation constraints on the heliosphere models, it is commonly believed that Voyager 1 (V1) crossed the TS for the first time at the heliocentric distance ~94 AU on 2004 December 16 (Burlaga et al. 2005; Decker et al. 2005; Gurnett & Kurth 2005; Stone et al. 2005), and Voyager 2 (V2) at ~84 AU on 2007 August 30 (Burlaga et al. 2008; Decker et al. 2008; Gurnett & Kurth 2008; Richardson et al. 2008). The 10 AU difference in the crossing distance indicates heliospheric asymmetries that could result from the ISMF, the asymmetric SW dynamic pressure, or the motion of TS caused by any time-dependent phenomena (Stone et al. 2008).
Summary of models indicating the strength and orientation of the ISMF.
More recently, IBEX has completed sky maps that image energetic neutral atoms (ENAs). These maps reveal a bright ribbon of ENAs in the energy range ~0.2−6 keV (McComas et al. 2009; Funsten et al. 2009; Fuselier et al. 2009; Schwadron et al. 2009). We note that Cassini observed ~6−13 keV ENAs with a similar but broader structure (Krimigis et al. 2009). One possible explanation assumes that the ribbon discovered by IBEX is probably ordered by the ISMF interacting with the heliosphere (McComas et al. 2009; Heerikhuisen et al. 2010; Chalov et al. 2010). Because they provide global maps of the interstellar interaction, ENAs observations are highly complementary to and synergic with the detailed single in situ measurements provided by the Voyager probes.
Most of these observations as well as further measurements of the plasma flow and magnetic field in the inner heliosheath by Voyager 2, have spurred numerous attempts to determine the parameters of ISMF from MHD and neutrals modeling. Table 1 provides a list of papers in which the ISMF parameters have been estimated. A quick look shows that up to now no analysis thus far proposed has used the full set of observations. In fact, with the last test reported, it was not possible to get the ISMF strength and orientation consistently using the crossing TS distance from the Sun for V1 ~94 AU, for V2 ~84 AU, and for the IBEX ribbon angular location for the same initial SW conditions (Strumik et al. 2011).
Here, we focus on extending our previously reported work (Strumik et al. 2011), using a more accurate sampling of the parameters space of our MHD model. Therefore, for the period of 2002−2007, which covers both V1 and V2 crossings, we report a rich set of numerical simulations that include several strengths and orientations of the ISMF, many SW conditions at different epochs that describe its anisotropy, and a fine 3D grid. Our primary goal is to fit V1, V2, and IBEX observations simulatneously, which should provide an accurate measurement of the unperturbed ISMF vector at the actual Galactic position of our solar system. A comparison of our findings with the most recent reports on the ISMF vector is also provided.
2. Model and method
We use the 3D MHD time-dependent model in which the effects of the interplanetary magnetic field and the anisotropic solar wind are simulated. We solve the set of MHD equations with a constant flux of hydrogen (Ratkiewicz & Ben-Jaffel 2002). This assumption is validated afterward by comparing our final results to independent models that use a full kinetic description for neutrals (e.g., Sect. 3; Heerikhuisen & Pogorelov 2011). Furthermore, as a lever to uncover the ISMF vector, the TS asymmetry was shown to be unchanged by the treatment of neutrals, provided the density level at that position is consistent with observations (Alouani-Bibi et al. 2011; Izmodenov et al. 2003). In our calculations the coordinate system is Sun-centered, and the x-y plane contains the ISMF B∞ and velocity V∞ vectors, with the latter parallel to the x-axis direction. At the outer boundary we use an LISM with plasma density n∞ = 0.095 cm-3 and velocity V∞ = 26.4 km s-1, flowing from the He direction (255.4°,5.2°) in ecliptic coordinates and temperature T∞ = 6400 K (hereafter called Ulysses-based He parameters, Witte et al. 2004). To have the neutral H number density at the TS consistent with measurements, we choose 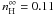 cm-3, which is still in the range 0.1−0.2 cm-3 indicated by Izmodenov et al. (2003) for the LISM. The unperturbed ISMF strength varies within the limit 1.5 to 3.0 μG. The orientation of the ISMF in space is defined by two angles: an inclination angle α (between inflow V∞ and magnetic field B∞ vectors) which varies from 0° to 90°, and a deviation angle β which varies from −90° to 90° and measures the angle of the x-y plane from the hydrogen deflection plane (HDP) (Lallement et al. 2010).
cm-3, which is still in the range 0.1−0.2 cm-3 indicated by Izmodenov et al. (2003) for the LISM. The unperturbed ISMF strength varies within the limit 1.5 to 3.0 μG. The orientation of the ISMF in space is defined by two angles: an inclination angle α (between inflow V∞ and magnetic field B∞ vectors) which varies from 0° to 90°, and a deviation angle β which varies from −90° to 90° and measures the angle of the x-y plane from the hydrogen deflection plane (HDP) (Lallement et al. 2010).
The anisotropy of the solar wind flow is included using slow and fast wind sectors that are estimated from yearly maps of observed interplanetary scintillations. According to these observations, for the period of 2001−2005, the slow SW cone was ~56 ± 6°, while for the period of 2006−2008, the cone was almost ~36 ± 6°. During the intermediate period of 2005−2006, the slow SW sector was assumed to shrink linearly between the two values (Tokumaru et al. 2010).
In addition to the two values assumed for the slow SW extent, we also considered several speeds at 1 AU in the range of 420 to 500 km s-1 for the slow component in order to cover most values thus far measured by the plasma detector on V2 and by the Advanced Composition Exoplorer (ACE), an Earth-orbiting satellite. For the fast SW component, a factor ~1.9 times the slow speed value is assumed (Tokumaru et al. 2010). For the TS crossing time reported so far for V1 and V2, the slow solar wind plasma density varies in the range of nSW ~ 4.5−6.5 cm-3, but was fixed at nSW = 5.2 cm-3 so that the corresponding SW dynamic pressure (in the range 1.4−2.1 nPa at 1 AU) follows the square of the SW speed variation. The solar equator is tilted 7.25° with respect to the ecliptic plane. The ecliptic longitude of the Sun’s ascending node is 75.77° (J2000). The Parker’s spiral model, which is assumed for the interplanetary magnetic field, has a radial component equal to 35.5 μG at 1 AU.
 |
Fig. 1 Contours of regions in ecliptic coordinates of ISMF orientations where the MHD model reproduces the TS crossing for V2 on 2007 August 30 for ISMF strengths equal to (blue) 1.8, (green) 2.0, (orange) 2.2, (red) 2.4, and (yellow) 3 μG (contours are shown from right to left in increasing strength). For the IBEX ribbon, the small black contour shows |B·R| < 0.025 obtained for 2.2 μG as the best fit. We note that the B·R = 0 condition is not sensitive to the ISMF strength and only the best solution is shown. (This figure is available in color in the electronic form.) |
In order to compare our MHD simulations to IBEX ribbon observations, we use the locations of enhanced emission of ENA fluxes as reported by Funsten et al. (2009). These locations are defined by ecliptic latitudes and longitudes at which we compute the B·R = 0 condition of perpendicularity between the line of sight of the observation and the magnetic field vector in the region outside the heliopause where the ISMF has its maximum strength (Heerikhuisen et al. 2010; Strumik et al. 2011). It is important to stress that modeling of the ENAs flux requires kinetic models for neutrals and is outside the scope of our study (Heerikhuisen et al. 2010).
In a first step, we simultaneously target the IBEX observation and the V2 TS crossing for which both plasma and field measurements exist. The angular grid for ISMF assumes a five degree regular step and strengths varying in the set 1.5, 1.8, 2.0, 2.4, and 3.0 μG. After an approximate solution is derived for the strength and orientation of the ISMF vector, we consider a finer grid (~2 degrees step) around that solution plus an additional value for the strength. Next, we consider the V1 TS crossing in 2004, using those SW speed and density values that are consistent with V2 plasma measurements obtained at the time of the V1 crossing and with ACE measurements conducted at 1 AU a year or so before its propagation to the V1 position. The approach described above should provide an ISMF vector consistent with all observations.
 |
Fig. 2 Comparison of the V2 plasma and field measurements (gray) and MHD model (black solid) for simulation parameters α = 42°, β = 0°, and ISMF strength 2.2 μG that correspond to the best solution obtained in Fig. 1 for the Ulysses He parameters. We also show MHD model (black dashed) for simulation parameters α = 45°, β = 0°, and ISMF strength 3.0 μG that correspond to a solution recently proposed when using IBEX-based He parameters (McComas et al. 2012; Bzowski et al. 2012). The SW speed is ~420 km s-1. From top to bottom, we show the plasma speed, density, and magnetic field strength. |
 |
Fig. 3 (Top) Comparison of the angular positions (ecliptic coordinates) of computed (solid line) and observed (stars) IBEX ribbon estimated for the best fit derived in Fig. 1 with SW parameters that best correspond to V2 TS-crossing time in 2007 (SW speed ~420 km s-1). (Bottom) Same but for SW parameters that best correspond to the V1 TS-crossing time in 2004 (SW speed ~466 km s-1). (This figure is available in color in the electronic form.) |
3. Results
Following the method described above, our first step is to conduct a sensitivity study by comparing our MHD simulations with the V2 TS crossing on 2007 August 30 and the IBEX ribbon observation. In Fig. 1, we compare ecliptic latitudes/longitudes regions for which the MHD model fits the plasma parameters distribution during the V2 TS crossing for different strengths of the ISMF. We note that the ensemble of solutions is very sensitive to the field strength and orientation. However, where the MHD model generally recovers the IBEX ribbon, the space regions are not very sensitive to the field strength, a finding that is consistent with previous studies (Strumik et al. 2011; Heerikhuisen & Pogorelov 2011). It appears that while the IBEX ribbon strongly constrains the ISMF orientation, it is less effective on the strength, which is better constrained by the V2 TS crossing. This means that we need both data sets to uniquely derive the ISMF strength and orientation. This statement is crucial for understanding the difference between our results and studies using the only IBEX ribbon data analysis. For clarity, a detailled comparison with the recent results of Mccomas et al. (2012) is provided at the end of this section as a reference.
Following the proposed step-by step analysis, our parametric study shows that our MHD model reproduces the position of the IBEX ribbon and the TS crossing conditions for V2 at ~83.7 AU, when the ISMF magnitude is in the range 2.0−2.4 μG and is pointing from a direction that corresponds to MHD space parameters α ~ 40−45° and β ~ (− 5)−5°. This solution was obtained for a slow solar wind sector of 36° with a density of ~5.2 cm-3 and a speed of ~420 km s-1 at 1 AU, consistent with measurements obtained respectively by V2 and by ACE before SW propagation to the TS crossing. To conclude this first step, we consider a finer grid in the ISMF space parameters and an additional strength of 2.2 μG as revealed from the previous analysis. As shown in Fig. 1, the best fit is obtained when the IBEX solution crosses the V2 TS solution for a ISMF vector with a strength of 2.2 ± 0.1 μG and pointing from ecliptic coordinates (224,36) ± 3°. This solution corresponds to space parameters α ~ 42 ± 2° and β ~ 0.0 ± 2° of our MHD simulation. The fit to the plasma parameters during the V2 TS crossing is shown in Fig. 2 (solid line), and the fit corresponding to the IBEX ribbon is shown at the top of Fig. 3.
The second step in our approach is to determine whether given the SW conditions that best correspond to the TS crossing on 2004 December 16, and with the ISMF vector derived in step 1, our MHD model provides a good fit to the position of the TS as measured by V1 in the interplanetary magnetic field. As shown in Fig. 4 (solid line) a rather good fit is obtained with the same ISMF strength and orientation obtained from V2 and IBEX data analysis but for SW speed ~466 km s-1 and density 5.2 cm-3 (SW ram pressure ~1.886 nPa). In addition, for the V1 plasma conditions derived above, a good fit is also obtained for the IBEX ribbon (Fig. 3, bottom), confirming the weak sensitivity of the outer heliosheath to SW conditions (Izmodenov et al. 2005). However, our sensitivity analysis shows that for the V1 events thus far reported in mid-2002 and early 2003 with the corresponding noisy IMF data (Burlaga et al. 2003), the TS position could be in the range 85−94 AU. Apparently, predicted positions of the TS are at or a few AU ahead of the V1 position, yet still close to it. Because of large uncertainties in plasma and field parameters, our results cannot distinguish between the two scenarios proposed so far for the 2002/2003 events (Krimigis et al. 2003; Jokipii et al. 2004; Krimigis et al. 2005). Ultimately, detailed modeling using the ISMF vector proposed here will be much needed in the future in order to check the flux level and energy range of particles measured by V1.
 |
Fig. 4 Comparison of V1 field measurements (gray) and MHD model (solid line) for simulation parameters α = 42°, β = 0°, and ISMF strength 2.2 μG that correspond to the best solution obtained in Fig. 1 but with SW speed ~466 km s-1 and Ulysses-based He parameters. We also show MHD model (black dashed) for simulation parameters α = 45°, β = 0°, and ISMF strength 3.0 μG that correspond to the IBEX-based He parameters (McComas et al. 2012). |
To clarify why it is critical to use most of the available in situ measurements and the remote observations to properly constrain the ISMF vector, we decided to compare our findings to the recent report on the ISMF strength and orientation derived from the only IBEX data set, including the new ISM He orientation, speed, and temperature (hereafter called IBEX-based He parameters) (Bzowski et al. 2012; McComas et al. 2012). Our simulations show that the corresponding MHD model (dashed line) does not correctly fit the in situ measurements obtained by V2 in 2007 (Fig. 2) and V1 in 2004 (Fig. 4). Because the obtained (dashed) curves fall on opposite sides of the TS position respectively observed by V1 and V2, we do not see how a stronger ISMF (≥ 3.0 μG) would help better fit both Voyager measurements. Because the Voyagers’ TS crossing and IBEX He data were obtained at different epochs, the obtained misfit may have several readings. First, our results cast doubt on the recently proposed strong ISMF solutions, and the consequent conclusions regarding the non-existence of the ISM bow shock (McComas et al. 2012). Second, for the newly assumed He parameters, other ISMF vector solutions may exist and should be tested in the future following the sensitivity approach sketched in Fig. 1. Finally, if a stronger ISMF is assumed, the misfit obtained here with the Voyager data could also indicate that either the IBEX He data should be critically re-analyzed (Möbius et al. 2012), or the IBEX He parameters reflect a real change in the ISM flow that occurred after the V2 TS crossing in 2007.
To further verify and extend the scope of our results, we tried to check their consistency. First, we point out that our analysis put the ISMF orientation very close to the observed HDP plane as reported by Lallement et al. (2010). Furthermore, both the orientation and strength derived here are consistent with the values obtained from an independent analysis constrained by the same HDP plane and a full kinetic treatment of neutrals (Heerikhuisen & Pogorelov 2011). This consistency between independent studies justifies our assumption of a constant H flux. In addition, we tried to compare the ISMF vector derived here to existing estimates obtained by other different techniques. Table 1 summarizes most of the reports on the ISMF derived from the V1 and V2 TS crossing and IBEX ribbon interpretation. Independently, Lyman-α sky-background observation, rotation measure and dispersion measure of radio pulsars, along with starlight polarization, provided an estimation of the ISMF vector in the solar system neighborhood (Ratkiewicz et al. 2008; Salvati 2010; Frisch et al. 2010). As shown in Fig. 5, the comparison of Galactic coordinates for the different estimates shows good convergence between the different techniques, lending credence to our results and the method utilized to obtain them.
 |
Fig. 5 Galactic coordinates of ISMF. (Yellow, hashed square) Sky background Lyman-α solutions (37 ± 14°, 49.5 ± 8.5°). (Red, small circle) Solutions from Voyager & IBEX data analysis (28,52) ± 3° (this work). (Blue, large hashed circle) Starlight polarization solutions (38,23) ± 35° (Frisch et al. 2010). Big cross shows the solution of the Faraday rotation measure and dispersion measure (5°, 41°) for 7 pulsars (Salvati 2010). Filled diamond is upwind direction. Angles increase counterclockwise. (This figure is available in color in the electronic form.) |
4. Summary and conclusions
We have shown that the asymmetries observed in the sky background Lyman-α emission deep in the heliosphere, in the TS position as measured by V1 and V2, and in the IBEX ribbon of ENAs, can all be explained with a rather weak |B∞| ~ 2.2 ± 0.1 μG ISMF pointing from Galactic coordinates (28,52) ± 3°. This direction makes an angle of ~42° with the Ulysses helium flow in agreement with the value first found by Ben-Jaffel et al. (2000). The ISMF vector derived here lies in the HDP plane (Lallement et al. 2010), consistent with an independent analysis of the SOHO/SWAN hydrogen flow deflection angle (Heerikhuisen & Pogorelov 2011). We have also shown that the magnetohydrodynamic modeling of the only V1 and V2 in situ measurements or IBEX data set does not lead to unique values of the ISMF strength and orientation as previously claimed (e.g., Fig. 1). The asymmetry thus far reported for the TS shape is not only the result of the ISMF effect but also of the SW anisotropy and time variation.
Our solution for the ISMF vector indicates a weak field that is consistent with all reported in situ measurements and remote observations. For the Ulysses-based He parameters thus far assumed for the interstellar flow, a bow shock must exist. By contrast, using a strong magnetic field (≥ 3.0 μG) making ~45° from the new IBEX-based He flow leads to a plasma configuration that is not consistent with the V2 and V1 TS crossing. Our results cast doubt on the strong ISMF solutions recently proposed by McComas et al. (2012). Yet for the newly proposed interstellar He parameters, further simulations are required before one might conclude whether the interstellar bow shock does disappear under those assumptions.
The ISMF derived here, at the actual Galactic position of the Sun, is in the range ~70−80° from the different estimations of the large-scale (kpc) Galactic magnetic field (e.g., Fig. 5). This finding is consistent with previous studies of rotation measure and dispersion measure of radio pulsars and from starlight polarization (Salvati 2010; Frisch et al. 2010).
Acknowledgments
L.B.J. acknowledges support from Université Pierre et Marie Curie (UPMC) and the Centre National de la Recherche Scientifique (CNRS) in France. R.R. acknowledges support from Foundation for Polish Science, contract Focus F3/07/2011. Authors acknowledge support from LEA ASTRO-PF.
References
- Alouani-Bibi, F., Opher, M., Alexashov, D., et al. 2011, ApJ, 734, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Ben-Jaffel, L., Puyoo, O., & Ratkiewicz, R. 2000, ApJ, 533, 924 [NASA ADS] [CrossRef] [Google Scholar]
- Bzowski, M., Kubiak, M. A., Mobius, E., et al. 2012, ApJS, 198, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Burlaga, L. F., Ness, N. F., Stone, E. C., et al. 2003, Geophys. Res. Lett., 30, 2072 [Google Scholar]
- Burlaga, L. F., Ness, N. F., Acuna, M. H., et al. 2005, Science, 309, 2027 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Burlaga, L. F., Ness, N. F., Acuna, M. H., et al. 2008, Nature, 454, 75 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Chalov, S. V., & Fahr, H. J. 1997, A&A, 326, 860 [NASA ADS] [Google Scholar]
- Chalov, S. V., Alexashov, D. B., McComas, D., et al. 2010, ApJ, 716, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Decker, R. B., Krimigis, S. M., Roelof, E. C., et al. 2005, Science, 309, 2020 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Decker, R. B., Krimigis, S. M., Roelof, E. C., et al. 2008, Nature, 454, 67 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fahr, H. J., Grzedzielski, S., & Ratkiewicz, R. 1988, Ann. Geophys., 6, 337 [NASA ADS] [Google Scholar]
- Florinski, V., Zank, G. P., Heerikhuisen, J., et al. 2010, ApJ, 719, 1097 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, P. C., Andersson, B. G., Berdyugin, A., et al. 2010, ApJ, 724, 1473 [NASA ADS] [CrossRef] [Google Scholar]
- Funsten, H. O., Allegrini, F., Crew, G. B., et al. 2009, Science, 326, 964 [Google Scholar]
- Fuselier, S. A., Allegrini, F., Funsten, H. O., et al. 2009, Science, 326, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Grygorczuk, J., Ratkiewicz, R., Strumik, M., & Grzedzielski, S. 2011, ApJ, 727, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Gurnett, D. A., & Kurth, W. S. 2005, Science, 309, 2025 [NASA ADS] [CrossRef] [Google Scholar]
- Gurnett, D. A., & Kurth, W. S. 2008, Nature, 454, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Han, J. L., Manchester, R. N., Lyne, A. G., et al. 2006, ApJ, 642, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Heerikhuisen, J., & Pogorelov, N. V. 2011, ApJ, 738, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Heerikhuisen, J., Pogorelov, N. V., Zank, G. P., et al. 2010, ApJ, 708, L126 [NASA ADS] [CrossRef] [Google Scholar]
- Izmodenov, V., Malama, Y. G., Gloeckler, G., & Geiss, J. 2003, ApJ, 594, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Izmodenov, V., Malama, Y. G., & Ruderman, M. S. 2005, A&A, 429, 1069 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jokipii, J. R., Giacalone, J., & Kota, J. 2004, ApJ, 611, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Krimigis, S. M., Decker, R. B., Hill, M. E., et al. 2003, Nature, 426, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Krimigis, S. M., Decker, R. B.„ Hill, M. E., & Roelof, C. E. 2005, In Solar Wind 11, eds. B. Fleck, & T. H. Zurbuchen, ESA SP-592, 22 [Google Scholar]
- Krimigis, S. M., Mitchell, D. G., Roelof, E. C., Hsieh, K. C., & McComas, D. J. 2005, Science, 326, 971 [Google Scholar]
- Lallement, R., Quemerais, E., & Bertaux, J. L., et al. 2005, Science, 307, 1447 [NASA ADS] [CrossRef] [Google Scholar]
- Lallement, R., Quemerais, E., Lampy, P., et al. 2010, ASPC, 428, 253 [NASA ADS] [Google Scholar]
- McComas, D. J., Allegrini, F., Bochsler, P., et al. 2009, Science, 326, 959 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- McComas, D. J., Alexashov, D., Bzowski, M., et al. 2012, Science, 336, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- Mc Donald, F. B., Stone, E. C., Cummings, A. C. et al. 2003, Nature, 426, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Möbius, E., Bochsler, P., Bzowski, M. et al. 2012, ApJS, 198, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Opher, M., Alouani Bibi, F., Toth, G., et al. 2009, Nature, 462, 1036 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pogorelov, N. V., Heerikhuisen, J., Mitchell, J. J. 2009, ApJ, 695, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Ratkiewicz, R., & Ben-Jaffel, L. 2002, J. Geophys. Res., 107, 1007 [CrossRef] [Google Scholar]
- Ratkiewicz, R., & Grygorczuk, J. 2008, Geophys. Res. Lett., 35, L23105 [NASA ADS] [CrossRef] [Google Scholar]
- Ratkiewicz, R., Barnes, A., Molvik, G. A., et al. 1998, A&A, 335, 363 [NASA ADS] [Google Scholar]
- Ratkiewicz, R., Ben-Jaffel, L., & Grygorczuk, J. 2008, ASP Conf. Ser., 385, 189 [NASA ADS] [Google Scholar]
- Richardson, J. D., Kasper, J. C., Wang, C. 2008, Nature, 454, 63 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Salvati, M. 2010, A&A, 513, A28 [Google Scholar]
- Schwadron, N. A., Bzowski, M., Crew, G. B., et al. 2009, Science, 326, 966 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stone, E. C., Cummings, A. C., McDonald, F. B., et al. 2005, Science, 309, 2017 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stone, E. C., Cummings, A. C., McDonald, F. B., et al. 2008, Nature, 454, 71 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Strumik, M., Ben-Jaffel, L., Ratkiewicz, R., & Grygorczyk, J. 2011, ApJ, 741, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Tokumaru, M., Kojima, M., & Fujiki, K. 2002, J. Geophys. Res., 115, A04102 [Google Scholar]
- Witte, M., Banaszkiewicz, M., Rosenbauer, H., & McMullin, D. 2004, Adv. Space Res., 34, 61 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Contours of regions in ecliptic coordinates of ISMF orientations where the MHD model reproduces the TS crossing for V2 on 2007 August 30 for ISMF strengths equal to (blue) 1.8, (green) 2.0, (orange) 2.2, (red) 2.4, and (yellow) 3 μG (contours are shown from right to left in increasing strength). For the IBEX ribbon, the small black contour shows |B·R| < 0.025 obtained for 2.2 μG as the best fit. We note that the B·R = 0 condition is not sensitive to the ISMF strength and only the best solution is shown. (This figure is available in color in the electronic form.) |
| In the text | |
 |
Fig. 2 Comparison of the V2 plasma and field measurements (gray) and MHD model (black solid) for simulation parameters α = 42°, β = 0°, and ISMF strength 2.2 μG that correspond to the best solution obtained in Fig. 1 for the Ulysses He parameters. We also show MHD model (black dashed) for simulation parameters α = 45°, β = 0°, and ISMF strength 3.0 μG that correspond to a solution recently proposed when using IBEX-based He parameters (McComas et al. 2012; Bzowski et al. 2012). The SW speed is ~420 km s-1. From top to bottom, we show the plasma speed, density, and magnetic field strength. |
| In the text | |
 |
Fig. 3 (Top) Comparison of the angular positions (ecliptic coordinates) of computed (solid line) and observed (stars) IBEX ribbon estimated for the best fit derived in Fig. 1 with SW parameters that best correspond to V2 TS-crossing time in 2007 (SW speed ~420 km s-1). (Bottom) Same but for SW parameters that best correspond to the V1 TS-crossing time in 2004 (SW speed ~466 km s-1). (This figure is available in color in the electronic form.) |
| In the text | |
 |
Fig. 4 Comparison of V1 field measurements (gray) and MHD model (solid line) for simulation parameters α = 42°, β = 0°, and ISMF strength 2.2 μG that correspond to the best solution obtained in Fig. 1 but with SW speed ~466 km s-1 and Ulysses-based He parameters. We also show MHD model (black dashed) for simulation parameters α = 45°, β = 0°, and ISMF strength 3.0 μG that correspond to the IBEX-based He parameters (McComas et al. 2012). |
| In the text | |
 |
Fig. 5 Galactic coordinates of ISMF. (Yellow, hashed square) Sky background Lyman-α solutions (37 ± 14°, 49.5 ± 8.5°). (Red, small circle) Solutions from Voyager & IBEX data analysis (28,52) ± 3° (this work). (Blue, large hashed circle) Starlight polarization solutions (38,23) ± 35° (Frisch et al. 2010). Big cross shows the solution of the Faraday rotation measure and dispersion measure (5°, 41°) for 7 pulsars (Salvati 2010). Filled diamond is upwind direction. Angles increase counterclockwise. (This figure is available in color in the electronic form.) |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


